Abstract
This paper presents an innovative design for reducing the impact of secondary flows on the aerodynamics of low-pressure turbine (LPT) stages. Starting from a state-of-the-art LPT stage, a local reshaping of the stator blade was introduced in the end-wall region in order to oppose the flow turning deviation. This resulted in an optimal stator shape, able to provide a more uniform exit flow angle. The detailed comparison between the baseline stator and the redesigned one allowed for pointing out that the rotor row performance increased thanks to the more uniform inlet flow, while the stator losses were not significantly affected. Moreover, it was possible to derive some design rules and to devise a general blade shape, named ‘snaked’, able to ensure such results. This generalization translated in an effective parametric description of the ‘snaked’ shape, in which few parameters are sufficient to describe the optimal shape modification starting from a conventional design. The “snaked” blade concept and its design have been patented by Avio Aero. The stator redesign was then applied to a whole LPT module in order to evaluate the potential benefit of the ‘snaked’ design on the overall turbine performance. Finally, the design was validated by means of an experimental campaign concerning the stator blade. The spanwise distributions of the flow angle and pressure loss coefficient at the stator exit proved the effectiveness of the redesign in providing a more uniform flow to the successive row, while preserving the original stator losses.
1. Introduction
Challenging issues are posed to the design of modern low-pressure turbine for turbofan applications. The high aspect ratio of low pressure turbine (LPT) blades, typically ranging from 3 to 7, makes the profile losses by far the largest contributor to the total losses and it justifies that, historically, the main efforts for improvements concentrated on the blade-to-blade flow [2].
However, due to the high levels of efficiency already reached, there seems to be little scope for improving the aerodynamic performance by reducing the profile losses [3]. On the contrary, a renewed interest is devoted to the other sources of loss, and namely to the secondary losses. This is particularly relevant, as, at the same time, great emphasis has been placed on the attempt to reduce the weight and the part count, while retaining a high level of performance. In fact, this leads towards high-lift profiles, which inherently causes an increase of secondary losses.
Several strategies have been so far proposed for reducing the secondary losses. These strategies can be divided in three main families, depending on the way secondary flows are hindered. The first one includes fence-like devices, whose goal is to disrupt the cross-flows associated with secondary flows, thus opposing their development [4,5]. The second one envisages a blade redesign, aimed at locally modifying the shape of a conventional design in order to mitigate the growth of the secondary flows [6,7]. Finally, the third family includes any possible intervention on the end-wall surfaces, from a simple end-wall profiling to a detailed non-axisymmetric shaping, aimed at weakening the gradients that drive the development of secondary flows [8,9]. A comprehensive review of the end-wall treatments for reducing secondary flows in axial turbines has been recently published by [10].
The design approach presented in this paper fits in the second family. A novel kind of turbine blade design, referred to as “snaked” blade design, is proposed. The underlying idea is that the blade shape can be modified close to the end-wall regions in order to smooth out its exit swirl distribution, thus mitigating the non-uniformities associated with the growth of the secondary flows. In doing so, the point does not necessarily consist of reducing the losses of the blade where secondary flows are generated, but rather in improving the operating conditions of the downstream blade row. This paper is divided in four sections. Firstly, the concept behind the “snaked” blade is discussed, and a method is presented to obtain a “snaked” blade by applying a shape morphing to a conventional blade. Then, the effectiveness of the concept is tested through a CFD-based redesign campaign, carried out on a single-stage of an actual LPT turbine. Prior to testing, the “snaked” blades in a multi-stage environment, the ability of the numerical setup to capture the flow mechanisms involved in this kind of design is demonstrated by comparing CFD results to experimental measurements. Measurements are available from a test rig equipped with both conventional and “snaked” blades, in terms of spanwise distributions of swirl angle and total pressure. Finally, the “snaked” blade concept is applied to a whole six-stage LPT module, so to test its potential on overall turbine performance.
2. The “Snaked” Blade Concept
Secondary flows have been investigated for a long time and several detailed and accurate descriptions of their pattern have been proposed [11,12]. The interaction between the end-wall boundary layer and the blade leads to a complex flow field characterized by cross-flow and vortices roll-up. Secondary flows reduce turbine performance by introducing additional losses in each row, and they alter the flow field with respect to the design intent at the row exit, thus affecting the aerodynamic performance of the successive row.
Figure 1 shows the typical impact of the secondary flows on the exit flow field downstream of a turbine blade. With respect to an ideal, smooth distribution, regions close to the end-walls exhibit a non-uniformity whose magnitude is proportional to the strength of the secondary flows generated within the blade passage. Such a non-uniformity, in turn, impacts the downstream rotor row, as the blade sections near the end-walls have to undergo non-optimal incidence and deflection due to the over-turning and under-turning of the upstream row.
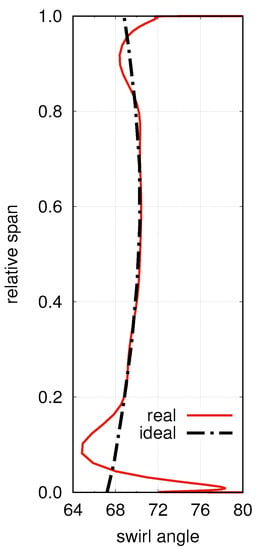
Figure 1.
“Snaked” blade concept.
Observing the radial distribution of the swirl angle suggests the idea of a local reshaping of the blade, able to hinder the over- and under-turning. The point does not necessarily consist of reducing the losses of the blade where secondary flows are generated, but rather in improving the operating conditions of the downstream blade. Therefore, the benefit brought about by the blade reshaping, and hence by the more uniform exit swirl angle, must be evaluated in terms of stage performance, rather than of single-row losses.
The discharge flow angle results from a number of design parameters, among which the most important is the so-called gauging angle, equivalent to the throat-to-pitch ratio. The underlying idea behind the “snaked” blade design is the following: at any spanwise position, the airfoil shape is locally modified in order to adjust the gauging angle, thus compensating the over- or under-turning with respect to the design intent.
Various strategies could be pursued to this end, which differ from one another in the way the airfoil shape modification is defined. In some effective parameterizations for turbine blades [13], the throat, and hence the gauging, is handled directly as an input parameter. Some other methods, instead, directly control the exit blade angle, so that the throat (gauging) can be varied indirectly, as a result of the imposition of other design parameters. In the present work, we have adopted a shape morphing approach, aimed at modifying the blade shape in order to match a desired value of the gauging. The outcome of such morphing is illustrated in Figure 2, where a given airfoil is re-shaped to increase/decrease the blade row gauging. As shown in this example, the airfoil morphing is carried out in such a way that the original axial chord as well as the leading edge part are preserved. As a result of the re-shaping, the rear part of the original airfoil section is twisted according to a morphing parameter, until the gauging angle meets a prescribed value.
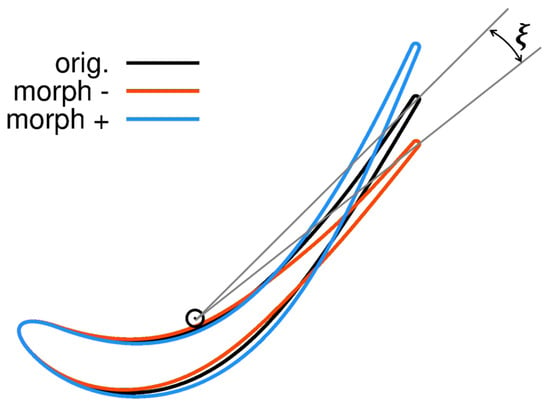
Figure 2.
Shape morphing approach.
3. Design of a “Snaked” Blade
An actual LPT module was selected to develop a proper CFD-based redesign activity and to test the effectiveness of the “snaked” blade concept. It is representative of a state-of-the-art, high-efficiency turbine operating in conditions consistent with the so called “aero-design point”. Figure 3 shows the flow path of the six-stage LPT and it points out the stage that was subjected to the redesign. Further details of the LPT module, of the thermodynamic cycle data as well as some geometrical and operating stage parameters can be found in previous works of the same authors [14,15].
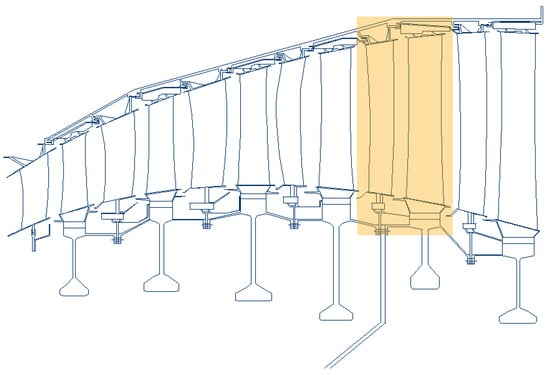
Figure 3.
LPT module.
Even if the “snaked” design can be applied to both stator and rotor rows, the redesign was carried out on the stator only. Too complex three-dimensional shapes of the blade are more critical for rotating rows, and they would require detailed integrity analysis.
The computational domain covered the turbine stage, and the increase of the stage efficiency was adopted as the major target of the redesign. An advanced optimization system, which consists of coupling CFD analyses with a response surface approach, was adopted as an effective strategy for the redesign campaign. Starting from the original blade shape, different stator geometries were obtained by means of the shape morphing. Applying perturbations of the morphing parameter along the span resulted in three-dimensional geometry modifications. As shown in Figure 4, the spanwise distribution of the morphing parameter was described by means of a B-spline with nine control points (CPs), which enables to reproduce very complex geometries.
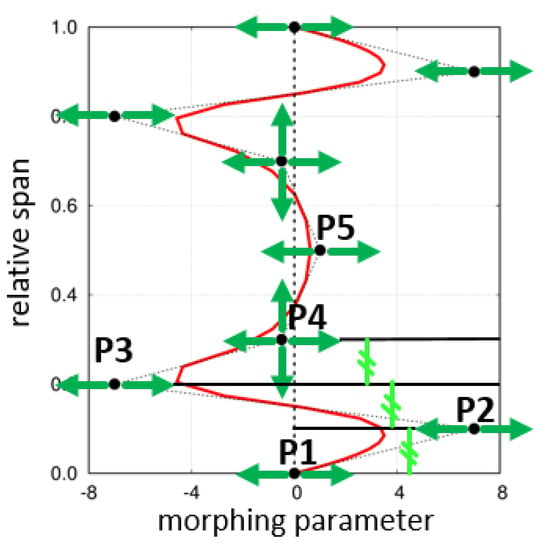
Figure 4.
Span-wise parameterization of the morphing parameter.
In Figure 4, the green arrows point out the 11 degrees of freedom (DOF) adopted for the present campaign. Nine parameters define the values of the morphing parameter at different spans. Only few parameters instead are used to perturb the spanwise positions of the CPs. The 5th point is fixed, and it is located at the midspan. In each half of the span, there are four CPs: the first one is placed on the end-wall while the remaining three are equally spaced. The last two DOF, therefore, concern only the spanwise position of the 4th and the 6th CPs. This set of parameters is selected in order to allow for maximum design generality, as the main intent is to look for an optimal blade shape able to increase the stage performance and not a priori a “snaked” geometry. Therefore, the adopted design space contained snake-like shapes, but also covered much different geometrical shapes. It is also important to bear in mind that the starting geometry was already been optimized in terms of spanwise “vortex” distribution by means of a parabolic shaping, therefore the present redesign is expected to mostly impact the near end-wall regions.
The performance of all the different geometries are evaluated by means of 3D CFD calculations, carried out by using the TRAF code [16]. The low-Reynolds version of the Wilcox’s model [17] is adopted for turbulence closure. The mesh size ( Mcells per blade passage) is selected on the basis of the authors’ previous experiences and the y+ of the first grid points from the wall is always kept around 1. The capability of the present numerical setup in assessing secondary flows for LPT blades has been recently discussed by [18,19,20]. These previous works show numerical accuracy comparing RANS results with both measurements and high fidelity data, showing the reliability of the present approach in predicting secondary flow vortex pattern and the associated secondary losses.
The proper inlet and outlet boundary conditions are derived from a 3D steady calculation of the whole LPT module.
Concerning the design space exploration, the response surface approach is based on an hybrid feed-forward artificial neural network (ANN), with two hidden layers in which hybridization was obtained by using different network architectures, initializations and training sets [21].
The stage efficiency is adopted as the objective function of the campaign while meeting several constraints. In order to ensure the matching of the optimized stator with the remaining part of the LPT module, the optimal solutions had to match the same overall operating point of the original one and therefore the same mass-averaged exit flow angle and mass flow rate. Finally, the morphing strategy allows for preserving the blade inlet angle as well as the axial row space.
3.1. Results of the Optimization
A summary of the optimization clouds is shown in Figure 5a, where the efficiency gain is reported as a function of the mass flow rate. Each symbol corresponds to a CFD calculation. The starting solution is reported as a black cross, the cloud of gray circles corresponds to the first set of geometries adopted to randomly populate the design space. The green circles represent the solutions suggested by the ANNs in order to refine the design space around the most promising regions. These solutions were exploited to improve the accuracy of meta-model that, finally, was used to find the optimal solutions (red squares in Figure 5a). These results clearly show that it was possible to increase the stage efficiency by about 0.3%. Figure 5c reports a comparison between the original and the optimized solutions in terms of the swirl angle at the stator exit, and it highlights how the optimal blade features a relevant reduction of the under- and over-turning.
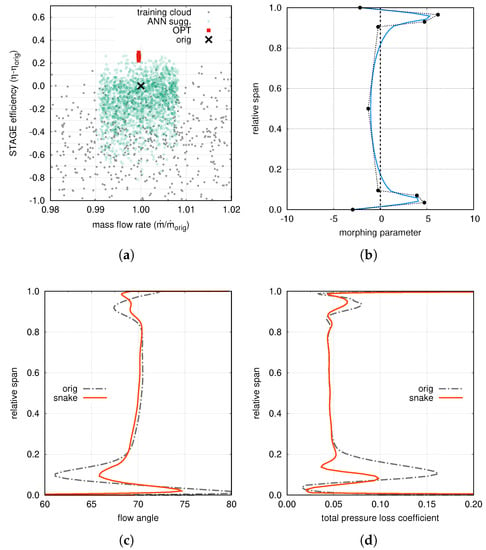
Figure 5.
Results of the “snaked” blade design: (a) optimization clouds; (b) morphing parameter distribution along the span; (c) swirl angle distribution for the original and the optimized stator; (d) spanwise distribution of the rotor total pressure loss coefficient.
The spanwise distribution of the morphing parameter of the optimum is shown in Figure 5b and the blade shape towards the end-walls is compared with the original one in Figure 6, where a three-dimensional view of the blade from the trailing edge (TE) is shown.A similar geometrical alteration was found near the hub and tip, as a quite symmetric distribution is exhibited by the morphing parameter along the span (see Figure 5b).
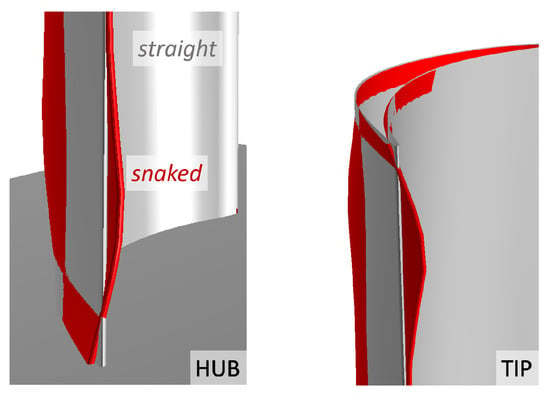
Figure 6.
Comparison between straight and “snaked” blades.
It is interesting to note that the “snaked” shape came as a result of this general optimization campaign, thus confirming the basic concept discussed above. Positive values of the morphing parameter are imposed in the first and last 10% span. This leads to a more tangential shape of the rear part of the airfoil and to an increased gauging angle that hinder the under-turning due to secondary flows.
In agreement with the “snaked” blade concept, the optimum features almost the same total pressure loss coefficient as the original one, and the efficiency gain is mainly due to the better performance of the rotor row. Moreover, these results allow for highlighting the main differences with respect to the classical end-bending shaping. In fact, at first glance, the airfoil modification may appear to be quite similar, but a deeper insight pinpoints some relevant differences. The classical end-bending consist of a 3D stacking of the airfoils close to the endwalls, whereas the snaking impacts on the rear part of the airfoil only and it implies a modification of the profile shape. These differences appear even more important considering that they reveal the different aims of the two approaches. If end-bending is mainly focused on the alteration of the pressure gradients in order to weaken secondary flows, the rationale of the snaking is in compensating the under- and over-turning by altering the gauging angle. It is clear that, even in this case, the pressure field is indirectly altered, but this is not the main driver of the new design.
Figure 5d reports a comparison of the spanwise distribution of the total pressure loss coefficient for the rotor row. The more uniform flow angle at the rotor inlet results in a relevant reduction of losses near the endwalls.
As already mentioned, the redesign was carried out considering a Reynolds number of about 300,000. It is well known, however, that, in the real operation, the engine undergoes conditions that differ from the cruise one, usually considered for the aerodynamic design. In particular, it is important to take into account the engine behaviour at lower Reynolds numbers, where a more laminar boundary layer may result in flow separations. Looking to the “snaked” blade, it is evident that some sections of the blade feature an increased loading in order to compensate for the under-turning. For these reasons, a particular attention was devoted to the performance of the “snaked” blade at low Reynolds. Some results of this campaign are reported in Figure 7 in terms of the total pressure loss coefficient and stage efficiency lapse rate (values are reported as variations with respect to the original blade at Re = 300,000). The benefit of the “snaked” blade is practically unchanged at varying the Reynolds number in terms of vane losses and stage efficiency. These results highlight that the new design is not associated with a steeper lapse-rate curve and therefore suggest that it does not feature a relevantly different behaviour with respect to the risk of separation. This conclusion is reinforced in Figure 8, where the boundary layer streamlines on the blade suction side are reported for the original and the “snaked” blade at the lowest Reynolds. Streamlines do not highlight any separation regions along the blade, thus confirming the promising behaviour of the new design even at low Reynolds.
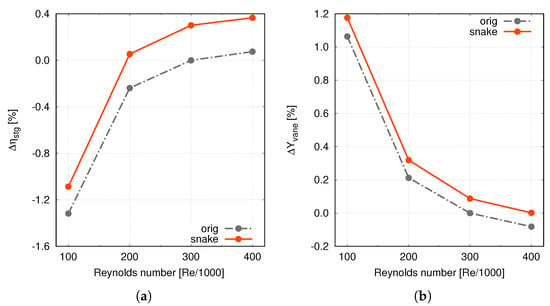
Figure 7.
Performance of the “snaked” blade at varying Reynolds number: (a) stage efficiency; (b) vane losses.

Figure 8.
Boundary layer (BL) streamlines on the blade suction side at Re = 100,000 (a) orig blade; (b) snaked blade.
The results reported in the present paper concerning the “snaked” concept were patented by [1].
3.2. Design Assessment: Impact of Numerical Modelling
The impact of two important features of the numerical framework was investigated to reinforce the solidity of the present design approach: the unsteady stator–rotor interaction, and the turbulence modelling.
Such sensitivity analysis was carried out comparing the performance of the optimal “snaked” design with the original one. Both the fully turbulent version of the Wilcox’s model, the low-Reynolds one [17], as well as the well known transition-sensitive model, were considered [22,23]. The main results are summarized in Table 1 in terms of stator loss coefficient and stage efficiency gain. In all of the calculations, the “snaked” stator features the same losses of the original one, but it provides a more uniform flow to the rotor row, thus resulting in an increased stage efficiency of about 0.3%.

Table 1.
Impact of numerical model.
Finally, an unsteady calculation was carried out in order to assess the impact of the steady assumption taken into account during the redesign. With the mixing-plane approach indeed, the effect of the vane secondary flows on the successive row is reduced to pitch-wise averaged values only. In a real case, instead, the complex vortex pattern that originates in the stator passage evolves in the downstream row, interacting with the rotor flow field. The unsteady calculations were carried out by means of a dual-time stepping approach with Phase-Lag BCs [24], adopting the same mesh and numerical set-up of the steady analysis. About 5–10 sub-iterations were computed per time step, considering a switching RMS residual value 10 times smaller than the single precision machine zero. The time-step was imposed as a trade-off between accuracy and computational costs, and it corresponded to 50 samplings of the rotor blade passing period. The unsteady calculation was iterated until reaching a satisfactory periodicity, which was evaluated by monitoring the variation over consecutive periods of the mass flow rate, the stage efficiency, and the unsteady blade loading.
The time-averaged stage efficiency and the stator loss coefficient were calculated using the time averages of mass-weighted total enthalpy and entropy, and the work-averaged total pressure [25].
As expected, the rotor-stator interaction did not relevantly affect the vane performance and, as reported in Table 1, the stator losses are practically unchanged. The stage efficiency gain is instead increased, coherently with the ability of the unsteady calculation to capture the impact of the stator secondary flows evolving in the rotor row. Figure 9 shows the instantaneous contours of axial vorticity at three different axial sections along the stage. In the first two sections, the vorticity associated with the stator secondary flows is clearly visible, and the traces of these vortices can be observed near the rotor leading edge.
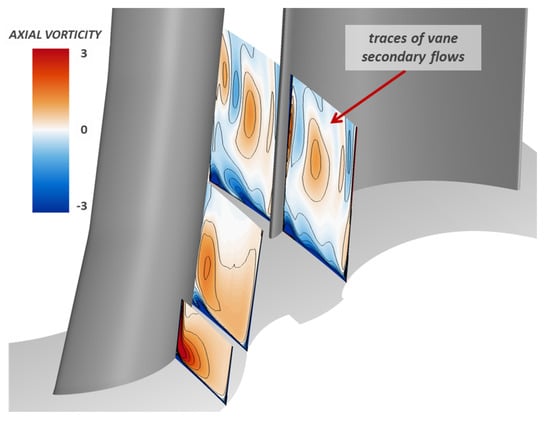
Figure 9.
Axial vorticity contours: unnsteady stator–rotor interaction.
The spanwise distribution of the time-averaged total pressure loss coefficient for the rotor row is shown in Figure 10. On one side, it is easy to note that the unsteady distribution of the original geometry features increased losses towards the endwalls. On the other side, the “snaked” stator, providing better inlet conditions for the rotor, ensures a relevant losses reduction.
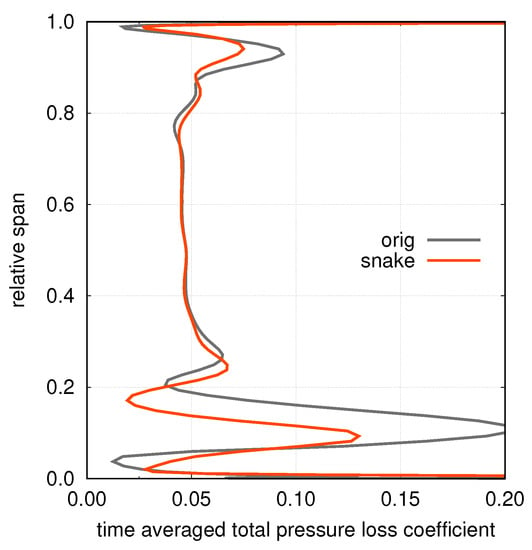
Figure 10.
Time averaged rotor losses.
3.3. Accounting for the Cavity Purge Flows
The flow in an actual turbine stage involves the presence of cavity purge flows, especially those related to the entry/exit from the shroud sealings (see Figure 11). To evaluate the impact of such additional distortions on the present design approach, the optimization campaign was repeated including the cavity flows within the computational domain.
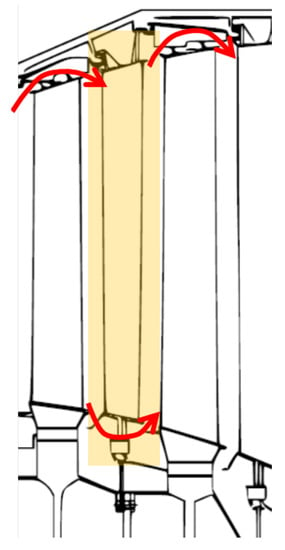
Figure 11.
Cavity purge flows.
The leakage flow from one blade row usually enters the downstream blade at a high negative incidence, thus intensifying secondary flows and losses in that blade row. In general, the flow in shrouded cavities is quite complex with axial, radial, and circumferential non uniformities. Fully three-dimensional, multi-block, unsteady computations including the mainstream, the shrouded cavities and the seal tooth regions are commonly used for specific investigations, but are time-consuming and not routinely practicable for design purposes. On the other hand, the most important features of the interaction between cavity flows and power stream can be provided by simple models, thus preventing a considerable growth of the computational cost.
In this campaign, the cavity flows were included using a simple one-dimensional model, which estimates the leakage mass flow, total enthalpy rise, and change in angular momentum through the seal cavity, given geometry parameters and the flow conditions at the interface between the cavity and primary flow path. The influence of the cavity flows on the power stream is accounted for by imposing coupled source/sink boundary conditions at the cavity/mainstream interface [26].
The main results of this new campaign are summarized in Figure 12c. Figure 12 shows the computational cloud, suggesting that the efficiency gain brought about by the snaking vane design is reduced with respect to the one attainable in case of “clean” end-walls (i.e., without cavity purge flows). This is consistent with the flow non-uniformity at the rotor inlet being not only due to the secondary flows from the upstream stator, but also to the highly swirled flow re-entering from the shroud cavity. As a consequence, the potential of the snaking to smooth out the non-uniformity is somehow reduced. Nevertheless, even if, to a lesser extent, the optimal solution from this campaign still shows the tendency to uniform the swirl at the stator exit (Figure 12a). In addition to that, as a major result, the optimal stator geometry does still clearly exhibit a “snaked” shape, as suggested by the shape of the morphing parameter (Figure 12b).
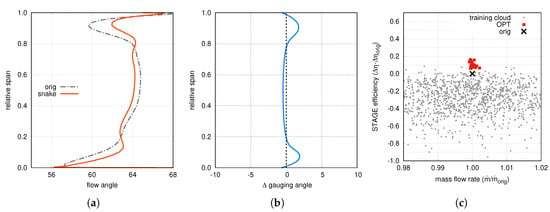
Figure 12.
Results of the design campaign with cavity purge flows included: (a) swirl angle distribution at stator exit; (b) morphing parameter distribution along the span; (c) optimization clouds.
4. Experimental Validation
The ability of the numerical setup to capture the development of secondary flows and their impact on the primary flow field, was demonstrated by comparing CFD results to experimental measurements.
Measurements were carried out in the blow-down wind tunnel installed at the Aerodynamics and Turbomachinery Laboratory of the University of Genova. The seven-blade, large-scale, linear cascade (see Figure 13a) was equipped with both the conventional and the “snaked” blades. Measurements were performed under steady inflow conditions, at a equal to 300 k.
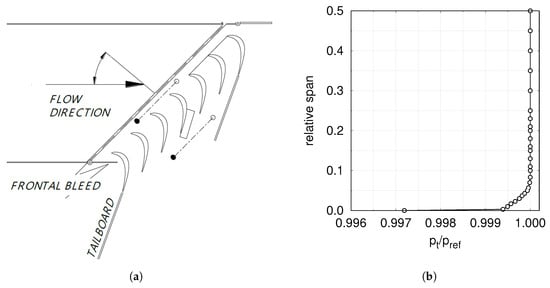
Figure 13.
Wind tunnel details: (a) sketch of the test-rig; (b) reference inlet BL.
Performance were evaluated in terms of spanwise distributions of swirl angle and total pressure losses. The details of test rig as well as of the adopted measurements techniques were provided by [27]. Turbulence boundary conditions for CFD calculations were derived from experimental data, imposing a turbulence level of about Tu = 4% at the cascade inlet. The inlet value of the turbulence length scale, instead, was established by matching the freestream turbulence decay upstream of the cascade. For the same facility, [18] already discussed the numerical setup, the mesh sensitivity as well as the importance of proper BCs when looking for a detailed comparison between CFD and experiments. In particular, it was proved that knowing the shape of the inlet BL close to the wall is crucial to set proper BCs in CFD calculations. To this end, detailed measurements of the inlet boundary layer were carried out by using a Kiel probe with a miniaturized head (1.2 mm), which allows for reducing as much as possible the distance of the first point from the wall. The measured inlet profile of total pressure is shown in Figure 13b.
Figure 14a–c summarize the comparison between numerical and experimental results. In particular, Figure 14a,b show the spanwise distributions in the first 50% span of exit flow angle and total pressure loss coefficient, for both the conventional and the “snaked” blades, while Figure 14c reports the contour-plots of total pressure loss downstream of the “snaked” blade for both CFD and experiments. In all cases, the agreement is quite satisfactory, proving that state-of-the-art CFD calculations are able to well capture the flow mechanisms involved in this kind of design. Moreover, the achievement of the design intent is confirmed by experiments, as the “snaked” blade reduces the under-turning while maintaining the same level of losses.
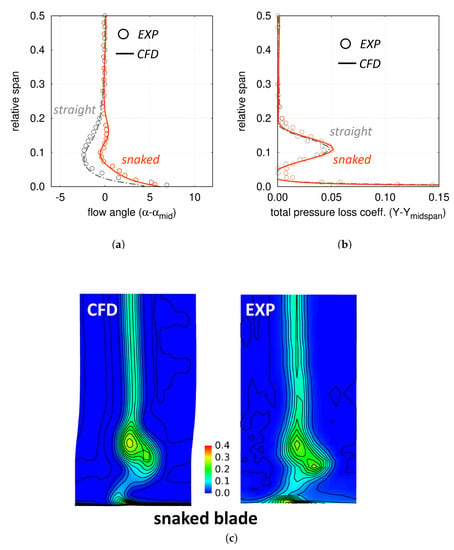
Figure 14.
Comparison between numerical and experimental results: (a) pitch-wise averaged swirl angle distribution; (b) pitch-wise averaged total pressure loss coefficient ; (c) 2D contour-plots of total pressure losses downstream of the snaked blade.
4.1. Linear Stage Environment
As already mentioned, cascade rigs do not allow for measuring the benefit of the “snaked” blade concept, as it affects stage performance rather than single-row losses. Benefits on efficiency, indeed, are due to carry-over effects connected with the more uniform flow guaranteed. However, before planning test at higher TRL, it is possible to further exploit cascade and CFD results to increase confidence in the potential benefit of the new design. With this intent, a linear, ‘stage-like’ environment was defined starting from the cascade one. The linear stage model was defined adopting the measured blade for the stator row and defining a linear, translating row for the rotor. The rotor row is identical to the stator one, but mirrored. The translational speed was selected in order to ensure the kinematic similarity between stator and rotor in terms of velocity diagrams, while the axial gap was defined consistently with the typical ones of the real engine. A sketch of the linear stage is reported in Figure 15.
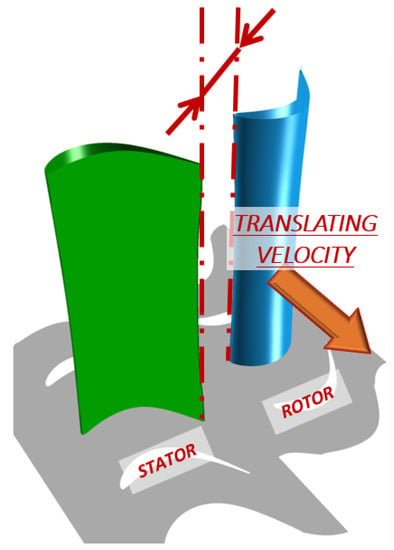
Figure 15.
Linear stage.
The same mesh and inlet BCs, Figure 13b, adopted for the single row calculation were adopted so that, apart from the potential interaction with the downstream row, the stator vane features exactly the same flow field as in the experimental environment. In this way, it was possible to assess the stage efficiency leveraging on the validated results on the cascade environment where the capability of the “snaked” blade to reduce over- and under-turning has been already proved. Calculations were performed in unsteady conditions, adopting 100 divisions per rotor passage to ensure a sufficiently fine time sampling. Table 2 shows the benefits provided by the “snaked” blade with a negligible increase in stator losses and a relevant improvement of the stage efficiency. Such results are consistent with the ones obtained in the engine environments, and they further increase the reliability of CFD estimation of the benefits of “snaked” blades.

Table 2.
“Snaked” blade benefits in a linear stage environment.
4.2. Performance at Varying Inlet BLs
In an actual turbine, the incoming BL is complex and a lot of uncertainties persist on its real conditions due to the interactions with the adjacent rows and with cavity purge flows. This relevantly impacts the strength of secondary flows. For this reason, a specific experimental campaign was carried out in order to measure the robustness of the “snaked” blade performance at varying the inlet BL. The three different boundary layers generated upstream of the blade LE for the present campaign are shown in Figure 16. As reported in [18], such differences in the BL thickness and near-wall shape have a strong impact on secondary losses, as well as on the flow distortion downstream of the blade. The measured and computed distributions of the exit flow angle are shown in Figure 17 for the “snaked” blade under the three different inlet BLs. It is worth noticing that, even in the worst case, the “snaked” blade features a rather uniform angle, with an under-turning always lower than 4 deg. At the same time, high values of over-turning persist near the wall. However, over-turning seems to have less impact on performance as these flows are confined very close to the wall, in a region of small mass flow, and then with a small contribution to the overall losses. Comparing Figure 14 and Figure 17, it is also clear that, as expected, “snaked” blades provide the best performance when operating under the conditions in which they were designed, but that they are also robust when facing different operating conditions. Finally, the comparison between CFD results and experiments in Figure 17, highlights once again a satisfactory agreement, suggesting the effectiveness of the adopted numerical approach as a design tool for reducing secondary flow losses.
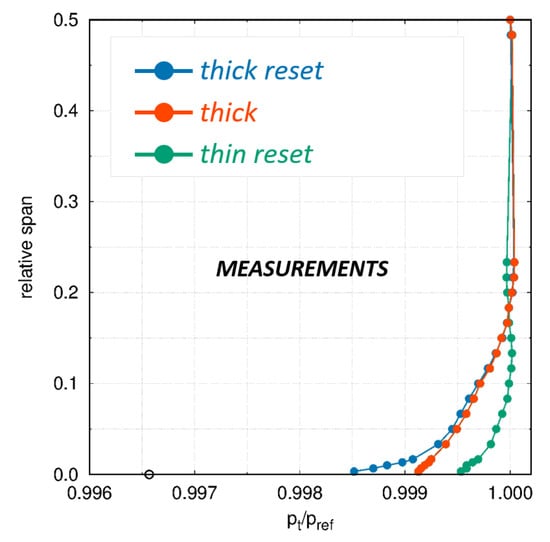
Figure 16.
Different BL profiles generated at the cascade inlet.
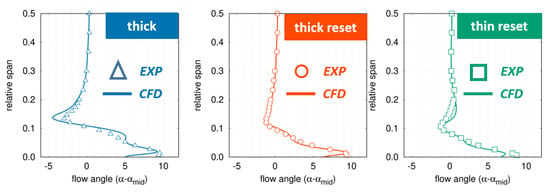
Figure 17.
“Snaked” blade robustness: measured and computed spanwise distributions of the exit blade-to-blade angle at varying inlet conditions
5. Design of a Whole LPT Module
The “snaked” blade concept was applied to all the stators of an actual LPT module, in order to test its potential on overall turbine performance. It is worth noticing that the “snaked” shape was obtained as a result of the single-stage campaigns, in which the morphing parameter had a quite general description, ensured by the high number of parameters. Despite this generality, the two single-stage campaigns led to relatively simple shapes, both when neglecting the cavity purge flows and when accounting for them. As a result of the single-stage design campaigns, a reduced set of parameters was identified in order to drastically reduce the number of degrees of freedom. An effective choice of parameters is shown in Figure 18a. It shows a simplified spanwise distribution of the morphing parameter, which requires only five parameters to reproduce the “snaked” shape. Looking at the figure, four parameters are used to describe the lower part of the distribution, from hub to mid-span. The upper part is handled by a single parameter (), which is simply a scaling factor applied to the upper control points with respect to the lower ones, and which ranges between 0.5 and 1.5. This is equivalent to assuming the shapes are similar near hub and near shroud, and that they possibly differ just in terms of magnitude of the morphing. With this simpler parameterization, the total number of degrees of freedom for the whole LPT module, composed of 6 stators, is 30.
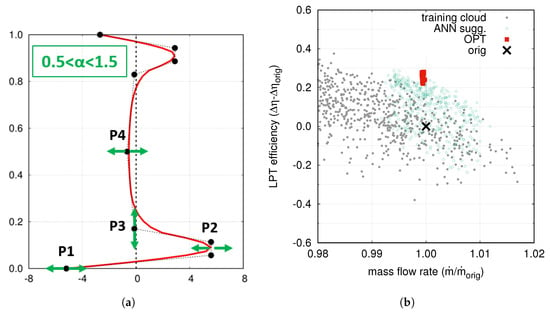
Figure 18.
Parameterization (a) and computational clouds (b) of the LPT redesign campaign.
As for the single-stage campaigns, steady calculations were carried out adopting the same numerical framework and the simplified model for cavity flows. The computational clouds of this six-stage campaign are reported in Figure 18b, which shows the efficiency gain on the overall module obtained applying “snaked” stator on all stages. An appreciable efficiency gain of about 0.3% was found on the overall module.
6. Conclusions
This work presents a new kind of turbine blade design aimed at reducing secondary losses. The underlying idea is that the blade shape can be modified close to the end-wall regions in order to smooth out the exit swirl distribution, by compensating the over- and under-turning associated with the secondary flows. A more uniform flow at the blade exit, indeed, is expected to improve the operating conditions of the downstream blade row. The paper presents a method to obtain the “snaked” blade by applying a shape morphing to an original, conventional blade. An actual LPT stage was selected to test the effectiveness of the snake-like blade concept, through a CFD-based redesign campaign. Two different optimizations were carried out with and without including the cavity flows within the computational domain. In all the cases, the optimal geometry clearly exhibited a snake-like shape, able to smooth out the swirl at the vane exit, thus resulting in interesting performance improvement. Then, “snaked” blades where validated, at low TRL, in a linear cascade environment. Experiments proved the capability of the new design to reduce under- and over-turning. The “snaked” blade performance was also tested at varying inlet BLs, and therefore at varying strengths of secondary flows.
Finally, the “snaked” blade concept was applied to all of the vanes of an actual LPT module. As a result of this six-stage campaign, an appreciable efficiency gain was found on the overall module, by applying optimal “snaked” vanes on all stages.
All in all, the present paper introduced a new near end-wall design that seems promising in improving LPT performance. At the same time, the paper presents an effective design strategy that, leveraging on accurate CFD calculations, can help the designer in facing the hard challenge of further improving turbine efficiency.
7. Patents
The “snaked” blade concept and its design have been patented by GE Avio [1].
Author Contributions
M.G., F.R., M.M., A.A. and F.B. contributed equally to this work.
Funding
This research activity received no external funding. The APC was funded by the Euroturbo Association.
Acknowledgments
This work is part of a joint research project between GE Avio, Univ. of Florence, and Univ. of Genova. The authors gratefully acknowledge GE Avio for granting permission to publish.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BL | Boundary Layer |
| CFD | Computational Fluid Dynamics |
| LPT | Low Pressure Turbine |
| RANS | Reynolds Averaged Navier-Stokes (equations) |
| RMS | Root Mean Square |
| TE | Trailing Edge |
References
- Bertini, F.; GE Avio, S.r.L. Method for Making a Shaped Turbine Aerofoil. U.S. Patent 9,506,348, 29 November 2016. [Google Scholar]
- Curtis, E.M.; Hodson, H.P.; Banieghbal, M.R.; Denton, J.D.; Howell, R.J.; Harvey, N.W. Development of blade profiles for low pressure turbine applications. ASME J. Turbomach. 1997, 119, 531–538. [Google Scholar] [CrossRef]
- Hodson, H.P.; Howell, R.J. The role of transition in high-lift low-pressure turbines for aeroengines. Prog. Aerosp. Sci. 2005, 41, 419–454. [Google Scholar] [CrossRef]
- Prümper, H. Application of boundary fences in turbomachinery. AGARD-AG 1972, 164, 315–331. [Google Scholar]
- Chung, J.T.; Simon, T.W. Effectiveness of the gas turbine endwall fences in secondary flow control at elevated freestream turbulence levels. In Proceedings of the ASME 1993 International Gas Turbine and Aeroengine Congress and Exposition, Cincinnati, OH, USA, 24–27 May 1993. ASME Paper 93–GT–051. [Google Scholar]
- Sauer, H.; Müller, R.; Vogeler, K. Reduction of secondary flow losses in turbine cascades by leading edge modifications at the endwall. ASME J. Turbomach. 2000, 123, 207–213. [Google Scholar] [CrossRef]
- Lyall, M.E.; King, P.I.; Clark, J.P.; Sondergaard, R. Endwall loss reduction of high lift low pressure turbine airfoils using profile contouring—Part I: Airfoil design. ASME J. Turbomach. 2014, 136, 081005. [Google Scholar] [CrossRef]
- Rose, M. Non-axisymmetric endwall profiling in the HP NGV’s of an axial flow gas turbine. In Proceedings of the ASME 1994 International Gas Turbine and Aeroengine Congress and Exposition, Cincinnati, Hague, The Netherlands, 13–16 June 1994. ASME Paper 94–GT–249. [Google Scholar]
- Praisner, T.J.; Allen-Bradley, E.; Grover, E.A.; Knezevici, D.C.; Sjolander, S.A. Application of nonaxisymmetric endwall contouring to conventional and high-lift turbine airfoils. ASME J. Turbomach. 2013, 135, 061006. [Google Scholar] [CrossRef]
- Kadhim, H.T.K.; Rona, A. Perspectives on the treatment of secondary flows in axial turbines. Energy Procedia 2017, 142, 1179–1184. [Google Scholar] [CrossRef]
- Sieverding, C.H. Recent progress in the understanding of basic aspects of secondary flows in turbine blade passages. ASME J. Turbomach. 1985, 107, 248–257. [Google Scholar] [CrossRef]
- Langston, L.S. Secondary flows in axial turbines—A review. Annals. N. Y. Acad. Sci. 2001, 934, 11–26. [Google Scholar] [CrossRef]
- Pritchard, L.J. An eleven parameter axial turbine airfoil geometry model. In Proceedings of the Gas Turbine Conference and Exhibit, Houston, TX, USA, 18–21 March 1985. ASME Paper 85–GT–219. [Google Scholar]
- Bertini, F.; Ampellio, E.; Marconcini, M.; Giovannini, M. A critical numerical review of loss correlation models and Smith diagram for modern low pressure turbine stages. In Proceedings of the ASME Turbo Expo, San Antonio, TX, USA, 3–7 June 2013. ASME Paper GT2013–94849. [Google Scholar]
- Bertini, F.; Credi, M.; Marconcini, M.; Giovannini, M. A path towards the aerodynamic robust design of low pressure turbines. ASME J. Turbomach. 2013, 135, 021018. [Google Scholar] [CrossRef]
- Arnone, A. Viscous analysis of three-dimensional rotor flow using a multigrid method. ASME J. Turbomach. 1994, 116, 435–445. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries Inc.: La Cañada, CA, USA, 1998; ISBN 1-928729-10-X. [Google Scholar]
- Giovannini, M.; Rubechini, F.; Marconcini, M.; Simoni, D.; Yepmo, V.; Bertini, F. Secondary flows in LPT cascades: Numerical and experimental investigation of the impact of the inner part of the boundary layer. ASME J. Turbomach. 2018, 140, 111002. [Google Scholar] [CrossRef]
- Pichler, R.; Zhao, Y.; Sandberg, R.; Michelassi, V.; Pacciani, R.; Marconcini, M.; Arnone, A. LES and RANS analysis of the end-wall flow in a linear LPT cascade with variable inlet conditions, Part I: Flow and secondary vorticity fields. In Proceedings of the ASME Turbo Expo, Oslo, Norway, 11–15 June 2018. ASME Paper GT2018–76233. [Google Scholar] [CrossRef]
- Marconcini, M.; Pacciani, R.; Arnone, A.; Michelassi, V.; Pichler, R.; Zhao, Y.; Sandberg, R. LES and RANS analysis of the end-wall flow in a linear LPT cascade with variable inlet conditions, Part II: Loss generation. ASME J. Turbomach. 2019, 141, 051004. [Google Scholar] [CrossRef]
- Rubechini, F.; Schneider, A.; Arnone, A.; Cecchi, S.; Malavasi, F. A redesign strategy to improve the efficiency of a 17-stage steam turbine. ASME J. Turbomach. 2012, 134, 031021. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. Predicting high-lift low-pressure turbine cascades flow using transition-sensitive turbulence closures. ASME J. Turbomach. 2014, 136, 051007. [Google Scholar] [CrossRef]
- Giovannini, M.; Marconcini, M.; Arnone, A.; Bertini, F. Evaluation of unsteady computational fluid dynamics models applied to the analysis of a transonic high-pressure turbine stage. IMechE Part A J. Power Energy 2014, 228, 813–824. [Google Scholar] [CrossRef]
- Cumpsty, N.A.; Horlock, J.H. Averaging nonuniform flow for a purpose. ASME J. Turbomach. 2006, 128, 120–129. [Google Scholar] [CrossRef]
- Rubechini, F.; Marconcini, M.; Arnone, A.; Cecchi, S.; Daccà, F. Some aspects of CFD modeling in the analysis of a low-pressure steam turbine. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; ASME Paper GT2007–27235. pp. 519–526. [Google Scholar]
- Simoni, D.; Berrino, M.; Ubaldi, M.; Zunino, P.; Bertini, F. Off-design performance of a highly loaded LP turbine cascade under steady and unsteady incoming flow conditions. ASME J. Turbomach. 2015, 137, 071009. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).