Abstract
A four stage helicoaxial pump was tested under varying operating conditions. A range of inlet pressures, rotational speeds (3000, 3600 rpm), and gas void fractures (GVFs) were considered for two fluid viscosities. The head developed and power input to run the pump were recorded. Head, power input and efficiency decrease as the GVF increases with best efficiency point (BEP) moving towards lower flow rate conditions. Dimensional analysis was conducted to evaluate the applicability of current affinity laws to the two-phase flow performance of the pump under consideration. Dimensionless head coefficient and power coefficients were defined for two-phase flow, considering the homogeneity in the two-phase fluid properties. Deviations in the two-phase affinity coefficients from the common law curve increases with GVF. To bridge this gap, a new correlation is proposed with a revised flow coefficient that allows all the head coefficient data to collapse on a single line with a greater degree of accuracy.
1. Introduction
Electrical submersible pumps (ESP) are a commonly used artificial lift system for upstream oil and gas production when the reservoir pressure is insufficient to meet the desired production rate. Reservoir production is quite often characterized by the presence of gas in liquid flow. Standard designs of mixed-flow pumps have limited gas-handling capabilities. Higher gas concentration may lead to gas lock, higher up-thrust, and accelerated wear of bearings due to gas in the bearing resulting in reduced run life. Evaluating gas presence in the working fluid is of significant research interest due to its effect on pump performance and reliability. Furthermore, the prediction of the multiphase flow condition of well fluid can help facilitate better well control and operation. Various researchers focused on understanding the performance of standard mixed-flow pumps under two-phase flow conditions, especially gas and liquid. Turpin and Bearden [1] first developed a model to predict the head capacity curve as a function of GVF and suction pressure. Cirilo [2] conducted two-phase flow testing of three different pumps for varying inlet pressures, speed, and number of pump stages using water and air as test fluids. The pump performance was characterized using inlet pressure, speed and number of stages. An empirical model was proposed for the threshold limit of GVF for stable pump operation. Romero [3] tested a 12-stage ESP with a specially designed impeller for two-phase flow. Based on the performance data, empirical correlations were developed to predict the two-phase flow head curve using dimensional analysis. Pessoa [4] investigated various conditions, such as surging and gas lock, as a function of liquid flow rates and GVF. Duran [5] used a drift flux model to correlate the performance for small no-slip GVF conditions in the bubbly flow regime. Zhou [6] presented an improved empirical model for the experimental data of Lea [7]. The model is used to evaluate head rise per stage under two-phase flow conditions. Pirouzpanah [8] developed a two-phase flow prediction model for split vane impeller pumps based on the concept of homogeneous head. The model utilizes dimensional analysis with head degradation, comparing with head developed for single-phase flow using head ratio. However, the analysis is limited to split vane impellers and does not apply well to high specific speed pumps such as a helicoaxial pump. So far, the development of predictive modeling has been mainly focused on standard mixed-flow pump performance. Helicoaxial pumps are a relatively new artificial lift technology first deployed by Total in 1992 [9] and mainly used as a retrofit. However, successful field trials and its ability to handle high GVF have made helicoaxial pumps a well-established alternative to conventional mixed-flow pump technology. Few studies have been focused on understanding the two-phase flow behavior and performance of the pump [10,11,12,13,14,15,16,17,18,19], however, not much has been done on modeling and predicting the performance of helicoaxial pumps operating with two-phase flow. The objective of this study is to evaluate the two-phase flow performance of a 4-stage helicoaxial, including two different liquid viscosities for a wide range of GVFs, and to develop dimensionless numbers to extend the affinity laws using homogeneous flow properties.
Helicoaxial Pump under Consideration: The multistage helicoaxial pump includes a series of pump stages, each of which consists of a rotational impeller and a stationary diffuser. Figure 1 depicts the solid model of a helicoaxial pump. The impeller has an outer diameter of 0.17 m and three blades. The diffusor’s inner diameter is 0.198 m and has nine blades. The impeller design is akin to the combination of a centrifugal pump and a screw compressor. The special helical design of the impeller can handle high GVF by balancing centrifugal forces with Coriolis (inertial) forces and by cross-channel mixing, induced by the shape of the hub as well as secondary flows, which reduces the tendency of phases to separate [20]. The geometry of a pump impeller can be described by its specific speed. The pump under consideration for this study has a specific speed of 6149 (5284), where the specific speed is defined as where N: 3600 rpm; Q: 232.12 m3/hr (1022 gpm); and H:18.5 m (60.82 ft).
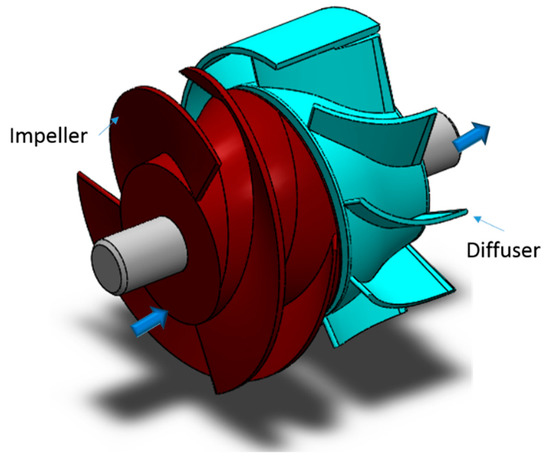
Figure 1.
Solid model of a helicoaxial pump stage.
2. Experimental Setup and Performance Parameters
Figure 2 shows the schematic of the test setup multiphase flow loop and a snapshot of the pump/motor assembly. The closed-loop test facility setup consists of a 5.6 m3 stainless steel tank/separator with a maximum pressure limit of 31 bar. Three major pipe lines are connected to this tank, each carrying liquid, gas, and mixture, respectively. Electro-pneumatic control valves, installed on each line and actuated via a Proportional/Integral (PI) controller, regulate the liquid flowrate, gas inlet pressure and inlet GVF. A 186 kW electrical motor drives the 4-stage pump via a variable frequency drive (VFD), with the maximum frequency limited to 60 Hz (3600 rpm) for this study. Rotational speed is measured using VFD as well as a tachometer. Deviation in both measurements was about . For two-phase flow operation, liquid is extracted from the bottom of the separator tank while air is extracted from the top and mixed with liquid at the pump inlet. Two-phase flow mixture from pump outlet is directed back to the separator which uses centrifugal action to separate the gas and liquid. Liquid temperature was maintained below 38 °C using a heat exchanger.
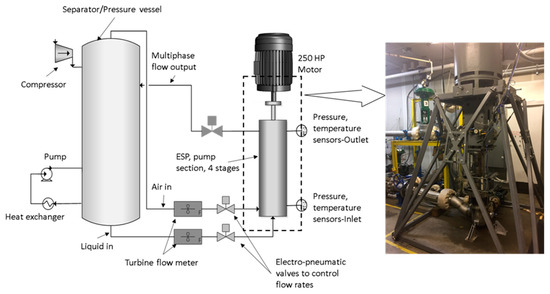
Figure 2.
Schematic of multiphase flow loop.
The power imparted to the fluid has two components, gas and liquid. The gas component can be characterized by using isothermal compression, due to high liquid capacitance. The liquid component can be calculated by using incompressible power output.
The sensors employed were calibrated before testing was initiated. Sensor information is provided in Appendix A. The uncertainty associated with the calculation of desired parameters is calculated based on the errors in the measurement of known parameters using the Kline-McClintock method [21]. This is detailed in Appendix A.
3. Results and Discussion
Effect of Inlet Pressure: This section presents the results for the pump-performance operating at the conditions listed in Table 1. Figure 3 represents the effect of inlet pressure at 15% GVF. It was expected that the head will increase as the inlet pressure increases, due to increased mass flowrate and lower separation losses in the pump stage. Contrary to expectation, there was a slight increase in power consumption as the inlet pressure decreased. This may be attributed to the reduced separation of liquid and gas in the main separator as the pressure increases, that may result in increased gas entrainment in liquid flow. Apparently, GVF may be higher at higher inlet pressures, however this aspect is not evaluated in this study and further data will be presented based on the recorded data.

Table 1.
Operational conditions and fluid properties.
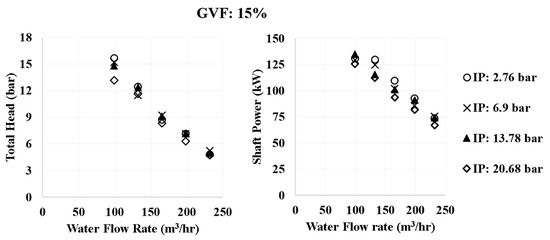
Figure 3.
Effect of inlet pressure on total head and shaft power.
Stagewise Head Performance: Figure 4 shows the stage-by-stage pump head performance at different GVFs. Stage 1 typically acts as a sacrificial member with a decreased head performance at low flow rate conditions. There is a significant increase in head performance for the second stage, and gradual increase, thereafter, for subsequent stages.
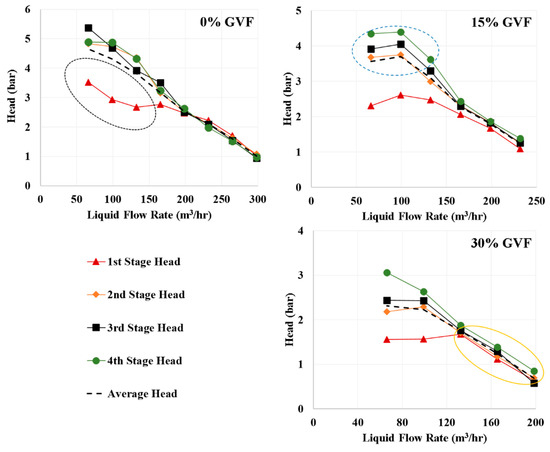
Figure 4.
Stage by stage pump head performance at different GVFs.
Figure 5, Figure 6 and Figure 7 display, respectively, the head, power, and efficiency performance, for a 13.7 bar inlet pressure at 3000, and 3600 rpm for 1 mPa.s (water) and 5 mPa.s fluids. Pump performance is described at low and high flowrate conditions, as below:
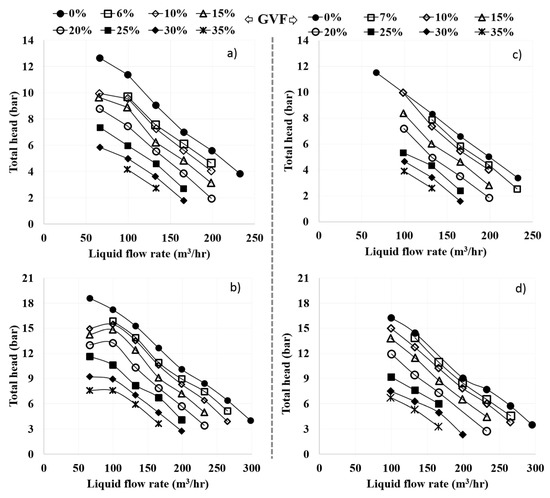
Figure 5.
Total pressure head developed by 4-stage helicoaxial pump: (a) 3000 rpm, water, (b) 3600 rpm, water, (c) 3000 rpm, 5 mPa.s, (d) 3600 rpm, 5 mPa.s.
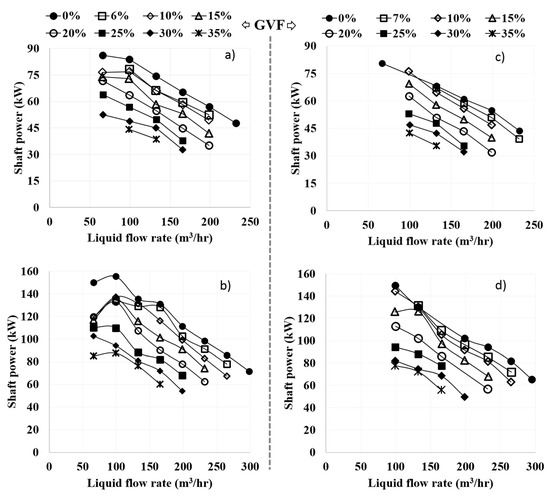
Figure 6.
Input shaft power for (a) 3000 rpm, water, (b) 3600 rpm, water, (c) 3000 rpm, 5 mPa.s, (d) 3600 rpm, 5 mPa.s.
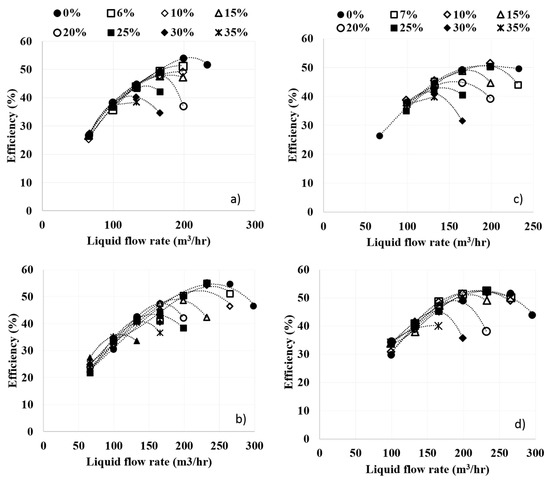
Figure 7.
Efficiency for (a) 3000 rpm, water, (b) 3600 rpm, water, (c) 3000 rpm, 5 mPa.s, (d) 3600 rpm, 5 mPa.s.
Pump Breakdown at Low Liquid Flowrate Conditions for Two-Phase Flow: At low flowrate condition, head developed by the pump is higher, which causes recirculation regions and the formation of vortices. The pump-performance head curve for the liquid-only phase is continuously decreasing, in accordance with the characteristic slope. Pump operation during two-phase flow conditions is dominated by liquid inertial forces and increased drag, causing higher separation among liquid, and gas, phases. This separation increases with a rise in GVF, reducing the slope and the range of the effective flow rate. This is evidenced in the head performance curve, as shown in the Figure 5. Reduced head by increasing the GVF at low flowrate condition also reduced the shaft input, as shown in Figure 6.
Pump Breakdown at High Liquid Flowrate Conditions for Two-Phase Flow: At high flow rate conditions, the dominance of the liquid phase allows two-phase mixture to move as a bulk flow, reducing the momentum losses due to reduced phase separation and slip velocities. However, with an increase in GVF the head and the required power input degrade. The point of breakdown moves towards lower flow rates as the GVF increases. Furthermore, the degradation increases with a decrease in rotational speed and saw an increase in liquid viscosity.
Effect of Viscosity: As expected, there is a slight decrease in single-phase flow performance with an increase in viscosity, however, there is no observable difference in deviation in two-phase flow performance due to the small difference in viscosity values.
Figure 7 shows the overall effect of the two-phase flow interaction on efficiency. Efficiency decreases as the GVF increases, and the BEP moved toward lower flow rates due to increased momentum losses as the gas phase becomes dominant with the decrease in total flow rate. These effects are prominent at lower viscosity.
Standard Affinity Laws Using Homogeneous Model Applied to Helico-Axial Pump
Usually affinity laws, derived from dimensional analysis by Buckingham [22], have been used to establish the correlations between co-dependent factors for turbomachines. It includes the effects of density, rotational speed, impeller size, and flowrate upon the pressure generated, and power required, to operate the pump. The pump performance map is characterized by using three distinct curves, head coefficiency (Ψ), defined based on incompressible pressure head,
The power input coefficient (П),
and pump efficiency (ƞ),
where all are a function of the flow coefficient ()
as the independent variable representing the condition for kinematic similarity. Two curves (Ψ vrs and П vrs ) define the entire performance curve for a single fluid property since the fourth non-dimensional group can be calculated from the other three, i.e., ƞ = f (, Ψ, П). If the properties of the pumped fluid remain close to the value used in the experimental test, to obtain the data for the flow map, it is still a good representation of the pump performance.
Figure 8 presents the standard affinity laws applied to the water data for different rotational speeds. Collapsing of the data onto a single curve demonstrates that the affinity laws work well for a constant fluid property for single phase flow.
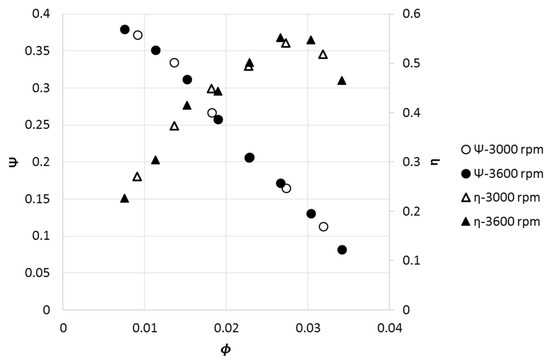
Figure 8.
Affinity law prediction using the pump head coefficient and efficiency at different rotational speeds, water.
Application of Affinity Law for Two-Phase Flow Condition: The energy loss across a pipe is characterized in terms of length, diameter, fluids properties and roughness. For two-phase pipe flow, mixture properties are mainly modeled by using homogenous flow with no slip between phases to predict the two-phase pressure drop. For instance, the homogeneous density is expressed as . Since pumps and compressors are rotating channels, a similar analysis characterizing the fluid friction loss should be applicable to the rotating devices. The affinity law coefficients are modified to include the effect of two-phase flow using weighted averages of properties as given below:
where is total volumetric flowrate. The density and viscosity of the mixture are the weighted averages of liquid and gas as given below:
where is the gas (air) volume fraction.
Head Coefficient for Two-Phase Flow ():Figure 9 shows the head coefficients for different rotational speeds and GVFs. The presence of gas has a direct impact on the pump performance, through the degradation of the head coefficient as the air fraction increases. The scatter is reduced with increased rotational speed and viscosity. The proposed dimensionless head coefficient, based on weighted properties, collapses the data, close to a single curve with increased deviation, as the GVF increases. Specifically, the divergence increases at low flow rate conditions. The standard affinity laws using homogeneous models may predict pump performance with greater degree of accuracy at low GVF.
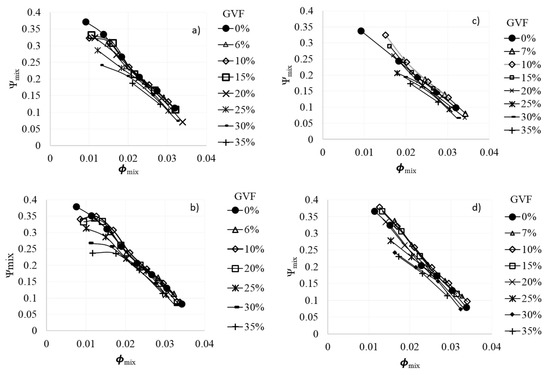
Figure 9.
Pump head coefficient for (a) 3000 rpm, water, (b) 3600 rpm, water, (c) 3000 rpm, 5 mPa.s, (d) 3600 rpm, 5 mPa.s.
Patil et al. [23] proposed a new method to predict the two-phase flow performance of the terry turbine. The method follows a model previously proposed by authors to characterize the effect of viscosity [24,25,26]. In the case of multiphase pumps working under multiphase flow conditions (liquid + gas), considering the velocity triangle at the impeller blade, the mixture velocity at the inlet depends upon the flow rate, while rotational Reynolds number represents the combined effect of inertial forces, due to rotational speed, and the frictional loss due to the two-phase fluid properties. Thus, for this analysis, the momentum loss is considered a function of the flow at the inlet, which is represented by the flow coefficient, and the rotational speed which is represented by the rotational Reynolds number. These two nondimensional groups are combined to represent the effects of two-phase flow. The independent variable is replaced by a new independent variable formed by multiplying the flow coefficient by the rotational Reynolds number raised to a power, , where Mo represents the Morrison number. The head coefficient plot vs. the revised independent variable, with varying values of the Mo. Using this developed correlation, the experimental data collapsed onto a single line with improved accuracy, as shown in the Figure 10.
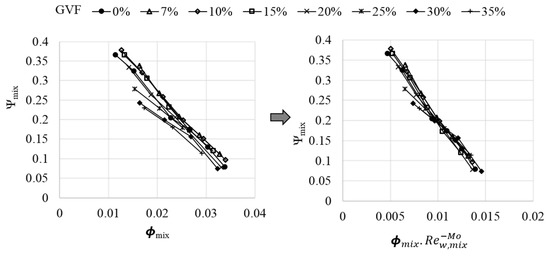
Figure 10.
Affinity laws modified to include the effect of gas for IP: 140.65 m, µ = 5 mPa.s, 3600 rpm.
Figure 11 shows how the Mo varies as a function of GVF for different rotational speeds and viscosities. Starting from 0% GVF, the value of the Mo increases for GVF up to 15% where it achieves a peak value. This flow regime is hypothesized to be homogeneous with the liquid fraction dominating the two-phase flow interaction. With further increase in the GVF, Mo decreases linearly, indicating a change in the flow regime as the dominance of gas phase increases. This linear decrease represents linear loss of momentum with GVF. The significance of this plot is knowing the water performance curve, the head performance can be predicted for different GVFs, knowing the value of the Morrison number. Due to the small difference in fluid viscosities (1 mPa.s and 5 mPa.s), the variation in performance degradation was smaller, which is reflected in Mo values. The Mo can be further analyzed to evaluate the stagewise-effect and characterization of different pump designs under two-phase flow conditions.
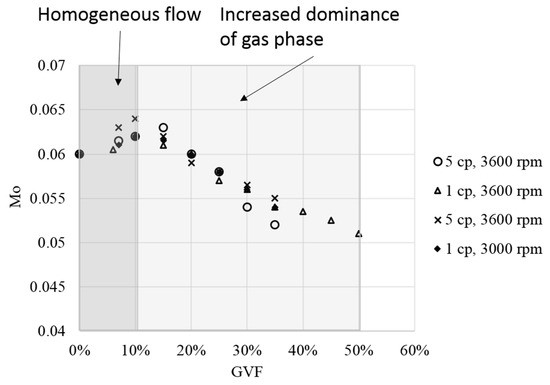
Figure 11.
Variation in Mo with GVF.
Power Input Coefficient: Power input is characterized in the terms of power coefficient. The power input coefficient is amicable to the predictions using standard affinity law coefficients with weighted average properties, except for the data at low load condition due to pump breakdown, as shown in Figure 12. This deviation from a single line follows a similar trend as with the in-head coefficient case (i.e., maximum deviation at low flow conditions). Additional analysis is in progress to further extend the proposed correlations for different pump types.
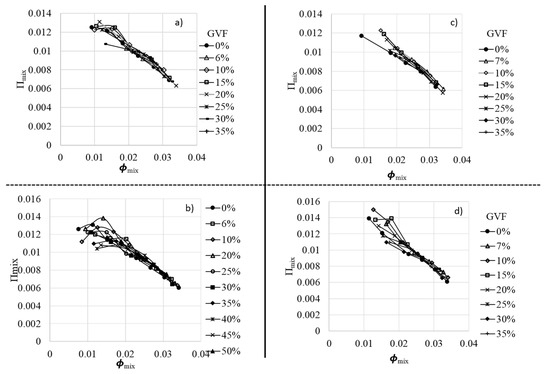
Figure 12.
Input shaft power for (a) 3000 rpm, water, (b) 3600 rpm, water, (c) 3000 rpm, 5 mPa.s, (d) 3600 rpm, 5 mPa.s.
4. Conclusions
The performance of a high-specific speed pump (helicoaxial type), under single-phase (100% liquid) and two-phase (air and liquid) flow mixtures, is investigated at different inlet pressures and rotational speeds. Pump-head and power input systematically degraded with an increase in GVF at the pump inlet. With an increase in liquid viscosity and GVF, the pump head further degraded, however, overall dispersion in data is similar, compared to air + water data. To characterize the pump performance while operating in two-phase flow, a dimensional analysis was performed and revised dimensionless numbers are proposed for two-phase flow, based on a homogeneous two-phase model. In accordance with the affinity law principle, head coefficient data collapsed on a common curve, however, with an increased deviation as the GVF increases. Proposed correlation is further modified by establishing new 2D plot, with a revised X axis that allows collapsing of all the data on a single curve with greater accuracy. Dimensionless number Mo is further characterized as a function of GVF and rotational speed. A new method was established, however, further development and improvement of this method will require collection, and analysis, of two-phase performance data of different pump types.
Author Contributions
Conceptualization, A.P.; data curation, S.G. and B.A.; formal analysis, A.P. and B.A.; funding acquisition, G.M.; investigation and methodology, A.P. and S.G.; resources, A.D.; writing—original draft, A.P.; writing—review and editing, B.A., A.D. and G.M.
Funding
This research was funded by Royal Dutch Shell.
Acknowledgments
The authors are grateful for the financial and technical support of this project by Royal Dutch Shell.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| BEP | Best Efficiency Point |
| BFSL | Best fit straight line |
| CFD | Computational Fluid Dynamics |
| Ds | Impeller outer diameter, m |
| ESP | Electrical Submersible Pump |
| g | Gravitational acceleration, m/s2 |
| GVF, α | Gas Void Fraction |
| N | rotational speed, rpm |
| Ns | Specific speed [US] |
| p | Pressure, bar |
| P | Power, kW |
| Q | Volumetric flow rate, m3/hr |
| H | Pump head |
| η | Efficiency |
| Torque, N.m | |
| μ | Dynamic viscosity, mPa.s |
| Φ | Flow rate coefficient |
| Power input coefficient | |
| Ψ | Head coefficient |
| ρ | Fluid density, kg/m3 |
| ω | Angular speed, rad/s |
Appendix A
Sensor Information:

Table A1.
List of flow meters.
Table A1.
List of flow meters.
| Flow Meter | Model No | Range | Accuracy (of Reading) |
|---|---|---|---|
| Water | Turbines Inc WM0600x6 | 56.8–567.8 m3/h | ±1% |
| Air | Omega-FTB-938 | 13.6–220.9 (Actual m3/h) * | ±1% |
| Water | Omega-FTB-1431 | 3.4–40.9 m3/h | ±1% |
| Air | Omega-FTB-933 | 1.7–17 (Actual m3/h) * | ±1% |
* Actual m3/h = m3/h × 213/ Pa × Ta/530 where Pa = Operation pressure (bar) Ta = Temperature in degrees Rankine.

Table A2.
List of pressure transducers.
Table A2.
List of pressure transducers.
| Transducer Type | Range (Bar) | Accuracy |
|---|---|---|
| Omega-PX 429-500 GI | 0–34.5 | ±0.08% |
| Omega-PX 429-750 GI | 0–51.7 | ±0.08% |
| Omega-PX481A-1000G5V | 0–69 | 0.3% |
Uncertainty Analysis of the Test Rig
The uncertainty (error) associated with the calculation of desired parameters is calculated based on the errors in the measurement of known parameters, using the Kline-McClintock method which shows accurate estimation of the uncertainties in each individual input by using a root-sum-square (RSS) operation. Even though repeated measurements should be statically analyzed for more accurate analysis, this method provides a simple answer for how errors in the variables are estimated and defined.
For instance, gas power (Pgas,isothermal) is a function of:
And, the uncertainty associated with the measurement of gas power Pgas,isothermal is given by the Equation (A-2), where p is a pressure and Q is the volumetric flow rate.
Similarly, uncertainties associated with other parameters were calculated as tabulated in Table A3.

Table A3.
Uncertainty associated to desired outcomes.
Table A3.
Uncertainty associated to desired outcomes.
| Outcomes | Uncertainty Interval |
|---|---|
| Efficiency | ±1.06% |
| Power input | ±1.04 kW |
| Head Output | ±3 m |
References
- Turpin, J.L.; Lea, J.F.; Bearden, J.L. Gas-Liquid Flow Through Centrifugal Pumps-Correlation of Data. In Proceedings of the Third International Pump Symposiun, Claremore, OK, USA, 1 January 1986; pp. 13–20. [Google Scholar]
- Cirilo, R. Air-Water Flow Through Electrical Submersible Pumps; The University of Tulsa: Tulsa, OK, USA, 1998. [Google Scholar]
- Romero, M. An Evaluation of An Electric Submersible Pumping System for High GOR Wells; University of Tulsa: Tulsa, OK, USA, 1999. [Google Scholar]
- Pessoa, R. Experimental Investigation of Two-Phase Flow Performance of Electrical Submersible Pump Stages; Society of Petroleum Engineers: New Orleans, LA, USA, 2000. [Google Scholar]
- Duran, J.; Prado, M. ESP Stages Air-Water Two-Phase Performance Modeling and Experimental Data; Society of Petroleum Engineers: Richardson, TX, USA, 2003. [Google Scholar]
- Zhou, D.; Sachdeva, R. Simple model of electric submersible pump in gassy well. J. Pet. Sci. Eng. 2010, 70, 204–213. [Google Scholar] [CrossRef]
- Lea, J.F.; Bearden, J.L. Effect of Gaseous Fluids on Submersible Pump Performance. J. Pet. Technol. 1982, 34, 2922–2930. [Google Scholar] [CrossRef]
- Pirouzpanah, S.; Gudigopuram, S.R.; Morrison, G.L. Two-phase flow characterization in a split vane impeller Electrical Submersible Pump. J. Pet. Sci. Eng. 2017, 148, 82–93. [Google Scholar] [CrossRef]
- Gié, P.; Buvat, P.; Bratu, C.; Durando, P. Poseidon Multiphase Pump: Field Tests Results. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 1992; p. 14. [Google Scholar]
- Zhang, J.; Cai, S.; Li, Y.; . Zhu, H.; Zhang, Y. Visualization study of gas–liquid two-phase flow patterns inside a three-stage rotodynamic multiphase pump. Exp. Therm. Fluid Sci. 2016, 70. [Google Scholar] [CrossRef]
- Kuchpil, C.; Souza, E.M.; Cerqueira, M.B.; Coelho, E.J.J.; Carbone, L.C.; Silva, L.T. Barracuda Subsea Helico-Axial Multiphase Pump Project. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2013. [Google Scholar]
- Charron, Y.; Pagnier, P.; Marchetta, E.; Stihle, S. Multiphase Flow Helico-Axial Turbine: Applications and Performance. In Proceedings of the Abu Dhabi International Conference and Exhibition; Society of Petroleum Engineers: Abu Dhabi, United Arab Emirates, 2004; p. 8. [Google Scholar]
- Hua, G.; Falcone, G.; Catalin, T.; Morrison, G. Comparison of Multiphase Pumping Technologies for Subsea and Downhole Applications. Oil Gas Facil. 2012, 1, 36–46. [Google Scholar] [CrossRef]
- Rojas, M.; Barrios, L.; Harris, G.; Cheah, K.W. Full-Scale Investigation of Gas-Handling Capabilities of High-Flow Helicoaxial ESP Stages for Deepwater Application. In SPE Electric Submersible Pump Symposium; Society of Petroleum Engineers: The Woodlands, TX, USA, 2017; p. 14. [Google Scholar]
- Simpson, A.; Rhys-Davies, J.; Husman, M.; Youri, E. A Tough, Truly Multiphase Downhole Pump for Unconventional Wells. In SPE Electric Submersible Pump Symposium; Society of Petroleum Engineers: The Woodlands, TX, USA, 2017; p. 20. [Google Scholar]
- Shang, S.; Bustamante, N.G. Understanding ESP Performance in Multiphase Flow Condition in SAGD Production Wells. In Abu Dhabi International Petroleum Exhibition Conference; Society of Petroleum Engineers: Abu Dhabi, UAE, 2017; p. 20. [Google Scholar]
- Xu, Y.; Cao, S.; Sano, T.; Wakai, T. Experimental Investigation on Transient Pressure Characteristics in a Helico-Axial Multiphase Pump. Energies 2019, 12, 461. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, L. Energy Performance and Pressure Fluctuation of a Multiphase Pump with Different Gas Volume Fractions. Energies 2018, 11, 1216. [Google Scholar] [CrossRef]
- Suh, J.W.; Kim, J.W.; Choi, Y.S.; Kim, J.H.; Joo, W.G.; Lee, K.Y. Multi-Objective Optimization of the Hydrodynamic Performance of the Second Stage of a Multi-Phase Pump. Energies 2017, 10, 1334. [Google Scholar] [CrossRef]
- Gulich, J.F. Centrifugal Pumps, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kline, S.J.; McClintock, F.A. Describing the uncertainity in single sample experiments. Mech. Eng. 1953, 3–8. [Google Scholar] [CrossRef]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Patil, A.; Sundar, S.; Wang, Y.; Solom, M.; Kirkland, K.V.; Morrison, G. Chatacterization of Steam Impulse Turbine for Two-Phase Flow. Int. J. Heat Fluid Flow 2019, 79, 108439. [Google Scholar]
- Morrison, G.; Wenjie, Y.; Rahul, A.; Abhay, P. Development of Modified Affinity Law for Centrifugal Pump to Predict the Effect of Viscosity. J. Energy Res. Technol. 2018, 140, 092005. [Google Scholar] [CrossRef]
- Patil, A.; Morrison, G. Affinity Law Modified to Predict the Pump Head Performance for Different Viscosities Using the Morrison Number. J. Fluids Eng. 2018, 141, 021203. [Google Scholar] [CrossRef]
- Patil, A.; Yin, W.; Agarwal, R.; Delgado, A.; Morrison, G. Extending Classical Friction Loss Modeling to Predict the Viscous Performance of Pumping Devices. J. Fluids Eng. 2019, 141, 101202. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).