Multiscale Simulation of the Hydroabrasive Erosion of a Pelton Bucket: Bridging Scales to Improve the Accuracy †
Abstract
:1. Introduction
2. Modeling Methodology
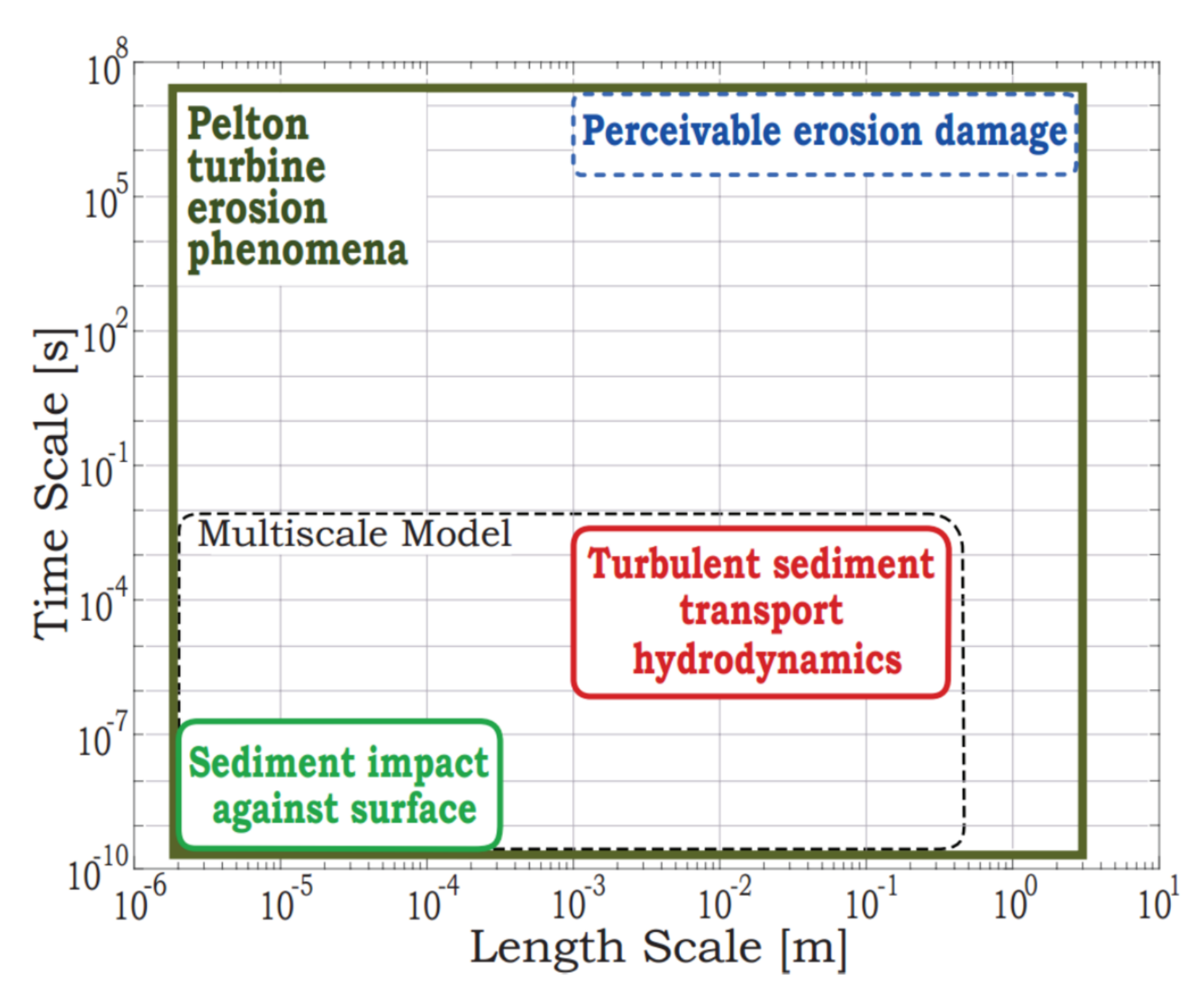
2.1. Multiscale Model of Erosion
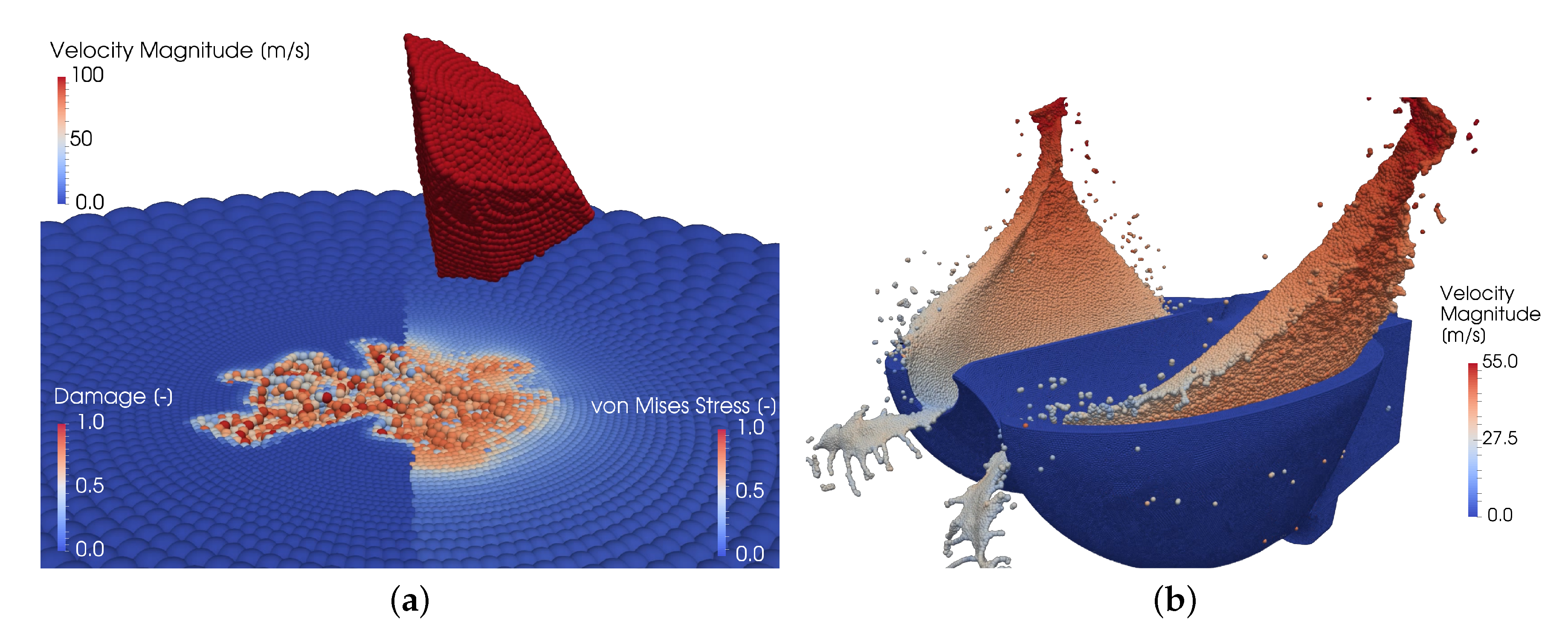
2.2. Microscale Model: Sediment Impacts
2.3. Macroscale Model: Turbulent Sediment Transport
2.4. Sequential Multiscale Coupling Strategy
2.5. The Finite Volume Particle Method
3. Test Case Description
4. Results
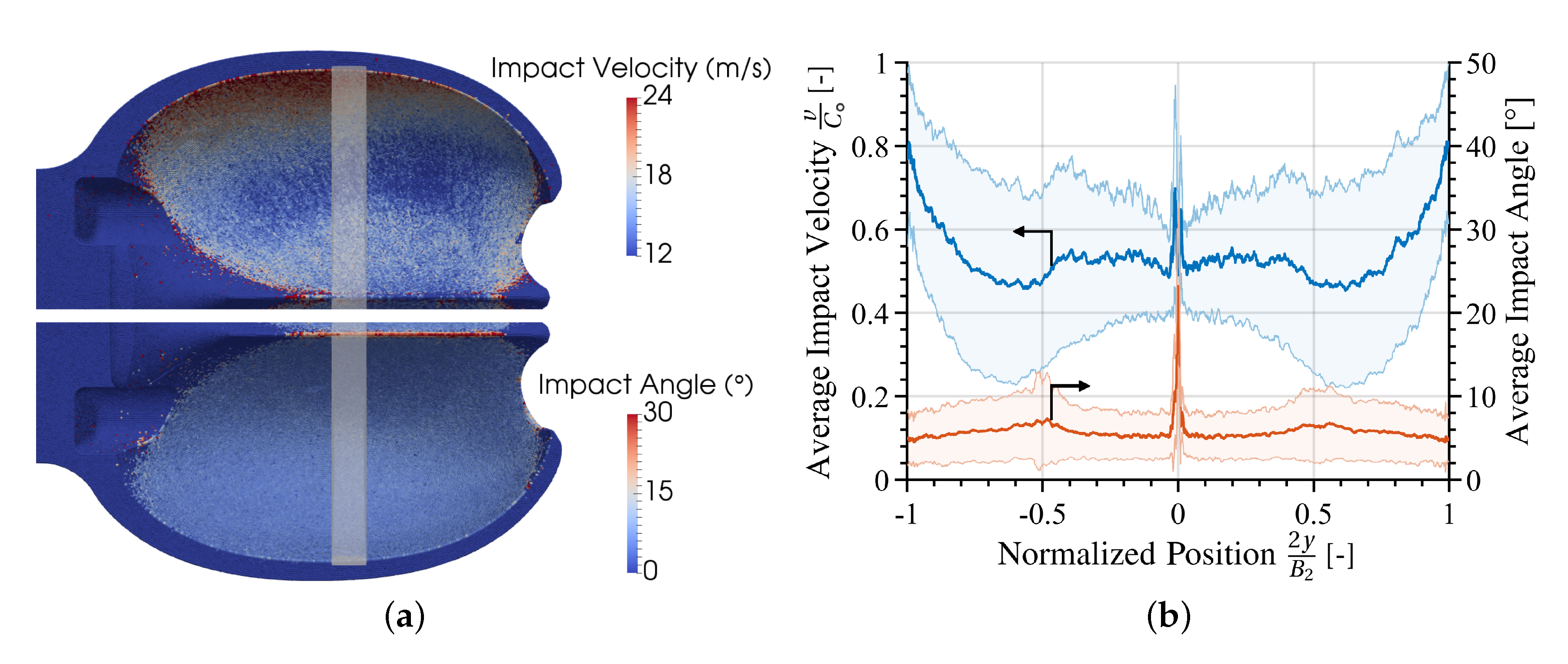
4.1. Distributions of Impact Conditions on the Bucket Surface
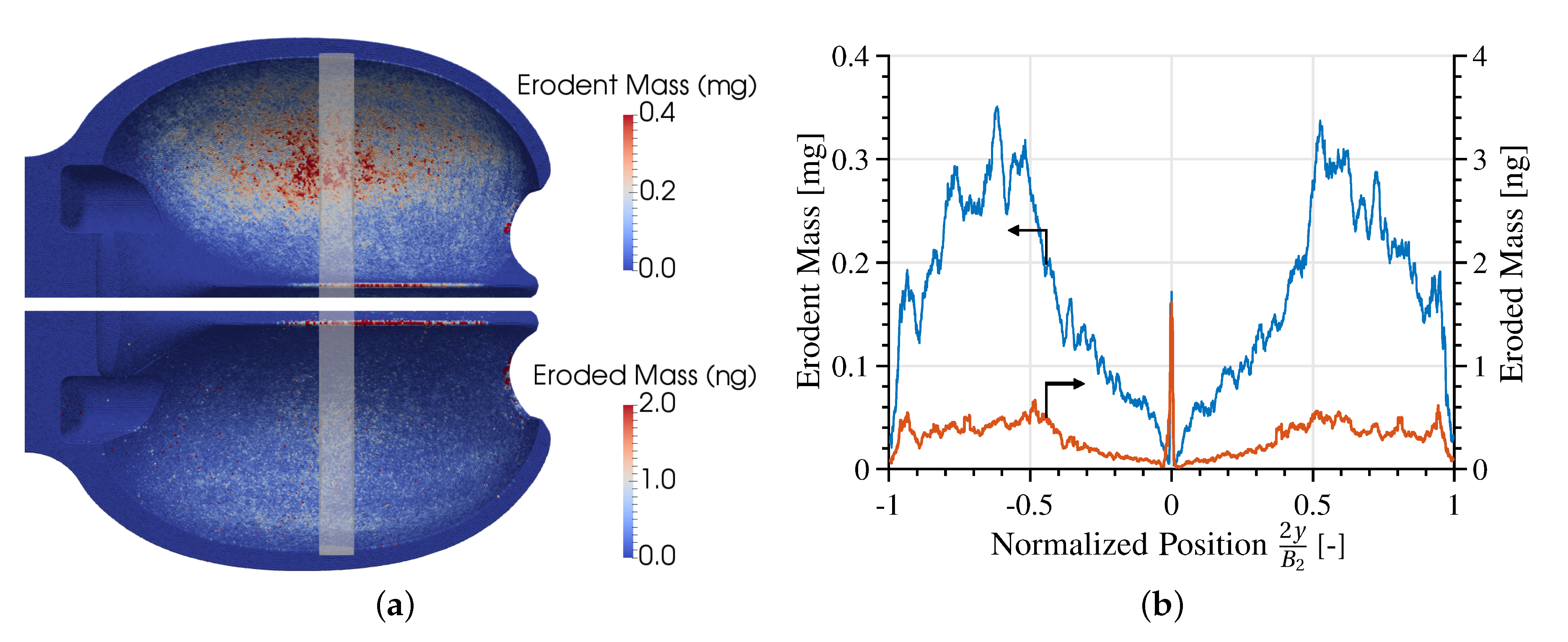
4.2. Erosion Distribution of the Bucket Surface
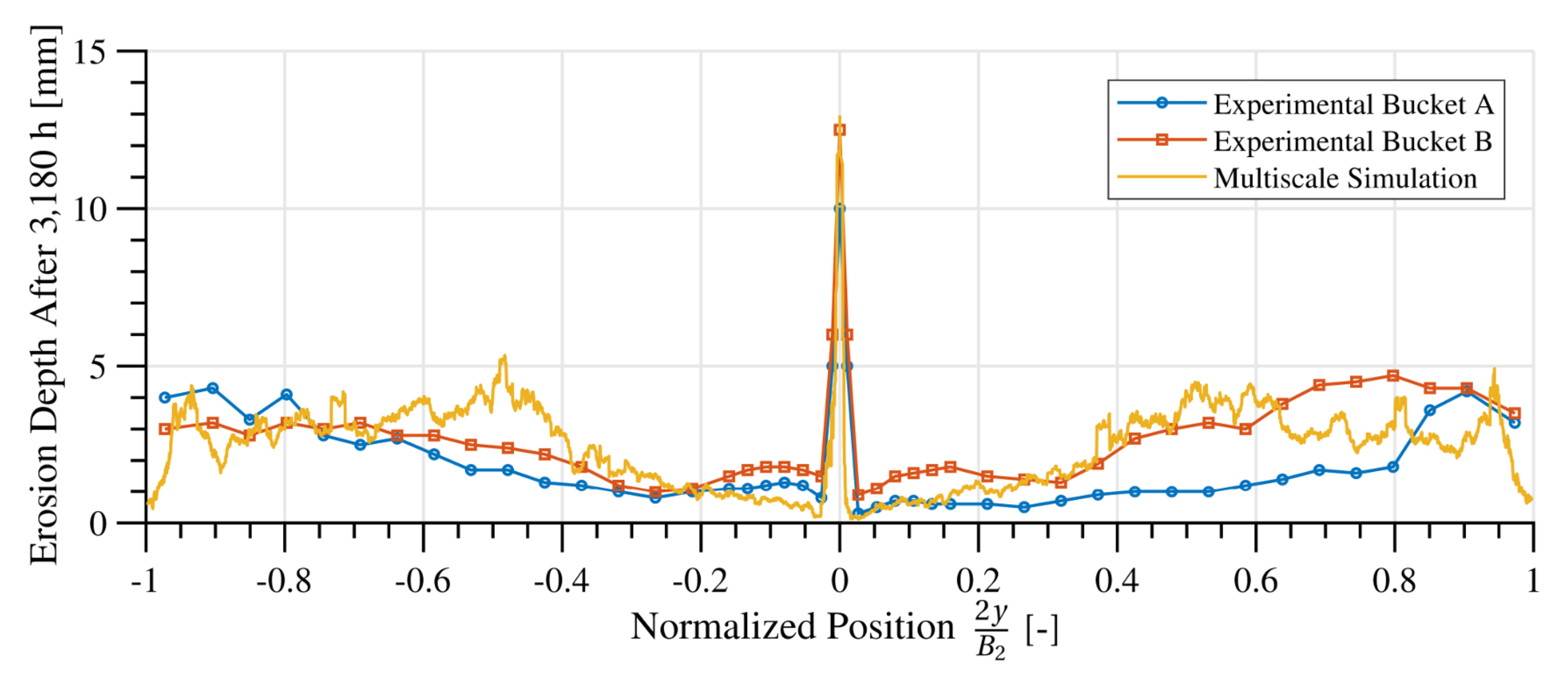
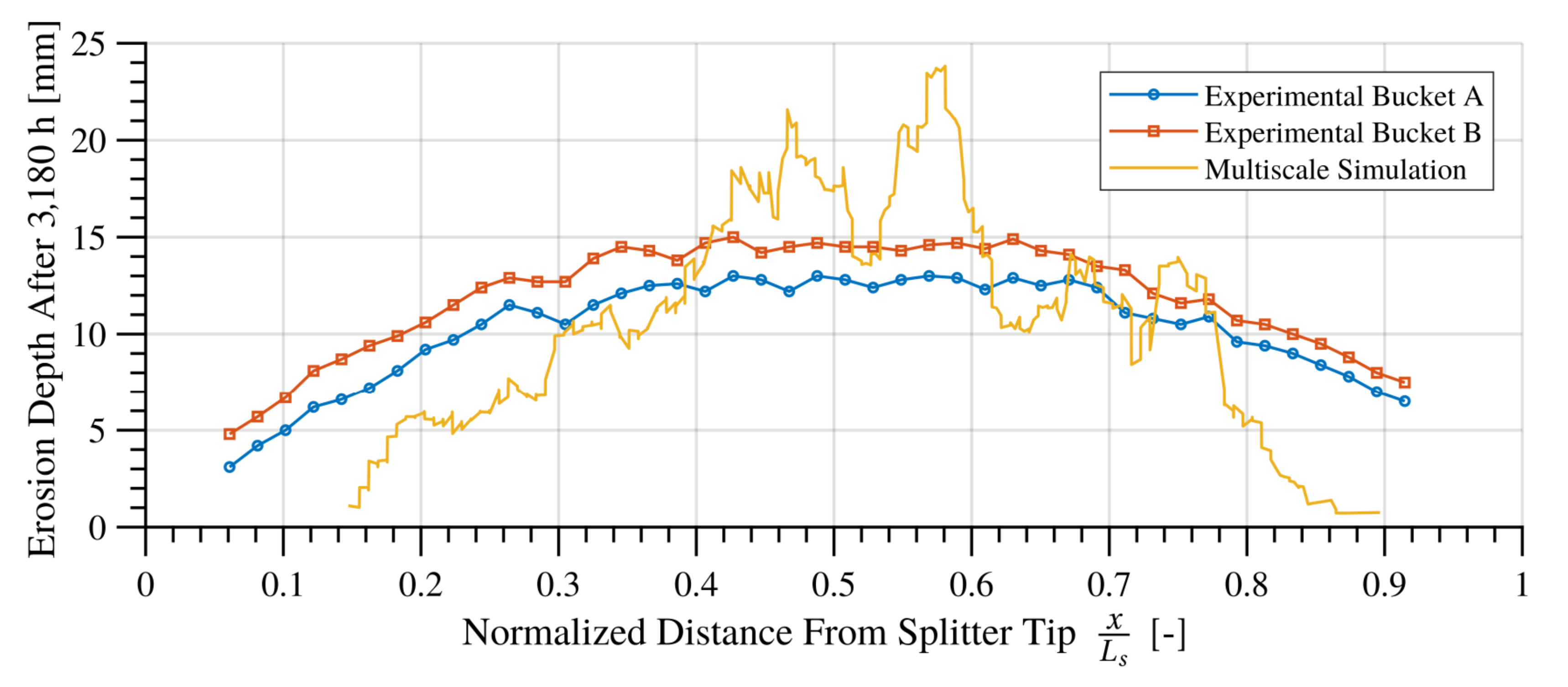
4.3. Erosion Depth Validation
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Variables | |
| Surface area | |
| Maximum internal bucket width | |
| Jet velocity | |
| Runner pitch diameter | |
| Jet diameter | |
| Jet length | |
| Splitter length | |
| c | Sediment concentration by mass |
| Sediment diameter below which x% of the cumulative mass distribution lies | |
| Eroded depth | |
| Extrapolation factor | |
| Eroded mass | |
| v | Sediment impact velocity |
| Number of buckets | |
| Jet impinging angle relative to the bucket plane | |
| Base material density | |
| Abbreviations | |
| ALE | Arbitrary Lagrangian-Eulerian |
| FVPM | Finite Volume Particle Method |
| GPU | Graphics Processing Unit |
References
- Grein, H.; Schachenmann, A. Solving problems of abrasion in hydroelectric machinery. Water Power Dam Construct. 1992, 44, 19–24. [Google Scholar]
- Chitrakar, S.; Neopane, H.; Gunnar, O. Study of the simultaneous effects of secondary flow and sediment erosion in Francis turbines. Renew. Energy 2016, 97, 881–889. [Google Scholar] [CrossRef]
- Felix, D.; Abgottspon, A.; Albayrak, I.; Boes, R. Hydro-abrasive erosion on coated Pelton runners: Partial calibration of the IEC model based on measurements in HPP Fieschertal. In Proceedings of the 28th IAHR Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016; Volume 49, p. 122009. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Finnie, I. Some observations on the erosion of ductile materials. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Shewmon, P.; Sundararajan, G. The erosion of metals. Annu. Rev. Mater. Sci. 1983, 13, 301–318. [Google Scholar] [CrossRef]
- Rai, A.; Kumar, A.; Staubli, T. Hydro-abrasive erosion in Pelton buckets: Classification and field study. Wear 2017, 392–393, 8–20. [Google Scholar] [CrossRef]
- Mann, B.; Arya, V. Abrasive and erosive wear characteristics of plasma nitriding and HVOF coatings: Their application in hydro turbines. Wear 2001, 249, 354–360. [Google Scholar] [CrossRef]
- Thapa, B.S.; Thapa, B.; Dahlhaug, O.G. Empirical modelling of sediment erosion in Francis turbines. Energy 2012, 41, 386–391. [Google Scholar] [CrossRef]
- Wang, Y.F.; Yang, Z.G. Finite element model of erosive wear on ductile and brittle materials. Wear 2008, 265, 871–878. [Google Scholar] [CrossRef]
- Balu, P.; Kong, F.; Hamid, S.; Kovacevic, R. Finite element modeling of solid particle erosion in AISI 4140 steel and nickel-tungsten carbide composite material produced by the laser-based power deposition process. Tribol. Int. 2013, 62, 18–28. [Google Scholar] [CrossRef]
- Wang, Y.F.; Yang, Z.G. A coupled finite element and meshfree analysis of erosive wear. Tribol. Int. 2009, 42, 373–377. [Google Scholar] [CrossRef]
- Takaffoli, M.; Papini, M. Material deformation and removal due to single particle impacts on ductile materials using smoothed particle hydrodynamics. Wear 2012, 274, 50–59. [Google Scholar] [CrossRef]
- Wang, M.H.; Huang, C.; Nandakumar, K.; Minev, P.; Luo, J.; Chiovelli, S. Computational fluid dynamics modelling and experimental study of erosion in slurry jet flows. Int. J. Comput. Fluid Dyn. 2009, 23, 155–172. [Google Scholar] [CrossRef]
- Grewal, H.S.; Singh, H.; Yoon, E.S. Interplay between erodent concentration and impingement angle for erosion in dilute water-sand flows. Wear 2015, 332, 1111–1119. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. The effect of sub-models and parametrizations in the simulation of abrasive jet impingement tests. Wear 2017, 370–371, 59–72. [Google Scholar] [CrossRef]
- Leguizamón, S.; Jahanbakhsh, E.; Maertens, A.; Alimirzazadeh, S.; Avellan, F. A multiscale model for sediment impact erosion simulation using the finite volume particle method. Wear 2017, 392–393, 202–212. [Google Scholar] [CrossRef]
- Abdulle, A.; Weinan, E.; Engquist, B.; Vanden-Eijnden, E. The heterogeoeous multiscale method. Acta Numer. 2012, 21, 1–87. [Google Scholar] [CrossRef]
- Walther, J.H.; Praprotnik, M.; Kotsalis, E.M.; Koumoutsakos, P. Multiscale simulation of water flow past a C-540 fullerene. J. Comput. Phys. 2012, 231, 2677–2681. [Google Scholar] [CrossRef]
- Saye, R.I.; Sethian, J.A. Multiscale modeling of membrane rearrangement, drainage, and rupture in evolving foams. Science 2013, 340, 720–724. [Google Scholar] [CrossRef] [PubMed]
- Yildirim, B.; Muftu, S.; Gouldstone, A. Modeling of high velocity impact of spherical particles. Wear 2011, 270, 703–713. [Google Scholar] [CrossRef]
- Leguizamón, S.; Jahanbakhsh, E.; Alimirzazadeh, S.; Maertens, A.; Avellan, F. FVPM numerical simulation of the effect of particle shape and elasticity on impact erosion. Wear 2019, 430–431, 108–119. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Leguizamón, S.; Jahanbakhsh, E.; Maertens, A.; Vessaz, C.; Alimirzazadeh, S.; Avellan, F. Impact erosion prediction using the finite volume particle method with improved constitutive models. In Proceedings of the 28th IAHR Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016; Volume 49, p. 122010. [Google Scholar] [CrossRef]
- Dehbi, A. Turbulent particle dispersion in arbitrary wall-bounded geometries: A coupled CFD-Langevin-equation based approach. Int. J. Multiphase Flow 2008, 34, 819–828. [Google Scholar] [CrossRef]
- Jahanbakhsh, E.; Vessaz, C.; Maertens, A.; Avellan, F. Development of a finite volume particle method for 3-D fluid flow simulations. Comput. Methods Appl. Mech. Eng. 2016, 298, 80–107. [Google Scholar] [CrossRef]
- Vessaz, C.; Jahanbakhsh, E.; Avellan, F. Flow simulation of jet deviation by rotating Pelton buckets using finite volume particle method. ASME J. Fluids Eng. 2015, 137, 074501. [Google Scholar] [CrossRef]
- Jahanbakhsh, E.; Maertens, A.; Quinlan, N.; Vessaz, C.; Avellan, F. Exact finite volume particle method with spherical-support kernels. Comput. Methods Appl. Mech. Eng. 2017, 317, 101–127. [Google Scholar] [CrossRef]
- Alimirzazadeh, S.; Jahanbakhsh, E.; Maertens, A.; Leguizamón, S.; Avellan, F. GPU-accelerated 3-D finite volume particle method. Comput. Fluids 2018, 171, 79–93. [Google Scholar] [CrossRef]
- Alimirzazadeh, S.; Kumashiro, T.; Leguizamón, S.; Maertens, A.; Jahanbakhsh, E.; Tani, K.; Avellan, F. GPU-accelerated Pelton turbine simulation using finite volume particle method coupled with linear eddy viscosity models. In Proceedings of the 29th IAHR Symposium on Hydraulic Machinery and Systems, Kyoto, Japan, 17–21 September 2018; Volume 240, p. 072018. [Google Scholar] [CrossRef]
- Perrig, A. Hydrodynamics of the Free Surface Flow in Pelton Turbine Buckets. Ph.D. thesis, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland, 2007. [Google Scholar] [CrossRef]
- Leguizamón, S.; Jahanbakhsh, E.; Maertens, A.; Alimirzazadeh, S.; Avellan, F. Simulation of the hydroabrasive erosion of a bucket: A multiscale model with projective integration to circumvent the spatio-temporal scale separation. In Proceedings of the 29th IAHR Symposium on Hydraulic Machinery and Systems, Kyoto, Japan, 17–21 September 2018; Volume 240, p. 072014. [Google Scholar] [CrossRef]
- Leguizamón, S.; Alimirzazadeh, S.; Jahanbakhsh, E.; Avellan, F. Multiscale simulation of erosive wear in a prototype-scale Pelton runner. Renew. Energy 2019, submit. [Google Scholar]
| c | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 375 | 1089 | 140 | 17 | 28.5 | 80 | 201 | 1174 | 6 | 27 | 134 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution NonCommercial NoDerivatives (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Leguizamón, S.; Jahanbakhsh, E.; Alimirzazadeh, S.; Maertens, A.; Avellan, F. Multiscale Simulation of the Hydroabrasive Erosion of a Pelton Bucket: Bridging Scales to Improve the Accuracy. Int. J. Turbomach. Propuls. Power 2019, 4, 9. https://doi.org/10.3390/ijtpp4020009
Leguizamón S, Jahanbakhsh E, Alimirzazadeh S, Maertens A, Avellan F. Multiscale Simulation of the Hydroabrasive Erosion of a Pelton Bucket: Bridging Scales to Improve the Accuracy. International Journal of Turbomachinery, Propulsion and Power. 2019; 4(2):9. https://doi.org/10.3390/ijtpp4020009
Chicago/Turabian StyleLeguizamón, Sebastián, Ebrahim Jahanbakhsh, Siamak Alimirzazadeh, Audrey Maertens, and François Avellan. 2019. "Multiscale Simulation of the Hydroabrasive Erosion of a Pelton Bucket: Bridging Scales to Improve the Accuracy" International Journal of Turbomachinery, Propulsion and Power 4, no. 2: 9. https://doi.org/10.3390/ijtpp4020009
APA StyleLeguizamón, S., Jahanbakhsh, E., Alimirzazadeh, S., Maertens, A., & Avellan, F. (2019). Multiscale Simulation of the Hydroabrasive Erosion of a Pelton Bucket: Bridging Scales to Improve the Accuracy. International Journal of Turbomachinery, Propulsion and Power, 4(2), 9. https://doi.org/10.3390/ijtpp4020009





