Adjoint-Based Multi-Point and Multi-Objective Optimization of a Turbocharger Radial Turbine †
Abstract
1. Introduction
2. Optimization Framework
2.1. Optimization Algorithm
2.2. Geometry Parameterization
2.3. Mesh Generation
2.4. Analysis Methods
2.4.1. CFD and Adjoint Solver
2.4.2. Moment of Inertia Computation
2.5. Gradient Evaluation
3. Problem Statement
4. Results
4.1. Optimization History
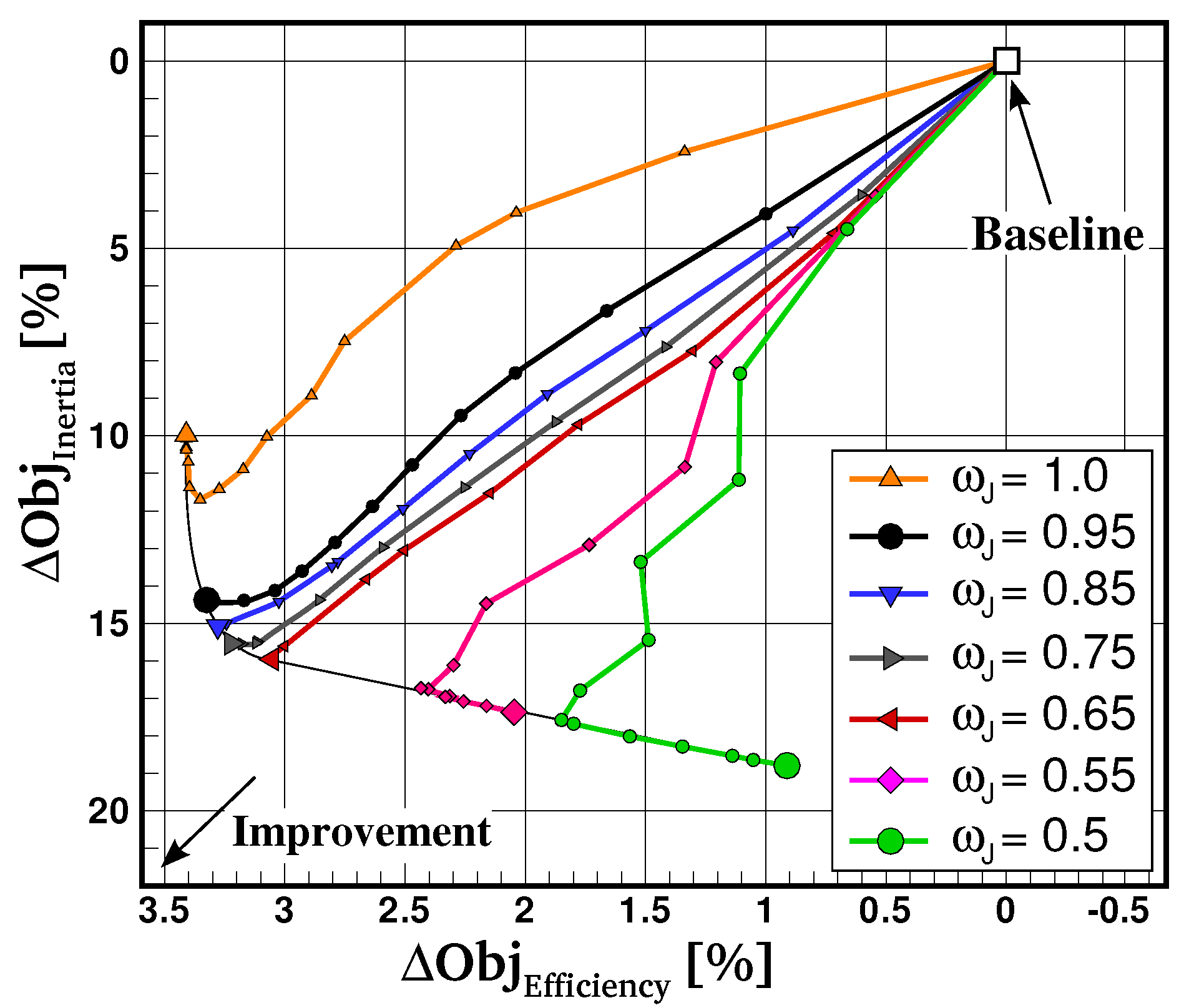
4.2. Influence of the Weight Coefficient
4.2.1. Performance Map
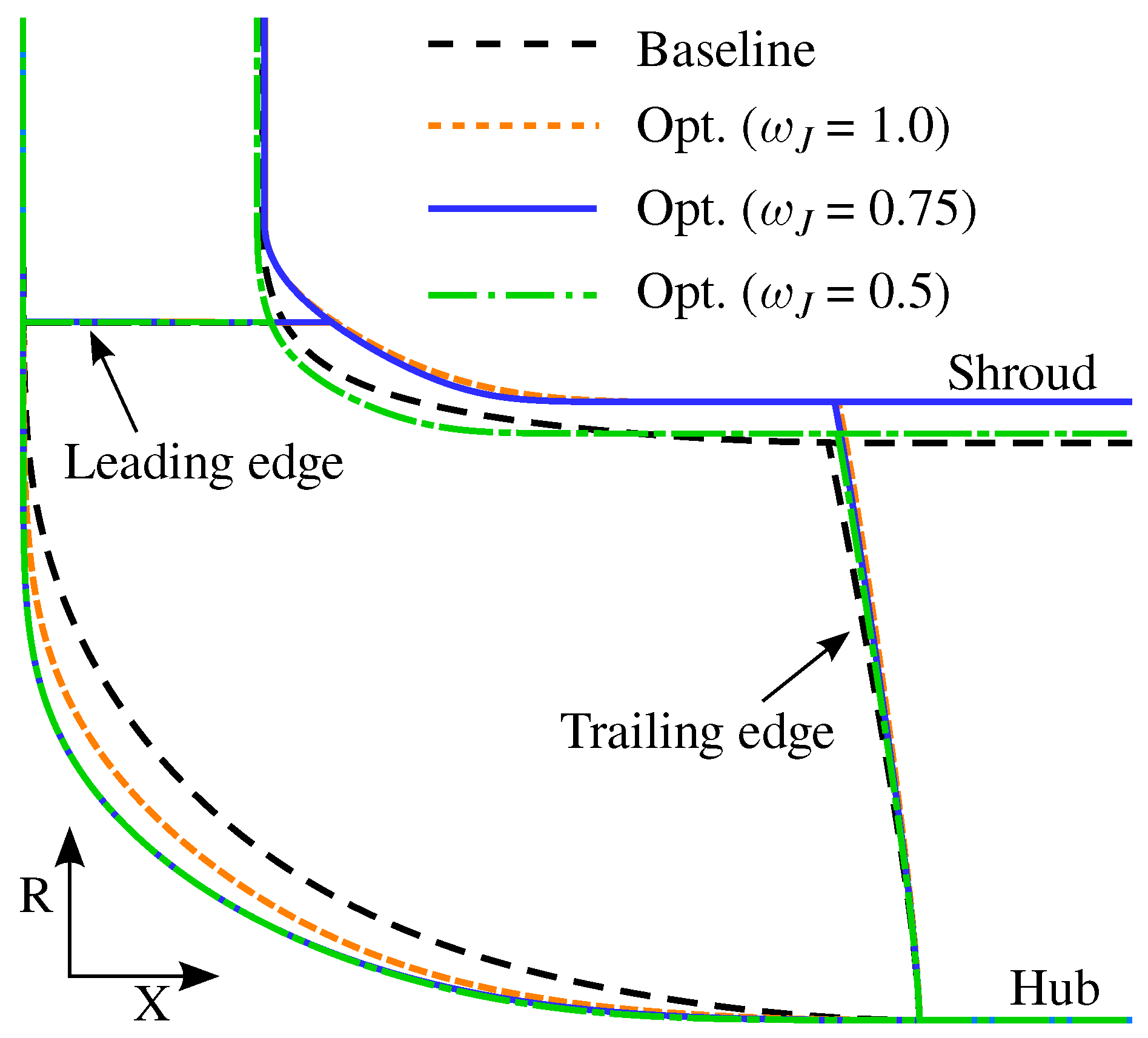
4.2.2. Meridional Shape
4.2.3. Blade Shape
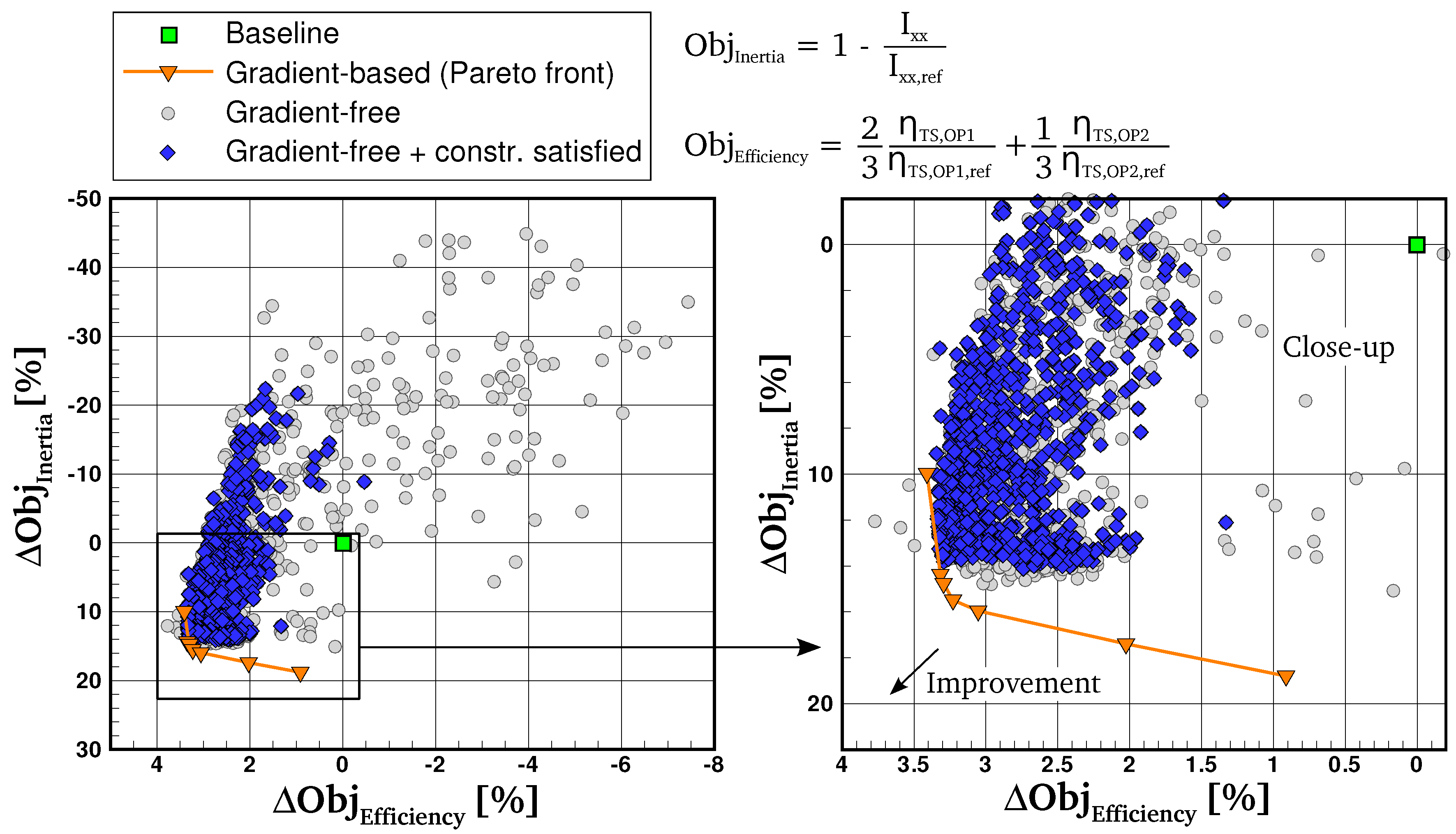
4.3. Comparison with the Gradient-Free Optimization Algorithm
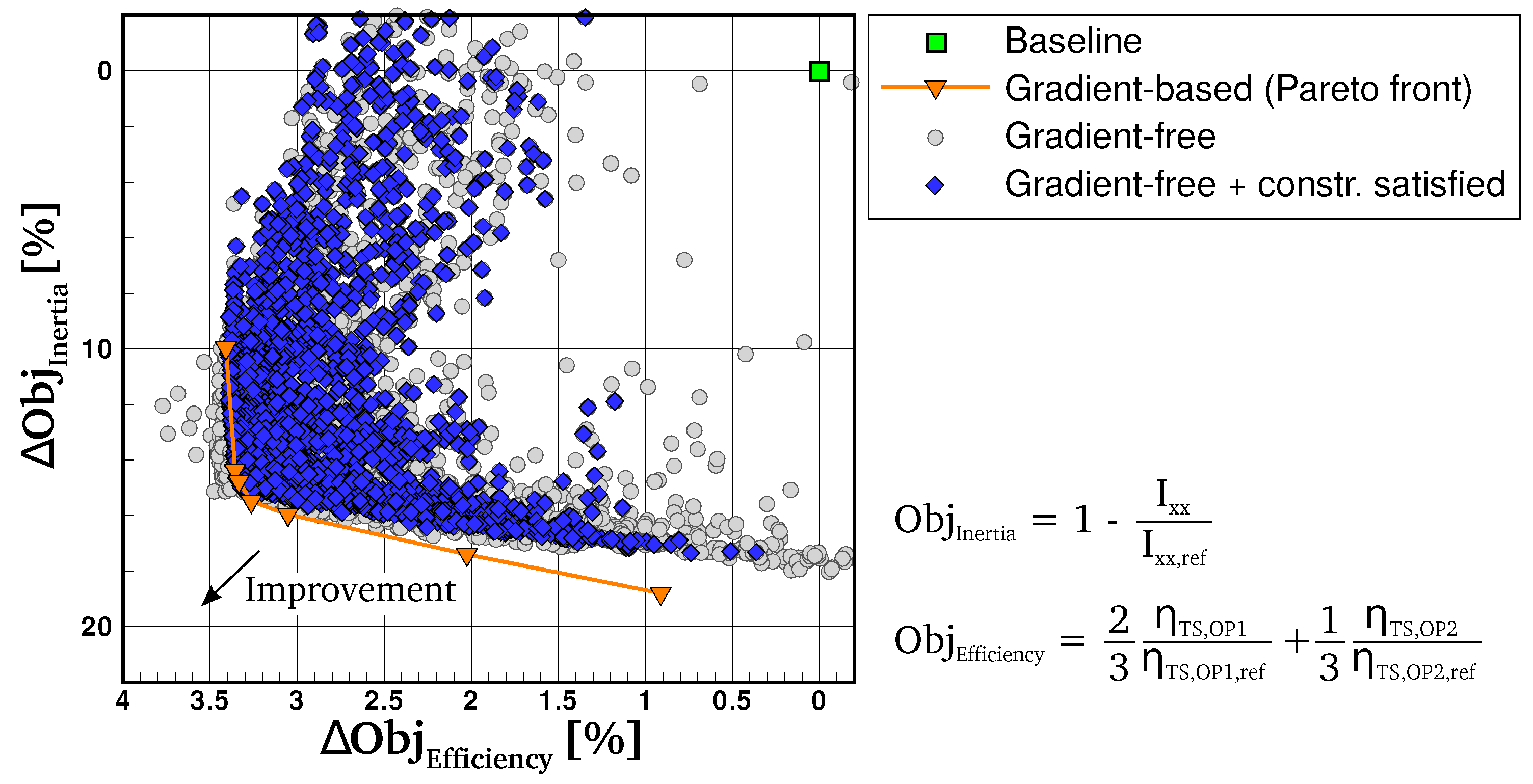
4.3.1. Results after 80 Generations
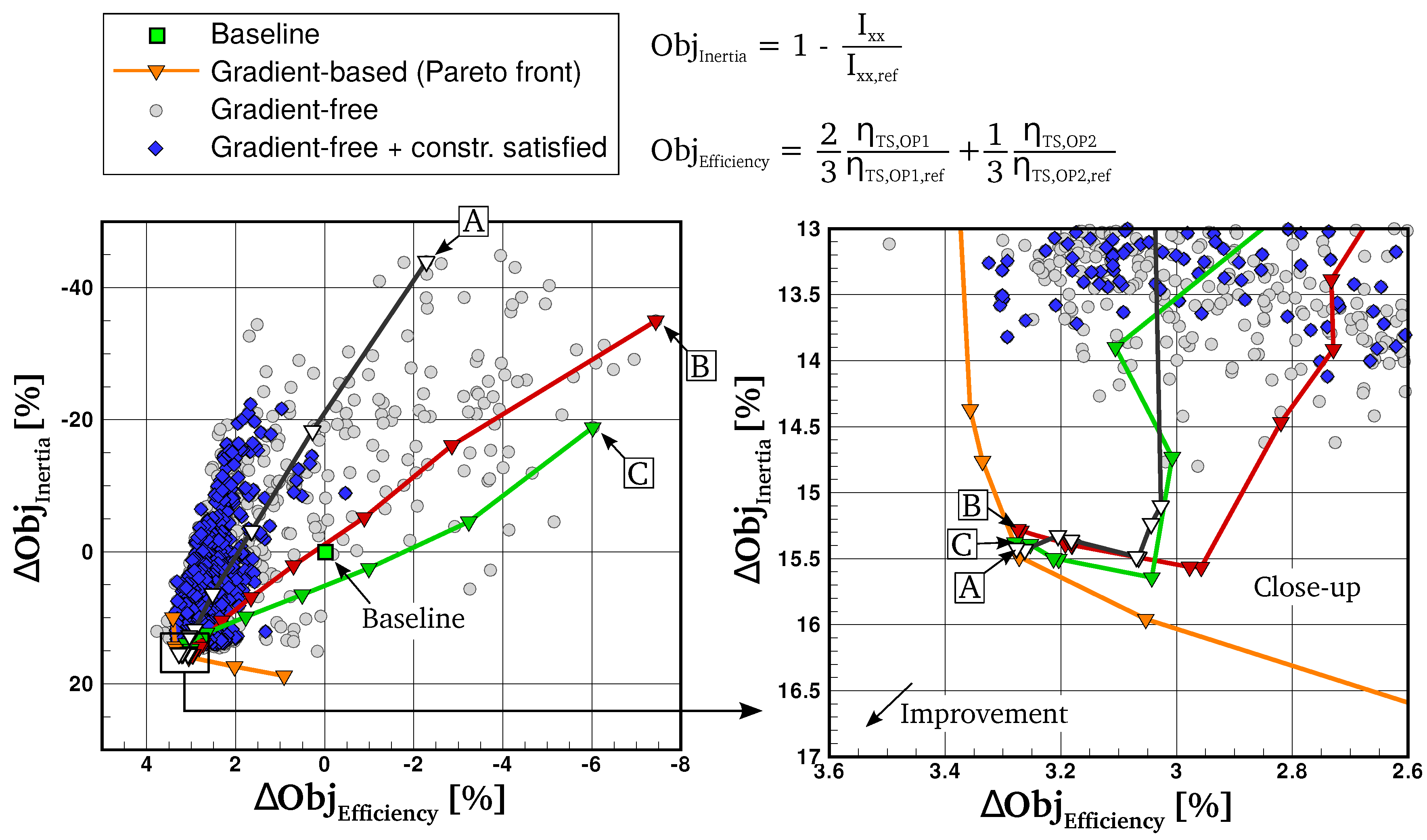
4.3.2. Results after 200 Generations
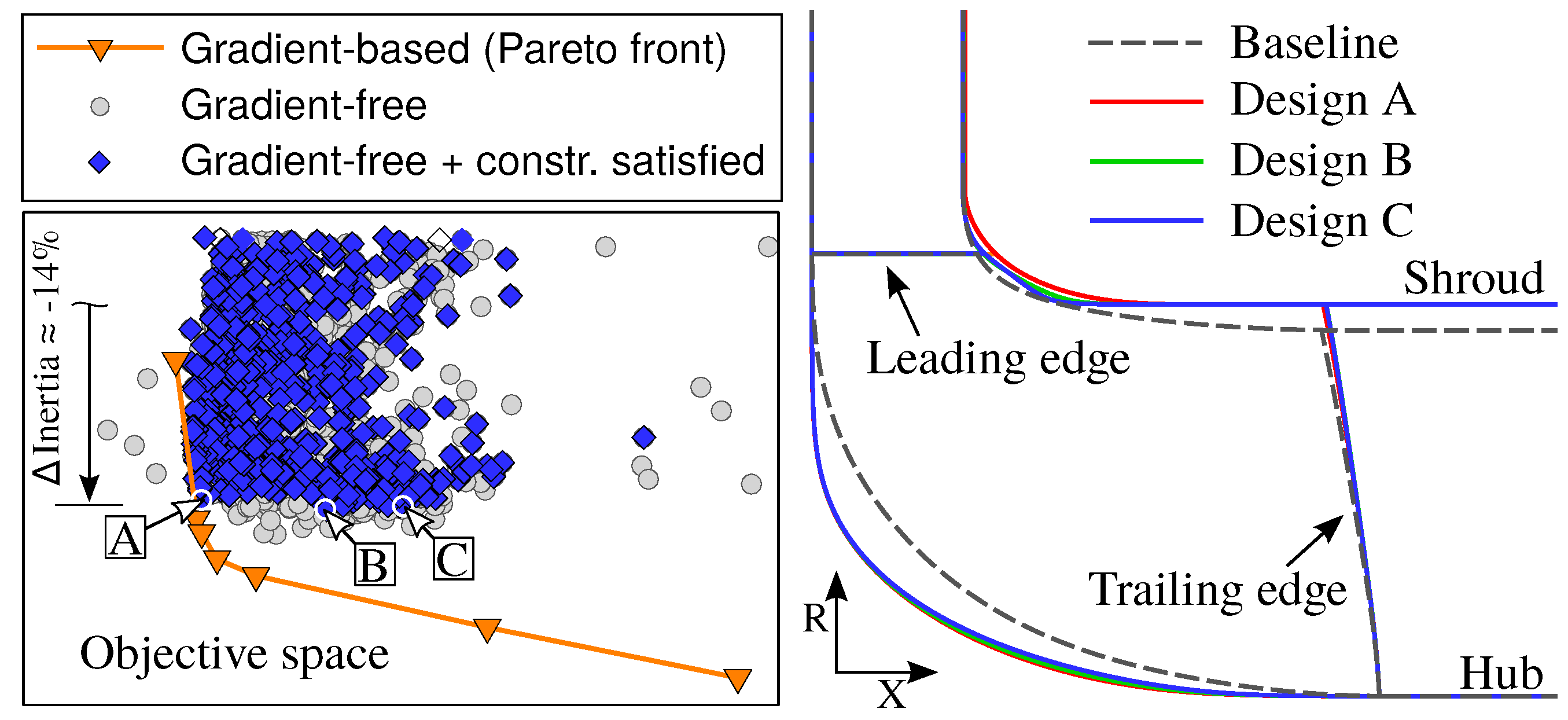
4.3.3. Influence of Initial Design
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Roman Symbols | |
| Moment of inertia | |
| J | Cost function |
| Mass flow | |
| Power | |
| Grid point coordinates | |
| Subscripts | |
| 0 | Total condition |
| 1 | Inlet |
| 2 | Outlet |
| is | Isentropic |
| ref | Reference |
| TS | Total-to-static |
| Greek Symbols | |
| Absolute flow angle | |
| Design variables | |
| Difference | |
| Efficiency | |
| Pressure ratio | |
| Weighting coefficient | |
| Abbrevations | |
| CADO | Computer Aided Design Optimization |
| CEV | 7 Constant Eddy Viscosity |
| Constr | Constraint |
| DE | Differential Evolution |
| JT-KIRK | Jacobian Trained Krylov Implicit Runge–Kutta |
| MUSCL | Monotonic Upstream-Centered Scheme for Conservation Laws |
| Obj | Objective |
| OP | Operating Point |
| RANS | Reynolds-Averaged Navier–Stokes |
| RPM | Revolutions per minute |
| SNOPT | Sparse Nonlinear OPTimizer |
| SQP | Sequential Quadratic Programming |
References
- Pironneau, O. On Optimum Design in Fluid Mechanics. J. Fluid Mech. 1974, 64, 97–110. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic Design via Control Theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Giles, M.B.; Duta, M.C.; Müller, J.-D.; Pierce, N.A. Algorithm Developments for Discrete Adjoint Methods. AIAA J. 2003, 41, 198–205. [Google Scholar] [CrossRef]
- Papadimitriou, D.I.; Giannakoglou, K.C. Total Pressure Loss Minimization in Turbomachinery Cascades Using a New Continuous Adjoint Formulation. J. Power Energy 2007, 221, 865–872. [Google Scholar] [CrossRef]
- Marta, A.C.; Shankaran, S.; Holmes, D.G.; Stein, A. Development of Adjoint Solvers for Engineering Gradient-Based Turbomachinery Design Applications. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 8–12 June 2009. [Google Scholar]
- Luo, J.; Liu, F.; McBean, I. Turbine Blade Row Optimization Through Endwall Contouring by an Adjoint Method. J. Propuls. Power 2015, 31, 505–518. [Google Scholar] [CrossRef]
- Corral, R.; Gisbert, F. Profiled End Wall Design Using an Adjoint Navier-Stokes Solver. J. Turbomach. 2008, 130, 021011. [Google Scholar] [CrossRef]
- Wang, D.X.; He, L. Adjoint Aerodynamic Design Optimization for Blades in Multi-Stage Turbomachines: Part 1—Methodology and Verification. J. Turbomach. 2010, 132, 021011. [Google Scholar] [CrossRef]
- Shahpar, S.; Caloni, S. Adjoint Optimisation of a High Pressure Turbine Stage for Lean-Burn Combustion System. In Proceedings of the 10th European Conference on Turbomachinery, Fluid Dynamics and Thermodynamics, Lappeenranta, Finland, 15–19 April 2013. [Google Scholar]
- Walther, B.; Nadarajah, S. Optimum Shape Design for Multirow Turbomachinery Configurations Using a Discrete Adjoint Approach and an Efficient Radial Basis Function Deformation Scheme for Complex Multiblock Grids. J. Turbomach. 2015, 137, 081006. [Google Scholar] [CrossRef]
- Mueller, L.; Verstraete, T. CAD Integrated Multipoint Adjoint-Based Optimization of a Turbocharger Radial Turbine. Int. J. Turbomach. Propuls. Power 2017, 2, 14. [Google Scholar] [CrossRef]
- Namgoong, H.; Crossley, W.; Lyrintzis, A.S. Global Optimization Issues for Transonic Airfoil Design. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002. [Google Scholar]
- Chernukhin, O.; Zingg, D.W. Multimodality and Global Optimization in Aerodynamic Design. AIAA J. 2013, 51, 1342–1354. [Google Scholar] [CrossRef]
- Zingg, D.W.; Nemec, M.; Pulliam, T.H. A Comparative Evaluation of Genetic and Gradient-Based Algorithms Applied to Aerodynamic Optimization. Eur. J. Comput. Mech. 2008, 17, 103–126. [Google Scholar] [CrossRef]
- Yu, Y.; Lyu, Z.; Xu, Z.; Martins, J.R.R.A. On the Influence of Optimization Algorithm and Initial Design on Wing Aerodynamic Shape Optimization. Aerosp. Sci. Technol. 2018, 15, 183–199. [Google Scholar] [CrossRef]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a Common Research Model for Applied CFD Validation Studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Koo, D.; Zingg, D.W. Investigation into Aerodynamic Shape Optimization of Planar and Nonplanar Wings. AIAA J. 2018, 56, 250–263. [Google Scholar] [CrossRef]
- Osusky, L.; Buckley, H.P.; Reist, T.A.; Zingg, D.W. Drag Minimization based on the Navier-Stokes Equations Using a Newton-Krylov Approach. AIAA J. 2015, 53, 1555–1577. [Google Scholar] [CrossRef]
- Buckley, H.P.; Zhou, B.Y.; Zingg, D.W. Airfoil Optimization Using Practical Aerodynamic Design Requirements. J. Aircr. 2010, 47, 1707–1719. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. An SQP Algorithm for Large-Scale Constrained Optimization. SIAM J. Optim. 2002, 12, 979–1006. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. User’s Guide for SNOPT Version 7: Software for Large-Scale Nonlinear Programming; University of California: San Diego, CA, USA, 2008. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. Some Theoretical Properties of an Augmented Lagrangian Merit Function; Technical Report SOL 86-6R; Stanford University: Stanford, CA, USA, 1986. [Google Scholar]
- Miller, P.L.; Olivier, J.H.; Miller, P.D.; Tweedt, D.L. BladeCAD: An Interactive Geometric Design Tool for Turbomachinery Blades; Technical Report TM-107262; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1996.
- Thompson, J.F.; Thames, F.C.; Mastin, C.W. Automatic Numerical Generation of Body-Fitted Curvilinear Coordinates for a Field Containing Any Number of Arbitrary Two-Dimensional Bodies. J. Comput. Phys. 1974, 15, 299–319. [Google Scholar] [CrossRef]
- Verstraete, T.; Mueller, L.; Müller, J.-D. CAD-Based Adjoint Optimization of the Stresses in a Radial Turbine. In Proceedings of the ASME Turbo Expo, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Roe, P.L. Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Harten, A.; Hyman, J.M. Self-Adjusting Grid Methods for One-Dimensional Hyperbolic Conservation Laws. J. Comput. Phys. 1983, 50, 235–269. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme. V. A Second Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Venkatakrishnan, V. On the Accuracy of Limiters and Convergence to Steady State Solutions. In Proceedings of the 31st AIAA Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
- Allmaras, S.R.; Johnson, F.T.; Spalart, P.R. Modifications and Clarifications for the Implementation of the Spalart-Allmaras Turbulence Model. In Proceedings of the 7th International Conference on Computational Fluid Dynamics (ICCFD7-1902), Big Island, HI, USA, 9–13 July 2012. [Google Scholar]
- Xu, S.; Radford, D.; Meyer, M.; Müller, J.-D. Stabilisation of Discrete Steady Adjoint Solvers. J. Comput. Phys. 2015, 299, 175–196. [Google Scholar] [CrossRef]
- Lyness, J.N.; Moler, C.B. Numerical Differentiation of Analytical Functions. SIAM J. Numer. Anal. 1967, 4, 202–210. [Google Scholar] [CrossRef]
- Martins, J.R.; Sturdza, P.; Alonso, J.J. The Complex-Step Derivative Approximation. ACM Trans. Math. Softw. 2003, 29, 245–262. [Google Scholar] [CrossRef]
- Mueller, L. Adjoint-Based Optimization of Turbomachinery with Applications to Axial and Radial Turbines. Ph.D. Thesis, Université libre de Bruxelles & von Karman Institute for Fluid Dynamics, Brussels, Belgium, 2019. [Google Scholar]
- Tonon, F. Explicit Exact Formulas for the 3-D Tetrahedron Inertia Tensor in Terms of its Vertex Coordinates. J. Math. Stat. 2004, 1, 8–11. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Verstraete, T. CADO: A Computer Aided Design and Optimization Tool for Turbomachinery Applications. In Proceedings of the 2nd International Conference on Engineering Optimization, Lisbon, Portugal, 6–9 September 2010. [Google Scholar]
- Dep, K.; Pratap, A.; Agarwal, S. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar]

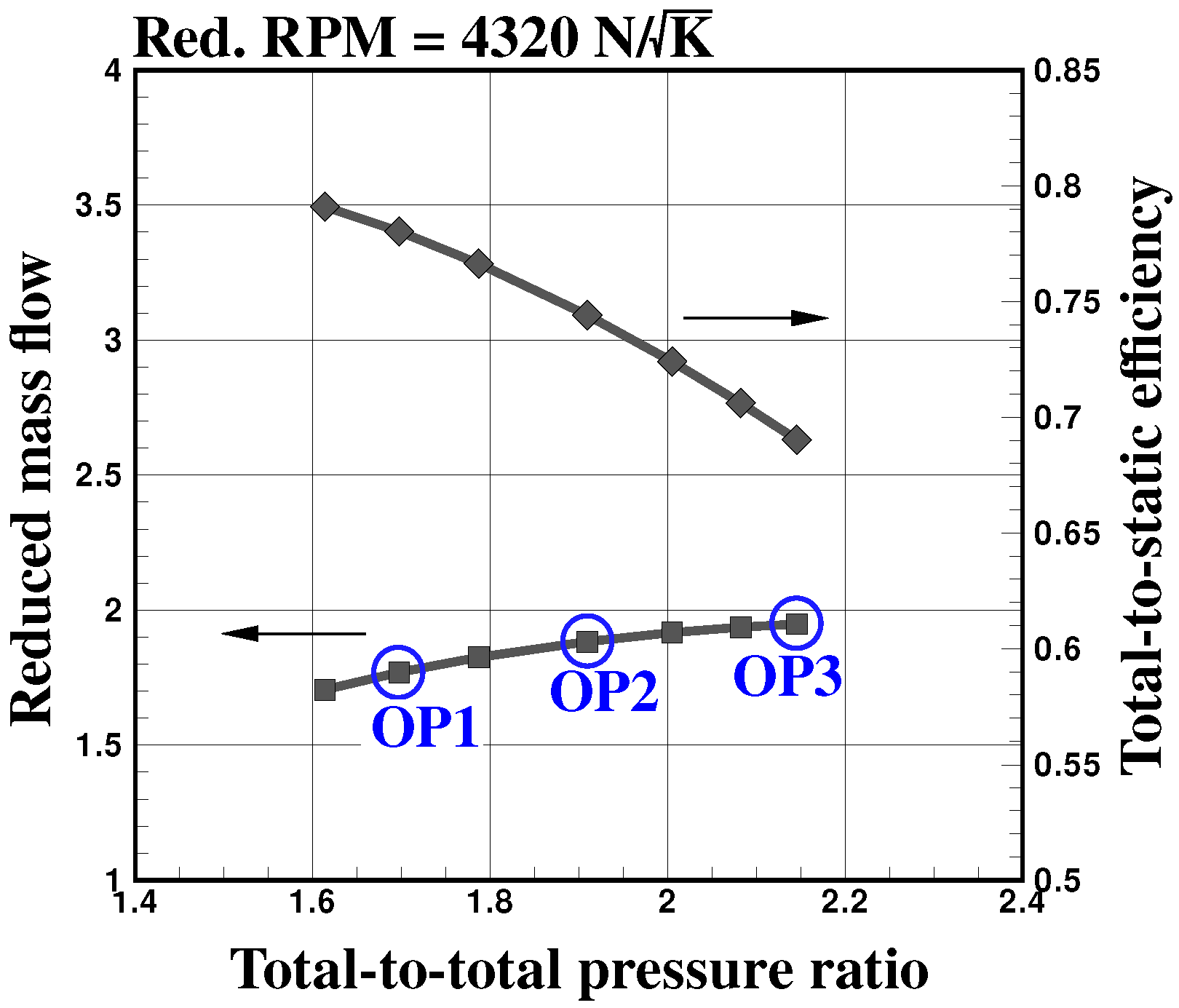




| Parameter | Symbol | Unit | OP1 | OP2 | OP3 |
|---|---|---|---|---|---|
| Inlet flow angle 1 | [] | 62 | |||
| Inlet total pressure | [bar] | - | - | 3.0 | |
| Inlet mass flow | [g/s] | 100 | 130 | - | |
| Inlet total temperature | [K] | 1050 | |||
| Exit static pressure 2 | [bar] | 1.013 | |||
| Rotational speed | [min−1] | 140,000 | |||
| Optimizer | Cost (CFD + Adjoint Evaluations) | |
|---|---|---|
| Gradient-free | 18,000 | |
| Gradient-based | 143 | |
| 146 | ||
| 140 | ||
| 137 | ||
| 143 | ||
| 155 | ||
| 158 | ||
| 1022 (in total) |
| Design | [%] | [%] |
|---|---|---|
| A | 3.277 | 15.421 |
| B | 3.275 | 15.298 |
| C | 3.279 | 15.374 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution NonCommercial NoDerivatives (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Mueller, L.; Verstraete, T. Adjoint-Based Multi-Point and Multi-Objective Optimization of a Turbocharger Radial Turbine. Int. J. Turbomach. Propuls. Power 2019, 4, 10. https://doi.org/10.3390/ijtpp4020010
Mueller L, Verstraete T. Adjoint-Based Multi-Point and Multi-Objective Optimization of a Turbocharger Radial Turbine. International Journal of Turbomachinery, Propulsion and Power. 2019; 4(2):10. https://doi.org/10.3390/ijtpp4020010
Chicago/Turabian StyleMueller, Lasse, and Tom Verstraete. 2019. "Adjoint-Based Multi-Point and Multi-Objective Optimization of a Turbocharger Radial Turbine" International Journal of Turbomachinery, Propulsion and Power 4, no. 2: 10. https://doi.org/10.3390/ijtpp4020010
APA StyleMueller, L., & Verstraete, T. (2019). Adjoint-Based Multi-Point and Multi-Objective Optimization of a Turbocharger Radial Turbine. International Journal of Turbomachinery, Propulsion and Power, 4(2), 10. https://doi.org/10.3390/ijtpp4020010




