1. Introduction
Not disregarding the classical CFD approaches [
1,
2,
3,
4,
5,
6], the design and/or analysis of aeronautical and marine propellers are generally carried out using many numerical methods such as lifting-line [
7,
8], lifting surface [
9,
10] and panel methods [
11,
12]. However, when compared with the classical engineering approach based on the momentum theory, these models have never shown a definitive improvement in the accuracy of the performance prediction and/or in the robustness of the numerical algorithm [
13]. For this reason, despite the great variety of more advanced methods, the simple and robust Blade-Element Momentum Theory is still the most used approach for the evaluation of propeller performance. This theory stems from the coupling of the Blade-Element Theory and of the Momentum Theory (MT). Two versions of this latter theory exist: the generalized (GMT) and the axial (AMT) Momentum Theory [
14]. While the former takes into account the wake rotation, the AMT completely disregards the tangential velocity, even in the wake. The MT relies on the steady, incompressible, axisymmetric, and inviscid flow assumptions. However, additional simplifying assumptions are typically introduced when the MT is used to evaluate local quantities such as the radial distribution of the axial velocity at the disk. Specifically, as shown in [
15,
16,
17,
18,
19], the AMT disregards the axial contribution of the pressure forces on the lateral surfaces of the infinitesimal streamtubes swallowed by the rotor. Due to the great relevance of this theory, the evaluation of its errors and the impact on the reliability of its results are of interest. Generally, the evaluation of these errors is carried out by comparing the MT results with those of more advanced actuator disk approaches which do not rely on the MT simplifying assumptions. For example, consider the nonlinear actuator disk of Wu [
20] further developed in [
21,
22,
23]. The method has been also extended to a ducted configuration in [
24,
25,
26,
27,
28,
29,
30]. The ring-vortex wake method proposed by Øye [
31] has also been employed by van Kuik and Lignarolo [
32] to verify the AMT when applied to a wind turbine. Sørensen and Mikkelsen [
33], Madsen et al. [
34], Sørensen [
35] and Madsen et al. [
36] also assessed the validity of the MT using several actuator disk approaches.
Despite the large amount of works on this topic, a precise evaluation of the AMT errors as applied to the classical uniformly loaded propeller is still missing. The relevance of this issue relies on the fact that the uniformly loaded disk still represents the benchmark model for two reasons. Firstly, thanks to its great simplicity, this model is the most studied and used approach. Secondly, it can be easily proven that a uniformly loaded disk is characterized by the maximum propulsive efficiency, thus making this oversimplified model a reference point for the performance estimation of real propellers. In this paper, the errors embodied in the AMT as applied to a uniformly loaded propeller are evaluated comparing its results with those of a free-wake ring-vortex actuator disk (FWRV-AD) method which models the wake through the superposition of ring vortices placed in the control points of
N straight panels [
37,
38]. The far wake is represented by a semi-infinite vortex cylinder. The velocity induced by a panel on itself is computed considering the wake curvature both in the cross and meridional plane. Two constrains are used to iteratively evaluate the wake shape and the density strengths of the vortices, i.e., the panels are required to be aligned with the overall flow field and to have a zero static pressure jump across them.
The article is organized as follows. Firstly, the typical simplifying assumptions used in the AMT are described in
Section 2. Then, most of the theoretical and numerical aspects of the FWRV-AD method are outlined, and its stability and convergence properties are discussed in some details (see
Section 3). Moreover, its results are verified in terms of global performance coefficients using the AMT in
Section 4.1. A further verification in terms of local flow quantities is carried out against a CFD actuator disk model (see
Section 4.2). Finally, in
Section 4.3, the AMT errors on the axial velocity at the disk, and on the axial induction factor are quantified.
2. The Axial Momentum Theory for the Uniformly Loaded Propeller: Review and Analysis of the Simplifying Assumptions
In the AMT, a uniformly loaded propeller is modelled by the steady, incompressible, inviscid, and axisymmetric flow through an actuator disk which experiences a uniform pressure jump across it. To fully take advantage of the axisymmetric flow assumption, a cylindrical coordinate system (
z,
r,
) is introduced. The
z axis is orthogonal to the disk face and, by convention, oriented in the downstream direction. Without loss of generality, the origin of the reference frame is placed at the disk center. Moreover, to further simplify the analysis, the tangential velocity is typically assumed to be zero everywhere, even in the wake. Obviously, for finite rotor angular velocity, this assumption contradicts the angular momentum equation. However, since the dynamic load associated with the change in the tangential velocity is usually small in comparison with the static load, the above assumption is generally accepted as a first approximation. Moreover, it can be easily proven [
15] that a uniformly loaded actuator disk without wake rotation is characterized by the maximum propulsive efficiency, thus making this oversimplified model a reference point for the performance of real propellers.
At upstream infinity, the axial velocity
and the static pressure
are considered to be uniform and, for the sake of simplicity, they are termed
and
, respectively. Across the disk, the axial
and the radial
velocity are supposed to be continuous (that is
and
). The axial and radial velocities at the disk are termed
and
, where the subscript
d stands for disk. While the velocity components are continuous functions across the disk, a radially uniform pressure jump
takes place there, i.e.,
At downstream infinity, the wake is supposed to be fully developed in the axial direction without a radial velocity component. Then, since there is no rotation in the wake, it is easy to show that the static pressure at downstream infinity is everywhere equal to
[
15], a fact that can be easily proven using the Bernoulli and the radial momentum equations. The wake axial velocity at downstream infinity
is termed
. This quantity can be related to the pressure jump across the disk by applying the Bernoulli equation to the streamtubes swallowed by the rotor. By so doing, it can be shown that
where
is the fluid density. The above equation implies that if a uniform pressure jump exists all along the rotor span, then the wake axial velocity at downstream infinity
must be uniform in the radial direction, too. Since
for a propeller, Equation (
1) also means that the axial velocity in the wake must be greater than
, so that, using the continuity equation, the streamtube swallowed by the disk must contract moving from upstream to downstream infinity.
A further relation between the rotor load and the wake velocity can be obtained by applying the axial momentum equation which returns [
15]
where
T is the propeller thrust and
is the rotor swept area. Moreover, if
r is the radius of a generic streamtube at
, then the function
returns the radius of that streamtube at downstream infinity. When a uniform pressure jump is used, Equation (
2) reduces to
In the above equation
is the area averaged axial velocity at the disk defined as
Then, from Equations (
1) and (
3), it is easy to prove that the averaged axial velocity at the disk is the arithmetic mean between the velocity at upstream and downstream infinity i.e.,
Under all the aforementioned simplifying assumptions, Equations (
1)–(
5) are exact. However, in the AMT, these equations are further simplified by adopting the following differential form of Equation (
2):
which, making use of Equation (
1), promptly returns the famous Froude law
Contrarily to Equation (
5), the above equation implies that for a uniform
, the axial velocity at the disk must be radially uniform, too. For this reason, the AMT is often considered a one-dimensional theory. However, as shown in [
16,
17,
32,
33], Equation (
6), and so (
7), are not exact since they disregard the effect of the pressure forces on the lateral surface of the infinitesimal streamtubes swallowed by the rotor. As discussed in [
16], this effect is intimately related to the wake contraction. In Equation (
7), the superscript AMT is used to denote the axial velocity at the disk evaluated under the simplifying assumptions of the AMT. Also note that Equations (
5) and (
7) readily yield
.
In the following sections, it is shown that, even if the load is uniform, the flow through a uniformly loaded disk is not one-dimensional since the axial velocity at the disk is not uniform. Moreover, the errors introduced in Equations (
6) and (
7) are evaluated comparing them with the results of the FWRV-AD model which does not rely on the simplifying assumption used to retrieve those equations.
3. The Free-Wake Ring-Vortex Model for the Uniformly Loaded Propeller without Wake Rotation
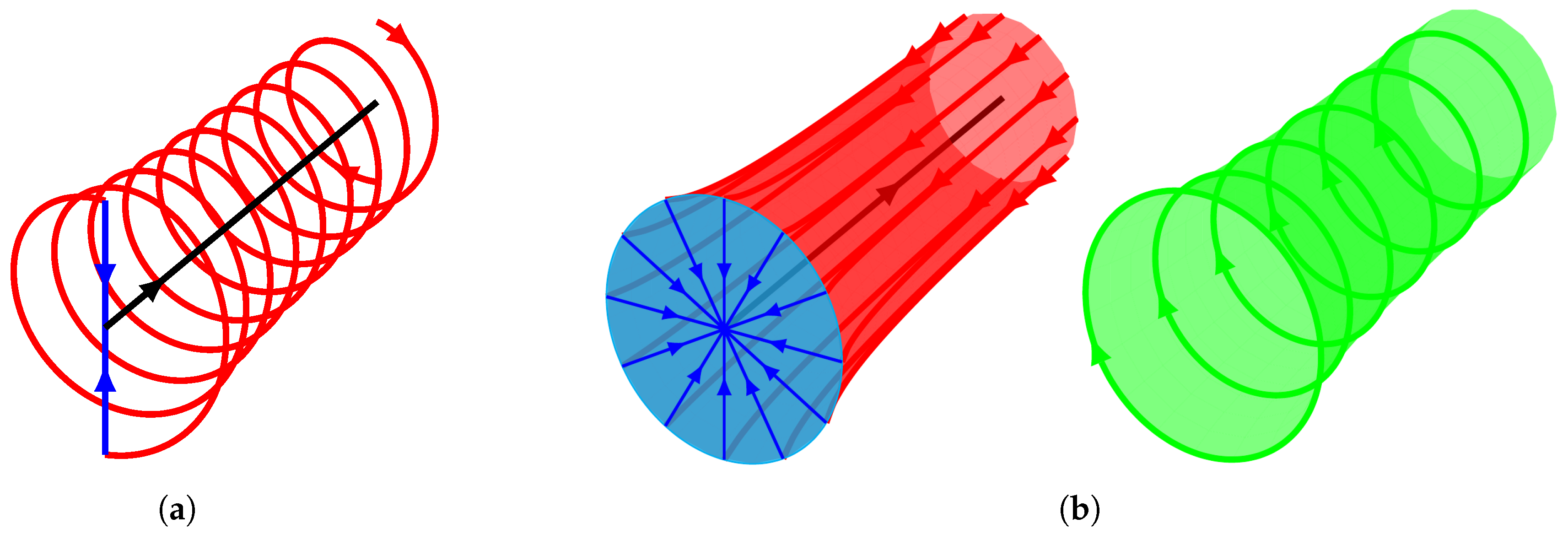
The actuator disk method described in this section stems from an infinite-blade variant of the Joukowsky vortex model [
39]. Basing on the Stokes and Kutta-Joukowsky theorems, this model represents each blade as a line vortex. In fact, a lift force is typically related to each blade section which, using the Kutta-Joukowsky theorem, must experience a bound circulation, too. Hence, from the Stokes theorem, a non-zero vorticity flux exists through any surface containing the blade section. This justifies the modelling of the blades through vortex lines. When a variation of the lift force takes place along the blade span, the associated vorticity flux must change accordingly. Since the vorticity is a solenoidal vector field, a trailing vorticity is also associated with the bound circulation variation. However, for a rotor with a uniform lift force distribution, the trailing vorticity is spread only from the tip and the root of the blades. Summarizing, three vortex systems are used to model the rotor: the blade bound vorticity, a straight line vortex representing the vorticity originating by the roots of the blades, and helicoidal vortex filaments for the vorticity spread by the blade tips (see
Figure 1a). This filament is customarily decomposed in a tangential and in a meridional wake vortex system [
40].
In the limiting case of infinite blades, the two components of the wake vortex filaments are spread over the wake boundary-surface to obtain two contoured cylindrical sheet-vortices (see
Figure 1b) whose strengths are directed in the meridional and tangential direction, respectively. The blade line-vortices are also uniformly distributed on the swept disk surface, while the root vortex is unchanged.
Please note that the tangential vorticity induces an axial and a radial velocity, whereas the meridional component of the vorticity can also induce a tangential velocity. Hence, to obtain the classical actuator disk without wake rotation by the Joukowsky model, the blade, the root, and the meridional wake vorticity must be neglected, while the sole tangential vortex-sheet of the wake has to be used.
The geometry and the strength distribution of this tangential vortex-sheet, which represents the boundary of the wake, are not known a priori, and they must be computed using two different conditions. Firstly, the sheet must be aligned with the overall flow field, a condition which allows evaluation of the wake geometry. Secondly, the stability of the wake edge has to be enforced by requiring that the static pressure just beneath and above the sheet is the same, i.e.,
, where the subscript
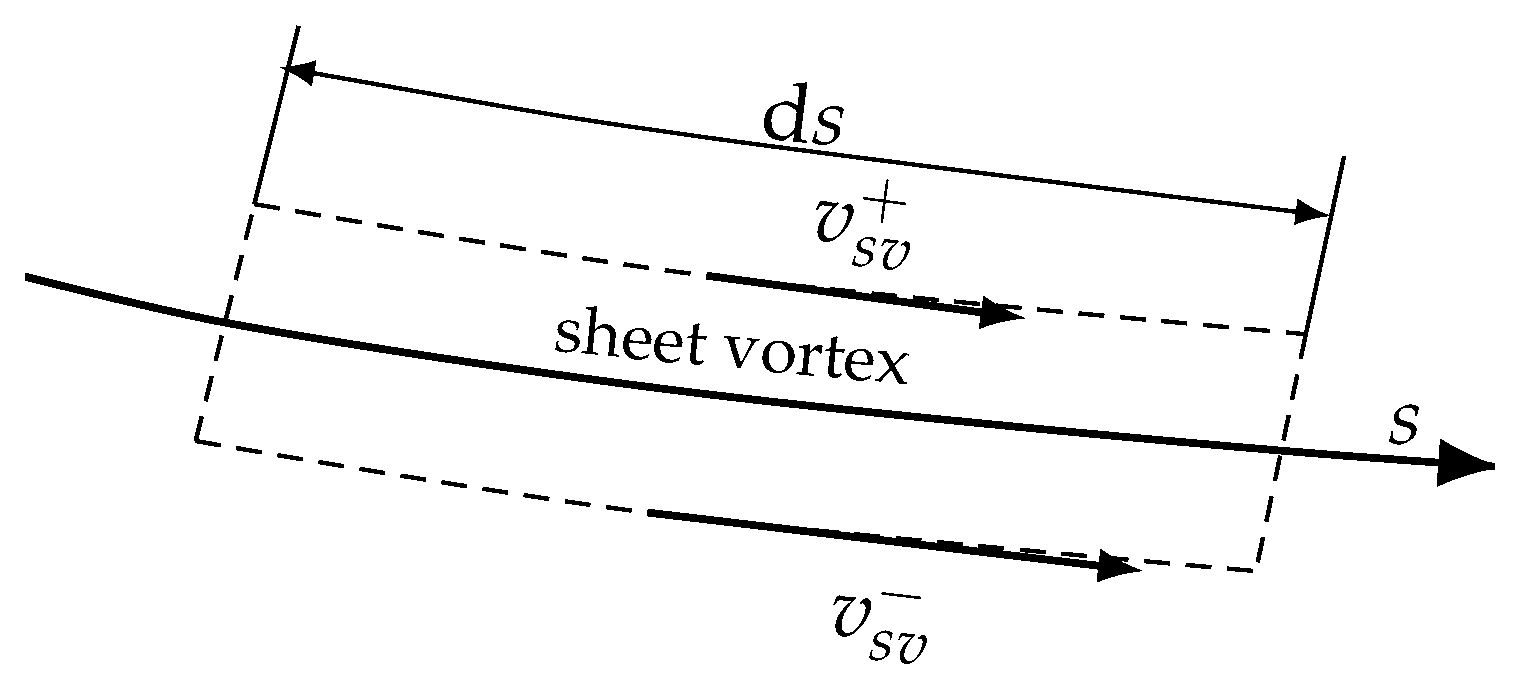
stands for sheet vortex. By so doing, the strength distribution of the sheet vortex can be evaluated as described in the following. First, it is convenient to introduce a curvilinear abscissa
s along the wake edge, with
at the rim of the disk. Then, a density strength distribution
is also introduced along the sheet, so that the strength of a sheet-element with infinitesimal length
becomes
(see
Figure 2).
By convention,
is considered to be clockwise-positive around the positive z axis, and thus, from the Stokes theorem, the strength
is equal to the clockwise velocity circulation around the dashed curve reported in
Figure 2. Then, it is easy to prove that
where
and
are the velocities just beneath and above the sheet, respectively. Please note that since the velocity in a propeller wake is higher than that outside it (
),
is a negative quantity all along the wake.
To enforce the free-force condition
on the wake edge, consider now the total pressure distribution inside and outside the wake. As stressed in the previous section, the axial and radial velocities are supposed to be continuous functions across the disk (
and
), whereas no tangential velocity exists both ahead and behind the disk. Then, the uniform pressure jump across the rotor plane is directly associated with a uniform total pressure jump there, namely
where
is the thrust coefficient, while
and
are the uniform total pressure inside and outside the wake, respectively. The same total pressure jump also exists across the sheet vortex which actually separates the wake from the stream not swallowed by the rotor. Hence, the static pressure difference across the sheet readily reads
Consequently, the sheet stability condition
returns
which, with the help of Equations (
8) and (
9), promptly becomes
In the above equation,
is the velocity at the sheet defined as
, while
and
. Please note that hereafter the disk radius
R and the freestream velocity
are used as reference in all dimensionless quantities. The free-force condition (
10) implies that the product
must be uniform on the sheet vortex, and it can be used to evaluate the density strength along the wake edge once the sheet velocity distribution and the thrust coefficient are known. At downstream infinity, the stability condition (
10) can be cast in a simplified form. Recall that as stressed in the previous section, the static pressure tends to
as
. Thus, from Equation (
9), the wake axial velocity at downstream infinity becomes
Glauert [
15] showed that the axial velocity outside the wake must reach the freestream velocity
as
. Therefore, at downstream infinity, the sheet velocity becomes
, while the density strength reads
3.1. The Discrete Free-Wake Ring-Vortex Model
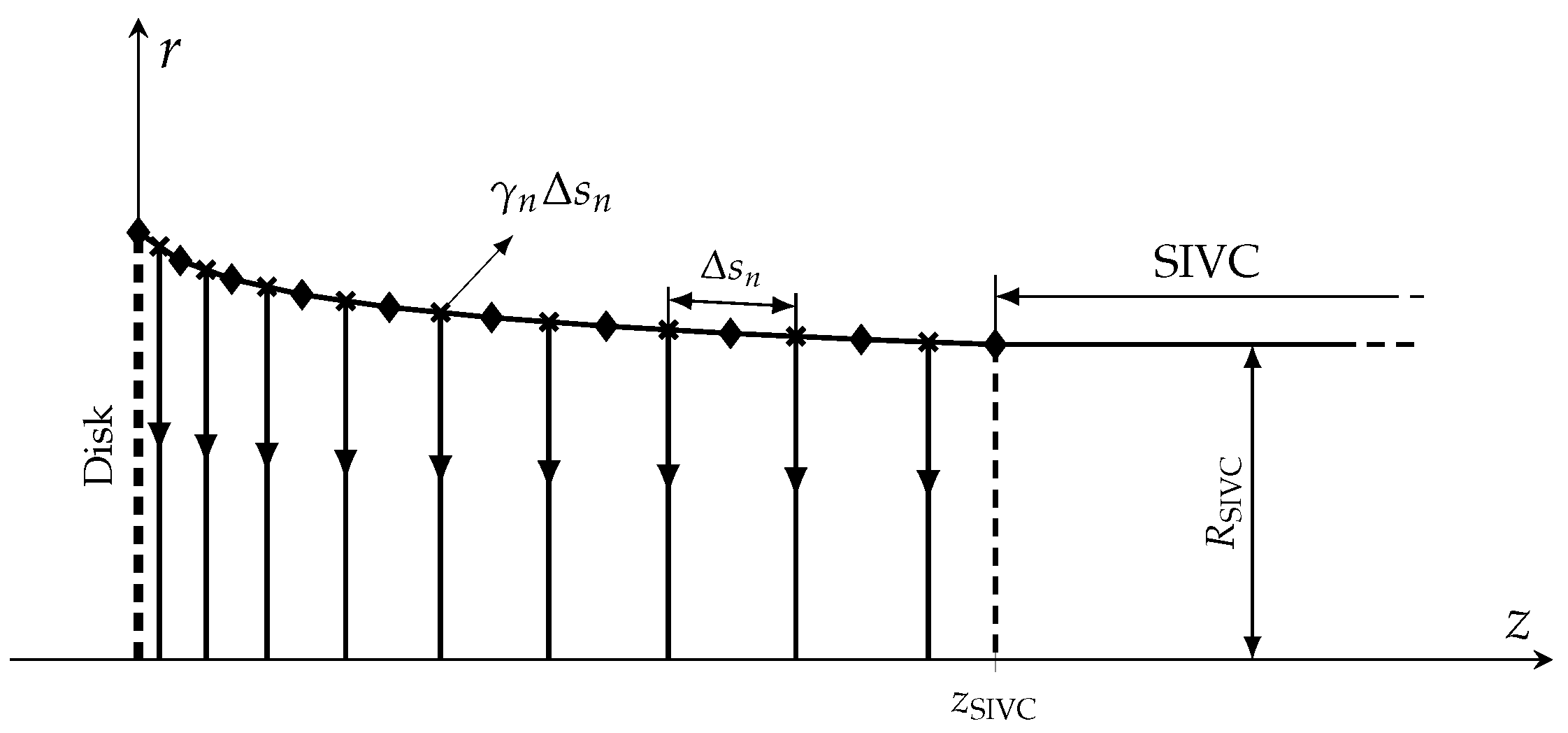
The tangential sheet vortex can be modelled as the superposition of ring vortices placed in the control points of
N annular panels. Furthermore, a semi-infinite vortex cylinder (SIVC), aimed at modelling the fully developed far wake, is also introduced.
Figure 3 shows a sketch of this model in the meridional view.
The diamonds represent the endpoints of the panels whose lengths are with . Crosses are used to denote the control points of the panels where the anticlockwise ring vortices are located. The density strength of the n-th ring-vortex, with center at and radius , is , where is obviously the unknown density strength. The SIVC begins at , while is the radius of this vortex element and is its density strength.
The overall velocity induced at the control point of the
m-th panel can be expressed as the sum of four contributions, viz. the self-induced velocity by the
m-th panel, the velocity induced by the other
ring vortices, the one induced by the SIVC, and, finally, the free stream contribution. Thus, the axial and radial velocity components at the
m-th panel can be written in dimensionless form as
respectively. In the above equation,
is the overall axial velocity induced on the
m-th panel, while
and
are the axial velocities induced on the control point of the
m-th panel by the
n-th ring vortex and by the SIVC, respectively. A similar notation is used for the radial velocities. However, in order to use Equation (
13), the velocities induced by a ring vortex and a SIVC must be evaluated. In the following, the expressions used to compute the velocity components induced by a ring vortex are first given. Then, the SIVC flow field is described.
Considering the generic point
P with coordinates
, the axial and radial velocities induced by the
n-th ring vortex at
P can be cast in the following form [
41]:
where
and
. As customary,
and
are used to denote the complete elliptic integrals of the first and second kind with modulus
. For
, the value of these two special functions can be numerically computed using several approaches, viz. series expansions, integration-based methods, duplication techniques, look-up table, polynomial approximations etcetera. All these methods show some pros and contra. For example, series expansion approaches require a significant computational cost to obtain high accuracy, while the convergence rate of integration methods is quite slow moving towards the singular point
. For this reason, the more efficient Arithmetic-Geometric Mean method [
42] is used in this work.
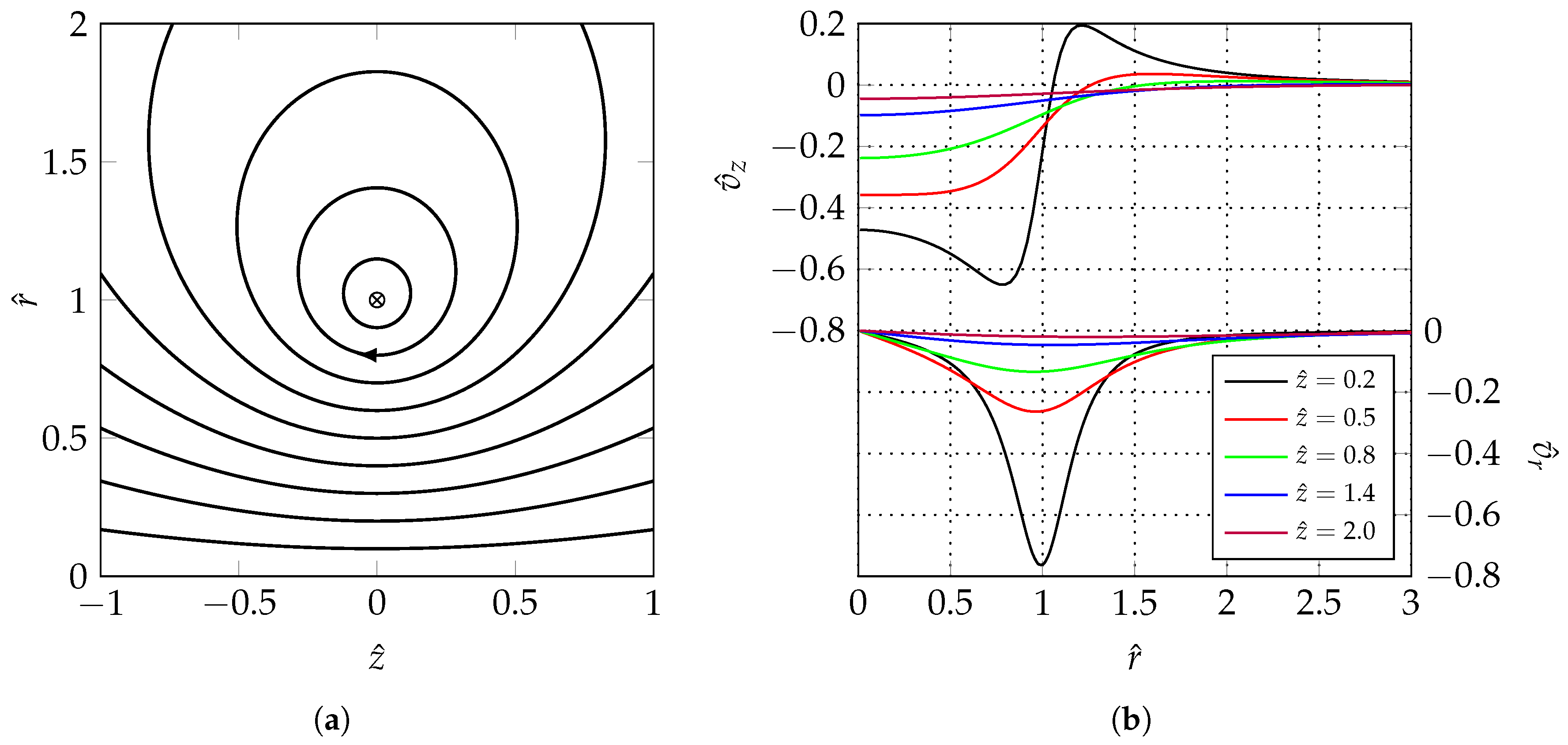
Figure 4a shows the streamlines of the flow induced by a unit strength ring vortex with center in
and unity radius. This figure also clarifies the adopted convention for the sign of the ring-vortex strength. The radial profiles of the axial and radial velocity at different axial stations are reported in
Figure 4b.
The self-induced velocity (
) of a rectilinear panel is evaluated following the approach proposed by Lewis [
43]. The latter expressed the self-induced velocity as the sum of two contributions associated with the sheet curvature in the (
r,
) and (
z,
r) planes, respectively. For the sake of simplicity, Lewis [
43] assumed that both curvatures act independently and their contributions can be estimated separately. The contribution due to the curvature in the
plane is assumed to be equal to the self-induced velocity of a planar rectilinear panel; an assumption that returns a reasonable accuracy provided
is small. The contribution associated with the
curvature can be evaluated considering the approximate Lamb [
44] formula for the self-induced velocity of a smoke ring vortex. Specifically, this contribution has been evaluated in [
45,
46] adapting the Lamb [
44] expression to a ring surface vorticity element. Having said that, the axial and radial components of the overall self-induced velocity can be written as [
43]
where
is the slope of the panel.
The last vortex element to be analyzed is the SIVC. Its induced velocity can be retrieved by directly integrating the Biot-Savart law along the lateral surface of the cylinder [
47]. By so doing, the axial and radial velocity components induced at
read
where
,
,
for
,
for
and
for
. Moreover,
is the complete elliptic integral of the third kind with modulus
and characteristic
. This special function, which is evaluated using the duplication algorithm proposed in [
48,
49], exhibits a singular behavior when
tends to the unity. However, since the quantity
goes to zero as
, the axial velocity can be also expressed through the following asymptotic relation:
Finally, to give an idea of the characteristics of the flow field induced by a SIVC,
Figure 5 shows the contours of the axial and radial velocity components along with the streamlines.
3.2. Solution Algorithm
Having said that, the iterative solution algorithm used to evaluate the unknown wake shape and the density strength distribution can be outlined as follows. The thrust coefficient is a user-defined input parameter. Thus, the SIVC density strength is directly evaluated by Equation (
12) which returns
. Please note that this value remains the same throughout the whole solution procedure. Then, the panel density strengths and the wake shape are initialized imposing
,
and
for
. The axial coordinates of the panel endpoints are evaluated adopting a cosine stretching law with a higher panel density in the proximity of the disk rim.
The iterative procedure begins locating the
N control points in the middle of each panel. Then, the overall flow field is evaluated there using the velocity expressions (
14)–(
20) in Equation (
13). The density strength distribution is now updated imposing the free-force condition (
10) which gives
, where
. As previously stated, the wake shape is updated requiring that all panels are aligned with the overall flow field. This is simply achieved computing the change in the endpoint coordinates as
and
. Then, the coordinates of the endpoints are evaluated by integration through
with
and
. In this wake updating process, an under-relaxation factor is typically used to preserve the stability of the iterative procedure, especially for high
values. Finally, the radial coordinate of the last endpoint is used to update
and convergence is checked. Then, a new iteration is started by computing the coordinates of the newly obtained control points and repeating the previously described steps.
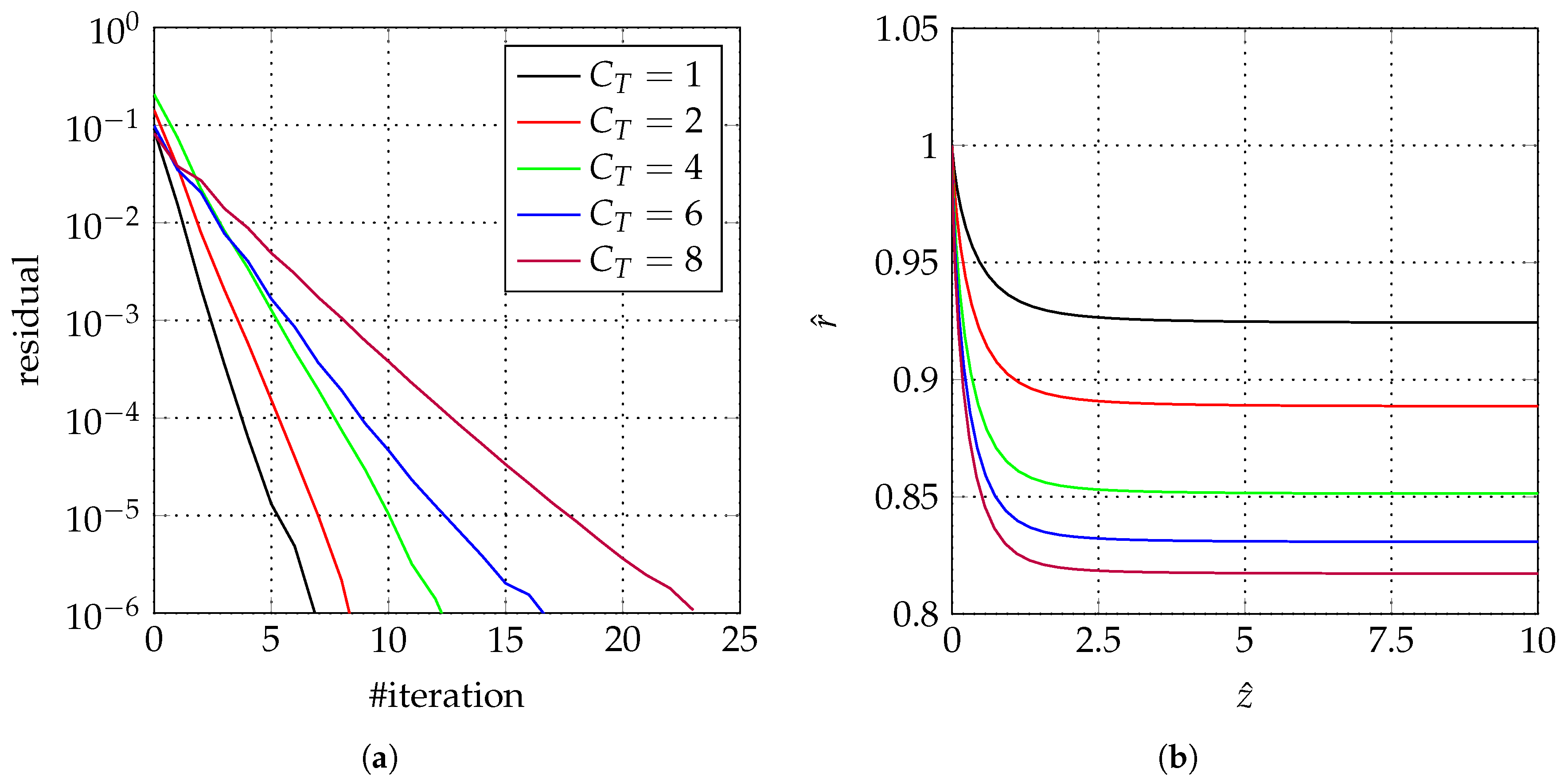
3.3. Analysis of the Results
Figure 6 shows the convergence history and the final wake shape for different values of the thrust coefficient. The residual is defined as the magnitude of the difference between the values of the SIVC radius at two successive iterations. To preserve the stability of the iterative procedure, an under-relaxation factor
is introduced for high values of
. Specifically, considering the cases reported in
Figure 6, no under-relaxation is used for
, 2 and 4, while
and 0.3 is used for
and
, respectively.
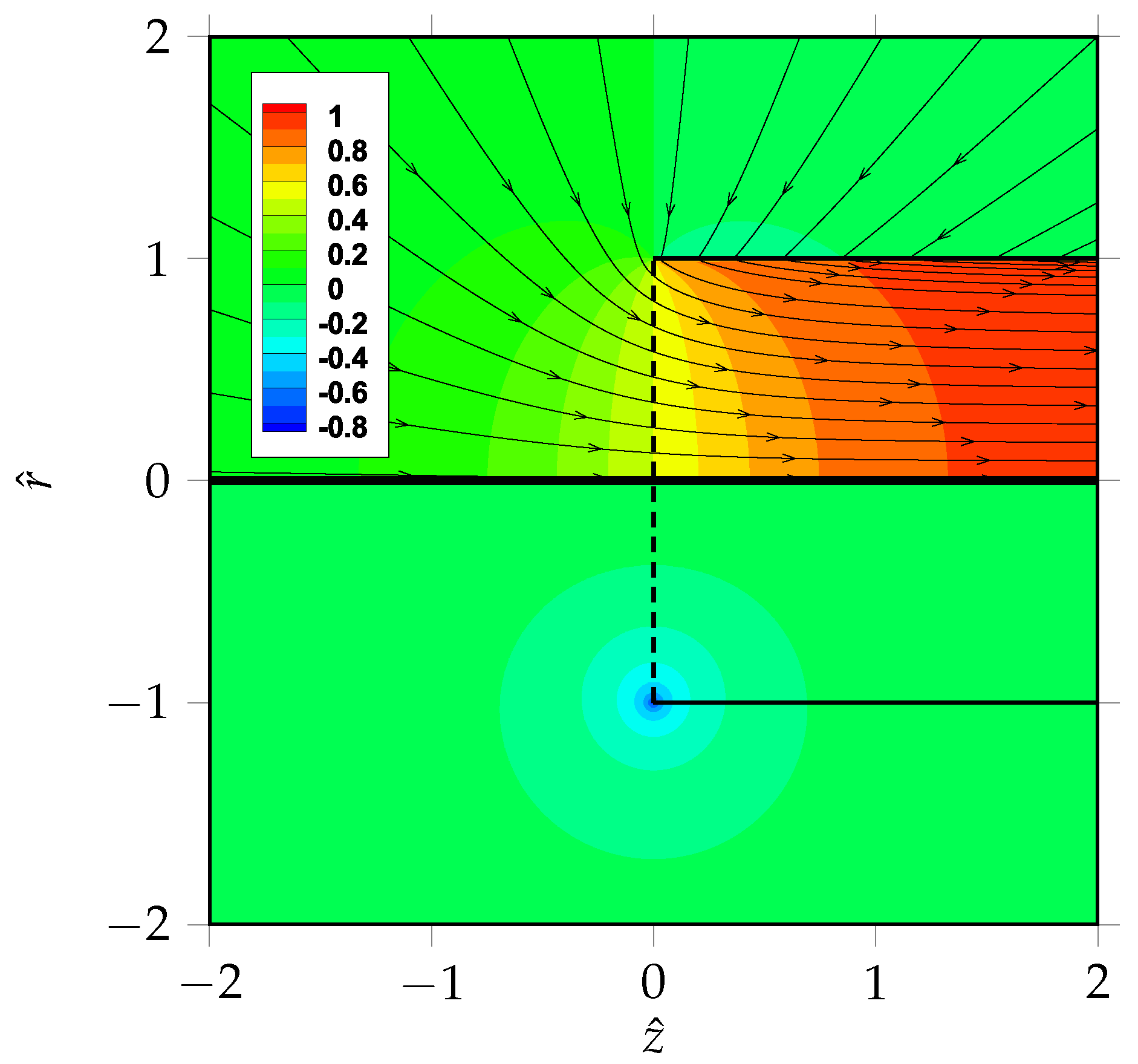
Finally, to give an idea of the flow field induced by a uniformly loaded disk without wake rotation, the contours of the velocity magnitude and pressure coefficient are reported in
Figure 7 along with the vector field and the streamlines. The thrust coefficient is set equal to 5, while as customary, the pressure coefficient is defined as
. The figure highlights the significant contraction of the wake for a highly loaded disk and the jet of the propeller. Also note that according to the free-force condition, no pressure jump occurs at the wake outer edge. Instead, along this edge, a velocity discontinuity exists due to the presence of the wake sheet vortex.
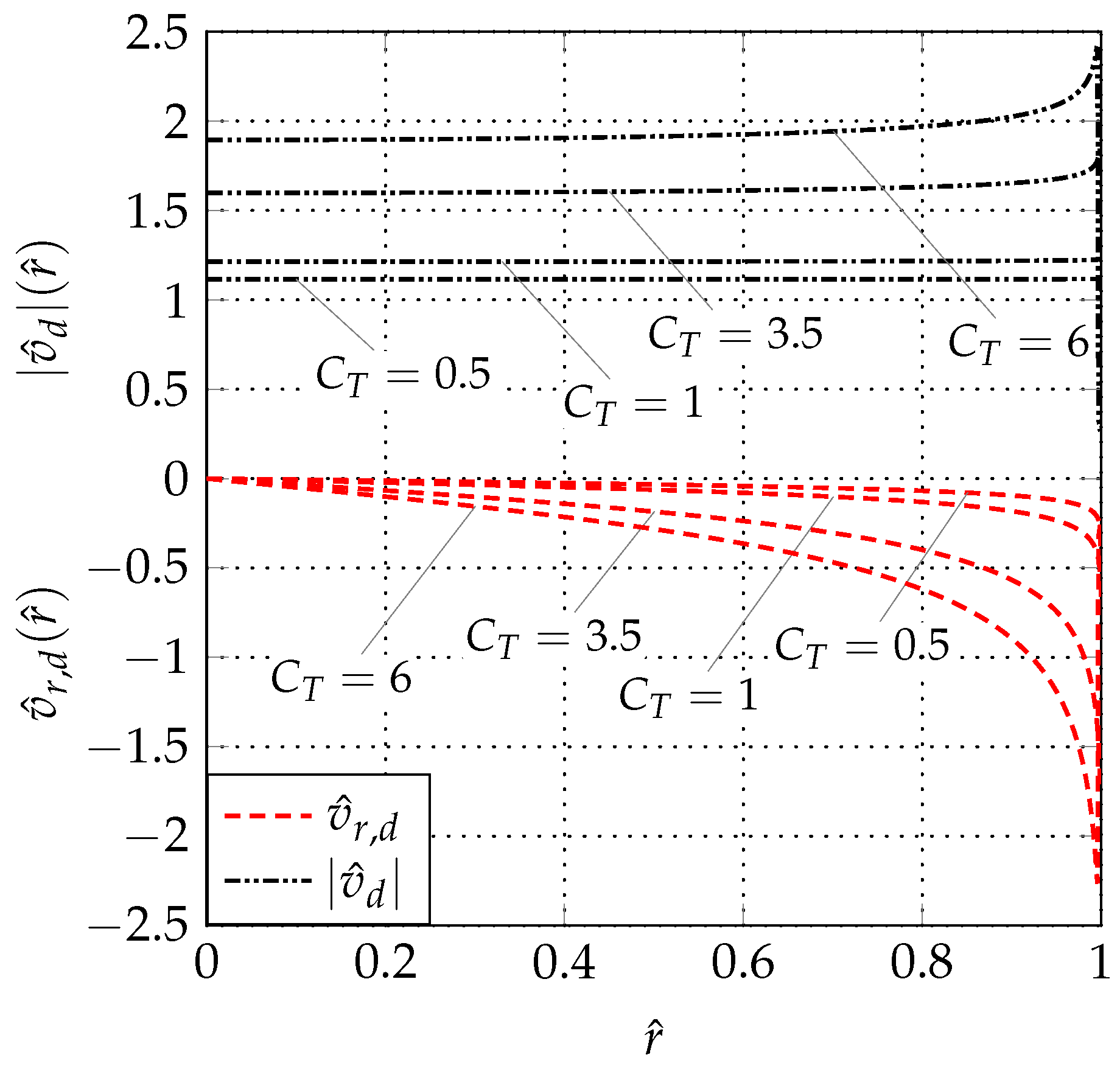
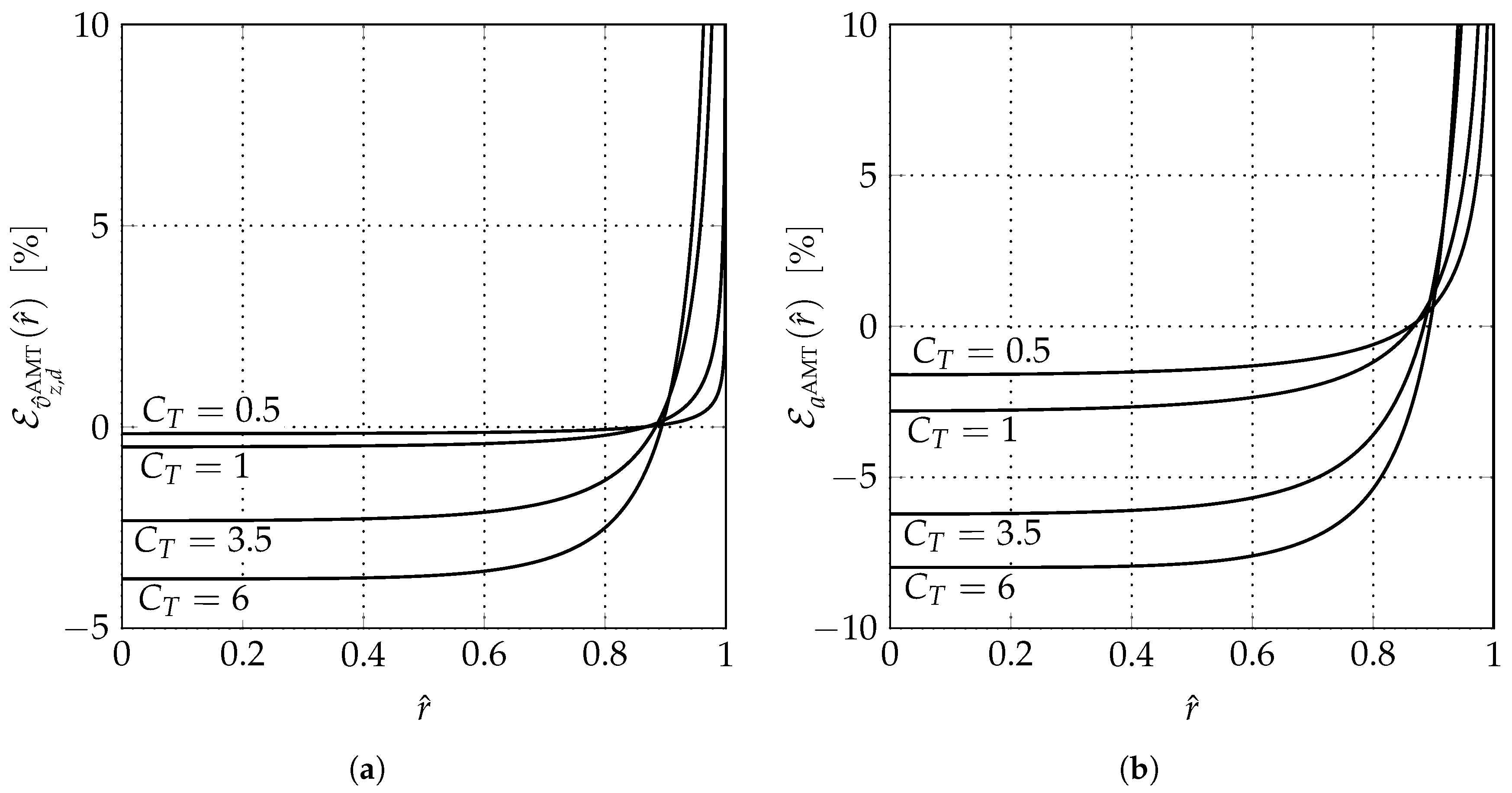
5. Conclusions
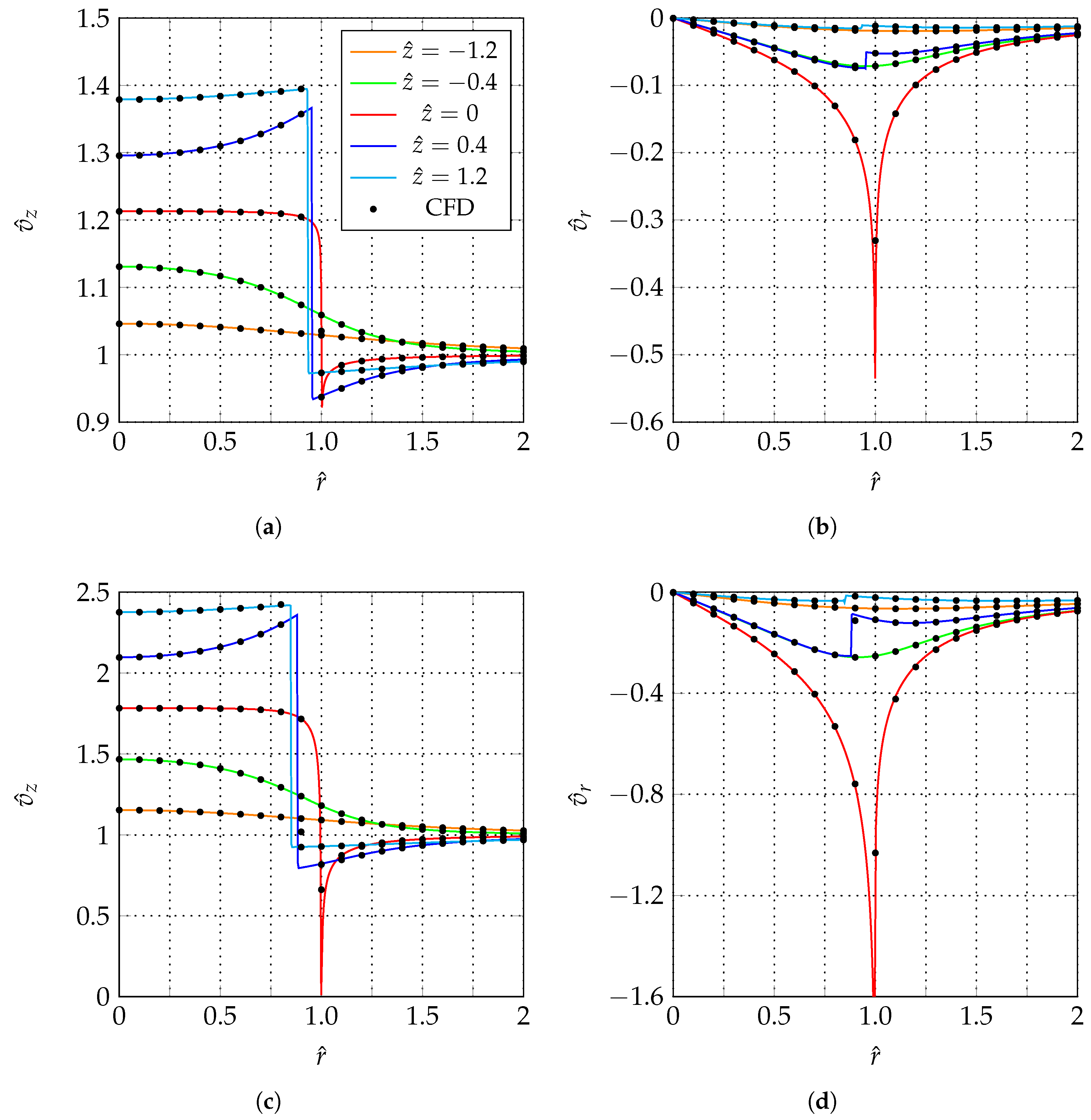
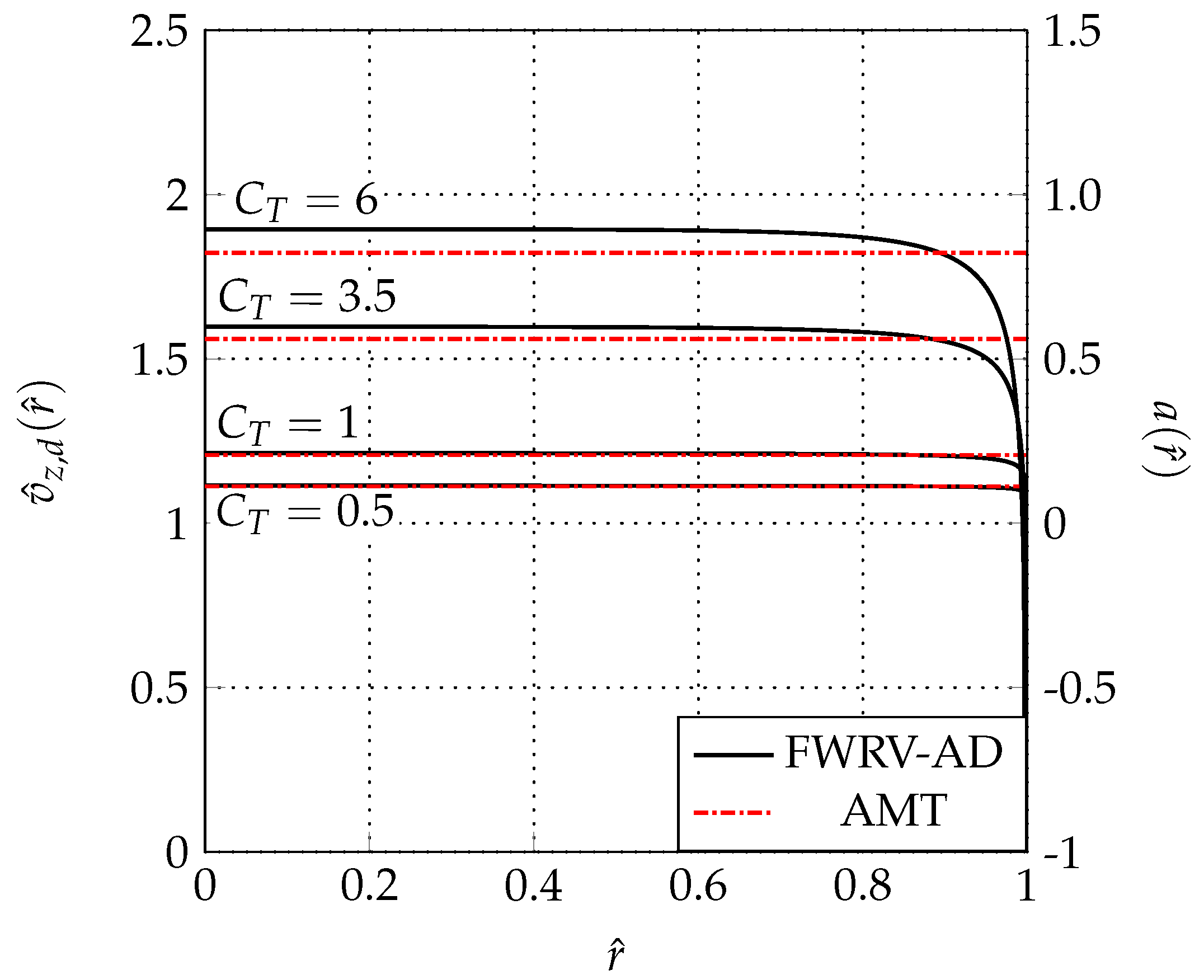
A free-wake ring-vortex actuator disk method is used to evaluate the errors embodied in the AMT when applied to a uniformly loaded propeller. The method, which represents the wake as a set of ring vortices, has been presented along with a discussion on its convergence and stability properties. It has been also verified in terms of global performance coefficients against the AMT which returns exact values of these quantities. For , the differences between the numerical and the exact values are globally less or equal than 1‰. A further verification is offered comparing the FWRV-AD results with those of a CFD actuator disk approach. For and 0, a very good agreement has been found between the radial distributions of the velocity components as evaluated by the two methods. Then, the FWRV-AD model has been used to quantify the errors in and introduced by the simplified version of the AMT. It has been shown that , despite the uniform load, is far from being uniform, especially at the tip where it exhibits a singular behavior. Moreover, as in the case of an energy-extracting disk, the velocity magnitude is uniform along the disk for . However, for , is also not uniform with a remarkable increment moving towards the tip. Significant errors have been detected also in the remaining part of the disk. At the hub (resp. at the mid-span region) the relative error in a is (resp. −2.56%) when , while it increases to (resp. −7.84%) for . Finally, the velocity magnitude at the disk is also not uniform for .