Characterization of the Unsteady Aerodynamics of Optimized Turbine Blade Tips through Modal Decomposition Analysis †
Abstract
1. Introduction
2. Research Methodology
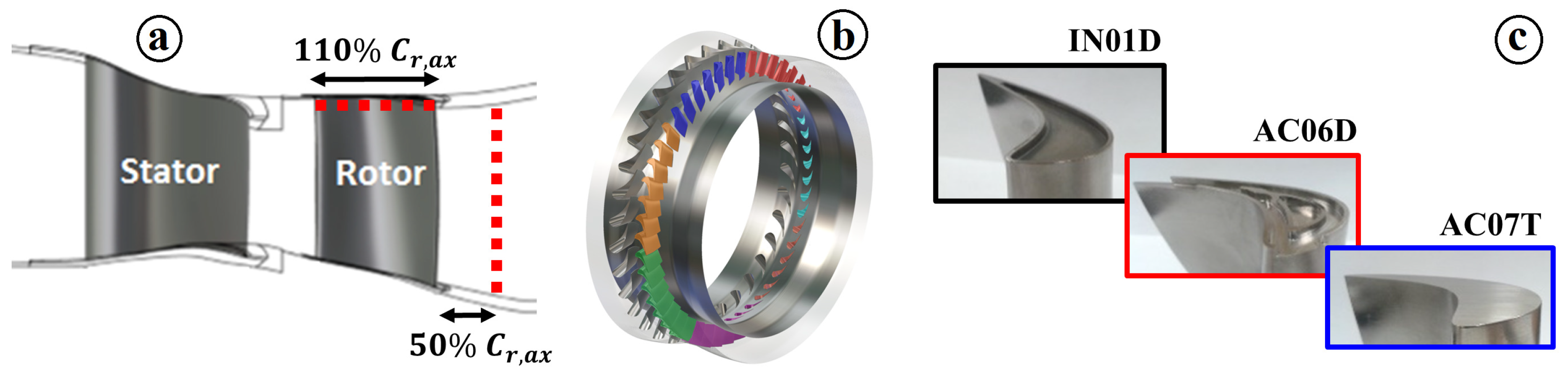
2.1. Experimental Setup
2.1.1. Test Article
2.1.2. Operating Conditions
2.1.3. Measurement Setup
2.1.4. Signal Acquisition
2.2. Numerical Setup
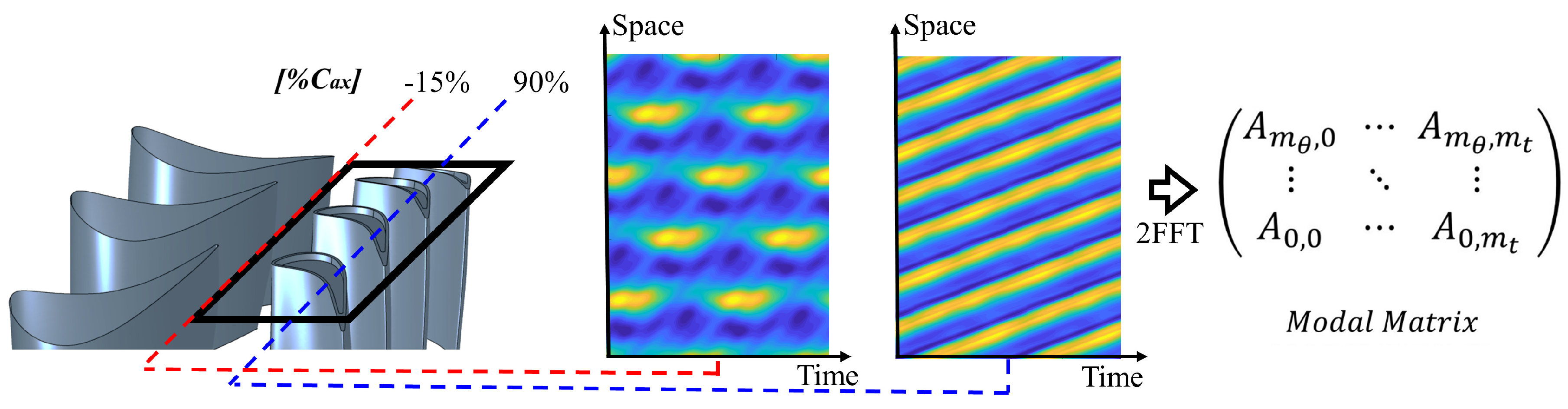
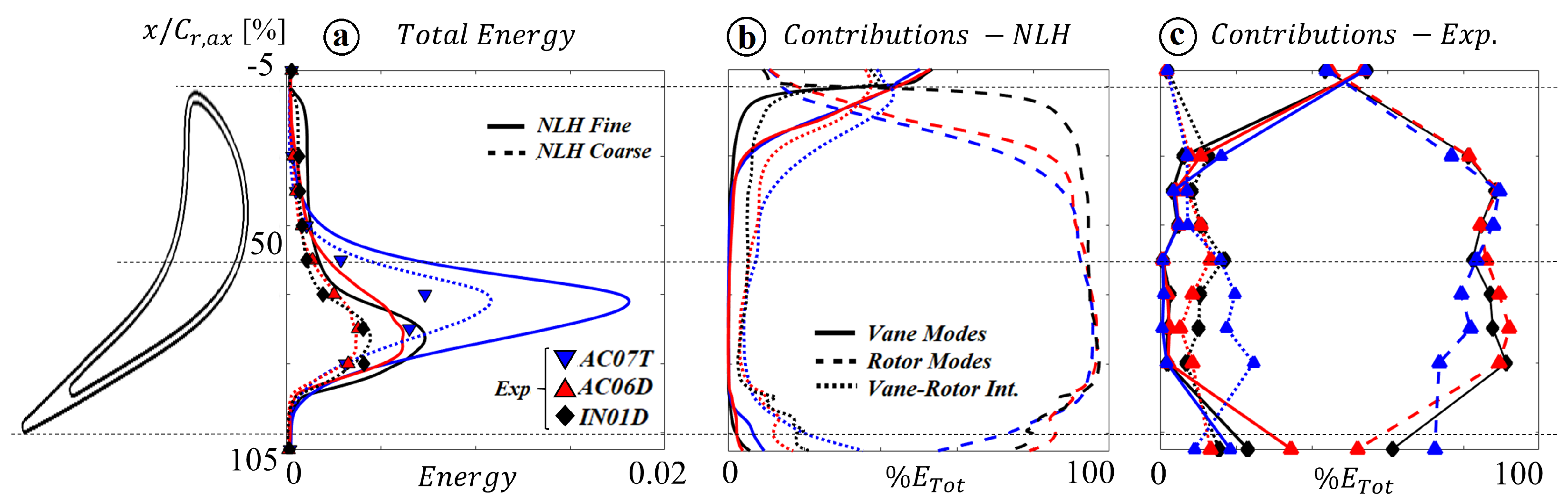
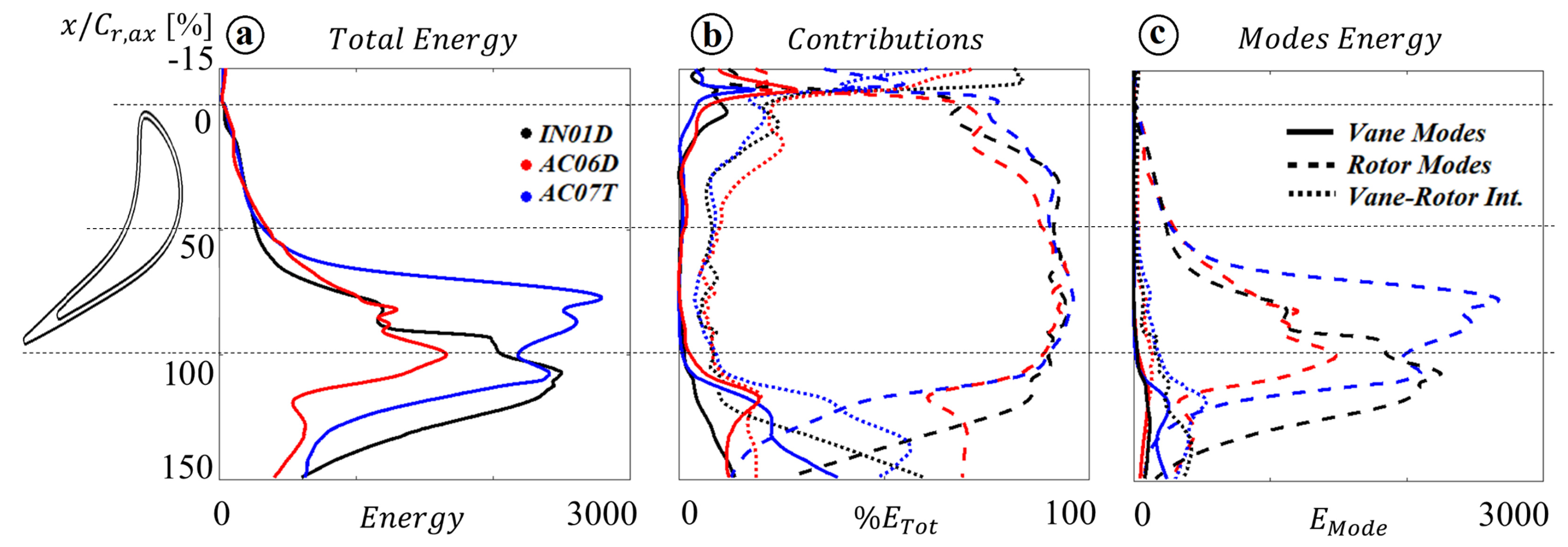
2.3. Modal Analysis
3. Results
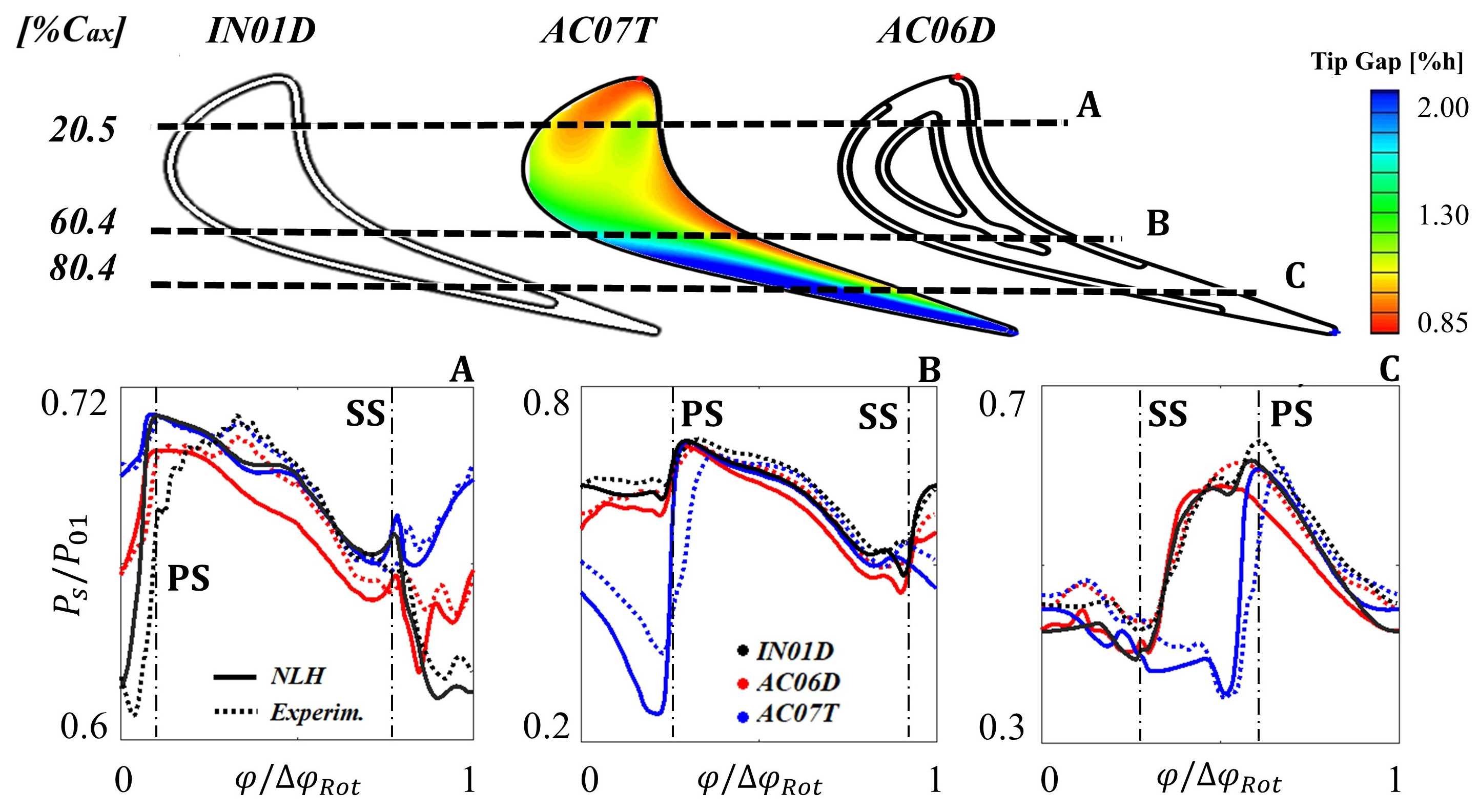
3.1. Over-Tip Flow
3.1.1. Blade Passing Effect
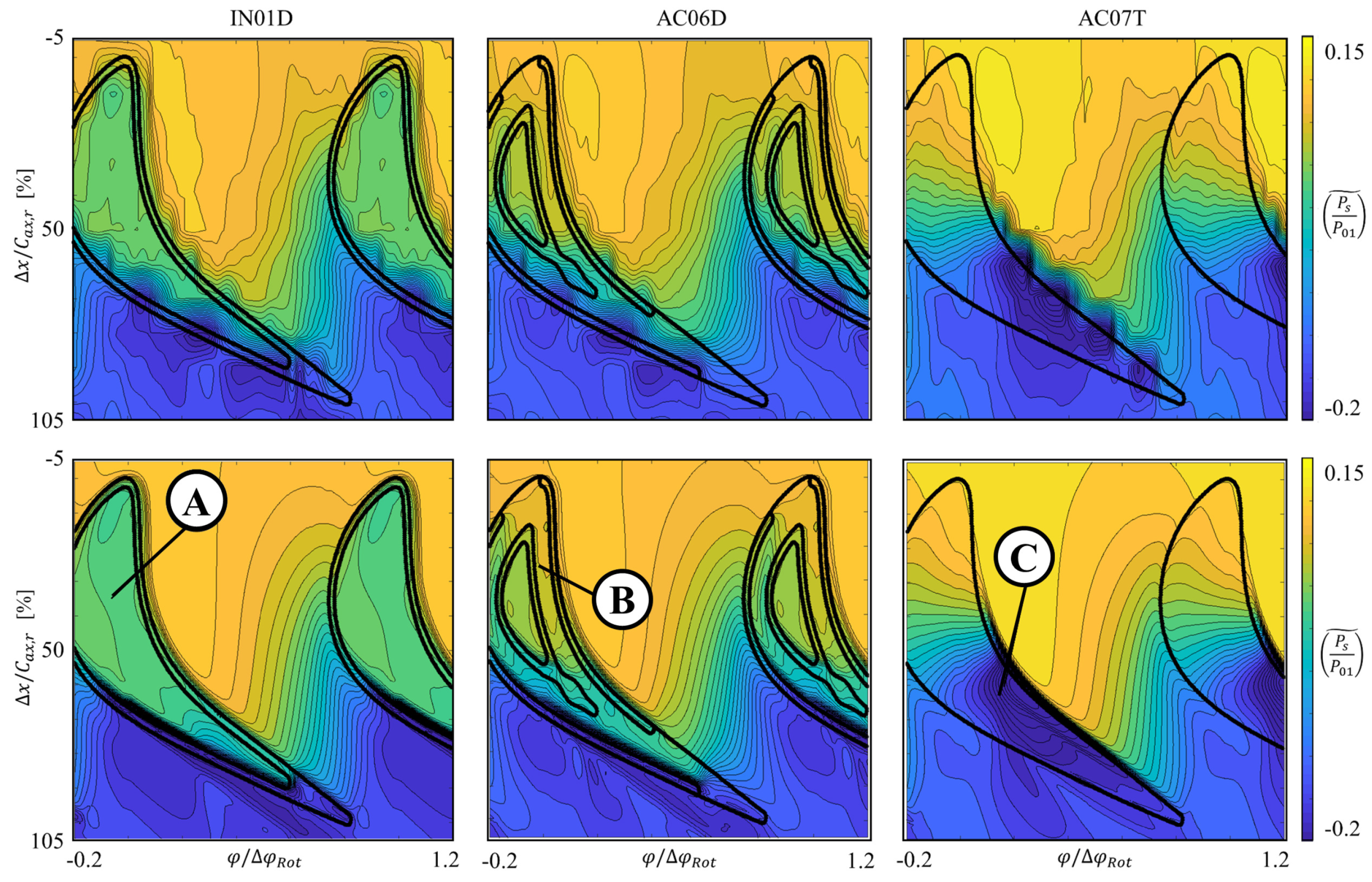
3.1.2. Casing Pressure Field
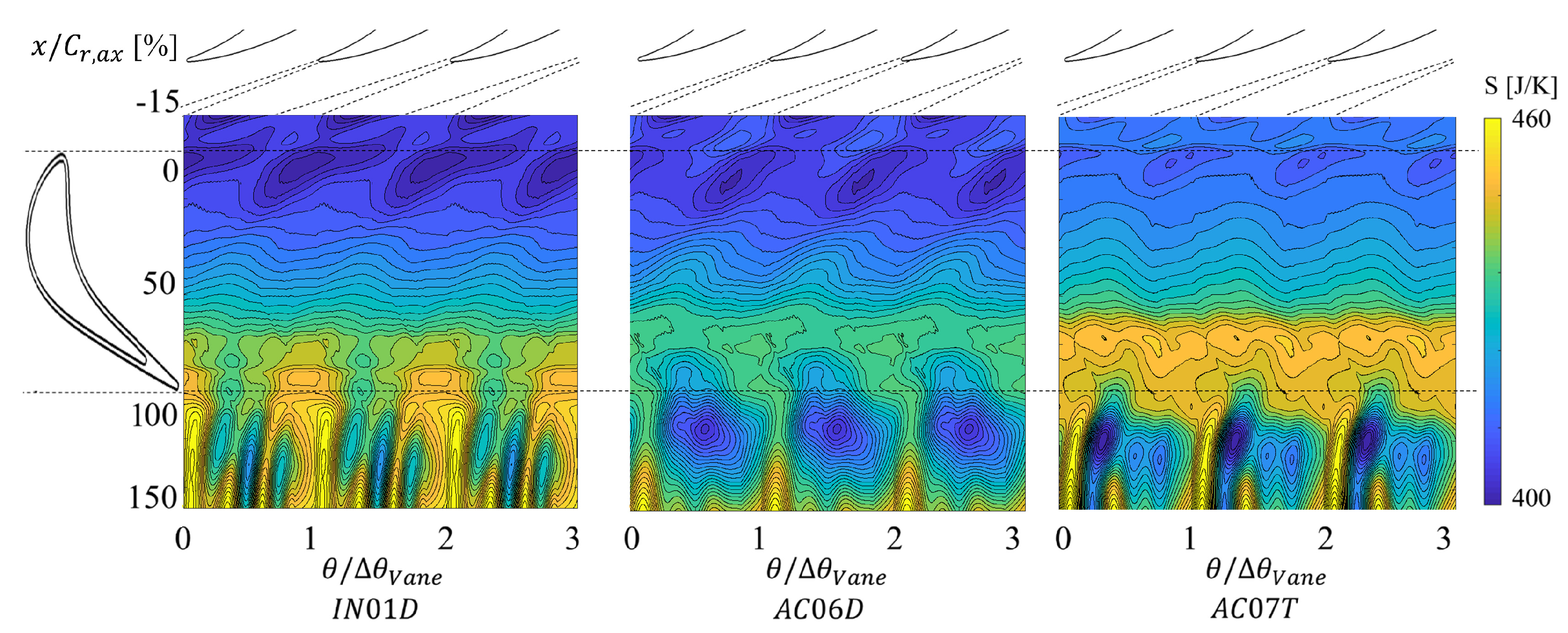
3.1.3. Mid-gap Entropy Field
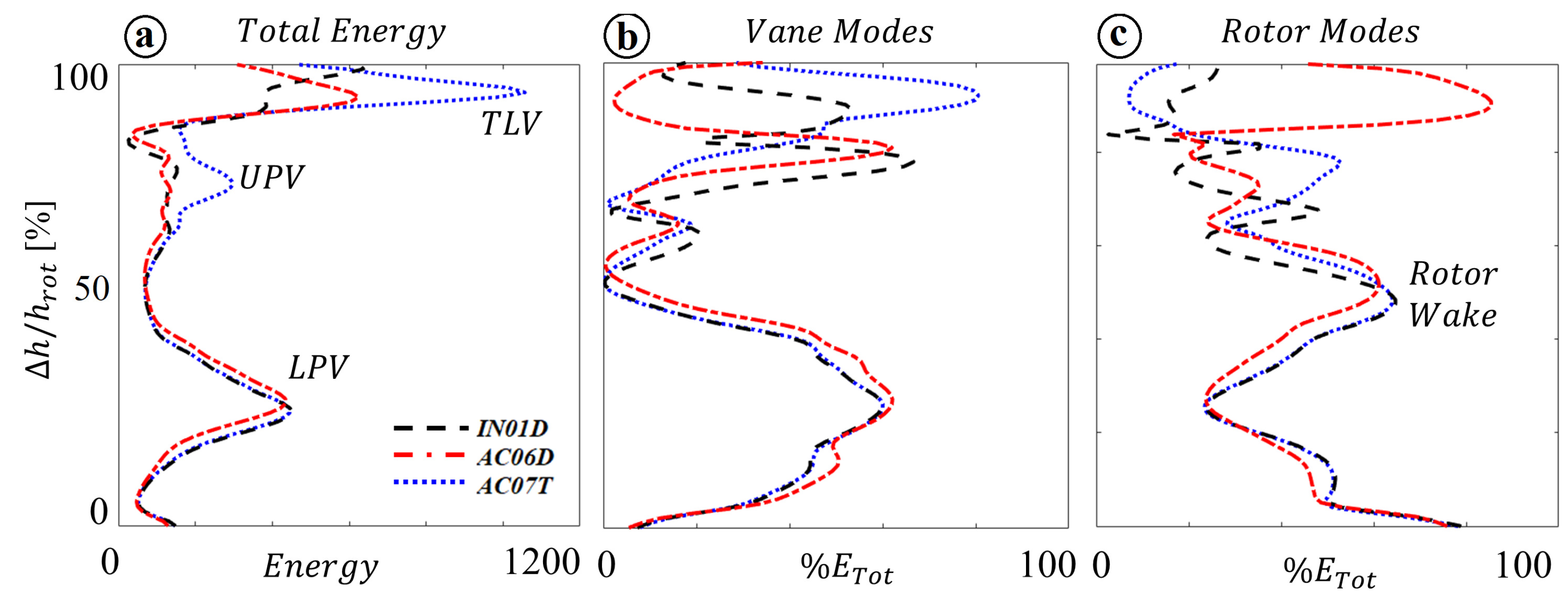
3.2. Stage Outlet Flow
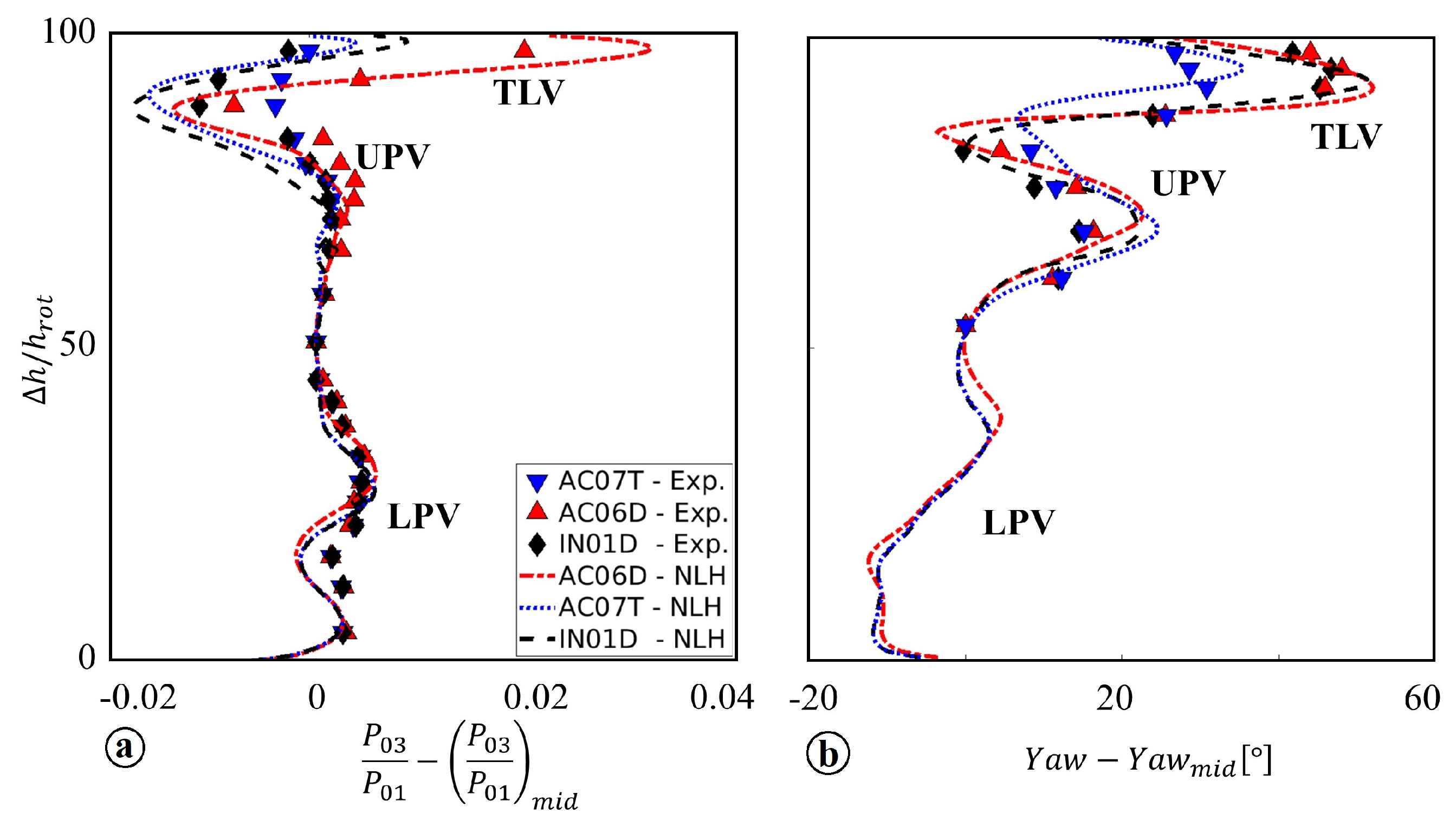
3.2.1. Time Average Radial Profiles
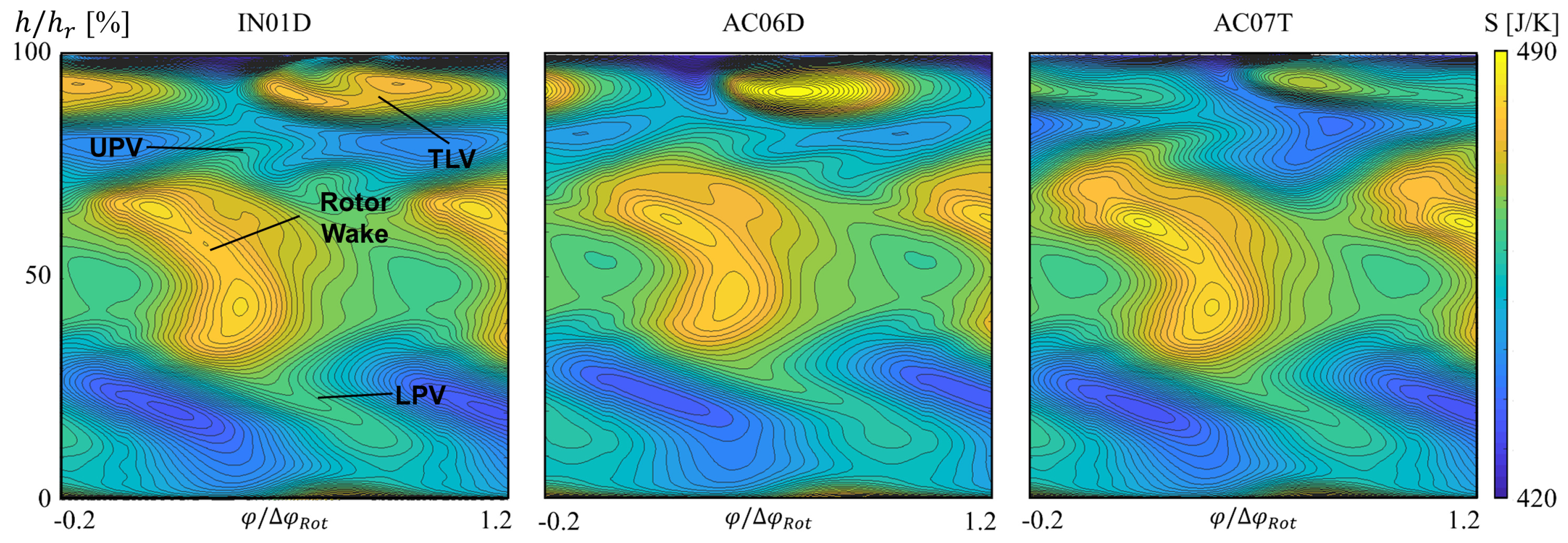
3.2.2. Rotor Entropy Field
3.2.3. Time-Mean Entropy Field
3.3. Modal Decomposition
3.3.1. Over-Tip Modes
3.3.2. Outlet Modes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Amplitude |
| Absolute flow angle () | |
| Rotor axial chord (m) | |
| E | Modal Energy |
| Rotor phase | |
| Rotor blade span (m) | |
| High pressure turbine | |
| Lower passage vortex | |
| m | Mode number |
| Stage inlet total pressure (bar) | |
| Static pressure (bar) | |
| S | Entropy (J/K) |
| t | Time |
| Vane phase | |
| Tip leakage vortex | |
| Upper passage vortex | |
| Non-dimensional first cell size |
References
- Bindon, J.P. Pressure distributions in the tip clearance region of an unshrouded axial turbine as affecting the problem of tip burnout. In Proceedings of the ASME 1987 International Gas Turbine Conference and Exhibition. American Society of Mechanical Engineers, Anaheim, CA, USA, 31 May–4 June 1987. [Google Scholar]
- Collins, M.; Chana, K.; Povey, T. Improved Methodologies for Time-Resolved Heat Transfer Measurements, Demonstrated on an Unshrouded Transonic Turbine Casing. J. Turbomach. 2016, 138, 111007. [Google Scholar] [CrossRef]
- Bunker, R.S. A Review of Turbine Blade Tip Heat Transfer. Ann. N. Y. Acad. Sci. 2001, 934, 64–79. [Google Scholar] [CrossRef]
- Shyam, V.; Ameri, A.; Chen, J.P. Analysis of Unsteady Tip and Endwall Heat Transfer in a Highly Loaded Transonic Turbine Stage. J. Turbomach. 2011, 134, 041022. [Google Scholar] [CrossRef]
- Hofer, T.; Arts, T. Aerodynamic Investigation of the Tip Leakage Flow for Blades With Different Tip Squealer Geometries at Transonic Conditions. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009; pp. 1051–1061. [Google Scholar] [CrossRef]
- Kwak, J.S.; Ahn, J.; Han, J.C.; Lee, C.P.; Bunker, R.S.; Boyle, R.; Gaugler, R. Heat Transfer Coefficients on the Squealer Tip and Near-Tip Regions of a Gas Turbine Blade With Single or Double Squealer. J. Turbomach. 2003, 125, 778–787. [Google Scholar] [CrossRef]
- Heyes, F.J.G.; Hodson, H.P.; Dailey, G.M. The Effect of Blade Tip Geometry on the Tip Leakage Flow in Axial Turbine Cascades. J. Turbomach. 1992, 114, 643–651. [Google Scholar] [CrossRef]
- Shyam, V.; Ameri, A. Comparison of Various Supersonic Turbine Tip Designs to Minimize Aerodynamic Loss and Tip Heating. In Proceedings of the TURBO EXPO 2011, Vancouver, BC, Canada, 6–10 June 2011; pp. 887–895. [Google Scholar] [CrossRef]
- Zhang, Q.; He, L. Tip-Shaping for HP Turbine Blade Aerothermal Performance Management. J. Turbomach. 2013, 135, 051025. [Google Scholar] [CrossRef]
- Dring, R.; Joslyn, H.D.; Hardin, L.; Wagner, J. Turbine rotor-stator interaction. J. Eng. Power 1982, 104, 729–742. [Google Scholar] [CrossRef]
- Joslyn, D.; Dring, R. Three-Dimensional Flow in an Axial Turbine: Part 1—Aerodynamic Mechanisms. J. Turbomach. 1992, 114, 61–70. [Google Scholar] [CrossRef]
- Zaccaria, M.; Lakshminarayana, B. An eXperimental Investigation of Steady and Unsteady Flow Field in an Axial Flow Turbine, NASA Contractor Report 4778, 1997. Available online: ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19970021336.pdf (accessed on 25 May 2019).
- Dénos, R.; Paniagua, G. Effect of vane-rotor interaction on the unsteady flowfield downstream of a transonic high pressure turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2005, 219, 431–442. [Google Scholar] [CrossRef]
- Krishnababu, S.; Newton, P.; Dawes, W.; Lock, G.D.; Hodson, H.; Hannis, J.; Whitney, C. Aerothermal Investigations of Tip Leakage Flow in Axial Flow Turbines—Part I: Effect of Tip Geometry and Tip Clearance Gap. J. Turbomach. 2009, 131, 011006. [Google Scholar] [CrossRef]
- Thorpe, S.; Yoshino, S.; Ainsworth, R.; Harvey, N. An investigation of the heat transfer and static pressure on the over-tip casing wall of an axial turbine operating at engine representative flow conditions (II). Time-resolved results. Int. J. Heat Fluid Flow 2004, 25, 945–960. [Google Scholar] [CrossRef]
- Cernat, B.C.; Pátỳ, M.; De Maesschalck, C.; Lavagnoli, S. Experimental and Numerical Investigation of Optimized Blade Tip Shapes—Part I: Turbine Rainbow Rotor Testing and Numerical Methods. J. Turbomach. 2019, 141, 011006. [Google Scholar] [CrossRef]
- Courtiade, N.; Ottavy, X.; Gourdain, N. Modal decomposition for the analysis of the rotor-stator interactions in multistage compressors. J. Therm. Sci. 2012, 21, 276–285. [Google Scholar] [CrossRef]
- Sieverding, C.; Arts, T. The VKI compression tube annular cascade facility CT3. In Proceedings of the ASME 1992 International Gas Turbine and Aeroengine Congress and Exposition, Cologne, Germany, 1–4 June 1992. [Google Scholar]
- Paniagua, G.; Sieverding, C.; Arts, T. Review of the von Karman Institute compression tube facility for turbine research. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- De Maesschalck, C.; Lavagnoli, S.; Paniagua, G. Blade tip carving effects on the aerothermal performance of a transonic turbine. J. Turbomach. 2015, 137, 021005. [Google Scholar] [CrossRef]
- De Maesschalck, C.; Lavagnoli, S.; Paniagua, G.; Verstraete, T.; Olive, R.; Picot, P. Heterogeneous Optimization Strategies for Carved and Squealer-Like Turbine Blade Tips. J. Turbomach. 2016, 138, 121011. [Google Scholar] [CrossRef]
- Cernat, B.C.; Paty, M.; Lavagnoli, S. On the Unsteady Aerodynamics of a High-Speed Turbine with Squealer Blade Tips. In Proceedings of the Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; p. 4434. [Google Scholar]
- Kupferschmied, P.; Köppel, P.; Gizzi, W.; Roduner, C.; Gyarmathy, G. Time-resolved flow measurements with fast-response aerodynamic probes in turbomachines. Meas. Sci. Technol. 2000, 11, 1036. [Google Scholar] [CrossRef]
- Lakshminarayana, B. Fluid Dynamics and Heat Transfer of Turbomachinery; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Pátỳ, M.; Cernat, B.; De Maesschalck, C.; Lavagnoli, S. Experimental and Numerical Investigation of Optimized Blade Tip Shapes: Part II—Tip Flow Analysis and Loss Mechanisms. J. Turbomach. 2019, 141, 011006. [Google Scholar] [CrossRef]
- Tyler, J.M.; Sofrin, T.G. Axial Flow Compressor Noise Studies; Technical Report, SAE Technical Paper; SAE: Warrendale, PA, USA, 1962. [Google Scholar]
- Lengani, D.; Spataro, R.; Peterleithner, J.; Göttlich, E. Unsteady Flow Evolution Through a Turning Midturbine Frame Part 2: Spectral Analysis. J. Propuls. Power 2015, 31, 1597–1606. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Cernat, B.C.; Lavagnoli, S. Characterization of the Unsteady Aerodynamics of Optimized Turbine Blade Tips through Modal Decomposition Analysis. Int. J. Turbomach. Propuls. Power 2019, 4, 12. https://doi.org/10.3390/ijtpp4020012
Cernat BC, Lavagnoli S. Characterization of the Unsteady Aerodynamics of Optimized Turbine Blade Tips through Modal Decomposition Analysis. International Journal of Turbomachinery, Propulsion and Power. 2019; 4(2):12. https://doi.org/10.3390/ijtpp4020012
Chicago/Turabian StyleCernat, Bogdan C., and Sergio Lavagnoli. 2019. "Characterization of the Unsteady Aerodynamics of Optimized Turbine Blade Tips through Modal Decomposition Analysis" International Journal of Turbomachinery, Propulsion and Power 4, no. 2: 12. https://doi.org/10.3390/ijtpp4020012
APA StyleCernat, B. C., & Lavagnoli, S. (2019). Characterization of the Unsteady Aerodynamics of Optimized Turbine Blade Tips through Modal Decomposition Analysis. International Journal of Turbomachinery, Propulsion and Power, 4(2), 12. https://doi.org/10.3390/ijtpp4020012





