Effect of a Recirculating Type Casing Treatment on a Highly Loaded Axial Compressor Rotor
Abstract
:1. Introduction
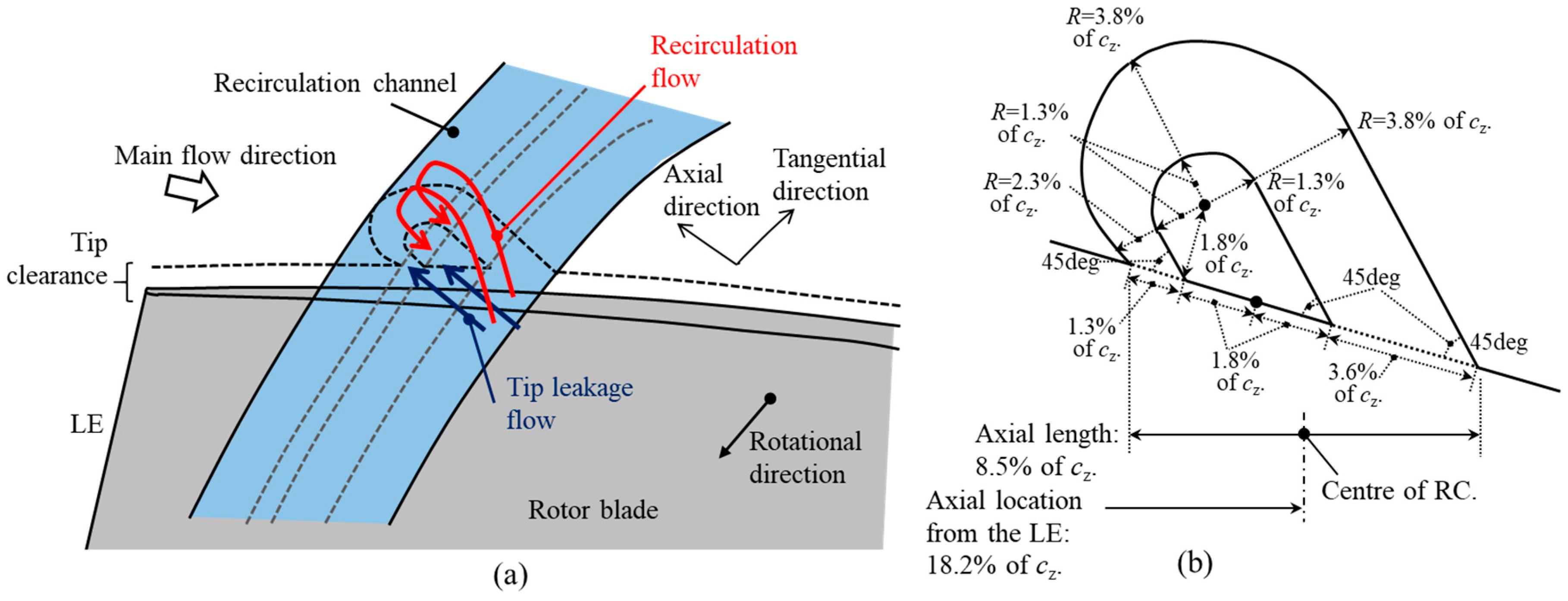
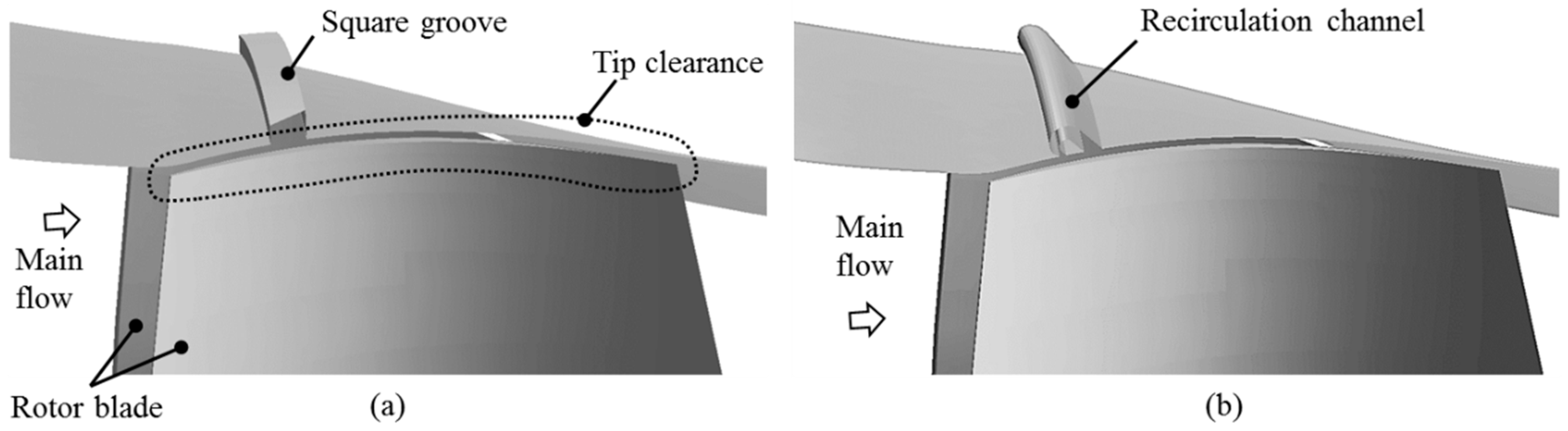
2. Axisymmetric Recirculation Channel Design for Axial Rotors
3. Numerical Approach for Validating the Design
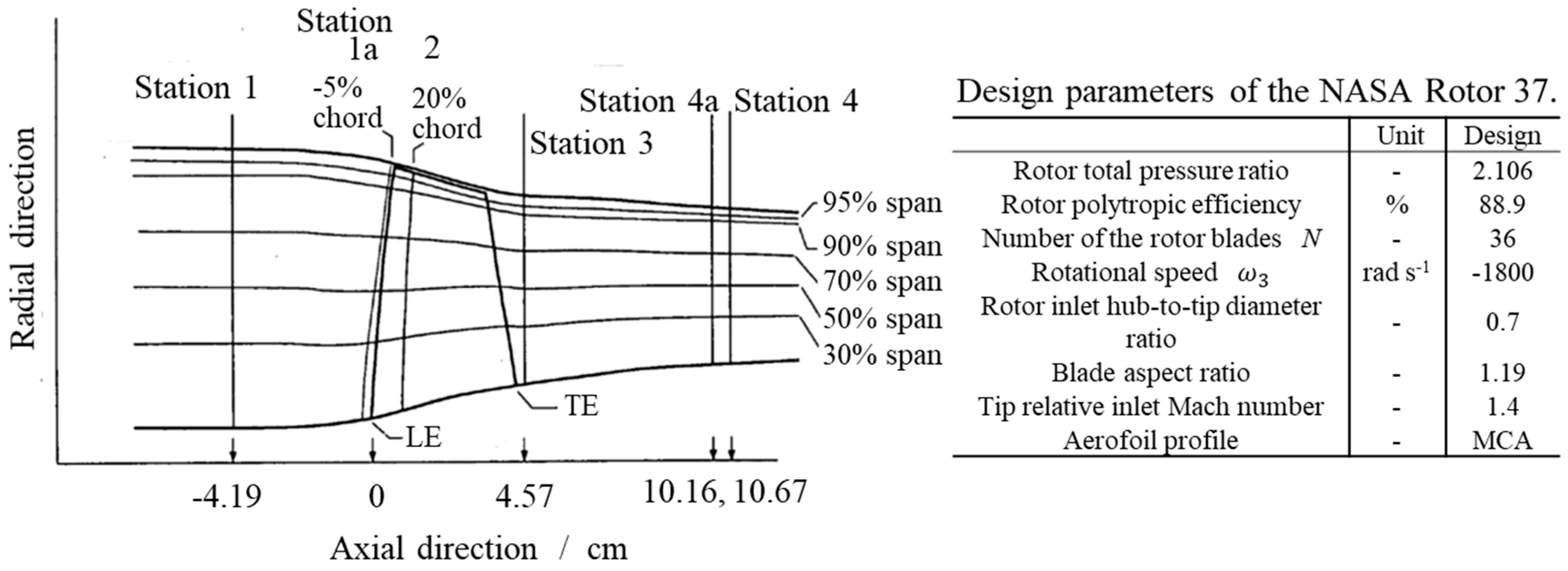
3.1. Axial Compressor Test Case
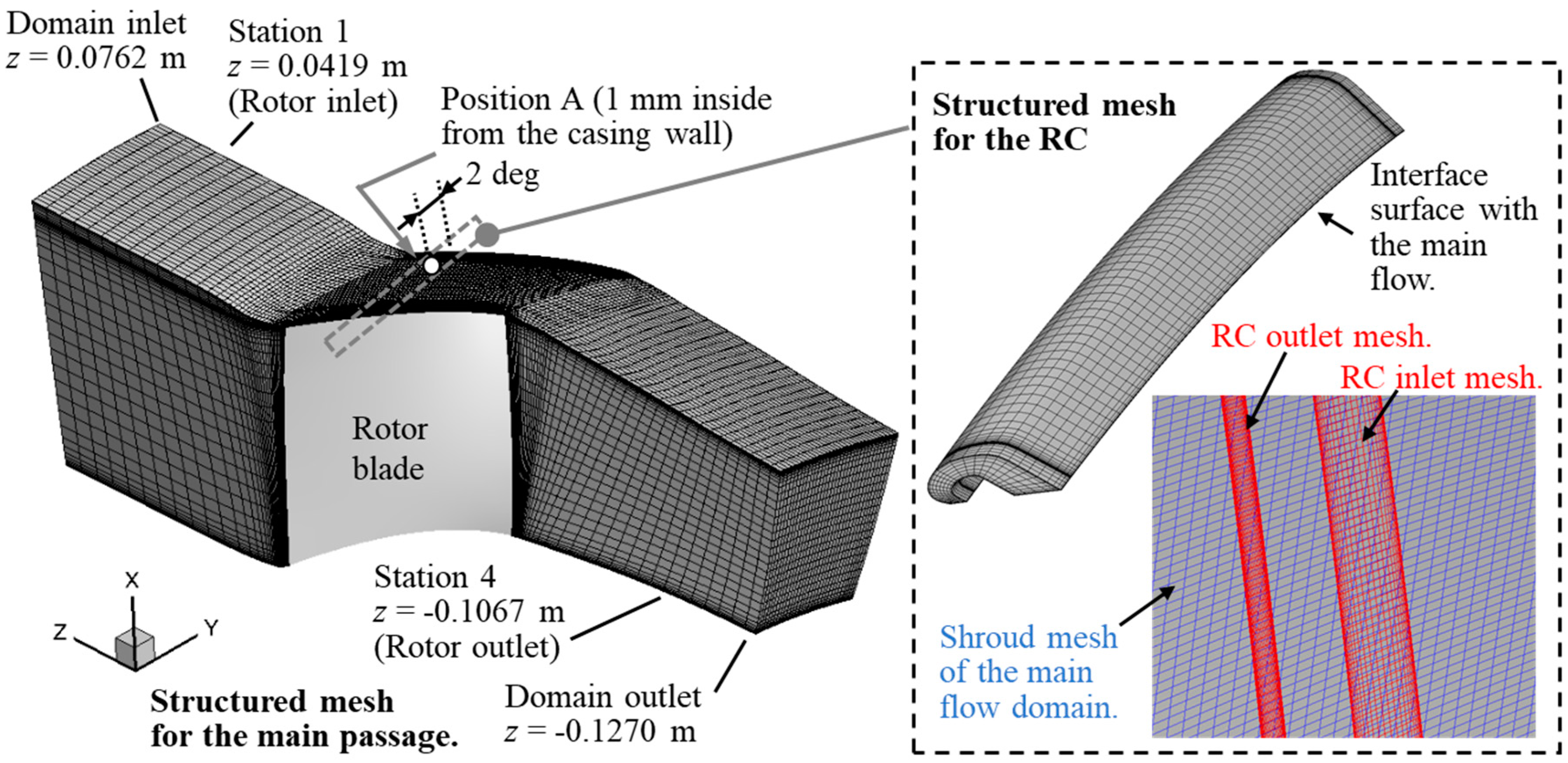
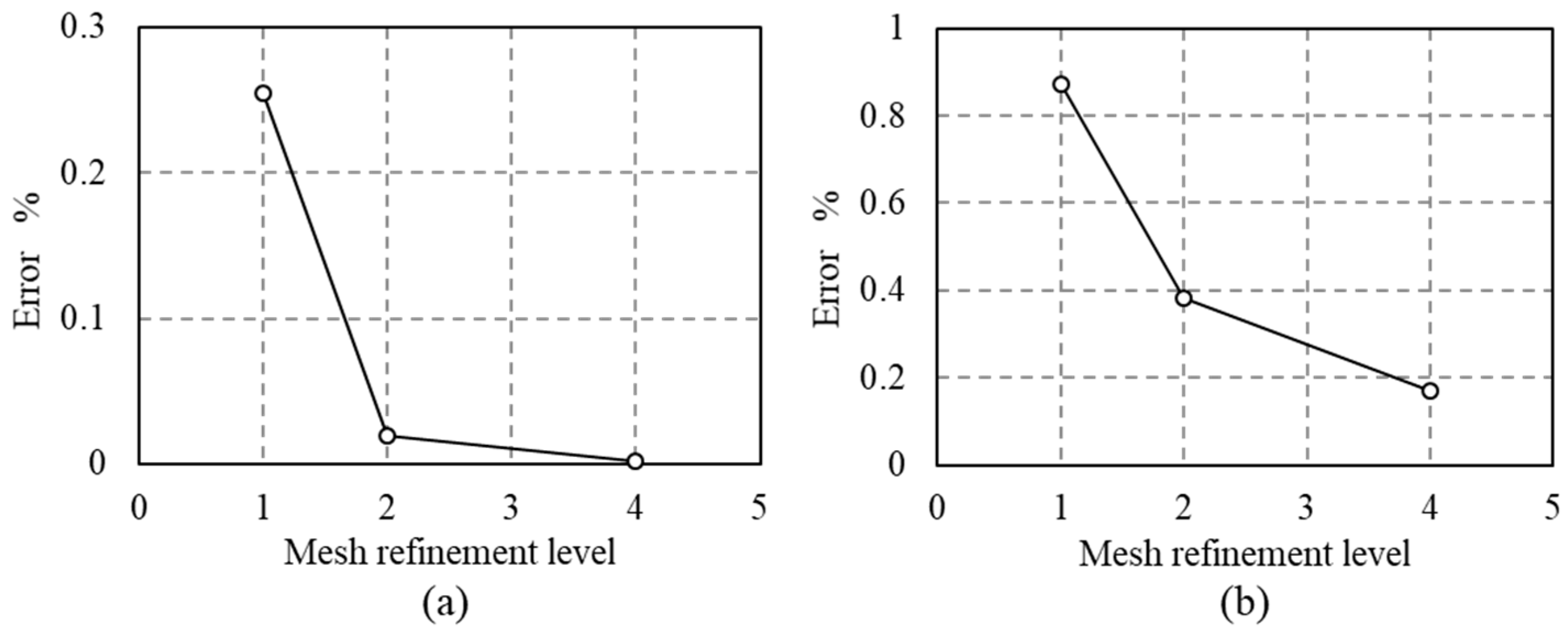
3.2. Computational Grid
3.3. Numerical Modeling
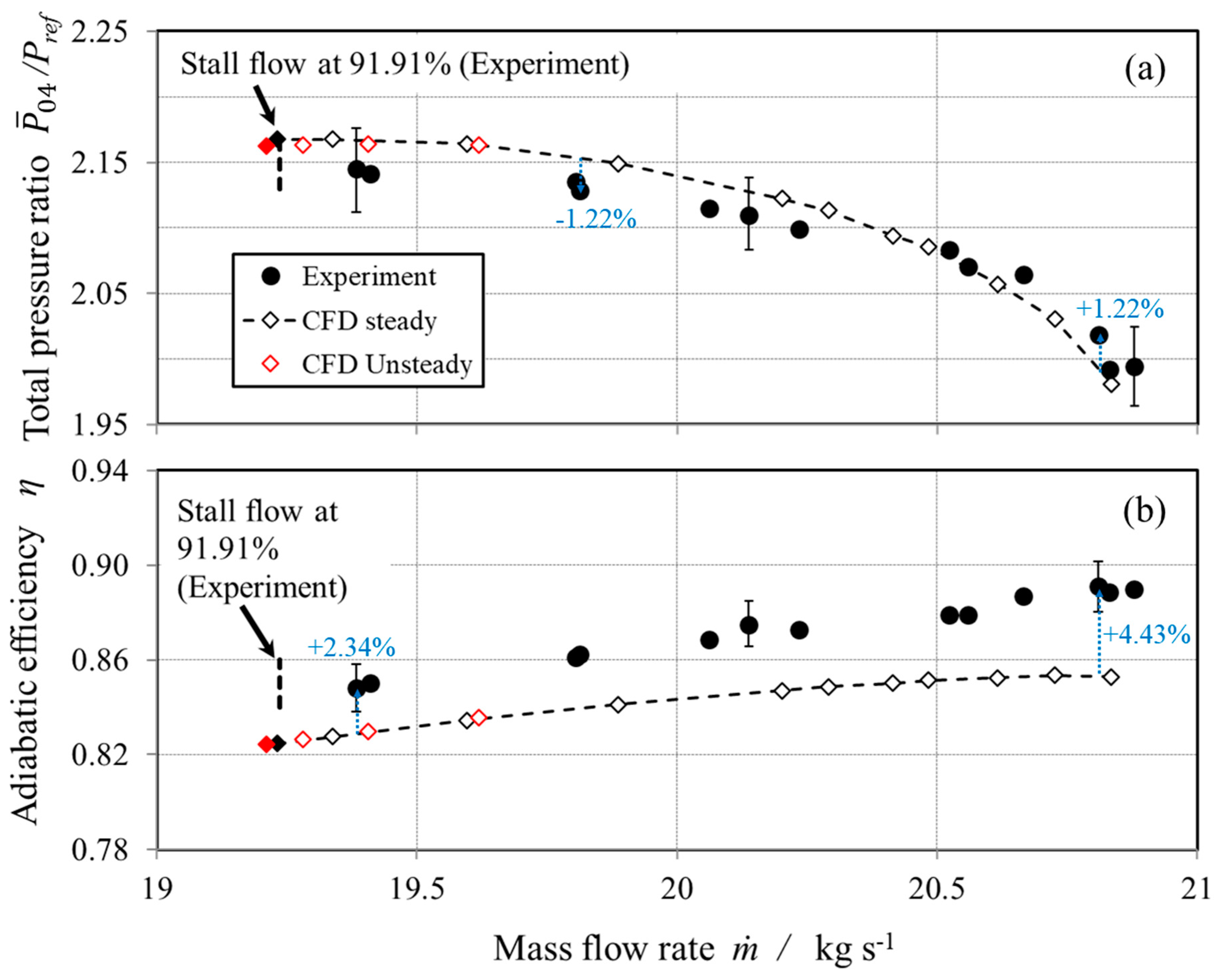
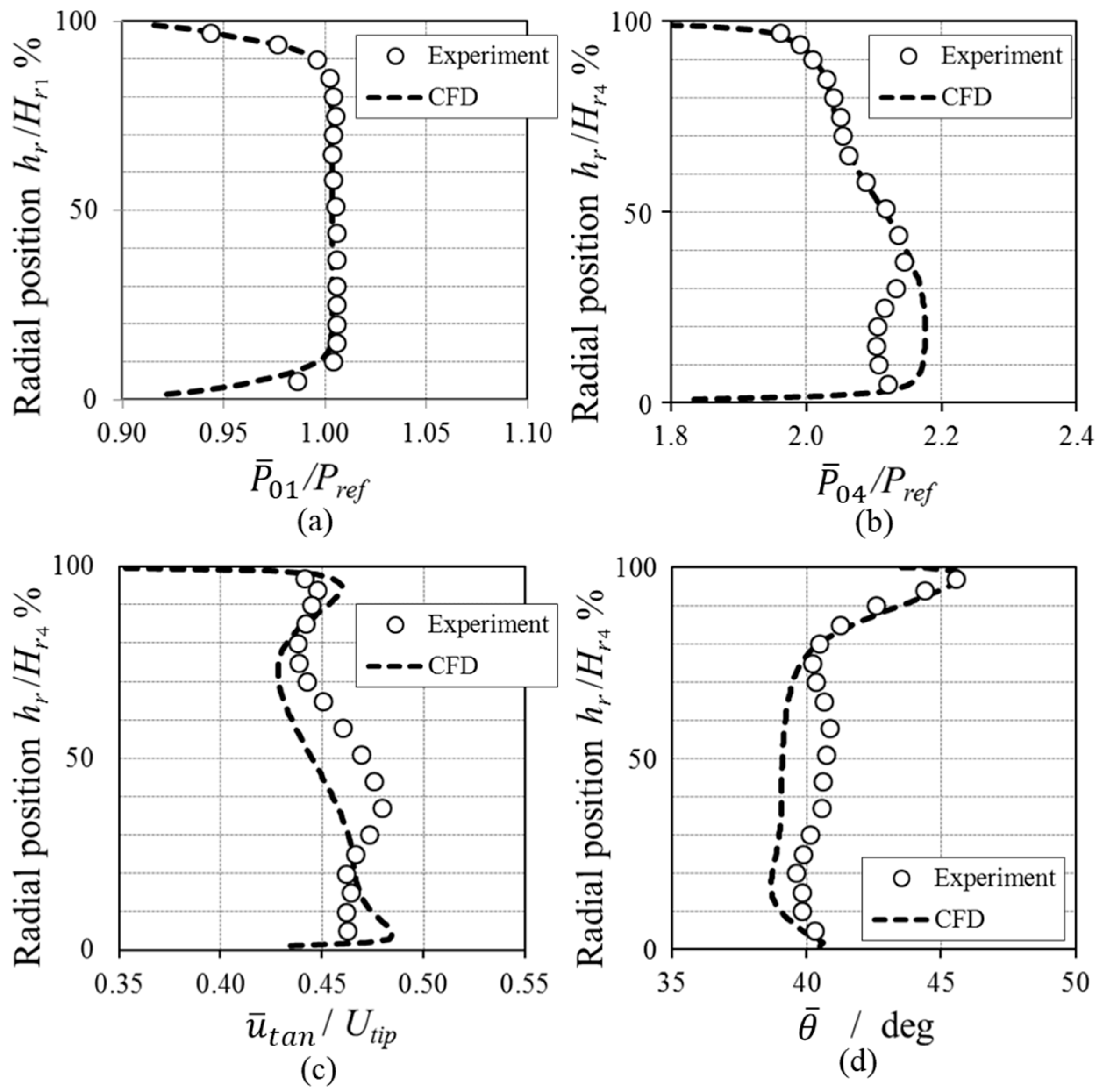
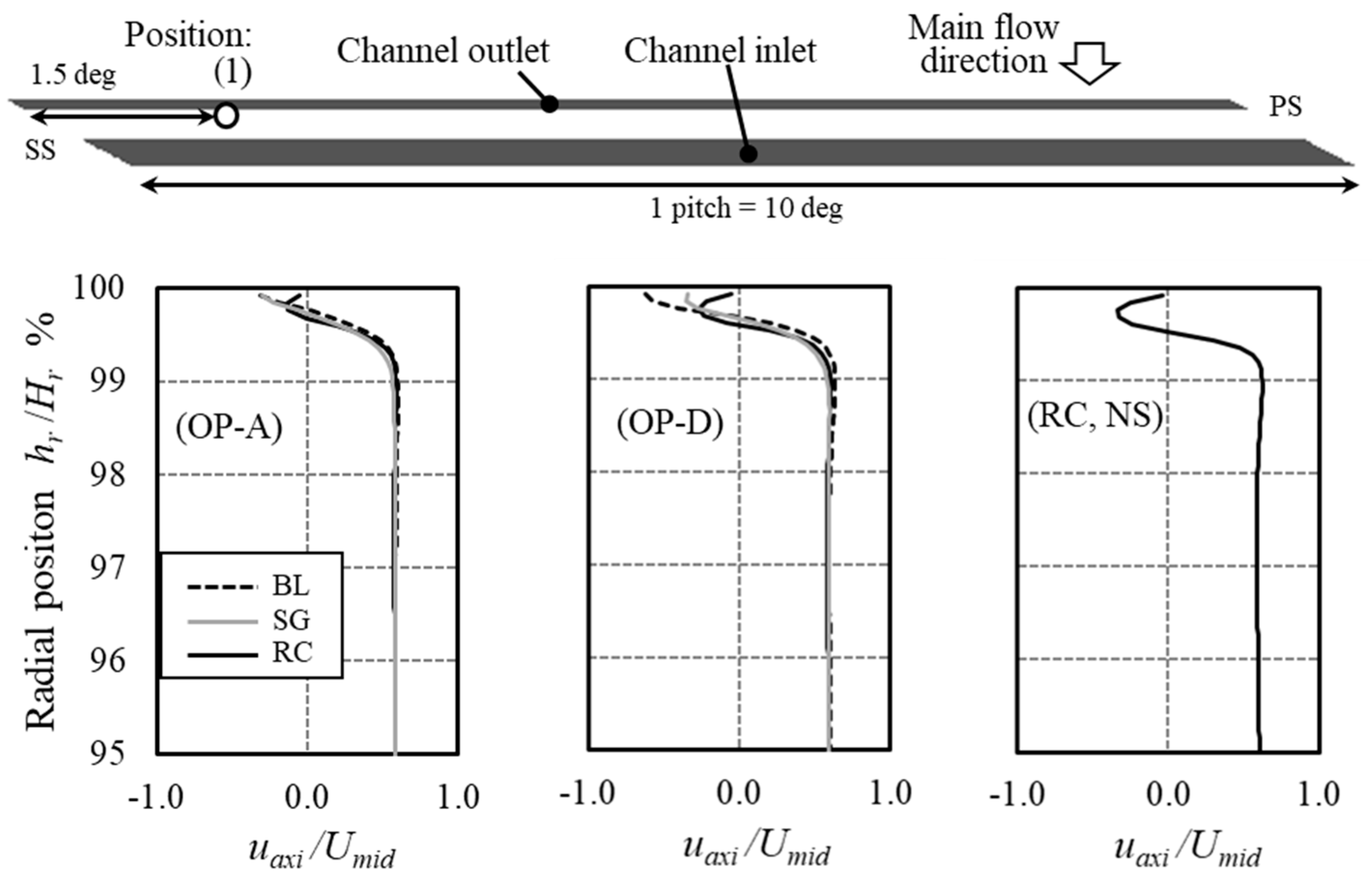
4. Validation of the Numerical Model
5. Results and Discussions
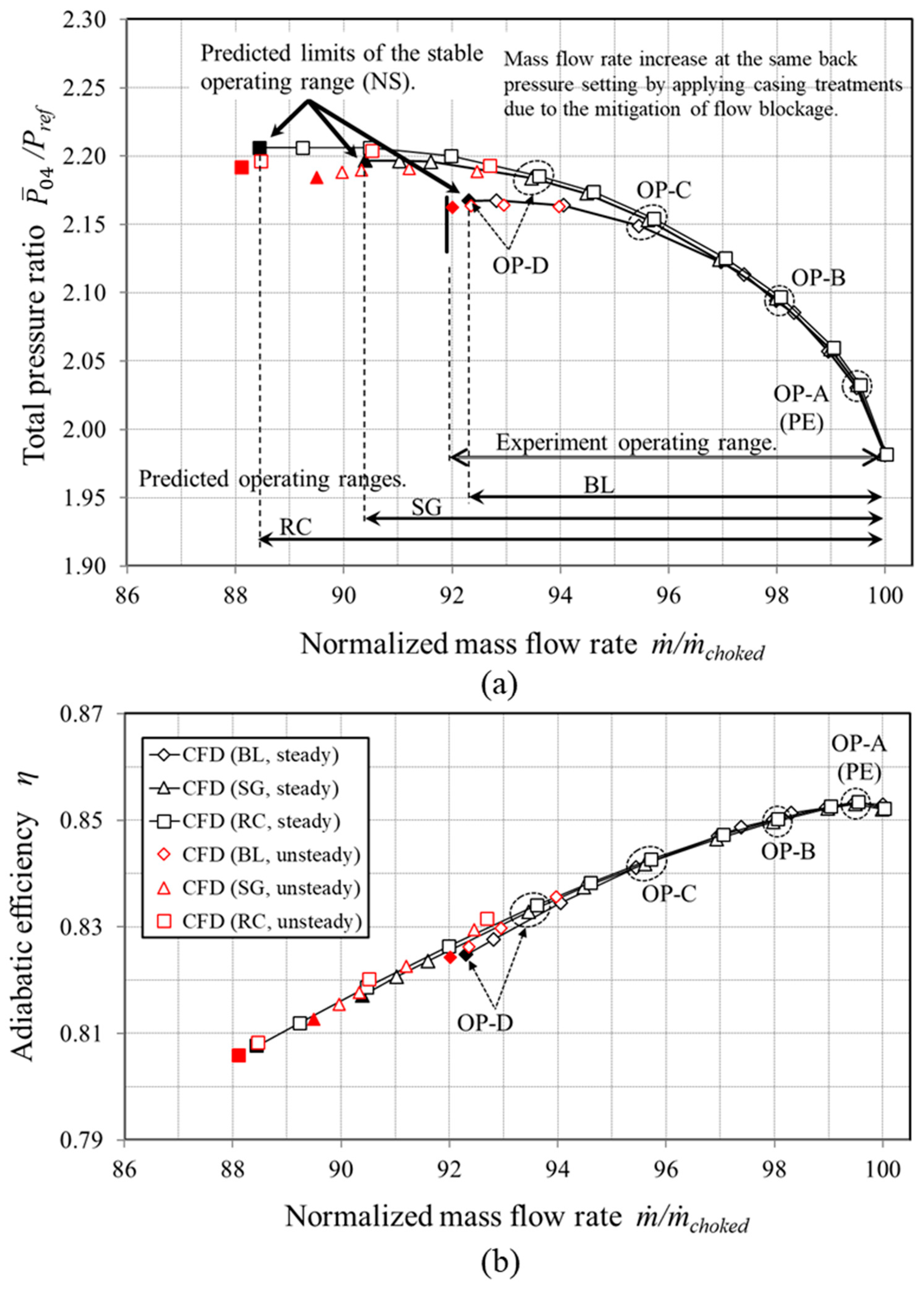
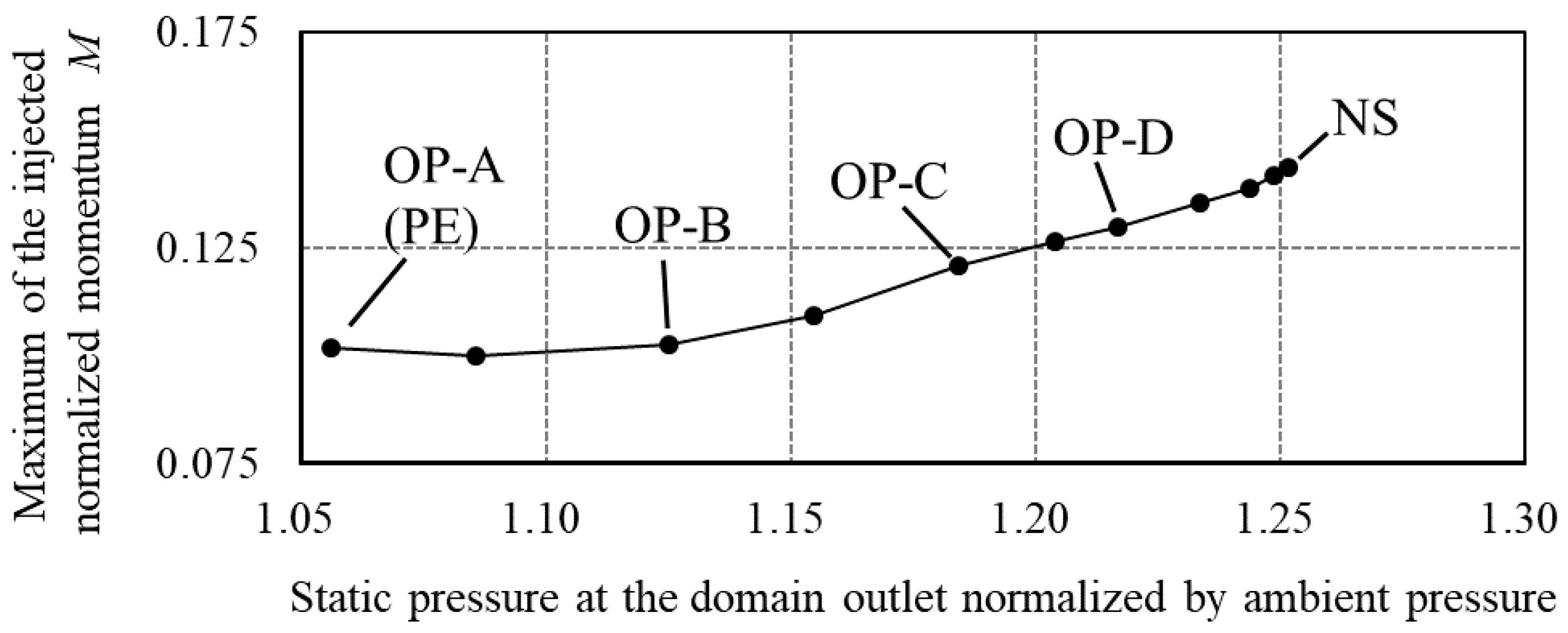
5.1. Overall Compressor Performance Characteristics
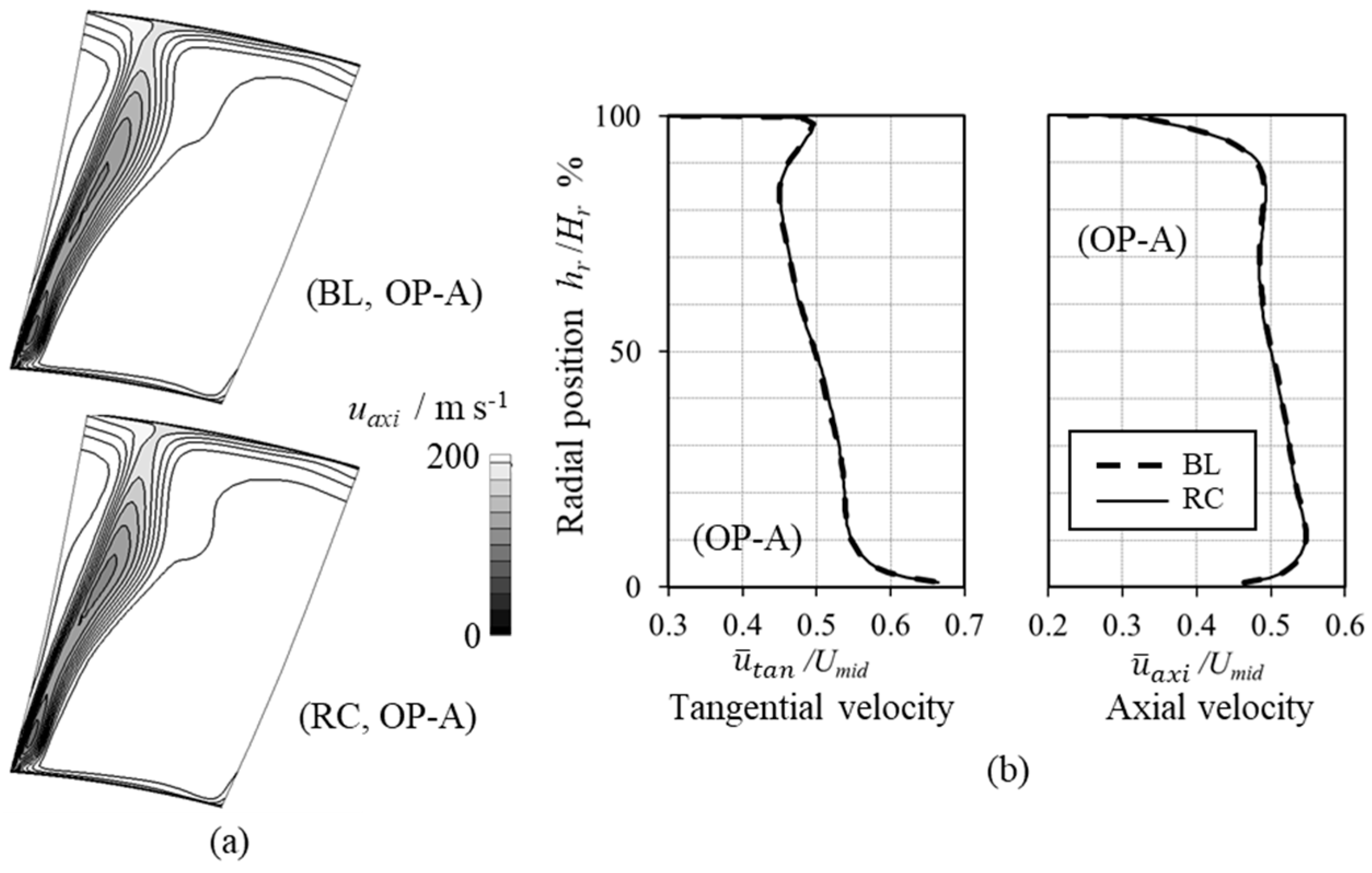
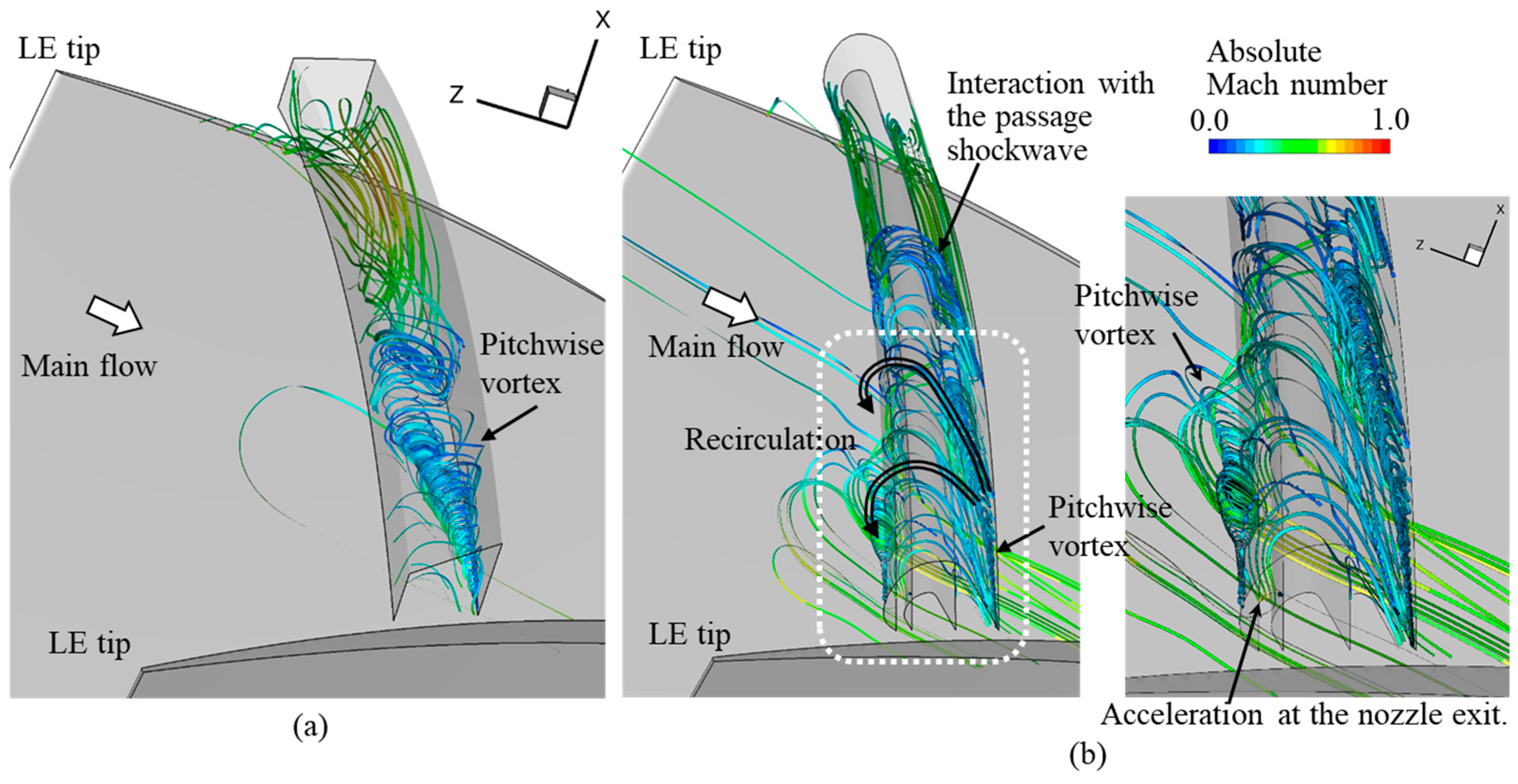
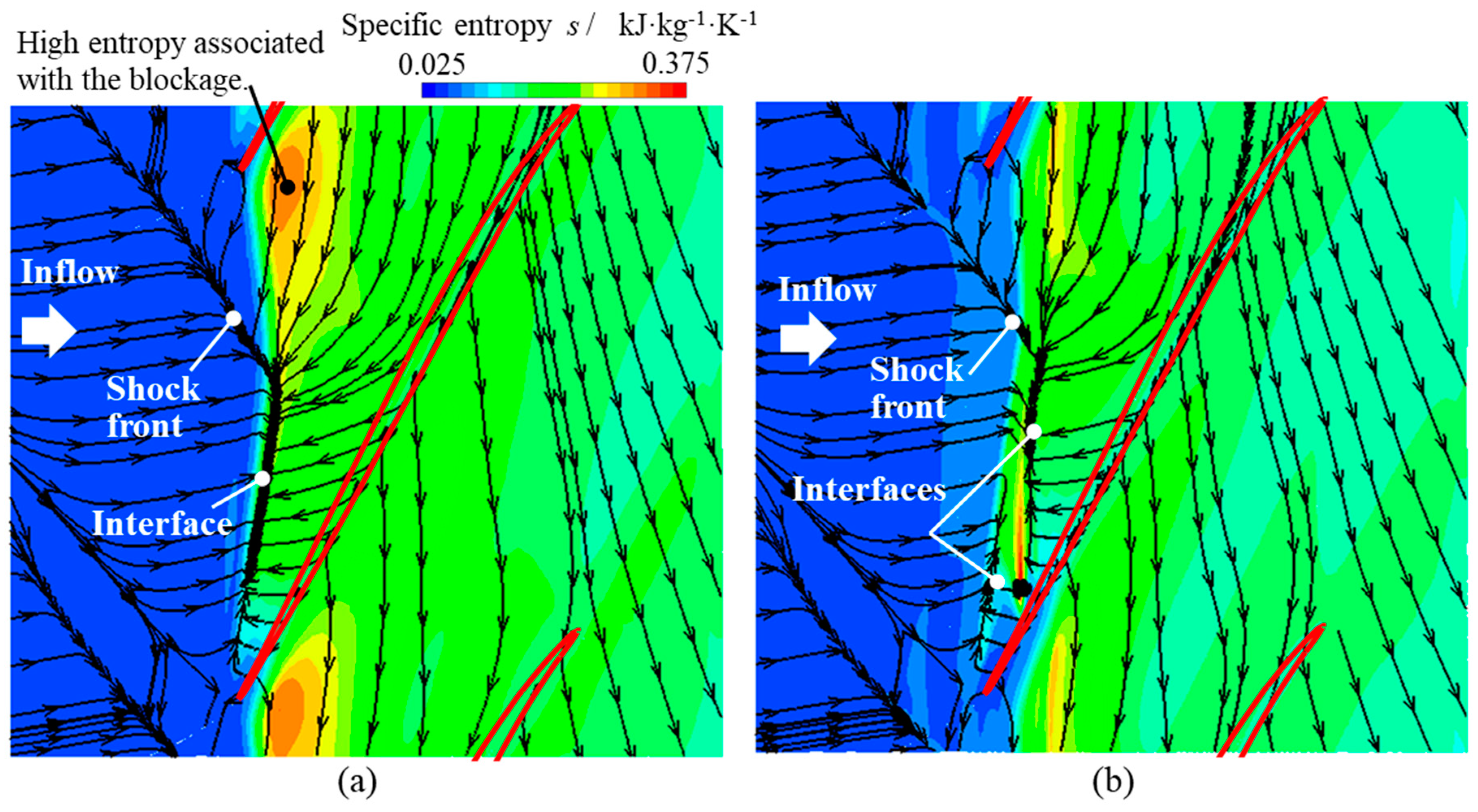
5.2. Analysis of the Passage Flow Structures
5.3. Flow Structure Inside the Casing Treatments
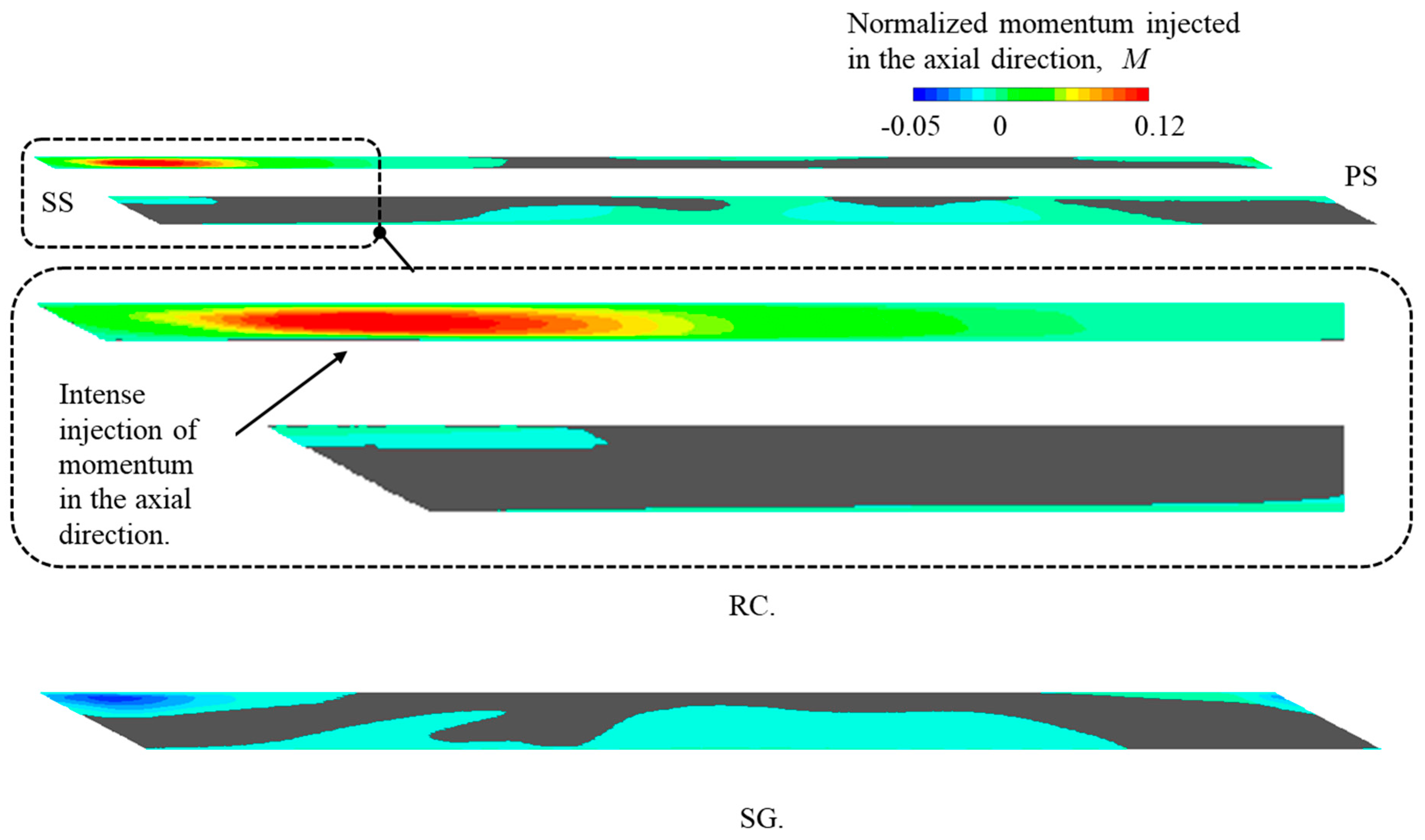
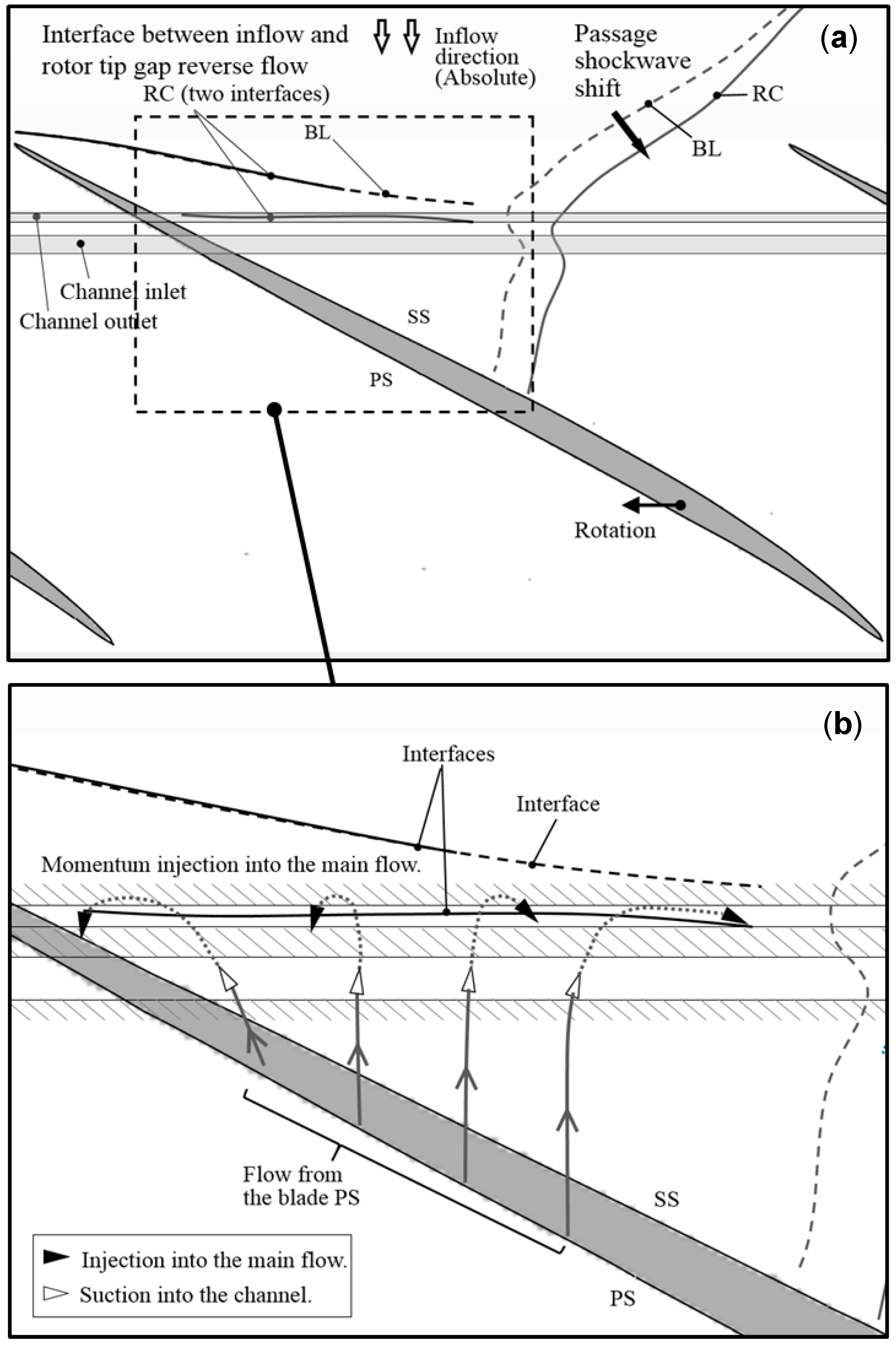
5.4. Flow Structures over the Casing Wall
5.5. Summary of the Working Principle of the Casing Channel
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| rotor blade tip axial chord, m | |
| e | relative error |
| radial position, m | |
| height of the main passage, m | |
| I | turbulence intensity |
| l | turbulence length scale, m |
| M | normalized momentum |
| mass flow rate, kg s−1 | |
| N | number of rotor blades |
| P | pressure, Pa |
| refinement ratio | |
| u | fluid velocity, m s−1 |
| U | rotor blade speed, m s−1 |
| y+ | near-wall resolution |
| γ | specific heat ratio |
| η | adiabatic efficiency |
| θ | flow angle, deg |
| κ | thermal conductivity, W m−1 K−1 |
| ρ | density, kg m−3 |
| rotational speed, rad s−1 | |
| Subscripts | |
| axi | axial direction |
| choked | choked condition |
| in | computational domain inlet boundary |
| mid | mid-span of the rotor blade |
| n | mesh index |
| out | computational domain outflow boundary |
| R | Richardson’s extrapolation |
| rad | radial direction |
| ref | reference |
| tan | tangential direction |
| tip | tip of the rotor blade |
| 0 | stagnation condition |
| 1 | station 1 |
| 4 | station 4 |
| Superscripts | |
| - | mass-averaged value |
| Abbreviations | |
| BL | baseline |
| LE | rotor blade tip leading edge |
| RC | recirculation channel |
| SG | square groove |
References
- Camp, T.R.; Day, I.J. A Study of Spike and Modal Stall Phenomena in a Low-Speed Axial Compressor. J. Turbomach. 1997, 120, 393–401. [Google Scholar] [CrossRef]
- Davis, R.L.; Yao, J. Computational Approach for Predicting Stall Inception in Multistage Axial Compressors. J. Propuls. Power 2007, 23, 257–265. [Google Scholar] [CrossRef]
- Owczarek, J.A. On Initiation of Stall in Axial Flow Compressors. Int. J. Turbomach. Propuls. Power 2017, 2, 5. [Google Scholar] [CrossRef]
- Haug, J.P.; Niehuis, R. Full Annulus Simulations of a Transonic Axial Compressor Stage with Distorted Inflow at Transonic and Subsonic Blade Tip Speed. Int. J. Turbomach. Propuls. Power 2018, 3, 7. [Google Scholar] [CrossRef]
- Gallimore, S.J.; Bolger, J.J.; Cumpsty, N.A.; Taylor, M.J.; Wright, P.I.; Place, J.M.M. The Use of Sweep and Dihedral in Multistage Axial Flow Compressor Blading—Part 1: University Research and Methods Development. J. Turbomach. 2002, 124, 521–532. [Google Scholar] [CrossRef]
- Gallimore, S.J.; Bolger, J.J.; Cumpsty, N.A.; Taylor, M.J.; Wright, P.I.; Place, J.M.M. The Use of Sweep and Dihedral in Multistage Axial Flow Compressor Blading—Part 2: Low and High-Speed Designs and Test Verification. J. Turbomach. 2002, 124, 533–541. [Google Scholar] [CrossRef]
- Vo, H.D. Rotating Stall Suppression in Axial Compressors with Casing Plasma Actuation. J. Propuls. Power 2010, 26, 808–818. [Google Scholar] [CrossRef]
- Reutter, O.; Rozanski, M.; Hergt, A.; Nicke, E. Advanced Endwall Contouring for Loss Reduction and Outflow Homogenization for an Optimized Compressor Cascade. Int. J. Turbomach. Propuls. Power 2017, 2, 1. [Google Scholar] [CrossRef]
- Osborn, M.W.; Lewis, W.G., Jr.; Heidelberg, J.L. Effect of Several Porous Casing Treatments on Stall Limit and on Overall Performance of an Axial-Flow Compressor Rotor; No. NASA/TN D-6537; NASA: Washington, DC, USA, 1971.
- Schnell, R.; Voges, M.; Mönig, R.; Müller, M.W.; Zschnerp, C. Investigation of Blade Tip Interaction with Casing Treatment in a Transonic Compressor—Part 2: Numerical Results. J. Turbomach. 2010, 133, 011008. [Google Scholar] [CrossRef]
- Gourdain, N.; Leboeuf, F. Unsteady Simulation of an Axial Compressor Stage with Casing and Blade Passive Treatment. J. Turbomach. 2009, 131, 021013. [Google Scholar] [CrossRef]
- Wadia, A.R.; James, F.D. F110-GE-132: Enhanced Power Through Low-Risk Derivative Technology. J. Turbomach. 2000, 123, 544–551. [Google Scholar] [CrossRef]
- Legras, G.; Trébinjac, I.; Gourdain, N.; Ottavy, X.; Castillon, L. A Novel Approach to Evaluate the Benefits of Casing Treatment in Axial Compressors. Int. J. Rotating Mach. 2012, 2012, 1–19. [Google Scholar] [CrossRef]
- Chen, H.; Huang, X.; Shi, K.; Fu, S.; Ross, M.; Bennington, M.A.; Cameron, J.D.; Morris, S.C.; McNulty, S.; Wadia, A. A Computational Fluid Dynamics Study of Circumferential Groove Casing Treatment in a Transonic Axial Compressor. J. Turbomach. 2014, 136, 031003. [Google Scholar] [CrossRef]
- Cevik, M.; Vo, H.D.; Yu, H. Casing Treatment for Desensitization of Compressor Performance and Stability to Tip Clearance. J. Turbomach. 2016, 138, 121008. [Google Scholar] [CrossRef]
- Houghton, T.; Day, I. Enhancing the Stability of Subsonic Compressors Using Casing Grooves. J. Turbomach. 2010, 133, 021007. [Google Scholar] [CrossRef]
- Houghton, T.; Day, I. Stability Enhancement by Casing Grooves: The Importance of Stall Inception Mechanism and Solidity. J. Turbomach. 2011, 134, 021003. [Google Scholar] [CrossRef]
- Sakuma, Y.; Watanabe, T.; Himeno, T.; Kato, D.; Murooka, T.; Shuto, Y. Numerical Analysis of Flow in a Transonic Compressor with a Single Circumferential Casing Groove: Influence of Groove Location and Depth of Flow Instability. J. Turbomach. 2013, 136, 031017. [Google Scholar] [CrossRef]
- Mao, X.; Liu, B.; Zhao, H. Numerical Investigation for the Impact of Single Groove on the Stall Margin Improvement and the Unsteadiness of Tip Leakage Flow in a Counter-Rotating Axial Flow Compressor. Energies 2017, 10, 1153. [Google Scholar] [CrossRef]
- Koff, S.G.; Mazzawy, R.S.; Nikkanen, J.P.; Nolcheff, N.A. Case Treatment for Compressor. U.S. Patent 5,282,718, 3 August 1992. [Google Scholar]
- Hathaway, M.D. Self-Recirculating Casing Treatment Concept for Enhanced Compressor Performance; No. NASA/TM-2002-211569; NASA: Washington, DC, USA, 2002.
- Dinh, C.T.; Ma, S.B.; Kim, K.Y. Effect of a Circumferential Feed-Back Channel on Aerodynamic Performance of a Single-Stage Transonic Axial Compressor. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. Paper No. GT2017-63536. [Google Scholar] [CrossRef]
- Yang, M.; Martinez-Botas, R.; Zhang, Y.; Zheng, X. Effect of Self-Recirculation-Casing Treatment on High Pressure Ratio Centrifugal Compressor. J. Propul. Power 2016, 32, 602–610. [Google Scholar] [CrossRef]
- Tesla, N. Valvular Conduit. U.S. Patent 1,329,559, 2 February 1916. [Google Scholar]
- Reid, L.; Moore, D. Design and Overall Performance of Four Highly Loaded, High-Speed Inlet Stages for an Advanced High-Pressure-Ratio Core Compressor; No. NASA/TP-1337; NASA: Washington, DC, USA, 1978.
- Dunham, J. CFD Validation for Propulsion System Components; No. AGRAD-AR-355; The Advisory Group for Aerospace Research and Development (NATO): Neuilly sur Seine, France, 1998. [Google Scholar]
- Arima, T.; Sonoda, T.; Shirotori, M.; Tamura, A.; Kikuchi, K. A Numerical Investigation of Transonic Axial Compressor Rotor Flow Using a Low-Reynolds-Number k-ε Turbulence Model. J. Turbomach. 1999, 121, 44–58. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluid. Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-ε Eddy-Viscosity Model for high Reynolds Number Turbulent Flows—Model Development and Validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Tsederberg, N.V. Thermal Conductivity of Gases and Liquids; Edward Arnold: London, UK, 1965; ISBN 026220004X. [Google Scholar]
- Roe, P.L. Characteristic-Based Schemes for the Euler Equations. Annu. Rev. Fluid Mech. 1986, 18, 337–365. [Google Scholar] [CrossRef]
- Weiss, J.M.; Maruszewski, J.P.; Smith, W.A. Implicit Solution of the Navier-Stokes Equations on Unstructured Meshes. In Proceedings of the 13th Computational Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. Paper No. AIAA-97-2103. [Google Scholar] [CrossRef]
- Denton, J.D. Lessons from Rotor 37. J. Therm. Sci. 1997, 6, 1–13. [Google Scholar] [CrossRef]
- Suder, K. Experimental Investigation of the Flow Field in a Transonic, Axial Flow Compressor with Respect to the Development of Blockage and Loss; No. NASA/TM-107310; NASA: Washington, DC, USA, 1996.
- Hah, C. Large Eddy Simulation of Transonic Flow Field in NASA Rotor 37; No. NASA/TM-2009-215627; NASA: Washington, DC, USA, 2009.
- Kim, D.-W.; Kim, J.-H.; Kim, K.-Y. Aerodynamic Performance of an Axial Compressor with a Casing Groove Combined with Injection. In Proceedings of the 13th Computational Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. Paper No. AIAA-97-2103. [Google Scholar] [CrossRef]
- Cumpsty, N.A. Compressor Aerodynamics; Longman Scientific & Technical: London, UK, 1989; ISBN 058201364x. [Google Scholar]
- Cumpsty, N.A. Jet Propulsion: A Simple Guide to the Aerodynamic and Thermodynamic Design and Performance of Jet Engine; Cambridge University Press: Cambridge, UK, 1997; ISBN 0521596742. [Google Scholar]

| Variables | Values | ||
|---|---|---|---|
| Inlet | Total pressure, P0in | kPa | 101.325 |
| Total temperature, T0in | K | 288.15 | |
| Turbulence intensity, I | % | 3 | |
| Turbulence length scale, l | m | 0.0114 | |
| Outlet | Static pressure, Pout | kPa | Varied from 101.3 to stall inception. |
| Choked Mass Flow Rate (kg s−1) | Normalized Mass Flow Rate at Near-Stall Condition (%) | |
|---|---|---|
| Experiment | 20.93 | 91.9 (Stalled flow) |
| Kawase and Rona (this study) | 20.84 | 92.3 |
| Arima et al. [27] | 20.77 | 92.4 |
| Sakuma et al. [18] | 20.78 | 92.1 |
| Hah [35] | 20.92 | 92.3 |
| Kim et al. [36] | - | 90.3 |
| BL | SG | RC | ||
|---|---|---|---|---|
| Stall Margin (SM) | % | 13.07 | 15.93 | 18.14 |
| ΔSM | % | 0.00 | 2.85 | 5.07 |
| Choked mass flow rate choked | kg s−1 | 20.83 | 20.83 | 20.84 |
| Adiabatic peak efficiency η | % | 85.337 | 85.306 | 85.341 |
| Δη | % | 0.00 | −0.031 | +0.004 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Kawase, M.; Rona, A. Effect of a Recirculating Type Casing Treatment on a Highly Loaded Axial Compressor Rotor. Int. J. Turbomach. Propuls. Power 2019, 4, 5. https://doi.org/10.3390/ijtpp4010005
Kawase M, Rona A. Effect of a Recirculating Type Casing Treatment on a Highly Loaded Axial Compressor Rotor. International Journal of Turbomachinery, Propulsion and Power. 2019; 4(1):5. https://doi.org/10.3390/ijtpp4010005
Chicago/Turabian StyleKawase, Motoyuki, and Aldo Rona. 2019. "Effect of a Recirculating Type Casing Treatment on a Highly Loaded Axial Compressor Rotor" International Journal of Turbomachinery, Propulsion and Power 4, no. 1: 5. https://doi.org/10.3390/ijtpp4010005
APA StyleKawase, M., & Rona, A. (2019). Effect of a Recirculating Type Casing Treatment on a Highly Loaded Axial Compressor Rotor. International Journal of Turbomachinery, Propulsion and Power, 4(1), 5. https://doi.org/10.3390/ijtpp4010005





