Numerical Investigation of Secondary Flow and Loss Development in a Low-Pressure Turbine Cascade with Divergent Endwalls †
Abstract
:1. Introduction
2. Experimental Reference Data
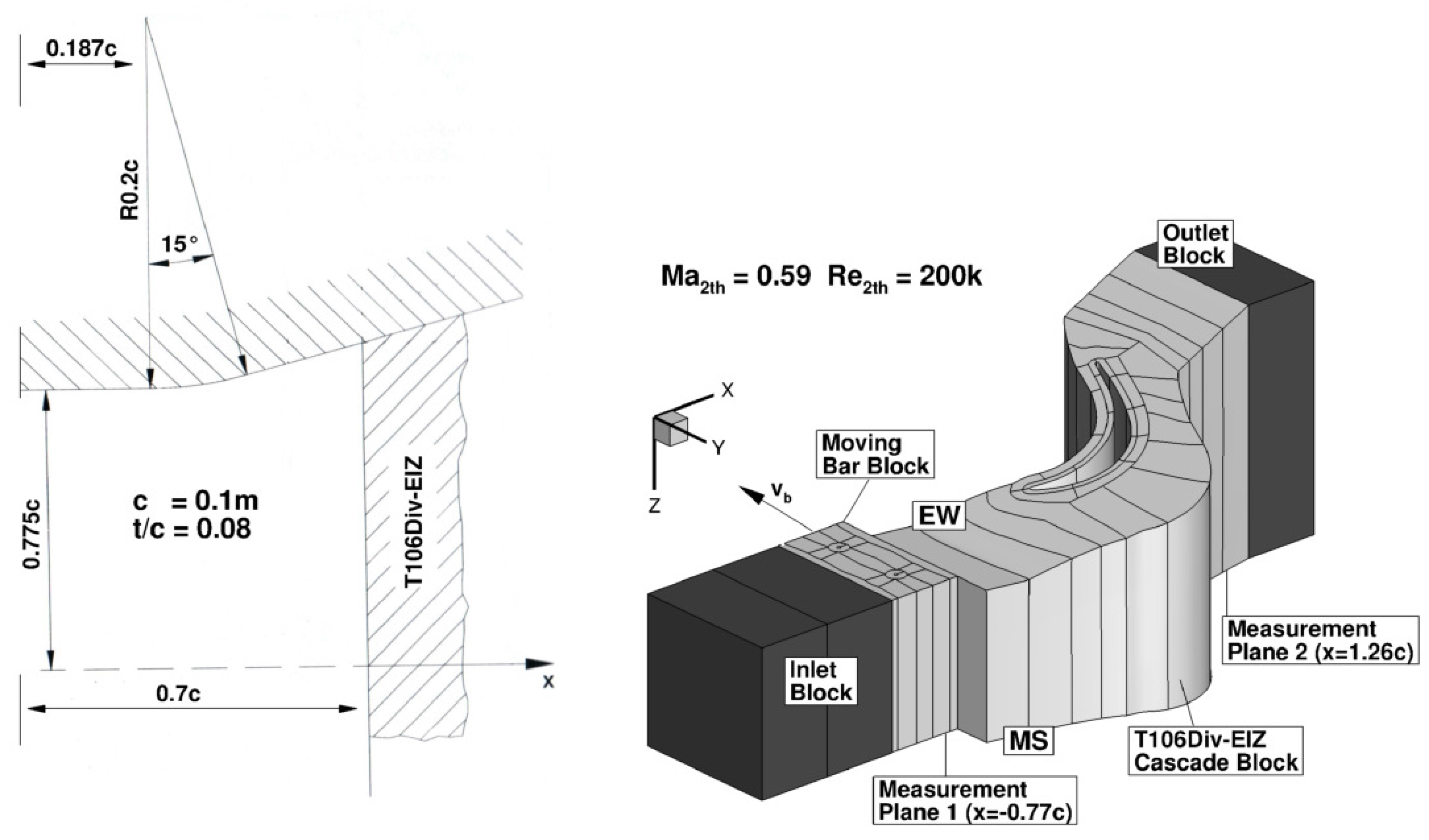
3. Investigated Test Cascade and Configurations
4. CFD Setup
4.1. Flow Solver and Domain Discretization
4.2. Domain Definition and Boundary Conditions
5. Results
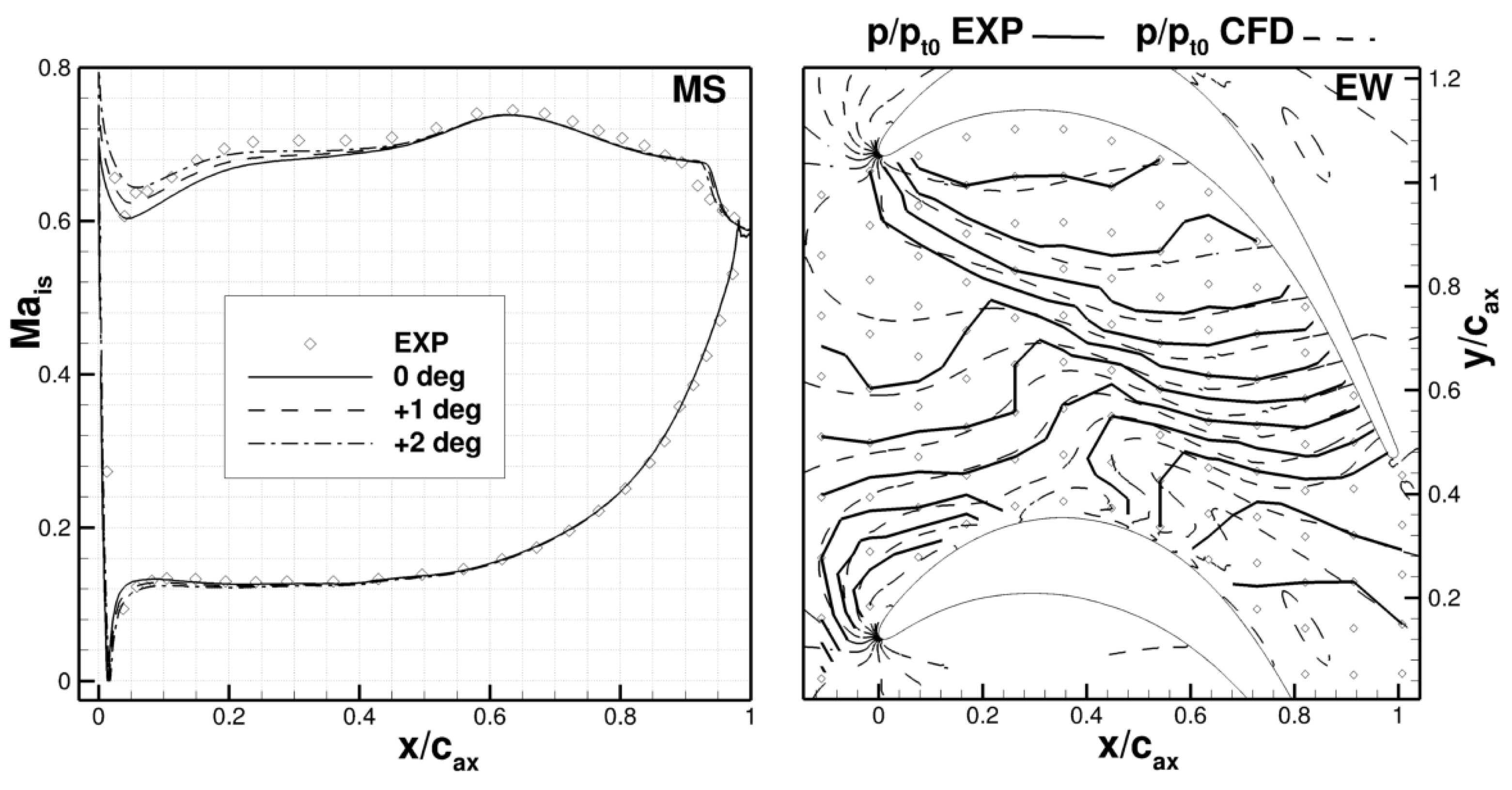
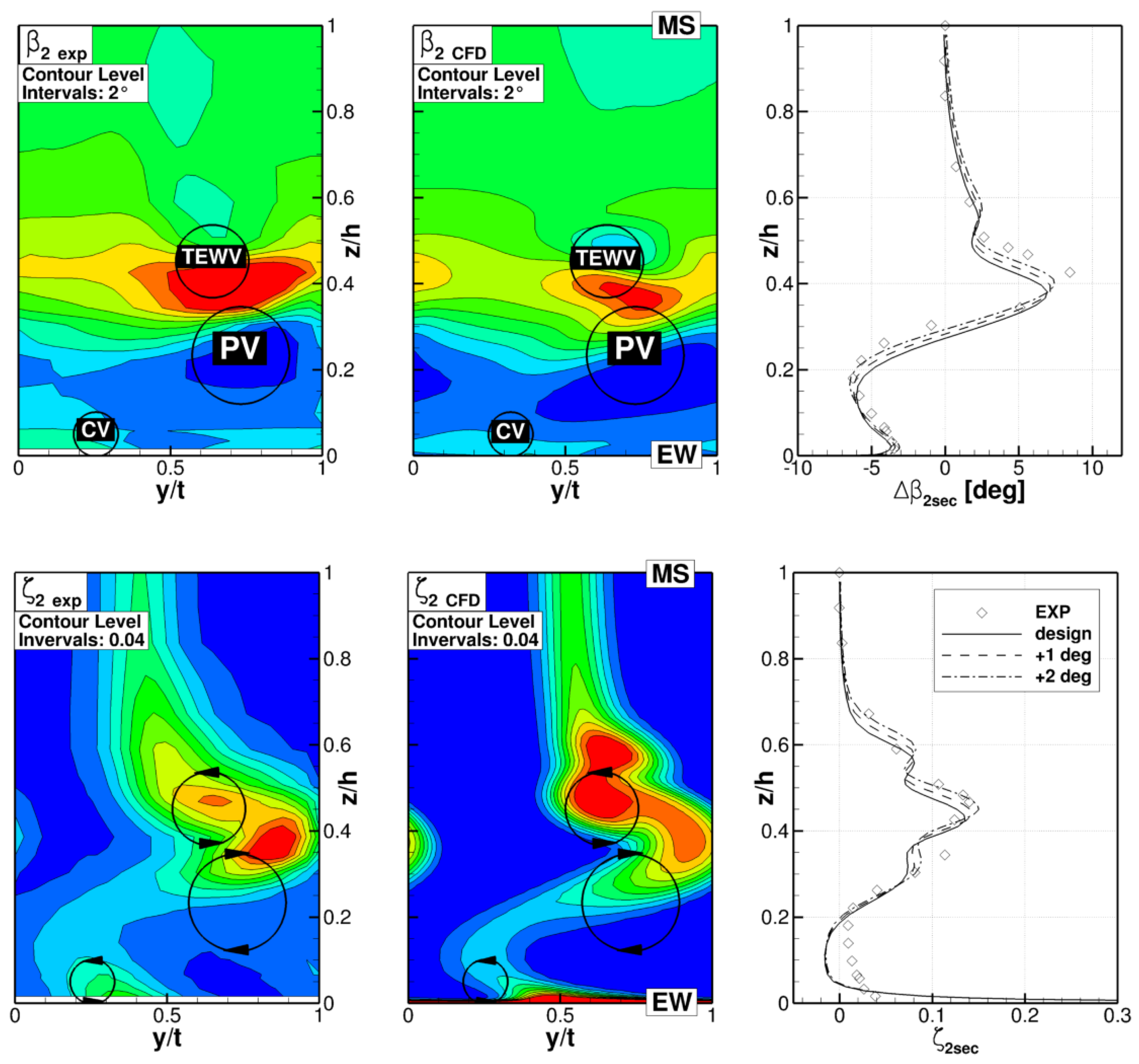
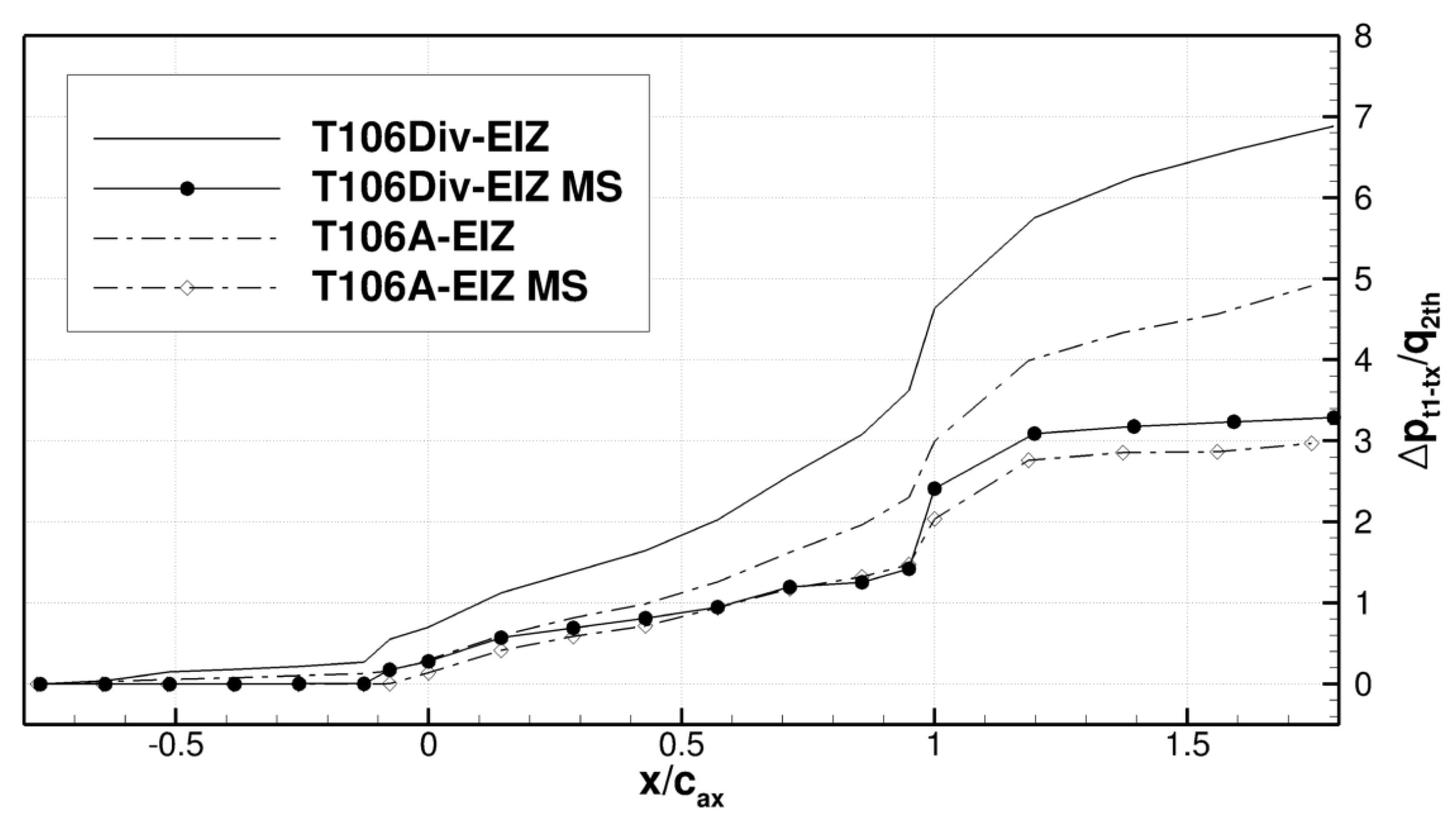
5.1. Comparison with Measured Data
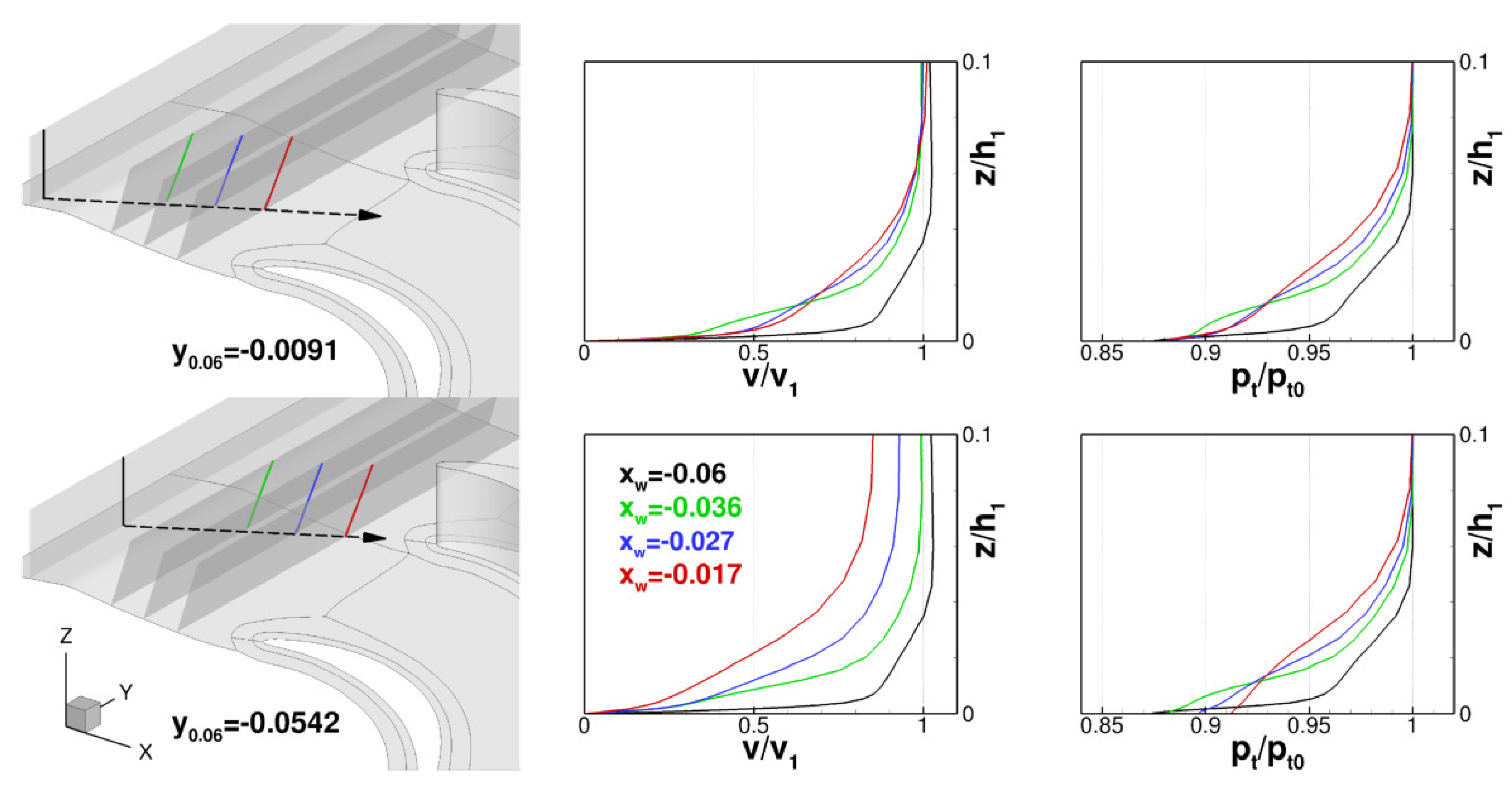
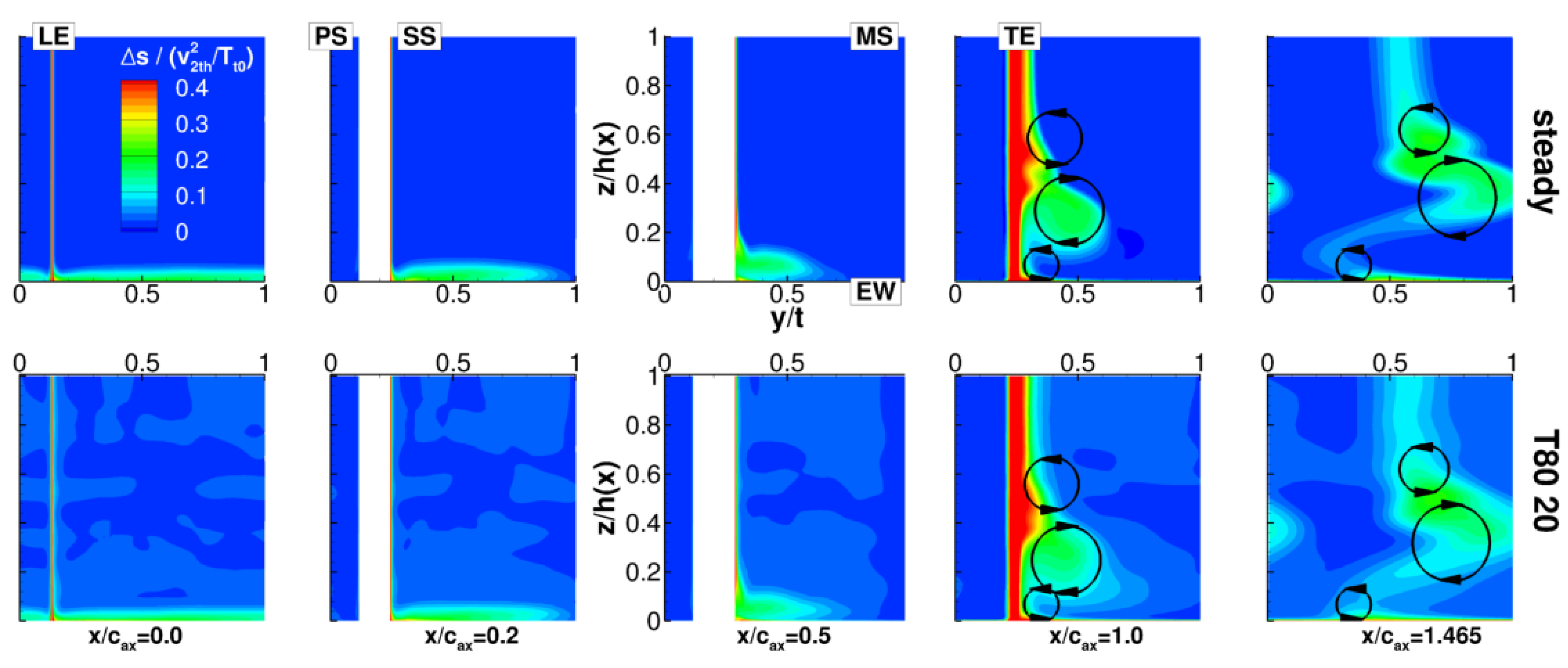
5.2. Steady Numerical Analysis
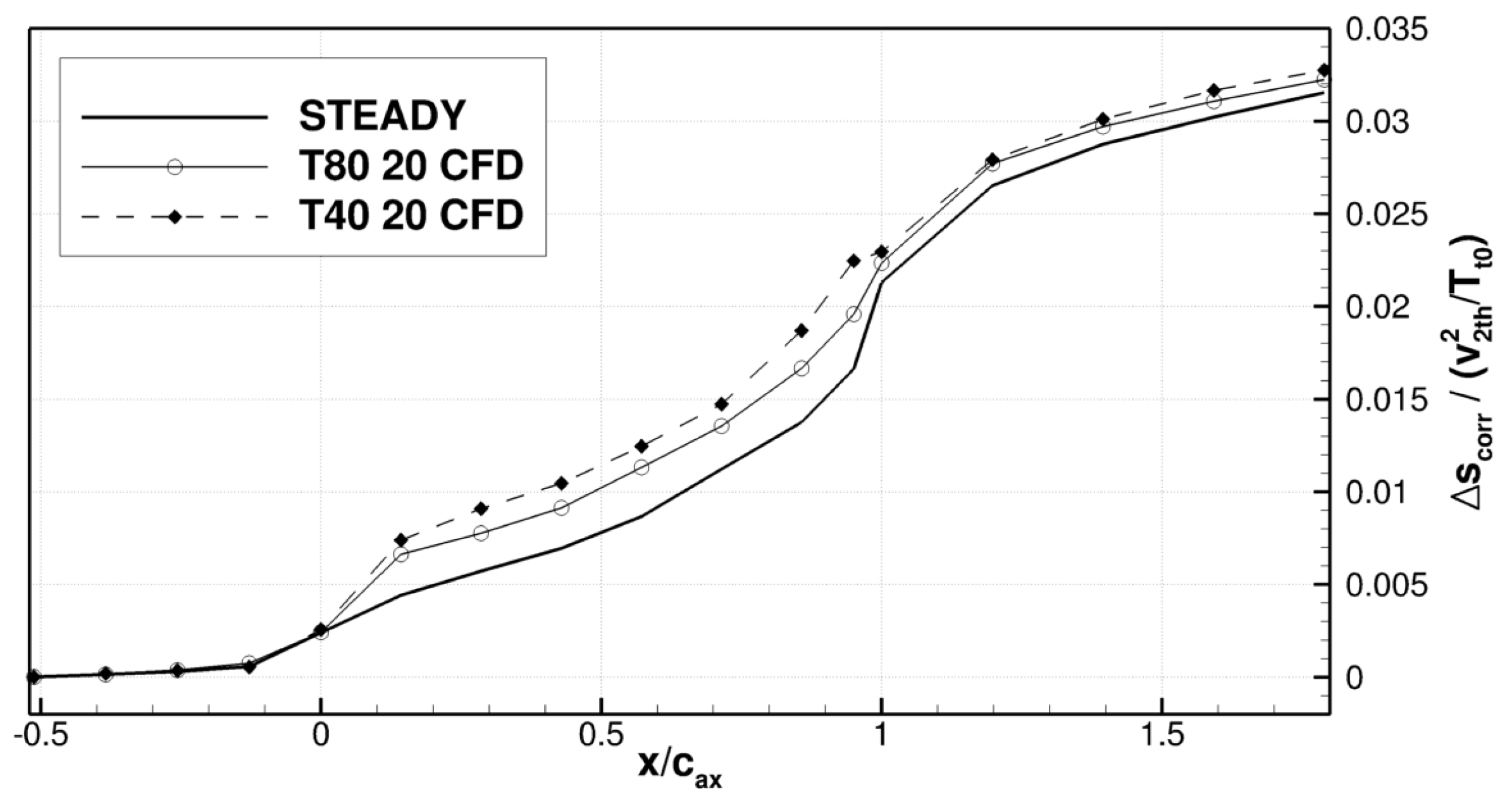
5.3. Steady and Unsteady Comparison
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| c | chord length |
| H, h | height in spanwise direction, |
| Ma | Mach number |
| p | pressure |
| q | dynamic pressure |
| Re | Reynolds number |
| s | entropy |
| Sr | Strouhal number, |
| T | temperature |
| t | pitch |
| v | velocity |
| x | axial coordinate |
| y | pitch-wise coordinate |
| z | span-wise coordinate |
| Greek Symbols | |
| yaw (pitch-wise) angle | |
| total pressure losses | |
| entropy generation | |
| flow coefficient, | |
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| CV | Corner Vortex |
| DNS | Direct Numerical Simulation |
| EIZ | Erzeuger Instationärer Zuströmung |
| (wake generator) | |
| EW | EndWall |
| EXP | Experimental |
| LPT | Low-Pressure Turbine |
| MS | Mid-Span |
| PV | Passage Vortex |
| TEWV | Trailing Edge Wake Vortex |
| (U)RANS | (Unsteady) Reynolds-Averaged Navier-Stokes equations |
| Subscripts | |
| 0 | domain inlet |
| 1,2 | measurement planes |
| ax | axial |
| b | bar |
| corr | corrected |
| t | total |
| th | theoretical |
| sec | secondary |
References
- Denton, J.D. The 1993 IGTI Scholar Lecture: Loss Mechanisms in Turbomachines. J. Turbomach. 1993, 115, 621–656. [Google Scholar] [CrossRef]
- Cui, J.; Tucker, P.G. Numerical Study of Purge and Secondary Flows in a Low Pressure Turbine. J. Turbomach. 2017, 139, 021007. [Google Scholar] [CrossRef]
- Ciorciari, R.; Kirik, I.; Niehuis, R. Effects of Unsteady Wakes on the Secondary Flows in the Linear T106 Turbine Cascade. J. Turbomach. 2014, 136, 091010. [Google Scholar] [CrossRef]
- Koschichow, D.; Fröhlich, J.; Kirik, I.; Niehuis, R. DNS of the Flow Near the Endwall in a Linear Low Pressure Turbine Cascade with Periodically Passing Wakes. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. Paper No. GT2014-25071. [Google Scholar]
- Volino, R.; Galvin, C.D.; Ibrahim, M. Effects of Periodic Unsteadiness on Secondary Flows in High Pressure Turbines. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. Paper No. GT2013-95881. [Google Scholar]
- Volino, R. Effects on Endwall Boundary Layer Thickness and Blade Tip Geometry on Flow Through High Pressure Turbine Passages. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. Paper No. GT2014-27013. [Google Scholar]
- Wakelam, C.T.; Höger, M.; Niehuis, R. A Comparison of Three Low Pressure Turbine Designs. J. Turbomach. 2013, 135, 051026. [Google Scholar] [CrossRef]
- Muth, B.; Niehuis, R. Axial Loss Development in Low Pressure Turbine Cascades. J. Turbomach. 2013, 135, 041024. [Google Scholar] [CrossRef]
- Praisner, T.J.; Grover, E.A.; Knezevici, D.C.; Popovis, I.; Sjolander, S.A.; Clark, J.P.; Sondergaard, R. Toward the Expansion of Low-Pressure-Turbine Airfoil Design Space. J. Turbomach. 2013, 135, 061007. [Google Scholar] [CrossRef]
- Weiss, A.P.; Fottner, L. The Influence of Load Distribution on Secondary Flow in Straight Turbine Cascades. J. Turbomach. 1995, 117, 133–141. [Google Scholar] [CrossRef]
- Kirik, I.; Niehuis, R. Comparing the Effect of Unsteady Wakes on Parallel and Divergent Endwalls in a LP Turbine Cascade (T106A-EIZ and T106D-EIZ). In Proceedings of the 11th International Gas Turbine Congress, Tokyo, Japan, 15–20 November 2015. [Google Scholar]
- Duden, A. Strömungsbeeinflussung zur Reduzierung der Sekundärströmungen in Turbinengittern. Ph.D. Thesis, Universität der Bundeswehr München, München, Germany, 1999. [Google Scholar]
- Acton, P. Untersuchungen des Grenzschichtumschlages an Einem Hochbelasteten Turbinengitter unter Inhomogenen und Instationären Zuströmbedingungen. Ph.D. Thesis, Universität der Bundeswehr München, München, Germany, 1988. [Google Scholar]
- Stadtmüller, P. Grenzschichtentwicklung und Verlustverhalten von Hochbelasteten Turbinengittern unter Einfluß Periodisch Instationärer Zuströmung. Ph.D. Thesis, Universität der Bundeswehr München, München, Germany, 2002. [Google Scholar]
- Ciorciari, R.; Kirik, I.; Niehuis, R. Investigating Unsteady Secondary Flows in a Linear Low Pressure Turbine: A Combined Experimental and Numerical Study. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Madrid, Spain, 23–27 March 2015. Paper No. ETC2015-134. [Google Scholar]
- DLR TRACE User Guide. Available online: http://www.trace-portal.de/userguide/trace/index.html (accessed on 9 January 2016).
- Eulitz, F. Numerische Simulation und Modellierung der Instationären Strömung in Turbomaschinen. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2000. [Google Scholar]
- Yang, H.; Kügeler, E.; Weber, A. A Conservative Zonal Approach with Applications to Unsteady Turbomachinery Flows. Presented at the DGLR Jahrestagung, Stuttgart, Germany, 23–26 September 2002. Paper No. DGLR-JT2002-073. [Google Scholar]
- Nürnberger, D. Impliziete Zeitintegration für die Simulation von Turbomaschinenströmungen. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2004. [Google Scholar]
- Kügeler, E. Numerisches Verfahren zur genauen Analyse der Kühleffektivität filmgekühlter Turbinenschaufeln. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2014. [Google Scholar]
- Yang, H.; Nürnberger, D.; Kersken, H.-P. Toward Excellence in Turbomachinery Computational Fluid Dynamics: A Hybrid Structured-Unstructured Reynolds-Averaged Navier-Stokes Solver. J. Turbomach. 2006, 128, 390–402. [Google Scholar] [CrossRef]
- Becker, K.; Heitkamp, K.; Kügeler, E. Recent Progress in a Hybrid-Grid CFD Solver for Turbomachinery Flows. In Proceedings of the Fifth European Conference on Computational Fluid Dynamics (ECCOMAS CFD 2010), Lisbon, Portugal, 14–17 June 2010. [Google Scholar]
- Kato, M.; Launder, B. The Modelling of Turbulent Flow Around Stationary and Vibrating Square Cylinders. Turbul. Shear Flow 1993, 1, 10-4. [Google Scholar]
- Kozulovic, D.; Röber, T.; Kügeler, E.; Nürnberger, D. Modifications of a Two-Equation Turbulence Model for Turbomachinery Fluid Flows. Presented at the DGLR Jahrestagung, Dresden, Germany, 20 September 2002. [Google Scholar]
- Marciniak, V.; Kügeler, E.; Franke, M. Predicting Transition on Low-Pressure Turbine Profiles. In Proceedings of the Fifth European Conference on Computational Fluid Dynamics (ECCOMAS CFD 2010), Lisbon, Portugal, 14–17 June 2010. [Google Scholar]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables: Part I—Model Formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Michelassi, V.; Chen, L.-W.; Pichler, R.; Sandberg, R.D. Compressible Direct Numerical Simulation of Low-Pressure Turbines: Part II—Effect of Inflow Disturbances. J. Turbomach. 2015, 137, 071005. [Google Scholar] [CrossRef]
- Pichler, R.; Sandberg, R.D.; Michelassi, V.; Bhaskaran, R. Investigation of the Accuracy of RANS Models to Predict the Flow Through a Low-Pressure Turbine. J. Turbomach. 2016, 138, 121009. [Google Scholar] [CrossRef]
- Adami, P.; Montomoli, F.; Belardini, E.; Martelli, F. Interaction Between Wake and Film Cooling Jets: Numerical Analysis. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. Paper No. GT2004-53178. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Ciorciari, R.; Schubert, T.; Niehuis, R. Numerical Investigation of Secondary Flow and Loss Development in a Low-Pressure Turbine Cascade with Divergent Endwalls. Int. J. Turbomach. Propuls. Power 2018, 3, 5. https://doi.org/10.3390/ijtpp3010005
Ciorciari R, Schubert T, Niehuis R. Numerical Investigation of Secondary Flow and Loss Development in a Low-Pressure Turbine Cascade with Divergent Endwalls. International Journal of Turbomachinery, Propulsion and Power. 2018; 3(1):5. https://doi.org/10.3390/ijtpp3010005
Chicago/Turabian StyleCiorciari, Roberto, Tobias Schubert, and Reinhard Niehuis. 2018. "Numerical Investigation of Secondary Flow and Loss Development in a Low-Pressure Turbine Cascade with Divergent Endwalls" International Journal of Turbomachinery, Propulsion and Power 3, no. 1: 5. https://doi.org/10.3390/ijtpp3010005
APA StyleCiorciari, R., Schubert, T., & Niehuis, R. (2018). Numerical Investigation of Secondary Flow and Loss Development in a Low-Pressure Turbine Cascade with Divergent Endwalls. International Journal of Turbomachinery, Propulsion and Power, 3(1), 5. https://doi.org/10.3390/ijtpp3010005






