Reducing Gas Accumulation in Horizontal Diffusers Under Two-Phase Flow Using Upstream Cross-Flow Steps †
Abstract
1. Introduction
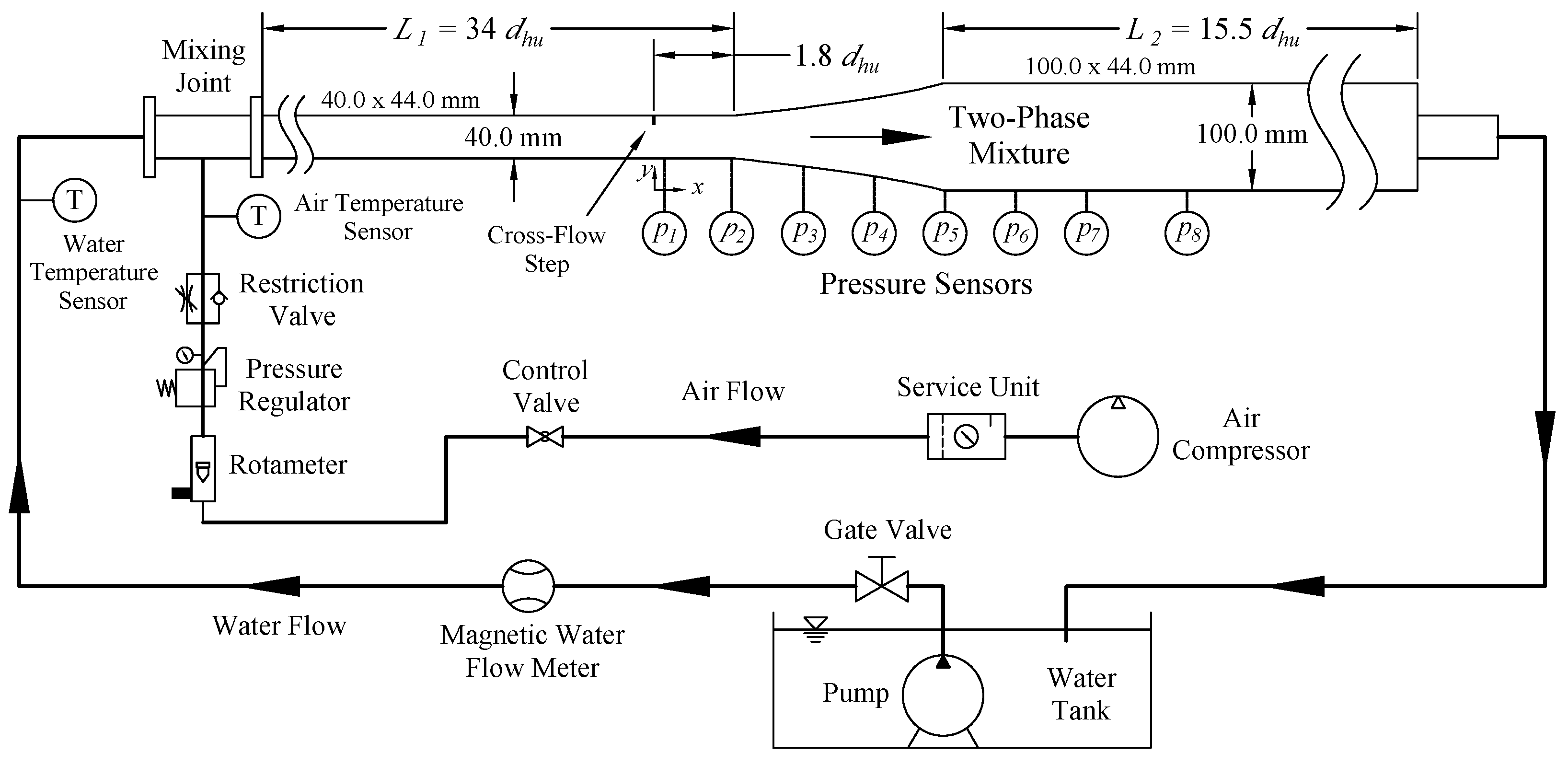
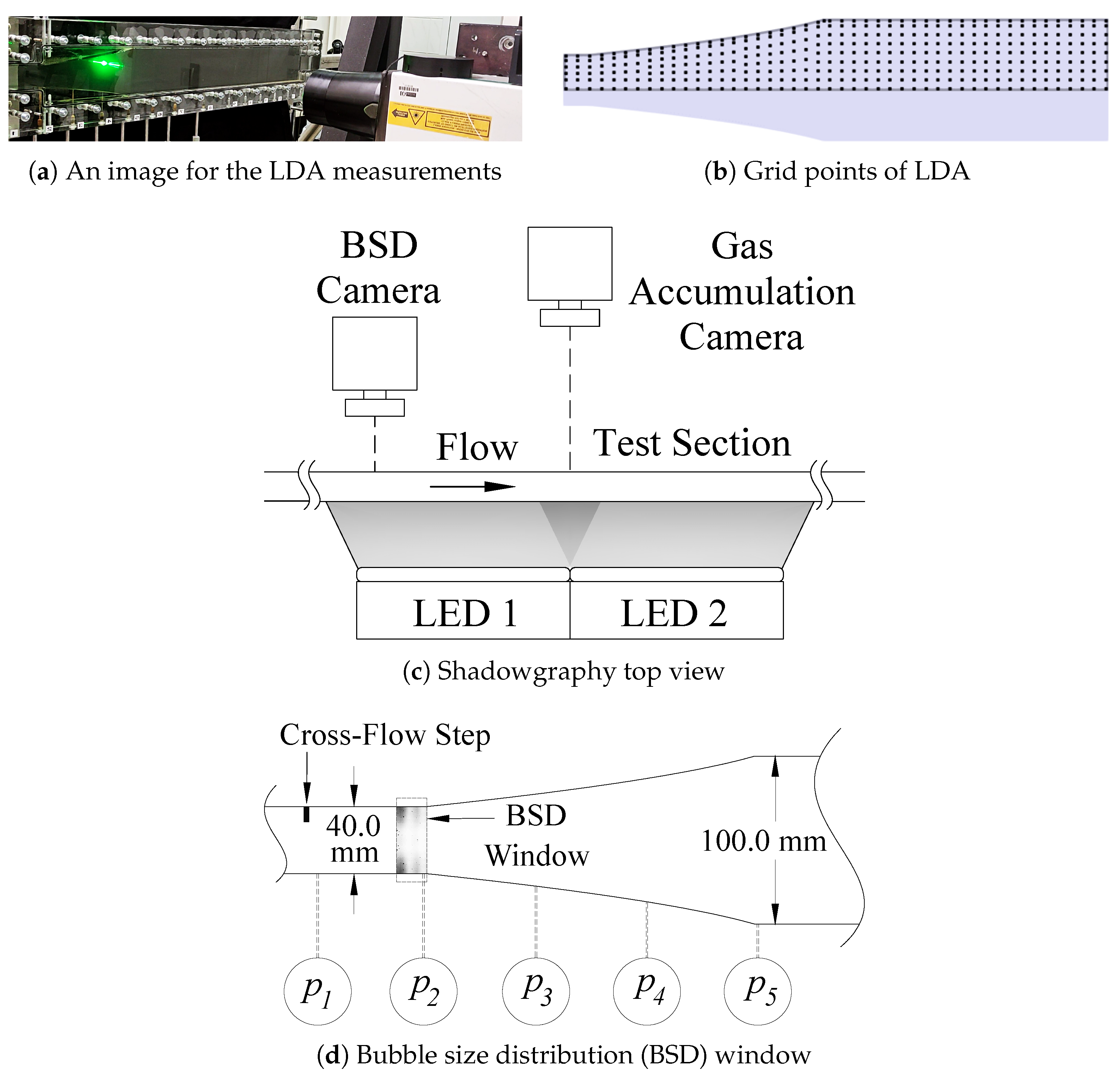
2. Experimental Setup
3. Results
3.1. Measurements of Single-Phase Velocities
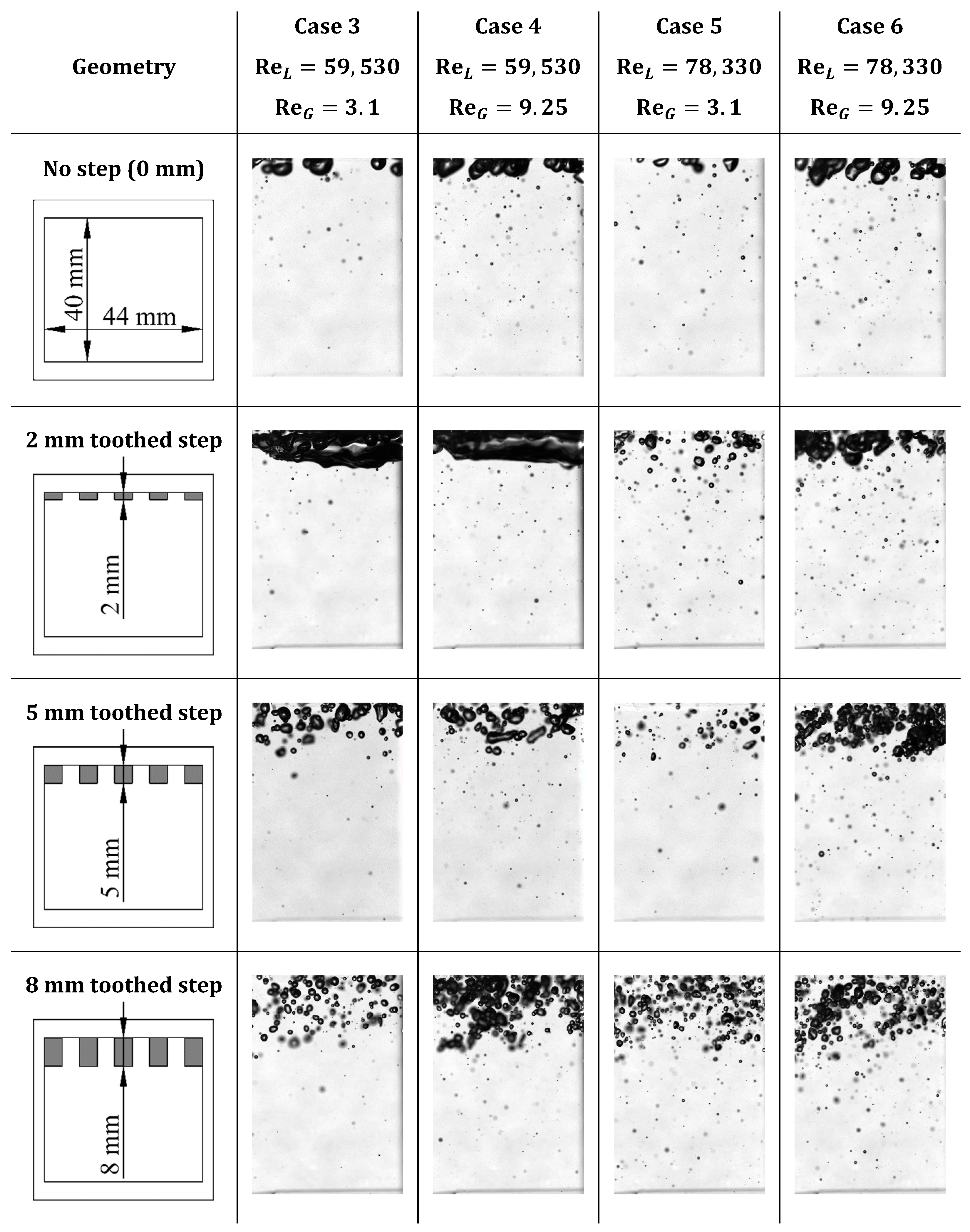
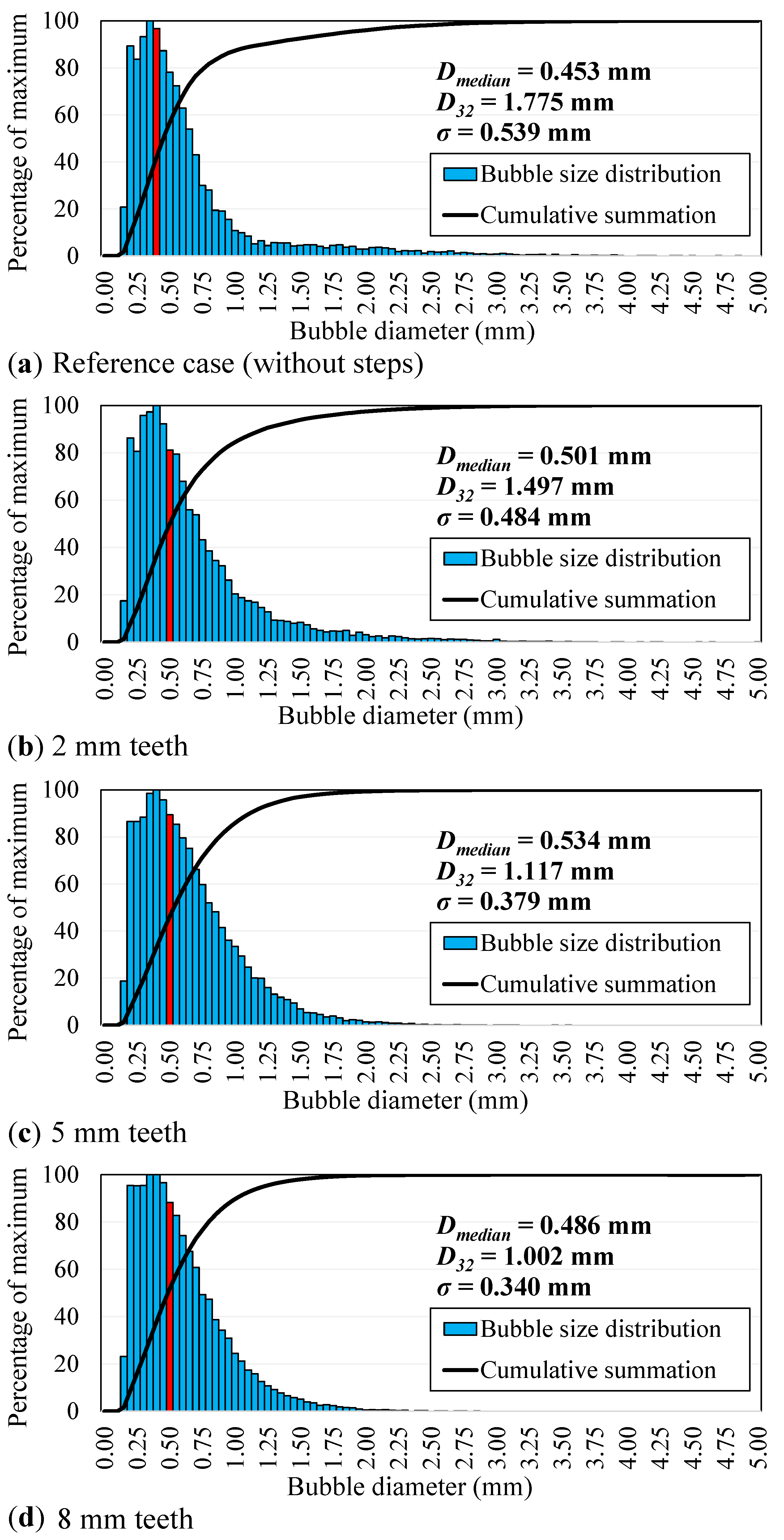
3.2. Measurements of Two-Phase Flow Conditions (Bubble Dispersion and Size Distributions)
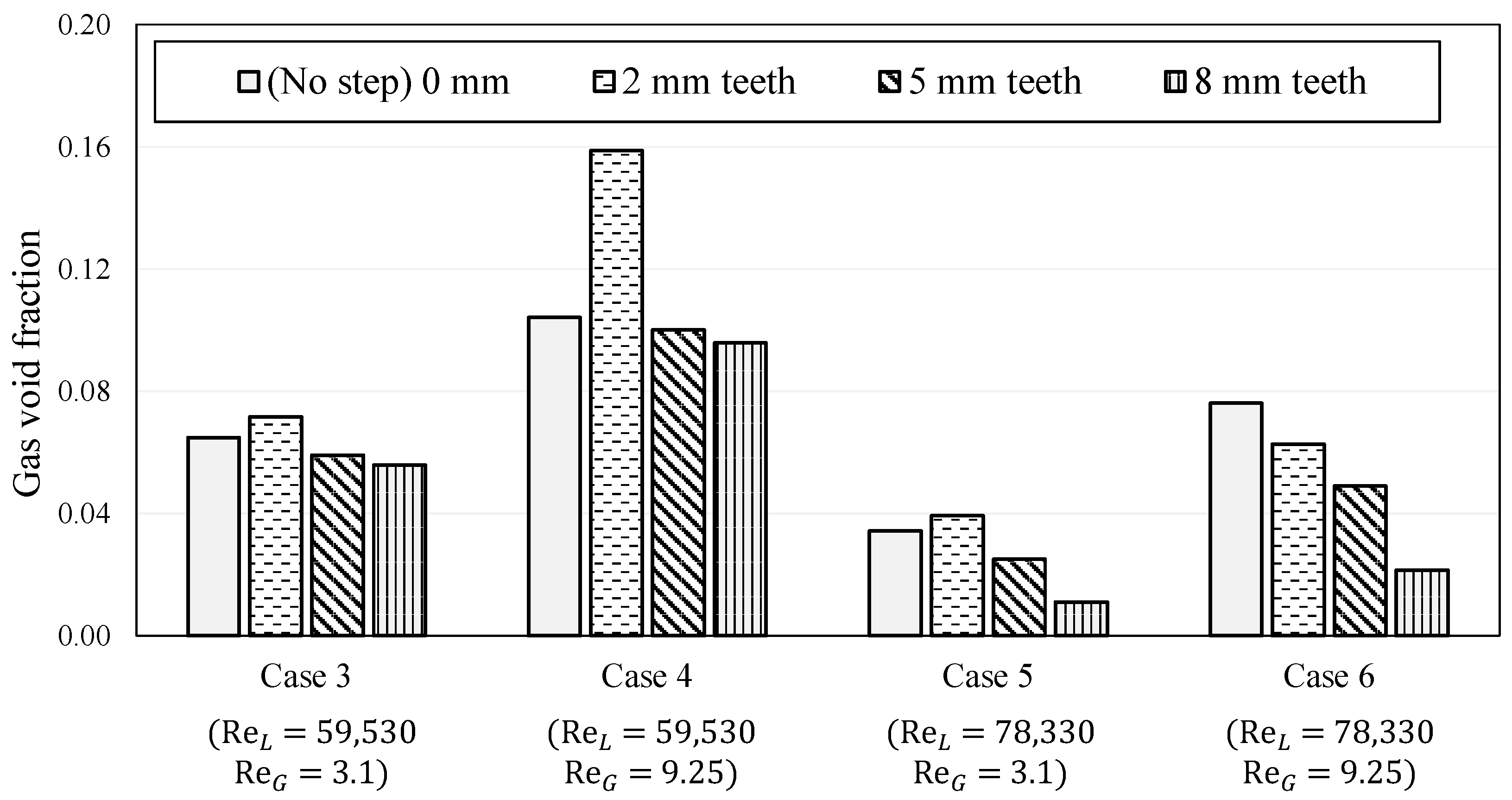
3.3. Measurements of Gas Accumulation
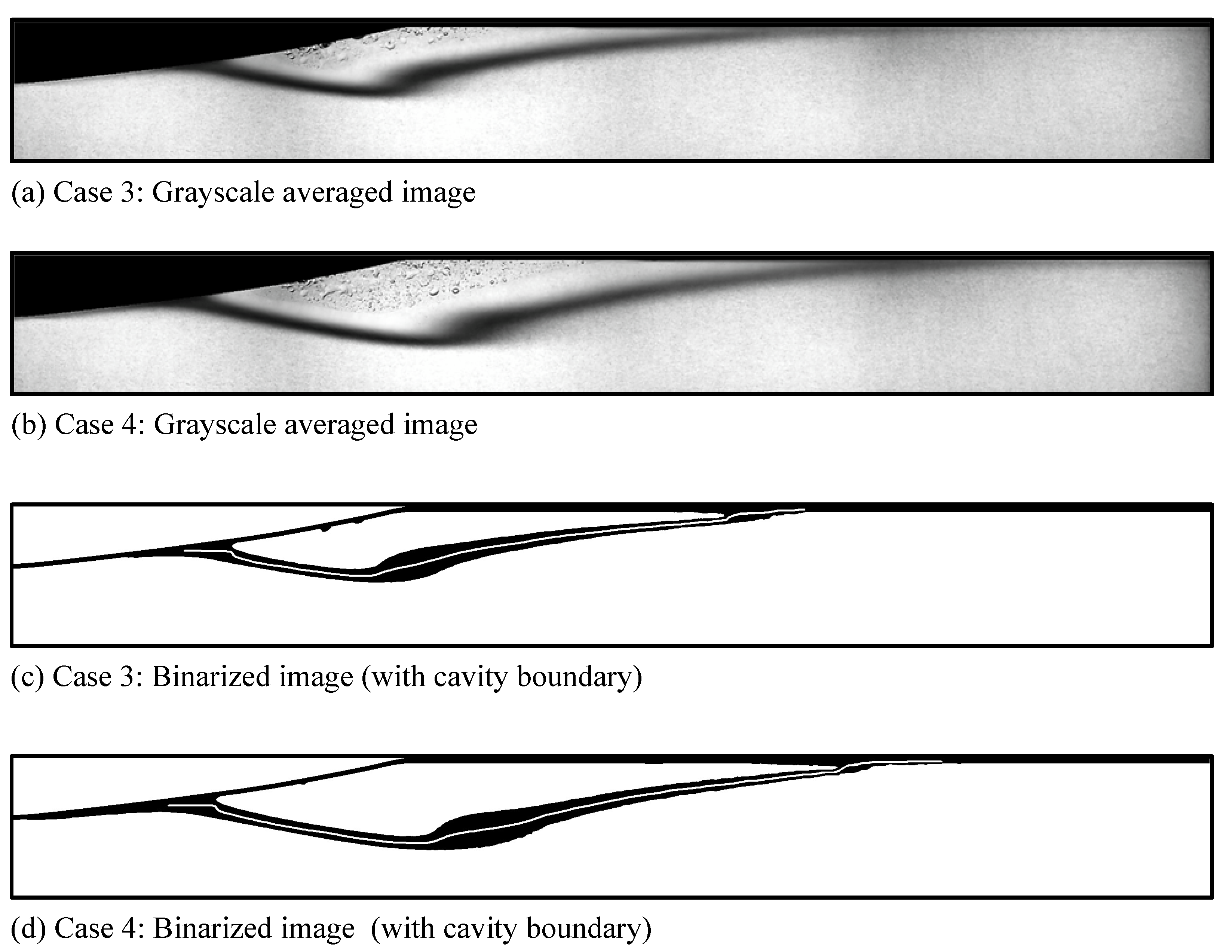
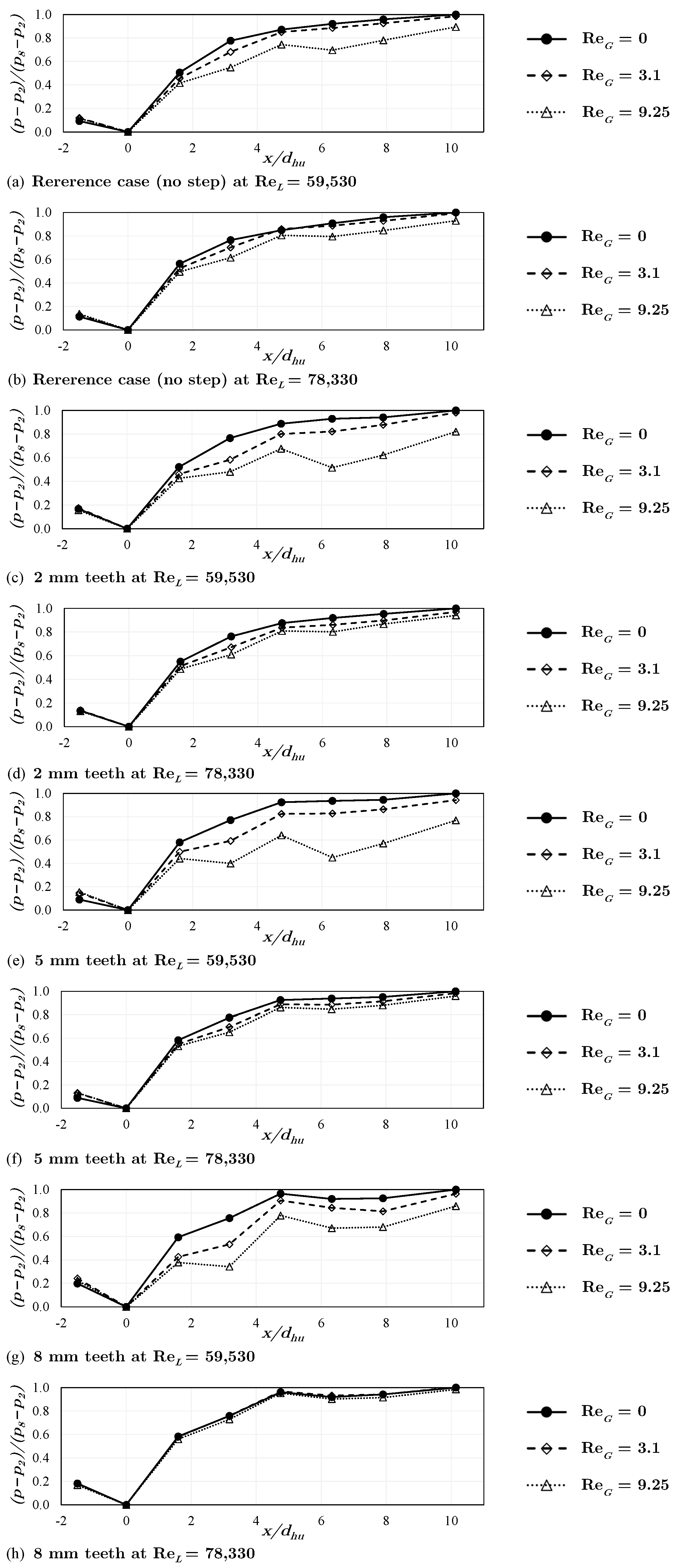
3.4. Pressure Recovery
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures and Abbreviations
| Roman characters | ||
| upstream cross-sectional area | () | |
| Sauter mean diameter | (mm) | |
| median diameter | (mm) | |
| downstream hydraulic diameter | (m) | |
| upstream hydraulic diameter | (m) | |
| I | light intensity | (cd) |
| upstream straight pipe length | (m) | |
| downstream straight pipe length | (m) | |
| reference pressure (sensor 2) | (mbar) | |
| p | local pressure | (mbar) |
| gas volume flow rate | (L/h) | |
| liquid volume flow rate | () | |
| superficial gas Reynolds number | ||
| superficial liquid Reynolds number | ||
| superficial gas velocity | (m/s) | |
| superficial liquid velocity | (m/s) | |
| x | axial distance | (m) |
| y | vertical distance | (m) |
| Greek characters | ||
| gas volume fraction | (%) | |
| density of gas | () | |
| density of liquid | () | |
| standard deviation of BSD | (mm) | |
| viscosity of gas | () | |
| viscosity of liquid | () | |
| Subscripts | ||
| d | downstream | |
| G | gas | |
| h | hydraulic | |
| L | liquid | |
| u | upstream | |
| Abbreviations | ||
| % RD | percentage of reading (for accuracy quantification) | |
| BSD | bubble size distribution | |
| LDA | Laser Doppler Anemometry | |
| LED | Light Emitting Diode | |
| LES | large eddy simulation | |
| RSM | Reynolds stress model | |
| RTD | Resistance Temperature Detector | |
| VOF | volume of fluid |
References
- Ewing, M.E.; Weinandy, J.J.; Christensen, R.N. Observations of Two-Phase Flow Patterns in a Horizontal Circular Channel. Heat Transf. Eng. 1999, 20, 9–14. [Google Scholar] [CrossRef]
- Chen, I.Y.; Tseng, C.Y.; Lin, Y.T.; Wang, C.C. Two-phase flow pressure change subject to sudden contraction in small rectangular channels. Int. J. Multiph. Flow 2009, 35, 297–306. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.; Chen, C.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Mansour, M.; Wunderlich, B.; Thévenin, D. Effect of tip clearance gap and inducer on the transport of two-phase air-water flows by centrifugal pumps. Exp. Therm. Fluid Sci. 2018, 99, 487–509. [Google Scholar] [CrossRef]
- Manzano Ruiz, J.J. Experimental and Theoretical Study of Two-Phase Flow in Centrifugal Pumps. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1980. Available online: https://hdl.handle.net/1721.1/15856 (accessed on 22 July 2025).
- Zhu, Z.; Xie, P.; Ou, G.; Cui, B.; Li, Y. Design and Experimental Analyses of Small-flow High-head centrifugal-vortex Pump for Gas-Liquid Two-phase Mixture. Chin. J. Chem. Eng. 2008, 16, 528–534. [Google Scholar] [CrossRef]
- Barrios, L.; Prado, M.G. Experimental Visualization of Two-Phase Flow Inside an Electrical Submersible Pump Stage. J. Energy Resour. Technol. 2011, 133, 042901. [Google Scholar] [CrossRef]
- Mansour, M.; Wunderlich, B.; Thévenin, D. Experimental study of two-phase air/water flows in a centrifugal pump working with a closed or a semi-open impeller. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; p. V009T27A012. [Google Scholar] [CrossRef]
- Mansour, M.; Kopparthy, S.; Thévenin, D. Investigations on the effect of rotational speed on the transport of air-water two-phase flows by centrifugal pumps. Int. J. Heat Fluid Flow 2022, 94, 108939. [Google Scholar] [CrossRef]
- Hundshagen, M.; Skoda, R. State of the art on two-phase non-miscible liquid/gas flow transport analysis in radial centrifugal pumps Part C: CFD approaches with emphasis on improved models. Int. J. Turbomach. Propuls. Power 2023, 8, 15. [Google Scholar] [CrossRef]
- Mansour, M.; Thévenin, D. State of the art on two-phase non-miscible liquid/gas flow transport analysis in radial centrifugal pumps Part B: Review of experimental investigations. Int. J. Turbomach. Propuls. Power 2023, 8, 42. [Google Scholar] [CrossRef]
- Müller, T.; Limbach, P.; Skoda, R. Numerical 3D RANS simulation of gas-liquid flow in a centrifugal pump with an Euler-Euler two-phase model and a dispersed phase distribution. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Madrid, Spain, 23–27 March 2015; Available online: https://euroturbo.eu/publications/proceedings-papers/etc2015-076/ (accessed on 22 July 2025).
- Mansour, M.; Kováts, P.; Wunderlich, B.; Thévenin, D. Experimental investigations of a two-phase gas/liquid flow in a diverging horizontal channel. Exp. Therm. Fluid Sci. 2018, 93, 210–217. [Google Scholar] [CrossRef]
- Kopparthy, S.; Mansour, M.; Janiga, G.; Thévenin, D. Numerical investigations of turbulent single-phase and two-phase flows in a diffuser. Int. J. Multiph. Flow 2020, 130, 103333. [Google Scholar] [CrossRef]
- Hundshagen, M.; Mansour, M.; Thévenin, D.; Skoda, R. Numerical investigation of two-phase air-water flow in a centrifugal pump with closed or semi-open impeller. In Proceedings of the 13th European Turbomachinery Conference on Turbomachinery Fluid Dynamics and Thermodynamics, ETC 2019, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar] [CrossRef]
- Poullikkas, A. Effects of two-phase liquid–gas flow on the performance of nuclear reactor cooling pumps. Prog. Nucl. Energy 2003, 42, 3–10. [Google Scholar] [CrossRef]
- Caridad, J.; Asuaje, M.; Kenyery, F.; Tremante, A.; Aguillón, O. Characterization of a centrifugal pump impeller under two-phase flow conditions. J. Pet. Sci. Eng. 2008, 63, 18–22. [Google Scholar] [CrossRef]
- Amoresano, A.; Langella, G.; Niola, V.; Quaremba, G. Advanced Image Analysis of Two-Phase Flow inside a Centrifugal Pump. Adv. Mech. Eng. 2014, 6, 958320. [Google Scholar] [CrossRef]
- Zhu, J.; Guo, X.; Liang, F.; Zhang, H.Q. Experimental study and mechanistic modeling of pressure surging in electrical submersible pump. J. Nat. Gas Sci. Eng. 2017, 45, 625–636. [Google Scholar] [CrossRef]
- Monte Verde, W.; Biazussi, J.L.; Sassim, N.A.; Bannwart, A.C. Experimental study of gas-liquid two-phase flow patterns within centrifugal pumps impellers. Exp. Therm. Fluid Sci. 2017, 85, 37–51. [Google Scholar] [CrossRef]
- Mansour, M.; Kopparthy, S.B.; Thévenin, D. Improving air-water two-phase flow pumping in centrifugal pumps using novel grooved front shrouds. Chem. Eng. Res. Des. 2023, 197, 173–191. [Google Scholar] [CrossRef]
- Chen, I.Y.; Chen, Y.M.; Yang, B.C.; Wang, C.C. Two-phase flow pattern and frictional performance across small rectangular channels. Appl. Therm. Eng. 2009, 29, 1309–1318. [Google Scholar] [CrossRef]
- Wambsganss, M.; Jendrzejczyk, J.; France, D.; Obot, N. Frictional pressure gradients in two-phase flow in a small horizontal rectangular channel. Exp. Therm. Fluid Sci. 1992, 5, 40–56. [Google Scholar] [CrossRef]
- Vallée, C.; Höhne, T.; Prasser, H.M.; Sühnel, T. Experimental investigation and CFD simulation of horizontal stratified two-phase flow phenomena. Nucl. Eng. Des. 2008, 238, 637–646. [Google Scholar] [CrossRef]
- Aziz, W.; Chaturvedi, S.; Kheireddine, A. Thermodynamic analysis of two-component, two-phase flow in solar collectors with application to a direct-expansion solar-assisted heat pump. Energy 1999, 24, 247–259. [Google Scholar] [CrossRef]
- Chen, I.Y.; Liu, C.C.; Chien, K.H.; Wang, C.C. Two-phase flow characteristics across sudden expansion in small rectangular channels. Exp. Therm. Fluid Sci. 2007, 32, 696–706. [Google Scholar] [CrossRef]
- Abdelall, F.F.; Hahn, G.; Ghiaasiaan, S.M.; Abdel-Khalik, S.I.; Jeter, S.S.; Yoda, M.; Sadowski, D.L. Pressure drop caused by abrupt flow area changes in small channels. Exp. Therm. Fluid Sci. 2005, 29, 425–434. [Google Scholar] [CrossRef]
- Ahmed, W.H.; Ching, C.Y.; Shoukri, M. Development of two-phase flow downstream of a horizontal sudden expansion. Int. J. Heat Fluid Flow 2008, 29, 194–206. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Modeling of turbulent heat-transfer augmentation in gas-droplet non-boiling flow in diverging and converging axisymmetric ducts with sudden expansion. Energies 2022, 15, 5861. [Google Scholar] [CrossRef]
- Anupriya, S.; Jayanti, S. Experimental and modelling studies of gas–liquid vertical annular flow through a diverging section. Int. J. Multiph. Flow 2014, 67, 180–190. [Google Scholar] [CrossRef]
- Hwang, J.J.; Tseng, F.G.; Pan, C. Ethanol-CO2 two-phase flow in diverging and converging microchannels. Int. J. Multiph. flow 2005, 31, 548–570. [Google Scholar] [CrossRef]
- Deniz, E.; Eskin, N. Hydrodynamic characteristics of two-phase flow through horizontal pipe having smooth expansion. ISI Bilim. Ve Tek. Derg.-J. Therm. Sci. Technol. 2015, 35, 1–9. [Google Scholar]
- Kourakos, V.G.; Rambaud, P.; Chabane, S.; Pierrat, D.; Buchlin, J.M. Two-phase flow modelling within expansion and contraction singularities. Comput. Methods Multiph. Flow V 2009, 63, 27. [Google Scholar] [CrossRef]
- Deniz, E.; Eskin, N. Experimental and Numerical Investigation of Two-Phase Flow through Enlarging Singularity. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 16–19 July 2012; pp. 1–9. Available online: https://docs.lib.purdue.edu/iracc/1254/ (accessed on 22 July 2025).
- Eskin, N.; Deniz, E. Pressure drop of two-phase flow through horizontal channel with smooth expansion. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 16–19 July 2012; pp. 1–10. Available online: https://docs.lib.purdue.edu/iracc/1255/ (accessed on 22 July 2025).
- Ahmadpour, A.; Noori Rahim Abadi, S.; Kouhikamali, R. Numerical simulation of two-phase gas–liquid flow through gradual expansions/contractions. Int. J. Multiph. Flow 2016, 79, 31–49. [Google Scholar] [CrossRef]
- Ding, G.; Chen, J.; Li, Z. An investigation on the bubble breakup characteristics by recirculation flow in a venturi channel. In Proceedings of the Fluids Engineering Division Summer Meeting, Online, 10–12 August 2021; Volume 3, Fluid Mechanics; Micro and Nano Fluid Dynamics; Multiphase Flow. p. V003T08A002. [Google Scholar] [CrossRef]
- Hundshagen, M.; Mansour, M.; Thévenin, D.; Skoda, R. 3D simulation of gas-laden liquid flows in centrifugal pumps and the assessment of two-fluid CFD methods. Exp. Comput. Multiph. Flow. 2021, 3, 186–207. [Google Scholar] [CrossRef]
- Nguyen, B.D.; Popp, S.; Hundshagen, M.; Skoda, R.; Mansour, M.; Thévenin, D.; Hasse, C. Large eddy simulations of turbulent gas-liquid flows in a diverging horizontal channel using a hybrid multiphase approach. J. Fluids Eng. 2022, 145, 031501. [Google Scholar] [CrossRef]
- Mansour, M.; Zanini, N.; Shenouda, M.; Pinelli, P.; Thévenin, D.; Suman, A.; Thévenin, D. Minimizing gas accumulation in two-phase flow within a diverging horizontal channel using cross-flow millimeter-size steps. In Proceedings of the 16th European Turbomachinery Conference on Turbomachinery Fluid Dynamics and Thermodynamics ETC16, Hannover, Germany, 24–28 March 2025. [Google Scholar]
- Mansour, M. Transport of Two-Phase Air-Water Flows in Radial Centrifugal Pumps. Ph.D. Thesis, University of Magdeburg, Magdeburg, Germany, 2020. [Google Scholar] [CrossRef]

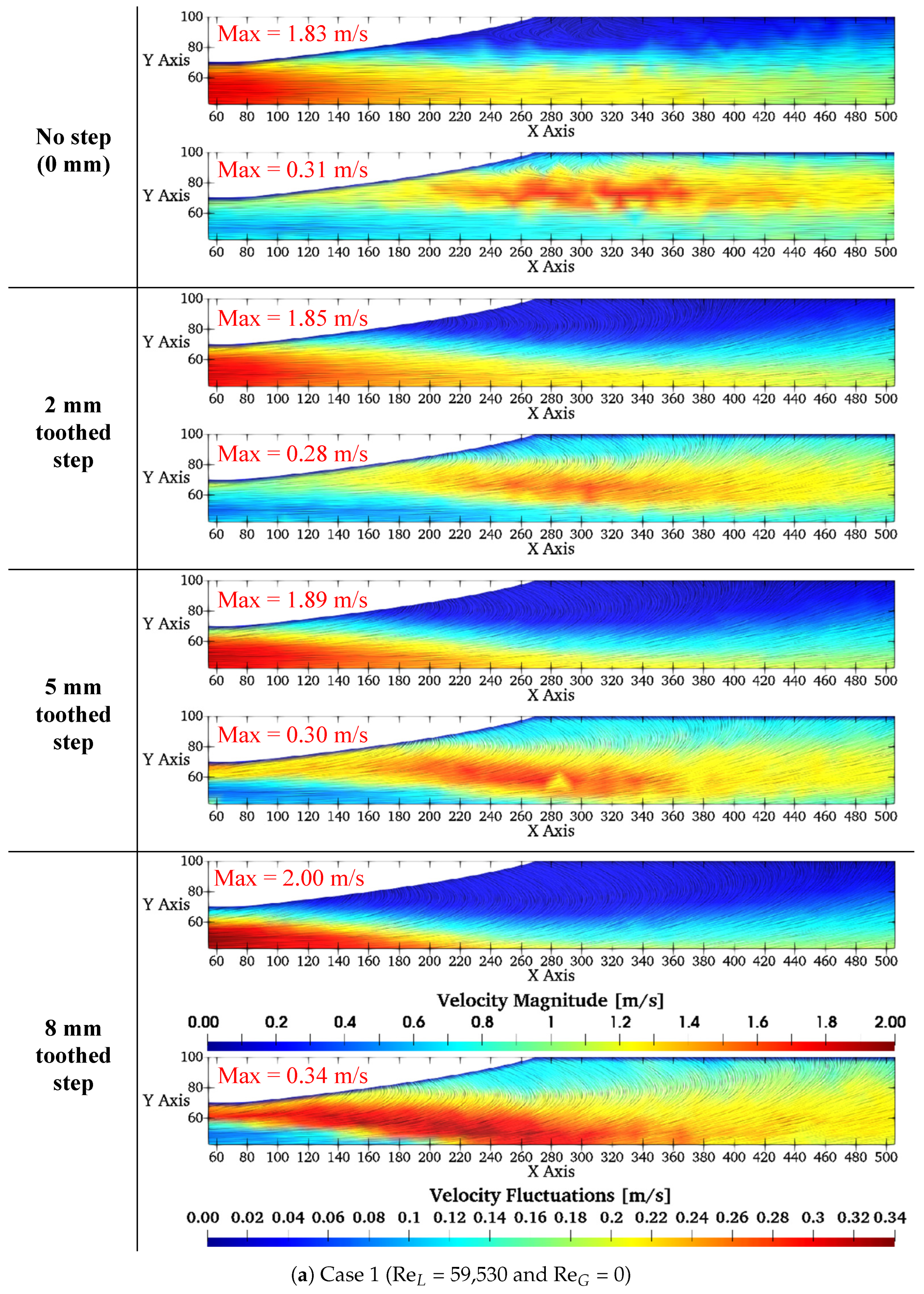
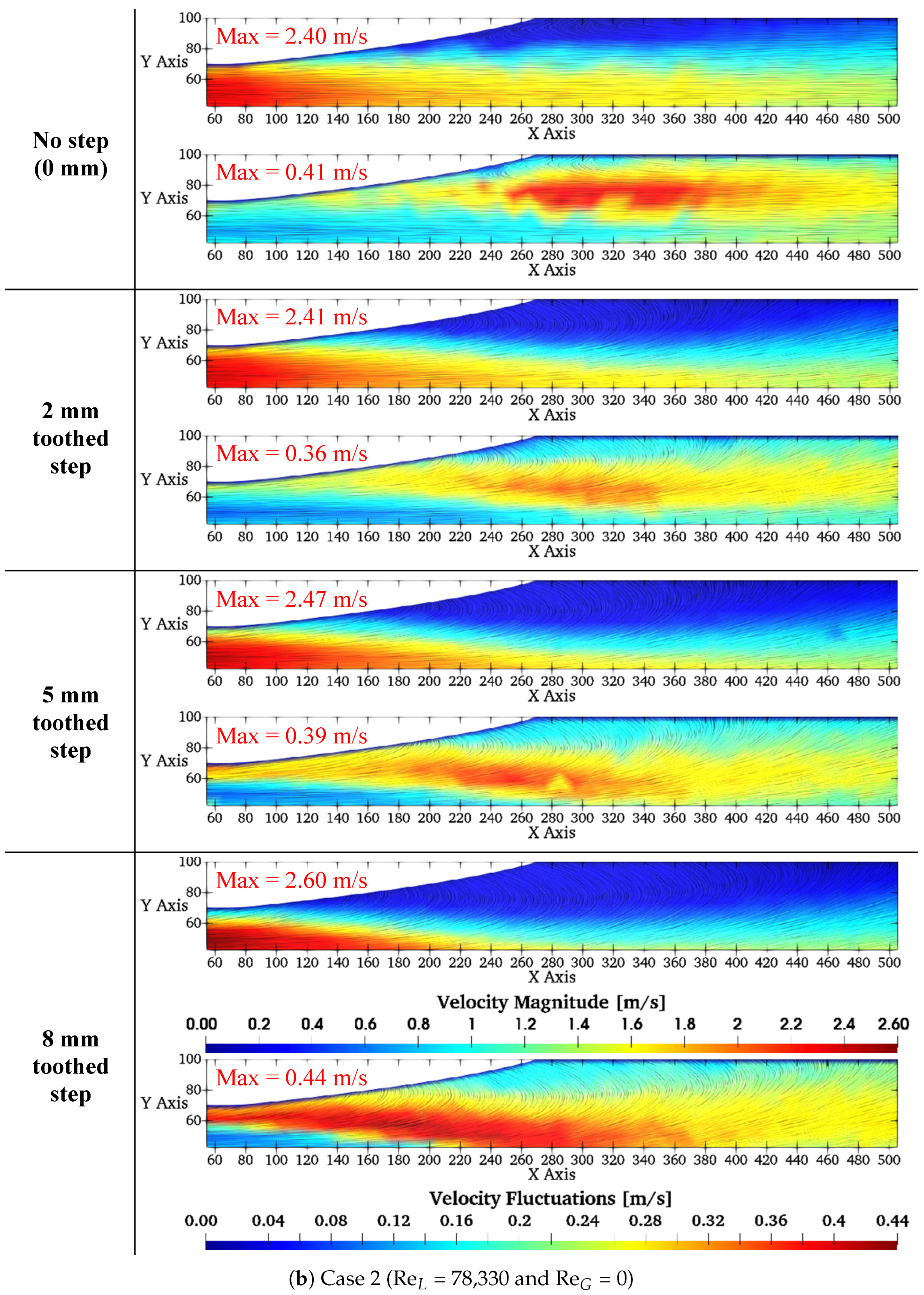



| Case no. | (m3/h) | (L/h) | ReL | ReG | (%) |
|---|---|---|---|---|---|
| 1 | 9.5 | 0 | 59,530 | 0 | 0 |
| 2 | 12.5 | 0 | 78,330 | 0 | 0 |
| 3 | 9.5 | 7.07 | 59,530 | 3.10 | 0.074 |
| 4 | 9.5 | 21.21 | 59,530 | 9.25 | 0.223 |
| 5 | 12.5 | 7.07 | 78,330 | 3.10 | 0.056 |
| 6 | 12.5 | 21.21 | 78,330 | 9.25 | 0.169 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Mansour, M.; Zanini, N.; Shenouda, M.; Pinelli, M.; Suman, A.; Thévenin, D. Reducing Gas Accumulation in Horizontal Diffusers Under Two-Phase Flow Using Upstream Cross-Flow Steps. Int. J. Turbomach. Propuls. Power 2025, 10, 20. https://doi.org/10.3390/ijtpp10030020
Mansour M, Zanini N, Shenouda M, Pinelli M, Suman A, Thévenin D. Reducing Gas Accumulation in Horizontal Diffusers Under Two-Phase Flow Using Upstream Cross-Flow Steps. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(3):20. https://doi.org/10.3390/ijtpp10030020
Chicago/Turabian StyleMansour, Michael, Nicola Zanini, Mena Shenouda, Michele Pinelli, Alessio Suman, and Dominique Thévenin. 2025. "Reducing Gas Accumulation in Horizontal Diffusers Under Two-Phase Flow Using Upstream Cross-Flow Steps" International Journal of Turbomachinery, Propulsion and Power 10, no. 3: 20. https://doi.org/10.3390/ijtpp10030020
APA StyleMansour, M., Zanini, N., Shenouda, M., Pinelli, M., Suman, A., & Thévenin, D. (2025). Reducing Gas Accumulation in Horizontal Diffusers Under Two-Phase Flow Using Upstream Cross-Flow Steps. International Journal of Turbomachinery, Propulsion and Power, 10(3), 20. https://doi.org/10.3390/ijtpp10030020







