As the reference case for this work, the ACAT fan blade tested in AneCom AeroTest [
29] and extensively employed by the UPM turbomachinery group for aeroelastic and noise analyses [
25,
26] is used. The blade is isolated from the intake and the remainder of the stage for this test. The main characteristics of the blade are summarized in
Table 1. This configuration has 20 blades. To simplify the test of the present work, a quasi-2D annular approximation of the geometry is used. For this purpose, a radial section of the ACAT rotor 1 blade is taken at approximately 60% of the blade span. The operating point is based on sea-level static conditions from the experimental reference.
Two configurations are used in this work based on the reference geometry: a single-passage configuration (
Figure 3), and a full annulus configuration. In both cases, Riemann boundary conditions are used at the inlet of the domain. The reference velocity, static pressure, and static temperature are imposed at the inlet based on a 3D configuration defined by Chennuru et al. [
25]. In this case, a 3D configuration with an axisymmetric intake design was evaluated at take-off conditions with no crosswind. Static pressure is fixed at the domain exit. The inlet Mach number of the section is
. In the single-passage configuration, periodic boundary conditions are imposed at the lateral sides of the blade passage. Viscous adiabatic walls are applied to blade surfaces. The top and bottom parts of the domain are modeled by symmetry boundary conditions. Spalart–Allmaras with wall functions is used as the turbulence closure model for this configuration. A
of between 30 and 100 is set for all the surfaces. A total of 35,000 nodes are used per passage. The fan operational speed is fixed to 70% of the maximum fan speed. The Reynolds number for this case is approximately
. In all cases of this study, the flow is initialized from an undisturbed base flow field obtained by steady RANS computation (
Figure 4). The different cases evaluated in this work, and their respective CFD setups are summarized in
Table 2.
3.1. Low-Frequency Application: Single Passage with Static Pressure Perturbation
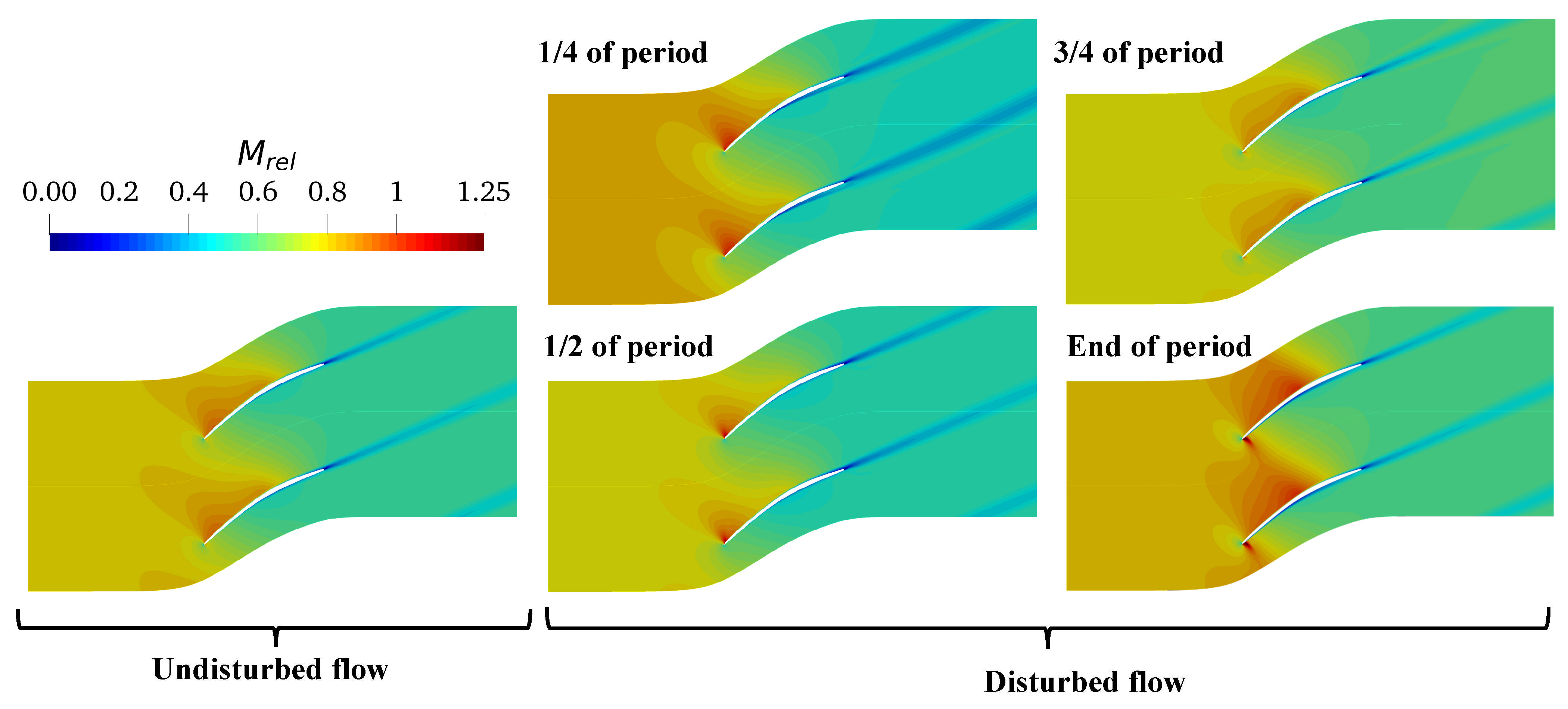
As an initial case to demonstrate the applicability of the PSpTM method to transonic turbomachinery design, a low-frequency static pressure uniform perturbation at the inlet is proposed for a single-passage domain (Case A in
Table 2). This results in a wave perturbation at the inlet, with wave number
. The fundamental frequency of the perturbation is equal to the fan rotation frequency. This results in a Strouhal number of approximately
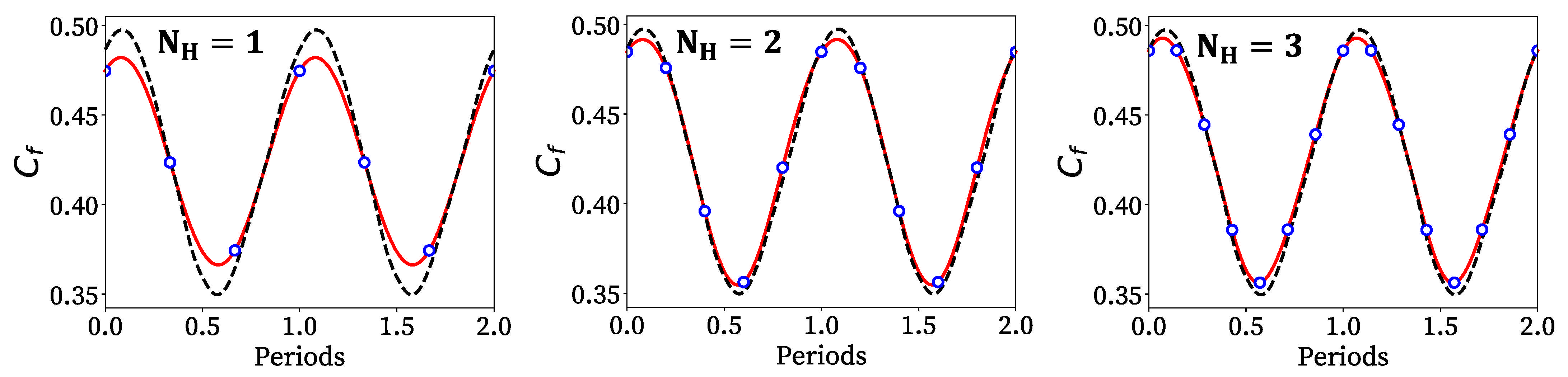
. The amplitude of the perturbation is set to 10% of the reference inlet static pressure. This results in notable variations on the aerodynamics of the blade section (
Figure 4), with nonlinear phenomena such as shock waves migrating from the pressure to the suction side during the period of the perturbation. This case is intended to mimic a pressure perturbation created by the intake’s nonaxisymmetric geometry. In these cases, the local geometry changes result in a quasi-steady, low engine order, azimuthal variation of the static pressure along the intake duct. This perturbation becomes unsteady in the fan domain with the fan rotation as the fundamental frequency. The perturbation has been exaggerated to demonstrate the method’s capabilities. The PSpTM method is applied with an increasing number of harmonics in the solution, with
,
, and
. The BDF2 method is used to benchmark the PSpTM method.
For the BDF2 approach, 100 time steps are used per fundamental period with the aim of capturing events of higher frequency. To obtain an equivalent level of convergence, the BDF2 method is set to have 20 and 40 Newton and Jacobi inner iterations per physical time step, respectively. The maximum CFL for the implicit DTS scheme is set to 50. The case is run for 25 fundamental periods to evaluate the system convergence. To benchmark the PSpTM method, it is necessary to guarantee an appropriate level of accuracy in the time solution. This convergence strategy was selected from different combinations to obtain sufficient time convergence in the solution for a reasonable computational cost. In many industrial applications, a much lower number of internal iterations is normally used. However, this can result in a notable reduction in time accuracy, despite achieving periodic convergence. Hence, to enable an adequate comparison between the BDF2 and the PSpTM approach, a highly converged temporal solution is used.
As defined in the previous section, in the PSpTM method, the number of time steps required per period is a function of the number of harmonics of the solution. Thus, the number of time steps will change for each of the four values of
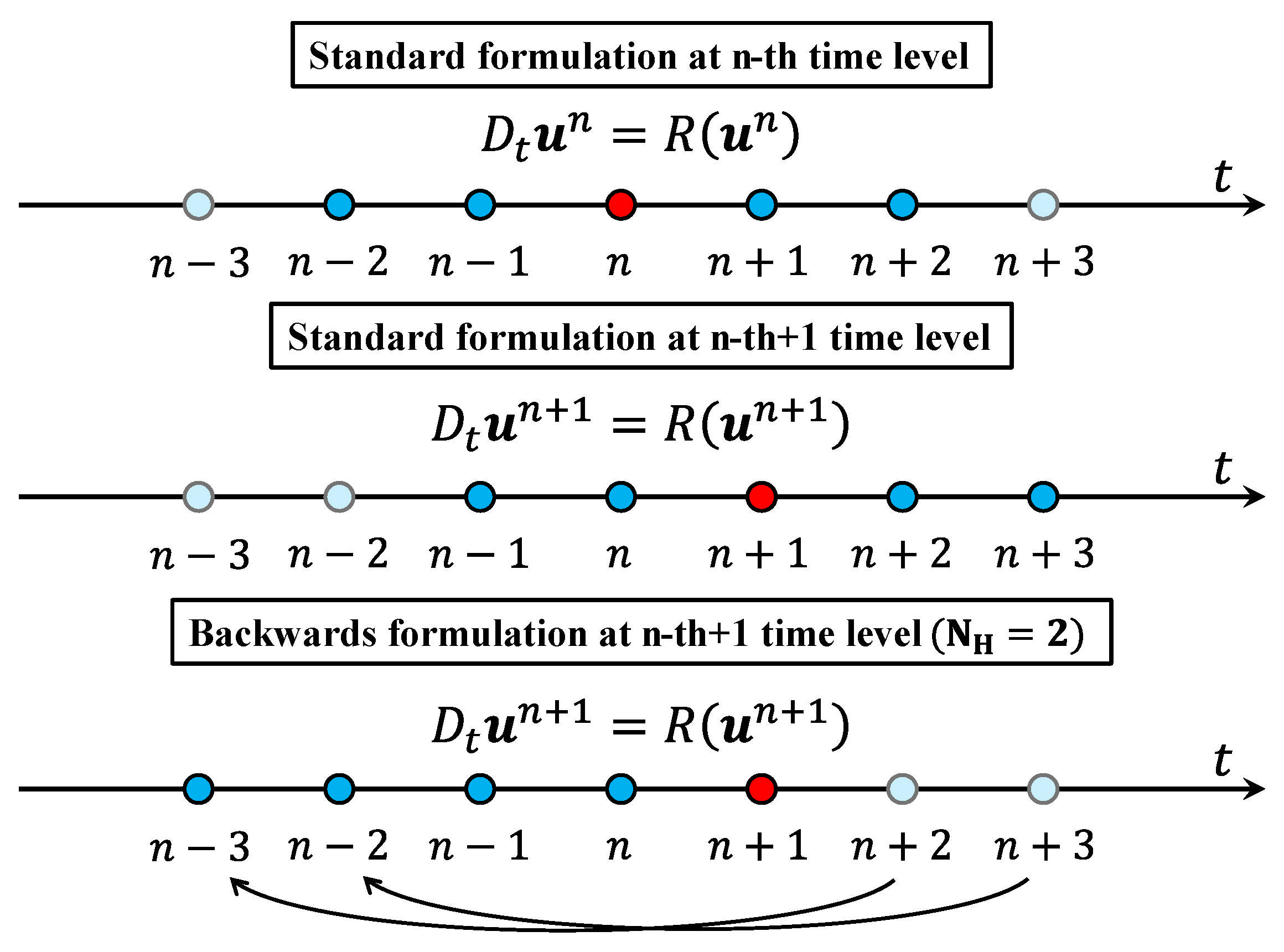
of this test. Due to the DTS-PI (
Section 2.2) approach [
22] in the PSpTM method, the PSpTM method ends requiring fewer internal iterations in the DTS to achieve the required convergence level. This contributes substantially to the reduction in the computational cost of this method. For this reason, for the current case, the number of inner iterations was set to 5 and 25 for the Newton and Jacobi iterations, respectively. This results in a much lower cost per time step than the BDF2 method. The maximum CFL for the inner iterations is set to 50.
To compare the accuracy of the PSpTM method with the BDF2 approach, the mass-weighted average of the total pressure at the outlet plane is used. The total pressure is scaled as a total pressure ratio with the time average of the total pressure value at the inlet (
Figure 5). The PSpTM method only requires a few temporal time steps per period, so it is not simple to directly observe the temporal evolution of the variables. The temporal derivative of the PSpTM method is based on a harmonic series. Thus, to adequately visualize the temporal evolution of the solution, a Fourier series fitted for the fundamental frequency and the number of harmonics is included based on the actual values at each time step (
Figure 5).
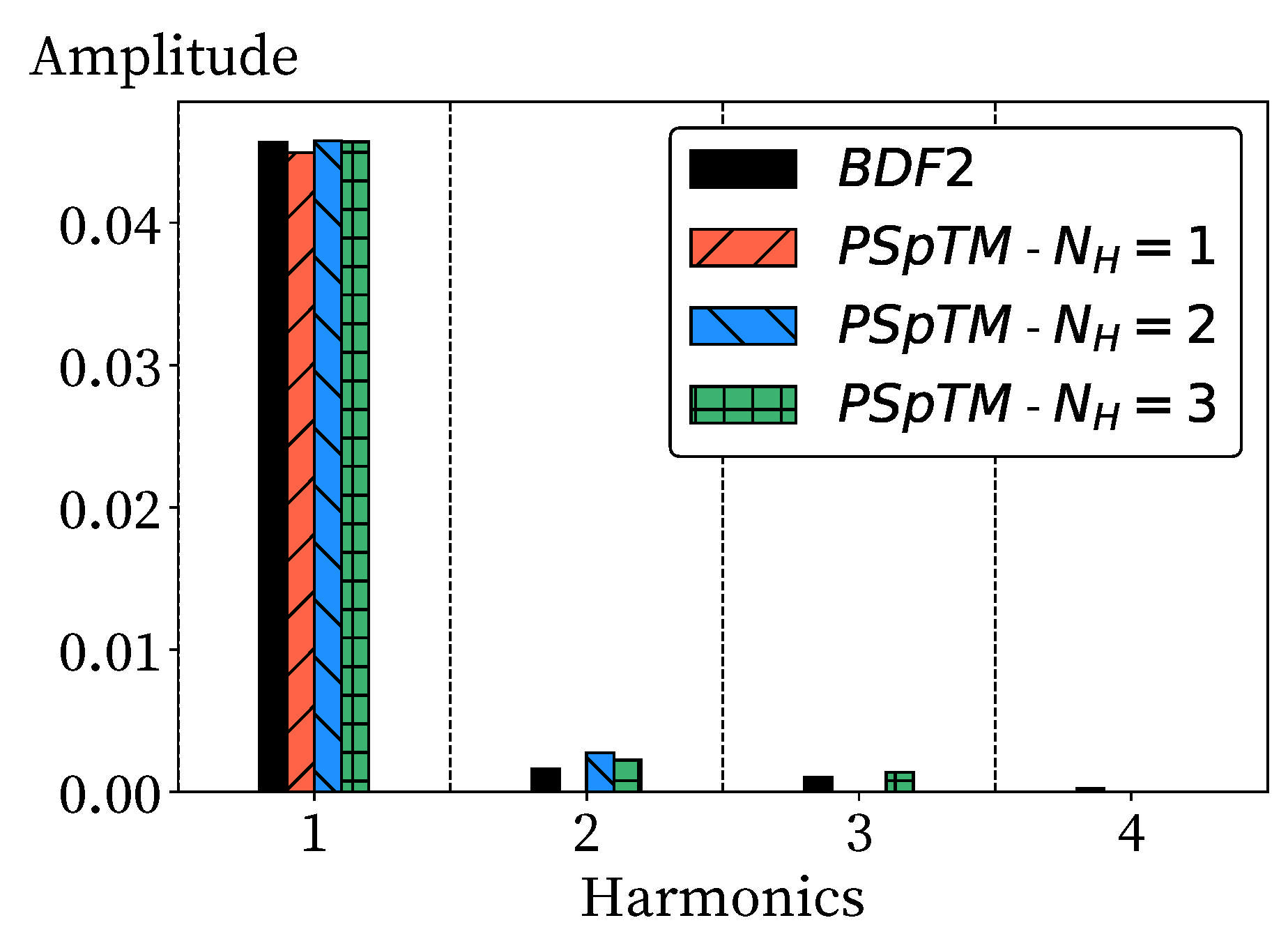
Given the amplitude of the inlet perturbation, the temporal variation of the flow is mostly defined by the first harmonic of the solution of the PSpTM method. Second-order contributions of the higher harmonics are present due to the flow nonlinearities, such as shock waves. The accuracy of the PSpTM method increases progressively with the number of harmonics included in the solution (
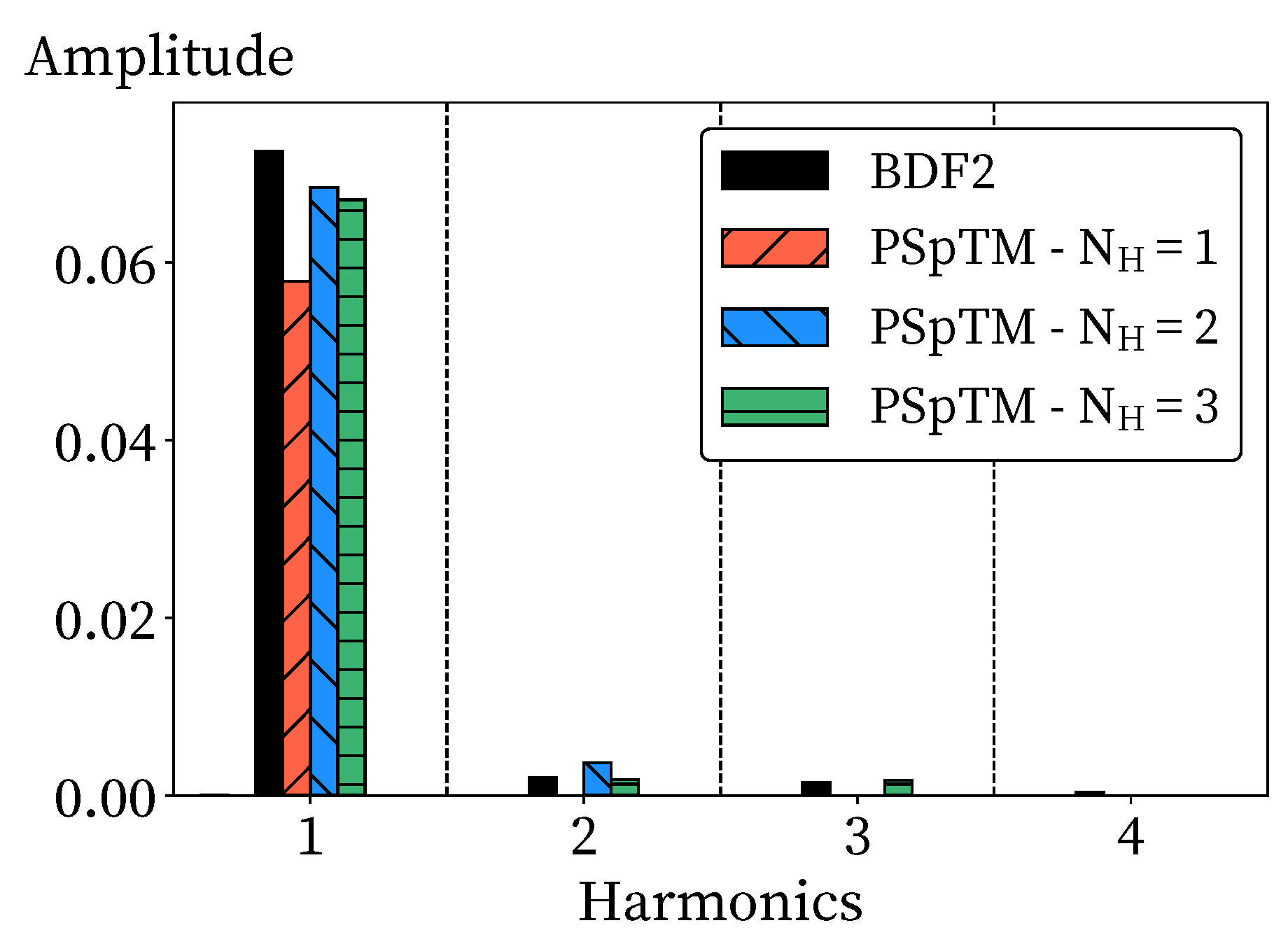
Figure 5). However, after retaining two harmonics, the gains in accuracy are marginal. In order to further illustrate this, a Fourier transform (FT) is applied to the temporal variation of the mass weighted value of the total pressure ratio at the outlet for both the BDF2 and the different PSpTM method (
Figure 6). As mentioned, the accuracy of the predicted amplitude of the method increases with the number of harmonics. The first harmonic contains most of the amplitude of the solution, with a second-order contribution from the second and third harmonics.
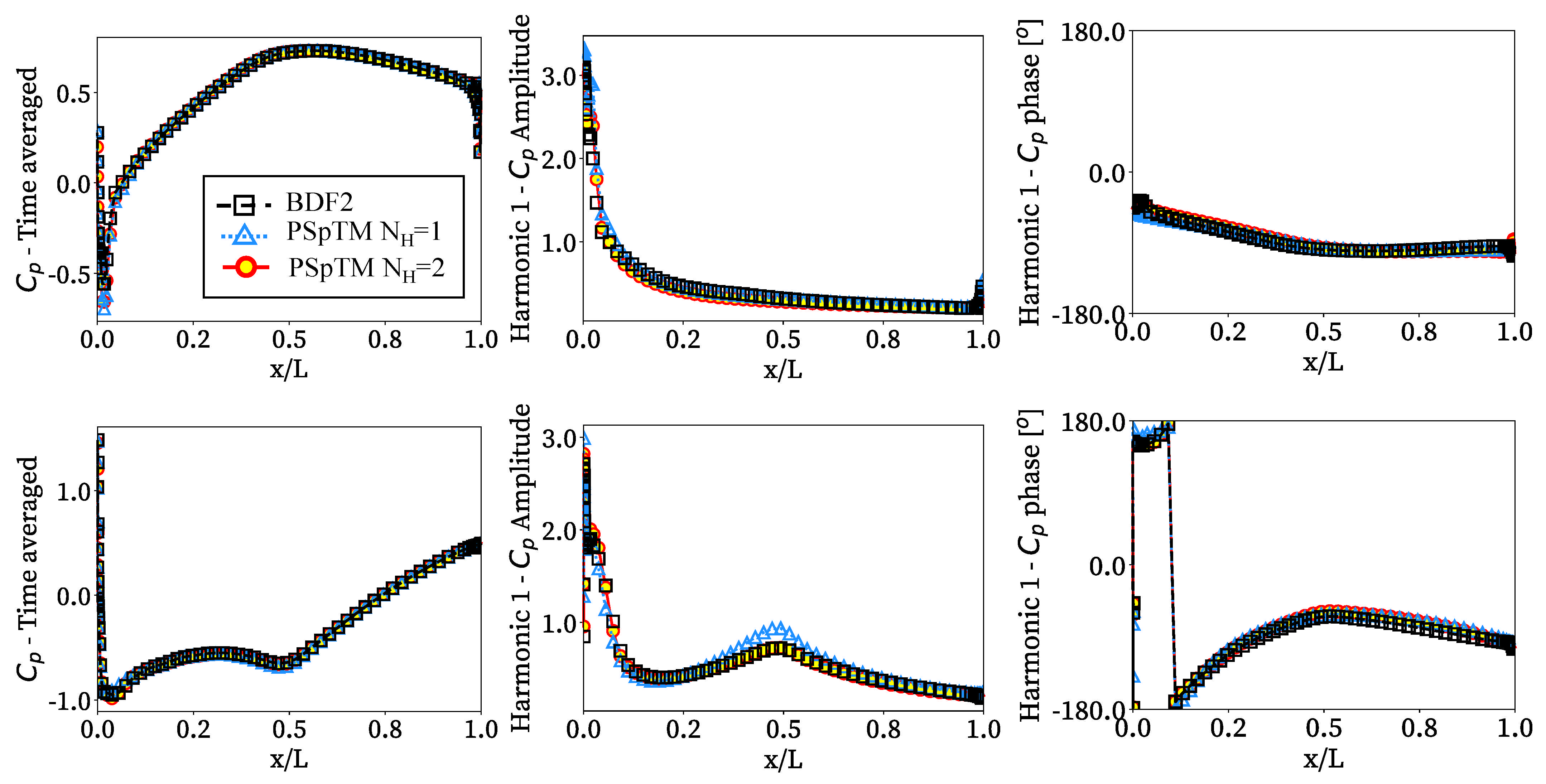
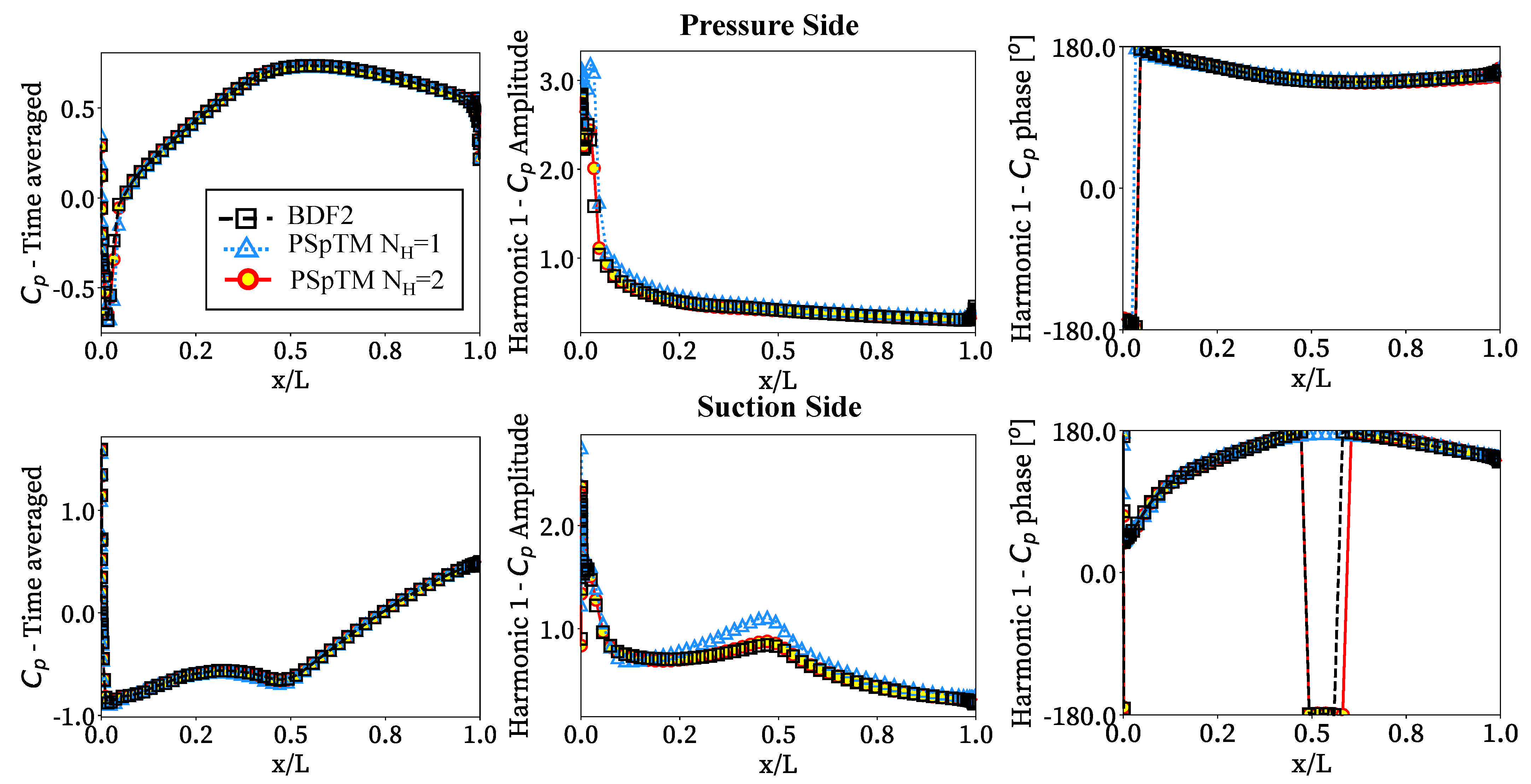
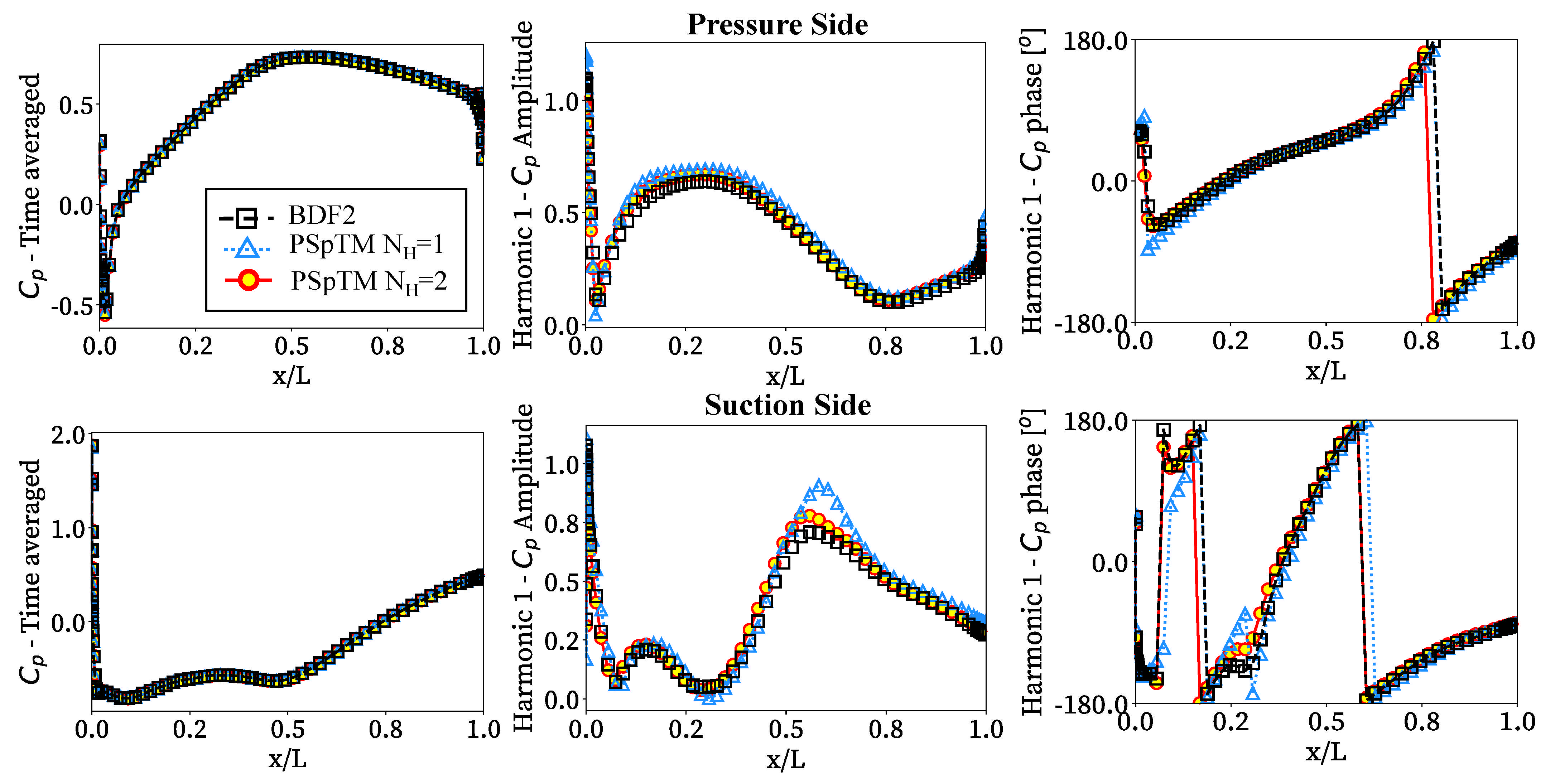
Figure 7 compares the time average and the amplitude and phase of the first harmonic of the pressure coefficient,
, along the blade to assess the PSpTM’s capability to capture the local flow variations over time. Since no notable variations were observed between the
and
solutions of the first harmonic, only the
case is included. Overall, the PSpTM method has adequate agreement with the BDF2 baseline in the time-averaged pressure distribution. The method can also capture some flow nonlinearities, such as the shock waves emerging near the leading edge in both the pressure and suction side and given time instants (
Figure 4). The shock wave at the pressure side also reaches the suction side of the contiguous blade around half of the chord. Some discrepancies are observed between the BDF2 and PSpTM in the amplitude of the first harmonic when only a single harmonic is retained (
). These are more noticeable on the leading edge of the pressure side and around the center of the blade chord of the suction side. These two regions of uncertainty are the result of the same shock wave that expands through the blade passage (
Figure 4). That shock blocking the passage triggers higher harmonics on the flow that the case with
cannot accurately capture. Nevertheless, the cases with a higher number of harmonics correctly include the effects of the shock wave and other second-order effects. Finally, some differences are observed in the solution phase for both harmonics. However, the general distribution of the first harmonic phase is properly captured with both cases in the PSpTM. Thus, the method can accurately capture the main flow unsteadiness over the blade.
Once the accuracy of the PSpTM method has been addressed, it is necessary to compare the performance of the PSpTM method with the reference BDF2 approach. For this purpose, the periodic norm
is used: In this case, the periodic norm of the static pressure,
, nondimensionalized with the isentropic dynamic head at the exit,
, is evaluated in the whole domain.
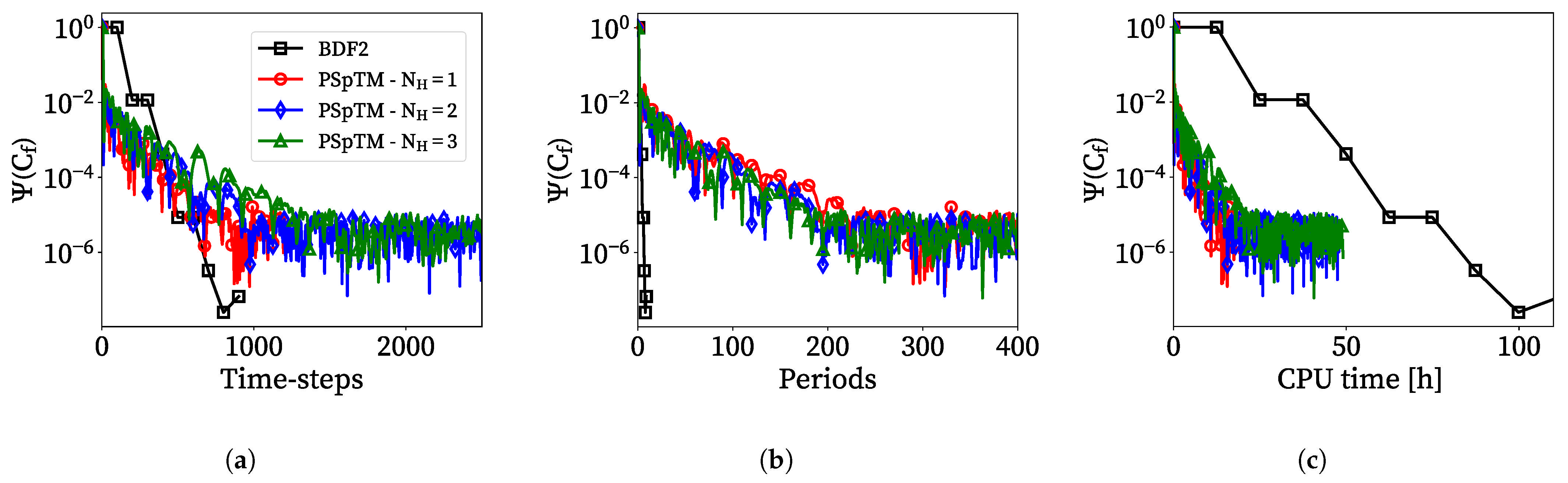
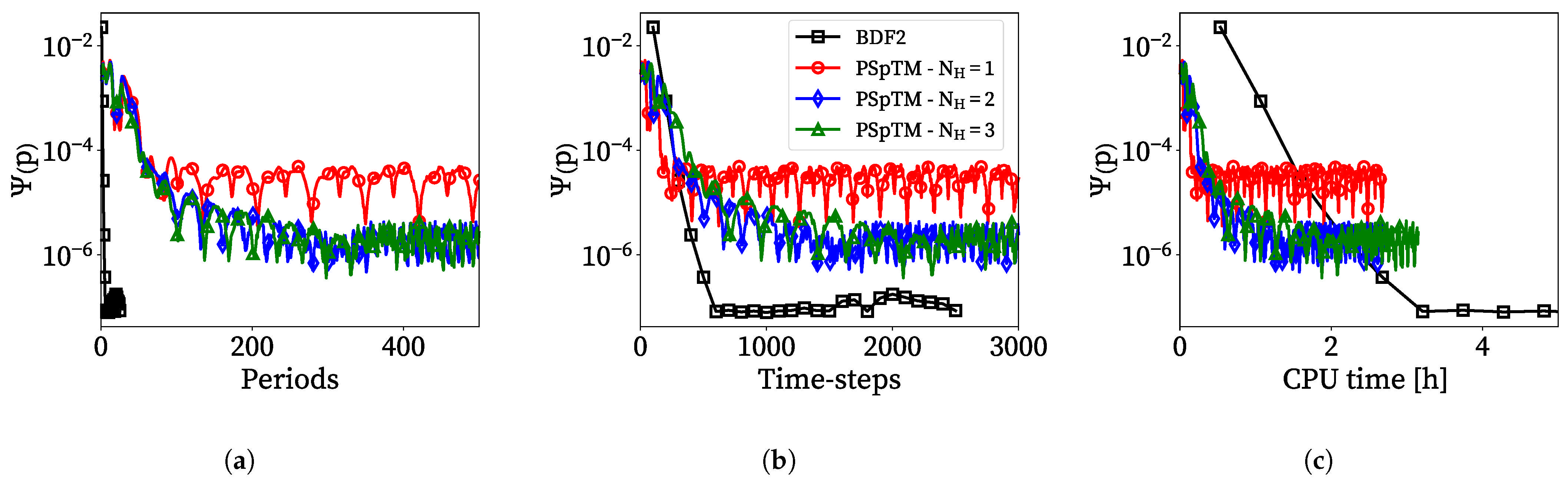
Figure 8 displays the periodic norm as a function of the number of periods, time steps, and the overall computational cost required for convergence. The CPU time unit is defined as the actual time multiplied by the number of CPU cores used in the simulation, which is an approximation of the computational time in a serial machine.
Figure 8a shows that the PSpTM method requires substantially more periods to achieve a periodic convergence than the BDF2 approach. However, this slow convergence rate does not result in a significant penalty in the number of time steps required to achieve periodic convergence (
Figure 8b). This is due to the much lower number of time steps required per period in the PSpTM method. One of the key advantages of the PSpTM is that it requires fewer inner iterations to achieve a similar level of convergence per time step than conventional approaches such as the BDF2 method. This significantly reduces the overall computational cost by a factor of ~4 for the
case, and approximately 2 and 3 for the
and
cases, respectively. Despite that, the slow convergence of the PSpTM could have some negative implications for more complex cases.
One potential contributor to the slow convergence rate on the PSpTM is believed to be the initialization. The solution is started from a converged steady simulation. This initialization is set equal to the previous steps of the method. Thus, while the unsteady conditions are established during the initial transient, the PSpTM method is still far from a periodic solution. Thus, the additional source term has not yet been set properly. For this reason, the method requires additional periods to smoothly transition to the time-periodic solution. Further studies are required to optimize the PSpTM method’s convergence and increase the overall computational gains. A potential fix for this would be the application of a hybrid method with a BDF2 initialization. This initialization should have sufficient time steps to capture some of the first flow harmonics with moderate accuracy. This should also last enough to reach a quasi-periodic state to cancel out any non-harmonic contribution of the initial transient. The pertinent time steps would be introduced on the PSpTM solution. Future work is required to analyze the impact of this strategy.
3.2. High-Frequency Case: Rotor/Stator Potential Interaction
A rotor/stator potential interaction case is emulated with the ACAT B1 domain as an additional test using the single-passage domain (Case B in
Table 2). Although in this case the stator is excluded, a similar problem can be formulated by adding a sinusoidal pressure wave at the domain inlet of
with a fundamental frequency equal to the blade passing frequency. In normal conditions, the potential perturbation would be downstream of the rotor. However, given the dimensions of the domain, the potential perturbation could be cut off. Thus, for this case, the potential perturbation was moved upstream to demonstrate the method’s capabilities. This is analogous to an EO20 problem, and it is used to test the method at high frequencies (
). The amplitude of the perturbation is set to 5% of the reference inlet static pressure.
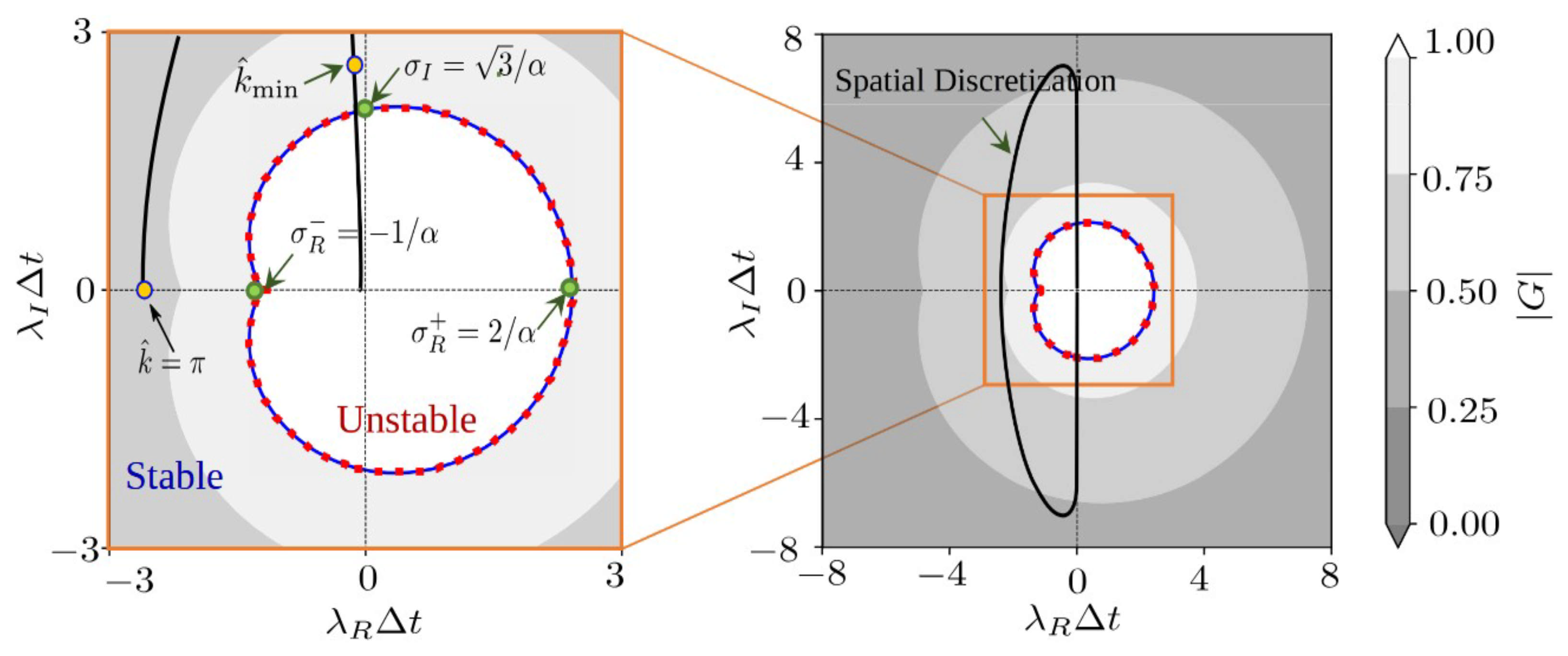
The convergence strategy of both the BDF2 and the PSpTM methods was adjusted to this case. For the BDF2 approach, 100 time steps are used per fundamental period to capture events of higher frequency and obtain a good temporal resolution for comparison purposes. To obtain an equivalent level of convergence, the BDF2 method is set to have 30 and 50 Newton and Jacobi inner iterations, respectively. The maximum CFL for the implicit DTS scheme is set to 50. The case is run for 25 fundamental periods to evaluate the system convergence. The PSpTM method is conditionally stable (
Appendix A), with some stability restrictions when modes with frequencies lower than the fundamental frequency of the problem are present in the problem. For this reason, at higher frequencies, it is advisable to apply a more conservative convergence strategy. For the current case, the number of inner iterations was set to 5 and 30 for the Newton and Jacobi iterations, respectively, to increase PSpTM’s stability. This results in a much lower cost per time step than the BDF2 method. The maximum CFL for the inner iterations is set to 15. Each PSpTM case is run for 500 periods.
As in the previous case, to monitor the accuracy of the solution, the dimensionless mass-averaged total pressure value at the exit is used as the reference metric.
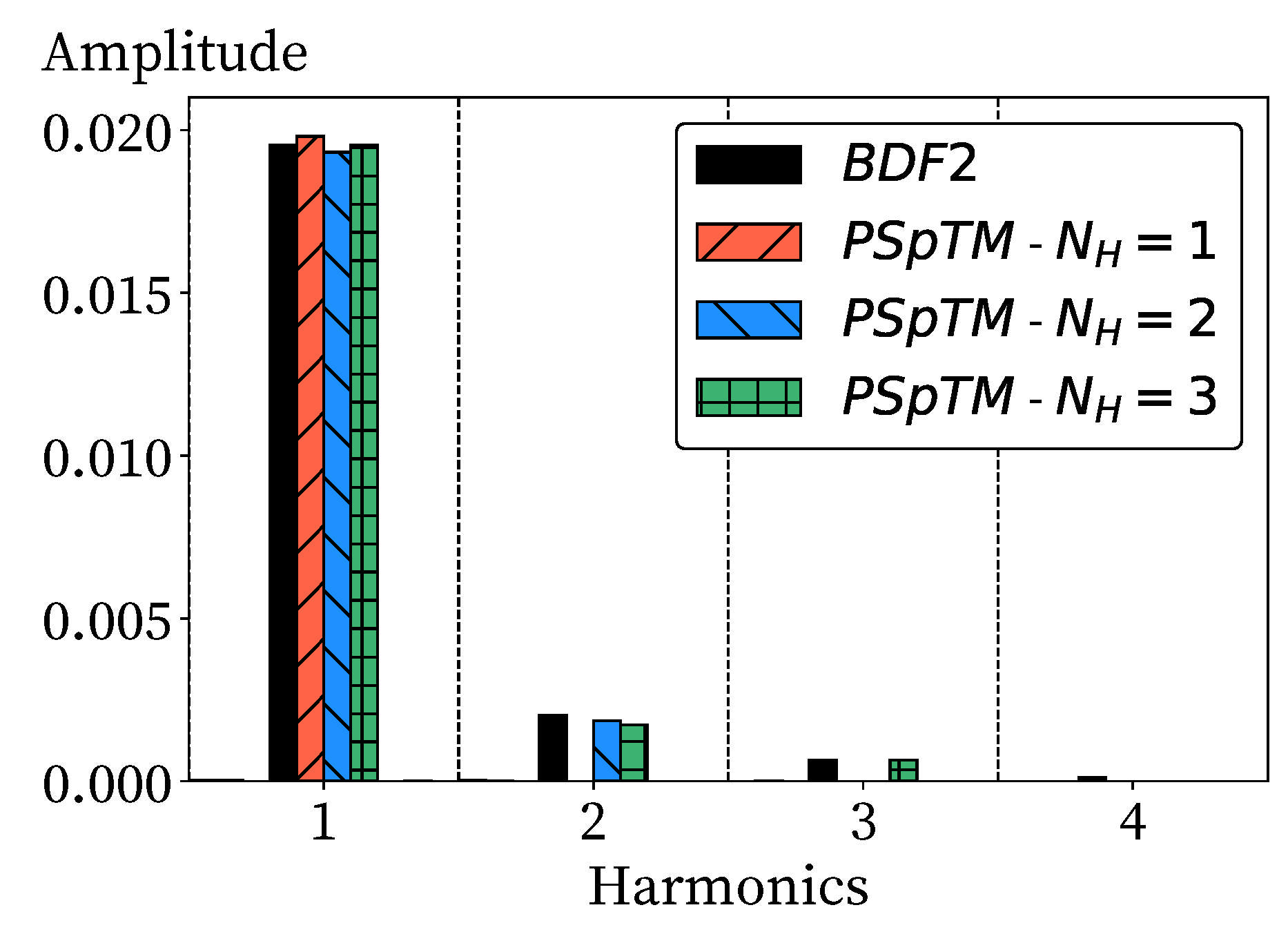
Figure 9 displays the spectrum of dimensionless total pressure at the exit. In this case, the first harmonic of the solution contains most of the energy. However, the second harmonic, while smaller, is still noticeable. The PSpTM method with
captures the amplitude of the first harmonic, but some additional energy is retained in the solution. This results in an excess in the amplitude prediction of about 1.4% compared with the BDF2 value. The accuracy of the solution increases with the number of harmonics, and the excess energy is moved towards the second harmonic. In the
and
cases, the relative error is reduced to −0.4% and −0.01%, respectively.
Figure 10 compares the time average and the first harmonic amplitude and phase of the pressure coefficient,
, along the blade to assess the PSpTM’s capability to capture the local flow variations over time. In this case, while the time average
is similar for all cases, some important differences are observed between the BDF2 and the PSpTM method with
. The latter overestimates the amplitude of the first harmonic both in the pressure and the suction side of the blade. Some noticeable differences are also spotted in the phase of the first harmonic for the
case. The accuracy in the prediction of the phase and amplitude increases significantly when two or more harmonics are retained. However, only some marginal gains in accuracy were achieved when more than two harmonics were included.
Figure 11 displays the periodic norm as a function of the number of periods, time speeds, and total computational cost. As in the low-frequency case, the PSpTM has a poor convergence rate in terms of the number of periods required to achieve the desired level of accuracy. As mentioned, this is attributed to an effect of the initialization of the method and the initial difficulty to reach a time-periodic solution (
Figure 11a). However, for this case, the BDF2 approach also presents a slow convergence, which is much lower than the low-frequency one. This is because of the increase in frequency. As the frequency rises in comparison with the flow convection, the convergence time is dominated by the through-flow time instead of the number of periods of the fundamental frequency. This results in a higher number of iterations required to achieve the same level of periodic accuracy (
Figure 11b). Hence, for a similar level of periodic convergence, the PSpTM method provides significant savings in computational cost, with a speed-up factor of approximately ten for the case with
, five for the case with
, and above 3 for
.
3.3. Inlet Distortion Effects: 1st EO Potential Perturbation
To evaluate the method for other representative turbomachinery cases, a full annulus configuration of the quasi-2D fan has been chosen (Case C in
Table 2). To model an intake distortion profile with EO1, a sinusoidal pressure perturbation is introduced at the inlet (
) (
Figure 12). The fundamental frequency of the perturbation is set to the fan rotational frequency. This results in a Strouhal number of approximately
. The amplitude of the perturbation is set to 7.5% of the reference inlet static pressure, which is large enough to give rise to nonlinear effects. The PSpTM method is applied with an increasing number of harmonics in the solution from
to
.
For the BDF2 approach, 100 time steps are used per period. To obtain an equivalent level of convergence, the BDF2 method is set to have 20 and 40 Newton and Jacobi inner iterations, respectively. The maximum CFL for the implicit DTS scheme is set to 40. The case is run for 10 fundamental periods. This convergence strategy was selected from different combinations to obtain sufficient time convergence in the solution for a reasonable computational cost. As explained in previous sections, the PSpTM requires fewer pseudo-time iterations to converge each time step. Thus, the number of DTS iterations was set to 6 and 30 for the Newton and Jacobi iterations, respectively. This results in a much lower cost per time step than the BDF2 method. The maximum CFL for the inner iterations is set to 40.
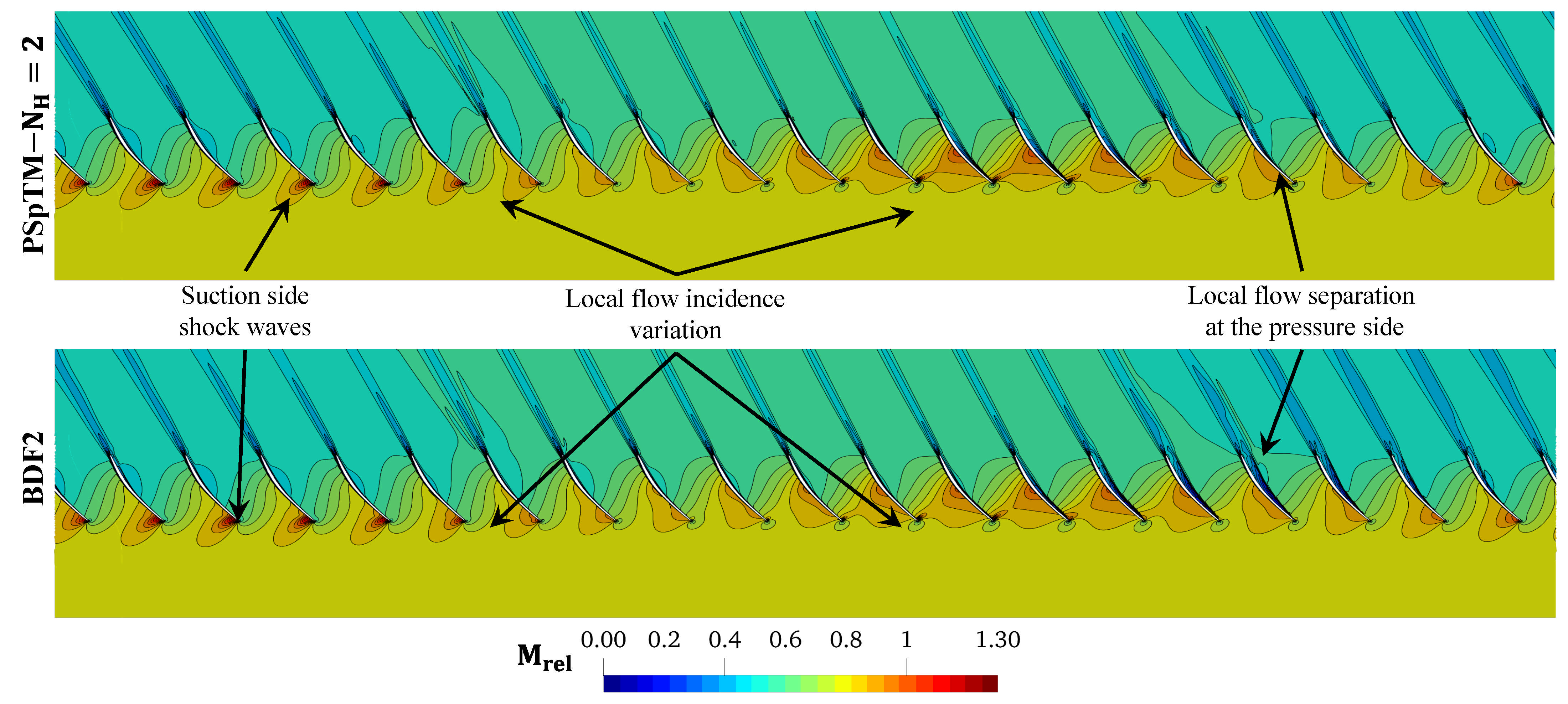
Given that each blade travels through a wide range of pressure ratios, the blade experiences a broad set of flow conditions within a rotation cycle (
Figure 12). This includes notable changes in the flow incidence that displace the shock-wave from the leading-edge to the middle of the suction side. As such, notable changes in the blade forces take place during the fan rotating cycle. For this reason, to evaluate the accuracy of the model the module of the total force over one blade is tracked over time (
). This is normalized by the area of the blade and the reference dynamic pressure at the inlet as a force coefficient:
The large variation of the flow conditions allows for testing the method in the presence of significant flow nonlinearities, including shock waves and synchronous flow separation (
Figure 12). The robust operation of the PSpTM under these flow conditions is an apparent step-up from nonlinear methods built on top of linear methods [
11,
12], which have some limitations in the presence of large perturbations.
In a first evaluation, the solution that retains a single harmonic fails to capture the amplitude of the temporal variation of
(
Figure 13 and
Figure 14). A notable increase in accuracy is observed when two or more harmonics are retained. A marginal gain in accuracy is appreciated with
. However, when the amplitude of the signal is studied in depth, it appears that most of the energy is contained in the first harmonic, and the higher harmonics only contain second-order contributions. This is in line with the previous works where it has been shown that shock-wave discontinuities give rise to higher harmonics [
15]. When higher harmonics (or more time steps per fundamental period) are included in the PSpTM method, the energy is distributed in higher harmonics, slightly decreasing the amplitude of the first harmonic. Overall, despite not fully matching the BDF2 results, a sufficient level of agreement with the BDF2 approach is observed with the PSpTM method with
.
From the instant flow fields obtained by both methods (
Figure 12), it is understood that the PSpTM under-predicts the magnitude of the flow separation at the pressure side, compared with the BDF2 case. The flow separation could be triggered at a different offset in each temporal scheme due to the temporal accuracy of each method for a given spatial discretization. The sensitivity to the time stepper is higher for low spatial resolution. Nevertheless, without a higher-order reference, it cannot be concluded which result is the most representative of the actual flow separation. Despite this, an adequate agreement in the overall flow field is observed for both temporal schemes.
Figure 15 represents the variation of the pressure coefficient,
, distribution over time on the pressure and suction side of the blade. The objective is to further analyze the method’s accuracy. Only the first two cases (i.e.,
and 2) are included, since no significant changes were observed between the
and
cases. Some discrepancies between the BDF2 and the PSpTM methods are observed for the
case. The solution with
improves significantly with respect to the single harmonic case, with only minor differences in the prediction of the phase and magnitude of the first harmonic of the solution.
Finally, to evaluate the periodic convergence of the solution, the periodic norm of the force coefficient is defined as
where the force magnitude over the blade is normalized by the dynamic pressure of reference and the area of the blade. As in previous cases, a slow convergence rate is observed for the PSpTM method due to the solver initialization (
Figure 16). Nevertheless, a speed-up factor of approximately 4 and 3 is achieved by the PSpTM method with
and
, respectively. The case with a single harmonic included does not match the same level of accuracy as the cases with higher harmonics. However, this case can achieve a speed-up factor of approximately 5.
 ), the PSpTM solution (
), the PSpTM solution ( ), and the Fourier fit of the PSpTM solution (
), and the Fourier fit of the PSpTM solution ( ).
).
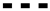 ), the PSpTM solution (
), the PSpTM solution ( ), and the Fourier fit of the PSpTM solution (
), and the Fourier fit of the PSpTM solution ( ).
).

 ), the PSpTM solution (
), the PSpTM solution ( ), and the Fourier fit of the PSpTM solution (
), and the Fourier fit of the PSpTM solution ( ).
).
 ), the PSpTM solution (
), the PSpTM solution ( ), and the Fourier fit of the PSpTM solution (
), and the Fourier fit of the PSpTM solution ( ).
).