Cavity Flow Instabilities in a Purged High-Pressure Turbine Stage †
Abstract
1. Introduction
2. Experimental Setup
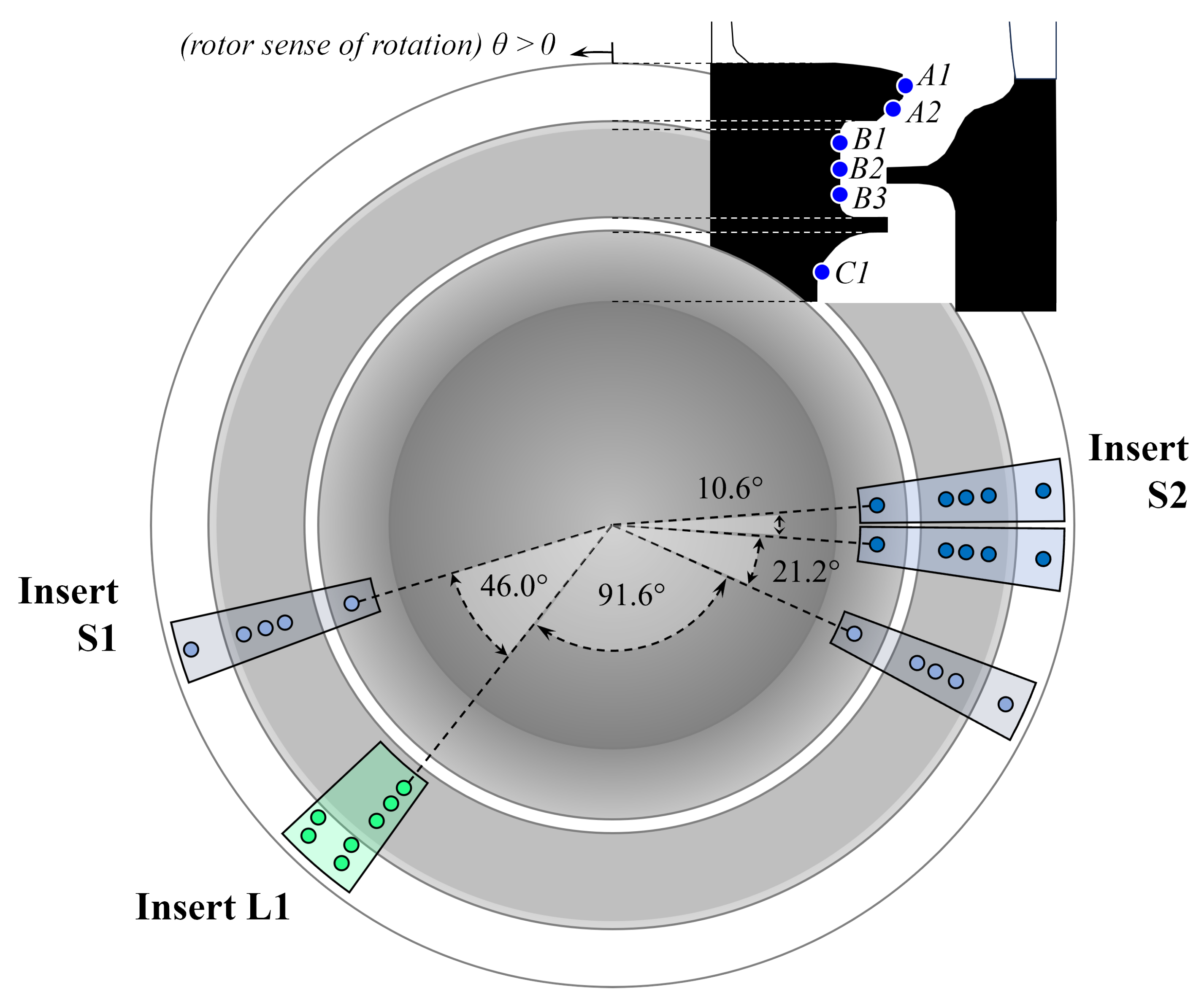
2.1. Test Article
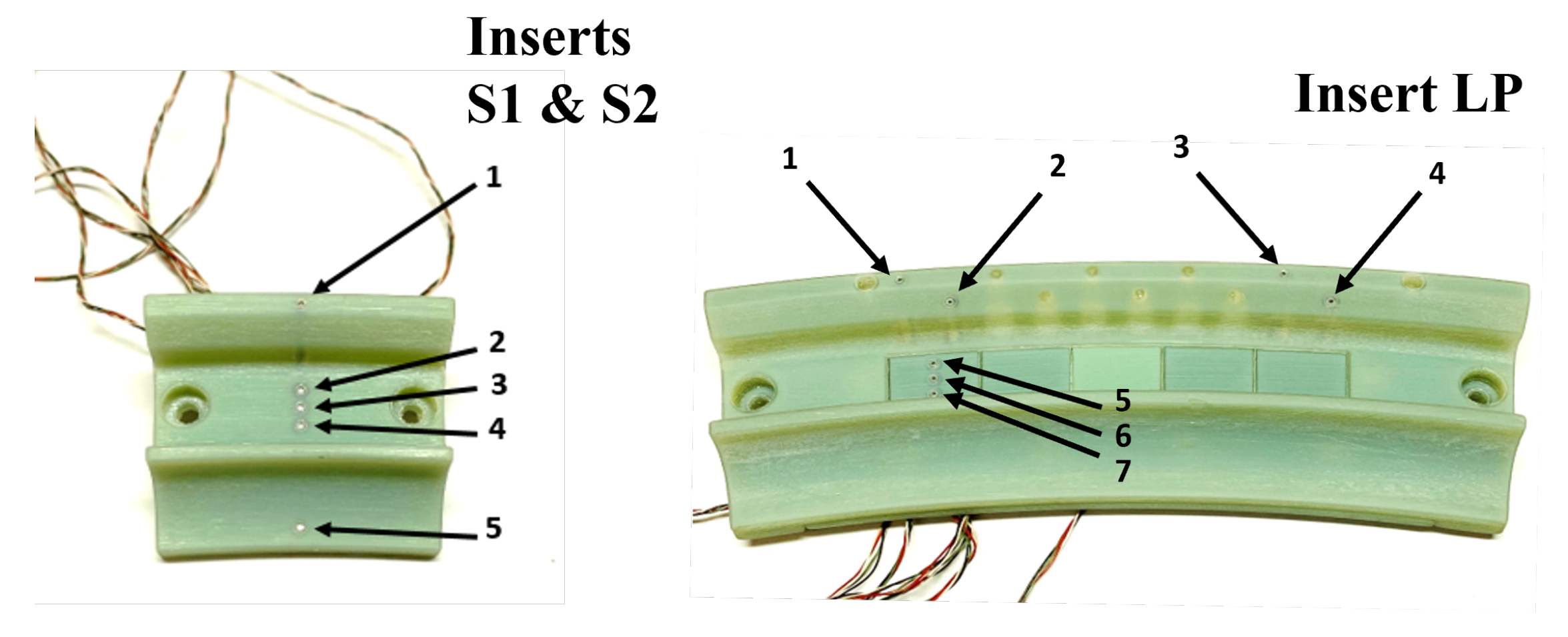
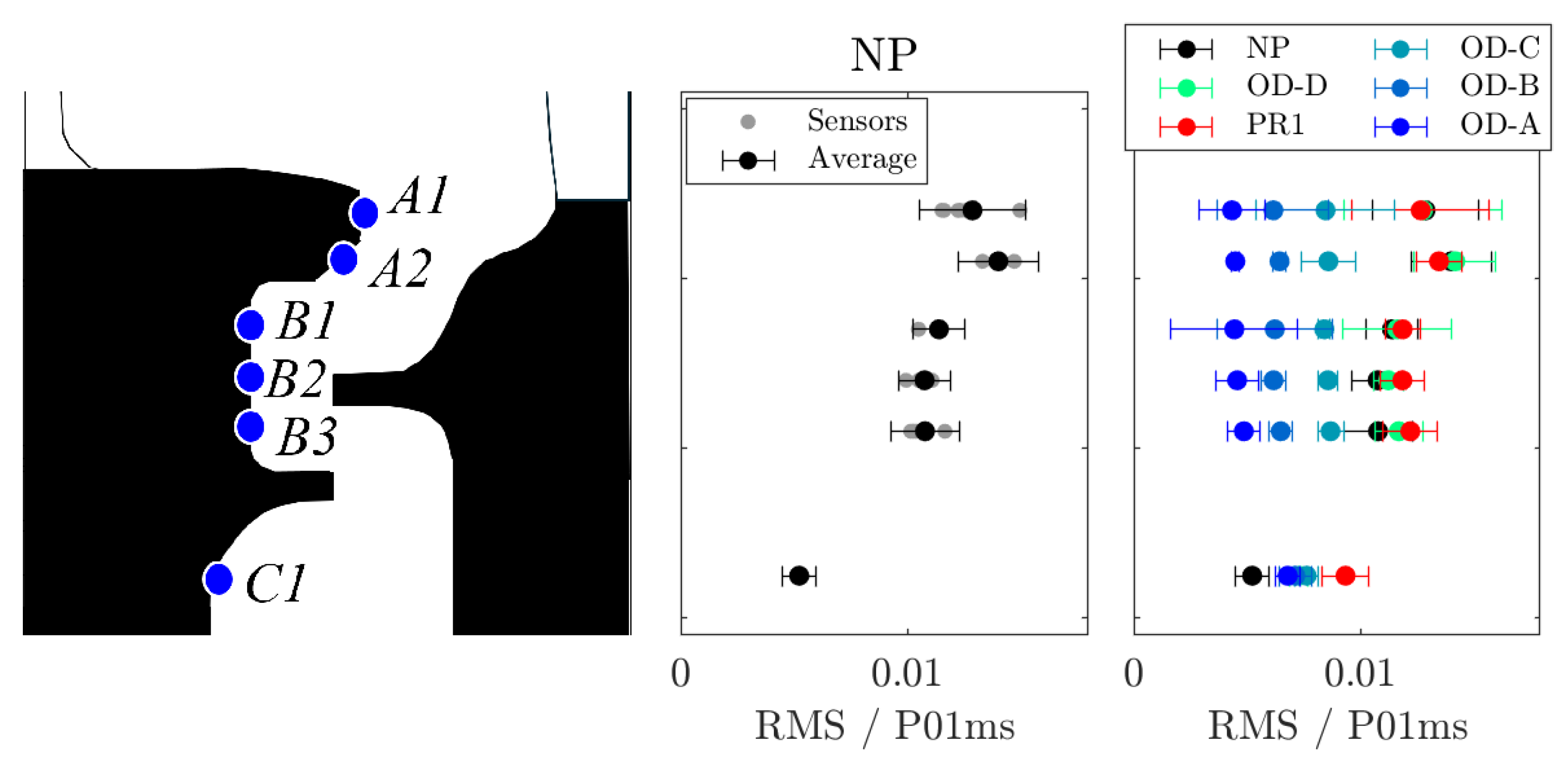
2.2. Instrumentation
2.3. Signal Acquisition
3. Methodology
3.1. Spectral Analysis
3.2. Instability Intensity Quantification
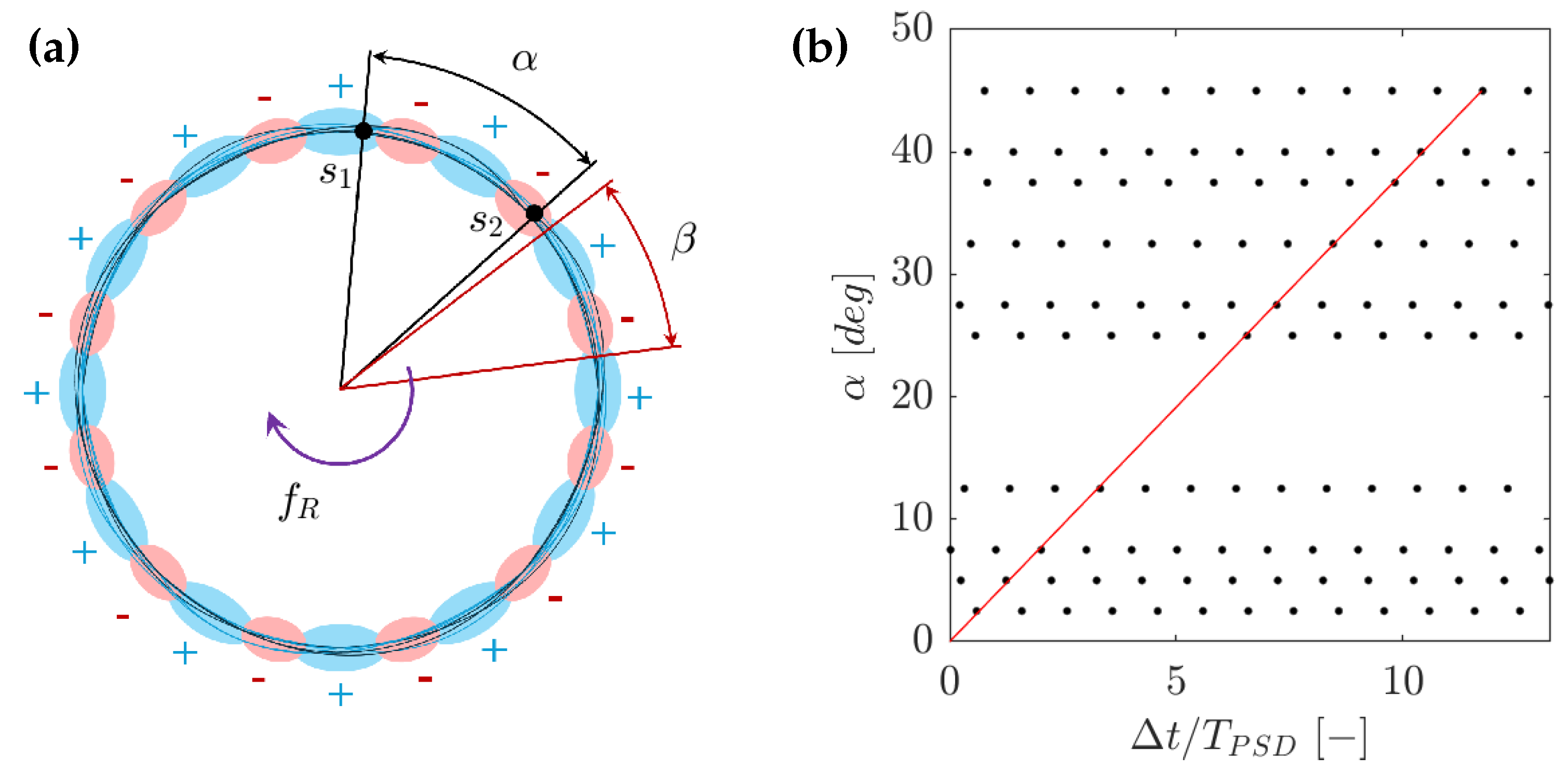
3.3. Cavity Mode Analysis
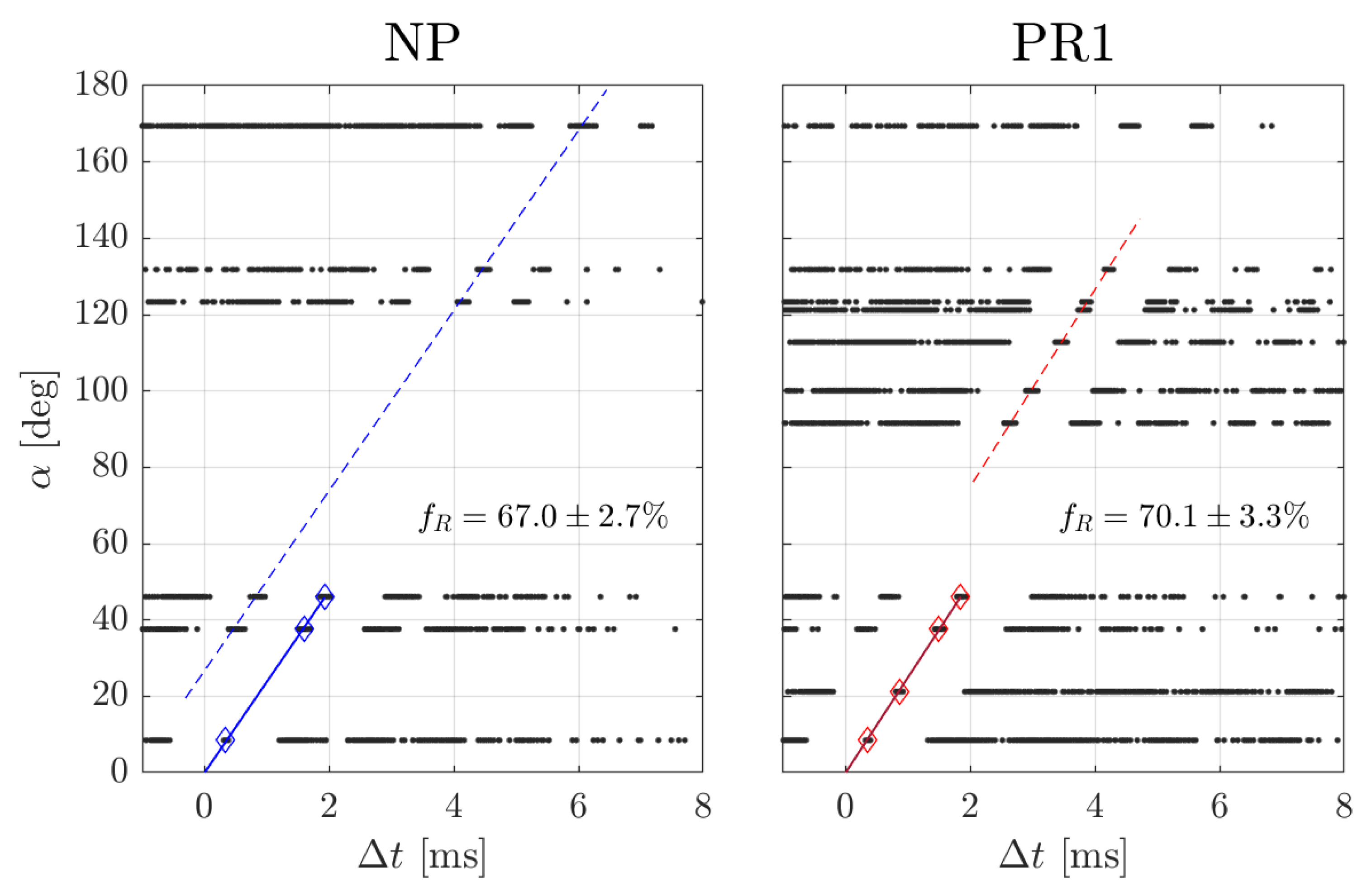
3.3.1. Cross-Correlation Method
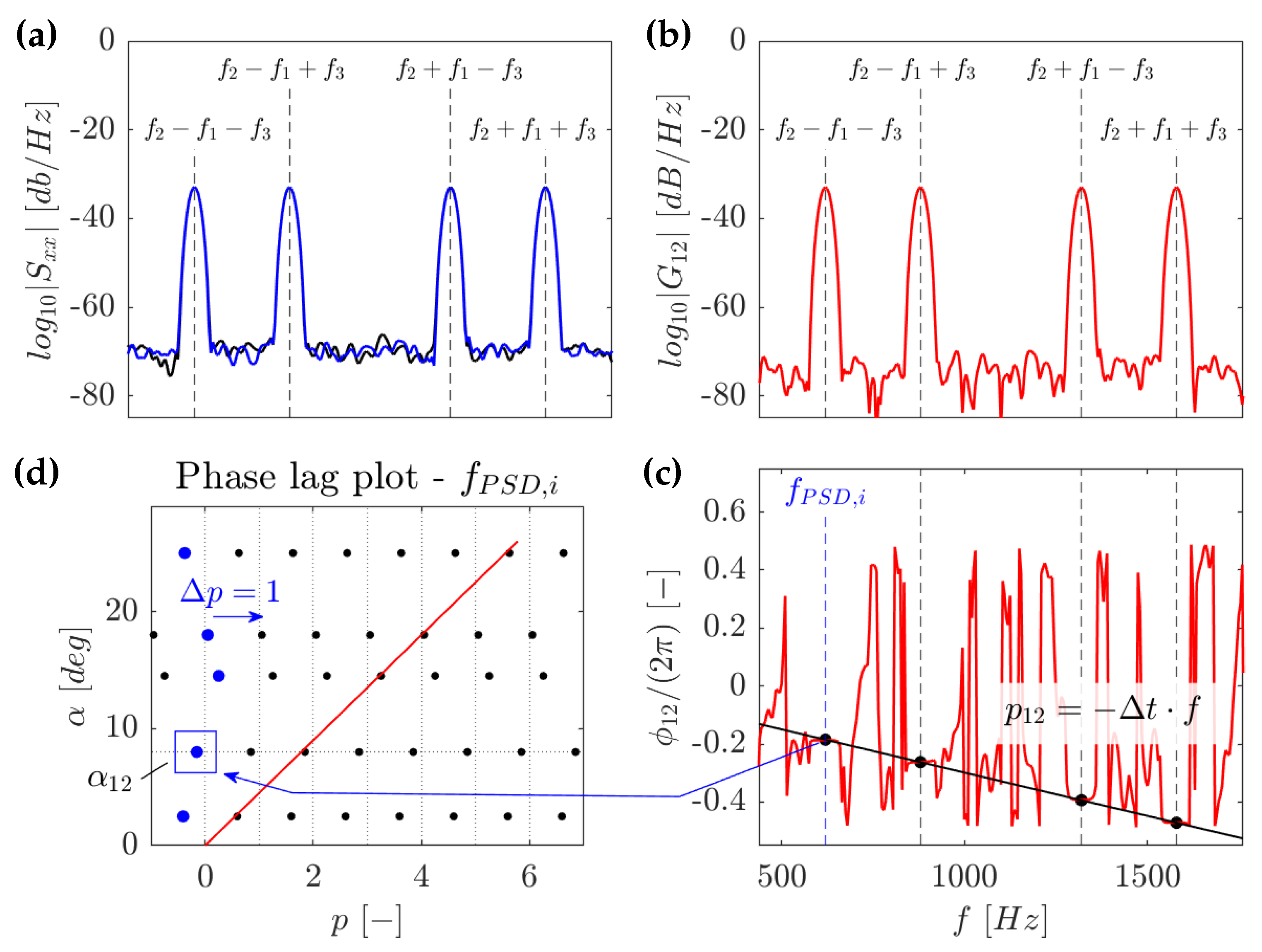
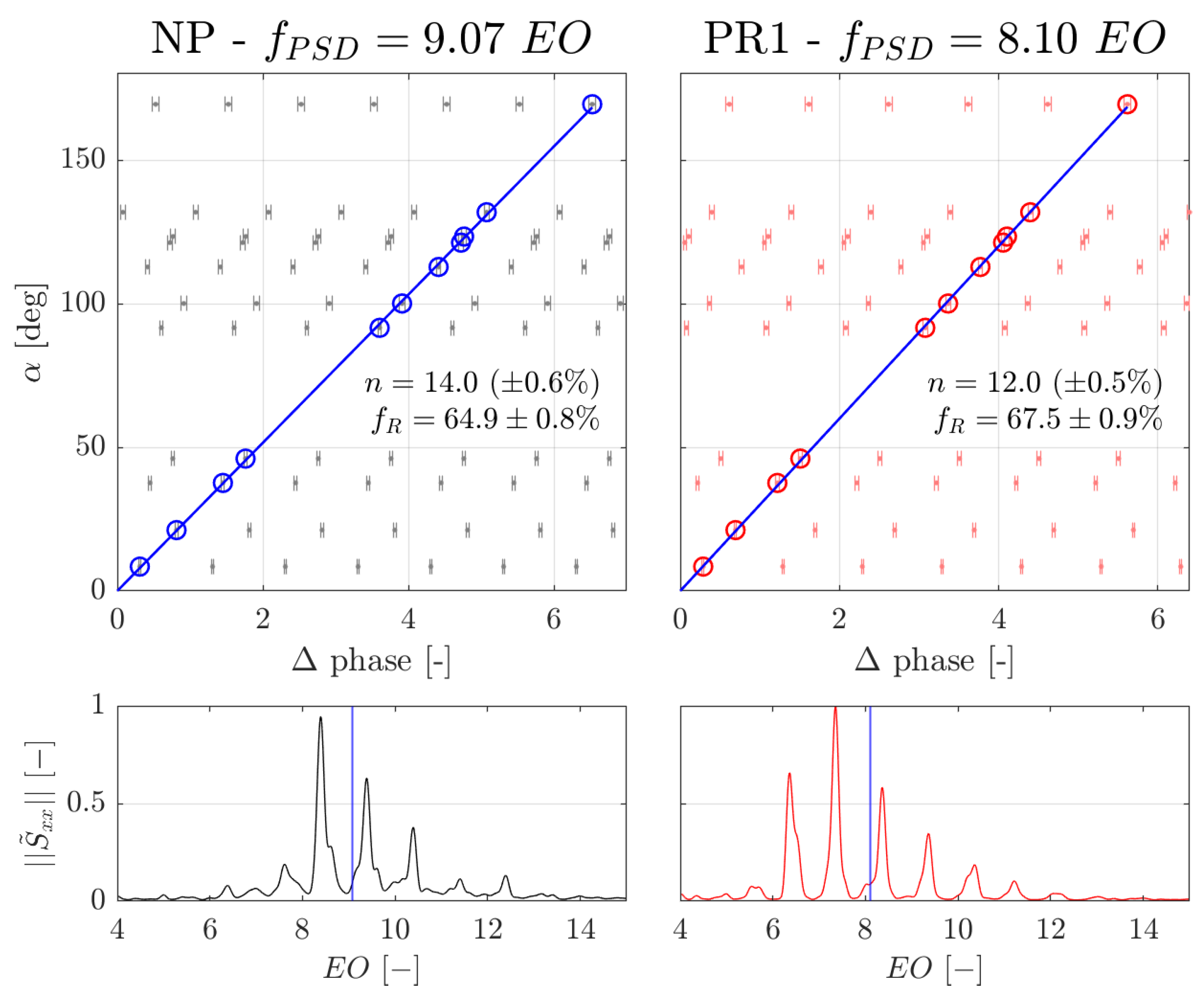
3.3.2. Cross-Power Spectral Density Method
4. Results and Discussion
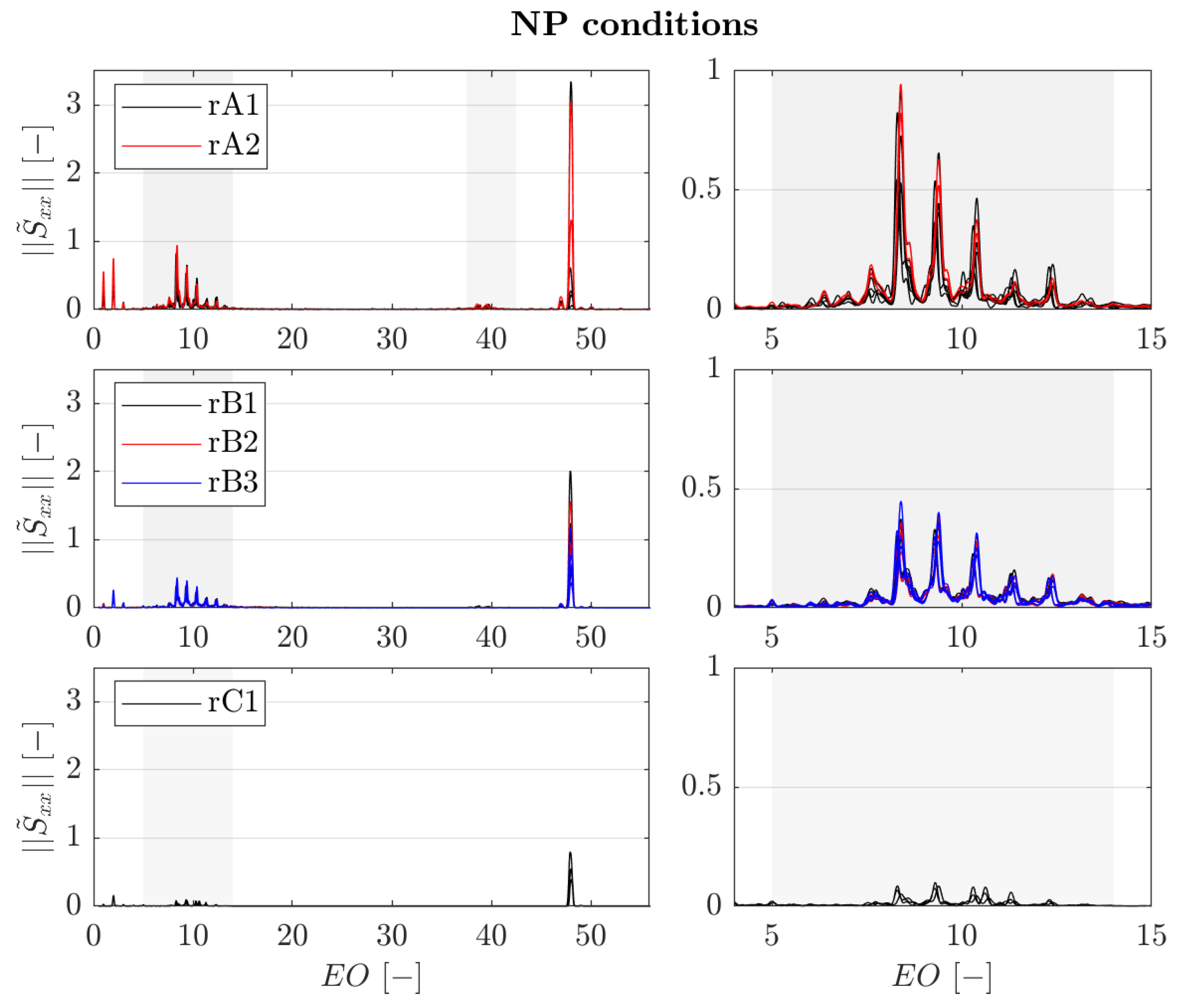
4.1. Spectra Analysis
4.2. Cavity Mode Characteristics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | |
| HPT | High-Pressure Turbine |
| PR | Purge Rate |
| CPSD | Cross-Power Spectral Density |
| CM | Cavity Mode |
| RMS | Root Mean Square |
| VKI | von Karman Institute for Fluid Dynamics |
| NP | Nominal Purge Condition |
| PR1 | Off-Design at PR = 1.00% |
| OD-A,-B,-C,-D | Extra Off-Design Conditions |
| LF | Signal Low-Frequency Content |
| HF | Signal High-Frequency Content |
| EO | Engine Order |
| CI | Confidence Interval |
| Probability Density Function | |
| H1(2,3,4) | Hub Insert Designs |
| T1(2) | Tip Insert Designs |
| L1, S1, S2 | ABS Inserts |
| Subscripts | |
| r | Rotor |
| Axial | |
| h | Hub |
| s | Stator |
| 0 | Total quantities |
| Planes 1, 2, and 3 | |
| Average |
| Variables | |
| Reynolds number | |
| M | Mach number |
| Rotor axial chord | |
| P | Pressure |
| T | Temperature |
| Rotational Reynolds number | |
| Rotational speed [rpm] | |
| Sensor angular distance | |
| Structures’ length scale | |
| n | Number of lobes |
| Structures’ rotating speed | |
| Structures’ rotating frequency | |
| Time lag (delay) |
| Time lag unit | |
| Phase lag (delay) | |
| Cross-power spectral density phase | |
| (Definition of ) | |
| Cross-correlation | |
| Power spectral density | |
| Cross-power spectral density |
References
- Scobie, J.A.; Sangan, C.M.; Michael Owen, J.; Lock, G.D. Review of Ingress in Gas Turbines. J. Eng. Gas Turbines Power 2016, 138, 120801. [Google Scholar] [CrossRef]
- Paniagua, G.; Dénos, R.; Almeida, S. Effect of the Hub Endwall Cavity Flow on the Flow-Field of a Transonic High-Pressure Turbine. J. Turbomach. 2004, 126, 578–586. [Google Scholar] [CrossRef]
- Schuepbach, P.; Abhari, R.S.; Rose, M.G.; Germain, T.; Raab, I.; Gier, J. Effects of Suction and Injection Purge-Flow on the Secondary Flow Structures of a High-Work Turbine. J. Turbomach. 2010, 132, 021021. [Google Scholar] [CrossRef]
- Regina, K.; Kalfas, A.I.; Abhari, R.S. Experimental Investigation of Purge Flow Effects on a High Pressure Turbine Stage. J. Turbomach. 2015, 137, 041006. [Google Scholar] [CrossRef]
- Chew, J.W.; Gao, F.; Palermo, D.M. Flow mechanisms in axial turbine rim sealing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 7637–7657. [Google Scholar] [CrossRef]
- Horwood, J.; Hualca Tigsilema, F.P.; Wilson, M.; Scobie, J.; Sangan, C.; Lock, G.; Dahlqvist, J.; Fridh, J. Flow Instabilities in Gas Turbine Chute Seals. J. Eng. Gas Turbines Power 2020, 142, 021019. [Google Scholar] [CrossRef]
- Rozman, M.; DeShong, E.T.; Thole, K.A.; Berdanier, R.A.; Robak, C. Characterizing Flow Instabilities During Transient Events in the Turbine Rim Seal Cavity. J. Turbomach. 2022, 145, 031014. [Google Scholar] [CrossRef]
- Gao, F.; Chew, J.W.; Beard, P.F.; Amirante, D.; Hills, N.J. Large-eddy simulation of unsteady turbine rim sealing flows. Int. J. Heat Fluid Flow 2018, 70, 160–170. [Google Scholar] [CrossRef]
- Monge-Concepción, I.; Siroka, S.; Berdanier, R.A.; Barringer, M.D.; Thole, K.A.; Robak, C. Influence of Vane Trailing Edge Flow on the Formation of Cavity Cells and Rim Sealing. J. Turbomach. 2022, 144, 061014. [Google Scholar] [CrossRef]
- Vella, S.; Tang, H.; Carnevale, M.; Scobie, J.A.; Lock, G.D.; Salvatori, F.; Sangan, C.M. On the Relationship Between Swirl and Unsteadiness Within Turbine Rim Seals. J. Eng. Gas Turbines Power 2025, 147, 041031. [Google Scholar] [CrossRef]
- Beard, P.F.; Gao, F.; Chana, K.S.; Chew, J. Unsteady Flow Phenomena in Turbine Rim Seals. J. Eng. Gas Turbines Power 2017, 139, 032501. [Google Scholar] [CrossRef]
- Gao, F.; Chew, J.W.; Marxen, O. Inertial waves in turbine rim seal flows. Phys. Rev. Fluids 2020, 5, 024802. [Google Scholar] [CrossRef]
- Bru Revert, A.; Beard, P.F.; Chew, J.W. Measurement of Inertial and Acoustic Waves in a Turbine Chute Rim Seal Cavity. J. Eng. Gas Turbines Power 2023, 145, 061021. [Google Scholar] [CrossRef]
- Horwood, J.; Hualca, F.; Scobie, J.; Wilson, M.; Sangan, C.; Lock, G. Experimental and Computational Investigation of Flow Instabilities in Turbine Rim Seals. J. Eng. Gas Turbines Power 2019, 141, 011028. [Google Scholar] [CrossRef]
- Iranidokht, V.; Kalfas, A.; Abhari, R.; Senoo, S.; Momma, K. Sensitivity analysis on the impact of geometrical and operational variations on turbine hub cavity modes and practical methods to control them. J. Glob. Power Propuls. Soc. 2021, 5, 66–78. [Google Scholar] [CrossRef]
- Town, J.; Averbach, M.; Camci, C. Experimental and Numerical Investigation of Unsteady Structures Within the Rim Seal Cavity in the Presence of Purge Mass Flow. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016. [Google Scholar] [CrossRef]
- Savov, S.S.; Atkins, N.R.; Uchida, S. A Comparison of Single and Double Lip Rim Seal Geometries. J. Eng. Gas Turbines Power 2017, 139, 112601. [Google Scholar] [CrossRef]
- Graikos, D.; Carnevale, M.; Sangan, C.M.; Lock, G.D.; Scobie, J.A. Influence of Flow Coefficient on Ingress Through Turbine Rim Seals. J. Eng. Gas Turbines Power 2021, 143, 111010. [Google Scholar] [CrossRef]
- Chilla, M.; Hodson, H.; Newman, D. Unsteady Interaction Between Annulus and Turbine Rim Seal Flows. J. Turbomach. 2013, 135, 051024. [Google Scholar] [CrossRef]
- Da Valle, L.; Torre, A.F.M.; Merli, F.; Cernat, B.C.; Lavagnoli, S. Cavity Instabilities in a High-Speed Low-Pressure Turbine Stage. Int. J. Turbomach. Propuls. Power 2025, 10, 4. [Google Scholar] [CrossRef]
- Da Valle, L.; Cernat, B.C.; Lavagnoli, S. Cavity Flow Instabilities in a Purged High-Pressure Turbine Stage. In Proceedings of the 16th European Turbomachinery Conference (ETC16): Turbomachinery Fluid Dynamics and Thermodynamics, Paper No. ETC16-291, Hannover, Germany, 24–28 March 2025; Available online: https://www.euroturbo.eu/publications/conference-proceedings-repository/ (accessed on 8 April 2025).
- Paniagua, G.; Sieverding, C.H.; Arts, T. Review of the von Karman Institute Compression Tube Facility for Turbine Research. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar] [CrossRef]
- Cernat, B.C.; Pinho, J.; Okada, M.; Lavagnoli, S. Experimental Investigation of a High-Speed Turbine with Rainbow Rotor and Rim Seal Purge Flow. J. Turbomach. 2023, 145, 071014. [Google Scholar] [CrossRef]
- Burigana, M.; Verstraete, T.; Lavagnoli, S. Turbine Endwall Contouring Through Advanced Optimization Techniques. J. Turbomach. 2023, 145, 081011. [Google Scholar] [CrossRef]
- Dénos, R. Influence of temperature transients and centrifugal force on fast-response pressure transducers. Exp. Fluids 2002, 33, 256–264. [Google Scholar] [CrossRef]
- Wiener–Khinchin Theorem, Wikipedia. Available online: https://en.wikipedia.org/w/index.php?title=Wiener%E2%80%93Khinchin_theorem&oldid=1218075429 (accessed on 8 October 2024).





| NP Conditions | PR1 Conditions | |||
|---|---|---|---|---|
| Parameter | Mean | Rep. 95% | Mean | Rep. 95% |
| [mbar] | 1037.9 | 0.7% | 1037.9 | 0.6% |
| [K] | 439.4 | 1.3% | 434.5 | 1.3% |
| 2.195 | 0.6% | 2.199 | 0.6% | |
| 2.214 | 0.5% | 2.219 | 0.5% | |
| 1.247 | 1.5% | 1.247 | 1.5% | |
| [rpm] | 5920 | 0.3% | 5920 | 0.3% |
| 0.78 | (-) | 0.78 | (-) | |
| [] | 2.76 | (-) | 2.76 | (-) |
| n∘ of tests | 155 | 71 | ||
| Purge Condition | Purge Rate (=) [%] | n∘ of Tests |
|---|---|---|
| Nominal, NP | 1.74% | 155 |
| Off-Design, PR1 | 1.00% | 71 |
| Off-Design, OD-A | −0.19% | 2 |
| Off-Design, OD-B | 0.15% | 2 |
| Off-Design, OD-C | 0.53% | 2 |
| Off-Design, OD-D | 1.38% | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Da Valle, L.; Cernat, B.C.; Lavagnoli, S. Cavity Flow Instabilities in a Purged High-Pressure Turbine Stage. Int. J. Turbomach. Propuls. Power 2025, 10, 15. https://doi.org/10.3390/ijtpp10030015
Da Valle L, Cernat BC, Lavagnoli S. Cavity Flow Instabilities in a Purged High-Pressure Turbine Stage. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(3):15. https://doi.org/10.3390/ijtpp10030015
Chicago/Turabian StyleDa Valle, Lorenzo, Bogdan Cezar Cernat, and Sergio Lavagnoli. 2025. "Cavity Flow Instabilities in a Purged High-Pressure Turbine Stage" International Journal of Turbomachinery, Propulsion and Power 10, no. 3: 15. https://doi.org/10.3390/ijtpp10030015
APA StyleDa Valle, L., Cernat, B. C., & Lavagnoli, S. (2025). Cavity Flow Instabilities in a Purged High-Pressure Turbine Stage. International Journal of Turbomachinery, Propulsion and Power, 10(3), 15. https://doi.org/10.3390/ijtpp10030015








