A Quasi-Direct Numerical Simulation of a Compressor Blade with Separation Bubbles and Inflow Turbulence †
Abstract
1. Introduction
2. Case Description
3. Numerical Setup
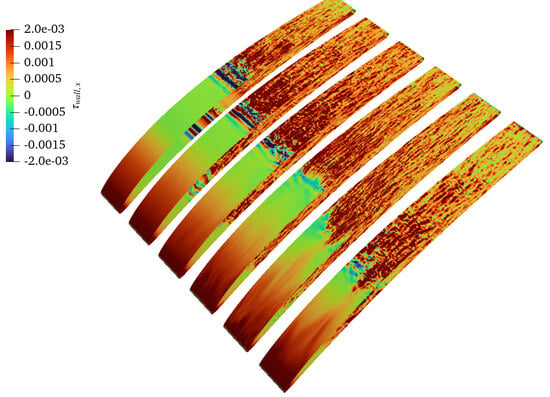
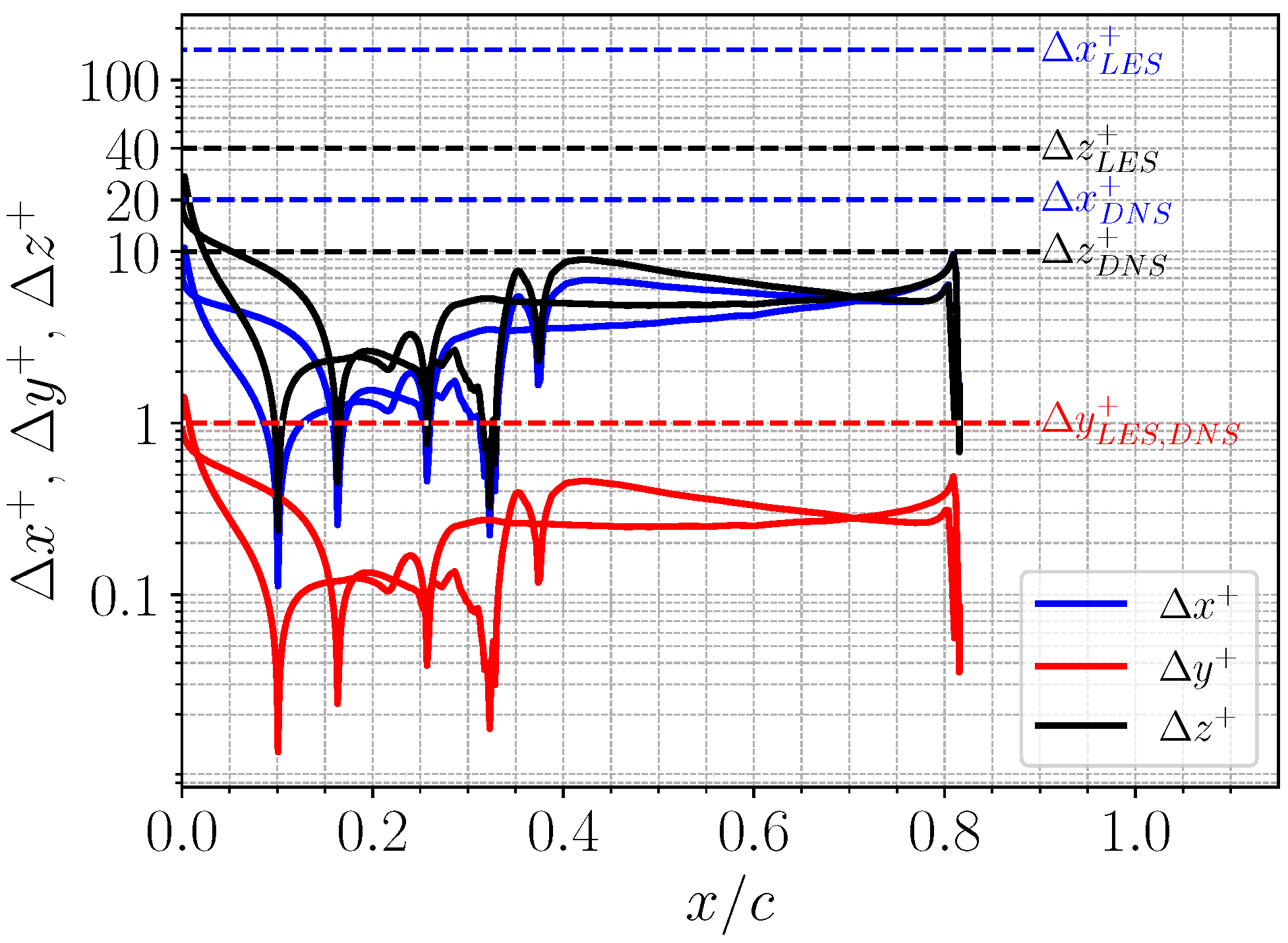
3.1. Meshing
3.2. Solver
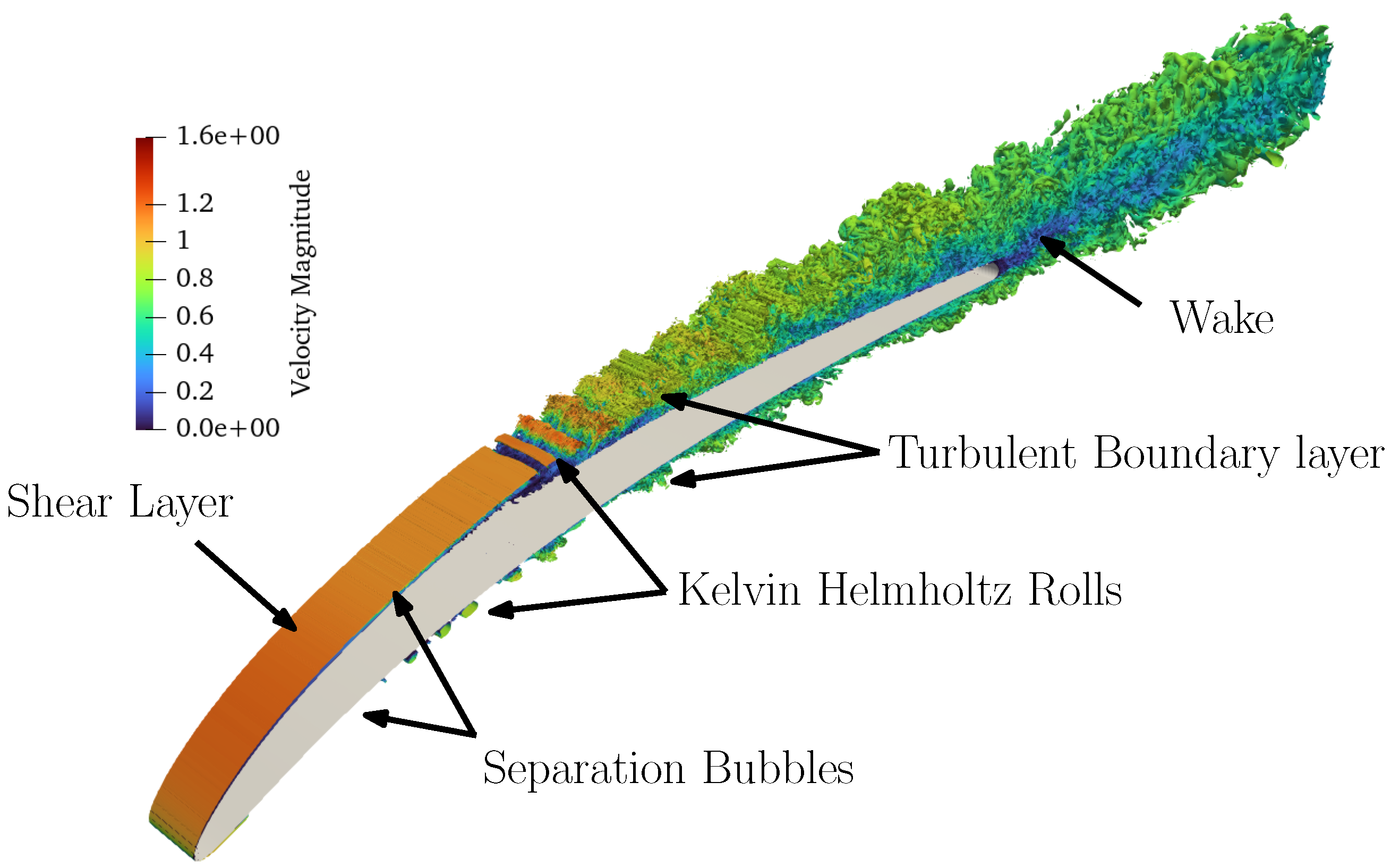
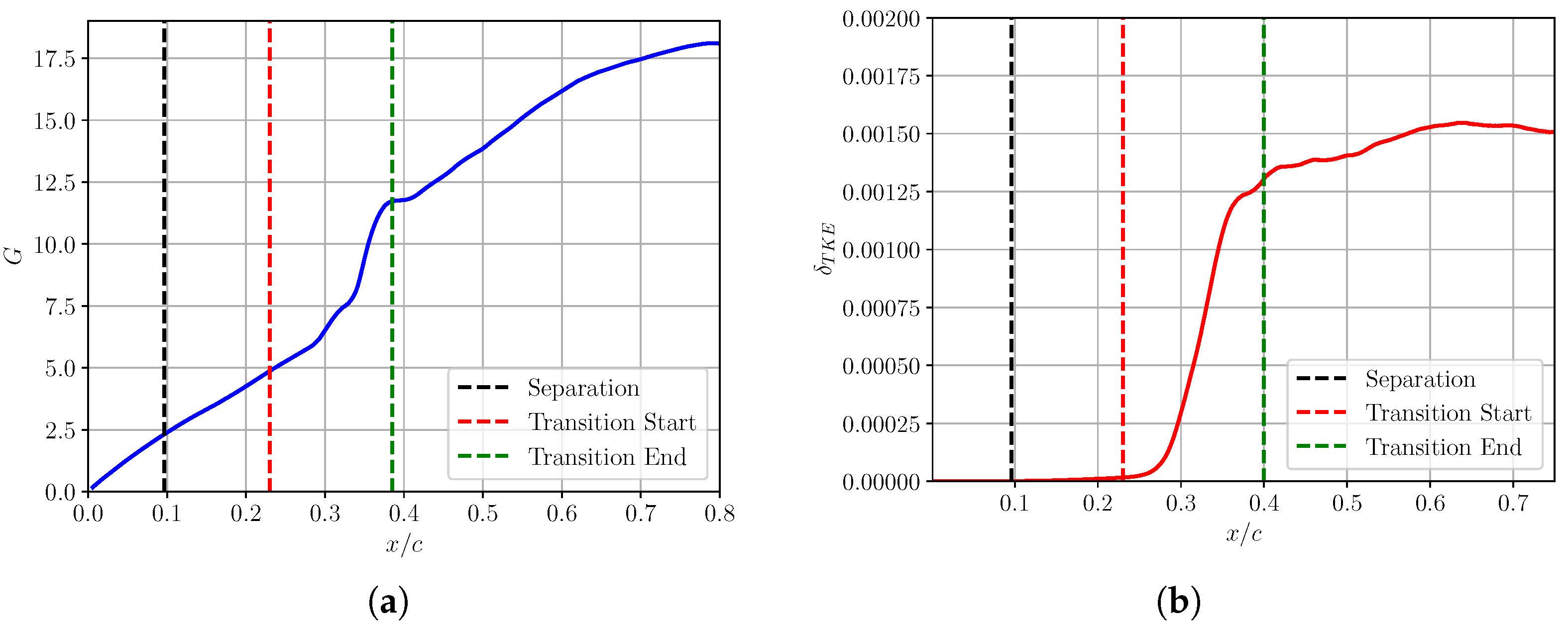
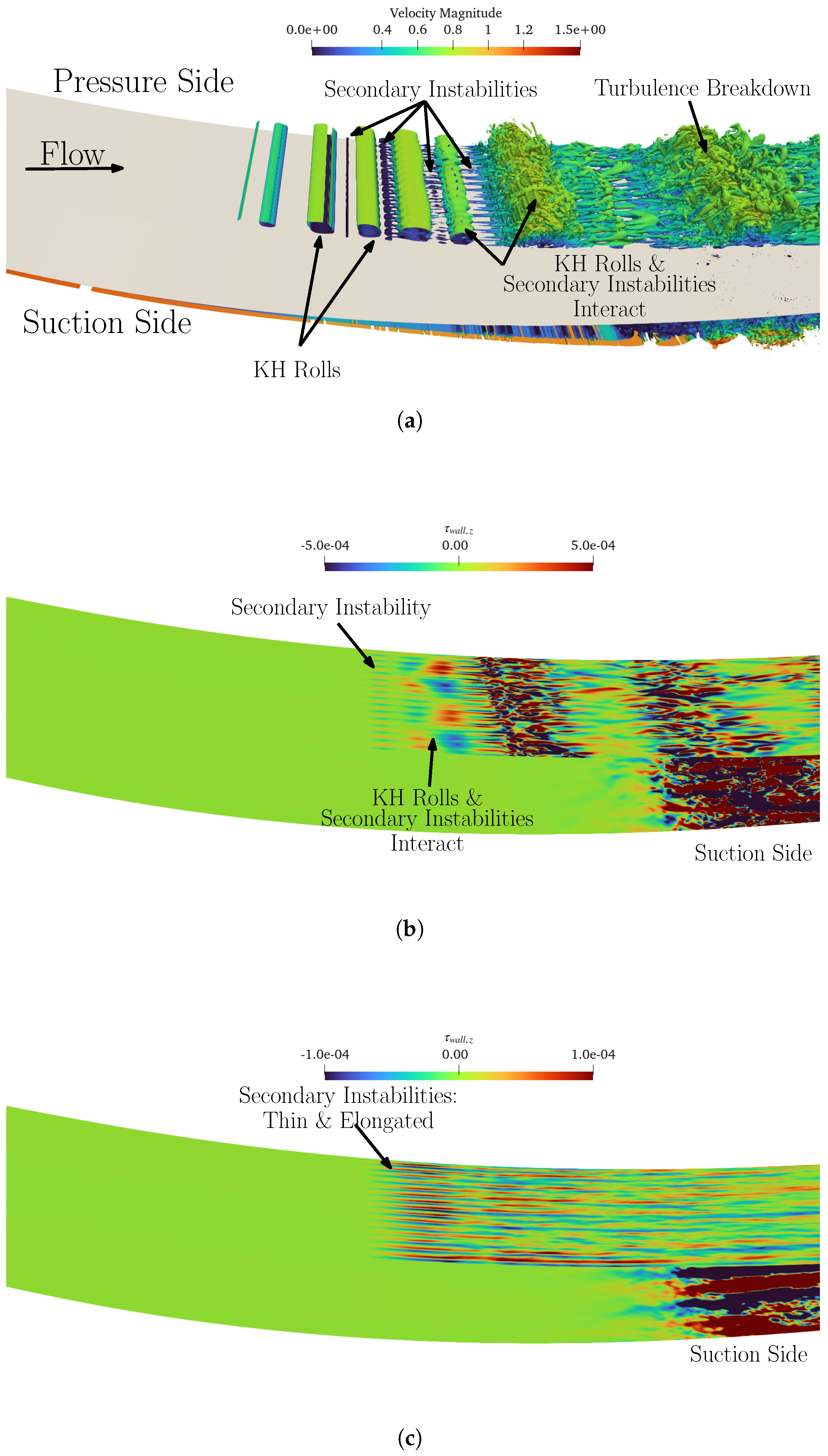
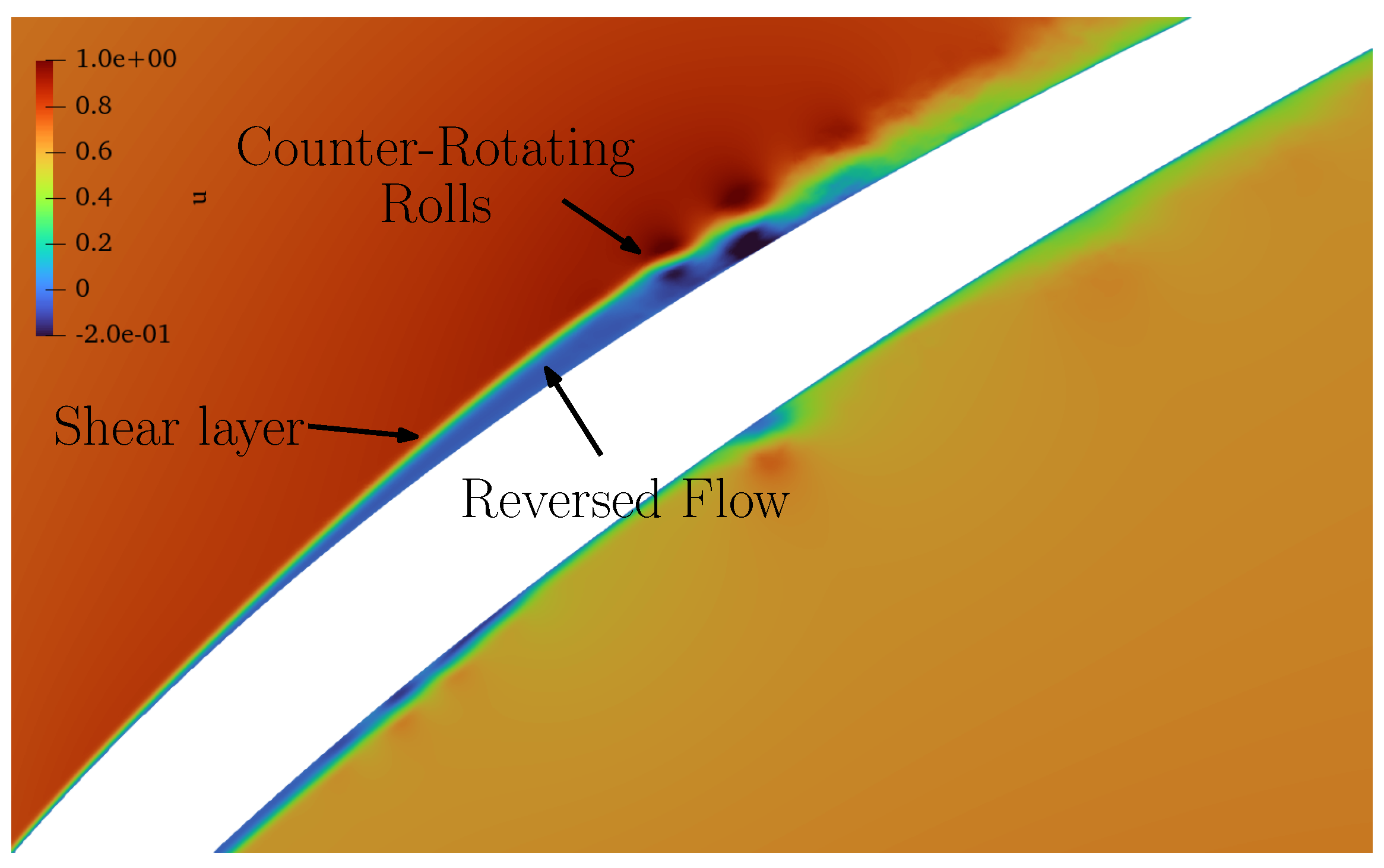
4. Clean Inflow
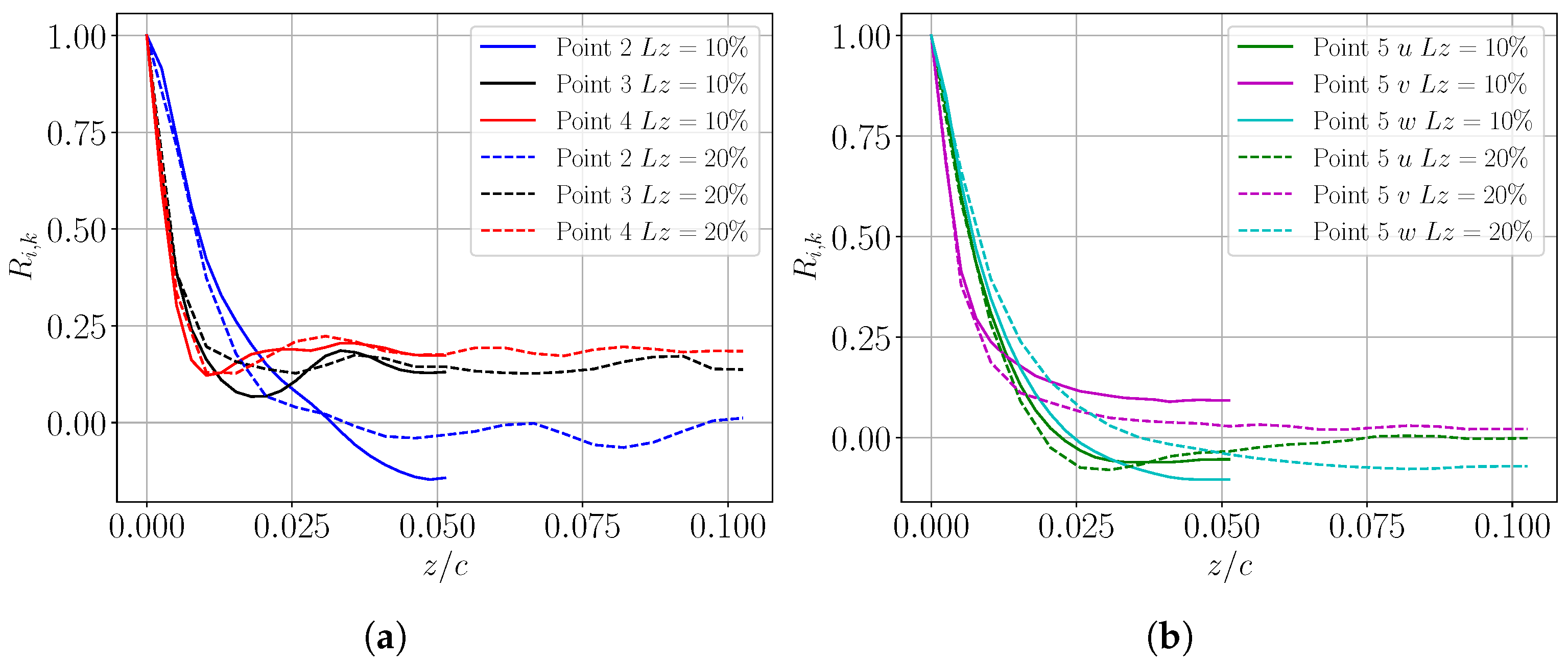
5. Extrusion Length-Clean Inflow
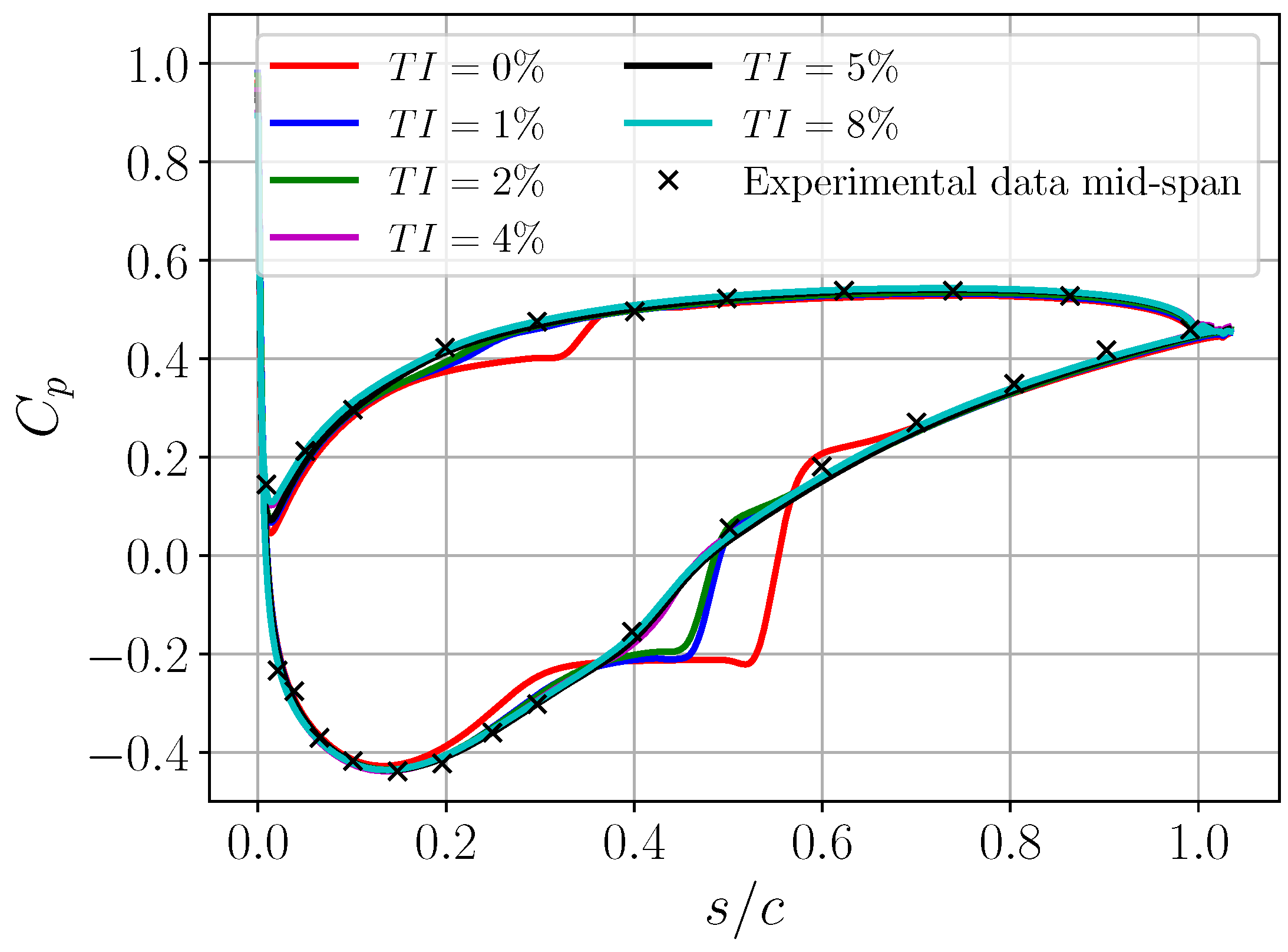
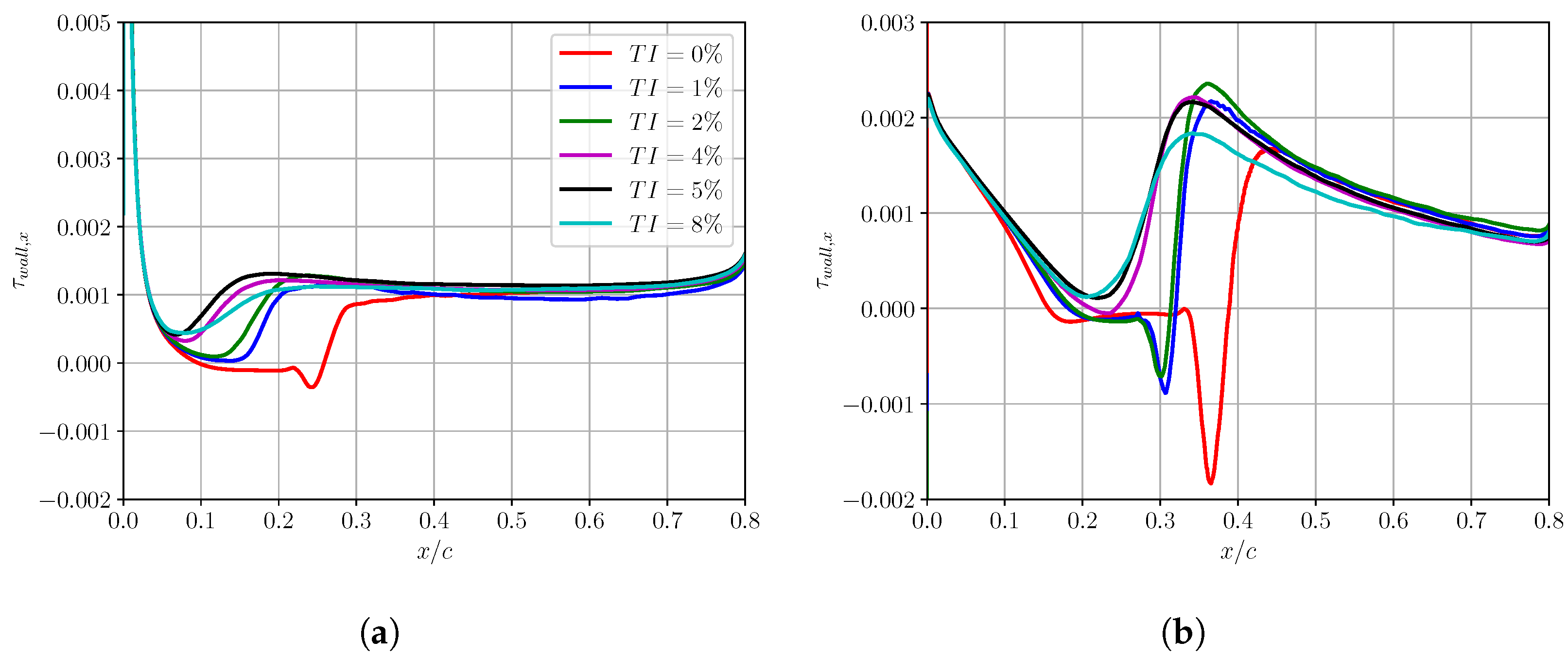
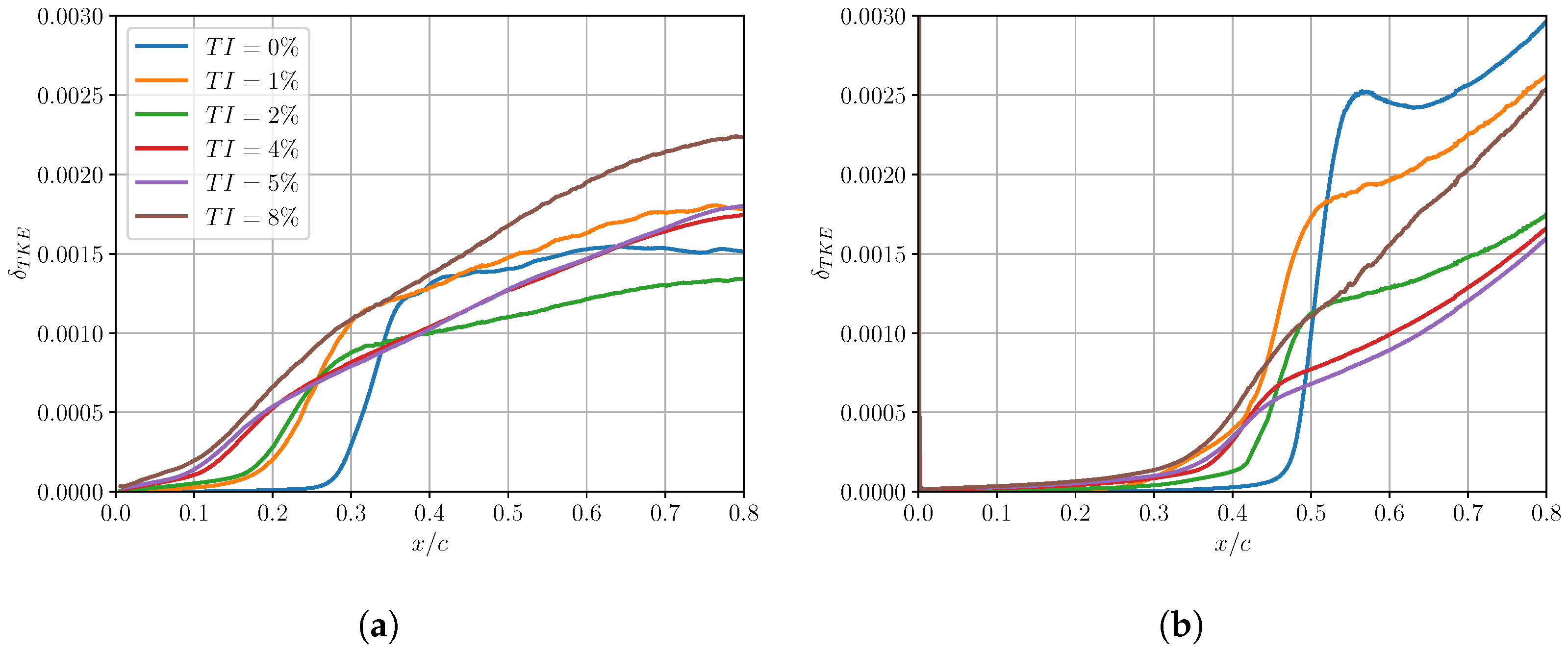
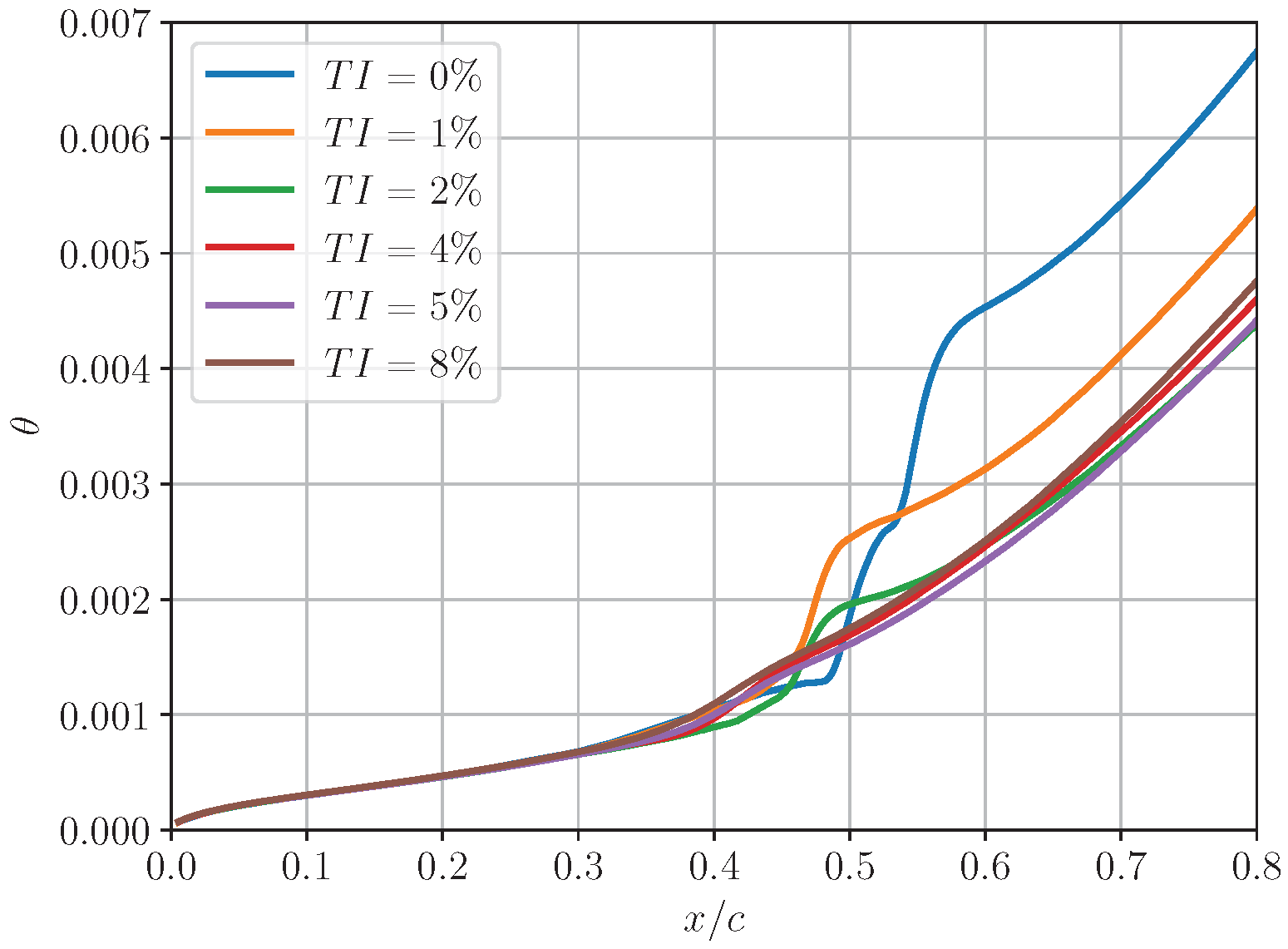
6. Turbulent Inflow
7. Costs
8. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Latin Symbols | Greek Symbols | Acronyms |
| c: True Chord | : Dynamic Viscosity | CFD: Computational Fluid Dynamics |
| : Pressure Coefficient | : Difference | DNS: Direct Numerical Simulation |
| f: Frequency | : Boundary Layer Height | FD: Finite Difference |
| G: Görtler Number | : Blackwelder Parameter | FE: Finite Element |
| : Spanwise Length | : Displacement Thickness | FV: Finite Volume |
| : Number of Fourier Modes | : Shear Stresses | GB: Gigabyte |
| P: Pressure | ∇: Differential Operator | GHz: Gigahertz |
| p: Polynomial Order | : Momentum Thickness | KH: Kelvin–Helmholtz |
| R: Radius of Curvature | LES: Large Eddy Simulation | |
| : Autocorrelation | Superscripts and Subscripts | iLES: Implicit LES |
| : Reynolds Number | +: Near-Wall Distances | PSD: Power Spectral Density |
| : Spectral Vanishing Viscosity | −: Time-Average | TI: Turbulence Intensity |
| t: Time | ′: Fluctuating Component | TS: Tollmien–Schlichting |
| V: Velocity Magnitude | : No-Slip Wall | RANS: Reynolds-Averaged Navier–Stokes |
| : Velocity Vector | : Max Amplification | |
| x: Axial Coordinate | ||
| y: Pitchwise Coordinate | ||
| z: Spanwise Coorinate |
Appendix A. Inflow Turbulence Boundary Condition
Appendix B. Boundary Layer δ99 and uδ99 Calculation
References
- Michelassi, V. Turbomachinery research and design: The role of DNS and LES in industry. In Proceedings of the Progress in Hybrid RANS-LES Modelling: Papers Contributed to the 7th Symposium on Hybrid RANS-LES Methods, Berlin, Germany, 17–19 September 2018; Springer: Berlin, Germany, 2020; pp. 55–69. [Google Scholar]
- Sandberg, R.D.; Michelassi, V. The current state of high-fidelity simulations for main gas path turbomachinery components and their industrial impact. Flow Turbul. Combust. 2019, 102, 797–848. [Google Scholar] [CrossRef]
- Wang, Z. High-order computational fluid dynamics tools for aircraft design. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130318. [Google Scholar] [CrossRef] [PubMed]
- Zaki, T.A.; Wissink, J.G.; Rodi, W.; Durbin, P.A. Direct numerical simulations of transition in a compressor cascade: The influence of free-stream turbulence. J. Fluid Mech. 2010, 665, 57–98. [Google Scholar] [CrossRef]
- McMullan, W.; Page, G.J. Large eddy simulation of a compressor cascade and the influence of spanwise domain. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 817–831. [Google Scholar] [CrossRef]
- McMullan, W.A.; Page, G.J. Large eddy simulation of a controlled diffusion compressor cascade. Flow Turbul. Combust. 2011, 86, 207–230. [Google Scholar] [CrossRef]
- McMullan, W.; Page, G. Towards large eddy simulation of gas turbine compressors. Prog. Aerosp. Sci. 2012, 52, 30–47. [Google Scholar] [CrossRef]
- Hah, C. Large eddy simulation of transonic flow field in NASA rotor 37. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 1061. [Google Scholar]
- Leggett, J.; Priebe, S.; Shabbir, A.; Michelassi, V.; Sandberg, R.; Richardson, E. Loss prediction in an axial compressor cascade at off-design incidences with free stream disturbances using large eddy simulation. J. Turbomach. 2018, 140, 071005. [Google Scholar] [CrossRef]
- Leggett, J.; Sandberg, R.D. Highly Resolved Simulations of a CDA Compressor Cascade: Effect of Reynolds Number on Losses. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Virtual, 7–11 June 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 84904, p. V02AT31A009. [Google Scholar]
- Leggett, J.; Sandberg, R. Exploring the Presence of Pressure Waves in Axial Compressor Cascades. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Virtual, 21–25 September 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84065, p. V02AT32A066. [Google Scholar]
- Wang, M.; Li, Z.; Yang, C.; Han, G.; Zhao, S.; Lu, X. Numerical investigations of the separated transitional flow over compressor blades with different loading distributions. Aerosp. Sci. Technol. 2020, 106, 106113. [Google Scholar] [CrossRef]
- Kozul, M.; Nardini, M.; Przytarski, P.J.; Solomon, W.; Shabbir, A.; Sandberg, R.D. Direct Numerical Simulation of Riblets Applied to Gas Turbine Compressor Blades at On-and Off-Design Incidences. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers, Boston, MA, USA, 26–30 June 2023; Volume 87080, p. V13AT29A006. [Google Scholar]
- Przytarski, P.J.; Wheeler, A.P.S.; Lengani, D.; Simoni, D. Data-Driven Analysis of High Fidelity Simulation of Multi-Stage Compressor. In Proceedings of the 14th European Turbomachinery Conference, Gdansk, Poland, 24–28 April 2021; p. ETC2021-628. [Google Scholar]
- Dawkins, I.; Taylor, J.; Ottavy, X.; Miller, R. The Unsteady Topology of Corner Separations. J. Turbomach. 2022, 144, 111001. [Google Scholar] [CrossRef]
- Karniadakis, G.; Sherwin, S.J. Spectral/hp Element Methods for Computational Fluid Dynamics; Oxford University Press: Oxford, MS, USA, 2005. [Google Scholar]
- Nektar++ Spectral/hp Element Framework Project. Available online: https://www.nektar.info/ (accessed on 10 July 2024).
- Cantwell, C.D.; Moxey, D.; Comerford, A.; Bolis, A.; Rocco, G.; Mengaldo, G.; De Grazia, D.; Yakovlev, S.; Lombard, J.E.; Ekelschot, D.; et al. Nektar++: An open-source spectral/hp element framework. Comput. Phys. Commun. 2015, 192, 205–219. [Google Scholar] [CrossRef]
- Moxey, D.; Cantwell, C.D.; Bao, Y.; Cassinelli, A.; Castiglioni, G.; Chun, S.; Juda, E.; Kazemi, E.; Lackhove, K.; Marcon, J.; et al. Nektar++: Enhancing the capability and application of high-fidelity spectral/hp element methods. Comput. Phys. Commun. 2020, 249, 107110. [Google Scholar] [CrossRef]
- Vivarelli, G.; Isler, J.A.; Montomoli, F.; Cantwell, C.; Sherwin, S.J.; Frey-Marioni, Y.; Vazquez-Diaz, R. Applications and Recent Developments of the Open-Source Computational Fluid Dynamics High-Fidelity Spectral/Hp Element Framework Nektar++ for Turbomachinery Configurations. In Proceedings of the Turbo Expo Power Land Sea Air, London, UK, 24–28 June 2024; Volume 88070, p. V12CT32A022. [Google Scholar]
- Vivarelli, G.; Isler, J.A.; Cantwell, C.D.; Montomoli, F.; Sherwin, S.J.; Frey-Marioni, Y.; Meyer, M.; Naqavi, I.; Vazquez-Diaz, R. A Quasi-Direct Numerical Simulation of a Compressor Blade with Separation Bubbles and Inflow Turbulence. In Proceedings of the 16th European Turbomachinery Conference, Hannover, Germany, 24–28 March 2025; p. ETC2025-325. Available online: https://www.euroturbo.eu/publications/conference-proceedings-repository/ (accessed on 5 May 2025).
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Karniadakis, G. Spectral element-Fourier methods for incompressible turbulent flows. Comput. Methods Appl. Mech. Eng. 1990, 80, 367–380. [Google Scholar] [CrossRef]
- Bolis, A.; Cantwell, C.D.; Moxey, D.; Serson, D.; Sherwin, S.J. An adaptable parallel algorithm for the direct numerical simulation of incompressible turbulent flows using a Fourier spectral/hp element method and MPI virtual topologies. Comput. Phys. Commun. 2016, 206, 17–25. [Google Scholar] [CrossRef]
- Mayle, R.E. The 1991 IGTI Scholar Lecture: The Role of Laminar-Turbulent Transition in Gas Turbine Engines. J. Turbomach. 1991, 113, 509–536. [Google Scholar] [CrossRef]
- Georgiadis, N.J.; Rizzetta, D.P.; Fureby, C. Large-eddy simulation: Current capabilities, recommended practices, and future research. AIAA J. 2010, 48, 1772–1784. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Israeli, M.; Orszag, S.A. High-order splitting methods for the incompressible Navier-Stokes equations. J. Comput. Phys. 1991, 97, 414–443. [Google Scholar] [CrossRef]
- Tadmor, E. Convergence of spectral methods for nonlinear conservation laws. SIAM J. Numer. Anal. 1989, 26, 30–44. [Google Scholar] [CrossRef]
- Cassinelli, A. A Spectral/hp Element DNS Tudy of Flow Past Low-Pressure Turbine Cascades and the Effects of Inflow Conditions. Ph.D. Thesis, Imperial College London, London, UK, 2020. [Google Scholar]
- Moura, R.C.; Sherwin, S.J.; Peiró, J. Eigensolution analysis of spectral/hp continuous Galerkin approximations to advection–diffusion problems: Insights into spectral vanishing viscosity. J. Comput. Phys. 2016, 307, 401–422. [Google Scholar] [CrossRef]
- Kirby, R.M.; Sherwin, S.J. Stabilisation of spectral/hp element methods through spectral vanishing viscosity: Application to fluid mechanics modelling. Comput. Methods Appl. Mech. Eng. 2006, 195, 3128–3144. [Google Scholar] [CrossRef]
- Davidson, L.; Billson, M. Hybrid LES-RANS using synthesized turbulent fluctuations for forcing in the interface region. Int. J. Heat Fluid Flow 2006, 27, 1028–1042. [Google Scholar] [CrossRef]
- Davidson, L. Using isotropic synthetic fluctuations as inlet boundary conditions for unsteady simulations. Adv. Appl. Fluid Mech. 2007, 1, 1–35. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Griffin, K.P.; Fu, L.; Moin, P. General method for determining the boundary layer thickness in nonequilibrium flows. Phys. Rev. Fluids 2021, 6, 024608. [Google Scholar] [CrossRef]
- Montomoli, F.; Hodson, H.; Haselbach, F. Effect of roughness and unsteadiness on the performance of a new low pressure turbine blade at low Reynolds numbers. J. Turbomach. 2010, 132, 031018. [Google Scholar] [CrossRef]
- Walker, G. Transitional flow on axial turbomachine blading. AIAA J. 1989, 27, 595–602. [Google Scholar] [CrossRef]
- Obremski, H.; Morkovin, M.V.; Landahl, M.; Wazzan, A. A Portfolio of Stability Characteristics of Incompressible Boundary Layers; Fluid Dynamics Panel of Advisory Group For Aerospace Research & Development (AGARD) of Northern Atlantic Treaty Organisation (NATO): Neuilly sur Seine, France, 1969. [Google Scholar]
- Roberts, S.K.; Yaras, M.I. Large-eddy simulation of transition in a separation bubble. J. Fluids Eng. 2006, 128, 232–238. [Google Scholar] [CrossRef]






| Symbol | Name | Value |
|---|---|---|
| V | Inflow Velocity | |
| c | True Chord | |
| Dynamic Viscosity | ||
| t | Reference Time | |
| f | Reference Frequency | |
| Turbulence Intensity | ||
| l | Turbulent Length Scale |
| Nodes | 5860 (5276 standard/584 high-memory) |
| Processor | 2 × AMD EPYCTM 7742, 2.25 GHz, 64-core |
| Memory per node | 256 GB (standard), 512 GB (high-memory) |
| Memory per core | 2 GB (standard), 4 GB (high memory) |
| Case | t | Nodes | Hours | Cost (£) | |||
|---|---|---|---|---|---|---|---|
| Clean inflow | 10 | 40 | 58 | 2320 | |||
| Clean inflow | 10 | 80 | 61 | 4880 | |||
| 10 | 40 | 30 | 1200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Vivarelli, G.; Isler, J.A.; Cantwell, C.D.; Montomoli, F.; Sherwin, S.J.; Frey-Marioni, Y.; Meyer, M.; Naqavi, I.; Vazquez-Diaz, R. A Quasi-Direct Numerical Simulation of a Compressor Blade with Separation Bubbles and Inflow Turbulence. Int. J. Turbomach. Propuls. Power 2025, 10, 8. https://doi.org/10.3390/ijtpp10020008
Vivarelli G, Isler JA, Cantwell CD, Montomoli F, Sherwin SJ, Frey-Marioni Y, Meyer M, Naqavi I, Vazquez-Diaz R. A Quasi-Direct Numerical Simulation of a Compressor Blade with Separation Bubbles and Inflow Turbulence. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(2):8. https://doi.org/10.3390/ijtpp10020008
Chicago/Turabian StyleVivarelli, Guglielmo, João Anderson Isler, Chris D. Cantwell, Francesco Montomoli, Spencer J. Sherwin, Yuri Frey-Marioni, Marcus Meyer, Iftekhar Naqavi, and Raul Vazquez-Diaz. 2025. "A Quasi-Direct Numerical Simulation of a Compressor Blade with Separation Bubbles and Inflow Turbulence" International Journal of Turbomachinery, Propulsion and Power 10, no. 2: 8. https://doi.org/10.3390/ijtpp10020008
APA StyleVivarelli, G., Isler, J. A., Cantwell, C. D., Montomoli, F., Sherwin, S. J., Frey-Marioni, Y., Meyer, M., Naqavi, I., & Vazquez-Diaz, R. (2025). A Quasi-Direct Numerical Simulation of a Compressor Blade with Separation Bubbles and Inflow Turbulence. International Journal of Turbomachinery, Propulsion and Power, 10(2), 8. https://doi.org/10.3390/ijtpp10020008