Preliminary Assessment of Geometric Variability Effects Through a Viscous Through-Flow Model Applied to Modern Axial-Flow Compressor Blades †
Abstract
1. Introduction
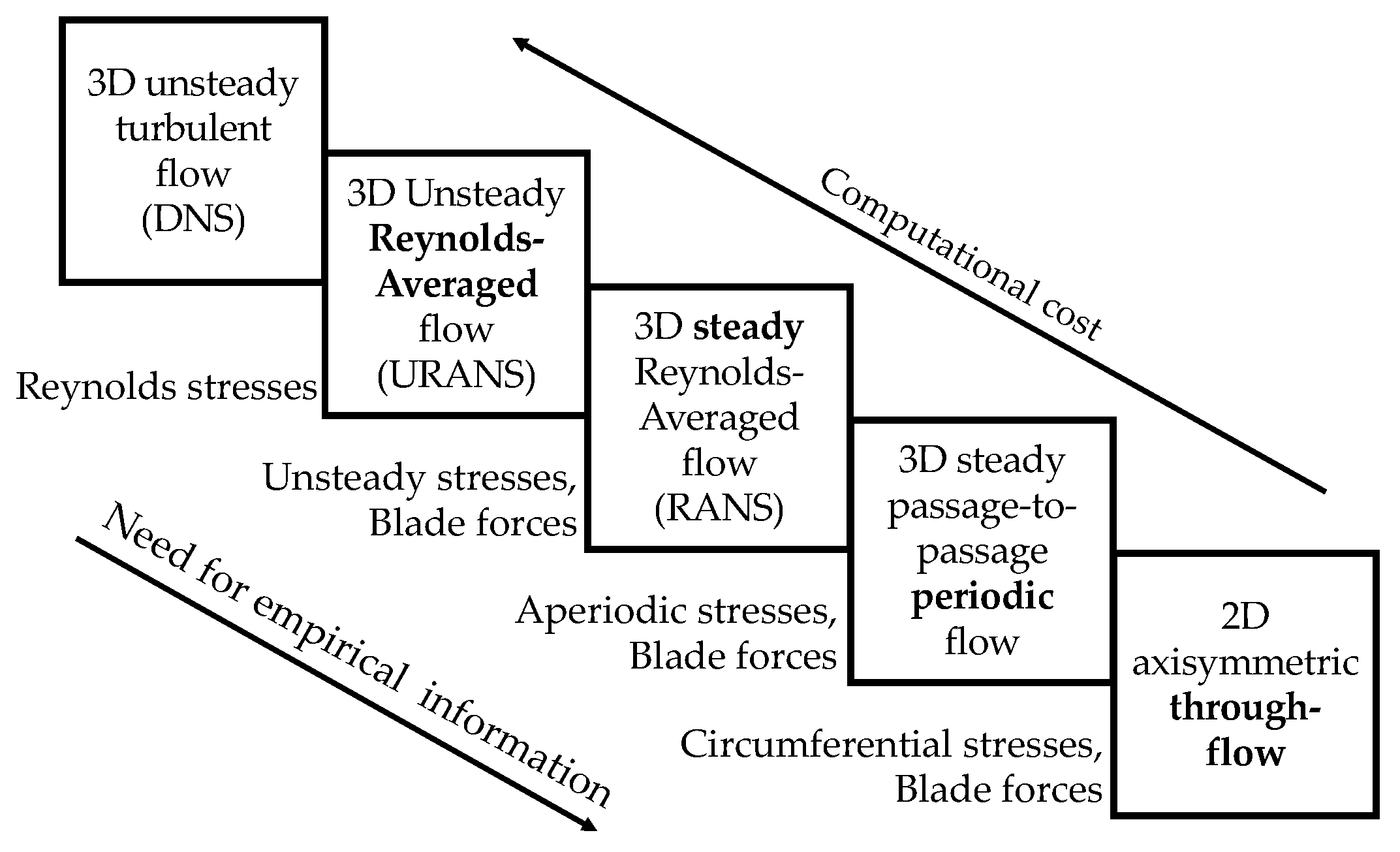
2. Through-Flow Model
2.1. Adamczyk’s Cascade
2.2. Viscous Through-Flow Equations
2.2.1. Closure Models
2.2.2. Numerical Implementation
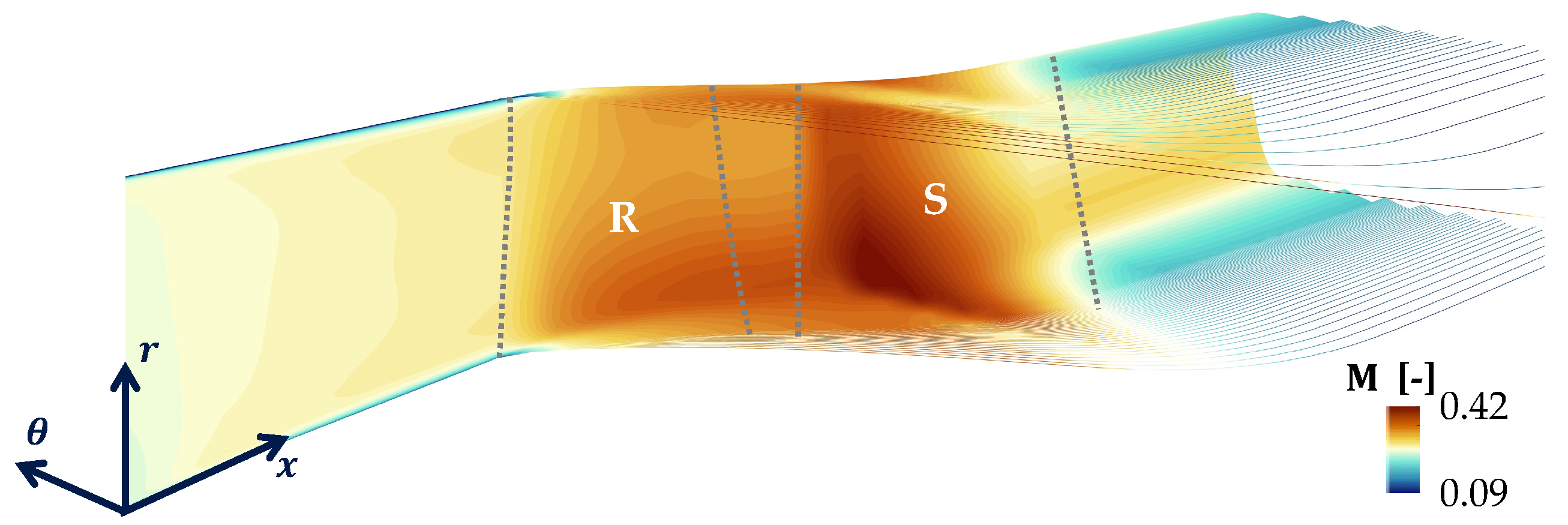
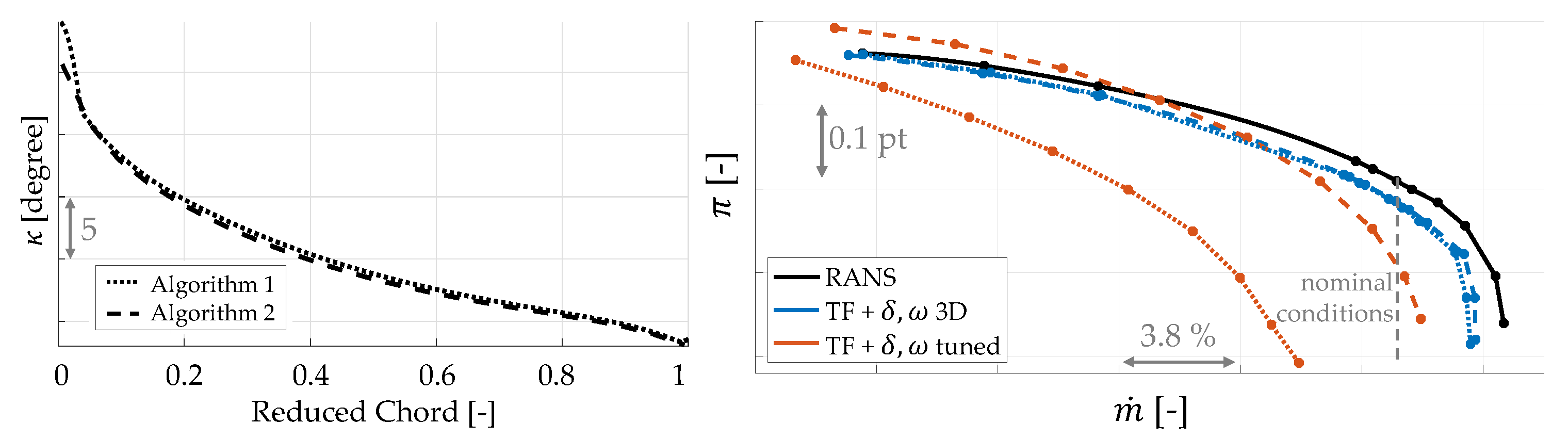
2.2.3. Solver Assessment
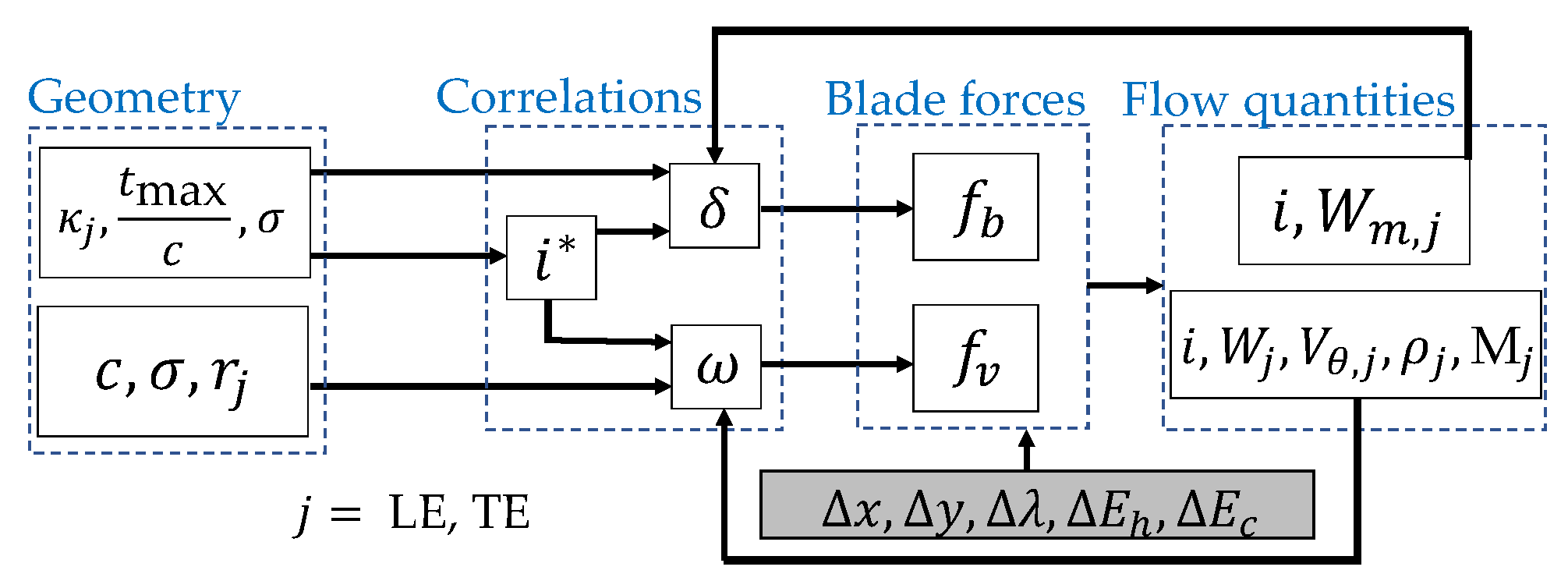
2.3. Correlations
2.4. Incidence Correction
2.5. Camber Line Computation
3. Analysis of the Effect of Geometric Variabilities
3.1. Manufacturing Variability
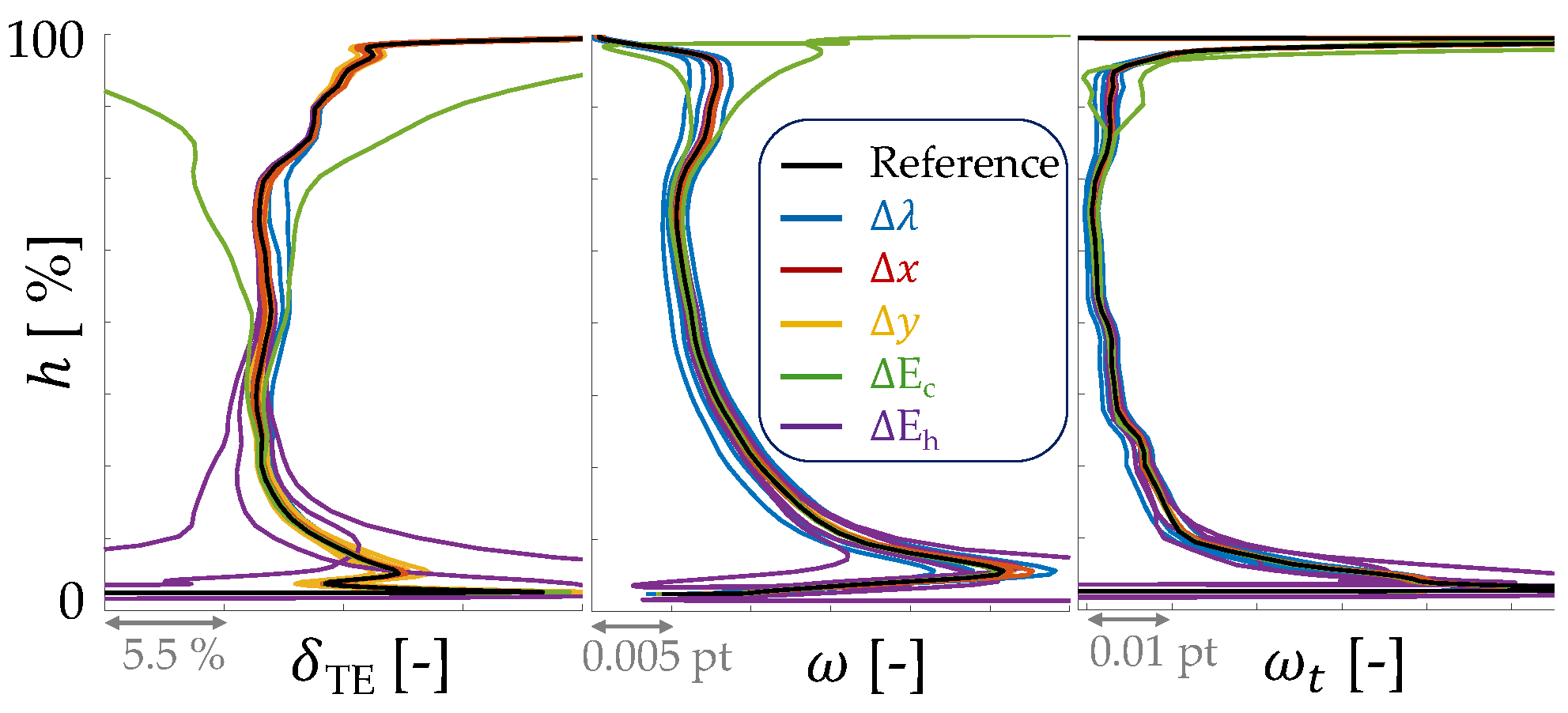
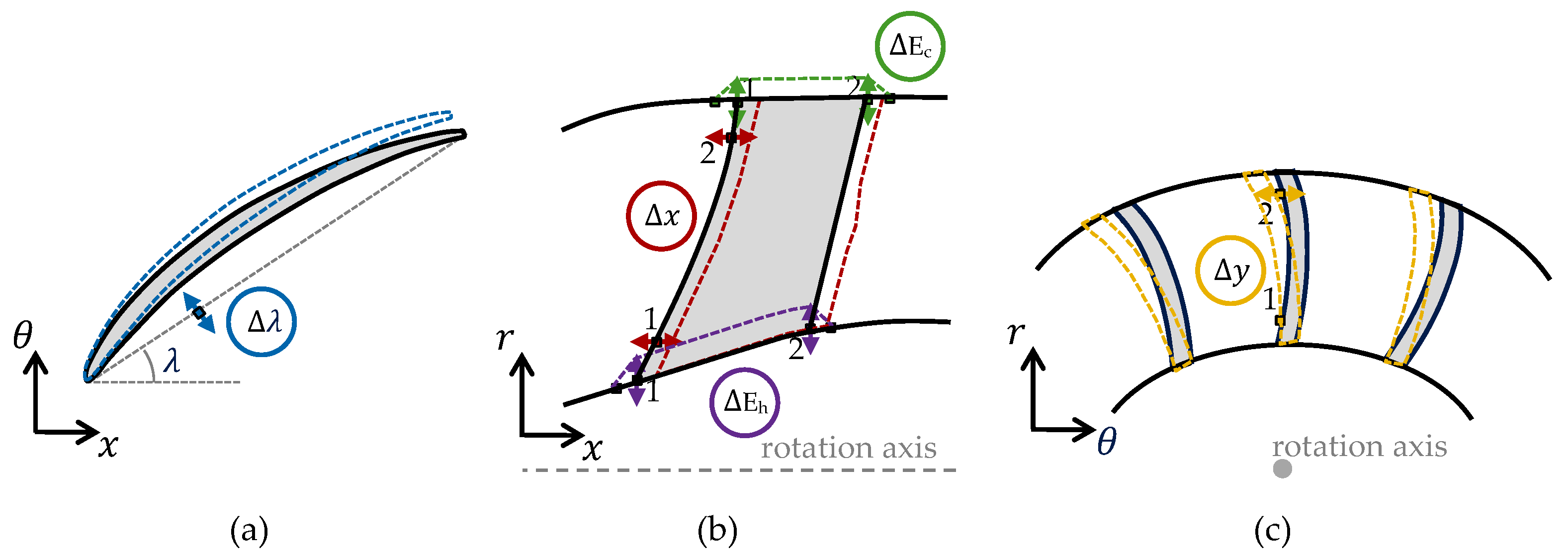
3.1.1. Imposed Geometric Variations
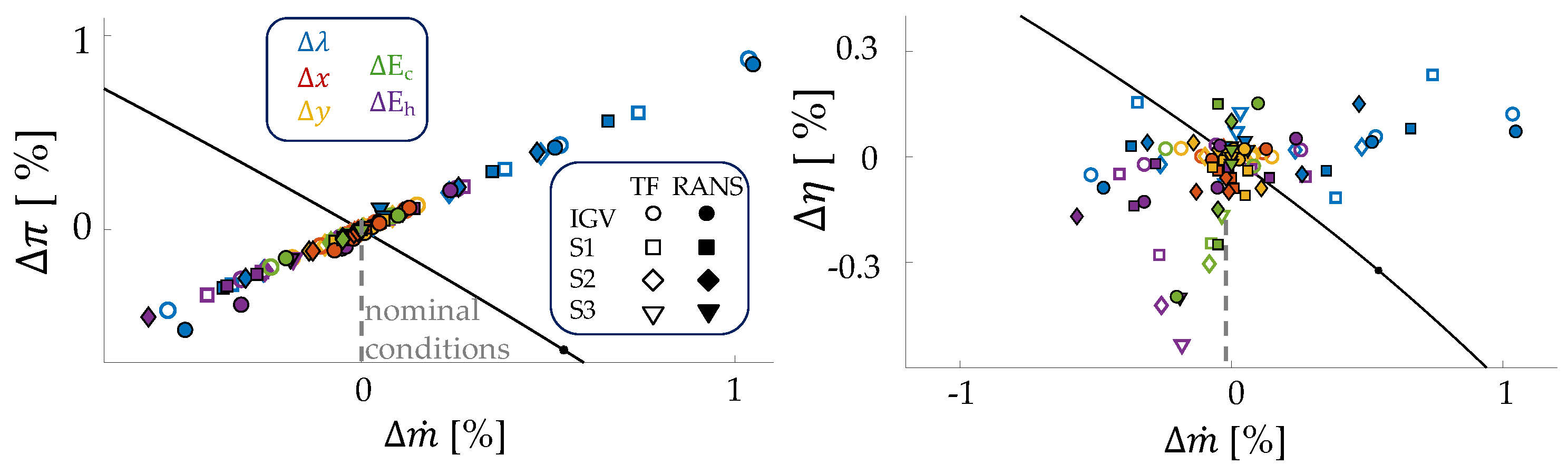
3.1.2. Sensitivity Analysis
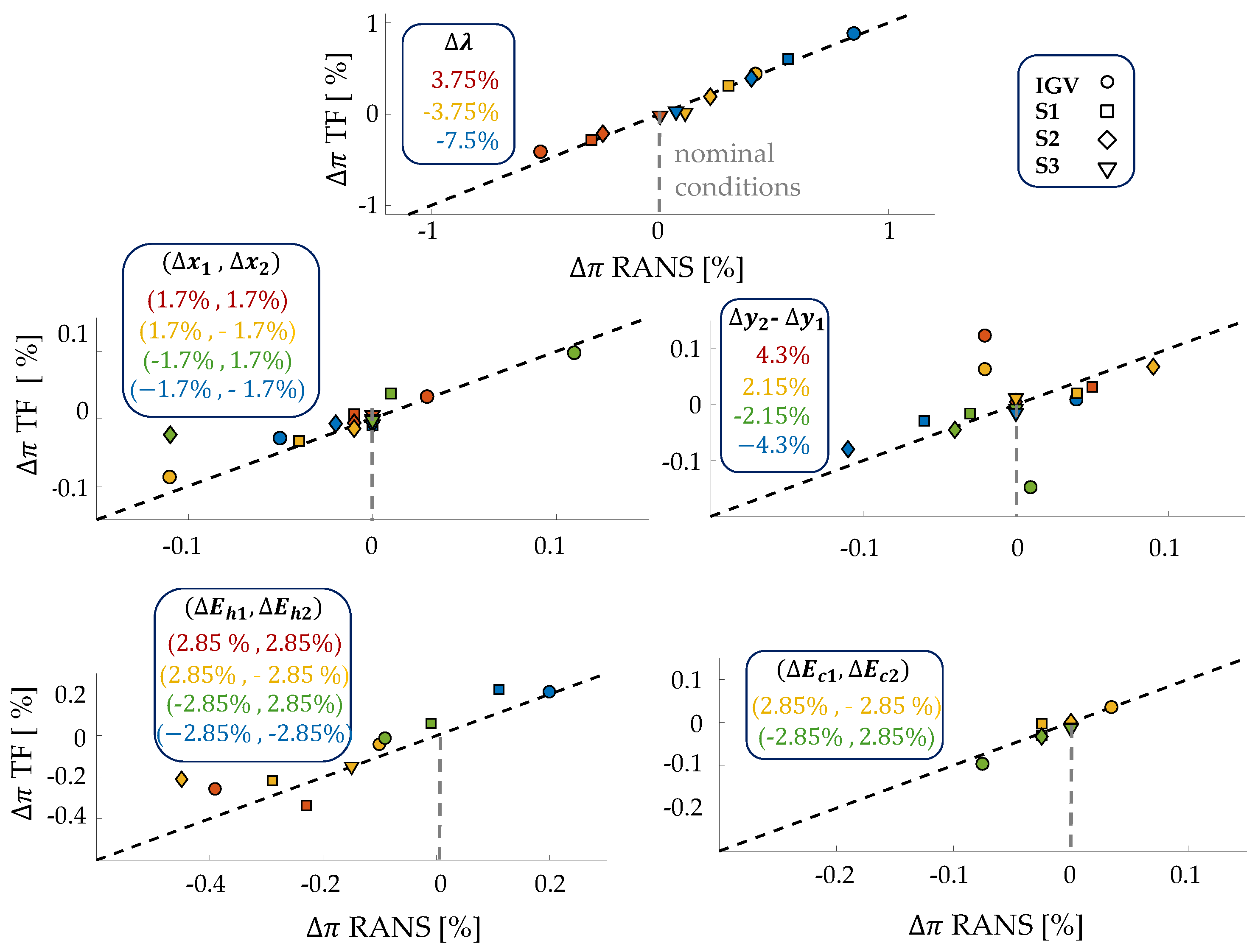
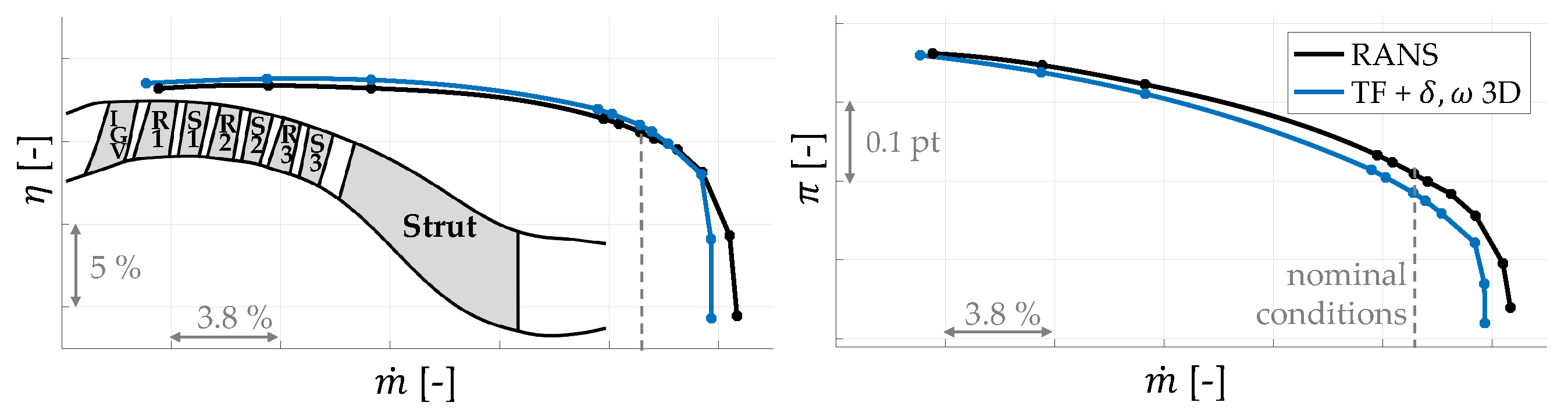
3.2. Evaluation of the Effects of Modeling Aspects on Variability Impact at Leading Edge
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| LE | Leading edge |
| RANS | Reynolds-averaged Navier–Stokes |
| TE | Trailing edge |
| TF | Through-flow |
Nomenclature
| b | tangential blockage factor [-] |
| specific heat coefficient at constant pressure [] | |
| c | blade chord [] |
| E | total energy |
| f | body force |
| h | normed blade span [-] |
| i | incidence angle [-] |
| l | streamline length [] |
| mass-flow rate | |
| M | Mach number [-] |
| N | number of blades per row [-] |
| p | pressure [] |
| source terms/body forces | |
| s | entropy [] |
| R | ideal gas constant [] |
| t | blade thickness [] |
| T | temperature [] |
| velocity in the absolute/relative frame [] | |
| x, r, | cylindrical coordinates |
| Greek symbols: | |
| tangential flow angle [-] | |
| variation | |
| deviation angle [-] | |
| isentropic efficiency [-] | |
| blade angle [-] | |
| stagger angle [-] | |
| total pressure ratio [-] | |
| density [] | |
| shear stress [] | |
| wake momentum thickness [] | |
| angular velocity of the shaft [] | |
| loss coefficient [-] | |
| Super-/Subscripts: | |
| * | optimal conditions |
| b | blade force |
| c/h | casing/hub |
| camber line | |
| inviscid/viscous | |
| m | meridional |
| s | stress |
| t | total quantities |
References
- Dow, E.A.; Wang, Q. The Implications of Tolerance Optimization on Compressor Blade Design. J. Turbomach. 2015, 137, 101008. [Google Scholar] [CrossRef]
- Bestle, D.; Flassig, P. Optimal Aerodynamic Compressor Blade Design Considering Manufacturing Noise. In Proceedings of the ISSMO Conference, London, UK, 8–9 July 2010. [Google Scholar]
- Garzon, V.E.; Darmofal, D.L. Impact of Geometric Variability on Axial Compressor Performance. J. Turbomach. 2003, 125, 692–703. [Google Scholar] [CrossRef]
- Nigro, R. Uncertainty Quantification for Robust Design of Axial Compressors. Ph.D. Thesis, University of Mons, Mons, Belgium, 2018. [Google Scholar]
- Lange, A.; Voigt, M.; Vogeler, K.; Johann, E.; Royce, R.; Kg, C.; Dahlewitz, D. Principal Component Analysis On 3D Scanned Compressor Blades For Probabilistic CFD Simulation. In Proceedings of the AIIA Conference, Granada, Spain, 3–7 September 2012; pp. 1–16. [Google Scholar] [CrossRef]
- Goodhand, M.N.; Miller, R.J.; Lung, H.W. The Impact of Geometric Variation on Compressor Two-Dimensional Incidence Range. J. Turbomach. 2014, 137, 021007. [Google Scholar] [CrossRef]
- Simon, J.F. Contribution to Throughflow Modelling for Axial Flow Turbomachines. Ph.D. Thesis, University of Liège, Liège, Belgium, 2007. [Google Scholar]
- Baralon, S.; Erikson, L.E.; Hall, U. Validation of a Throughflow Time-Marching Finite-Volume Solver for Transonic Compressors. In Proceedings of the ASME Turbo Expo, Stockholm, Sweden, 1–4 June 1998. [Google Scholar]
- Lange, A.; Vogeler, K.; Gümmer, V.; Schrapp, H.; Clemen, C. Introduction of A Parameter Based Compressor Blade Model For Considering Measured Geometry Uncertainties In Numerical Simulation. ASME J. Turbomach. 2009, 48876, 1113–1123. [Google Scholar]
- Wu, C.H. A General Theory of Three-Dimesional Flow in Subsonic and Supersonic Turbomachines of Axial-, Radial-, and Mixed-Flow Types; Technical Report; NACA: Washington, DC, USA, 1952. [Google Scholar]
- Pacciani, R.; Rubechini, F.; Marconcini, M.; Arnone, A.; Cecchi, S.; Daccà, F. A CFD-based throughflow method with an explicit body force model and an adaptive formulation for the S2 streamsurface. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 16–28. [Google Scholar] [CrossRef]
- Righi, M.; Pachidis, V.; Könözsy, L.; Pawsey, L. Three-Dimensional Through-Flow Modelling of Axial Flow Compressor Rotating Stall and Surge. Aerosp. Sci. Technol. 2018, 78, 271–279. [Google Scholar] [CrossRef]
- Föllner, S.; Amedick, V.; Bonhoff, B.; Brillert, D.; Benra, F.K. Model validation of an Euler-based 2D-Throughflow Approach For multistage Axial Turbine Analysis. In Proceedings of the ASME Turbo Expo, London, UK, 22–26 June 2020; Volume 29, pp. 185–186. [Google Scholar]
- Jian, L.; Dongrun, W.; Jinfang, T.; Mingmin, Z.; Xiaoqing, Q. The Effects of Incidence and Deviation on the CFD-Based Throughflow Analysis. In Proceedings of the ASME Turbo Expo, London, UK, 22–26 June 2020; pp. 1–9. [Google Scholar]
- Adamczyk, J.J. Model Equation for Simulating Flows in Multistage Turbomachinery; Technical Report TM-86869; NASA: Cleveland, OH, USA, 1984. [Google Scholar]
- Adamczyk, J.J. Aerodynamic Analysis of Multistage Turbomachinery Flows in Support of Aerodynamic Design. ASME J. Turbomach. 1999, 122, 189–217. [Google Scholar] [CrossRef]
- Budo, A.; Terrapon, V.E.; Arnst, M.; Hillewaert, K.; Mouriaux, S.; Rodriguez, B.; Bartholet, J. Application of a Viscous Through-Flow Model to a Modern Axial Low-Pressure Compressor. In Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers; American Society of Mechanical Engineers: New York City, NY, USA, 2021. [Google Scholar] [CrossRef]
- Smith, B.R. A Near Wall Model for The k-l Two Equation Turbulence Model. In Proceedings of the AIIA Conference, Austin, TX, USA, 31 May–3 June 1994; pp. 1–8. [Google Scholar] [CrossRef]
- Jameson, A.; Schmidt, W.; Turkel, E. Numerical solution of the Euler equations by finite volume methods using Runge Kutta time stepping schemes. In Proceedings of the 14th Fluid and Plasma Dynamics Conference, Palo Alto, CA, USA, 23–25 June 1981. [Google Scholar]
- Lieblein, S. Incidence and Deviation-Angle Correlations for Compressor Cascades. ASME J. Turbomach. 1960, 82, 575–584. [Google Scholar] [CrossRef]
- Aungier, R.H. Axial-Flow Compressors; The American Society of Mechanical Engineers: New York City, NY, USA, 2003. [Google Scholar]
- Carter, A. The Low Speed Performance Of Related Aerofoils In Cascades; Technical Report 19; Aeronautical Research Council: London, UK, 1950. [Google Scholar]
- Johnsen, I.; Bullock, R. Aerodynamic Design of Axial-Flow Compressors; Number SP-36; NASA: Washington, DC, USA, 1965; pp. 1–507. [Google Scholar]
- Pollard, D.; Gostelow, J.P. Some Experiments at Low Speed on Compressor Cascades. J. Eng. Gas Turbines Power 1967, 89, 427–436. [Google Scholar] [CrossRef]
- Kónig, W.M.; Hennecke, D.K.; Fottner, L. Improved Blade Profile Loss And Deviation Angle Models For Advanced Transonic Compressor Bladings: Part I—A Model For Subsonic Flow. ASME J. Turbomach. 1994, 118, 73–80. [Google Scholar] [CrossRef]
- Cao, T.; Hield, P.; Tucker, P.G. Hierarchical Immersed Boundary Method with Smeared Geometry. J. Propuls. Power 2017, 33, 1151–1163. [Google Scholar] [CrossRef]
- Budo, A.; Hillewaert, K.; Bartholet, J.; Terrapon, V.E. Assessment of geometrical variability effects through a viscous through-flow model applied to modern axial-flow compressor blades. In Proceedings of the 15th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Budapest, Hungary, 24–28 April 2023; Available online: https://www.euroturbo.eu/publications/proceedings-papers/etc2023-307/ (accessed on 1 November 2024).
- Budo, A.; Hillewaert, K.; Arnst, M.; Le Man, T.; Terrapon, V.E. Quantification of geometric variability effects through a viscous through-flow model: Sensitivity analysis of the manufacturing tolerance effects on performance of modern axial-flow compressor blades. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York City, NY, USA, 2023; Available online: https://asmedigitalcollection.asme.org/GT/proceedings-pdf/GT2023/87103/V13CT32A023/7045776/v13ct32a023-gt2023-102800.pdf (accessed on 1 November 2024). [CrossRef]



| DOFs | Relative Variations [%] |
|---|---|
| ; | |
| ; | |
| ; | |
| ; |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Budo, A.; Bartholet, J.; Le Men, T.; Hillewaert, K.; Terrapon, V.E. Preliminary Assessment of Geometric Variability Effects Through a Viscous Through-Flow Model Applied to Modern Axial-Flow Compressor Blades. Int. J. Turbomach. Propuls. Power 2025, 10, 6. https://doi.org/10.3390/ijtpp10020006
Budo A, Bartholet J, Le Men T, Hillewaert K, Terrapon VE. Preliminary Assessment of Geometric Variability Effects Through a Viscous Through-Flow Model Applied to Modern Axial-Flow Compressor Blades. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(2):6. https://doi.org/10.3390/ijtpp10020006
Chicago/Turabian StyleBudo, Arnaud, Jules Bartholet, Thibault Le Men, Koen Hillewaert, and Vincent E. Terrapon. 2025. "Preliminary Assessment of Geometric Variability Effects Through a Viscous Through-Flow Model Applied to Modern Axial-Flow Compressor Blades" International Journal of Turbomachinery, Propulsion and Power 10, no. 2: 6. https://doi.org/10.3390/ijtpp10020006
APA StyleBudo, A., Bartholet, J., Le Men, T., Hillewaert, K., & Terrapon, V. E. (2025). Preliminary Assessment of Geometric Variability Effects Through a Viscous Through-Flow Model Applied to Modern Axial-Flow Compressor Blades. International Journal of Turbomachinery, Propulsion and Power, 10(2), 6. https://doi.org/10.3390/ijtpp10020006