Considerations for High-Fidelity Modeling of Unsteady Flows in a Multistage Axial Compressor
Abstract
1. Introduction
2. Computational Methodology
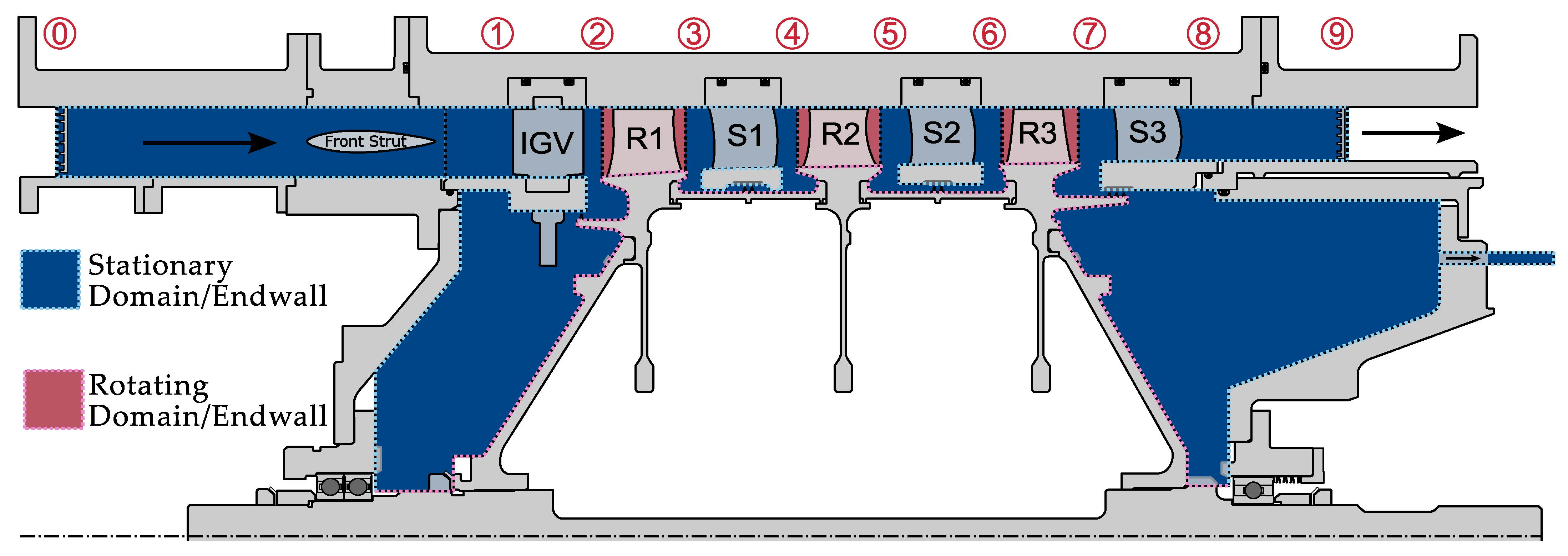
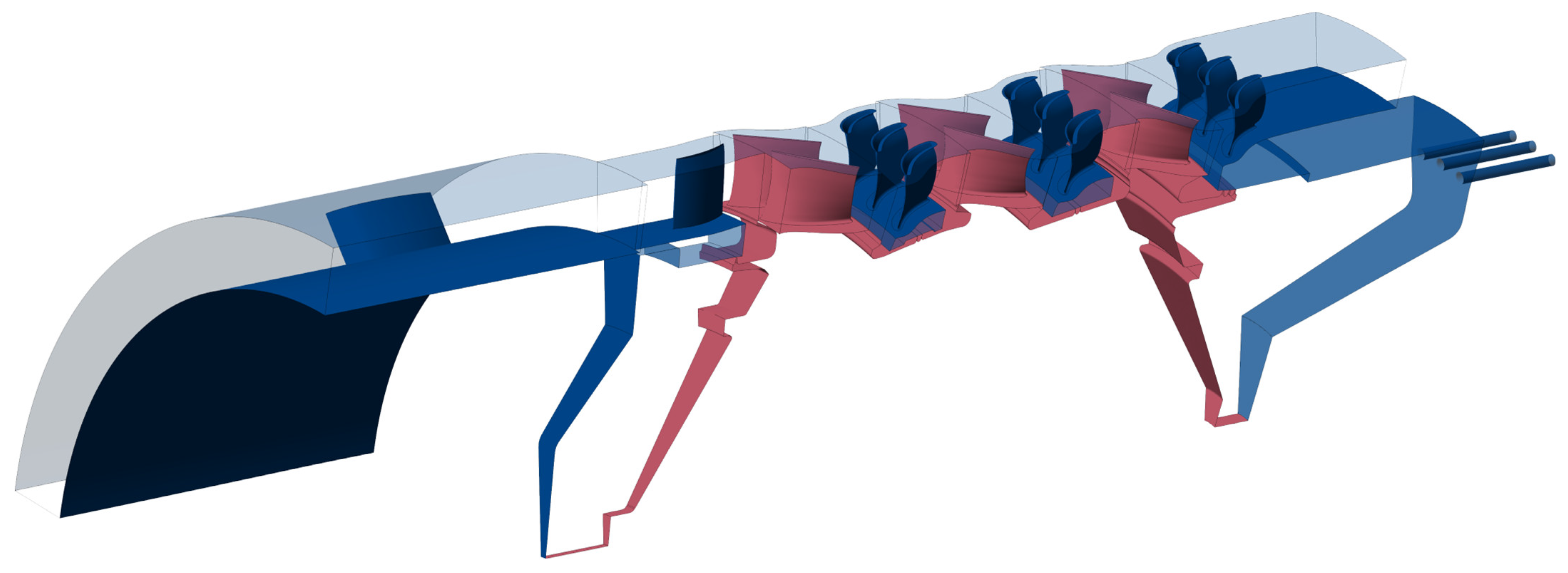
2.1. Scope of the Computational Domain and Geometric Definitions
2.2. Ansys CFX-5 Solver
2.3. Boundary Conditions and Modeling
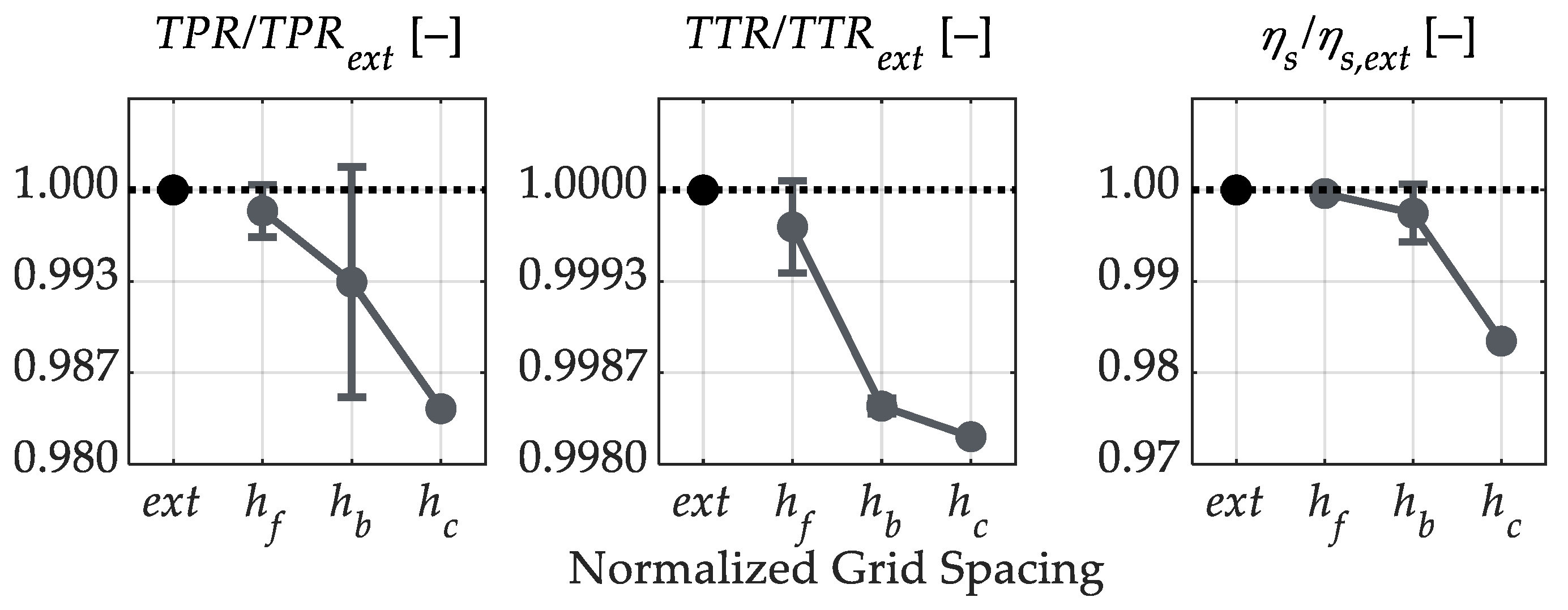
2.4. Spatial Discretization and Grid Sensitivity
2.5. Transient Blade Row Model
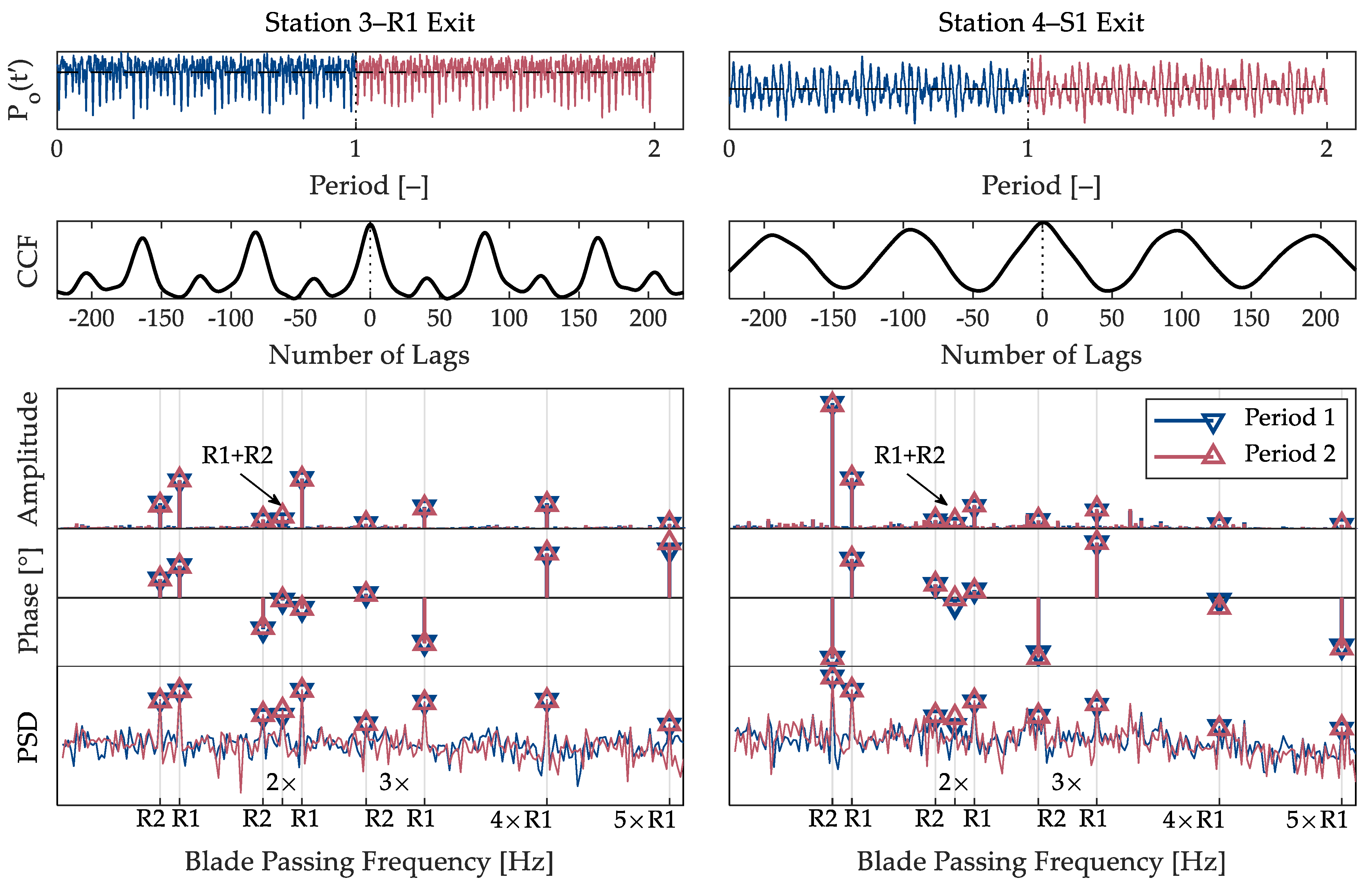
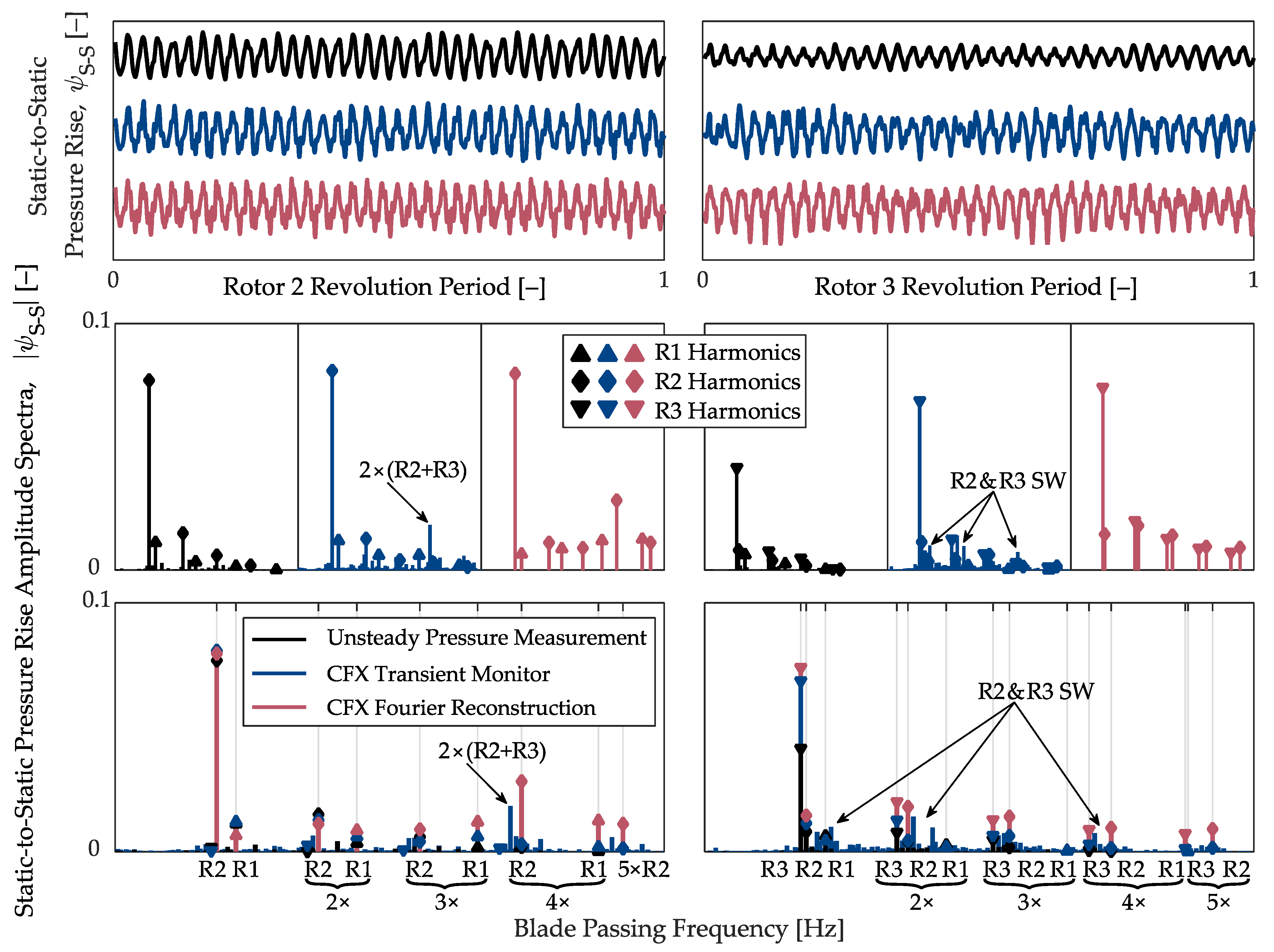
2.6. Assessing Periodic-Unsteady Convergence
- (1)
- Conservation equation residuals have reduced orders of magnitude (typically 4–6, highly dependent on model complexity), reaching a level below a predefined threshold.
- (2)
- Global and domain imbalances of mass, momentum, energy, and other scalar quantities are near zero (less than 1%).
- (3)
- The solution’s figures of merit no longer change with subsequent iterations (e.g., TPR, TTR, mass flow rate, torque, entropy).
- (1)
- Each monitor point location has unchanging temporal means between periods and an associated membership grade of one (fM = 1.00).
- (2)
- High membership grades are associated with the amplitude and phase of the fundamental through fifth harmonic of the upstream R1 blade-passing frequency (BPF) (fA, fϕ > 0.85) and the fundamental through third harmonic of the downstream R2 blade-passing frequency (fA, fϕ > 0.88).
- (3)
- The cross-correlation function (CCF) applied to the successive periods shows minimal time lag between the signals. The associated membership grade (fS > 0.94) is the value of the cross-correlation function at zero time lag and indicates a consistent signal shape between periods.
- (4)
- Membership grades (fS > 0.89) of the fractional signal power set parameter computed from the PSD estimate include the same frequencies chosen for the amplitude and phase spectra, indicating that most of the signal power is accounted for in the chosen frequencies.
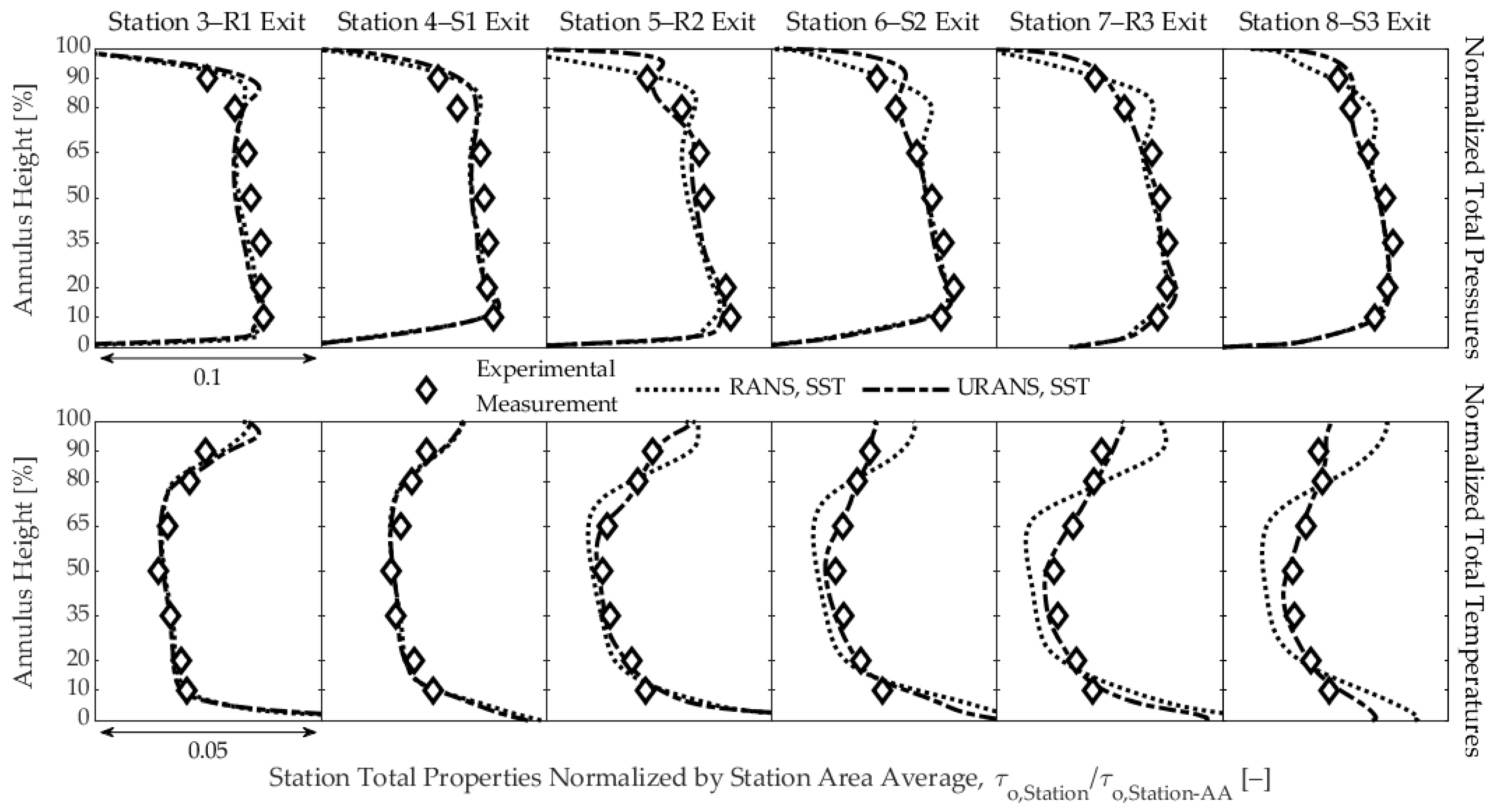
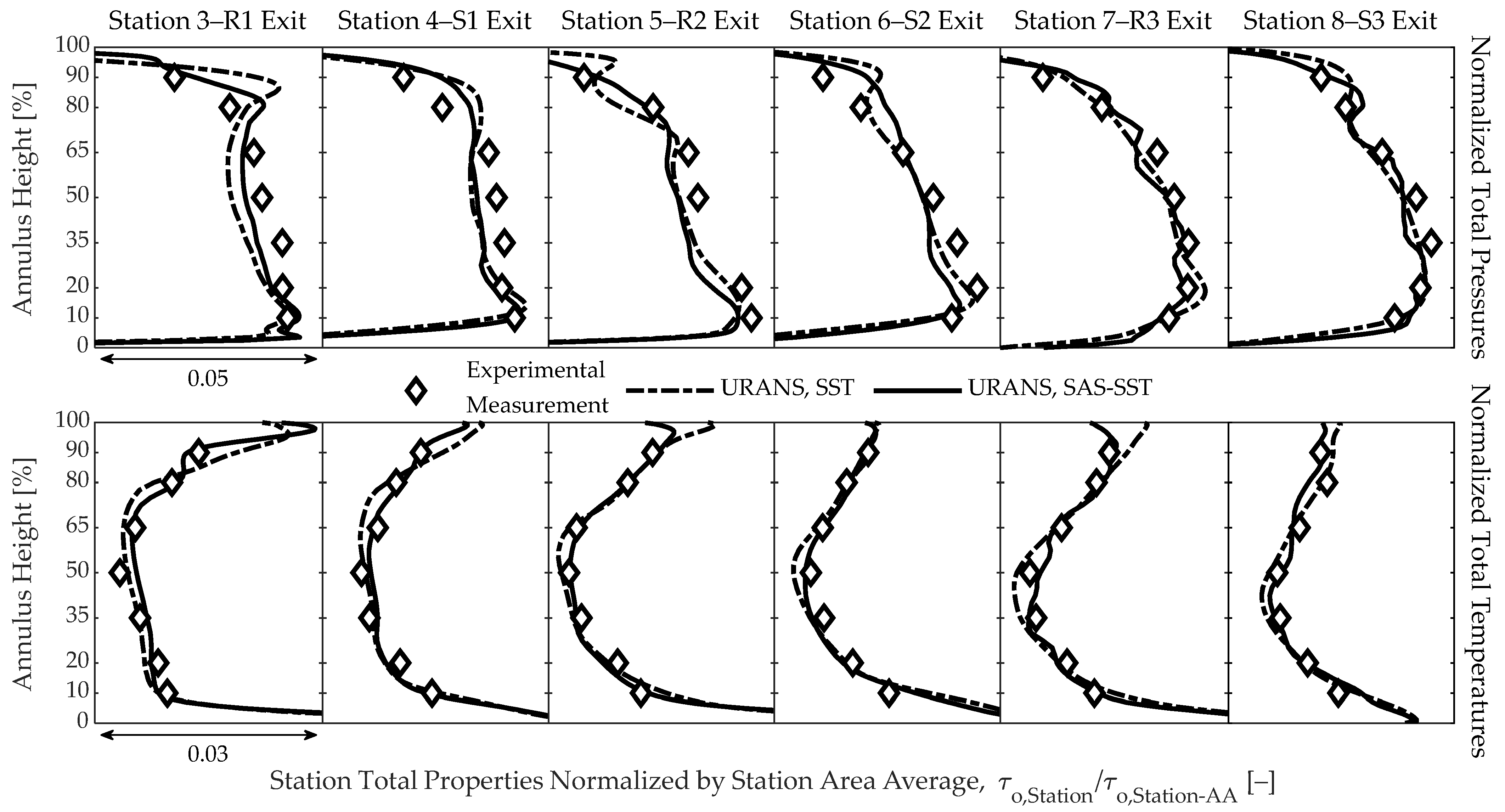
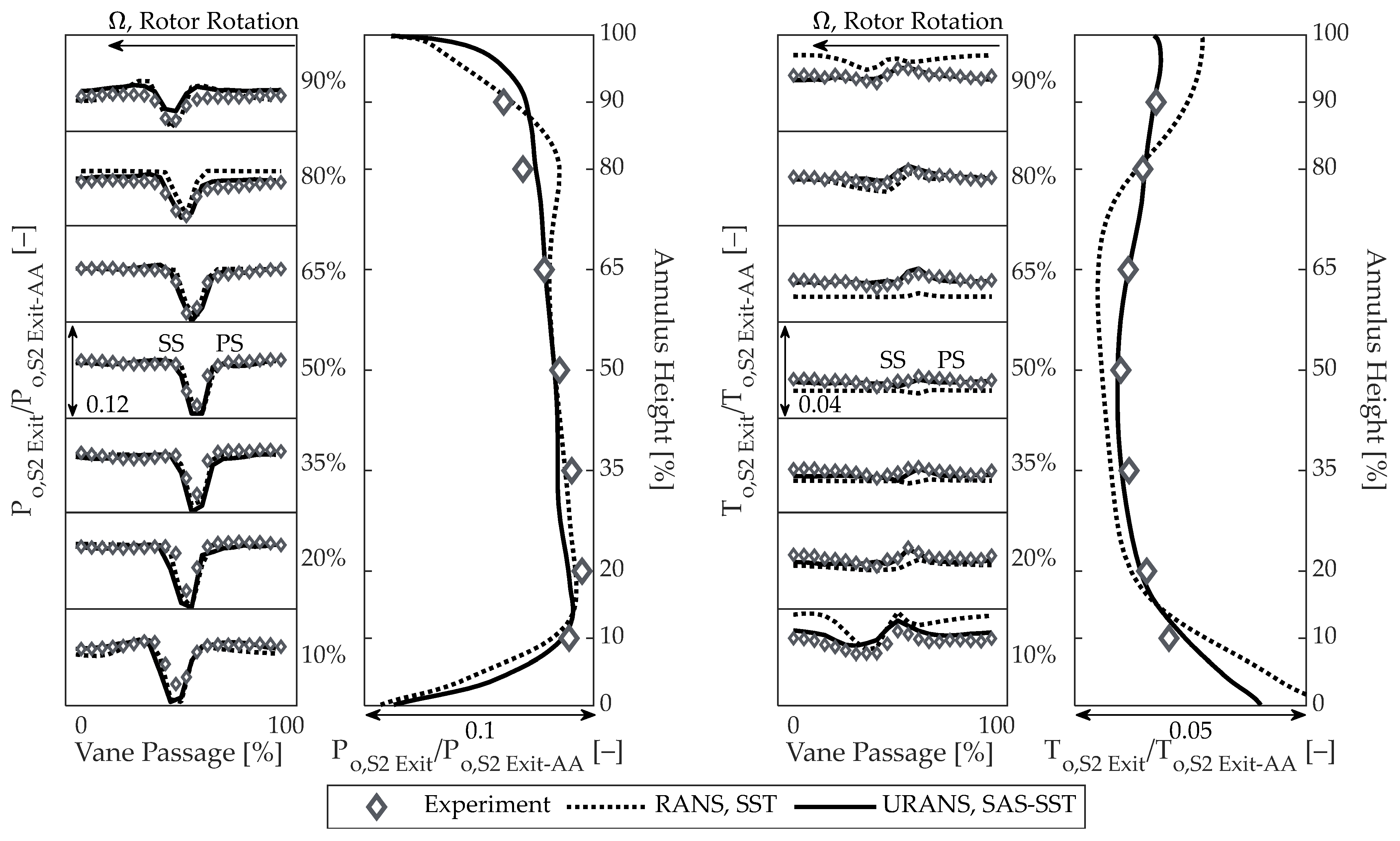
3. Comparing CFD Methods with Experimental Measurements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kormanik, N.J., III; Matthews, D.R.; Key, N.L.; King, A.J. Lessons Learned for Developing an Effective High-Speed Research Compressor Facility. Aerospace 2024, 11, 949. [Google Scholar] [CrossRef]
- Denton, J.D. Some Limitations of Turbomachinery CFD. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; Volume 7: Turbomachinery, Parts A, B, and C, pp. 735–745. [Google Scholar] [CrossRef]
- Adkins, G.G.; Smith, L.H. Spanwise Mixing in Axial-Flow Turbomachines. J. Eng. Power 1982, 104, 97–110. [Google Scholar] [CrossRef]
- Gallimore, S.J.; Cumpsty, N.A. Spanwise Mixing in Multistage Axial Flow Compressors: Part I—Experimental Investigation. J. Turbomach. 1986, 108, 2–9. [Google Scholar] [CrossRef]
- Gallimore, S.J. Spanwise Mixing in Multistage Axial Flow Compressors: Part II—Throughflow Calculations Including Mixing. J. Turbomach. 1986, 108, 10–16. [Google Scholar] [CrossRef]
- Wisler, D.C.; Bauer, R.C.; Okiishi, T.H. Secondary Flow, Turbulent Diffusion, and Mixing in Axial-Flow Compressors. J. Turbomach. 1987, 109, 455–469. [Google Scholar] [CrossRef]
- Roberts, W.B. Discussion: “Secondary Flow, Turbulent Diffusion, and Mixing in Axial-Flow Compressors” (Wisler, D.C., Bauer, R.C., and Okiishi, T.H., 1987, ASME J. Turbomach., 109, pp. 455–469). J. Turbomach. 1987, 109, 477. [Google Scholar] [CrossRef]
- Cozzi, L.; Rubechini, F.; Giovannini, M.; Marconcini, M.; Arnone, A.; Schneider, A.; Astrua, P. Capturing Radial Mixing in Axial Compressors With Computational Fluid Dynamics. J. Turbomach. 2019, 141, 031012. [Google Scholar] [CrossRef]
- Matthews, D.R. The Influence of Stator Endwall Clearances on Multistage Axial Compressor Aerodynamics. Ph.D. Thesis, School of Aeronautics and Astronautics, Purdue University, West Lafayette, IN, USA, 2024. [Google Scholar]
- ANSYS, Inc. ANSYS CFX Release 2023 R2 Documentation 2023; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Giles, M.B. Calculation of Unsteady Wake/Rotor Interaction. J. Propuls. Power 1988, 4, 356–362. [Google Scholar] [CrossRef]
- Cornelius, C.; Biesinger, T.; Zori, L.; Campregher, R.; Galpin, P.; Braune, A. Efficient Time Resolved Multistage CFD Analysis Applied to Axial Compressors; American Society of Mechanical Engineers Digital Collection: Düsseldorf, Germany, 2014. [Google Scholar] [CrossRef]
- Shabbir, A.; Turner, M.G. A Wall Function for Calculating the Skin Friction With Surface Roughness; American Society of Mechanical Engineers Digital Collection: Vienna, Austria, 2004; pp. 1661–1671. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Smirnov, P.E.; Menter, F.R. Sensitization of the SST Turbulence Model to Rotation and Curvature by Applying the Spalart–Shur Correction Term. J. Turbomach. 2009, 131, 041010. [Google Scholar] [CrossRef]
- Menter, F.; Egorov, Y. A Scale Adaptive Simulation Model Using Two-Equation Models. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F.R.; Lechner, R.; Cokljat, D. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 2: Application to Complex Flows. Flow Turbul. Combust 2010, 85, 139–165. [Google Scholar] [CrossRef]
- Eiseman, P.R.; Rajagopalan, K. Automatic Topology Generation. In New Developments in Computational Fluid Dynamics; Fujii, K., Nakahashi, K., Obayashi, S., Komurasaki, S., Eds.; Springer: Berlin, Heidelberg, 2005; pp. 112–124. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- American Institute of Aeronautics and Astronautics. Guide for the Verification and Validation of Computational Fluid Dynamics Simulations (G-077-1998(2002)); American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1998. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001–078004. [Google Scholar] [CrossRef]
- Kormanik, N.J., III. Characterization of Aerodynamic Forcing Functions for Embedded Rotor Resonant Response in a Multistage Compressor. Master’s Thesis, School of Aeronautics and Astronautics, Purdue University, West Lafayette, IN, USA, 2017. [Google Scholar]
- Brown, J.; Kormanik, N.J., III; Matthews, D.R.; Key, N.L. Experimental and Computational Analysis of Heat Transfer Effects on the Performance of a Multistage Axial Compressor. In Proceedings of the ETC15: Proceedings of 15th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Budapest, Hungary, 24–28 April 2023. [Google Scholar]
- Clark, J.P.; Grover, E.A. Assessing Convergence in Predictions of Periodic-Unsteady Flowfields. J. Turbomach. 2007, 129, 740–749. [Google Scholar] [CrossRef]
- Kerrebrock, J.L.; Mikolajczak, A.A. Intra-Stator Transport of Rotor Wakes and Its Effect on Compressor Performance. J. Eng. Power 1970, 92, 359–368. [Google Scholar] [CrossRef]
- Montomoli, F.; Naylor, E.; Hodson, H.P.; Lapworth, L. Unsteady Effects in Axial Compressors: A Multistage Simulation. J. Propuls. Power 2013, 29, 1001–1008. [Google Scholar] [CrossRef]
- Tyler, J.M.; Sofrin, T.G. Axial Flow Compressor Noise Studies; SAE Technical Paper 620532; SAE International: Warrendale, PA, USA, 1962. [Google Scholar] [CrossRef]
- Silkowski, P.D.; Hall, K.C. 1997 Best Paper Award—Structures and Dynamics Committee: A Coupled Mode Analysis of Unsteady Multistage Flows in Turbomachinery. J. Turbomach. 1998, 120, 410–421. [Google Scholar] [CrossRef]
- Leng, Y.; Key, N.L. Utilization of Fast Response Pressure Measurements to Non-Intrusively Monitor Blade Vibration in Axial Compressors. J. Turbomach. 2020, 142, 031001. [Google Scholar] [CrossRef]




| TPR [–] | TTR [–] | ηs [–] | ||||
|---|---|---|---|---|---|---|
| Stg2 | Ovr | Stg2 | Ovr | Stg2 | Ovr | |
| 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | |
| 1.5 | 1.5 | 2.0 | 2.0 | 2.0 | 2.0 | |
| 1.000 | 0.998 | 1.000 | 1.000 | 1.001 | 1.000 | |
| 0.999 | 0.993 | 0.999 | 0.998 | 1.004 | 0.997 | |
| 0.995 | 0.984 | 0.999 | 0.998 | 0.993 | 0.983 | |
| 0.001 | 0.010 | 0.001 | 0.002 | −0.002 | 0.002 | |
| 0.006 | 0.026 | 0.001 | 0.002 | 0.007 | 0.014 | |
| 0.10% | 0.52% | 0.05% | 0.13% | 0.29% | 0.21% | |
| 0.49% | 1.46% | 0.08% | 0.15% | 0.82% | 1.63% | |
| p | 3.75 | 2.14 | 1.09 | 2.55 | 1.94 | 2.71 |
| 1.001 | 1.005 | 0.221 | 0.029 | 0.997 | 1.002 | |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 1.000 | 1.000 | 0.999 | 0.998 | 1.008 | 1.000 | |
| 0.10% | 0.52% | 0.05% | 0.13% | 0.29% | 0.21% | |
| 0.38% | 0.93% | 0.02% | 0.02% | 1.10% | 1.40% | |
| 0.01% | 0.15% | 0.05% | 0.03% | 0.10% | 0.04% | |
| 0.11% | 0.67% | 0.02% | 0.00% | 0.38% | 0.25% | |
| 0.01% | 0.19% | 0.06% | 0.03% | 0.13% | 0.05% | |
| 0.14% | 0.85% | 0.03% | 0.01% | 0.48% | 0.32% | |
| Fuzzy Set Parameter | Parameter Description | Consistent Signal Representation |
|---|---|---|
| Temporal History and Mean | Mean Level | |
| Spectra Amplitude for Chosen Signal Components | Amplitude | |
| Spectra Phase for Chosen Signal Components | Phase Angle | |
| Cross-Correlation of Cycles 1 and 2 | Overall Signal Shape | |
| Power Spectral Density Estimate | Fractional Signal Power | |
| Overall Convergence Level | ||
| Fuzzy Set | Membership Grade | Fuzzy Set | Membership Grade | ||||
|---|---|---|---|---|---|---|---|
| R1 BPF | Station 3– R1 Exit | Station 4– S1 Exit | R2 BPF | Station 3– R1 Exit | Station 4– S1 Exit | ||
| fA | R1 | 0.983 | 0.989 | fA | R2 | 0.925 | 0.987 |
| fϕ | R1 | 0.995 | 0.997 | fϕ | R2 | 0.999 | 0.989 |
| fA | 2 × R1 | 0.988 | 0.935 | fA | 2 × R2 | 0.898 | 0.887 |
| fϕ | 2 × R1 | 0.999 | 0.984 | fϕ | 2 × R2 | 0.976 | 0.994 |
| fA | 3 × R1 | 0.959 | 0.890 | fA | 3 × R2 | 0.996 | 0.983 |
| fϕ | 3 × R1 | 0.984 | 0.996 | fϕ | 3 × R2 | 0.989 | 0.933 |
| fA | 4 × R1 | 0.951 | 0.855 | ||||
| fϕ | 4 × R1 | 0.984 | 0.890 | ||||
| fA | 5 × R1 | 0.902 | 0.912 | fA | R1 + R2 | 0.606 | 0.276 |
| fϕ | 5 × R1 | 0.888 | 0.968 | fϕ | R1 + R2 | 0.993 | 0.903 |
| Station 3–R1 Exit | Station 4–S1 Exit | ||||||
| fM | 1.000 | fM | 1.000 | ||||
| fS | 0.945 | fS | 0.968 | ||||
| fP | 0.904 | fP | 0.895 | ||||
| Upstream R2 | Upstream R3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unsteady Measurement | CFX Transient Monitor | CFX Fourier Reconstruction | Unsteady Measurement | CFX Transient Monitor | CFX Fourier Reconstruction | ||||||
| BPF | BPF | BPF | BPF | BPF | BPF | ||||||
| 0.0771 | 0.0810 | 0.0798 | 0.0418 | 0.0688 | 0.0743 | ||||||
| 0.0154 | 0.0188 | 0.0286 | 0.0085 | 0.0145 | 0.0205 | ||||||
| 0.0117 | 0.0131 | 0.0130 | 0.0082 | 0.0130 | 0.0184 | ||||||
| 0.0064 | 0.0125 | 0.0125 | 0.0067 | 0.0119 | 0.0150 | ||||||
| 0.0047 | 0.0069 | 0.0116 | 0.0053 | 0.0104 | 0.0145 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Matthews, D.R.; Key, N.L. Considerations for High-Fidelity Modeling of Unsteady Flows in a Multistage Axial Compressor. Int. J. Turbomach. Propuls. Power 2025, 10, 5. https://doi.org/10.3390/ijtpp10010005
Matthews DR, Key NL. Considerations for High-Fidelity Modeling of Unsteady Flows in a Multistage Axial Compressor. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(1):5. https://doi.org/10.3390/ijtpp10010005
Chicago/Turabian StyleMatthews, Douglas R., and Nicole L. Key. 2025. "Considerations for High-Fidelity Modeling of Unsteady Flows in a Multistage Axial Compressor" International Journal of Turbomachinery, Propulsion and Power 10, no. 1: 5. https://doi.org/10.3390/ijtpp10010005
APA StyleMatthews, D. R., & Key, N. L. (2025). Considerations for High-Fidelity Modeling of Unsteady Flows in a Multistage Axial Compressor. International Journal of Turbomachinery, Propulsion and Power, 10(1), 5. https://doi.org/10.3390/ijtpp10010005





