Computational Design of an Energy-Efficient Small Axial-Flow Fan Using Staggered Blades with Winglets
Abstract
:1. Introduction
2. Computational Methodology
2.1. Governing Flow Equations
2.2. Blade Model Design
2.3. Computational Domain and Boundary Conditions
2.4. Fluid Flow Solver
3. Results and Discussion
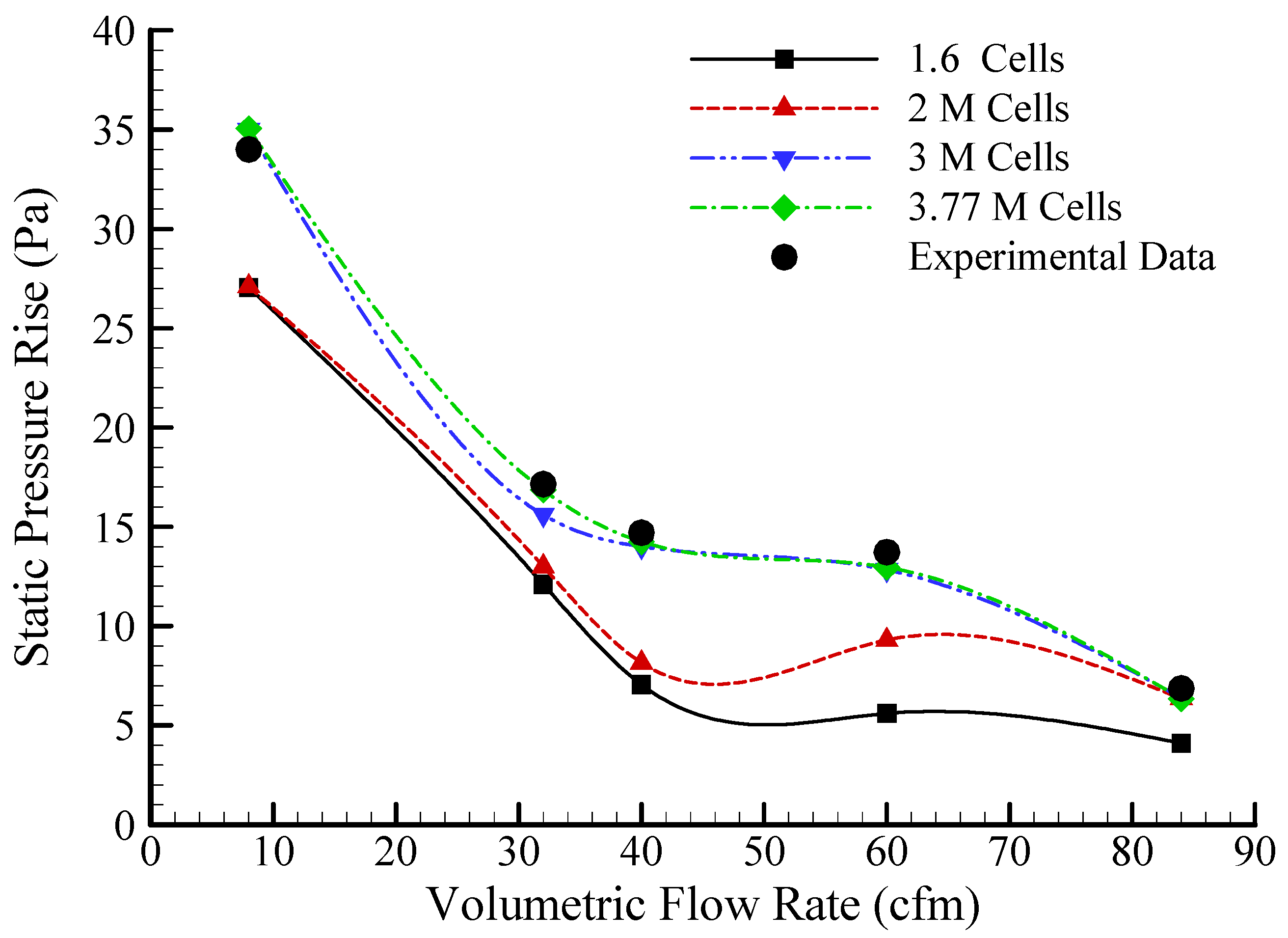
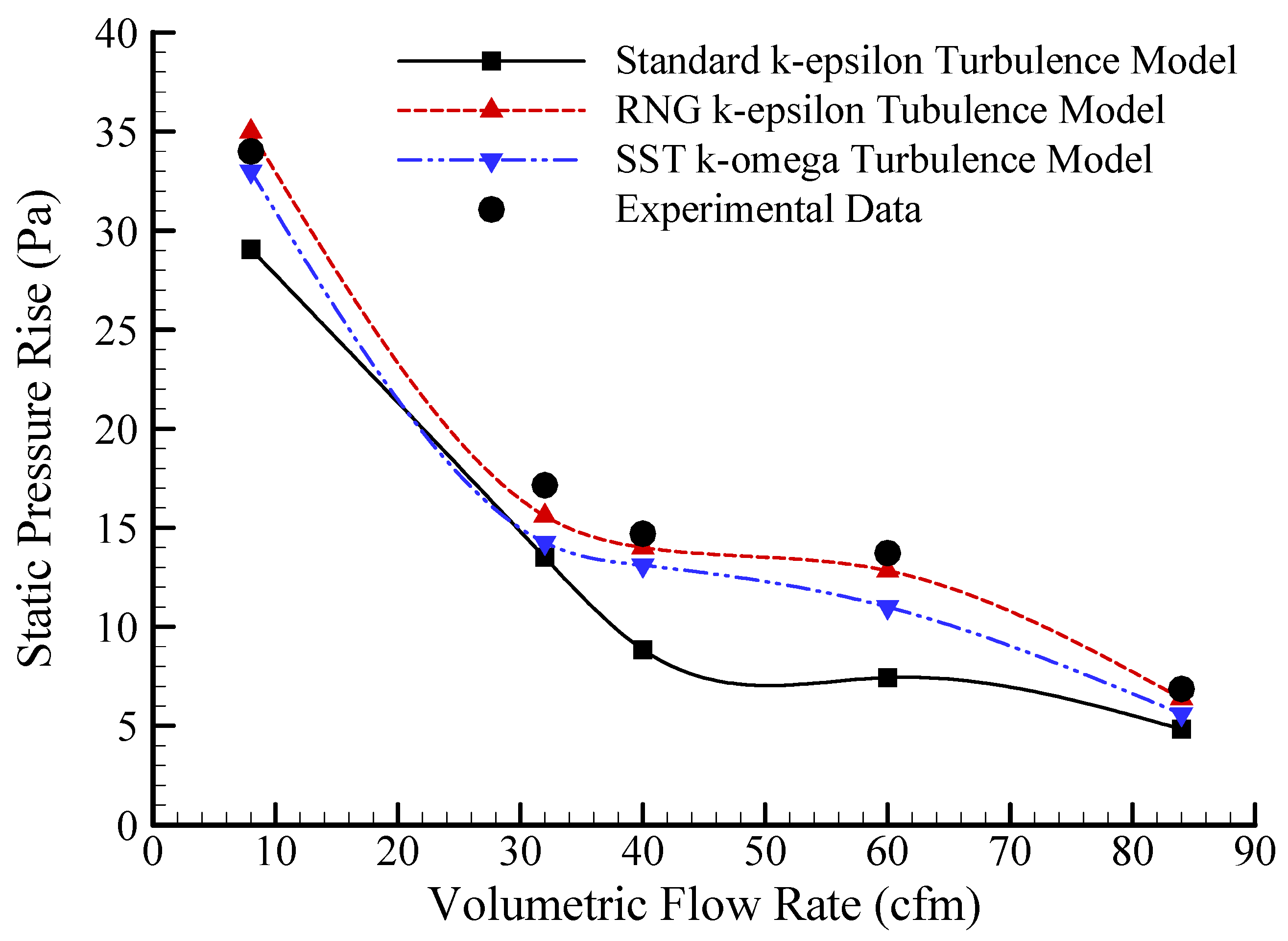
3.1. Model Validation
3.2. The Effect of Design Parameters
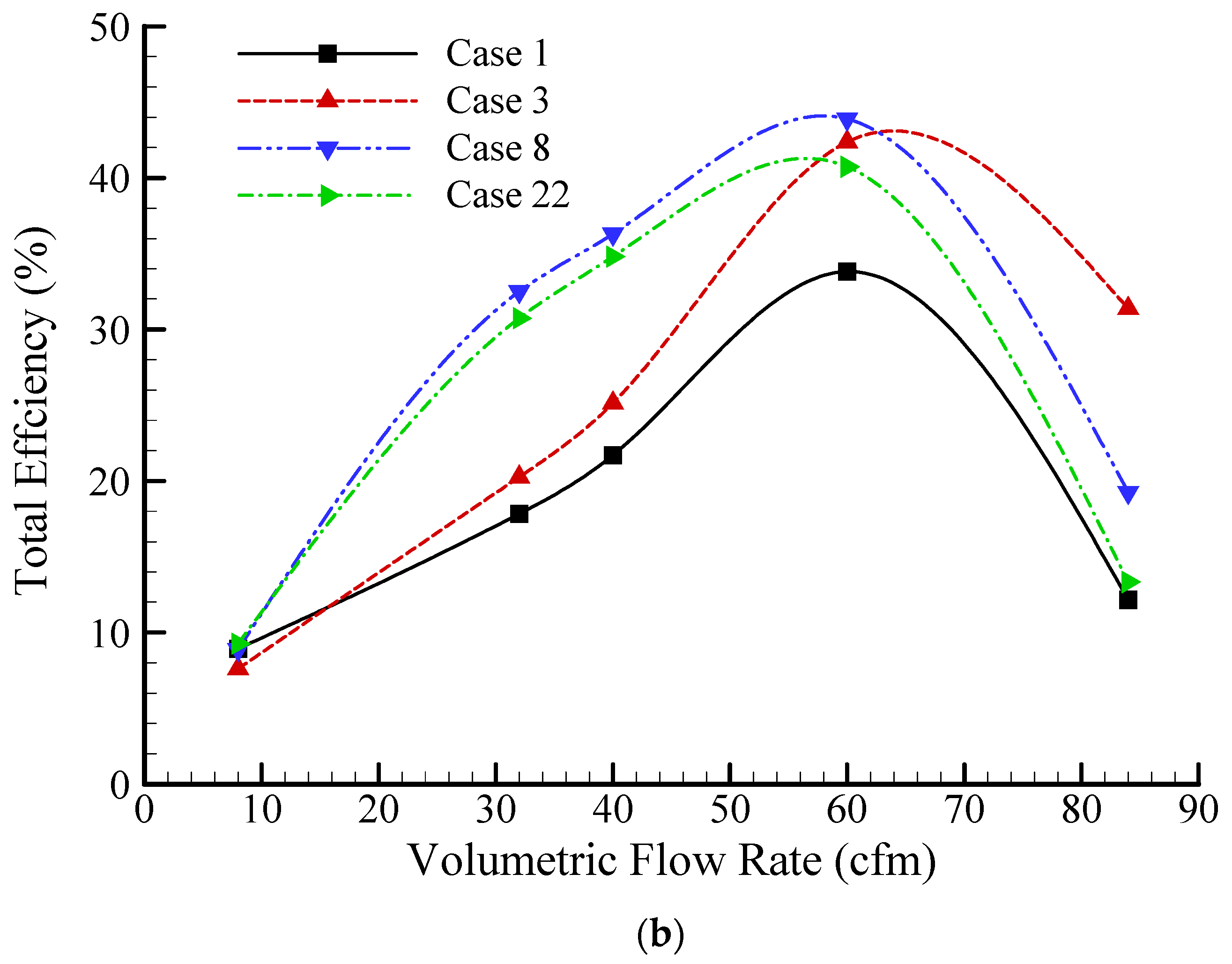
3.2.1. Fan Performance Curves
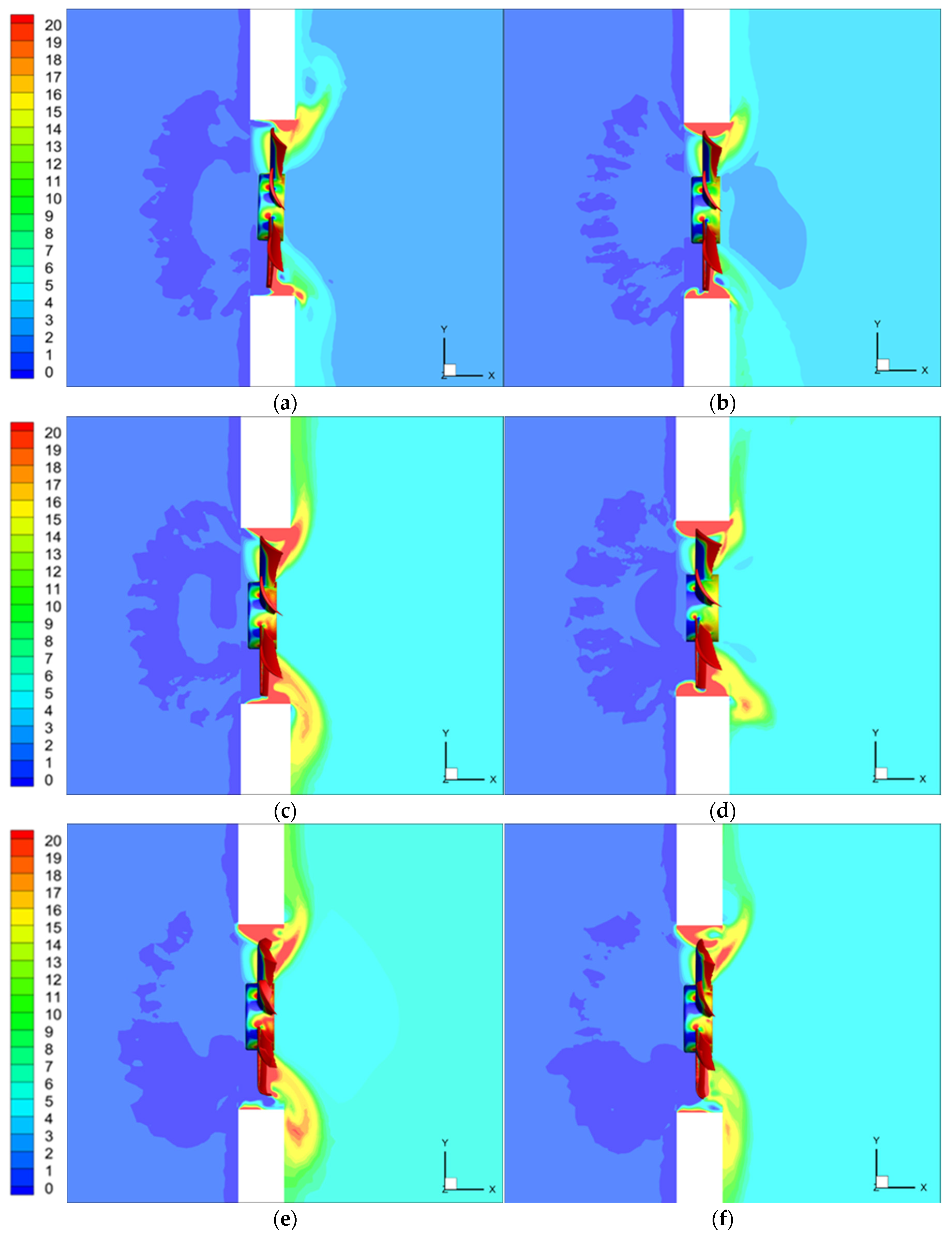
3.2.2. Pressure Contours
3.2.3. Streamlines and Velocity Contours
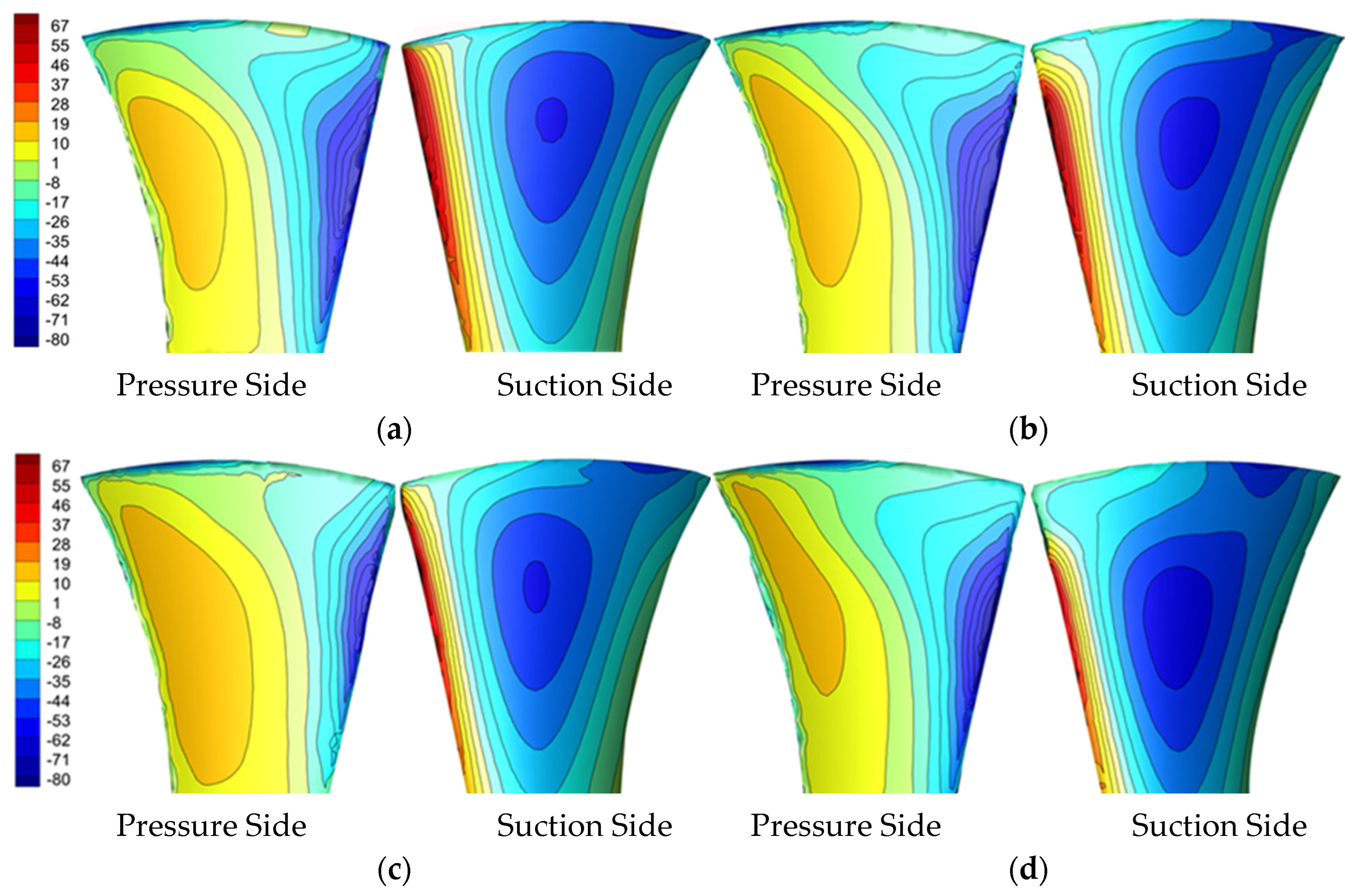
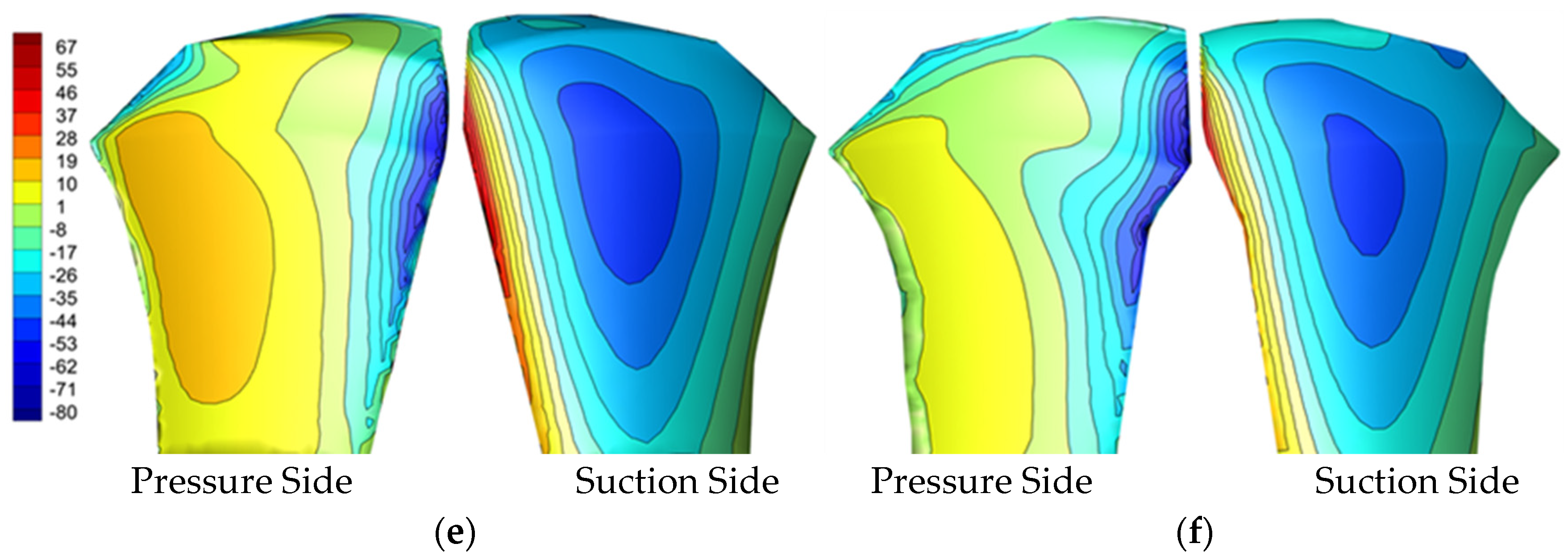
3.2.4. Suction and Pressure Side Pressure Contours
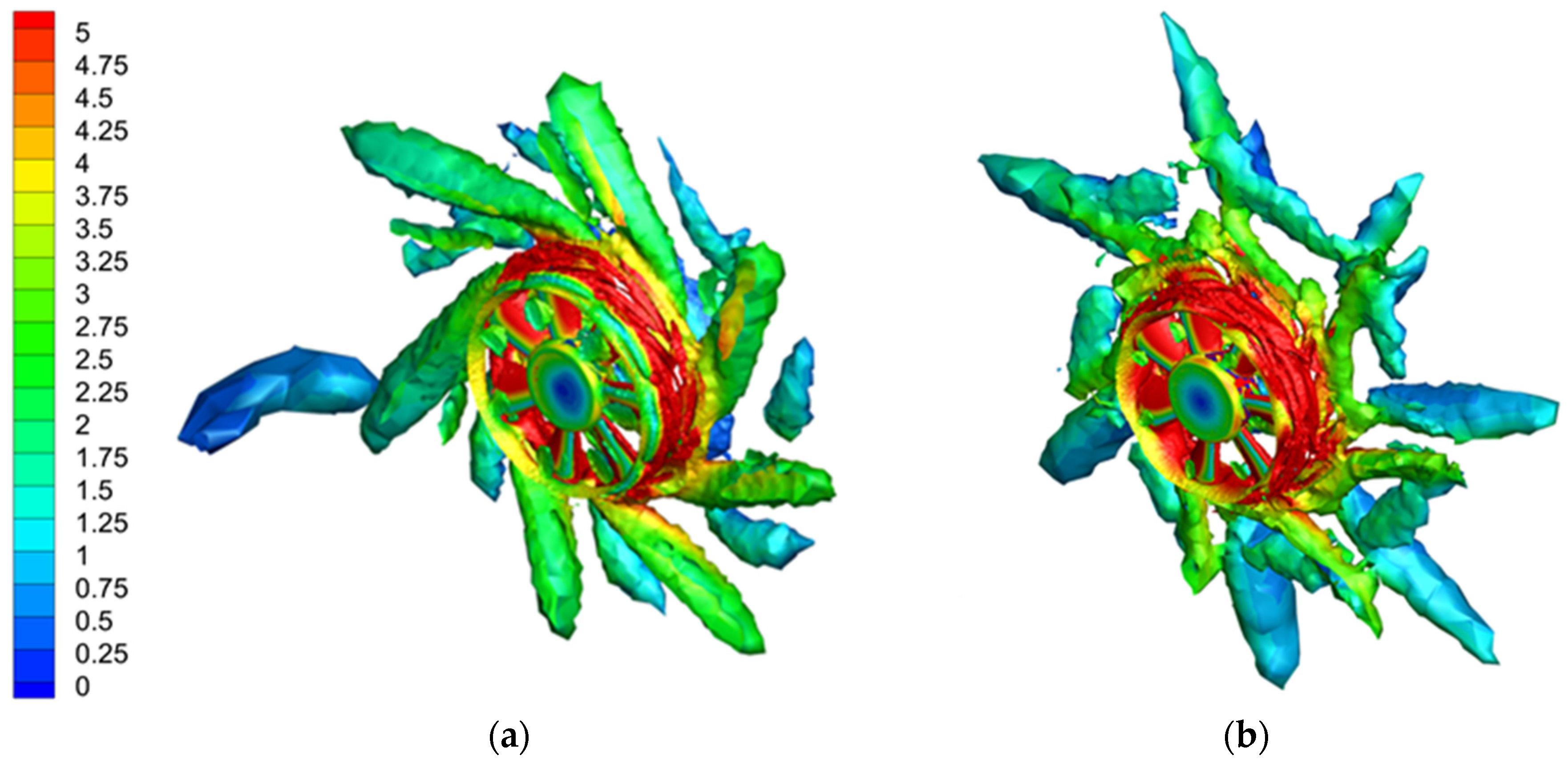
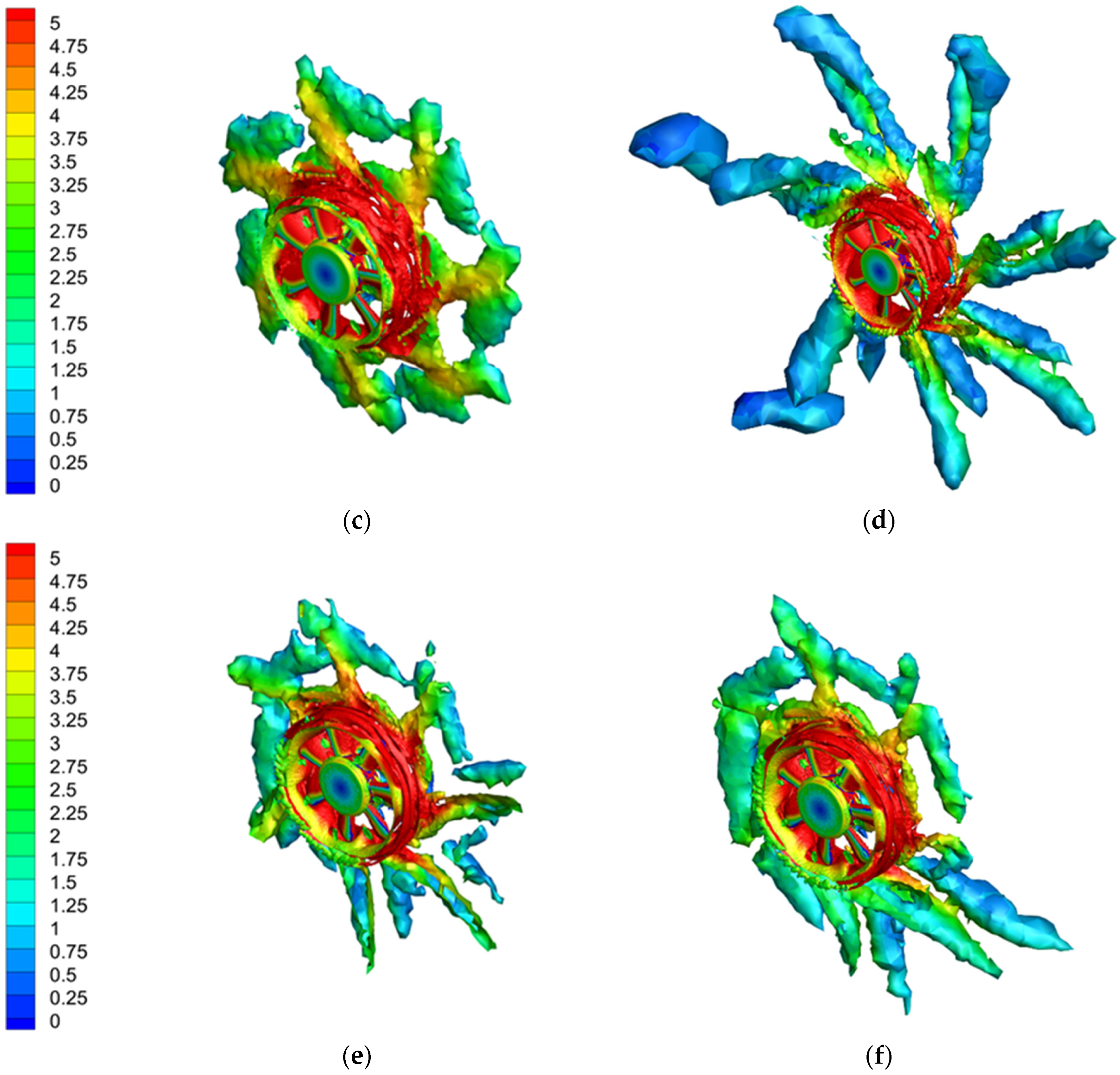
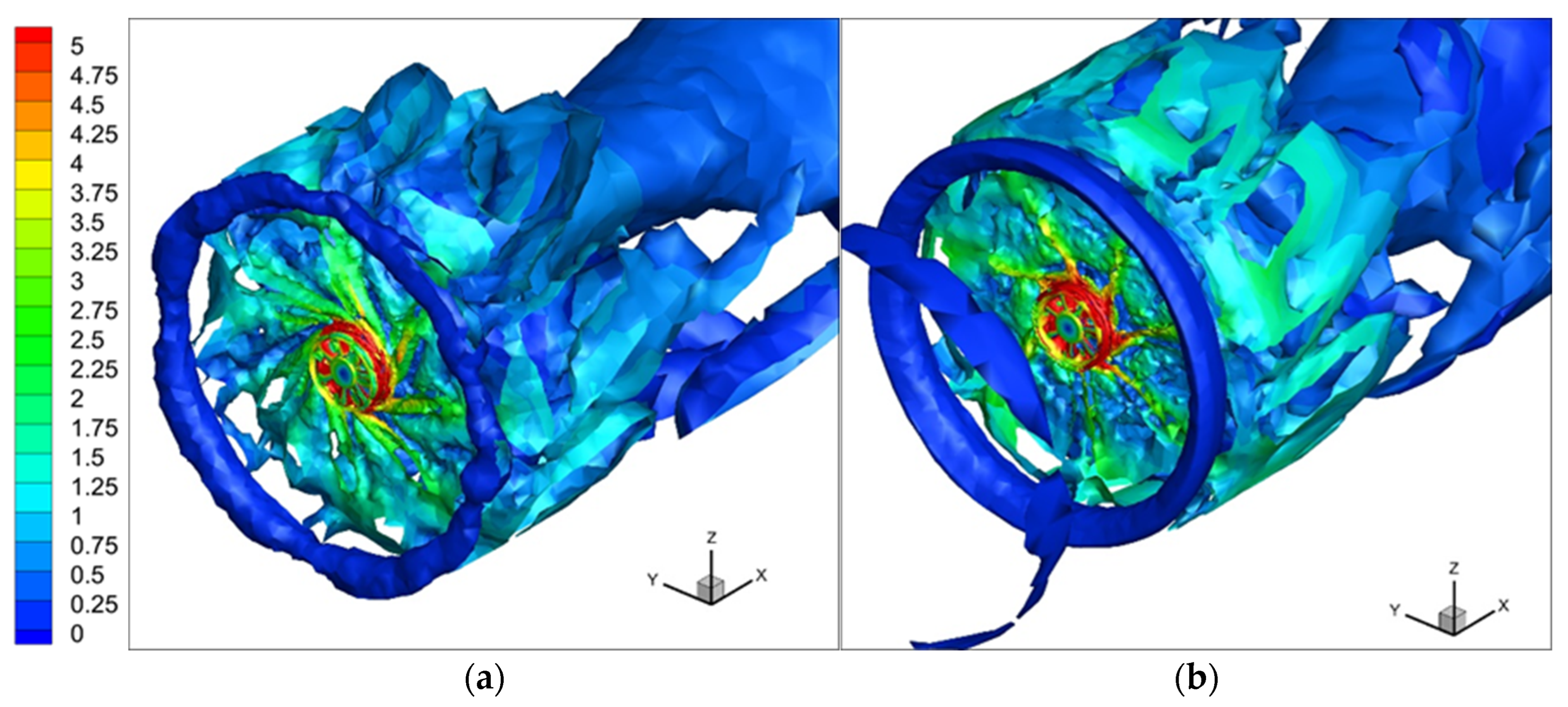
3.2.5. Q–Criterion Contours
4. Conclusions
- The stagger angle and winglet both have a significant influence on the performance characteristics of the small axial-flow fan. The total pressure rise across the fan and the total fan efficiency curve are both highly dependent on the stagger angle and the winglet which may have a positive or negative influence on the fan performance characteristics depending on the choice of values of these two parameters.
- The fan performance can be significantly improved using a critical value of the stagger angle together with an implementation of the winglet on the tip of the rotor blade. Considering the total efficiency for the investigated operation range, the fan attains the best performance with an additional stagger angle of +10° and a winglet with a curvature radius of 6.77 mm and a twist angle of −7° for the investigated dimensioning range. In the stall region, all staggered blades with and without winglets reproduce better efficiency curves than that of the baseline blade.
- The use of different additional stagger angles shifts the best efficiency point (BEP) for the flow rate ranging from 55 cfm to 65 cfm while the use of different winglet configurations does not alter the BEP which is found to be around 60 cfm as observed for the baseline blade geometry.
- The present three-dimensional (3-D) Reynolds-averaged Navier–Stokes (RANS) equation-based RNG k–ε turbulence modeling approach coupled with the multiple reference frame (MRF) technique which adopts a multi-block topology generation meshing method successfully resolves the rotating flow around the fan. The computed results compare well with the experimental data and suggest that the present computational methodology can be used with confidence for such flow analysis.
- The near-wake flow characteristics of the fan which are governed by the flow separation and associated vortical structures generated from the tip of the blade are significantly affected by the blade geometry. The variation in behavior of vortex shedding and the formation of the recirculation zone depending on the blade geometry directly affects the near-wake total pressure distribution and hence the fan performance. The wingletted blade better controls the flow in the very near-wake region of the fan.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Babu, A.M.; Gangadhar, V.V.R.L.S.; Reddy, A.C.S. Modeling and analysis of tube axial flow fan by comparison of material used and changing the number of blades. Int. J. Sci. Eng. Technol. Res. 2014, 3, 4730–4736. [Google Scholar]
- Dwivedi, D.; Dandotiya, D.S. CFD Analysis of axial flow fans with skewed blades. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 741–752. [Google Scholar]
- Lin, S.-C.; Tsai, M.-L. An integrated study of the design method for small axial-flow fans, based on the airfoil theory. Int. J. Adv. Eng. Innov. Technol. 2010, 225, 885–895. [Google Scholar] [CrossRef]
- Zhou, J.-H.; Yang, C.-X. Parametric design and numerical simulation of the axial-flow fan for electronic devices. IEEE Trans. on Comp. Pack. Technol. 2010, 33, 287–297. [Google Scholar] [CrossRef]
- Quin, D.; Grimes, R. The effect of Reynolds number on microaxial flow fan performance. J. Fluids Eng. 2008, 130, 101101. [Google Scholar] [CrossRef]
- Sahu, M.D.; Bartaria, V.N. Characteristic curve determination of the analyzed impellers in axial flow fan. Int. J. Appl. Eng. Technol. 2016, 4, 452–456. [Google Scholar]
- Yadav, A.; Pathak, M.; Sharman, P.K. Numerical analysis of aerofoil section of blade of axial flow fan at different angle of attack. Int. J. Adv. Res. Ideas Innov. Technol. 2017, 3, 63–74. [Google Scholar]
- Liu, S.H.; Huang, R.F.; Chen, L.J. Performance and inter-blade flow of axial flow fans with different blade angles of attack. J. Chin. Inst. Eng. 2011, 34, 141–153. [Google Scholar] [CrossRef]
- Izadi, M.J.; Falahat, A. Effect of blade angle of attack and hub to tip ratio on mass flow rate in an axial fan at a fixed rotational speed. In Proceedings of the ASME Fluids Engineering Division Summer Conference, Jacksonville, FL, USA, 10–14 August 2008. [Google Scholar] [CrossRef]
- Hirano, T.; Otaka, T.; Minorikawa, G. Study on optimum design method for small axial fan. In Proceedings of the 4th International Conference on Design Engineering and Science ICDES 2017, Aachen, Germany, 17–19 September 2017. [Google Scholar]
- Luo, D.; Huang, D.; Sun, X.; Chen, X.; Zheng, Z. A computational study on the performance improvement of low-speed axial flow fans with microplates. J. Appl. Fluid Mech. 2017, 10, 1537–1546. [Google Scholar] [CrossRef]
- Ye, X.; Ding, X.; Zhang, J.; Li, C. Numerical simulation of pressure pulsation and transient flow field in an axial flow fan. Energy 2017, 129, 185–200. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, Y.; Dou, H.; Jin, Y. Numerical and experimental investigation on aerodynamic performance of small axial flow fan with hollow blade root. J. Therm. Sci. 2013, 22, 424–432. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, Y. Effect of blade numbers on aerodynamic performance and noise of small axial flow fan. Adv. Mater. Res. 2011, 199–200, 796–900. [Google Scholar] [CrossRef]
- Mao, H.; Wang, Y.; Lin, P.; Jin, Y.; Setoguchi, T.; Kim, H.D. Influence of tip end-plate on noise of small axial fan. J. Therm. Sci. 2017, 26, 30–37. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, Z.; Lin, P.; Jin, Y.; Setoguchi, T.; Kim, H.D. Effect of inlet guide vanes on the performance of small axial fan. J. Therm. Sci. 2017, 26, 504–513. [Google Scholar] [CrossRef]
- Moosania, M.; Zhou, C.; Hu, S. Effect of tip geometry on the performance of low-speed axial flow fan. Int. J. Ref. 2022, 134, 16–23. [Google Scholar] [CrossRef]
- Pretorius, J.P.; Erasmus, J.A. Effect of tip vortex reduction on air-cooled condenser axial flow fan performance: An experimental investigation. J. Turbomach. 2022, 144, 031001. [Google Scholar] [CrossRef]
- Dellacasagrande, M.; Canepa, E.; Cattanei, A.; Moradi, M. Characterization of unsteady leakage flow in an axial fan. Int. J. Turbomach. Propuls. Power 2023, 8, 34. [Google Scholar] [CrossRef]
- Yadegari, M.; Ommi, F.; Aliabadi, S.K.; Saboohi, Z. Reducing the aerodynamic noise of the axial flow fan with perforated surface. App. Acoust. 2023, 215, 109720. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, C.; Zheng, Z.; Hu, X.; Mao, Y. Experimental study of the parameter effects on the flow and noise characteristics for a contra-rotating axial fan. Front. Phys. 2023, 11, 1153380. [Google Scholar] [CrossRef]
- Masi, M.; Danieli, P.; Lazzaretto, A. Effect of solidity and aspect ratio on the aerodynamic performance of axial-flow fans with 0.2 hub-to-tip ratio. J. Turbomach. 2023, 145, 081008. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, Y.; Jin, Y. Effect of tip flange on tip leakage flow of small axial flow fans. J. Therm. Sci. 2014, 23, 45–52. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, Z.; Lin, P.; Jin, Y.; Setoguchi, T.; Kim, H.D. Effect of the uneven circumferential blade space on the performance of small axial flow fan. J. Therm. Sci. 2016, 25, 492–500. [Google Scholar] [CrossRef]
- Cavazzini, G.; Giacomel, F.; Ardizzon, G.; Casari, N.; Fadiga, E.; Pinelli, M.; Suman, A.; Montomoli, F. CFD-based optimization of scroll compressor design and uncertainty quantification of the performance under geometrical variations. Energy 2020, 209, 118382. [Google Scholar] [CrossRef]
- Bianchi, S.; Corsini, A.; Sheard, A.G.; Tortora, C. A critical review of stall control techniques in industrial fans. ISRN Mech. Eng. 2013, 2013, 526192. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N. Aerodynamic Investigation of Winglets on Wind Turbine Blades Using CFD; Report No. Riso-R-1543(EN); Riso National Laboratory: Roskilde, Denmark, 2006. [Google Scholar]
- Li, W. Research on the Actuation Technology of Variable Height and Cant Winglet. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2012. [Google Scholar] [CrossRef]
- Saravanan, P.; Parammasivam, K.M.; Selvi Rajan, S. Experimental investigation on small horizontal axis wind turbine rotor using winglets. J. Appl. Sci. Eng. 2013, 16, 159–164. [Google Scholar] [CrossRef]
- Zhang, T.-T.; Elsakka, M.; Huang, W.; Wang, Z.-G.; Ingham, D.B.; Ma, L.; Pourkashanian, M. Winglet design for vertical axis wind turbines based on a design of experiment and CFD approach. Energy Convers. Manag. 2019, 195, 712–726. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, Y.; Ding, W.X.; Bian, S.X. The aerodynamic performance of H-type Darrieus VAWT rotor with and without winglets: CFD simulations. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 2625–2636. [Google Scholar] [CrossRef]
- Dejene, G.; Ramayya, V.; Bekele, A. Investigation of NREL Phase VI wind turbine blade with different winglet configuration for performance augmentation. Int. J. Sustain. Energy 2024, 43, 2321622. [Google Scholar] [CrossRef]
- Ansys Fluent, Version 19.1, User’s Manual. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 5 May 2018).
- Wang, Z.; Liu, J.; Wang, H.; Zhang, B.; Liu, W.; Ozdemir, E.D.; Aksel, M.H. Numerical and experimental investigation on the integrate performance of axial flow cooling fan and heat exchanger. Appl. Therm. Eng. 2024, 245, 122814. [Google Scholar] [CrossRef]
- Chen, F.; Zhu, G.; Xi, D.; Miao, B. Air volume flow rate optimization of the guide vanes in an axial flow fan based on DOE and CFD. Sci. Rep. 2023, 13, 4439. [Google Scholar] [CrossRef]
- Fakhari, S.M.; Mrad, H. Optimization of an axial-flow mine ventilation fan based on effects of design parameters. Results Eng. 2024, 21, 101662. [Google Scholar] [CrossRef]
- Amin, G.; Salunkhe, P.; Kini, C. Numerical analysis of a novel casing treatment in an axial flow fan. J. Propuls. Power 2024, 40, 818–832. [Google Scholar] [CrossRef]
- Song, Y.G.; Ryu, S.Y.; Cheong, C.; Lee, I. Improvement in flow and noise performances of small axial-flow fan for automotive fine dust sensor. J. Acoust. Soc. Korea 2023, 41, 7–15. [Google Scholar] [CrossRef]
- Hur, K.H.; Haider, B.A.; Sohn, C.H. Trailing edge serrations for noise control in axial-flow automotive cooling fans. Int. J. Aeroacoustics 2023, 22, 713–730. [Google Scholar] [CrossRef]
- Hashim, H.M.; Dogruoz, B.; Arik, M.; Parlak, M. An investigation into performance characteristics of an axial flow fan using CFD for electronic devices. In Proceedings of the ASME 2015 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems InterPACK2015, San Francisco, CA, USA, 6–9 July 2015. [Google Scholar]

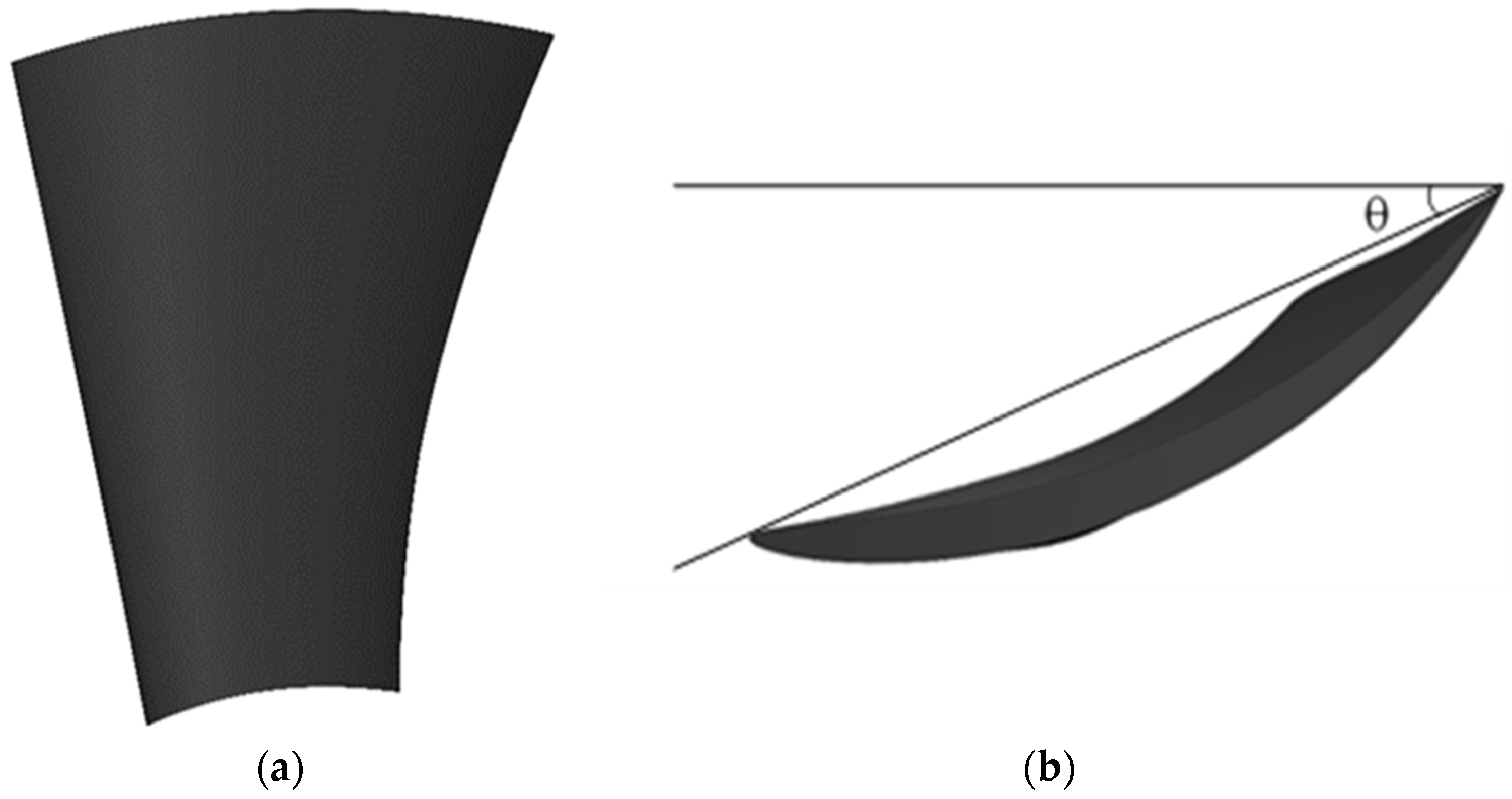
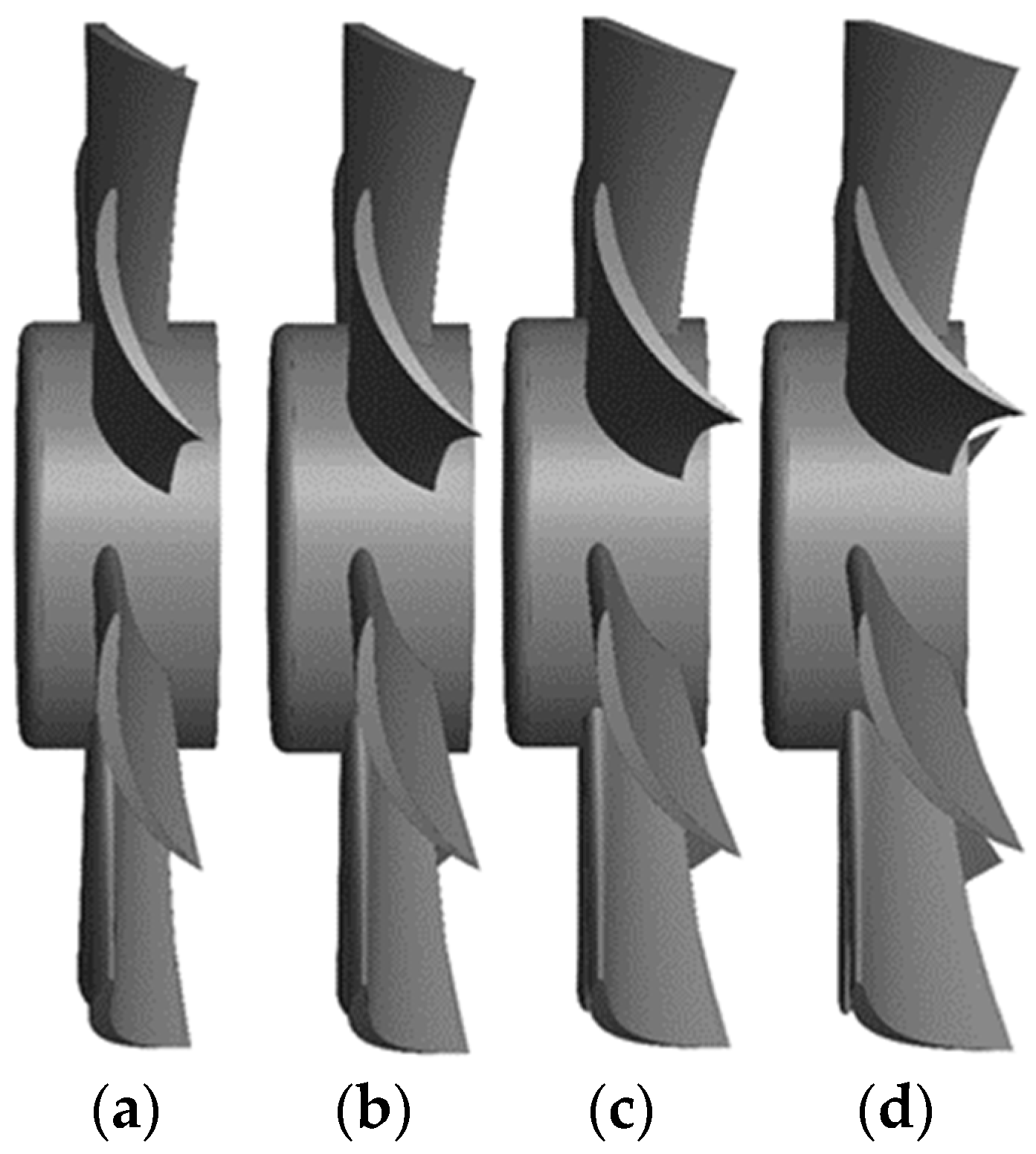

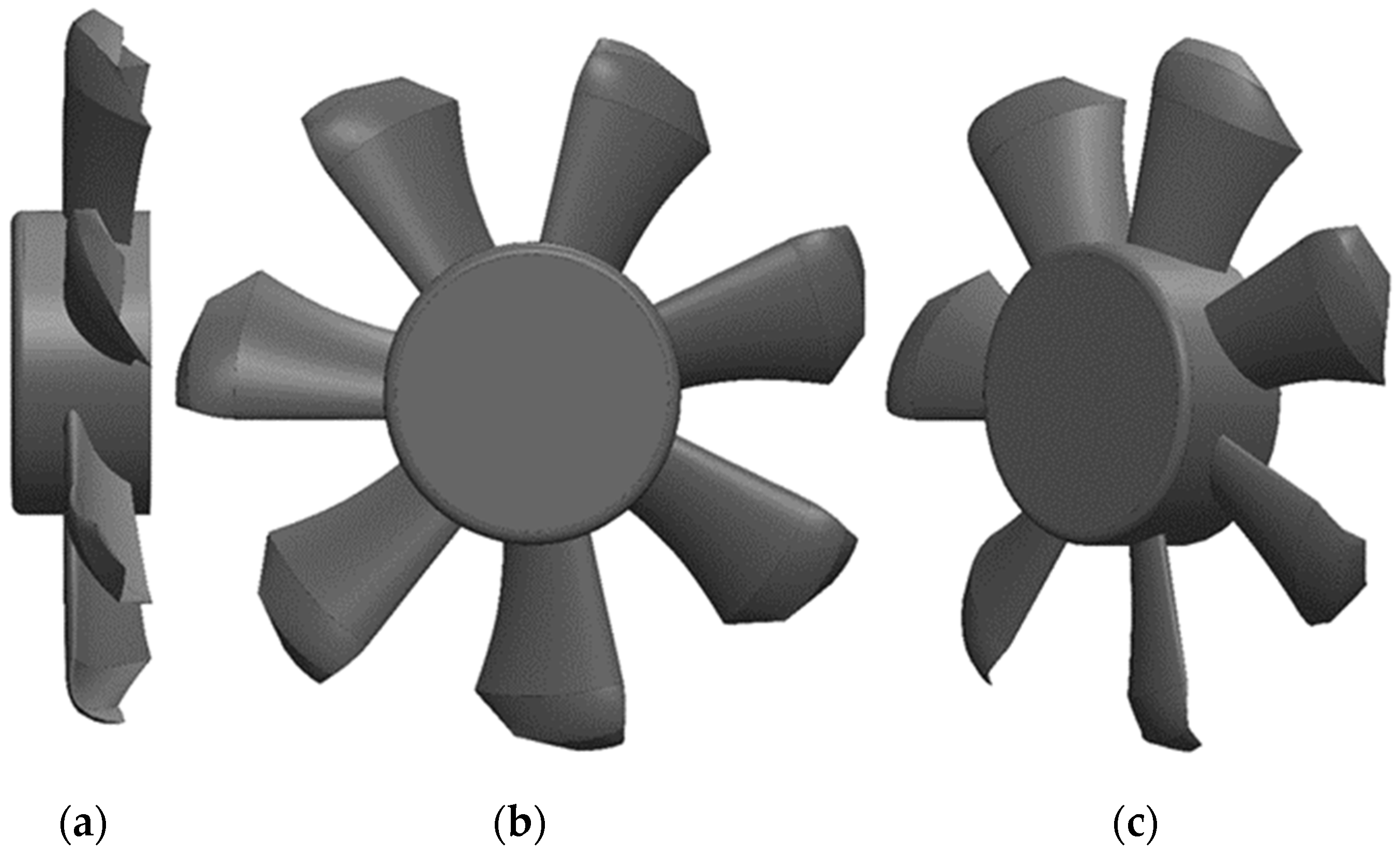
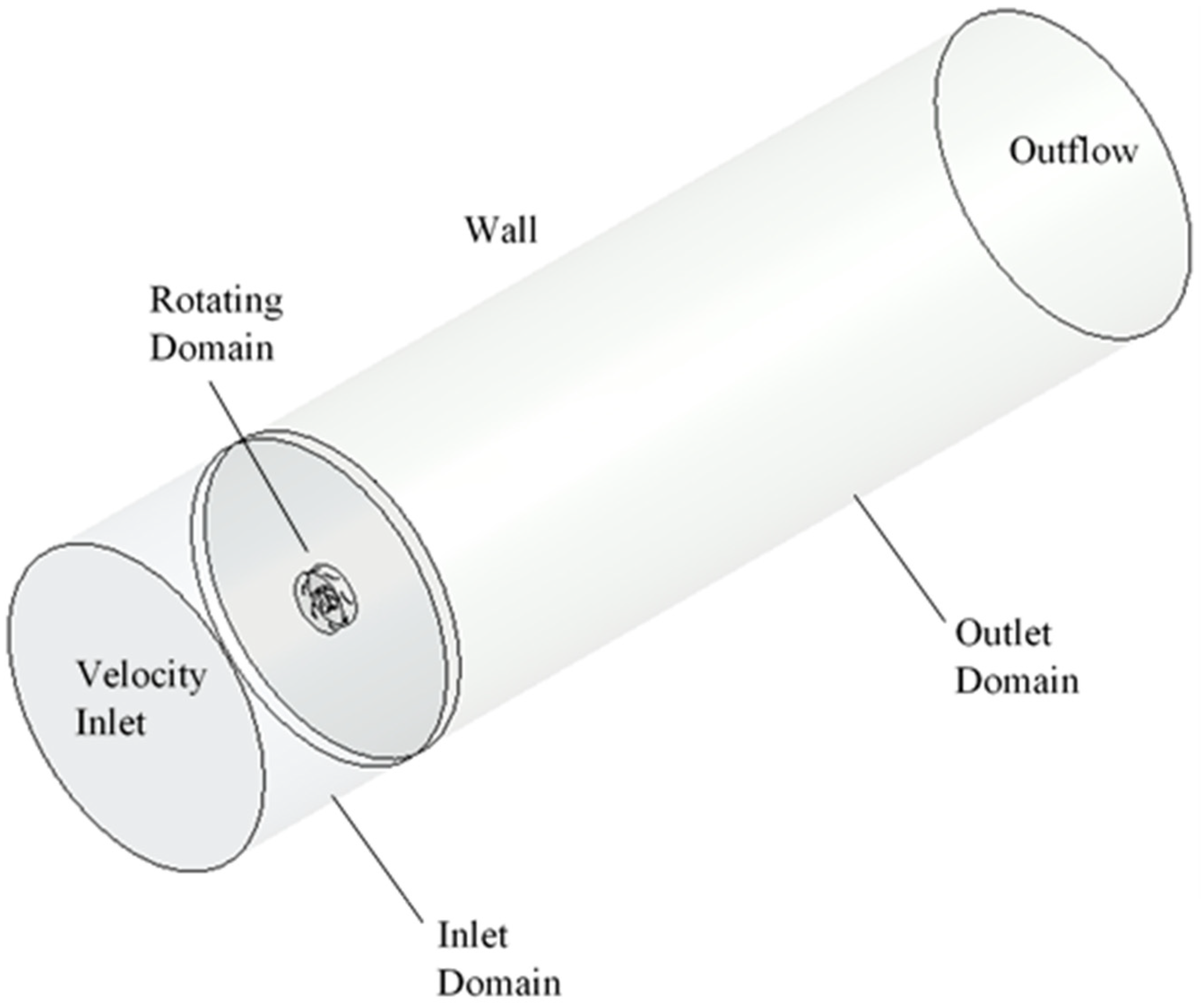





| Segment Number | Radius (mm) | Chord Length (mm) | Setting Angle (Degree) | Airfoil Type |
|---|---|---|---|---|
| 1 | 23.0 | 18.6 | 39.9 | 4420 |
| 2 | 26.7 | 21.2 | 39.7 | 4418 |
| 3 | 30.4 | 23.6 | 39.5 | 4416 |
| 4 | 34.2 | 26.2 | 39.3 | 4414 |
| 5 | 37.9 | 28.9 | 38.9 | 4412 |
| 6 | 41.6 | 31.6 | 38.6 | 4410 |
| 7 | 45.3 | 34.2 | 38.2 | 4408 |
| 8 | 49.1 | 36.6 | 37.7 | 4406 |
| 9 | 52.8 | 39.1 | 37.0 | 4406 |
| 10 | 56.5 | 41.6 | 36.0 | 4406 |
| Mesh Size | y+ | Quality | Aspect Ratio | Skewness | Orthogonal Quality |
|---|---|---|---|---|---|
| 1.6 M Cells | 0–9 | Minimum | 1.15 | 3.00 × 10−9 | 4.40 × 10−2 |
| Average | 2.18 | 0.226 | 0.77 | ||
| Maximum | 135.46 | 0.89 | 0.99 | ||
| 2 M Cells | 0–10 | Minimum | 1.15 | 3.00 × 10−9 | 4.40 × 10−2 |
| Average | 2.09 | 0.222 | 0.77 | ||
| Maximum | 135.46 | 0.89 | 0.99 | ||
| 3 M Cells | 0–4.5 | Minimum | 1.157 | 1.00 × 10−8 | 5.40 × 10−2 |
| Average | 2.8 | 0.225 | 0.77 | ||
| Maximum | 131.41 | 0.91 | 0.99 | ||
| 3.77 M Cells | 0–4.5 | Minimum | 1.157 | 2.40 × 10−9 | 5.40 ×10−2 |
| Average | 2.6 | 0.221 | 0.78 | ||
| Maximum | 131.41 | 0.91 | 0.99 |
| Type | Case No | Additional Stagger Angle (°) | Ctip (mm) | HW (mm) | RCR (mm) | σ (°) | η (%) |
|---|---|---|---|---|---|---|---|
| Baseline Geometry | 1 | – | – | – | – | – | 33.80 |
| Additional Stagger Angle | 2 | 5 | – | – | – | – | 29.30 |
| 3 | 10 | – | – | – | – | 42.30 | |
| 4 | 15 | – | – | – | – | 31.30 | |
| Winglet | 5 | 10 | 10 | 10 | 6.77 | 0 | 41.20 |
| 6 | 7 | 41.90 | |||||
| 7 | 14 | 41.80 | |||||
| 8 | −7 | 43.80 | |||||
| 9 | −14 | 42.10 | |||||
| 10 | 7.1 | 0 | 40.90 | ||||
| 11 | 7 | 41.16 | |||||
| 12 | 14 | 41.65 | |||||
| 13 | −7 | 42.71 | |||||
| 14 | −14 | 40.91 | |||||
| 15 | 7.3 | 0 | 41.44 | ||||
| 16 | 7 | 42.70 | |||||
| 17 | 14 | 41.40 | |||||
| 18 | −7 | 41.31 | |||||
| 19 | −14 | 40.94 | |||||
| 20 | 9.71 | 0 | 41.15 | ||||
| 21 | 7 | 41.32 | |||||
| 22 | 14 | 40.40 | |||||
| 23 | −7 | 42.71 | |||||
| 24 | −14 | 41.84 | |||||
| 25 | 12.67 | 0 | 41.93 | ||||
| 26 | 7 | 41.90 | |||||
| 27 | 14 | 42.30 | |||||
| 28 | −7 | 41.32 | |||||
| 29 | −14 | 41.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Tutar, M.; Cam, J.B. Computational Design of an Energy-Efficient Small Axial-Flow Fan Using Staggered Blades with Winglets. Int. J. Turbomach. Propuls. Power 2025, 10, 1. https://doi.org/10.3390/ijtpp10010001
Tutar M, Cam JB. Computational Design of an Energy-Efficient Small Axial-Flow Fan Using Staggered Blades with Winglets. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(1):1. https://doi.org/10.3390/ijtpp10010001
Chicago/Turabian StyleTutar, Mustafa, and Janset Betul Cam. 2025. "Computational Design of an Energy-Efficient Small Axial-Flow Fan Using Staggered Blades with Winglets" International Journal of Turbomachinery, Propulsion and Power 10, no. 1: 1. https://doi.org/10.3390/ijtpp10010001
APA StyleTutar, M., & Cam, J. B. (2025). Computational Design of an Energy-Efficient Small Axial-Flow Fan Using Staggered Blades with Winglets. International Journal of Turbomachinery, Propulsion and Power, 10(1), 1. https://doi.org/10.3390/ijtpp10010001





