Methylparaben Adsorption onto Activated Carbon and Activated Olive Stones: Comparative Analysis of Efficiency, Equilibrium, Kinetics and Effect of Graphene-Based Nanomaterials Addition
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Adsorbents Preparation
2.2.2. Effect of Experimental Parameters on Adsorption Process
2.2.3. Equilibrium and Kinetic Experiments
2.2.4. Mathematical Models
Equilibrium Studies
Kinetic Studies
Adsorption Mechanism
- The adsorbate molecules diffuse from the bulk solution to the external surface of the adsorbent (boundary layer diffusion);
- The adsorbate molecules diffuse through the interior of the adsorbent particles (intraparticle diffusion).
3. Results and Discussion
3.1. Effect of Experimental Parameters
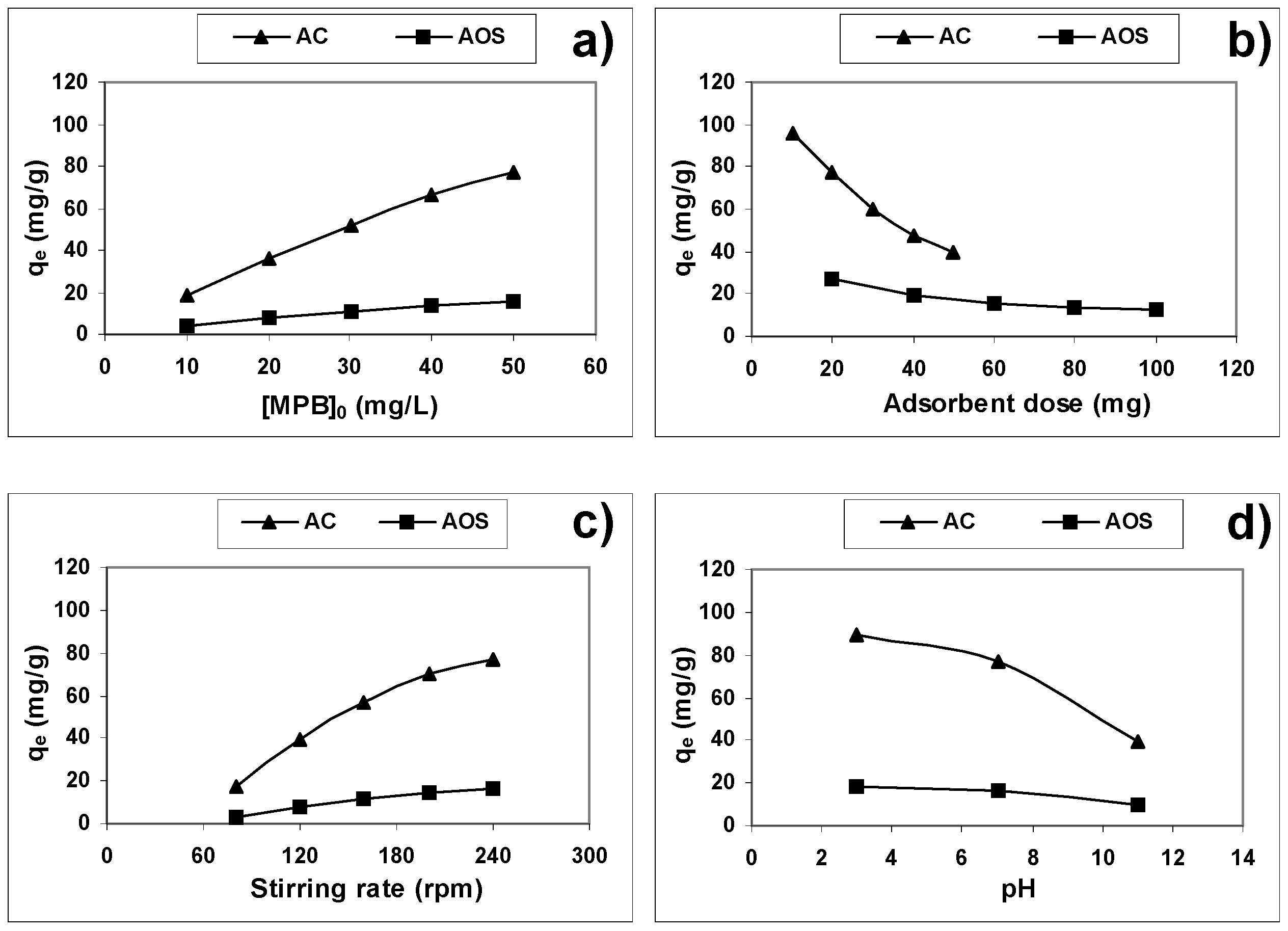
3.1.1. Effect of the Initial Methylparaben Concentration
3.1.2. Effect of Adsorbent Dose
3.1.3. Effect of Stirring Speed
3.1.4. Effect of the Initial pH of Methylparaben Solution
3.1.5. Selected Standard Experimental Conditions
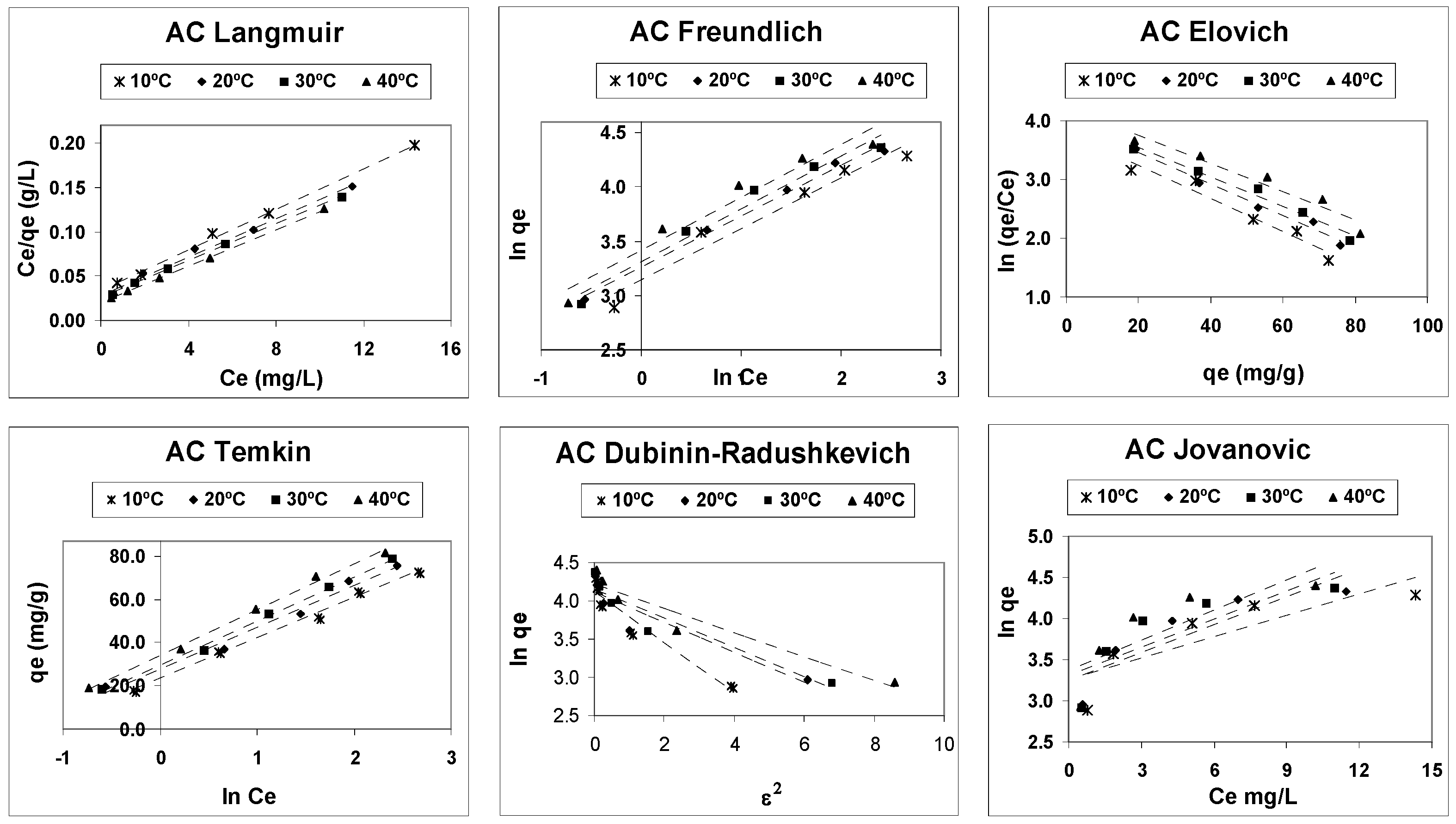
3.2. Adsorption Equilibrium
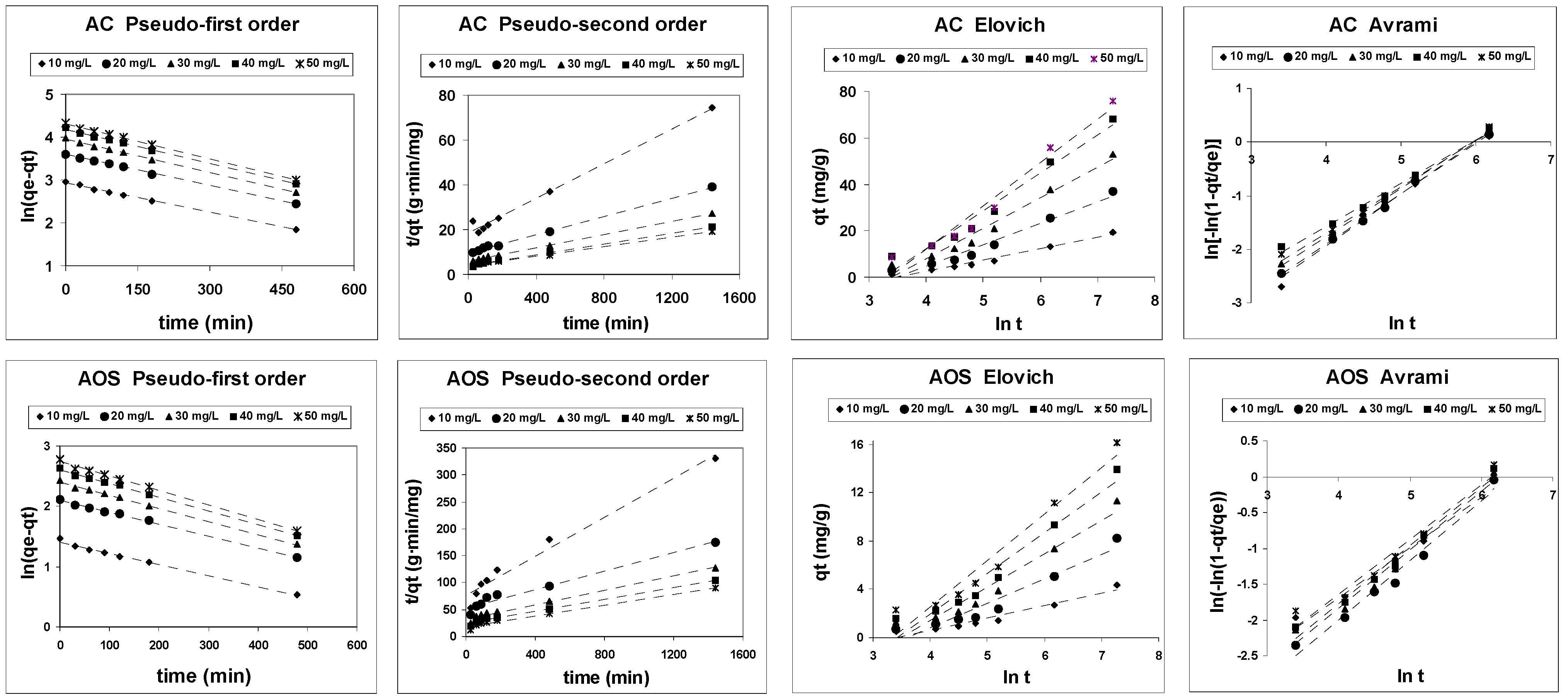
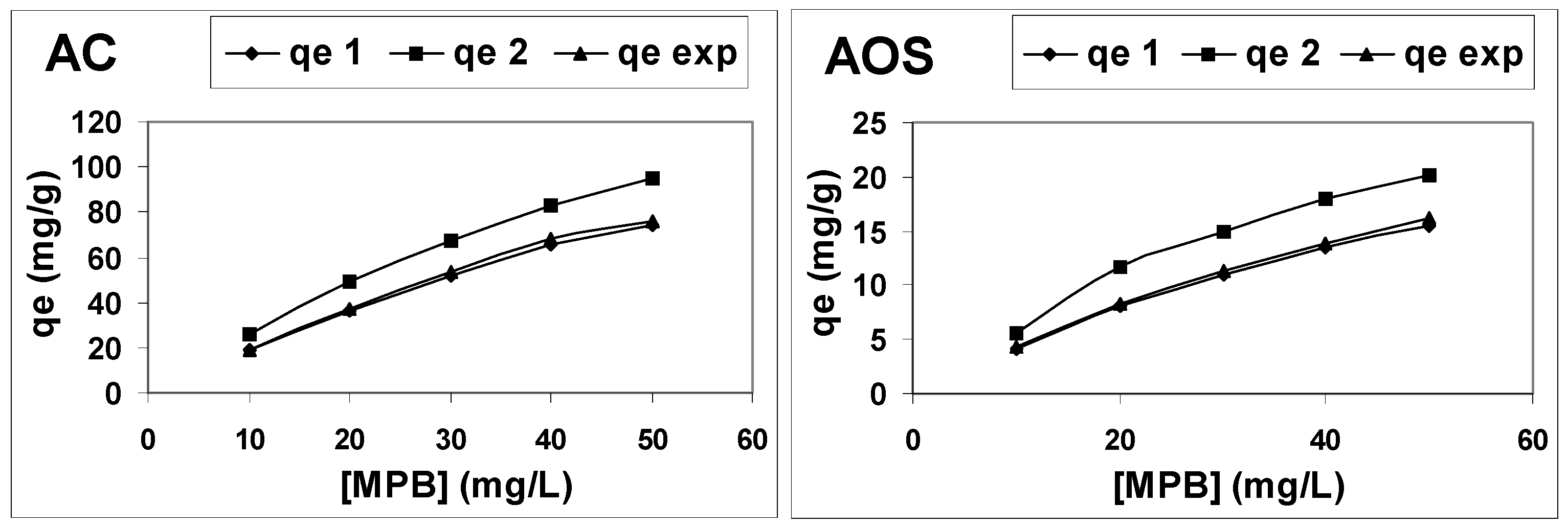
3.3. Adsorption Kinetics
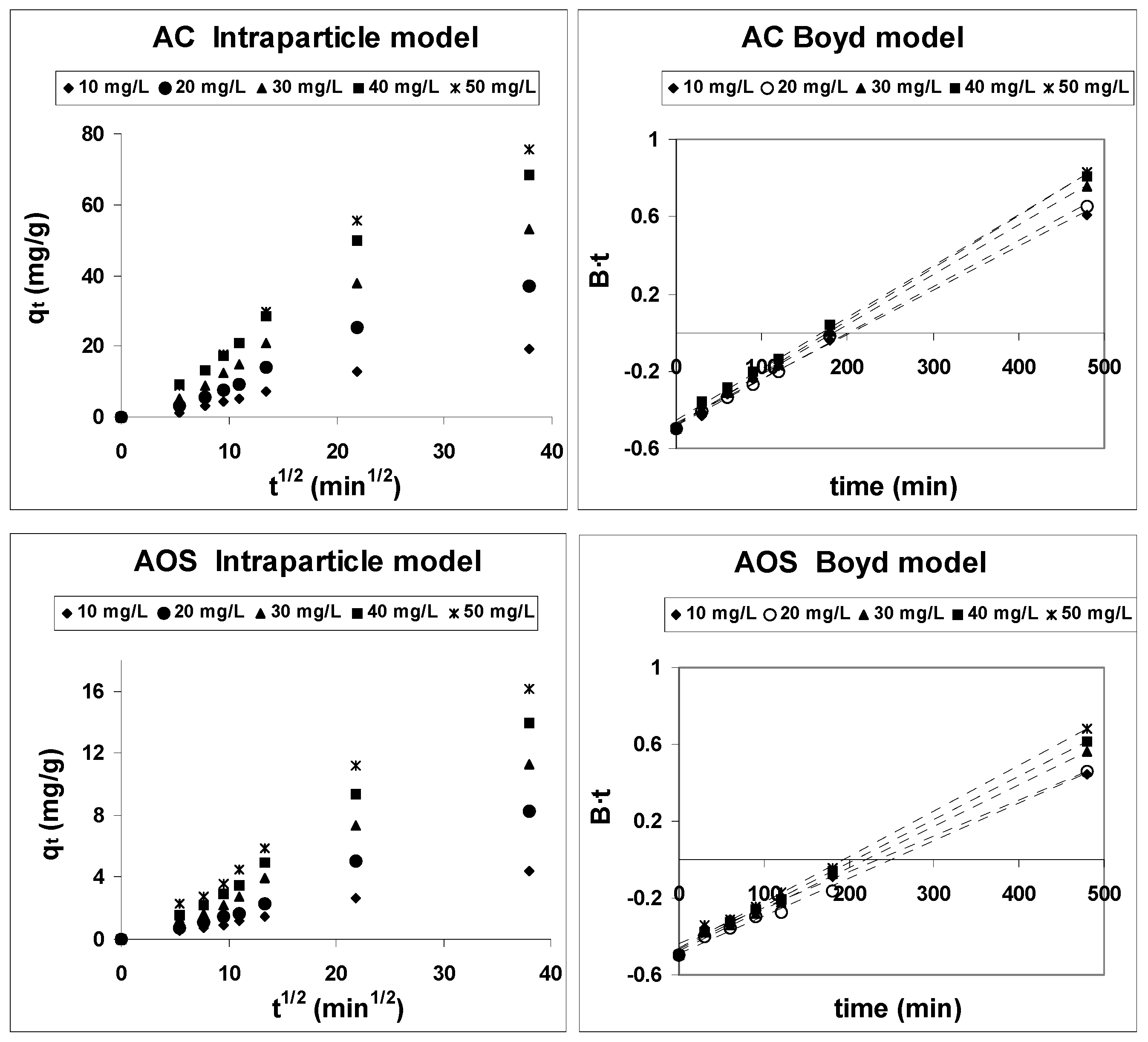
3.4. Adsorption Mechanism
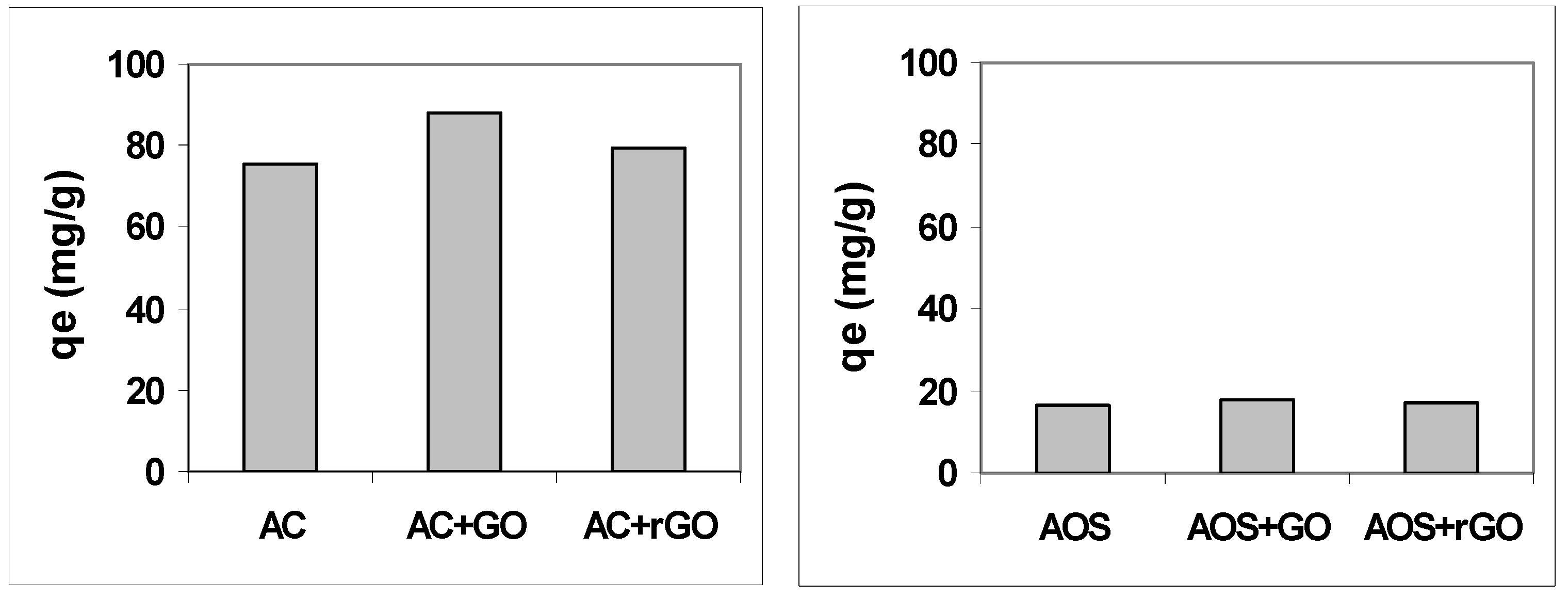
3.5. Effect of the Presence of Graphene-Based Nanomaterials in Adsorbents on Methylparaben Adsorption
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Senthil-Rathi, B.; Senthil-Kumar, P.; Dai-Viet, N.V. Critical review on hazardous pollutants in water environment: Occurrence, monitoring, fate, removal technologies and risk assessment. Sci. Total Environ. 2021, 797, 149134. [Google Scholar] [CrossRef] [PubMed]
- Barceló, D. Emerging pollutants in water analysis. Trends Anal. Chem. 2003, 22, xiv–xvi. [Google Scholar] [CrossRef]
- Dulio, V.; Van Bavel, B.; Brorström-Lundén, E.; Harmsen, J.; Hollender, J.; Schlabach, M.; Slobodnik, J.; Thomas, K.; Koschorreck, J. Emerging pollutants in the EU: 10 years of NORMAN in support of environmental policies and regulations. Environ. Sci. Eur. 2018, 30, 5. [Google Scholar] [CrossRef] [PubMed]
- la Farré, M.; Pérez, S.; Kantiani, L.; Barceló, D. Fate and toxicity of emerging pollutants, their metabolites and transformation products in the aquatic environment. Trends Anal. Chem. 2008, 27, 991–1007. [Google Scholar] [CrossRef]
- Haman, C.; Dauchy, X.; Rosin, C.; Muñoz, J.F. Occurrence, fate and behavior of parabens in aquatic environments: A review. Water Res. 2015, 68, 1–11. [Google Scholar] [CrossRef]
- Gmurek, M.; Rossi, A.F.; Martins, R.C.; Quinta-Ferreira, R.M.; Ledakowicz, S. Photodegradation of single and mixture of parabens—Kinetic, by-products identification and cost-efficiency analysis. Chem. Eng. J. 2015, 276, 303–314. [Google Scholar] [CrossRef]
- Lincho, J.; Martins, R.C.; Gomes, J. Paraben Compounds—Part I: An Overview of Their Characteristics, Detection, and Impacts. Appl. Sci. 2021, 11, 2307. [Google Scholar] [CrossRef]
- Chang, X.; He, Y.; Song, L.; Ding, J.; Ren, S.; Lv, M.; Chen, L. Methylparaben toxicity and its removal by microalgae Chlorella vulgaris and Phaeodactylum tricornutum. J. Hazard. Mater. 2023, 454, 131528. [Google Scholar] [CrossRef]
- Sánchez-Martin, J.; Beltran-Heredia, J.; Dominguez, J.R. 2013. Advanced photochemical degradation of emerging pollutants: Methylparaben. Water Air Soil. Pollut. 2013, 224, 1483. [Google Scholar] [CrossRef]
- Lin, Y.; Ferronato, C.; Deng, N.; Wu, F.; Chovelon, J.M. Photocatalytic degradation of methylparaben by TiO2: Multivariable experimental design and mechanism. Appl. Catal. B–Environ. 2009, 88, 32–41. [Google Scholar] [CrossRef]
- Zúñiga-Benítez, H.; Peñuela, G.A. Methylparaben removal using heterogeneous photocatalysis: Effect of operational parameters and mineralization/biodegradability studies. Environ. Sci. Pollut. Res. 2017, 24, 6022–6030. [Google Scholar] [CrossRef] [PubMed]
- Bernal-Romero, M.A.; Boluda-Botella, N.; Prats-Rico, D. Removal of emerging pollutants in water treatment plants: Adsorption of methyl and propylparaben onto powdered activated carbon. Adsorption 2019, 25, 983–999. [Google Scholar] [CrossRef]
- Bernal, V.; Giraldo, L.; Moreno-Piraján, J.C.; Balsamo, M.; Erto, A. Mechanisms of Methylparaben Adsorption onto Activated Carbons: Removal Tests Supported by a Calorimetric Study of the Adsorbent–Adsorbate Interactions. Molecules 2019, 24, 413. [Google Scholar] [CrossRef] [PubMed]
- Shirasangi, R.; Kohli, H.P.; Gupta, S.; Chakraborty, M. Separation of methylparaben by emulsion liquid membrane: Optimization, characterization, stability and multiple cycles studies. Colloids Surf. A 2020, 597, 124761. [Google Scholar] [CrossRef]
- Hidalgo, A.M.; León, G.; Murcia, M.D.; Gómez, M.; Gómez, E.; Gómez, J.L. Using Pressure-Driven Membrane Processes to Remove Emerging Pollutants from Aqueous Solutions. Int. J. Environ. Res. Public Health 2021, 18, 4036. [Google Scholar] [CrossRef]
- Heo, J.; Kwon, D.; Beirns, E.; Tan, G.Y.A.; Lee, P.H.; Kim, J. Superior methylparaben removal by anaerobic fluidized bed ceramic membrane bioreactor with PVDF tubular fluidized biocarrier: Reactor performance and microbial community. J. Environ. Chem. Eng. 2023, 11, 109153. [Google Scholar] [CrossRef]
- Mutar, Z.H.; Mohammed, A.A.; Al-Baldawi, I.A. Optimization of Acetaminophen and Methylparaben Removal within Subsurface Batch Constructed Wetland Systems. J. Ecol. Eng. 2022, 23, 228–239. [Google Scholar] [CrossRef]
- Steter, J.R.; Brillas, E.; Sirés, I. On the selection of the anode material for the electrochemical removal of methylparaben from different aqueous media. Electrochim. Acta 2016, 222, 1464–1474. [Google Scholar] [CrossRef]
- Steter, J.R.; Dionisio, D.; Lanza, M.R.V.; Motheo, A.J. Electrochemical and sonoelectrochemical processes applied to the degradation of the endocrine disruptor methyl paraben. J. Appl. Electrochem. 2014, 44, 1317–1325. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mishra, R.; Saha, P.; Kushwaha, P. Adsorption thermodynamics, kinetics and isosteric heat of adsorption of malachite green onto chemically modified rice husk. Desalination 2011, 265, 159–168. [Google Scholar] [CrossRef]
- Crini, G.; Lichtfouse, E. Advantages and disadvantages of techniques used for wastewater treatment. Environ. Chem. Lett. 2019, 17, 145–155. [Google Scholar] [CrossRef]
- Mezohegyi, G.; van der Zee, F.P.; Font, J.; Fortuny, A.; Fabregat, A. Towards advanced aqueous dye removal processes: A short review on the versatile role of activated carbon. J. Environ. Manag. 2012, 102, 148–164. [Google Scholar] [CrossRef] [PubMed]
- Halim, A.A.; Aziz, H.A.; Johari, M.A.M.; Ariffin, K.S. Comparison study of ammonia and COD adsorption on zeolite, activated carbon and composite materials in landfill leachate treatment. Desalination 2010, 262, 31–35. [Google Scholar] [CrossRef]
- Bedia, J.; Peñas-Garzón, M.; Gómez-Avilés, A.; Rodriguez, J.J.; Belver, C. A Review on the Synthesis and Characterization of Biomass-Derived Carbons for Adsorption of Emerging Contaminants from Water. C–J. Carbon Res. 2018, 4, 63. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, J.; Du, Q.; Zhang, H.; Cui, Y. Antibiotic removal by agricultural waste biochars with different forms of iron oxide. RSC Adv. 2019, 9, 14143. [Google Scholar] [CrossRef]
- Matei, E.; Râpă, M.; Predescu, A.M.; Turcanu, A.A.; Vidu, R.; Predescu, C.; Bobirica, C.; Bobirica, L.; Orbec, C. Valorization of Agri-Food Wastes as Sustainable Eco-Materials for Wastewater Treatment: Current State and New Perspectives. Materials 2021, 14, 4581. [Google Scholar] [CrossRef]
- El-Bakouri, H.; Usero, J.; Morillo, J.; Ouassini, A. Adsorptive features of acid-treated olive stones for drin pesticides: Equilibrium, kinetic and thermodynamic modeling studies. Biores. Technol. 2009, 100, 4147–4155. [Google Scholar] [CrossRef]
- León, G.; Saura, F.; Hidalgo, A.M.; Miguel, B. Activated olive stones as a low-cost and environmentally friendly adsorbent for removing cephalosporin C from aqueous solutions. Int. J. Environ. Res. Public Health 2021, 18, 4489. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, Mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption isotherm models: Classification, physical meaning, application and solving method. Chemosphere 2020, 258, 127279. [Google Scholar] [CrossRef]
- Weber, T.; Chakravorti, R. Pore and solid diffusion models for fixed-bed adsorbers. AIChE J. 1974, 20, 228–238. [Google Scholar] [CrossRef]
- Freundlich, H. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385–471. [Google Scholar]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Al-Ghouti, M.A.; Da’ana, D.A. Guidelines for the use and interpretation of adsorption isotherm models: A review. J. Hazard. Mater. 2020, 393, 122383. [Google Scholar] [CrossRef]
- Gök, Ö.; Özcan, A.; Erdem, B.; Özcan, A.S. Prediction of the kinetics, equilibrium and thermodynamic parameters of adsorption of copper(II) ions onto 8-hydroxy quinoline immobilized bentonite. Coll. Surf. A Physicochem. Eng. Aspects 2008, 317, 174–185. [Google Scholar] [CrossRef]
- Temkin, M.; Pyzhev, V. Kinetics of Ammonia synthesis on promoted Iron catalysts. Acta. Physicochim. URSS 1940, 12, 327–356. [Google Scholar]
- Rajahmundry, G.K.; Garlapati, C.; Kumar, P.S.; Alwi, R.S.; Vo, D.V.N. Statistical analysis of adsorption isotherm models and its appropriate selection. Chemosphere 2021, 276, 130176. [Google Scholar] [CrossRef] [PubMed]
- León, G.; García, F.; Miguel, B.; Bayo, J. Equilibrium, kinetics and thermodynamic studies of methyl orange removal by adsorption onto granular activated carbon. Desal. Water Treat. 2016, 57, 17104–17117. [Google Scholar] [CrossRef]
- Jovanovic, D.S. Physical adsorption of gases. I: Isotherms for monolayer and multilayer adsorption. Kolloid-Z. Z. Polym. 1969, 235, 1203–1213. [Google Scholar] [CrossRef]
- Saadi, R.; Saadi, Z.; Fazaeli, R.; Fard, N. Monolayer and multilayer adsorption isotherm models for sorption from aqueous media. Korean J. Chem. Eng. 2015, 32, 787–799. [Google Scholar] [CrossRef]
- Dubinin, M.M.; Radushkevich, L.V. The equation of the characteristic curve of the activated charcoal. Proc. Acad. Sci. USSR Phys. Chem. Sect. 1947, 55, 331–337. [Google Scholar]
- Dubinin, M. The potential theory of adsorption of gases and vapors for adsorbents with energetically non-uniform surfaces. Chem. Rev. 1960, 60, 235–241. [Google Scholar] [CrossRef]
- Lagergren, S. About the theory of so-called adsorption of soluble substances. K. Sven. Vetenskap. Handl. 1898, 24, 1–39. [Google Scholar]
- Tseng, R.L.; Wu, F.C.; Juang, R.S. Characteristics and applications of the Lagergren’s first-order equation for adsorption kinetics. J. Taiwan Inst. Chem. Eng. 2010, 41, 661–669. [Google Scholar] [CrossRef]
- Ho, Y.S. Review of second-order model for adsorption systems. J. Hazard. Mater. 2006, 136, 681–689. [Google Scholar] [CrossRef]
- Hubbe, M.A.; Azizian, S.; Douven, S. Implications of apparent pseudo-second-order adsorption kinetics onto cellulosic materials: A review. BioRes. 2019, 14, 7582–7626. [Google Scholar] [CrossRef]
- Elovich, S.Y.; Larinov, O.G. Theory of adsorption from solutions of non-electrolytes on solid (I) equation adsorption from solutions and the analysis of its simplest form, (II) verification of the equation of adsorption isotherm from solutions. Izv. Akad. Nauk. SSSR Otd. Khim. Nauk. 1962, 2, 209–216. [Google Scholar]
- Chien, S.H.; Clayton, W.R. Application of Elovich equation to the kinetics of phosphate release and sorption in soils. Soil Sci. Soc. Am. J. 1980, 44, 265–268. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase changes I General theory. J. Chem. Phys. 1940, 7, 1103–1112. [Google Scholar] [CrossRef]
- Vargas, A.M.M.; Cazetta, A.L.; Kunita, M.H.; Silva, T.L.; Almeida, V.C. Adsorption of methylene blue on activated carbon produced from flamboyant pods (Delonix regia): Study of adsorption isotherms and kinetic models. Chem. Eng. J. 2011, 168, 722–730. [Google Scholar] [CrossRef]
- Acharya, J.; Sahu, J.N.; Sahoo, B.K.; Mohanty, C.R.; Meikap, B.C. Removal of chromium(VI) from wastewater by activated carbon developed from Tamarind wood activated with zinc chloride. Chem. Eng. J. 2009, 150, 25–39. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Kinetics of adsorption on carbon from solution. ASCE Sanit. Eng. Div. J. 1963, 1, 31–59. [Google Scholar] [CrossRef]
- Boyd, G.E.; Adamson, A.W.; Myers, L.S. The exchange adsorption of ions from aqueous solutions by organic zeolites. II. Kinetics. J. Am. Chem. Soc. 1947, 69, 2836–2848. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.S.; Ramakrishnan, K.; Kirupha, S.D.; Sivanesan, S. Thermodynamic, kinetic, and equilibrium studies on phenol removal by use of cashew nut shell. Can. J. Chem. Eng. 2011, 89, 284–291. [Google Scholar] [CrossRef]
- Lin, K.; Pan, J.; Chen, Y.; Cheng, R.; Xu, X. Study the adsorption of phenol from aqueous solution on hydroxyapatite nanopowders. J. Hazard. Mater. 2009, 161, 231–240. [Google Scholar] [CrossRef] [PubMed]
- Ahn, C.K.; Park, D.; Woo, S.H.; Park, J.M. Removal of cationic heavy metal from aqueous solution by activated carbon impregnated with anionic surfactants. J. Hazard. Mater. 2009, 164, 1130–1136. [Google Scholar] [CrossRef] [PubMed]
- Figueiredo, J.L.; Pereira, M.F.R.; Freitas, M.M.A.; Orfao, J.J.M. Modification of the surface chemistry of activated carbons. Carbon 1999, 37, 1379–1389. [Google Scholar] [CrossRef]
- Montes-Morán, M.A.; Suárez, D.; Menéndez, J.A.; Fuente, E. On the nature of basic sites on carbon surfaces: An overview. Carbon 2004, 42, 1219–1225. [Google Scholar] [CrossRef]
- Bohli, T.; Ouederni, A.; Fiol, N.; Villaescusa, I. Evaluation of an activated carbon from olive stones used as an adsorbent for heavy metal removal from aqueous phases. Comptes Rendus Chim. 2015, 18, 88–99. [Google Scholar] [CrossRef]
- Shahrin, E.W.E.S.; Narudin, N.A.K.; Shahri, N.N.M.; Verinda, S.B.; Nur, M.; Hobley, J.; Usman, A. Adsorption Behavior and Dynamic Interactions of Anionic Acid Blue 25 on Agricultural Waste. Molecules 2022, 27, 1718. [Google Scholar] [CrossRef]
- Asbollah, M.A.; Sahid, M.S.M.; Shahrin, E.W.E.S.; Narudin, N.A.K.; Kusrini, E.; Shahri, N.N.M.; Hobley, J.; Usman, A. Dynamics and thermodynamics for competitive adsorptive removal of methylene blue and rhodamine B from binary aqueous solution onto durian rind. Environ. Monit. Assess. 2022, 194, 645. [Google Scholar] [CrossRef] [PubMed]
- Shahrin, E.W.E.S.; Narudin, N.A.K.; Shahri, N.N.M.; Nur, M.; Lim, J.W.; Bilad, M.R.; Mahadi, A.H.; Hobley, J.; Usman, A. A comparative study of adsorption behavior of rifampicin, streptomycin, and ibuprofen contaminants from aqueous solutions onto chitosan: Dynamic interactions, kinetics, diffusions, and mechanisms. Emerg. Contam. 2023, 9, 100199. [Google Scholar] [CrossRef]
- Kumar, V.; Lee, Y.S.; Shin, J.W.; Kim, K.H.; Kukkar, D.; Tsangd, Y.F. Potential applications of graphene-based nanomaterials as adsorbent for removal of volatile organic compounds. Environ. Int. 2020, 135, 105356. [Google Scholar] [CrossRef] [PubMed]
- Faysal-Hossain, M.D.; Akther, N.; Zhou, Y. Recent advancements in graphene adsorbents for wastewater treatment: Current status and challenges. Chin. Chem. Lett. 2020, 31, 2525–2538. [Google Scholar] [CrossRef]
- Brisebois, P.P.; Siaj, M. Harvesting graphene oxide—Years 1859 to 2019: A review of its structure, synthesis, properties and exfoliation. J. Mater. Chem. C 2020, 8, 1517–1547. [Google Scholar] [CrossRef]
- Tadyszak, K.; Wychowaniec, J.K.; Litowczenko, J. Biomedical Applications of Graphene-Based Structures. Nanomaterials 2018, 8, 944. [Google Scholar] [CrossRef]

| Model | Linearized Equation | Plot | Model Parameters |
|---|---|---|---|
| Langmuir [29,30,31] | Ce/qe against Ce | qm: maximum monolayer adsorption capacity (mg/g) KL: Langmuir adsorption constant (L/mg) | |
| Freundlich [32,33,34] | lnqe against lnCe | KF: constant related to the adsorption capability (mg/g)·(L/mg)1/n n: constant related to adsorption intensity | |
| Elovich [35] | ln(qe/Ce) against qe | qmE: maximum Elovich adsorption capacity (mg/g) KE: Elovich equilibrium constant (L/mg) | |
| Temkin [36,37,38] | qe against lnCe | A: adsorption equilibrium constant (L/mg) B: the Temkin constant (mg/g) | |
| Jovanovic [39,40] | lnqe against Ce | qm: maximum adsorption capacity (mg/g) KJ is the Jovanovic constant (L/mg) | |
| Dubinin–Radushkevich [41,42] | E = (2·K)−1/2 | lnqe against ε2 | qm: maximum adsorption capacity (mg/g) K: constant related to the sorption energy (mol2/J2) ε: adsorption potential (J/mol) E: mean free energy of adsorption |
| Model | Linearized Equation | Plot | Model Parameters |
|---|---|---|---|
| Pseudo-first order [43,44] | ln(qe − qt) against t | ksp1: pseudo-first order adsorption rate constant (1/min) qeps1: equilibrium adsorption capacity estimated by the model (mg/g) | |
| Pseudo-second order [45,46] | t/qt against t | kps2: pseudo-second order adsorption rate constant (L/mol·min) qeps2: equilibrium adsorption capacity estimated by the model (mg/g) | |
| Elovich [47,48] | qt against lnt | α: initial adsorption rate (mg/g·min) β: constant related to the number of available adsorption sites (g/mg) | |
| Avrami [49,50] | ln[−ln(1 − qt/qe)] against lnt | Kav: Avrami’s constant rate (min−1) nav: Avrami’s order model. |
| Model | Linearized Equation | Plot | Model Parameters |
|---|---|---|---|
| Weber-Morris [52] | qt against t1/2 | kintp: intraparticle diffusion rate constant (mg/g·h1/2) Ci: contribution of the boundary layer diffusion | |
| Boyd [53] | B⋅t against t |
| Langmuir Isotherm | Freundlich Isotherm | Elovich Isotherm | ||||||||
| Temperature (K) | qm (mg/g) | KL (L/mg) | RL | R2 | n | KF (mg/g)·(L/mg)1/n | R2 | qmE (mg/g) | KE (L/g) | R2 |
| 283 | 86.9565 | 0.3412 | 0.0554 | 0.9965 | 2.1277 | 23.2174 | 0.9561 | 35.7143 | 1.2451 | 0.9481 |
| 293 | 92.5926 | 0.3763 | 0.0505 | 0.9916 | 2.1418 | 26.1723 | 0.9901 | 36.7647 | 1.4985 | 0.9825 |
| 303 | 95.2381 | 0.4086 | 0.0467 | 0.9991 | 2.0509 | 27.3523 | 0.9687 | 39.8406 | 1.4412 | 0.9758 |
| 313 | 98.0392 | 0.4976 | 0.0386 | 0.9997 | 2.0631 | 30.5266 | 0.9537 | 41.6667 | 1.6557 | 0.9428 |
| Temkin isotherm | Jovanovic isotherm | Dubinin–Radushkevich isotherm | ||||||||
| Temperature (K) | A (L/mg) | B (mg/g) | R2 | qm (mg/g) | KJ (L/mg) | R2 | qm (mg/g) | K (mol2/L2) | E (Jmol) | R2 |
| 283 | 3.5135 | 18.7006 | 0.9941 | 25.9378 | 0.0868 | 0.7008 | 61.2767 | 0.3284 | 1.2339 | 0.9305 |
| 293 | 4.1867 | 19.3489 | 0.9828 | 25.9352 | 0.1116 | 0.7689 | 61.3626 | 0.1978 | 1.5899 | 0.8620 |
| 303 | 4.2481 | 20.4452 | 0.9969 | 27.3086 | 0.1144 | 0.6915 | 63.5991 | 0.1904 | 1.6205 | 0.8993 |
| 313 | 5.0017 | 21.1908 | 0.9945 | 28.9595 | 0.1222 | 0.6542 | 68.1492 | 0.1581 | 1.7784 | 0.9211 |
| Langmuir Isotherm | Freundlich Isotherm | Elovich Isotherm | ||||||||
| Temperature (K) | qm (mg/g) | KL (L/mg) | RL | R2 | N | KF (mg/g)·(L/mg)1/n | R2 | qmE (mg/g) | KE (L/g) | R2 |
| 283 | 24.8756 | 0.0503 | 0.2846 | 0.9964 | 1.5601 | 1.8016 | 0.9923 | 14.8368 | 0.0958 | 0.9887 |
| 293 | 27.3224 | 0.0540 | 0.2701 | 0.9987 | 1.5413 | 2.0311 | 0.9903 | 16.4474 | 0.1015 | 0.9909 |
| 303 | 27.8552 | 0.0604 | 0.2487 | 0.9984 | 1.5309 | 2.2001 | 0.9852 | 16.1290 | 0.1495 | 0.9708 |
| 313 | 28.4900 | 0.0723 | 0.2167 | 0.9947 | 1.6116 | 2.6966 | 0.9920 | 17.1527 | 0.1092 | 0.9940 |
| Temkin isotherm | Jovanovic isotherm | Dubinin–Radushkevich isotherm | ||||||||
| Temperature (K) | A (L/mg) | B (mg/g) | R2 | qm (mg/g) | KJ (L/mg) | R2 | qm (mg/g) | K (mol2/L2) | E (Jmol) | R2 |
| 283 | 1.9362 | 5.3355 | 0.9890 | 4.0020 | 0.0582 | 0.8876 | 12.4572 | 3.9969 | 0.3537 | 0.8882 |
| 293 | 1.7755 | 5.8183 | 0.9920 | 4.6409 | 0.0532 | 0.8649 | 13.6331 | 3.2111 | 0.3946 | 0.9019 |
| 303 | 1.6175 | 6.0015 | 0.9962 | 4.7870 | 0.0580 | 0.8475 | 13.8696 | 2.5785 | 0.4404 | 0.9222 |
| 313 | 1.3474 | 6.1344 | 0.9881 | 5.2169 | 0.0613 | 0.8644 | 14.8530 | 1.7796 | 0.5301 | 0.8911 |
| Pseudo-First Order | Pseudo-Second Order | Elovich | Avrami | ||||||||||
| Co (mg/L) | qe,exp | kps1 (1/min) | qe,ps1 (mg/g) | R2 | ksp2 (g/mg·min) | qe,ps2 (mg/g) | R2 | α (mg/g·min) | β (g/mg) | R2 | kAV (1/min) | nAV | R2 |
| 10 | 19.3673 | 0.002284 | 18.7994 | 0.9956 | 0.00008153 | 25.8184 | 0.9899 | 0.1506 | 0.2081 | 0.9742 | 0.00288 | 0.9786 | 0.9854 |
| 20 | 36.9137 | 0.002395 | 36.3182 | 0.9981 | 0.00004340 | 49.0798 | 0.9979 | 0.2838 | 0.1083 | 0.9652 | 0.00346 | 0.9406 | 0.9978 |
| 30 | 53.1282 | 0.002578 | 51.8823 | 0.9990 | 0.00003762 | 67.6956 | 0.9984 | 0.4431 | 0.0762 | 0.9694 | 0.00462 | 0.9028 | 0.9986 |
| 40 | 68.2462 | 0.002653 | 65.2040 | 0.9973 | 0.00003767 | 83.0841 | 0.9946 | 0.6347 | 0.0613 | 0.9670 | 0.00821 | 0.8085 | 0.9905 |
| 50 | 75.7463 | 0.002720 | 74.3646 | 0.9986 | 0.00002845 | 95.2381 | 0.9932 | 0.6503 | 0.0537 | 0.9608 | 0.00584 | 0.8627 | 0.9880 |
| Pseudo-First Order | Pseudo-Second Order | Elovich | Avrami | ||||||||||
| Co (mg/L) | qe,exp | kps1 (1/min) | qe,ps1 (mg/g) | R2 | kps2 (g/mg·min) | qe,ps2 (mg/g) | R2 | α (mg/g·min) | β (g/mg) | R2 | kAV (1/min) | nAV | R2 |
| 10 | 5.9873 | 0.001861 | 4.1049 | 0.9904 | 0.00043281 | 5.5131 | 0.9714 | 0.0344 | 0.9907 | 0.9315 | 0.0112 | 0.7004 | 0.9800 |
| 20 | 10.6883 | 0.001953 | 8.1424 | 0.9960 | 0.00014076 | 11.6198 | 0.9668 | 0.0552 | 0.4960 | 0.9241 | 0.0048 | 0.8351 | 0.9771 |
| 30 | 14.3992 | 0.002161 | 11.0262 | 0.9979 | 0.00014026 | 14.9403 | 0.9810 | 0.0846 | 0.3637 | 0.9426 | 0.0060 | 0.8188 | 0.9749 |
| 40 | 18.7234 | 0.002265 | 13.5256 | 0.9979 | 0.00012871 | 17.9775 | 0.9856 | 0.1093 | 0.2966 | 0.9479 | 0.0066 | 0.8122 | 0.9808 |
| 50 | 18.7234 | 0.002381 | 15.5235 | 0.9960 | 0.00013105 | 20.2020 | 0.9821 | 0.1365 | 0.2606 | 0.9446 | 0.0093 | 0.7604 | 0.9590 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
León, G.; Hidalgo, A.M.; Martínez, A.; Guzmán, M.A.; Miguel, B. Methylparaben Adsorption onto Activated Carbon and Activated Olive Stones: Comparative Analysis of Efficiency, Equilibrium, Kinetics and Effect of Graphene-Based Nanomaterials Addition. Appl. Sci. 2023, 13, 9147. https://doi.org/10.3390/app13169147
León G, Hidalgo AM, Martínez A, Guzmán MA, Miguel B. Methylparaben Adsorption onto Activated Carbon and Activated Olive Stones: Comparative Analysis of Efficiency, Equilibrium, Kinetics and Effect of Graphene-Based Nanomaterials Addition. Applied Sciences. 2023; 13(16):9147. https://doi.org/10.3390/app13169147
Chicago/Turabian StyleLeón, Gerardo, Asunción María Hidalgo, Antonio Martínez, María Amelia Guzmán, and Beatriz Miguel. 2023. "Methylparaben Adsorption onto Activated Carbon and Activated Olive Stones: Comparative Analysis of Efficiency, Equilibrium, Kinetics and Effect of Graphene-Based Nanomaterials Addition" Applied Sciences 13, no. 16: 9147. https://doi.org/10.3390/app13169147
APA StyleLeón, G., Hidalgo, A. M., Martínez, A., Guzmán, M. A., & Miguel, B. (2023). Methylparaben Adsorption onto Activated Carbon and Activated Olive Stones: Comparative Analysis of Efficiency, Equilibrium, Kinetics and Effect of Graphene-Based Nanomaterials Addition. Applied Sciences, 13(16), 9147. https://doi.org/10.3390/app13169147







