Bias-Corrected CMIP5 Projections for Climate Change and Assessments of Impact on Malaria in Senegal under the VECTRI Model
Abstract
1. Introduction
2. Materials and Methods
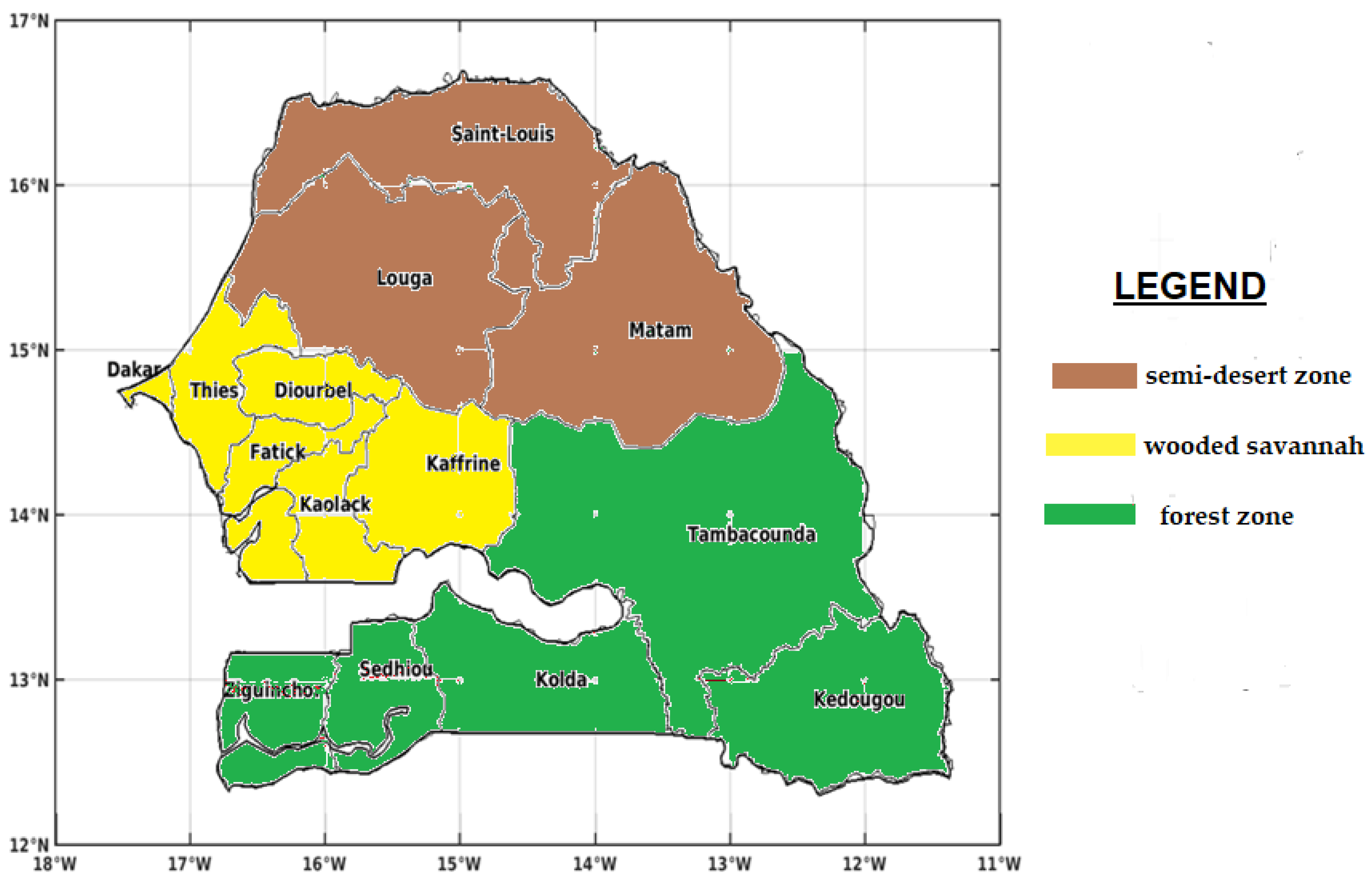
2.1. Study Area
2.2. Climate Data
2.3. GCM Models Used (Bias-Corrected CMIP5)
2.4. Malaria Impact Model Used (VECTRI)
2.5. Methods
3. Results
3.1. Validation of the Rainfall and Temperature Inputs
3.2. Evaluation of the Performance of the VECTRI Model with GCM
3.2.1. Spatio-Temporal Variability of the EIR for the Validation of the GCM
3.2.2. Taylor Diagram for Rainfall, Temperature and EIR Variable
3.3. Projected Changes in Malaria Index (EIR)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, S.; Hill, A.V.S. Dynamic Interactions in Malaria: Host Heterogeneity Meets Parasite Polymorphism. Proc. R. Soc. London. Ser. B Biol. Sci. 1995, 261, 271–277. [Google Scholar] [CrossRef]
- Carnevale, P.; Robert, V. (Eds.) Faciès et typologie du paludisme en Afrique sud-saharienne. In Les Anophèles: Biologie, Transmission du Plasmodium et Lutte Antivectorielle; Didactiques; IRD Éditions: Marseille, France, 2017; pp. 187–223. ISBN 978-2-7099-2283-8. [Google Scholar]
- Alonso, D.; Bouma, M.J.; Pascual, M. Epidemic Malaria and Warmer Temperatures in Recent Decades in an East African Highland. Proc. R. Soc. B Biol. Sci. 2011, 278, 1661–1669. [Google Scholar] [CrossRef] [PubMed]
- World Malaria Report 2021|Medicines for Malaria Venture. Available online: https://www.mmv.org/newsroom/publications/world-malaria-report-2021 (accessed on 18 March 2023).
- Konaté, L.; Faye, O.; Gaye, O.; Sy, N.; Diop, A.; Diouf, M.; Trape, J.-F.; Molez, J.-F. Zoophagie et hôtes alternatifs des vecteurs du paludisme au Sénégal. Parasite 1999, 6, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Faye, O.; Konate, L.; Fontenille, D.; Gaye, O.; Sy, N.; Hébrard, G.; Hervé, J.-P.; Touré, Y.T. Variations Saisonnières des Populations d’Anopheles Gambiae s.l. et Transmission du Paludisme dans un Village de Savane Soudanienne du Sud-Est du Sénégal. Bull. L’institut Fondam D’afrique Noire Cheihk Anta Diop Dakar Série A 1995, 48, 57–66. [Google Scholar]
- Robert, V.; Dieng, H.; Lochouarn, L.; Traoré, S.F.; Trape, J.-F.; Simondon, F.; Fontenille, D. La Transmission du Paludisme dans La Zone de Niakhar, Sénégal. Trop. Med. Int. Health 1998, 3, 667–677. [Google Scholar] [CrossRef]
- Christensen, J.H.; Hewitson, B.; Busuioc, A.; Chen, A.; Gao, X.; Held, I.; Jones, R.; Kolli, R.K.; Kwon, W.-T.; Mearns, L.; et al. Regional Climate Projections. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; pp. 847–940. [Google Scholar]
- Kouassi, A.; Assamoi, P.; Bigot, S.; Diawara, A.; Schayes, G.; Yoroba, F.; Kouassi, B. Étude du climat Ouest-Africain à l’aide du modèle atmosphérique régional M.A.R. Climatologie 2010, 7, 39–55. [Google Scholar] [CrossRef]
- Berry, H.L.; Bowen, K.; Kjellstrom, T. Climate Change and Mental Health: A Causal Pathways Framework. Int. J. Public Health 2010, 55, 123–132. [Google Scholar] [CrossRef]
- Diouf, I.; Rodriguez Fonseca, B.; Caminade, C.; Thiaw, W.M.; Deme, A.; Morse, A.P.; Ndione, J.-A.; Gaye, A.T.; Diaw, A.; Ndiaye, M.K.N. Climate Variability and Malaria over West Africa. Am. J. Trop. Med. Hyg. 2020, 102, 1037–1047. [Google Scholar] [CrossRef]
- Fall, P.; Diouf, I.; Deme, A.; Sene, D. Assessment of Climate-Driven Variations in Malaria Transmission in Senegal Using the VECTRI Model. Atmosphere 2022, 13, 418. [Google Scholar] [CrossRef]
- Lindsay, S.W.; Martens, W.J. Malaria in the African Highlands: Past, Present and Future. Bull. World Health Organ. 1998, 76, 33–45. [Google Scholar]
- Paaijmans, K.P.; Wandago, M.O.; Githeko, A.K.; Takken, W. Unexpected High Losses of Anopheles Gambiae Larvae Due to Rainfall. PLoS ONE 2007, 2, e1146. [Google Scholar] [CrossRef] [PubMed]
- Caminade, C.; Kovats, S.; Rocklov, J.; Tompkins, A.M.; Morse, A.P.; Colón-González, F.J.; Stenlund, H.; Martens, P.; Lloyd, S.J. Impact of Climate Change on Global Malaria Distribution. Proc. Natl. Acad. Sci. USA 2014, 111, 3286–3291. [Google Scholar] [CrossRef] [PubMed]
- Costello, A.; Abbas, M.; Allen, A.; Ball, S.; Bell, S.; Bellamy, R.; Friel, S.; Groce, N.; Johnson, A.; Kett, M.; et al. Managing the Health Effects of Climate Change. Lancet 2009, 373, 1693–1733. [Google Scholar] [CrossRef]
- Dufresne, L.; Cadule, P.; Caubel, A.; Chauvin, F.; Déqué, M.; Douville, H.; Fairhead, L.; Fichefet, T.; Foujols, A.; Grandpeix, Y.; et al. Simulation de l’évolution récente et future du climat par les modèles du CNRM et de l’IPSL. Météorologie 2006, 55, 45–59. [Google Scholar] [CrossRef]
- Bonnardot, V.; Carey, V.; Madelin, M.; Cautenet, S.; Coetzee, Z.; Quénol, H. Using atmospheric and statistical models to understand local climate and assess spatial temperature variability at a fine scale over the stellenbosch wine district, south africa. Int. J. Vine Wine Sci. 2012, 46, 1–13. [Google Scholar]
- Giorgi, F. Regional Climate Modeling: Status and Perspectives. J. Phys. IV Fr. 2006, 139, 101–118. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Errico, R.M.; Giorgi, F.; Bates, G.T. A Regional Climate Model for the Western United States. Clim. Chang. 1989, 15, 383–422. [Google Scholar] [CrossRef]
- Giorgi, F. Simulation of Regional Climate Using a Limited Area Model Nested in a General Circulation Model. J. Clim. 1990, 3, 941–963. [Google Scholar] [CrossRef]
- Wang, Y.; Leung, L.R.; McGREGOR, J.L.; Lee, D.-K.; Wang, W.-C.; Ding, Y.; Kimura, F. Regional Climate Modeling: Progress, Challenges, and Prospects. J. Meteorol. Soc. Japan. Ser. II 2004, 82, 1599–1628. [Google Scholar] [CrossRef]
- Crétat, J.; Pohl, B.; Richard, Y. Les modèles climatiques régionaux: Outils de décomposition des échelles spatio-temporelles. In Proceedings of the Hyper Article en Ligne—Sciences de l’Homme et de la Société, Besançon, France, 23 February 2011. [Google Scholar]
- Richard, Y.; Roucou, P.; Cretat, J.; Castel, T.; Pohl, B. Modeles de climats regionaux: Potentiels et limites. In Proceedings of the Actes du 25e Colloque de l’Association Internationale de Climatologie (AIC), Grenoble, France, 14–25 May 2012; p. 6. [Google Scholar]
- Dosio, A.; Panitz, H.-J.; Schubert-Frisius, M.; Lüthi, D. Dynamical Downscaling of CMIP5 Global Circulation Models over CORDEX-Africa with COSMO-CLM: Evaluation over the Present Climate and Analysis of the Added Value. Clim. Dyn. 2015, 44, 2637–2661. [Google Scholar] [CrossRef]
- Famien, A.M.; Janicot, S.; Ochou, A.D.; Vrac, M.; Defrance, D.; Sultan, B.; Noël, T. A Bias-Corrected CMIP5 Dataset for Africa Using the CDF-t Method—A Contribution to Agricultural Impact Studies. Earth Syst. Dynam. 2018, 9, 313–338. [Google Scholar] [CrossRef]
- Lim Kam Sian, K.T.C.; Hagan, D.F.T.; Ayugi, B.O.; Nooni, I.K.; Ullah, W.; Babaousmail, H.; Ongoma, V. Projections of Precipitation Extremes Based on Bias-Corrected CMIP6 Models Ensemble over Southern Africa. Int. J. Climatol. 2022, 42, 8269–8289. [Google Scholar] [CrossRef]
- Tompkins, A.M.; Ermert, V. A Regional-Scale, High Resolution Dynamical Malaria Model That Accounts for Population Density, Climate and Surface Hydrology. Malar. J. 2013, 12, 65. [Google Scholar] [CrossRef] [PubMed]
- Ndiaye, O.; Goddard, L.; Ward, M.N. Using Regional Wind Fields to Improve General Circulation Model Forecasts of July-September Sahel Rainfall. Int. J. Climatol. 2009, 29, 1262–1275. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A State-of-the-Art Global Reanalysis Dataset for Land Applications; Data, Algorithms, and Models. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Novella, N.S.; Thiaw, W.M. African Rainfall Climatology Version 2 for Famine Early Warning Systems. J. Appl. Meteorol. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing Objective Techniques for Gauge-Based Analyses of Global Daily Precipitation. J. Geophys. Res. 2008, 113, D04110. [Google Scholar] [CrossRef]
- Bony, S.; Bellon, G.; Klocke, D.; Sherwood, S.; Fermepin, S.; Denvil, S. Robust Direct Effect of Carbon Dioxide on Tropical Circulation and Regional Precipitation. Nat. Geosci. 2013, 6, 447–451. [Google Scholar] [CrossRef]
- Wigley, T.M.L.; Jones, P.D. Influences of Precipitation Changes and Direct CO2 Effects on Streamflow. Nature 1985, 314, 149–152. [Google Scholar] [CrossRef]
- Michelangeli, P.-A.; Vrac, M.; Loukos, H. Probabilistic Downscaling Approaches: Application to Wind Cumulative Distribution Functions. Geophys. Res. Lett. 2009, 36, L11708. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next Generation of Scenarios for Climate Change Research and Assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.-L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Chapter 12—Long-Term Climate Change: Projections, Commitments and Irreversibility. In Climate Change 2013: The Physical Science Basis. IPCC Working Group I Contribution to AR5; IPCC, Ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Vrac, M.; Drobinski, P.; Merlo, A.; Herrmann, M.; Lavaysse, C.; Li, L.; Somot, S. Dynamical and Statistical Downscaling of the French Mediterranean Climate: Uncertainty Assessment. Nat. Hazards Earth Syst. Sci. 2012, 12, 2769–2784. [Google Scholar] [CrossRef]
- Lavaysse, C.; Vrac, M.; Drobinski, P.; Lengaigne, M.; Vischel, T. Statistical Downscaling of the French Mediterranean Climate: Assessment for Present and Projection in an Anthropogenic Scenario. Nat. Hazards Earth Syst. Sci. 2012, 12, 651–670. [Google Scholar] [CrossRef]
- Vautard, R.; Noël, T.; Li, L.; Vrac, M.; Martin, E.; Dandin, P.; Cattiaux, J.; Joussaume, S. Climate Variability and Trends in Downscaled High-Resolution Simulations and Projections over Metropolitan France. Clim. Dyn. 2013, 41, 1419–1437. [Google Scholar] [CrossRef]
- Franklin, C.N.; Sun, Z.; Bi, D.; Dix, M.; Yan, H.; Bodas-Salcedo, A. Evaluation of Clouds in ACCESS Using the Satellite Simulator Package COSP: Regime-Sorted Tropical Cloud Properties. J. Geophys. Res. Atmos. 2013, 118, 6663–6679. [Google Scholar] [CrossRef]
- Chylek, P.; Li, J.; Dubey, M.K.; Wang, M.; Lesins, G. Observed and Model Simulated 20th Century Arctic Temperature Variability: Canadian Earth System Model CanESM2; Aerosols/Atmospheric Modelling/Troposphere/Physics (physical properties and processes); 2011; preprint. [Google Scholar]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Sanna, A.; Fogli, P.G.; Manzini, E.; Vichi, M.; Oddo, P.; Navarra, A. Effects of Tropical Cyclones on Ocean Heat Transport in a High-Resolution Coupled General Circulation Model. J. Clim. 2011, 24, 4368–4384. [Google Scholar] [CrossRef]
- Voldoire, A.; Sanchez-Gomez, E.; Salas y Mélia, D.; Decharme, B.; Cassou, C.; Sénési, S.; Valcke, S.; Beau, I.; Alias, A.; Chevallier, M.; et al. The CNRM-CM5.1 Global Climate Model: Description and Basic Evaluation. Clim. Dyn. 2013, 40, 2091–2121. [Google Scholar] [CrossRef]
- The CSIRO-Mk3.6.0 Atmosphere-Ocean GCM: Participation in CMIP5 and Data Publication. In Proceedings of the MODSIM2011, 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011. Modelling and Simulation Society of Australia and New Zealand (MSSANZ).
- Griffies, S.M.; Winton, M.; Donner, L.J.; Horowitz, L.W.; Downes, S.M.; Farneti, R.; Gnanadesikan, A.; Hurlin, W.J.; Lee, H.-C.; Liang, Z.; et al. The GFDL CM3 Coupled Climate Model: Characteristics of the Ocean and Sea Ice Simulations. J. Clim. 2011, 24, 3520–3544. [Google Scholar] [CrossRef]
- Dunne, J.P.; John, J.G.; Adcroft, A.J.; Griffies, S.M.; Hallberg, R.W.; Shevliakova, E.; Stouffer, R.J.; Cooke, W.; Dunne, K.A.; Harrison, M.J.; et al. GFDL’s ESM2 Global Coupled Climate–Carbon Earth System Models. Part I: Physical Formulation and Baseline Simulation Characteristics. J. Clim. 2012, 25, 6646–6665. [Google Scholar] [CrossRef]
- Dunne, J.P.; John, J.G.; Shevliakova, E.; Stouffer, R.J.; Krasting, J.P.; Malyshev, S.L.; Milly, P.C.D.; Sentman, L.T.; Adcroft, A.J.; Cooke, W.; et al. GFDL’s ESM2 Global Coupled Climate–Carbon Earth System Models. Part II: Carbon System Formulation and Baseline Simulation Characteristics*. J. Clim. 2013, 26, 2247–2267. [Google Scholar] [CrossRef]
- Volodin, E.M.; Dianskii, N.A.; Gusev, A.V. Simulating Present-Day Climate with the INMCM4.0 Coupled Model of the Atmospheric and Oceanic General Circulations. Izv. Atmos. Ocean. Phys. 2010, 46, 414–431. [Google Scholar] [CrossRef]
- Dufresne, J.-L.; Foujols, M.-A.; Denvil, S.; Caubel, A.; Marti, O.; Aumont, O.; Balkanski, Y.; Bekki, S.; Bellenger, H.; Benshila, R.; et al. Climate Change Projections Using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5. Clim. Dyn. 2013, 40, 2123–2165. [Google Scholar] [CrossRef]
- Abiodun, B.J.; Adeyewa, Z.D.; Oguntunde, P.G.; Salami, A.T.; Ajayi, V.O. Modeling the Impacts of Reforestation on Future Climate in West Africa. Appl. Clim. 2012, 110, 77–96. [Google Scholar] [CrossRef]
- Asare, E.O.; Tompkins, A.M.; Bomblies, A. A Regional Model for Malaria Vector Developmental Habitats Evaluated Using Explicit, Pond-Resolving Surface Hydrology Simulations. PLoS ONE 2016, 11, e0150626. [Google Scholar] [CrossRef]
- Tompkins, A.M.; Thomson, M.C. Uncertainty in Malaria Simulations in the Highlands of Kenya: Relative Contributions of Model Parameter Setting, Driving Climate and Initial Condition Errors. PLoS ONE 2018, 13, e0200638. [Google Scholar] [CrossRef]
- Hoshen, M.B.; Morse, A.P. A Weather-Driven Model of Malaria Transmission. Malar. J. 2004, 3, 32. [Google Scholar] [CrossRef]
- Kelly-Hope, L.A.; McKenzie, F.E. The Multiplicity of Malaria Transmission: A Review of Entomological Inoculation Rate Measurements and Methods across Sub-Saharan Africa. Malar. J. 2009, 8, 19. [Google Scholar] [CrossRef]
- Craig, M.H.; Snow, R.W.; le Sueur, D. A Climate-Based Distribution Model of Malaria Transmission in Sub-Saharan Africa. Parasitol. Today 1999, 15, 105–111. [Google Scholar] [CrossRef]
- Navarro-Racines, C.; Tarapues, J.; Thornton, P.; Jarvis, A.; Ramirez-Villegas, J. High-Resolution and Bias-Corrected CMIP5 Projections for Climate Change Impact Assessments. Sci. Data 2020, 7, 7. [Google Scholar] [CrossRef]
- Iizumi, T.; Takikawa, H.; Hirabayashi, Y.; Hanasaki, N.; Nishimori, M. Contributions of Different Bias-Correction Methods and Reference Meteorological Forcing Data Sets to Uncertainty in Projected Temperature and Precipitation Extremes. J. Geophys. Res. Atmos. 2017, 122, 7800–7819. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Kante, I.K.; Badiane, D.; Sall, S.M.; Deme, A.; Diedhiou, A. Comparative Study of the West African Continental, Coastal and Marine Atmospheric Profiles during the Summer of 2006. Int. J. Geophys. 2012, 2012, 603949. [Google Scholar] [CrossRef]
- Bomblies, A. Modeling the Role of Rainfall Patterns in Seasonal Malaria Transmission. Clim. Chang. 2012, 112, 673–685. [Google Scholar] [CrossRef]
- Eikenberry, S.E.; Gumel, A.B. Mathematical Modeling of Climate Change and Malaria Transmission Dynamics: A Historical Review. J. Math. Biol. 2018, 77, 857–933. [Google Scholar] [CrossRef]
- Pascual, M.; Cazelles, B.; Bouma, M.J.; Chaves, L.F.; Koelle, K. Shifting Patterns: Malaria Dynamics and Rainfall Variability in an African Highland. Proc. R. Soc. B Biol. Sci. 2008, 275, 123–132. [Google Scholar] [CrossRef]
- Dev, V.; Dash, A.P. Rainfall and Malaria Transmission in North–Eastern India. Ann. Trop. Med. Parasitol. 2007, 101, 457–459. [Google Scholar] [CrossRef]
- Diouf, I.; Deme, A.; Ndione, J.-A.; Gaye, A.T.; Rodríguez-Fonseca, B.; Cissé, M. Climate and Health: Observation and Modeling of Malaria in the Ferlo (Senegal). Comptes Rendus Biol. 2013, 336, 253–260. [Google Scholar] [CrossRef]
- Mbouna, A.D.; Tompkins, A.M.; Lenouo, A.; Asare, E.O.; Yamba, E.I.; Tchawoua, C. Modelled and Observed Mean and Seasonal Relationships between Climate, Population Density and Malaria Indicators in Cameroon. Malar. J. 2019, 18, 359. [Google Scholar] [CrossRef]
- Jean, M.; Pierre, C.; Marc, C. Biodiversité du Paludisme Dans le Monde; John Libbey Eurotext: Montrouge, France, 2004; ISBN 978–2-7420–1304-3. [Google Scholar]
- Kapwata, T.; Wright, C.Y.; du Preez, D.J.; Kunene, Z.; Mathee, A.; Ikeda, T.; Landman, W.; Maharaj, R.; Sweijd, N.; Minakawa, N.; et al. Exploring Rural Hospital Admissions for Diarrhoeal Disease, Malaria, Pneumonia, and Asthma in Relation to Temperature, Rainfall and Air Pollution Using Wavelet Transform Analysis. Sci. Total Environ. 2021, 791, 148307. [Google Scholar] [CrossRef] [PubMed]
- Shah, M.M.; Krystosik, A.R.; Ndenga, B.A.; Mutuku, F.M.; Caldwell, J.M.; Otuka, V.; Chebii, P.K.; Maina, P.W.; Jembe, Z.; Ronga, C.; et al. Malaria Smear Positivity among Kenyan Children Peaks at Intermediate Temperatures as Predicted by Ecological Models. Parasites Vectors 2019, 12, 288. [Google Scholar] [CrossRef] [PubMed]
- Sultan, B.; Janicot, S.; Diedhiou, A. The West African Monsoon Dynamics. Part I: Documentation of Intraseasonal Variability. J. Clim. 2003, 16, 3389–3406. [Google Scholar] [CrossRef]
- Redelsperger, J.-L.; Diedhiou, A.; Flamant, C.; Janicot, S.; Lafore, J.-P.; Lebel, T.; Polcher, J.; Caniaux, G.; de Rosnay, P.; Desbois, M.; et al. Amma, une étude multidisciplinaire de la mousson ouest-africaine. Météorologie 2006, 8, 22. [Google Scholar] [CrossRef]
- Bodian, A.; Diop, L.; Panthou, G.; Dacosta, H.; Deme, A.; Dezetter, A.; Ndiaye, P.M.; Diouf, I.; Vischel, T. Recent Trend in Hydroclimatic Conditions in the Senegal River Basin. Water 2020, 12, 436. [Google Scholar] [CrossRef]
- Ryan, S.J.; McNally, A.; Johnson, L.R.; Mordecai, E.A.; Ben-Horin, T.; Paaijmans, K.; Lafferty, K.D. Mapping Physiological Suitability Limits for Malaria in Africa Under Climate Change. Vector Borne Zoonotic Dis. 2015, 15, 718–725. [Google Scholar] [CrossRef]
- Abiodun, G.J.; Maharaj, R.; Witbooi, P.; Okosun, K.O. Modelling the Influence of Temperature and Rainfall on the Population Dynamics of Anopheles Arabiensis. Malar. J. 2016, 15, 364. [Google Scholar] [CrossRef]
- Metcalf, C.J.E.; Walter, K.S.; Wesolowski, A.; Buckee, C.O.; Shevliakova, E.; Tatem, A.J.; Boos, W.R.; Weinberger, D.M.; Pitzer, V.E. Identifying Climate Drivers of Infectious Disease Dynamics: Recent Advances and Challenges Ahead. Proc. R. Soc. B 2017, 284, 20170901. [Google Scholar] [CrossRef]
- Bayoh, M.N.; Lindsay, S.W. Effect of Temperature on the Development of the Aquatic Stages of Anopheles Gambiae Sensu Stricto (Diptera: Culicidae). Bull. Entomol. Res. 2003, 93, 375–381. [Google Scholar] [CrossRef]
- McMichael, C. Climate Change—Related Migration and Infectious Disease. Virulence 2015, 6, 548–553. [Google Scholar] [CrossRef]
- Diouf, I.; Rodriguez-Fonseca, B.; Deme, A.; Caminade, C.; Morse, A.; Cisse, M.; Sy, I.; Dia, I.; Ermert, V.; Ndione, J.-A.; et al. Comparison of Malaria Simulations Driven by Meteorological Observations and Reanalysis Products in Senegal. Int. J. Environ. Res. Public Health 2017, 14, 1119. [Google Scholar] [CrossRef]
- Aflahah, E.; Latifah, A.L.; Hidayat, R.; Hidayati, R.; Ihwan, A. Inter-Comparison of Multiple Global Climate Model (GCM) Data Based on Spatial Pattern of Rainfall over Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2019, 284, 012017. [Google Scholar] [CrossRef]
- Mordecai, E.A.; Paaijmans, K.P.; Johnson, L.R.; Balzer, C.; Ben-Horin, T.; de Moor, E.; McNally, A.; Pawar, S.; Ryan, S.J.; Smith, T.C.; et al. Optimal Temperature for Malaria Transmission Is Dramatically Lower than Previously Predicted. Ecol. Lett. 2013, 16, 22–30. [Google Scholar] [CrossRef]
- Deme, A.; Gaye, A.T.; Hourdin, F. Chapter 3. Climate Projections in West Africa: The Obvious and the Uncertain. In Rural Societies in the Face of Climatic and Environmental Changes in West Africa; Sultan, B., Lalou, R., Sanni, M.A., Oumarou, A., Arame Soumaré, M., Eds.; IRD Éditions: Montpellier, France, 2017; pp. 61–86. ISBN 978-2-7099-2424-5. [Google Scholar]
- Mordecai, E.A.; Caldwell, J.M.; Grossman, M.K.; Lippi, C.A.; Johnson, L.R.; Neira, M.; Rohr, J.R.; Ryan, S.J.; Savage, V.; Shocket, M.S.; et al. Thermal Biology of Mosquito-borne Disease. Ecol. Lett. 2019, 22, 1690–1708. [Google Scholar] [CrossRef]
- Sultan, B.; Roudier, P.; Quirion, P.; Alhassane, A.; Muller, B.; Dingkuhn, M.; Ciais, P.; Guimberteau, M.; Traore, S.; Baron, C. Assessing Climate Change Impacts on Sorghum and Millet Yields in the Sudanian and Sahelian Savannas of West Africa. Environ. Res. Lett. 2013, 8, 014040. [Google Scholar] [CrossRef]
- Yamana, T.K.; Eltahir, E.A. Early Warnings of the Potential for Malaria Transmission in Rural Africa Using the Hydrology, Entomology and Malaria Transmission Simulator (HYDREMATS). Malar. J. 2010, 9, 323. [Google Scholar] [CrossRef]
- Ngarakana-Gwasira, E.T.; Bhunu, C.P.; Masocha, M.; Mashonjowa, E. Assessing the Role of Climate Change in Malaria Transmission in Africa. Malar. Res. Treat. 2016, 2016, 7104291. [Google Scholar] [CrossRef]
- Ermert, V.; Fink, A.H.; Morse, A.P.; Paeth, H. The Impact of Regional Climate Change on Malaria Risk Due to Greenhouse Forcing and Land-Use Changes in Tropical Africa. Environ. Health Perspect. 2012, 120, 77–84. [Google Scholar] [CrossRef]
- Gething, P.W.; Patil, A.P.; Smith, D.L.; Guerra, C.A.; Elyazar, I.R.; Johnston, G.L.; Tatem, A.J.; Hay, S.I. A New World Malaria Map: Plasmodium Falciparum Endemicity in 2010. Malar. J. 2011, 10, 378. [Google Scholar] [CrossRef]
- Béguin, A.; Hales, S.; Rocklöv, J.; Åström, C.; Louis, V.R.; Sauerborn, R. The Opposing Effects of Climate Change and Socio-Economic Development on the Global Distribution of Malaria. Glob. Environ. Chang. 2011, 21, 1209–1214. [Google Scholar] [CrossRef]
- Gething, P.W.; Smith, D.L.; Patil, A.P.; Tatem, A.J.; Snow, R.W.; Hay, S.I. Climate Change and the Global Malaria Recession. Nature 2010, 465, 342–345. [Google Scholar] [CrossRef] [PubMed]
- Vrac, M.; Friederichs, P. Multivariate—Intervariable, Spatial, and Temporal—Bias Correction. J. Clim. 2015, 28, 218–237. [Google Scholar] [CrossRef]
- Vrac, M.; Noël, T.; Vautard, R. Bias Correction of Precipitation through Singularity Stochastic Removal: Because Occurrences Matter. J. Geophys. Res. Atmos. 2016, 121, 5237–5258. [Google Scholar] [CrossRef]
















| Climate Datasets | Definition | Resolution | References |
|---|---|---|---|
| ERA5 (Rainfall at temperature) | European ReAnalysis | 0.25° × 0.25° | [30] |
| CHIRPS (Rainfall) | Climate Hazards InfraRed Rainfall with Station data | 0.05° × 0.05° | [32] |
| ARC2 (Rainfall) | Africa Rainfall Climatology, version 2 | 0.1° × 0.1° | [33] |
| CPC (Rainfall) | Climate Prediction Center | 0.25° × 0.25° | [34] |
| Model | Institute | Resolution | Reference |
|---|---|---|---|
| ACCESS1–3 | Australian Community Climate and Earth System Simulator, Australia | 1.25° × 1.9°, L38 | [43] |
| CanESM2 | Canadian Centre for Climate Modeling and Analysis, Canada | 2.8° 9 × 2.8°, L35 | [44] |
| CMCC-CM | Centro Euro-Mediterraneo per I Cambiamenti Climatici, Italy | 0.75° × 0.75°, L31 | [45] |
| CMCC-CMS | Centro Euro-Mediterraneo per I Cambiamenti Climatici, Italy | 0.75° × 0.75°, L31 | [45] |
| CNRM-CM5 | Centre National de Recherches Météorologiques, France | 1.4° × 1.4°, L31 | [46] |
| CSIRO-Mk3–6-0 | CSIRO-QCCCE, Australia | 1.9° × 1.9°, L18 | [47] |
| GFDL-CM3 | Geophysical Fluid Dynamics Laboratory-Climate Model version 3, USA | 2° × 2.5°, L48 | [48] |
| GFDL-ESM2G | Geophysical Fluid Dynamics Laboratory-Earth System Models version 2G, USA | 2° × 2.5°, L48 | [49] |
| GFDL-ESM2M | Geophysical Fluid Dynamics Laboratory Earth System Models version 2M, USA | 2° × 2.5°, L48 | [50] |
| Inmcm4 | Institute for Numerical Mathematics, Russia | 2° × 1.5°, L21 | [51] |
| IPSL-CM5B-LR | Institut Pierre-Simon Laplace, France | 1.895° × 3.75°, L39 | [52] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fall, P.; Diouf, I.; Deme, A.; Diouf, S.; Sene, D.; Sultan, B.; Famien, A.M.; Janicot, S. Bias-Corrected CMIP5 Projections for Climate Change and Assessments of Impact on Malaria in Senegal under the VECTRI Model. Trop. Med. Infect. Dis. 2023, 8, 310. https://doi.org/10.3390/tropicalmed8060310
Fall P, Diouf I, Deme A, Diouf S, Sene D, Sultan B, Famien AM, Janicot S. Bias-Corrected CMIP5 Projections for Climate Change and Assessments of Impact on Malaria in Senegal under the VECTRI Model. Tropical Medicine and Infectious Disease. 2023; 8(6):310. https://doi.org/10.3390/tropicalmed8060310
Chicago/Turabian StyleFall, Papa, Ibrahima Diouf, Abdoulaye Deme, Semou Diouf, Doudou Sene, Benjamin Sultan, Adjoua Moïse Famien, and Serge Janicot. 2023. "Bias-Corrected CMIP5 Projections for Climate Change and Assessments of Impact on Malaria in Senegal under the VECTRI Model" Tropical Medicine and Infectious Disease 8, no. 6: 310. https://doi.org/10.3390/tropicalmed8060310
APA StyleFall, P., Diouf, I., Deme, A., Diouf, S., Sene, D., Sultan, B., Famien, A. M., & Janicot, S. (2023). Bias-Corrected CMIP5 Projections for Climate Change and Assessments of Impact on Malaria in Senegal under the VECTRI Model. Tropical Medicine and Infectious Disease, 8(6), 310. https://doi.org/10.3390/tropicalmed8060310










