Exploring Emergent Features of Student Interaction within an Embodied Science Learning Simulation
Abstract
1. Introduction
1.1. Embodied Learning Environments
1.2. Embodiment and Multimodal Learning
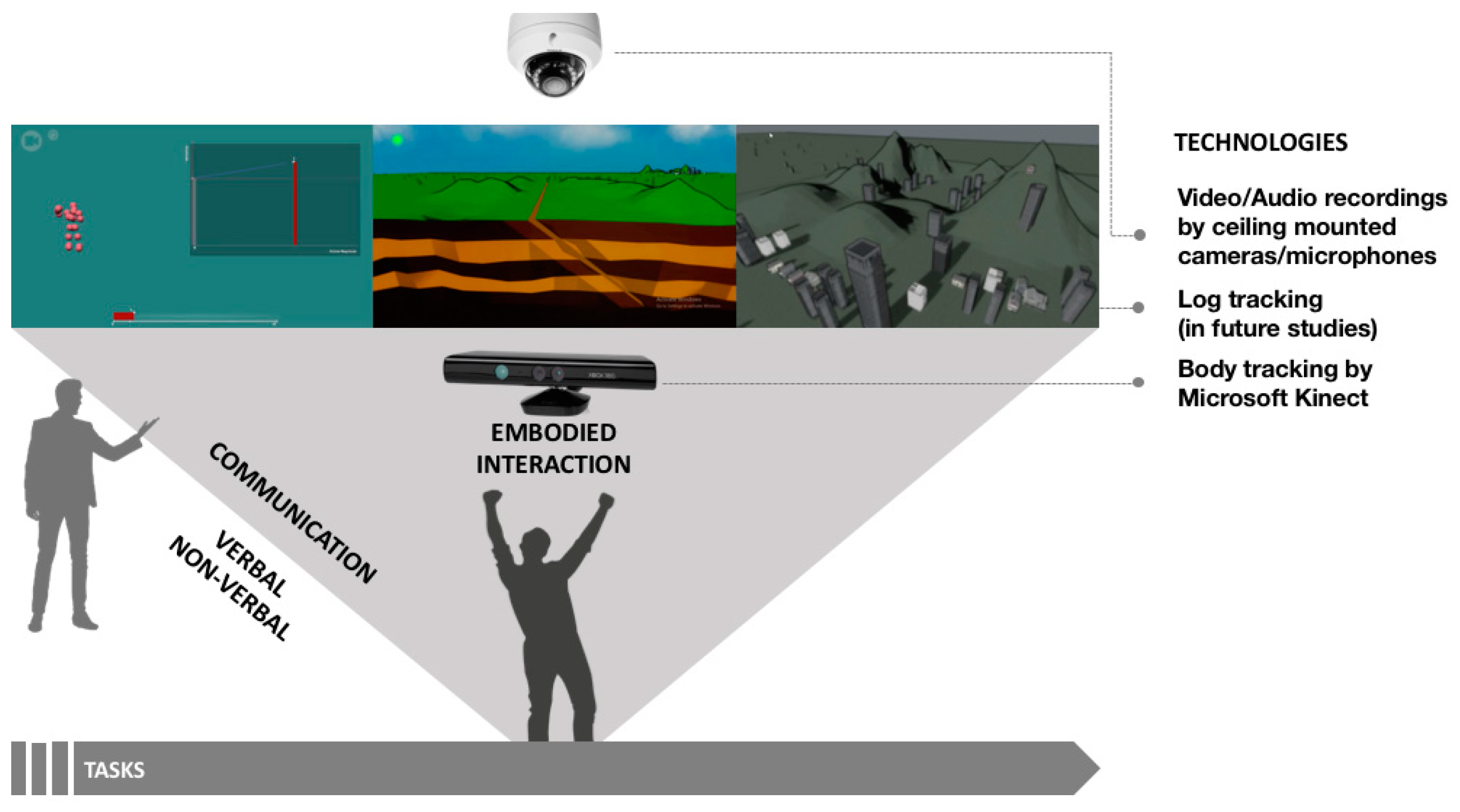
1.3. ELASTIC3S
- What multimodal interaction metrics are available to capture student behavior as they engage with cross-cutting science concepts within an embodied learning simulation?
- How does the multimodal learning environment allow students, or not allow them, to progress in their understanding of non-linear growth?
2. Materials and Methods
2.1. Participants
2.2. Data Sources
2.2.1. Conceptual Measures
2.2.2. Simulation Metrics
2.3. Methods
3. Results
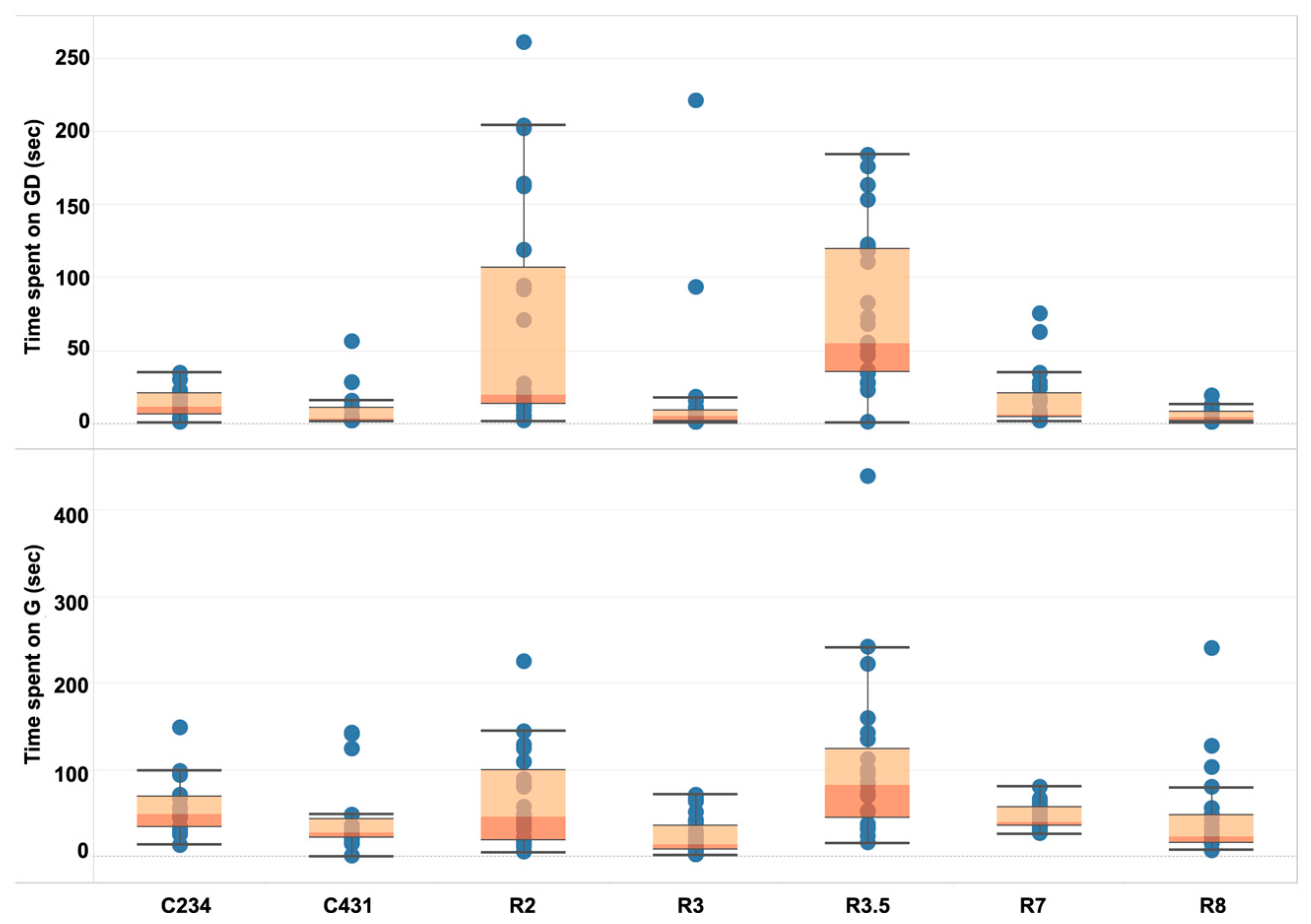
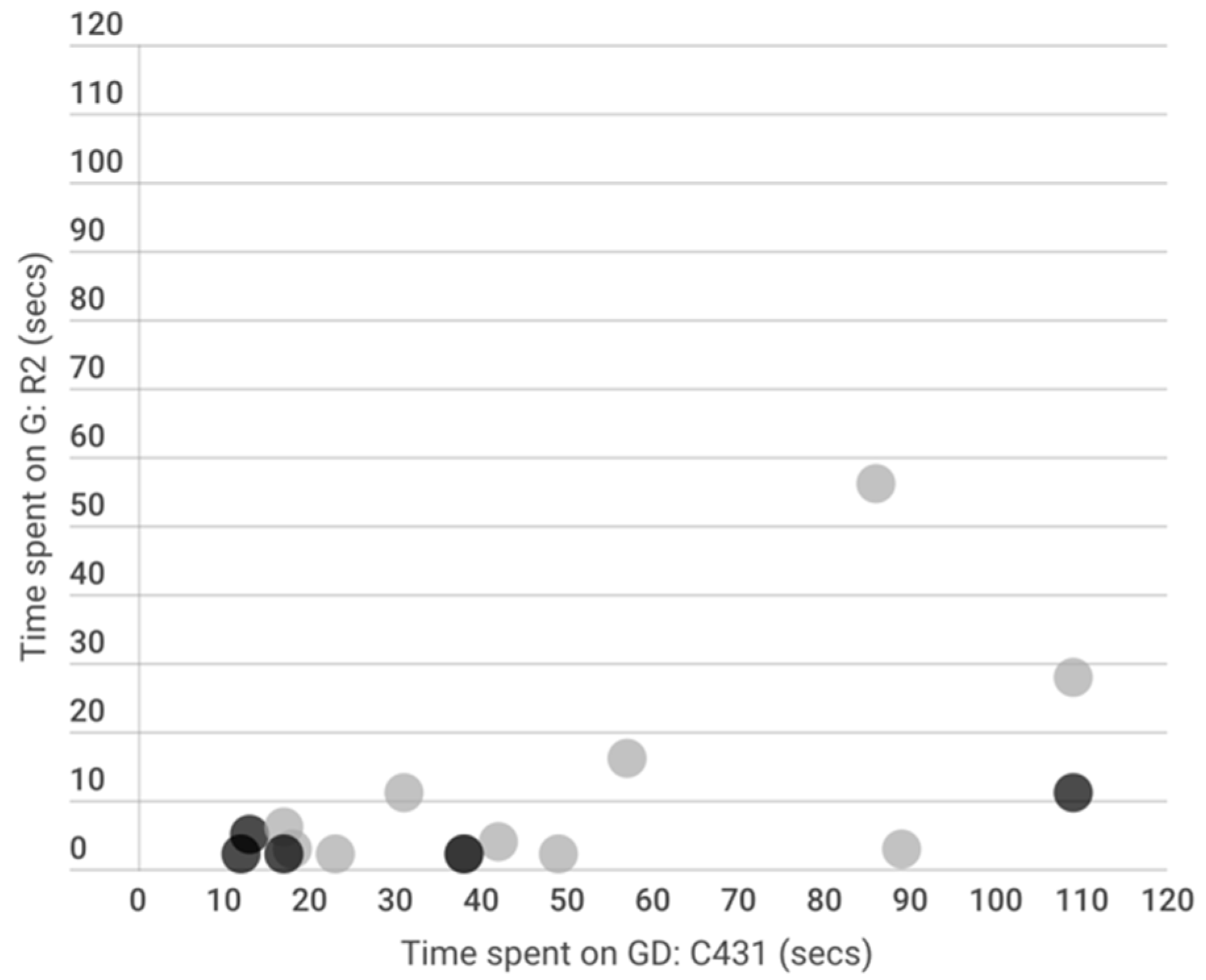
3.1. Relationship between Embodied Interaction Metrics
3.2. Descriptive Cases
3.2.1. Gestural Time Spent
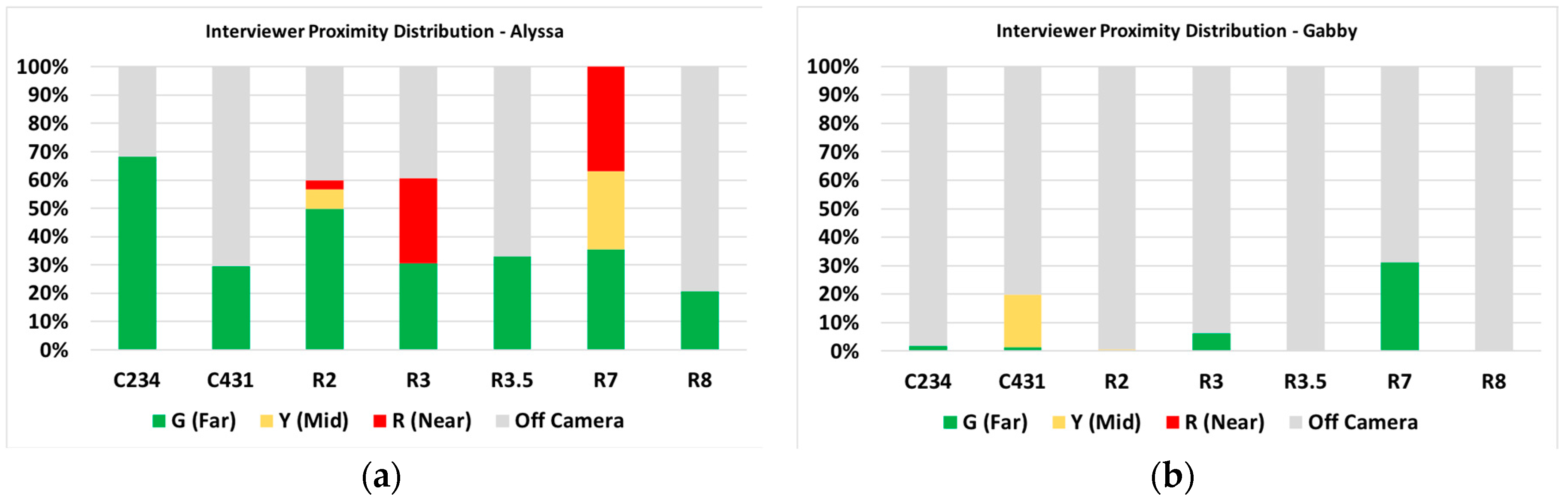
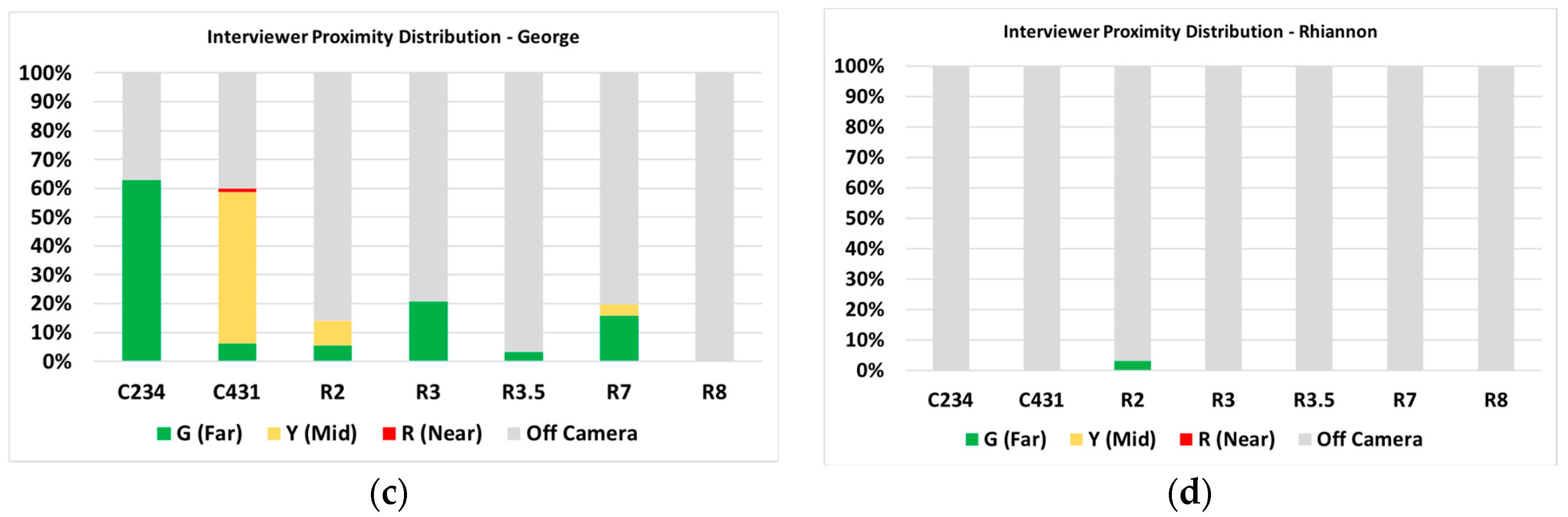
3.2.2. Proximity between a Student and Interviewer
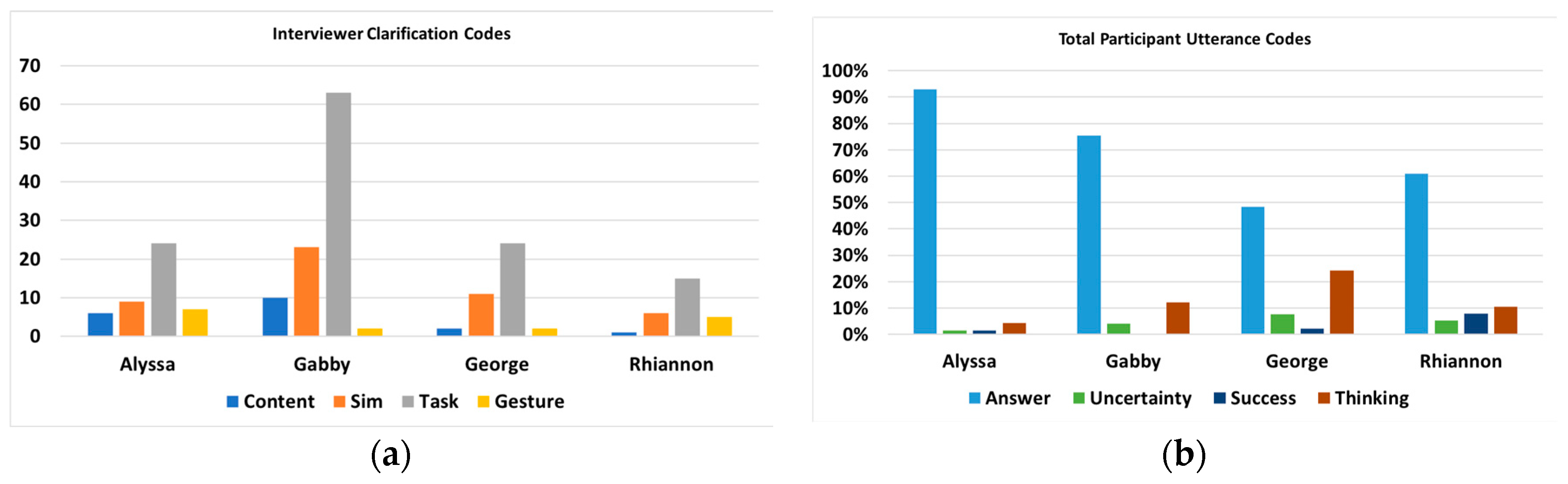
3.2.3. Verbal Discourse
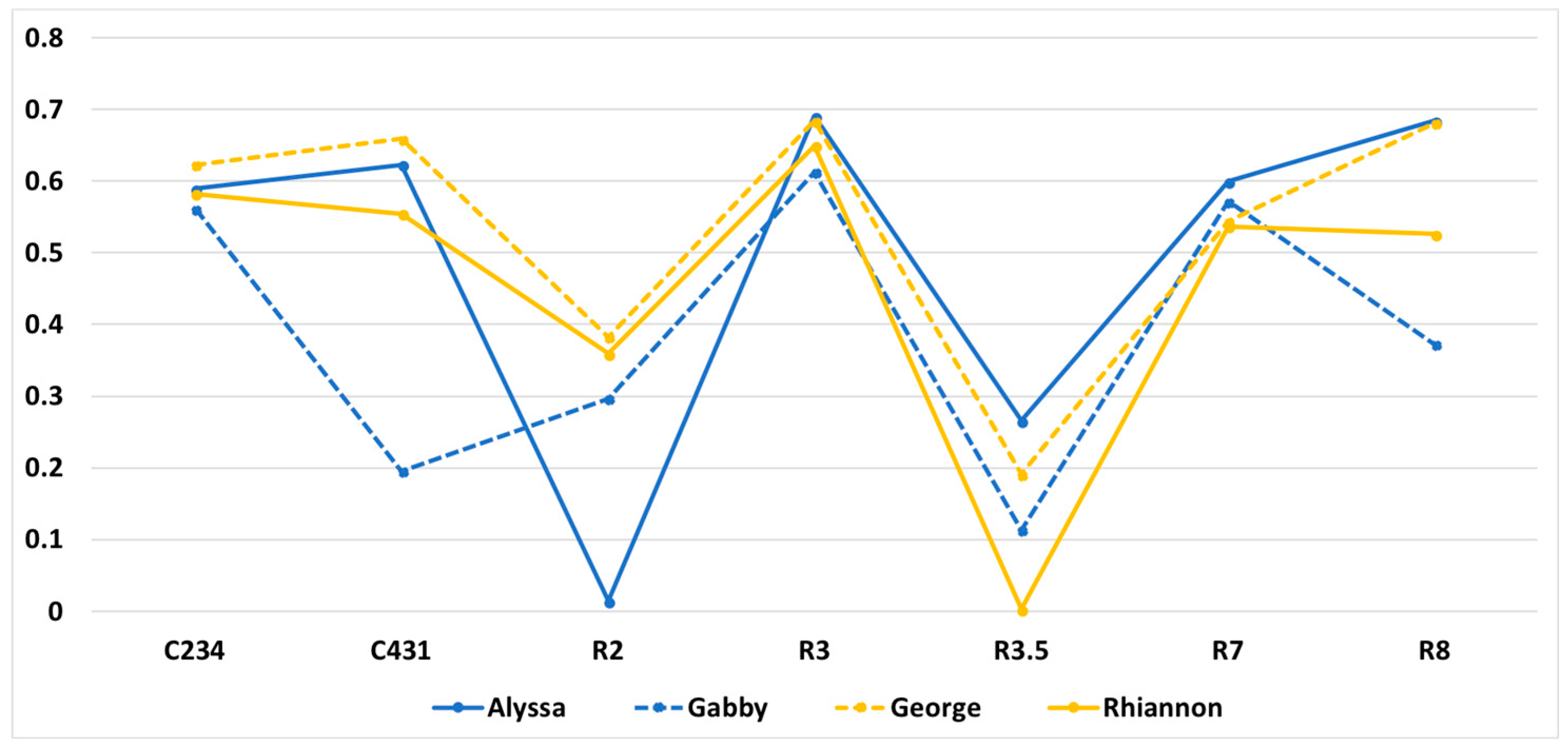
3.2.4. Learning as Multimodal: Alyssa versus Gabby
4. Discussion
4.1. Multimodal Interaction Metrics
4.2. Implications for the Design of Multimodal Learning Environment
5. Study Limitations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- NGSS Lead States. Next Generation Science Standards; The National Academies Press: Washington, DC, USA, 2013. [Google Scholar]
- Abrahamson, D.; Lindrgen, R. Embodiment and embodied design. In the Cambridge Handbook of the Learning Sciences, 2nd ed.; Sawyer, R.K., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 358–376. [Google Scholar]
- Black, J.B.; Segal, A.; Vitale, J.; Fadjo, C.L. Embodied cognition and learning environment design. In Theoretical Foundations of Learning Environments, 2nd ed.; Jonassen, D., Land, S., Eds.; Routledge, Taylor & Francis Group: Florence, SC, USA, 2012; pp. 198–223. [Google Scholar]
- DeSutter, D.; Stieff, M. Teaching students to think spatially through embodied actions: Design principles for learning environments in science, technology, engineering, and mathematics. Cogn. Res. 2017. [Google Scholar] [CrossRef] [PubMed]
- Lindgren, R.; Johnson-Glenberg, M. Emboldened by embodiment six precepts for research on embodied learning and mixed reality. Educ. Res. 2013, 42, 445–452. [Google Scholar] [CrossRef]
- Enyedy, N.; Danish, J.A.; Delacruz, G.; Kumar, M. Learning physics through play in an augmented reality environment. Int. J. Comput. Support. Collab. Learn. 2012, 7, 347–378. [Google Scholar] [CrossRef]
- Johnson-Glenberg, M.C.; Birchfield, D.A.; Tolentino, L.; Koziupa, T. Collaborative embodied learning in mixed reality motion-capture environments: Two science studies. J. Educ. Psychol. 2014, 106, 86–104. [Google Scholar] [CrossRef]
- Lindgren, R.; Tscholl, M.; Wang, S.; Johnson, E. Enhancing learning and engagement through embodied interaction within a mixed reality simulation. Comput. Educ. 2016, 95, 174–187. [Google Scholar] [CrossRef]
- Blikstein, P.; Worsley, M.A.B. Multimodal learning analytics and education data mining: Using computational technologies to measure complex learning tasks. J. Learn. Anal. 2016, 3, 220–238. [Google Scholar] [CrossRef]
- Smith, C.; King, B.; Gonzalez, D. Using Multimodal Learning Analytics to Identify Patterns of Interactions in a Body-Based Mathematics Activity. J. Interact. Learn. Res. 2016, 27, 355–379. [Google Scholar]
- Ainsworth, S.; Prain, V.; Tytler, R. Drawing to Learn in Science. Science 2011, 333, 1096–1097. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim-Didi, K.; Hackling, M.W.; Ramseger, J.; Sherriff, B. Embodied Strategies in the Teaching and Learning of Science. In Quality Teaching in Primary Science Education; Springer: Cham, Switzerland, 2017; pp. 181–221. ISBN 978-3-319-44381-2. [Google Scholar]
- Barsalou, L.W. Perceptions of perceptual symbols. Behav. Brain Sci. 1999, 22, 637–660. [Google Scholar] [CrossRef]
- Johnson, M. The Body in the Mind: The Bodily Basis of Meaning, Imagination, and Reason; University of Chicago Press: Chicago, IL, USA, 1987. [Google Scholar]
- Barsalou, L.W. Grounded Cognition: Past, Present, and Future. Top. Cogn. Sci. 2010, 2, 716–724. [Google Scholar] [CrossRef] [PubMed]
- Glenberg, A.M. Embodiment as a unifying perspective for psychology. Wiley Interdiscip. Rev. Cogn. Sci. 2010, 1, 586–596. [Google Scholar] [CrossRef] [PubMed]
- Wilson, M. Six views of embodied cognition. Psychon. Bull. Rev. 2002, 9, 625–636. [Google Scholar] [CrossRef] [PubMed]
- Tomasino, B.; Nobile, M.; Re, M.; Bellina, M.; Garzitto, M.; Arrigoni, F.; Molteni, M.; Fabbro, F.; Brambilla, P. The mental simulation of state/psychological verbs in the adolescent brain: An fMRI study. Brain Cogn. 2018, 123, 34–46. [Google Scholar] [CrossRef] [PubMed]
- Milgram, P.; Kishino, F.A. Taxonomy of Mixed Reality Visual Displays. IEICE Trans. Inf. Syst. 1994, 77, 1321–1329. [Google Scholar]
- Alibali, M.W.; Nathan, M.J. Embodiment in Mathematics Teaching and Learning: Evidence From Learners’ and Teachers’ Gestures. J. Learn. Sci. 2012, 21, 247–286. [Google Scholar] [CrossRef]
- Goldin-Meadow, S.; Cook, S.W.; Mitchell, Z.A. Gesturing gives children new ideas about math. Psychol. Sci. 2009, 20, 267–272. [Google Scholar] [CrossRef] [PubMed]
- Roth, W.M. Gestures: Their role in teaching and learning. Rev. Educ. Res. 2001, 71, 365–392. [Google Scholar] [CrossRef]
- Crowder, E.M. Gestures at work in sense-making science talk. J. Learn. Sci. 1996, 5, 173–208. [Google Scholar] [CrossRef]
- Niebert, K.; Gropengießer, H. Understanding the greenhouse effect by embodiment—Analysing and using students’ and scientists’ conceptual resources. Int. J. Sci. Educ. 2014, 36, 277–303. [Google Scholar] [CrossRef]
- Birchfield, D.; Thornburg, H.; Megowan-Romanowicz, M.C.; Hatton, S.; Mechtley, B.; Dolgov, I.; Burleson, W. Embodiment, multimodality, and composition: Convergent themes across HCI and education for mixed-reality learning environments. Adv. Hum. Comput. Interact. 2008. [Google Scholar] [CrossRef]
- Gellevij, M.; Van Der Meij, H.; De Jong, T.; Pieters, J. Multimodal versus Unimodal Instruction in a Complex Learning Context. J. Exp. Educ. 2002, 70, 215–239. [Google Scholar] [CrossRef]
- Flood, V.J.; Amar, F.G.; Nemirovsky, R.; Harrer, B.W.; Bruce, M.R.; Wittmann, M.C. Paying attention to gesture when students talk chemistry: Interactional resources for responsive teaching. J. Chem. Educ. 2014, 92, 11–22. [Google Scholar] [CrossRef]
- Sankey, M.; Birch, D.; Gardiner, M. Engaging students through multimodal learning environments: The journey continues. In Proceedings of the ASCILITE 2010: 27th Annual Conference of the Australasian Society for Computers in Learning in Tertiary Education: Curriculum, Technology and Transformation for an Unknown Future, Sydney, Australia, 5–8 December 2010; University of Queensland: Brisbane, Australia, 2010; pp. 852–863. [Google Scholar]
- Prain, V.; Waldrip, B. An Exploratory Study of Teachers’ and Students’ Use of Multi-modal Representations of Concepts in Primary Science. Int. J. Sci. Educ. 2006, 28, 1843–1866. [Google Scholar] [CrossRef]
- Frymier, A. A model of immediacy in the classroom. Commun. Q. 1994, 42, 133–144. [Google Scholar] [CrossRef]
- Richmond, V.; Gorham, J.; McCroskey, V. The Relationship between Selected Immediacy Behaviors and Cognitive Learning. In Communication Yearbook 10; McLaughlin, M., Ed.; Sage: Newbury Park, CA, USA, 1987; pp. 574–590. [Google Scholar]
- Andersen, J. Teacher immediacy as a predictor of teacher effectiveness. In Communication Yearbook 3; Nimmo, D., Ed.; Transaction Books: New Brunswick, NJ, USA, 1979; pp. 543–559. [Google Scholar]
- Pogue, L.L.; Ahyun, K. The effect of teacher nonverbal immediacy and credibility on student motivation and affective learning. Commun. Educ. 2006, 55, 331–344. [Google Scholar] [CrossRef]
- Seifert, T. Understanding student motivation. Educ. Res. 2004, 46, 137–149. [Google Scholar] [CrossRef]
- Witt, P.L.; Wheeless, L.R.; Allen, M. A meta-analytical review of the relationship between teacher immediacy and student learning. Commun. Monogr. 2004, 71, 184–207. [Google Scholar] [CrossRef]
- Márquez, C.; Izquierdo, M.; Espinet, M. Multimodal science teachers’ discourse in modeling the water cycle. Sci. Educ. 2006, 90, 202–226. [Google Scholar] [CrossRef]
- Ainsworth, S.; Th Loizou, A. The effects of self-explaining when learning with text or diagrams. Cogn. Sci. 2003, 27, 669–681. [Google Scholar] [CrossRef]
- Ainsworth, S.; Iacovides, I. Learning by constructing self-explanation diagrams. In Proceedings of the 11th Biennial Conference of European Association for Research on Learning and Instruction, Nicosia, Cyprus, 23–27 August 2005. [Google Scholar]
- Cooper, M.M.; Williams, L.C.; Underwood, S.M. Student understanding of intermolecular forces: A multimodal study. J. Chem. Educ. 2015, 92, 1288–1298. [Google Scholar] [CrossRef]
- Won, M.; Yoon, H.; Treagust, D.F. Students’ learning strategies with multiple representations: Explanations of the human breathing mechanism. Sci. Educ. 2014, 98, 840–866. [Google Scholar] [CrossRef]
- Morphew, J.W.; Lindgren, R.; Alameh, S. Embodied ideas of scale: Learning and engagement with a whole-body science simulation. In Proceedings of the Annual Meeting American Educational Research Association, New York, NY, USA, 13–17 April 2018. [Google Scholar]
- Junokas, M.J.; Lindgren, R.; Kang, J.; Morphew, J.W. Enhancing multimodal learning through personalized gesture recognition. J. Comp. Asst. Learn. 2018. [Google Scholar] [CrossRef]
- Alameh, S.; Morphew, J.W.; Mathayas, N.; Lindgren, R. Exploring the relationship between gesture and student reasoning regarding linear and exponential growth. In Proceedings of the International Conference of the Learning Sciences, Singapore, 20–24 June 2016; pp. 1006–1009. [Google Scholar]
- Creswell, J.W. Research Design: Qualitative, Quantitative, and Mixed Methods Approaches; Sage: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Yin, R.K. Case Study Research: Design and Methods, 3rd ed.; Sage: Thousand Oaks, CA, USA, 2003. [Google Scholar]
- Oltmann, S. Qualitative interviews: A methodological discussion of the interviewer and respondent contexts. Qual. Soc. Res. 2016, 17. [Google Scholar] [CrossRef]
- Datavyu Team. Datavyu: A Video Coding Tool; Databrary Project; New York University: New York, NY, USA, 2014. [Google Scholar]
- Cowan, J. The potential of cognitive think-aloud protocols for educational action-research. Act. Learn. High. Educ. 2017. [Google Scholar] [CrossRef]
- Marco-Ruiz, L.; Bønes, E.; de la Asunción, E.; Gabarron, E.; Aviles-Solis, J.C.; Lee, E.; Traver, V.; Sato, K.; Bellika, J.G. Combining multivariate statistics and the think-aloud protocol to assess Human-Computer Interaction barriers in symptom checkers. J. Biomed. Inform. 2017, 74, 104–122. [Google Scholar] [CrossRef] [PubMed]
- Vandevelde, S.; Van Keer, H.; Schellings, G.; Van Hout-Wolters, B. Using think-aloud protocol analysis to gain in-depth insights into upper primary school children’s self-regulated learning. Learn. Individ. Differ. 2015, 43, 11–30. [Google Scholar] [CrossRef]
- Worsley, M.; Blikstein, P. Leveraging Multimodal Learning Analytics to Differentiate Student Learning Strategies. In Proceedings of the Fifth International Conference on Learning Analytics and Knowledge (LAK ’15), Poughkeepsie, NY, USA, 16–20 March 2015; ACM: New York, NY, USA, 2015; pp. 360–367. [Google Scholar]

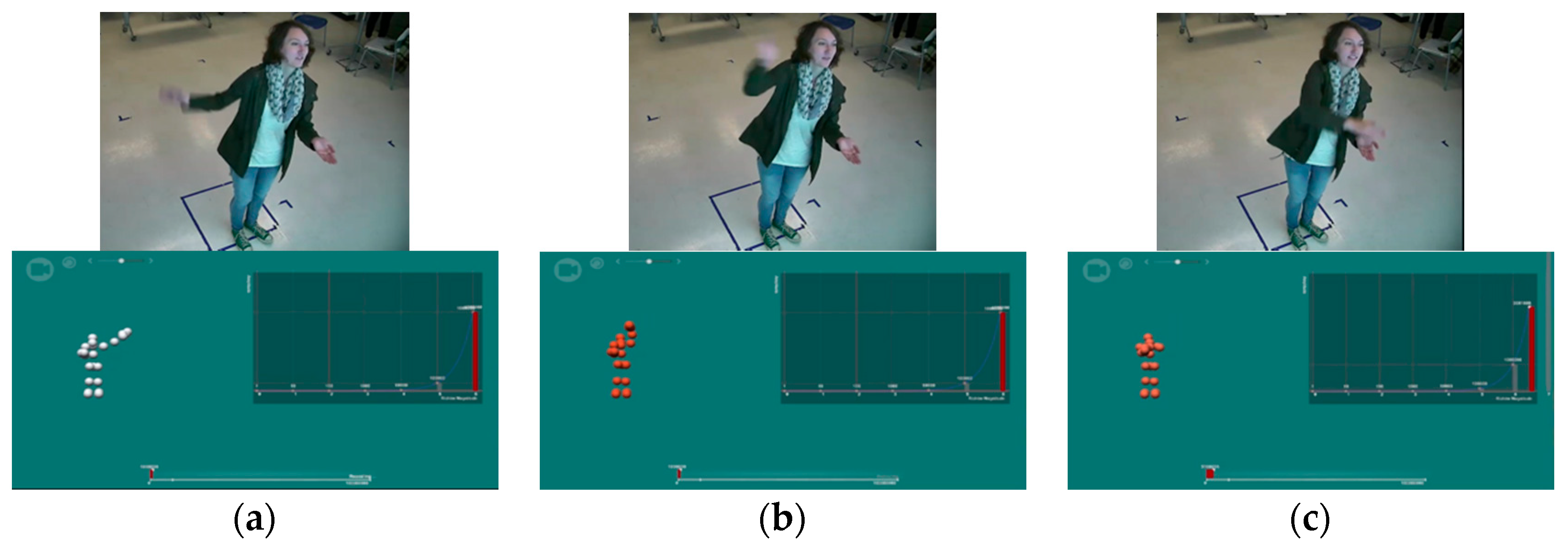


| Code | Definition | Sample Dialog | |
|---|---|---|---|
| Interviewer | Queries | Questions from interviewer (types: content, simulation, gesture, task) | “Now we want to make 300 cubes. How do you think that we can make 300 with the least number of gestures?” “Describe the damage caused by this earthquake.” |
| Clarifications | Supporting statements from the interviewer to the students during tasks (types: content, simulation, gesture, task) | “So, what are you trying to do?” “Do you want to try to get to that and we can see?” “Think about what you would start with...” | |
| Student | Queries | Questions from student (types: content, simulation, gesture, task) | “I should’ve added three, right?” |
| Utterances | Responses or other verbalizations from the student (types: answer, uncertainty, thinking aloud, success) | “Oh, wait, wait...never mind, I know what I am going to do.” “I think that’s where it will damage it.” “Which graph? Looks like J?” |
| C234 | C431 | R2 | R3.5 | R7 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GD | G | GD | G | GD | G | GD | G | GD | G | ||
| C234 | GD | 1 | |||||||||
| G | 0.155 | 1 | |||||||||
| C431 | GD | −0.192 | −0.123 | 1 | |||||||
| G | −0.462 | −0.028 | 0.692 ** | 1 | |||||||
| R2 | GD | 0.140 | 0.093 | −0.040 | −0.333 | 1 | |||||
| G | 0.161 | 0.793 ** | 0.567 * | 0.077 | 0.143 | 1 | |||||
| R3.5 | GD | 0.227 | 0.443 | −0.248 | −0.198 | 0.300 | 0.306 | 1 | |||
| G | −0.190 | 0.315 | 0.063 | 0.251 | −0.011 | 0.267 | −0.041 | 1 | |||
| R7 | GD | −0.128 | 0.087 | −0.269 | 0.286 | −0.083 | 0.066 | 0.006 | −0.134 | 1 | |
| G | 0.047 | 0.340 | −0.115 | −0.082 | 0.146 | 0.340 | 0.504 * | 0.238 | 0.174 | 1 | |
| Interviewer | Gabby |
|---|---|
| Think about what you would start with... | Uh... |
| I can help you | Um... |
| Ok, so you’ve got four. | |
| So, what are you adding to get to? | [mumbling]...400, and then...31 [mumbling then begins using add gesture] 31 |
| Can you think of a way that might be quicker? | Yeah... there is probably a faster way. |
| I can give you a hint... What’s a quick way you can get to 403? Here, we can do it together. | Um... |
| Step one, I’d say make four cubes, right? | Yeah [gestures to add four] |
| Now, the next number we need is three... Right? | Multiply by 10 then add [gestures times 10] |
| So, what do we have to do to get to 43 now? | [gestures to add three] |
| And then... now we need to get to 431. So, what can we do to get to 430? | Multiply by 10? |
| Ok, yeah... Give that a shot. | [gestures times 10] And then one... [gestures to add one] |
| How are you doing? | Good |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.; Lindgren, R.; Planey, J. Exploring Emergent Features of Student Interaction within an Embodied Science Learning Simulation. Multimodal Technol. Interact. 2018, 2, 39. https://doi.org/10.3390/mti2030039
Kang J, Lindgren R, Planey J. Exploring Emergent Features of Student Interaction within an Embodied Science Learning Simulation. Multimodal Technologies and Interaction. 2018; 2(3):39. https://doi.org/10.3390/mti2030039
Chicago/Turabian StyleKang, Jina, Robb Lindgren, and James Planey. 2018. "Exploring Emergent Features of Student Interaction within an Embodied Science Learning Simulation" Multimodal Technologies and Interaction 2, no. 3: 39. https://doi.org/10.3390/mti2030039
APA StyleKang, J., Lindgren, R., & Planey, J. (2018). Exploring Emergent Features of Student Interaction within an Embodied Science Learning Simulation. Multimodal Technologies and Interaction, 2(3), 39. https://doi.org/10.3390/mti2030039




