An Empirical Evaluation of the Critical Population Size for “Knowledge Spillover” Cities in China: The Significance of 10 Million
Abstract
1. Introduction
2. Literature Review
3. Data & Methods
3.1. Data Sources and Preprocessing
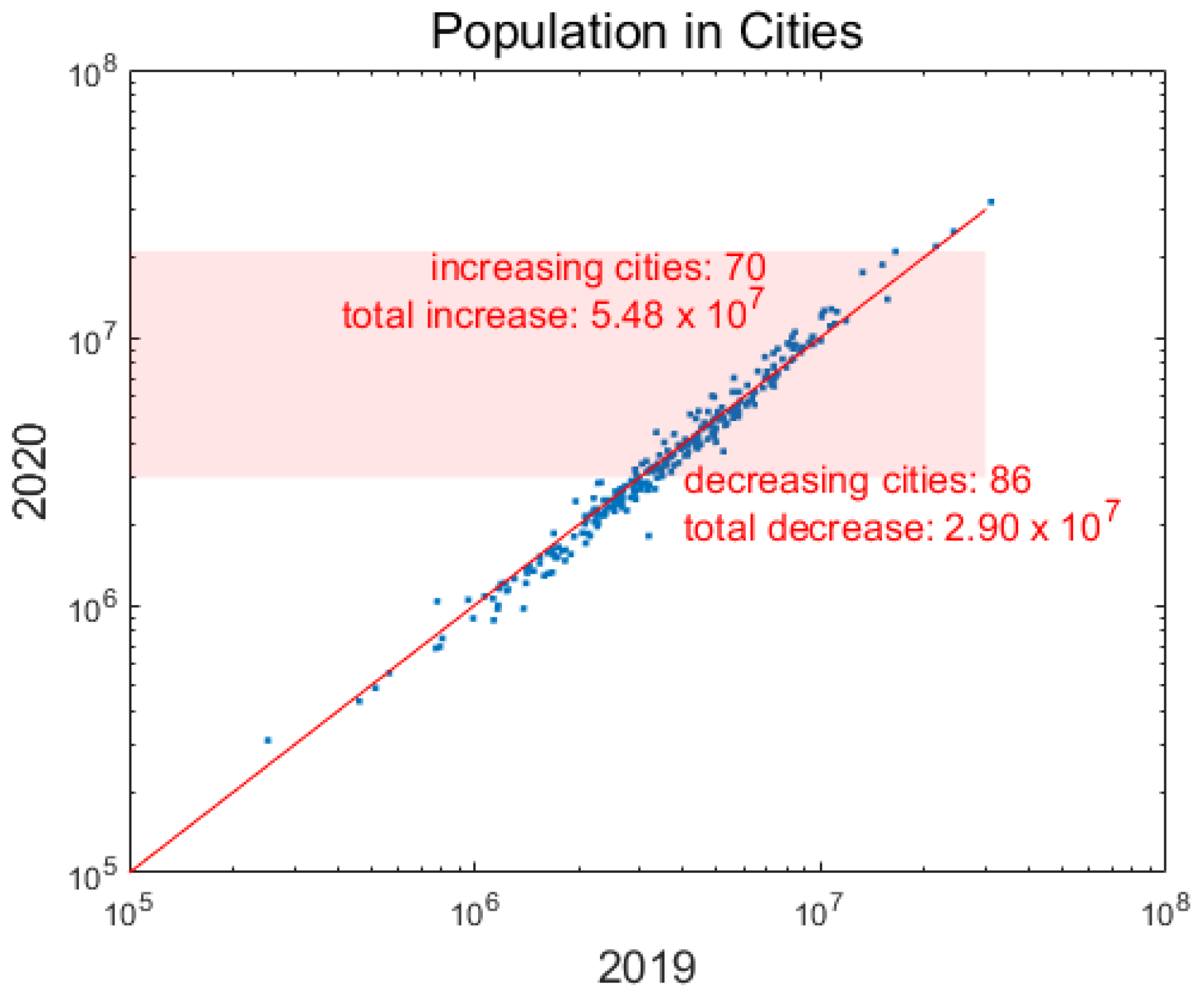
3.1.1. Resident Population Data for Cities from 2004 to 2019
3.1.2. 280 Cities and 19 Industries
3.2. Investigate How the Comparative Advantage Evolves with Population Size
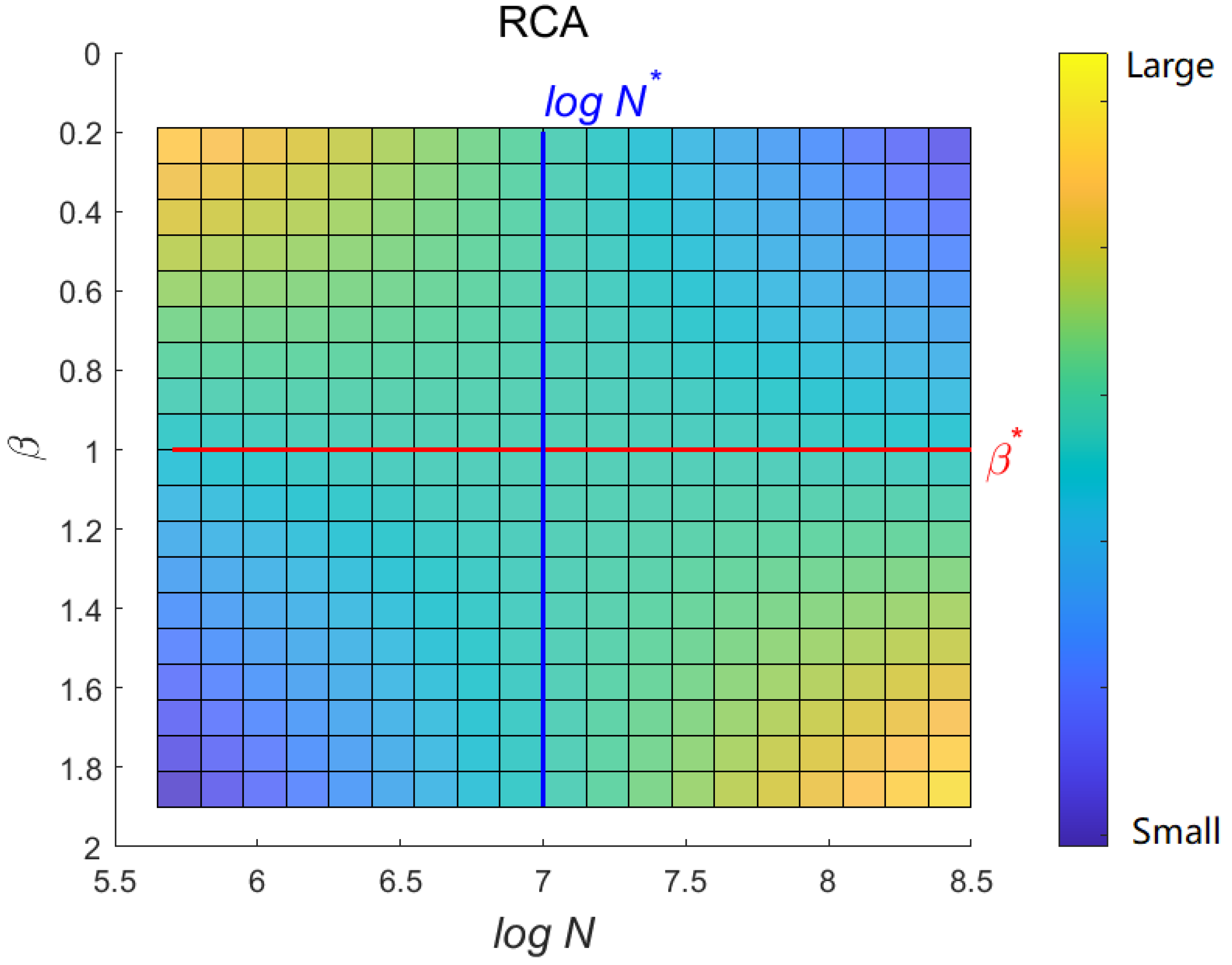
3.3. The Comparative Advantage of Industries and Its Critical Point Analysis
4. Results
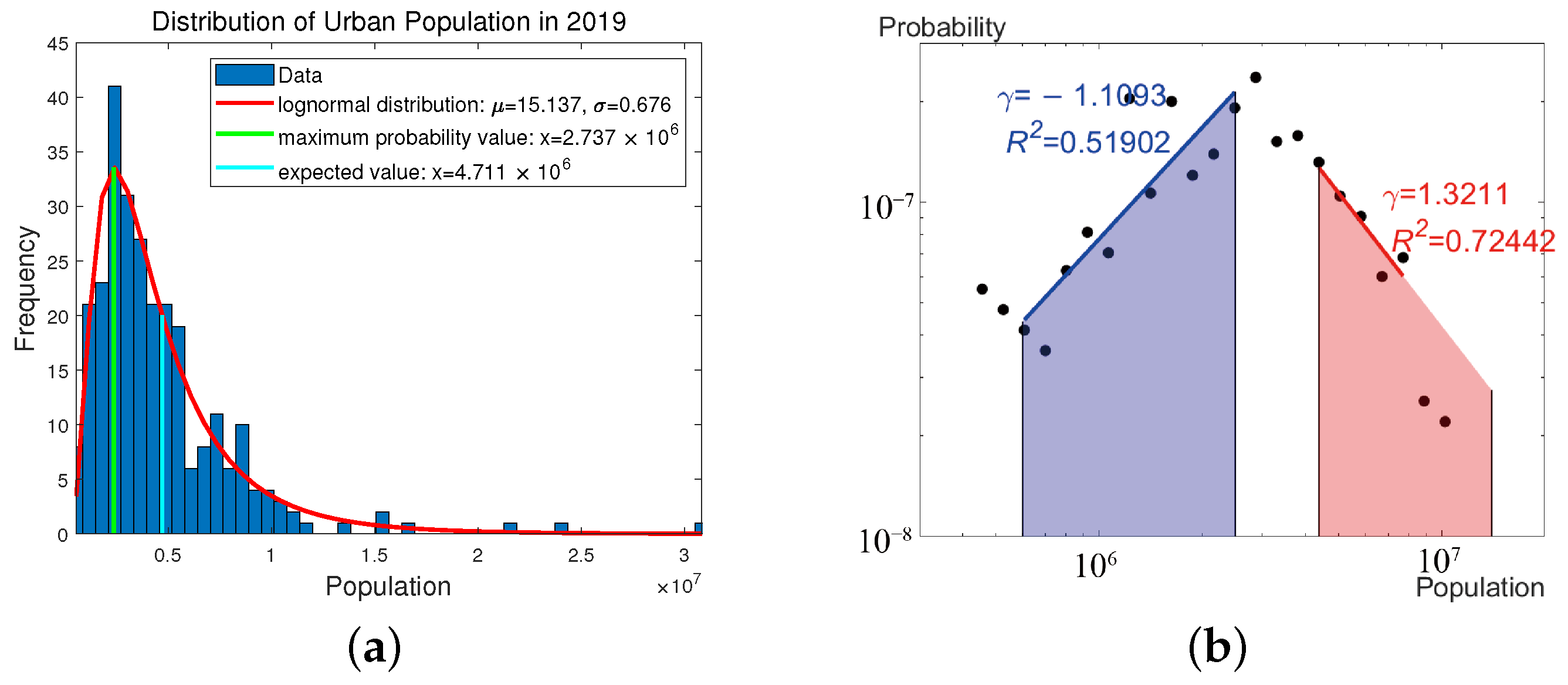
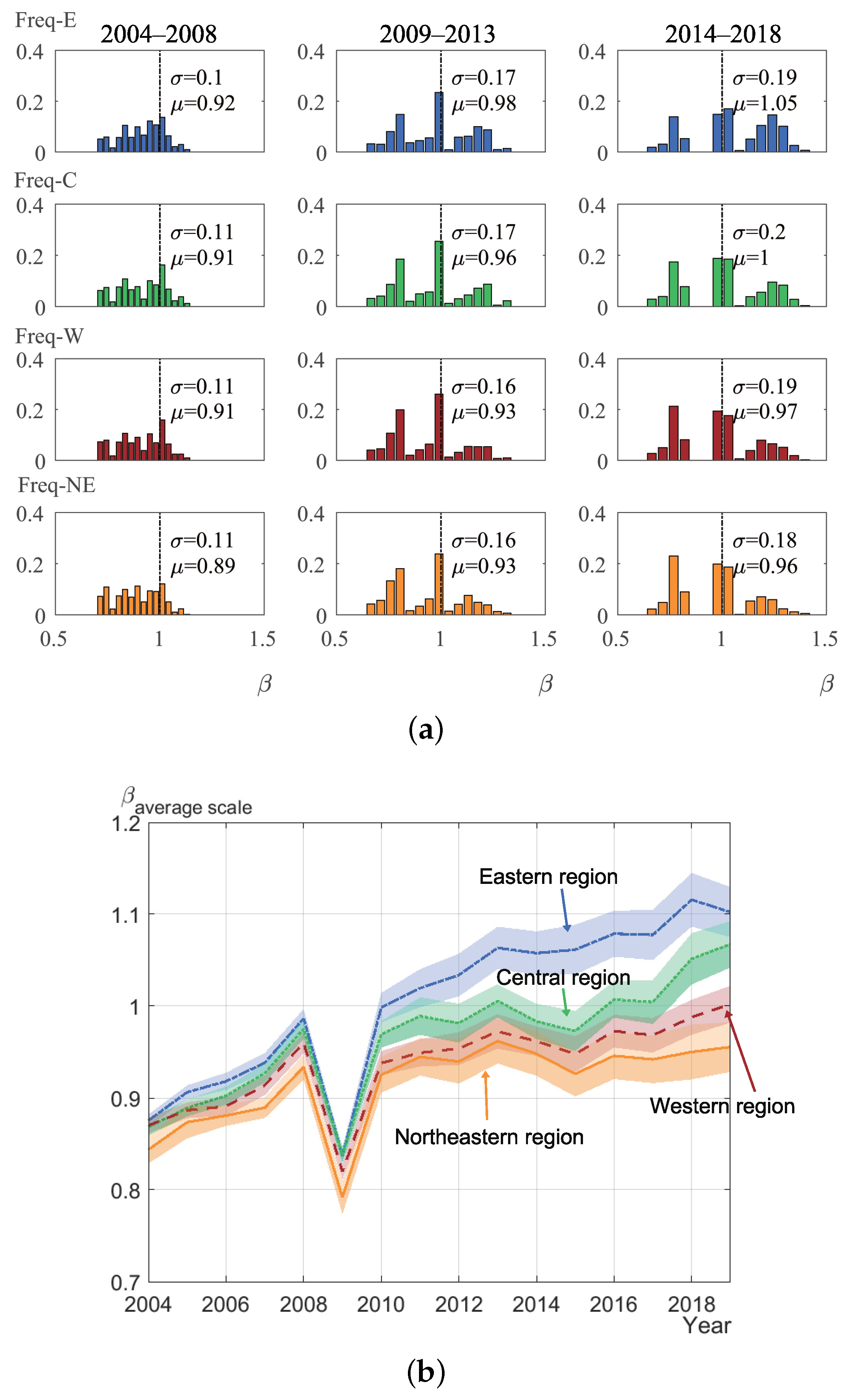
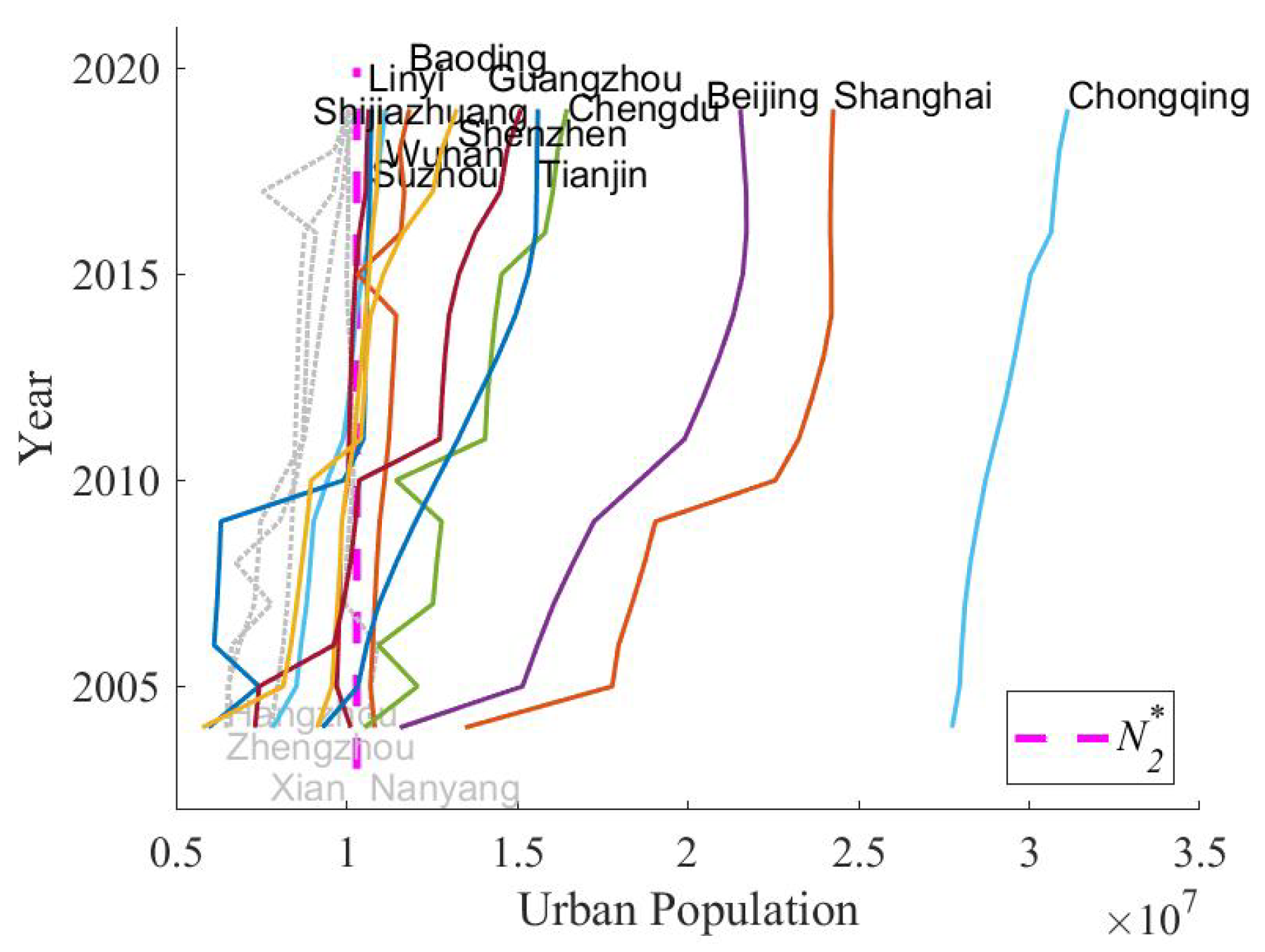
4.1. Distribution and Evolution of Scale Characteristics
4.1.1. Evolution of Scale Characteristics
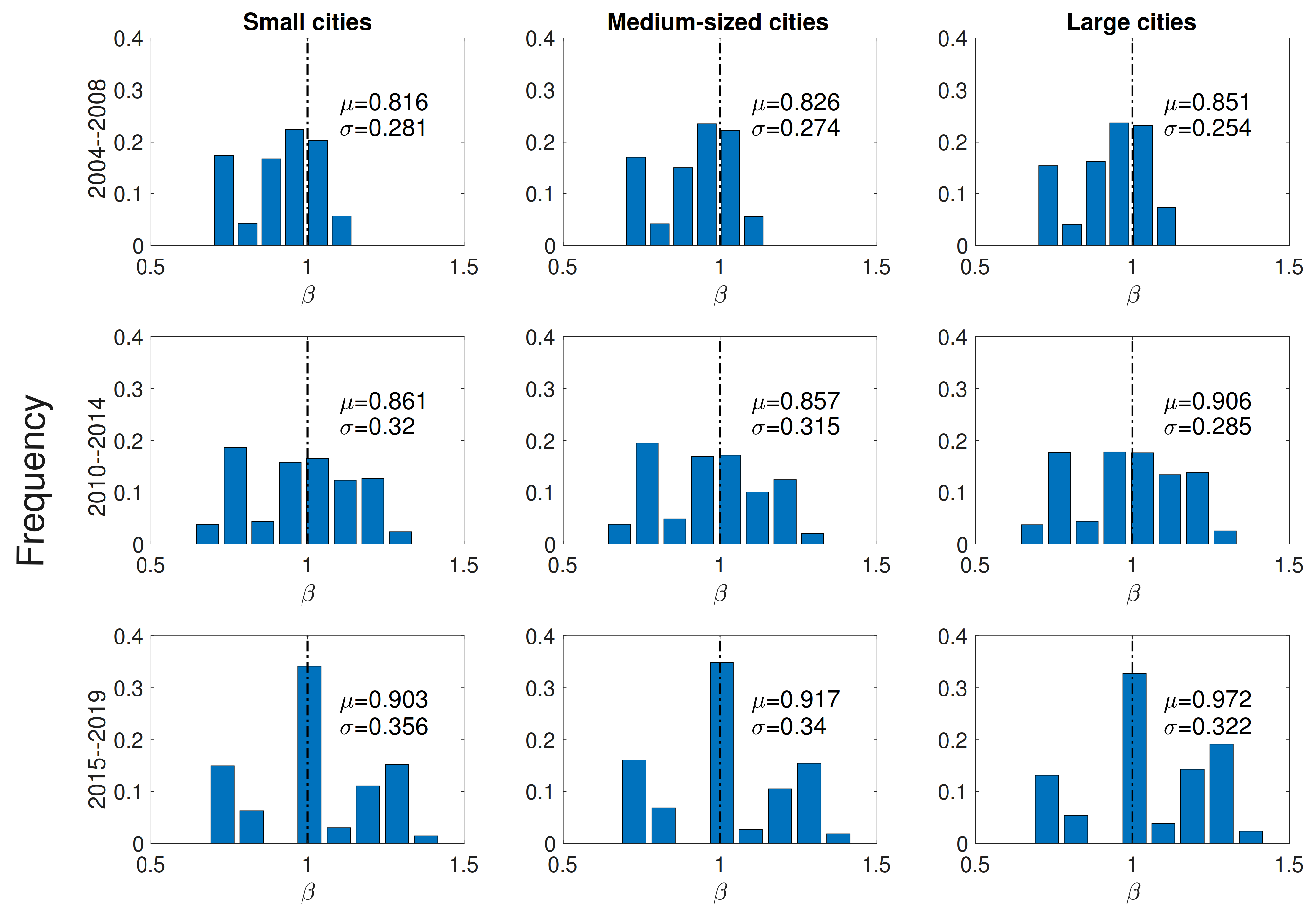
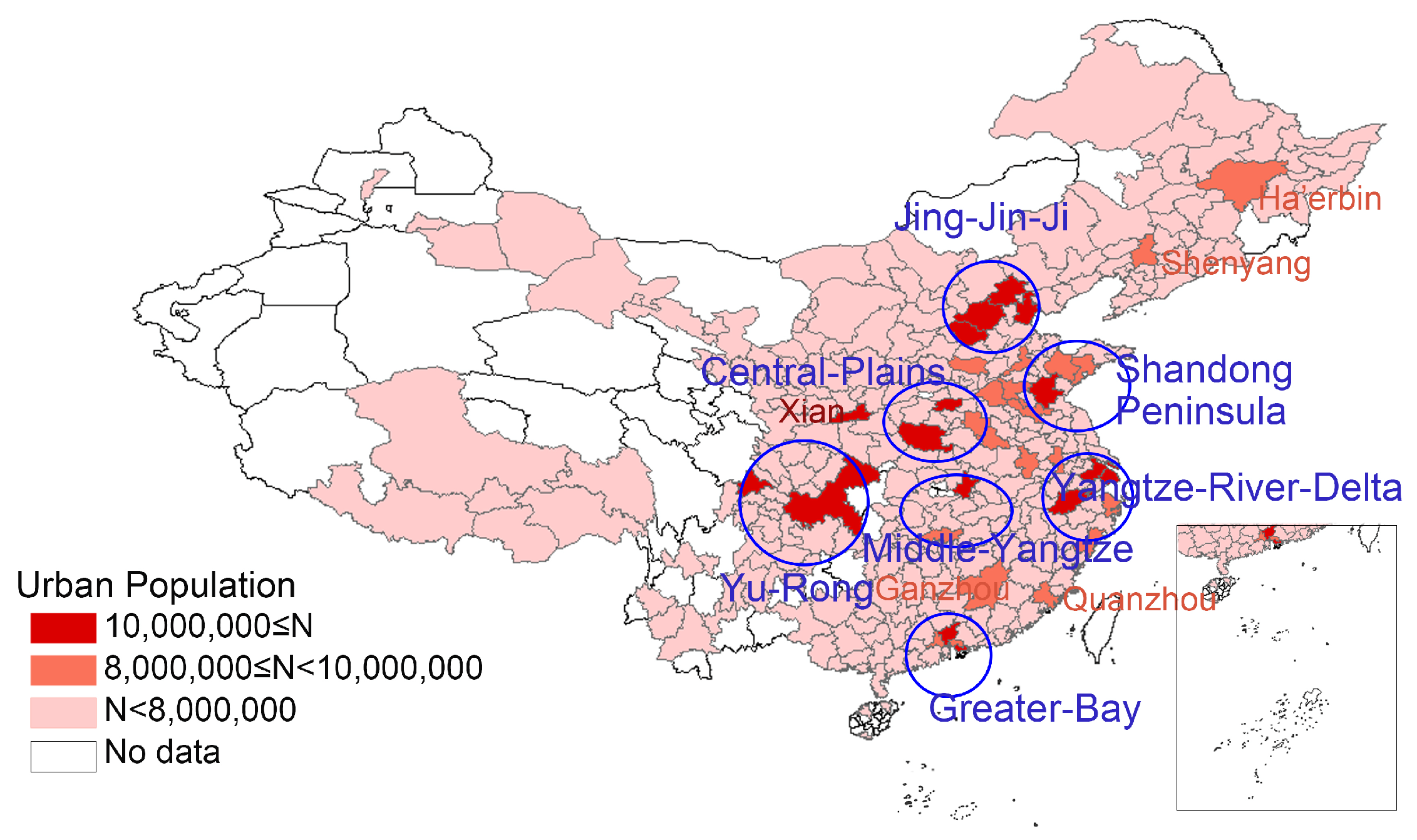
4.1.2. Distribution of Scale Characteristics in Different Cities
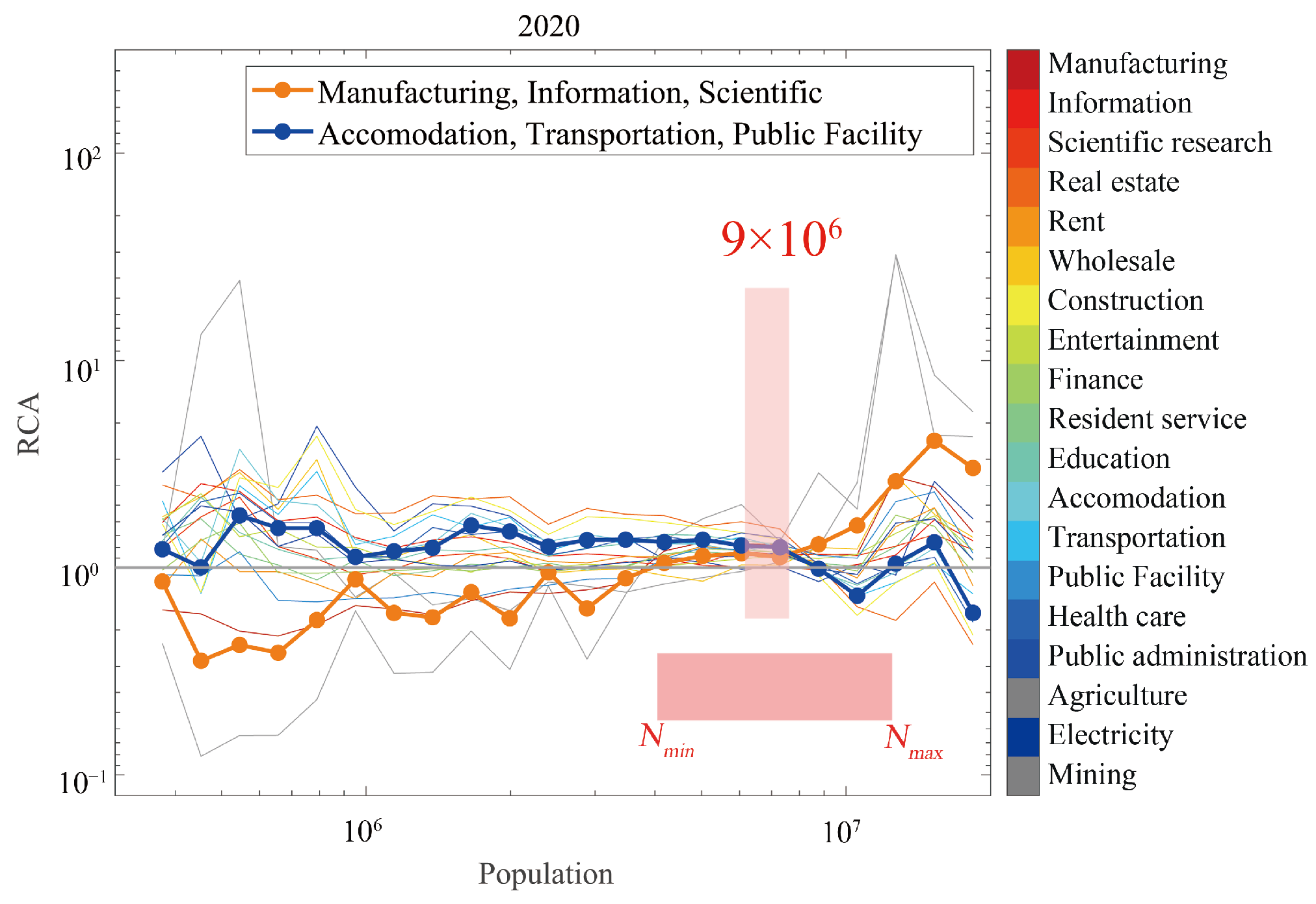
4.2. Labour Demand of “Knowledge Spillover” Development
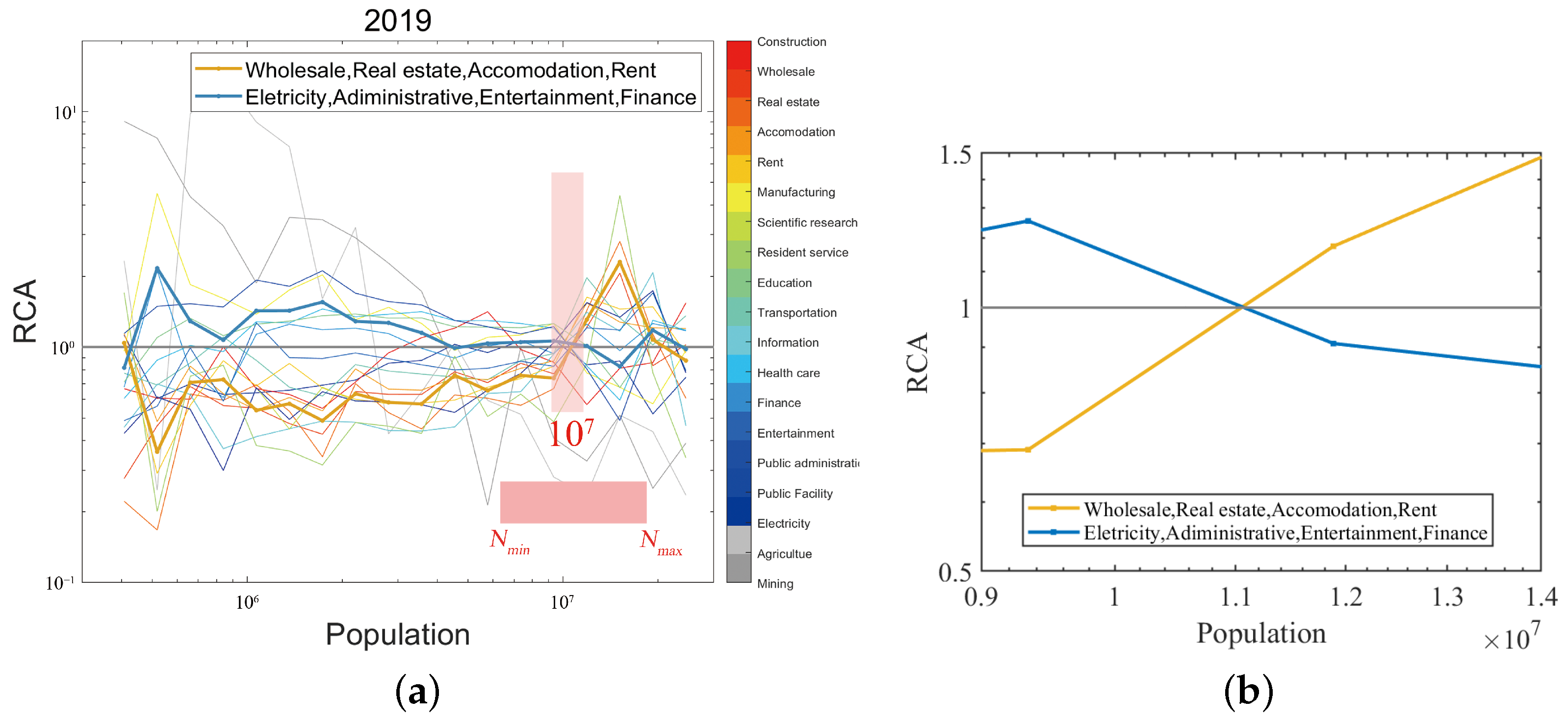
4.2.1. Evolution of Knowledge Spillover Industries
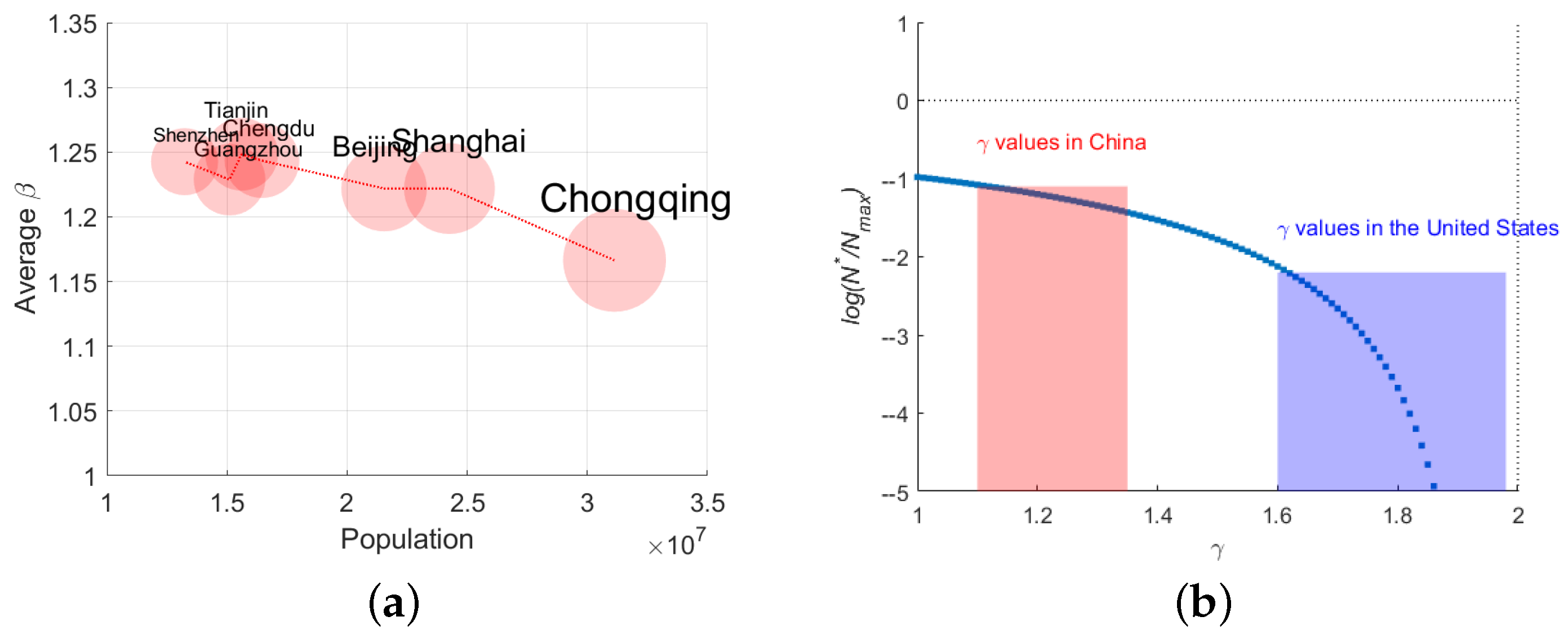
4.2.2. Comparison with the Optimal City Size Model
4.2.3. Limitations of Urban Innovation in China
4.2.4. Influence of Population Distribution Characteristics
5. Conclusions and Suggestions
5.1. The Comparative Advantage of “Knowledge Spillover” Industries Requires a Critical Urban Population Size
5.2. The Critical Population Size of 10 Million for China
5.3. Future Prospects for China
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources and Statistical Analyses
Appendix A.1. Cities and Industries
Appendix A.1.1. Cities in China
Appendix A.1.2. Municipalities and Prefecture-Level Cities
Appendix A.1.3. 19 Industries
Appendix A.2. Data Sources
Appendix A.2.1. Explanation of the Time Interval of the Data
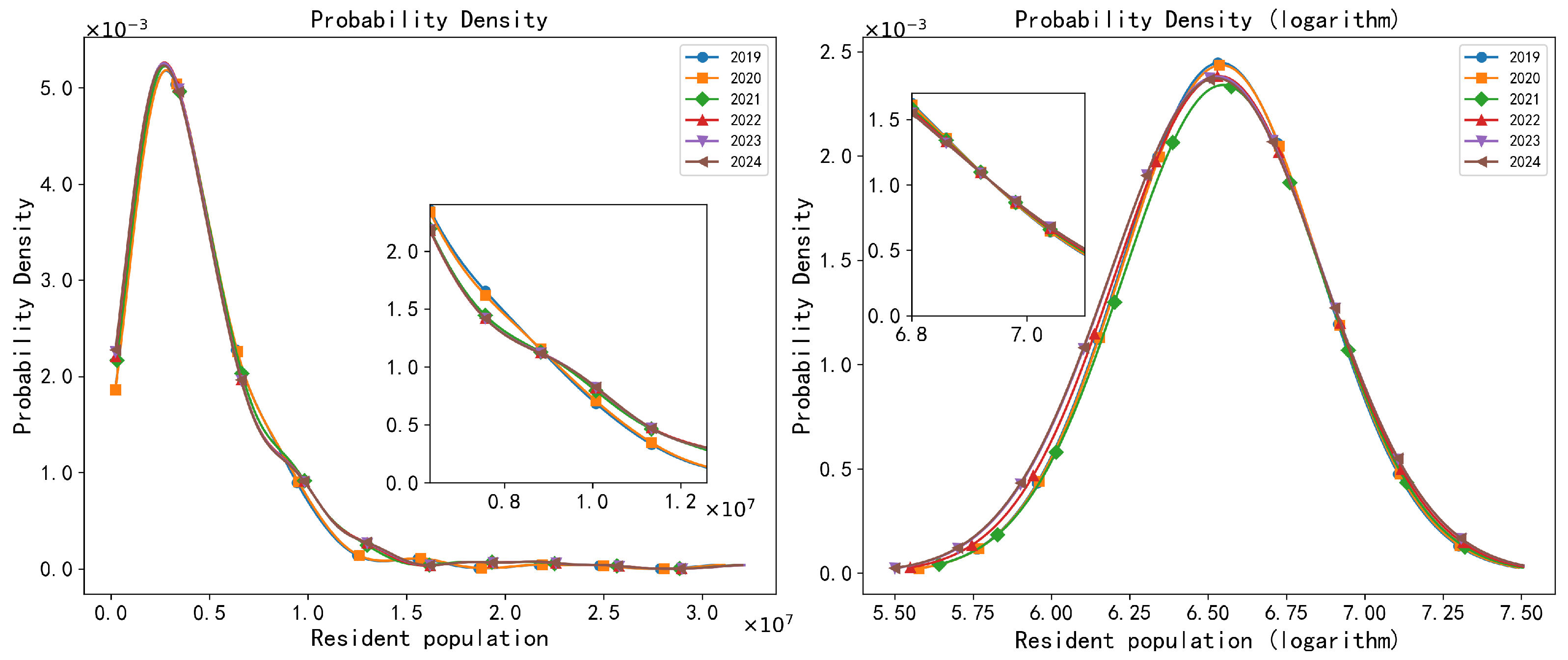
Appendix A.2.2. Data Interpolation Method
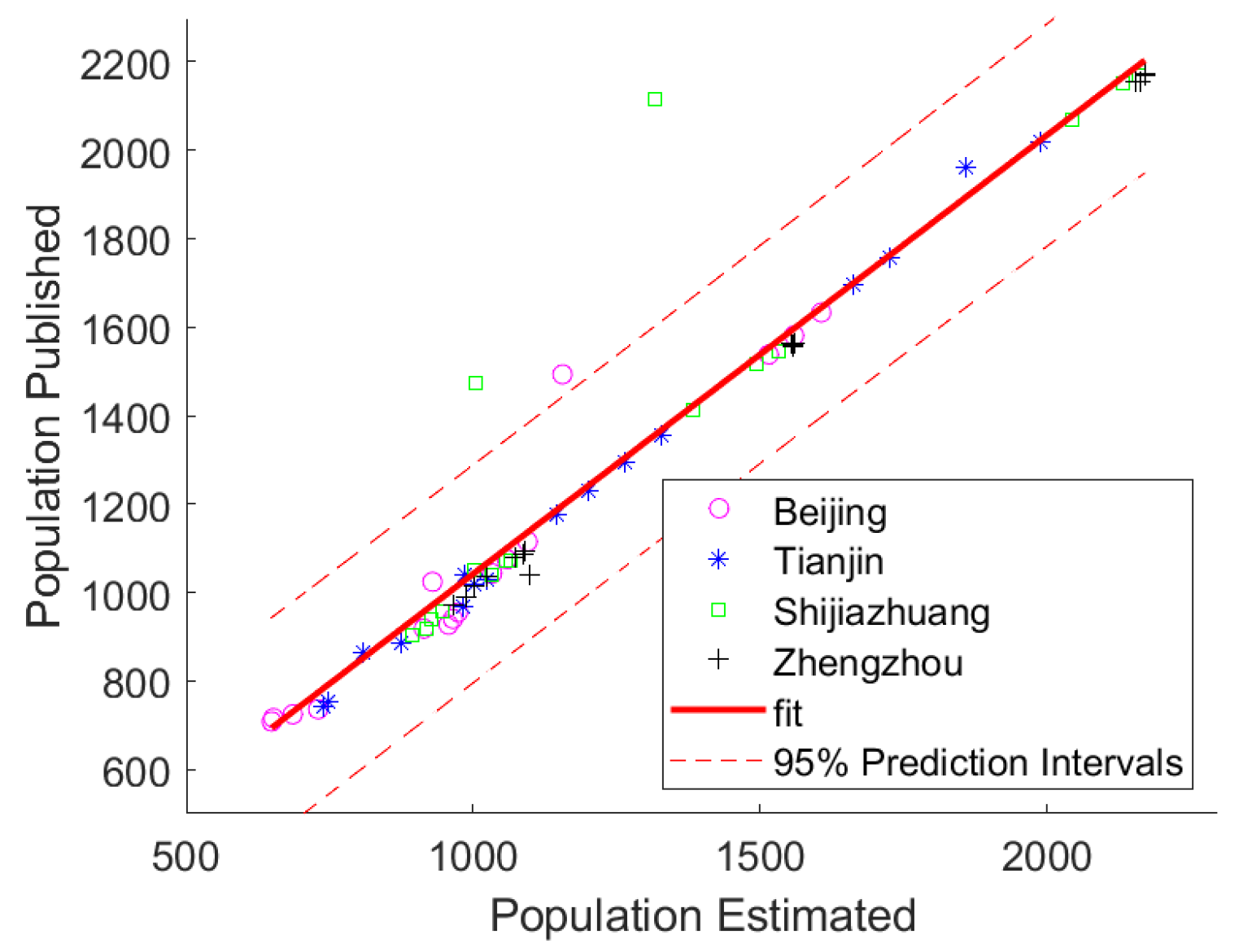
Appendix A.2.3. Logarithmic Linear Correlation of the Population and Employment in Specific Industries
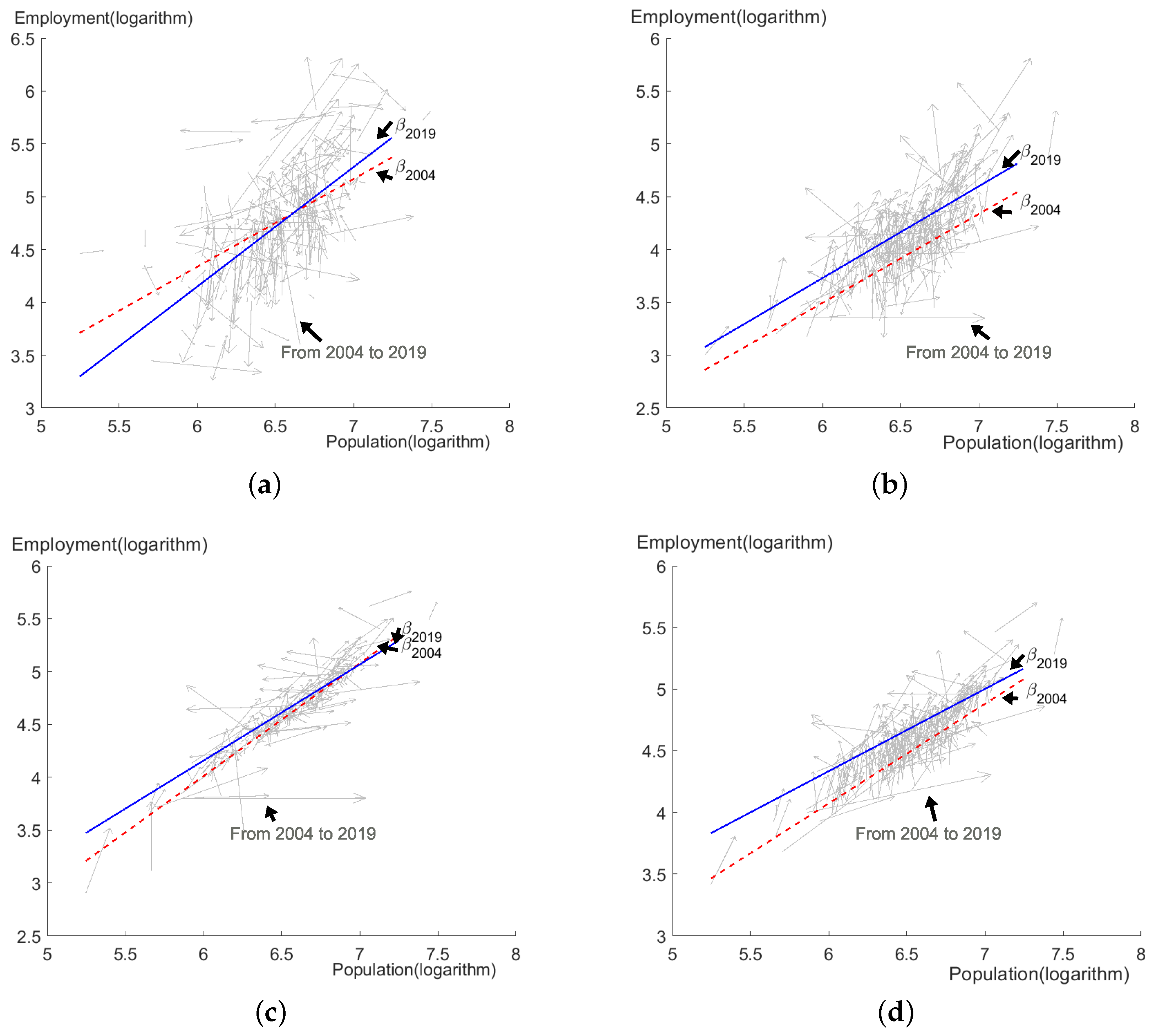
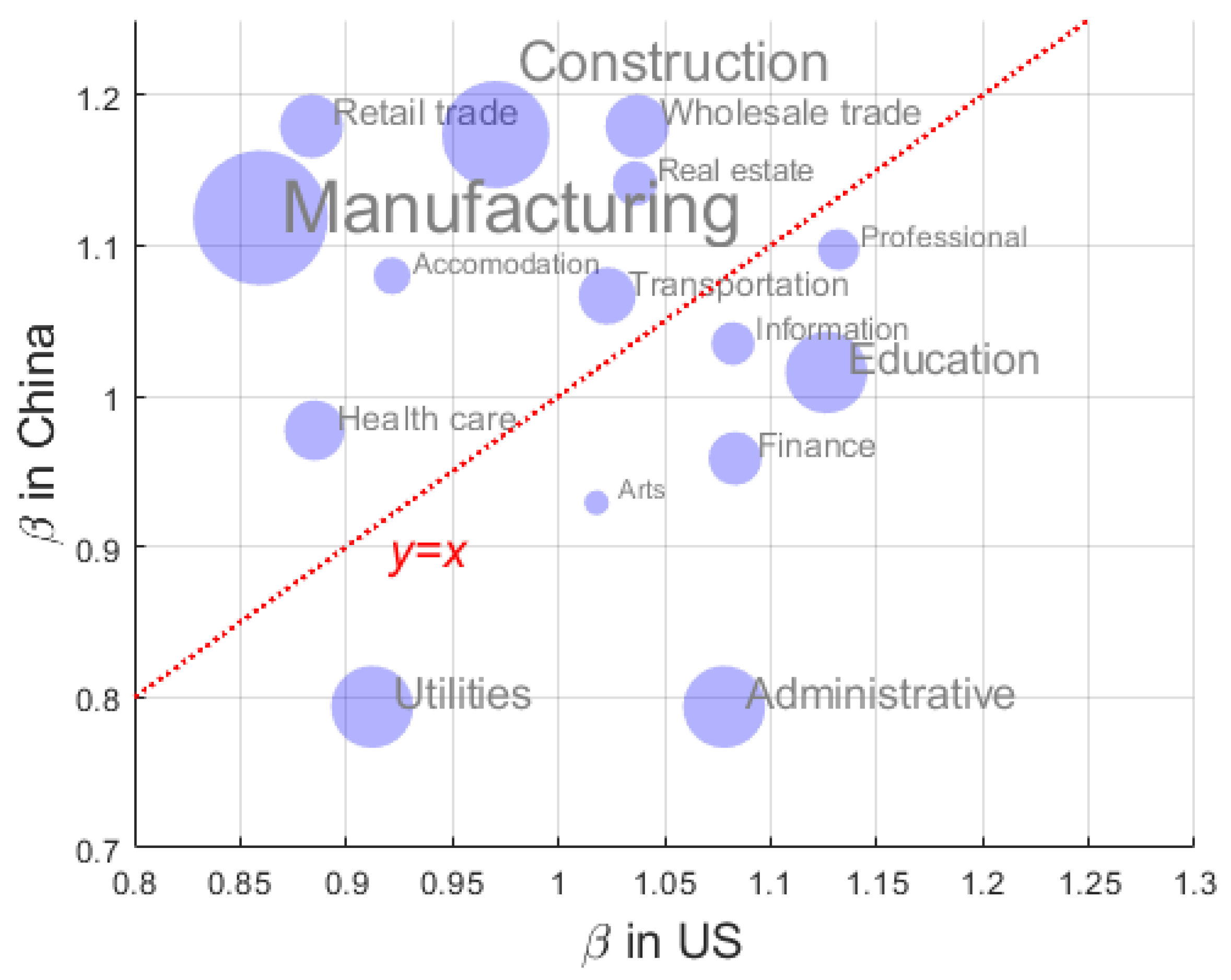
Appendix A.2.4. The Different βi Values for China and the United States
Appendix B. The Theoretical Model and Derivation Process
Appendix B.1. The Scaling Laws for Cities
| Industry | ||||
|---|---|---|---|---|
| Agriculture, forestry, animal husbandry and fishery | 0.24 | 0.05 | 0.01 | 0.05 |
| Mining | 0.09 | 0.68 | 0.00 | 0.85 |
| Manufacturing | 1.32 ** | 0.00 | 0.52 | 0.00 |
| Production and supply of electricity, heating, gas, and water | 0.73 ** | 0.00 | 0.36 | 0.00 |
| Construction industry | 1.35 ** | 0.00 | 0.53 | 0.00 |
| Wholesale and retail | 1.35 ** | 0.00 | 0.61 | 0.00 |
| Transportation, warehousing, and postal services | 1.16 ** | 0.00 | 0.56 | 0.00 |
| Accommodation and catering industry | 1.29 ** | 0.00 | 0.44 | 0.00 |
| Information transmission, computing and services, and software | 1.24 ** | 0.00 | 0.54 | 0.00 |
| Finance | 1.01 ** | 0.00 | 0.57 | 0.00 |
| Real estate industry | 1.26 ** | 0.00 | 0.53 | 0.00 |
| Rent | 1.21 ** | 0.00 | 0.49 | 0.00 |
| Scientific research, technical services and geological survey | 1.26 ** | 0.00 | 0.51 | 0.00 |
| Public facilities management industry | 1.25 ** | 0.00 | 0.51 | 0.00 |
| Residential services, repair and other services | 1.38 ** | 0.00 | 0.41 | 0.00 |
| Educational Services | 1.05 ** | 0.00 | 0.93 | 0.00 |
| Health care and social work | 0.98 ** | 0.00 | 0.88 | 0.00 |
| Culture, sports and entertainment | 1.03 ** | 0.00 | 0.53 | 0.00 |
| Public administration, social security and social organization | 0.76 ** | 0.00 | 0.80 | 0.00 |
Appendix B.2. The Comparative Advantage Function
Appendix B.3. Changes in Comparative Advantage
- Changes with N.when , ; when , ; and when , .
- Changes with ..In 2019,, , , when , . When , ; when , ; and when , ., , , when , . When , ; when , ; and when , .
Appendix C. Other Results
Appendix C.1. The Derivation Process for the 2020 Data
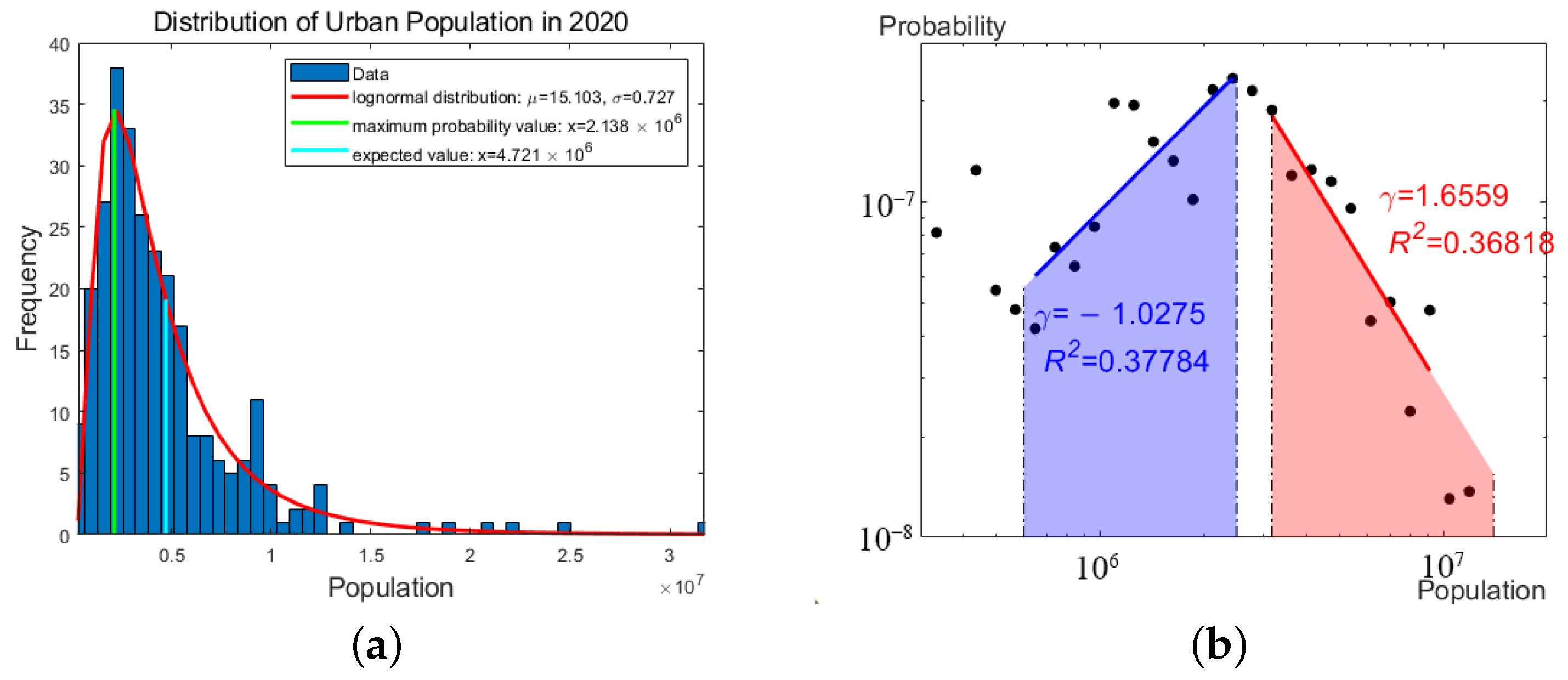
Appendix C.2. Labour Demand of “Knowledge Spillover” Cities in China
| Year | ||
|---|---|---|
| 2004 | ||
| 2005 | ||
| 2006 | ||
| 2007 | ||
| 2008 | ||
| 2009 | ||
| 2010 | ||
| 2011 | ||
| 2012 | ||
| 2013 | ||
| 2014 | ||
| 2015 | ||
| 2016 | ||
| 2017 | ||
| 2018 | ||
| 2019 | ||
| 2020 |
| Year | Million | Million | Million | LLR p-Value | Population |
|---|---|---|---|---|---|
| 2004 | 8 | 9 | ∞ | 0.002 * | 0.000 * |
| 2005 | 8 | 9 | ∞ | 0.000 * | 0.000 * |
| 2006 | 8 | 9 | ∞ | 0.000 * | 0.000 * |
| 2007 | 8 | 9 | ∞ | 0.000 * | 0.001 * |
| 2008 | 8 | 9 | ∞ | 0.008 * | 0.010 * |
| 2009 | 8 | 10 | ∞ | 0.001 * | 0.003 * |
| 2010 | 8 | 10 | ∞ | 0.007 * | 0.009 * |
| 2011 | 8 | 10 | ∞ | 0.000 * | 0.001 * |
| 2012 | 7 | 10 | ∞ | 0.005 * | 0.008 * |
| 2013 | 10 | 11 | ∞ | 0.002 * | 0.005 * |
| 2014 | 10 | 11 | ∞ | 0.003 * | 0.005 * |
| 2015 | 10 | 11 | ∞ | 0.001 * | 0.002 * |
| 2016 | 10 | 11 | ∞ | 0.005 * | 0.007 * |
| 2017 | 10 | 11 | ∞ | 0.002 * | 0.004 * |
| 2018 | 10 | 11 | ∞ | 0.002 * | 0.003 * |
| 2019 | 10 | 11 | ∞ | 0.007 * | 0.008 * |
| 2020 | 8 | 10 | ∞ | 0.009 * | 0.010 * |
Appendix C.3. Comparison with the Optimal City Size
| a | ||||
|---|---|---|---|---|
| China | 245.471 | 0.1064 | 0.3528 | 1.13 × 107 |
| United States | 131.978 | 0.0994 | 0.3393 | 1.22 × 106 |
Appendix C.4. Differences in Cities’ Economic Regions
| Region | Provinces |
|---|---|
| Eastern Region | Beijing, Tianjin, Hebei, Shanghai, Jiangsu, Zhejiang, Fujian, Shandong, Guangdong, Hainan, Taiwan, Hong Kong SAR, Macao SAR |
| Central Region | Shanxi, Anhui, Jiangxi, Henan, Hubei, Hunan |
| Western Region | Inner Mongolia Autonomous Region, Guangxi Zhuang Autonomous Region, Chongqing Municipality, Sichuan, Guizhou, Yunnan, Tibet Autonomous Region, Shaanxi, Gansu, Qinghai, Ningxia Hui Autonomous Region, Xinjiang Uygur Autonomous Region |
| Northeast Region | Liaoning, Jilin, Heilongjiang |
Appendix C.5. The Recapitulation of Industries
| Industry | Score |
|---|---|
| Manufacturing | 0.75 * |
| Production and supply of electricity, heating, gas, and water | 0.93 * |
| Construction industry | 0.42 |
| Wholesale and retail | 0.68 * |
| Transportation, warehousing, and postal services | 0.83 * |
| Accommodation and catering industry | 0.85 * |
| Information transmission, computing services, and software | 0.67 * |
| Finance | 0.61 * |
| Real estate industry | 0.91 * |
| Rent | 0.83 * |
| Scientific research, technical services, and geological survey | 0.77 * |
| Public facilities management industry | −0.91 |
| Residential services, repair, and other services | 0.73 * |
| Educational services | 0.83 * |
| Health care and social work | 0.42 |
| Culture, sports, and entertainment | 0.82 * |
| Public administration, social security, and social organization | 0.60 * |
References
- Bettencourt, L.M.; West, G. A unified theory of urban living. Nature 2010, 467, 912–913. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Zhang, H.; Liu, W.; Zhang, W. The global pattern of urbanization and economic growth: Evidence from the last three decades. PLoS ONE 2014, 9, e103799. [Google Scholar] [CrossRef] [PubMed]
- United Nations. World Urbanization Prospects: The 2014 Revision; United Nations Department of Economic and Social Affairs Population Division: New York, NY, USA, 2015; Volume 41. [Google Scholar]
- Balland, P.A.; Jara-Figueroa, C.; Petralia, S.G.; Steijn, M.P.; Rigby, D.L.; Hidalgo, C.A. Complex economic activities concentrate in large cities. Nat. Hum. Behav. 2020, 4, 248–254. [Google Scholar] [CrossRef]
- Xu, H.; Jiao, M. City size, industrial structure and urbanization quality—A case study of the Yangtze River Delta urban agglomeration in China. Land Use Policy 2021, 111, 105735. [Google Scholar] [CrossRef]
- Zheng, S.; Du, R. How does urban agglomeration integration promote entrepreneurship in China? Evidence from regional human capital spillovers and market integration. Cities 2020, 97, 102529. [Google Scholar] [CrossRef]
- Hong, I.; Frank, M.R.; Rahwan, I.; Jung, W.S.; Youn, H. The universal pathway to innovative urban economies. Sci. Adv. 2020, 6, eaba4934. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef]
- Bettencourt, L.M. The Origins of Scaling in Cities. Science 2013, 340, 1438–1441. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Lobo, J.; West, G.B. Why are large cities faster? Universal scaling and self-similarity in urban organization and dynamics. Eur. Phys. J. B 2008, 63, 285–293. [Google Scholar] [CrossRef]
- Pumain, D.; Paulus, F.; Vacchiani-Marcuzzo, C.; Lobo, J. An evolutionary theory for interpreting urban scaling laws. Cybergeo Eur. J. Geogr. 2006, 2006, 1–20. [Google Scholar] [CrossRef]
- Youn, H.; Bettencourt, L.; Lobo, J.; Strumsky, D.; Samaniego, H.; West, G. Scaling and universality in urban economic diversification. J. R. Soc. Interface 2016, 13, 20150937. [Google Scholar] [CrossRef] [PubMed]
- Misra, S.B. Revisiting Rural Non-farm Sector Employment in India: Trends from 1993-94 to 2023-24. Indian J. Hum. Dev. 2025, 09737030251322830. [Google Scholar] [CrossRef]
- Ge, P.; Sun, W.; Zhao, Z. Employment structure in China from 1990 to 2015. J. Econ. Behav. Organ. 2021, 185, 168–190. [Google Scholar] [CrossRef]
- Arif, I. Productive knowledge, economic sophistication, and labor share. World Dev. 2021, 139, 105303. [Google Scholar] [CrossRef]
- Li, X.; Huang, S.; Chen, Q. Analyzing the driving and dragging force in China’s inter-provincial migration flows. Int. J. Mod. Phys. C 2019, 30, 1940015. [Google Scholar] [CrossRef]
- Chen, Y. The evolution of Zipf’s law indicative of city development. Phys. A Stat. Mech. Its Appl. 2016, 443, 555–567. [Google Scholar] [CrossRef]
- Taylor, J.R. The China dream is an urban dream: Assessing the CPC’s national new-type urbanization plan. J. Chin. Political Sci. 2015, 20, 107–120. [Google Scholar] [CrossRef]
- Ye, X.; Xie, Y. Re-examination of Zipf’s law and urban dynamic in China: A regional approach. Ann. Reg. Sci. 2012, 49, 135–156. [Google Scholar] [CrossRef]
- Guan, X.; Wei, H.; Lu, S.; Dai, Q.; Su, H. Assessment on the urbanization strategy in China: Achievements, challenges and reflections. Habitat Int. 2018, 71, 97–109. [Google Scholar] [CrossRef]
- Chen, X.; Du, W. Too big or too small? The threshold effects of city size on regional pollution in China. Int. J. Environ. Res. Public Health 2022, 19, 2184. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, H.; Wang, Y.; Li, C.; Luo, Q.; Chen, S. Promoting coordinated spatial governance of mega-cities in China via spatial organization of metropolitan areas. Front. Urban Rural Plan. 2024, 2, 24. [Google Scholar] [CrossRef]
- Zheng, D.; Dong, S.; Lin, C. The Necessity and Control Strategy of “Medium Density” in Metropolis. Int. Urban Plan 2021, 36, 1–9. [Google Scholar]
- Zipf, G.K. Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology; Ravenio Books: London, UK, 2016. [Google Scholar]
- Hu, Y.; Connor, D.S.; Stuhlmacher, M.; Peng, J.; Turner Ii, B. More urbanization, more polarization: Evidence from two decades of urban expansion in China. npj Urban Sustain. 2024, 4, 33. [Google Scholar] [CrossRef]
- Bee, M.; Riccaboni, M.; Schiavo, S. The size distribution of US cities: Not Pareto, even in the tail. Econ. Lett. 2013, 120, 232–237. [Google Scholar] [CrossRef]
- Berry, B.J.; Okulicz-Kozaryn, A. The city size distribution debate: Resolution for US urban regions and megalopolitan areas. Cities 2012, 29, S17–S23. [Google Scholar] [CrossRef]
- Li, H.; Wei, Y.D.; Ning, Y. Spatial and temporal evolution of urban systems in China during rapid urbanization. Sustainability 2016, 8, 651. [Google Scholar] [CrossRef]
- Mori, T.; Smith, T.E.; Hsu, W.T. Common power laws for cities and spatial fractal structures. Proc. Natl. Acad. Sci. USA 2020, 117, 6469–6475. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Oehlers, M.; Moreno-Monroy, A.I.; Kropp, J.P.; Rybski, D. Association between population distribution and urban GDP scaling. PLoS ONE 2021, 16, e0245771. [Google Scholar] [CrossRef]
- Zhao, S.X.; Guo, N.S.; Li, C.L.K.; Smith, C. Megacities, the world’s largest cities unleashed: Major trends and dynamics in contemporary global urban development. World Dev. 2017, 98, 257–289. [Google Scholar] [CrossRef]
- Friedmann, J. Four theses in the study of China’s urbanization. Int. J. Urban Reg. Res. 2006, 30, 440–451. [Google Scholar] [CrossRef]
- Frank, M.R.; Sun, L.; Cebrian, M.; Youn, H.; Rahwan, I. Small cities face greater impact from automation. J. R. Soc. Interface 2018, 15, 20170946. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Shi, P.; Liu, Y. Society: Realizing China’s urban dream. Nat. News 2014, 509, 158. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.R.; Hui, E.C.M.; Choguill, C.; Jia, S.H. The new urbanization policy in China: Which way forward? Habitat Int. 2015, 47, 279–284. [Google Scholar] [CrossRef]
- Xu, Z.; Zhu, N. City size distribution in China: Are large cities dominant? Urban Stud. 2009, 46, 2159–2185. [Google Scholar] [CrossRef]
- Gao, B.; Huang, Q.; He, C.; Dou, Y. Similarities and differences of city-size distributions in three main urban agglomerations of China from 1992 to 2015: A comparative study based on nighttime light data. J. Geogr. Sci. 2017, 27, 533–545. [Google Scholar] [CrossRef]
- Fang, L.; Li, P.; Song, S. China’s development policies and city size distribution: An analysis based on Zipf’s law. Urban Stud. 2017, 54, 2818–2834. [Google Scholar] [CrossRef]
- Cai, E.; Zhang, S.; Chen, W.; Li, L. Spatio–temporal dynamics and human–land synergistic relationship of urban expansion in Chinese megacities. Heliyon 2023, 9, e19872. [Google Scholar] [CrossRef]
- ECNS. 17 Chinese Cities Have a Population of over 10 Million in 2021. 2022. Available online: https://www.ecns.cn/news/cns-wire/2022-05-26/detail-ihaytawr8118445.shtml (accessed on 21 May 2025).
- National Bureau of Statistics of China. China City Statistical Yearbook; Annual Publications from 2004 to 2020 Accessed from China Economic and Social Big Data Research Platform. Available online: https://data.oversea.cnki.net/en/trade/yearBook/single?zcode=Z009&id=N2025020156&pinyinCode=YZGCA (accessed on 25 May 2025).
- GB/T 4754-2017; Industrial Classification for National Economic Activities. National Bureau of Statistics of China: Beijing, China, 2017. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=A703F0E23DD165A5A1318679F312D158 (accessed on 21 May 2025).
- National Bureau of Statistics of China. China Statistical Yearbook for Regional Economy; Accessed from China Economic and Social Big Data Research Platform. Available online: https://data.oversea.cnki.net/en/trade/yearBook/single?zcode=Z009&id=N2015070200&pinyinCode=YZXDR (accessed on 25 May 2025).
- U.S. Bureau of Economic Analysis. GDP by County, Metro, and Other Areas; Data Released on December 4, 2024. Available online: https://www.bea.gov/data/gdp/gdp-county-metro-and-other-areas (accessed on 25 May 2025).
- U.S. Census Bureau, Population Division. Metropolitan and Micropolitan Statistical Areas Population Totals and Components of Change: 2010–2019; Data Covering the Period from 2010 to 2019. Available online: https://www.census.gov/data/datasets/time-series/demo/popest/2010s-total-metro-and-micro-statistical-areas.html (accessed on 25 May 2025).
- U.S. Bureau of Economic Analysis. Regional Price Parities and Implicit Regional Price Deflators, by Metropolitan Area, 2020; Data in Millions of Constant (2012) Dollars. Available online: https://www.bea.gov/data/consumer-spending/real-consumer-spending-state (accessed on 25 May 2025).
- Liesner, H. The European Common Market and British Industry. Econ. J. 1958, 68, 302–316. [Google Scholar] [CrossRef]
- Levy, M. Gibrat’s Law for (All) Cities: Comment. Am. Econ. Rev. 2009, 99, 1672–1675. [Google Scholar] [CrossRef]
- Deng, Z.; Fan, H. Study on the law of urban population size distribution in China. Chin. J. Popul. Sci. 2016, 4, 48–60. [Google Scholar]
- Chen, D.; Yan, Z.; Wang, W. Urban population size, industrial agglomeration model and urban innovation: Empirical evidence from 271 cities at prefecture level and above. Chin. J. Popul. Sci. 2020, 34, 27–40. [Google Scholar]
- Dong, K. Research on Urban Power Law Distribution and Urban Allometric Scaling. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2019. [Google Scholar]
- Blank, A.; Solomon, S. Power laws in cities population, financial markets and internet sites (scaling in systems with a variable number of components). Phys. A Stat. Mech. Its Appl. 2000, 287, 279–288. [Google Scholar] [CrossRef]
- Gabaix, X. Power laws in economics: An introduction. J. Econ. Perspect. 2016, 30, 185–206. [Google Scholar] [CrossRef]
- González-Val, R.; Lanaspa, L.; Sanz-Gracia, F. New evidence on Gibrat’s law for cities. Urban Stud. 2014, 51, 93–115. [Google Scholar] [CrossRef]
- Lalanne, A. Zipf’s law and Canadian urban growth. Urban Stud. 2014, 51, 1725–1740. [Google Scholar] [CrossRef]
- Wei, S.; Sun, N.; Jiang, Y. Applicability of Zipf’s law and Gibrat’s law in urban size distribution in China. J. World Econ. 2018, 96–120. [Google Scholar]
- Eeckhout, J. Gibrat’s Law for (All) Cities. Am. Econ. Rev. 2004, 94, 1429–1451. [Google Scholar] [CrossRef]
- Malevergne, Y.; Pisarenko, V.; Sornette, D. Testing the Pareto against the lognormal distributions with the uniformly most powerful unbiased test applied to the distribution of cities. Phys. Rev. E 2011, 83, 036111. [Google Scholar] [CrossRef]
- Rabinowitz, P.H. (Ed.) Minimax Methods in Critical Point Theory with Applications to Differential Equations; Number 65; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Michaels, G.; Rauch, J.; Redding, S.J. Task Specialization in U.S. Cities from 1880 to 2000. J. Eur. Econ. Assoc. 2019, 17, 754–798. [Google Scholar] [CrossRef]
- Albouy, D.; Behrens, K.; Robert-Nicoud, F.; Seegert, N. The optimal distribution of population across cities. J. Urban Econ. 2019, 110, 102–113. [Google Scholar] [CrossRef]
- Henderson, J.V. Optimum city size: The external diseconomy question. J. Political Econ. 1974, 82, 373–388. [Google Scholar] [CrossRef]
- Capello, R.; Camagni, R. Beyond optimal city size: An evaluation of alternative urban growth patterns. Urban Stud. 2000, 37, 1479–1496. [Google Scholar] [CrossRef]
- Mizutani, F.; Tanaka, T.; Nakayama, N. Estimation of optimal metropolitan size in Japan with consideration of social costs. Empir. Econ. 2015, 48, 1713–1730. [Google Scholar] [CrossRef]
- Giesen, K.; Südekum, J. Zipf’s law for cities in the regions and the country. J. Econ. Geogr. 2011, 11, 667–686. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J.; Liu, Q. Zipf’s law for all the natural cities around the world. Int. J. Geogr. Inf. Sci. 2015, 29, 498–522. [Google Scholar] [CrossRef]
- Verbavatz, V.; Barthelemy, M. The growth equation of cities. Nature 2020, 587, 397–401. [Google Scholar] [CrossRef]
- Wang, X. Urbanization Path and City Scale in China: An Economic Analysis. Econ. Res. J. 2010, 10, 20–32. [Google Scholar]
- Carlino, G. Manufacturing agglomeration economies as returns to scale: A production function approach. In Papers of the Regional Science Association; Springer: Berlin/Heidelberg, Germany, 1982; Volume 50, pp. 95–108. [Google Scholar]
- Jin, X. Theories on the Optimum Scales of Cities and Empirical Study: Taking the Example of the Three Municipalities. Shanghai Econ. Rev. 2004, 2004, 35–43. [Google Scholar] [CrossRef]
- Zhang, Y. The Empirical Study of Optimal City Size in China: The Perspective of Economic Growth. Shanghai Econ. Rev. 2009, 5, 31–38. [Google Scholar]
- Jie, Z.; Yang, X. Optimal city size in China: An extended empirical study from the perspective of energy consumption. China City Plan. Rev. 2017, 26, 22–29. [Google Scholar]
- Sun, W.; Jones, J.; Gamber, M. A Turning Point for China’s Population: No Child and Long Illness. Aging Dis. 2023, 14, 1950–1952. [Google Scholar] [CrossRef] [PubMed]
- Wang, P. Population Decline Narrows, Population Quality Continues to Improve. National Bureau of Statistics of China. 2025. Available online: https://www.stats.gov.cn/sj/sjjd/202501/t20250117_1958337.html (accessed on 21 May 2025).
- United Nations. World Population Aging; Technical Report; Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2017. [Google Scholar]
- Liang, J. Prospects for Chinas drive for innovation: From the perspective of demographics. In China and the West; Edward Elgar Publishing: Cheltenham, UK, 2021; pp. 135–147. [Google Scholar]
- Yu, X.; Yi, T. Analysis on the Influencing Mechanism of Population Agglomeration, Industry Agglomeration and Innovation Agglomeration in Chinese Megacities. Commer. Res. 2020, 62, 145–152. [Google Scholar]
- National Bureau of Statistics of China. 7th National Population Census (2020). Available online: https://www.stats.gov.cn/sj/pcsj/rkpc/7rp/indexch.htm (accessed on 25 May 2025).
- Jiang, B.; Jia, T. Zipf’s law for all the natural cities in the United States: A geospatial perspective. Int. J. Geogr. Inf. Sci. 2011, 25, 1269–1281. [Google Scholar] [CrossRef]
- Hidalgo, C.A.; Hausmann, R. The building blocks of economic complexity. Proc. Natl. Acad. Sci. USA 2009, 106, 10570–10575. [Google Scholar] [CrossRef]
- Hausmann, R.; Hidalgo, C.A. The network structure of economic output. J. Econ. Growth 2011, 16, 309–342. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, Y. Analysis on the causes of frequent economic recession in Northeast China—The change from “industry absence” to “system solidification”. Soc. Sci. Front. 2017, 2, 48–57. [Google Scholar]

| Variable | Variable Description | Data Source |
|---|---|---|
| Employment in China | The employment of 19 industries in prefecture-level and above cities, annual data during 2004–2019, from “China City Statistical Yearbook” [41], 10 thousand people. | https://data.oversea.cnki.net/en/trade/yearBook/single?zcode=Z009&id=N2025020156&pinyinCode=YZGCA (accessed on 20 May 2025) |
| GRP, GRP (per capita) in China | The gross regional product and gross regional product per capita in prefecture-level and above cities of China, the annual data during 2004–2012 and 2014–2019 are from “China City Statistical Yearbook” [41], and the annual data in 2013 is from “China Statistical Yearbook for Regional Economy” [43], yuan. | https://data.oversea.cnki.net/en/trade/yearBook/single?zcode=Z009&id=N2025020156&pinyinCode=YZGCA (accessed on 20 May 2025); https://data.oversea.cnki.net/en/trade/yearBook/single?zcode=Z009&id=N2015070200&pinyinCode=YZXDR (accessed on 20 May 2025) |
| Sales of commodities in China | Total retail sales of consumer goods + total sales of commodities of enterprises above designated size in wholesale and retail trades prefecture-level and above cities of China, annual data in 2019, from “China City Statistical Yearbook” [41], 10,000 yuan. | https://data.oversea.cnki.net/en/trade/yearBook/single?zcode=Z009&id=N2025020156&pinyinCode=YZGCA (accessed on 20 May 2025) |
| GDP (per capita) in the United States | CAGDP1 gross domestic product (GDP) summary by metropolitan area, from U.S. Bureau of Economic Analysis [44], annual data during 2004–2019, thousands of chained 2012 dollars. | https://www.bea.gov/data/gdp/gdp-county-metro-and-other-areas (accessed on 20 May 2025) |
| Population in the United States | Annual estimates of the resident population for metropolitan statistical areas in the United States, from U.S. Census Bureau, Population Division [45], annual data in 2019, people. | https://www.census.gov/data/datasets/time-series/demo/popest/2010s-total-metro-and-micro-statistical-areas.html (accessed on 20 May 2025) |
| Sales of commodities in the United States | Real personal consumption expenditures by States, real personal income by metropolitan area, annual data in 2019, from U.S. Bureau of Economic Analysis, millions of constant (2012) dollars [46]. | https://www.bea.gov/data/consumer-spending/real-consumer-spending-state (accessed on 20 May 2025) |
| No. | Million | Million | Million | LLR p-Value | Population |
|---|---|---|---|---|---|
| 1 | 10 | 11 | ∞ | 0.007 * | 0.008 * |
| 2 | 6 | 7 | 10 | 0.205 | 0.206 |
| 3 | 5 | 6 | 10 | 0.012 | 0.012 |
| 4 | 4 | 5 | 10 | 0.022 | 0.023 |
| 5 | 3 | 4 | 10 | 0.061 | 0.062 |
| 6 | 2 | 3 | 10 | 0.539 | 0.539 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Chen, Q.; Zhou, Y.; Huang, S.; Shi, Y.; Li, X. An Empirical Evaluation of the Critical Population Size for “Knowledge Spillover” Cities in China: The Significance of 10 Million. Urban Sci. 2025, 9, 245. https://doi.org/10.3390/urbansci9070245
Gao X, Chen Q, Zhou Y, Huang S, Shi Y, Li X. An Empirical Evaluation of the Critical Population Size for “Knowledge Spillover” Cities in China: The Significance of 10 Million. Urban Science. 2025; 9(7):245. https://doi.org/10.3390/urbansci9070245
Chicago/Turabian StyleGao, Xiaohui, Qinghua Chen, Ya Zhou, Siyu Huang, Yi Shi, and Xiaomeng Li. 2025. "An Empirical Evaluation of the Critical Population Size for “Knowledge Spillover” Cities in China: The Significance of 10 Million" Urban Science 9, no. 7: 245. https://doi.org/10.3390/urbansci9070245
APA StyleGao, X., Chen, Q., Zhou, Y., Huang, S., Shi, Y., & Li, X. (2025). An Empirical Evaluation of the Critical Population Size for “Knowledge Spillover” Cities in China: The Significance of 10 Million. Urban Science, 9(7), 245. https://doi.org/10.3390/urbansci9070245