An Adaptive Selection of Urban Construction Projects: A Multi-Stage Model with Iterative Supercriterion Reduction
Abstract
1. Introduction
- -
- A multi-stage decision-making method for selecting urban construction projects has been proposed. It allows for the integration of regulatory, customer-oriented, and retrospective criteria. This ensures the possibility of considering not only regulatory and subjective requirements but also regional peculiarities of a project implementation of this type.
- -
- A logarithmic model for identifying weighting functions has been developed, enabling the numerical expression of the impact of criterion values on the project success factor. This approach allows for the straightforward derivation of quantitative characteristics based on small data samples.
- -
- An iterative approach to reducing the number of criteria in the task of multi-criteria optimization for construction project selection has been proposed. A reduction in criteria enables a semi-automated process of finding an alternative that best satisfies the two constructed supercriteria.
- -
- An experimental verification of the developed method has been conducted for the task of selecting investment projects in construction in the western region of Ukraine.
2. Literature Review
3. Materials and Methods
3.1. Problem Analysis and Verbal–Mathematical Problem Formulation
- -
- Financial risks (inflation and poor budget planning);
- -
- Technical challenges (insufficient preparation and planning errors);
- -
- Delays due to bureaucracy (regulatory barriers and document approval);
- -
- The impact of macroeconomic and political factors (crises, pandemics, and instability), etc.
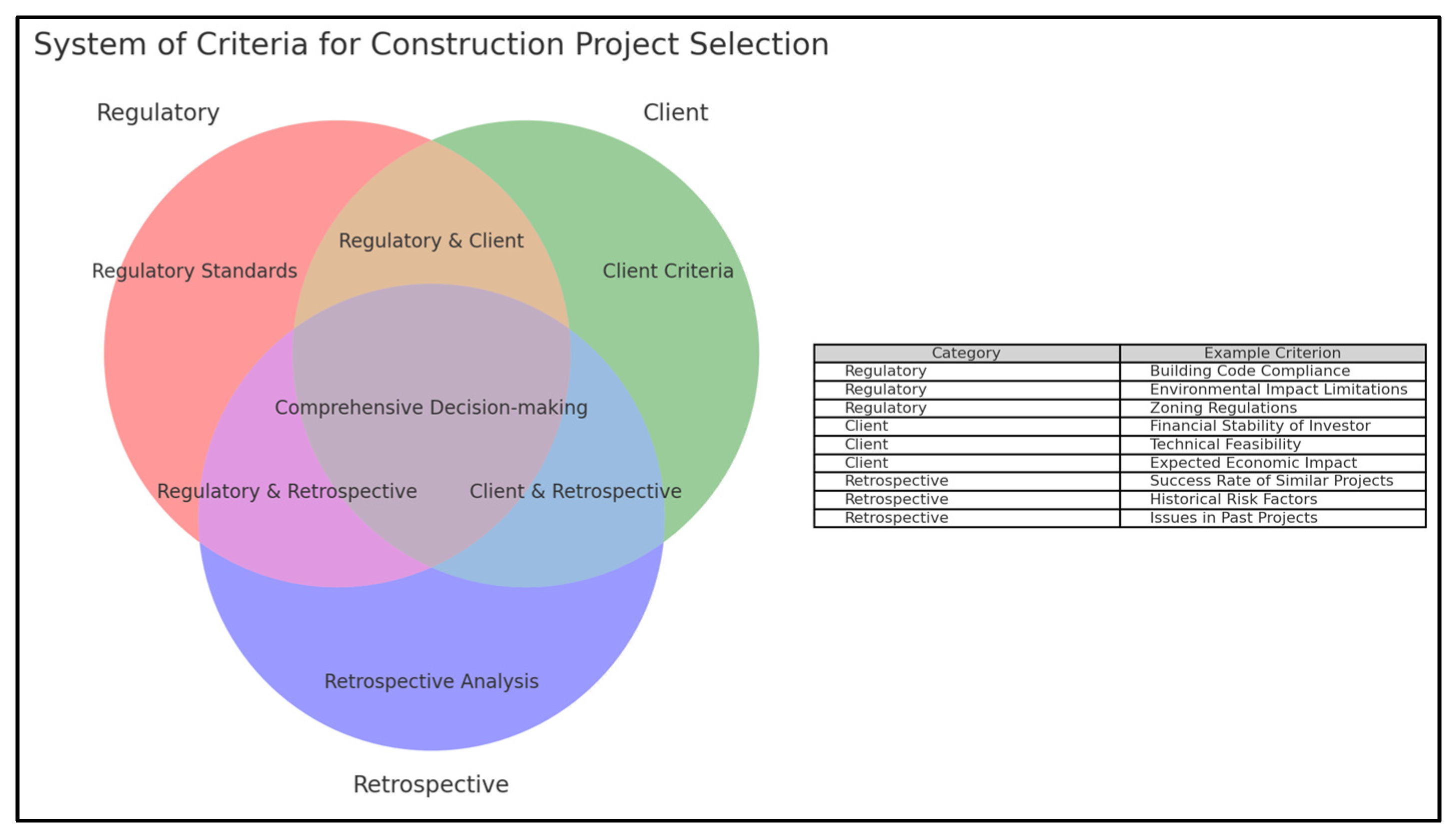
- Let us introduce the notation. —the set of indices of criteria provided by the regulators;
- —indices of criteria provided by customers;
- —indices of criteria obtained based on retrospective data analysis.
3.2. Method for Selecting Investment Projects in Urban Construction
- -
- The hypothesis of project independence, according to which all considered projects (alternatives) are independent of each other;
- -
- The hypothesis of the relative stability of project implementation conditions, according to which regulatory, economic, and political conditions are assumed to be conditionally unchanged during the period covered by the model;
- -
- The hypothesis of data reliability: all data are assumed to be accurate and representative.
- -
- The determination of criterion weights reflecting their importance in the selection process;
- -
- The formation of super-criteria that aggregate criteria of different types;
- -
- The construction of a multi-criteria model for evaluating alternatives.
3.2.1. Logarithmic Model for Identifying Weighting Functions
- -
- The first type includes projects that were successfully completed;
- -
- The second type includes projects that were completed but during their implementation faced difficulties that led to a deterioration of the expected result;
- -
- To the third group, we assign projects that, for certain reasons, were not completed.
- -
- The logarithmic function allows us to interpret the ratio between types of projects in negative, zero, or positive values: when the number of successful and unsuccessful projects is equal, the weight equals zero; if there are more successful ones, the weight is positive, and vice versa. This enables the use of weighting function values in score-based models.
- -
- The logarithmic function smooths out sharp fluctuations in small samples, making it resistant to local peaks and instability—unlike linear or power functions.
- -
- -
- Parameter indicates to what extent projects of the second group (those that encountered certain problems during implementation) can be considered successful. If , they are considered unsuccessful and formally assigned to the third group; if , they are considered successful and assigned to the first group. In all other cases, for , they are partially assigned to the first and third groups in proportions . This allows us to tune the model to the specifics of the risk acceptance policy.
- -
- Parameter > 0 in model (3) prevents instability in calculations. Its use guarantees that neither the numerator nor the denominator of the fraction equals zero, and the argument of the logarithmic function stays within permissible bounds. The closer this parameter is to zero, the less it affects the values of the weighting functions.
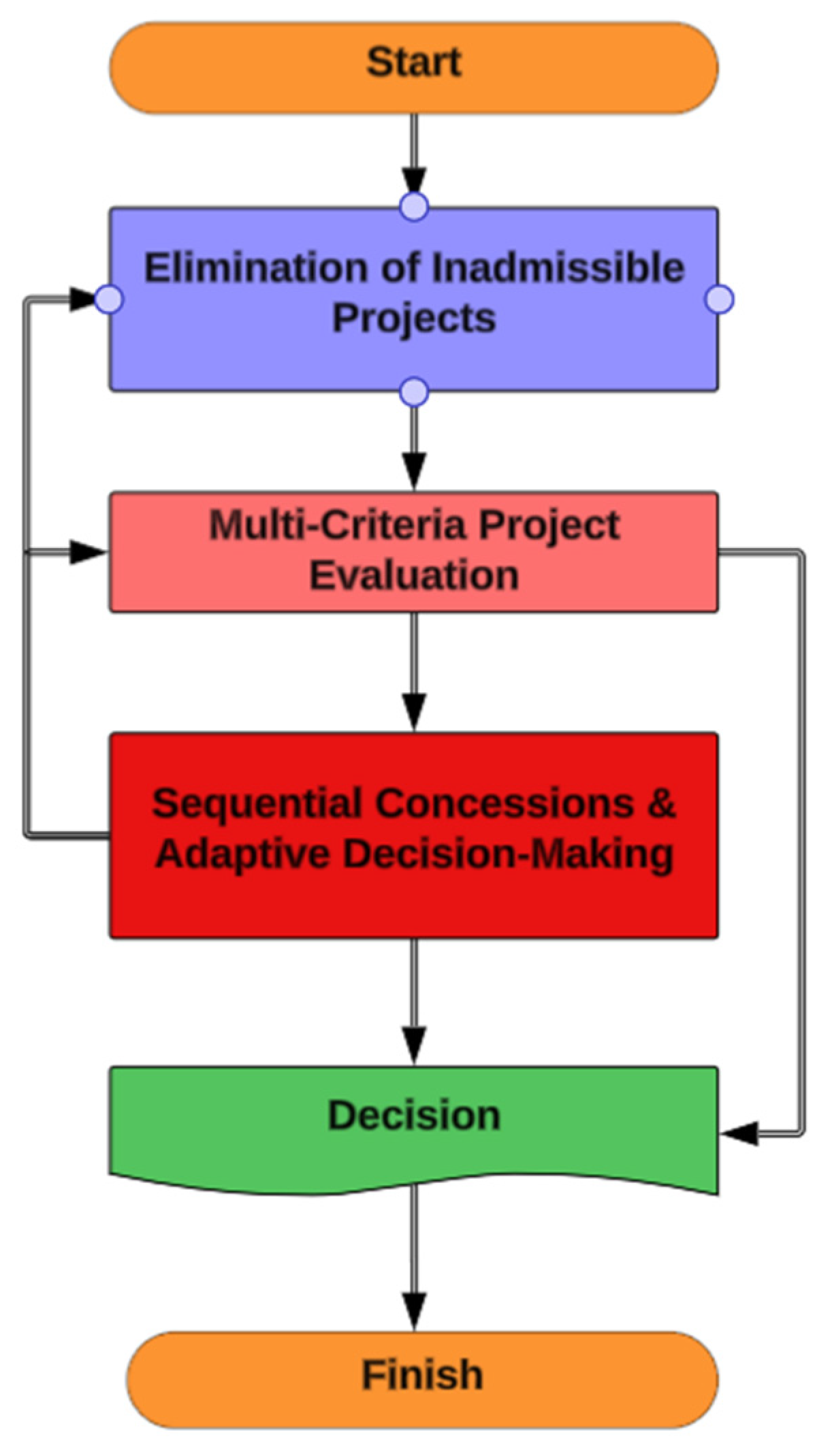
3.2.2. Procedure for Sequential Analysis of Alternatives for Elimination of Unpromising Projects
3.2.3. Model of Multi-Criteria Selection Based on Supercriteria
3.2.4. Method of Iterative Reduction in Supercriteria via Internal Optimization
4. Results
4.1. Collection of Data
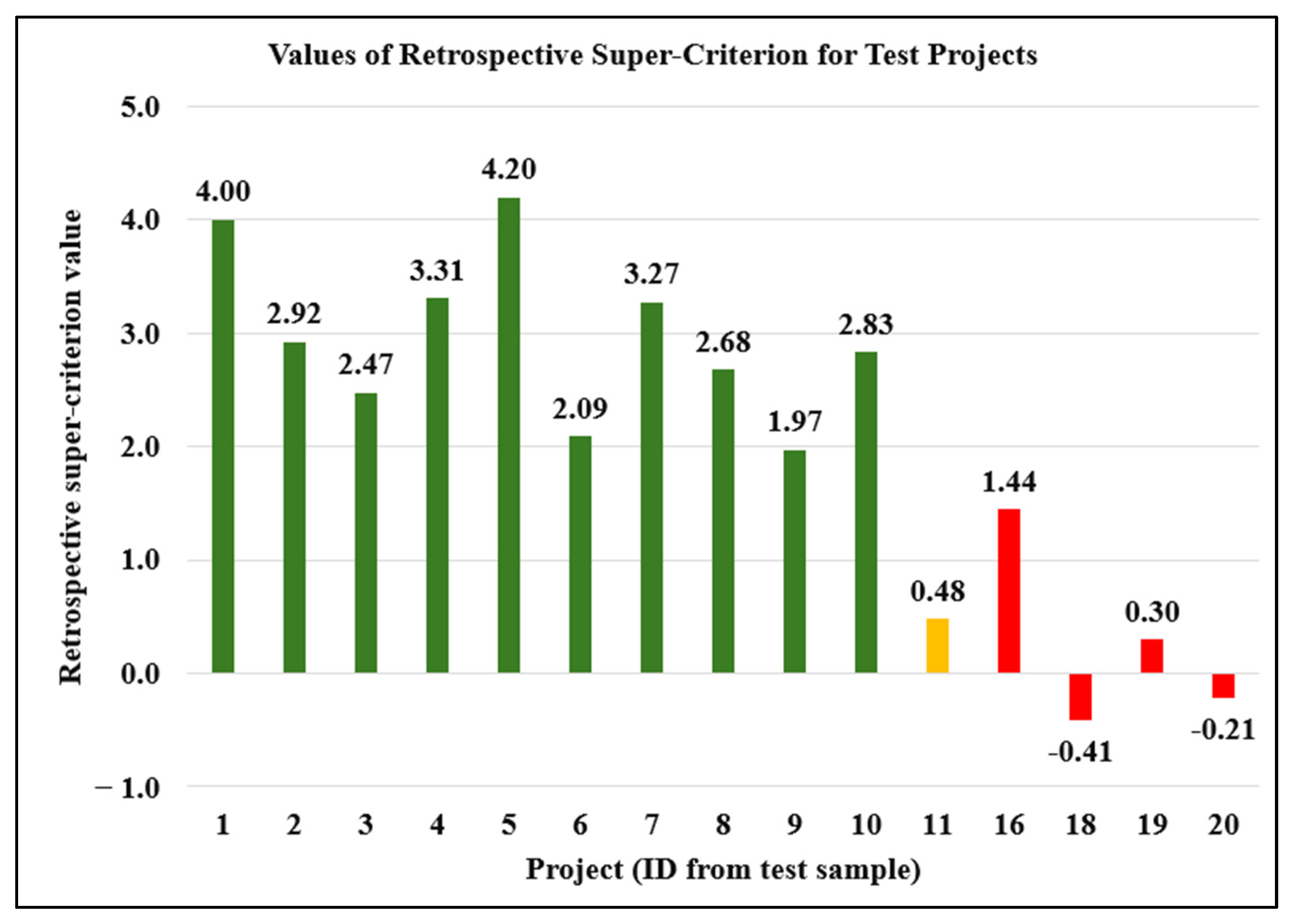
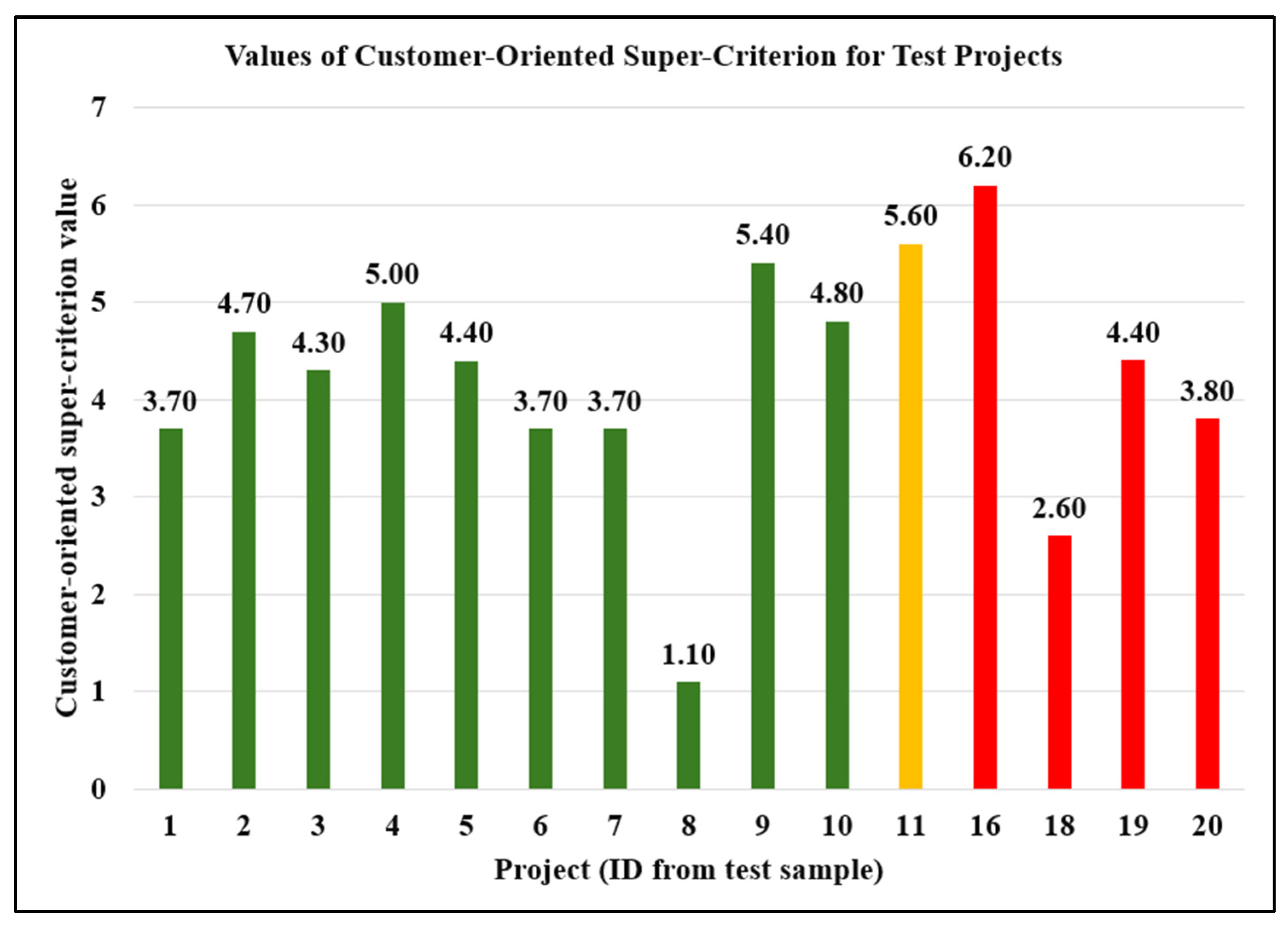
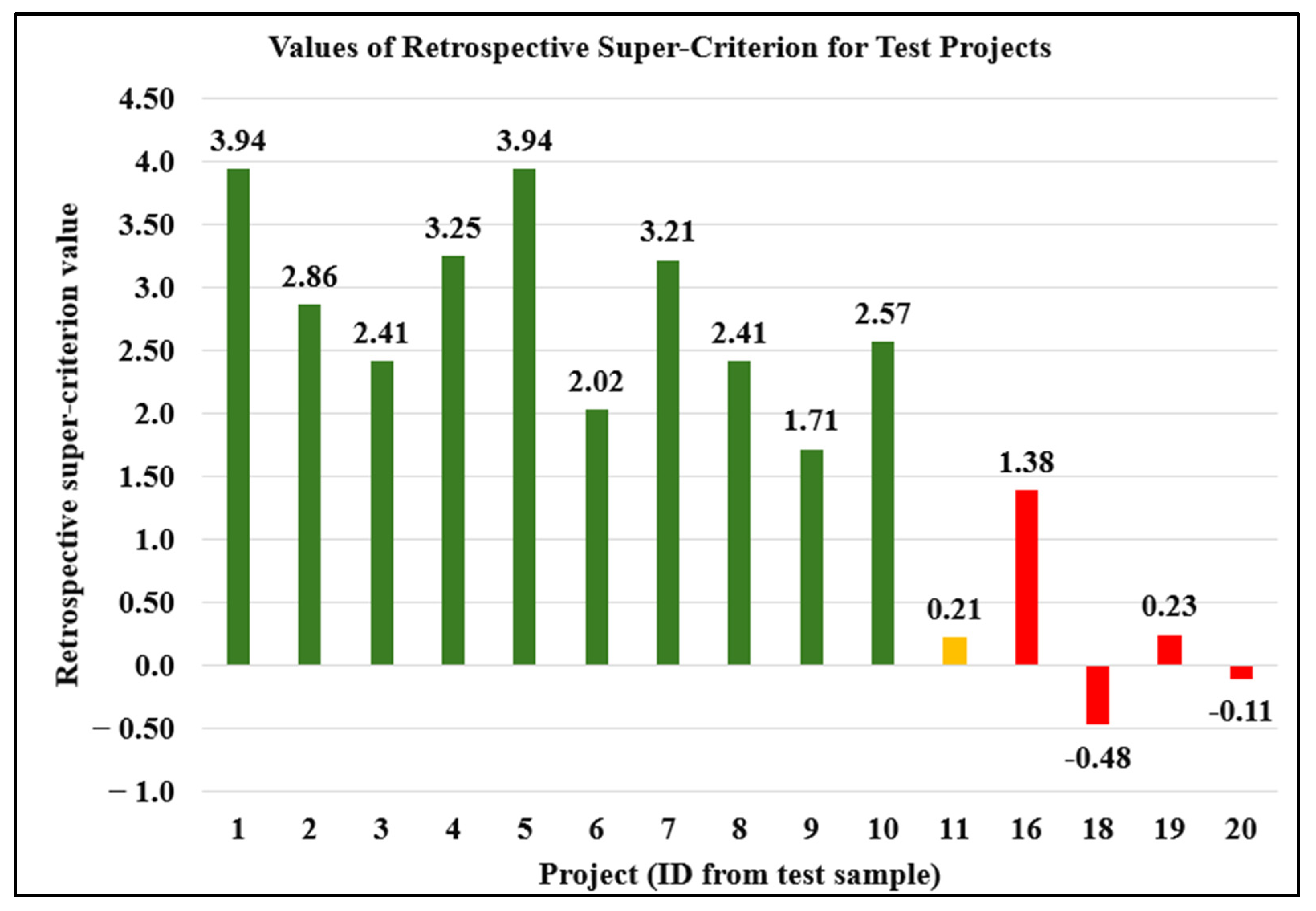
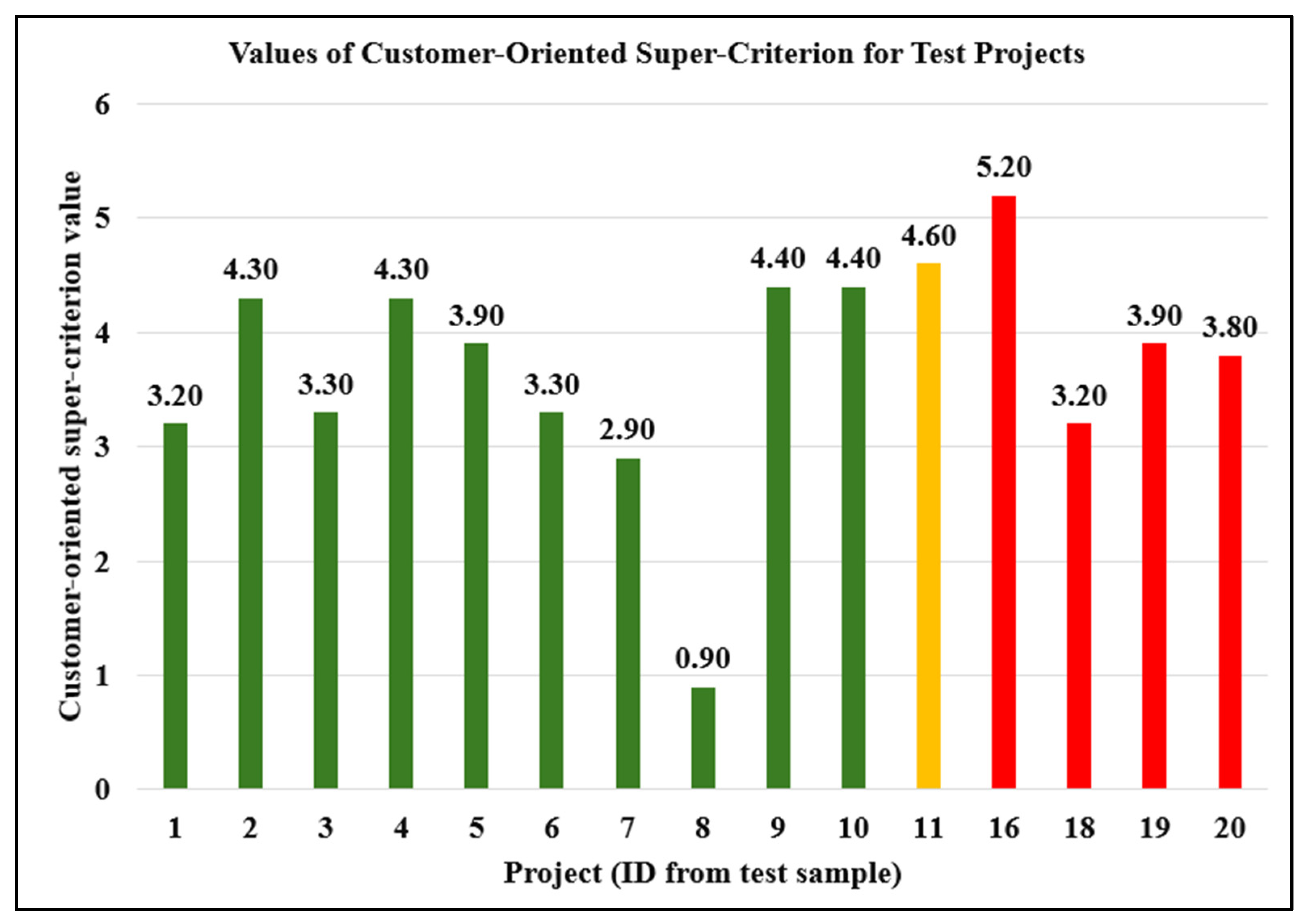
4.2. The Results of Applying the Developed Method
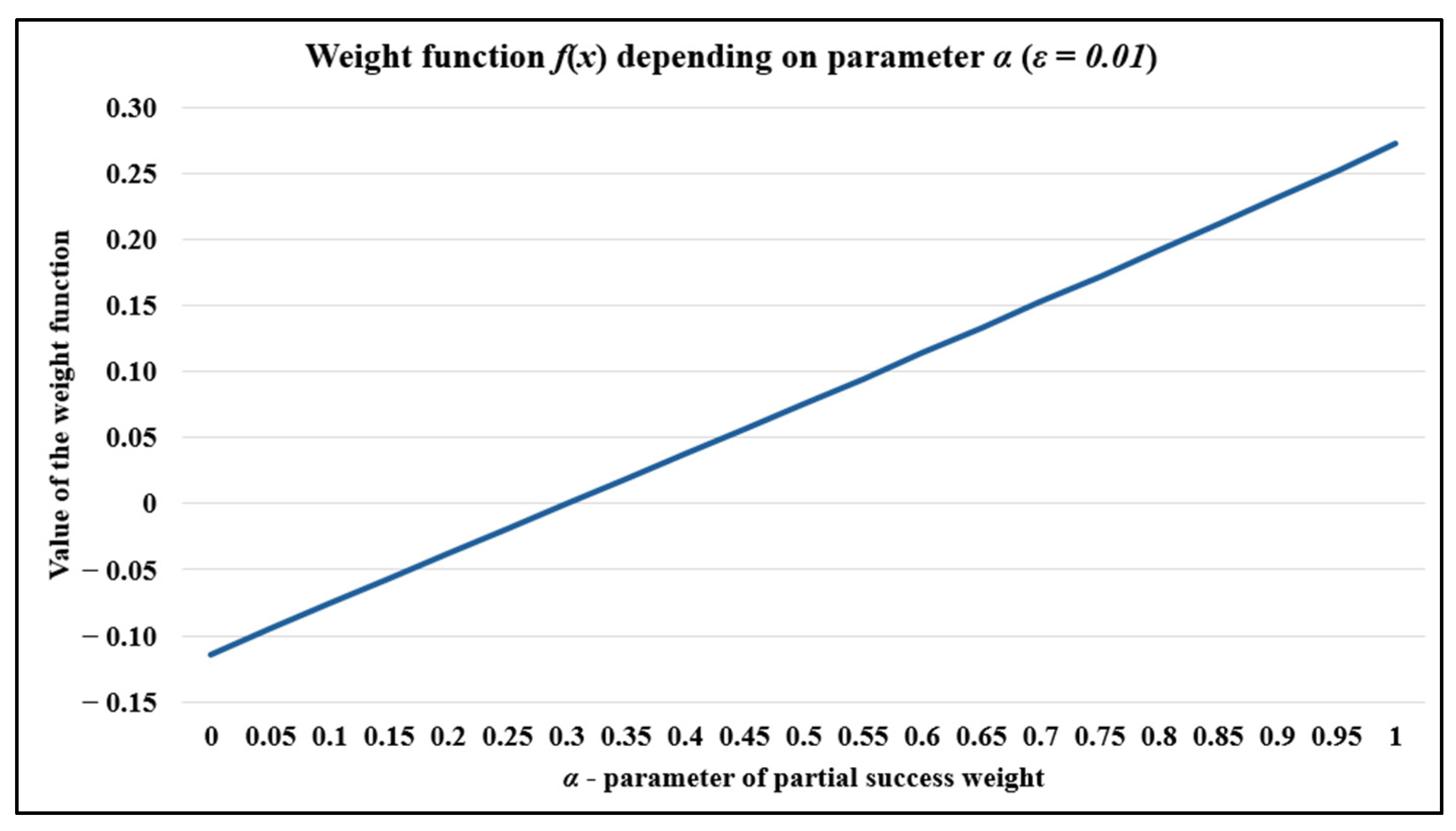
4.3. A Sensitivity Analysis of the Logarithmic Model
5. Discussion
5.1. Interpretation of Results
5.2. Comparison with Classical Multi-Criteria Decision-Making Methods
5.3. The Key Properties and Application Potential of the Method
- -
- The availability of retrospective data on previously implemented projects in the corresponding area;
- -
- Regulatory constraints that projects must comply with;
- -
- Constraints provided by the customer;
- -
- A tool for performing calculations.
6. Conclusions
- -
- The necessity of having retrospective data. In the absence of such data, the method is reduced to a single-criterion selection problem and may be less reliable.
- -
- The method does not provide project ranking, as it is designed to select one of the potentially effective projects.
- -
- When using continuous criteria, it is necessary to divide them into intervals.
- -
- The modification of the method for analyzing projects that are already in the implementation phase;
- -
- The integration of the model with artificial intelligence technologies (in particular, machine learning) for automatic parameter tuning and adaptation to new data;
- -
- The enhancement of the logarithmic model to account for weighting functions in the context of continuous data without discretization.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Number | Criterion Name | Value Range | Regulatory Constraint |
|---|---|---|---|
| 1 | Urban Planning Compliance | Yes/No | Must fully comply with urban zoning and general plan |
| 2 | Land Tenure Status | Owned/Leased/Not Available | Land must be legally owned or leased for project use |
| 3 | Building Code (DBN) Compliance | Yes/No | Project design must meet DBN construction code requirements |
| 4 | Energy Efficiency Class | Class A/B/C/D | Energy efficiency class must not be lower than Class C |
| 11 | Availability of Urban Infrastructure | Yes/No | Must be within reach of existing city infrastructure (utilities, roads) |
| 15 | Environmental Zone Restrictions | Yes/No | Construction not allowed if territory falls under environmental restriction |
| Number | Criterion Name | Value Range | Weight Coefficients |
|---|---|---|---|
| 4 | Energy Efficiency Class | Class A/B/C/D | {‘Class A’: 1.0, ‘Class B’: 0.7, ‘Class C’: 0.4, ‘Class D’: 0.1} |
| 5 | Price per m2 | <USD 600/USD 600–800/>USD 800 | {‘<USD 600’: 1.0, ‘USD 600–800’: 0.6, ‘>USD 800’: 0.2} |
| 6 | Construction Duration | <12/12–24/>24 months | {‘<12’: 1.0, ‘12–24’: 0.6, ‘>24 months’: 0.2} |
| 7 | Experience in Social Housing | Yes/Partial/No | {‘Yes’: 1.0, ‘Partial’: 0.5, ‘No’: 0.1} |
| 10 | Use of Local Contractors | Yes/No | {‘Yes’: 1.0, ‘No’: 0.0} |
| 13 | Ownership of Construction Equipment | Low/Medium/High | {‘High’: 1.0, ‘Medium’: 0.5, ‘Low’: 0.2} |
| 14 | Public Benefit Index | Low/Medium/High | {‘High’: 1.0, ‘Medium’: 0.6, ‘Low’: 0.2} |
| Number | Price per m2 | Construction Duration | Experience in Social Housing | Share of Failed Projects | Completion Rate of Previous Projects | Number of Completed Projects | Group | Use of Local Contractors | Ownership of Construction Equipment | Public Benefit Index |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | >800 | >24 months | Yes | 0% | 50–80% | 0 | Successful | No | Low | Medium |
| 2 | USD 600–800 | >24 months | Yes | >25% | >80% | 1–5 | Successful | Yes | Medium | High |
| 3 | USD 600–800 | 12–24 | Yes | 0% | 50–80% | 1–5 | Successful | Yes | Medium | Medium |
| 4 | USD 600–800 | 12–24 | Yes | 1–25% | 50–80% | 1–5 | Successful | No | Medium | Medium |
| 5 | <600 | >24 months | Yes | 0% | >80% | >5 | Successful | No | Medium | High |
| 6 | USD 600–800 | <12 | Yes | 0% | 50–80% | 1–5 | Successful | No | Medium | High |
| 7 | >800 | 12–24 | Yes | 0% | >80% | 1–5 | Successful | Yes | Medium | Medium |
| 8 | >800 | >24 months | No | 1–25% | >80% | >5 | Successful | Yes | Low | Low |
| 9 | USD 600–800 | <12 | Yes | 0% | 50–80% | >5 | Successful | No | Low | Medium |
| 10 | USD 600–800 | >24 months | Yes | 1–25% | <50% | >5 | Successful | Yes | High | Medium |
| 11 | USD 600–800 | <12 | Partial | 1–25% | >80% | >5 | Partially Successful | Yes | Medium | High |
| 16 | USD 600–800 | >24 months | Yes | 0% | 50–80% | 1–5 | Unsuccessful | Yes | High | Medium |
| 18 | >800 | >24 months | Yes | 0% | 50–80% | 1–5 | Unsuccessful | No | Medium | Medium |
| 19 | >800 | <12 | Yes | 0% | 5–80% | 1–5 | Unsuccessful | Yes | Medium | Low |
| 20 | >800 | 12–24 | Yes | 1–25% | >80% | >5 | Unsuccessful | Yes | Medium | Medium |
References
- Pooja. Urbanization and Its Influence on Worldwide Construction. Civil Engineering, Construction. Available online: https://www.gcelab.com/blog/urbanization-and-its-influence-on-worldwide-construction (accessed on 29 March 2025).
- Yang, Z.; Cao, Y.; Du, J. The Impact of New Urbanization Construction on Sustainable Economic Growth of Resource-Based Cities. Environ. Sci. Pollut. Res. 2023, 30, 96860–96874. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Qian, P.; Yang, L.; Tian, Z.; Luo, J. Analysis of the Impact of Urban Infrastructure on Urbanization Processes at Different Levels from a Spatiotemporal Perspective. Sustainability 2024, 16, 6888. [Google Scholar] [CrossRef]
- Alyamani, R.; Long, S.; Nurunnabi, M. Evaluating Decision Making in Sustainable Project Selection Between Literature and Practice. Sustainability 2021, 13, 8216. [Google Scholar] [CrossRef]
- Lannyati, N.; Sarwono, A.P.; Sami’an, S.; Taufiq, T.; Soeharto, A. Legal and Financial Risk Management in Large-Scale Construction Projects. Sch. Int. J. Law Crime Justice 2024, 7, 316–322. [Google Scholar] [CrossRef]
- Holt, G.D.; Olomolaiye, P.O.; Harris, F.C. A Review of Contractor Selection Practice in the U.K. Construction Industry. Build. Environ. 1995, 30, 553–561. [Google Scholar] [CrossRef]
- Hashemizadeh, A.; Ju, Y. Project Portfolio Selection for Construction Contractors by MCDM–GIS Approach. Int. J. Environ. Sci. Technol. 2019, 16, 8283–8296. [Google Scholar] [CrossRef]
- Mulesa, O.; Horvat, P.; Radivilova, T.; Sabadosh, V.; Baranovskyi, O.; Duran, S. Design of Mechanisms for Ensuring the Execution of Tasks in Project Planning. East.-Eur. J. Enterp. Technol. 2023, 2, 16–22. [Google Scholar] [CrossRef]
- Göküz, B.; Akıner, İ. Investigating Key Factors Influencing the Success of Construction Projects at International Level. Discov. Civ. Eng. 2025, 2, 30. [Google Scholar] [CrossRef]
- Rane, N.L.; Achari, A.; Choudhary, S.P. Multi-Criteria Decision-Making (MCDM) as a powerful tool for sustainable development: Effective applications of AHP, FAHP, TOPSIS, ELECTRE, and VIKOR in sustainability. Int. Res. J. Mod. Eng. Technol. Sci. 2023, 5, 2654–2670. [Google Scholar] [CrossRef]
- Vargas, R.V. Using the Analytic Hierarchy Process (Ahp) to Select and Prioritize Projects in a Portfolio. In Proceedings of the PMI® Global Congress 2010, Washington, DC, USA, 10–12 October 2010; Project Management Institute North America: Washington, DC, USA; Newtown Square, PA, USA, 2010. [Google Scholar]
- Belekar, S.; Jamadar, S.; Manjarekar, J.; Singh, R.; Kazi, A. Application of Analytical Hierarchy Process (AHP) in Construction Works. Int. J. Eng. Res. Technol. 2020, 9, 134–137. Available online: https://www.ijert.org/application-of-analytical-hierarchy-process-ahp-in-construction-works (accessed on 24 April 2025).
- Uzun, B.; Taiwo, M.; Syidanova, A.; Uzun Ozsahin, D. The Technique For Order of Preference by Similarity to Ideal Solution (TOPSIS). In Application of Multi-Criteria Decision Analysis in Environmental and Civil Engineering; Uzun Ozsahin, D., Gökçekuş, H., Uzun, B., LaMoreaux, J., Eds.; Professional Practice in Earth Sciences; Springer International Publishing: Cham, Switzerland, 2021; pp. 25–30. ISBN 978-3-030-64764-3. [Google Scholar]
- Madanchian, M.; Taherdoost, H. A Comprehensive Guide to the TOPSIS Method for Multi-Criteria Decision Making. Sustain. Soc. Dev. 2023, 1, 2220. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Tüysüz, F. An In-Depth Review of Theory of the TOPSIS Method: An Experimental Analysis. J. Manag. Anal. 2020, 7, 281–300. [Google Scholar] [CrossRef]
- Chatterjee, P.; Athawale, V.M.; Chakraborty, S. Materials Selection Using Complex Proportional Assessment and Evaluation of Mixed Data Methods. Mater. Des. 2011, 32, 851–860. [Google Scholar] [CrossRef]
- Maceika, A.; Bugajev, A.; Šostak, O.R.; Vilutienė, T. Decision Tree and AHP Methods Application for Projects Assessment: A Case Study. Sustainability 2021, 13, 5502. [Google Scholar] [CrossRef]
- Kabir, G.; Sadiq, R.; Tesfamariam, S. A Review of Multi-Criteria Decision-Making Methods for Infrastructure Management. Struct. Infrastruct. Eng. 2014, 10, 1176–1210. [Google Scholar] [CrossRef]
- Dursun, M.; Liliç, M. An Integrated Fuzzy MCDM Method for the Evaluation of R&D Projects. Acad. Platf. J. Eng. Smart Syst. 2023, 11, 1–10. [Google Scholar] [CrossRef]
- Hsieh, T.-Y.; Lu, S.-T.; Tzeng, G.-H. Fuzzy MCDM Approach for Planning and Design Tenders Selection in Public Office Buildings. Int. J. Proj. Manag. 2004, 22, 573–584. [Google Scholar] [CrossRef]
- Arabiat, A.; Al-Bdour, H.; Bisharah, M. Predicting the Construction Projects Time and Cost Overruns Using K-Nearest Neighbor and Artificial Neural Network: A Case Study from Jordan. Asian J. Civ. Eng. 2023, 24, 2405–2414. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R.; Dronyuk, I.; Tkachenko, P.; Gregus, M.; Rashkevych, M. Predictive Modeling Based on Small Data in Clinical Medicine: RBF-Based Additive Input-Doubling Method. Math. Biosci. Eng. 2021, 18, 2599–2613. [Google Scholar] [CrossRef]
- Melnykova, N.; Shakhovska, N.; Ml, M.G.; Melnykov, V. Using Big Data for Formalization the Patient’s Personalized Data. Procedia Comput. Sci. 2019, 155, 624–629. [Google Scholar] [CrossRef]
- Mulesa, O.; Ondrejicka, V.; Yehorchenkov, O.; Yehorchenkova, N.; Jamecny, L.; Marusynets, M. Development of a Semi-Automated Decision-Making Method for the Resilience of Urban Healthcare Systems in Crisis Situations. Urban Sci. 2025, 9, 15. [Google Scholar] [CrossRef]
- Mulesa, O.; Yatsyna, O.; Melnyk, O.; Myronyuk, I.; Povkhan, I.; Batyuk, A. Prediction of the Occurrence of Threatening Conditions in Individuals as a Problem of Assigning an Object to a Class. In Proceedings of the 2022 IEEE 17th International Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 10–12 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 332–335. [Google Scholar]
- Ashtari, M.A.; Ansari, R.; Hassannayebi, E.; Jeong, J. Cost Overrun Risk Assessment and Prediction in Construction Projects: A Bayesian Network Classifier Approach. Buildings 2022, 12, 1660. [Google Scholar] [CrossRef]
- Chandanshive, V.; Kambekar, A. Prediction of Building Construction Project Cost Using Support Vector Machine. Ind. Eng. Strateg. Manag. 2021, 1, 31–42. [Google Scholar] [CrossRef]
- Yan, A.; Cheng, Z. A Review of the Development and Future Challenges of Case-Based Reasoning. Appl. Sci. 2024, 14, 7130. [Google Scholar] [CrossRef]
- Xie, L.; Wu, S.; Chen, Y.; Chang, R.; Chen, X. A Case-Based Reasoning Approach for Solving Schedule Delay Problems in Prefabricated Construction Projects. Autom. Constr. 2023, 154, 105028. [Google Scholar] [CrossRef]
- Renugadevi, N.; Mehta, M.; Gideon Daniel Giftson, T. A Review of Urban Heat Island Mapping Approaches with a Special Emphasis on the Indian Region. Environ. Monit. Assess. 2025, 197, 365. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, H.; Zhang, Z. Monitoring and Assessing the Growth Law of Urban Land Using Multi-Source Data: A Case Study of Five East African Countries. Land Use Policy 2025, 153, 107530. [Google Scholar] [CrossRef]
- Hajarian, A. Spatial Analysis of the Relationship between Smart Cities and Urban Livability (Case Study: Neighborhoods of Isfahan). Geogr. Environ. Sustain. 2025, 15, 97–114. [Google Scholar] [CrossRef]
- Buyana, K.; Walubwa, J.; Mukwaya, P.; Sseviiri, H.; Byarugaba, D.; Nsangi, G. The Role of Visual Ethnography in Co-Producing Climate Information Services in Cities. Glob. Soc. Chall. J. 2025, 4, 63–82. [Google Scholar] [CrossRef]
- The Business Research Company. Construction Global Market Report 2025—By Type of Construction (Buildings Construction, Heavy and Civil Engineering Construction, Specialty Trade Contractors, Land Planning and Development), by Type of Contractor (Large Contractor, Small Contractor), by End-Use Sector (Public, Private)—Market Size, Trends, and Global Forecast 2025–2034; The Business Research Company: Telangana, India, 2025. [Google Scholar]
- Fraga, B. Why Do Projects Fail? Available online: https://www.mbpce.com/blog/why-do-projects-fail/ (accessed on 16 March 2025).
- Rivera, A.; Le, N.; Kashiwagi, J.; Kashiwagi, D. Identifying the Global Performance of the Construction Industry. J. Adv. Perform. Inf. Value 2016, 8, 7. [Google Scholar] [CrossRef]
- Abbasi, O.; Noorzai, E.; Gharouni Jafari, K.; Golabchi, M. Exploring the Causes of Delays in Construction Industry Using a Cause-and-Effect Diagram: Case Study for Iran. J. Archit. Eng. 2020, 26, 05020008. [Google Scholar] [CrossRef]
- Zidane, Y.J.-T.; Andersen, B. The Top 10 Universal Delay Factors in Construction Projects. Int. J. Manag. Proj. Bus. 2018, 11, 650–672. [Google Scholar] [CrossRef]
- Durdyev, S.; Hosseini, M.R. Causes of Delays on Construction Projects: A Comprehensive List. Int. J. Manag. Proj. Bus. 2019, 13, 20–46. [Google Scholar] [CrossRef]
- Sharifi, M.; Ebrahimi, M.; Seifollahi, F. Landfill Site Selection for Construction and Demolition Waste in Plain and Desert Cities Using Spatial Information System and TOPSIS (Case Study: Yazd City). Geogr. Environ. Plan. 2024, 35, 47–82. Available online: https://gep.ui.ac.ir/article_29072.html (accessed on 16 March 2025).
- Masi, M.; Arrighi, C.; Piragino, F.; Castelli, F. Participatory Multi-Criteria Decision Making for Optimal Siting of Multipurpose Artificial Reservoirs. J. Environ. Manag. 2024, 370, 122904. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, M.; Chen, L.; Luo, L.; Wang, W.; Zhu, X.; Sun, Y. Multi-Objective Optimization of Urban Gas Station Site Selection Under Territorial Spatial Planning Constraints. ISPRS Int. J. Geo-Inf. 2024, 13, 375. [Google Scholar] [CrossRef]
- Oruc, S.; Dikbas, H.A.; Gumus, B.; Yucel, I. The Impact of Climate Change on Construction Activity Performance. Buildings 2024, 14, 372. [Google Scholar] [CrossRef]
- Agresti, A. Statistical Methods for the Social Sciences; Pearson: London, UK, 2018; Volume 5, ISBN 978-0-13-450710-1. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning. In Information Science and Statistics, 1st ed.; Springer: New York, NY, USA, 2016; ISBN 978-1-4939-3843-8. [Google Scholar]
- Hnatienko, H.; Domanetska, I.; Hnatiienko, O.; Khrolenko, Y. Scheme of Sequential Analysis of Options for Creating an Intelligent System for Analyzing Competitive Proposals for Urban Transformation; CEUR: Kyiv, Ukraine, 2024. [Google Scholar]
- Szukits, Á.; Móricz, P. Towards Data-Driven Decision Making: The Role of Analytical Culture and Centralization Efforts. Rev. Manag. Sci. 2024, 18, 2849–2887. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, T.; Wang, X. High-Speed Railways Reduces Carbon Emissions: Mediating Effects of Green Innovation and the Resilience of Environmental Investment. Humanit. Soc. Sci. Commun. 2024, 11, 1127. [Google Scholar] [CrossRef]
- Ren, X.; Zeng, G.; Zhao, Y. Digital Finance and Corporate ESG Performance: Empirical Evidence from Listed Companies in China. Pac.-Basin Financ. J. 2023, 79, 102019. [Google Scholar] [CrossRef]

| Number | Criterion Name | Criterion Type | Value Range | Comment |
|---|---|---|---|---|
| 1 | Urban Planning Compliance | Normative | Yes/No | Compliance with city master plan (mandatory) |
| 2 | Land Tenure Status | Normative, Retrospective | Owned/Leased/Not Available | Impact on timing and stability |
| 3 | Building Code (DBN) Compliance | Normative | Yes/No | Technical compliance check |
| 4 | Energy Efficiency Class | Normative, Customer | Class A/B/C/D | Regulated and of interest to customer |
| 5 | Price per m2 | Customer, Retrospective | <USD 600/USD 600–800/>USD 800 | Sale or construction price |
| 6 | Construction Duration | Customer, Retrospective | <12/12–24/>24 months | Project implementation timeline |
| 7 | Experience in Social Housing | Customer, Retrospective | Yes/Partial/No | Relevance of experience to customer |
| 8 | Share of Failed Projects | Retrospective | 0%/1–25%/>25% | Risk indicator |
| 9 | Completion Rate of Previous Projects | Retrospective | <50%/50–80%/>80% | Ratio of completed to total projects |
| 10 | Use of Local Contractors | Customer | Yes/No | Support for local economy |
| 11 | Availability of Urban Infrastructure | Normative | Yes/No | Access to networks and transport |
| 12 | Number of Completed Projects | Retrospective | 0/1–5/>5 | Access to networks and transport |
| 13 | Ownership of Construction Equipment | Customer | Low/Medium/High | Level of contractor’s independence |
| 14 | Public Benefit Index | Customer | Low/Medium/High | Social significance of project |
| 15 | Environmental Zone Restrictions | Normative | Yes/No | Construction restrictions on site |
| Criterion | Criterion Value | Successful | Conditionally Successful | Unsuccessful | (x) |
|---|---|---|---|---|---|
| Land Tenure Status | Owned | 15 | 1 | 2 | 0.733423 |
| Leased | 4 | 5 | 8 | −0.37971 | |
| Not Available | 2 | 1 | 2 | −0.10431 | |
| Price per m2 | <USD 600 | 2 | 4 | 7 | −0.56032 |
| USD 600–800 | 14 | 3 | 3 | 0.431453 | |
| >USD 800 | 5 | 0 | 2 | 0.396642 | |
| Construction Duration | <12 | 4 | 3 | 10 | −0.43007 |
| 12–24 | 7 | 4 | 1 | 0.268369 | |
| >24 Months | 10 | 0 | 1 | 0.996113 | |
| Experience in Social Housing | Yes | 14 | 2 | 1 | 0.742023 |
| Partial | 5 | 2 | 6 | −0.14819 | |
| No | 2 | 3 | 5 | −0.45318 | |
| Share of Failed Projects | 0% | 7 | 1 | 2 | 0.409229 |
| 1–25% | 13 | 6 | 7 | 0.080344 | |
| >25% | 1 | 0 | 3 | −0.47425 | |
| Completion Rate of Previous Projects | <50% | 3 | 3 | 7 | −0.41608 |
| 50–80% | 3 | 1 | 4 | −0.17564 | |
| >80% | 15 | 3 | 1 | 0.660649 | |
| Number of Completed Projects | 0 | 2 | 1 | 2 | −0.10431 |
| 1–5 | 11 | 4 | 7 | 0.063224 | |
| >5 | 8 | 2 | 3 | 0.261095 |
| Criterion | AHP/TOPSIS/VIKOR | The Proposed Method |
|---|---|---|
| Type of Data | Subjective expert assessments | Retrospective empirical data |
| Dependence on Experts | High | Minimal |
| Possibility to Consider Regional Specificity | Limited | Direct integration through historical data |
| Weight Coefficient Formation | Method of pairwise comparisons/heuristics | Automatic, logarithmic function based on frequency |
| Adaptive Criterion Reduction | Absent | Via iterative procedure |
| Alternative Ranking | Yes | After repeated execution of the procedure |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulesa, O. An Adaptive Selection of Urban Construction Projects: A Multi-Stage Model with Iterative Supercriterion Reduction. Urban Sci. 2025, 9, 146. https://doi.org/10.3390/urbansci9050146
Mulesa O. An Adaptive Selection of Urban Construction Projects: A Multi-Stage Model with Iterative Supercriterion Reduction. Urban Science. 2025; 9(5):146. https://doi.org/10.3390/urbansci9050146
Chicago/Turabian StyleMulesa, Oksana. 2025. "An Adaptive Selection of Urban Construction Projects: A Multi-Stage Model with Iterative Supercriterion Reduction" Urban Science 9, no. 5: 146. https://doi.org/10.3390/urbansci9050146
APA StyleMulesa, O. (2025). An Adaptive Selection of Urban Construction Projects: A Multi-Stage Model with Iterative Supercriterion Reduction. Urban Science, 9(5), 146. https://doi.org/10.3390/urbansci9050146






