Enhancing PM2.5 Air Pollution Prediction Performance by Optimizing the Echo State Network (ESN) Deep Learning Model Using New Metaheuristic Algorithms
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Used
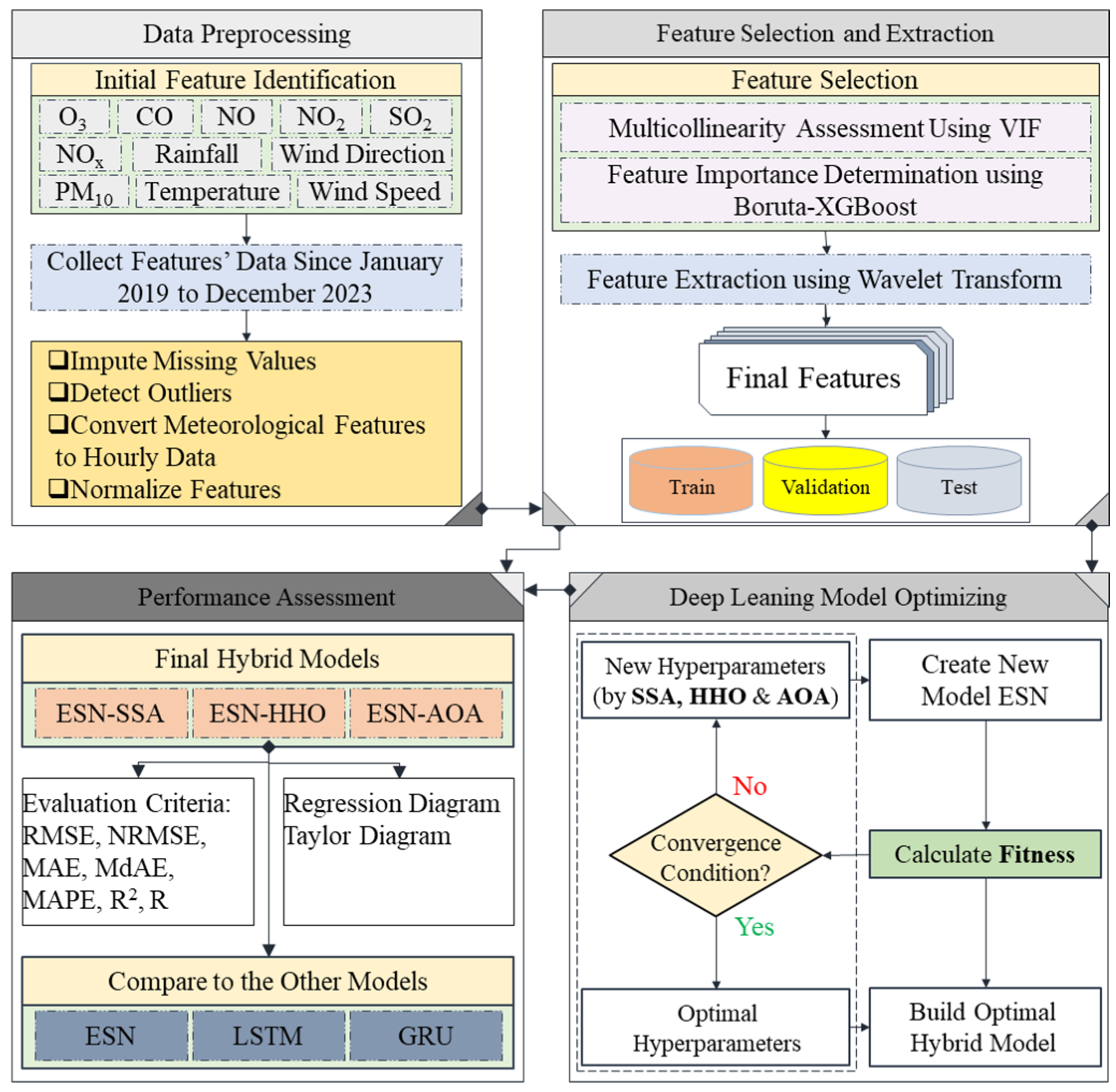
2.2. Proposed Methodology
| Algorithm 1. Pseudo-code of the proposed methodology. | |
| 1. Data Preprocessing | |
| |
2. Feature Selection
| |
| 4. For 1 to 200: | |
| 5. Execution of metaheuristic (SSA, HHO, AOA) operators | |
| 6. Model training | |
| 7. Calculate objective function (0.8 × RMSETraining + 0.2 × RMSEValidation) | |
| 8. Update best solution | |
| 9. End (end of metaheuristic algorithms) | |
| 10. Return the best solution (optimal hyperparameters and weights vectors) | |
2.3. Boruta-XGBoost
2.4. ESN
2.5. Metaheuristic Algorithms
| Algorithm 2. Pseudo-code of metaheuristic algorithms for hyperparameter tuning | |
| 1. Inputs: the population size and maximum number of iterations | |
| 2. Outputs: the location of the best solution and its objective function value | |
| 3. Initial metaheuristic parameter (if needed) | |
| 4. Initial candidate solution | |
| 5. While (the stopping condition is not met) do: | |
| 6. Execution of metaheuristic operators | |
| 7. Calculating the objective function value | |
| 8. Updating the best solution | |
| 9. End (end of metaheuristic algorithms) | |
| 10. Return the best solution | |
2.5.1. AOA
2.5.2. HHO
2.5.3. SSA
2.6. Evaluation Criteria
3. Results
3.1. Data Preprocessing
3.2. Feature Selection and Extraction
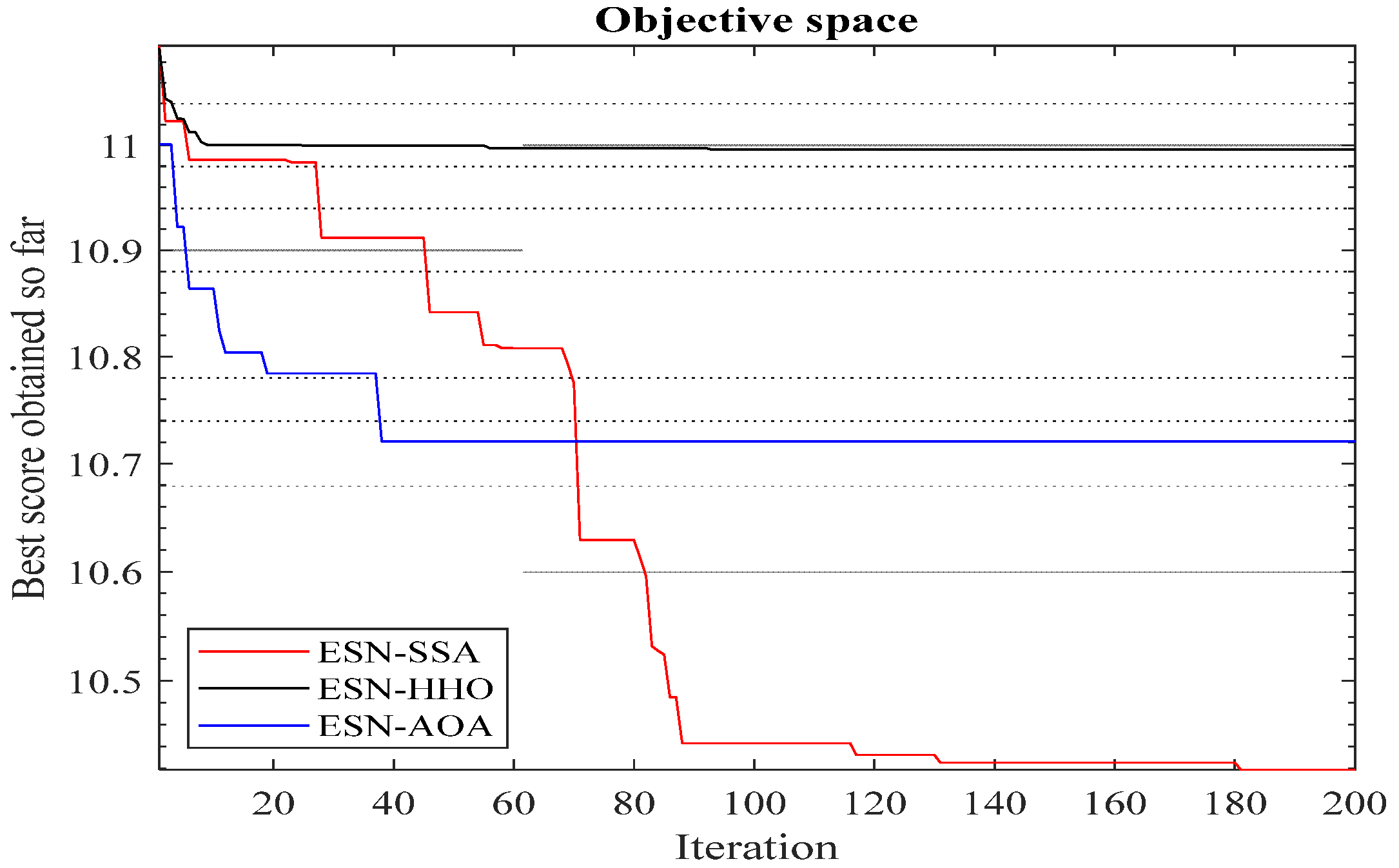
3.3. Deep Leaning Model Optimizing
3.4. Performance Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Yao, L.; Xu, Y.; Sun, S.; Li, T. Potential Heterogeneity in the Relationship between Urbanization and Air Pollution, from the Perspective of Urban Agglomeration. J. Clean. Prod. 2021, 298, 126822. [Google Scholar] [CrossRef]
- Bai, K.; Li, K.; Sun, Y.; Wu, L.; Zhang, Y.; Chang, N.-B.; Li, Z. Global Synthesis of Two Decades of Research on Improving PM2.5 Estimation Models from Remote Sensing and Data Science Perspectives. Earth-Sci. Rev. 2023, 241, 104461. [Google Scholar] [CrossRef]
- Luan, T.; Guo, X.; Guo, L.; Zhang, T. Quantifying the Relationship between PM2.5 Concentration, Visibility and Planetary Boundary Layer Height for Long-Lasting Haze and Fog–Haze Mixed Events in Beijing. Atmos. Chem. Phys. 2018, 18, 203–225. [Google Scholar] [CrossRef]
- Chuang, K.-J.; Chan, C.-C.; Su, T.-C.; Lee, C.-T.; Tang, C.-S. The Effect of Urban Air Pollution on Inflammation, Oxidative Stress, Coagulation, and Autonomic Dysfunction in Young Adults. Am. J. Respir. Crit. Care Med. 2007, 176, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Mills, N.L.; Donaldson, K.; Hadoke, P.W.; Boon, N.A.; MacNee, W.; Cassee, F.R.; Sandström, T.; Blomberg, A.; Newby, D.E. Adverse Cardiovascular Effects of Air Pollution. Nat. Clin. Pract. Cardiovasc. Med. 2009, 6, 36–44. [Google Scholar] [CrossRef]
- Wu, R.; Dai, H.; Geng, Y.; Xie, Y.; Masui, T.; Liu, Z.; Qian, Y. Economic Impacts from PM2.5 Pollution-Related Health Effects: A Case Study in Shanghai. Environ. Sci. Technol. 2017, 51, 5035–5042. [Google Scholar] [CrossRef]
- Global Burden of Disease Collaborative Network Global Burden of Disease Study 2019 (GBD 2019) Air Pollution Exposure Estimates 1990–2019; Institute for Health Metrics and Evaluation (IHME): Seattle, WA, USA, 2021. [CrossRef]
- Pandey, A.; Brauer, M.; Cropper, M.L.; Balakrishnan, K.; Mathur, P.; Dey, S.; Turkgulu, B.; Kumar, G.A.; Khare, M.; Beig, G. Health and Economic Impact of Air Pollution in the States of India: The Global Burden of Disease Study 2019. Lancet Planet. Health 2021, 5, e25–e38. [Google Scholar] [CrossRef]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The Contribution of Outdoor Air Pollution Sources to Premature Mortality on a Global Scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef]
- IQAir. World Air Quality Report: Region & City PM2.5 Ranking 2022. Available online: https://www.greenpeace.org/static/planet4-india-stateless/2023/03/2fe33d7a-2022-world-air-quality-report.pdf (accessed on 21 February 2025).
- Faridi, S.; Bayat, R.; Cohen, A.J.; Sharafkhani, E.; Brook, J.R.; Niazi, S.; Shamsipour, M.; Amini, H.; Naddafi, K.; Hassanvand, M.S. Health Burden and Economic Loss Attributable to Ambient PM2.5 in Iran Based on the Ground and Satellite Data. Sci. Rep. 2022, 12, 14386. [Google Scholar] [CrossRef]
- GBD Compare. GBD Compare 2021. Available online: https://vizhub.healthdata.org/gbd-compare/ (accessed on 21 February 2025).
- Kazemi, Z.; Yunesian, M.; Hassanvand, M.S.; Daroudi, R.; Ghorbani, A.; Sefiddashti, S.E. Hidden Health Effects and Economic Burden of Stroke and Coronary Heart Disease Attributed to Ambient Air Pollution (PM2.5) in Tehran, Iran: Evidence from an Assessment and Forecast up to 2030. Ecotoxicol. Environ. Saf. 2024, 286, 117158. [Google Scholar] [CrossRef]
- Abbasi, M.T.; Alesheikh, A.A.; Jafari, A.; Lotfata, A. Spatial and Temporal Patterns of Urban Air Pollution in Tehran with a Focus on PM2.5 and Associated Pollutants. Sci. Rep. 2024, 14, 25150. [Google Scholar] [CrossRef] [PubMed]
- Anchan, A.; Shedthi, B.S.; Manasa, G. Models Predicting PM2.5 Concentrations—A Review. In Recent Advances in Artificial Intelligence and Data Engineering; Shetty, D.P., Shetty, S., Eds.; Advances in Intelligent Systems and Computing; Springer Singapore: Singapore, 2022; Volume 1386, pp. 65–83. ISBN 9789811633416. [Google Scholar]
- Zhou, S.; Wang, W.; Zhu, L.; Qiao, Q.; Kang, Y. Deep-Learning Architecture for PM2.5 Concentration Prediction: A Review. Environ. Sci. Ecotechnol. 2024, 21, 100400. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Ning, M.; Lei, Y.; Sun, Y.; Liu, W.; Wang, J. Defending Blue Sky in China: Effectiveness of the “Air Pollution Prevention and Control Action Plan” on Air Quality Improvements from 2013 to 2017. J. Environ. Manag. 2019, 252, 109603. [Google Scholar] [CrossRef] [PubMed]
- Zamani Joharestani, M.; Cao, C.; Ni, X.; Bashir, B.; Talebiesfandarani, S. PM2.5 Prediction Based on Random Forest, XGBoost, and Deep Learning Using Multisource Remote Sensing Data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef]
- Rad, A.K.; Razmi, S.-O.; Nematollahi, M.J.; Naghipour, A.; Golkar, F.; Mahmoudi, M. Machine Learning Models for Predicting Interactions between Air Pollutants in Tehran Megacity, Iran. Alex. Eng. J. 2024, 104, 464–479. [Google Scholar] [CrossRef]
- Salehie, O.; Jamal, M.H.B.; Shahid, S. Characterization and Prediction of PM2.5 Levels in Afghanistan Using Machine Learning Techniques. Theor. Appl. Climatol. 2024, 155, 9081–9097. [Google Scholar] [CrossRef]
- Masood, A.; Ahmad, K. A Model for Particulate Matter (PM2.5) Prediction for Delhi Based on Machine Learning Approaches. Procedia Comput. Sci. 2020, 167, 2101–2110. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Wang, X. PM2.5 Prediction Based on Modified Whale Optimization Algorithm and Support Vector Regression. Sci. Rep. 2024, 14, 23296. [Google Scholar] [CrossRef]
- Oprea, M.; Mihalache, S.F.; Popescu, M. Computational Intelligence-Based PM2.5 Air Pollution Forecasting. Int. J. Comput. Commun. Control 2017, 12, 365–380. [Google Scholar] [CrossRef]
- Shah, J.; Mishra, B. Analytical Equations Based Prediction Approach for PM2.5 Using Artificial Neural Network. SN Appl. Sci. 2020, 2, 1516. [Google Scholar] [CrossRef]
- Xie, X.; Semanjski, I.; Gautama, S.; Tsiligianni, E.; Deligiannis, N.; Rajan, R.T.; Pasveer, F.; Philips, W. A Review of Urban Air Pollution Monitoring and Exposure Assessment Methods. ISPRS Int. J. Geo-Inf. 2017, 6, 389. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Z.; Qu, L. A Novel Machine Learning-Based Artificial Intelligence Method for Predicting the Air Pollution Index PM2.5. J. Clean. Prod. 2024, 468, 143042. [Google Scholar] [CrossRef]
- Peng, L.; Zhu, Q.; Lv, S.-X.; Wang, L. Effective Long Short-Term Memory with Fruit Fly Optimization Algorithm for Time Series Forecasting. Soft Comput. 2020, 24, 15059–15079. [Google Scholar] [CrossRef]
- Wang, Z.; Crooks, J.L.; Regan, E.A.; Karimzadeh, M. High-Resolution Estimation of Daily PM2.5 Levels in the Contiguous US Using Bi-LSTM with Attention. Remote Sens. 2025, 17, 126. [Google Scholar] [CrossRef]
- Kim, Y.; Park, S.-B.; Lee, S.; Park, Y.-K. Comparison of PM2.5 Prediction Performance of the Three Deep Learning Models: A Case Study of Seoul, Daejeon, and Busan. J. Ind. Eng. Chem. 2023, 120, 159–169. [Google Scholar] [CrossRef]
- Govande, A.; Attada, R.; Shukla, K.K. Predicting PM2.5 Levels over Indian Metropolitan Cities Using Recurrent Neural Networks. Earth Sci. Inform. 2025, 18, 1–16. [Google Scholar] [CrossRef]
- Wei, M.; Du, X. Apply a Deep Learning Hybrid Model Optimized by an Improved Chimp Optimization Algorithm in PM2.5 Prediction. Mach. Learn. Appl. 2025, 19, 100624. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H. Grey Wolf Optimization–Based Deep Echo State Network for Time Series Prediction. Front. Energy Res. 2022, 10, 858518. [Google Scholar] [CrossRef]
- Na, X.; Han, M.; Ren, W.; Zhong, K. Modified BBO-Based Multivariate Time-Series Prediction System with Feature Subset Selection and Model Parameter Optimization. IEEE Trans. Cybern. 2020, 52, 2163–2173. [Google Scholar] [CrossRef]
- Qiao, J.; Li, F.; Han, H.; Li, W. Growing Echo-State Network with Multiple Subreservoirs. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 391–404. [Google Scholar] [CrossRef]
- Yang, C.; Yang, S.; Tang, J.; Li, B. Design and Application of Adaptive Sparse Deep Echo State Network. IEEE Trans. Consum. Electron. 2023, 70, 3582–3592. [Google Scholar] [CrossRef]
- Xu, X.; Ren, W. Application of a Hybrid Model Based on Echo State Network and Improved Particle Swarm Optimization in PM2.5 Concentration Forecasting: A Case Study of Beijing, China. Sustainability 2019, 11, 3096. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.; Chen, Q. An Echo State Network with Adaptive Improved Pigeon-Inspired Optimization for Time Series Prediction. Appl. Intell. 2025, 55, 443. [Google Scholar] [CrossRef]
- Chen, H.-C.; Wei, D.-Q. Chaotic Time Series Prediction Using Echo State Network Based on Selective Opposition Grey Wolf Optimizer. Nonlinear Dyn. 2021, 104, 3925–3935. [Google Scholar] [CrossRef]
- Heidari, A.A.; Akhoondzadeh, M.; Chen, H. A Wavelet PM2.5 Prediction System Using Optimized Kernel Extreme Learning with Boruta-XGBoost Feature Selection. Mathematics 2022, 10, 3566. [Google Scholar] [CrossRef]
- Zhu, S.; Lian, X.; Liu, H.; Hu, J.; Wang, Y.; Che, J. Daily Air Quality Index Forecasting with Hybrid Models: A Case in China. Environ. Pollut. 2017, 231, 1232–1244. [Google Scholar] [CrossRef]
- Xing, G.; Zhao, E.; Zhang, C.; Wu, J. A Decomposition-Ensemble Approach with Denoising Strategy for PM2.5 Concentration Forecasting. Discret. Dyn. Nat. Soc. 2021, 2021, 5577041. [Google Scholar] [CrossRef]
- Shu, Y.; Ding, C.; Tao, L.; Hu, C.; Tie, Z. Air Pollution Prediction Based on Discrete Wavelets and Deep Learning. Sustainability 2023, 15, 7367. [Google Scholar] [CrossRef]
- Yang, Z. Hourly Ambient Air Humidity Fluctuation Evaluation and Forecasting Based on the Least-Squares Fourier-Model. Measurement 2019, 133, 112–123. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Xu, J.; Wei, Y.; Zeng, P. VMD-Based Iterative Boruta Feature Extraction and CNNA-BiLSTM for Short-Term Load Forecasting. Electr. Power Syst. Res. 2025, 238, 111172. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X. AQI Time Series Prediction Based on a Hybrid Data Decomposition and Echo State Networks. Environ. Sci. Pollut. Res. 2021, 28, 51160–51182. [Google Scholar] [CrossRef] [PubMed]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Kayhomayoon, Z.; Naghizadeh, F.; Malekpoor, M.; Arya Azar, N.; Ball, J.; Ghordoyee Milan, S. Prediction of Evaporation from Dam Reservoirs under Climate Change Using Soft Computing Techniques. Environ. Sci. Pollut. Res. 2023, 30, 27912–27935. [Google Scholar] [CrossRef]
- Rezaie, F.; Panahi, M.; Bateni, S.M.; Lee, S.; Jun, C.; Trauernicht, C.; Neale, C.M. Development of Novel Optimized Deep Learning Algorithms for Wildfire Modeling: A Case Study of Maui, Hawai ‘i. Eng. Appl. Artif. Intell. 2023, 125, 106699. [Google Scholar] [CrossRef]
- Almalawi, A.; Khan, A.I.; Alsolami, F.; Alkhathlan, A.; Fahad, A.; Irshad, K.; Alfakeeh, A.S.; Qaiyum, S. Arithmetic Optimization Algorithm with Deep Learning Enabled Airborne Particle-Bound Metals Size Prediction Model. Chemosphere 2022, 303, 134960. [Google Scholar] [CrossRef]
- Paryani, S.; Bordbar, M.; Jun, C.; Panahi, M.; Bateni, S.M.; Neale, C.M.; Moeini, H.; Lee, S. Hybrid-Based Approaches for the Flood Susceptibility Prediction of Kermanshah Province, Iran. Nat. Hazards 2023, 116, 837–868. [Google Scholar] [CrossRef]
- Marouane, B.; Mu’azu, M.A.; Petroselli, A. Prediction of Reservoir Evaporation Considering Water Temperature and Using ANFIS Hybridized with Metaheuristic Algorithms. Earth Sci. Inform. 2024, 17, 1779–1798. [Google Scholar] [CrossRef]
- Ge, Q.; Li, C.; Yang, F. Support Vector Machine to Predict the Pile Settlement Using Novel Optimization Algorithm. Geotech. Geol. Eng. 2023, 41, 3861–3875. [Google Scholar] [CrossRef]
- Dogan, M.; Taspinar, Y.S.; Cinar, I.; Kursun, R.; Ozkan, I.A.; Koklu, M. Dry Bean Cultivars Classification Using Deep Cnn Features and Salp Swarm Algorithm Based Extreme Learning Machine. Comput. Electron. Agric. 2023, 204, 107575. [Google Scholar] [CrossRef]
- Junninen, H.; Niska, H.; Tuppurainen, K.; Ruuskanen, J.; Kolehmainen, M. Methods for Imputation of Missing Values in Air Quality Data Sets. Atmos. Environ. 2004, 38, 2895–2907. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting. R Package Version 0.4-2 2015, 1, 1–4. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks-with an Erratum Note. Bonn Ger. Ger. Natl. Res. Cent. Inf. Technol. Gmd Tech. Rep. 2001, 148, 13. [Google Scholar]
- Rigamonti, M.; Baraldi, P.; Zio, E.; Roychoudhury, I.; Goebel, K.; Poll, S. Ensemble of Optimized Echo State Networks for Remaining Useful Life Prediction. Neurocomputing 2018, 281, 121–138. [Google Scholar] [CrossRef]
- Yusoff, M.-H.; Chrol-Cannon, J.; Jin, Y. Modeling Neural Plasticity in Echo State Networks for Classification and Regression. Inf. Sci. 2016, 364, 184–196. [Google Scholar] [CrossRef]
- Ozturk, M.C.; Xu, D.; Principe, J.C. Analysis and Design of Echo State Networks. Neural Comput. 2007, 19, 111–138. [Google Scholar] [CrossRef]
- Sun, C.; Song, M.; Hong, S.; Li, H. A Review of Designs and Applications of Echo State Networks. arXiv 2020, arXiv:2012.02974. [Google Scholar] [CrossRef]
- He, K.; Mao, L.; Yu, J.; Huang, W.; He, Q.; Jackson, L. Long-Term Performance Prediction of PEMFC Based on LASSO-ESN. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Jaeger, H. Echo State Network. Scholarpedia 2007, 2, 2330. [Google Scholar] [CrossRef]
- Marino, R.; Kirkpatrick, S. Hard Optimization Problems Have Soft Edges. Sci. Rep. 2023, 13, 3671. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Alesheikh, A.A.; Chatrsimab, Z.; Rezaie, F.; Lee, S.; Jafari, A.; Panahi, M. Land Subsidence Susceptibility Mapping Based on InSAR and a Hybrid Machine Learning Approach. Egypt. J. Remote Sens. Space Sci. 2024, 27, 255–267. [Google Scholar] [CrossRef]
- Jafari, A.; Alesheikh, A.A.; Zandi, I.; Lotfata, A. Spatial Prediction of Human Brucellosis Susceptibility Using an Explainable Optimized Adaptive Neuro Fuzzy Inference System. Acta Trop. 2024, 260, 107483. [Google Scholar] [CrossRef]
- Yousefi, Z.; Alesheikh, A.A.; Jafari, A.; Torktatari, S.; Sharif, M. Stacking Ensemble Technique Using Optimized Machine Learning Models with Boruta–XGBoost Feature Selection for Landslide Susceptibility Mapping: A Case of Kermanshah Province, Iran. Information 2024, 15, 689. [Google Scholar] [CrossRef]
- Jafari, A.; Alesheikh, A.A.; Rezaie, F.; Panahi, M.; Shahsavar, S.; Lee, M.-J.; Lee, S. Enhancing a Convolutional Neural Network Model for Land Subsidence Susceptibility Mapping Using Hybrid Meta-Heuristic Algorithms. Int. J. Coal Geol. 2023, 277, 104350. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B. Improved Arithmetic Optimization Algorithm and Its Application to Discrete Structural Optimization; Elsevier: Amsterdam, The Netherlands, 2022; Volume 35, pp. 748–764. [Google Scholar]
- Hu, G.; Zhong, J.; Du, B.; Wei, G. An Enhanced Hybrid Arithmetic Optimization Algorithm for Engineering Applications. Comput. Methods Appl. Mech. Eng. 2022, 394, 114901. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, H.; Heidari, A.A.; Chen, Y.; Wu, Z.; Cai, Z.; Liu, L. WHHO: Enhanced Harris Hawks Optimizer for Feature Selection in High-Dimensional Data. Clust. Comput. 2025, 28, 186. [Google Scholar] [CrossRef]
- Bilal, O.; Asif, S.; Zhao, M.; Khan, S.U.R.; Li, Y. An Amalgamation of Deep Neural Networks Optimized with Salp Swarm Algorithm for Cervical Cancer Detection. Comput. Electr. Eng. 2025, 123, 110106. [Google Scholar] [CrossRef]







| Index | O3 (ppb) | CO (ppm) | NO (ppb) | NO2 (ppb) | NOx (ppb) | SO2 (ppb) |
| Min. | −6.06 | −0.02 | −10.83 | 1.92 | 2.37 | 0.10 |
| Max. | 213.03 | 20.96 | 983.53 | 173.08 | 1093.01 | 190.71 |
| Std. | 24.84 | 1.54 | 102.88 | 23.07 | 116.84 | 4.71 |
| Mean | 21.87 | 1.90 | 68.97 | 47.88 | 116.60 | 5.52 |
| Median | 9.60 | 1.42 | 24.56 | 47.10 | 76.40 | 4.43 |
| Index | PM10 (μg/m3) | WD (c°) | WS (m/s) | TEMP (°C) | RAIN (mm) | PM2.5 (μg/m3) |
| Min. | 1.50 | 0.00 | 0.00 | 0.00 | 1.00 | 0.33 |
| Max. | 1654.50 | 97.00 | 9.00 | 9.00 | 9.00 | 293.60 |
| Std. | 50.91 | 15.10 | 2.85 | 1.52 | 0.89 | 21.65 |
| Mean | 79.03 | 10.30 | 2.54 | 1.16 | 1.75 | 32.76 |
| Median | 71.29 | 5.00 | 1.43 | 0.76 | 1.67 | 27.00 |
| Features | VIF | Features | VIF |
|---|---|---|---|
| O3 | 1.82 | PM10 | 1.38 |
| CO | 8.91 | WD | 1.23 |
| NO | 745.07 | WS | 2.51 |
| NO2 | 42.39 | TEMP | 2.47 |
| NOx | 971.67 | RAIN | 1.05 |
| SO2 | 1.23 |
| Hyperparameter | AOA | HHO | SSA |
|---|---|---|---|
| Sparse degree | 0.1000 | 0.1002 | 0.1001 |
| Spectral Radios | 0.2323 | 0.1000 | 0.8464 |
| Input scaling | 0.3254 | 0.1967 | 0.1003 |
| Model (Train) | RMSE | Rank | NRMSE | Rank | MAE | Rank | MdAE | Rank | MAPE | Rank | R2 | Rank | R | Rank |
| LSTM | 19.4500 | 5 | 3.0838 | 6 | 12.2742 | 5 | 6.7811 | 5 | 0.3509 | 5 | 0.1108 | 5 | 0.7155 | 5 |
| GRU | 19.6184 | 6 | 2.4687 | 5 | 12.8060 | 6 | 7.5866 | 6 | 0.3523 | 6 | 0.0953 | 6 | 0.7146 | 6 |
| ESN | 11.5334 | 4 | 0.6745 | 4 | 8.5224 | 4 | 6.4945 | 4 | 0.3356 | 4 | 0.6873 | 4 | 0.8291 | 4 |
| ESN-SSA | 10.3955 | 1 | 0.5691 | 1 | 7.5834 | 1 | 5.6488 | 1 | 0.3040 | 1 | 0.7460 | 1 | 0.8640 | 1 |
| ESN-HHO | 11.0180 | 3 | 0.6296 | 3 | 8.1018 | 3 | 6.1446 | 3 | 0.3213 | 3 | 0.7147 | 3 | 0.8454 | 3 |
| ESN-AOA | 10.7546 | 2 | 0.6039 | 2 | 7.9283 | 2 | 6.0373 | 2 | 0.3175 | 2 | 0.7281 | 2 | 0.8534 | 2 |
| Model (Test) | RMSE | Rank | NRMSE | Rank | MAE | Rank | MdAE | Rank | MAPE | Rank | R2 | Rank | R | Rank |
| LSTM | 22.1623 | 6 | 3.2319 | 6 | 13.8238 | 5 | 7.3085 | 4 | 0.3303 | 4 | 0.0928 | 6 | 0.7316 | 5 |
| GRU | 22.1448 | 5 | 2.6652 | 5 | 14.0515 | 6 | 7.7365 | 5 | 0.3288 | 3 | 0.0942 | 5 | 0.7224 | 6 |
| ESN | 15.1598 | 4 | 0.5695 | 3 | 10.4114 | 4 | 7.8797 | 6 | 0.3381 | 6 | 0.5755 | 4 | 0.8303 | 3 |
| ESN-SSA | 13.7503 | 1 | 0.5675 | 2 | 9.5149 | 1 | 6.8262 | 1 | 0.3123 | 1 | 0.6508 | 1 | 0.8353 | 2 |
| ESN-HHO | 14.7045 | 3 | 0.5520 | 1 | 10.1420 | 3 | 7.5664 | 3 | 0.3322 | 5 | 0.6006 | 3 | 0.8411 | 1 |
| ESN-AOA | 14.6121 | 2 | 0.5884 | 4 | 9.8715 | 2 | 7.0937 | 2 | 0.3165 | 2 | 0.6056 | 2 | 0.8197 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zandi, I.; Jafari, A.; Lotfata, A. Enhancing PM2.5 Air Pollution Prediction Performance by Optimizing the Echo State Network (ESN) Deep Learning Model Using New Metaheuristic Algorithms. Urban Sci. 2025, 9, 138. https://doi.org/10.3390/urbansci9050138
Zandi I, Jafari A, Lotfata A. Enhancing PM2.5 Air Pollution Prediction Performance by Optimizing the Echo State Network (ESN) Deep Learning Model Using New Metaheuristic Algorithms. Urban Science. 2025; 9(5):138. https://doi.org/10.3390/urbansci9050138
Chicago/Turabian StyleZandi, Iman, Ali Jafari, and Aynaz Lotfata. 2025. "Enhancing PM2.5 Air Pollution Prediction Performance by Optimizing the Echo State Network (ESN) Deep Learning Model Using New Metaheuristic Algorithms" Urban Science 9, no. 5: 138. https://doi.org/10.3390/urbansci9050138
APA StyleZandi, I., Jafari, A., & Lotfata, A. (2025). Enhancing PM2.5 Air Pollution Prediction Performance by Optimizing the Echo State Network (ESN) Deep Learning Model Using New Metaheuristic Algorithms. Urban Science, 9(5), 138. https://doi.org/10.3390/urbansci9050138





