Navigating Efficiency and Uncertainty: Risks of Relying on an At-Will Workforce in Urban Meal Delivery
Abstract
1. Introduction
2. Literature Review
3. Developing the Environment and Replicating Delivery Operations
3.1. The Meal Delivery Problem
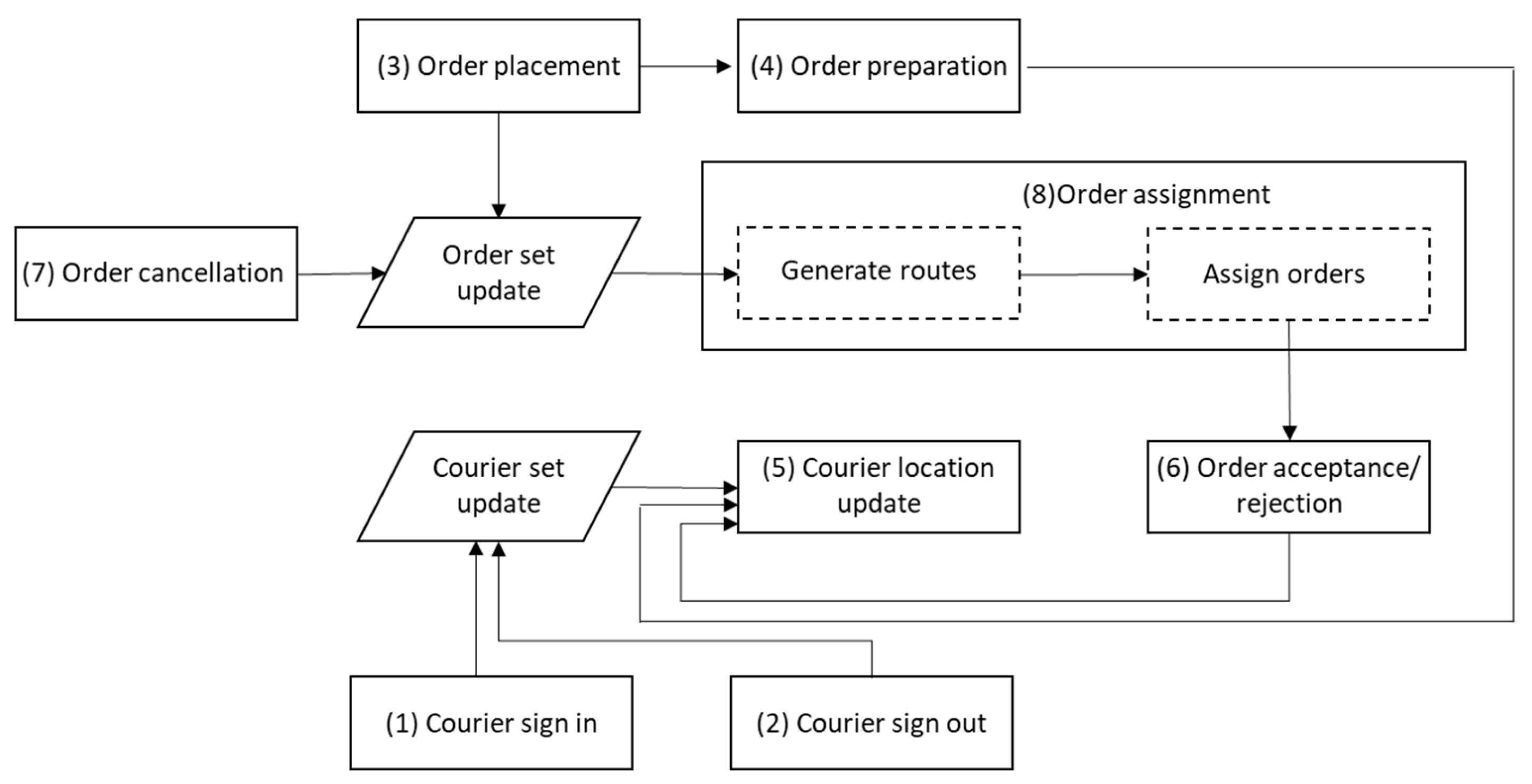
3.2. Simulating the Meal Delivery Environment with Fixed or At-Will Couriers
- (1)
- Courier sign in
- (2)
- Courier sign out
- (3)
- Order placement
- (4)
- Order preparation
- (5)
- Courier location update
- (6)
- Order acceptance/rejection
- (7)
- Order cancellation
- (8)
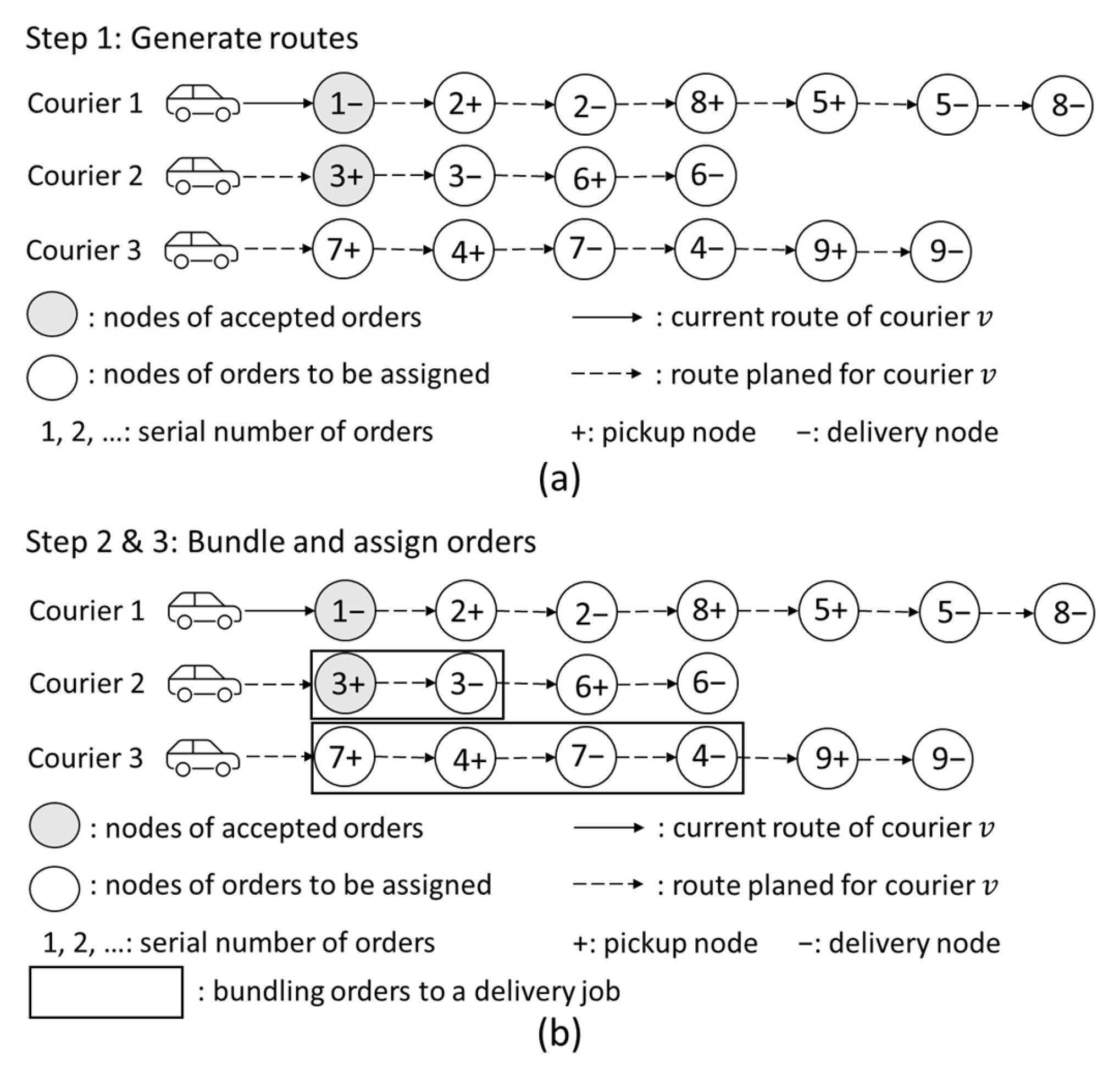
- Order assignment
| Algorithm 1. Tabu search procedure for route generation |
|
Input: tabu tenure , number of decomposition cycles , subsets , and stopping criteria parameter {Initialization} Generate initial solution For decomposition cycle : {Diversification phase} Decompose to disjoint subsets of routes Any routes with centroids contained in the same sector in a sweep are included in the same subset {Intensification phase} For from 1 to : While is updated in the last neighbor search moves: Generate neighboring solutions to via Neighborhood Search through Ejection Chain Update with best nontabu solution among neighboring solutions If objective value of is better than , then {Update tabu list} Return |
3.3. Simulating the Meal Delivery Environment with Fixed Fleet
4. Evaluating the Risk of Late Delivery
| Algorithm 2. CVaR measurement procedure |
| Input: tolerance level, , for 1, and number of simulation replications, Let Repeat simulation times, for each run storing CtD times of all orders in Count total number of orders in , Sort CtD times in in descending order and find cutoff point at Calculate CVaR as the average of the first CtD times in sorted Output computed CVaR value |
5. Case Study
5.1. Experiment Design
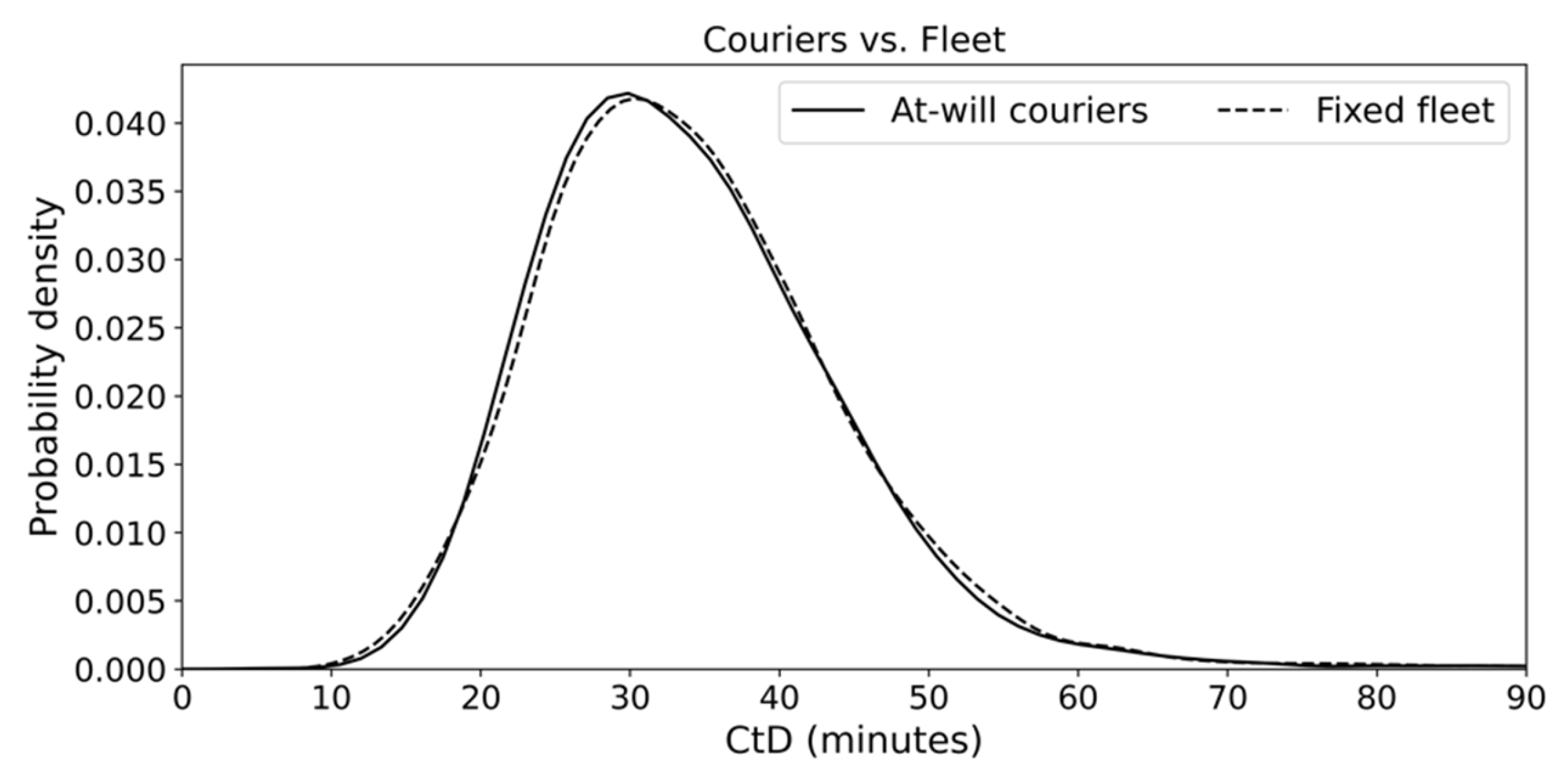
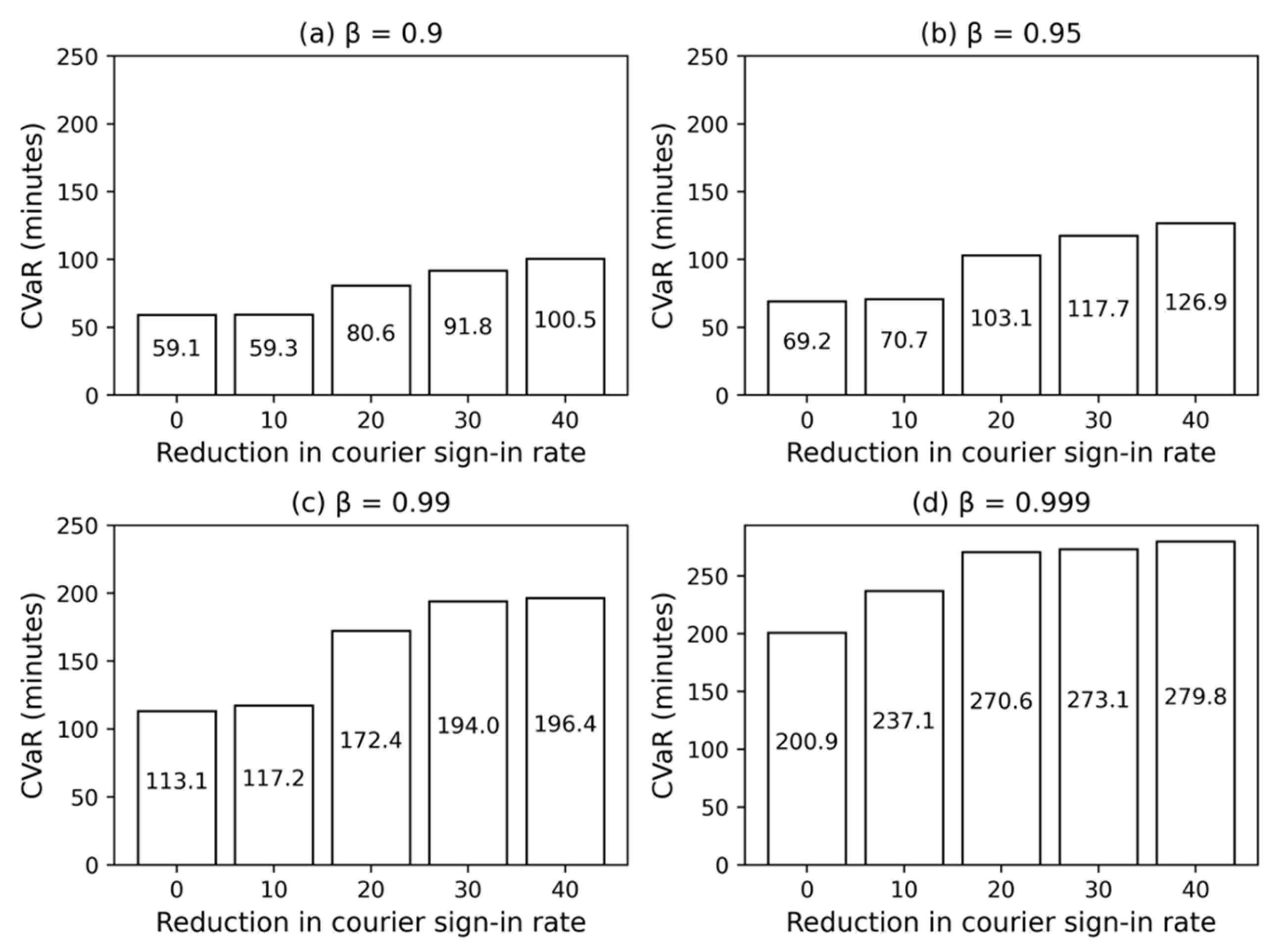
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McKinsey & Company Ordering in: The Rapid Evolution of Food Delivery. Available online: https://www.mckinsey.com/industries/technology-media-and-telecommunications/our-insights/ordering-in-the-rapid-evolution-of-food-delivery (accessed on 25 November 2022).
- Erera, A.L.; Reyes, D.; Savelsbergh, M.; O’Neil, R.J.; Sahasrabudhe, S. The Meal Delivery Routing Problem. Optim. Online 2018. Available online: https://optimization-online.org/2018/04/6571/ (accessed on 25 November 2022).
- Fotouhi, H.; Mori, N.; Miller-Hooks, E.; Sokolov, V.; Sahasrabudhe, S. Assessing the Effects of Limited Curbside Pickup Capacity in Meal Delivery Operations for Increased Safety during a Pandemic. Transp. Res. Rec. 2021, 2675, 436–452. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Thomas, B.W.; Campbell, A.M.; Woyak, N. The Restaurant Meal Delivery Problem: Dynamic Pickup and Delivery with Deadlines and Random Ready Times. Transp. Sci. 2021, 55, 75–100. [Google Scholar] [CrossRef]
- US Census Bureau Annual Retail Trade Survey Shows Impact of Online Shopping on Retail Sales during COVID-19 Pandemic. Available online: https://www.census.gov/library/stories/2022/04/ecommerce-sales-surged-during-pandemic.html (accessed on 16 January 2024).
- Archetti, C.; Savelsbergh, M.; Speranza, M.G. The Vehicle Routing Problem with Occasional Drivers. Eur. J. Oper. Res. 2016, 254, 472–480. [Google Scholar] [CrossRef]
- Dayarian, I.; Savelsbergh, M. Crowdshipping and Same-Day Delivery: Employing In-Store Customers to Deliver Online Orders. Prod. Oper. Manag. 2020, 29, 2153–2174. [Google Scholar] [CrossRef]
- Arslan, A.M.; Agatz, N.; Kroon, L.; Zuidwijk, R. Crowdsourced Delivery—A Dynamic Pickup and Delivery Problem with Ad Hoc Drivers. Transp. Sci. 2019, 53, 222–235. [Google Scholar] [CrossRef]
- Mancini, S.; Gansterer, M. Bundle Generation for Last-Mile Delivery with Occasional Drivers. Omega 2022, 108, 102582. [Google Scholar] [CrossRef]
- Yildiz, B.; Savelsbergh, M. Provably High-Quality Solutions for the Meal Delivery Routing Problem. Transp. Sci. 2019, 53, 1372–1388. [Google Scholar] [CrossRef]
- Steever, Z.; Karwan, M.; Murray, C. Dynamic Courier Routing for a Food Delivery Service. Comput. Oper. Res. 2019, 107, 173–188. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Bozanta, A.; Cevik, M.; Kavuk, E.M.; Tosun, A.; Sonuc, S.B.; Kosucu, B.; Başar, A. A Deep Reinforcement Learning Approach for the Meal Delivery Problem. Knowl.-Based Syst. 2022, 243, 108489. [Google Scholar] [CrossRef]
- Yildiz, B.; Savelsbergh, M. Service and Capacity Planning in Crowd-Sourced Delivery. Transp. Res. Part C Emerg. Technol. 2019, 100, 177–199. [Google Scholar] [CrossRef]
- Alvarez-Palau, E.J.; Calvet-Liñán, L.; Viu-Roig, M.; Gandouz, M.; Juan, A.A. Economic Profitability of Last-Mile Food Delivery Services: Lessons from Barcelona. Res. Transp. Bus. Manag. 2022, 45, 100659. [Google Scholar] [CrossRef]
- Bi, H.; Zhu, X.; Lu, F.; Huang, M. The Meal Delivery Routing Problem in E-Commerce Platforms under the Shared Logistics Mode. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1799–1819. [Google Scholar] [CrossRef]
- Zhou, W.; Fotouhi, H.; Miller-Hooks, E. Decision Support through Deep Reinforcement Learning for Maximizing a Courier’s Monetary Gain in a Meal Delivery Environment. In review by Decision Support Systems.
- Liu, Y. An Optimization-Driven Dynamic Vehicle Routing Algorithm for on-Demand Meal Delivery Using Drones. Comput. Oper. Res. 2019, 111, 1–20. [Google Scholar] [CrossRef]
- Zhao, Q.; Lu, F.; Wang, L.; Wang, S. Research on Drones and Riders Joint Take-out Delivery Routing Problem. Comput. Eng. Appl. 2022, 58, 269–278. [Google Scholar] [CrossRef]
- Liao, W.; Zhang, L.; Wei, Z. Multi-Objective Green Meal Delivery Routing Problem Based on a Two-Stage Solution Strategy. J. Clean. Prod. 2020, 258, 120627. [Google Scholar] [CrossRef]
- Gurvich, I.; Lariviere, M.; Moreno, A. Operations in the On-Demand Economy: Staffing Services with Self-Scheduling Capacity. In Sharing Economy: Making Supply Meet Demand; Hu, M., Ed.; Springer Series in Supply Chain Management; Springer International Publishing: Cham, Switzerland, 2019; pp. 249–278. ISBN 978-3-030-01863-4. [Google Scholar]
- Gendreau, M.; Guertin, F.; Potvin, J.-Y.; Séguin, R. Neighborhood Search Heuristics for a Dynamic Vehicle Dispatching Problem with Pick-Ups and Deliveries. Transp. Res. Part C Emerg. Technol. 2006, 14, 157–174. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of Conditional Value-at-Risk. JOR 2000, 2, 21–41. [Google Scholar] [CrossRef]

| Citation | Driver Category | Sign in Uncertainty | Sign out (or Work-Duration) Uncertainty | Order Rejection | Travel Time Uncertainty | Order Arrival Uncertainty | Order Preparation Uncertainty | Application Size |
|---|---|---|---|---|---|---|---|---|
| Erera et al. [2] | At-will couriers | ✓ Historical data | ✓ Historical data | ✓ | ✓ Historical data | ✓ Historical data | Instances with hundreds of restaurants | |
| Yildiz and Savelsbergh [10] | Occasional couriers | Same set as in Erera et al. [2] | ||||||
| Yildiz and Savelsbergh [13] | Fixed fleet supplements at-will couriers | ✓ | ✓ Sign out if idle time exceeds a threshold | ✓ Probability of rejecting orders | ✓ | Focus on single restaurant | ||
| Steever et al. [11] | Occasional couriers | 14 and 34 restaurants | ||||||
| Ulmer et al. [4] | Fixed fleet | ✓ | ✓ | 110 restaurants | ||||
| Jahanshahi et al. [12] | Occasional couriers | ✓ | ✓ | Orders randomly generated over space—no restaurants | ||||
| Fotouhi et al. [3] | At-will couriers | ✓ | ✓ Sign out after a predetermined sign-out time | ✓ Probability of rejecting orders | ✓ | ✓ | ✓ | Replications with 500 restaurants |
| Alvarez-Palau et al. [14] | At-will couriers OR fixed fleet | ✓ Historical data | ✓ Historical data | ✓ Historical data | ✓ Historical data | Real-world delivery data, number of restaurants not mentioned | ||
| Zhou et al. [16] | Single-driver perspective | ✓ | ✓ Sign out after a predetermined sign-out time | ✓ Reject orders with information | ✓ | ✓ | ✓ | Replications with 25 restaurants |
| Math Symbols | Description |
|---|---|
| set of orders, | |
| set of customers, | |
| set of restaurants, | |
| set of fixed-fleet or couriers, | |
| support set for uncertainty | |
| time period of meal delivery | |
| the restaurant in which order is prepared | |
| the customer associated with order | |
| the fixed-fleet driver or a courier who deliver the order | |
| the placement time of order | |
| the ready time of order | |
| the pickup time of order | |
| the delivery time of order | |
| expected delivery time for order | |
| delivery time requirement | |
| parameter of exponential distribution, which denotes the new couriers sign in rate at time | |
| sign in location of courier | |
| sign in time of courier | |
| pre-defined sign out time of courier | |
| the courier ’s willingness-to-wait time threshold | |
| courier ’s planned work duration | |
| location from where the courier need to pick up order | |
| customer index for order | |
| Location to where the courier need to deliver order |
| Uncertainty Categories | Description |
|---|---|
| Order placement | The time between the placement of consecutive orders at each restaurant follows an exponential distribution , where follows a uniform distribution . This allows the generation of restaurants with varying popularity. is a time-based parameter that reflects the temporal influence on the arrival of couriers. For the eight-hour meal delivery period, . |
| Order preparation times | The preparation time of each order follows a truncated normal distribution over interval (5, 120) with mean 17 and standard deviation 10; units in minutes. |
| Pickup and drop-off service times | The pickup service time at restaurants and drop-off service time at customers follow truncated normal distributions, both within interval (1, 4) with mean 2.5 and standard deviation 0.5. |
| Courier sign-in time | The time between the sign in of consecutive couriers into the platform follows an exponential distribution . denotes the base arrival rate, reflects the temporal influence on the arrival of the couriers, capturing that more couriers may sign in at the height of demand. Thus, the actual number of at-will couriers present at any point in time will fluctuate over the meal delivery period. |
| Courier sign-in location | The sign-in location along horizontal and vertical axes follows a truncated normal distribution within (0, 10) with mean 5 and standard deviation 3, units in miles. |
| Courier working duration | A courier’s work duration follows a truncated normal distribution within (0, 480) with mean 120 and standard deviation 30, units in minutes. |
| Courier response time | A courier’s response time for accepting or rejecting an order follows a truncated normal distribution within (0.1, 1) with mean 0.3 and standard deviation 0.2, units in minutes. |
| Courier willingness to wait while idle | A courier’s willingness to stay in the platform while idle follows a truncated normal distribution within (8, 22) with mean 15 and standard deviation 5, units in minutes. |
| Order rejection | Couriers reject a delivery job with probability = 0.2. |
| Order cancellation | Duration a customer is willing to wait until his/her order is successfully assigned to a courier before canceling the order follows a truncated normal distribution in the range of (17, 60) with mean 27 and standard deviation 5 with all units in minutes. |
| Average Number | CtD | Freshness | Delivery Resource (Vehicle Hours) | Resources Per Order (Vehicle Hours) | |
|---|---|---|---|---|---|
| Fixed fleet drivers | 32 | 35.26 | 15.99 | 481 | 0.80 |
| At-will couriers | 126 (total over 14 h with 2-h desired work duration) | 35.21 | 16.03 | 295.01 | 0.49 |
| Fixed-Fleet Drivers | At-Will Couriers | |
|---|---|---|
| 0.9 | 60.11 | 59.12 |
| 0.91 | 61.39 | 60.46 |
| 0.92 | 62.90 | 62.02 |
| 0.93 | 64.68 | 63.92 |
| 0.94 | 66.86 | 66.27 |
| 0.95 | 69.62 | 69.30 |
| 0.96 | 73.32 | 73.47 |
| 0.97 | 78.65 | 79.60 |
| 0.98 | 86.92 | 89.88 |
| 0.99 | 101.85 | 113.12 |
| 0.995 | 112.95 | 139.91 |
| 0.999 | 133.16 | 200.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Miller-Hooks, E.; Sahasrabudhe, S. Navigating Efficiency and Uncertainty: Risks of Relying on an At-Will Workforce in Urban Meal Delivery. Urban Sci. 2024, 8, 17. https://doi.org/10.3390/urbansci8010017
Zhou W, Miller-Hooks E, Sahasrabudhe S. Navigating Efficiency and Uncertainty: Risks of Relying on an At-Will Workforce in Urban Meal Delivery. Urban Science. 2024; 8(1):17. https://doi.org/10.3390/urbansci8010017
Chicago/Turabian StyleZhou, Weiwen, Elise Miller-Hooks, and Sagar Sahasrabudhe. 2024. "Navigating Efficiency and Uncertainty: Risks of Relying on an At-Will Workforce in Urban Meal Delivery" Urban Science 8, no. 1: 17. https://doi.org/10.3390/urbansci8010017
APA StyleZhou, W., Miller-Hooks, E., & Sahasrabudhe, S. (2024). Navigating Efficiency and Uncertainty: Risks of Relying on an At-Will Workforce in Urban Meal Delivery. Urban Science, 8(1), 17. https://doi.org/10.3390/urbansci8010017






