Analysis of Overpass Displacements Due to Subway Construction Land Subsidence Using Machine Learning
Abstract
1. Introduction
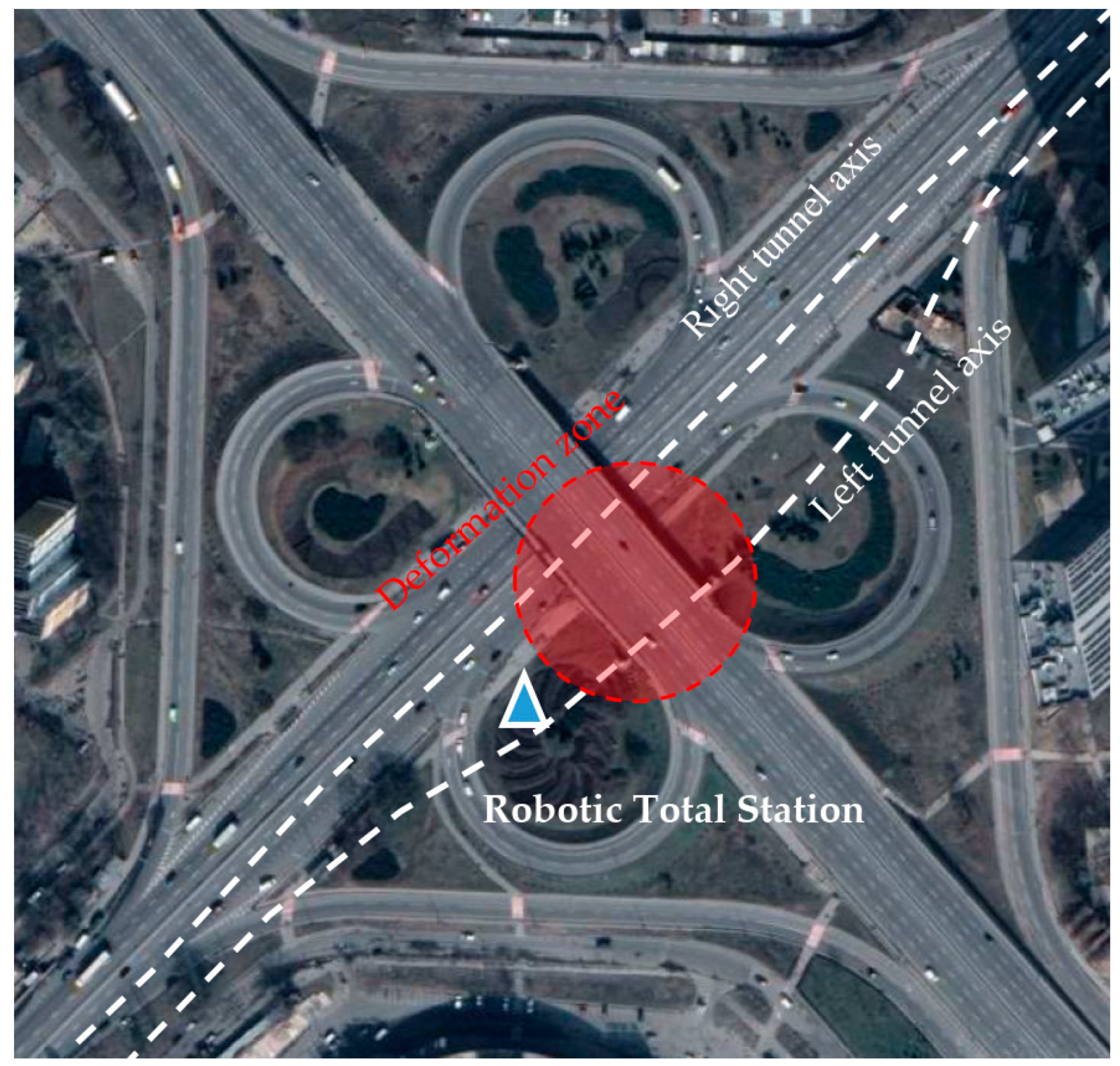
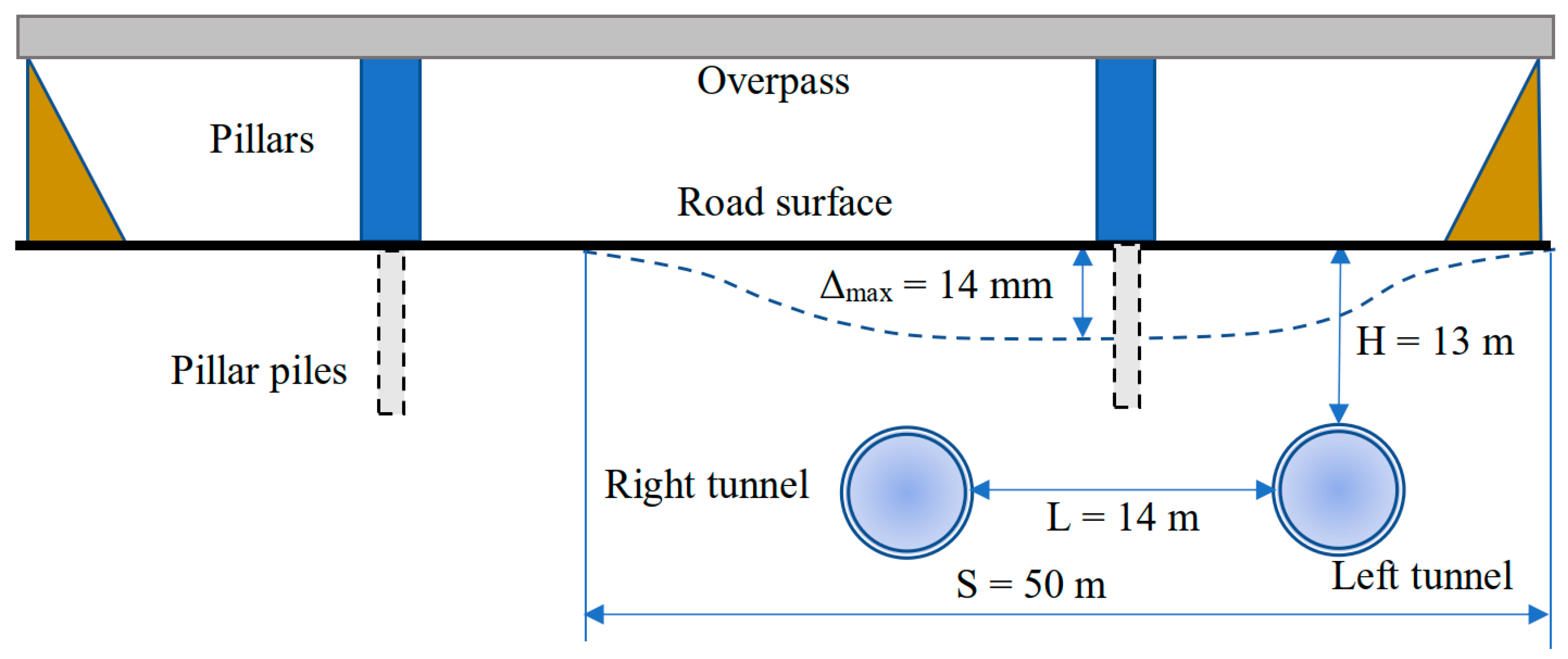
2. Study Object
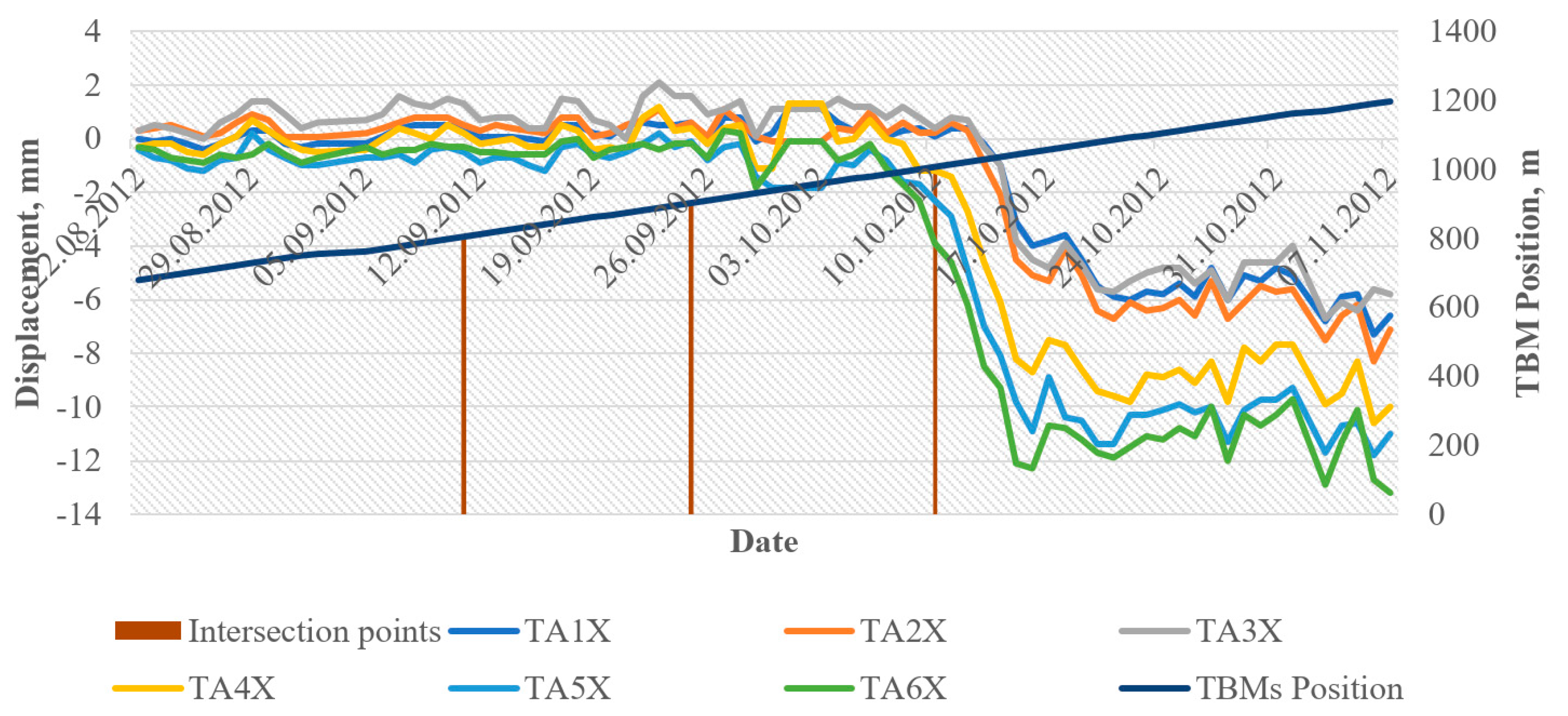
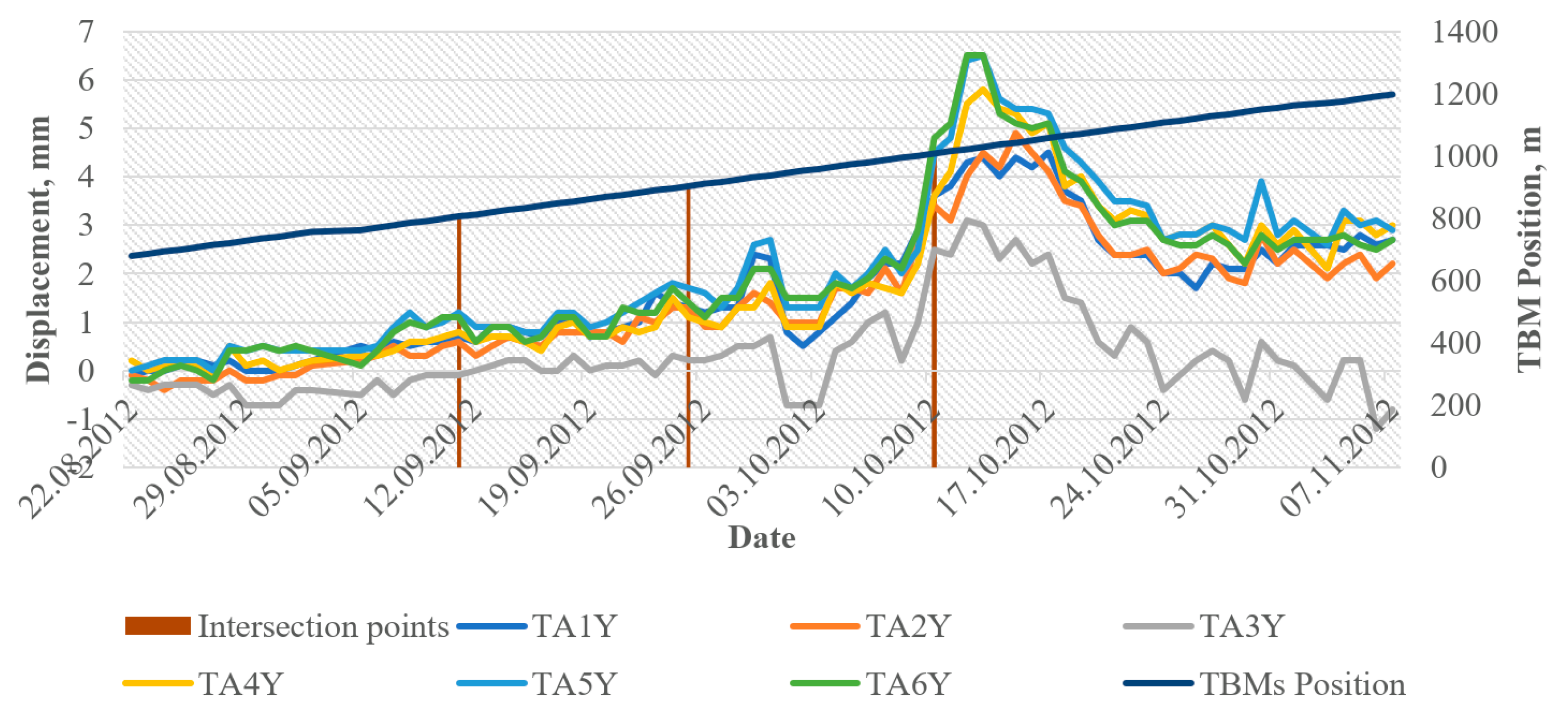
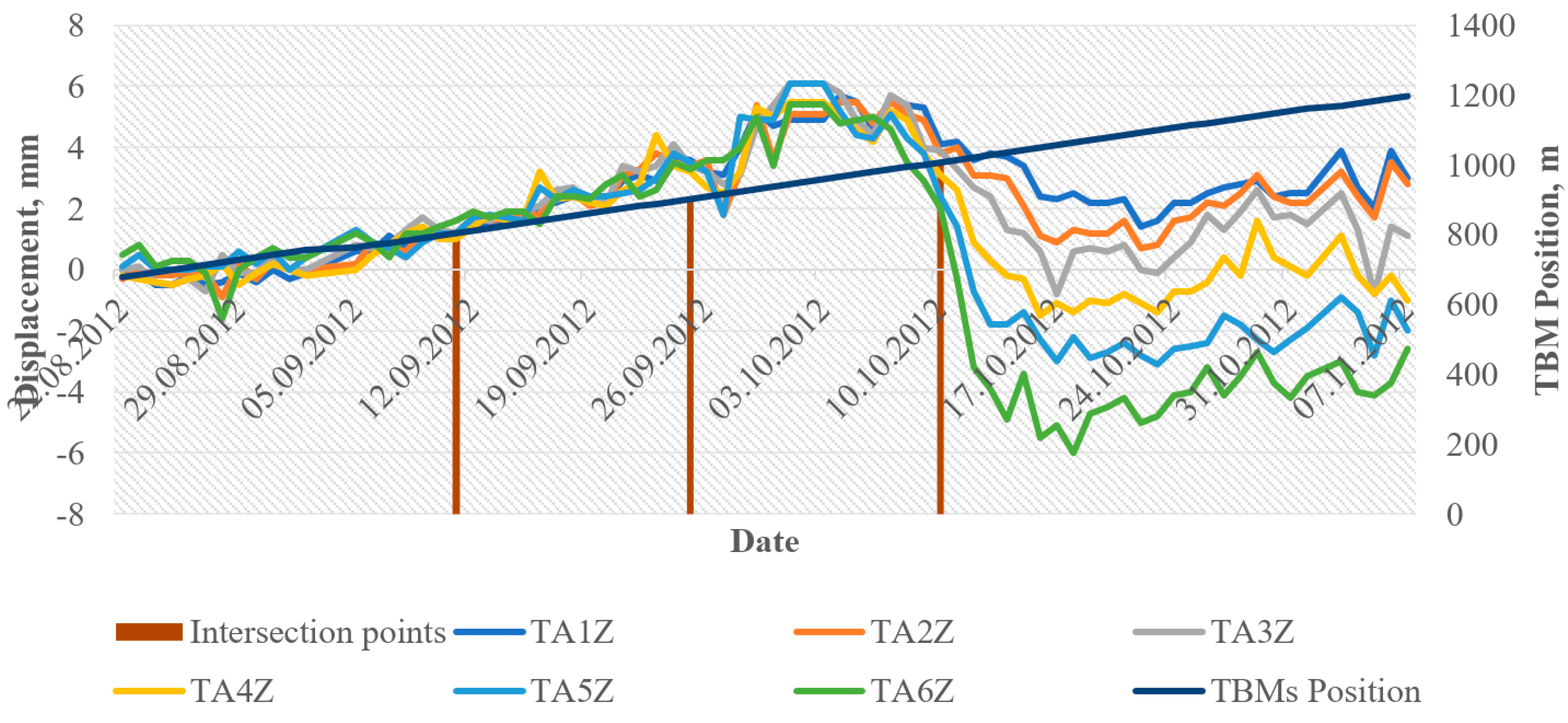
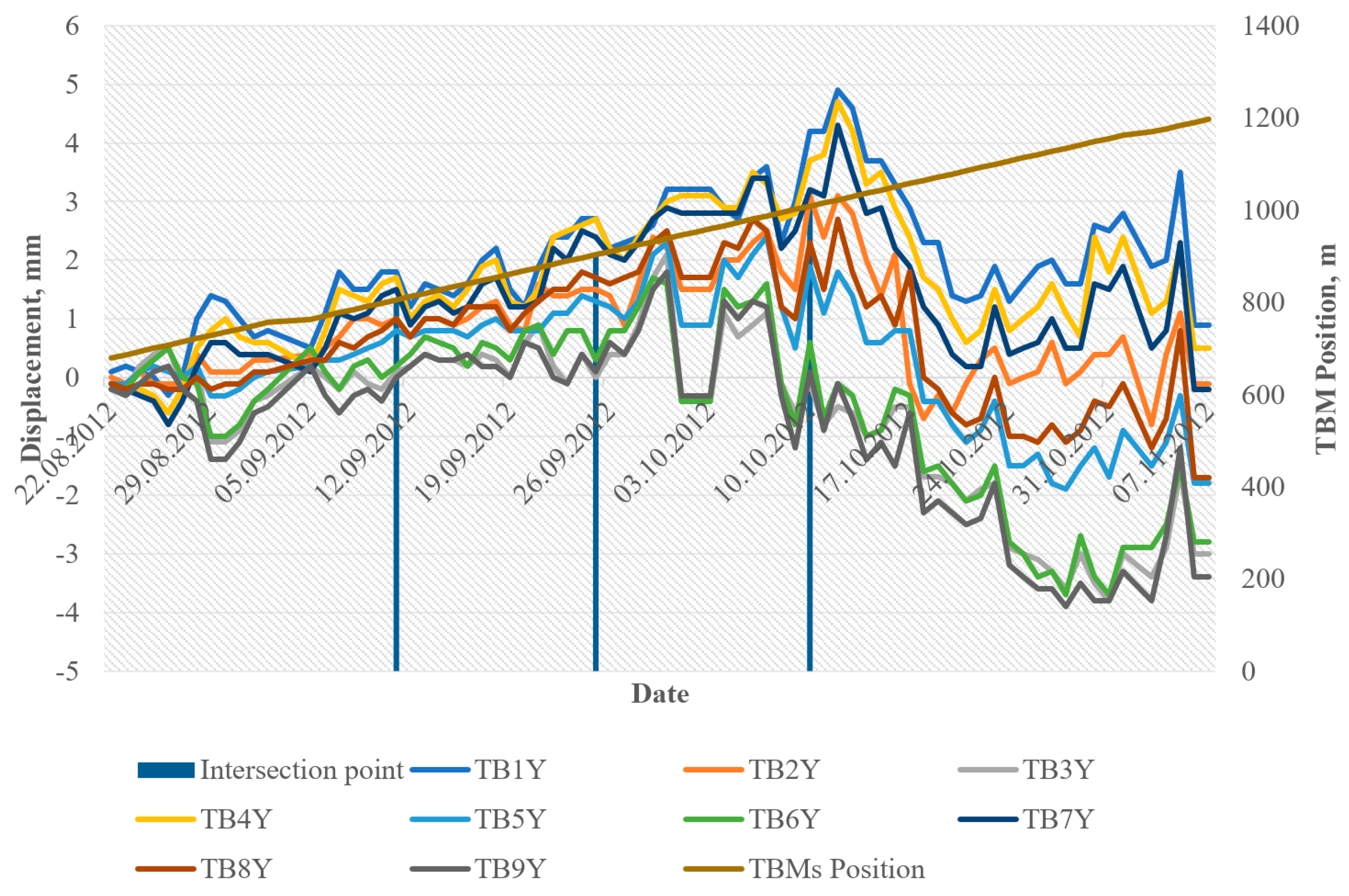
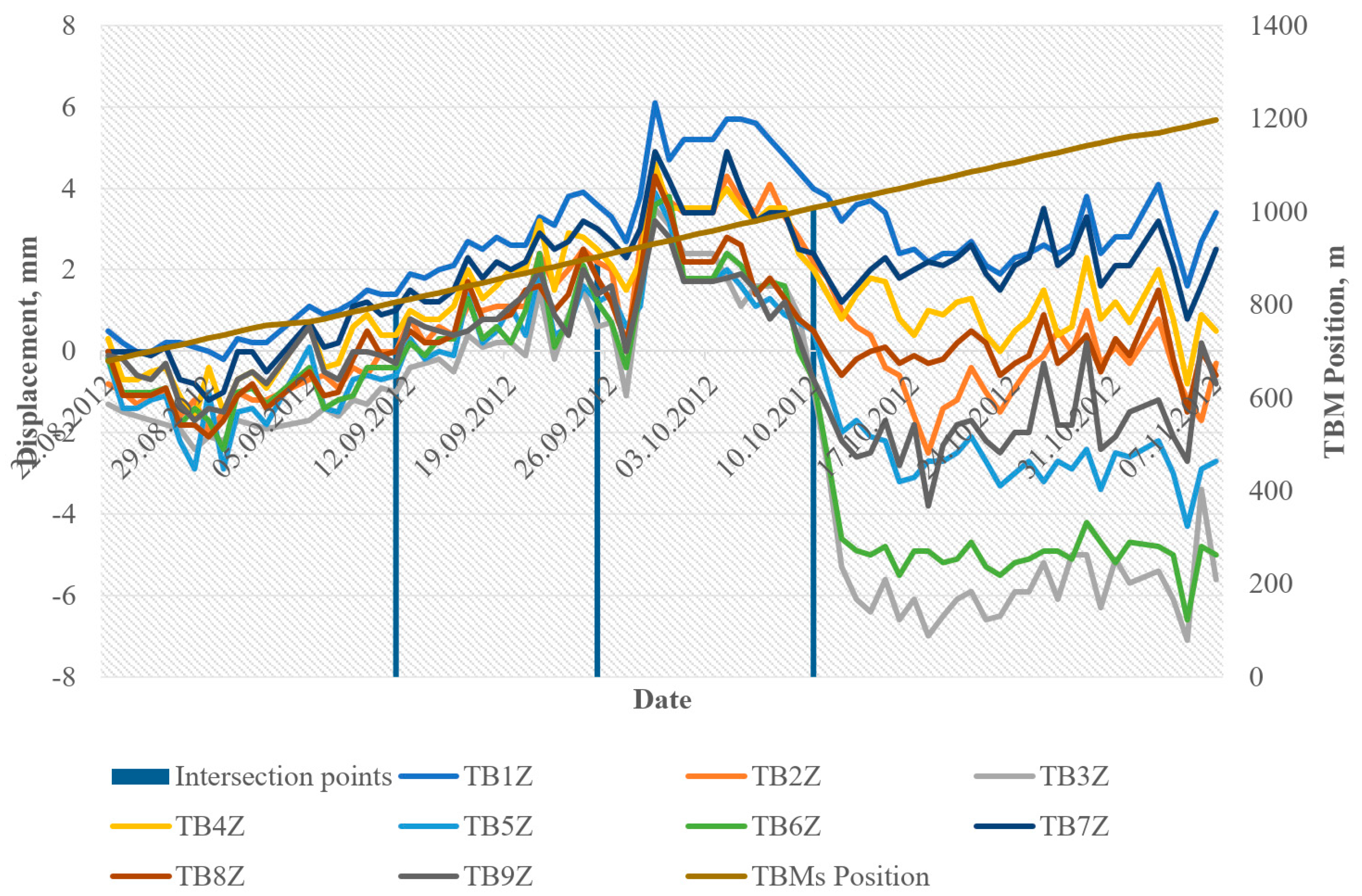
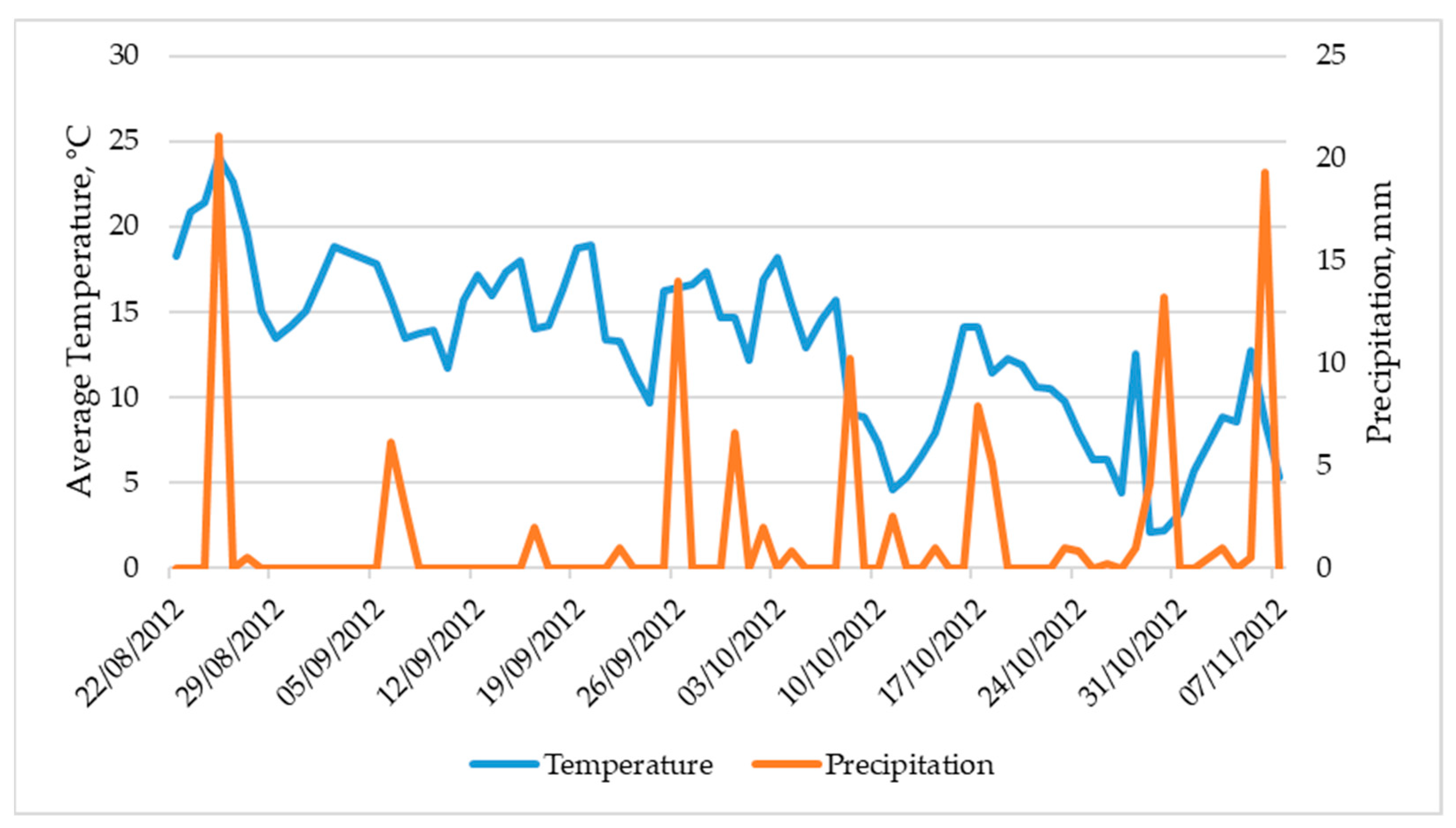
3. Initial Data for Model Simulations
4. Results and Discussions
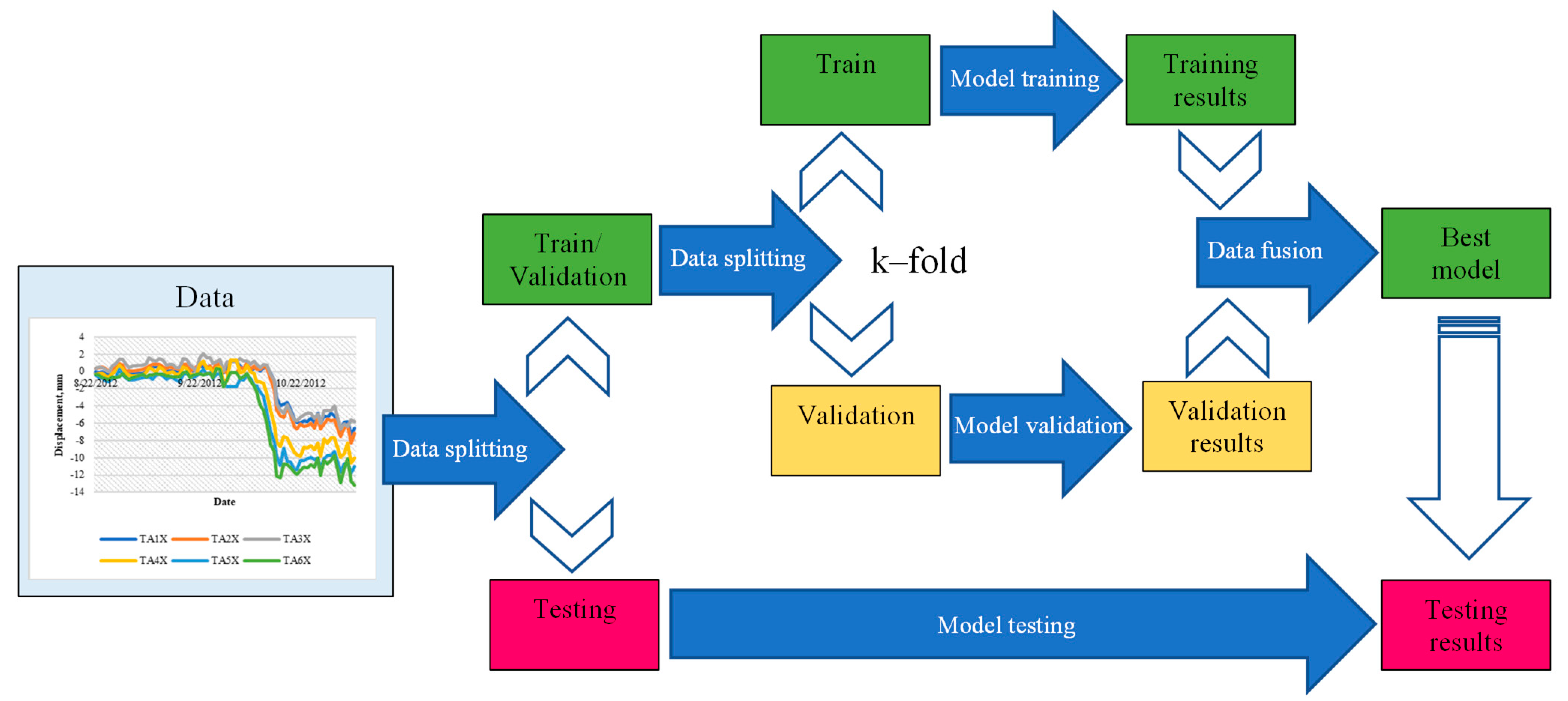
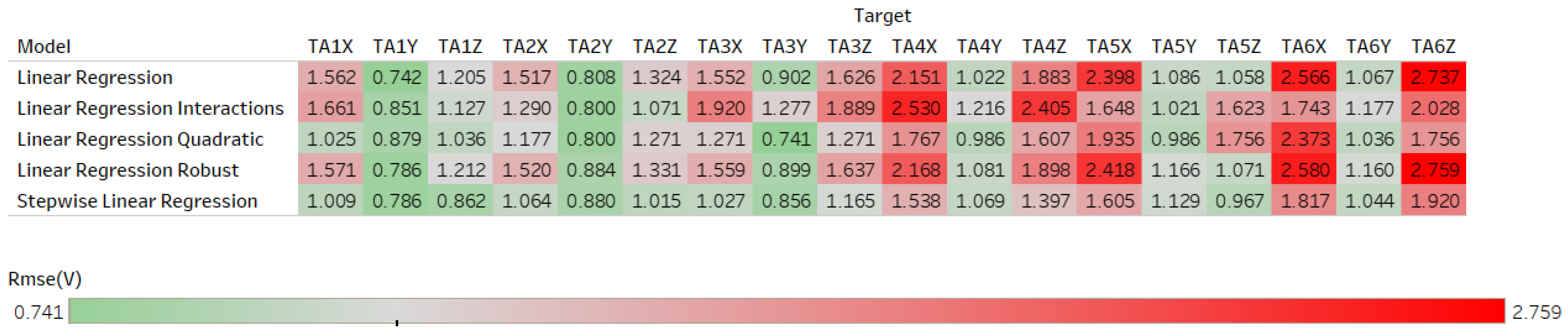
4.1. Regression Analysis Results
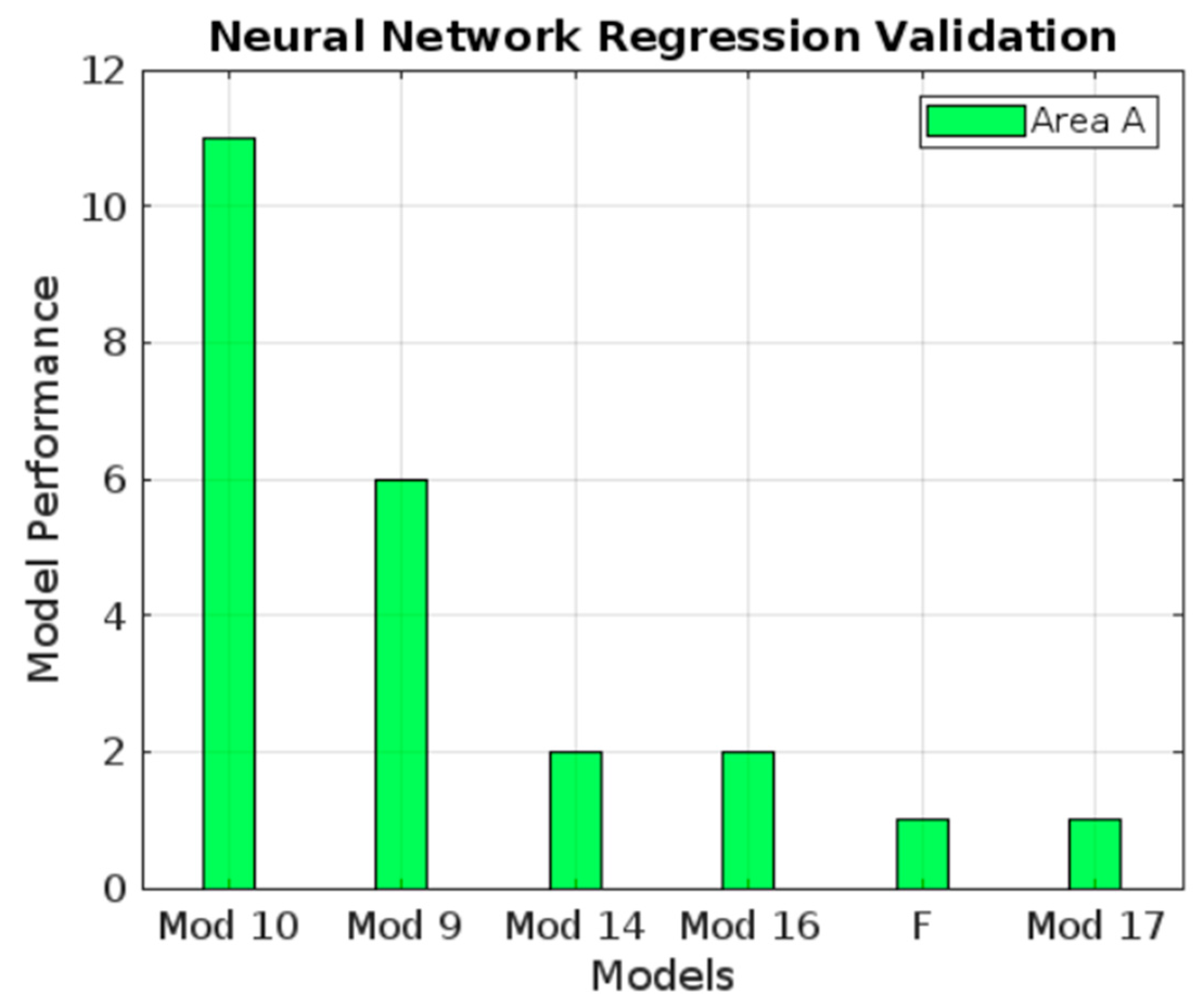
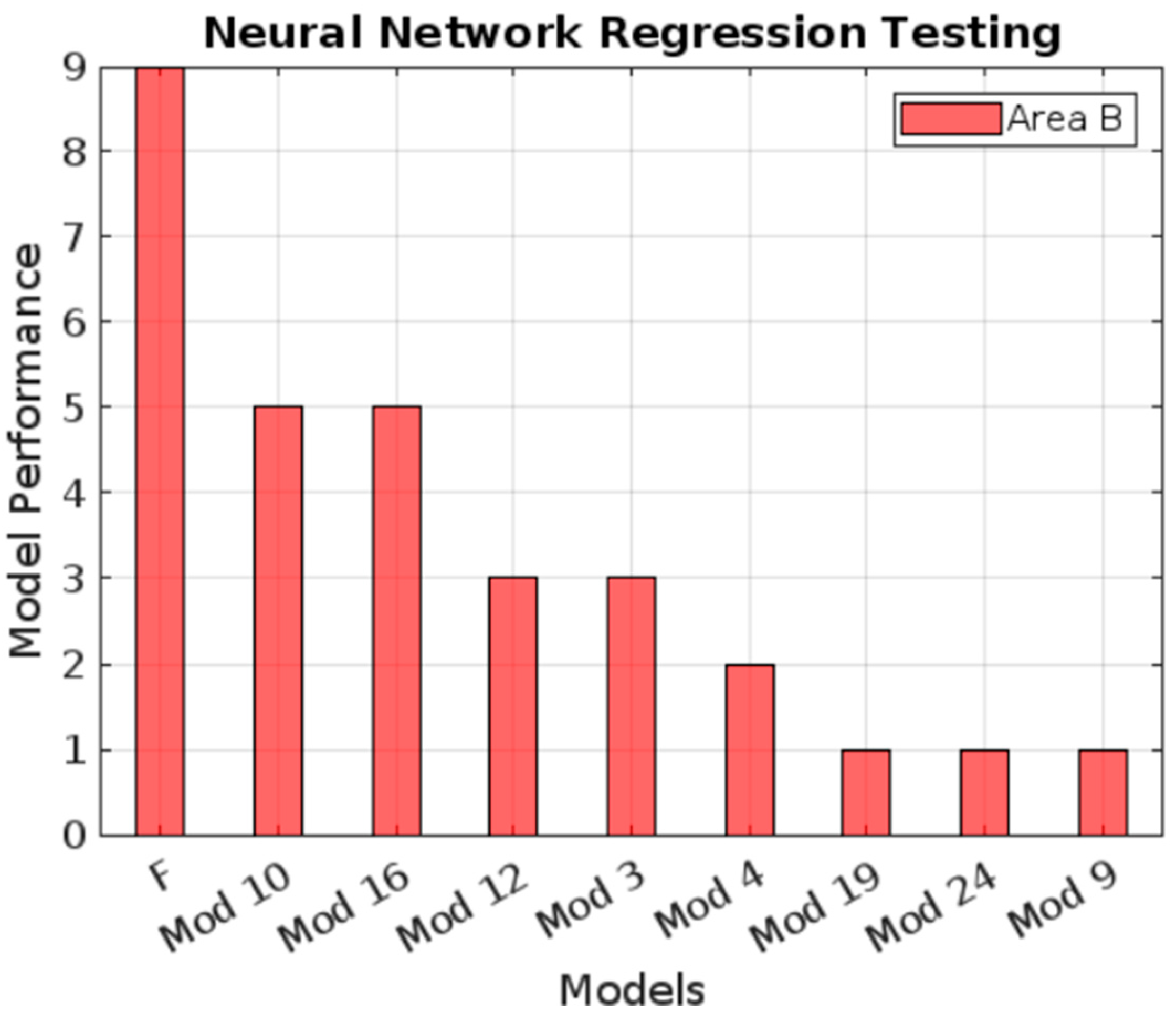
4.2. Neural Network Regression Results
- rectified linear unit function ;
- hyperbolic tangent function ;
- the sigmoid function ;
- identity function .
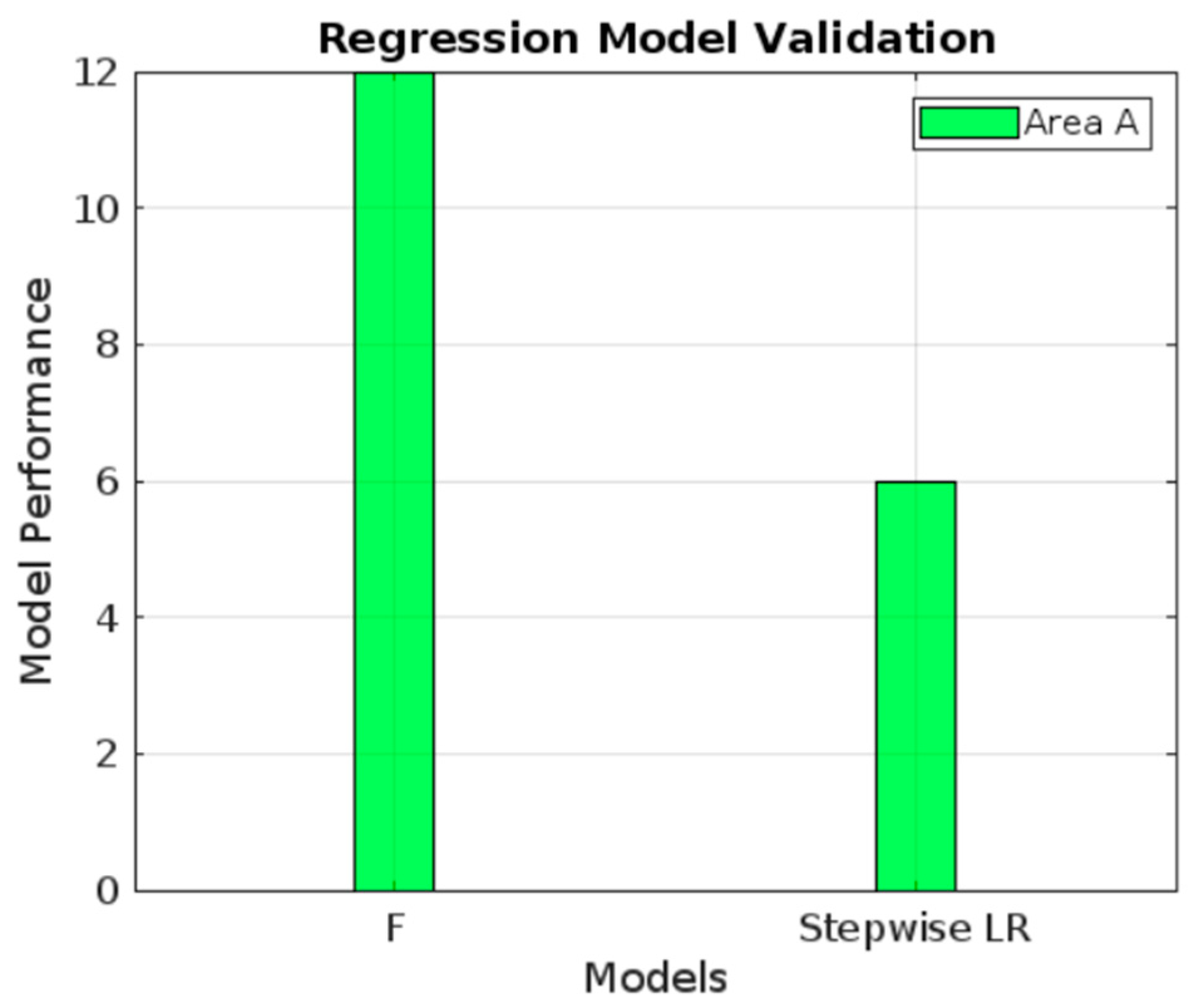
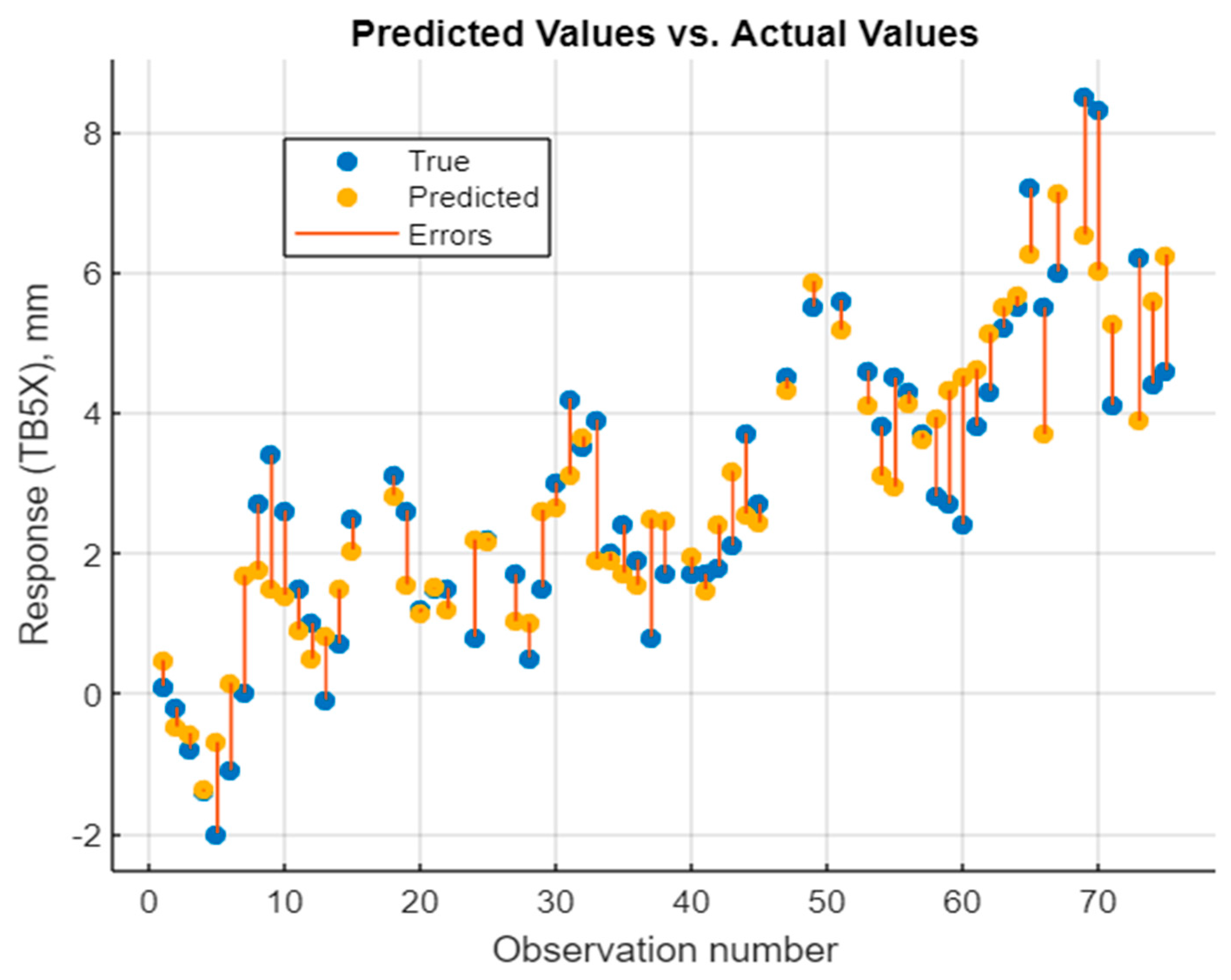
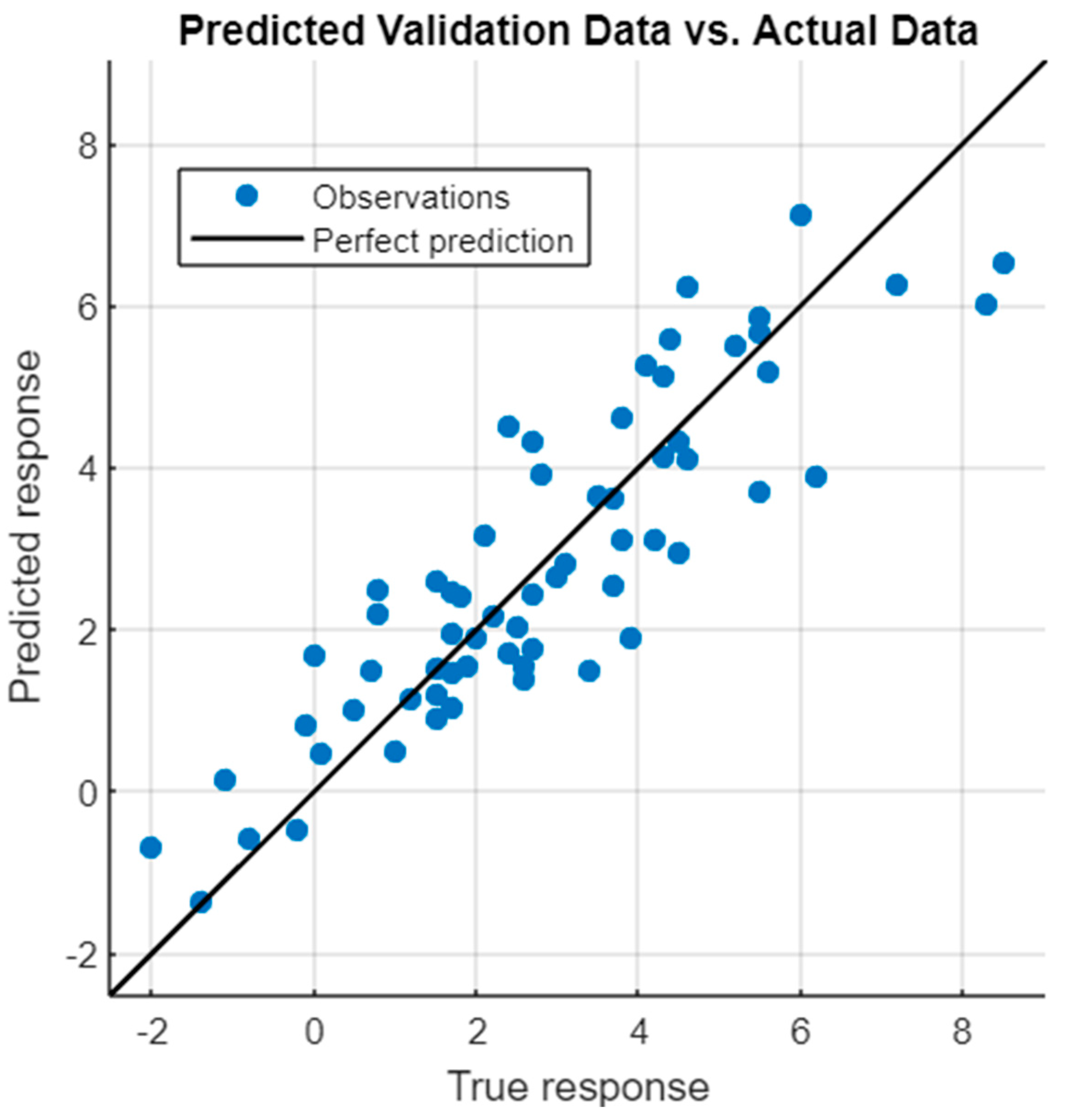
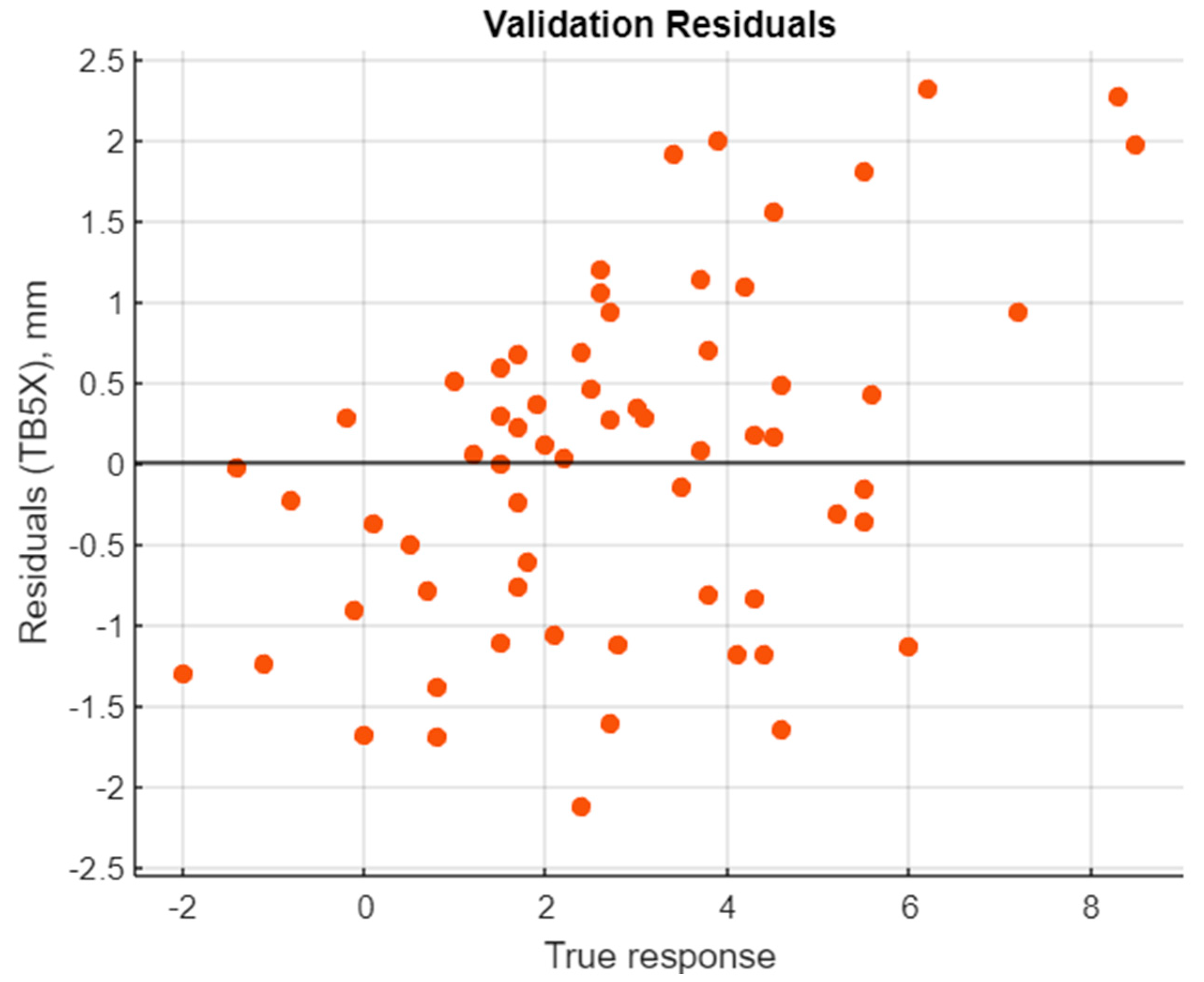
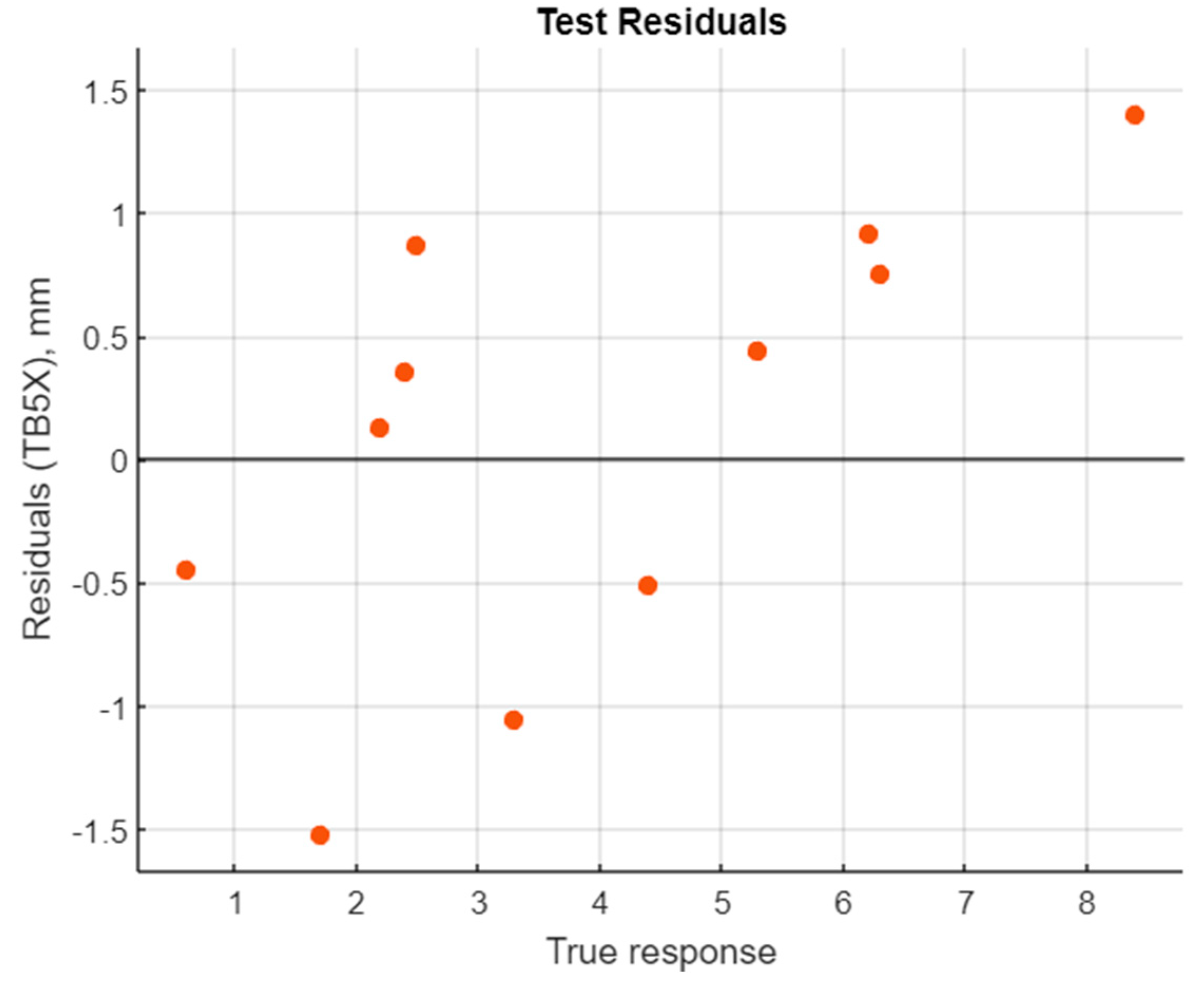
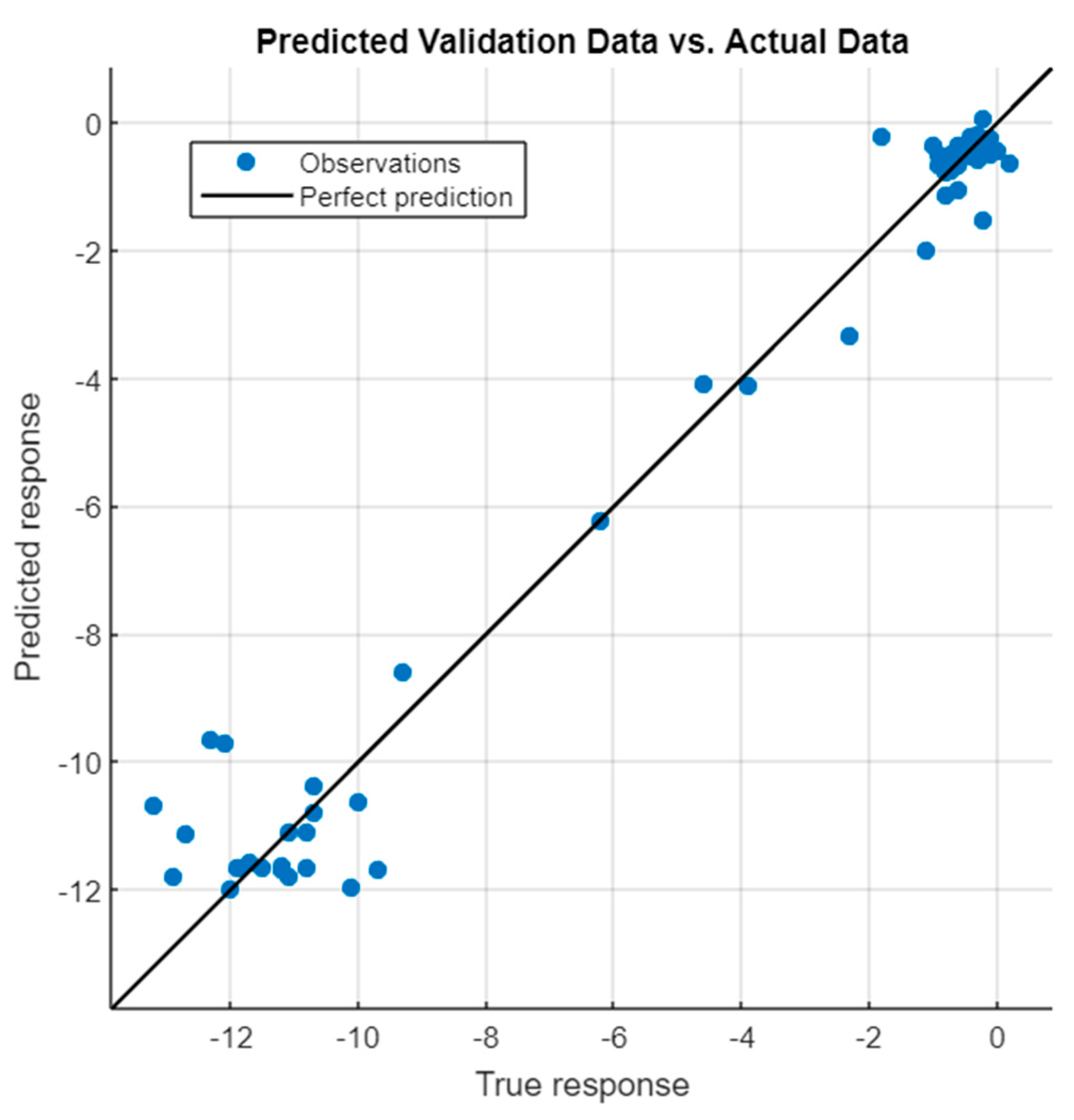
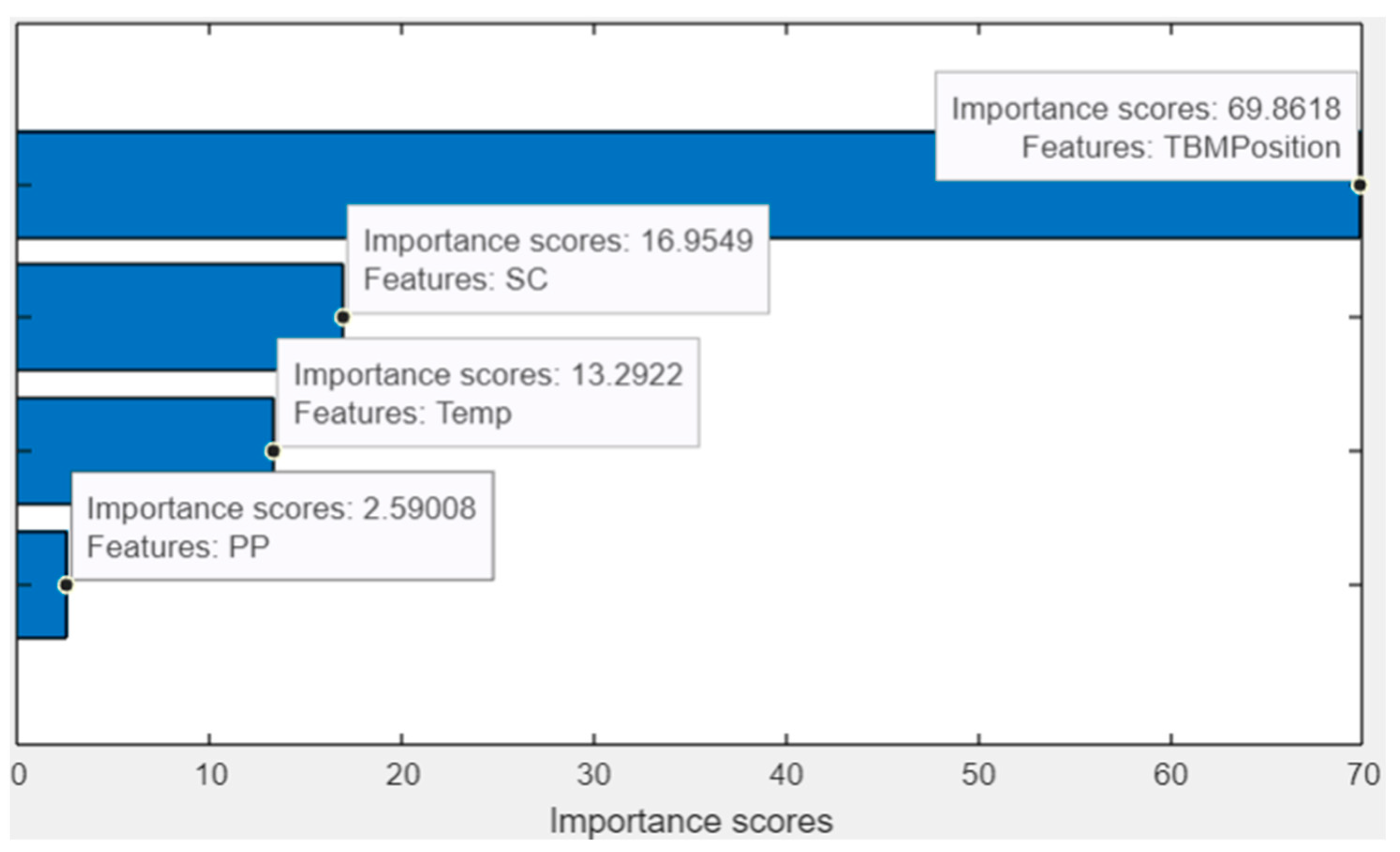
4.3. Best Model Performance Analysis and Discussions
- (1)
- Assigning the validation procedure. For small datasets (up to 300 responses), this is a k-fold validation with at least ten folds, and for large datasets (more than 1000 responses), a hold-out validation procedure.
- (2)
- Assigning the testing data subset, which is 15–20%, depending on the dataset size.
- (3)
- Choosing the set of parameters (predictors).
- (4)
- Choosing the optimizable hyperparameters (activation function, number of layers, and outputs).
- (5)
- Assigning the activation function (hyperbolic tangent or sigmoid).
- (6)
- Optimizing the number of layers and the number of outputs.
- (7)
- Comparing the estimation metrics.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lepadatu, A.; Tiberius, C. GPS for structural health monitoring—Case study on the Basarab overpass cable-stayed bridge. J. Appl. Geod. 2013, 8, 65–86. [Google Scholar] [CrossRef][Green Version]
- Ono, M.N.; Agbo, J.A.; Ijioma, D.I.; Chubado, M. Establishment of Baseline Data for Monitoring of Deformation of Murtala Mohammed Bridge (MMB) Lokoja Kogi State, using GPS. Int. J. Sci. Technol. 2014, 4, 86–92. [Google Scholar]
- Raziq, N.; Collier, P. GPS deflection monitoring of the West Gate Bridge. J. Appl. Geod. 2007, 1, 34–44. [Google Scholar] [CrossRef]
- Roberts, G.W.; Brown, C.J.; Xiaolin, X.T.; Ogundipe, M.O. A Tale of Five Bridges; the use of GNSS for Monitoring the Deflections of Bridges. J. Appl. Geod. 2014, 8, 241–264. [Google Scholar] [CrossRef]
- Stiros, S.C. GNSS (GPS) Monitoring of Dynamic Deflections of Bridges: Structural Constraints and Metrological Limitations. Infrastructures 2021, 6, 23. [Google Scholar] [CrossRef]
- Vazquez, E.G.; Gaxiola-Camacho, R.; Bennett, R.; Guzman-Acevedo, M.; Gaxiola-Camacho, I. Structural evaluation of dynamic and semi-static displacements of the Juarez Bridge using GPS technology. Measurement 2017, 110, 146–153. [Google Scholar] [CrossRef]
- Avşar, Ö.; Akca, D.; Altan, O. Photogrammetric Deformation Monitoring of the Second Bosphorus Bridge in Istanbul. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-5, 71–76. [Google Scholar] [CrossRef]
- Maas, H.-G.; Hampel, U. Photogrammetric Techniques in Civil Engineering Material Testing and Structure Monitoring. Photogramm. Eng. Remote Sens. 2006, 72, 39–45. [Google Scholar] [CrossRef]
- Fradelos, Y.; Thalla, O.; Biliani, I.; Stiros, S. Study of lateral displacements and natural frequency of a pedestrian bridge using low-cost cameras. Sensors 2020, 20, 3217. [Google Scholar] [CrossRef]
- Mill, T.; Ellmann, A.; Kiisa, M.; Idnurm, J.; Idnurm, S.; Horemuz, M.; Aavik, A. Geodetic Monitoring of Bridge Deformations Occurring During Static Load Testing. Balt. J. Road Bridge Eng. 2015, 10, 17–27. [Google Scholar] [CrossRef]
- Erdélyi, J.; Kopáčik, A.; Lipták, I.; Kyrinovič, P. Pedestrian bridge monitoring using terrestrial laser scanning. In Advances and Trends in Engineering Sciences and Technologies—Proceedings of the International Conference on Engineering Sciences and Technologies; EsaT, Tatranská Štrba, High Tatras Mountains-Slovak Republic, 27–29 May 2015; CRC Press: Boca Raton, FL, USA, 2015; pp. 51–56. [Google Scholar]
- Gawronek, P.; Makuch, M. TLS Measurement during Static Load Testing of a Railway Bridge. ISPRS Int. J. Geo-Inf. 2019, 8, 44. [Google Scholar] [CrossRef]
- Erdélyi, J.; Kopáčik, A.; Kyrinovič, P. Spatial Data Analysis for Deformation Monitoring of Bridge Structures. Appl. Sci. 2020, 10, 8731. [Google Scholar] [CrossRef]
- Psimoulis, P.A.; Stiros, S.C. Measuring Deflections of a Short-Span Railway Bridge Using a Robotic Total Station. J. Bridge Eng. 2013, 18, 182–185. [Google Scholar] [CrossRef]
- Braun, J.; Štroner, M. Geodetic Measurement of Longitudinal Displacements of the Railway Bridge. In Proceedings of the 6th International Conference on Engineering Surveying “INGEO 2014”, Prague, Czech Republic, 3–4 April 2014; pp. 231–236. Available online: http://www.svf.stuba.sk/docs/web_katedry/gde/ingeo/TS7-02_Braun.pdf (accessed on 16 September 2023).
- Shults, R.; Roshchyn, O. Preliminary determination of spatial geodetic monitoring accuracy for free station method. Geod. List 2016, 70, 355–370. [Google Scholar]
- Zhang, L.; Zha, X. Monitoring and result analysis of temporary railway bridge construction. J. Geomat. 2018, 43, 113–116. [Google Scholar] [CrossRef]
- Lipták, I. Monitoring the Dynamic Deformation of the Bridge Structures by Accelerometers. Rep. Geod. 2013, 94, 37–46. [Google Scholar] [CrossRef]
- Lipták, I.; Kopáčik, A.; Erdélyi, J.; Kyrinovič, P. Dynamic Deformation Monitoring of a Bridge Structure. SSP—J. Civ. Eng. 2013, 8, 13–20. [Google Scholar] [CrossRef]
- Bianchi, S.; Biondini, F.; Rosati, G.; Anghileri, M.; Capacci, L.; Cazzulani, G.; Benedetti, L. Structural Health Monitoring of Two Road Bridges in Como, Italy. In EUROSTRUCT 2021: Proceedings of the 1st Conference of the European Association on Quality Control of Bridges and Structures; Lecture Notes in Civil Engineering; Pellegrino, C., Faleschini, F., Zanini, M.A., Matos, J.C., Casas, J.R., Strauss, A., Eds.; Springer: Cham, Swizerland, 2022; Volume 200. [Google Scholar] [CrossRef]
- Meng, X. Real-Time Deformation Monitoring of Bridges Using GPS/Accelerometers. PhD Thesis, University of Nottingham, Nottingham, UK, 2002; 259p. Available online: http://eprints.nottingham.ac.uk/10279/1/Meng%27s_full_thesis.pdf (accessed on 20 September 2023).
- Wegner, J.D.; Cong, X.Y.; Paffenholz, J.-A.; Rehr, I.; Strübing, T. Geodetic Monitoring and Deformation Analysis of a Vertical Lift Bridge. In Proceedings of the XXIII FIG Congress “Shaping the Change”, Munich, Germany, 8–13 October 2006; 15pAvailable online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2006/papers/ts58/ts58_03_wegner_etal_0608.pdf (accessed on 16 September 2023).
- Lõhmus, H.; Ellmann, A.; Märdla, S.; Idnurm, S. Terrestrial laser scanning for the monitoring of bridge load tests—Two case studies. Surv. Rev. 2018, 50, 270–284. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Ferreira, J.; Martins, T. Non-contact measurement of the dynamic displacement of railway bridges using an advanced video-based system. Eng. Struct. 2014, 75, 164–180. [Google Scholar] [CrossRef]
- Stiros, S.; Psimoulis, P.; Moschas, F.; Saltogianni, V.; Tsantopoulos, E.; Triantafyllidis, P. Multi-sensor measurement of dynamic deflections and structural health monitoring of flexible and stiff bridges. Bridg. Struct. 2019, 15, 43–51. [Google Scholar] [CrossRef]
- Kovačič, B.; Kamnik, R.; Kapović, Z. Mathematical Analysis of Measured Displacements with Emphasis on Polynomial Interpolation. Geod. List 2009, 4, 315–327. [Google Scholar]
- Milovanović, B.; Mišković, Z.; Gospavić, Z.; Vulić, M. Modelling Behaviour of Bridge Pylon for Test Load Using Regression Analysis with Linear and Non-Linear Process. Geod. List 2011, 3, 205–220. [Google Scholar]
- Beshr, A.A.E.-W. Structural Deformation Monitoring and Analysis of Highway Bridge Using Accurate Geodetic Techniques. Engineering 2015, 7, 488–498. [Google Scholar] [CrossRef]
- Wieser, A.; Brunner, F.K. Analysis of bridge deformations using continuous GPS measurements. In Proceedings of the INGEO2002, 2nd Conference of Engineering Surveying, Bratislava, Slovakia, 11–13 November 2002; Kopacik, A., Kyrinovic, P., Eds.; Slovak University of Technology: Bratislava, Czech Republic, 2002; pp. 45–52. [Google Scholar]
- Shults, R.; Annenkov, A.; Seitkazina, G.; Soltabayeva, S.; Kozhayev, Z.; Khailak, A.; Nikitenko, K.; Sossa, B.; Kulichenko, N. The Displacements Analysis for Pipeline Overpasses Monitoring by Geodetic Measurements Results. J. Geod. Geodyn. 2022, 13, 50–71. [Google Scholar] [CrossRef]
- Eichhorn, A. Tasks and Newest Trends in Geodetic Deformation Analysis: A Tutorial. In Proceedings of the 15th European Signal Processing Conference (EUSIPCO 2007): Selected Papers, Poznan, Poland, 3–7 September 2007; EURASIP: Poznan, Poland, 2007; pp. 1156–1160. [Google Scholar]
- Shults, R. The Models of Structural Mechanics for Geodetic Accuracy Assignment: A Case Study of the Finite Element Method. In Contributions to International Conferences on Engineering Surveying; Springer Proceedings in Earth and Environmental Sciences; Kopáčik, A., Kyrinovič, P., Erdélyi, J., Paar, R., Marendić, A., Eds.; Springer: Cham, Swizerland, 2020. [Google Scholar] [CrossRef]
- Shults, R.; Soltabayeva, S.; Seitkazina, G.; Nukarbekova, Z.; Kucherenko, O. Geospatial Monitoring and Structural Mechanics Models: A Case Study of Sports Structures. In Proceedings of the International Conference “Environmental Engineering”, Vilnius, Lithuania, 21–22 May 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Kamnik, R.; Kovačić, B.; Štrukelj, A. Deformation Analysis of Bridges in Exceptional Transports in Slovenia. Traffic Transp. 2012, 22, 15–22. [Google Scholar] [CrossRef]
- Kafle, B.; Zhang, L.; Mendis, P.; Herath, N.; Maizuar, M.; Duffield, C.; Thompson, R.G. Monitoring the Dynamic Behavior of The Merlynston Creek Bridge Using Interferometric Radar Sensors and Finite Element Modeling. Int. J. Appl. Mech. 2017, 9, 1750003. [Google Scholar] [CrossRef]
- Demirkaya, S. Deformation Analysis of an Arch Dam Using ANFIS. In Proceedings of the Second International Workshop (AIEG 2010) “Application of Artificial Intelligence in Engineering Geodesy”: Selected Papers, Braunschweig, Austria, 21–31 June 2010. [Google Scholar]
- Demirkaya, S.; Balcilar, S. The Contribution of Soft Computing Techniques for the Interpretation of Dam Deformation. In Proceedings of the FIG Working Week 2012 Knowing to Manage the Territory, Protect the Environment, Evaluate the Cultural Heritage, Rome, Italy, 6–10 May 2012; 15pAvailable online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2012/papers/ts01f/TS01F_demirkaya_balcilar_5866.pdf (accessed on 16 September 2023).
- Heine, K. Fuzzy Technology and ANN for Analysis of Deformation processes. In Proceedings of the First International Workshop (AIEG 2008) Application of Artificial Intelligence in Engineering Geodesy: Selected Papers, Vienna, Austria, 9–25 December 2008. [Google Scholar]
- Miima, J.B.; Niemeier, W. Adapting neural networks for modelling structural behavior in geodetic deformation monitoring. ZFV—Z. Geodäsie Geoinf. Landmanag. 2004, 129, 160–167. Available online: http://geodaesie.info/zfv/zfv-32004/1319 (accessed on 16 September 2023).
- Cross, E.J.; Koo, K.-Y.; Brownjohn, J.; Worden, K. Long-term monitoring and data analysis of the Tamar Bridge. Mech. Syst. Signal Process. 2013, 35, 16–34. [Google Scholar] [CrossRef]
- Pantazis, G.; Alevizakou, E.-G. The Use of Artificial Neural Networks in Predicting Vertical Displacements of Structures. Int. J. Appl. Sci. Technol. 2013, 3, 1–8. Available online: http://www.ijastnet.com/journals/Vol_3_No_5_May_2013/1.pdf (accessed on 20 September 2023).
- Zhao, S.; Li, P.; Li, H.; Zhang, T.; Wang, B. Monitoring and Comparative Analysis of Hohhot Subway Subsidence Using StaMPS-PS Based on Two DEMS. Remote Sens. 2023, 15, 4011. [Google Scholar] [CrossRef]
- Yan, Y.; Doin, M.-P.; Lopez-Quiroz, P.; Tupin, F.; Fruneau, B.; Pinel, V.; Trouve, E. Mexico City Subsidence Measured by InSAR Time Series: Joint Analysis Using PS and SBAS Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1312–1326. [Google Scholar] [CrossRef]
- Fernández-Torres, E.A.; Cabral-Cano, E.; Novelo-Casanova, D.A.; Solano-Rojas, D.; Havazli, E.; Salazar-Tlaczani, L. Risk Assessment of Land Subsidence and Associated Faulting in Mexico City Using InSAR. Nat. Hazards 2022, 112, 37–55. [Google Scholar] [CrossRef]
- Luo, X.G.; Wang, J.; Xu, Z.; Zhu, S.; Meng, L.; Liu, J.; Cui, Y. Dynamic Analysis of Urban Ground Subsidence in Beijing Based on the Permanent Scattering InSAR Technology. JARS 2018, 12, 026001. [Google Scholar] [CrossRef]
- Wang, H.; Feng, G.; Xu, B.; Yu, Y.; Li, Z.; Du, Y.; Zhu, J. Deriving Spatio-Temporal Development of Ground Subsidence Due to Subway Construction and Operation in Delta Regions with PS-InSAR Data: A Case Study in Guangzhou, China. Remote Sens. 2017, 9, 1004. [Google Scholar] [CrossRef]
- Wang, R.; Yang, M.; Dong, J.; Liao, M. Investigating Deformation along Metro Lines in Coastal Cities Considering Different Structures with InSAR and SBM Analyses. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103099. [Google Scholar] [CrossRef]
- Espiritu, K.W.; Reyes, C.J.; Benitez, T.M.; Tokita, R.C.; Galvez, L.J.; Ramirez, R. Sentinel-1 Interferometric Synthetic Aperture Radar (InSAR) Reveals Continued Ground Deformation in and around Metro Manila, Philippines, Associated with Groundwater Exploitation. Nat. Hazards 2022, 114, 3139–3161. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Radman, A.; Akhoondzadeh, M.; Hosseiny, B. Integrating InSAR and deep-learning for modeling and predicting subsidence over the adjacent area of Lake Urmia, Iran. GIScience Remote Sens. 2021, 58, 1413–1433. [Google Scholar] [CrossRef]
- Han, Y.; Liu, G.; Liu, J.; Yang, J.; Xie, X.; Yan, W.; Zhang, W. Monitoring and Analysis of Land Subsidence in Jiaozuo City (China) Based on SBAS-InSAR Technology. Sustainability 2023, 15, 11737. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Zhang, H.; Liu, J.; Jing, Z. Land Subsidence Monitoring and Building Risk Assessment Using InSAR and Machine Learning in a Loess Plateau City—A Case Study of Lanzhou, China. Remote Sens. 2023, 15, 2851. [Google Scholar] [CrossRef]
- Sun, H.; Peng, H.; Zeng, M.; Wang, S.; Pan, Y.; Pi, P.; Xue, Z.; Zhao, X.; Zhang, A.; Liu, F. Land Subsidence in a Coastal City Based on SBAS-InSAR Monitoring: A Case Study of Zhuhai, China. Remote Sens. 2023, 15, 2424. [Google Scholar] [CrossRef]
- Fu, G.; Schmid, W.; Castellazzi, P. Understanding the Spatial Variability of the Relationship between InSAR-Derived Deformation and Groundwater Level Using Machine Learning. Geosciences 2023, 13, 133. [Google Scholar] [CrossRef]
- Yazbeck, J.; Rundle, J.B. Predicting Short-Term Deformation in the Central Valley Using Machine Learning. Remote Sens. 2023, 15, 449. [Google Scholar] [CrossRef]
- Zhang, J.; Ke, C.; Shen, X.; Lin, J.; Wang, R. Monitoring Land Subsidence along the Subways in Shanghai on the Basis of Time-Series InSAR. Remote Sens. 2023, 15, 908. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Kim, D. GPS-structural health monitoring of a long span bridge using neural network adaptive filter. Surv. Rev. 2014, 46, 7–14. [Google Scholar] [CrossRef]
- Behkamal, B.; Entezami, A.; De Michele, C.; Arslan, A.N. Elimination of Thermal Effects from Limited Structural Displacements Based on Remote Sensing by Machine Learning Techniques. Remote Sens. 2023, 15, 3095. [Google Scholar] [CrossRef]
- Gomez-Cabrera, A.; Escamilla-Ambrosio, P.J. Review of Machine-Learning Techniques Applied to Structural Health Monitoring Systems for Building and Bridge Structures. Appl. Sci. 2022, 12, 10754. [Google Scholar] [CrossRef]









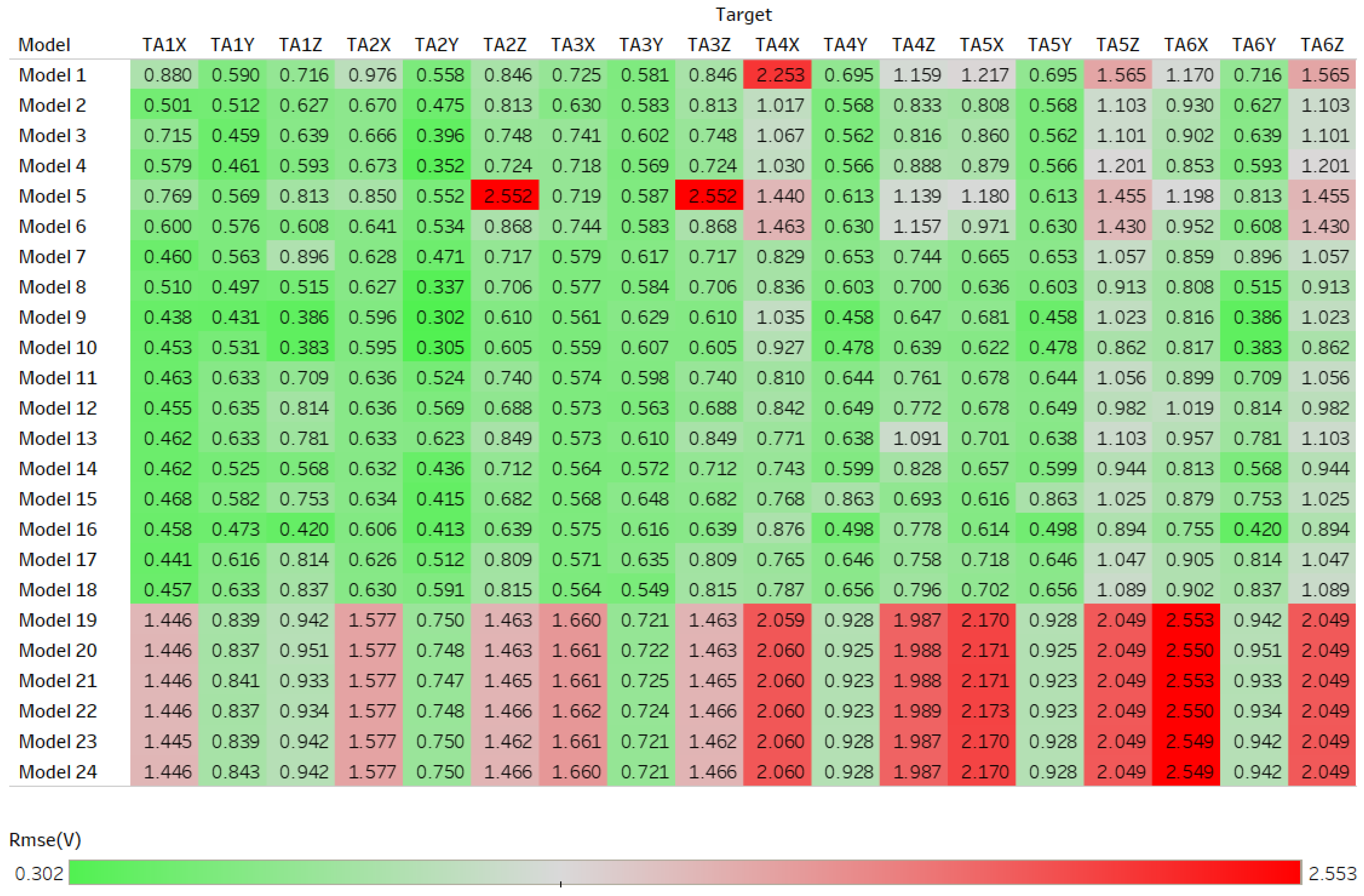
















| Model | Activation Function | Number of Layers | Number of Outputs in Each Layer |
|---|---|---|---|
| Model 1 | Rectified linear unit | 1 | 10 |
| Model 2 | 2 | 10, 10 | |
| Model 3 | 3 | 10, 10, 10 | |
| Model 4 | 3 | 30, 20, 10 | |
| Model 5 | 1 | 20 | |
| Model 6 | 1 | 50 | |
| Model 7 | Hyperbolic tangent | 1 | 10 |
| Model 8 | 2 | 10, 10 | |
| Model 9 | 3 | 10, 10, 10 | |
| Model 10 | 3 | 30, 20, 10 | |
| Model 11 | 1 | 20 | |
| Model 12 | 1 | 50 | |
| Model 13 | Sigmoid function | 1 | 10 |
| Model 14 | 2 | 10, 10 | |
| Model 15 | 3 | 10, 10, 10 | |
| Model 16 | 3 | 30, 20, 10 | |
| Model 17 | 1 | 20 | |
| Model 18 | 1 | 50 | |
| Model 19 | Identity function | 1 | 10 |
| Model 20 | 2 | 10, 10 | |
| Model 21 | 3 | 10, 10, 10 | |
| Model 22 | 3 | 30, 20, 10 | |
| Model 23 | 1 | 20 | |
| Model 24 | 1 | 50 |
| Target | Validation | Testing |
|---|---|---|
| TA1X | Stepwise Linear Regression | Linear Regression Quadratic |
| TA2X | Stepwise Linear Regression | Linear Regression Quadratic |
| TA3X | Stepwise Linear Regression | Linear Regression Quadratic |
| TA4X | F | F |
| TA5X | F | F |
| TA6X | F | F |
| TA1Y | Stepwise Linear Regression | Linear Regression Quadratic |
| TA2Y | F | F |
| TA3Y | F | F |
| TA4Y | F | F |
| TA5Y | F | F |
| TA6Y | F | F |
| TA1Z | Stepwise Linear Regression | Stepwise Linear Regression |
| TA2Z | F | Linear Regression Quadratic |
| TA3Z | F | Linear Regression Quadratic |
| TA4Z | F | F |
| TA5Z | Stepwise Linear Regression | F |
| TA6Z | F | F |
| Target | Validation | Testing |
|---|---|---|
| TB1X | Stepwise Linear Regression | Linear Regression Quadratic |
| TB2X | Stepwise Linear Regression | F |
| TB3X | Stepwise Linear Regression | Linear Regression Quadratic |
| TB4X | Linear Regression | Linear Regression Quadratic |
| TB5X | Stepwise Linear Regression | Stepwise Linear Regression |
| TB6X | Stepwise Linear Regression | Linear Regression Quadratic |
| TB7X | Stepwise Linear Regression | F |
| TB8X | Stepwise Linear Regression | Linear Regression Robust |
| TB9X | F | F |
| TB1Y | F | F |
| TB2Y | F | F |
| TB3Y | Stepwise Linear Regression | Linear Regression Quadratic |
| TB4Y | F | F |
| TB5Y | Stepwise Linear Regression | Stepwise Linear Regression |
| TB6Y | Stepwise Linear Regression | Linear Regression Quadratic |
| TB7Y | F | Linear Regression Quadratic |
| TB8Y | Stepwise Linear Regression | Linear Regression Quadratic |
| TB9Y | Stepwise Linear Regression | F |
| TB1Z | Stepwise Linear Regression | F |
| TB2Z | Stepwise Linear Regression | F |
| TB3Z | F | F |
| TB4Z | F | Stepwise Linear Regression |
| TB5Z | F | Stepwise Linear Regression |
| TB6Z | F | F |
| TB7Z | Stepwise Linear Regression | F |
| TB8Z | F | Stepwise Linear Regression |
| TB9Z | F | F |
| Target | Validation | Testing |
|---|---|---|
| TA1X | Model 17 | Model 7, 11, 12 |
| TA2X | Model 9,10 | Model 6 |
| TA3X | Model 9, 10, 14 | Model 17, 18 |
| TA4X | Model 14 | Model 10 |
| TA5X | Model 16 | Model 8 |
| TA6X | Model 16 | Model 8 |
| TA1Y | Model 9, 10 | Model 9, 10 |
| TA2Y | Model 9, 10 | Model 9, 10 |
| TA3Y | F | F |
| TA4Y | Model 9 | Model 9 |
| TA5Y | Model 9 | Model 16 |
| TA6Y | Model 10 | Model 16 |
| TA1Z | Model 10 | Model 16 |
| TA2Z | Model 10 | Model 2, 13 |
| TA3Z | Model 10 | Model 2, 7, 13 |
| TA4Z | Model 10 | Model 16 |
| TA5Z | Model 10 | Model 9 |
| TA6Z | Model 10 | Model 9 |
| Target | Validation | Testing |
|---|---|---|
| TB1X | Model 16 | Model 3 |
| TB2X | Model 22 | Model 3 |
| TB3X | Model 18, 21, 22 | Model 19 |
| TB4X | Model 5 | Model 16 |
| TB5X | Model 22 | F |
| TB6X | F | Model 24 |
| TB7X | Model 6 | F |
| TB8X | F | F |
| TB9X | F | F |
| TB1Y | F | Model 16 |
| TB2Y | Model 8 | Model 4 |
| TB3Y | Model 18 | Model 10, 12 |
| TB4Y | Model 7 | F |
| TB5Y | Model 7 | F |
| TB6Y | Model 11, 14 | Model 10 |
| TB7Y | Model 11, 13 | Model 12 |
| TB8Y | Model 11, 13 | Model 12 |
| TB9Y | Model 7, 13, 18 | Model 16 |
| TB1Z | Model 16 | Model 4 |
| TB2Z | Model 13 | Model 3, 10 |
| TB3Z | Model 10, 16 | Model 9, 16 |
| TB4Z | Model 15 | F |
| TB5Z | Model 10 | Model 10 |
| TB6Z | Model 10 | Model 10 |
| TB7Z | Model 16 | Model 16 |
| TB8Z | F | F |
| TB9Z | F | F |
| Layer 1 | Layer 2 | Layer 3 | Activation Function | MSE | Validation RMSE, mm | Validation R-Square | Testing RMSE, mm | Testing R-Square |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 68 | Hyperbolic tangent | 0.56 | 0.75 | 0.77 | 0.78 | 0.72 |
| 1 | 300 | - | Hyperbolic tangent | 0.63 | 0.74 | 0.77 | 0.80 | 0.70 |
| 1 | 4 | 46 | Sigmoid | 0.59 | 0.76 | 0.76 | 0.79 | 0.71 |
| 2 | - | - | Sigmoid | 0.60 | 0.78 | 0.75 | 0.71 | 0.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shults, R.; Bilous, M.; Ormambekova, A.; Nurpeissova, T.; Khailak, A.; Annenkov, A.; Akhmetov, R. Analysis of Overpass Displacements Due to Subway Construction Land Subsidence Using Machine Learning. Urban Sci. 2023, 7, 100. https://doi.org/10.3390/urbansci7040100
Shults R, Bilous M, Ormambekova A, Nurpeissova T, Khailak A, Annenkov A, Akhmetov R. Analysis of Overpass Displacements Due to Subway Construction Land Subsidence Using Machine Learning. Urban Science. 2023; 7(4):100. https://doi.org/10.3390/urbansci7040100
Chicago/Turabian StyleShults, Roman, Mykola Bilous, Azhar Ormambekova, Toleuzhan Nurpeissova, Andrii Khailak, Andriy Annenkov, and Rustem Akhmetov. 2023. "Analysis of Overpass Displacements Due to Subway Construction Land Subsidence Using Machine Learning" Urban Science 7, no. 4: 100. https://doi.org/10.3390/urbansci7040100
APA StyleShults, R., Bilous, M., Ormambekova, A., Nurpeissova, T., Khailak, A., Annenkov, A., & Akhmetov, R. (2023). Analysis of Overpass Displacements Due to Subway Construction Land Subsidence Using Machine Learning. Urban Science, 7(4), 100. https://doi.org/10.3390/urbansci7040100






