Uncovering the Socioeconomic Structure of Spatial and Social Interactions in Cities
Abstract
1. Introduction
2. Materials and Methods
2.1. From Data to Networks
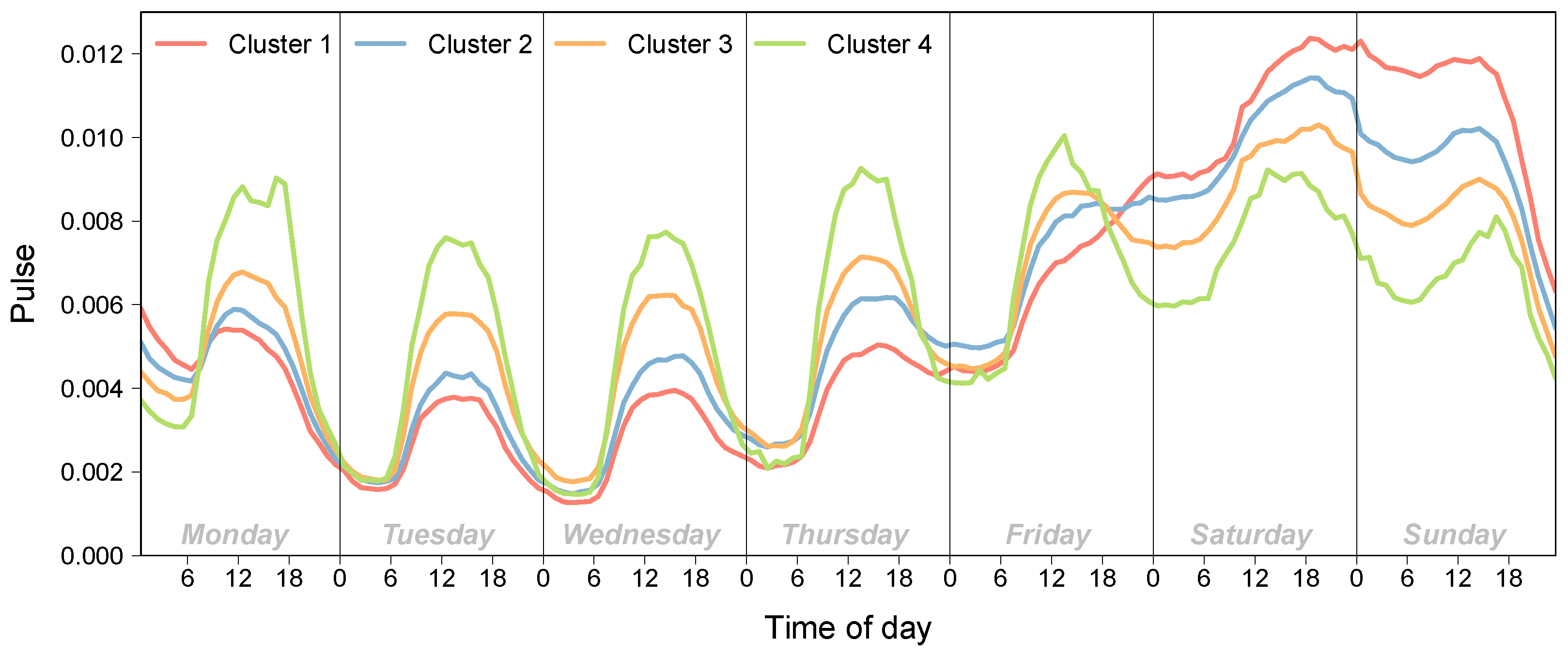
2.2. Pulse of a Location
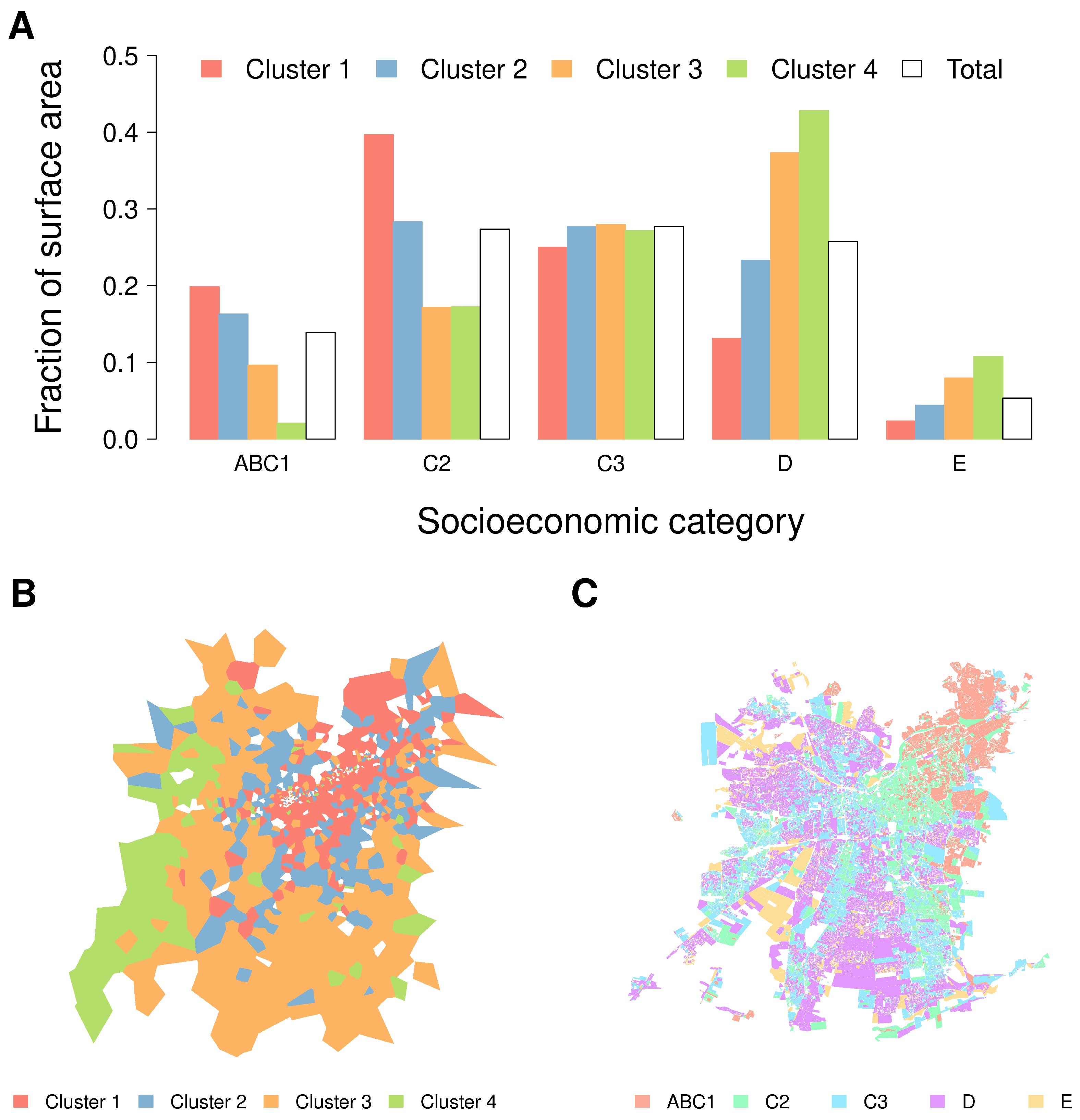
2.3. Cluster Analysis
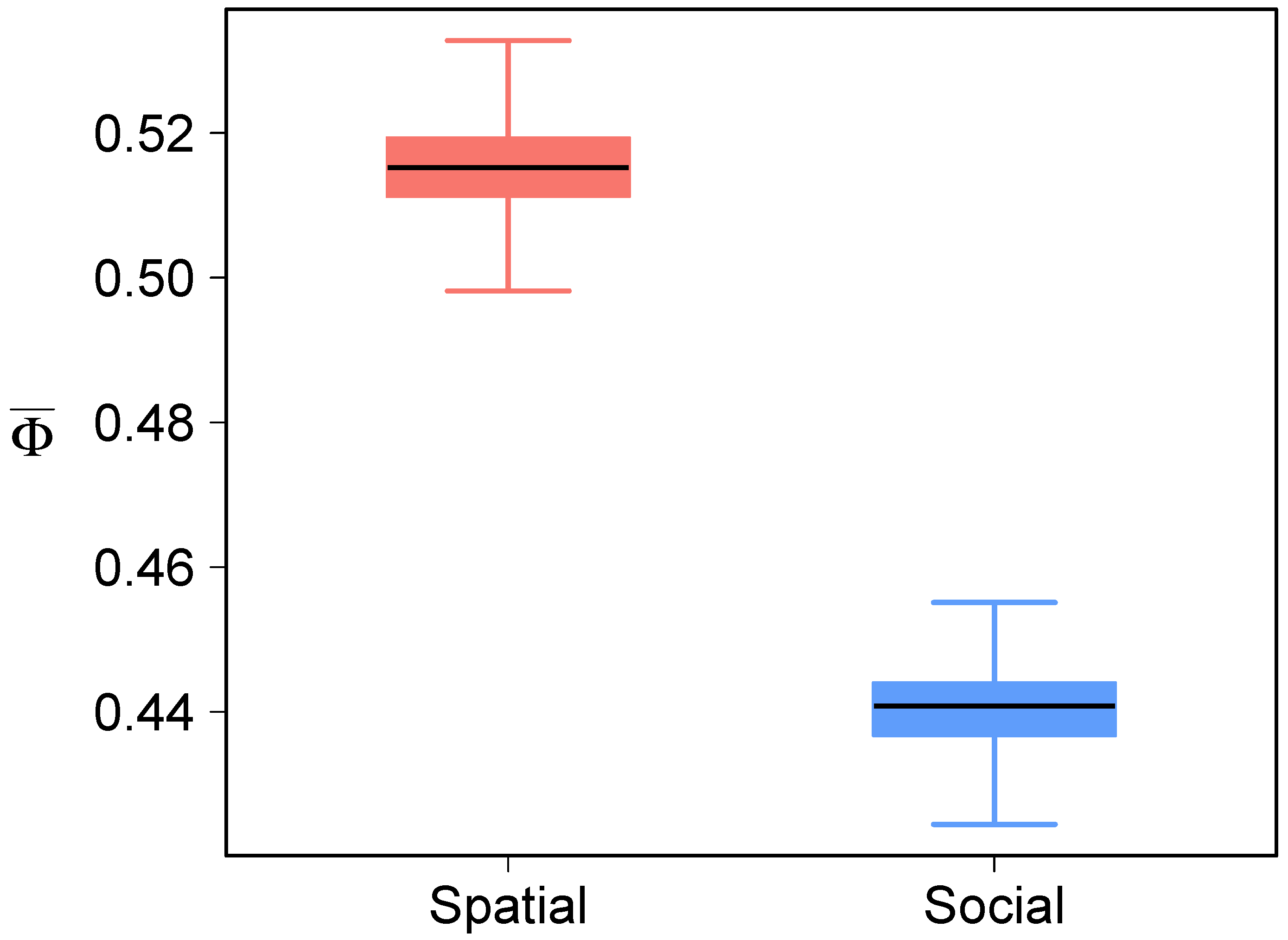
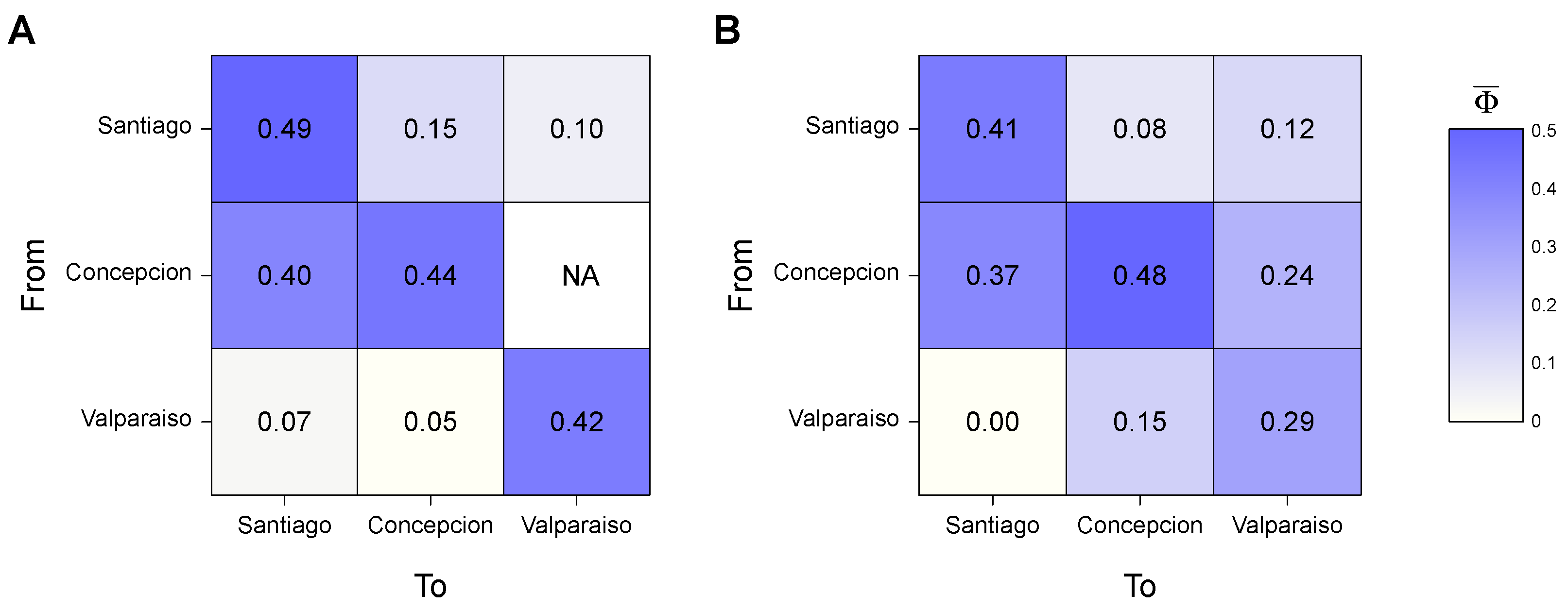
2.4. Measuring Spatial and Social Interactions
3. Results
3.1. Pulse of a Location and Socioeconomic Structure
3.2. Socio-Spatial Interactions Analysis
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Preprocessing
Appendix A.1. Call and Location History
Appendix A.2. Identification of the Users’ Place of Residence
- First, we focused on the user’s spatial events occurring during nighttime hours (between 9 pm and 8 am included). Only days of the week from Monday to Thursday were considered ( h in total). We note that is the number of events occurring during nighttime hours.
- We applied here a first filter by considering only users with a number of spatial events higher than a fraction of the total number of nighttime hours.
- We identified the location in which the user has localized the highest number of spatial events during nighttime hours. We define this location as her or his home location.
- A second filter was also implemented to select only users whose fraction of events occurring at their home location during nighttime is larger than a fraction of the total number of events during nighttime.

| Date | # Users (All) | # Reliable Users |
|---|---|---|
| 15 to 21 March 2015 | 3,292,923 | 1,657,048 |
| 10 to 16 May 2015 | 3,292,647 | 1,598,571 |
| 2 to 8 August 2015 | 3,236,122 | 1,539,621 |
| Total | 4,064,476 | 2,565,365 |
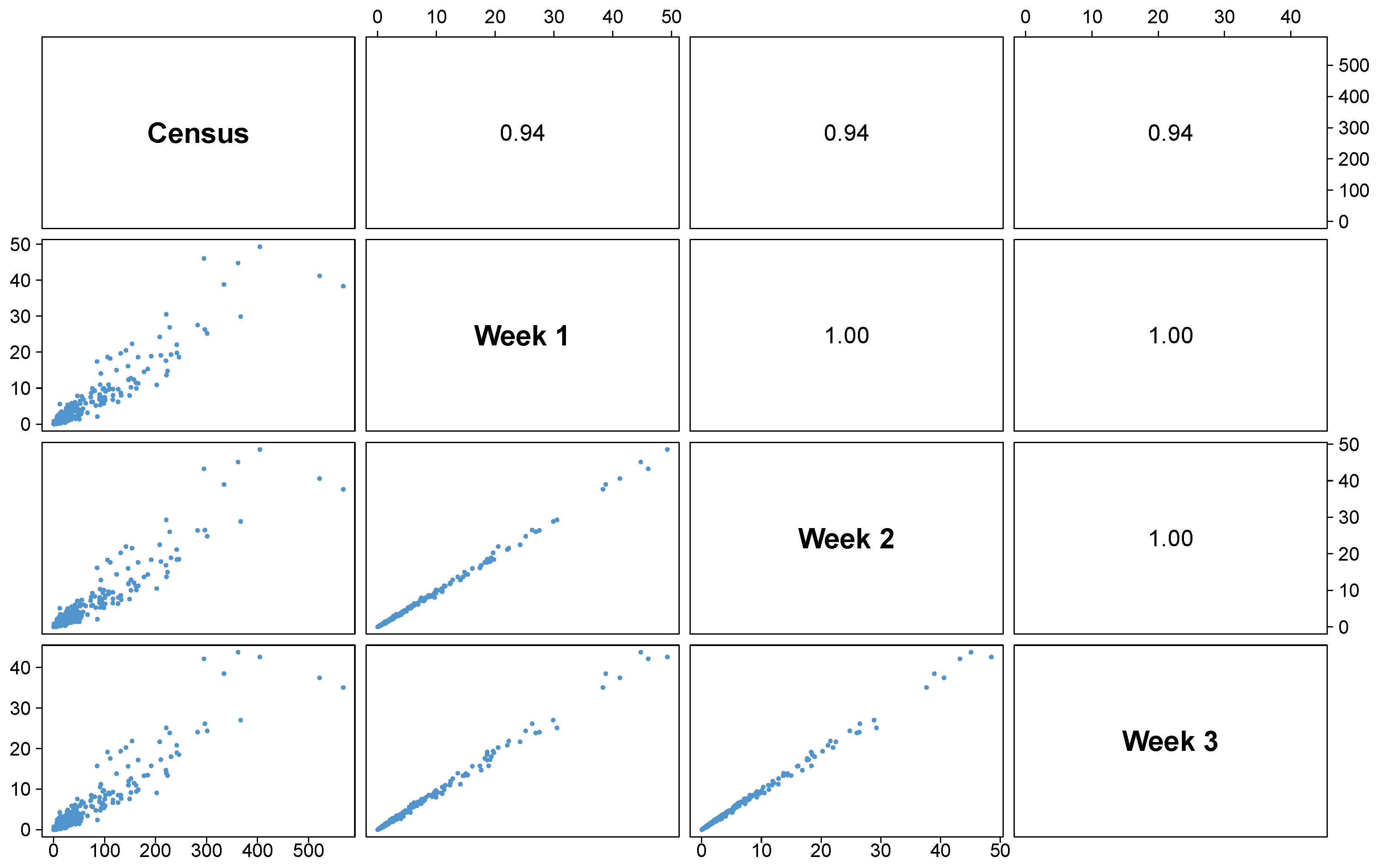
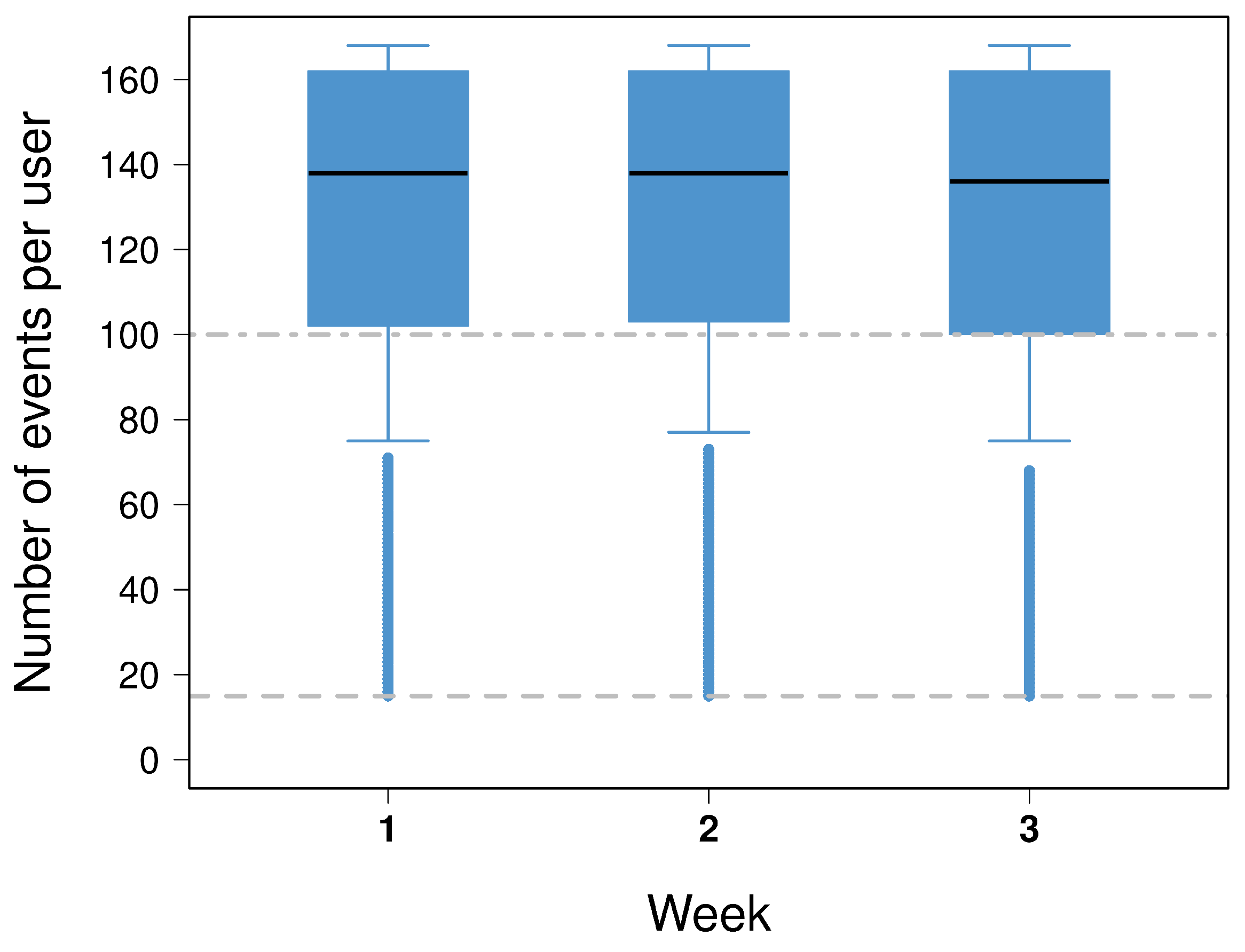
Appendix A.3. From Events to Networks
| Date | #Reliable Users | #Spatial Events | #Social Events |
|---|---|---|---|
| 15 to 21 March 2015 | 1,657,048 | 129,760,887 | 4,433,505 |
| 10 to 16 May 2015 | 1,598,571 | 126,359,359 | 4,207,538 |
| 2 to 8 August 2015 | 1,539,621 | 120,960,807 | 3,905,935 |
| Total | 3,023,946 | 377,081,053 | 12,546,978 |
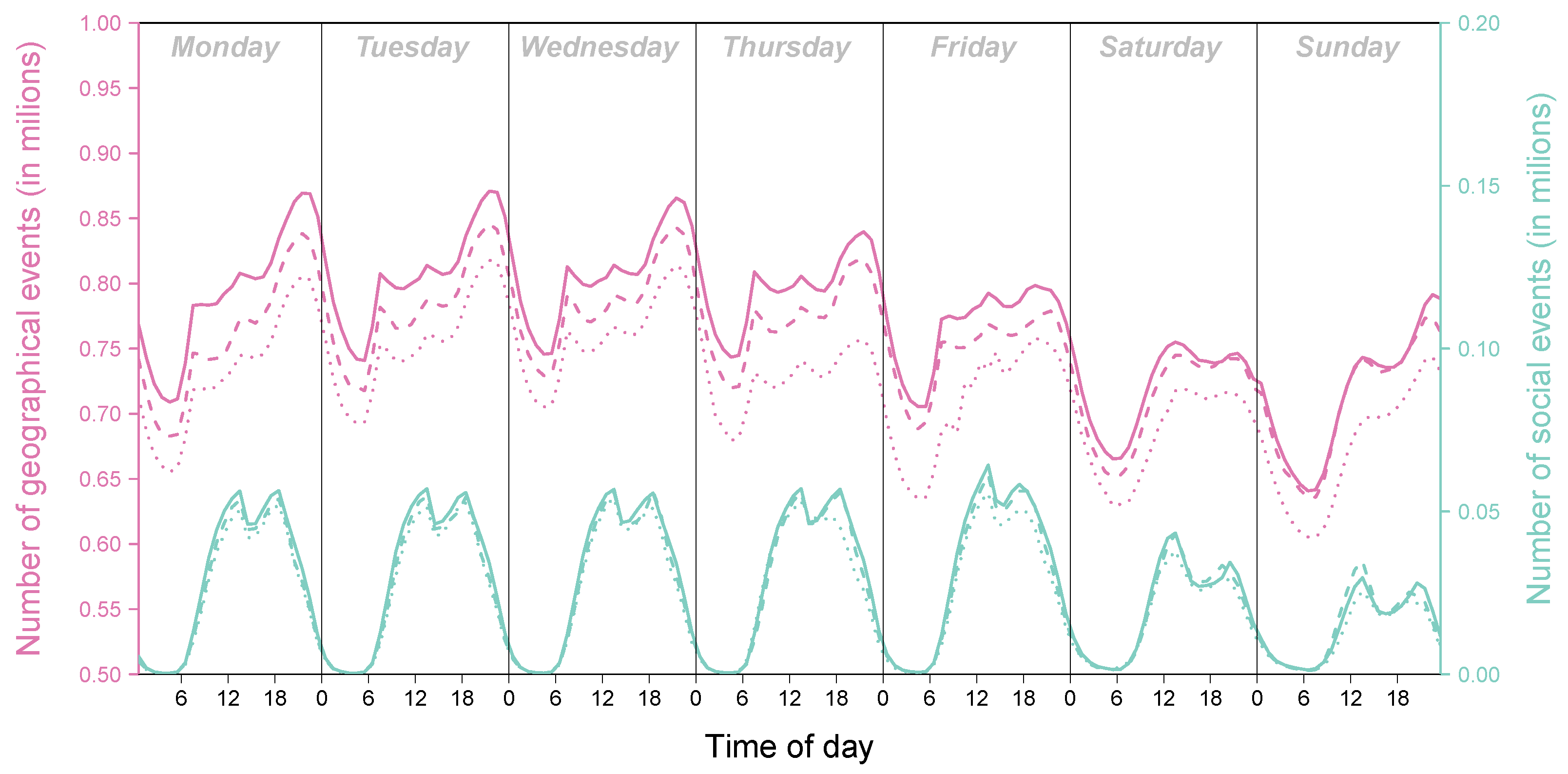
Appendix B. Socioeconomic Structure of the Locations
- Antofagasta in 2002 available at https://ideocuc-ocuc.hub.arcgis.com/datasets/fbde68b6c3d547c8adfcc17d196e1e88_0, last accessed 6 December 2022.
- Coquimbo y La Serena in 2002 available at https://ideocuc-ocuc.hub.arcgis.com/, last accessed 6 December 2022.
- Gran Concepción in 2002 available at https://ideocuc-ocuc.hub.arcgis.com/datasets/f62f12fae97548fd8c71cb405d40e5f2_0, last accessed 6 December 2022.
- Gran Santiago in 2012 available at https://ideocuc-ocuc.hub.arcgis.com/datasets/c264bc8bca7f45bc8ae74329557628b2_0, last accessed 6 December 2022.
- Puerto Montt and Puerto Varas in 2002 available at https://ideocuc-ocuc.hub.arcgis.com/datasets/91deae3707ff447f961b4e2a5cf2300d_0, last accessed 6 December 2022.
- Valparaíso in 2002 available at https://ideocuc-ocuc.hub.arcgis.com/datasets/b9458dbbc94343e58ea5fc9c5def03f9_0, last accessed 6 December 2022.
Appendix C. Clustering Analysis
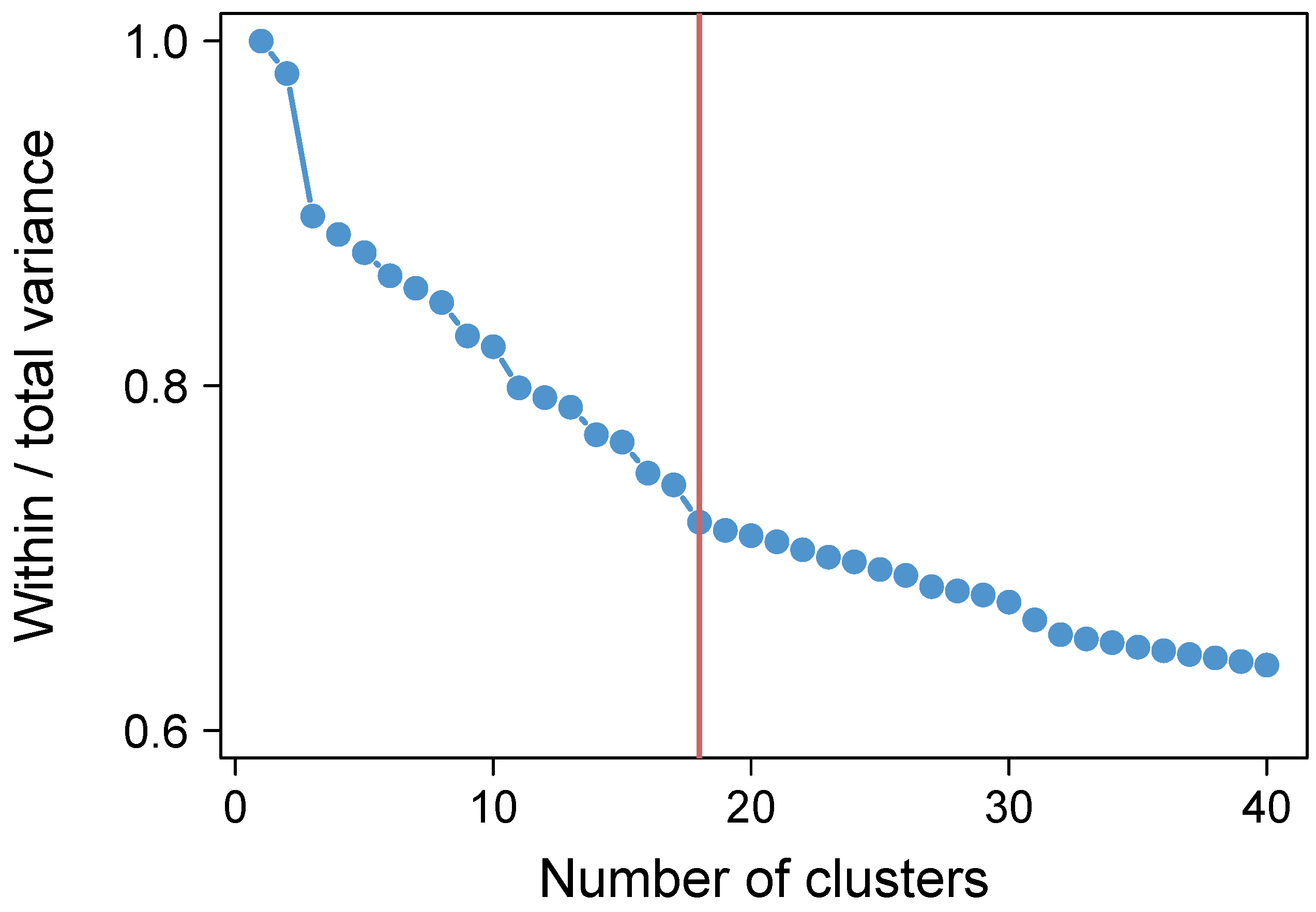
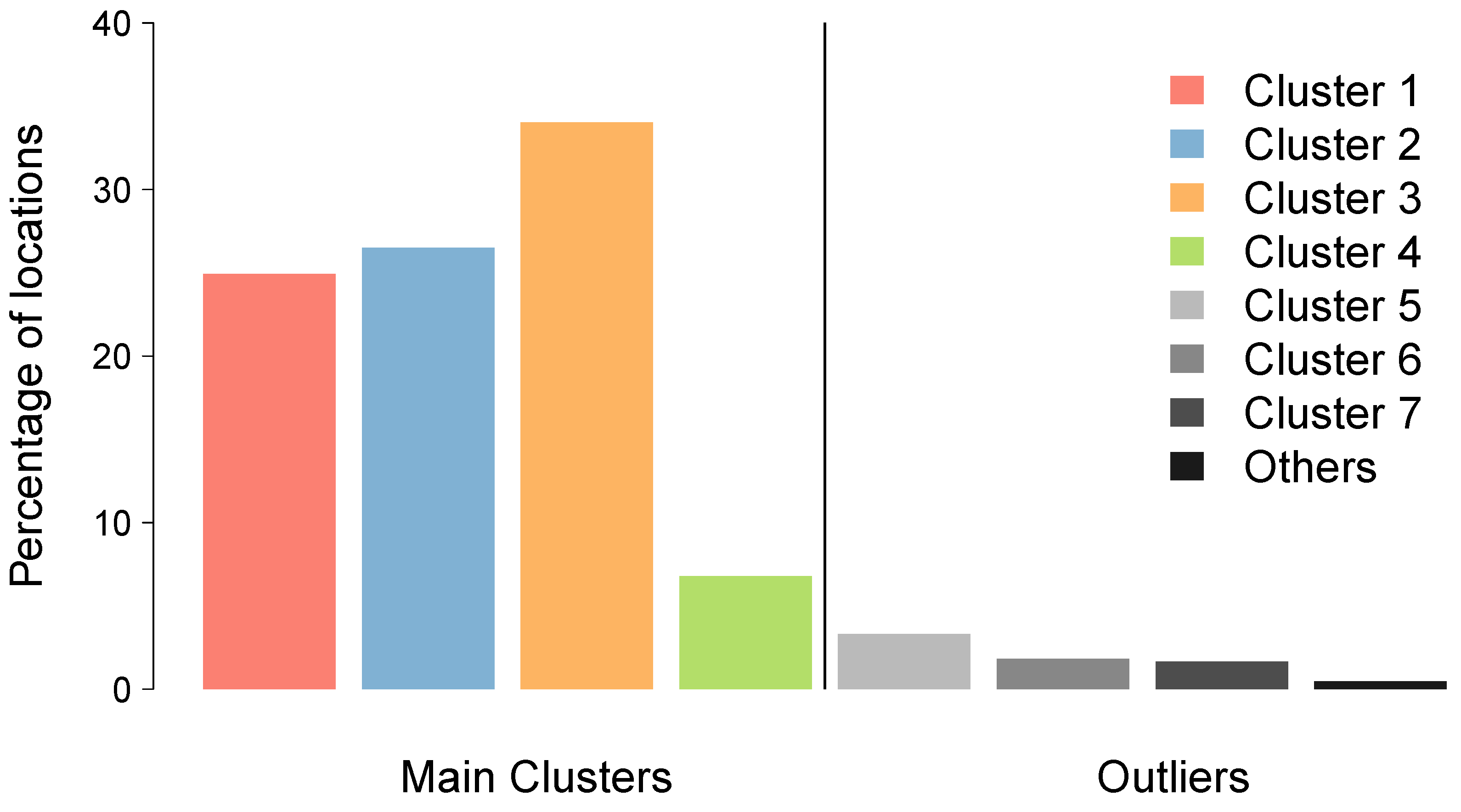
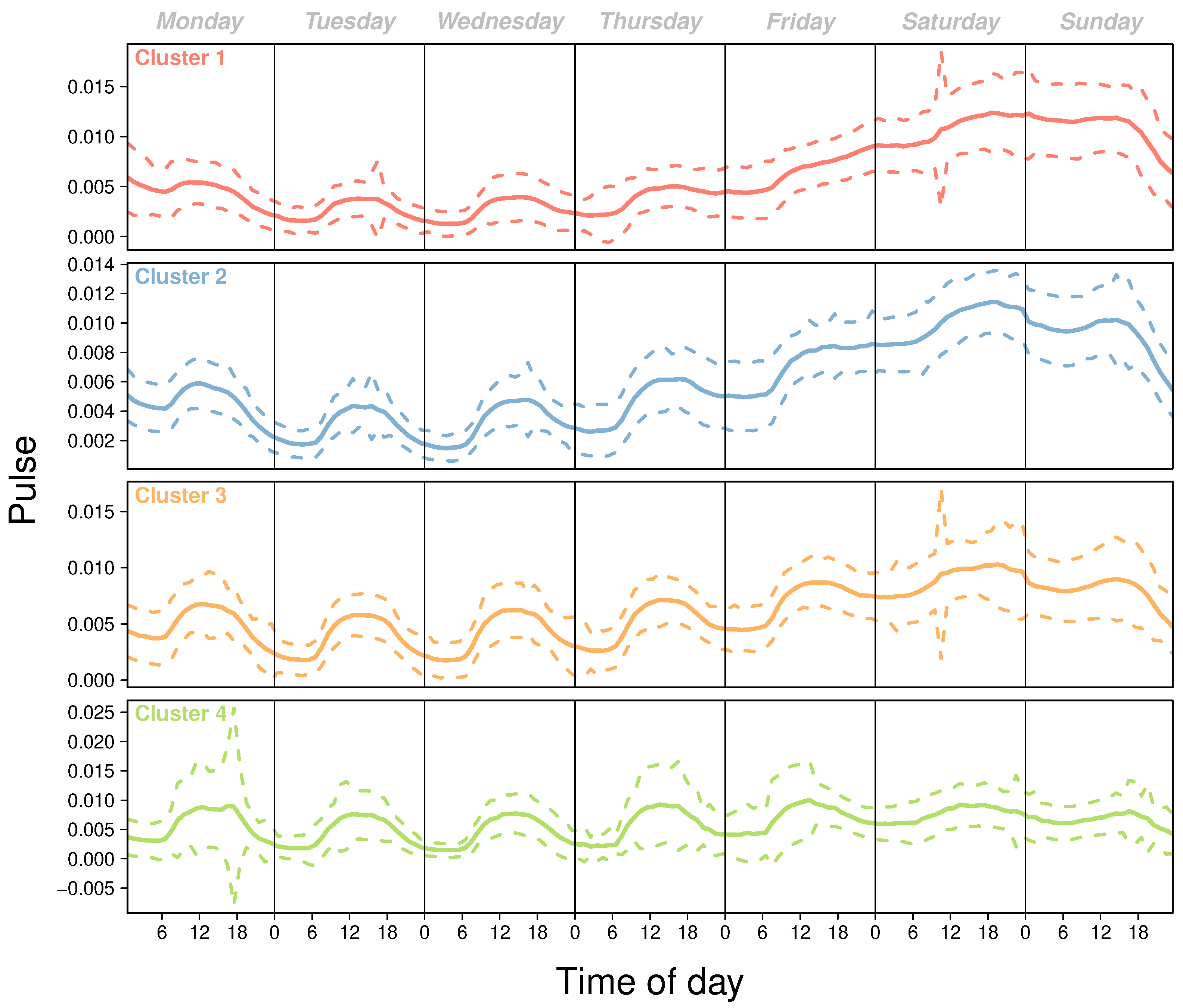
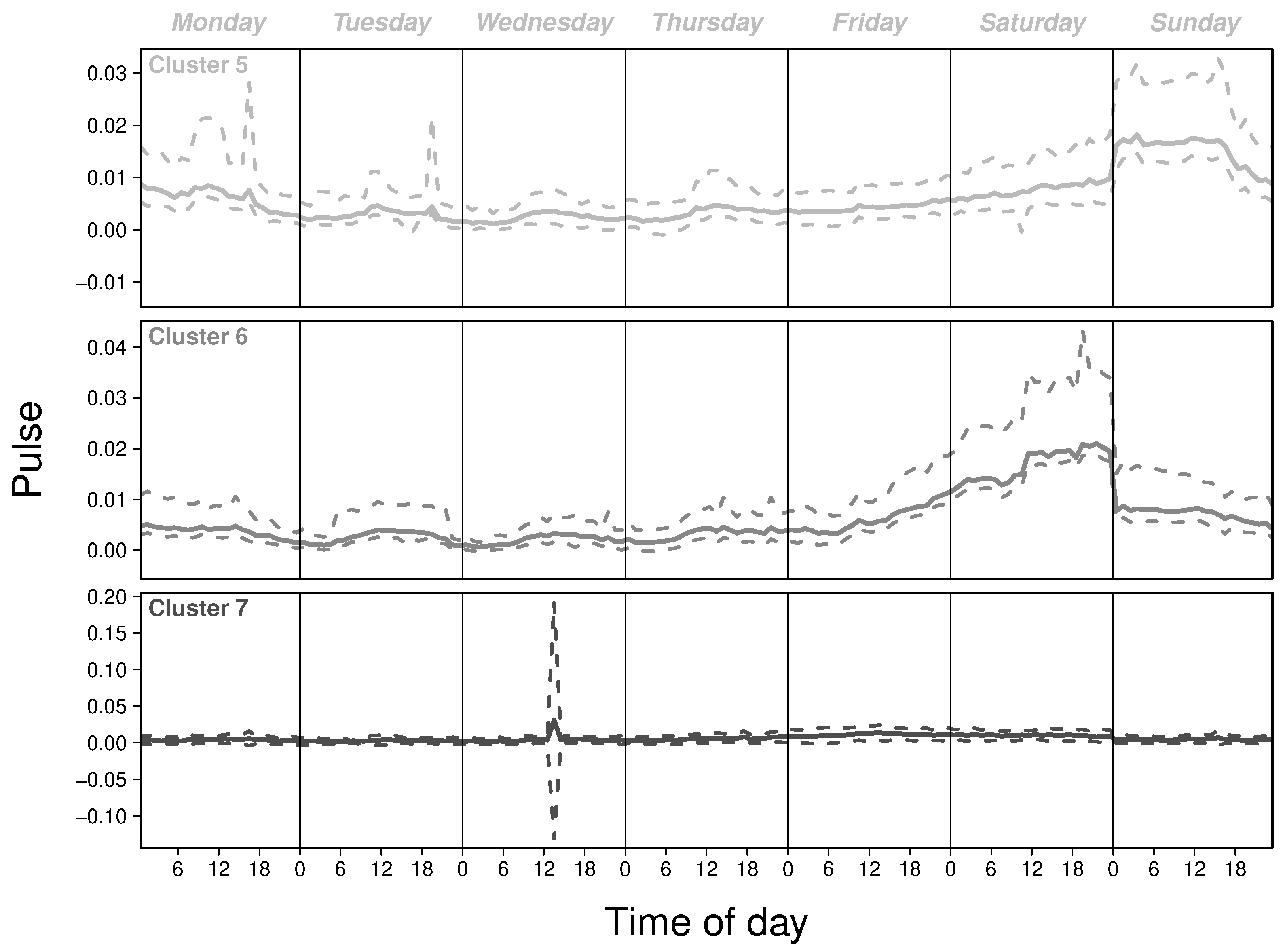
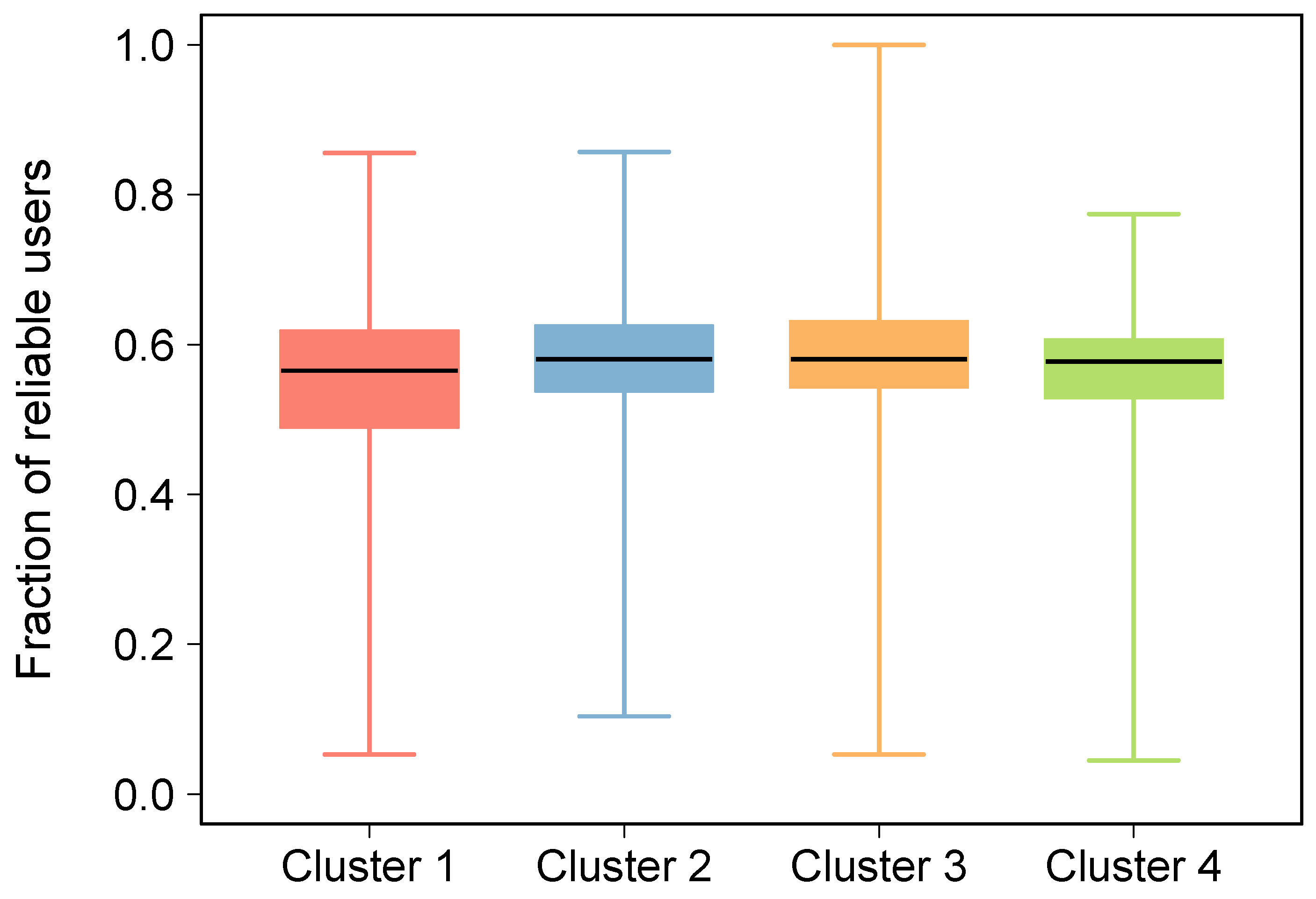
Appendix D. Null Model
References
- Hall, P.; Tewdwr-Jones, M. Urban and Regional Planning; Routledge: Oxfordshide, UK, 2019. [Google Scholar]
- Alvaredo, F.; Chancel, L.; Piketty, T.; Saez, E.; Zucman, G. World Inequality Report 2018; Belknap Press: Cambridge, MA, USA, 2018. [Google Scholar]
- El-Geneidy, A.; Levinson, D.; Diab, E.; Boisjoly, G.; Verbich, D.; Loong, C. The cost of equity: Assessing transit accessibility and social disparity using total travel cost. Transp. Res. Part A Policy Pract. 2016, 91, 302–316. [Google Scholar] [CrossRef]
- Jones, M.; Pebley, A.R. Redefining neighborhoods using common destinations: Social characteristics of activity spaces and home census tracts compared. Demography 2014, 51, 727–752. [Google Scholar] [CrossRef] [PubMed]
- Lenormand, M.; Samaniego, H.; Chaves, J.; da Fonseca Vieira, V.; Silva, M.; Evsukoff, A. Entropy as a Measure of Attractiveness and Socioeconomic Complexity in Rio de Janeiro Metropolitan Area. Entropy 2020, 22, 368. [Google Scholar] [CrossRef]
- Steele, J.E.; Sundsøy, P.R.; Pezzulo, C.; Alegana, V.A.; Bird, T.J.; Blumenstock, J.; Bjelland, J.; Engø-Monsen, K.; de Montjoye, Y.A.; Iqbal, A.M.; et al. Mapping poverty using mobile phone and satellite data. J. R. Soc. Interface 2017, 14, 20160690. [Google Scholar] [CrossRef] [PubMed]
- Dannemann, T.; Sotomayor-Gómez, B.; Samaniego, H. The Time Geography of Segregation during Working Hours. R. Soc. Open Sci. 2018, 5, 180749. [Google Scholar] [CrossRef]
- Cottineau, C.; Vanhoof, M. Mobile phone indicators and their relation to the socioeconomic organisation of cities. ISPRS Int. J. -Geo-Inf. 2019, 8, 19. [Google Scholar] [CrossRef]
- Alessandretti, L.; Aslak, U.; Lehmann, S. The scales of human mobility. Nature 2020, 587, 402–407. [Google Scholar] [CrossRef]
- De Montjoye, Y.A.; Hidalgo, C.A.; Verleysen, M.; Blondel, V.D. Unique in the Crowd: The privacy bounds of human mobility. Sci. Rep. 2013, 3, 1376. [Google Scholar] [CrossRef]
- Blondel, V.D.; Decuyper, A.; Krings, G. A survey of results on mobile phone datasets analysis. EPJ Data Sci. 2015, 4, 10. [Google Scholar] [CrossRef]
- Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.J.; Simini, F.; Tomasini, M. Human mobility: Models and applications. Phys. Rep. 2018, 734, 1–74. [Google Scholar] [CrossRef]
- Lenormand, M.; Louail, T.; Barthelemy, M.; Ramasco, J.J. Is spatial information in ICT data reliable? arXiv 2016, arXiv:1609.03375. [Google Scholar]
- Lenormand, M.; Murillo Arias, J.; San Miguel, M.; Ramasco, J.J. On the importance of trip destination for modeling individual human mobility patterns. J. R. Soc. Interface 2020, 17, 20200673. [Google Scholar] [CrossRef] [PubMed]
- Entwisle, B. Putting people into place. Demography 2007, 44, 687–703. [Google Scholar] [CrossRef] [PubMed]
- Shelton, T.; Poorthuis, A.; Zook, M. Social media and the city: Rethinking urban socio-spatial inequality using user-generated geographic information. Landsc. Urban Plan. 2015, 142, 198–211. [Google Scholar] [CrossRef]
- Salganik, M.J. Bit by Bit: Social Research in the Digital Age; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Blumenstock, J.; Cadamuro, G.; On, R. Predicting poverty and wealth from mobile phone metadata. Science 2015, 350, 1073–1076. [Google Scholar] [CrossRef]
- Frias-Martinez, V.; Virseda, J. On the relationship between socio-economic factors and cell phone usage. In Proceedings of the Fifth International Conference on Information and Communication Technologies and Development, ICTD ‘12, Atlanta, GA, USA, 12–15 March 2012; pp. 76–84. [Google Scholar]
- Lenormand, M.; Picornell, M.; Garcia Cantú, O.; Tugores, A.; Louail, T.; Herranz, R.; Barthelemy, M.; Frías-Martínez, E.; Ramasco, J.J. Comparing and modeling land use organization in cities. R. Soc. Open Sci. 2015, 2, 150459. [Google Scholar] [CrossRef]
- Pappalardo, L.; Vanhoof, M.; Gabrielli, L.; Smoreda, Z.; Pedreschi, D.; Giannotti, F. An analytical framework to nowcast well-being using mobile phone data. Int. J. Data Sci. Anal. 2016, 2, 75–92. [Google Scholar] [CrossRef]
- Alessandretti, L.; Sapiezynski, P.; Sekara, V.; Lehmann, S.; Baronchelli, A. Evidence for a conserved quantity in human mobility. Nat. Hum. Behav. 2018, 2, 485–491. [Google Scholar] [CrossRef]
- Barbosa, H.; Hazarie, S.; Dickinson, B.; Bassolas, A.; Frank, A.; Kautz, H.; Sadilek, A.; Ramasco, J.J.; Ghoshal, G. Uncovering the socioeconomic facets of human mobility. arXiv 2020, arXiv:2012.00838. [Google Scholar] [CrossRef]
- Jiron, P. Mobility on the Move: Examining Urban Daily Mobility Practices in Santiago de Chile. Ph.D. Thesis, London School of Economics and Political Science, London, UK, 2009. [Google Scholar]
- Gauvin, L.; Tizzoni, M.; Piaggesi, S.; Young, A.; Adler, N.; Verhulst, S.; Ferres, L.; Cattuto, C. Gender gaps in urban mobility. Humanit. Soc. Sci. Commun. 2020, 7, 11. [Google Scholar] [CrossRef]
- Lotero, L.; Hurtado, R.G.; Floría, L.M.; Gómez-Gardeñes, J. Rich do not rise early: Spatio-temporal patterns in the mobility networks of different socio-economic classes. R. Soc. Open Sci. 2016, 3, 150654. [Google Scholar] [CrossRef] [PubMed]
- Palmer, J.R.B.; Espenshade, T.J.; Bartumeus, F.; Chung, C.Y.; Ozgencil, N.E.; Li, K. New Approaches to Human Mobility: Using Mobile Phones for Demographic Research. Demography 2013, 50, 1105–1128. [Google Scholar] [CrossRef] [PubMed]
- McLuhan, M. The Medium Is the Message; Routledge: Oxfordshire, UK, 1964. [Google Scholar]
- Yeung, H.W.C. Capital, State and Space: Contesting the Borderless World. Trans. Inst. Br. Geogr. 1998, 23, 291–309. [Google Scholar] [CrossRef]
- Bagrow, J.P.; Liu, X.; Mitchell, L. Information flow reveals prediction limits in online social activity. Nat. Hum. Behav. 2019, 3, 122–128. [Google Scholar] [CrossRef]
- Song, C.; Qu, Z.; Blumm, N.; Barabasi, A.L. Limits of Predictability in Human Mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Urry, J. Social networks, travel and talk. Br. J. Sociol. 2003, 54, 155–175. [Google Scholar] [CrossRef]
- Netto, V.M.; Meirelles, J.; Ribeiro, F.L.; Federal, U.; Uff, F. Social Interaction and the City: The Effect of Space on the Reduction of Entropy. Complexity 2017, 2017, 6182503. [Google Scholar] [CrossRef]
- Cho, E.; Myers, S.A.; Leskovec, J. Friendship and mobility: User movement in location-based social networks. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ‘11, San Diego, CA, USA, 21–24 August 2011; pp. 1082–1090. [Google Scholar]
- Le Roux, G.; Vallée, J.; Commenges, H. Social segregation around the clock in the Paris region (France). J. Transp. Geogr. 2017, 59, 134–145. [Google Scholar] [CrossRef]
- Carrasco, J.A.; Hogan, B.; Wellman, B.; Miller, E.J. Agency in social activity interactions: The role of social networks in time and space. Tijdschr. Econ. Soc. Geogr. 2008, 99, 562–583. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabási, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779. [Google Scholar] [CrossRef]
- Miranda, F.; Doraiswamy, H.; Lage, M.; Zhao, K.; Gonçalves, B.; Wilson, L.; Hsieh, M.; Silva, C.T. Urban Pulse: Capturing the Rhythm of Cities. IEEE Trans. Vis. Comput. Graph. 2017, 23, 791–800. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 5th ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Bassolas, A.; Barbosa-Filho, H.; Dickinson, B.; Dotiwalla, X.; Eastham, P.; Gallotti, R.; Ghoshal, G.; Gipson, B.; Hazarie, S.A.; Kautz, H.; et al. Hierarchical Organization of Urban Mobility and Its Connection with City Livability. Nat. Commun. 2019, 10, 4817. [Google Scholar] [CrossRef] [PubMed]
- Jiron, P.; Carrasco, J.A. Understanding Daily Mobility Strategies through Ethnographic, Time Use, and Social Network Lenses. Sustainability 2020, 12, 312. [Google Scholar] [CrossRef]
- Garreton, M.; Basauri, A.; Valenzuela, L. Exploring the correlation between city size and residential segregation: Comparing Chilean cities with spatially unbiased indexes. Environ. Urban. 2020, 32, 569–588. [Google Scholar] [CrossRef]
- Wang, Q.; Phillips, N.E.; Small, M.L.; Sampson, R.J. Urban mobility and neighborhood isolation in America’s 50 largest cities. Proc. Natl. Acad. Sci. USA 2018, 115, 7735–7740. [Google Scholar] [CrossRef]
- Xu, Y.; Santi, P.; Ratti, C. Beyond Distance Decay: Discover Homophily in Spatially Embedded Social Networks. Ann. Am. Assoc. Geogr. 2021, 112, 505–521. [Google Scholar] [CrossRef]
- Mena, G.E.; Martinez, P.P.; Mahmud, A.S.; Marquet, P.A.; Buckee, C.O.; Santillana, M. Socioeconomic status determines COVID-19 incidence and related mortality in Santiago, Chile. Science 2021, 372, eabg5298. [Google Scholar] [CrossRef]
- Beiró, M.G.; Bravo, L.; Caro, D.; Cattuto, C.; Ferres, L.; Graells-Garrido, E. Shopping Mall Attraction and Social Mixing at a City Scale. EPJ Data Sci. Data 2018, 7, 49. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, J.; Liu, G.; Fu, Y.; Aggarwal, C. Ensemble-Spotting: Ranking Urban Vibrancy via POI Embedding with Multi-view Spatial Graphs. In Proceedings of the 2018 SIAM International Conference on Data Mining (SDM), San Diego, CA, USA, 3–5 May 2018; pp. 351–359. [Google Scholar]
- Liu, H.; Guo, Q.; Zhu, H.; Fu, Y.; Zhuang, F.; Ma, X.; Xiong, H. Characterizing and Forecasting Urban Vibrancy Evolution: A Multi-View Graph Mining Perspective. ACM Trans. Knowl. Discov. Data 2022. accepted. [Google Scholar] [CrossRef]
- Small, M.L.; Adler, L. The Role of Space in the Formation of Social Ties. Annu. Rev. Sociol. 2019, 45, 111–132. [Google Scholar] [CrossRef]
- Pappalardo, L.; Ferres, L.; Sacasa, M.; Cattuto, C.; Bravo, L. Evaluation of home detection algorithms on mobile phone data using individual-level ground truth. EPJ Data Sci. 2021, 10, 29. [Google Scholar] [CrossRef] [PubMed]
- Graells-Garrido, E.; Caro, D.; Parra, D. Inferring modes of transportation using mobile phone data. EPJ Data Sci. 2018, 7, 49. [Google Scholar] [CrossRef]
- Gozzi, N.; Tizzoni, M.; Chinazzi, M.; Ferres, L.; Vespignani, A.; Perra, N. Estimating the effect of social inequalities on the mitigation of COVID-19 across communities in Santiago de Chile. Nat. Commun. 2021, 12, 2429. [Google Scholar] [CrossRef] [PubMed]
- Sotomayor-Gómez, B.; Samaniego, H. City limits in the age of smartphones and urban scaling. Comput. Environ. Urban Syst. 2020, 79, 101423. [Google Scholar] [CrossRef]
- Onnela, J.P.; Arbesman, S.; González, M.C.; Barabási, A.L.; Christakis, N.A. Geographic constraints on social network groups. PLoS ONE 2011, 6, e16939. [Google Scholar] [CrossRef] [PubMed]
- Pumain, D. An evolutionary theory of urban systems. In International and Transnational Perspectives on Urban Systems; Springer: Singapore, 2018; pp. 3–18. [Google Scholar]
- Adimark. Mapa Socioeconómico de Chile. 2009. Available online: https://ideocuc-ocuc.hub.arcgis.com/ (accessed on 6 December 2022).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenormand, M.; Samaniego, H. Uncovering the Socioeconomic Structure of Spatial and Social Interactions in Cities. Urban Sci. 2023, 7, 15. https://doi.org/10.3390/urbansci7010015
Lenormand M, Samaniego H. Uncovering the Socioeconomic Structure of Spatial and Social Interactions in Cities. Urban Science. 2023; 7(1):15. https://doi.org/10.3390/urbansci7010015
Chicago/Turabian StyleLenormand, Maxime, and Horacio Samaniego. 2023. "Uncovering the Socioeconomic Structure of Spatial and Social Interactions in Cities" Urban Science 7, no. 1: 15. https://doi.org/10.3390/urbansci7010015
APA StyleLenormand, M., & Samaniego, H. (2023). Uncovering the Socioeconomic Structure of Spatial and Social Interactions in Cities. Urban Science, 7(1), 15. https://doi.org/10.3390/urbansci7010015






