Urban Expansion Simulated by Integrated Cellular Automata and Agent-Based Models; An Example of Tallinn, Estonia
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.3. Data Analysis
2.3.1. Image Processing
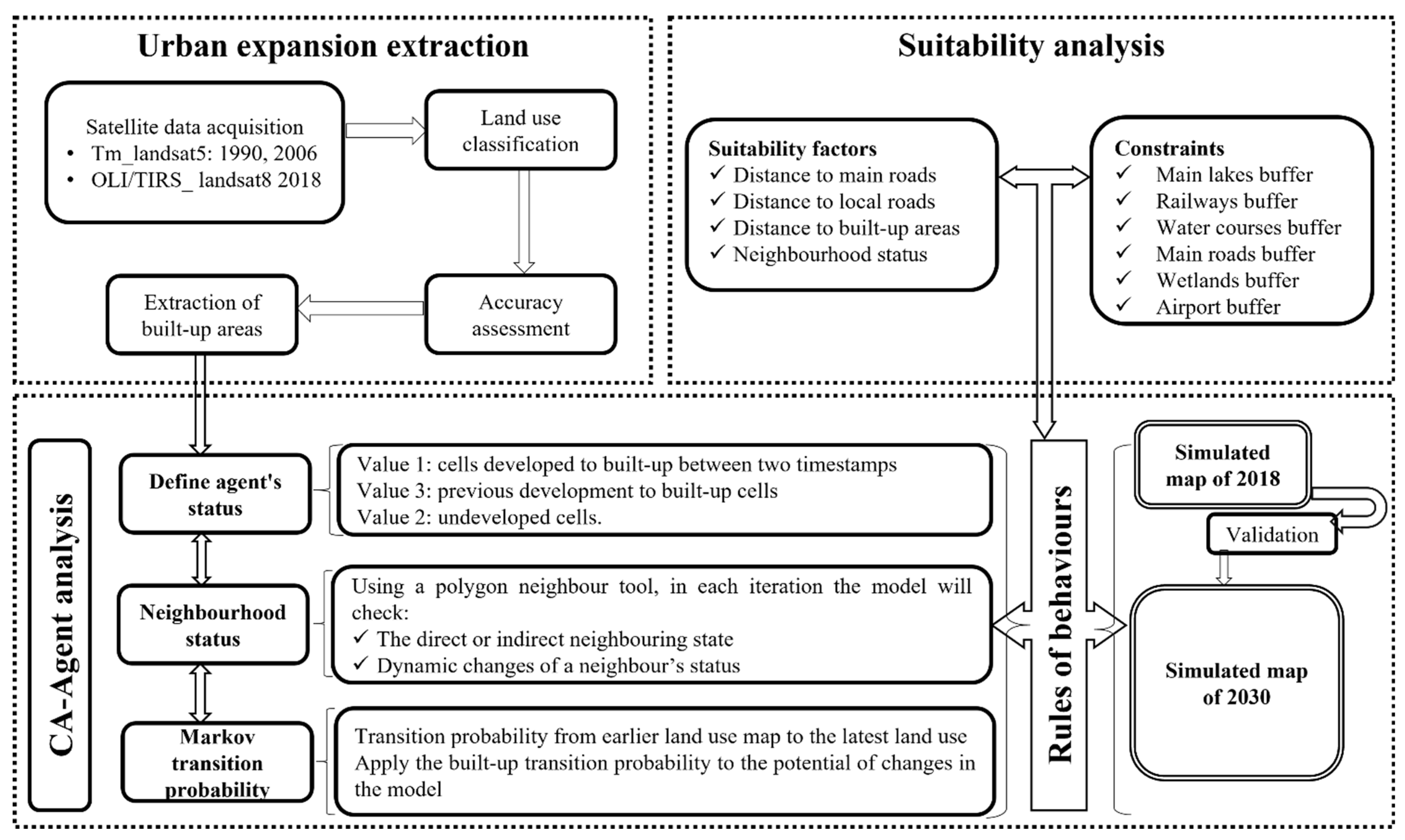
2.3.2. CA–Agent Model Framework
3. Results
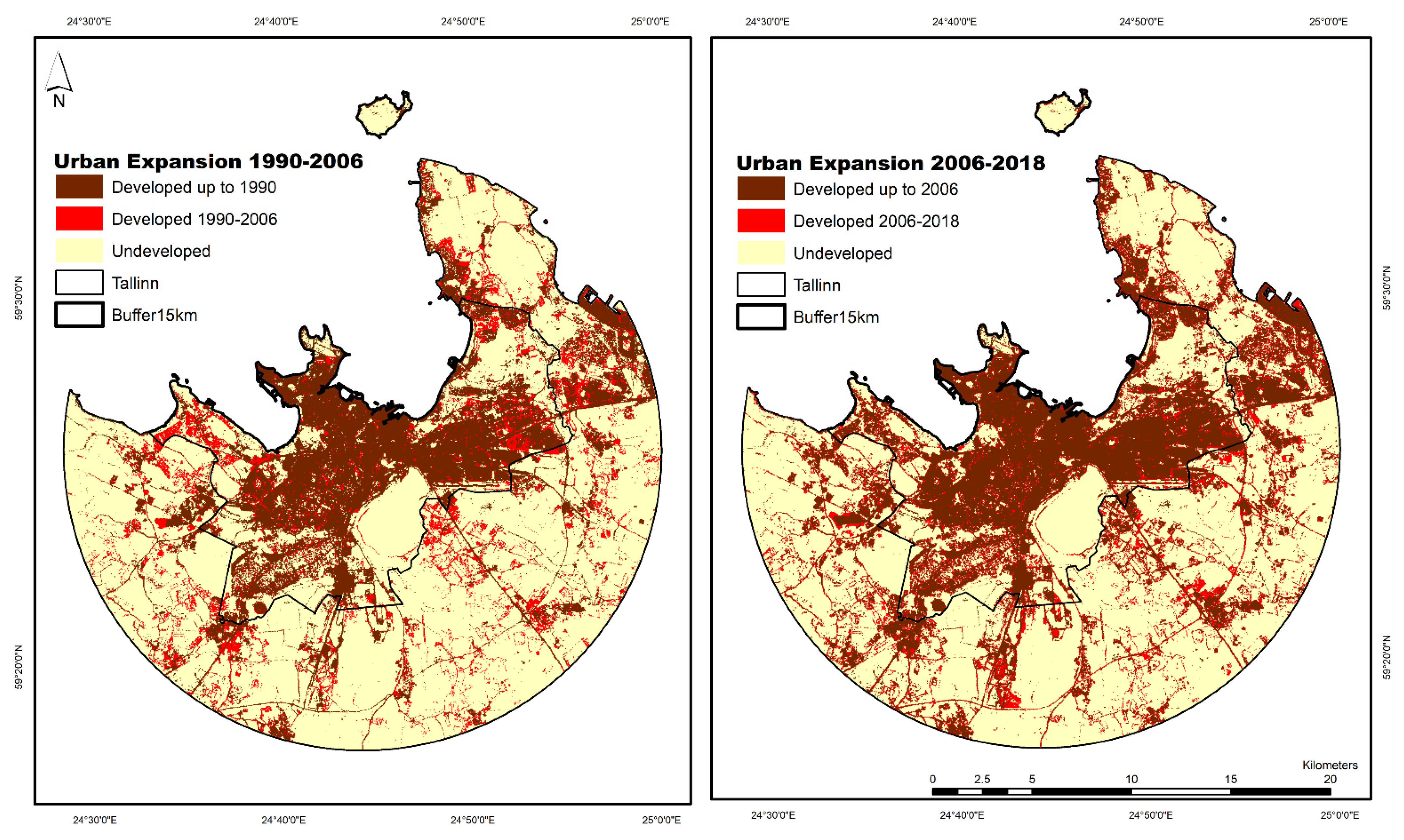
3.1. Spatiotemporal Patterns of Urban Expansion from 1990 to 2018
3.2. Application of CA–Agent Model in Tallinn and Its Buffer Zone
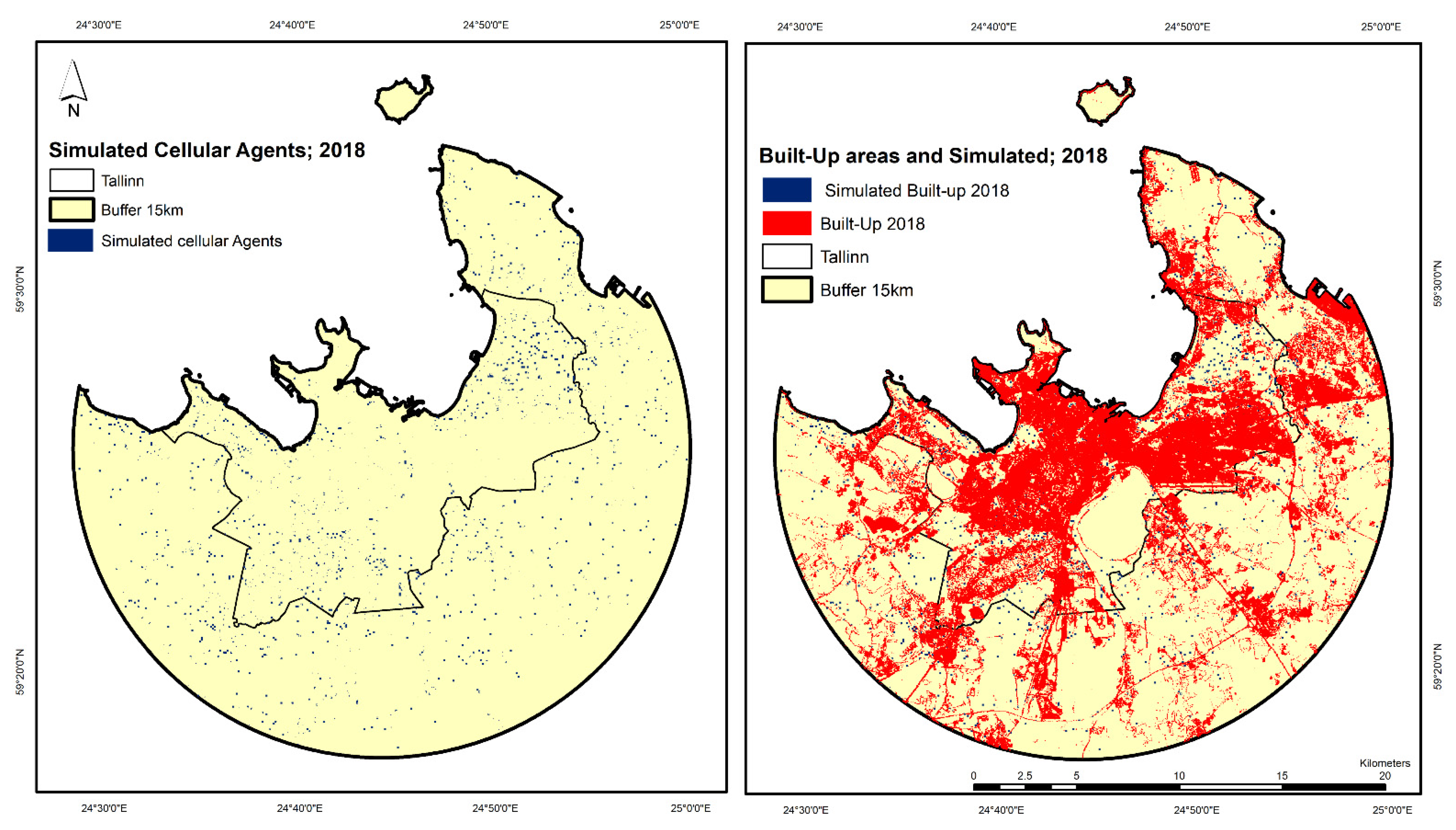
3.3. Simulation of Urban Expansion by 2018
3.4. Simulation Validation Results
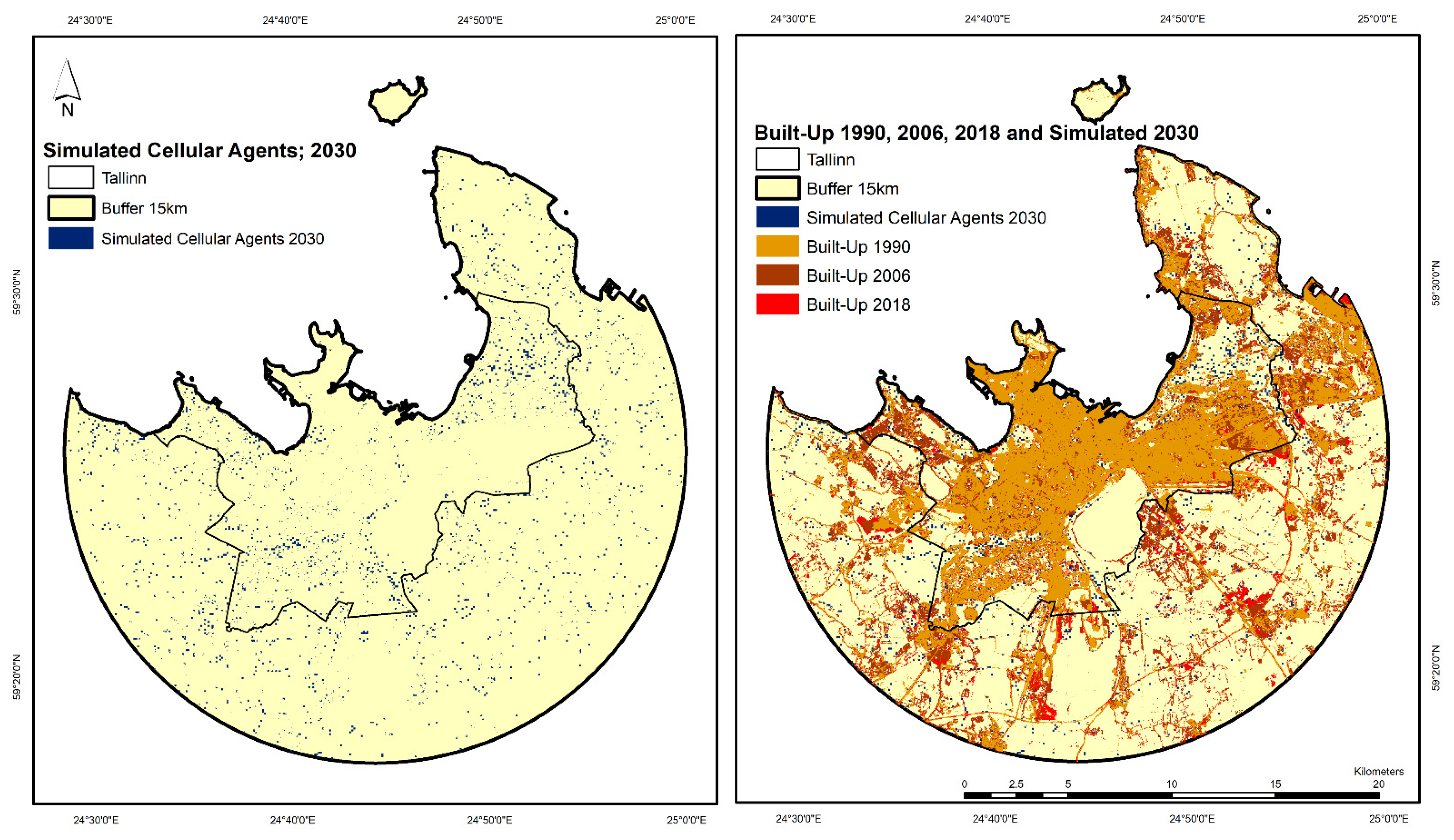
3.5. Simulation of Urban Expansion by 2030
4. Discussion
4.1. Interactions of Cellular Agents
4.2. Applying the Adjacent Neighborhood
4.3. State of the Cellular Agent
4.4. Coupling Markovian Transition Probability with CA–Agent
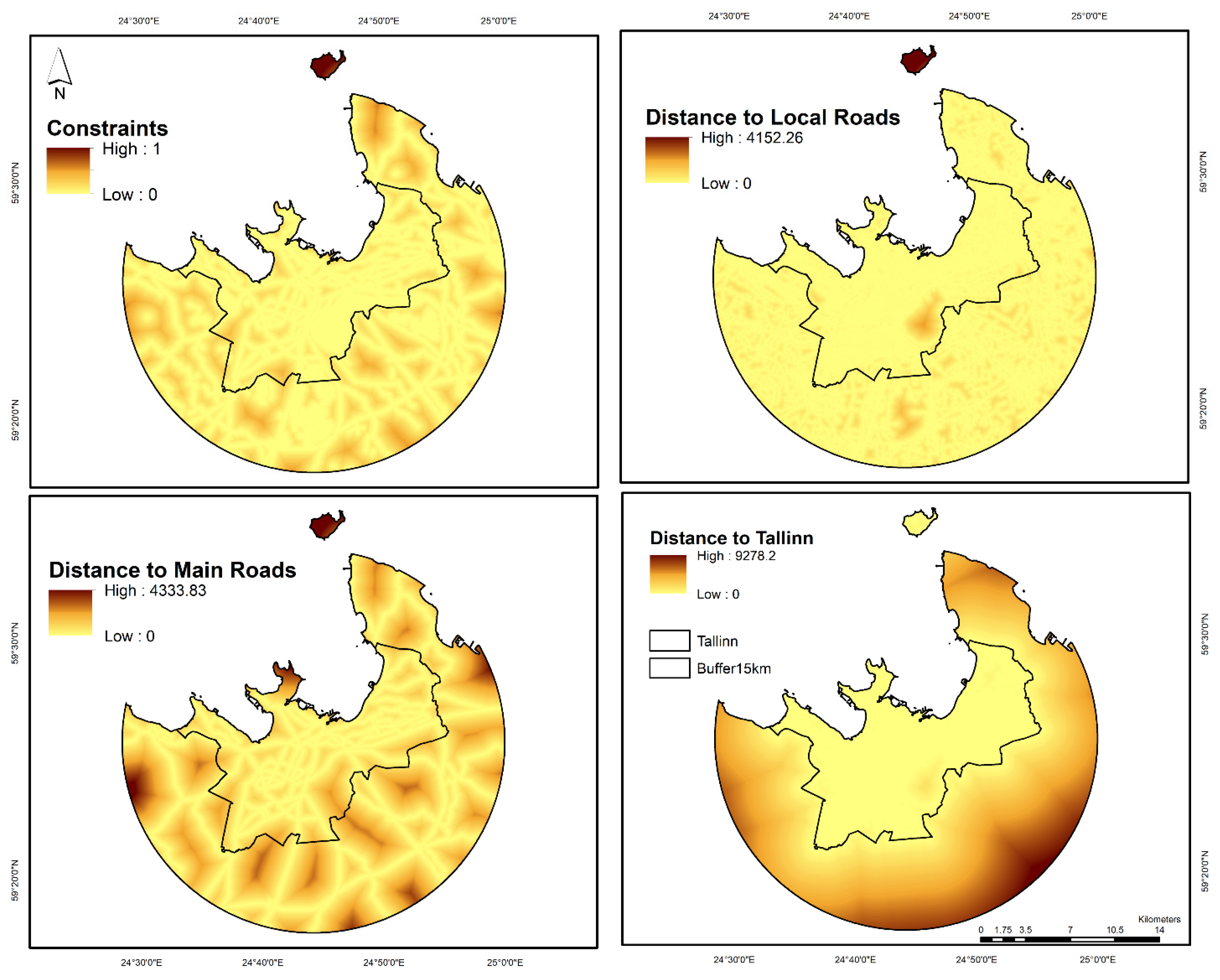
4.5. Configuration of Suitability Factors
4.6. Urban Expansion Simulation
4.7. Research Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, C.; Liu, Z.; Gou, S.; Zhang, Q.; Zhang, J.; Xu, L. Detecting Global Urban Expansion over the Last Three Decades Using a Fully Convolutional Network. Environ. Res. Lett. 2019, 14, 034008. [Google Scholar] [CrossRef]
- Haregeweyn, N.; Fikadu, G.; Tsunekawa, A.; Tsubo, M.; Meshesha, D.T. The Dynamics of Urban Expansion and Its Impacts on Land Use/Land Cover Change and Small-Scale Farmers Living near the Urban Fringe: A Case Study of Bahir Dar, Ethiopia. Landsc. Urban Plan. 2012, 106, 149–157. [Google Scholar] [CrossRef]
- Forkuor, G.; Cofie, O. Dynamics of Land-Use and Land-Cover Change in Freetown, Sierra Leone and Its Effects on Urban and Peri-Urban Agriculture—A Remote Sensing Approach. Int. J. Remote Sens. 2011, 32, 1017–1037. [Google Scholar] [CrossRef]
- Bolca, M.; Turkyilmaz, B.; Kurucu, Y.; Altinbas, U.; Esetlili, M.T.; Gulgun, B. Determination of Impact of Urbanization on Agricultural Land and Wetland Land Use in Balçovas’ Delta by Remote Sensing and GIS Technique. Environ. Monit. Assess. 2007, 131, 409–419. [Google Scholar] [CrossRef] [PubMed]
- Salghuna, N.N.; Rama Chandra Prasad, P.; Asha Kumari, J. Assessing the Impact of Land Use and Land Cover Changes on the Remnant Patches of Kondapalli Reserve Forest of the Eastern Ghats, Andhra Pradesh, India. Egypt. J. Remote Sens. Space Sci. 2018, 21, 419–429. [Google Scholar] [CrossRef]
- Bala, G.; Caldeira, K.; Wickett, M.; Phillips, T.J.; Lobell, D.B.; Delire, C.; Mirin, A. Combined Climate and Carbon-Cycle Effects of Large-Scale Deforestation. Proc. Natl. Acad. Sci. USA. 2007, 104, 6550–6555. [Google Scholar] [CrossRef]
- Huang, J.; Zhan, J.; Yan, H.; Wu, F.; Deng, X. Evaluation of the Impacts of Land Use on Water Quality: A Case Study in the Chaohu Lake Basin. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- McGrane, S.J. Impacts of Urbanisation on Hydrological and Water Quality Dynamics, and Urban Water Management: A Review. Hydrol. Sci. J. 2016, 61, 2295–2311. [Google Scholar] [CrossRef]
- Patra, S.; Sahoo, S.; Mishra, P.; Mahapatra, S.C. Impacts of Urbanization on Land Use /Cover Changes and Its Probable Implications on Local Climate and Groundwater Level. J. Urban Manag. 2018, 7, 70–84. [Google Scholar] [CrossRef]
- Bhat, P.A.; ul Shafiq, M.; Mir, A.A.; Ahmed, P. Urban Sprawl and Its Impact on Landuse/Land Cover Dynamics of Dehradun City, India. Int. J. Sustain. Built Environ. 2017, 6, 513–521. [Google Scholar] [CrossRef]
- Li, C.; Zhao, J.; Thinh, N.X.; Xi, Y. Assessment of the Effects of Urban Expansion on Terrestrial Carbon Storage: A Case Study in Xuzhou City, China. Sustainability 2018, 10, 647. [Google Scholar] [CrossRef]
- Zubair, O.A.; Ji, W.; Weilert, T.E. Modeling the Impact of Urban Landscape Change on Urban Wetlands Using Similarityweighted Instance-Based Machine Learning and Markov Model. Sustainability. 2017, 9, 2223. [Google Scholar] [CrossRef]
- Kelobonye, K.; Xia, J.C.; Swapan, M.S.H.; McCarney, G.; Zhou, H. Drivers of Change in Urban Growth Patterns: A Transport Perspective from Perth, Western Australia. Urban Sci. 2019, 3, 40. [Google Scholar] [CrossRef]
- Qian, Y.; Wu, Z. Study on Urban Expansion Using the Spatial and Temporal Dynamic Changes in the Impervious Surface in Nanjing. Sustainability 2019, 11, 933. [Google Scholar] [CrossRef]
- Mohapatra, S.N.; Pani, P.; Sharma, M. Rapid Urban Expansion and Its Implications on Geomorphology: A Remote Sensing and GIS Based Study. Geogr. J. 2014, 2014. [Google Scholar] [CrossRef]
- D’Amour, C.B.; Reitsma, F.; Baiocchi, G.; Barthel, S.; Güneralp, B.; Erb, K.H.; Haberl, H.; Creutzig, F.; Seto, K.C. Future Urban Land Expansion and Implications for Global Croplands. Proc. Natl. Acad. Sci. USA 2017, 114, 8939–8944. [Google Scholar] [CrossRef]
- Castle, C.J.E.; Crooks, A. Principles and Concepts of Agent-Based Modelling for Developing Geospatial Simulations. Available online: https://discovery.ucl.ac.uk/id/eprint/3342/1/3342.pdf (accessed on 1 September 2006).
- Wang, J.; Gao, W.; Gao, Z.; Yin, J.; Xu, S. Urban Expansion and Landscape Diversity Change of Shanghai City. Available online: https://www.researchgate.net/publication/252987453_Urban_Expansion_and_Landscape_Diversity_Change_of_Shanghai_City_China (accessed on 12 August 2010).
- Dahal, K.R.; Benner, S.; Lindquist, E. Analyzing Spatiotemporal Patterns of Urbanization in Treasure Valley, Idaho, USA. Appl. Spat. Anal. Policy 2016, 11, 205–226. [Google Scholar] [CrossRef]
- Van Truong, T.; Van Cu, P.; Laffly, D. Urban Expansion and Landscape Change Analysis Using Remote Sensing and Survey: A Case Study in Ha Long Bay Area, Vietnam. In Proceedings of the IEEE 2016 Eighth International Conference on Knowledge and Systems Engineering (KSE), Hanoi, Vietnam, 6–8 October 2016; pp. 315–320. [Google Scholar] [CrossRef]
- Zhao, P.; Lü, B.; de Roo, G. Urban Expansion and Transportation: The Impact of Urban Form on Commuting Patterns on the City Fringe of Beijing. Environ. Plan. Econ. Space 2010, 42, 2467–2486. [Google Scholar] [CrossRef]
- Zhao, P. Sustainable Urban Expansion and Transportation in a Growing Megacity: Consequences of Urban Sprawl for Mobility on the Urban Fringe of Beijing. Habitat Int. 2010, 34, 236–243. [Google Scholar] [CrossRef]
- Rimal, B.; Zhang, L.; Keshtkar, H.; Haack, B.N.; Rijal, S.; Zhang, P. Land Use/Land Cover Dynamics and Modeling of Urban Land Expansion by the Integration of Cellular Automata and Markov Chain. ISPRS Int. J. Geo-Inf. 2018, 7, 154. [Google Scholar] [CrossRef]
- Xu, S.; Sun, Y.; Zhao, S. Contemporary Urban Expansion in the First Fastest Growing Metropolitan Region of China: A Multicity Study in the Pearl River Delta Urban Agglomeration from 1980 to 2015. Urban Sci. 2021, 5, 11. [Google Scholar] [CrossRef]
- Deep, S.; Saklani, A. Urban Sprawl Modeling Using Cellular Automata. Egypt. J. Remote Sens. Space Sci. 2014, 17, 179–187. [Google Scholar] [CrossRef]
- Wang, R.; Hou, H.; Murayama, Y. Scenario-Based Simulation of Tianjin City Using a Cellular Automata-Markov Model. Sustainability 2018, 10, 2633. [Google Scholar] [CrossRef]
- Chen, G.; Li, X.; Liu, X.; Chen, Y.; Liang, X.; Leng, J.; Xu, X.; Liao, W.; Qiu, Y.; Wu, Q.; et al. Global Projections of Future Urban Land Expansion under Shared Socioeconomic Pathways. Nat. Commun. 2020, 11, 1–12. [Google Scholar] [CrossRef]
- Harb, M.; Garschagen, M.; Cotti, D.; Krätzschmar, E.; Baccouche, H.; Ben Khaled, K.; Bellert, F.; Chebil, B.; Ben Fredj, A.; Ayed, S.; et al. Integrating Data-Driven and Participatory Modeling to Simulate Future Urban Growth Scenarios: Findings from Monastir, Tunisia. Urban Sci. 2020, 4, 10. [Google Scholar] [CrossRef]
- Mustafa, A.; Cools, M.; Saadi, I.; Teller, J. Coupling Agent-Based, Cellular Automata and Logistic Regression into a Hybrid Urban Expansion Model (HUEM). Land Use Policy 2017, 69, 529–540. [Google Scholar] [CrossRef]
- Falah, N.; Karimi, A.; Tavakoli Harandi, A. Urban Growth Modeling Using Cellular Automata Model and AHP (Case Study: Qazvin City). Model. Earth Syst. Environ. 2020, 6, 235–248. [Google Scholar] [CrossRef]
- Benchelha, M.; Benzha, F.; Rhinane, H.; Benchelha, S.; Benchelha, T. Modeling of Urban Growth Using Cellular Automata and GIS Case of Benslimane in Morocco. Available online: https://doi.org/10.20944/preprints202011.0287.v1 (accessed on 9 November 2020).
- Liu, Y.; Batty, M.; Wang, S.; Corcoran, J. Modelling Urban Change with Cellular Automata: Contemporary Issues and Future Research Directions. Prog. Hum. Geogr. 2021, 45, 3–24. [Google Scholar] [CrossRef]
- Guan, D.; Zhao, Z.; Tan, J. Dynamic Simulation of Land Use Change Based on Logistic-CA-Markov and WLC-CA-Markov Models: A Case Study in Three Gorges Reservoir Area of Chongqing, China. Environ. Sci. Pollut. Res. 2019, 26, 20669–20688. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, M.; Liu, X.; Chen, Z.; Wei, X.; Che, W. MCR-Modified CA-Markov Model for the Simulation of Urban Expansion. Sustainability 2018, 10, 3116. [Google Scholar] [CrossRef]
- Guan, D.J.; Li, H.F.; Inohae, T.; Su, W.; Nagaie, T.; Hokao, K. Modeling Urban Land Use Change by the Integration of Cellular Automaton and Markov Model. Ecol. Model. 2011, 222, 3761–3772. [Google Scholar] [CrossRef]
- Sarkar, A.; Chouhan, P. Modeling Spatial Determinants of Urban Expansion of Siliguri a Metropolitan City of India Using Logistic Regression. Model. Earth Syst. Environ. 2020, 6, 2317–2331. [Google Scholar] [CrossRef]
- Salem, M.; Tsurusaki, N.; Divigalpitiya, P. Analyzing the Driving Factors Causing Urban Expansion in the Peri-Urban Areas Using Logistic Regression: A Case Study of the Greater Cairo Region. Infrastructures 2019, 4, 4. [Google Scholar] [CrossRef]
- Siddiqui, A.; Siddiqui, A.; Maithani, S.; Jha, A.K.; Kumar, P.; Srivastav, S.K. Urban Growth Dynamics of an Indian Metropolitan Using CA Markov and Logistic Regression. Egypt. J. Remote Sens. Space Sci. 2018, 21, 229–236. [Google Scholar] [CrossRef]
- Koch, J.; Dorning, M.A.; Van Berkel, D.B.; Beck, S.M.; Sanchez, G.M.; Shashidharan, A.; Smart, L.S.; Zhang, Q.; Smith, J.W.; Meentemeyer, R.K. Modeling Landowner Interactions and Development Patterns at the Urban Fringe. Landsc. Urban Plan. 2019, 182, 101–113. [Google Scholar] [CrossRef]
- Hosseinali, F.; Alesheikh, A.A.; Nourian, F. Agent-Based Modeling of Urban Land-Use Development, Case Study: Simulating Future Scenarios of Qazvin City. Cities 2013, 31, 105–113. [Google Scholar] [CrossRef]
- Xu, T.; Gao, J.; Coco, G.; Wang, S. Urban Expansion in Auckland, New Zealand: A GIS Simulation via an Intelligent Self-Adapting Multiscale Agent-Based Model. Int. J. Geogr. Inf. Sci. 2020, 34, 2136–2159. [Google Scholar] [CrossRef]
- Zhou, X.; Fu, W. A Multi-Agent Simulation Method of Urban Land Layout Structure Based on FPGA. Mob. Netw. Appl. 2020, 25, 1572–1581. [Google Scholar] [CrossRef]
- Langton, C.G. Self-reproduction in cellular automata. Mar. Sci. Bull. 1984, 10, 135–144. [Google Scholar] [CrossRef]
- Liao, J.; Tang, L.; Shao, G.; Qiu, Q.; Wang, C.; Zheng, S.; Su, X. A Neighbor Decay Cellular Automata Approach for Simulating Urban Expansion Based on Particle Swarm Intelligence. Int. J. Geogr. Inf. Sci. 2014, 28, 720–738. [Google Scholar] [CrossRef]
- Ma, J.; Bi, Q.; Zhang, J.; Zhou, H. Using Cellular Automaton to Simulate Urban Expansion in Changchun, China. Sens. Transducers 2014, 169, 159–164. [Google Scholar]
- White, R.; Engelen, G.; Uljee, I. The Use of Constrained Cellular Automata for High-Resolution Modelling of Urban Land-Use Dynamics. Environ. Plan. B Plan. Des. 1997, 24, 323–343. [Google Scholar] [CrossRef]
- Mozaffaree Pour, N.; Oja, T. Simulation of Urban Expansion in Estonia for 2046 Using Cellular Automata Model Based on the CORINE Land Cover Database. In Proceedings of the 3rd International Conference on Geoinformatics and Data Analysis (ICGDA 2020), Marseille, France, 15–17 April 2020; pp. 14–18. [Google Scholar] [CrossRef]
- Li, X.; Gong, P. Urban Growth Models: Progress and Perspective. Sci. Bull. 2016, 61, 1637–1650. [Google Scholar] [CrossRef]
- Jafari, M.; Majedi, H.; Monavari, S.M.; Alesheikh, A.A.; Zarkesh, M.K. Dynamic Simulation of Urban Expansion Based on Cellular Automata and Logistic Regression Model: Case Study of the Hyrcanian Region of Iran. Sustainability 2016, 8, 810. [Google Scholar] [CrossRef]
- Mustafa, A.; Heppenstall, A.; Omrani, H.; Saadi, I.; Cools, M.; Teller, J. Modelling Built-up Expansion and Densification with Multinomial Logistic Regression, Cellular Automata and Genetic Algorithm. Comput. Environ. Urban Syst. 2018, 67, 147–156. [Google Scholar] [CrossRef]
- Li, X.; Gong, P.; Yu, L.; Hu, T. A Segment Derived Patch-Based Logistic Cellular Automata for Urban Growth Modeling with Heuristic Rules. Comput. Environ. Urban Syst. 2017, 65, 140–149. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; Kainz, W.; Boloorani, A.D. Integration of Logistic Regression, Markov Chain and Cellular Automata Models to Simulate Urban Expansion. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 265–275. [Google Scholar] [CrossRef]
- Liu, D.; Zheng, X.; Wang, H. Land-Use Simulation and Decision-Support System (LandSDS): Seamlessly Integrating System Dynamics, Agent-Based Model, and Cellular Automata. Ecol. Model. 2020, 417, 108924. [Google Scholar] [CrossRef]
- Santé, I.; García, A.M.; Miranda, D.; Crecente, R. Cellular Automata Models for the Simulation of Real-World Urban Processes: A Review and Analysis. Landsc. Urban Plan. 2010, 96, 108–122. [Google Scholar] [CrossRef]
- Qian, Y.; Xing, W.; Guan, X.; Yang, T.; Wu, H. Coupling Cellular Automata with Area Partitioning and Spatiotemporal Convolution for Dynamic Land Use Change Simulation. Sci. Total Environ. 2020, 722, 137738. [Google Scholar] [CrossRef]
- Xia, C.; Wang, H.; Zhang, A.; Zhang, W. A High-Performance Cellular Automata Model for Urban Simulation Based on Vectorization and Parallel Computing Technology. Int. J. Geogr. Inf. Sci. 2018, 32, 399–424. [Google Scholar] [CrossRef]
- Gao, C.; Feng, Y.; Tong, X.; Lei, Z.; Chen, S.; Zhai, S. Modeling Urban Growth Using Spatially Heterogeneous Cellular Automata Models: Comparison of Spatial Lag, Spatial Error and GWR. Comput. Environ. Urban Syst. 2020, 81, 101459. [Google Scholar] [CrossRef]
- Zhou, L.; Dang, X.; Sun, Q.; Wang, S. Multi-Scenario Simulation of Urban Land Change in Shanghai by Random Forest and CA-Markov Model. Sustain. Cities Soc. 2020, 55, 102045. [Google Scholar] [CrossRef]
- Aburas, M.M.; Ho, Y.M.; Ramli, M.F.; Ash’aari, Z.H. The Simulation and Prediction of Spatio-Temporal Urban Growth Trends Using Cellular Automata Models: A Review. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 380–389. [Google Scholar] [CrossRef]
- Groff, E.R.; Johnson, S.D.; Thornton, A. State of the Art in Agent-Based Modeling of Urban Crime: An Overview. J. Quant. Criminol. 2019, 35, 155–193. [Google Scholar] [CrossRef]
- Ramachandra, T.V.; Sellers, J.M.; Bharath, H.A.; Vinay, S. Modeling Urban Dynamics along Two Major Industrial Corridors in India. Spat. Inf. Res. 2019, 27, 37–48. [Google Scholar] [CrossRef]
- Wu, H.; Liu, L.; Yu, Y.; Peng, Z.; Jiao, H.; Niu, Q. An Agent-Based Model Simulation of Human Mobility Based on Mobile Phone Data: How Commuting Relates to Congestion. ISPRS Int. J. Geo-Inf. 2019, 8, 313. [Google Scholar] [CrossRef]
- Tian, G.; Ma, B.; Xu, X.; Liu, X.; Xu, L.; Liu, X.; Xiao, L.; Kong, L. Simulation of Urban Expansion and Encroachment Using Cellular Automata and Multi-Agent System Model—A Case Study of Tianjin Metropolitan Region, China. Ecol. Indic. 2016, 70, 439–450. [Google Scholar] [CrossRef]
- Johnston, K.M. AgentAnalyst: Agent-Based Modeling in ArcGIS; Esri Press: Redlands, CA, USA, 2013; ISBN 9781589483231. [Google Scholar]
- Ebrahimipour, A.; Saadat, M.; Farshchin, A. Prediction of Urban Growth through Cellular Automata-Markov Chain. Bull. Soc. R. Sci. Liège 2016, 85, 824–839. [Google Scholar]
- Jafari, M.; Majedi, H.; Monavari, S.M.; Alesheikh, A.A.; Zarkesh, M.K. Dynamic Simulation of Urban Expansion through a CA-Markov Model Case Study: Hyrcanian Region, Gilan, Iran. Eur. J. Remote Sens. 2016, 49, 513–529. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; de Noronha Vaz, E. Spatiotemporal Simulation of Urban Growth Patterns Using Agent-Based Modeling: The Case of Tehran. Cities 2013, 32, 33–42. [Google Scholar] [CrossRef]
- Aburas, M.M.; Ho, Y.M.; Ramli, M.F.; Ash’aari, Z.H. Improving the Capability of an Integrated CA-Markov Model to Simulate Spatio-Temporal Urban Growth Trends Using an Analytical Hierarchy Process and Frequency Ratio. Int. J. Appl. Earth Obs. Geoinformation 2017, 59, 65–78. [Google Scholar] [CrossRef]
- Xu, T.; Gao, J.; Coco, G. Simulation of Urban Expansion via Integrating Artificial Neural Network with Markov Chain—Cellular Automata. Int. J. Geogr. Inf. Sci. 2019, 33, 1960–1983. [Google Scholar] [CrossRef]
- Rimal, B.; Zhang, L.; Keshtkar, H.; Wang, N.; Lin, Y. Monitoring and Modeling of Spatiotemporal Urban Expansion and Land-Use/Land-Cover Change Using Integrated Markov Chain Cellular Automata Model. ISPRS Int. J. Geo-Inf. 2017, 6, 288. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, X.; Huang, H.; Ma, S. Simulating Urban Growth Boundaries Using a Patch-Based Cellular Automaton with Economic and Ecological Constraints. Int. J. Geogr. Inf. Sci. 2019, 33, 55–80. [Google Scholar] [CrossRef]
- Wahyudi, A.; Liu, Y. Spatial Dynamic Models for Inclusive Cities: A Brief Concept of Cellular Automata (CA) and Agent-Based Model (ABM). J. Reg. City Plan. 2015, 26, 54–70. [Google Scholar] [CrossRef][Green Version]
- Dahal, K.R.; Chow, T.E. An Agent-Integrated Irregular Automata Model of Urban Land-Use Dynamics. Int. J. Geogr. Inf. Sci. 2014, 28, 2281–2303. [Google Scholar] [CrossRef]
- Mozaffaree Pour, N.; Oja, T. A Comparative Analysis of “Urban Expansion” Using Remotely Sensed Data of CORINE Land Cover and Global Human Settlement Layer in Estonia. In Proceedings of the 6th International Conference on Geographical Information Systems Theory, Applications and Management, Prague, Czech Republic, 7–9 May 2020; SCITEPRESS—Science and Technology Publications: Prague, Czech Republic, 2020; pp. 143–150. [Google Scholar] [CrossRef]
- Reimets, R.; Uuemaa, E.; Oja, T.; Sisas, E.; Mander, Ü. Urbanisation-Related Landscape Change in Space and Time along Spatial Gradients near Roads: A Case Study from Estonia. Landsc. Res. 2015, 40, 192–207. [Google Scholar] [CrossRef]
- Samarüütel, A.; Steen Selvig, S.; Holt-Jensen, A. Urban Sprawl and Suburban Development around Pärnu and Tallinn, Estonia. Nor. Geogr. Tidsskr-Nor. J. Geogr. 2010, 64, 152–161. [Google Scholar] [CrossRef]
- Tammaru, T.; Leetmaa, K.; Silm, S.; Ahas, R. Temporal and Spatial Dynamics of the New Residential Areas around Tallinn. Eur. Plan. Stud. 2009, 17, 423–439. [Google Scholar] [CrossRef]
- Congedo, L. Semi-Automatic Classification Plugin Documentation Release 7.5.5.1. Available online: https://fromgistors.blogspot.com/p/semi-automatic-classification-plugin.html (accessed on 27 August 2021).
- Oja, T. Change of land-use: Distortion of the meaning of urban and rural. In Estonian Human Development Report 2019/2020 Spatial Choices for an Urbanised Society; Tallinn: SA Eesti Koostöö kogu, Estonia, 2020; pp. 34–43. Available online: https://inimareng.ee (accessed on 1 December 2020).
- Bharath, H.A.; Chandan, M.C.; Vinay, S.; Ramachandra, T.V. Modelling Urban Dynamics in Rapidly Urbanising Indian Cities. Egypt. J. Remote Sens. Space Sci. 2018, 21, 201–210. [Google Scholar] [CrossRef]
- Wakode, H.B.; Baier, K.; Jha, R.; Azzam, R. Analysis of Urban Growth Using Landsat TM/ETM Data and GIS-a Case Study of Hyderabad, India. Arab. J. Geosci. 2014, 7, 109–121. [Google Scholar] [CrossRef]
- Kityuttachai, K.; Tripathi, N.K.; Tipdecho, T.; Shrestha, R. CA-Markov Analysis of Constrained Coastal Urban Growth Modeling: Hua Hin Seaside City, Thailand. Sustainability 2013, 5, 1480–1500. [Google Scholar] [CrossRef]
- Dan-Jumbo, N.; Metzger, M.; Clark, A. Urban Land-Use Dynamics in the Niger Delta: The Case of Greater Port Harcourt Watershed. Urban Sci. 2018, 2, 108. [Google Scholar] [CrossRef]
- Abdelkareem, O.E.A.; Elamin, H.M.A.; Eltahir, M.E.S.; Adam, H.E.; Elhaja, M.E.; Rahamtalla, A.M.; Babatunde, O.; Elmar, C. Accuracy Assessment of Land Use Land Cover in Umabdalla Natural Reserved Forest, South Kordofan, Sudan. Int. J. Agric. Environ. Sci. 2018, 3, 5–9. [Google Scholar]
- Rwanga, S.S.; Ndambuki, J.M. Accuracy Assessment of Land Use/Land Cover Classification Using Remote Sensing and GIS. Int. J. Geosci. 2017, 8, 611–622. [Google Scholar] [CrossRef]
- Li, N. Adding complexity to polygon agents using an urban. In Agent Analyst; Agent-Based Modeling in ArcGIS; Esri Press: Redlands, CA, USA, 2013; pp. 239–308. [Google Scholar]
- Kozlowski, J. Threshold theory and the sub-regional plan. Town Plan. Rev. 1968, 39, 99–116. [Google Scholar] [CrossRef]
- Cao, M.; Tang, G.; Shen, Q.; Wang, Y. A New Discovery of Transition Rules for Cellular Automata by Using Cuckoo Search Algorithm. Int. J. Geogr. Inf. Sci. 2015, 29, 806–824. [Google Scholar] [CrossRef]
- Eastman, J.R. TerrSet; Geospatial Monitoring and Modeling System. In TerrSet Tutorial; Clark Labs, Clark University: Worcester, MA, USA, 2016. [Google Scholar]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of Quantity Disagreement and Allocation Disagreement for Accuracy Assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Pickard, B.; Gray, J.; Meentemeyer, R. Comparing Quantity, Allocation and Configuration Accuracy of Multiple Land Change Models. Land 2017, 6, 52. [Google Scholar] [CrossRef]
- Kong, L.; Tian, G.; Ma, B.; Liu, X. Embedding Ecological Sensitivity Analysis and New Satellite Town Construction in an Agent-Based Model to Simulate Urban Expansion in the Beijing Metropolitan Region, China. Ecol. Indic. 2017, 82, 233–249. [Google Scholar] [CrossRef]
- Tan, R.; Liu, Y.; Zhou, K.; Jiao, L.; Tang, W. A Game-Theory Based Agent-Cellular Model for Use in Urban Growth Simulation: A Case Study of the Rapidly Urbanizing Wuhan Area of Central China. Comput. Environ. Urban Syst. 2015, 49, 15–29. [Google Scholar] [CrossRef]
- Liu, Y.; Kong, X.; Liu, Y.; Chen, Y. Simulating the Conversion of Rural Settlements to Town Land Based on Multi-Agent Systems and Cellular Automata. PLoS ONE 2013, 8, e79300. [Google Scholar] [CrossRef]
- Couclelis, H. From Cellular Automata to Urban Models: New Principles for Model Development and Implementation. Environ. Plan. B Plan. Des. 1997, 24, 165–174. [Google Scholar] [CrossRef]
- Tian, G.; Ouyang, Y.; Quan, Q.; Wu, J. Simulating Spatiotemporal Dynamics of Urbanization with Multi-Agent Systems—A Case Study of the Phoenix Metropolitan Region, USA. Ecol. Model. 2011, 222, 1129–1138. [Google Scholar] [CrossRef]
- Pinto, N.; Antunes, A.P.; Roca, J. Applicability and Calibration of an Irregular Cellular Automata Model for Land Use Change. Comput. Environ. Urban Syst. 2017, 65, 93–102. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, X.; Ai, B.; Li, S. Capturing the Varying Effects of Driving Forces over Time for the Simulation of Urban Growth by Using Survival Analysis and Cellular Automata. Landsc. Urban Plan. 2016, 152, 59–71. [Google Scholar] [CrossRef]
- Pinto, N.N.; Antunes, A.P. A Cellular Automata Model Based on Irregular Cells: Application to Small Urban Areas. Environ. Plan. B Plan. Des. 2010, 37, 1095–1114. [Google Scholar] [CrossRef]
- Musa, S.I.; Hashim, M.; Reba, M.N.M. Geospatial Modelling of Urban Growth for Sustainable Development in the Niger Delta Region, Nigeria. Int. J. Remote Sens. 2019, 40, 3076–3104. [Google Scholar] [CrossRef]
- Feng, Y.; Qi, Y. Modeling Patterns of Land Use in Chinese Cities Using an Integrated Cellular Automata Model. ISPRS Int. J. Geo-Inf. 2018, 7, 403. [Google Scholar] [CrossRef]
- Al-sharif, A.A.A.; Pradhan, B. A Novel Approach for Predicting the Spatial Patterns of Urban Expansion by Combining the Chi-Squared Automatic Integration Detection Decision Tree, Markov Chain and Cellular Automata Models in GIS. Geocarto Int. 2015, 30, 858–881. [Google Scholar] [CrossRef]
- Berberoğlu, S.; Akın, A.; Clarke, K.C. Cellular Automata Modeling Approaches to Forecast Urban Growth for Adana, Turkey: A Comparative Approach. Landsc. Urban Plan. 2016, 153, 11–27. [Google Scholar] [CrossRef]

| Product Description | Date of Acquisition | Ground Resolution |
|---|---|---|
| TM_Landsat5 | 1990/05/13 | 30 m |
| TM_ Landsat5 | 2006/06/10 | 30 m |
| OLI/TIRS_Landsat8 | 2018/05/26 | 30 m |
| Landsat Images | Accuracy Assessment | |
|---|---|---|
| Overall Accuracy (%) | Kappa Hat Classification | |
| TM_Landsat5 (1990) | 98.20 | 0.96 |
| TM_Landsat5 (2006) | 97.80 | 0.96 |
| OLI/TIRS_Landsat8 (2018) | 97.00 | 0.95 |
| Cellular Agent | Adjacent Neighbors | Number of Neighbors |
|---|---|---|
| 4 | 13,586, 14,345, 21,995, 22,301, 28,192, 30,848, 55,813, 62,819, 62,831, 62,857 | 10 |
| 5 | 9226, 11,980, 64,507 | 3 |
| 6 | 3788, 6010, 14,613, 58,190, 68,473, 68,575 | 6 |
| 7 | 855, 1223, 9146, 16,959, 21,055, 23,646, 26,114, 26,526 | 8 |
| Built-Up Areas | Increased Area by sq. km | Percentage of Change | ||||||
|---|---|---|---|---|---|---|---|---|
| 1990 | 2006 | 2018 | 1990–2006 | 2006–2018 | 1990–2018 | 1990–2006 | 2006–2018 | 1990–2018 |
| 122.22 | 149.32 | 163.02 | 27.10 | 13.70 | 40.80 | 18.15 | 8.40 | 25.03 |
| Probability Definitions | Probability in Model (Range between 0 and 1) | Markovian Transition Probability (Range between 0 and 1) |
|---|---|---|
| Development probability of large cells | 0.35 | |
| Development probability of isolated cells | 0.05 | 0.84 |
| Development probability of cells in Tallinn | 0.30 | |
| Development probability of cells in the buffer zone | 0.14 |
| Properties | Simulation 2018 |
|---|---|
| Total cells | 73,815 |
| Total undeveloped cells | 54,707 |
| Total unbuildable cells | 1770 |
| Suitability threshold | 88 |
| Total number of developed cellular agents | 1736 |
| Total area of developed cellular agents | 7.06 sq.km |
| Image Comparison Results (Degree from 0–1) | |
|---|---|
| Kstandard | 0.86 |
| Klocation | 0.89 |
| MediumGrid (m) | 0.91 |
| Qdisagreement | 0.02 |
| Adisagreement | 0.07 |
| Properties | Simulation 2030 |
|---|---|
| Total cells | 69,624 |
| Total undeveloped cells | 58,236 |
| Total unbuildable cells | 2342 |
| Suitability threshold | 94 |
| Total number of developed cellular agents | 2881 |
| Total area of developed cellular agents | 12.22 sq.km |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mozaffaree Pour, N.; Oja, T. Urban Expansion Simulated by Integrated Cellular Automata and Agent-Based Models; An Example of Tallinn, Estonia. Urban Sci. 2021, 5, 85. https://doi.org/10.3390/urbansci5040085
Mozaffaree Pour N, Oja T. Urban Expansion Simulated by Integrated Cellular Automata and Agent-Based Models; An Example of Tallinn, Estonia. Urban Science. 2021; 5(4):85. https://doi.org/10.3390/urbansci5040085
Chicago/Turabian StyleMozaffaree Pour, Najmeh, and Tõnu Oja. 2021. "Urban Expansion Simulated by Integrated Cellular Automata and Agent-Based Models; An Example of Tallinn, Estonia" Urban Science 5, no. 4: 85. https://doi.org/10.3390/urbansci5040085
APA StyleMozaffaree Pour, N., & Oja, T. (2021). Urban Expansion Simulated by Integrated Cellular Automata and Agent-Based Models; An Example of Tallinn, Estonia. Urban Science, 5(4), 85. https://doi.org/10.3390/urbansci5040085






