1. Introduction
Migration of human beings has always been an important dynamics of our history and is an important, multidimensional and complex issue [
1]. Historical data show that human migration may be temporary or permanent in nature, with the intention of moving to a new land, place or country. Population migration is primarily classified as internal or international, and often analysed separately. However, the underlying economic, social, political and cultural drivers initiating and perpetuating both types of migration are similar and differ predominantly in their relative importance [
2]. A fundamental difference, however, is the role of the state and regulations to control international migration. While international migration has gathered more attention due to its policy implications, internal migration, with an estimated total of 740 million people (
of the world population) in 2000, is much larger than an estimated 200 million international migrants [
2]. Research on internal migration is important, as it is a key aspect of the population dynamics of a country. Even though administrative structures can be hard to compare, the United Nations’ Department of Economic and Social Affairs shows that five-year migration rates between the smallest administrative units in countries worldwide can vary between
and
[
3]. Migration events within these regions would even further increase these migration rates.
Migration may involve individuals, family units or large groups. Sjaastad [
4] beglieved that migration cannot be viewed in isolation, as human decision making is usually collective (influenced by an individuals social network) and shaped by individual behaviour. Broadly, the migration decision entails weighing the costs versus the benefits of migration. It has been discovered that the choice to move to a certain destination is likely influenced by its economic prospects [
5], the availability of amenities [
6,
7], the travel distance [
8], information distance [
9] and social distance [
10] between both locations. The way in which these variables influence the migration decision differs for each individual. After all, each individual has different personal connections [
11,
12], motivations [
9] and aspirations [
13,
14].
Migration theories can be classified according to the level they focus on. Micro-level theories focus on individual migration decisions, whereas macro-level theories look at aggregate migration trends and explain these trends with macro-level explanations. Neoclassical macro-level migration theories postulate that migration is determined by the expected increase in earnings weighted by the probability on employment [
15,
16]. A different view is posed in the historical approach of the World Systems theory [
17]. In this theory, migration is treated as a consequence of “capitalist expansion of neoclassical governments and multinationals”. In the Dual Labour Market theory [
18], emphasis is placed on a secondary labour market for unskilled jobs which fluctuates according to the business cycle, making it unstable and unattractive to local workers. This would in turn lead to migration of unskilled labour from poorer regions. Micro-level theories focus on the behaviour of individuals. For example, Wolpert’s stress-threshold theory [
19], which assumes individuals have a threshold level of satisfaction that is a function of their current state in relation to the environment. The Human capital theory [
20] advances the neoclassical macro-theory by incorporating socio-demographic characteristic of individuals. Hein de Haas argued that existing theories on social capital of migration explain the growth of already-established migrant networks, but fail to explain their creation, different trajectories and subsequent collapse [
21]. Similarly, there are cognitive theories such as value-expectancy [
22] in which migrants make conscious decisions based on various non-economic factors: autonomy, security and self-fulfilment.
Based on the above theories, several types of mathematical and micro simulation models of migration have been created to understand and forecast migration at various temporal and spatial scales. Hoda Rahmati and Tularam [
23] presented a comprehensive review of the state-of-art in modelling human migration. Each type of models uses many different variables in a different way. Economic models focus on “economic, non- economic, psychological costs, distance, income, unemployment, educational, population, urbanisation, and human capital investment variables”. This can be seen in statistical time series models, which incorporate wage, unemployment and population density. Agent-based models often include other non-economic variables, such as adaptation behaviours, subjective norm, perceived behavioural control, rainfall assets, livestock asset, occupation, experience and general information about migration, age, gender, marital status, rainfall condition, and migration information and consideration. Other types of models have a more long-term focus, such as Markov chain models and optimisation models. The first make a link between the perpetuation of migration and population flows and can be either discrete or continuous, while the latter include return migration but also focus on age, asset and GDP parameters. Another type of model that is popular for migration analysis is the gravity model. The notion of applying the gravity law to population movement was introduced by John Q. Stewart who founded the “social physics” school [
24]. The gravity model has been the most frequently-used paradigm for understanding migration flows between cities, countries and regions. The gravity model owes its success to, “firstly, its intuitive consistency with migration theories; secondly, ease of estimation in its simplest form; and, thirdly, goodness of fit in most applications” [
25]. Recently, Ramos et. al. used a gravity model for nearly 200 countries between 1960 and 2010 to demonstrate an increase in migratory pressures from European Neighbouring Countries to the EU [
26]. Gravity models can easily be augmented to include different additional controls (e.g., economic situation, transportation, etc.) and policy variables (e.g., economic zones, housing policies, etc.). In these extended gravity models, interactions between different locations are specified as a direct function of their mutual geographical distance and their population mass as proxy to the economic prospects of a location. A new type of migration models that has also become popular are the radiation models [
27], which have been applied and extended further [
28,
29,
30]. In these models, residents create intervening opportunities for migrants, which means that geographical distance only has an indirect influence on the generated migration flows. Both types of models can come in different forms. A good example of this variety in models is an artificial neural network model that included both the traditional variables, as well as intervening variables and amenity variables [
31]. However, the above theories and models do not account for regional identity in the analysis of migration.
Identity is a latent variable and often not included in models due to lack of data. In this paper, we overcome this problem by using both Dutch administrative regions as well as historic literature to form identity regions. These identity regions can help separate the effects of distance and identity, and present a more accurate picture of the effect of distance. As distance has a direct effect in the gravity model, we expand this model with identity regions, which in turn allows us to quantify the effect of identity on the migration from a given municipality. Having an easily accessible way of including identity into a migration model could help policymakers, as better migration predictions would allow them to improve their future policies at a low cost.
In this paper, we show that identity plays an important role in Dutch internal migration, as people are
times as likely to move to a municipality when it is located within the same historic identity region.
Section 2 provides a description of the methodologies and data used, and the definition of these regional cultural identities. In
Section 3, the models are developed, and parameters are estimated based on survey data. These models are then used in
Section 4, where we test the impact of regional identity by comparing randomly spatially clustered and optimised identity regions to show that the effects we attribute to regional identity could not be attributed due to chance. Including these identity regions in the migration model decreases the deviation of the model by 10.7%. Finally,
Section 5 concludes with a discussion of the results and a way forward.
2. Methodologies
In this section, we first specify a basic gravity model for human migration, after which this model is fitted on Dutch data collected between 1996 and 2016. Using three different sets of identity regions we specify, we introduce the identity regions to the gravity model. After creating this model, we define a way of comparing the influence of identity on migration for different identity sets, and define ways to create and optimise the definitions of such regional identities.
2.1. Used Migration Data
Part of the internal migration events within the Netherlands take place within municipalities, whereas the other events take place between two different municipalities. This means that both intra-municipal and inter-municipal migration data should be used, as we want to include all internal migration events. Such migration data are available for the years 1995–2016 via Statistics Netherlands [
32].
The migration data were collected directly from the Dutch civil registration database. Even though no data are available on the percentage of unregistered movements, this shortcoming is not expected to have a large effect on the outcomes of this research: research by CBS showed that in 2016
% (95% CI [
%,
%]) of Dutch citizens were registered at the correct address [
32].
For each year, the number of inter-municipal migrants between every combination of municipalities is recorded, as well as the number of intra-municipal migrants. This does not mean that data for the same number of municipalities are recorded each year: because of merges of municipalities, the number of municipalities has decreased from 625 in 1996 to 390 in 2016. To be able to create maps and compare migration data in different years, we artificially merge municipalities to form the municipalities that existed in 2016 [
32].
2.2. Model Specification
As mentioned in the Introduction, several types of models are often used to model migration. Even though other model types might have a slightly better performance, a gravity model is considered here. The decisive factor in this choice is that a gravity model explicitly uses the distance variable, whereas the radiation model uses the distances variable indirectly [
33]. The influence of distance on the migration process and the impact of the introduction of identity regions on that distance variable would otherwise be hard to determine.
The most basic gravity model often used to model human migration is shown in Equation (
1). Within this equation, the populations
and
of municipalities
a and
b are positively related to the number of people that migrate from municipality
a to
b,
. When more people live in municipality
a, a larger number of people can leave that municipality, and when there are more people living in municipality
b, it is likely that there are more opportunities in that municipality [
9]. This could make people more willing to move there.
Alongside the influences of the population sizes of both municipalities, the distance
between those two municipalities is also included in this model. This distance can compensate for the influence of travel distance and information distance between two municipalities. As the distance between two municipalities becomes larger, it becomes less likely that individuals move between those two municipalities. The
G variable is a proportionality constant that differs depending on the geographical context and time scale in which the function is applied.
This equation can then be rewritten in a linear form through taking the logarithm of both sides, as shown in Equation (
2). By doing this, a generalised linear regression (GLM) can be applied to find the values of
,
,
and
. The
variable is introduced to accurately determine the value of
G, which equals
.
2.3. Fitting a Standard Gravity Model for Human Migration
To be able to fit the gravity model to the migration data, we also need to have data on the population size of all municipalities and data on the distances between all municipalities. While municipal population data can be acquired through Statistics Netherlands, it is harder to acquire data on the distance travelled by each individual [
32].
The distance travelled by every migrant is approximated by the length of the straight line between the geographical centres of both municipalities in kilometres. This can be done because this distance is highly correlated with the travel time between two locations [
34]. Even though there are cases where this assumption does not hold, such as when certain geographical boundaries cannot be crossed or the population centre is located far from the geographical centre of a municipality, we assume this does not have a significant impact. This is an assumption that works for the Netherlands, because it is flat and there are many roads and bridges—except perhaps for the two municipalities that are located at opposite shores of the IJsselmeer. When travel times do not necessarily correlate with the geographical distance, it might be better to find the actual travel times between two municipalities instead—taking into account the location of the population centres within those municipalities as well.
This way of approximating the distance travelled cannot be used for the intra-municipal migration data. The distance between the centre of a municipality and the centre of that very same municipality is always zero. Under the assumption that most migration movements take place over shorter distances, we estimate the intra-municipal travel distance to be about
instead. This means that the model parameters are calculated using the data sources presented in
Table 1.
The linear form of the gravity model presented in Equation (
2) can then be fitted on the data using a Generalised Linear Model (GLM). GLMs are flexible generalisations of linear regressions, in which the response variables can have a non-normal error distribution model [
35]. Because logarithms are used in this linear form and it is impossible to take the logarithm of zero, the cases in which no people migrate between two municipalities should be processed before fitting the equation.
There are two options to solve this problem: disregard the migration data when no migrants move between two municipalities in a certain year, or modify all the measured migration data in such a way that all connections have some migrants. Because choosing the first approach would mean that information is lost on municipalities that did not attract migrants, we choose the second option. Every number of migrants is increased by two, as with this value the deviation of the model is minimised. A regression on these data resulted in Equation (
3) (
= 4,750,471) = 1.4232
,
).
2.4. Expansion of the Gravity Model
The impact of the regional identities can be examined by expanding the gravity model with a categorical variable
that is true if both municipalities have the same regional identity and false if they do not. Following this introduction, the linear version of the gravity model is also adjusted to Equation (
5). The used parameters are shown in
Table 2.
In this paper, three different sets of regional cultural identities are used. We define a regional identity as a region in which municipalities have a shared political history as proxy for cultural. This shared history is something which can be quantified and documented relatively easily, whereas researching and determining similarities in cultural traditions would be much more difficult. Each of the three sets consists of a different numbers of identity regions, as shown in
Table 3. Comparing the effects that the three different sets have might help to comprehend both the importance of identity in regions of certain sizes and the significance of choosing the right clusters of municipalities.
2.4.1. Specification of Regional Identities
In this paper, three different sets of regional identities are used. The three sets with different numbers of identity regions are shown in
Table 3. Comparing the effects that the three different sets have might help to comprehend both the importance of identity in regions of certain sizes and the significance of choosing the right clusters of municipalities. Each of the three sets of regions has a shared history, which would have allowed each of the regions to develop their own cultural identity.
The first two sets of identity regions consist of administrative regions, which are designed to compare regions of certain sizes within the European Union. The first set consists of the twelve NUTS 2 regions or provinces [
36], which can be traced back to the historical medieval states that merged to become the Netherlands. Some provinces such as Friesland or Noord-Brabant have strong provincial identities through historical cultural and political traditions, whereas provinces with more heterogeneous populations such as Overijssel and Gelderland do not. The second set of forty NUTS 3 regions [
36] can be traced back to the COROP regions defined in the early 1970s. These regions were based on the catchment areas of large Dutch cities, by analysing daily commutes. This can indicate historical dependency. In the creation of these regions, no provincial boundaries were crossed to make the regions easier to use.
Because these two sets of regions were created for an administrative use, it can be the case that multiple cultural identity regions were merged to create the right number of regions with a certain population threshold. Regions within both sets must have a minimal number of residents to allow for accurate statistic comparison [
37]. In the case of migration modelling, we might however want to keep the combination of different cultural identities to a minimum.
The third set of identity regions is manually specified through a literature study. It consists of seventy long-standing historical identity regions. The municipalities within each region have a shared history, and therefore often have similar traditions and dialect. Details on these historical regions can be found in [
38]. Maps of each of the sets of regions can be found in
Section 1 of the Supplementary Materials.
2.4.2. Introduction of the Different Sets of Identity Regions
Using the same data as before, new models can be fitted on each of the three predefined sets of identity regions. The formula fitted on the NUTS 2 regions is shown in Equation (
6) (
= 4,750,471) =
,
), the formula generated using the NUTS 3 regions in Equation (
7) (
= 4,750,471) =
,
) and the formula that is based on the historic regions in Equation (
8) (
= 4,750,471) =
,
). This means that the deviance is decreased by, respectively, 1.4%, 10.6% and 10.7%. In all cases, the coefficient for the identity influence is significant (
).
In these three equations, two variables have changed by more than one tenth:
and
. The
variable would previously have contained part of the
variable, and is likely to have a lower value when the
variable is introduced. Likewise, the value of
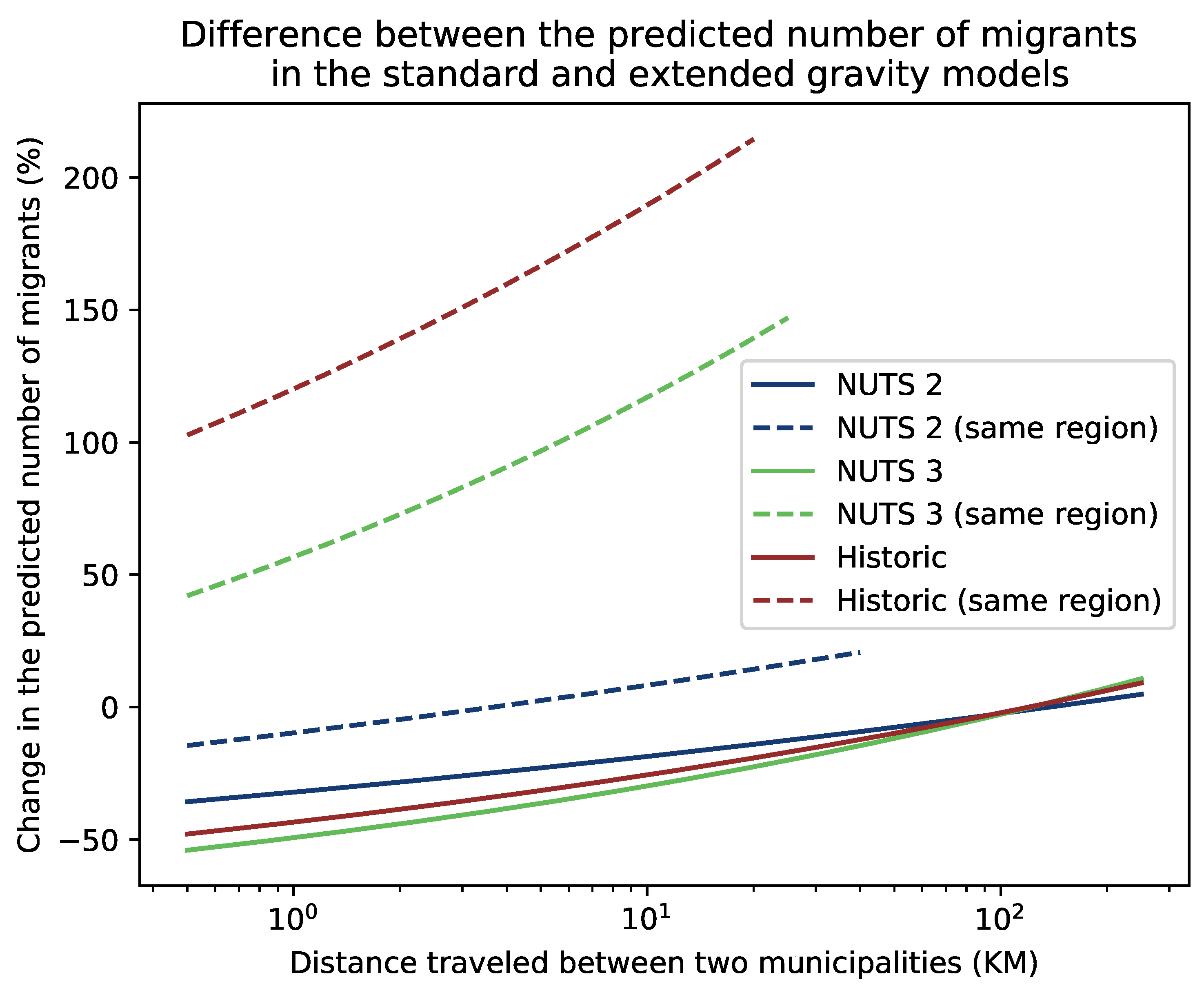
is lowered because the variable would no longer have to account for the effects that identity has on shorter distance migration. A comparison between the effects of the new equations on the predicted number of migrants at certain distances is shown in
Section 4.1.
This way of identity regions assumes that the strength of each of these regional identities is similar, as the expected number of migrants is constantly increased by the same factor when two municipalities are located within the same identity region. In practice, this is not always the case. Identity may for example play a different role in more urbanised environments than in the countryside. Adjusting the model to understand those differences is very difficult, as fitting individual parameters for the influence of each single identity region could lead to over-fitting. Different ways of defining identity regions are discussed in
Section 2 of the Supplementary Materials.
2.5. Comparison of the Importance of Identity in Different Sets of Regions
When comparing the importance of identity in the different sets of identity regions, the parameter values of the
variables that are found in Equations (
6)–(
8) cannot be compared, because the values of the
,
,
and
parameters differ as well. However, we can use the basic gravity model specified in Equation (
3) to find and compare the influence of identity on human migration. This can be done by comparing the differences in the predicted numbers of migrants and the actual number of migrants for both the intraregional and interregional migration, the
. This means that the
values are first split into two different categories as specified in Equation (
9).
A two-sample Kolmogorov–Smirnov test between the distribution of all values and the distribution of all values reveals that both distributions are not the same for each of the three sets of pre-specified identity regions (). This means that there are differences between interregional and intramunicipal migration flows that cannot be explained by the basic gravity model.
As a tool to compare the influence of identity in different municipalities, the formula for a municipalities’ Identity Comparison Measure (
) is specified in Equation (
10). The
value takes on positive values when the basic model is worse at explaining migration inside a region than migration outside a region. Considering that the basic model is fitted on all migration data, this means that people in that region are more likely to move towards municipalities that are located in the same area than towards municipalities that are not.
This value can thus tell us about the difference between the variance that can be explained in the intraregional migration flows, and the explained variance in the interregional migration data. A positive value indicates that the model has more difficulties to explain the intraregional migration behaviour than it has to explain the interregional migration behaviour. An value can be calculated for each separate municipality. This is done by only using all and values for all migration flows originating in that particular municipality. Which migration flows are part of the intraregional migration figures and which flows are part of interregional migration figures depends on the used identity regions.
A comparison between these different values can give an indication as to what regions contain stronger identities, or whether the municipality is part of the right identity region. This does not imply that an value can be translated directly to the influence regional identity has on migration. Instead, the value defines the unexplained differences in the remaining deviance that could not be included in the and variables.
2.6. Creation of Randomly Generated Identity Regions
Apart from defining the predefined identity regions, we randomly generate identity regions to be able to analyse the quality to those predefined identity regions. The fact that a certain set of identity regions produces positive values does not mean much, as such values could also occur in randomly generated regions, just because the municipalities within each region are located in proximity to one another.
Using entirely randomly generated regions as a comparison would not be realistic; municipalities located within the same identity regions are generally not scattered all over the country, but present in a cluster of municipalities. A more realistic approach to generating random regions would thus enforce that municipalities located within a region should at least form a spatial cluster together.
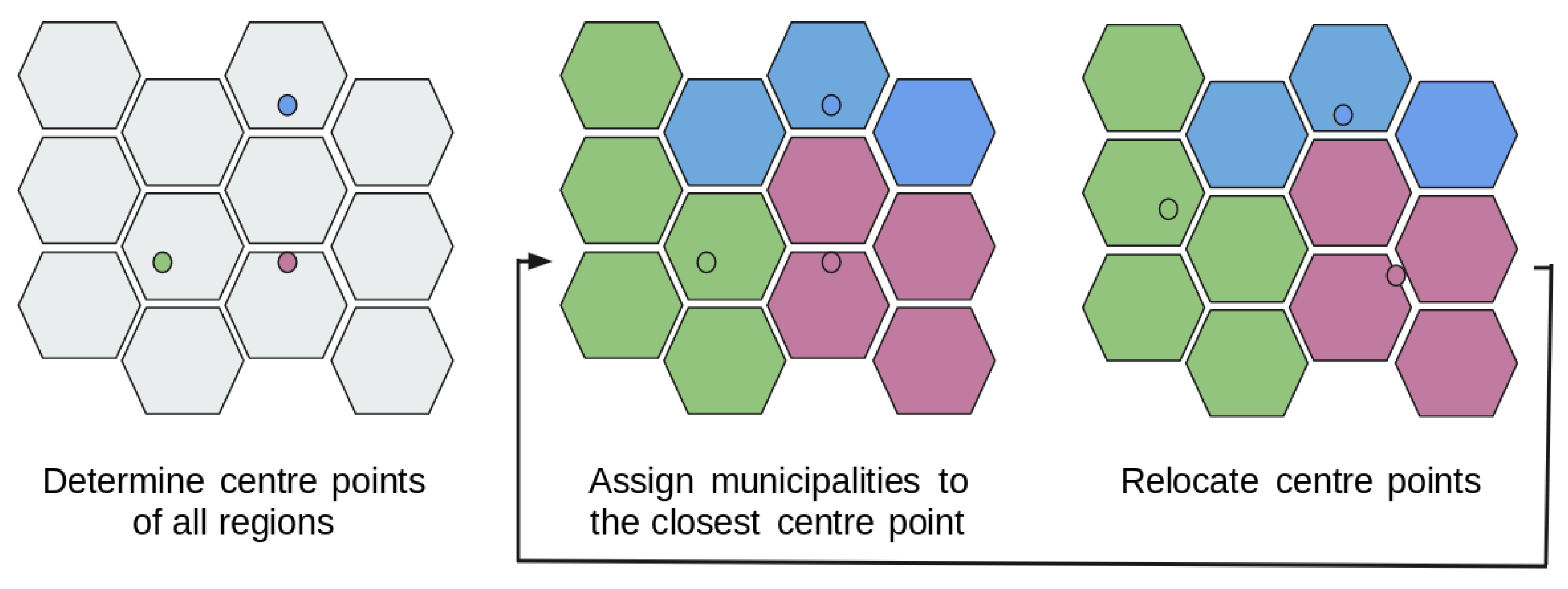
The k-means algorithm is used to create such spatial clusters of municipalities [
39]. Instead of randomly assigning each municipality to a region, a random centre point is assigned to each region. Each municipality is then assigned to the closest centre point, after which the centre point of each region becomes the geographical centre of the municipalities belonging to that region. Some municipalities might then be located closer to the centre point of another region, which means that the that municipality is relocated to that other region. This process is repeated until no more municipalities are reassigned to another region. A visual representation of this algorithm is shown in
Figure 1.
Optimisation of a Set of Identity Regions
By optimising the predefined identity regions and the randomly spatially clustered regions to generate higher
values, we can get a better understanding of the regions used. This can be done by comparing the mean and median
values of the non-optimised and optimised regions. A set of regions can be optimised by increasing the average
value for each region. As this value increases, the differences in the predictive value of the model between the interregional and intraregional migration are enlarged. When this difference becomes larger, the strength of the identity contained within the defined regions also becomes larger. For the algorithm behind our optimisation strategy, see
Section 3 of the Supplementary Materials.
4. Discussion
4.1. Effect on the Influence of the Distance Parameter
When the three different sets of identity regions were introduced to the gravity model, the parameter, which controls the influence of distance on the number of migrants, changed. It decreased from in the original model to (NUTS 2 regions), (NUTS 3 regions) and (historic regions). This mainly has a big influence on the predicted number of migrants over smaller distances, as it is at these distances that migrants can choose to move within or outside their identity region. This means for instance that if the parameter were used as a descriptive characteristic of a population, then an error would be introduced in its inference if the confounding effect of identity would not be into account.
4.2. Model Limitations
An assumption made in this model is that we expect amenities to to be uniformly distributed over the country, which means that they should therefore have no effect on the value. Examples of such amenities are industrial areas, natural parks, and available housing. If this were not true, then it would be possible that strong migration patterns due to amenities are mistakenly inferred as being intra-regional or inter-regional, which could, respectively, inflate or deflate the strength of identity regions that we find. However, some amenities can start to have unequal effects when there are large regional differences in the availability of amenities, rather than large local differences. For example, when employment possibilities in a certain identity region are very low, people could be forced to migrate towards another region where they can get a job. This migration would not be related to their identity, but to employment opportunities. Similar situations can occur when certain educational possibilities are not available within the identity region. On the other hand, certain amenities can also increase the value. When the industry in a region is highly specialised, we might find that people are more likely to move within their region than outside the region because they want to keep working in the same industry, and receive specialised education. Taking the availability of different amenities into account could improve the estimate of the relative role of identity regions. However, since the main point of the present article is to demonstrate that the role of identity is significant, not so much its exact value, we leave this for future work.
Forced migration is another case of migration that can have a big negative effect on the value of a region. However, in the Netherlands, it is quite rare: in our dataset, the relocation of hundreds of newly registered asylum seekers to other immigration centres is the only example of such forced migration events.
While incorporating more variables will create more exact and accurate values, we do not expect this to change our overall conclusion. Identity plays a significant role in the modelling of human migration, and is an effect which is not to be ignored.
4.2.1. Strong Geographical Identities Require Little Displacement
Something that has to be kept in mind when applying this model in other situations is that analysing Dutch cultural identity can differ from analysing other cultural identities. Within the Netherlands, most of these Dutch identities are bound to a specific geographical region, something that might not be the case in other countries. In other areas of the world, where there is a lot of internal displacement of people due to natural disasters, conflicts and forced movement, it can be much more difficult to pinpoint cultural identities to geographical regions. This means that the model might not be applied as is to, for example, African or Southeast Asian migration patterns. An analysis of cultural similarities between different displaced or migrated communities could provide the information needed to include the concept of identity into a model instead. A similar approach might be needed for research in Australia or the United States, areas in which people tend to have less strong ties to certain smaller geographical regions as well.
4.2.2. Identity Regions
In this research, we assumed that historical political boundaries relate to the cultural identity of the residents in an area. This approach allows the idea of identity to be implemented into a model, without requiring extensive research into local and regional culture. However, the used sets of regions are not always perfect. In all three sets of regions, some municipalities can be relocated to other regions in such a way that their negative values become positive, or to seriously increase their value. This could mean that some municipalities are not located in the right cultural identity region, or that other variables such as the availability of certain amenities outweigh the influence of identity in these areas.
The presence of such municipalities might indicate that the regions could still be improved, but does not mean that those sets of regions are not well defined at all. A comparison between the NUTS 3 regions and their randomly generated spatially clustered counterparts shows that the mean value of the NUTS 3 regions set is always larger, and the median value in the NUTS 3 regions set is similar to the highest median values found in the randomly generated spatially clustered regions. This means that the regions defined in the NUTS 3 set perform better than the randomly generated spatially clustered regions. The same reasoning also holds for the set of historic regions.
4.3. Development of Identity Influence over Time
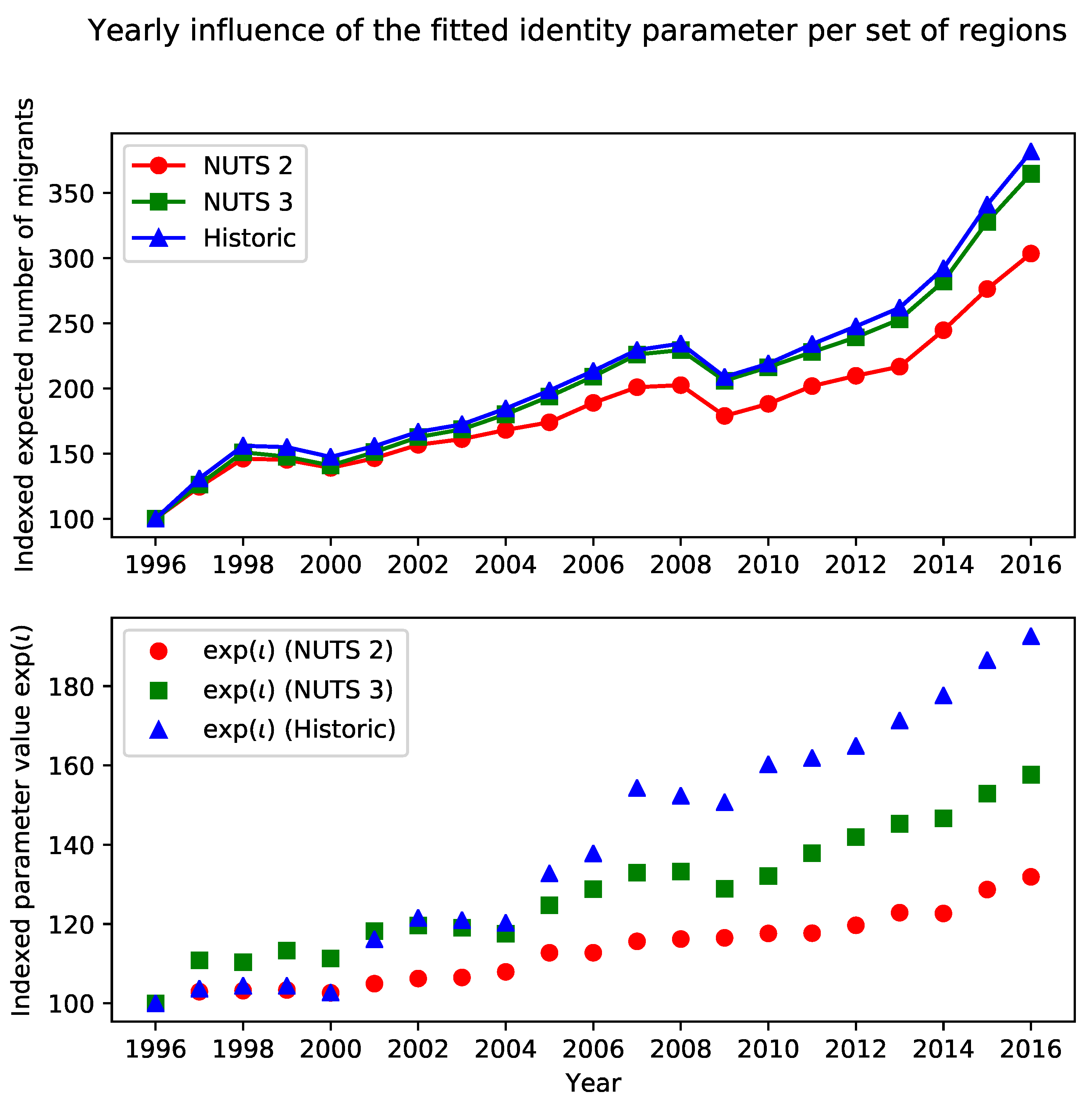
The same extended migration models can also be fitted on yearly data instead. The resulting developments in both the predicted numbers of migrants and the influence of identity over time are shown in
Figure 3.
Between 1996 and 2016, we observe a tripling in the expected number of migrants, and a gradual increase in the exp() values. In the case of the NUTS 2 regions, we observe a nearly 60% increase in the value of exp(). The importance of regional identity in the migration decision is lowered at two different moments: around 2000 and in 2009. This correlates with the moments at which the total numbers of expected migrants is lowered as well. While a link might be made to the economic recession in both years, further investigation on the nature of these patterns is needed.
5. Conclusions
The expansion of the gravity model with one of three different sets of identity regions results in three different sets of parameter values in Equation (
6) that showed how the influence of these identity regions should be incorporated into the model. In particular, when the NUTS 3 and historic regions are added to the gravity model, the resulting Equations (
7) and (
8) show that Dutch people are, respectively,
and
times as likely to move to a municipality within the same identity. NUTS 2 regions turn out to have less predictive value, as Equation (
6) shows that people were
times more likely to move towards a municipality within the same NUTS 2 region.
Including either the NUTS 3 or historic regions in the migration model decreases the deviation of the model by, respectively,
and
. Again, the larger NUTS 2 regions seem to have less predictive power: including the NUTS 2 regions only decreased the deviation of the model by
.
Table 4 shows further evidence that the NUTS 3 and historic regions are more relevant; the median
values of both sets of regions are similar to their randomly generated spatially clustered counterparts, whereas the
values of the NUTS 2 regions are not. This is strange, as randomly clustered regions should have a very similar structure to the original sets of regions, and the median ICM values should be similar. The same applies to their optimised counterparts. This further supports the use of smaller sized regions whenever this is possible.
We have demonstrated that the incorporation of identity regions does not have to be difficult. By choosing to model the identity regions with strict boundaries, we created a way of incorporating identity regions that can easily be used in other regions as well. Through literature research, it should be possible to specify sets of historic identity regions in these other regions too. Overall, this makes us believe that introducing regional identities in human migration models is an easy way to enhance their performance.
Because regional identity seems to be an important factor in the human migration decision, it would be interesting to embed these identity regions in other types of human migration models as well. When such models are used on regions in different circumstances, this could provide more information about the influence of regional identity itself. It would be interesting to see what would happen in more segregated societies, or in societies where most people regularly travel over larger distances than in the Dutch society. The value could also be used to detect the formation of regions over time. This could be particularly useful in areas that were colonised or have seen enormous change in society. This variable could help to map these changes in society onto changes in local migration behaviour, which in turn might help in understanding the regional identities in a certain area.