Street Network Models and Measures for Every U.S. City, County, Urbanized Area, Census Tract, and Zillow-Defined Neighborhood
Abstract
:1. Introduction
2. Background
2.1. Street Network Models
2.2. Street Network Data
3. Methods
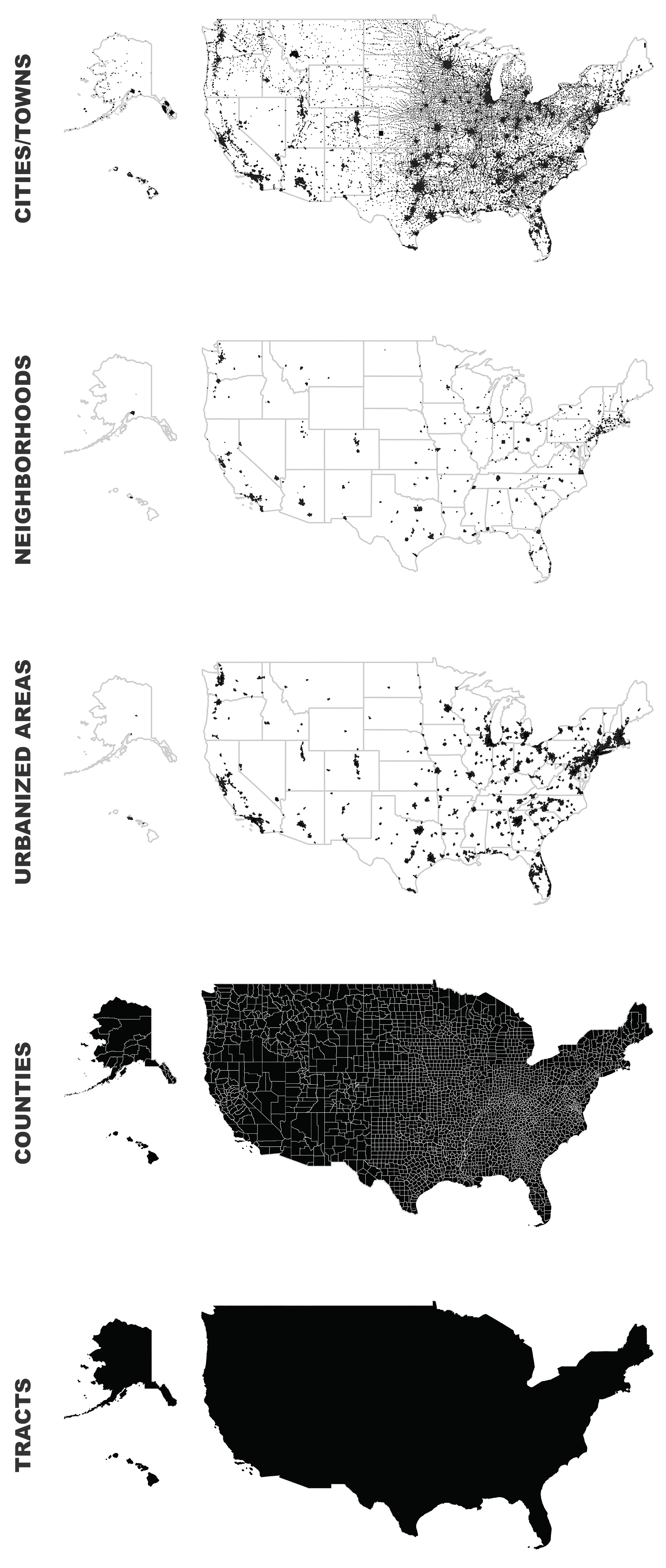
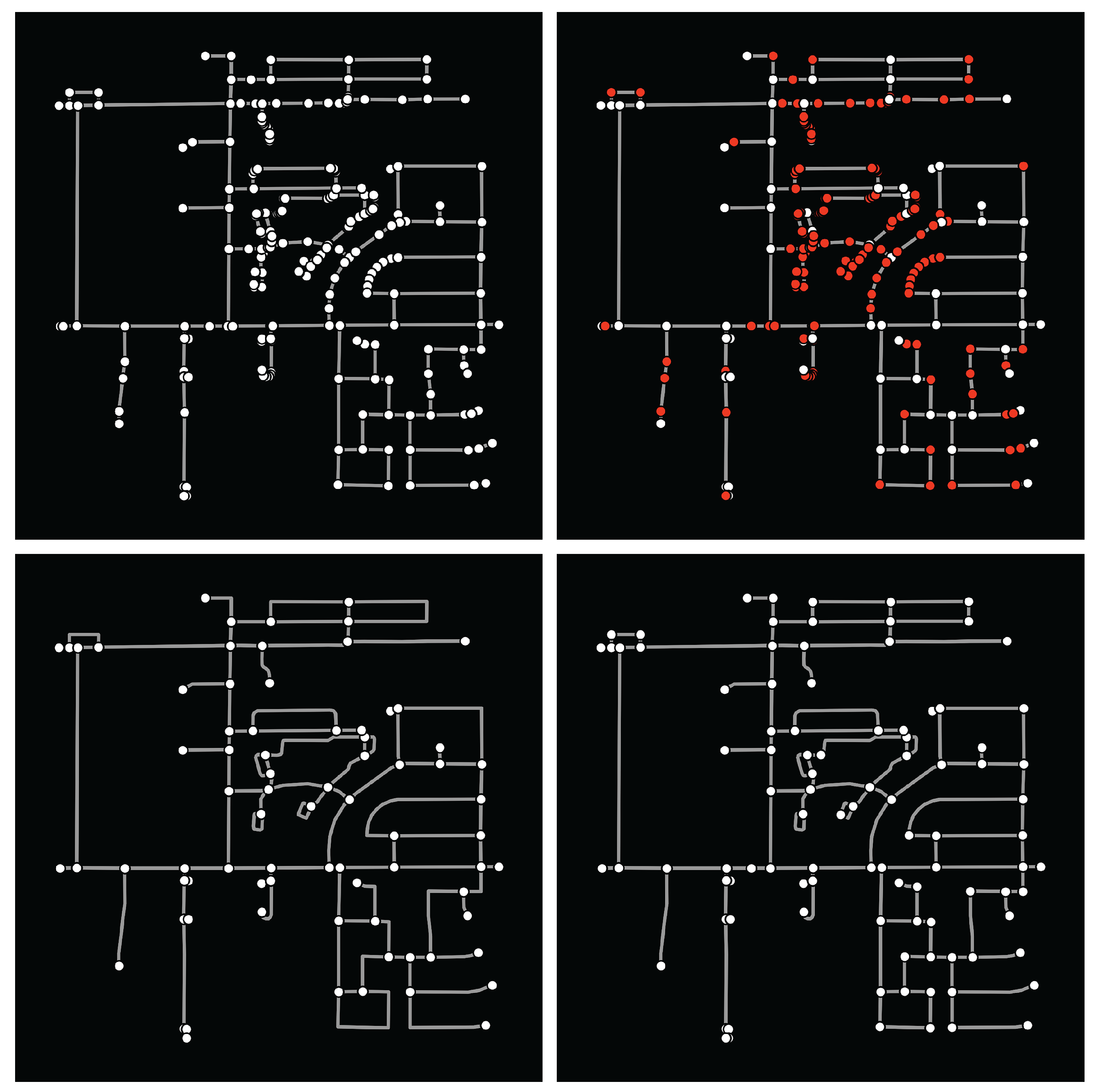
3.1. Graph Production
- U.S. census bureau 2017 places shapefiles for all 50 states. Census “places” comprise cities, towns, equivalent entities, and census-designated places. For this project, we discard the latter (small unincorporated communities) to retain and analyze every city and town (N = 19,678) in the U.S.
- U.S. census bureau 2017 nationwide counties (N = 3233) shapefile.
- U.S. census bureau 2017 nationwide urban areas shapefile. Census “urban areas” comprise urbanized areas and urban clusters. For this project, we discard the latter (small agglomerations) to retain and analyze every urbanized area (N = 497) in the U.S. [83].
- U.S. census bureau 2017 nationwide census tracts (N = 74,133) shapefile.
3.2. Graph Analysis
3.3. Data and Code Availability
- Boeing, G. U.S. Street Network Shapefiles, Node/Edge Lists, and GraphML Files. Harvard Dataverse, v2. https://doi.org/10.7910/DVN/CUWWYJ (2018)
- Boeing, G. U.S. Street Network Analytic Measures. Harvard Dataverse, v2. https://doi.org/10.7910/DVN/F5UNSK (2018)
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Levinson, D. Network Structure and City Size. PLoS ONE 2012, 7, e29721. [Google Scholar] [CrossRef] [PubMed]
- Cervero, R.; Kockelman, K. Travel Demand and the 3 Ds: Density, Diversity, and Design. Transp. Res. Part D Transp. Environ. 1997, 2, 199–219. [Google Scholar] [CrossRef]
- Ewing, R.; Cervero, R. Travel and the Built Environment: A Meta-Analysis. J. Am. Plan. Assoc. 2010, 76, 265–294. [Google Scholar] [CrossRef]
- Talen, E. Measuring Urbanism: Issues in Smart Growth Research. J. Urban Des. 2003, 8, 195–215. [Google Scholar] [CrossRef]
- Grannis, R. The Importance of Trivial Streets: Residential Streets and Residential Segregation. Am. J. Sociol. 1998, 103, 1530–1564. [Google Scholar] [CrossRef]
- Southworth, M.; Ben-Joseph, E. Streets and the Shaping of Towns and Cities; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Marshall, W.; Garrick, N. Street network types and road safety: A study of 24 California cities. Urban Des. Int. 2010, 15, 133–147. [Google Scholar] [CrossRef]
- Marshall, W.; Piatkowski, D.; Garrick, N. Community design, street networks, and public health. J. Transp. Health 2014, 1, 326–340. [Google Scholar] [CrossRef]
- Karimi, K. A configurational approach to analytical urban design: “Space syntax” methodology. Urban Des. Int. 2012, 17, 297–318. [Google Scholar] [CrossRef]
- Horner, M.W.; Murray, A.T. Excess commuting and the modifiable areal unit problem. Urban Stud. 2002, 39, 131–139. [Google Scholar] [CrossRef]
- Dessemontet, P.; Kaufmann, V.; Jemelin, C. Switzerland as a Single Metropolitan Area? A Study of its Commuting Network. Urban Stud. 2010, 47, 2785–2802. [Google Scholar] [CrossRef]
- Lee, J.; Sohn, K. Identifying the Impact on Land Prices of Replacing At-grade or Elevated Railways with Underground Subways in the Seoul Metropolitan Area. Urban Stud. 2014, 51, 44–62. [Google Scholar] [CrossRef]
- Porta, S.; Romice, O.; Maxwell, J.A.; Russell, P.; Baird, D. Alterations in scale: Patterns of change in main street networks across time and space. Urban Stud. 2014, 51, 3383–3400. [Google Scholar] [CrossRef]
- Porta, S.; Latora, V.; Strano, E. Networks in Urban Design: Six Years of Research in Multiple Centrality Assessment. In Network Science: Complexity in Nature and Technology; Estrada, E., Fox, M., Higham, D.J., Oppo, G.L., Eds.; Springer: London, UK, 2010; pp. 107–129. [Google Scholar]
- Porta, S.; Latora, V.; Wang, F.; Rueda, S.; Strano, E.; Scellato, S.; Cardillo, A.; Belli, E.; Càrdenas, F.; Cormenzana, B.; et al. Street Centrality and the Location of Economic Activities in Barcelona. Urban Stud. 2012, 49, 1471–1488. [Google Scholar] [CrossRef]
- Hajrasouliha, A.; Yin, L. The impact of street network connectivity on pedestrian volume. Urban Stud. 2015, 52, 2483–2497. [Google Scholar] [CrossRef]
- Parthasarathi, P.; Levinson, D.; Hochmair, H. Network Structure and Travel Time Perception. PLoS ONE 2013, 8, e77718. [Google Scholar] [CrossRef] [PubMed]
- Parthasarathi, P.; Hochmair, H.; Levinson, D. Street network structure and household activity spaces. Urban Stud. 2015, 52, 1090–1112. [Google Scholar] [CrossRef]
- Knight, P.L.; Marshall, W.E. The metrics of street network connectivity: Their inconsistencies. J. Urban. Int. Res. Placemak. Urban Sustain. 2015, 8, 241–259. [Google Scholar] [CrossRef]
- Xiao, Y.; Webster, C.; Orford, S. Identifying house price effects of changes in urban street configuration: An empirical study in Nanjing, China. Urban Stud. 2016, 53, 112–131. [Google Scholar] [CrossRef]
- Zhong, C.; Arisona, S.M.; Huang, X.; Batty, M.; Schmitt, G. Detecting the dynamics of urban structure through spatial network analysis. Int. J. Geograph. Inf. Sci. 2014, 28, 2178–2199. [Google Scholar] [CrossRef]
- Zhong, C.; Schläpfer, M.; Arisona, S.M.; Batty, M.; Ratti, C.; Schmitt, G. Revealing centrality in the spatial structure of cities from human activity patterns. Urban Stud. 2017, 54, 437–455. [Google Scholar] [CrossRef]
- Barthelemy, M. From paths to blocks: New measures for street patterns. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 256–271. [Google Scholar] [CrossRef]
- Barrington-Leigh, C.; Millard-Ball, A. A century of sprawl in the United States. Proc. Natl. Acad. Sci. USA 2015, 112, 8244–8249. [Google Scholar] [CrossRef] [PubMed]
- Boeing, G. Measuring the Complexity of Urban Form and Design. Urban Des. Int. 2018, 23, 281–292. [Google Scholar] [CrossRef]
- Rose-Redwood, R.; Bigon, L. Gridded Worlds: An Urban Anthology; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Barthelemy, M. Betweenness centrality in large complex networks. Eur. Phys. J. B Condens. Matter Complex Syst. 2004, 38, 163–168. [Google Scholar] [CrossRef]
- Barthelemy, M.; Flammini, A. Modeling Urban Street Patterns. Phys. Rev. Lett. 2008, 100, 138702. [Google Scholar] [CrossRef] [PubMed]
- Barthelemy, M. Morphogenesis of Spatial Networks; Springer: New York, NY, USA, 2017. [Google Scholar]
- Barthelemy, M.; Bordin, P.; Berestycki, H.; Gribaudi, M. Self-organization versus top-down planning in the evolution of a city. Sci. Rep. 2013, 3, 2153. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Costa, L.D.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Dorogovtsev, S.; Mendes, J. Evolution of networks. Adv. Phys. 2002, 51, 1079–1187. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Porta, S. Centrality measures in spatial networks of urban streets. Phys. Rev. E 2006, 73, 036125. [Google Scholar] [CrossRef] [PubMed]
- Crucitti, P.; Latora, V.; Porta, S. Centrality in networks of urban streets. Chaos Interdiscip. J. Nonlinear Sci. 2006, 16, 015113. [Google Scholar] [CrossRef] [PubMed]
- Buhl, J.; Gautrais, J.; Reeves, N.; Solé, R.V.; Valverde, S.; Kuntz, P.; Theraulaz, G. Topological patterns in street networks of self-organized urban settlements. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 49, 513–522. [Google Scholar] [CrossRef]
- Chan, S.H.Y.; Donner, R.V.; Lämmer, S. Urban road networks—Spatial networks with universal geometric features? Eur. Phys. J. B 2011, 84, 563–577. [Google Scholar] [CrossRef]
- Strano, E.; Nicosia, V.; Latora, V.; Porta, S.; Barthelemy, M. Elementary processes governing the evolution of road networks. Sci. Rep. 2012, 2, 296. [Google Scholar] [CrossRef] [PubMed]
- Strano, E.; Viana, M.; da Fontoura Costa, L.; Cardillo, A.; Porta, S.; Latora, V. Urban Street Networks, a Comparative Analysis of Ten European Cities. Environ. Plan. B Plan. Des. 2013, 40, 1071–1086. [Google Scholar] [CrossRef]
- Louf, R.; Barthelemy, M. A typology of street patterns. J. R. Soc. Interface 2014, 11, 20140924. [Google Scholar] [CrossRef] [PubMed]
- Gudmundsson, A.; Mohajeri, N. Entropy and order in urban street networks. Sci. Rep. 2013, 3, 3324. [Google Scholar] [CrossRef] [PubMed]
- Mohajeri, N.; Gudmundsson, A. The Evolution and Complexity of Urban Street Networks: Urban Street Networks. Geograph. Anal. 2014, 46, 345–367. [Google Scholar] [CrossRef]
- Li, W.; Hu, D.; Liu, Y. An improved measuring method for the information entropy of network topology. Trans. GIS 2018, 22, 1632–1648. [Google Scholar] [CrossRef]
- Courtat, T.; Gloaguen, C.; Douady, S. Mathematics and morphogenesis of cities: A geometrical approach. Phys. Rev. E 2011, 83, 036106. [Google Scholar] [CrossRef] [PubMed]
- Boeing, G. OSMnx: New Methods for Acquiring, Constructing, Analyzing, and Visualizing Complex Street Networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Boeing, G. A Multi-Scale Analysis of 27,000 Urban Street Networks: Every US City, Town, Urbanized Area, and Zillow Neighborhood. Environ. Plan. B Urban Anal. City Sci. 2018. [Google Scholar] [CrossRef]
- Newman, M.E.J. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Trudeau, R.J. Introduction to Graph Theory, 2nd ed.; Dover Publications: New York, NY, USA, 1994. [Google Scholar]
- Vespignani, A. Twenty years of network science. Nature 2018. [Google Scholar] [CrossRef] [PubMed]
- Brandes, U.; Erlebach, T. (Eds.) Network Analysis: Methodological Foundations; Number 3418 in Lecture Notes in Computer Science; Springer: Berlin, Germany, 2005. [Google Scholar]
- Gastner, M.T.; Newman, M.E.J. The spatial structure of networks. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 49, 247–252. [Google Scholar] [CrossRef]
- Marshall, S.; Gil, J.; Kropf, K.; Tomko, M.; Figueiredo, L. Street Network Studies: From Networks to Models and their Representations. Netw. Spat. Econ. 2018. [Google Scholar] [CrossRef]
- Aldous, D.J. Routed Planar Networks. Electron. J. Graph Theory Appl. 2016, 4, 42–59. [Google Scholar] [CrossRef]
- Boeing, G. Planarity and Street Network Representation in Urban Form Analysis. Environ. Plan. B Urban Anal. City Sci. 2018. [Google Scholar] [CrossRef]
- Boyer, J.M. Subgraph Homeomorphism via the Edge Addition Planarity Algorithm. J. Graph Algorithms Appl. 2012, 16, 381–410. [Google Scholar] [CrossRef]
- Cardillo, A.; Scellato, S.; Latora, V.; Porta, S. Structural properties of planar graphs of urban street patterns. Phys. Rev. E 2006, 73, 066107. [Google Scholar] [CrossRef] [PubMed]
- Chimani, M.; Gutwenger, C. Non-planar core reduction of graphs. Discret. Math. 2009, 309, 1838–1855. [Google Scholar] [CrossRef]
- Chimani, M.; Hliněný, P.; Mutzel, P. Vertex insertion approximates the crossing number of apex graphs. Eur. J. Comb. 2012, 33, 326–335. [Google Scholar] [CrossRef]
- Eppstein, D.; Goodrich, M.T. Studying (Non-planar) Road Networks Through an Algorithmic Lens. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, GIS ’08, Irvine, CA, USA, 5–7 November 2008; p. 16. [Google Scholar]
- Fohl, P.; Curtin, K.M.; Goodchild, M.F.; Church, R.L. A non-planar, lane-based navigable data model for ITS. In Proceedings of the Seventh International Symposium on Spatial Data Handling, Delft, The Netherlands, 12–16 August 1996; pp. 17–29. [Google Scholar]
- Hopcroft, J.; Tarjan, R. Efficient Planarity Testing. J. ACM 1974, 21, 549–568. [Google Scholar] [CrossRef]
- Liebers, A. Planarizing graphs—A survey and annotated bibliography. J. Graph Algorithms Appl. 2001, 5, 257–330. [Google Scholar] [CrossRef]
- Masucci, A.P.; Smith, D.; Crooks, A.; Batty, M. Random planar graphs and the London street network. Eur. Phys. J. B Condens. Matter Complex Syst. 2009, 71, 259–271. [Google Scholar] [CrossRef]
- Székely, L.A. A successful concept for measuring non-planarity of graphs: The crossing number. Discret. Math. 2004, 276, 331–352. [Google Scholar] [CrossRef]
- Viana, M.P.; Strano, E.; Bordin, P.; Barthelemy, M. The simplicity of planar networks. Sci. Rep. 2013, 3, 3495. [Google Scholar] [CrossRef] [PubMed]
- Law, S. Defining Street-based Local Area and measuring its effect on house price using a hedonic price approach. Cities 2017, 60, 166–179. [Google Scholar] [CrossRef]
- Dill, J. Measuring network connectivity for bicycling and walking. In Proceedings of the Transportation Research Board 83rd Annual Meeting, Washington, DC, USA, 11–15 January 2004. [Google Scholar]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plan. B Plan. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A dual approach. Phys. A Stat. Mech. Appl. 2006, 369, 853–866. [Google Scholar] [CrossRef]
- Ratti, C. Space syntax: Some inconsistencies. Environ. Plan. B Plan. Des. 2004, 31, 487–499. [Google Scholar] [CrossRef]
- Batty, M. Network geography: Relations, interactions, scaling and spatial processes in GIS. In Re-Presenting GIS; Unwin, D.J., Fisher, P., Eds.; John Wiley & Sons: Chichester, UK, 2005; pp. 149–170. [Google Scholar]
- Barthelemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- O’Sullivan, D. Spatial Network Analysis. In Handbook of Regional Science; Fischer, M.M., Nijkamp, P., Eds.; Springer: Berlin, Germany, 2014; pp. 1253–1273. [Google Scholar]
- Frizzelle, B.; Evenson, K.; Rodriguez, D.; Laraia, B. The importance of accurate road data for spatial applications in public health: Customizing a road network. Int. J. Health Geogr. 2009, 8, 24. [Google Scholar] [CrossRef] [PubMed]
- Barrington-Leigh, C.; Millard-Ball, A. The world’s user-generated road map is more than 80% complete. PLoS ONE 2017, 12, e0180698. [Google Scholar] [CrossRef] [PubMed]
- Jokar Arsanjani, J.; Zipf, A.; Mooney, P.; Helbich, M. (Eds.) OpenStreetMap in GIScience; Lecture Notes in Geoinformation and Cartography; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Karduni, A.; Kermanshah, A.; Derrible, S. A protocol to convert spatial polyline data to network formats and applications to world urban road networks. Sci. Data 2016, 3, 160046. [Google Scholar] [CrossRef] [PubMed]
- Boeing, G. Methods and Measures for Analyzing Complex Street Networks and Urban Form. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2017. [Google Scholar]
- Lu, B.; Sun, H.; Harris, P.; Xu, M.; Charlton, M. Shp2graph: Tools to Convert a Spatial Network into an Igraph Graph in R. ISPRS Int. J. Geo-Inf. 2018, 7, 293. [Google Scholar] [CrossRef]
- Foti, F. Behavioral Framework for Measuring Walkability and its Impact on Home Values and Residential Location Choices. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2014. [Google Scholar]
- Sevtsuk, A.; Mekonnen, M. Urban network analysis. A new toolbox for ArcGIS. Revue Internationale de Géomatique 2012, 22, 287–305. [Google Scholar] [CrossRef]
- U.S. Census Bureau. 2010 Census Urban and Rural Classification and Urban Area Criteria. 2010. Available online: https://www.census.gov/geo/reference/ua/urban-rural-2010.html (accessed on 2 January 2019).
- Schernthanner, H.; Asche, H.; Gonschorek, J.; Scheele, L. Spatial Modeling and Geovisualization of Rental Prices for Real Estate Portals. In Computational Science and Its Applications—ICCSA 2016; Gervasi, O., Murgante, B., Misra, S., Rocha, A.M.A.C., Torre, C.M., Taniar, D., Apduhan, B.O., Stankova, E., Wang, S., Eds.; Number 9788 in Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; pp. 120–133. [Google Scholar]
- Besbris, M.; Faber, J.W.; Rich, P.; Sharkey, P. Effect of neighborhood stigma on economic transactions. Proc. Natl. Acad. Sci. USA 2015, 112, 4994–4998. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, J.; Abramovitz, M. Indicator Analysis for Unpacking Poverty in New York City; Technical Report; CUNY: New York, NY, USA, 2014. [Google Scholar]
- Gil, J. Street network analysis “edge effects”: Examining the sensitivity of centrality measures to boundary conditions. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 819–836. [Google Scholar] [CrossRef]
- ESRI. Shapefile Technical Description; White Paper J-7855; Environmental Systems Research Institute: Redlands, CA, USA, 1998. [Google Scholar]
- Brandes, U.; Eiglsperger, M.; Herman, I.; Himsolt, M.; Marshall, M.S. GraphML Progress Report: Structural Layer Proposal. In Graph Drawing; Goos, G., Hartmanis, J., van Leeuwen, J., Mutzel, P., Jünger, M., Leipert, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2265, pp. 501–512. [Google Scholar]
- Hagberg, A.; Conway, D. Hacking Social Networks Using the Python Programming Language. Presented at the Sunbelt 2010: International Network for Social Network Analysis, Riva del Garda, Italy, 29 June–4 July 2010. [Google Scholar]
- Giacomin, D.J.; Levinson, D.M. Road network circuity in metropolitan areas. Environ. Plan. B Plan. Des. 2015, 42, 1040–1053. [Google Scholar] [CrossRef]
- Boeing, G. The Morphology and Circuity of Walkable and Drivable Street Networks. In The Mathematics of Urban Morphology; D’Acci, L., Ed.; Birkhäuser: Basel, Switzerland, 2019. [Google Scholar]
- Boeing, G. Urban Spatial Order: Street Network Orientation, Configuration, and Entropy. arXiv, 2019; arXiv:1808.00600. [Google Scholar] [CrossRef]
- Beineke, L.W.; Oellermann, O.R.; Pippert, R.E. The Average Connectivity of a Graph. Discret. Math. 2002, 252, 31–45. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. Integration of space syntax into GIS: New perspectives for urban morphology. Trans. GIS 2002, 6, 295–309. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. Topological Analysis of Urban Street Networks. Environ. Plan. B Plan. Des. 2004, 31, 151–162. [Google Scholar] [CrossRef]
- Jiang, B. A Topological Pattern of Urban Street Networks: Universality and Peculiarity. Phys. A Stat. Mech. Appl. 2007, 384, 647–655. [Google Scholar] [CrossRef]
- Mandloi, D.; Thill, J.C. Object-Oriented Data Modeling of an Indoor/Outdoor Urban Transportation Network and Route Planning Analysis. In Geospatial Analysis and Modelling of Urban Structure and Dynamics; Jiang, B., Yao, X., Eds.; Springer: Dordrecht, The Netherlands, 2010; Volume 99, pp. 197–220. [Google Scholar]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Agryzkov, T.; Oliver, J.L.; Tortosa, L.; Vicent, J.F. An algorithm for ranking the nodes of an urban network based on the concept of PageRank vector. Appl. Math. Comput. 2012, 219, 2186–2193. [Google Scholar] [CrossRef]
- Chin, W.C.B.; Wen, T.H. Geographically Modified PageRank Algorithms: Identifying the Spatial Concentration of Human Movement in a Geospatial Network. PLoS ONE 2015, 10, e0139509. [Google Scholar] [CrossRef] [PubMed]
- Dankelmann, P.; Oellermann, O.R. Bounds on the average connectivity of a graph. Discret. Appl. Math. 2003, 129, 305–318. [Google Scholar] [CrossRef]
- Cranmer, S.J.; Leifeld, P.; McClurg, S.D.; Rolfe, M. Navigating the range of statistical tools for inferential network analysis. Am. J. Polit. Sci. 2017, 61, 237–251. [Google Scholar] [CrossRef]
- Opsahl, T.; Panzarasa, P. Clustering in weighted networks. Soc. Netw. 2009, 31, 155–163. [Google Scholar] [CrossRef]
- Gleich, D.F. PageRank Beyond the Web. SIAM Rev. 2015, 57, 321–363. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Y.; Ma, C.; Yang, J.; Ye, X.; Zhang, C. TrajGraph: A Graph-Based Visual Analytics Approach to Studying Urban Network Centralities Using Taxi Trajectory Data. IEEE Trans. Vis. Comput. Graph. 2016, 22, 160–169. [Google Scholar] [CrossRef] [PubMed]
- Barron, C.; Neis, P.; Zipf, A. A Comprehensive Framework for Intrinsic OpenStreetMap Quality Analysis. Trans. GIS 2014, 18, 877–895. [Google Scholar] [CrossRef]
- Basiri, A.; Jackson, M.; Amirian, P.; Pourabdollah, A.; Sester, M.; Winstanley, A.; Moore, T.; Zhang, L. Quality assessment of OpenStreetMap data using trajectory mining. Geospat. Inf. Sci. 2016, 19, 56–68. [Google Scholar] [CrossRef]
- Corcoran, P.; Mooney, P.; Bertolotto, M. Analysing the growth of OpenStreetMap networks. Spat. Stat. 2013, 3, 21–32. [Google Scholar] [CrossRef]
- Girres, J.F.; Touya, G. Quality Assessment of the French OpenStreetMap Dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Haklay, M. How Good is Volunteered Geographical Information? A Comparative Study of OpenStreetMap and Ordnance Survey Datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Maron, M. How complete is OpenStreetMap? Mapbox. 19 November 2015. Available online: https://www.mapbox.com/blog/how-complete-is-openstreetmap/ (accessed on 2 January 2019).
- Neis, P.; Zielstra, D.; Zipf, A. The Street Network Evolution of Crowdsourced Maps: OpenStreetMap in Germany 2007–2011. Future Internet 2011, 4, 1–21. [Google Scholar] [CrossRef]
- Zielstra, D.; Hochmair, H.H.; Neis, P. Assessing the Effect of Data Imports on the Completeness of OpenStreetMap—A United States Case Study. Trans. GIS 2013, 17, 315–334. [Google Scholar] [CrossRef]
| Measure | Definition |
|---|---|
| area | land area of cities, counties, and urbanized areas; gross area of neighborhoods (km2)) |
| mean avg neighborhood degree | mean of all average neighborhood degrees in network |
| avg weighted neighborhood degree | mean degree of nodes in the neighborhood of each node, weighted by edge length |
| mean avg weighted neighborhood degree | mean of all weighted average neighborhood degrees in network |
| avg circuity | total edge length divided by sum of great circle distances between the nodes incident to each edge |
| avg clustering coefficient | mean of clustering coefficients (extent to which node’s neighborhood forms a complete graph) of all nodes |
| avg weighted clustering coefficient | mean of weighted clustering coefficients of all nodes |
| avg degree centrality | mean of all degree centralities in network |
| avg edge length | mean edge length in network (m) |
| total edge length | sum of edge lengths in network (m) |
| edge density | total edge length divided by area |
| intersection count | number of intersections in network |
| intersection density | intersection count divided by area |
| dead-end count | number of dead-end nodes in the network |
| dead-end proportion | proportion of nodes that are dead-ends |
| three-way intersection count | number of three-way intersection in the network |
| three-way intersection proportion | proportion of nodes that are three-way intersections |
| four-way intersection count | number of four-way intersection in the network |
| four-way intersection proportion | proportion of nodes that are four-way intersections |
| n | number of nodes in network |
| m | number of edges in network |
| avg node degree () | mean number of inbound and outbound edges incident to the nodes |
| node density | n divided by area in square kilometers |
| maximum PageRank | highest PageRank (ranking of nodes based on structure of incoming edges) value of any node in the graph |
| minimum PageRank | lowest PageRank value of any node in the graph |
| self-loop proportion | proportion of edges that have a single incident node (i.e., edge where ) |
| street density | total street length divided by area in square kilometers |
| avg street segment length | mean edge length in undirected representation of network (m) |
| total street length | sum of edge lengths in undirected representation of network (m) |
| count of street segments | number of edges in undirected representation of network |
| avg streets per node | mean number of physical streets that emanate from each node (intersections and dead-ends) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boeing, G. Street Network Models and Measures for Every U.S. City, County, Urbanized Area, Census Tract, and Zillow-Defined Neighborhood. Urban Sci. 2019, 3, 28. https://doi.org/10.3390/urbansci3010028
Boeing G. Street Network Models and Measures for Every U.S. City, County, Urbanized Area, Census Tract, and Zillow-Defined Neighborhood. Urban Science. 2019; 3(1):28. https://doi.org/10.3390/urbansci3010028
Chicago/Turabian StyleBoeing, Geoff. 2019. "Street Network Models and Measures for Every U.S. City, County, Urbanized Area, Census Tract, and Zillow-Defined Neighborhood" Urban Science 3, no. 1: 28. https://doi.org/10.3390/urbansci3010028
APA StyleBoeing, G. (2019). Street Network Models and Measures for Every U.S. City, County, Urbanized Area, Census Tract, and Zillow-Defined Neighborhood. Urban Science, 3(1), 28. https://doi.org/10.3390/urbansci3010028





