Modeling Determinants of Urban Growth in Conakry, Guinea: A Spatial Logistic Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Methods
3. Logistic Regression Model
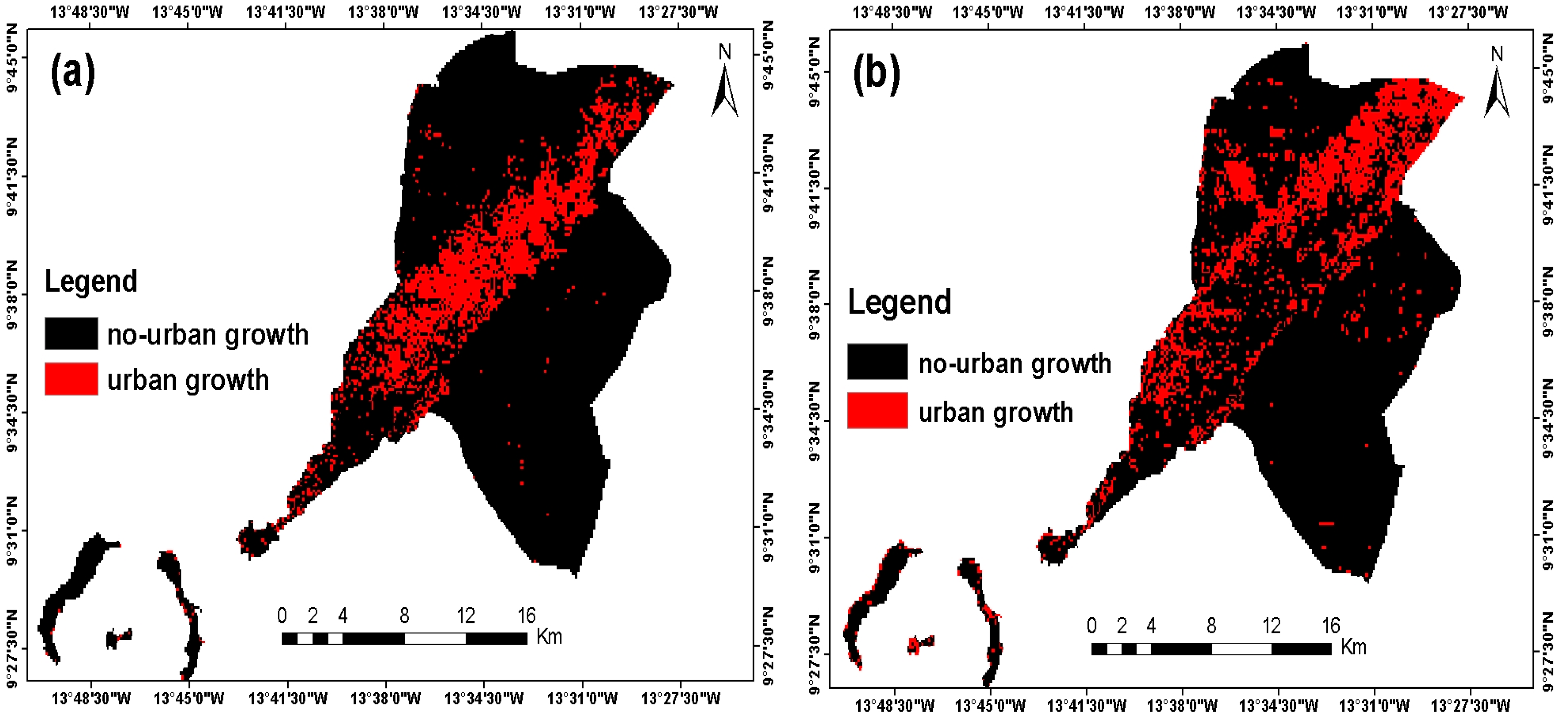
3.1. Dependent Variable
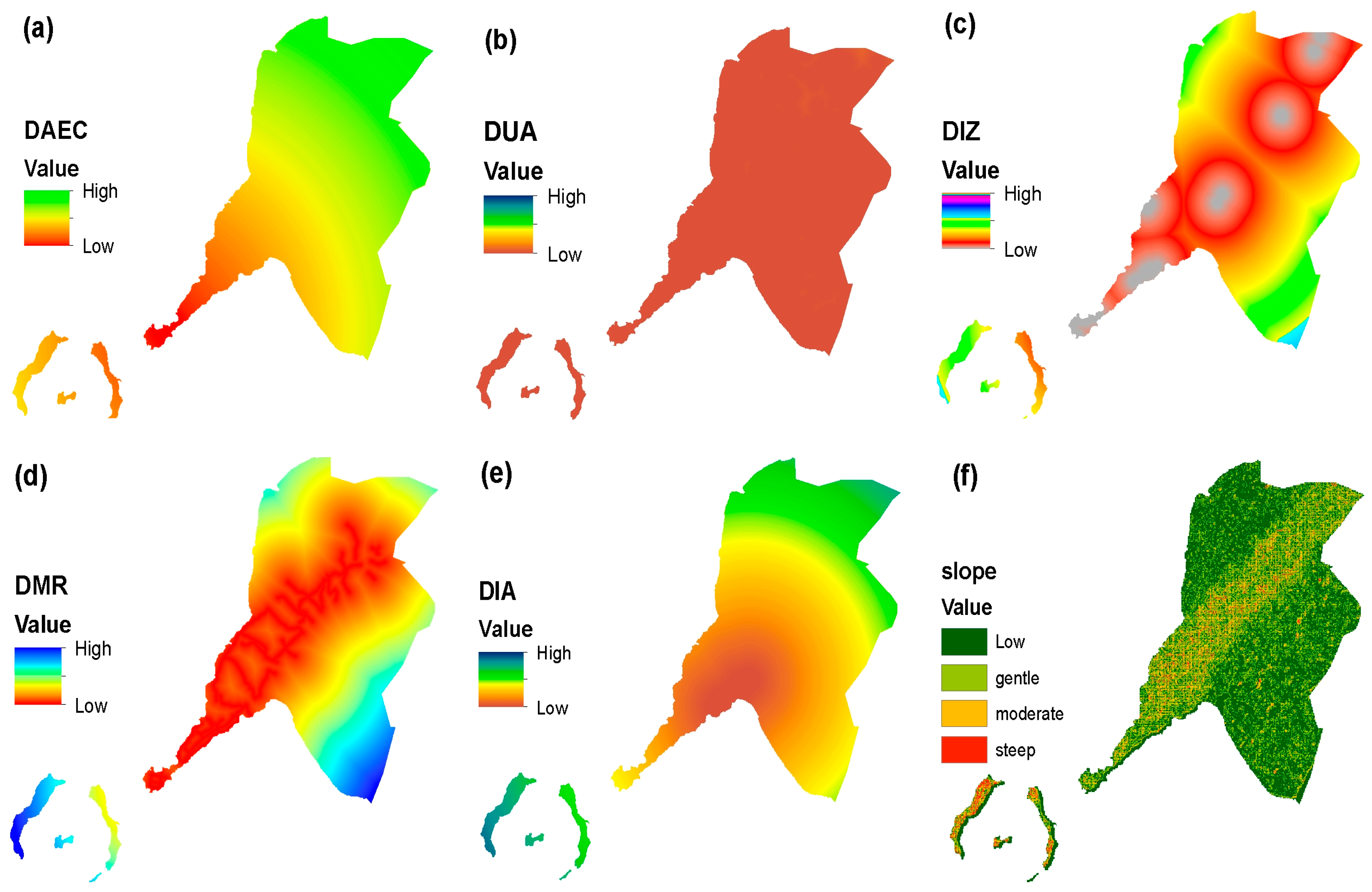
3.2. Explanatory Variables of Urban Growth
3.3. Multicollinearity Analysis of the Explanatory Variables
3.4. Statistical Test for Association between Dependent and Explanatory Variables: Cramer’s V Test
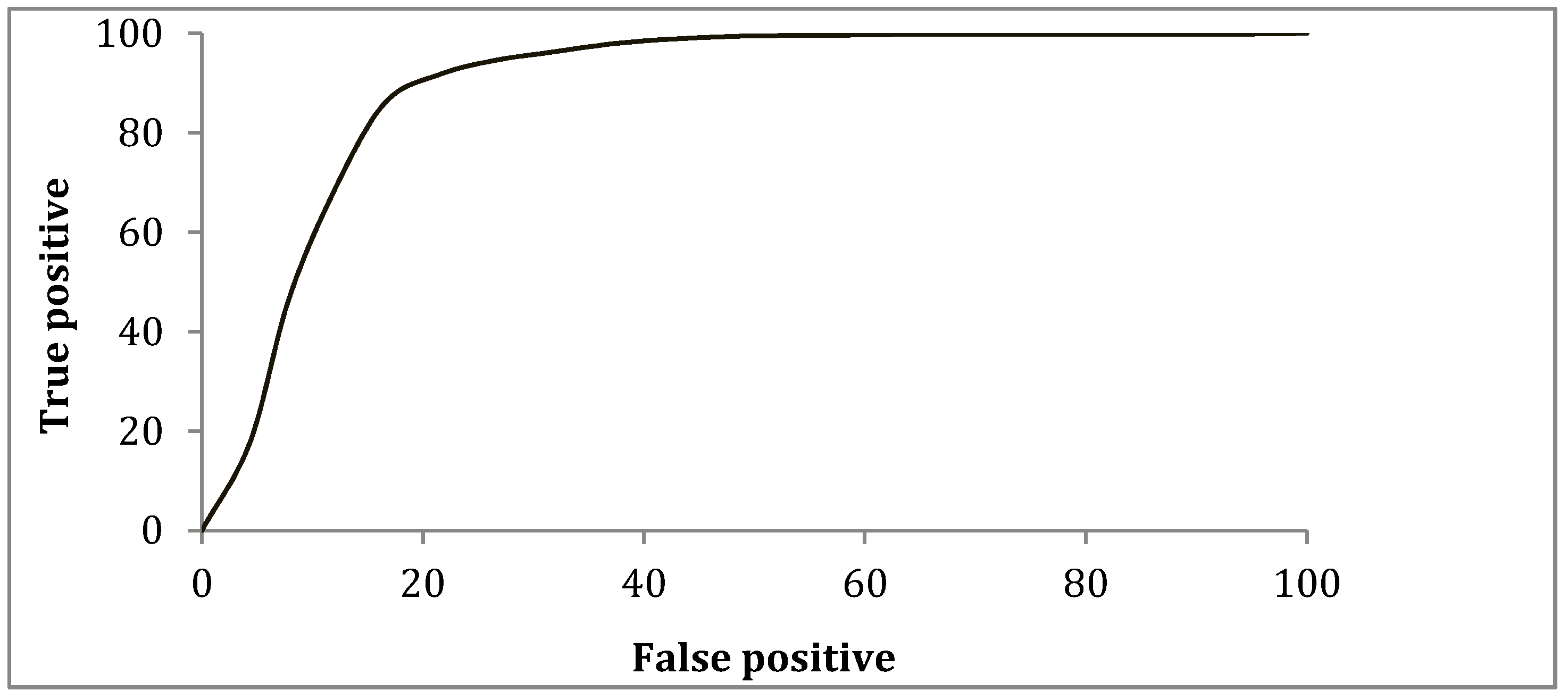
3.5. Model Validation Using the ROC Technique
4. Results
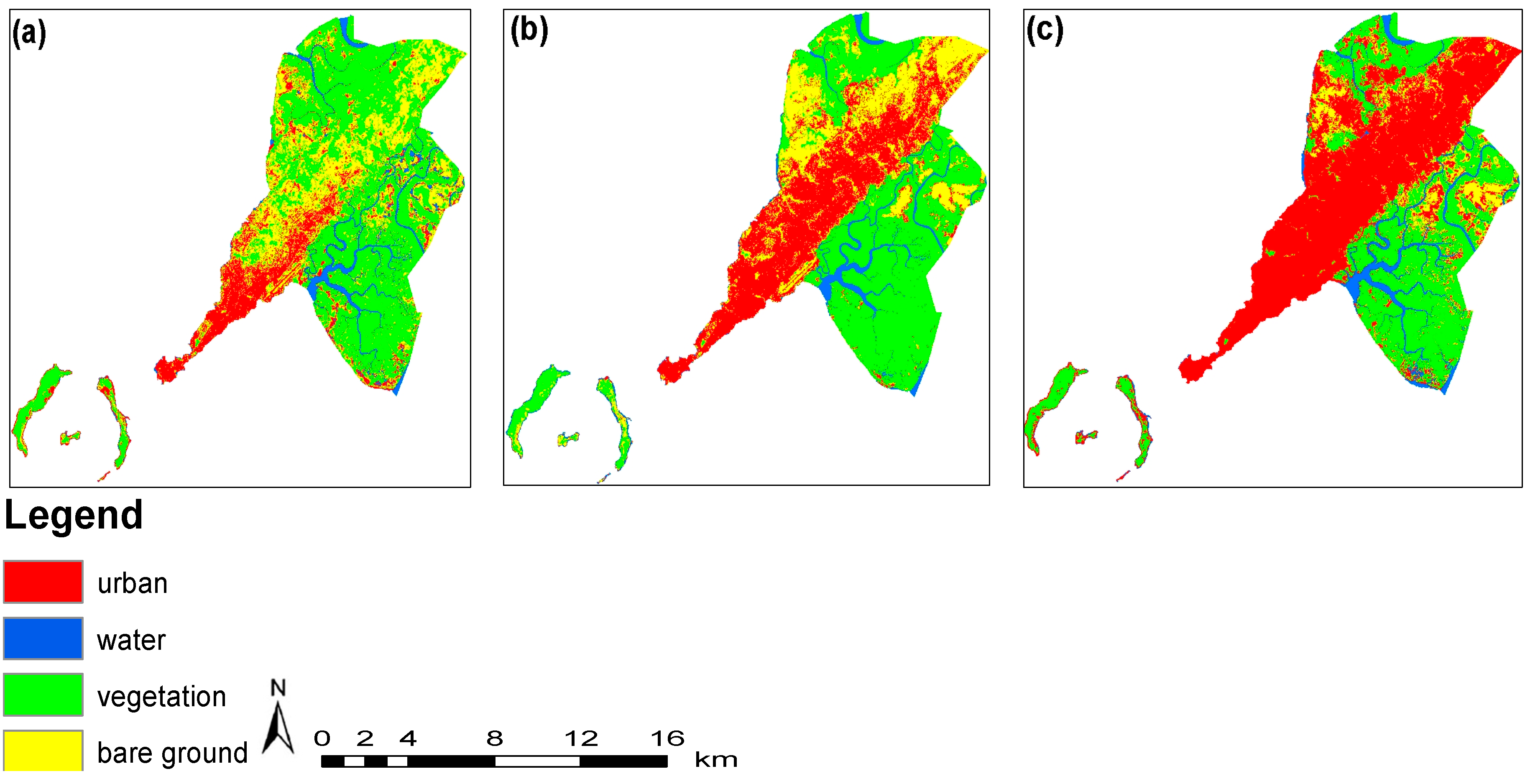
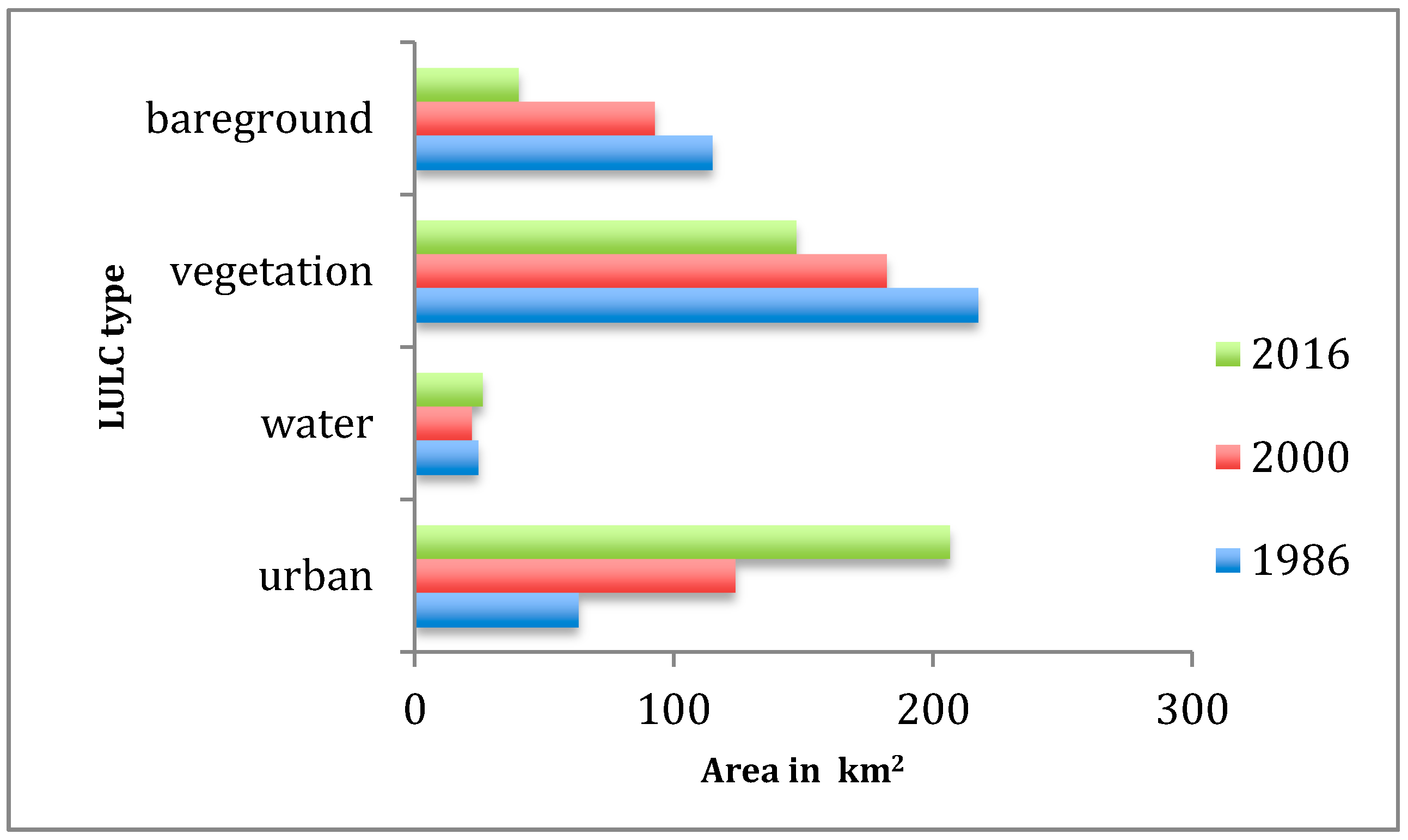
4.1. LULC Change Analysis
4.2. Logistic Regression Analysis
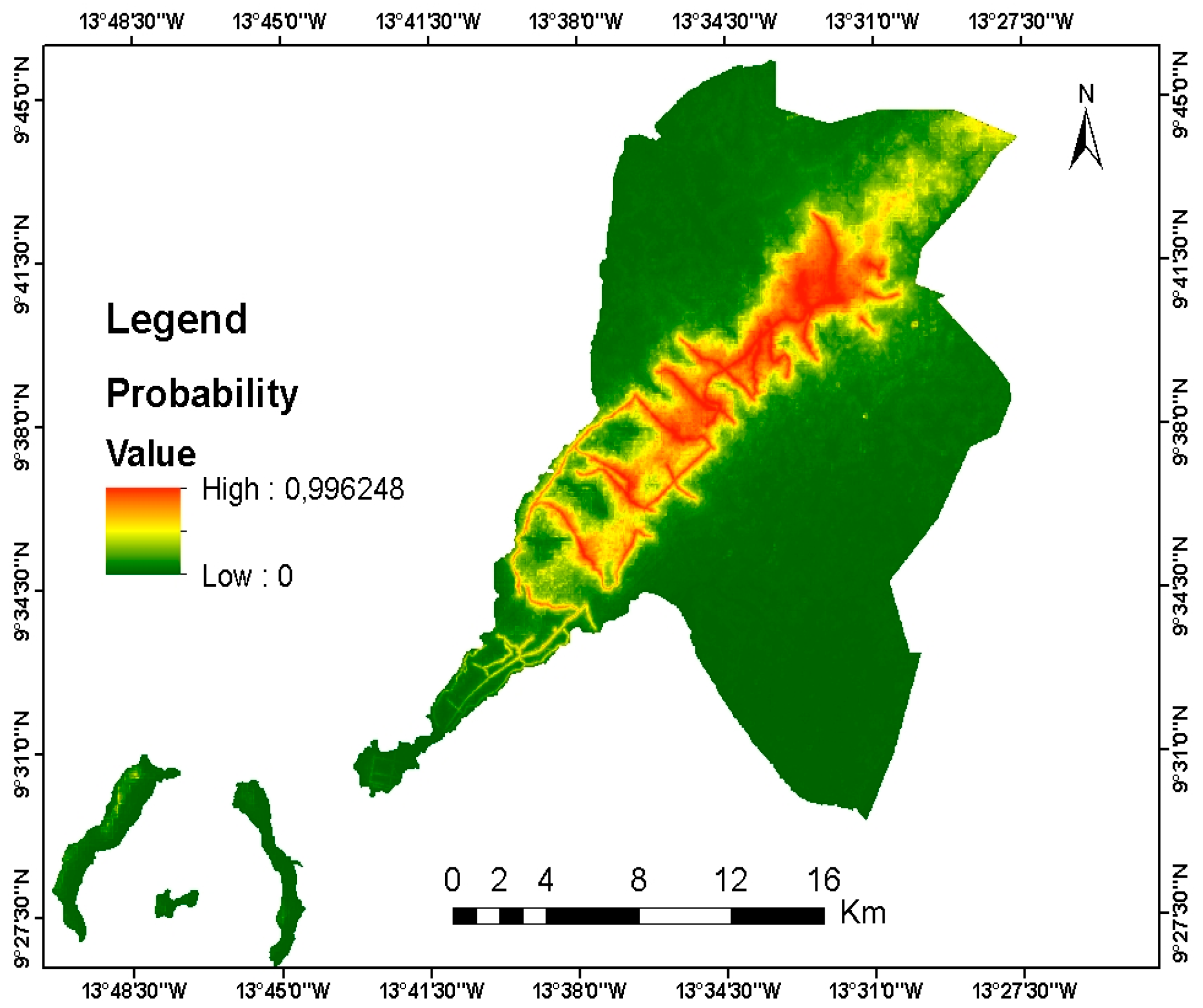
4.3. Urban Growth Probability Map for 2016
5. Discussion
5.1. LULC Change
5.2. LRM
5.3. Weakness of This Study
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- United Nations. World Urbanization Prospects 2014: Highlights; United Nations Environment Programme; United Nations: New York, NY, USA, 2014. [Google Scholar]
- Linard, C.; Tatem, A.J.; Gilbert, M. Modelling spatial patterns of urban growth in Africa. Appl. Geogr. 2013, 44, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Pickett, S.T.A.; Cadenasso, M.L.; Grove, J.M.; Boone, C.G.; Groffman, P.M.; Irwin, E.; Kaushal, S.S.; Marshall, V.; McGrath, B.P.; Nilon, C.H.; et al. Urban ecological systems: Scientific foundations and a decade of progress. J. Environ. Manag. 2011, 92, 331–362. [Google Scholar] [CrossRef] [PubMed]
- Aguayo, M.; Wiegand, T.; Azócar, G.; Wiegand, K.; Vega, C. Revealing the Driving Forces of Mid-Cities Urban Growth Patterns Using Spatial Modeling: A Case Study of Los Ángeles, Chile. Ecol. Soc. 2007, 12. Article 13. [Google Scholar] [CrossRef]
- Goerg, O. Conakry. Capital Cities in Africa Power Powerlessness. 2011. Available online: http://www.codesria.org/spip.php?article1603 (accessed on 7 March 2017).
- Jasse, A. Image of the Day. Available online: https://earthobservatory.nasa.gov (accessed on 7 April 2017).
- Sylla, L.; Xiong, D.; Zhang, H.Y.; Bangoura, S.T. A GIS technology and method to assess environmental problems from land use/cover changes: Conakry, Coyah and Dubreka region case study. Egypt. J. Remote Sens. Space Sci. 2012, 15, 31–38. [Google Scholar] [CrossRef]
- The World Bank. Guinea—Conakry Urban Development Project; The World Bank: Washington, DC, USA, 1984. [Google Scholar]
- Lagarias, A. Urban sprawl simulation linking macro-scale processes to micro-dynamics through cellular automata, an application in Thessaloniki, Greece. Appl. Geogr. 2012, 34, 146–160. [Google Scholar] [CrossRef]
- Yue, W.; Liu, Y.; Fan, P. Measuring urban sprawl and its drivers in large Chinese cities: The case of Hangzhou. Land Use Policy 2013, 31, 358–370. [Google Scholar] [CrossRef]
- Yusuf, A.Y.; Biswajeet, P.; Mohammed, O.I. Spatio-temporal Assessment of Urban Heat Island Effects in Kuala Lumpur Metropolitan City Using Landsat Images. J. Indian Soc. Remote Sens. 2014, 42, 829–837. [Google Scholar] [CrossRef]
- Triantakonstantis, D. Urban growth prediction: A review of computational models and human perceptions. J. Geogr. Inf. Syst. 2012, 4, 555–587. [Google Scholar] [CrossRef]
- Gao, J.; Li, S. Detecting spatially non-stationary and scale-dependent relationships between urban landscape fragmentation and related factors using Geographically Weighted Regression. Appl. Geogr. 2011, 31, 292–302. [Google Scholar] [CrossRef]
- Luo, J.; Wei, Y.H.D. Modeling spatial variations of urban growth patterns in Chinese cities: The case of Nanjing. Landsc. Urban Plan. 2009, 91, 51–64. [Google Scholar] [CrossRef]
- Jokar Arsanjani, J.; Helbich, M.; Kainz, W.; Darvishi Boloorani, A. Integration of logistic regression, Markov chain and cellular automata models to simulate urban expansion. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 265–275. [Google Scholar] [CrossRef]
- Pradhan, B. Flood susceptible mapping and risk area delineation using logistic regression, GIS and remote sensing. J. Spat. Hydrol. 2009, 9, 1–18. [Google Scholar]
- Aly, B.C.; Malick, S. Infrastructures Urbaines 1. 2012. Available online: http://www.disonslaveriteguinee.net/wp-content/uploads/2014/01/french_-_infrastructures_urbaines.pdf (accessed on 7 April 2017).
- Audits Urban, Oganisationnel et Financier de la Ville et des Communes de Conakry; Tunis, 2007. Available online: http://documents.worldbank.org/curated/en/274401468035962158/pdf/33541.pdf (accessed on 7 April 2017).
- Nong, Y.; Du, Q. Urban growth pattern modeling using logistic regression. Geo-Spat. Inf. Sci. 2011, 14, 62–67. [Google Scholar] [CrossRef]
- Sweet, S.A.; Grace-Martin, K.A. Data Analysis with SPSS: A First Course in Applied Statistics, 4th ed. Available online: https://www.pearsonhighered.com/program/Sweet-Data-Analysis-with-SPSS-A-First-Course-in-Applied-Statistics-4th-Edition/PGM334221.html (accessed on 7 January 2017).
- Kleinbaum, D.G.; Klein, M. Logistic Regression: A Self-Learning Text Statistics for Biology and Health, 3rd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Huang, B.; Zhang, L.; Wu, B. Spatiotemporal analysis of rural–urban land conversion. Int. J. Geogr. Inf. Sci. 2009, 23, 379–398. [Google Scholar] [CrossRef]
- Mahiny, A.S.; Turner, B.J. Modeling Past Vegetation Change through Remote Sensing and GIS: A Comparison of Neural Networks and Logistic Regression Methods. In Proceedings of the 7th International Conference on Geocomputation, University of Southampton, Southampton, UK, 8–10 September 2003. [Google Scholar]
- Lin, Y.P.; Chu, H.J.; Wu, C.F.; Verburg, P.H. Predictive Ability of Logistic Regression, Auto-Logistic Regression and Neural Network Models in Empirical Land-Use Change Modeling—A case study. Int. J. Geogr. Inf. Sci. 2011, 25, 65–87. [Google Scholar] [CrossRef]
- Eyoh, A.; Olayinka, N.; Nwilo, P.; Okwuashi, O.; Isong, M.; Udoudo, D. Modelling and Predicting Future Urban Expansion of Lagos, Nigeria from Remote Sensing Data Using Logistic Regression and GIS. Int. J. Appl. Sci. Technol. 2012, 2, 116–124. [Google Scholar]
- Parks, J.J.; Champagne, A.R.; Costi, T.A.; Shum, W.W.; Pasupathy, A.N.; Neuscamman, E.; Flores-Torres, S.; Cornaglia, P.S.; Aligia, A.A.; Balseiro, C.A.; et al. Mechanical control of spin states in spin-1 molecules and the underscreened Kondo effect. Science 2010, 328, 1370–1373. [Google Scholar] [CrossRef] [PubMed]
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance Inflation Factor: As a Condition for the Inclusion of Suppressor Variable(s) in Regression Analysis. Open J. Stat. 2015, 5, 754–767. [Google Scholar] [CrossRef]
- Midi, H.; Sarkar, S.K.; Rana, S. Collinearity diagnostics of binary logistic regression model. J. Interdiscip. Math. 2010, 13, 253–267. [Google Scholar] [CrossRef]
- Menard, S. Six approaches to calculating standardized logistic regression coefficients. Am. Stat. 2004, 58, 218–223. [Google Scholar] [CrossRef]
- Alsharif, A.A.A.; Pradhan, B. Urban Sprawl Analysis of Tripoli Metropolitan City (Libya) Using Remote Sensing Data and Multivariate Logistic Regression Model. J. Indian Soc. Remote Sens. 2014, 42, 149–163. [Google Scholar] [CrossRef]
- Eastman, J.R. IDRISI Selva Tutorial. Man. Version 17. 2012. Available online: http://uhulag.mendelu.cz/files/pagesdata/eng/gis/idrisi_selva_tutorial.pdf (accessed on 15 January 2017).
- Pontius., R.G., Jr.; Batchu, K. Using the Relative Operating Characteristic to Quantify Certainty in Prediction of Location of Land Cover Change in India. Trans. GIS 2003, 7, 467–484. [Google Scholar] [CrossRef]
- Pontius, R.G.; Schneider, L.C. Land-cover change model validation by an ROC method for the Ipswich watershed, Massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Hosmer, T.; le Cessie, S.; Lemeshow, S. A comparison of goodness-of-fit tests for the logistic regression model. Stat. Med. 1997, 16, 965–980. [Google Scholar] [CrossRef]
- Menard, S. Quantitative Applications in the Social Sciences, 2nd ed.; SAGE Publication, Inc.: Thousand Oaks, CA, USA, 1995; Volume 106. [Google Scholar]
- Clark, W.; Hosking, P. Statistical Methods for Geographers; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Hensher, D.A.; Johnson, L.W. Applied Discrete Choice Modelling. 1981. Available online: https://trid.trb.org/view.aspx?id=1206392 (accessed on 23 August 2016).
- World Bank. Poverty and Urban Mobility in Conakry. Available online: http://www.gtkp.com/assets/uploads/20091127-171237-6675-Conakry_en.pdf (accessed on 3 October 2016).
- UNU-IDHP Coastal Zones and Urbanization: Summary for Decision-Makers. Available online: http://www.futureearth.org/sites/default/files/files/IHDP%20SDM%20costalzones_and_urbanization-1.pdf (accessed on 3 November 2016).

| Data | Data Source |
|---|---|
| Landsat (TM 1986) | USGS Earth Explorer |
| Landsat (ETM +2000) | USGS Earth Explorer |
| Landsat (OLI 2016) | USGS Earth explorer |
| Administrative boundary map | Diva-GIS |
| Aster DEM | USGS Earth Explorer |
| Roads Network | Diva-GIS |
| Active Economic Center | Google Earth, digitized |
| International Airport | Google Earth digitized |
| Industrial | Open Street Map downloaded |
| Ground controll point data | Garmin GPS |
| Variable | Description | Nature |
|---|---|---|
| Dependent (Y) | 1 Urban growth, 0 no urban growth | Dummy |
| Explanatory variable | ||
| Socioeconomic factors | ||
| DAEC | Distance to active economic center | Continuous |
| DUA | Distance to urbanized areas | Continuous |
| DIZ | Distance to industrial zones | Continuous |
| DMR | Distance to major roads | Continuous |
| DIA | Distance to international airport | Continuous |
| Topography factors | ||
| Slope | Percentage rise | Continuous |
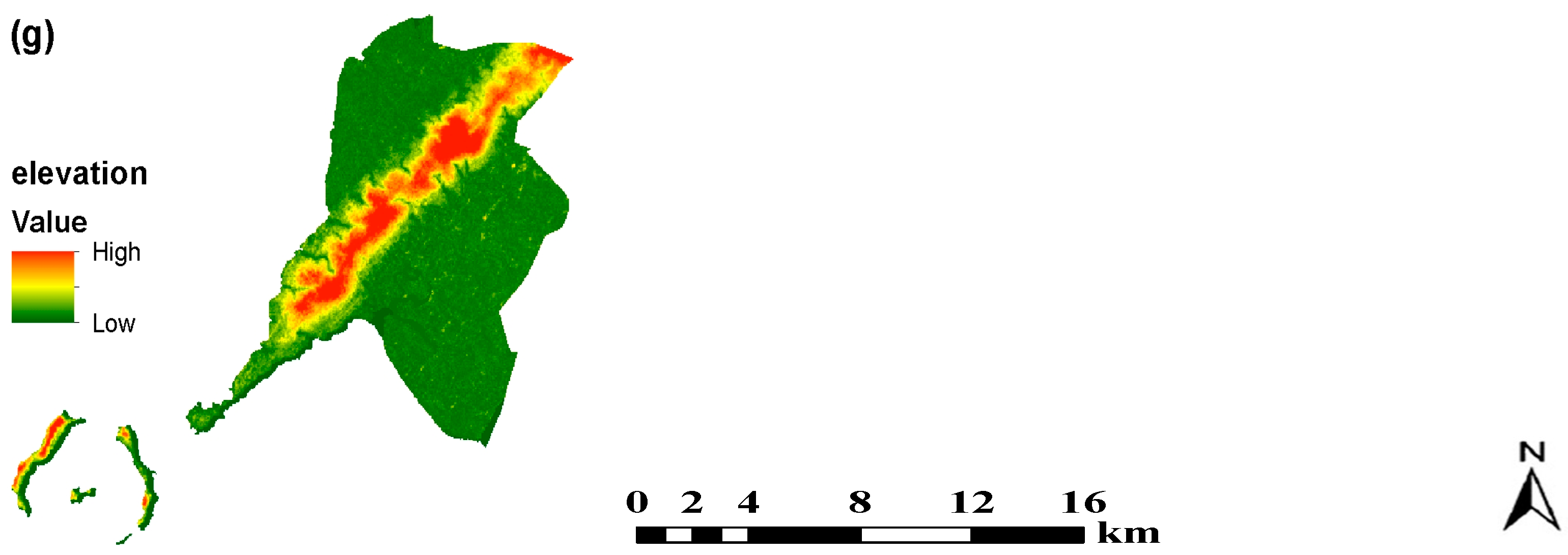
| Elevation | Elevation | Continuous |
| Variable | DAEC | DUA | DIZ | DMR | DIA | Slope | Elevation | VIF |
|---|---|---|---|---|---|---|---|---|
| DAEC | 1 | 0.029 | 0.44 | 0.31 | 0.30 | 0.09 | 0.13 | 1.99 |
| DUA | 1 | 0.58 | 0.53 | 0.50 | −0.48 | −0.46 | 1.62 | |
| DIZ | 1 | 0.75 | 0.51 | −0.32 | −0.41 | 7.84 | ||
| DMR | 1 | 0.58 | −0.43 | −0.54 | 5.86 | |||
| DIA | 1 | −0.24 | −0.26 | 3.20 | ||||
| Slope | 1 | 0.58 | 1.21 | |||||
| Elevation | 1 | 1.17 |
| Explanatory Variables | Cramer’s V | p Value |
|---|---|---|
| DAEC | 0.15 | 0.00 |
| DUA | 0.22 | 0.00 |
| DIZ | 0.32 | 0.00 |
| DMR | 0.39 | 0.00 |
| DIA | 0.22 | 0.00 |
| Slope | 0.32 | 0.00 |
| Elevation | 0.42 | 0.00 |
| Actual Map | Total | |||
|---|---|---|---|---|
| Urban Growth (1) | No-Urban Growth (0) | |||
| Predicted Image | Urban growth (1) | A | B | A+B |
| No-urban growth (0) | C | D | C+D | |
| Total | A + C = 95,941 | B + D = 1,613,435 | A + B + C + D = 1,709,376 | |
| Year | 1986 | 2000 | 2016 | |||
|---|---|---|---|---|---|---|
| LULC | Area (km2) | Area (%) | Area (km2) | Area (%) | Area (km2) | Area (%) |
| urban | 63.03 | 0.15 | 123.76 | 0.29 | 206.58 | 0.49 |
| water | 24.63 | 0.05 | 21.80 | 0.05 | 26.10 | 0.06 |
| vegetation | 217.48 | 0.51 | 181.86 | 0.43 | 147.32 | 0.35 |
| bare ground | 114.76 | 0.27 | 92.49 | 0.22 | 39.88 | 0.09 |
| Total | 419.90 | 1.00 | 419.90 | 1.00 | 419.90 | 1.00 |
| Variable | Coefficient | |
|---|---|---|
| Intercept | 7.03 | |
| DAEC | −0.01 | |
| DUA | 0.39 | |
| DIZ | 0.02 | |
| DMR | 0.67 | |
| DIA | −0.06 | |
| Slope | 0.27 | |
| Elevation | 1.76 | |
| Number of Total Observation | 1,709,376 |
|---|---|
| Number of 0 | 1,619,469 |
| Number of 1 | 89,907 |
| −2logLo | 67,290.6403 |
| −2log(likelihood) | 32,635.0373 |
| pseudo R2 | 0.5150 |
| Goodness of Fit | 202,668.3024 |
| Chi-Square(7) | 34,655.6030 |
| ROC | 0.96 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traore, A.; Watanabe, T. Modeling Determinants of Urban Growth in Conakry, Guinea: A Spatial Logistic Approach. Urban Sci. 2017, 1, 12. https://doi.org/10.3390/urbansci1020012
Traore A, Watanabe T. Modeling Determinants of Urban Growth in Conakry, Guinea: A Spatial Logistic Approach. Urban Science. 2017; 1(2):12. https://doi.org/10.3390/urbansci1020012
Chicago/Turabian StyleTraore, Arafan, and Teiji Watanabe. 2017. "Modeling Determinants of Urban Growth in Conakry, Guinea: A Spatial Logistic Approach" Urban Science 1, no. 2: 12. https://doi.org/10.3390/urbansci1020012
APA StyleTraore, A., & Watanabe, T. (2017). Modeling Determinants of Urban Growth in Conakry, Guinea: A Spatial Logistic Approach. Urban Science, 1(2), 12. https://doi.org/10.3390/urbansci1020012




