Module-Lattice-Based Key-Encapsulation Mechanism Performance Measurements

Abstract

Key exchange mechanisms are foundational to secure communication, yet traditional methods face challenges from quantum computing. The Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) is a post-quantum cryptographic key exchange protocol with unknown successful quantum vulnerabilities. This study evaluates the ML-KEM using experimental benchmarks. We implement the ML-KEM in Python for clarity and in C++ for performance, demonstrating the latter’s substantial performance improvements. The C++ implementation achieves microsecond-level execution times for key generation, encapsulation, and decapsulation. Python, while slower, provides a user-friendly introduction to the ML-KEM’s operation. Moreover, our Python benchmark confirmed that the ML-KEM consistently outperformed RSA in execution speed across all tested parameters. Beyond benchmarking, the ML-KEM is shown to handle the computational hardness of the Module Learning With Errors (MLWE) problem, ensuring resilience against quantum attacks, classical attacks, and Artificial Intelligence (AI)-based attacks, since the ML-KEM has no pattern that could be detected. To evaluate its practical feasibility on constrained devices, we also tested the C++ implementation on a Raspberry Pi 4B, representing IoT use cases. Additionally, we attempted to run integration and benchmark tests for the ML-KEM on microcontrollers such as the ESP32 DevKit, ESP32 Super Mini, ESP8266, and Raspberry Pi Pico, but these trials were unsuccessful due to memory constraints. The results showed that while the ML-KEM can operate effectively in such environments, only devices with sufficient resources and runtimes can support its computational demands. While resource-intensive, the ML-KEM offers scalable security across diverse domains such as IoT, cloud environments, and financial systems, making it a key solution for future cryptographic standards.

1. Introduction

Post-quantum cryptography, or quantum encryption, is an area that involves the construction of cryptography systems on regular hardware and software resources available in today’s internet connections and which are resistant to quantum attacks. Traditional cryptographic algorithms rely on mathematical one-way functions, particularly RSA (Rivest–Shamir–Adleman), ECC (elliptic curve cryptography), Diffie–Hellman, and others. Quantum computers, however, have efficient solutions for these problems, such as Shor’s algorithm and its variants. The Shor family of algorithms solves prime factorization and discrete logarithms, both in modular arithmetic and in elliptic curves, in polynomial or even linear time. This makes current encryption systems weak in the quantum computing era [1].

To strengthen crypto-systems, newly proposed post-quantum cryptographic mechanisms rely on other types of mathematical structures, which are intractable for both classical and quantum systems. Key approaches can be identified as lattice-based cryptography, multivariate cryptography, and hash-based cryptography [2,3]. Lattice-based cryptography has gained significant attention because the mathematical problems it relies on, such as Learning With Errors (LWE) and the Shortest Vector Problem (SVP), are considered difficult for both classical and quantum computers [4]. Currently, no efficient quantum algorithms are known to solve these problems.

Since 2016, the National Institute of Standards and Technology (NIST) has been working to define post-quantum cryptography standards for securing data in the quantum age. In 2022, NIST released the first draft of post-quantum cryptography standards to defend against quantum threats. These standards cover digital signatures and general encryption, with enough privacy protection even against quantum computers [5]. In August 2024, NIST approved and made public three post-quantum encryption standard algorithms: the Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM), Module-Lattice-Based Digital Signature Algorithm (ML-DSA), and Stateless Hash-Based Digital Signature Algorithm (SLH-DSA) [6]. In March 2025, NIST approved the final post-quantum algorithm for key exchange, called HQC, an alternative for the ML-KEM, which is expected to be standardized by 2027 [7]. These algorithms are expected to provide the fix for a consequential cyber hazard [8].

The post-quantum cryptographic standards apply to two areas: identity verification using digital signatures and secure key exchange using key-encapsulation mechanisms (KEM). Post-quantum cryptography introduces other, more reliable techniques, such as the Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) [9].

Our research uses the ML-KEM. Key-encapsulation mechanisms (KEMs) protect information by making keys travel securely through the network. Based on combined lattice-related cryptography, the protection applied to the ML-KEM relies on the difficult nature of lattice problems and thus resists quantum-based attacks [4,10]. Lattice-based cryptography has been acclaimed for optimality and security compared to its counterparts. Thus, multi-dimensional structures called lattices are used to construct cryptographic schemes resistant to quantum computers. The ML-KEM uses this concept to facilitate secure key encapsulation by solving lattice-based problems that are still hard for quantum computers [11,12].

Furthermore, this work connects theoretical advancements in cryptographic techniques with real-world applications of lattice-based encryption. One important contribution of this research lies in its insight into an enhanced understanding of lattice-based cryptography and the work of the ML-KEM toward key encapsulation, which is fit for the 21st-century threat. The current work adds to the conviction that people must embrace post-quantum cryptographic techniques as the world moves to the new quantum computing paradigm.

2. Review of the Literature and Previous Research Findings

2.1. Literature Review

Key exchange mechanisms represent some of the most central protocols in secure communication, allowing cryptographic key exchange over channels that are not necessarily safe. The emergence of quantum computing, however, has exposed traditional key exchange protocols to significant vulnerabilities, and thus, their quantum-resistant alternatives have been widely welcomed. These emerging solutions are key-encapsulation methods (KEMs), as these methods do not require key consensus between the communicating partners prior to the actual communication.

One of the most innovative approaches is integrating machine learning into the ML-KEM, which offers enhanced robustness and adaptability to cryptographic systems. This review discusses the state of research before the ML-KEM, the role of machine learning in cryptography, and how the ML-KEM compares to other quantum-resistant algorithms.

Before the development of the ML-KEM, traditional KEMs relied on well-established hard mathematical problems, such as integer factorization, applied in RSA, and discrete logarithms, applied by Diffie–Hellman. These methods worked well in classical settings but are vulnerable to Shor’s algorithm [13] when implemented on quantum computers.

In response to these vulnerabilities, quantum-resistant alternatives, including lattice-based cryptography, code-based schemes, and multivariate polynomial cryptography, have emerged. Among these, the lattice-based schemes such as the NTRU (Nth Degree Truncated Polynomial Ring Unit) and ML-KEM, which rely on the hardness of the Learning With Errors (LWE) problem [14] and its generalization and the Module Learning With Errors (MLWE) problem [14], have received considerable attention.

The MLWE problem is based on computational problems in module lattices [14], allowing strong security guarantees even against quantum attacks. Furthermore, the ML-KEM applies the Fujisaki–Okamoto transform [14] to its underlying public-key encryption scheme to turn it into a key-encapsulation mechanism that can boast strong security properties such as IND-CCA2 (Indistinguishability under Adaptive Chosen Ciphertext Attack) security [14]. Similarly, code-based schemes, such as McEliece [15], are considered robust in the post-quantum cryptography regime due to the hardness of decoding linear codes, for example, Goppa codes. Despite McEliece having large public keys, the small ciphertext size and strong security guarantees make it a very attractive option in post-quantum cryptography, even when the public keys are large [15,16].

2.2. Previous Research Findings

2.2.1. Study of ML-KEM

A key-encapsulation mechanism (KEM) is a critical component of modern cryptographic systems that enables secure key exchange over potentially insecure networks. In other words, a KEM is a scheme for securely exchanging symmetric keys over public channels between two interacting entities. It employs asymmetric (public-key) cryptography to encapsulate the symmetric key within a ciphertext, ensuring confidentiality during transmission. Once the symmetric key has been securely exchanged, it serves as the foundation for encrypting larger amounts of data efficiently, while maintaining the computational advantages of symmetric encryption [17].

Powerful quantum algorithms, such as Shor’s and Grover’s, pose significant threats to today’s encryption systems. Shor’s algorithm can solve integer factorization and discrete logarithm problems in polynomial time. These problems form the building blocks of many asymmetric cryptographic systems, such as RSA and Diffie–Hellman [1]. Grover’s algorithm provides a quadratic speedup for brute-force attacks, effectively reducing the security level of symmetric encryption by half. However, this can be mitigated by increasing key sizes; for instance, AES-256 provides an equivalent of 128-bit security against quantum attacks [8,18].

Unlike asymmetric encryption, which is fundamentally broken by Shor’s algorithm, symmetric encryption remains secure as long as sufficiently large keys are used [1,18]. This implies that symmetric encryption can resist quantum attacks through larger key sizes, whereas asymmetric key exchange mechanisms remain vulnerable to quantum threats [1,18]. To address this, post-quantum key-encapsulation mechanisms (KEMs), such as the ML-KEM, ultimately work with one encryption–decryption key per message, and thus provide a secure and quantum-resistant method for key exchange, ensuring the confidentiality of communications even in the presence of quantum adversaries [14,18].

The three main algorithms or steps employed by a key-encapsulation mechanism (KEM) include key generation (KeyGen), encapsulation (Encaps), and decapsulation (Decaps). The KeyGen algorithm generates a pair of keys consisting of a public encapsulation key and a private decapsulation key using a probabilistic method. Once generated, the public key is shared with the intended recipient. The Encaps algorithm, also probabilistic, uses the public key to produce a shared secret key alongside the ciphertext, which is transmitted securely. Finally, Decaps is a deterministic algorithm that utilizes the private key and the received ciphertext to extract the shared secret key. This procedure guarantees that only the intended recipient, who holds the private decapsulation key, can derive the shared secret key [14,17].

The Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) is a specialized form of KEMs that employs lattice-based cryptography. This branch of cryptography is designed to resist attacks from quantum computers. Unlike traditional KEMs that rely on RSA or elliptic curve cryptography, the ML-KEM utilizes advanced mathematical structures called module lattices. These structures are based on the Module Learning With Errors (MLWE) problem, a computationally challenging problem that is the foundation of ML-KEM’s security. The ML-KEM is a key component of the post-quantum cryptography initiative. By relying on the complexity of the MLWE problem, the ML-KEM provides a reliable and safe mechanism for exchanging cryptographic keys, even in the presence of powerful quantum adversaries and sophisticated threats [14,19].

A lattice is a structured grid of points in multi-dimensional space. The strength of lattice-based schemes lies in the complexity of problems defined on such structures, such as the Shortest Vector Problem (SVP) and Learning With Errors (LWE), which have no known polynomial solutions, even for advanced quantum algorithms [4].

Several lattice-based cryptographic schemes are built upon the Learning With Errors (LWE) problem. LWE involves solving linear equations that are intentionally “noisy” due to the addition of small random errors. Formally, the goal is to recover a secret vector (s) from a set of linear equations affected by the noise. This added noise makes these equations computationally difficult to solve using traditional methods, even with significant computational resources [3].

The Module Learning With Errors (MLWE) problem generalizes LWE by working with module lattices, which are more structured and efficient than general lattices. In MLWE, the secret and noise vectors belong to a module over a ring, usually a ring of integers modulo a prime. This structure enables cryptographic schemes to achieve greater efficiency and compactness while retaining the computational difficulty of the problem [14].

How the ML-KEM Works

The Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) enables the secure exchange of cryptographic keys. It is built upon the public-key encryption scheme K-PKE, which employs lattice-based computations and randomization to ensure unpredictable cryptographic outputs. While K-PKE serves as the core of the ML-KEM, it is not a standalone key exchange method. As mentioned above, the ML-KEM operates through three main processes: key generation, encapsulation, and decapsulation.

Additionally, the ML-KEM includes internal routines to optimize computational efficiency. However, access to these internal routines is restricted as part of its implementation requirements [14].

Key Generation Process in the ML-KEM

The key generation process in the ML-KEM involves the ML-KEM.KeyGen() function producing a pair of cryptographic keys: the encapsulation key (ek) and the decapsulation key (dk). This process begins by generating two random 32-byte seeds, denoted as (d) and (z). These seeds are crucial for ensuring the strength and uniqueness of the keys. They serve as deterministic inputs, allowing the same key pair to be regenerated when the same seeds are reused.

Once the seeds are generated, the ML-KEM.KeyGen() function invokes the internal routine ML-KEM.KeyGen_internal(), passing (d) and (z) as parameters. This internal function performs the core operations to derive the encapsulation and decapsulation keys [14].

Within ML-KEM.KeyGen_internal(), the function K-PKE.KeyGen() is called using the seed (d). This step generates the key pair for the underlying lattice-based encryption scheme, resulting in a public encryption key (ek_PKE) and a private decryption key (dk_PKE). The public key comprises a lattice matrix (Â) and a computed component (t = Â · s + e), where (s) is the secret vector and (e) is the noise vector. The private key includes the secret vector (s), which is critical for decryption. These components form the cryptographic foundation of the keys. The security of K-PKE is based on the computational difficulty of the Module Learning With Errors (MLWE) problem, providing strong resistance against quantum attacks [14].

In the ML-KEM, the encapsulation key (ek) is derived directly from the public encryption key (ek_PKE) generated by K-PKE.KeyGen(). In contrast, the decapsulation key (dk) is built upon the private decryption key (dk_PKE) by incorporating additional elements to enhance security. Specifically, the decapsulation key includes the private decryption key, the encapsulation key, the hash of the encapsulation key, and the random seed (z). Embedding the encapsulation key (ek) within the decapsulation key (dk) ensures its integrity and guarantees that the correct key pair is used during decryption. Furthermore, including (z) facilitates the implicit rejection of invalid ciphertexts during decapsulation, safeguarding the system against compromise [14].

Encapsulation Process in the ML-KEM

The ML-KEM.Encaps() function initiates the encapsulation process, which generates both a shared secret key (k) and a corresponding ciphertext (c). This function is responsible for securely transmitting the symmetric key to the recipient while maintaining confidentiality.

The process begins by generating a randomized 32-byte seed (m), which is then passed along with the encapsulation key (ek) to the internal routine ML-KEM.Encaps_internal() [14].

Within ML-KEM.Encaps_internal(), the shared secret key (k) and the randomness (r) are derived by hashing the concatenation of the seed (m) and the hash of the encapsulation key (ek). This step ensures that both the shared secret key and the randomness are cryptographically secure [14].

The K-PKE.Encrypt() algorithm is then used to encrypt the seed (m) with the encapsulation key (ek) and the derived randomness (r). This encryption process produces the ciphertext (c), which securely encapsulates the seed. The use of lattice-based computations in K-PKE.Encrypt() ensures strong resistance against potential adversaries [14].

Decapsulation Process in the ML-KEM

The decapsulation process is executed by the ML-KEM.Decaps() function, which allows the recipient to securely recover the shared secret key (k) using their private decapsulation key (dk) and the received ciphertext (c). This deterministic process ensures that the shared key is reliably and securely retrieved [14].

The ML-KEM.Decaps() function invokes the internal routine ML-KEM.Decaps_internal(), which decrypts the ciphertext (c) using the private decapsulation key (dk) through the K-PKE.Decrypt() algorithm. This decryption step recovers the original seed (m) that was encapsulated during the encryption process [14].

Once the seed (m) is retrieved, it is combined with the hash of the encapsulation key to recompute the shared secret key (k) and the derived randomness (r′) using a secure hashing function. To verify the integrity of the ciphertext, the seed (m) and the derived randomness (r′) are re-encrypted with the encapsulation key (ek) to produce a new ciphertext (c′). If this re-encrypted ciphertext (c′) matches the received ciphertext (c), the shared secret key (k) is considered valid and returned [14].

If the ciphertext validation fails, the system activates an implicit rejection mechanism. In such cases, the shared secret key is replaced with a hash of a predefined random value and the ciphertext. This ensures that no valid key is derived from tampered or invalid ciphertexts. As a result, only a legitimate decapsulation key can derive the shared secret key, offering strong resistance against both classical and quantum attacks [14].

2.2.2. Key Findings

In terms of performance, the ML-KEM exhibits strong encapsulation and decapsulation capabilities, along with effective procedures for cryptographic key exchange. These secure operations are made possible by their dependence on module-lattice structures. However, this design results in higher computational overhead compared to traditional KEMs. Enhancing the encapsulation and decapsulation processes for improved execution speed is important for ensuring practical usability in secure communication [18].

By leveraging the complexity of the Module Learning With Errors (MLWE) problem, the ML-KEM offers strong resistance against both classical and quantum attacks. This includes protection against Shor’s and Grover’s algorithms [4,5,6]. To further strengthen the unpredictability and integrity of the keys, the ML-KEM incorporates randomness injection alongside deterministic elements. This combination ensures that generated keys remain secure while preventing predictability vulnerabilities [20].

Although the ML-KEM offers superior security and quantum resistance, it also comes with higher resource consumption, requiring more memory and processing power compared to traditional KEMs [18]. Despite this, the trade-offs are considered acceptable due to the advanced security features it offers. The ML-KEM effectively protects communications from advanced threats, such as quantum attackers [8].

Its robust design and quantum-resistant architecture make the ML-KEM a vital component of post-quantum cryptographic solutions. It is well-suited to meet the requirements of secure data exchange in future computing environments.

2.2.3. The Security and Performance Evaluation

The security and performance evaluation methods discussed here are based on existing research and studies in the field. These include the following:

• Threat modeling: Threat modeling in ML-KEM design anticipates several attack scenarios and considers classical and quantum-type attacks. Threat modeling aimed to verify resistance against computational attacks, ciphertext tampering, and interception by the quantum adversary. In this relation, the possible attack vectors would encompass adversarial inputs, brute-force attacks, and vulnerabilities in models to ensure thorough research of the security aspects.
• Verification of scalability and adjustability: The ML-KEM has undergone benchmarking in real-world utilization with diverse hardware configurations and communication contexts. The problem at the heart of the ML-KEM, called MLWE, has been subjected to extensive tests concerning cryptographic hardness. Simulated attack attempts were made to ensure that the algorithm maintains the expected security levels when deployed in the real world [5].
• Impact of Evaluation: Security assessment and threat modeling ensured the applicability of the ML-KEM to post-quantum cryptography requirements by verifying it against all known quantum algorithms. This process also identified critical aspects, such as potential model poisoning and improper noise handling, which need to be implemented with care to avoid vulnerabilities.
• Efficiency validation: The benchmarking showed that the ML-KEM has a certain computational overhead compared to conventional KEMs; however, this effectiveness is enough for practical applications even in high-security settings [21,22]. Testing in different scenarios also proved the ML-KEM’s versatility for various application cases, such as secure communications and data sharing across public networks [8,20].

2.2.4. Threat Model

• Security Assumptions

In adversarial scenarios, the use of deterministic randomness and sufficient entropy helps protect the algorithm from adaptive adversaries who adjust their strategies based on partial decryption results. The ML-KEM employs ciphertext rejection techniques, which reduce the attacker’s ability to manipulate distorted inputs or extract sensitive information [2,4].

In classical contexts, the ML-KEM’s threat model also considers traditional computational attacks, including known-plaintext, chosen-ciphertext, and brute-force attacks. Its noise-based security mechanisms ensure resilience against such threats, enhancing the overall encryption reliability in both classical and quantum environments [6].

• Secure Channel Assumptions

The integrity and validity of private keys and encapsulation keys are vital for maintaining security. Classical attacks, such as ciphertext tampering intended to induce incorrect decapsulation, are part of the threat landscape. The ML-KEM provides support for ensuring the integrity of ciphertexts using cryptographic hashes and rejecting tampered inputs [14].

Moreover, the intrinsic complexity of the MLWE problem makes attacks such as brute force and linear analysis computationally infeasible, further strengthening the scheme’s security model [3,10].

2.2.5. Vulnerabilities of the ML-KEM

Although the Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) is resistant to quantum attacks, it is not entirely free from some vulnerabilities that arise from its dependency on the module-lattice cryptographic structure and its implementation. In particular, potential issues can arise from parameter misconfiguration and the improper handling of intermediate values [14].

Parameter Selection

Parameter selection is an essential part of post-quantum cryptography since it directly affects the effectiveness and security of key-encapsulation methods (KEMs). These specific parameters determine the mathematical structure, processing needs, and adversarial attack resistance of the ML-KEM. ML-KEM-512, ML-KEM-768, and ML-KEM-1024 are the three parameter sets that make up the ML-KEM. Each of these encompasses five additional parameters: k, η₁, η₂, d_u, and d_v, along with two constants: n = 256 and q = 3329 [14]. Understanding these specific parameters is necessary to evaluate the scheme’s resistance to both classical and quantum assaults [14].

• The parameter k determines the dimensions of the matrix  used in K-PKE algorithm key generation (K-PKE.KeyGen) and encryption (K-PKE.Encrypt) algorithms. It also defines the dimensions of critical vectors s and e in key generation and y and e1 in encryption [14]. System efficiency is impacted by the additional computational overhead, even though a higher k number improves security.
• The error distribution parameters, η₁ and η₂, are essential for maintaining the strength of the cryptographic scheme. η₁ is crucial for defining the distribution used to generate the K-PKE.KeyGen vectors s and e, as well as the K-PKE.Encrypt vector y. As for η₂, it is necessary for defining the distribution used in K-PKE.Encrypt to generate the vectors e₁ and e₂ [14].
• Moreover, the compression parameters du and dv are essential to maximize storage and transmission efficiency. The Compress, Decompress, ByteEncode, and ByteDecode operations in encryption (K-PKE.Encrypt) and decryption (K-PKE.Decrypt) are controlled by these parameters [14]. All of these methods were described above.

Table 1. Key and ciphertext sizes in the ML-KEM (bytes) [14].

ML-KEM Parameter Set	Encapsulation Key Size	Decapsulation Key Size	Ciphertext Size
ML-KEM-512	800 bytes	1632 bytes	768 bytes
ML-KEM-768	1184 bytes	2400 bytes	1088 bytes
ML-KEM-1024	1568 bytes	3168 bytes	1568 bytes

illustrates how the ML-KEM differs from traditional cryptography, where security parameters are often linked to key length.

The parameter selection can become a vulnerability if not carefully aligned with the security and performance requirements. The parameter set, which includes ML-KEM-512, ML-KEM-768, and ML-KEM-1024, offers a trade-off of computing efficiency and security. The ML-KEM-512, for instance, increases the computational efficiency but decreases the security, which then leaves a system vulnerable, especially in high-security applications due to advanced adversaries. On the other hand, ML-KEM-1024 might increase computational overhead, which would hamper performance for those situations where such a high level of security is not called for. Because it offers a significant security margin at a manageable performance cost, NIST advises using ML-KEM-768 as the default parameter set [14].

NIST has assigned a security category to each ML-KEM parameter set, as shown in

Table 2. ML-KEM parameter sets and security category [14].

ML-KEM Parameter Set	Security Category	Equivalent Symmetric Key Strength
ML-KEM-512	Category 1	Comparable to AES-128
ML-KEM-768	Category 3	Comparable to AES-192
ML-KEM-1024	Category 5	Comparable to AES-256

. These ratings indicate a similar security level against classical and quantum attackers, ensuring an acceptable trade-off between protection and efficiency.

The Destruction of Intermediate Values

The destruction of intermediate values in the ML-KEM is essential for maintaining the confidentiality and integrity of cryptographic procedures. These values are produced during the ML-KEM.KeyGen, ML-KEM.Encaps, and ML-KEM.Decaps processes and include temporary internal data such as random integers, partial computations, and the sensitive components of private or shared secret keys.

NIST does not explicitly list the intermediate values for the ML-KEM to prevent potential security vulnerabilities. This omission is intentional to avoid disclosing computational data that attackers could exploit to reconstruct secret keys, thereby compromising the entire cryptographic system [14].

Each cryptographic algorithm has its own intermediate values, which are specific to its mathematical structure and operation. For example, RSA and ECC have different internal computations and transient data during key generation, encapsulation, and decapsulation. The secure handling of these values is addressed in NIST’s broader cryptography standards and guidelines [23].

However, not all intermediate values require deletion. NIST identifies two exceptions:

• The seed (d, z) used in ML-KEM.KeyGen: Since the decapsulation key can be reconstructed using this seed, it may be stored for later use.
• Matrix  in K-PKE.KeyGen and K-PKE.Encrypt: To avoid recomputation, the matrix can be retained for future operations.

Thus, although intermediate values are crucial for computing operations, the improper management of transient data introduces vulnerabilities that could grant attackers access to critical keys. This highlights the importance of securely and promptly destroying intermediate values during cryptographic operations.

The ML-KEM’s security depends on the proper selection of parameters and the secure deletion of intermediate values. Negligence of either of these two factors may degrade the performance or leak sensitive cryptographic information.

2.2.6. Security Comparison Between the ML-KEM and RSA

Ensuring the security of transmitted messages is a primary concern in cryptography, as various attacks, such as interception and content modification, can compromise data integrity. To mitigate these risks, cryptographic algorithms like the ML-KEM and RSA are widely used to establish secure key exchanges. The security of public-key systems generally relies on the difficulty of solving certain mathematical problems. For RSA, security depends on the complexity of factoring large integers. While this remains secure against classical attacks, the introduction of quantum algorithms like Shor’s algorithm has significantly weakened RSA by making integer factorization efficient [1].

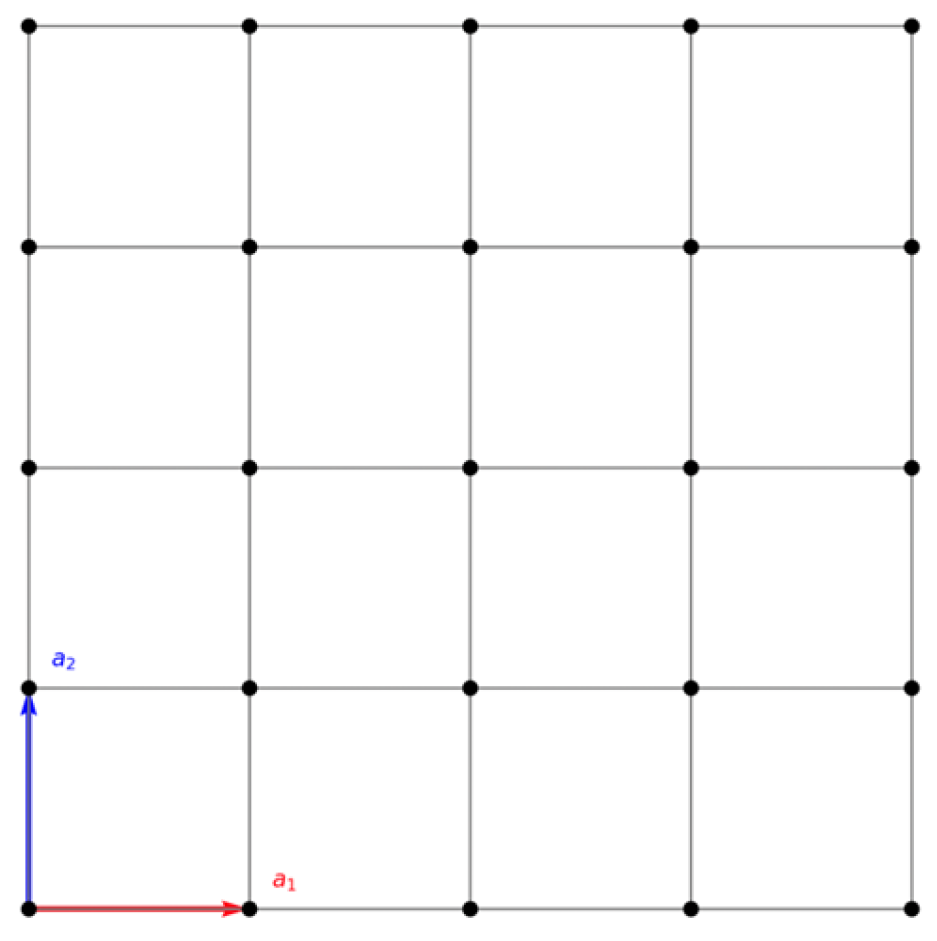
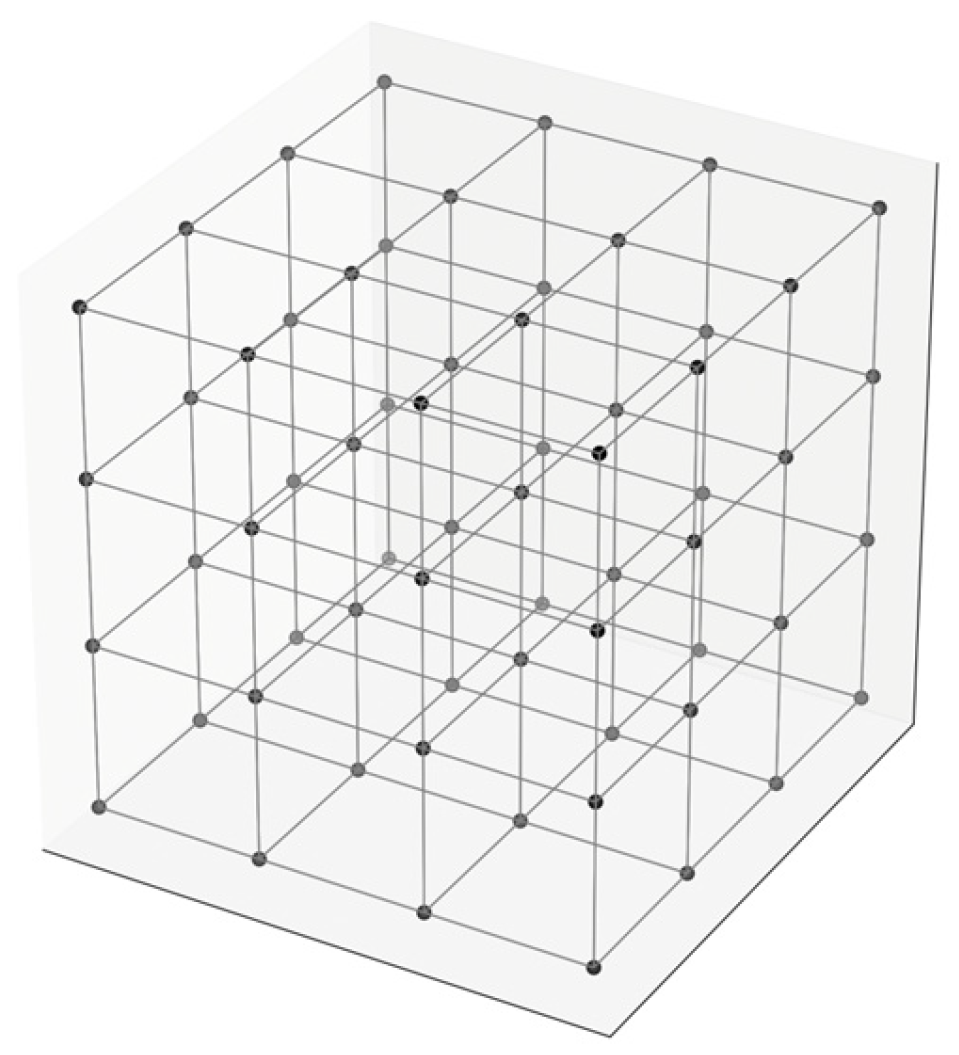
In contrast, the ML-KEM, which is based on lattice cryptography, presents greater resistance to cryptanalysis and poses a greater computational challenge than the integer factorization problem that RSA is based on [14]. The ML-KEM derives its security from hard problems in lattice theory, such as the Shortest Vector Problem and the Closest Vector Problem [2]. These problems refer to high-dimensional lattices, often possessing hundreds of dimensions; these structures are significantly more complex than those in two- or three-dimensional space (Figure 1 and Figure 2). The big dimensionality boosts this problem’s difficulty, making it computationally impossible to solve, even for quantum computers.

In addition to its solid security base, Module Learning With Errors (MLWE) is also lattice-based and forms one of the core foundations of the ML-KEM. The MLWE enhances its complexity using Learning with Errors (LWE), another key element of lattice cryptography. LWE is widely used in many cryptographic schemes for generating encryption keys that enhance security by eliminating the threat of side-channel attacks, ensuring that an attacker cannot reconstruct the decryption keys [3]. Meanwhile, RSA is highly vulnerable to side-channel attacks and other cryptanalytic techniques, such as the Number Field Sieve (NFS), which is currently the most effective classical algorithm for factoring large integers. Since an attacker can shorten the time required to recover private keys by utilizing the NFS, this renders RSA vulnerable even in the classical era [24].

Another significant difference between the ML-KEM and RSA lies in the use of the Fujisaki–Okamoto (FO) transformation in the ML-KEM, which enhances its security properties. This transformation converts a weakly secure lattice-based encryption scheme into a more robust key-encapsulation mechanism (KEM) [14]. It allows the ML-KEM to achieve IND-CCA2, ensuring that even if an attacker can manipulate ciphertexts and observe their decryptions, no meaningful information about the underlying plaintext or shared secret can be extracted [14,25]. This directly mitigates chosen-ciphertext attacks (CCAs), where adversaries attempt to tamper with ciphertexts in order to recover sensitive key material [25].

Basic RSA, on the other hand, lacks any built-in mechanism to withstand CCAs, making it easier for attackers to extract private keys. Once an attacker obtains the private key, they can decrypt the ciphertext, compromising one of the most critical aspects of security: confidentiality [12]. However, not all RSA variants are vulnerable to such attacks. RSA with padding schemes, such as Optimal Asymmetric Encryption Padding (RSA-OAEP), and RSA using the Key-Encapsulation Mechanism (RSA-KEM) incorporate specific defenses against CCAs [26,27]. Still, despite these safeguards, both remain vulnerable to quantum attacks, as Shor’s algorithm can efficiently break their underlying number-theoretic assumptions.

Due to these essential security distinctions, the ML-KEM has been officially acknowledged by NIST as a component of its post-quantum cryptography standards [14]. Although RSA remains widely used in many applications today, its mathematical foundation will not withstand future quantum threats. In comparison, the ML-KEM offers superior protection, making it a critical component in next-generation cryptographic systems.

2.2.7. A Performance Comparison Between the ML-KEM and RSA

Cryptographic performance is influenced by computational efficiency, key size, and system overhead. The RSA and ML-KEM were based on different mathematical algorithms, so performance was executed differently for each algorithm. Despite offering a strong defense against quantum threats, the ML-KEM’s processing requirements raise system overhead due to complex polynomial multiplications and high-dimensional operations, unlike RSA, which relies on modular exponentiation and multiplication. These elements have an impact on performance, particularly in contexts with limited resources, as they demand a lot more processing power.

Moreover, the enhanced security offered by the ML-KEM is at the cost of larger ciphertext and key sizes, as shown in Table 1. These sizes are significantly larger compared to RSA-2048 and RSA-3072, which, respectively, only need 256 and 384 bytes [28]. The creation of large keys and ciphertexts increases the bandwidth and storage requirements, posing challenges in bandwidth-constrained environments. This illustrates the trade-off between security and efficiency, as even the lowest parameter set, ML-KEM-512, is still significantly larger than RSA keys.

Table 3. Performance comparison between the ML-KEM and RSA [14,28].

Feature	ML-KEM	RSA
Mathematical Foundation	Lattice-based (MLWE)	Integer factorization
Quantum Resistance	Yes	No
Typical Key Sizes	800–3168 bytes	256–384 bytes
Ciphertext Size	768–1568 bytes	≈256–384 bytes
Computational Complexity	High (polynomial/lattice operations)	Moderate (modular arithmetic)
Memory and Processing Requirements	High	Low to moderate
Implementation Maturity	Emerging	Mature

below summarizes key performance characteristics between the ML-KEM and RSA.

To summarize, resorting to the ML-KEM is a trade-off between security and performance: to obtain robust security against the threats from quantum computers, compromises are needed concerning computational efficiency and resource demands, whereas RSA, in the context of classical cryptography, has the best performance due to the lightweight nature of the underlying operations and smaller key sizes. In contrast, the ML-KEM provides resistance to quantum attacks only at the expense of heavier computations and greater key sizes. As a result, as cryptographic methods continue to evolve, the balance between security and efficiency will drive the adoption of both the ML-KEM and RSA, demonstrating the need for adaptable encryption techniques in a progressively complex digital era.

3. Gap Analysis in Existing Research

While the ML-KEM has been formally standardized and endorsed as a preferred and viable option in the post-quantum key-encapsulation realm, there is often a reliance on theoretical construction and proof of security while disregarding the details of deployment and practically implementing the ML-KEM. It follows that, looking at existing work, the broad scope, depth, and applicability for the practice of such evaluation can be severely lacking. The limitations of the existing research identified in the previous section are depicted in

Table 4. Identified gaps in existing ML-KEM research across security, implementation, and deployment.

Aspect	What the Literature Covers	Gap Identified
Quantum Security Evaluation	Theoretical resilience to Shor’s and Grover’s algorithms is established [1,4,5,14].	Lack of empirical testing or simulation under realistic quantum adversarial models
Parameter Set Selection	Parameter trade-offs for ML-KEM-512, -768, and -1024 are outlined in standards [14].	Limited studies on real-world misconfigurations or adaptive attacks exploiting weak parameter choices
Performance in Constrained Devices	General benchmarking on standard computing systems [18,21].	Absence of performance profiling on mobile, IoT, or low-power embedded devices
Intermediate Value Handling	NIST notes risks of improper management and exemptions [14,23].	No in-depth implementation guidance on secure deletion, memory management, or attack surface reduction
Side-Channel Resilience	Cryptographic structure discussed; FO transform used for CCA security [14,25].	Very few studies evaluate practical side-channel threats like timing, power, or fault injection
Protocol Integration	ML-KEM evaluated as a standalone mechanism.	Lack of research on integration with TLS, VPNs, or hybrid classical–post-quantum systems [29,30]
Security Benchmarking Frameworks	Threat modeling includes ciphertext tampering, brute-force, and chosen-ciphertext attacks [2,4,6].	Lacks standardized benchmarking across different deployment scenarios and attacker models

.

The gap analysis presented in Table 4 shows that thus far the research focus has amounted to difficultly engaging in the critical evaluation of the ML-KEM for the first two related issues, purposefully related to the theoretical construction or post-quantum soundness of the design, while seemingly willfully sidelining all consideration of deployment, integration in a system, and a full analysis of possible limitations at the physical layer. Most publications emphasizing ML-KEM’s performance tend not to mention resource-constrained environments that are feasible to deploy in practice, and there is often a neglect of spaces regarding attack surfaces such as physical-memory leakage, fault recovery, and side-channel attacks. At present, there is little coverage or understanding of working with the safe implementation of the coordinates of the parameter set, as well as covering intermediate values in the course of securely designing real-world cryptographic systems, to make the neutrality of any of these discussions feasible. There is an importance for future research to align and ensure that work is complementing the theory with full evaluations at deployment to capture space in the studies of the work, covering operational resilience and working with integration in modern network protocols.

4. Applications

The ML-KEM has significant potential across diverse domains, particularly in securing environments vulnerable to emerging quantum threats. It ensures secure communication between constrained devices like smart sensors, industrial machines, and home appliances in IoT ecosystems, where computational efficiency and low energy consumption are critical. However, its implementation in IoT requires optimization due to its higher computational demands and memory usage compared to traditional cryptographic methods. For instance, smart home systems could rely on the ML-KEM to establish secure encryption keys for device communication. Similarly, in cloud security, the ML-KEM protects data in transit and at rest by securing the key exchange process, enabling robust encryption for sensitive information. Its use in quantum-resistant environments is critical for long-term data protection in finance, government, and blockchain technology, safeguarding against future quantum-based cryptographic attacks [29,31].

Additionally, the ML-KEM enhances security in mobile systems, ensuring that the sensitive information stored and transmitted remains confidential even in quantum-capable adversarial scenarios. Organizations across various sectors, such as banking, telecommunications, and technology firms like Microsoft, are actively exploring quantum-resistant cryptography to address security challenges in enterprise environments [31,32]. By enhancing key exchange mechanisms with quantum-resistant shared secret generation, the ML-KEM secures current systems and lays the foundation for future-proof cryptographic frameworks. Its adaptability across various applications highlights its versatility, and its role in facilitating the transition to post-quantum cryptography enables industries to secure their digital infrastructures while minimizing operational disruption [29,31].

5. Experiment

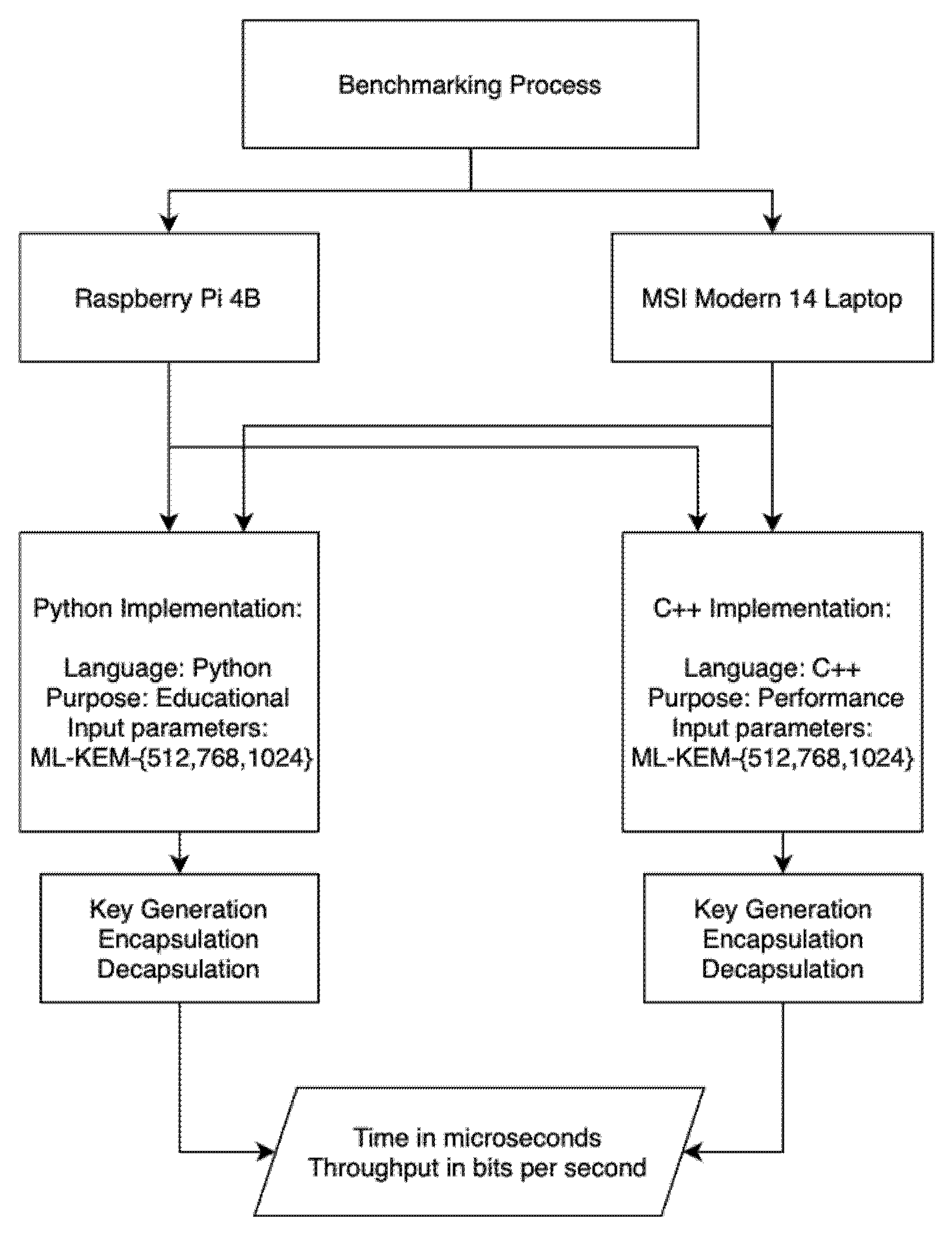
5.1. Python vs. C++ Comparsion

We analyzed two implementations using the method shown in Figure 3:

• Python Implementation: Educational, written with clarity in mind, with very little thought to performance [32,33].
• C++ Implementation: High-performance, constexpr-style system with a focus on minimizing runtime [33,34].

Figure 3. Python vs. C++ comparison experiment overview diagram.

Figure 3. Python vs. C++ comparison experiment overview diagram.

5.1.1. Experiment Setup

• Hardware:

  ○

  Raspberry Pi 4B: ARM Cortex-A72 (1.5 GHz), 8 GB RAM, representing IoT-grade hardware.

  ○

  MSI Modern 14 Laptop: Intel Core i7-12th Gen (1.70 GHz), 16 GB RAM, representing a modern desktop system.

• Parameters: ML-KEM-512, ML-KEM-768, and ML-KEM-1024 (NIST security levels 1, 3, and 5).
• Metrics:

  ○

  Execution Time: Mean real-time (µs) for key generation (KeyGen), encapsula-tion (Encap), and decapsulation (Decap).

  ○

  Throughput: Operations per second (items/s).

• Experimental Procedure: Each cryptographic operation was executed 10 times per parameter set on each hardware platform. The average of these 10 iterations was taken to obtain stable and representative values for execution time and throughput.

5.1.2. Benchmark Results

Execution Time

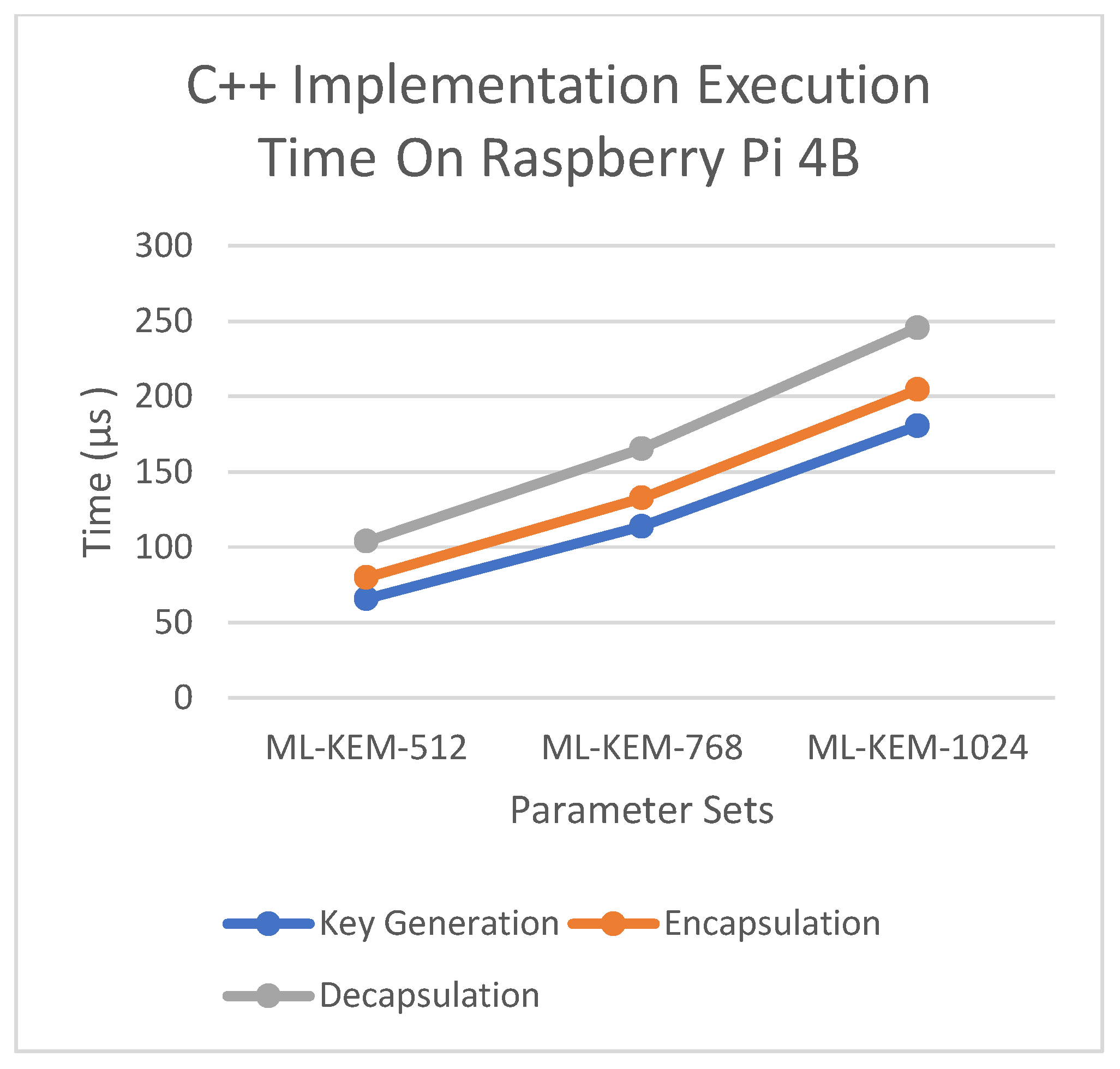
According to

Table 5. Execution time (mean) by implementation and device.

Parameter	Operation	Raspberry Pi 4B (C++)	MSI Laptop (C++)	Raspberry Pi 4B (Python)	MSI Laptop (Python)
ML-KEM-512	KeyGen	65.6 µs	14.7 µs	5486 µs (5.49 ms)	1650 µs (1.65 ms)
	Encap	79.8 µs	17.7 µs	8240 µs (8.24 ms)	2383 µs (2.38 ms)
	Decap	103.8 µs	22.6 µs	11,711 µs (11.71 ms)	3304 µs (3.30 ms)
ML-KEM-768	KeyGen	113.8 µs	24.7 µs	9491 µs (9.49 ms)	2980 µs (2.98 ms)
	Encap	132.6 µs	28.9 µs	12,918 µs (12.92 ms)	4044 µs (4.04 ms)
	Decap	165.4 µs	35.1 µs	17,515 µs (17.52 ms)	5549 µs (5.55 ms)
ML-KEM-1024	KeyGen	180.6 µs	38.8 µs	14,512 µs (14.51 ms)	5135 µs (5.14 ms)
	Encap	204.5 µs	43.2 µs	18,791 µs (18.79 ms)	6456 µs (6.46 ms)
	Decap	245.7 µs	52.4 µs	24,429 µs (24.43 ms)	8495 µs (8.50 ms)

, the ML-KEM’s native C++ implementation achieves sub-200 µs key generation on Raspberry Pi 4B (65.6 µs at 512-bit and 180.6 µs at 1024-bit). In contrast, executing the same KEM routines in Python 3.11.2 on the Pi 4B suffers a minimum quadrillion factor increase in latency (~5.49 ms vs. 65.6 µs for ML-KEM-512 KeyGen). This is due to CPython’s byte array marshaling, type checking, and C library calls.

Examining “Raspberry Pi 4B (C++)” and comparing it with “MSI Laptop (C++)” illustrates how the latter completes each operation 3–5 times faster. The MSI system with 12 cores at 1.7 GHz x86_64 had a 14.7 µs ML-KEM-512 KeyGen while the PI performed at 65.6 µs, equating to 4.5x speedup. On Pi, ML-KEM-1024 Decap was 245.7 µs whilst it was 52.4 µs on the MSI, achieving approximately 4.7x speedup. All three parameters exhibit the same 3–5x gap attributed to clock speed, the CPU microarchitecture (wider SIMD, out-of-order execution), and memory subsystem. Figure 4 and Figure 5 present the execution times of the C++ implementation for ML-KEM operations on the MSI Laptop and Raspberry Pi 4B, respectively, highlighting performance differences across parameter sets.

Using Python on the MSI platform, the times surpass 1 ms with the smallest parameter set. However, MSI still outperforms the Pi by approximately two to three times when Python is implemented. For instance, ML-KEM-512 Encap takes 2383 µs on MSI while RPi requires 8240 µs (≈3.5×). Notice that the Python interpreter overhead dominates to the point where hardware discrepancies partially “flatten” the results. In C++, the gap is about four times, while in Python, it shrinks to three times due to the interpreter’s overhead, which overshadows the computation. 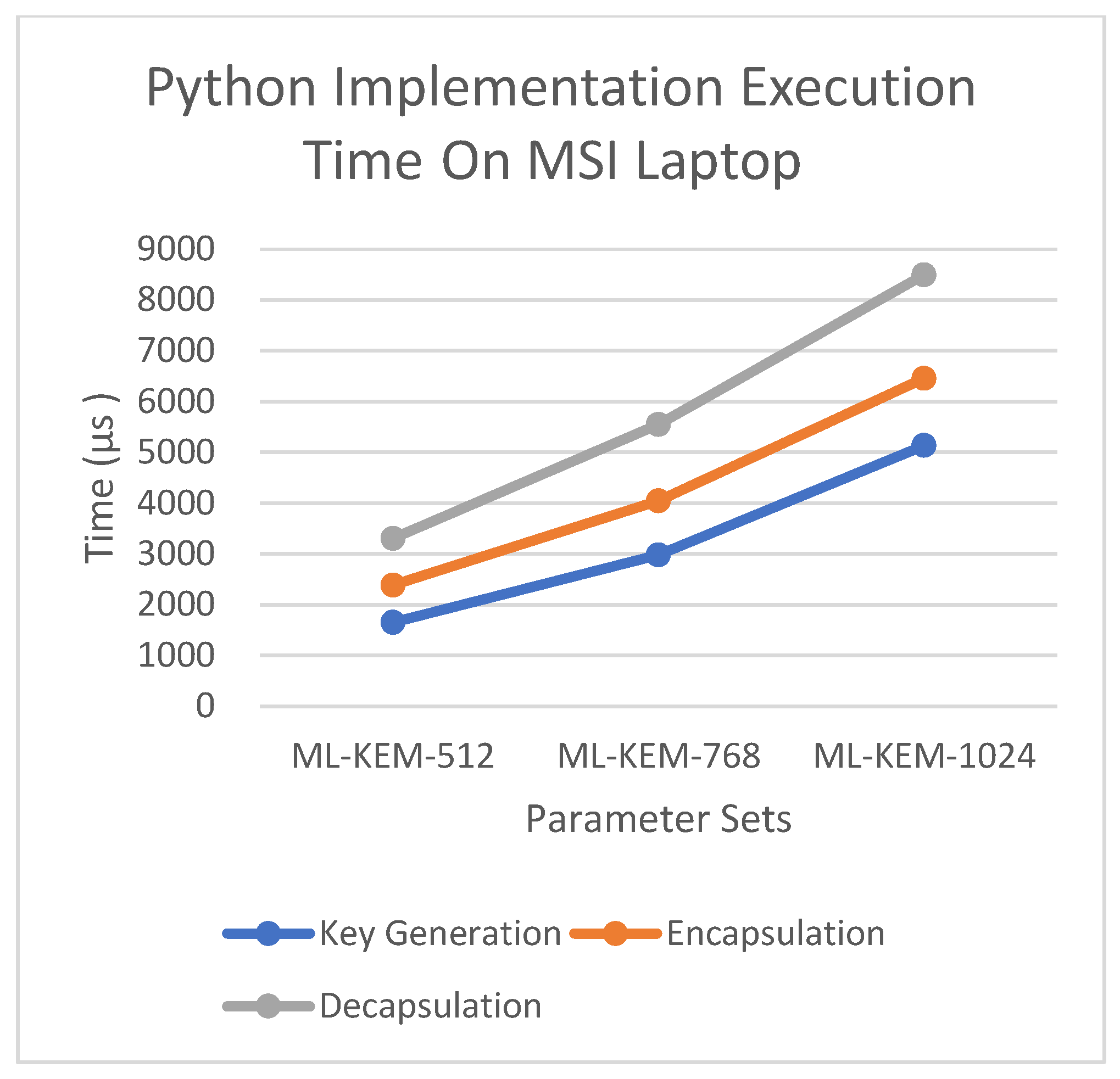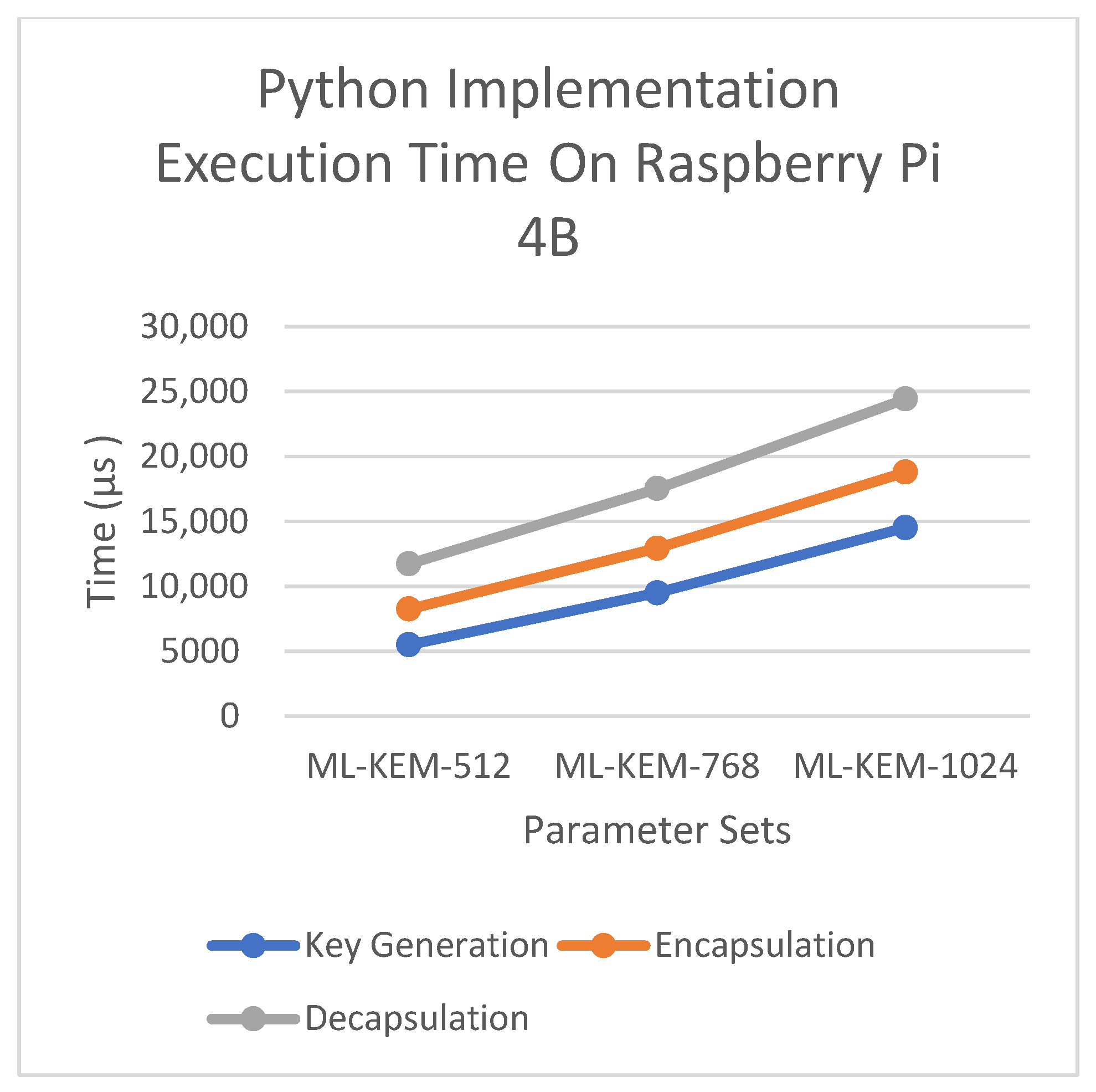Figure 6 and Figure 7 present the Python implementation execution times for ML-KEM operations on the MSI Laptop and Raspberry Pi 4B, respectively.

Lastly, on the Pi, ML-KEM-512 in Python with KeyGen taking 5486 µs remains outperforming the C++ version on the same hardware with KeyGen at 65.6 µs by approximately 35 times. In reality, post-quantum KEMs implemented in Python are only acceptable for IoT devices in infrequent key exchange scenarios. For real-time or battery-sensitive scenarios, C/C++ implementations are essential.

Concise Overview

• C++ executes in dozens of microseconds on both devices, whereas Python incurs costs in milliseconds.
• The MSI Laptop outperforms the former by 3–5× on C++ and 2–3× on Python.
• Increasing security parameters (512→1024) approximately quadruples or triples execution time.

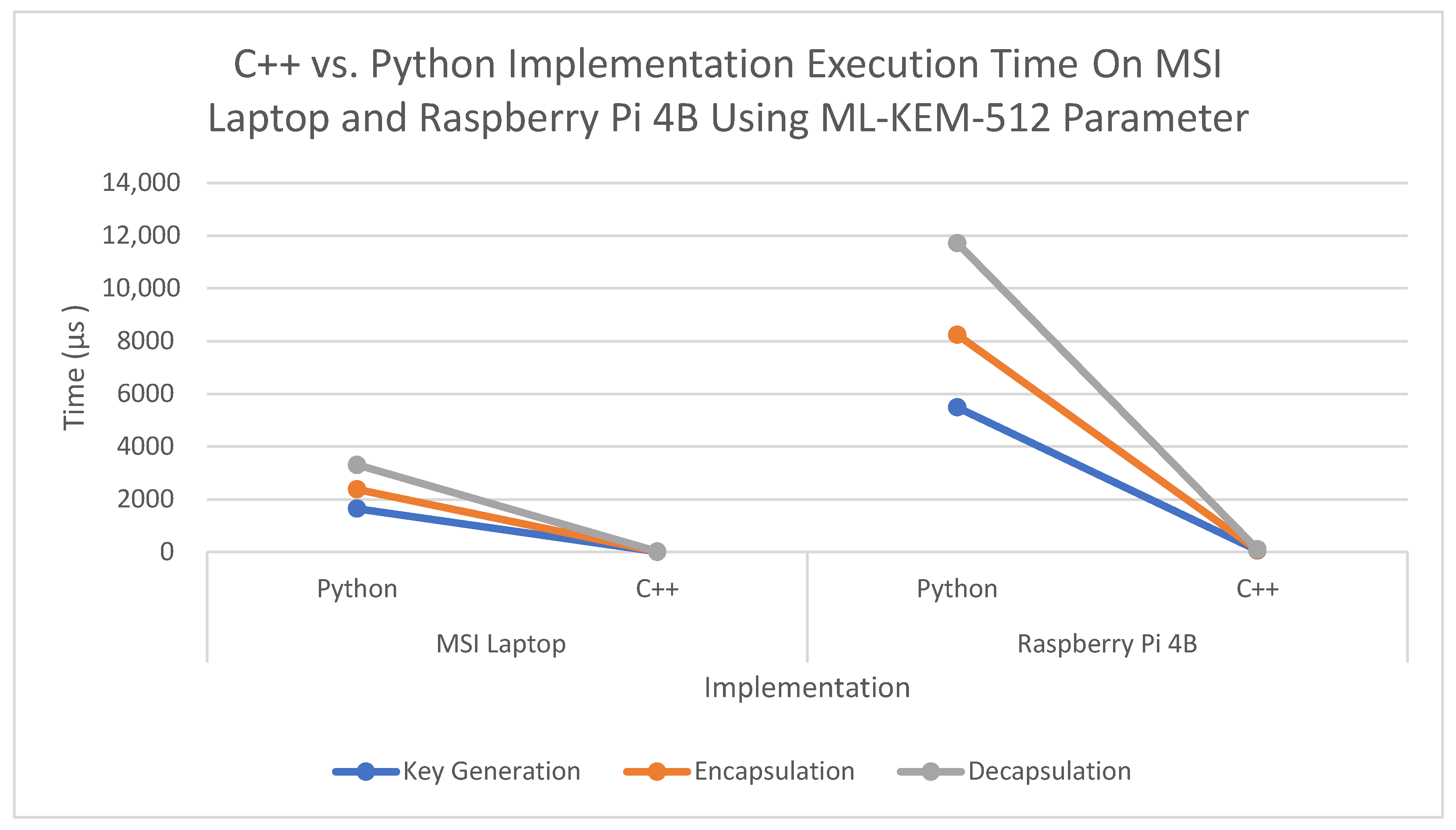
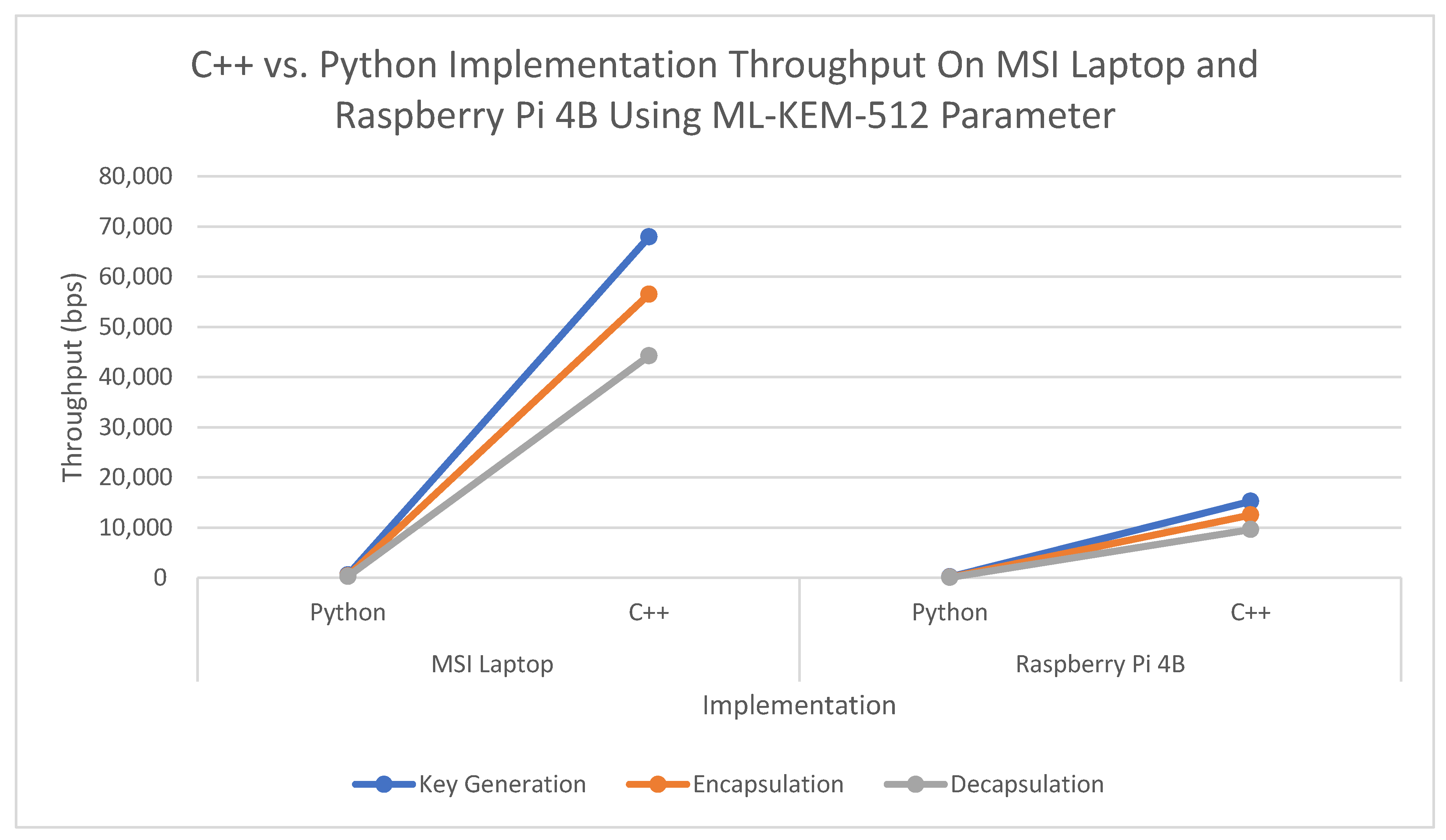
Figure 8 provides a side-by-side comparison of C++ and Python implementation execution times for ML-KEM-512 across both the MSI Laptop and Raspberry Pi 4B. It clearly illustrates the stark performance gap between the two programming environments.

Throughput

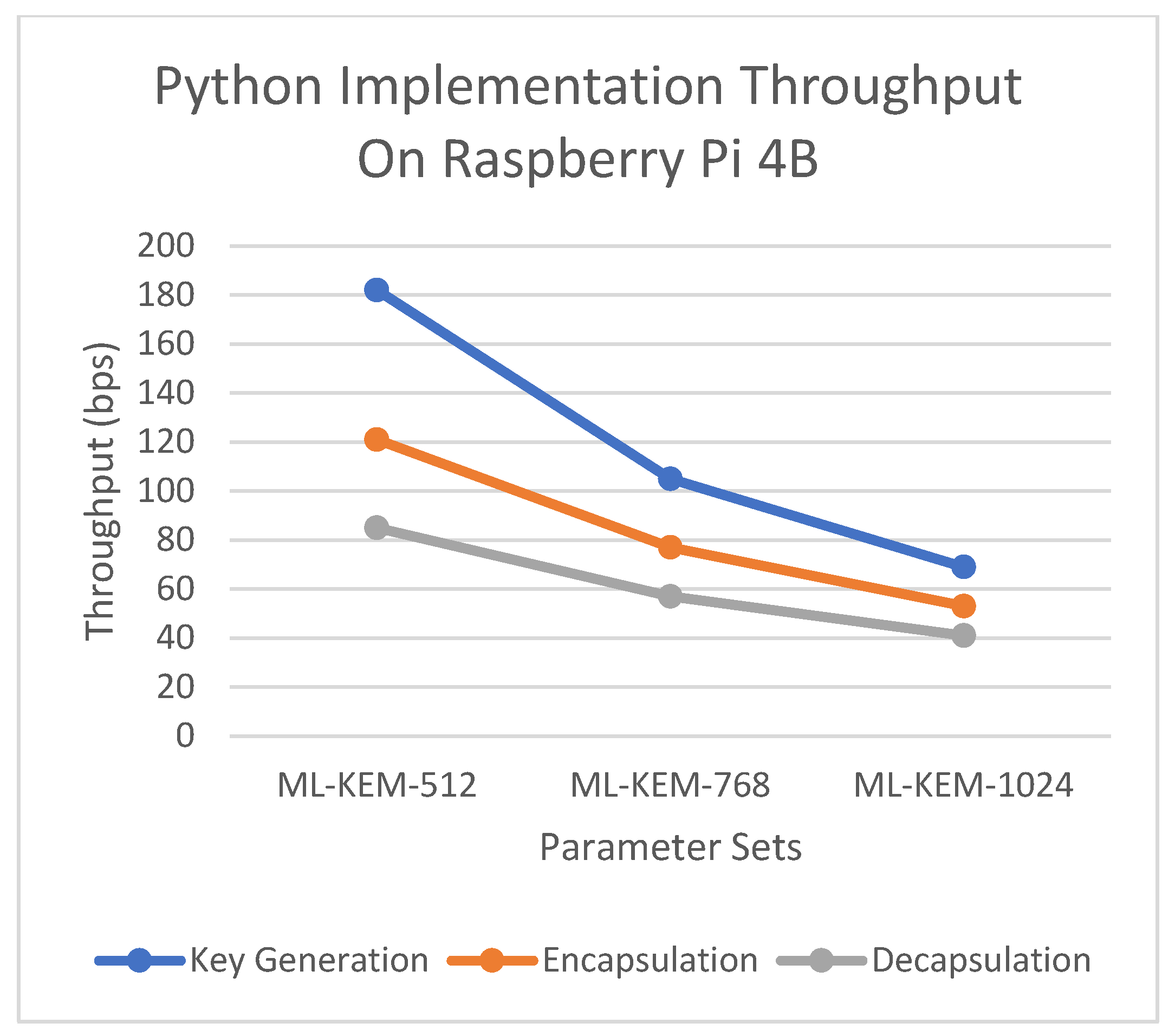
In analyzing

Table 6. Throughput per implementation and device.

Parameter	Operation	Raspberry Pi 4B (C++)	MSI Laptop (C++)	Raspberry Pi 4B (Python)	MSI Laptop (Python)
ML-KEM-512	KeyGen	15,243	67,932	182	606
	Encap	12,541	56,497	121	420
	Decap	9637	44,248	85	303
ML-KEM-768	KeyGen	8792	40,485	105	336
	Encap	7542	34,602	77	247
	Decap	6049	28,490	57	180
ML-KEM-1024	KeyGen	5541	25,773	69	195
	Encap	4893	23,148	53	155
	Decap	4072	19,084	41	118

, we notice that since the throughput =1/(avg execution time), Pi’s C++ throughput is about 15 k ops/sec with ML-KEM-512 KeyGen and 5.5 k ops/sec with ML-KEM-1024 KeyGen. For the MSI, the throughput increases to about 68 k ops/sec with ML-KEM-512 KeyGen and decreases to 25.8 k ops/sec with ML-KEM-1024 KeyGen. In Python, on the Pi, the throughput drops to an astonishing 182 ops/sec with ML-KEM-512 KeyGen, demonstrating that Python is 100 times slower than C++ for pure operational throughput on the same hardware. On the MSI using Python, 182 ops with ML-KEM-512 KeyGen makes these benchmarks roughly 112 times slower compared to the MSI C++ figures.

For the console output, we narrowed it down to the lower bounds of throughput metrics that dramatically impact high-frequency key exchanges in a densely populated Internet of Things environment: Under these conditions, a Pi 4B running C++ ML-KEM can perform a KEM handshake several thousand times, a feat not possible on Python from the same board.

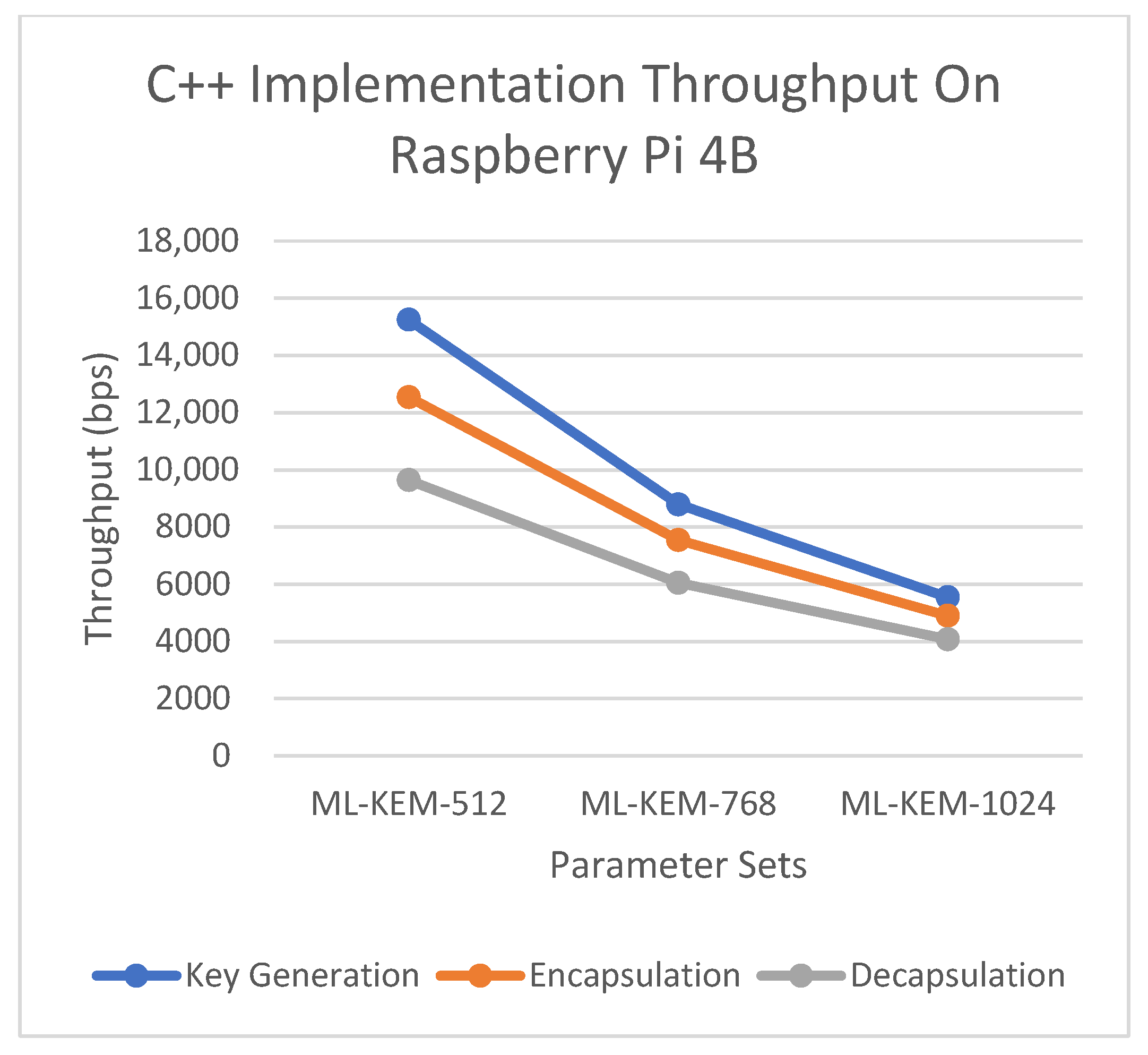
Figure 9, Figure 10, Figure 11 and Figure 12 illustrate the execution time performance of the ML-KEM across Python and C++ implementations on both the MSI Laptop and Raspberry Pi 4B. These visualizations provide a clear view of the disparities in speed, which directly impact throughput and suitability for high-frequency post-quantum key exchanges in constrained and desktop-grade environments.

Concise Overview

• A C++ application executed on the Pi gives a throughput of 5 k to 15 k KEM ops per second, while for the MSI it is between 20K and 68k ops/s.
• The best performance that can be achieved by running a Python application on the Pi is 40 to 180 ops/s, while the MSI can achieve 118 to 606 ops/s, far too low to be considered for bulk applications.
• Throughput diminishes as parameters increase due to the time required for operations.

Figure 13 illustrates the throughput performance of C++ and Python implementations for ML-KEM-512 on both the MSI Laptop and Raspberry Pi 4B.

5.1.3. Performance Comparison of C++ and Python

In comparison to Python, C++ proves to be approximately 75× to 200× faster based on wall-clock time measurements. This is due to the following:

• Native Compilation (C++): Each line of C++ code undergoes a series of advanced optimization techniques, such as -O3 and link-time optimizations, which enable parallel processing on CPUs. Additionally, in the case of x86_64, AVX2 and neon technology on ARM Cortex-A72 also utilize SIMD/Vectorial functions for its parallel processing capabilities. For the implementation of polynomial arithmetic, Montgomery multiplication, and NTT transforms, C++ proves to be far more efficient during execution because intricate loops are used.
• Interpreter Overhead (Python): In Python, function calls from higher levels incur a penalty. In this case, calling “keypair()” or “encapsulation()” can be performed within a Python vm. This requires a full cycle of bytecode fetching, dynamic type verification, memory allocation, object creation, garbage collection, etc. Passing Python objects, returning bytes and byte arrays, and interfacing with C are performed through “kyber-py” or “ml-kem-py”. The C portions of the code are nowhere near the computational efficiency that such overhead is today. Such a system adds latency that dwarfs the cost of pure arithmetic.

For example:

• ML-KEM-512 KeyGen on MSI:

  ○

  C++: 14.7 μs;

  ○

  Python: 1650 μs;

  ▪

  → C++ is ~112 × faster.

• ML-KEM-1024 Decap on Raspberry Pi 4B:

  ○

  C++: 245.7 μs;

  ○

  Python: 24,429 μs;

  ▪

  → C++ is ~99 × faster.

Therefore, in the context of real-time or batch processing scenarios, particularly on a constrained device like an IoT peripheral or a Raspberry Pi 4B, the C++ implementation becomes nearly indispensable. Python should only be used for research and design, as its capableness does not extend to production-grade security protocols.

5.1.4. Hardware Impact

In the context of C++ implementations, the MSI Modern 14 laptop not only outperforms the Raspberry Pi 4B but does so by approximately three to five times, depending on the operation and parameter set. Such a difference is a result of not only the clock speed but also the architectural supremacy of the x86_64 platform. The Raspberry Pi 4B lags in performance due to its lack of out-of-order execution and the absence of advanced features like AVX2 and large (multi-megabyte) L3 caches compared to the Pi’s 1 MB L2 caches that improve computational throughput and memory locality.

The MSI system utilizes an Intel-based architecture running at 1.7 GHz and incorporates more advanced microarchitectural features. The Raspberry Pi 4B, by comparison, runs at 1.5 GHz and uses a Cortex-A72 processor with a 128-bit NEON SIMD pipeline, which is narrower than the vector capabilities of most modern x86 CPUs. Although it is true that ARM cores are considerably cheaper and consume less power than x86 chips, they are far less effective when it comes to single-thread compute-intensive tasks like lattice-based cryptography.

Additionally, tasks that are memory bandwidth-sensitive, such as operating on large buffers, are also impacted by the difference in available memory bandwidth—DDR4 available on the MSI with ~50 GB/s compared to LPDDR4 on the Pi with 15 GB/s—particularly when dealing with large structures such as 3328-byte ciphertexts or 2560-byte public keys.

Empirical benchmarks confirm these architectural limitations. On the Raspberry Pi 4B, ML-KEM-512 key generation takes 65.6 µs, while on the MSI laptop it is 14.7 µs, which is ~4.5× slower. For ML-KEM-1024 decapsulation, it takes 245.7 µs on the Pi and 52.4 µs on the MSI, which is ~4.7× slower. Even though Python’s interpreter overhead dampens some of the hardware advantage on the Pi, the MSI consistently leads by 2× to 3×. For instance, ML-KEM-512 encapsulation in Python takes 2383 µs on the MSI and 8240 µs on the Pi, yielding a difference of ~3.5×.

5.1.5. Parameter Scalability

Moving from ML-KEM-512 to ML-KEM-1024, execution times scale almost linearly in relation to the security parameter increase. This aligns with expectations, since the higher order polynomial and larger matrices mean more arithmetic operations and buffers proportional to the work required.

In the C++ implementation on the Raspberry Pi 4B, the key generation shifts from 65.6 µs to 113.8 µs (ML-KEM-768) and 180.6 µs (ML-KEM-1024), while decapsulation increases from 103.8 µs to 165.4 µs and 245.7 µs, respectively.

On the MSI laptop using the Python implementation, the key generation time rose from 1650 µs to 2980 µs and then 5135 µs, with decapsulation rising from 3304 µs to 8495 µs, all within the same parameters.

These findings demonstrate the need for larger buffers to handle keys and ciphertexts, as well as the extra time needed for more random sampling operations. This logic is supported by the observed linear growth. Lower-latency configurations like ML-KEM-512 or ML-KEM-768 might be better for designers who are interested in creating effective IoT systems. Although it satisfies NIST Level 5 requirements and offers the highest security level, ML-KEM-1024 might not be feasible in environments with limited resources.

5.1.6. Failure on Resource-Constrained Devices

In reference to our practical assessment, we focused on running benchmarks as well as integration tests for the ML-KEM on IoT devices such as the ESP32 DevKit, ESP32 Super Mini, ESP8266, and Raspberry Pi Pico. The intention was to ascertain whether the implementation of post-quantum KEMs (key-encapsulation mechanisms) would be feasible on microcontrollers typical of low-power or embedded systems.

We encountered significant limitations across most platforms, particularly those lacking electronic vector arithmetic capabilities or hardware encryption acceleration units. The ML-KEM and other post-quantum KEMs based on CRYSTALS or “Kyber” have high computational requirements alongside memory constraints, which offer very little room for integration outside of the more powerful devices.

Relatively, the ML-KEM’s polynomial arithmetic, NTT tables, and other buffers generate internal data structures that require kilobytes of memory just for the buffer alone. As an example, the Kyber implementation performed on the ESP32 microcontroller required heavy memory optimization [30,34]. Higher parameter sets like ML-KEM-1024 are far worse in terms of resource-per-augmentation demand. This mirrors issues seen in other lattice-based systems such as LEDAcrypt, where higher security levels increase decoding failures and memory requirements [30,35].

These constraints are compounded by practical limits on hardware capability, which also pose challenges. Even the better microcontroller units (MCUs) have a drawn-out processing time for encapsulation, decapsulation, and key generation processes. While some attempts have been made to leverage hardware accelerators, such as ESP32’s hardware encryptors (AES and SHA units) or dual-core microcontrollers [30,34], the performance gains are minimal. For example, 80 MHz ES8266 and 133 Mhz Cortex-M0+ remain far too slow for practical ML-KEM use. Furthermore, full Kyber encryption has been proved to be extremely resource-heavy, especially on constrained devices [35,36]. With respect to IoT use cases (latency sensitive), such delay becomes intolerable.

Architecturally, MCUs such as the Raspberry Pi Pico and ESP32 lack the necessary hardware capabilities for efficient polynomial or modular computation. Pico’s Cortex-M0+ processor lacks digital signal processing (DSP) and SIMD units and includes only a 32-bit multiplier. Similarly, the ESP8266 and ESP32 do not support large-integer arithmetic, forcing them into inefficient software solutions. While parallelism using dual cores may help somewhat, it does not meet the needs of real-time or low-latency environments.

Network and energy costs surge as well. The public keys and ciphertexts for the ML-KEM and Kyber-768 consume over a kilobyte each (they use ~1.1 kB and ~2.3 kB, respectively). Such sizes are problematic in lossy or bandwidth-limited networks, common in IoT. Furthermore, energy metrics associated with devices like the Raspberry Pi Pico W suggest that post-quantum Kyber handshakes require substantially higher energy than classical handshakes, adversely affecting the battery in mobile or remote-sensor applications [36,37].

Given these observations, we conclude that the ML-KEM is currently unsuitable for low-end microcontrollers, whether implemented in C++ or Python. Even optimized-for-resources versions of lattice-based KEMs are infeasible within low-power MCUs. In practice, there are four IoT options. (1) Offload KEM computations to more advanced edge devices or gateways. (2) Employ other lightweight PQC met schemas tailored to constrained environments. (3) Blend classical and post-quantum protocols to reduce the number of KEM operations required on the end node. (4) Shift all computationally intensive operations to more advanced edge devices or gateways and retain only control functions on the node level [37,38].

5.1.7. Recommendations

For Learning/Prototyping

• For an introduction to the ML-KEM and experimentation with various parameter sets, Python is recommended. Its clear, well-documented API makes it an excellent starting point.

For Performance-Sensitive Applications

• C++ is recommended for real-world, high-security systems where speed is critical. Its performance (~139.5× faster on average) enables it to meet the demands of production environments.

Important Security Notice

While these implementations follow the ML-KEM Standard (NIST FIPS 203) [14] and are accompanied by comprehensive tutorials to support learning and experimentation, they have not been formally audited for cryptographic security. As such, they may remain vulnerable to implementation-level threats, such as side-channel attacks.

These implementations are excellent educational resources but should not be used in production systems without rigorous, independent security reviews. Any deployment in sensitive or high-assurance environments must undergo a formal audit process to ensure they meet stringent cryptographic standards and are resilient against practical attack vectors.

5.1.8. Logical Opinion

The Python implementation offers an excellent avenue for learning but lacks the performance and security needed for real-world applications. The C++ implementation utilizes advanced techniques and low-level details, such as constexpr, to achieve both compile-time evaluation and optimized runtime performance.

In contrast, C++ requires a more advanced understanding of cryptography fundamentals and modern software development techniques due to its inherent complexities.

5.2. ML-KEM + AES-192 vs. RSA + AES-192: Performance and Practicality Comparison

5.2.1. Experimental Setup

We presented our experimental implementation in Figure 14.

• Hardware:

  ○

  MSI Modern 14 Laptop with Intel Core i7 12th Gen CPU (1.70 GHz), 16 GB RAM.

• Parameters: ML-KEM-512, ML-KEM-768, ML-KEM-1024; RSA-2048, RSA-3072, RSA-4096.
• Metrics:

  ○

  Execution Time: Mean real-time (µs) for KeyGen, Encap, and Decap, AES Encrypt, AES Decrypt, Total Time.

• Procedure: All cryptographic operations were implemented and benchmarked using Python [32]. Each operation was executed 10 times per configuration to compute an average execution time. The message “Post-Quantum Technology” was used as the plaintext input for AES-192 encryption and decryption, ensuring consistency across all experiments.

5.2.2. Comparison Overview

To evaluate post-quantum readiness and practical efficiency, we benchmarked a hybrid system using ML-KEM-512, ML-KEM-768, and ML-KEM-1024 for key-encapsulation and AES-192 for symmetric encryption and decryption. We then contrasted them with traditional RSA-2048, RSA-3072, and RSA-4096 hybrids using AES-192. To maintain uniformity and isolate the effectiveness of key-encapsulation mechanisms, AES-192 encryption and decryption were used consistently throughout all experiments. AES showed consistent timing across all parameters and contributed very little to the total execution time, as shown in

Table 7. Execution time comparison of ML-KEM and RSA parameters with AES-192.

Metric	ML-KEM-512	ML-KEM-768	ML-KEM-1024	RSA-2048	RSA-3072	RSA-4096
KeyGen Time	1650 µs	2980 µs	5135 µs	77,961.02 µs	195,401.31 µs	453,639.96 µs
Encaps Time	2383 µs	4044 µs	6456 µs	145.33 µs	160.00 µs	242.24 µs
Decaps Time	3304 µs	5549 µs	8495 µs	2284.85 µs	4969.77 µs	9096.71 µs
AES Encrypt	8.95 µs	9.82 µs	9.61 µs	22.28 µs	15.32 µs	17.92 µs
AES Decrypt	5.40 µs	5.59 µs	5.40 µs	7.14 µs	7.08 µs	7.54 µs
Total Time	8084.35 µs	12,588.41 µs	20,101.01 µs	80,420.62 µs	200,553.48 µs	462,004.3 µs

. This consistency confirms that the encapsulation scheme, not symmetric encryption, is the cause of the fundamental performance discrepancy and validates the configuration.

Despite being part of the theoretical comparison of cryptographic features in Table 3, no previous study has directly contrasted RSA’s practical runtime performance with the ML-KEM. The current benchmark study was therefore carried out in order to compare and empirically assess the execution speed of both the RSA and ML-KEM schemes across a variety of parameter sets. By comparing the two methods’ performance side by side, this evaluation closes a gap in the literature and identifies which approach is more effective in practical settings.

5.2.3. Hybrid RSA Setup

In this experiment, the RSA scheme based on RSA-OAEP is adapted to act as a key-encapsulation mechanism. A 192-bit random AES key is generated, encrypted using the recipient’s RSA public key, and decrypted with the corresponding private key. The recovered key is then used to perform the symmetric encryption and decryption of a fixed message using AES with a 192-bit key in Cipher Block Chaining (CBC) mode. This hybrid approach reflects traditional usage in secure communication protocols, where RSA is commonly used to encrypt symmetric session keys, while AES handles the confidentiality of the payload.

As mentioned in Section 2.2.6, basic RSA is vulnerable to chosen ciphertext attacks (CCAs). To ensure a fair and secure comparison, we employed RSA-OAEP, which is a widely adopted and secure variant of RSA in practice. This decision aligns the experiment with established cryptographic best practices and provides a realistic benchmark against which to evaluate the performance of the ML-KEM.

5.2.4. Analysis and Key Insights

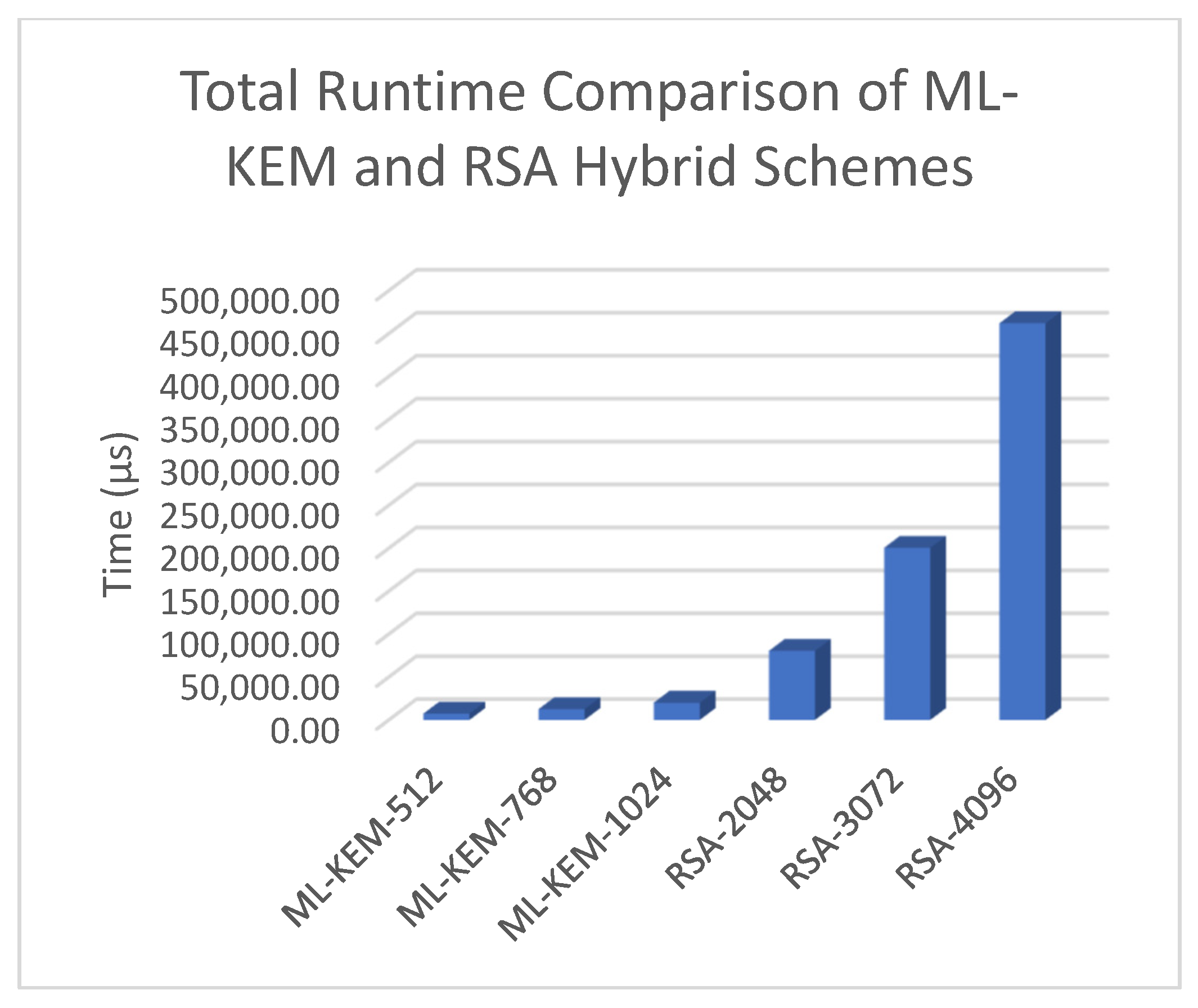
Table 7’s results show a sharp difference in performance between all ML-KEM and RSA parameter sets. ML-KEM-512, the most lightweight option, is nearly 10 times faster than RSA-2048 in total runtime. ML-KEM-768 performs more than 15 times faster than RSA-3072. ML-KEM-1024, although the most computationally intensive among the ML-KEM parameters, still outpaces RSA-4096 by more than 23 times. Notably, ML-KEM-1024 is still much faster than all tested RSA key sizes, despite being the largest and slowest of the three post-quantum parameters. This consistent superiority highlights the ML-KEM’s suitability for real-world, post-quantum-ready applications.

RSA’s key generation time is significantly longer for all parameter sets, even though it showed slightly faster encapsulation and decapsulation in isolation. For instance, ML-KEM-768 generates keys in 2980 microseconds, while RSA-3072 takes more than 195,000 microseconds. Similarly, ML-KEM-1024 generates keys in 5135 microseconds, while RSA-4096 takes over 453,000. Particularly when taking into account higher security levels, these values show a pronounced performance difference between the RSA and ML-KEM in terms of key establishment efficiency. The runtime disparities visualized in Figure 15 and Figure 16 reinforce the numerical insights from Table 7.

These findings are not surprising. Maletsky’s comparative analysis [38,39] shows that RSA is substantially slower than ECC for private key operations and key generation, and the difference becomes wider as security levels rise. The study reports RSA’s key generation to be up to 1000× slower than ECC, raising concerns about RSA’s practicality in performance-sensitive systems. Similarly, the comparative study by Lopez and Barsoum [39,40] explains that RSA’s inefficiency results from its dependence on modular exponentiation and large prime generation, both of which have significant computational costs. Despite the fact that both studies concentrate on ECC, they corroborate our empirical findings about the ML-KEM’s runtime effectiveness. In particular, the ML-KEM performs better than RSA because it uses structured lattice-based arithmetic, which is more compatible with contemporary CPU architectures.

Concise Overview

• The ML-KEM consistently achieves significantly faster total runtimes than RSA across all parameter levels.
• Although RSA has marginally faster encapsulation and decapsulation, its key generation time (e.g., 195,401.31 µs for RSA-3072 vs. 2980 µs for ML-KEM-768) is significantly higher than that of the ML-KEM across all parameter sets.AES-192 contributed minimally to runtime, reinforcing the validity of focusing on encapsulation differences.
• Even the largest ML-KEM parameter (1024) was faster in total runtime than RSA-2048, RSA-3072, and RSA-4096.
• The ML-KEM’s reliance on structured lattice-based arithmetic enables faster operations on modern CPUs than RSA’s number-theoretic operations.
• Increasing the ML-KEM parameters from 512 to 1024 results in a ~2.7× rise in runtime, while RSA’s rise across key sizes is exponentially higher.

6. Discussion

This research offered a comprehensive evaluation of ML-KEM performance in two implementation environments: Python for educational use and C++ for performance-sensitive applications. Although both implementations adhere to the ML-KEM standards, they present distinct trade-offs regarding performance, usability, and security.

6.1. Limitations

Despite the comprehensive nature of our experimental analysis, several limitations remain that affect the generalizability and applicability of our findings.

First, despite our evaluation of the ML-KEM on a Raspberry Pi 4B and a mid-range consumer laptop, as well as our attempts to deploy it on various microcontroller platforms (ESP32, ESP8266, and Raspberry Pi Pico), successful execution was only accomplished on the more powerful hardware. Memory constraints, the absence of SIMD or DSP units, and the lack of large-integer arithmetic support were the main reasons why the ML-KEM could not be run on ultra-constrained devices. The applicability of the ML-KEM in real-time or latency-sensitive IoT environments is restricted by these problems. This emphasizes the necessity of additional optimizations suited to hybrid offloading models or lightweight architectures.

Second, the Python implementation used in this study primarily served an instructional purpose. While useful for educational exploration and prototyping, it suffers from significant interpreter overhead, lacks hardware acceleration, and does not incorporate defenses against side-channel attacks. As such, it is unsuitable for production deployment in high-security or resource-constrained environments.

Third, although performance benchmarks were rigorously collected, this research does not include any formal cryptographic audits or side-channel resistance evaluations. Consequently, implementation-level vulnerabilities such as timing attacks or memory leakage remain unassessed. This gap must be addressed before any deployment in critical systems.

Fourth, not all RSA padding or configurations were assessed in this study. Other variations like RSA-PSS or configurations with different key management strategies were not tested, but RSA-OAEP was utilized to guarantee a fair comparison with the ML-KEM. This restricts how thorough the RSA performance evaluation can be.

Lastly, despite the significant implications of higher power demands, particularly for extended cryptographic operations on devices like the Raspberry Pi or low-power microcontrollers, our study did not incorporate direct energy consumption profiling. For battery-operated and remote IoT deployments, energy efficiency is an essential consideration. Power monitoring tools should be incorporated into future research to evaluate the complete feasibility of the ML-KEM in energy-constrained settings.

Collectively, these drawbacks highlight how crucial it is to keep improving and refining post-quantum cryptography techniques in order to guarantee their safe, effective, and useful implementation across a range of embedded and Internet of Things applications.

6.2. Future Directions and Research Opportunities

Future research into the ML-KEM presents numerous opportunities to enhance its capabilities and adapt to evolving security demands. One direction involves optimizing the ML-KEM for constrained environments, such as IoT devices, where energy efficiency and computational resource limitations are critical. This could involve developing lightweight variants that retain acceptable security margins while reducing resource usage [29,40].

In addition to optimization, integration with established cryptographic standards like TLS, VPNs, and blockchain protocols would promote smoother adoption and applicability across modern secure communications infrastructure [29].

Moreover, the use of deep learning methods could address automated and enhanced parameter selection and adaptation of the system. The incorporation of online learning models may enable dynamic key management systems, adapting key management as operating conditions change. An area of exploration supported by Zhang et al.’s deep learning work [41] is to enhance adaptability in system mechanisms and optimize performance enhancements to the operational components supporting cryptographic functions in real time, potentially increasing effectiveness.

Another important area for development is addressing the robustness of the system to uncertainty or variability conditions. As an example, Zhang et al. [42] introduced a work in device-free localization variance-constrained local–global modeling to accommodate uncertainty. Variance-controlled or multi-distribution approaches to ML-KEM systems, incorporating assessments to adapt or modify behavior (security) based on the changing conditions of the environment and threats, would be one field to explore.

Research can also investigate models consolidating hybrid cryptography, combining the ML-KEM with post-quantum algorithms and evaluating the benefits or novel advantages this would provide in countering threats more securely. Testing to identify real-world exposures to adversarial conditions will help evaluate the resilience of the model but also recognize exploitable vulnerabilities.

Empirical energy profiling is an important avenue for the future. Direct power consumption measurements for ML-KEM operations were not included in this study, despite the fact that energy efficiency has been recognized as a major constraint. In order to measure and analyze energy usage across different devices, future work should include tools like energy profilers, battery drain monitors, current sensors (like INA219), or simulation-based modeling. In battery-operated or intermittently powered IoT systems, where cryptographic efficiency directly affects device longevity and reliability, this is especially crucial for determining whether ML-KEM deployment is feasible.

Furthermore, to enable a more thorough and representative comparison with the ML-KEM in a variety of cryptographic applications, future research should investigate a larger range of RSA variants beyond RSA-OAEP, such as RSA-PSS and other configurations. This would assist in identifying the safest and most useful RSA substitute for hybrid deployments.

Finally, more benchmarking and hardware tests across other platforms like ARM, RISC-V, and FPGA, the incorporation of standardized audit processes, and other evaluation methods will facilitate our ability to record and preserve the sustainable adoption of the ML-KEM when deployed into production-grade environments.

In conclusion, while the ML-KEM provides a unique and relevant key-encapsulation solution that is secure against quantum computers from breaking the confidentiality or integrity of the key management it provides, there is much more research work to be determined or even to improve on the development of the ML-KEM in ways that can optimize, adaptively structure the key management actions, move towards a lightweight implementation, and be supports to integration processes within those efforts.

7. Conclusions

The research examined a groundbreaking post-quantum cryptographic technology, named the Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM). This cryptographic method addresses security vulnerabilities presented by legacy cryptographic systems such as RSA and ECC. Security is obtained by exploiting the computational hardness of MLWE (Module Learning with Errors), the ML-KEM provides security against both quantum and classical attackers, offering resistance to Grover’s search and Shor’s factorization algorithms. Beyond theoretical strengths, this paper involved conducting a live benchmark of the two implementations on both an MSI laptop and a Raspberry Pi 4B to analyze their real-world performance and feasibility. Additionally, integration trials on microcontrollers such as ESP32 variants, ESP8266, and Raspberry Pi Pico were unsuccessful due to architectural constraints and insufficient computational capabilities, underscoring the ML-KEM’s current limitations on low-end embedded platforms.

Furthermore, the computational benchmarks unveil notable performance differences between Python and C++ implementations of the ML-KEM. The C++ implementation proved to be efficient and was faster than Python by over 139.5× in key operations such as key generation, encapsulation, and decapsulation. To evaluate its feasibility on edge environments, the experiment was also conducted on a Raspberry Pi 4B to represent its suitability on IoT devices. The result, in the context of real-time or batch processing scenarios, showed that the C++ implementation is significantly better. In addition, our Python-based benchmarks showed that the ML-KEM consistently outperformed RSA across all parameter sets, with ML-KEM-768 over 15× faster than RSA-3072, and ML-KEM-1024 faster than RSA-4096, Nonetheless, these findings demonstrate the need for larger buffers to handle keys and ciphertext.

Apart from performance comparisons, this study tackles significant practical aspects of the ML-KEM that are often overlooked in the literature. These consist of the management and destruction of intermediate cryptographic values, the careful selection of parameters, and the impact of hardware characteristics on overall performance.

In spite of its advantages, the ML-KEM has drawbacks, particularly at the ML-KEM-1024 level, including high memory consumption and computational expense. These problems make it impractical to use on extremely constrained devices and emphasize the need for more study into lighter and more energy-efficient models. Even so, the ML-KEM continues to be a significant development in the field of post-quantum cryptography. Its practical value is confirmed by its incorporation into established protocols like TLS and its applicability in safeguarding cloud platforms, mobile systems, and blockchain apps. In order to increase overall security, future research should concentrate on hybrid cryptographic schemes that combine the ML-KEM with other quantum-resistant algorithms. For the sustainable and safe adoption of the ML-KEM, research into energy profiling, lightweight optimization, embedded systems, and benchmarking on various architectures like ARM, RISC-V, and FPGA will be crucial.

To conclude, this work provides useful insights into the practical implementation of the ML-KEM in addition to validating its theoretical merits. This study offers a thorough basis for the further research, development, and standardization of the ML-KEM in post-quantum security systems through empirical evaluation, performance benchmarking, and implementation analysis.