Near-Field Pressure Signature of New-Concept Supersonic Aircraft Obtained Using Open-Source Approach
Abstract
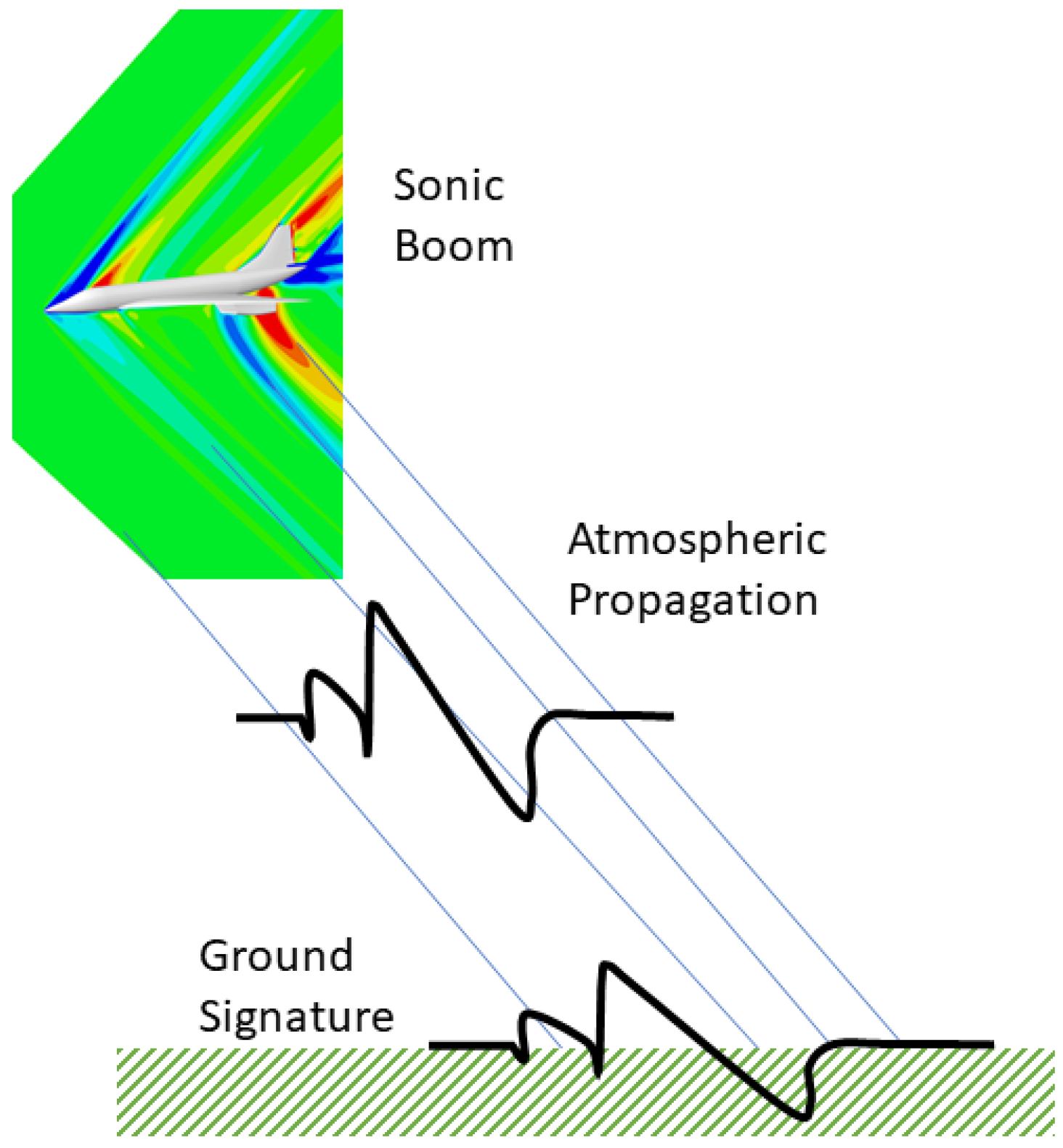
1. Introduction
2. Numerical Approach: Development and Validation
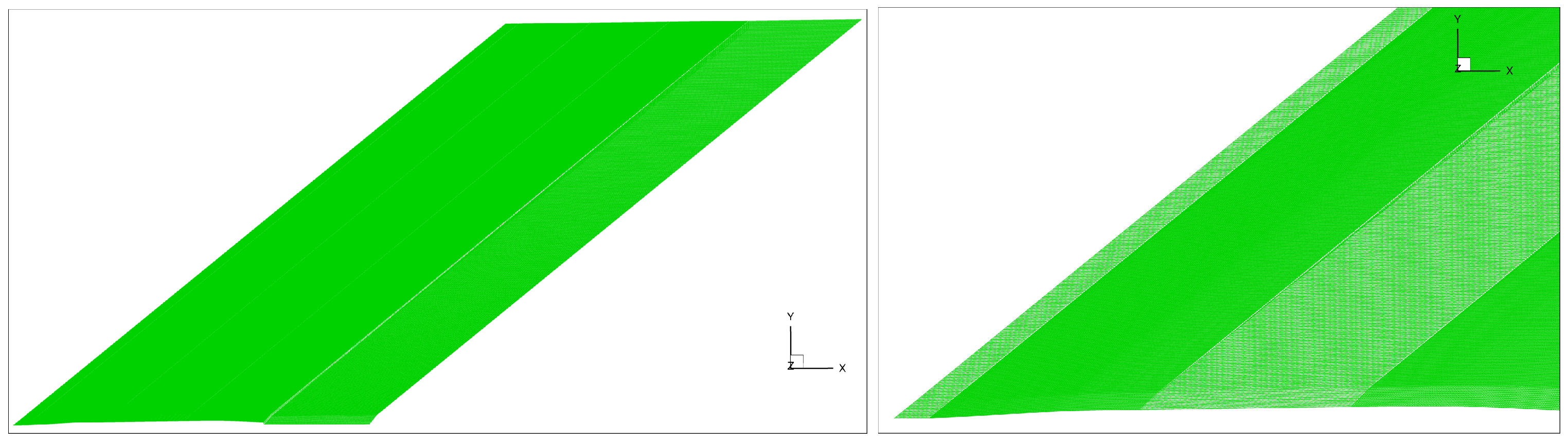
2.1. Numerical Setup
2.2. Test Cases
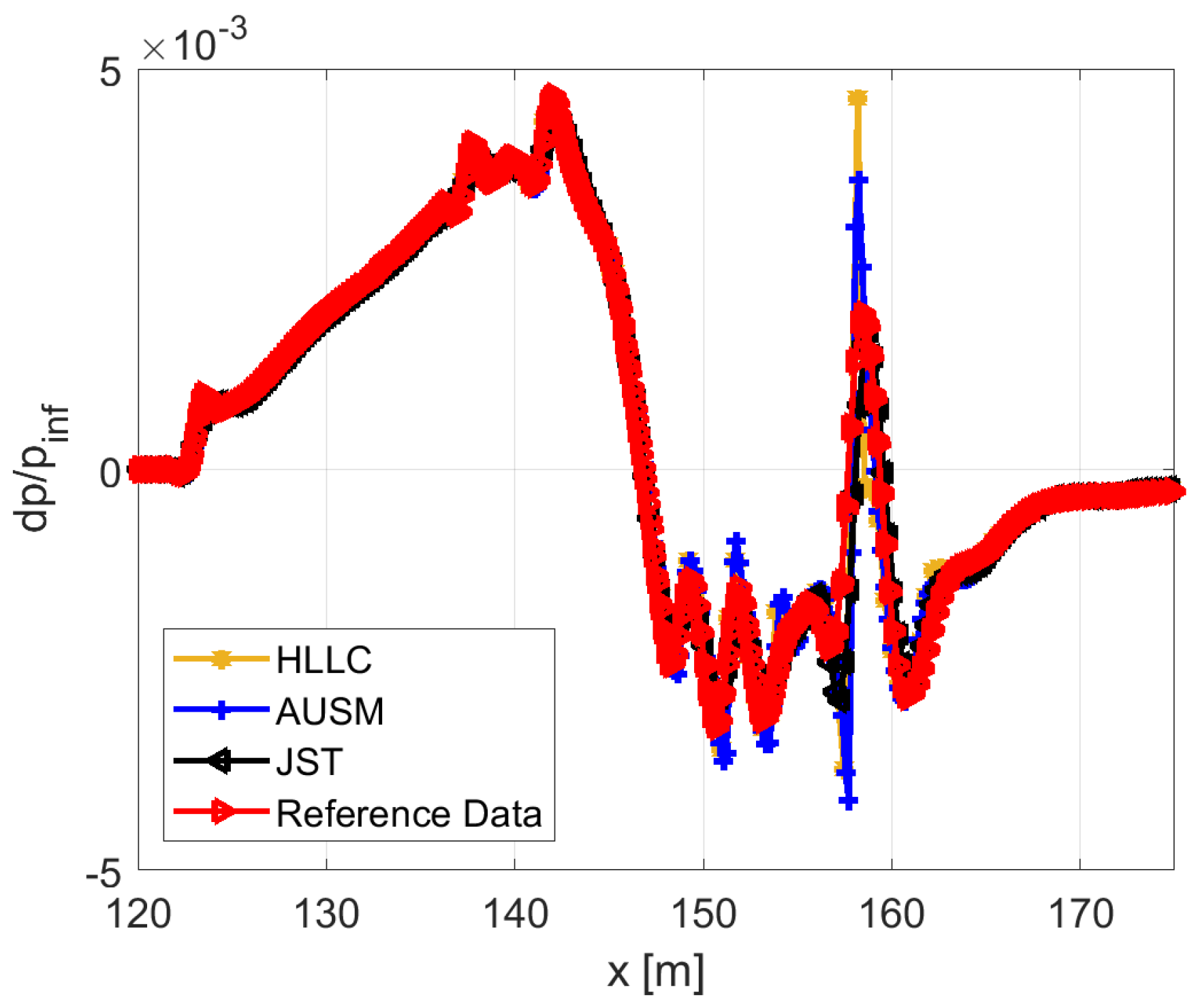
2.3. Validation Data
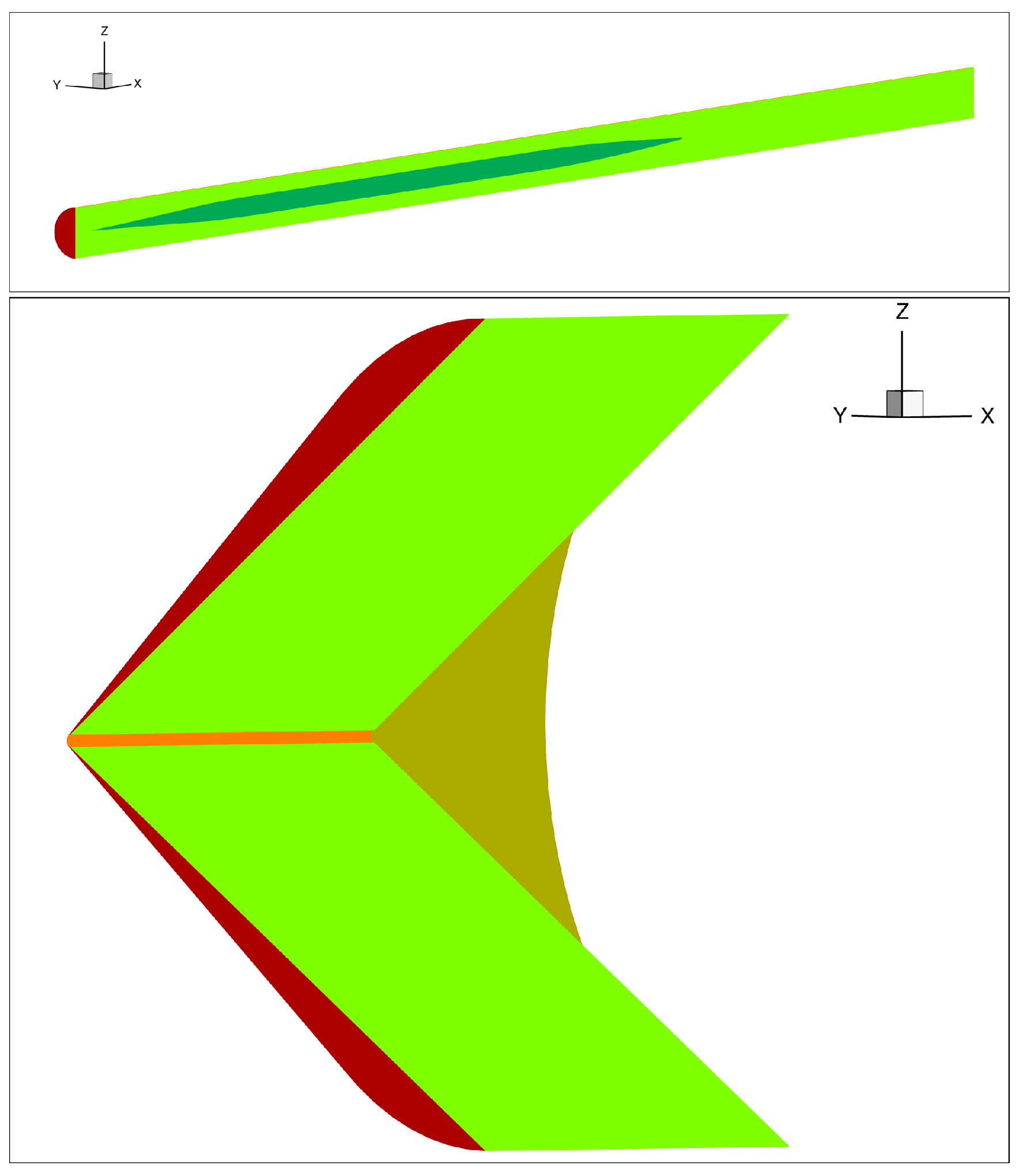
2.4. AXIE Geometry
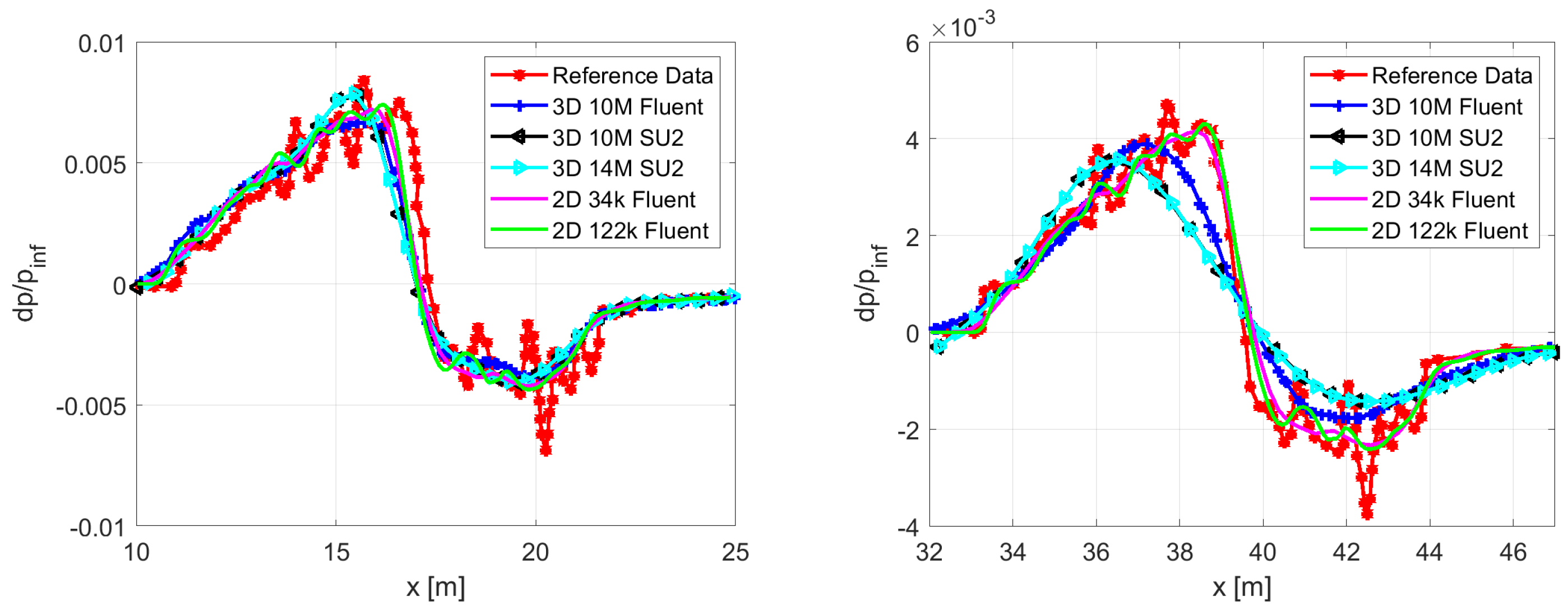
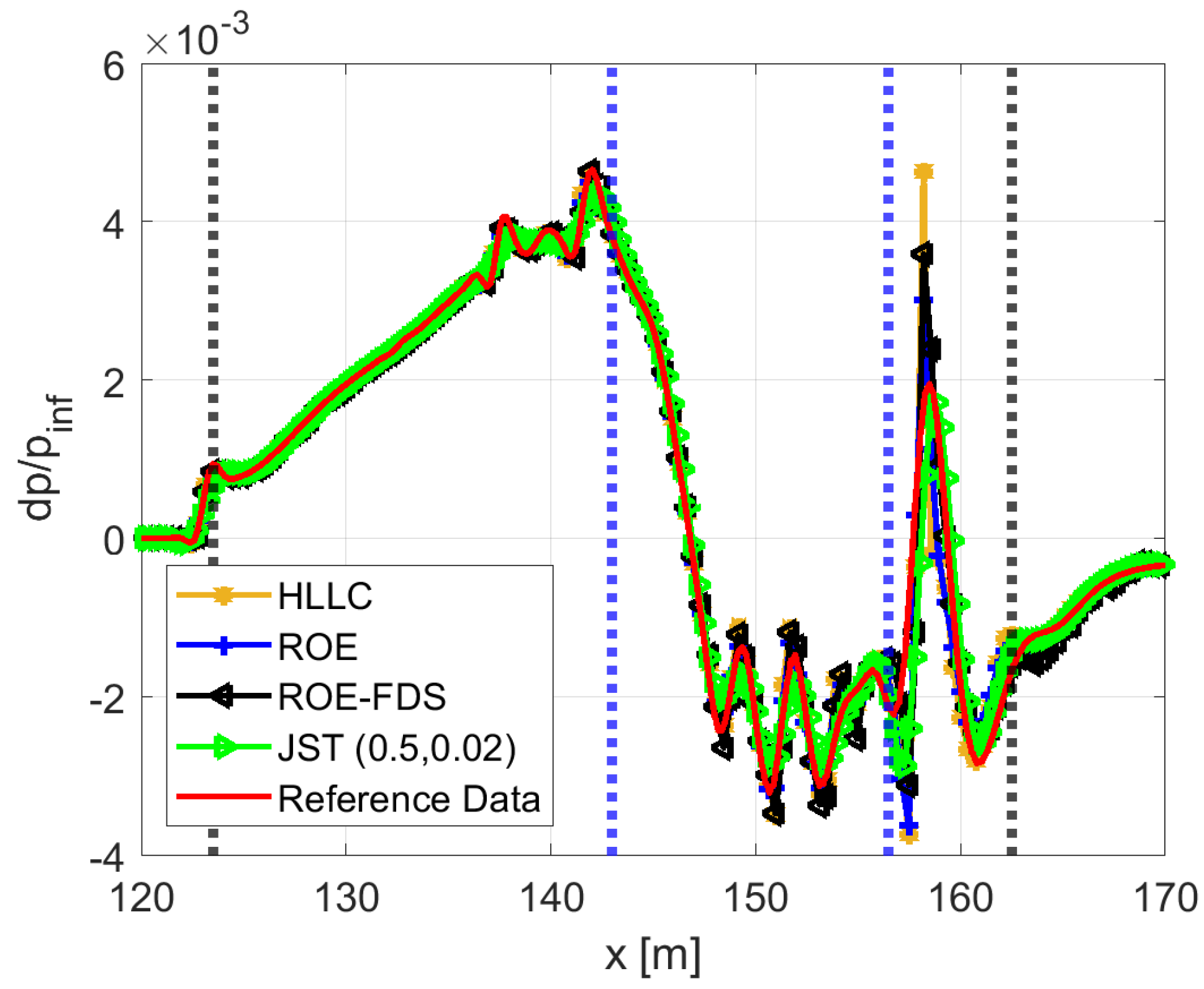
2.4.1. AXIE 2D Test Case
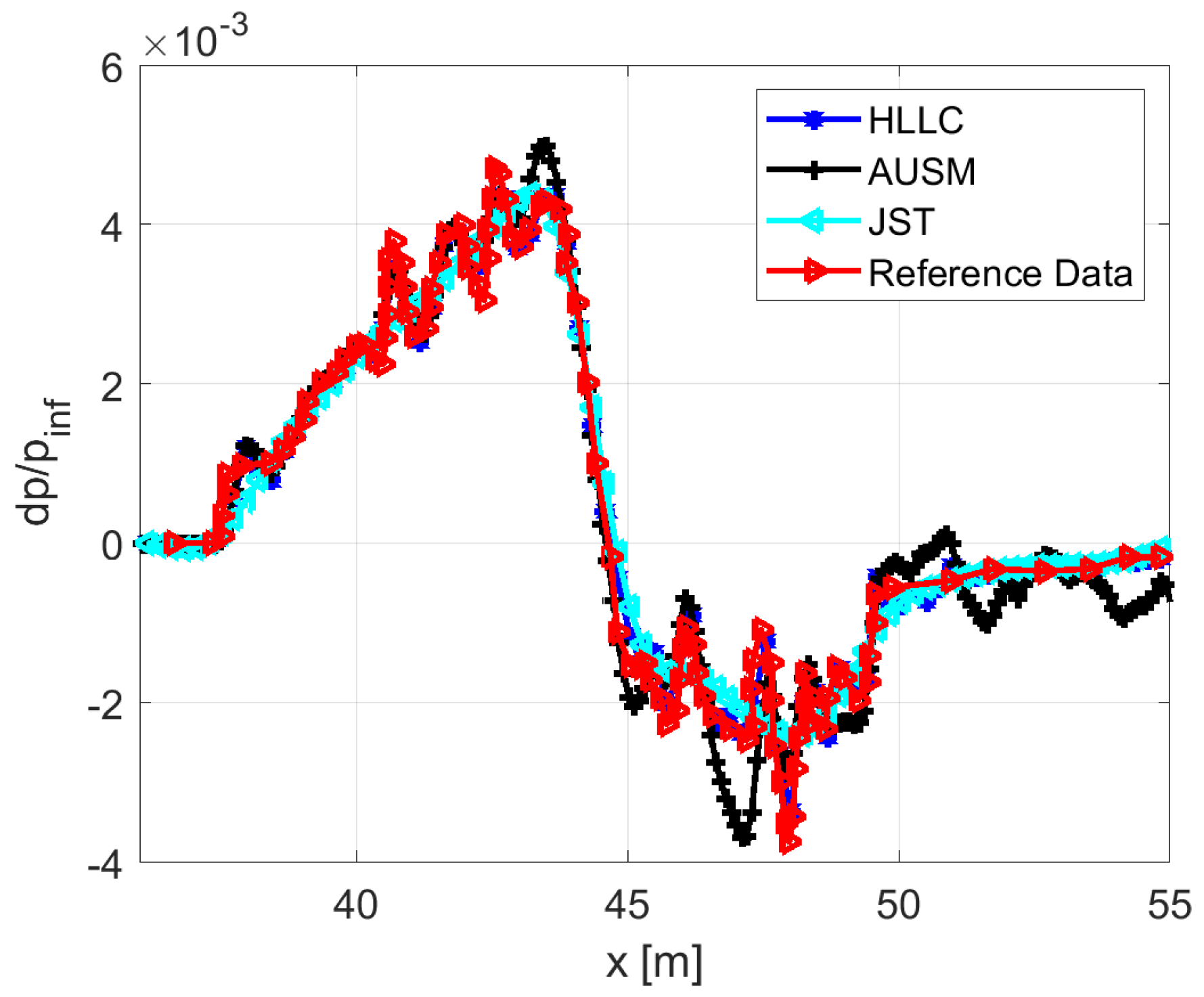
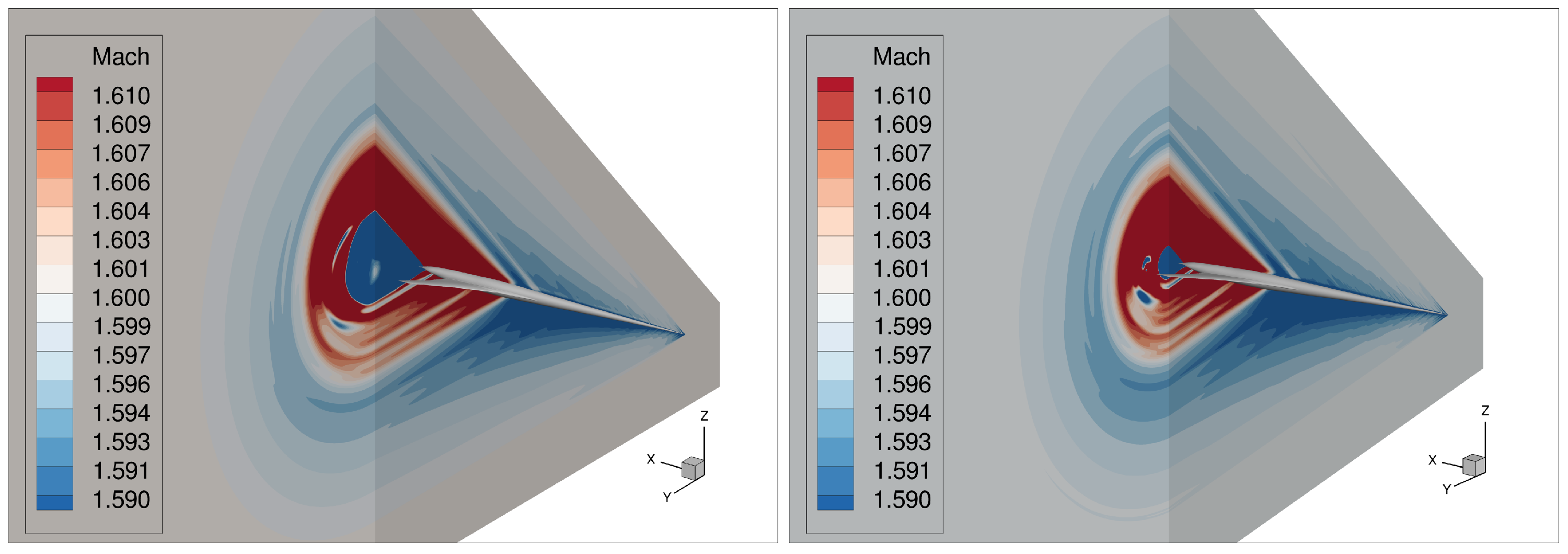
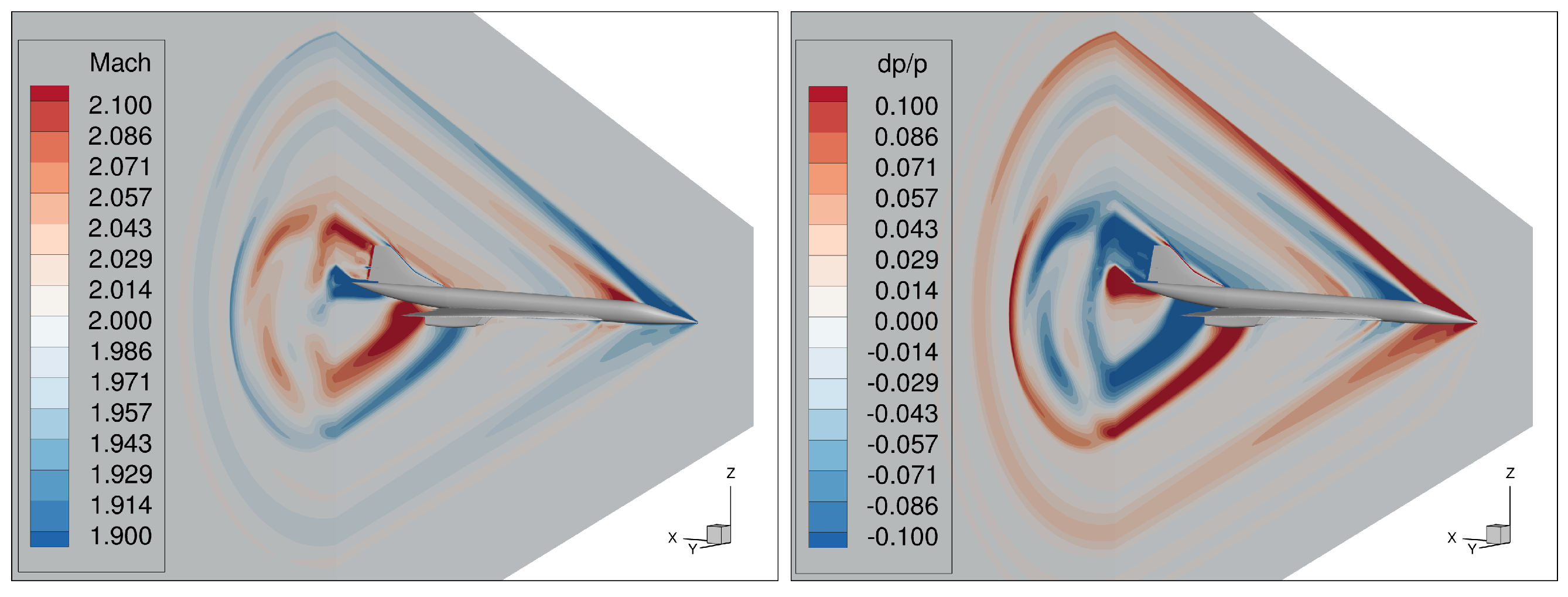
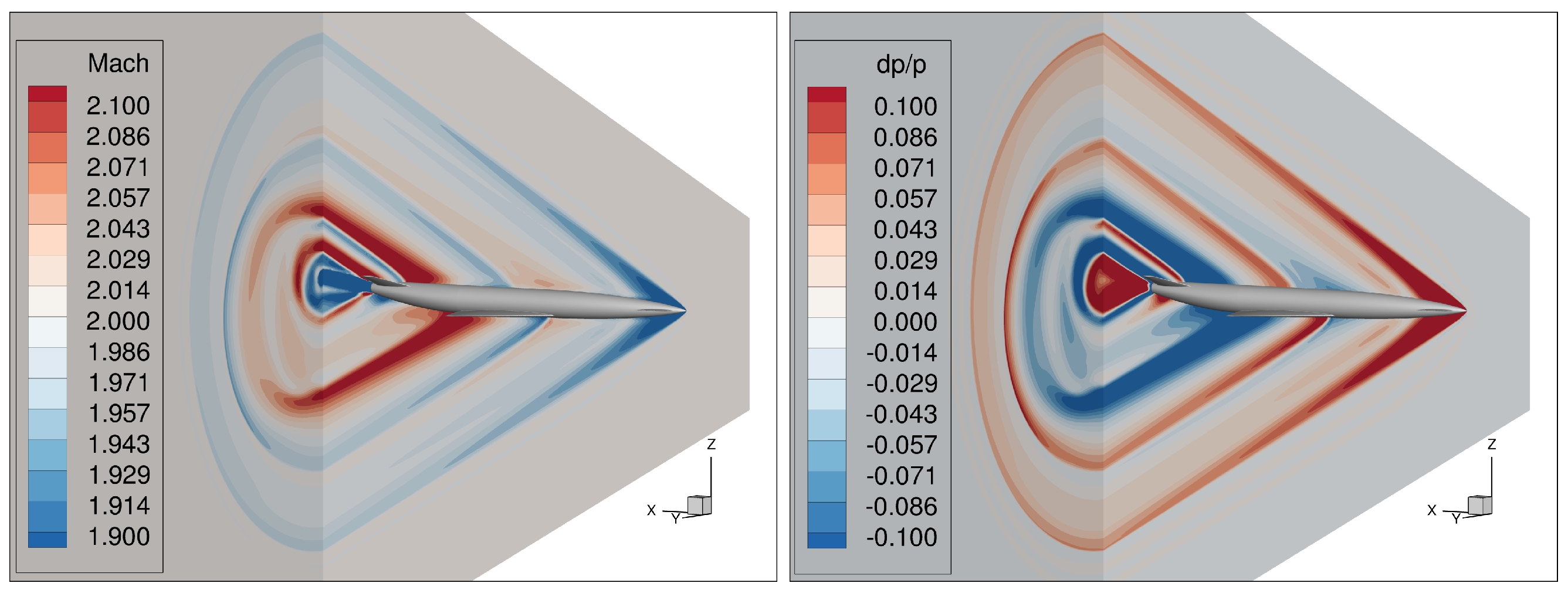
2.4.2. AXIE 3D Test Case
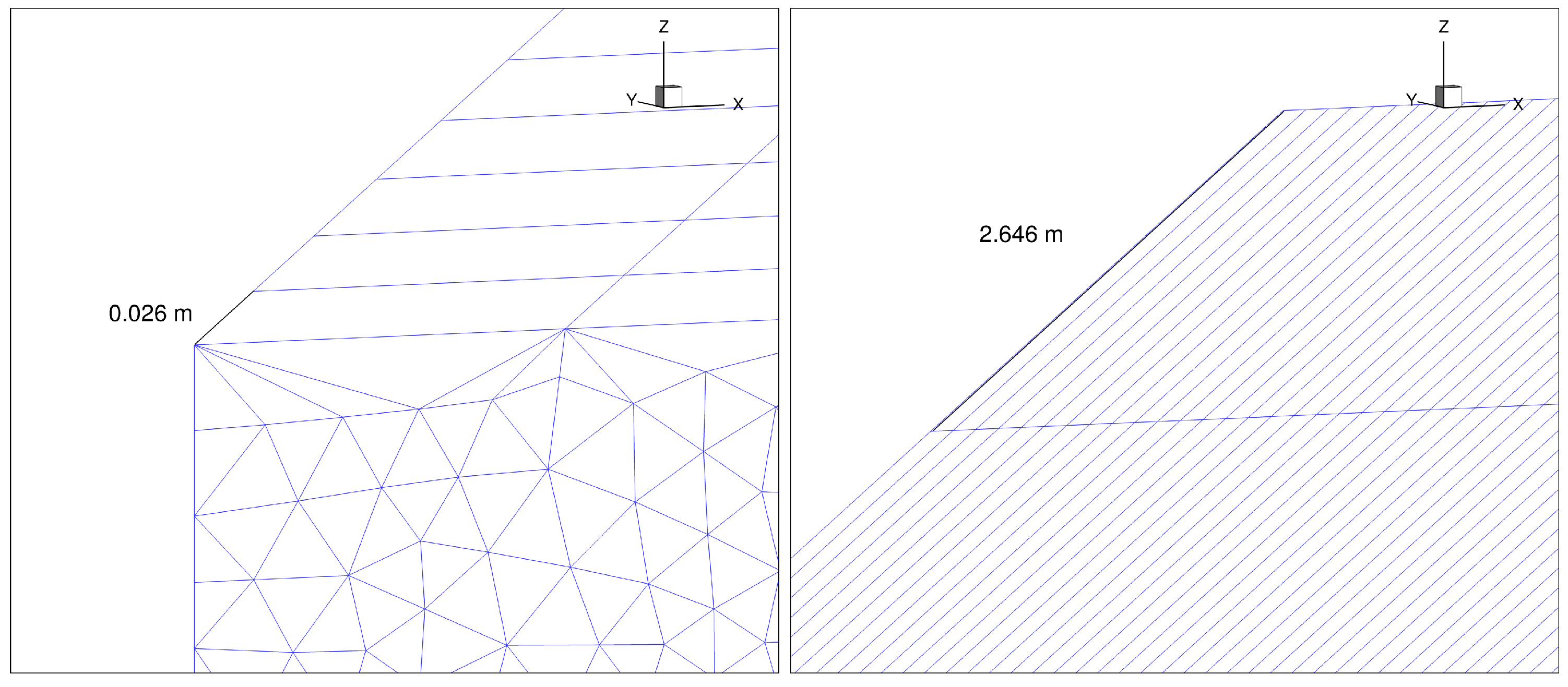
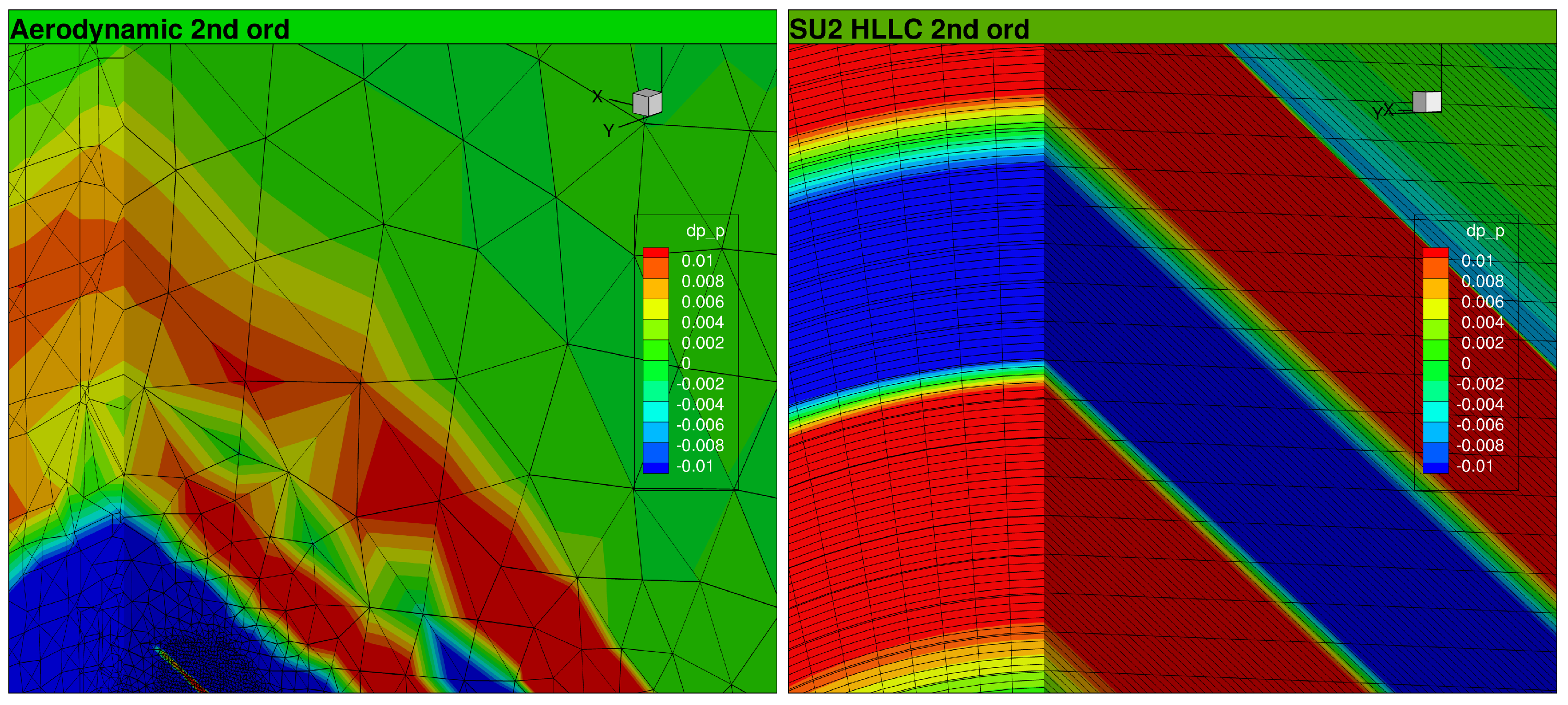
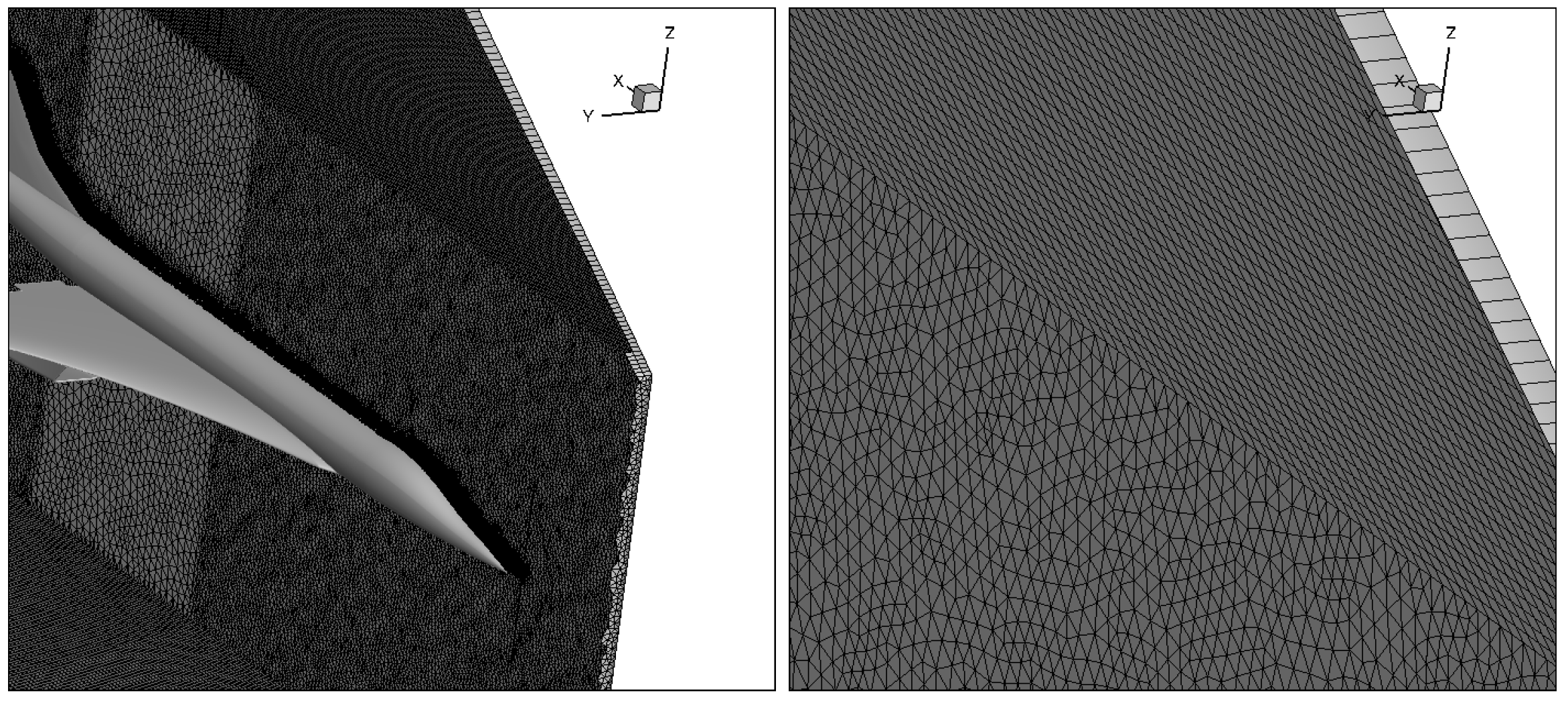
2.4.3. AXIE 3D Hybrid Grid
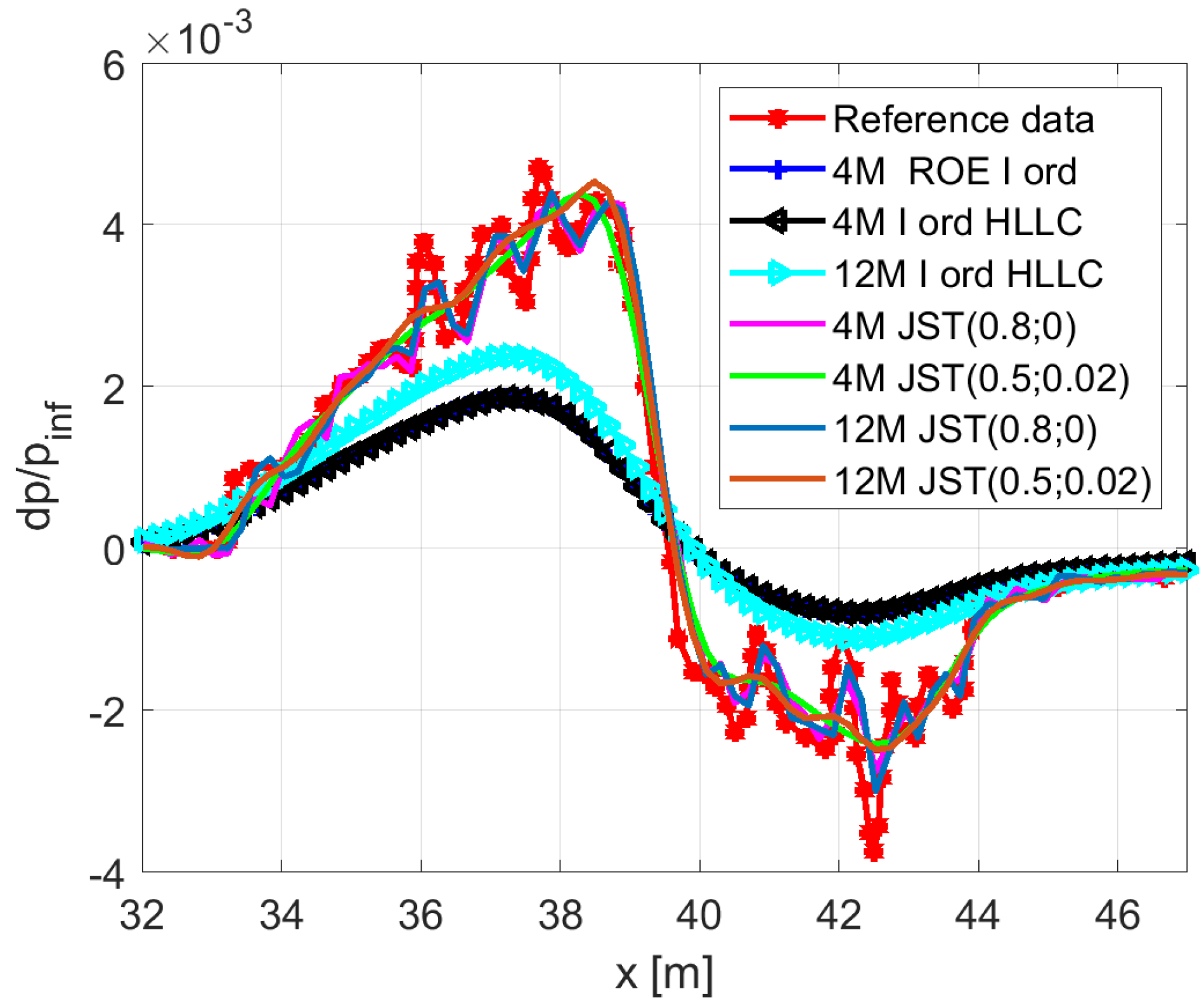
2.4.4. Different Refinement Laws
- Uniform law: All cells have the same size along the radial direction.
- Geometric law: Cell sizes increase progressively using a constant growth rate from the geometry outward.
2.5. JWB Geometry
2.5.1. JWB 3D Test Case
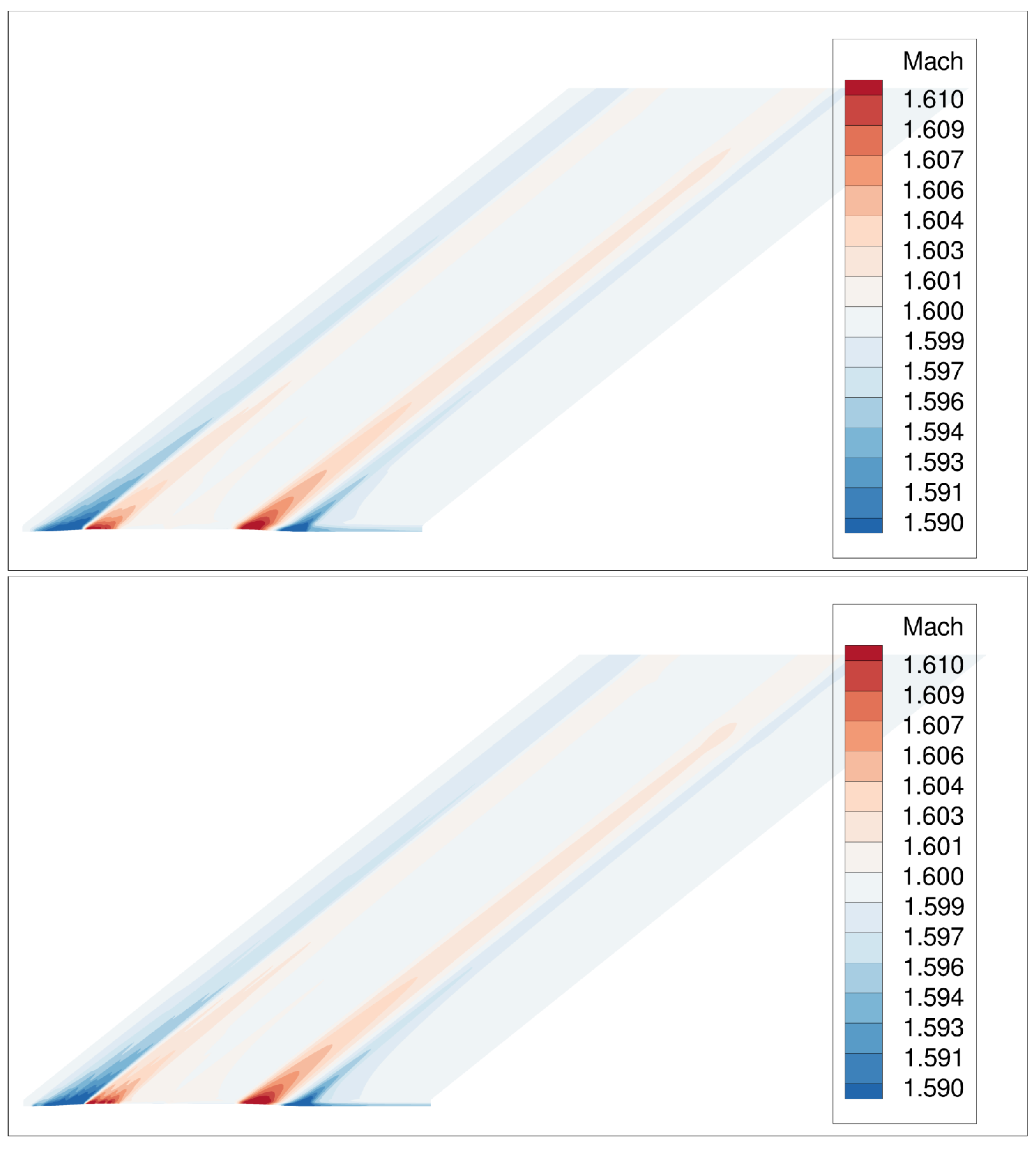
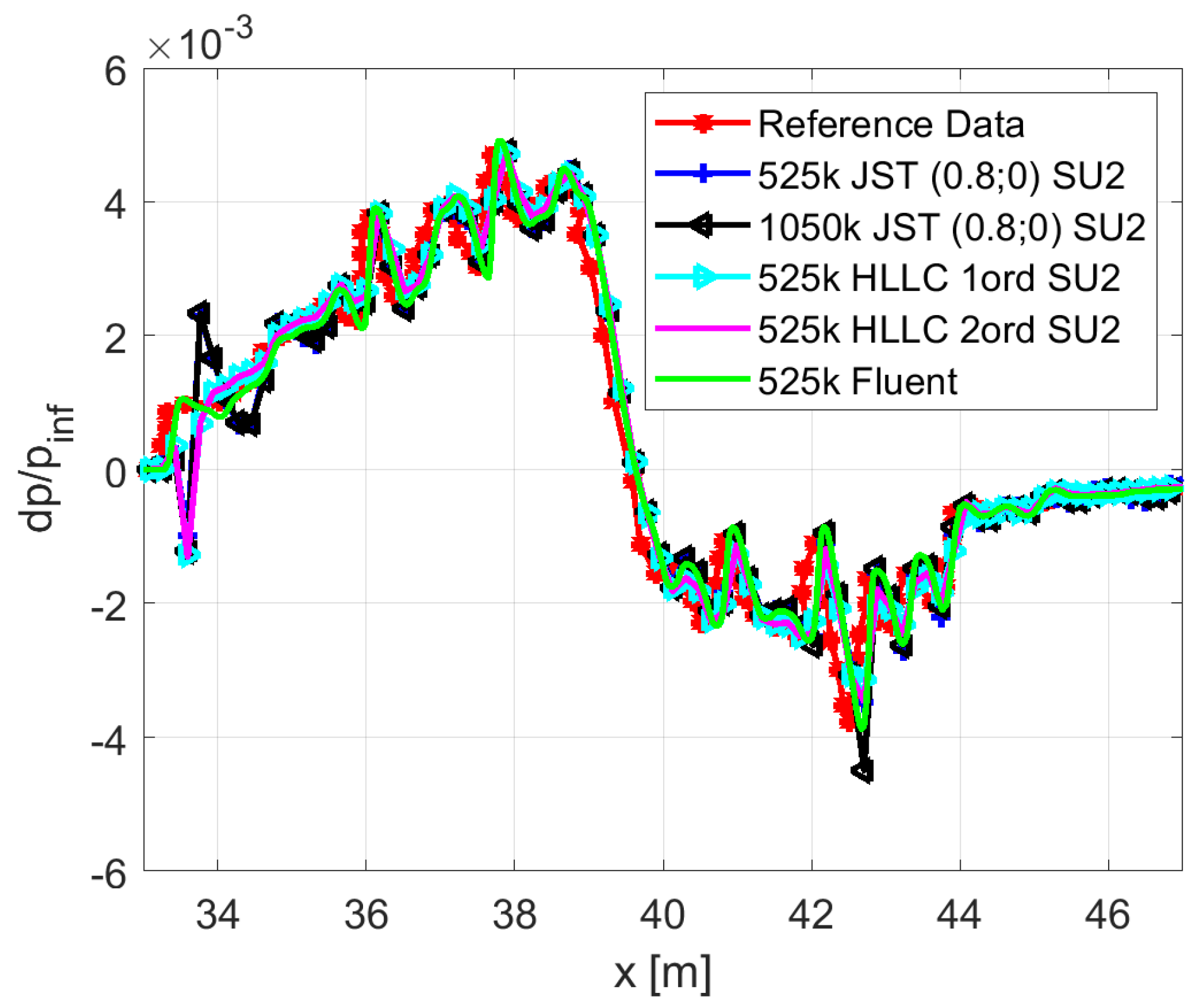
2.5.2. Refinement Strategy Effects for JWB
3. Conceptual Supersonic Aircraft
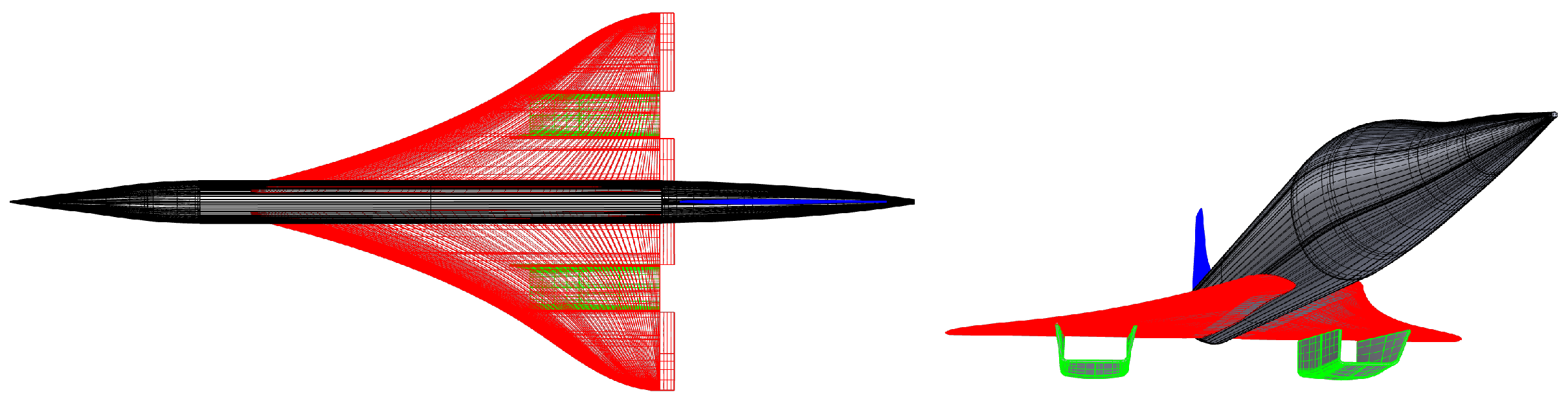
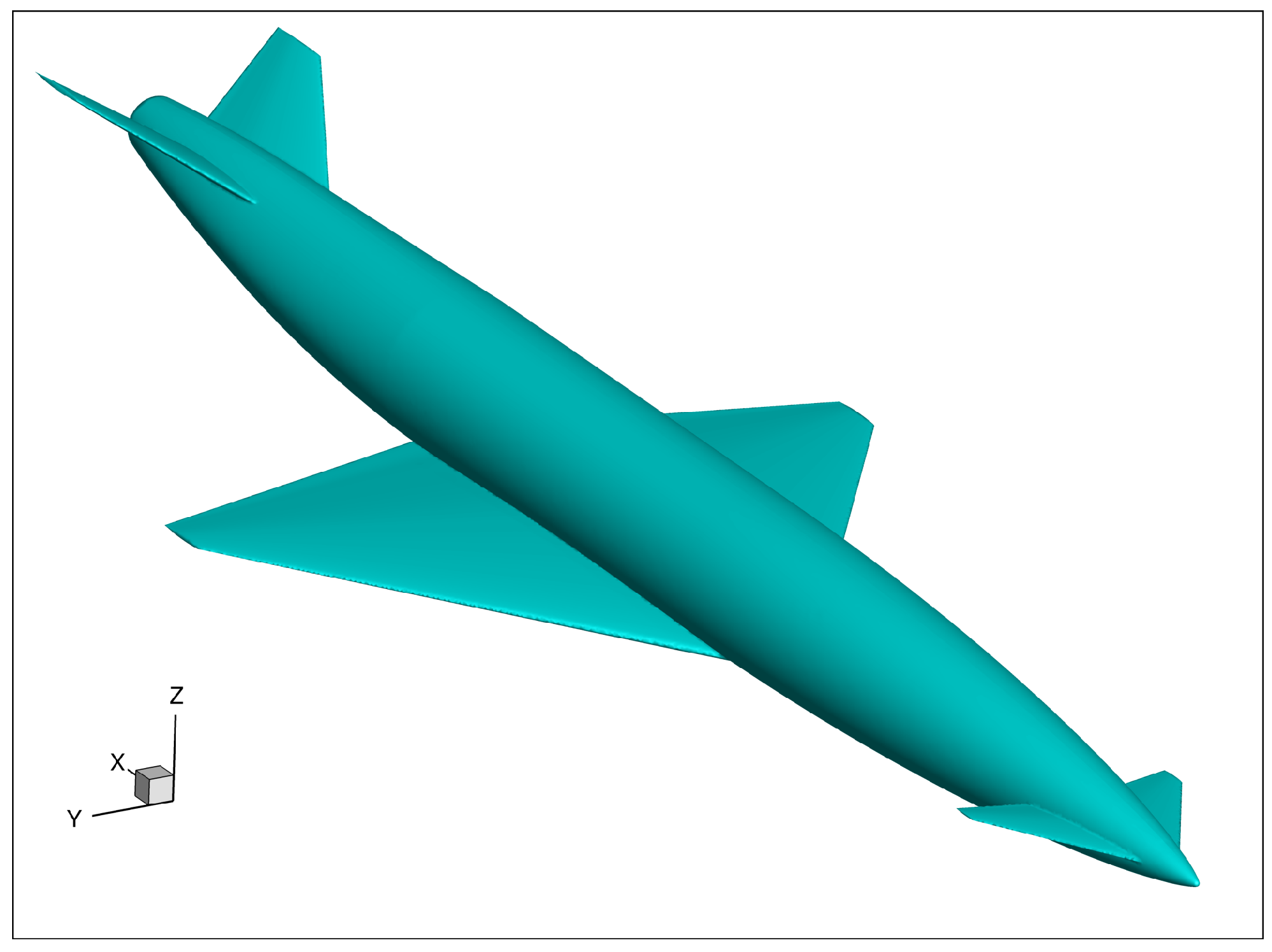
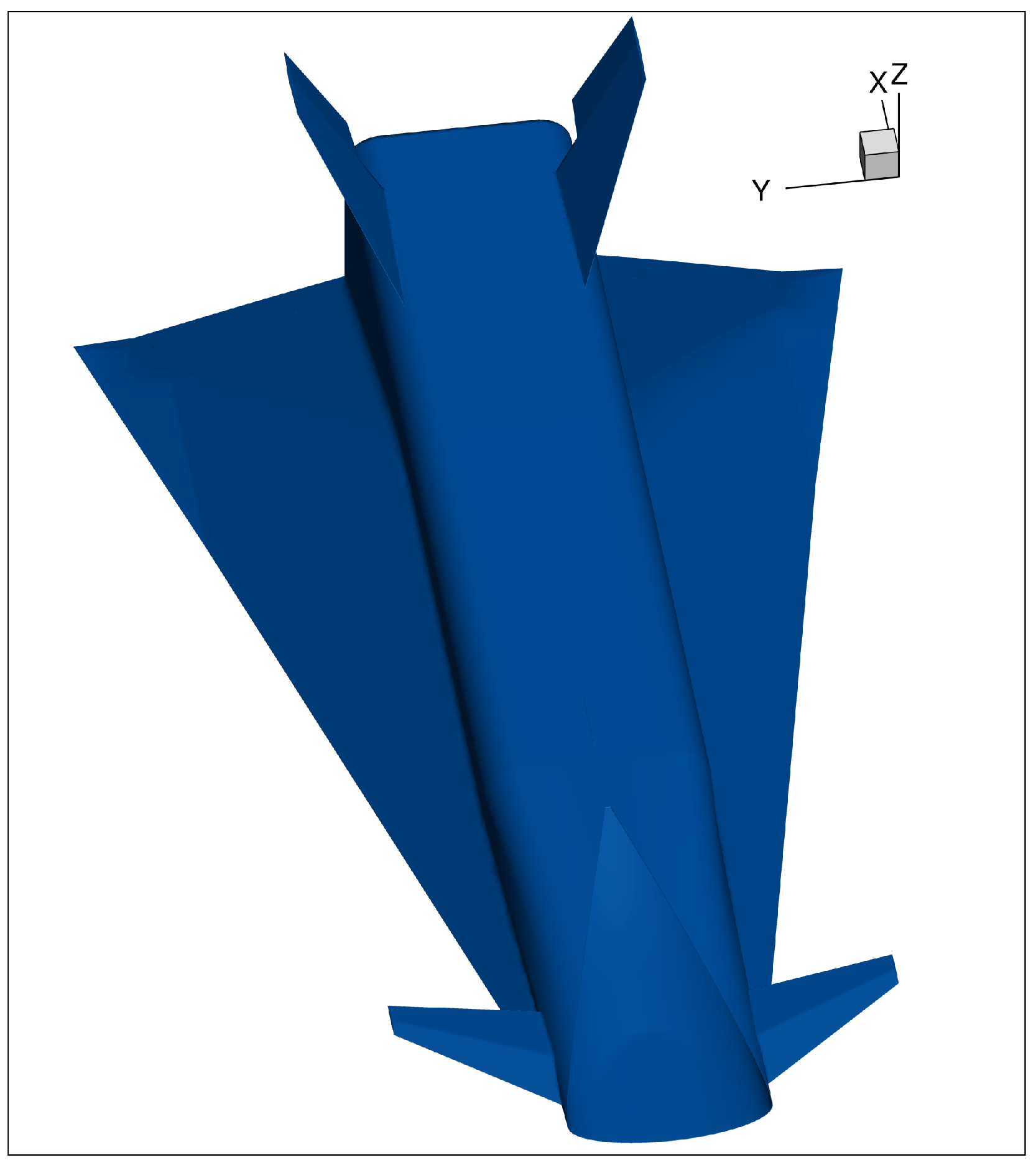
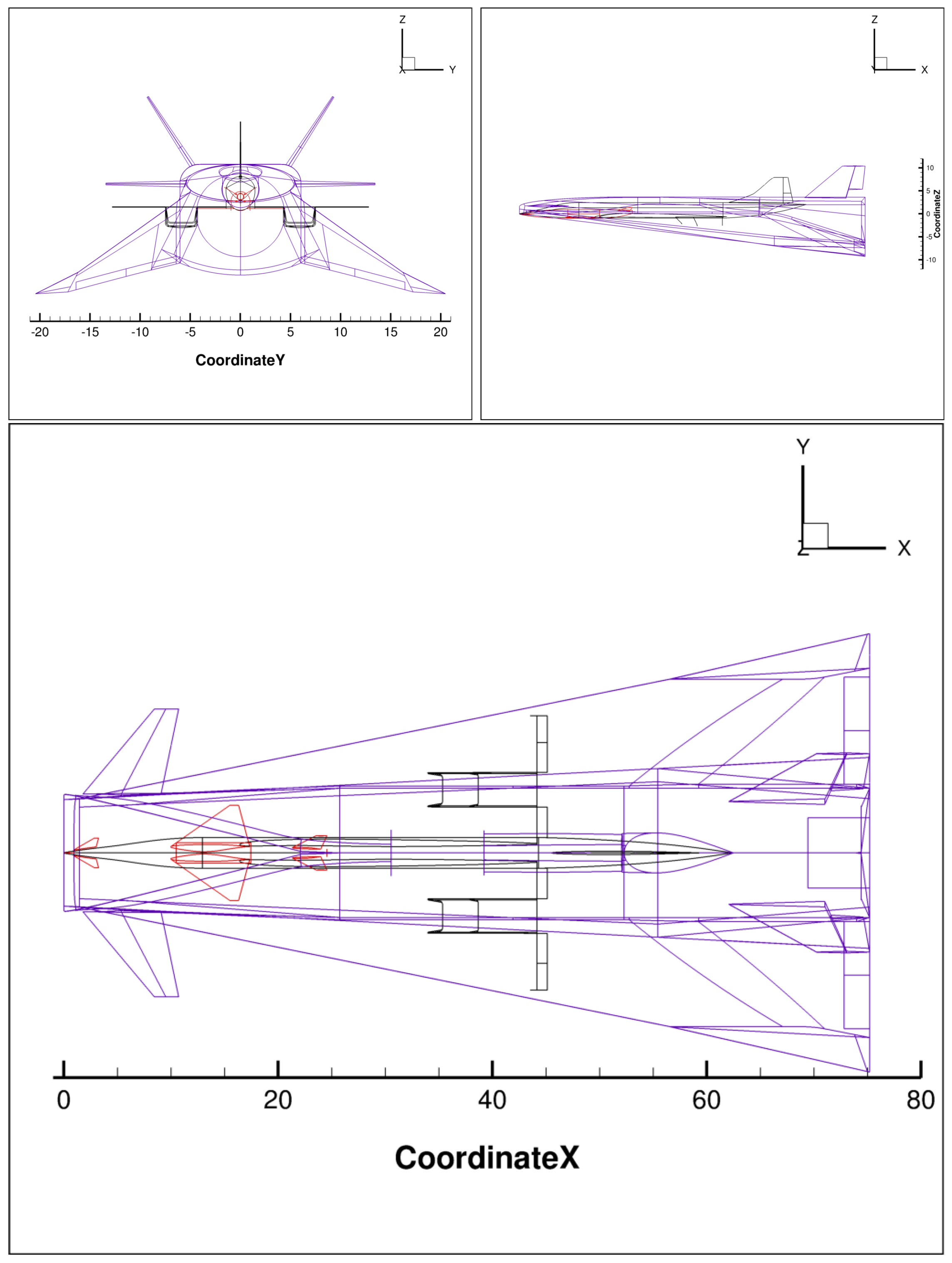
3.1. CS1 Geometry
3.2. CS2 Geometry
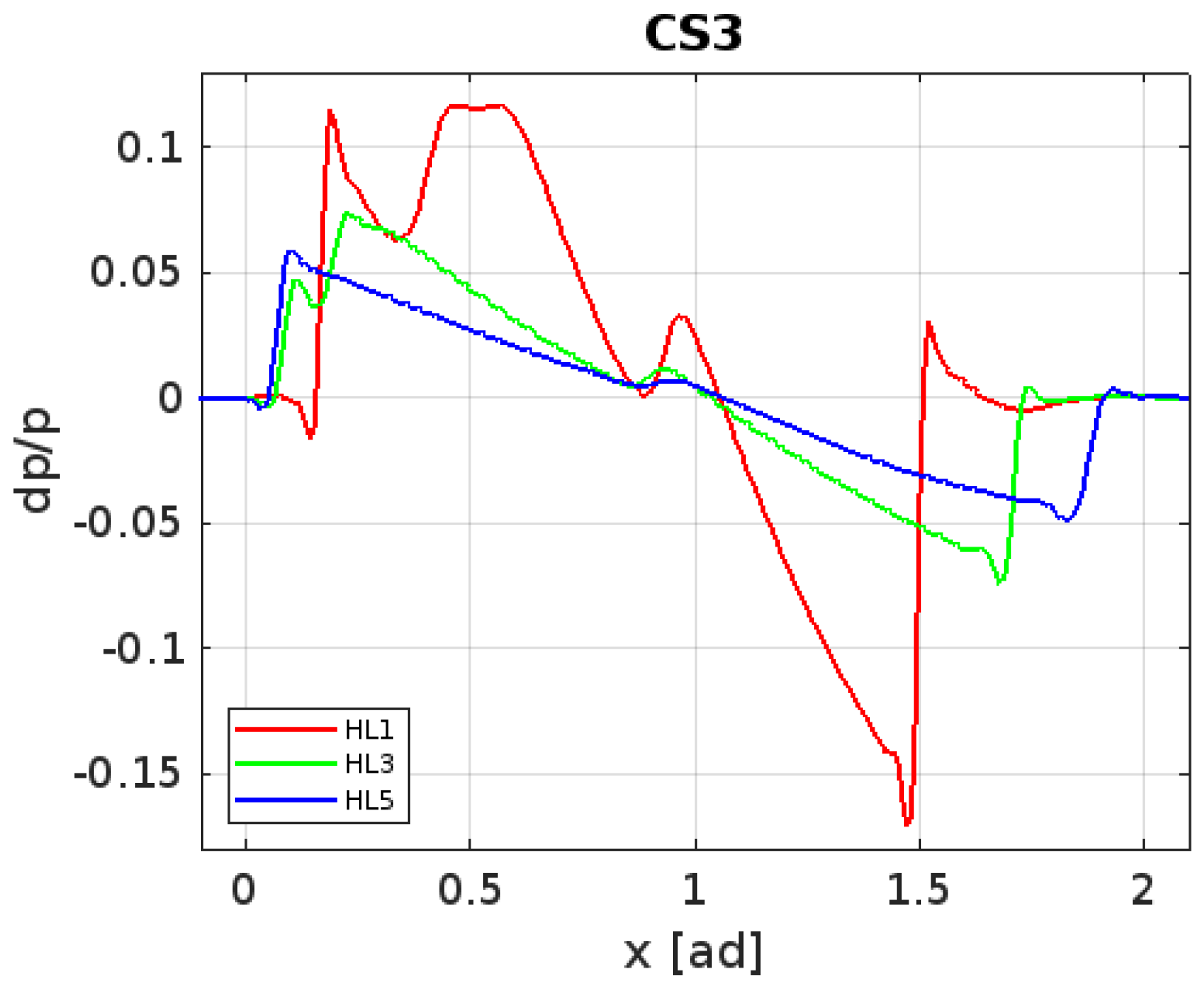
3.3. CS3 Geometry
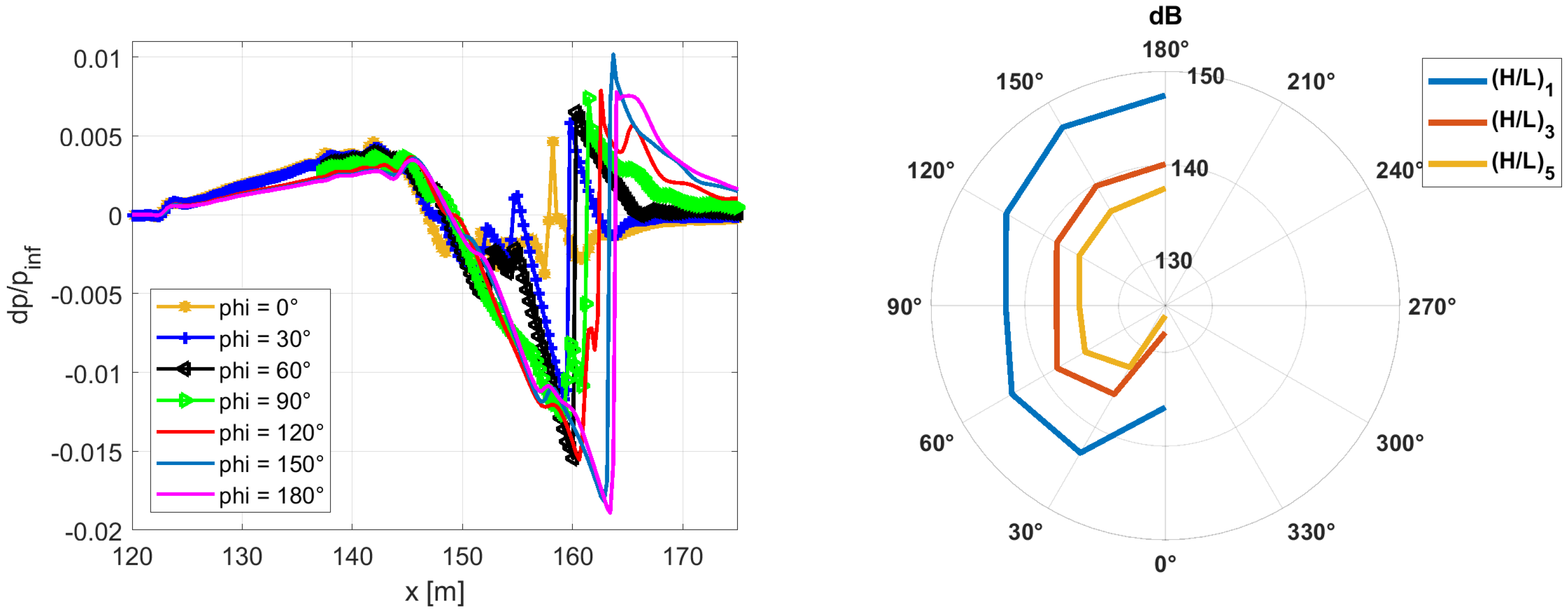
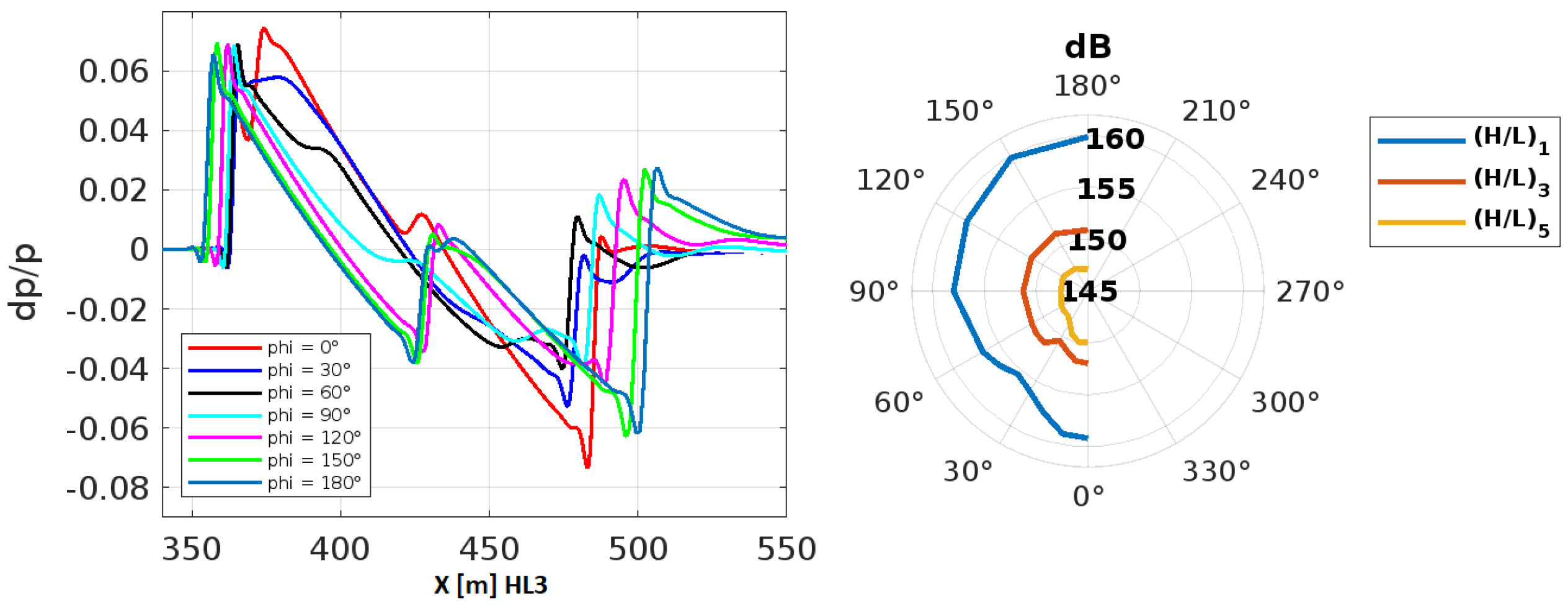
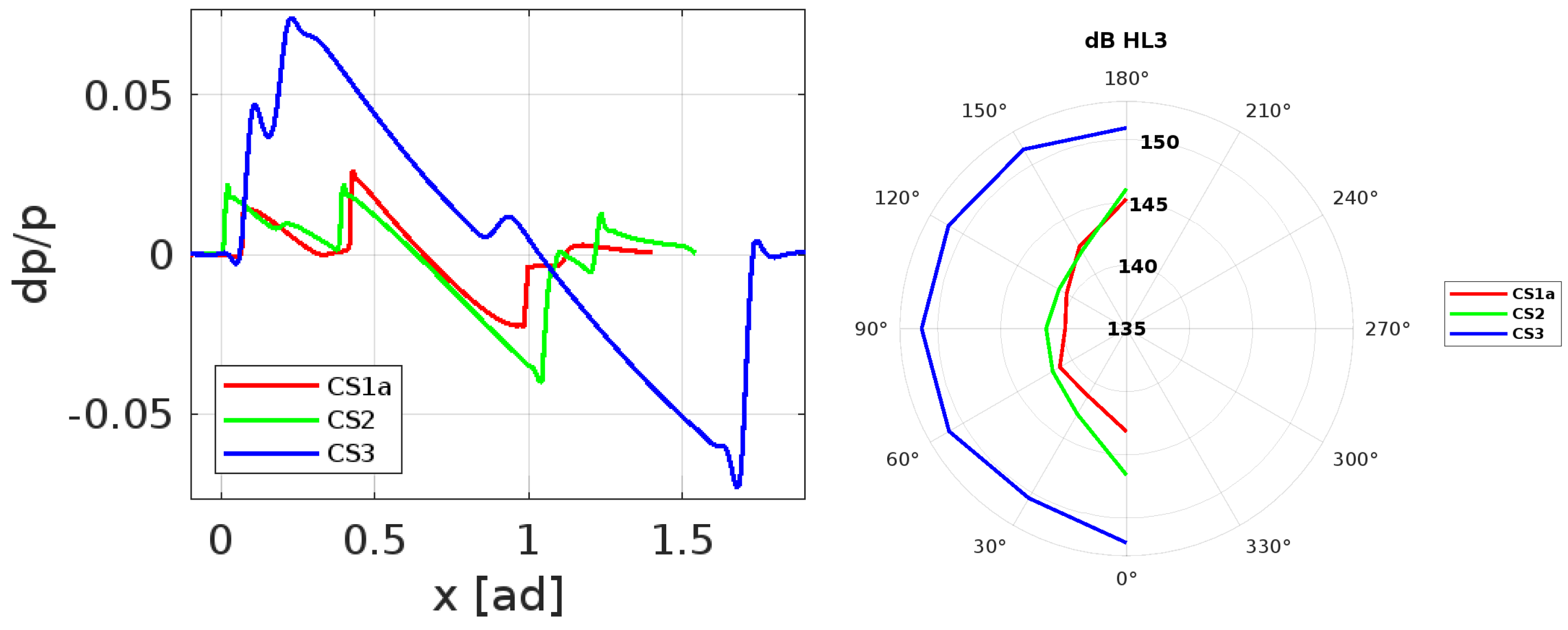
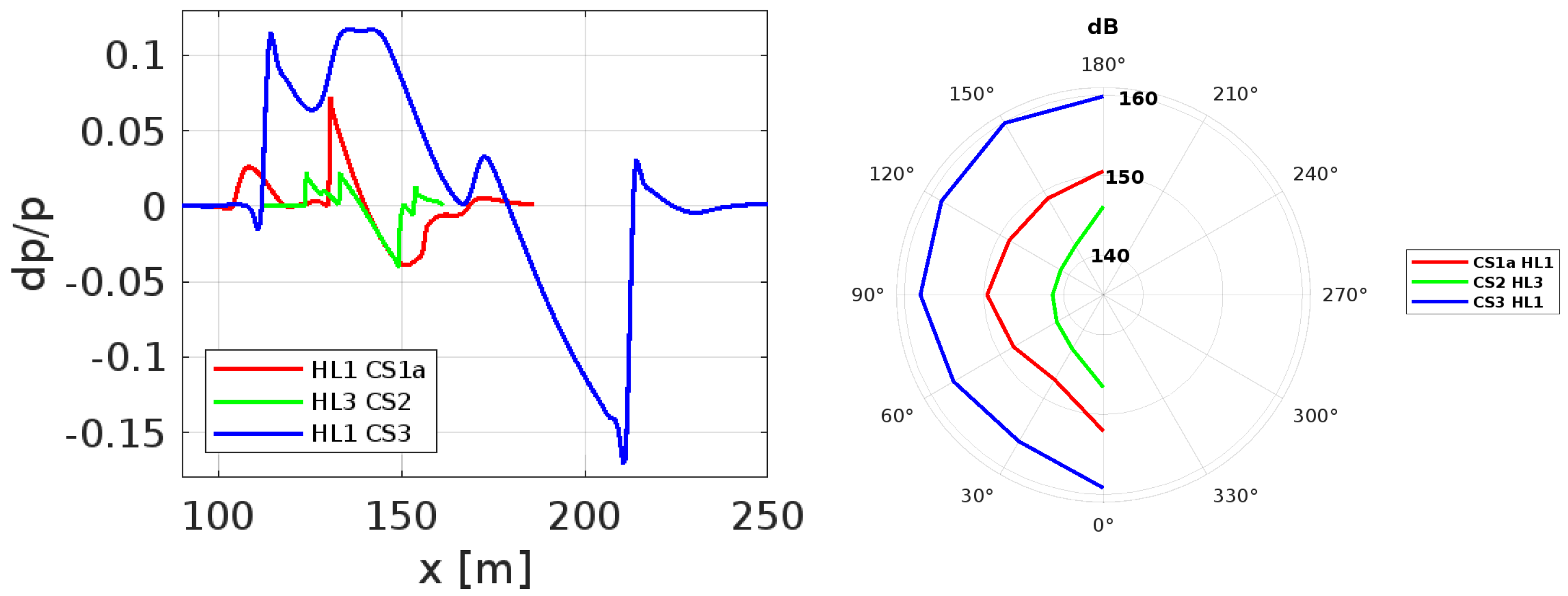
3.4. Comparison of Noise Performances
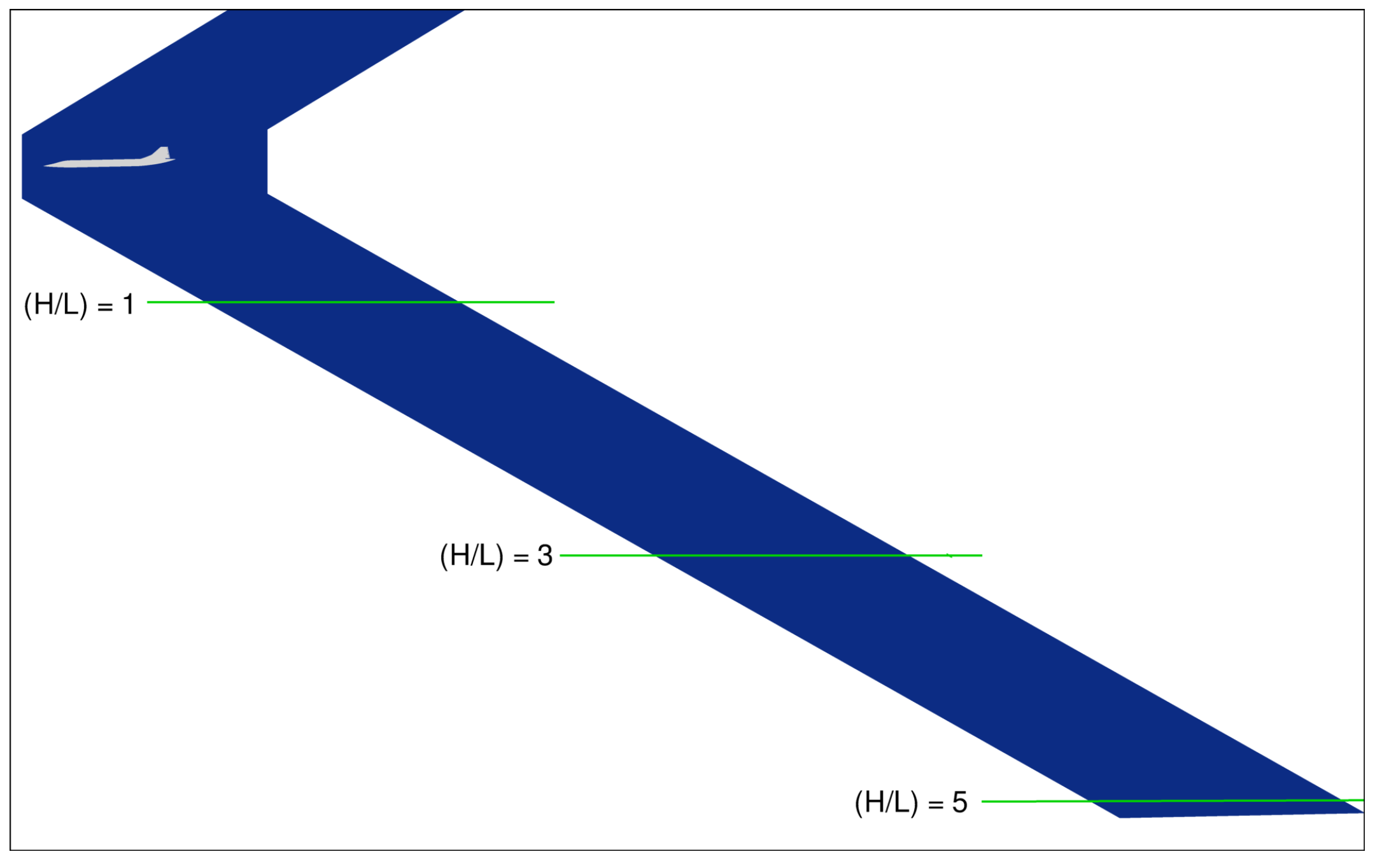
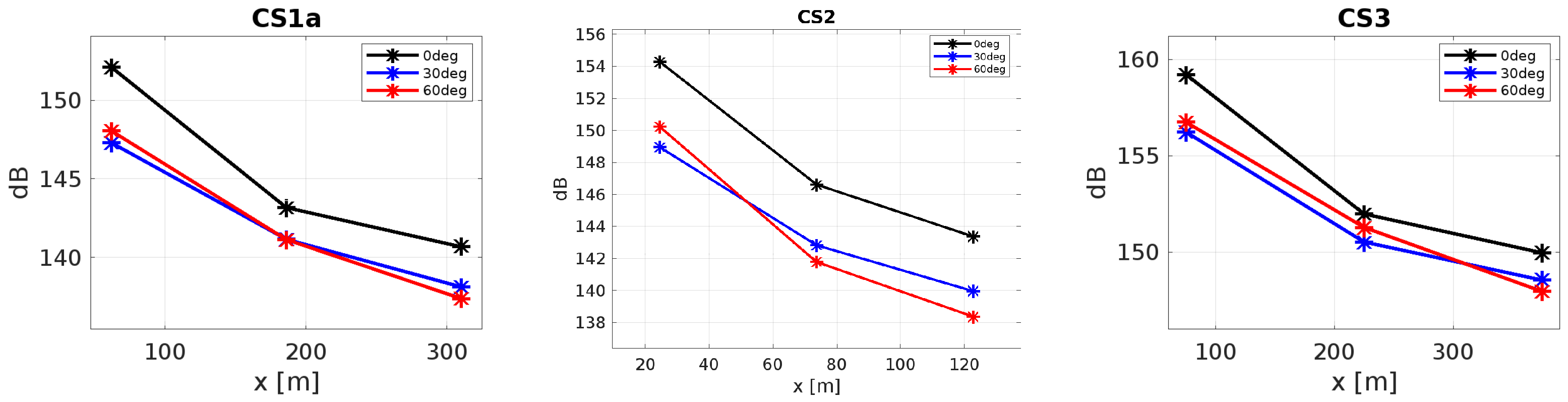
3.4.1. Noise Assessment at Non-Dimensionalized Distances
3.4.2. Noise Assessment at Equivalent Physical Distances
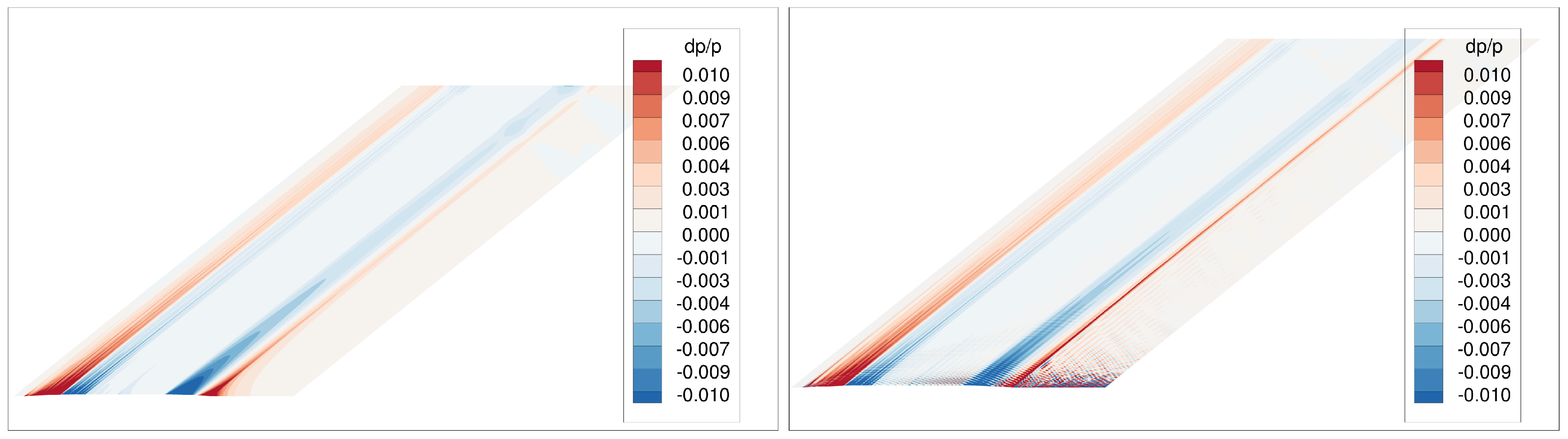
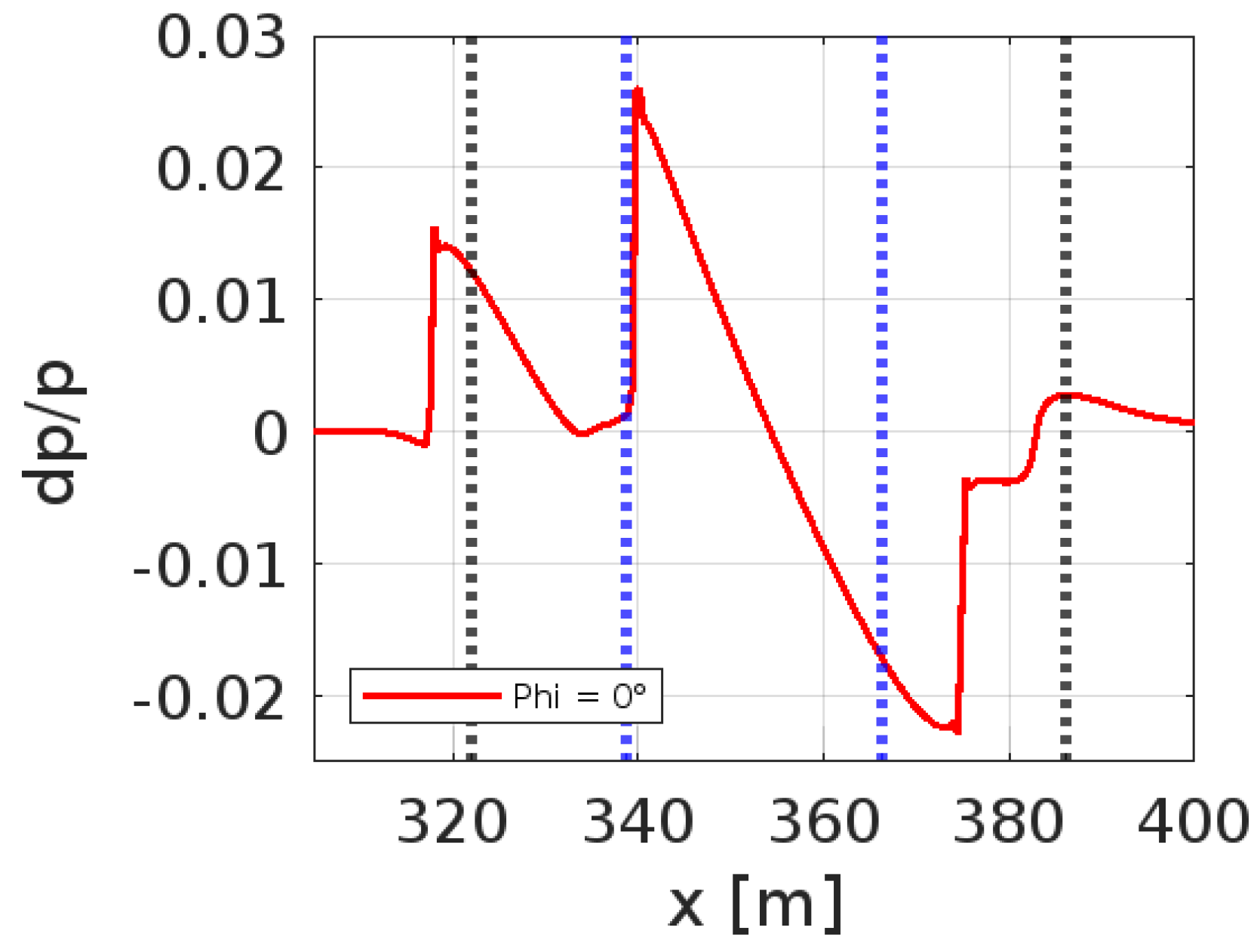
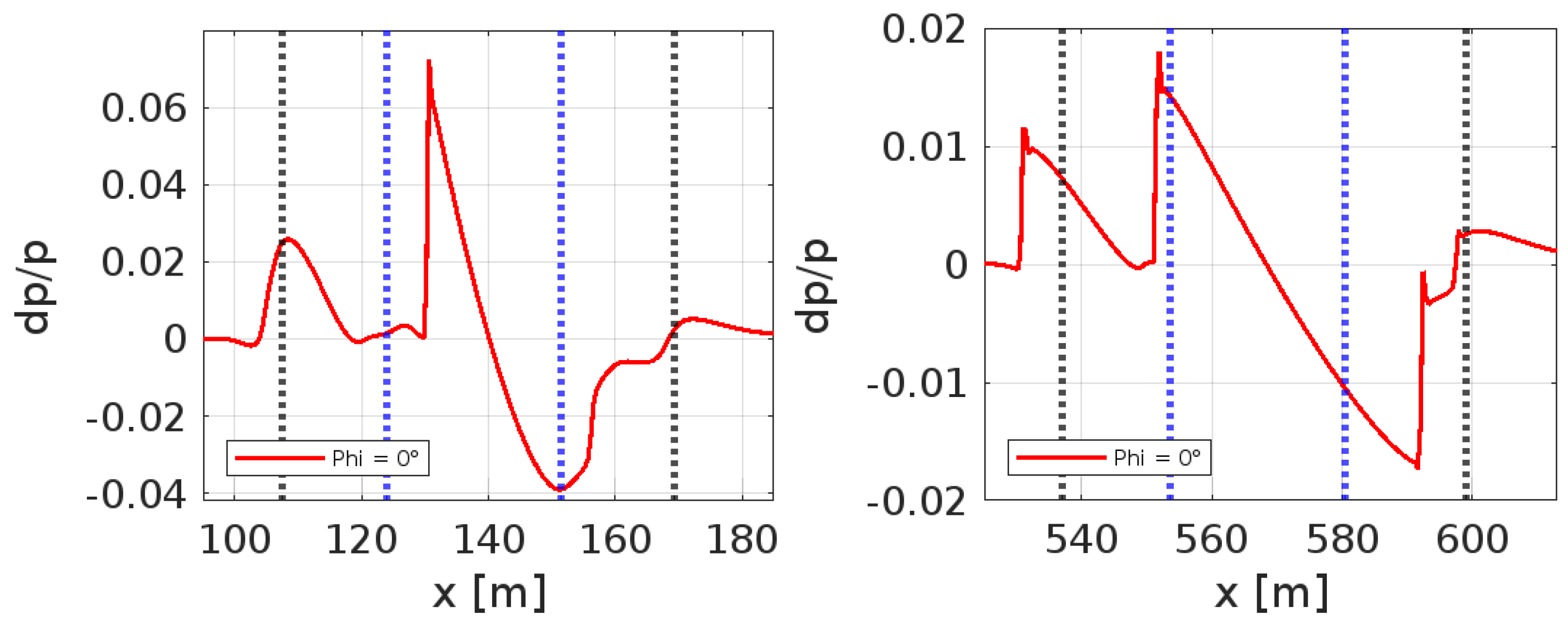
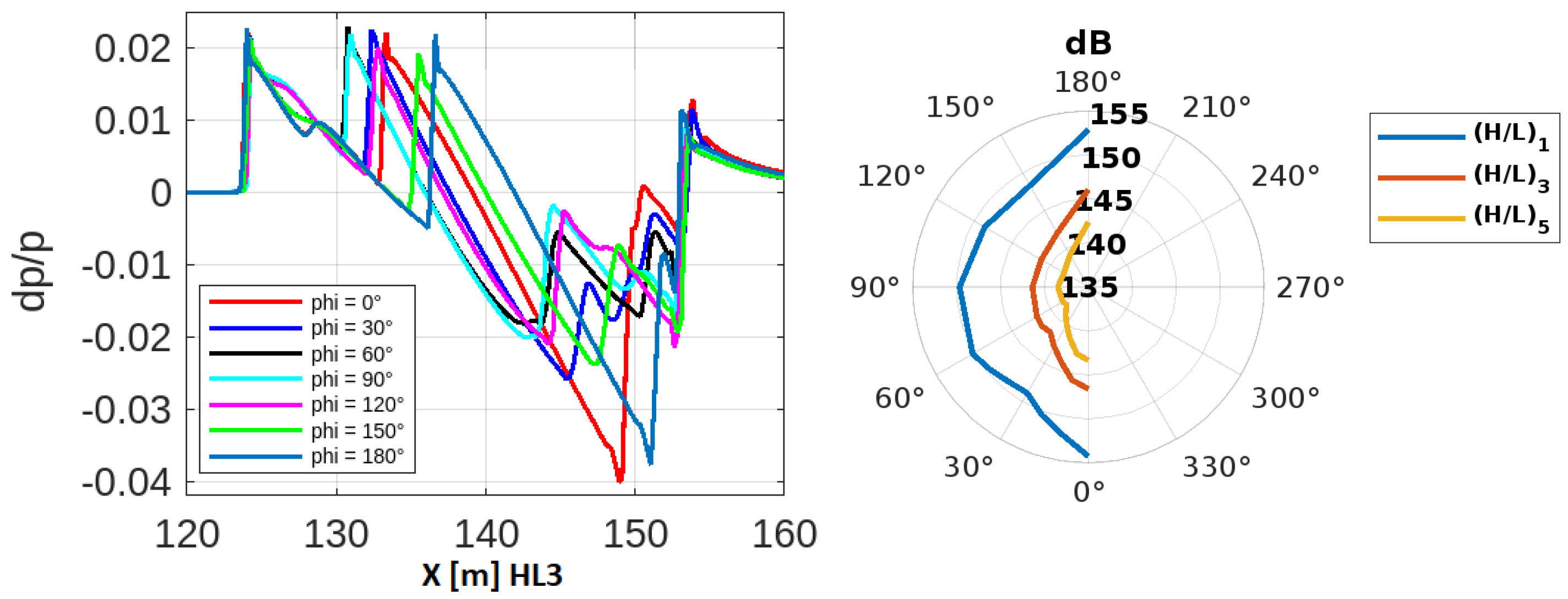
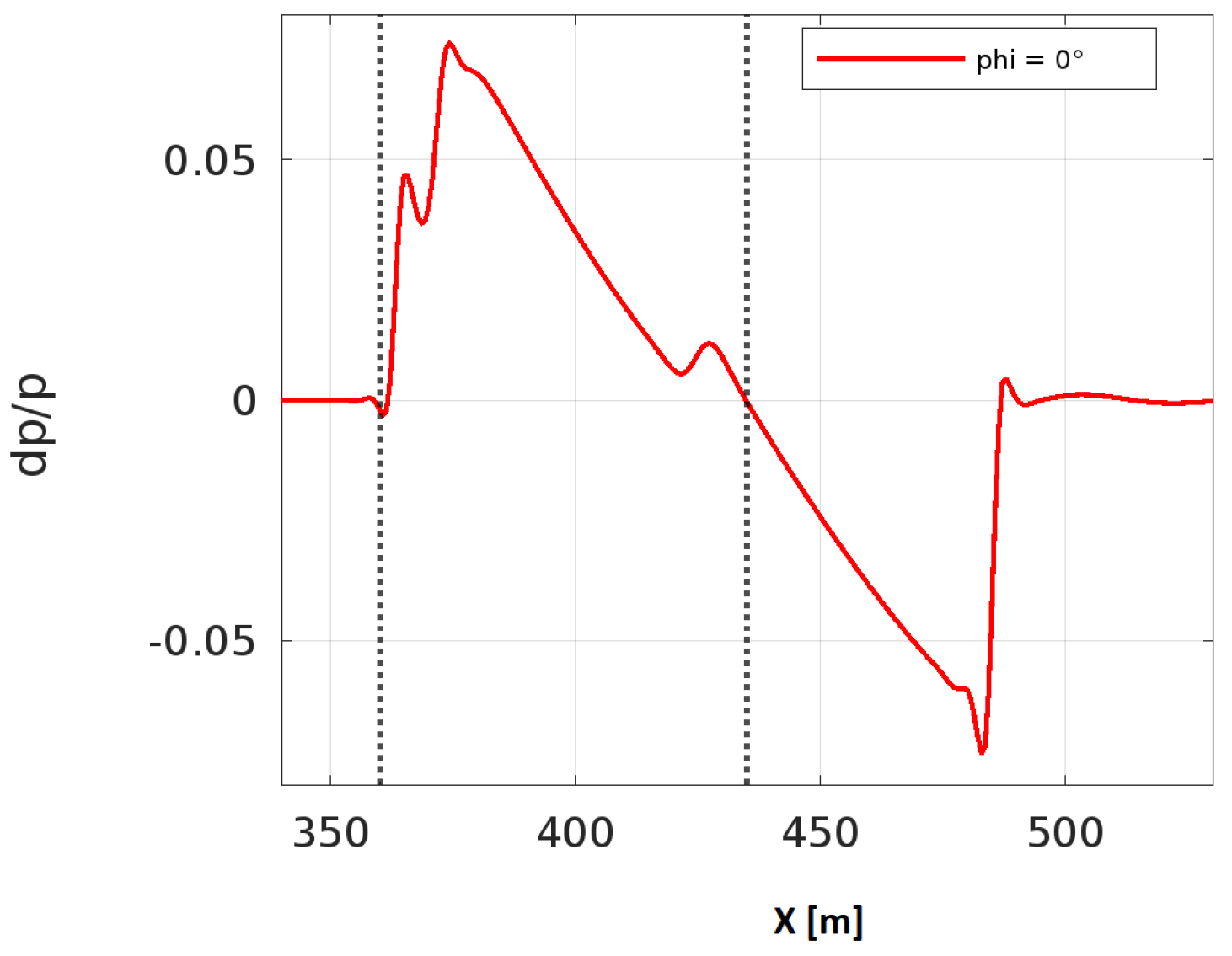
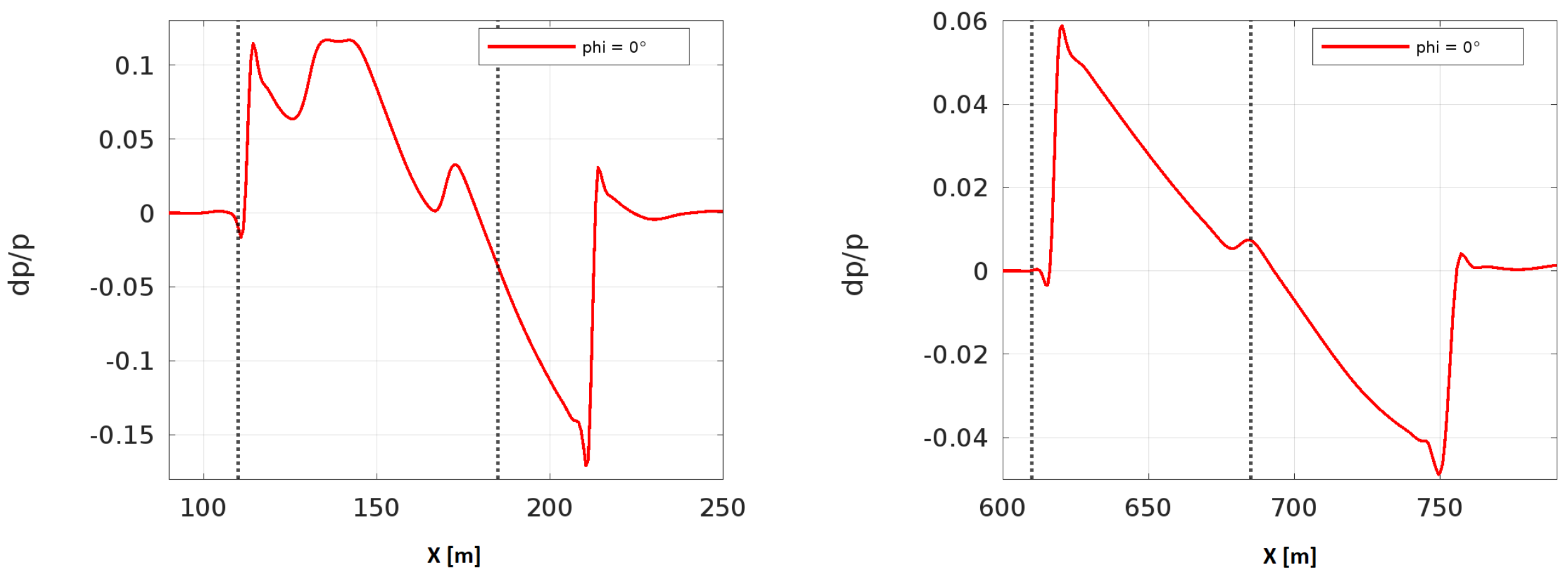
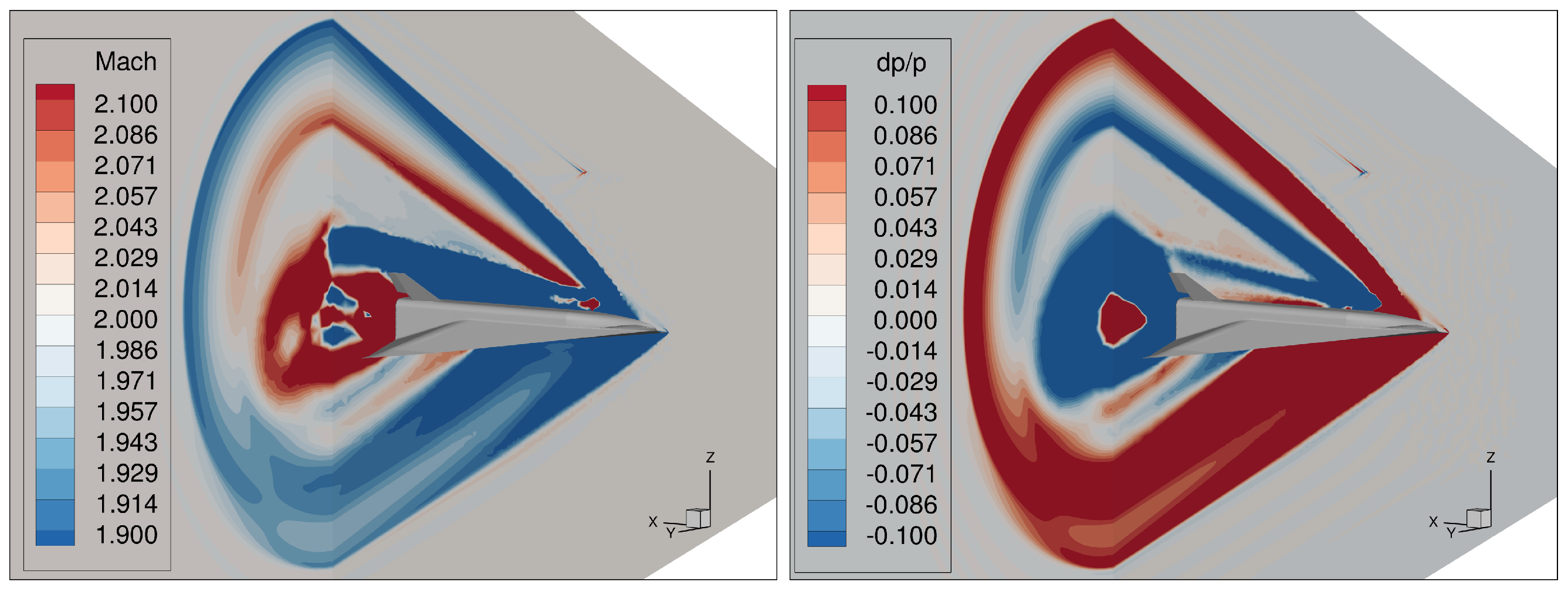
3.4.3. Propagation Effects in the Near-Field Domain
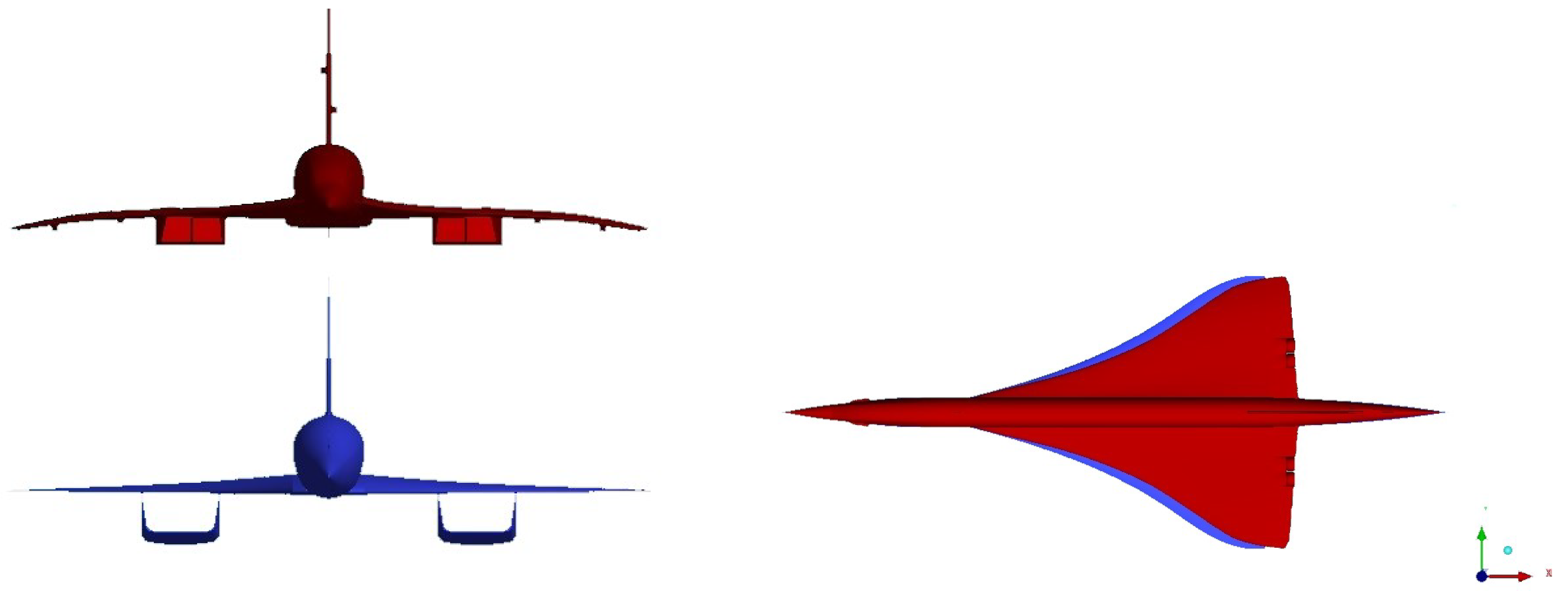
3.5. Influence of Geometry on the Pressure Signature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| dB | Decibel |
| PLdB | Perceived Level of Noise in Decibels |
| FAA | Federal Aviation Administration |
| ICAO | International Civil Aviation Organization |
| CFD | Computational Fluid Dynamics |
| SPL | Sound Pressure Level |
| SEL | Sound Exposure Level |
| OASPL | Overall Sound Pressure Level |
| SBPW | Sonic Boom Prediction Workshop |
| Pressure Coefficient | |
| M | Mach Number |
| RANS | Reynolds-Averaged Navier–Stokes |
| CFL | Courant Number |
References
- Liebhardt, B.; Lütjens, K. An Analysis of the Market Environment for Supersonic Business Jets. In Proceedings of the DLRK Tagungsband 2011: 60. Deutscher Luft- und Raumfahrtkongress in Bremen, Bremen, Germany, 27–29 September 2011; Available online: https://elib.dlr.de/75275/ (accessed on 3 September 2025).
- Herbert, S.R.; Hubbard, H.H. Sonic Boom Symposium. J. Acoust. Soc. Am. 1972, 51, 671. [Google Scholar] [CrossRef]
- Sparrow, V.W. Sonic Boom Symposium. J. Acoust. Soc. Am. 2002, 111, 479. [Google Scholar] [CrossRef]
- Maglieri, D.J. Some Effects of Airplane Operations and the Atmosphere on Sonic-Boom Signatures. J. Acoust. Soc. Am. 1966, 39, S36–S42. [Google Scholar] [CrossRef]
- Henderson, L.F.; Moore, F.K. The Approach to Far-Field Sonic Boom; NASA Conference Publication: Washington, DC, USA, 1968; p. 180. [Google Scholar]
- Caughey, D.A.; Gardner, J.H.; Hayes, W.D.; Weiskopf, F.B., Jr. Theoretical Problems Related to Sonic Boom; NASA Conference Publication: Washington, DC, USA, 1971; p. 255. [Google Scholar]
- Christine, M.D.; Powell, C.A. Status of Sonic Boom Methodology and Understanding; NASA Conference Publication: Washington, DC, USA, 1988; p. 3027. [Google Scholar]
- Giofriddo, T.A. Analysis of Sonic Boom Data to Quantify Distortions of Shock Profiles; NASA Conference Publication: Washington, DC, USA, 1992; p. 3172. [Google Scholar]
- Pierce, A.D. Progress in Modeling Atmospheric Propagation of Sonic Booms; NASA Conference Publication: Washington, DC, USA, 1993; p. 10132. [Google Scholar]
- Robinson, L.D. An Evaluation of Rise Time Characterization and Prediction Methods; NASA Conference Publication: Washington, DC, USA, 1994; p. 3279. [Google Scholar]
- Maglieri, D.J.; Bobbitt, P.J.; Plotkin, K.J.; Shepherd, K.P. Sonic Boom, Six Decades of Research; NASA, SP-2014-622; NASA Conference Publication: Washington, DC, USA, 2014. [Google Scholar]
- Kelly, R.; Laflin, S.M.K. A Hybrid Computational Fluid Dynamics Procedure for Sonic Boom Prediction. In Proceedings of the 24th Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- El Din, I.S.; Carrier, G.; Grenon, R.; Le Pape, M.C.; Minelli, A. Overview of Sonic Boom CFD Prediction Methodology in Use at ONERA and its Application to Supersonic Business Jet Configuration Design. In Proceedings of the 11th ONERA-DLR Aerospace Symposium, Toulouse, France, 9–11 February 2011. [Google Scholar]
- Park, M.A.; Nemec, M. Numerical and Mesh Resolution Requirements for Accurate Sonic Boom Prediction. J. Aircr. 2009, 46. [Google Scholar] [CrossRef]
- Park, M.; Morgenstern, J. Summary and Statistical Analysis of the First AIAA Sonic Boom Prediction Workshop. J. Aircr. 2014, 53, 578–598. [Google Scholar] [CrossRef]
- Park, M.A.; Nemec, M. Nearfield Summary and Statistical Analysis of the Second AIAA Sonic Boom Prediction Workshop. J. Aircr. 2019, 56, 851–875. [Google Scholar] [CrossRef]
- Park, M.A.; Carter, M.B. Nearfield Summary and Analysis of the Third AIAA Sonic Boom Prediction Workshop C608 Low Boom Demonstrator. In Proceedings of the 3rd AIAA Sonic Boom Workshop Report-Out II: Nearfield CFD Cases, Virtual Event, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Park, M.A.; Carter, M.B. Near Field Summary and Analysis of the Third AIAA Sonic Boom Prediction Workshop Shock-Plume Interaction Case. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Glorioso, A.; Petrosino, F.; Aprovitola, A.; Barbarino, M.; Pezzella, G. Sonic Boom generation using open source CFD approach. In Proceedings of the AIAA Aviation 2023 Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar] [CrossRef]
- Glorioso, A.; Petrosino, F.; Barbarino, M.; Pezzella, G.; Viviani, A. Improvement on Open Source CFD Methodology To Evaluate Near-Field Sonic Boom. In Proceedings of the 30th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 4–7 June 2024. [Google Scholar] [CrossRef]
- Glorioso, A.; Petrosino, F.; Barbarino, M.; Pezzella, G.; Viviani, A. Sonic Boom Analysis of Different Supersonic Aircraft. In Proceedings of the 34th ICAS Congress 2024, Firenze, Italy, 9–13 September 2024. [Google Scholar]
- Economon, T.D.; Palacios, F.; Copeland, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An Open-Source Suite for Multiphysics Simulation and Design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- Ansys Fluent Fluid Simulation Software, ANSYS, Inc.: Canonsburg, PA, USA, 2018.
- Horizon2020. MDO and REgulations for Low-boom and Environmentally Sustainable Supersonic aviation. Grant Agreem. 2021. [Google Scholar] [CrossRef]
- Roe, P.L. Characteristic-Based Schemes for the Euler Equations. Annu. Rev. Fluid Mech. 1986, 18, 337–365. [Google Scholar] [CrossRef]
- Jameson, A. Origins and Further Development of the Jameson–Schmidt–Turkel Scheme. AIAA J. 2017, 55, 1487–1510. [Google Scholar] [CrossRef]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Liou, M.S. Evolution of Advection Upstream Splitting Method Schemes. Def. Sci. J. 2010, 60, 606–613. [Google Scholar] [CrossRef]
- Palacios, F.; Lulaczyk, T.; Alonso, J.; Carrier, G.; Loselle, A. Stanford-Onera-INRIA contribution. In Proceedings of the 1st AIAA Sonic Boom Prediction Workshop, National Harbour, MA, USA, 11 January 2014. [Google Scholar]
- Ozoroski, L. Third AIAA Sonic Boom Prediction Workshop – Introduction. In Sonic Boom Prediction Workshop; NASA Langley Research Center: Hampton, VA, USA, 2020. [Google Scholar]
- Ueno, A.; Kanamori, M.; Makino, Y. Robust Low-Boom Design Based on Near-Field Pressure Signature in Whole Boom Carpet. J. Aircr. 2017, 54, 918–925. [Google Scholar] [CrossRef]
- Zore, K.; Ozcer, I.; Munholand, L.; Stokes, J. ANSYS CFD Simulations of Supersonic and Hypersonic Flows. In Proceedings of the 6th National Symposium on Shock Waves, Chennai, India, 26–28 February 2020. [Google Scholar]
- Viola, N.; Fusaro, R.; Gori, O.; Marini, M.; Roncioni, P.; Saccone, G.; Saracoglu, B.; Ispir, A.C.; Fureby, C.; Nilson, T.; et al. STRATOFLY MR3—How to reduce the environmental impact of high-speed transportation. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–21 January 2021. [Google Scholar] [CrossRef]












| Operating Conditions | Value |
|---|---|
| Mach number | 1.6 |
| Angle of attack [deg] | 0 |
| Altitude [m] | 15,760 |
| Pressure [Pa] | 10,684.3 |
| Temperature [K] | 216.6 |
| Operating Conditions | Value |
|---|---|
| Mach number | 2.0 |
| Angle of attack [deg] | 0 |
| Altitude [m] | 15,760 |
| Pressure [Pa] | 10,684.3 |
| Temperature [K] | 216.6 |
| Dimensions | CS1 | CS2 | CS3 |
|---|---|---|---|
| Body Length [m] | 62 | 75 | |
| Body Height [m] | 10 | ||
| Wing Span [m] | 26 | ||
| [m2] | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glorioso, A.; Petrosino, F.; Barbarino, M.; Pezzella, G. Near-Field Pressure Signature of New-Concept Supersonic Aircraft Obtained Using Open-Source Approach. Sci 2025, 7, 127. https://doi.org/10.3390/sci7030127
Glorioso A, Petrosino F, Barbarino M, Pezzella G. Near-Field Pressure Signature of New-Concept Supersonic Aircraft Obtained Using Open-Source Approach. Sci. 2025; 7(3):127. https://doi.org/10.3390/sci7030127
Chicago/Turabian StyleGlorioso, Antimo, Francesco Petrosino, Mattia Barbarino, and Giuseppe Pezzella. 2025. "Near-Field Pressure Signature of New-Concept Supersonic Aircraft Obtained Using Open-Source Approach" Sci 7, no. 3: 127. https://doi.org/10.3390/sci7030127
APA StyleGlorioso, A., Petrosino, F., Barbarino, M., & Pezzella, G. (2025). Near-Field Pressure Signature of New-Concept Supersonic Aircraft Obtained Using Open-Source Approach. Sci, 7(3), 127. https://doi.org/10.3390/sci7030127









