Computational Fluid Dynamics Analysis into the Comparison of Resistance Characteristics Between DARPA Suboff and Modified U209 Types of Submarines
Abstract
1. Introduction
1.1. Background
1.2. Aim of Present Work
2. Method
2.1. Background
2.2. Modeling
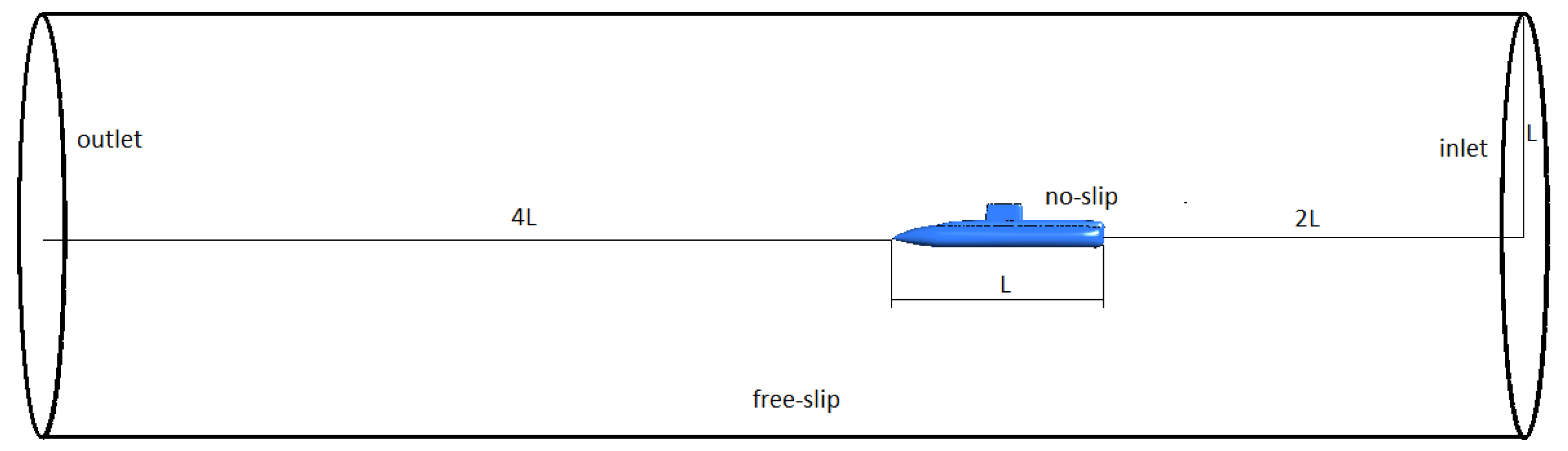
2.3. Domain
2.4. Grid Convergence Independence
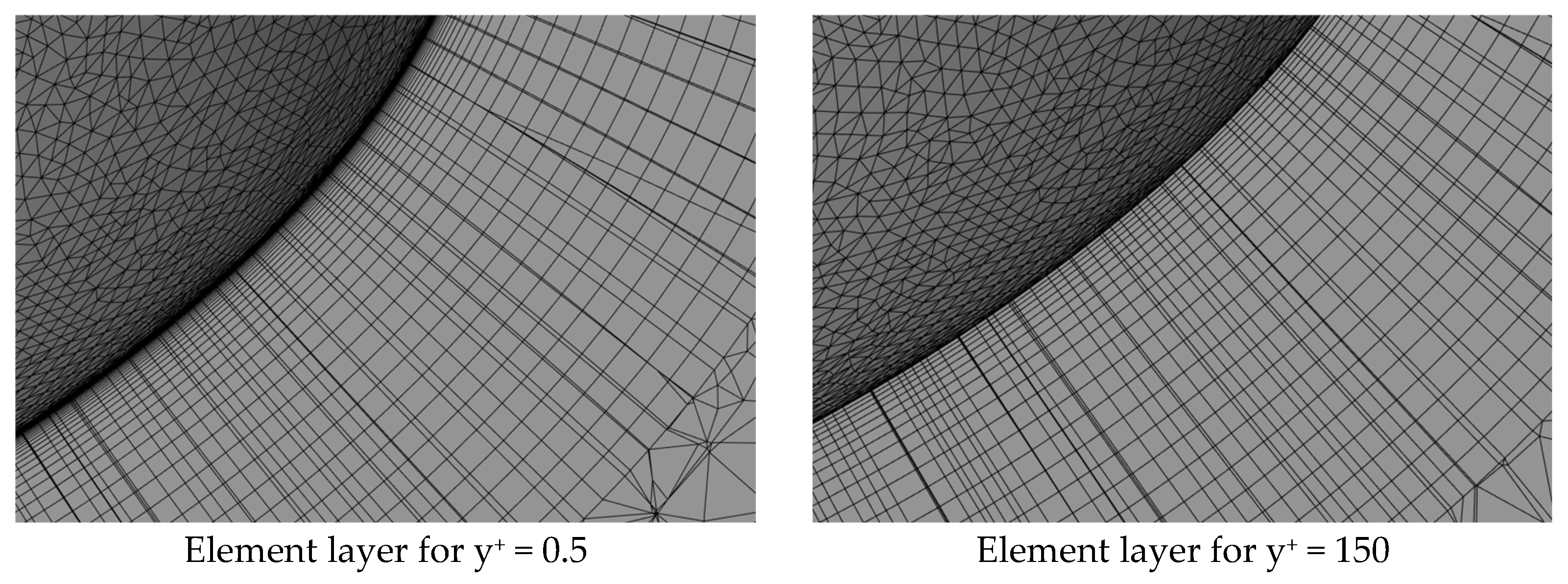
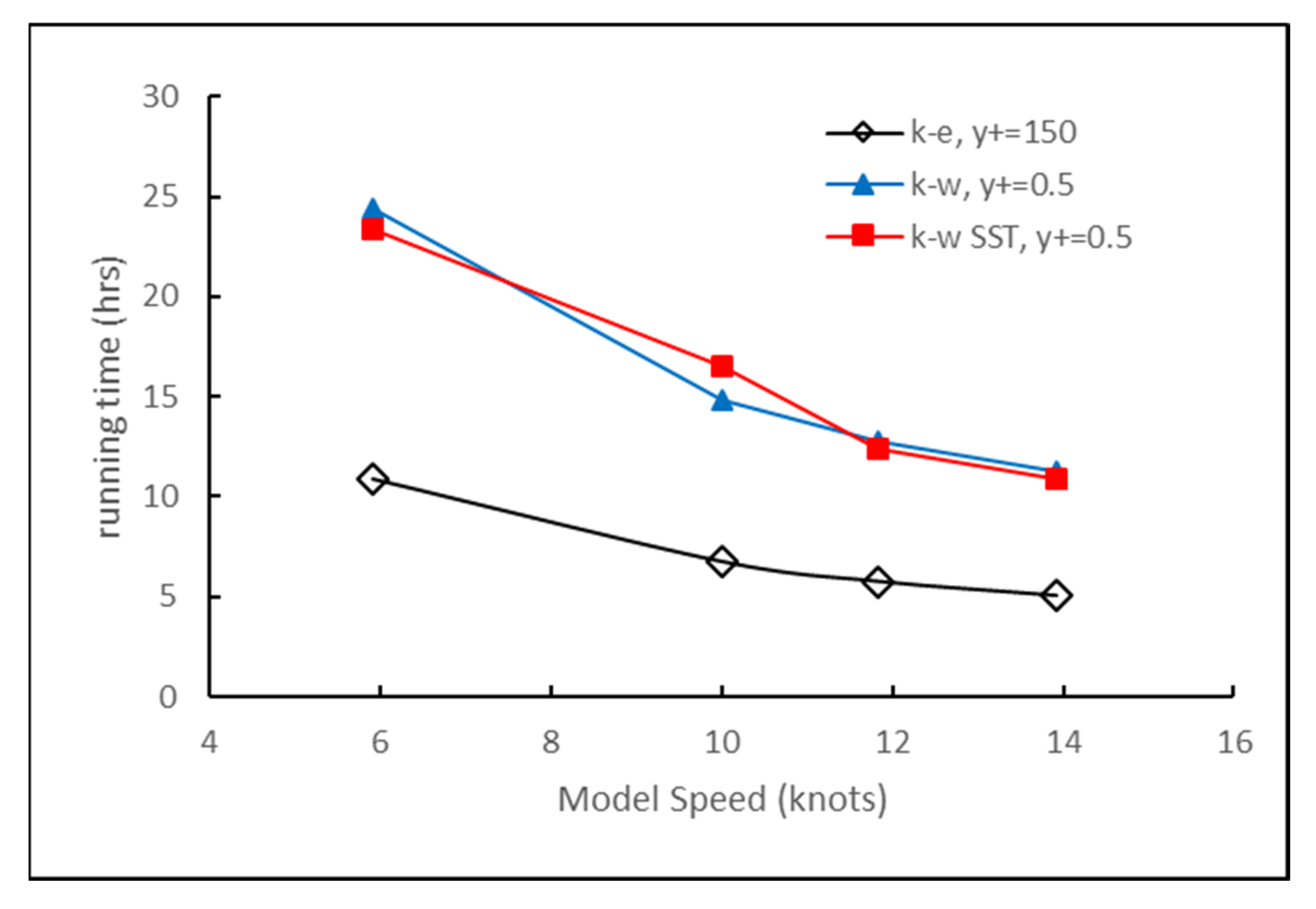
2.5. Turbulence Model Study
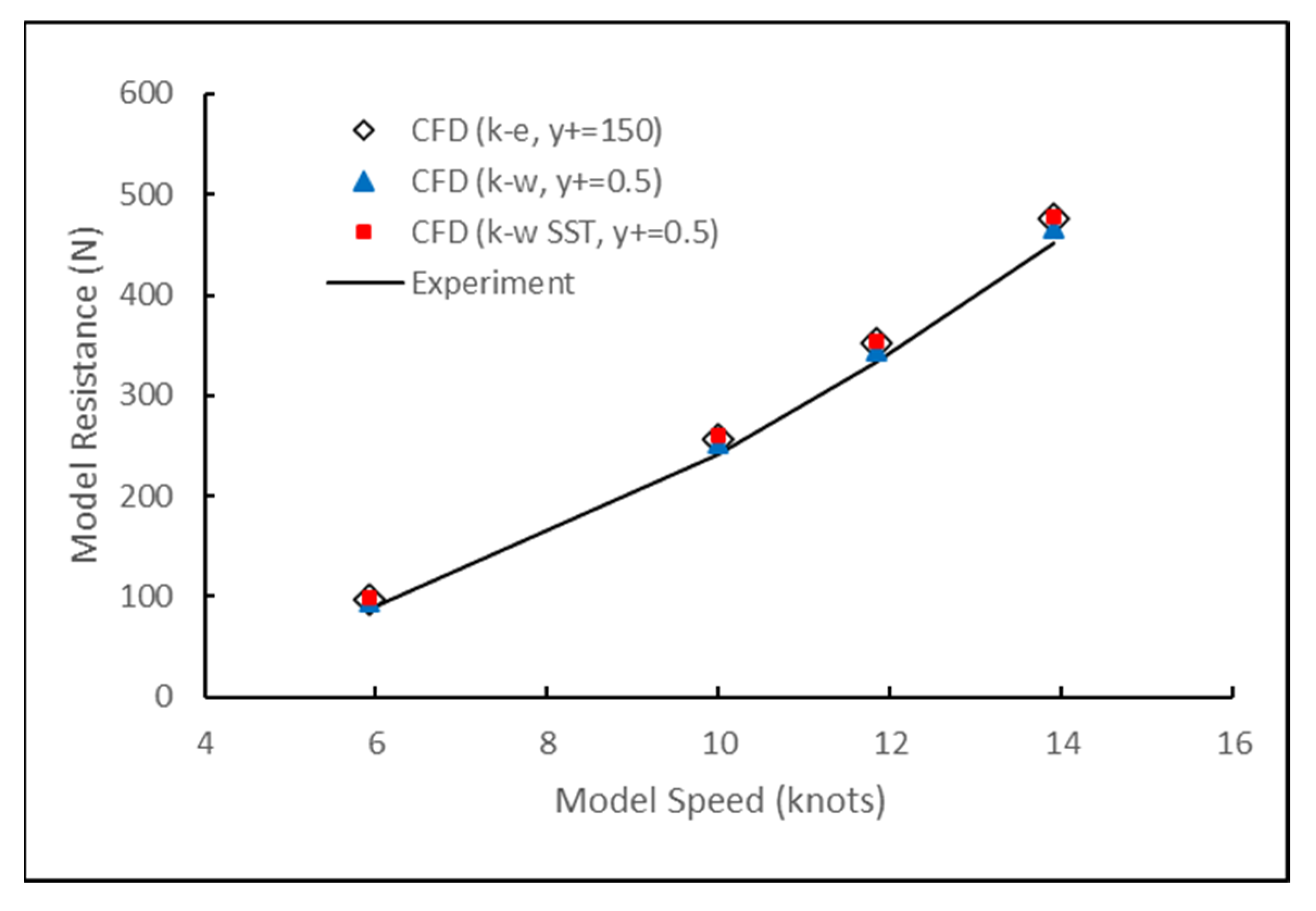
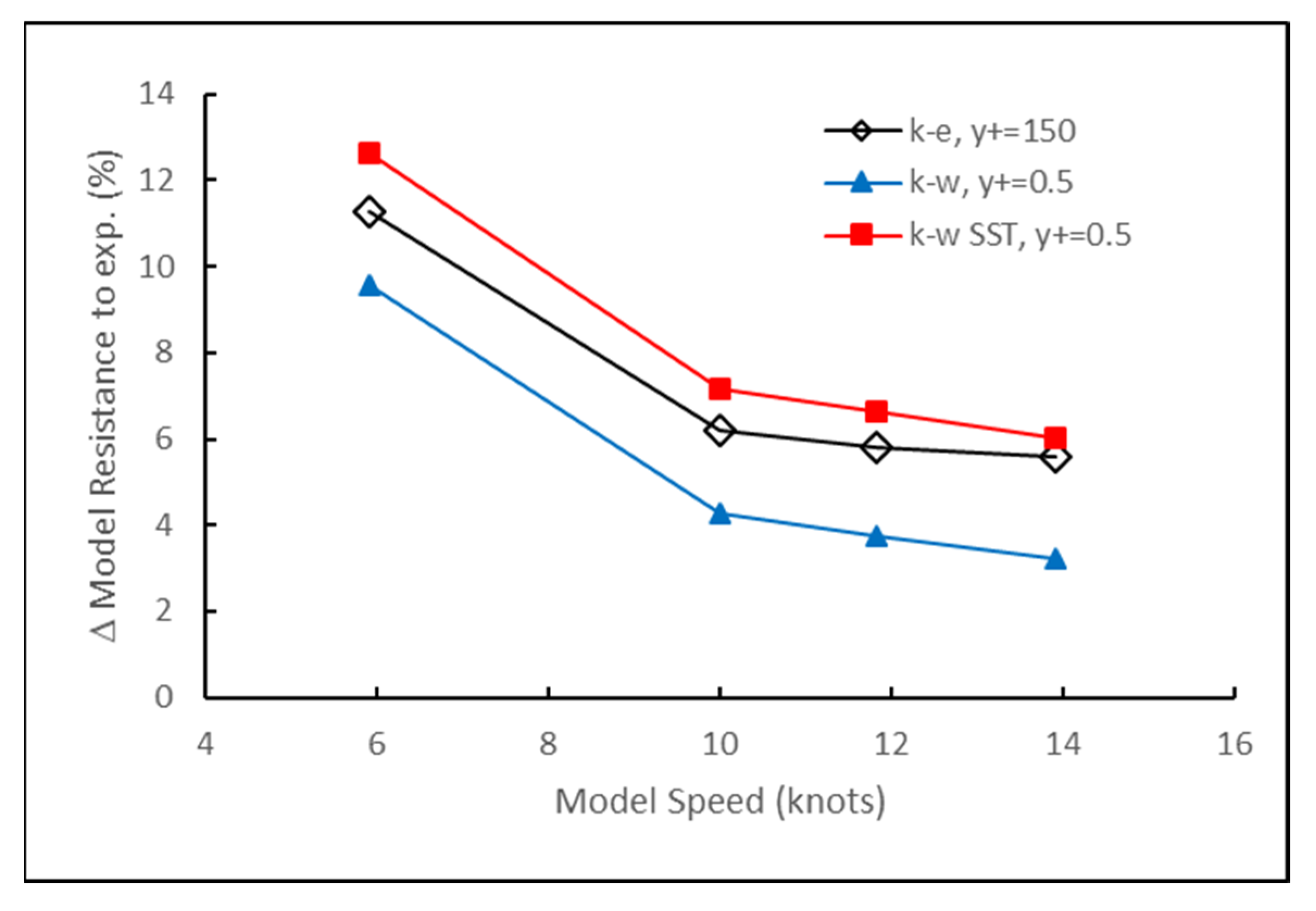
2.6. Validation Against Experimental Results
3. Results and Discussion
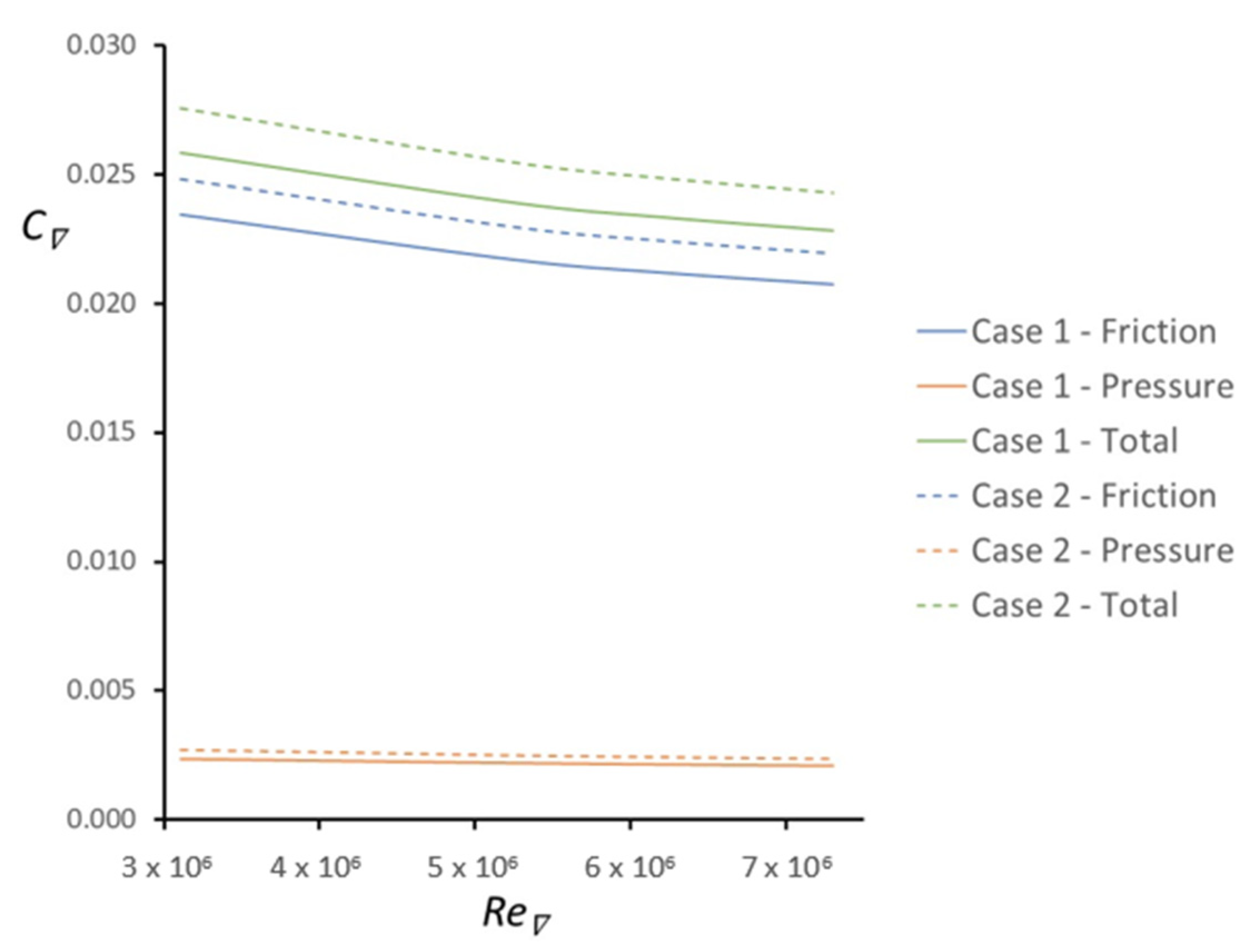
3.1. Influence of Hull Shape
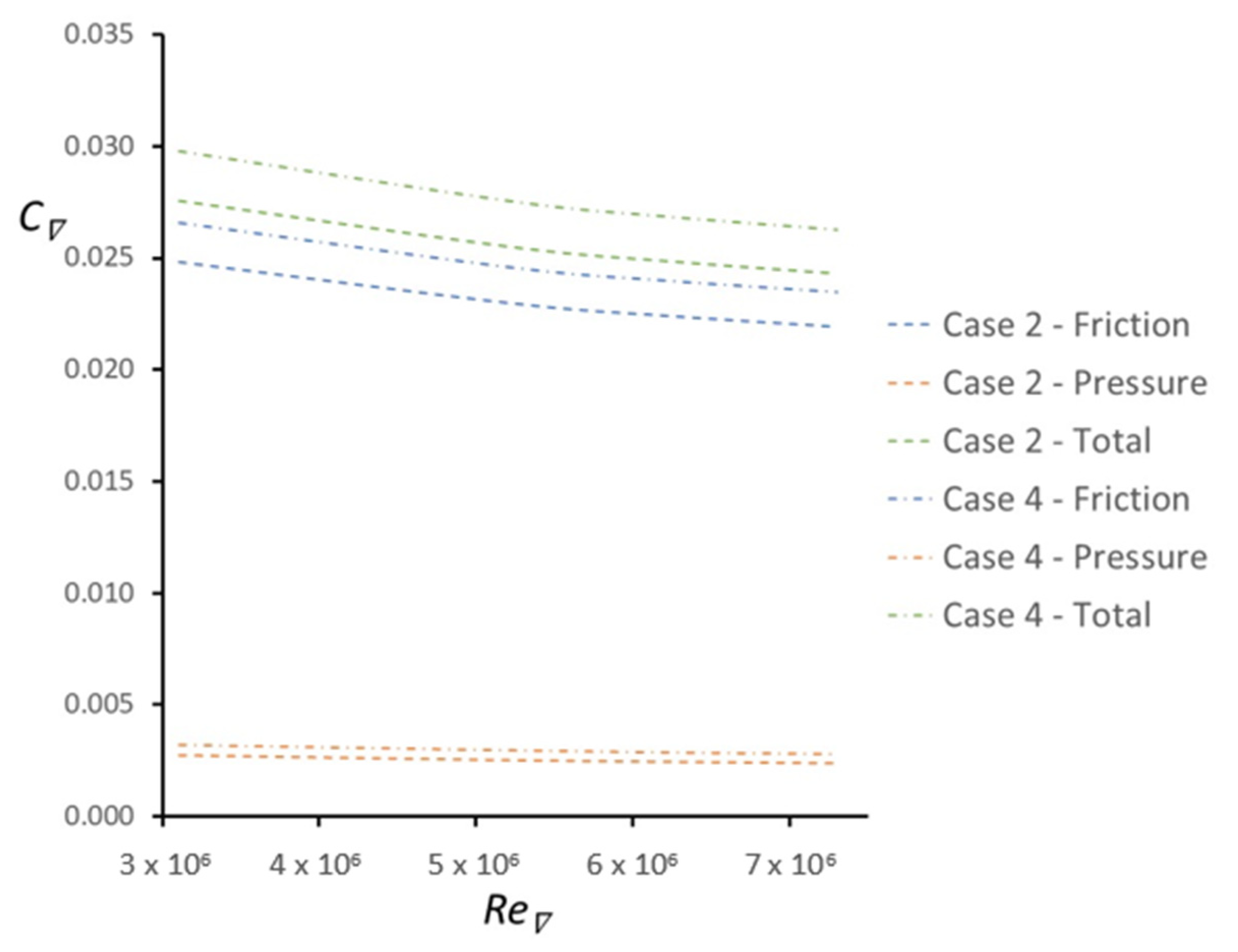
3.2. Influence of Casing
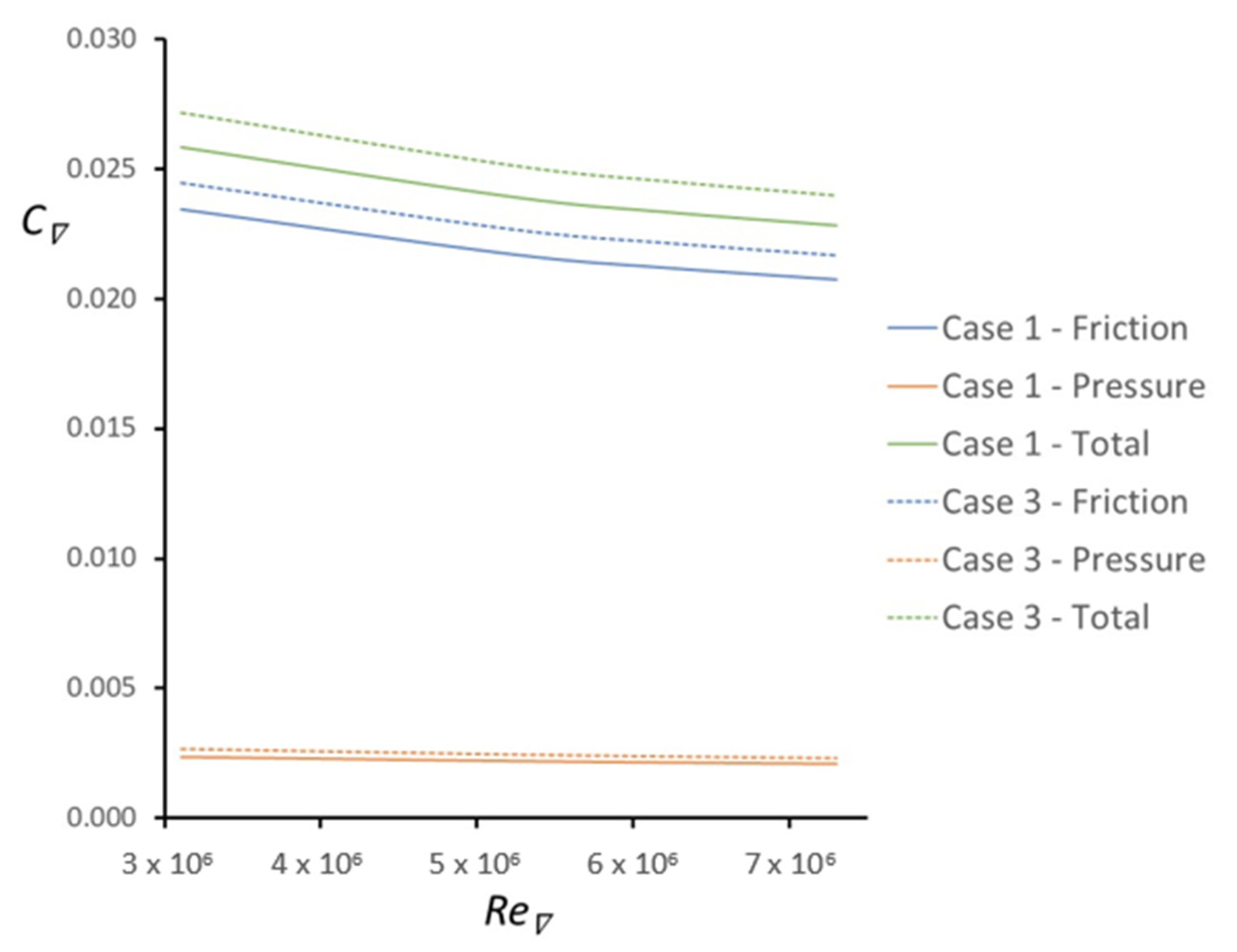
3.3. Influence of Sail
3.4. Comparison with Empirical Prediction
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clark, B. The Emerging Era in Undersea Warfare; The Center for Strategic and Budgetary Assessments (CSBA): Washington, DC, USA, 2015. [Google Scholar]
- Kiser, D.E. Indian, Japanese, and US Responses to Chinese Submarine Modernization. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2016. [Google Scholar]
- The 2021 Military Balance Chart: Submarines and Sub-surface Warfare. Mil. Balance 2021, 121, ci. [CrossRef]
- Chapter One: Defence and military analysis. Mil. Balance 2021, 121, 9–22. [CrossRef]
- Benere, D.E. A Critical Examination of the US Navy’s Use of Unrestricted Submarine Warfare in the Pacific Theater During World War II; Naval War College, Joint Operations Department: Newport, RI, USA, 1992. [Google Scholar] [CrossRef]
- Humphris, S.E. Vehicles for deep sea exploration. In Elements of Physical Oceanography: A Derivative of the Encyclopedia of Ocean Sciences; Academic Press: Cambridge, MA, USA, 2009; pp. 197–209. [Google Scholar] [CrossRef]
- Groves, N.C.; Huang, T.T.; Chang, M.S. Geometric Characteristics of DARPA SUBOFF Models (DTRC Model Nos. 5470 and 5471); David Taylor Research Center: Bethesda, MD, USA, 1989. [Google Scholar]
- Liu, H.L.; Huang, T.T. Summary of DARPA SUBOFF Experimental Program Data; Report Number: CRDKNSWC/HD-1298-11; Naval Surface Warfare Center Carderock (NSWCCD): Bethesda, MD, USA, 1998. [Google Scholar] [CrossRef]
- Renilson, M.R. Submarine Hydrodynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-319-79056-5. [Google Scholar]
- Zheku, V.V.; Villa, D.; Piaggio, B.; Gaggero, S.; Viviani, M. Assessment of Numerical Captive Model Tests for Underwater Vehicles: The DARPA SUB-OFF Test Case. J. Mar. Sci. Eng. 2023, 11, 2325. [Google Scholar] [CrossRef]
- Uzun, D.; Sezen, S.; Atlar, M.; Turan, O. Effect of biofouling roughness on the full-scale powering performance of a submarine. Ocean Eng. 2021, 238, 109773. [Google Scholar] [CrossRef]
- Utama, I.K.A.P.; Farhan, F.; Nasirudin, A.; Ariesta, R.C.; Renilson, M.R. CFD Analysis of Biofouling Effect on Submarine Resistance and Wake. J. Mar. Sci. Eng. 2023, 11, 1312. [Google Scholar] [CrossRef]
- Lyu, X.; Tang, H.; Sun, J.; Wu, X.; Chen, X. Simulation of microbubble resistance reduction on a suboff model. Brodogradnja 2014, 65, 23–32. [Google Scholar]
- Kinaci, O.K.; Gokce, M.K.; Alkan, A.D.; Kukner, A. On self-propulsion assessment of marine vehicles. Brodogradnja 2018, 69, 29–51. [Google Scholar] [CrossRef]
- Chase, N.; Carrica, P.M. Submarine propeller computations and application to self-propulsion of DARPA Suboff. Ocean Eng. 2013, 60, 68–80. [Google Scholar] [CrossRef]
- Byeon, C.Y.; Kim, J.I.; Park, I.R.; Seol, H.S. Resistance and self-propulsion simulations for the DARPA Suboff submarine by using RANS method. J. Compt. Fluids Eng. 2018, 23, 36–46. [Google Scholar] [CrossRef]
- Delen, C.; Kinaci, O.K. Direct CFD simulations of standard maneuvering tests for DARPA Suboff. Ocean Eng. 2003, 276, 114202. [Google Scholar] [CrossRef]
- Nugroho, W.H.; Purnomo, N.J.H.; Suwarni, E.; Priohutomo, R.K.; Mulyad. Slamming loads prediction on a submarine hull structure. J. Subsea Offshore 2016, 8, 15–21. [Google Scholar]
- Utama, I.K.A.P.; Aryawan, W.D.; Nasirudin, A.; Sutiyo; Yanuar. Numerical Investigation into the Pressure and Flow Velocity Distributions of a Slender-Body Catamaran Due to Viscous Interference Effects. Int. J. Technol. 2021, 149-162, 149–162. [Google Scholar] [CrossRef]
- Mikulec, M.; Piehl, H. Verification and validation of CFD simulations with full-scale ship speed/power trial data. Brodogradnja 2023, 74, 41–62. [Google Scholar] [CrossRef]
- Hadi, E.S.; Tuswan, T.; Azizah, G.; Ali, B.; Samuel, S.; Hakim, M.L.; Hadi, M.R.C.P.; Iqbal, M.; Sari, D.P.; Satrio, D. Influence of the canal width and depth on the resistance of 750 DWT Perintis ship using CFD simulation. Brodogradnja 2023, 74, 117–144. [Google Scholar] [CrossRef]
- Trimulyono, A.; Hakim, M.L.; Ardhan, C.; Ahmad, S.T.P.; Tuswan, T.; Santosa, A.W.B. Analysis of the double steps position effect on planing hull performances. Brodogradnja 2023, 74, 41–72. [Google Scholar] [CrossRef]
- Dai, K.; Li, Y.; Gong, J.; Fu, Z.; Li, A.; Zhang, D. Numerical study on propulsive factors in regular head and oblique waves. Brodogradnja 2022, 73, 37–56. [Google Scholar] [CrossRef]
- Querard, A.B.G.; Temarel, P.; Turnock, S.R. Influence of viscous effects on the hydrodynamics of ship-like sections undergoing symmetric and antisymmetric motions, using RANS. In Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering (OMAE), Estoril, Portugal, 5–20 June 2008; pp. 1–10. [Google Scholar] [CrossRef]
- Kim, S.P.; Lee, H.H. Fully nonlinear seakeeping analysis based on CFD simulations. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; pp. 970–974. [Google Scholar]
- Enger, S.; Peric, M.; Peric, R. Simulation of flow around KCS-hull. In Proceedings of the Gothenburg 2010—A Workshop on Numerical Ship Hydrodynamics, Gothenburg, Sweden, 8–10 December 2010. [Google Scholar]
- Tezdogan, T.; Demirel, Y.K.; Kellett, P.; Khorasanchi, M.; Incecik, A.; Turan, O. Full-scale unsteady RANS CFD simulations of ship behaviour and performance in head seas due to slow steaming. Ocean Eng. 2015, 97, 186–206. [Google Scholar] [CrossRef]
- Cakici, F.; Sukas, O.F.; Kinaci, O.K.; Alkan, A.D. Prediction of the vertical motions of dtmb 5415 ship using different numerical approaches. Brodogradnja 2017, 68, 29–44. [Google Scholar] [CrossRef]
- Park, J.; Seok, W. Computational analysis of strut effects on a BB2 submarine at drift angle 0, 6, and 12°. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100555. [Google Scholar] [CrossRef]
- Mai, T.L.; Jeon, M.; Vo, A.K.; Yoon, H.K.; Kim, S.; Lee, J. Establishment of empirical formula for hydrodynamic derivatives of submarine considering design parameters. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100537. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. ASME J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Bayraktar, E.; Mierka, O.; Turek, S. Benchmark computations of 3D laminar flow around a cylinder with CFX, OpenFOAM and FeatFlow. Int. J. Comput. Sci. Eng. 2012, 7, 253–266. [Google Scholar] [CrossRef]
- Julián, I.; Herguido, J.; Menéndez, M. Gas permeation effect on the two-section two-zone fluidized bed membrane reactor (TS-TZFBMR) fluid dynamics: A CFD simulation study. Chem. Eng. J. 2016, 305, 201–211. [Google Scholar] [CrossRef]
- Utama, I.K.A.P.; Suastika, I.K.; Sulisetyono, A.; Hermawan, Y.A.; Aryawan, W.D. Resistance Analysis of Rescue Boat in Calm Water Condition. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1052, p. 012062. [Google Scholar] [CrossRef]
- Leong, Z.Q. (Australian Maritime College, University of Tasmania, Launceston, Tasmania, Australia). Personal Communication, 2017.




| Case | Description | L (m) | D (m) | L/D | LPMB (m) | S (m2) | ∇ (m3) |
|---|---|---|---|---|---|---|---|
| 1 | Suboff bare hull only | 4.356 | 0.530 | 8.219 | 2.250 | 6.232 | 0.755 |
| 2 | U209 bare hull only (no casing/free flood space) | 4.484 | 0.495 | 9.058 | 2.793 | 6.424 | 0.755 |
| 3 | Suboff with Suboff sail | 4.356 | 0.530 | 8.219 | 2.250 | 6.379 | 0.757 |
| 4 | U209 with casing (no sail) | 4.484 | 0.495 | 9.058 | 2.793 | 6.931 | 0.822 |
| 5 | U209 with casing and Suboff sail | 4.484 | 0.495 | 9.058 | 2.793 | 7.073 | 0.824 |
| 6 | U209 with casing and U209 sail | 4.484 | 0.495 | 9.058 | 2.793 | 7.453 | 0.841 |
| Case | Estimated (m2) | Actual (m2) | Difference |
|---|---|---|---|
| 1 | 6.255 | 6.232 | −0.4% |
| 2 | 6.224 | 6.424 | −3.2% |
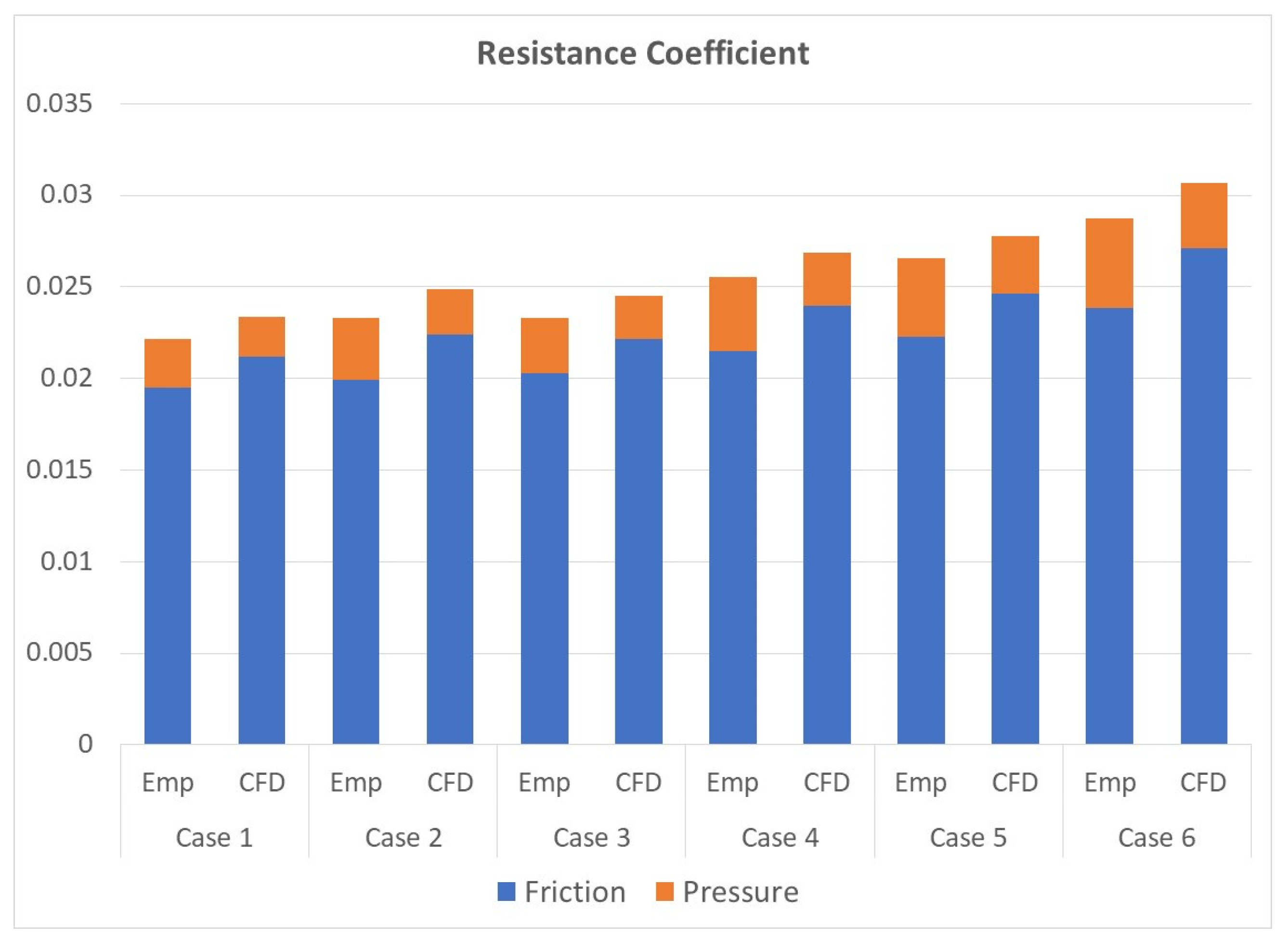
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Emp | CFD | % | Emp | CFD | % | Emp | CFD | % | Emp | CFD | % | Emp | CFD | % | Emp | CFD | % | |
| F | 19.5 | 21.2 | −8 | 19.9 | 22.4 | −11 | 20.3 | 22.1 | −8 | 21.5 | 24.0 | −10 | 22.2 | 24.6 | −10 | 23.8 | 27.1 | −12 |
| P | 2.7 | 2.1 | 25 | 3.3 | 2.4 | 36 | 3.0 | 2.4 | 26 | 4.0 | 2.9 | 40 | 4.3 | 3.2 | 37 | 4.9 | 3.6 | 38 |
| Total | 22.2 | 23.3 | −5 | 23.3 | 24.9 | −6 | 23.3 | 24.5 | −5 | 25.5 | 26.9 | −5 | 26.6 | 27.8 | −4 | 28.7 | 30.7 | −6 |
| Constant | Value |
|---|---|
| ξhull | 4 |
| ξPMB | 15 |
| nPMB | 3 |
| n | −1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasirudin, A.; Sutiyo; Yulianto, A.N.; Julianto, E.; Utama, I.K.A.P.; Renilson, M. Computational Fluid Dynamics Analysis into the Comparison of Resistance Characteristics Between DARPA Suboff and Modified U209 Types of Submarines. Sci 2025, 7, 82. https://doi.org/10.3390/sci7020082
Nasirudin A, Sutiyo, Yulianto AN, Julianto E, Utama IKAP, Renilson M. Computational Fluid Dynamics Analysis into the Comparison of Resistance Characteristics Between DARPA Suboff and Modified U209 Types of Submarines. Sci. 2025; 7(2):82. https://doi.org/10.3390/sci7020082
Chicago/Turabian StyleNasirudin, Ahmad, Sutiyo, Ardi Nugroho Yulianto, Eko Julianto, I Ketut Aria Pria Utama, and Martin Renilson. 2025. "Computational Fluid Dynamics Analysis into the Comparison of Resistance Characteristics Between DARPA Suboff and Modified U209 Types of Submarines" Sci 7, no. 2: 82. https://doi.org/10.3390/sci7020082
APA StyleNasirudin, A., Sutiyo, Yulianto, A. N., Julianto, E., Utama, I. K. A. P., & Renilson, M. (2025). Computational Fluid Dynamics Analysis into the Comparison of Resistance Characteristics Between DARPA Suboff and Modified U209 Types of Submarines. Sci, 7(2), 82. https://doi.org/10.3390/sci7020082








