The Dynamics of Aggregation of Polyamide Granule Clusters on a Water Surface

Abstract

The process of convergence and the aggregation of polyamide granules and clusters on a water surface has been studied. These granules are widely used to visualize flows on the surface and in the bulk of the water. It is shown that the law of particle motion during convergence corresponds to electrostatic interaction. Like other polymers, polyamide particles are easily charged owing to friction. The quantitative estimation of the surface charge of the granules gives values close to the results of other authors. The range of action of electrostatic forces is fractions of a millimeter, and the maximum velocities of the clusters and granules measured in the experiment do not exceed 1 mm/s when converging. Therefore, when studying flows, electrostatic interaction does not distort the velocity field if the concentration of the granules is low and the velocities of the flows are rather high.

1. Introduction

The interaction in the arrays of small particles at the liquid surface is important for various spectra of technologies starting from the flotation techniques for mineral processing in the extractive metallurgy to the novel building blocks of photonic crystals using dimeric or tetrahedral clusters. However, the aggregation processes of such particles strongly depend on the nature and properties of particles’ material as well as those of the liquid. This work is devoted to one of the important and weakly study cases, namely to the convergence and aggregation of polyamide granules and clusters on a water surface.

In experiments on vortex flows and turbulence in the bulk and on the surface of water, polyamide-12 granules with an average diameter of 30 µm are used. The density of the granules is close to that of water. Therefore, when moving in a liquid flow, these particles do not distort the velocity field and allow one to observe complex hydrodynamic processes using optical methods (see, for example, [1]).

The work of [2] describes the clusterization of polyamide granules on a water surface when an external action leading to the emergence of flows ceases. This means that there is an interaction between polyamide granules and the clusters consisting of them. Knowing the nature of this interaction is important for estimating the conditions under which the velocity field of a liquid medium will differ from the picture given by the observation of decorating particles.

The convergence of particles on the liquid surface and their aggregation with the formation of various structures have been studied for a long time. The nature of the interaction of these objects depends on their sizes. According to Smoluchowski’s theory [3], the factors that determine the process of clusterization (coagulation) of colloidal particles with a size of not more than 1 µm are Brownian motion and the action of van der Waals dispersion forces. Owing to their small size, gravity can be neglected for hydrophobic particles. These particles do not deform the liquid surface. Therefore, in this case, the action of surface tension forces can be neglected when investigating the clusterization process ([4,5,6,7,8,9]).

Another limiting case is objects floating at the surface of a liquid, the sizes of which have the scale of capillary length [10,11,12,13]. When they converge, the surface energy of the liquid decreases, and the clusterization process will be determined by surface tension forces and the presence of macroflows in the liquid [14,15].

In an intermediate case, which includes polyamide granules, particles have sizes from tens to hundreds of µm. Let us provide some examples. In [16,17], the clusterization of hydrophobic carbon rods with a length of 100–200 µm and glass beads with a diameter of 75 µm on the water surface was investigated. The fractal dimension of clusters formed from the rods turned out to be smaller than that of clusters formed from the glass beads. The authors explained that by the action of surface tension forces. The meniscus being radially symmetric in the case of the beads led to the formation of denser clusters. The liquid surface was more curved at the ends of the rods than along the sides. That resulted in the formation of a more dispersed structure of corresponding clusters. In [18], the convergence of two neutral and equally charged hydrophobic glass beads at the interface of two liquids under the action of surface tension forces was investigated. The diameter of the beads was about one-tenth of the capillary length. It turned out that the obtained experimental time dependence of distance between the beads agreed well with the theory. Pronounced hydrophobicity and a big difference between the density of particles and that of liquids in the experiments [16,17,18] led to significant curvature of the surface and, as a result, the formation of clusters under the action of surface tension forces.

The clusterization of hollow glass microspheres with an average diameter of 60 µm floating on the liquid helium surface was described in [19]. Although helium wets particles well, their density is close to that of liquid helium, and they slightly project over the surface. It was shown that surface tension forces worked efficiently in this case as well. The reason was the low temperatures and short capillary length of liquid helium compared to water.

The interaction between polyamide granules that are used in experiments to visualize flows on the water surface has an unusual character. It was demonstrated in [20] that they were heavier than water, were well wetted, did not sink, and were held at the water surface from inside under the action of van der Waals forces. Therefore, the surface remained flat. This means that forces under the action of which granules merged into clusters and clusters conglomerated together were not surface tension forces. If the surface tension is excluded, it is possible to state as follows: attraction forces, which lead to the convergence of polyamide granules and their conglomeration into clusters, have an electrostatic nature and long-range character and are characterized by power dependence on the distance between the particles, with power exponent depending on a specific type of electrostatic interaction. The aim of the present work was to investigate the process of granule aggregation and establish the law of their interaction.

2. Materials and Methods

The experiments were carried out with polyamide-12 granules; the density declared by the manufacturer was 0.99–1.01 g/cm³, and the diameter of the granules ranged from 10 to 80 µm. Two types of experiments were performed: observation of the clusterization of a large number of granules on the surface to study the macroscopic peculiarities of this process and video recording of the convergence and aggregation of two individual objects—a granule and a cluster or two clusters—using a microscope.

Polyamide granules were sputtered over the surface of a glass dish 17 cm in diameter with water. Clusterization was observed for 10 days. The water surface was regularly photographed. Successive clusterization stages can be seen in Figure 1. At the beginning of observations, the distance between individual clusters was fractions of a millimeter.

Figure 2 shows the results of polyamide granule clusterization on the water surface in a glass Petri dish with a diameter of 7 cm; then, 50 h after sputtering over the water surface, the granules merged into one large cluster with pronounced linear structures consisting of tens of particles. To exclude the motion of water when performing the experiments, the following measures were undertaken. The glass dish and the Petri dish were placed on an optical table to avoid the effect of external vibrations. The experiment was carried out in a room with constant temperature and poor lighting, which was not changed during the observations. To exclude the air motion, the dishes were covered with a glass. The thickness of the water layer did not exceed 1 cm, and the sizes of the vessels were small; therefore, there were no temperature gradients that could lead to the formation of convective flows.

For comparison, clusterization of hollow glass microspheres with an average diameter of 50 µm and a density of 0.125 g/cm³ was observed under the same conditions. The photos (Figure 3) taken using a microscope clearly show the difference in the character of clusterization of the polyamide granules and hollow glass microspheres on the water surface in the Petri dish.

For more detailed observation of clusterization, a Colling Tech microscope with a video camera connected to a computer was used. A layer of distilled water or a 4% solution of sodium chloride with a thickness of 5–6 mm was poured into a Petri dish with a diameter of 7 cm. The sodium chloride solution was used to establish the effect of a larger number of free ions of opposite signs than in water on the clusterization. Polyamide granules were sputtered over the liquid surface. Then, the dish was covered with a thin glass and placed on an observation table. By using differential screws, it was possible to move the microscope objective along the water surface. The size of the observed part of the surface was 1 mm × 0.7 mm. By the time the motion of water related to the dish movement stopped, many granules had already merged into small clusters. We managed to see and capture on video the convergence and aggregation of a granule and a cluster, as well as clusters of different sizes to each other. In total, 42 videos were recorded (see Supplementary Materials for some examples). Figure 4 depicts, as an example, photos of converging objects at the beginning of observations. The number of granules forming the clusters under study varied widely; therefore, the sizes of the clusters ranged from 30 to 400 µm. The clusters had different structures: densely packed, 2D cell, and pronounced linear ones. All of them were formed by one layer of granules. During video recording, no liquid motion was observed. In addition to converging particles, in the microscope field of view, there were other clusters and granules, which remained motionless.

3. Results and Discussion

3.1. The Law of Motion

When analyzing the process of multi-hour clusterization of polyamide granules, we conclude that the action of van der Waals forces between the polyamide particles cannot cause clusterization in its initial stage. Smoluchowski’s coagulation theory [3] uses the concept of a sphere of influence, the radius of which is taken as equal to that of colloidal micron-sized particles. It is assumed that when particles converge at this distance, they will conglomerate together under the action of dispersion forces. In our experiments, there is no motion of water that could lead to the convergence of particles. After sputtering at the beginning of the experiment, they are at a distance of hundreds of µm from each other; this is two orders of magnitude greater than the radius of the sphere of influence. This means that the electromagnetic forces that lead to the convergence should be described otherwise.

In the middle and late stages of observation, linear fragments can be seen in the structure of the clusters that are characteristic of the consolidation of dipoles [21,22,23], the formation of metal “leaves” during electrolysis of zinc sulfate [24], and the growth of dendrites from impurity barium particles in liquid helium in an electric field [25]. This suggests that the clusterization of polyamide granules occurs under the action of electrostatic forces.

It is known that a large static charge can accumulate on the surface of polymers, including polyamide [26]. There is a vast amount of literature on the study of the triboelectric effect, which is the emergence of electric charges on the dielectric surface because of friction. After applying various methods of electrization, some polymers can gain charges of opposite signs [27,28], which remain on the surface for a long time.

The triboelectric effect was investigated in granules of various polymers, including polyamide-12 [28]. The granules of the substances under study with a diameter of 3 mm, which were subjected to neutralization, were placed into a container made of the same material. There, they were mixed with an air jet and then poured into a separator. There, under the action of an electric field, they fell into different sections depending on the sign and value of an electric charge gained as a result of friction against each other and the container walls. Figures in the Ref [28] illustrate the dependence of an average density of the surface charge on polyamide-12 granules on the duration of mixing in the container. It shows that the granules gained charges of different signs, from $+3·{10}^{-6}$ to $-2·{10}^{-6}$ C/m², during electrization.

We assume that polyamide-12 granules may gain charges during manufacturing, packaging, transportation, and procedures when conducting experiments due to mutual friction. Moreover, electrization can be more efficient than in the experiments [28] since, in our case, the granules are smaller by two orders of magnitude.

Based on the method used in [21] for investigating an interaction between magnetic macrodipoles with opposite dipole moments, the law of motion of granules and clusters during their convergence can be established.

Particles are affected by electrostatic forces of attraction related to the presence of an electric charge on the granule surface. Moreover, neutral granules are attracted to charged ones due to polarization. We denote the force of electrostatic interaction by $F_{el}$. In addition, a moving particle is affected by the resistance force of the medium $F_{res}$, which is proportional to its velocity.

It is assumed that a cluster and a granule or two clusters do not have velocity components that are perpendicular to the conventional line connecting these two particles, i.e., that they move strictly toward each other.

We assume that the particle motion is completely dissipative, i.e., that the sum of the forces of electrostatic attraction $F_{el}$ and medium resistance $F_{res}$ acting upon each particle equals zero. Then, in the most general case, the law of motion for each particle will have the form

$$F_{el}+F_{res}=0, { F}_{el}~{\displaystyle \frac{1}{x^{c-1}}}, F_{res}~v.$$

(1)

where x is the distance between the particles, and $t$ is the time. In an ideal situation, if convergence occurs due to the presence of two opposite charges of particles, $c=3$. If one particle carries a charge of one sign, and another has a dipole moment, $c=4$. Two dipoles interact according to law (1), where $c=5$; in case of the interaction between charged and neutral particles, $c=6$. Approximation (1) is valid for point charges and dipoles.

As the origin of coordinates, we take the point where the particles will merge as a result of motion toward each other.

For the first and second particles, it follows from the equations of dissipative motion that

$${\displaystyle \frac{d{x}_1}{dt}}+{\displaystyle \frac{k_1}{{\left|x_1-x_2\right|}^{c-1}}}=0,{\displaystyle \frac{d{x}_2}{dt}}+{\displaystyle \frac{k_2}{{\left|x_1-x_2\right|}^{c-1}}}=0.$$

(2)

By summing up two Equation (3) for $x=\left|x_1-x_2\right|$, i.e., for the distance between the particles, we obtain the equation

$${\displaystyle \frac{dx}{dt}}+{\displaystyle \frac{k_1+k_2}{x^{c-1}}}=0$$

(3)

The integration gives

$$t=t_0-b{x}^c$$

(4)

3.2. Results of the Experiment

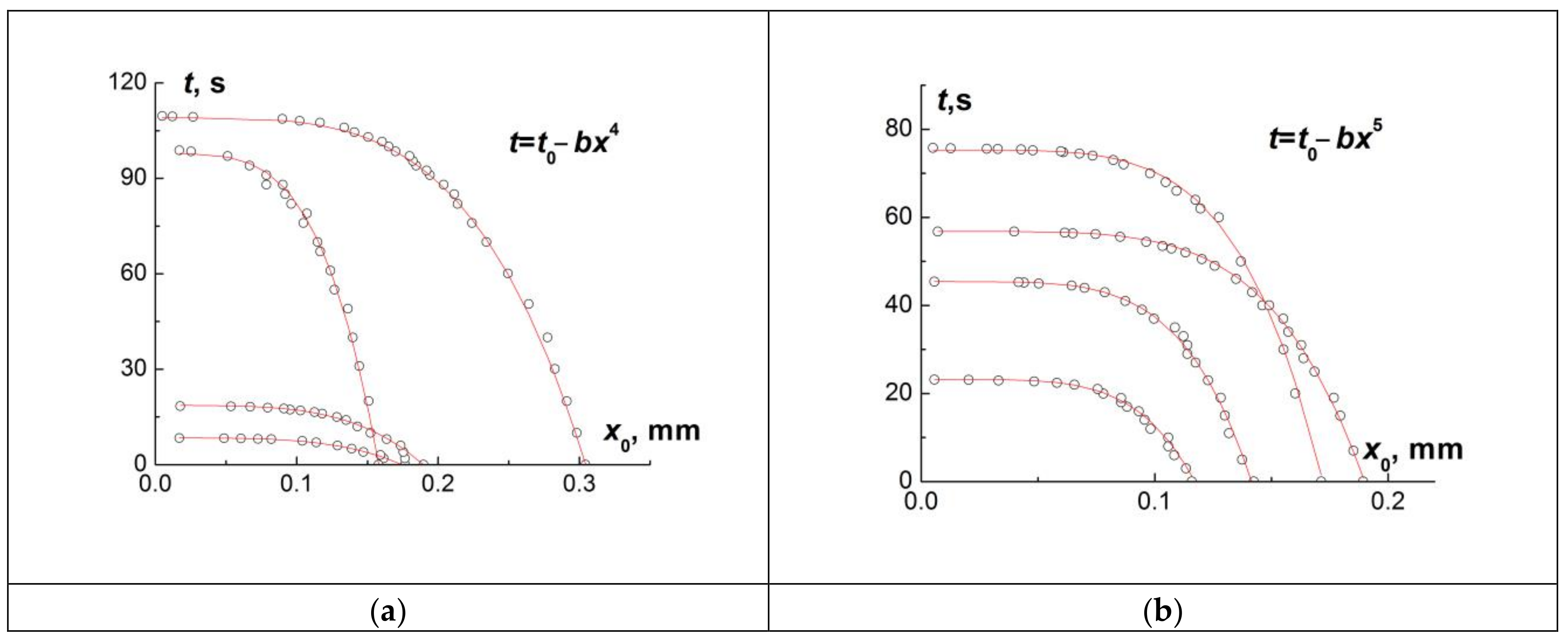
The dependence t(x) can be plotted from the video. The fitting of the obtained experimental dependence by a curve of the form (4) permits gives the values of b and c.

The dots in Figure 5 show the experimental values of x at the moments of time t, which were obtained when processing several videos. The dependencies are well fitted by curves of the form (4), for which c is 4 (a) and 5 (b). The standard deviation for c, which was calculated by the fitting procedure, did not exceed 5% for all 42 curves of this kind obtained from video processing.

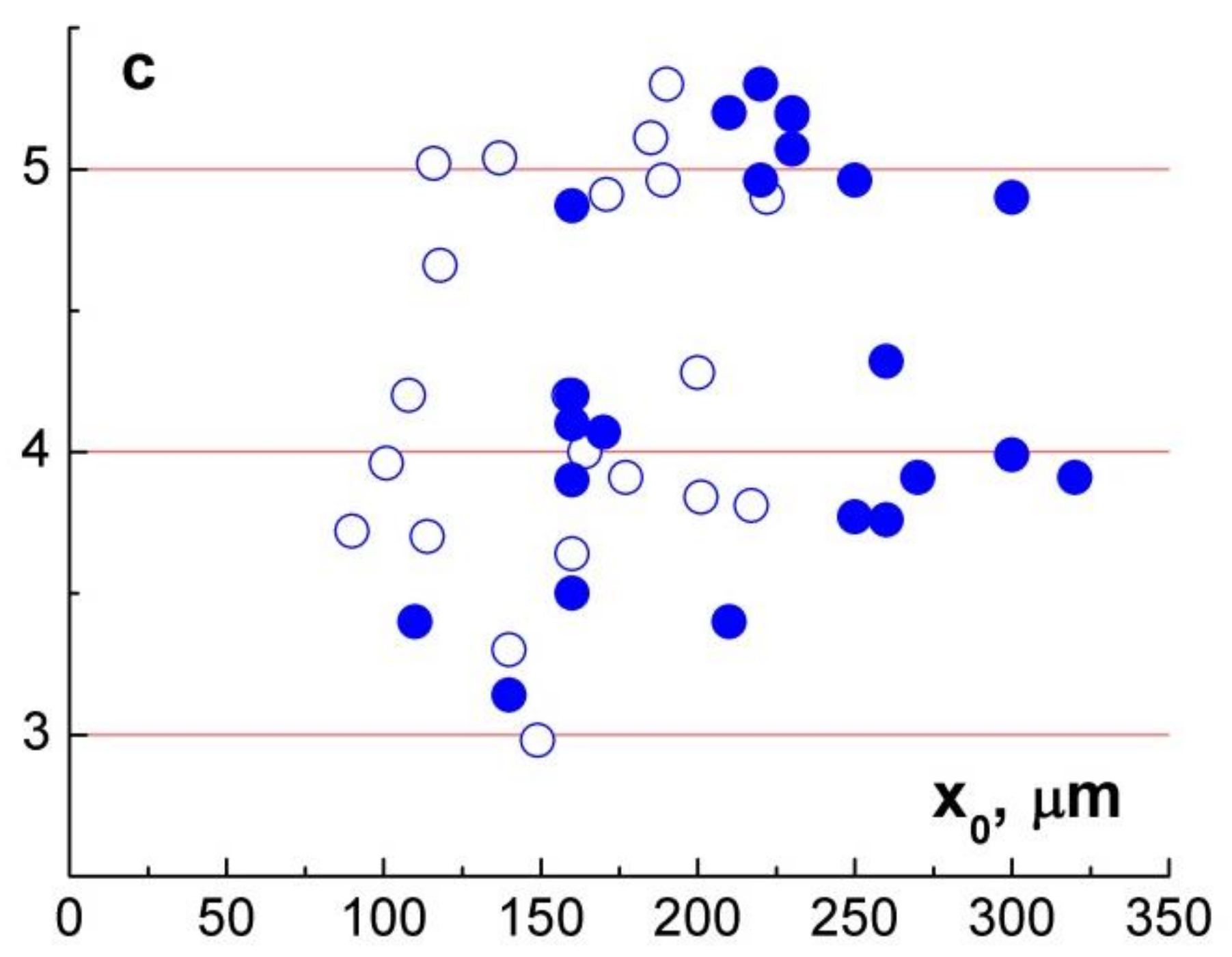
Figure 6 provides information about the times of observation t₀ in our series of experiments and the obtained values of the power exponent c (4). The observations in the sodium chloride solution and distilled water are shown with solid and open circles, respectively.

The values of $c$ vary from 3 to 5.3; at t₀ > 30 s, these values are near integers 4 and 5 for most observations. The ranges of values of $\mathrm{c}$ for distilled and salt water turned out to be the same.

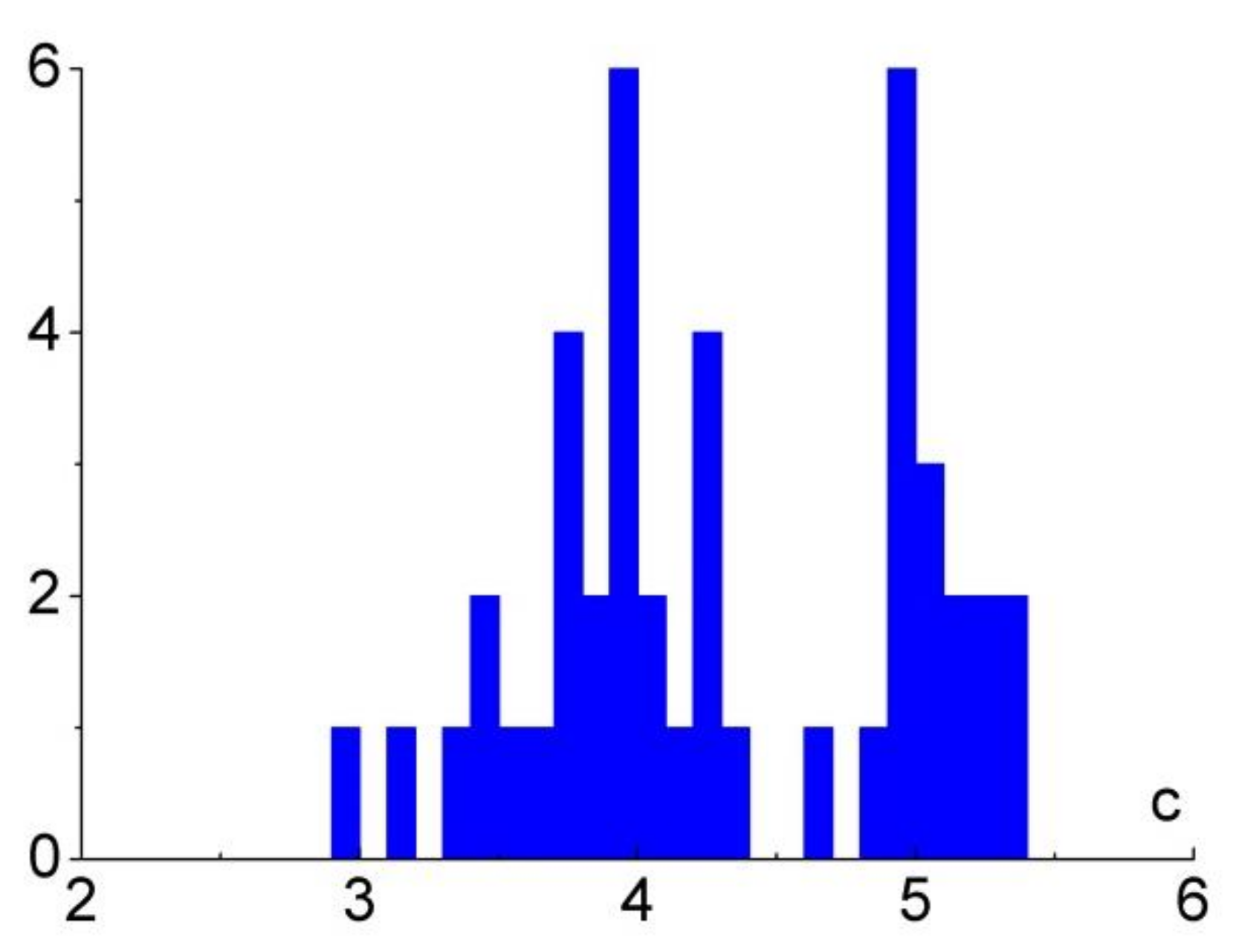
Figure 7 shows what values of c were obtained at different x₀, i.e., the distances between converging particles at the beginning of the video recording. Like c(t₀), the figure demonstrates the proximity of the power exponent to integers for a large number of observations. This fact is reflected in the histogram in Figure 8, in which there are two peaks near numbers 4 and 5 despite a small number of observations in terms of statistics.

The velocity v of convergence of the particles just before aggregation was calculated from the videos when the distance between them was about several µm. It turned out that the values of v did not exceed 1 mm/s. This means that the interaction of clusters should not distort the pattern of liquid flows if there are not too many decorating particles and characteristic flow velocities are significantly higher than v. The obtained maximum value of the velocity allows estimating the Reynolds number Re = vρr/η, where v = 0.1 cm/s, ρ = 1 g/cm³, r = 0.002 ÷ 0.02 cm, η = 0.01 g cm²/s, Re ≈ 0.02 ÷ 0.2, which rules out turbulence during the motion of clusters and granules.

3.3. Discussion

Assuming that there are charges of opposite signs on the granule surface, it is possible to interpret the results of processing the videos as follows. It is known [29] that if there is any generally neutral set of charges, far enough from this set, the potential created by it turns out to be dipole:

$${\phi }_p\left(R\right)={\displaystyle \frac{1}{4\pi {\epsilon }_0}}{\displaystyle \frac{p_R}{R^2}}.$$

(5)

Here, $\overrightarrow{p}=\sum q_i\overrightarrow{d_i},q_i$ is the value of an individual charge, $\overrightarrow{d_i}$ is the radius vector that determines the position of q_i relative to the origin of coordinates located inside the set of charges, and $p_R$ is the projection of $\overrightarrow{p}$ on the radius vector $\overrightarrow{R}$.

If the total charge of the cluster is $Q=\sum q_i\ne 0$, its potential has the form

$${\phi \left(R\right)=\phi }_p\left(R\right)+{\phi }_Q\left(R\right),{ \phi }_Q\left(R\right)={\displaystyle \frac{1}{4\pi {\epsilon }_0}}{\displaystyle \frac{Q}{R}}$$

(6)

When, during the processing of the videos, we obtain the values of $c$ (4) close to integers 3, 4, or 5, this can be interpreted as follows. In the first case, the dipole moments of the clusters ${\overrightarrow{p}}_1,{\overrightarrow{p}}_2$ are zero, and they interact as particles with opposite charges $Q_1,Q_2$. In the second case, the dipole moment of one of the clusters is nonzero, and its total charge is zero; for another cluster, the opposite is true. In the third case, the total charges of both clusters are zero, and the dipole moments are nonzero.

However, in our observations of the convergence of granules and clusters, the distances between them are comparable with the sizes of the interacting objects. Therefore, strictly speaking, they cannot be regarded as either point charges or point dipoles. Since the observed clusters are large, the granules they consist of carry charges of opposite signs, the distribution of which has a complex form. Nevertheless, the electrostatic interaction of granules and clusters as point dipoles and charges can be examined based on the following qualitative considerations.

Figure 9 shows two converged clusters. They consist of some number of granules, each of which can be neutral or charged. The structure of charges of the cluster should exhibit periodicity related to its formation from opposite charges. The action of positive and negative charges will be mostly compensated at some distance from the cluster; then, the electric field is generated by one or two opposite charges, which have a value greater than the average one and are located closest to the cluster with which the first cluster interacts. According to this scheme, the clusters in Figure 9 interact as two dipoles.

Following the proposed model, simple estimations of the density of a charge on the granules can be made. By comparing them with the values of $\mathsf{\sigma }\approx {10}^{-6}$ C/m² ([27,28]), it is possible to evaluate the degree of reliability of our conclusion about the nature of interaction between polyamide granules in water. We use the most general laws of electrostatics, considering water as a medium with the permittivity $\mathsf{\epsilon }$.

The estimations were made for the processes of convergence to which the values of $\mathrm{c}$ close to the integers 4 and 5 correspond. Let us assume that the action of charges of opposite signs that form the cluster is compensated in a place where another cluster or granule with which it interacts is located. Only one point charge or two point charges of opposite signs located near the cluster boundary determine electrostatic attraction. Its force is

$$F_{el}={\displaystyle \frac{1}{4\pi {\epsilon }_0\epsilon }}{\displaystyle \frac{{2Q}_1{p}_2}{x^3}}, F_{el}={\displaystyle \frac{1}{4\pi {\epsilon }_0\epsilon }}{\displaystyle \frac{{6p}_1{p}_2}{x^4}},$$

(7)

for the point charge $Q_1$ and the point dipole $p_2$ or two dipoles $p_1$ and $p_2$, respectively. Formula (7) is valid when the dipole moments lie in the plane of the water surface and are co-directional in case of the interaction between two dipoles.

The resistance force ${\mathrm{F}}_{\mathrm{r}\mathrm{e}\mathrm{s}}$ is estimated from Stokes’ formula:

$$F_{res}=6\pi \eta rv,$$

(8)

where $\eta$ is the dynamic viscosity coefficient, $\mathrm{r}$ is the radius of a moving spherical particle, and $\mathrm{v}$ is its velocity. In this approximation, a large cluster can be regarded as a disk. Then, in formula (8), $r=0.57D$, where $D$ is the radius of the disk. Strictly speaking, formula (8) cannot be used to describe the motion of particles near the liquid surface. However, our estimations do not claim to have good accuracy.

Taking into account (7) and (8), the law of motion of converging particles (4) takes the form

$$t=t_0-b{x}^4,b={\displaystyle \frac{3}{2}}{\displaystyle \frac{{\pi }^2{\epsilon }_0\epsilon \eta }{Q_1{p}_2}}{\displaystyle \frac{r_1{r}_2}{r_1+r_2}},$$

(9)

for the charge–dipole interaction and

$$t=t_0-b{x}^5,b={\displaystyle \frac{4}{5}}{\displaystyle \frac{{\pi }^2{\epsilon }_0\epsilon \eta }{p_1{p}_2}}{\displaystyle \frac{r_1{r}_2}{r_1+r_2}}$$

(10)

for the dipole–dipole interaction, respectively; indexes 1 and 2 correspond to the first and second particles.

The approximation of the experimental data by curves of the form (4) gives the value of the coefficient $b$ (4). The charge $Q_1$ and dipole moments $p_1$ and $p_2$ can be expressed in terms of the granule radius $a$, the dipole length $l$, and the charge density $\mathsf{\sigma }$:

$$Q_1=4\pi a_1^2\sigma ,{ p}_1=4\pi a_1^2\sigma l_1, p_2=4\pi a_2^2\sigma l_2.$$

From (9) and (10), we obtain an expression for the density of the surface charge on the granule:

$$\sigma ={\displaystyle \frac{1}{4a_1{a}_2}}\sqrt{{\displaystyle \frac{3}{2}}{\displaystyle \frac{{\epsilon }_0\epsilon \eta }{l_{2}b}}{\displaystyle \frac{r_1{r}_2}{r_1+r_2}}} or \sigma ={\displaystyle \frac{1}{4a_1{a}_2}}\sqrt{{\displaystyle \frac{4}{5}}{\displaystyle \frac{{\epsilon }_0\epsilon \eta }{l_1{l}_{2}b}}{\displaystyle \frac{r_1{r}_2}{r_1+r_2}}}$$

(11)

The estimation of $\mathsf{\sigma }$ was made by taking into account the sizes of the clusters and the granules forming them. The radius of the granules was in a range of 10–30 µm, and the length of the dipole is of 100 µm order. The sizes of the granules and clusters, which were observed in the experiments and determine $F_{res}$, can range from 30 to 200 µm.

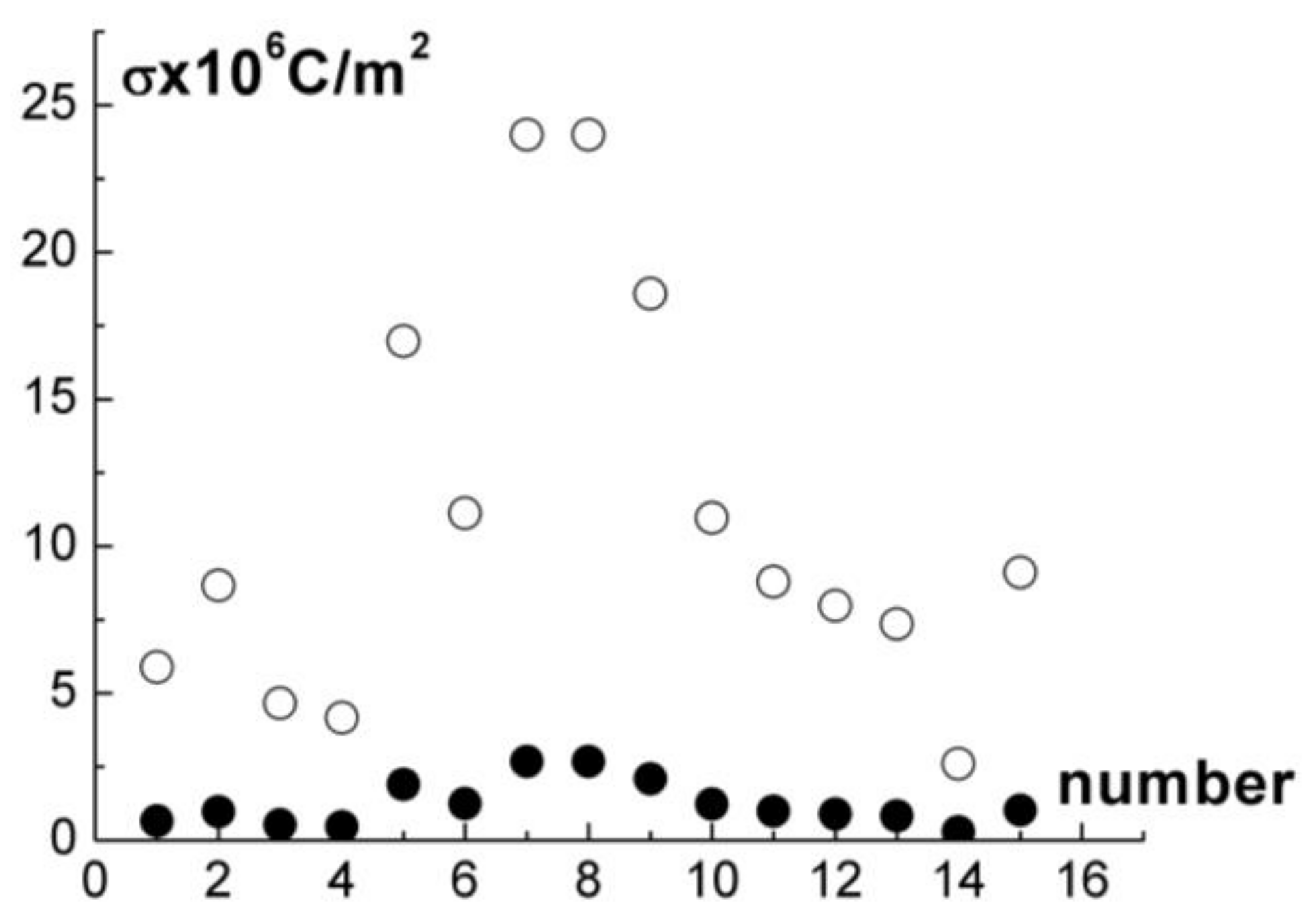
The values of $\sigma$ were calculated according to formulas (11) for 15 curves of the form (9) and (10) at $\epsilon =1$ and $\epsilon =$80, which are the permittivity of air and water. The results are demonstrated in Figure 10. For all experiments, our estimations give $\sigma <2.5·{10}^{-6}$ C/m² at $\epsilon =1$, which agrees with the results from [28]. Calculations at $\epsilon =$80 give overestimated values of $\sigma$ that correspond to the immersion of granules and clusters into water to a significant depth. Actually, they are separated from the interface by a very thin layer of water.

3.4. Effect of Screening

In water, and especially in a salt solution, there are positively and negatively charged ions. Owing to them, an electric field generated by the charges on the granules should be screened well. The length of screening in water can be estimated according to the Debye– Hückel theory for diluted electrolytes:

$$\lambda ={\displaystyle \frac{1}{zF}}\sqrt{{\displaystyle \frac{\epsilon RT}{8\pi c}}\approx } 1 \mathrm{\mu }\mathrm{m},$$

where $z=1$ is the ion charge, $\mathrm{F}$ is the Faraday constant, $T=300$ is the absolute temperature, $R$ is the gas constant, $\epsilon$= 80 is the permittivity of water, and $c={10}^{-7}$ mol/L is the ion concentration. A 4% NaCl solution is not a diluted electrolyte. In this case, the length of screening can be affected by many factors that we cannot take into consideration. The inefficiency of screening in our case may have two reasons. The characteristic size of the granules is 20 µm, and neighboring granules in the cluster may have opposite charges. If a neutral granule is adjacent to a charged one, a charge of the opposite sign is induced on the part of its surface that touches the charged granule. Therefore, ion clouds surrounding the granules have opposite charge signs and a significant overlap area. This is the first reason. The second one is that “submerged” granules and clusters are located at a micron distance from the water surface, which is characteristic of van der Waals forces. Hence, the electric field is not screened completely from the water–air interface. This is confirmed by a simple experiment. A voltage of 1 kV was applied to a test probe located 2–3 mm above the surface of water with polyamide clusters. A considerable number of clusters polarized by an external field and moving toward an increase in the electric field merged into a large cluster 5 min after applying the voltage (Figure 11). Therefore, an external electric field passes through a thin layer of water, and, hence, charged granules can interact in the absence of an external field due to the incomplete screening of the charge from the water–air interface.

It is possible to compare the electric field at the distance from which the clusters floated to the test probe to that generated by an individual charged granule at a distance characteristic of our observations of the cluster convergence. Under a voltage of 1 kV, the test probe with a radius of the hemispherical tip of 0.25 mm generates an electric field of ~2500 V/m at a distance of 1 cm. A spherical granule with a surface charge density of 10–6 C/m² and a radius of 20 µm generates an electric field of ~400 V/m at a distance of 100 µm. The estimations were made for the vacuum. In our experiments, the external field and the field of a charged granule were comparable in value.

4. Conclusions

In this paper, we considered a poorly studied case of particle interaction on a liquid surface—the clustering of polyamide granules on a water surface and the interactions in the observed two-dimensional system, leading to linear structures formation, are of considerable scientific interest. Since the polyamide granules are held near the water surface without deforming it, the observed process is somewhat different from the interaction of particles that deform the liquid surface and unite, including the influence of surface tension. The importance of this paper also lies in the broad prospects for using information about the patterns of such interaction processes in various fields of science and technology, such as crystal growing and polymer production technologies. It was shown in this work that the clusterization of polyamide granules on the water surface in the absence of flows occurs as a result of the electrostatic interaction. This interaction was due to the presence of charges of opposite signs on the granule surface gained as a result of friction. The screening of an electric field in water, which has high permittivity, was suppressed since the granules and clusters were a two-dimensional system located at a micron distance from the surface. The apparent radius of action of the attraction forces was 0.1–0.3 mm. This interaction should not distort the pattern of the velocity field when using granules to visualize macroflows. In our experiments, the maximum velocity of convergence of the clusters and granules did not exceed 1 mm/s. Therefore, the interaction of the granules would not affect the decoration of rather rapid flows. The latter conclusion is of no small importance, given the widespread use of granules in various hydrodynamic studies. The estimate of the density of the charge on the granule surface in order of magnitude agrees with the data from [27,28].