A Molecular Dynamics Perspective on the Impacts of Random Rough Surface, Film Thickness, and Substrate Temperature on the Adsorbed Film’s Liquid–Vapor Phase Transition Regime
Abstract
1. Introduction
2. MD Simulation Models and Methods
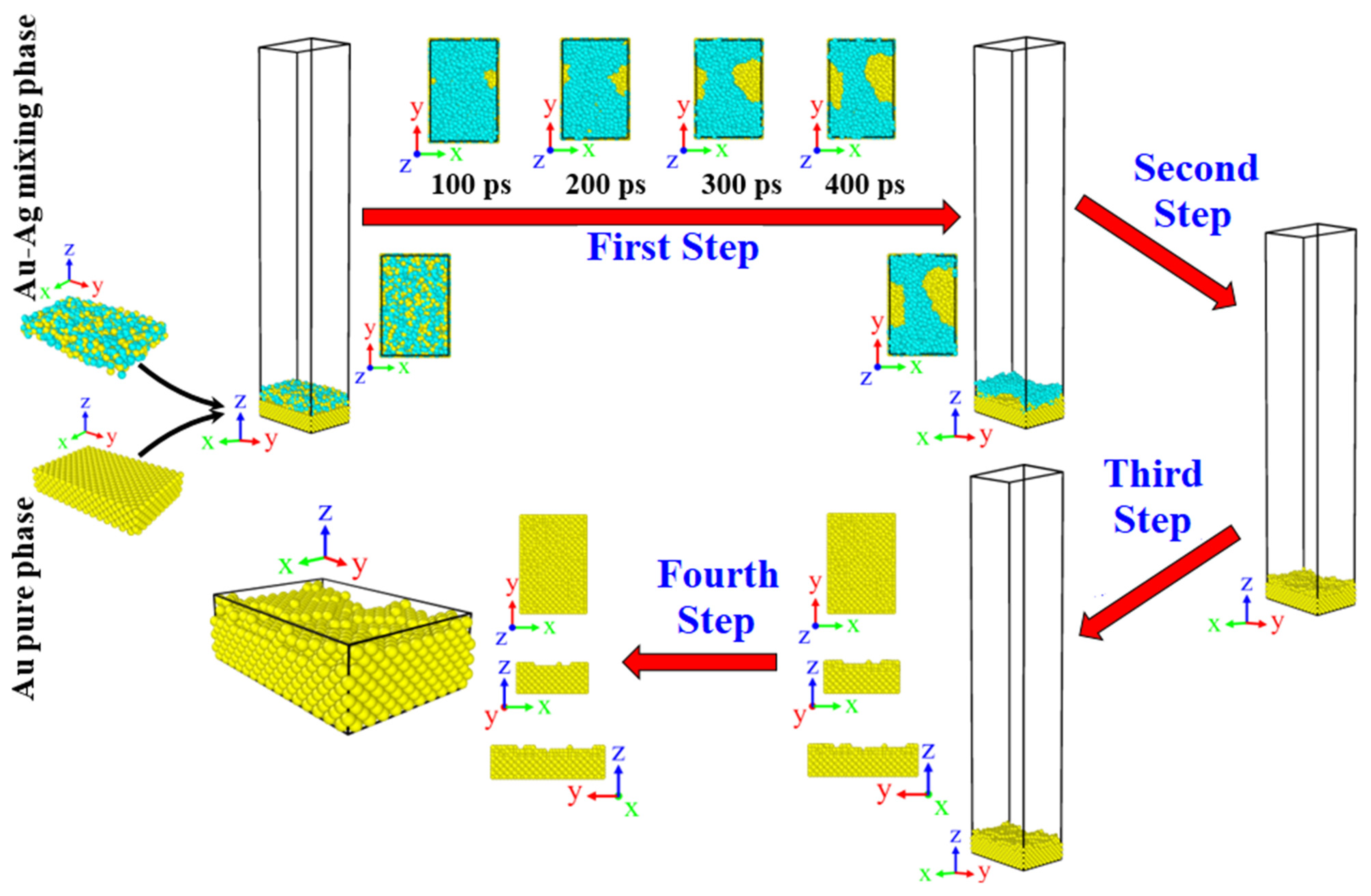
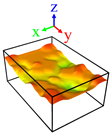
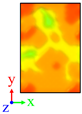
2.1. Innovative Method to Construct a Random Rough Au Surface
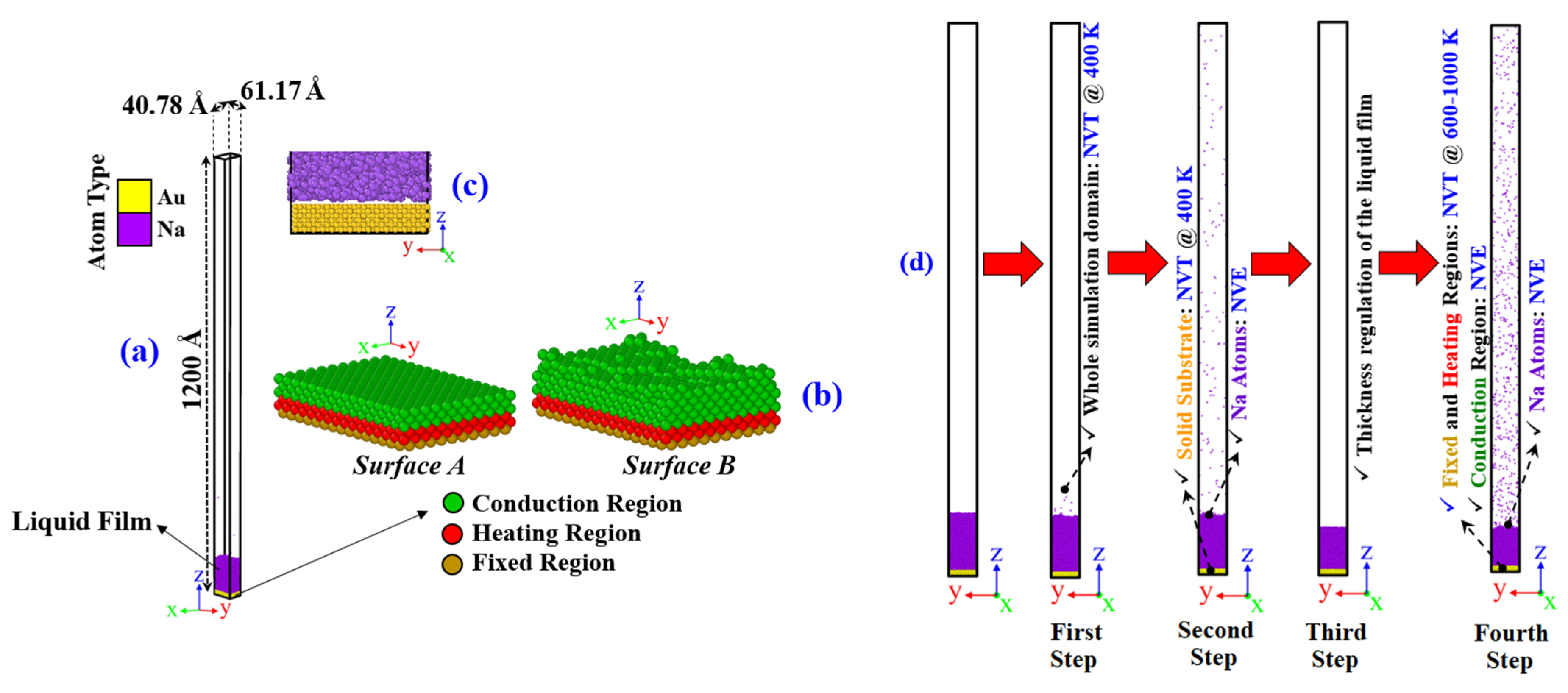
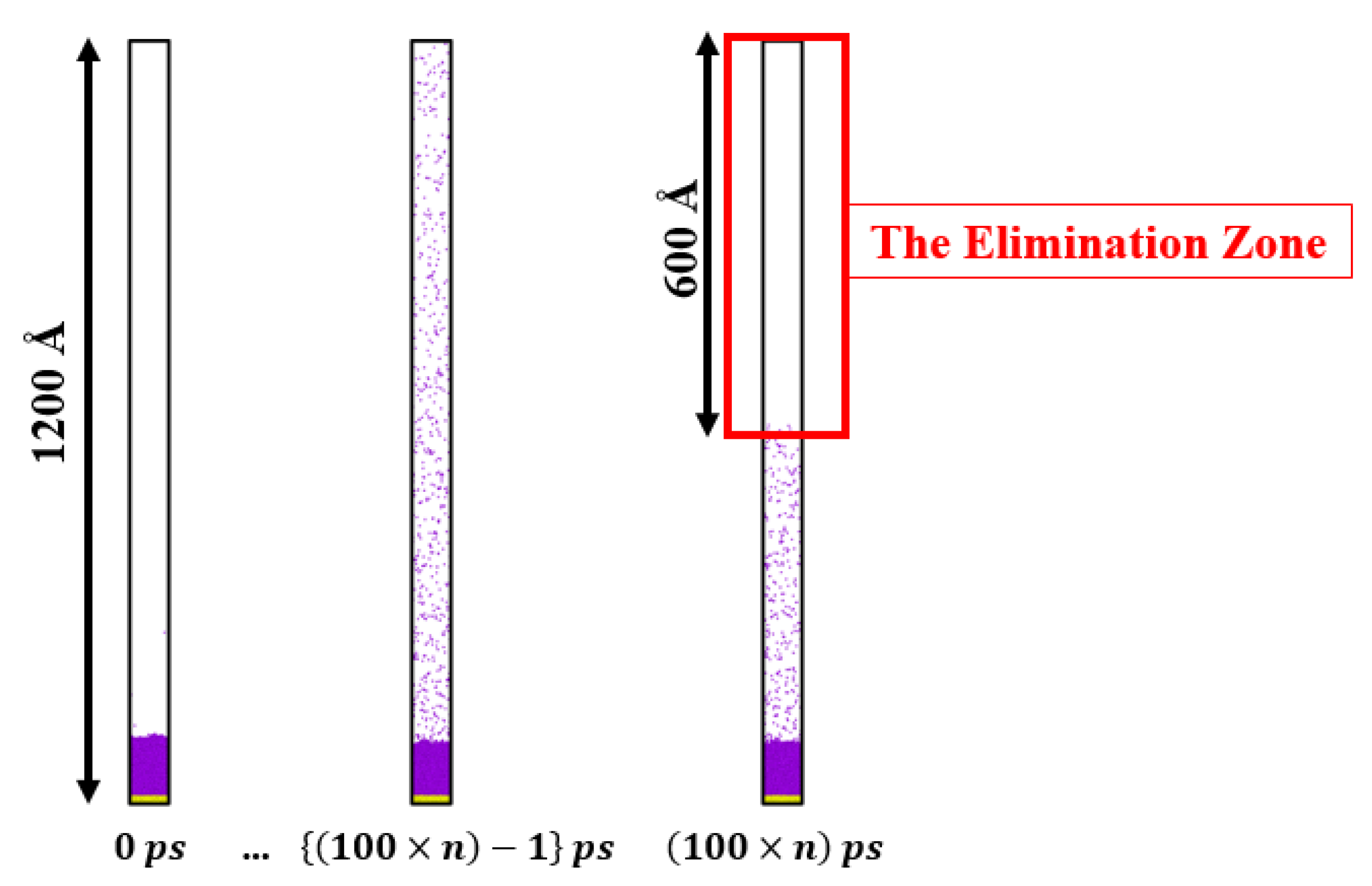
2.2. Liquid–Vapor Phase Transition Simulation
3. Result and Discussion
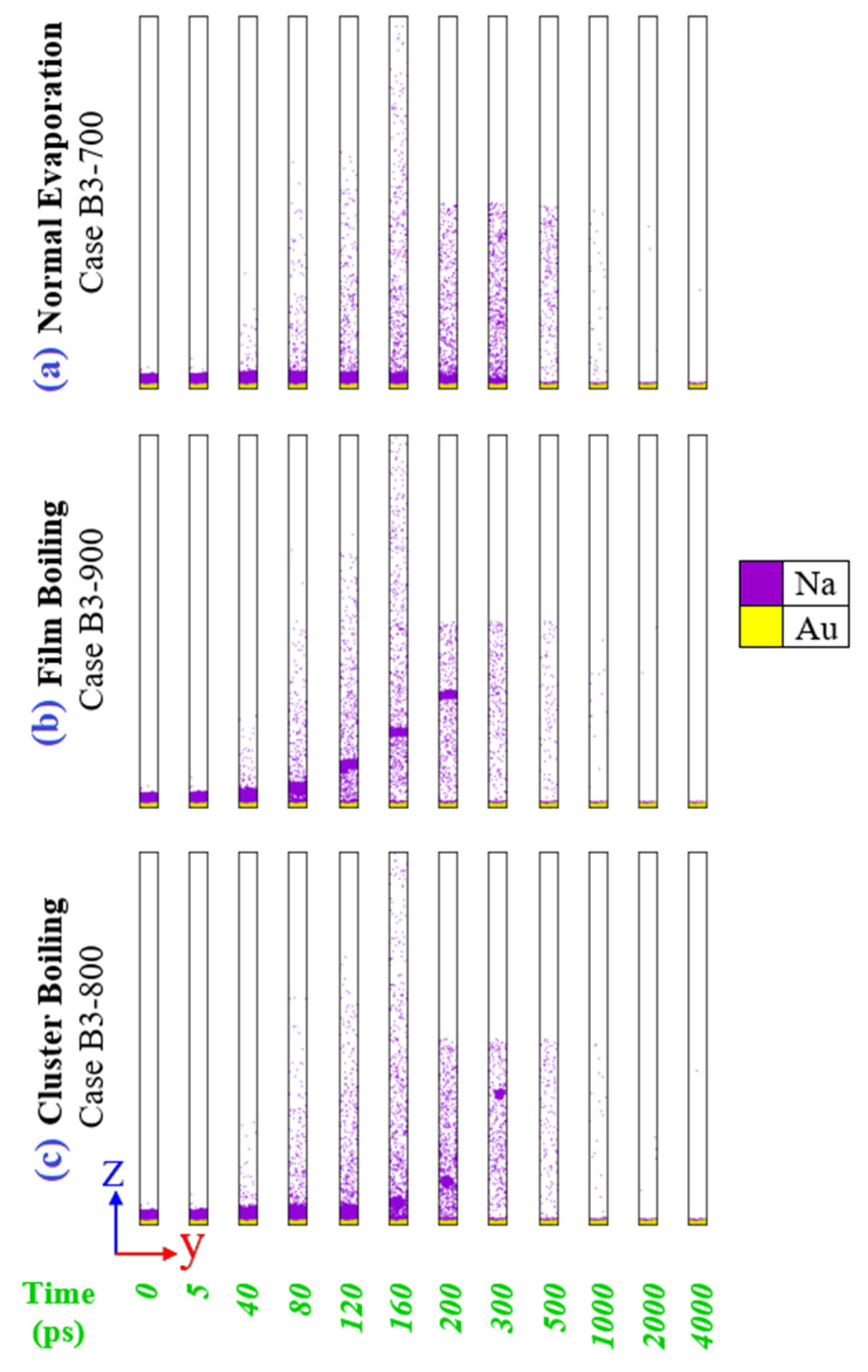
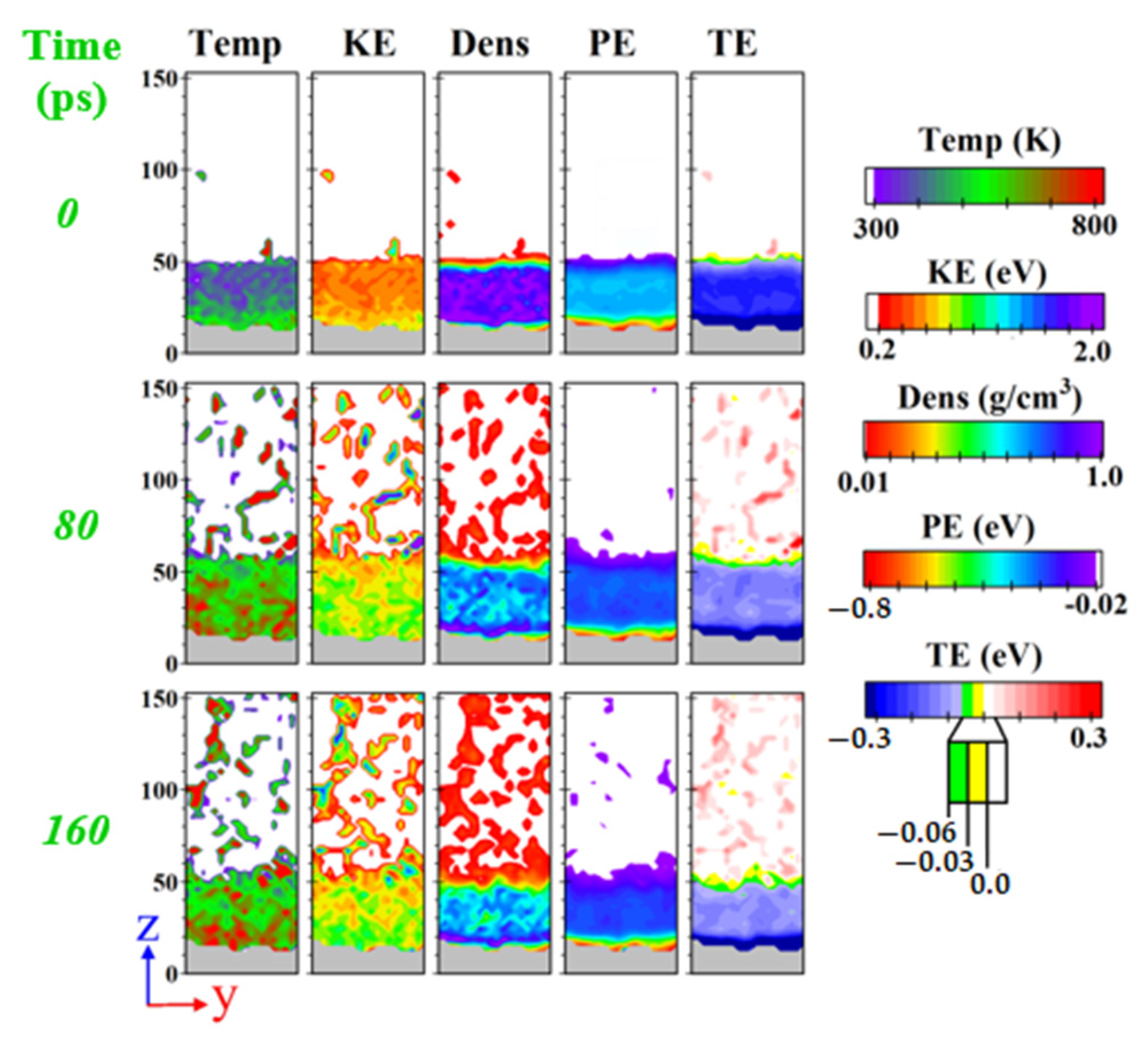
3.1. Overview of Phase Transition Regimes
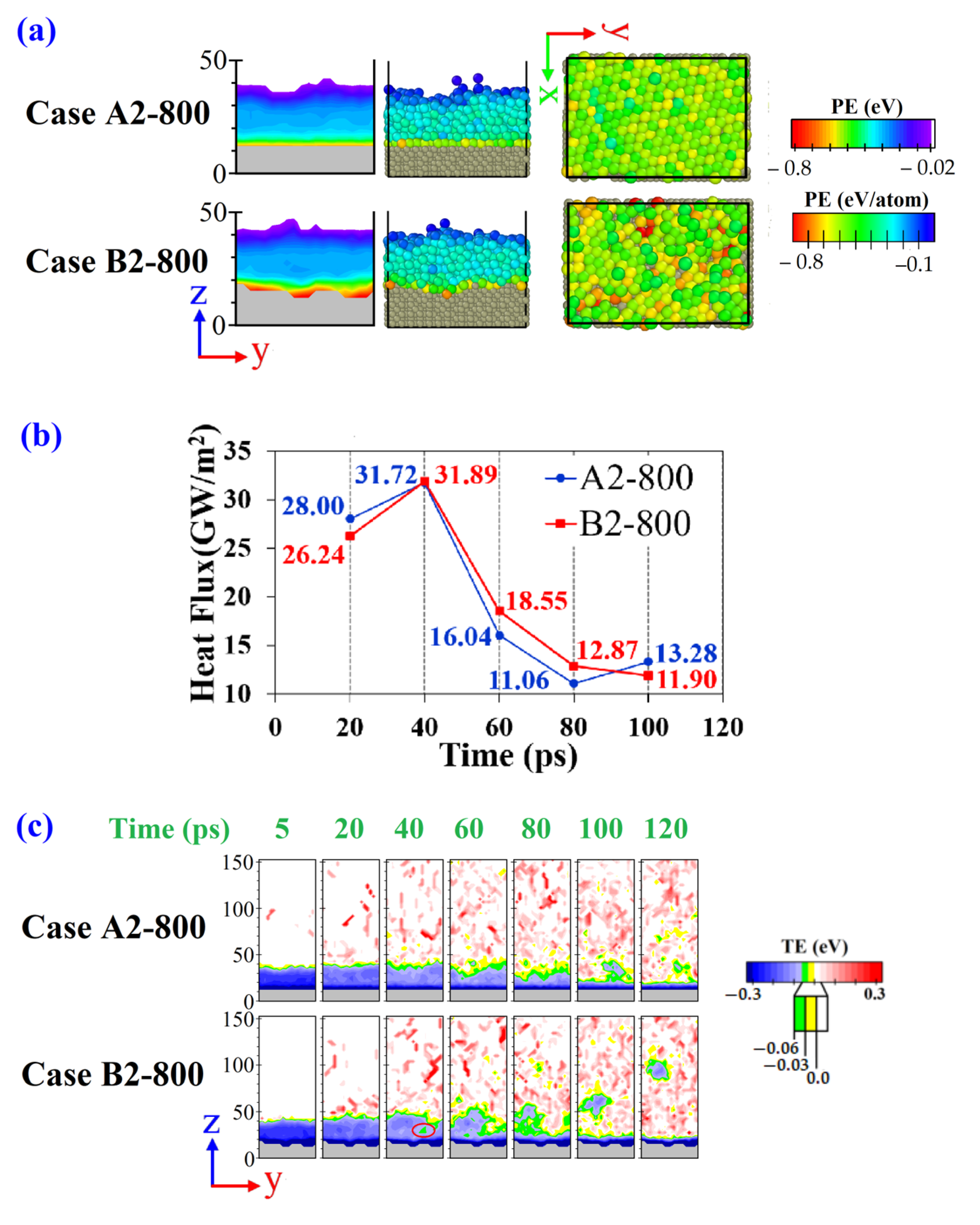
3.2. Transition from Normal Evaporation to Cluster/Film Boiling
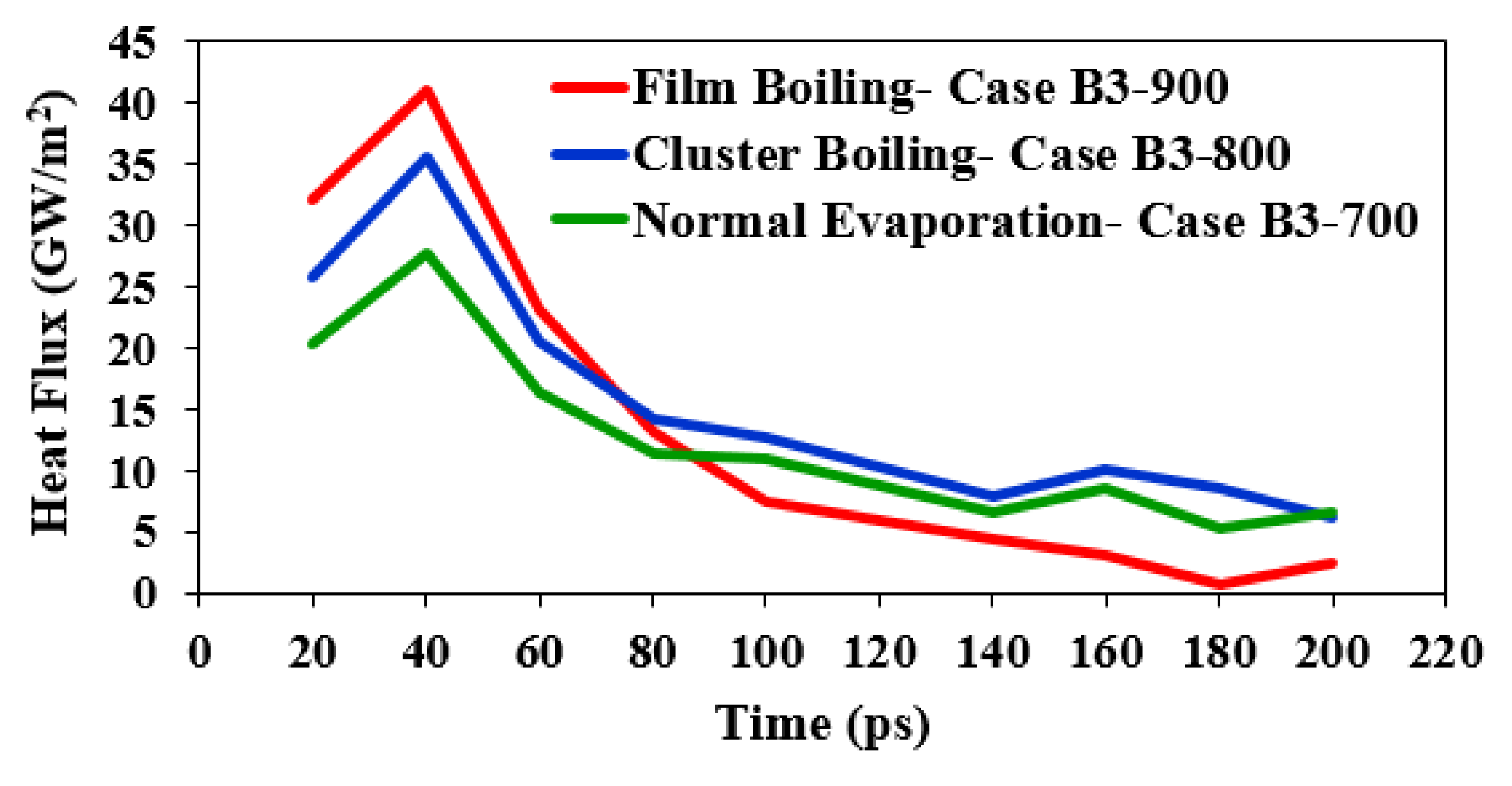
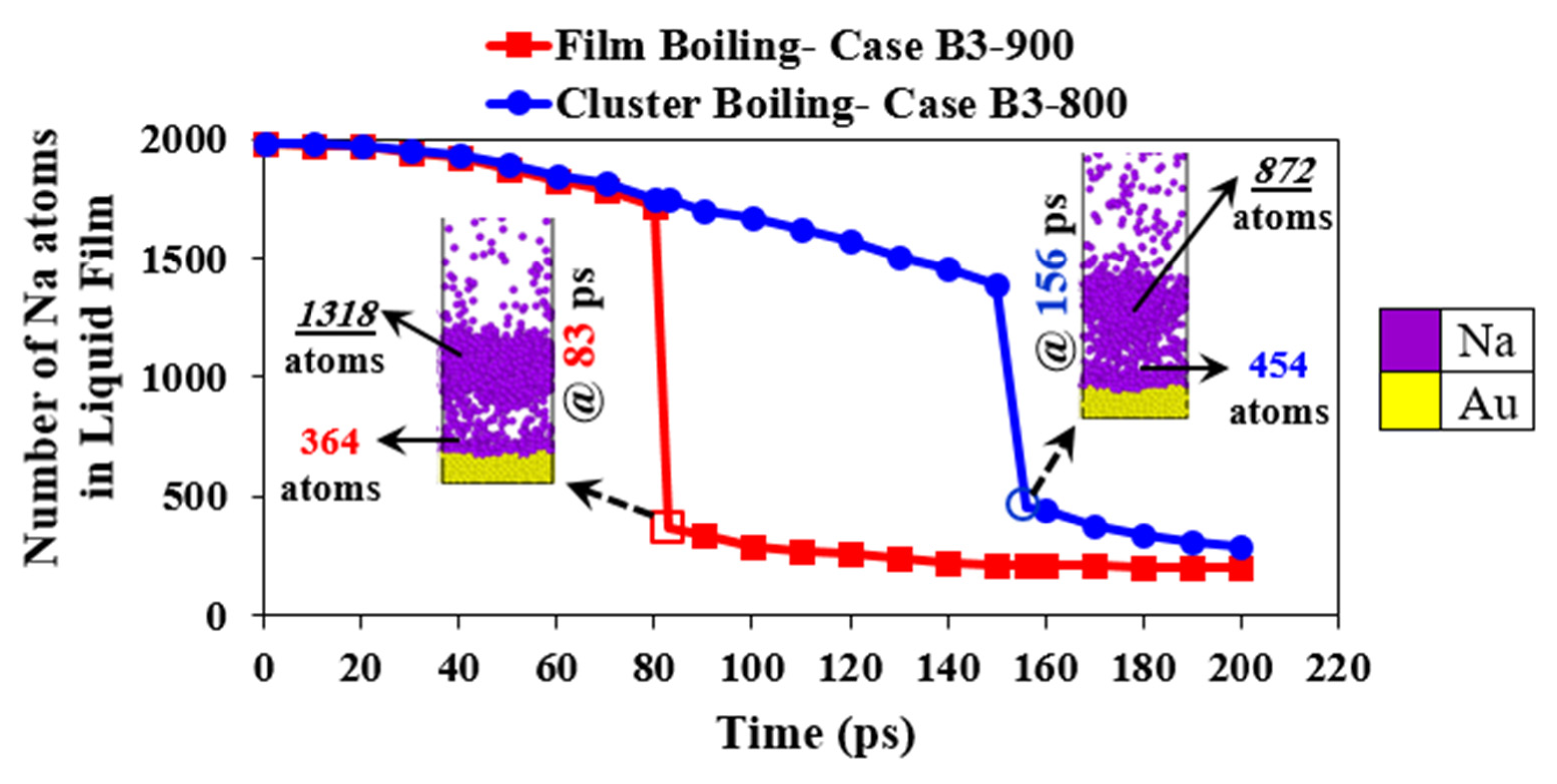
3.3. Transition from Cluster Boiling to Film Boiling
- Whenever TE in the near-wall zone goes to a zero value, a vapor layer starts forming, and it can ultimately yield either cluster or film boiling. Otherwise, normal evaporation will be observed.
- Following the formation of the vapor layer, if the number of liquid atoms that are about to evaporate is higher than a particular threshold, film boiling will appear; otherwise, cluster boiling will take place. From the results described above, it can be inferred that the minimum initial liquid film thickness of 3 nm is the threshold for the occurrence of film boiling.
3.4. Transition from Cluster Boiling to Film Boiling
4. Conclusions
- (1)
- The results illustrated that the value of the solid substrate temperature as well as the liquid film thickness are critical in determining the phase transition regime. Enhancing the solid substrate temperature and consequently the value of the absorbed thermal energy could result in changing the phase transition from a normal evaporation regime to cluster/film boiling and cluster boiling to film boiling if the liquid film had the minimum required thicknesses. Specifically, the minimum thickness for normal evaporation to cluster/film boiling transition was 2 nm, while it was 3 nm for cluster to film boiling transition.
- (2)
- Even though using the random rough surface can enhance the absorbed thermal energy, besides a specific film thickness (2 nm) and substrate temperature (800 K), it cannot change the phase transition regime. Mainly because its heat flux enhancement is not significant because of its low roughness ratio.
- (3)
- For the normal evaporation regime, two different modes (in terms of the heat fluxes) were identified. The influence of roughness on the mode of normal evaporation was negligible. For the normal evaporation transition mode, the liquid film thickness plays a significant role, even more than the solid substrate temperature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| 12-6 L-J | 12-6 Lennard-Jones potential |
| Å | Angstrom |
| Dens | Density [g/cm3] |
| EAM | Embedded Atom Model potential |
| eV | Electronvolt |
| FCC | Face-centered cubic |
| F | Embedding energy [eV] |
| fs | Femtosecond |
| g | Gram |
| GW | Gigawatt |
| K | Kelvin |
| KE | Kinetic energy [eV] |
| m | Meter |
| MD | Molecular dynamics |
| nm | Nanometer |
| ns | Nanosecond |
| NVE | Microcanonical ensemble |
| NVT | Canonical ensemble |
| OVITO | Open Visualization Tool software |
| PE | Potential energy [eV] |
| ps | Picosecond |
| rij | Distance between the atoms i and j [Å] |
| s | Second |
| TE | Total energy [eV] |
| Temp | Temperature [K] |
| Ui | Potential energy in the Embedded Atom Model potential [eV] |
| Uij | Potential energy in the Lennard-Jones 12-6 potential [eV] |
| WHP | Wicked heat pipe |
| Potential energy factor | |
| Lennard-Jones potential distance constant [Å] | |
| Micro | |
| Lennard-Jones potential energy constant [eV] | |
| Interatomic pair repulsion energy [eV] | |
| Subscripts | |
| Ag | Silver |
| Au | Gold |
| i | Atom i |
| j | Atom j |
| Na | Sodium |
References
- Rainieri, S.; Bozzoli, F.; Pagliarini, G. Effect of a Hydrophobic Coating on the Local Heat Transfer Coefficient in Forced Convection under Wet Conditions. Exp. Heat Transf. 2009, 22, 163–177. [Google Scholar] [CrossRef]
- Tang, H.; Xie, Y.; Xia, L.; Tang, Y.; Sun, Y. Review on the fabrication of surface functional structures for enhancing heat transfer of heat pipes. Appl. Therm. Eng. 2013, 226, 120337. [Google Scholar] [CrossRef]
- Solomon, A.B.; Ramachandran, K.; Pillai, B.C. Thermal performance of a heat pipe with nanoparticles coated wick. Appl. Therm. Eng. 2012, 36, 106–112. [Google Scholar] [CrossRef]
- Shahmardi, A.; Tammisola, O.; Chinappi, M.; Brandt, L. Effects of surface nanostructure and wettability on pool boiling: A molecular dynamics study. Int. J. Therm. Sci. 2021, 167, 106980. [Google Scholar] [CrossRef]
- Liu, H.; Ahmad, S.; Chen, J.; Zhao, J. Molecular dynamics study of the nanoscale boiling heat transfer process on nanostructured surfaces. Int. Commun. Heat Mass Transf. 2020, 119, 104963. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z.; Shao, W.; Cao, Q.; Cui, Z. Ultrathin liquid film nucleate boiling on grooved surfaces with variational aspect ratio. Therm. Sci. Eng. Prog. 2023, 43, 102023. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Tian, C.; Meng, X. Numerical experiments on evaporation and explosive boiling of ultra-thin liquid argon film on aluminum nanostructure substrate. Nanoscale Res. Lett. 2015, 10, 158. [Google Scholar] [CrossRef]
- Fu, T.; Mao, Y.; Tang, Y.; Zhang, Y.; Yuan, W. Effect of nanostructure on rapid boiling of water on a hot copper plate: A molecular dynamics study. Heat Mass Transf. 2015, 52, 1469–1478. [Google Scholar] [CrossRef]
- Fallahzadeh, R.; Bozzoli, F.; Cattani, L. Effect of closed-loop nanochannels on the onset of explosive boiling: A molecular dynamics simulation study. J. Phys. Conf. Ser. 2024, 2685, 012013. [Google Scholar] [CrossRef]
- Fallahzadeh, R.; Bozzoli, F.; Cattani, L.; Azam, M.W. Effect of Cross Nanowall Surface on the Onset Time of Explosive Boiling: A Molecular Dynamics Study. Energies 2024, 17, 1107. [Google Scholar] [CrossRef]
- Seyf, H.R.; Zhang, Y. Effect of nanotextured array of conical features on explosive boiling over a flat substrate: A nonequilibrium molecular dynamics study. Int. J. Heat Mass Transf. 2013, 66, 613–624. [Google Scholar] [CrossRef]
- Qasemian, A.; Qanbarian, M.; Arab, B. Molecular dynamics simulation on explosive boiling of thin liquid argon films on cone-shaped Al–Cu-based nanostructures. J. Therm. Anal. Calorim. 2020, 145, 269–278. [Google Scholar] [CrossRef]
- Fu, T.; Mao, Y.; Tang, Y.; Zhang, Y.; Yuan, W. Molecular Dynamics Simulation on Rapid Boiling of Thin Water Films on Cone-Shaped Nanostructure Surfaces. Nanoscale Microscale Thermophys. Eng. 2015, 19, 17–30. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, T.; Guo, K.; Wang, C.; Tian, W.; Qiu, S.; Su, G. Molecular dynamics simulation of the evaporation of thin liquid sodium film on the conical nanostructure surface. Prog. Nucl. Energy 2023, 162, 104795. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Z. Study of boiling heat transfer on concave hemispherical nanostructure surface with MD simulation. Int. J. Heat Mass Transf. 2019, 143, 118534. [Google Scholar] [CrossRef]
- Seyf, H.R.; Zhang, Y. Molecular Dynamics Simulation of Normal and Explosive Boiling on Nanostructured Surface. J. Heat Transf. 2013, 135, 121503. [Google Scholar] [CrossRef]
- Zhou, J.; Li, S.; Tang, S.-Z.; Zhang, D.; Tian, H. Effect of nanostructure on explosive boiling of thin liquid water film on a hot copper surface: A molecular dynamics study. Mol. Simul. 2021, 48, 221–230. [Google Scholar] [CrossRef]
- Liu, H.; Qin, X.; Ahmad, S.; Tong, Q.; Zhao, J. Molecular dynamics study about the effects of random surface roughness on nanoscale boiling process. Int. J. Heat Mass Transf. 2019, 145, 118799. [Google Scholar] [CrossRef]
- Liu, H.; Deng, W.; Ding, P.; Zhao, J. Investigation of the effects of surface wettability and surface roughness on nanoscale boiling process using molecular dynamics simulation. Nucl. Eng. Des. 2021, 382, 111400. [Google Scholar] [CrossRef]
- Guo, C.; Ji, C.; Kong, Y.; Liu, Z.; Guo, L.; Yang, Y. The Effect of Liquid–Solid Interactions upon Nucleate Boiling on Rough Surfaces: Insights from Molecular Dynamics. Materials 2023, 16, 1984. [Google Scholar] [CrossRef]
- Qun, C.; Zheng, C. Molecular dynamics simulations of the effects of surface sinusoidal nanostructures on nanoscale liquid film phase-change. J. Therm. Sci. 2020, 29, 1076–1084. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, T.; Guo, K.; Tian, W.; Qiu, S.; Su, G. The evaporation of nanoscale sodium liquid film on the non-ideal nanostructure surface: A molecular dynamics study. Int. J. Adv. Nucl. React. Des. Technol. 2023, 5, 1–8. [Google Scholar] [CrossRef]
- Cao, Q.; Li, Z.; Cui, Z. Nanoscale Investigation of Bubble Nucleation and Boiling on Random Rough Surfaces. Langmuir 2023, 39, 12754–12761. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Guye, K.; Dogruoz, B.; Agonafer, D. Molecular dynamics simulations of thin-film evaporation: The influence of interfacial thermal resistance on a graphene-coated heated silicon substrate. Appl. Therm. Eng. 2021, 195, 117142. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, D.; Qiu, S.; Tian, W.; Wu, Y.; Su, G. Study on the characteristics of the sodium heat pipe in passive residual heat removal system of molten salt reactor. Nucl. Eng. Des. 2013, 265, 691–700. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, K.; Wang, C.; Zhang, D.; Tian, W.; Qiu, S.; Su, G. Molecular dynamics study of liquid sodium film evaporation and condensation by Lennard-Jones potential. Nucl. Eng. Technol. 2022, 54, 3117–3129. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, T.; Guo, K.; Tian, W.; Qiu, S.; Su, G. Molecular dynamics study of the wettability effect on the evaporation of thin liquid sodium film. Nucl. Eng. Des. 2023, 405, 112183. [Google Scholar] [CrossRef]
- Leite, R.P.; de Koning, M. Nonequilibrium free-energy calculations of fluids using LAMMPS. Comput. Mater. Sci. 2019, 159, 316–326. [Google Scholar] [CrossRef]
- Hu, C.; Shi, L.; Yi, C.; Bai, M.; Li, Y.; Tang, D. Mechanism of enhanced phase-change process on structured surface: Evolution of solid-liquid-gas interface. Int. J. Heat Mass Transf. 2023, 205, 123915. [Google Scholar] [CrossRef]
- Asai, P.; Jin, J.; Deo, M.; Miller, J.D.; Butt, D. Non-equilibrium molecular dynamics simulation to evaluate the effect of confinement on fluid flow in silica nanopores. Fuel 2022, 317, 123373. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Liu, L.; Su, Z.; Du, Y.; Li, Y.; Han, H.; Zhu, J.; Sun, C. Molecular dynamics study on the enhancement of heterogeneous nucleate boiling of mixed liquid on superhydrophilic surfaces. Appl. Therm. Eng. 2023, 230, 120724. [Google Scholar] [CrossRef]
- Guillotte, M.; Godet, J.; Pizzagalli, L. A fully molecular dynamics-based method for modeling nanoporous gold. Comput. Mater. Sci. 2019, 161, 135–142. [Google Scholar] [CrossRef]
- Wu, C.-D.; Hong, G.-W. Effects of heating rate on morphological evolution, microstructure, and mechanical properties of nanoporous gold. J. Appl. Phys. 2022, 131, 224304. [Google Scholar] [CrossRef]
- Kraut, J.C.; Stern, W.B. The density of gold-silver-copper alloys and its calculation from the chemical composition. Gold Bull. 2000, 33, 52–55. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302–1322. [Google Scholar] [CrossRef]
- Krone, M.; Stone, J.E.; Ertl, T.; Schulten, K. Fast visualization of Gaussian density surfaces for molecular dynamics and particle system trajectories. In Proceedings of the Eurographics Conference on Visualization, Vienna, Austria, 5–8 June 2012. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Semiempirical, Quantum Mechanical Calculation of Hydrogen Embrittlement in Metals. Phys. Rev. Lett. 1983, 50, 1285–1288. [Google Scholar] [CrossRef]
- Ahmadi, V.; Fahim, A.H.; Neek, S.J.; Ghassemi, H. Molecular dynamic simulation of light alkanes flash evaporation. Therm. Sci. Eng. Prog. 2023, 46, 102211. [Google Scholar] [CrossRef]
- Delhommelle, J.; Millié, P. Inadequacy of the Lorentz-Berthelot combining rules for accurate predictions of equilibrium properties by molecular simulation. Mol. Phys. 2009, 99, 619–625. [Google Scholar] [CrossRef]
- Foiles, S.M.; Baskes, M.I.; Daw, M.S. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B 1986, 33, 7983–7991. [Google Scholar] [CrossRef]
- Hasan, M.N.; Shavik, S.; Rabbi, K.; Mukut, K.; Morshed, A. Phase Change Characteristics of Ultra-Thin Liquid Argon Film over different Flat Substrates at High Wall Superheat for Hydrophilic/Hydrophobic Wetting Condition: A Non-Equilibrium Molecular Dynamics Study. J. Chem. Eng. 2017, 29, 49–55. [Google Scholar] [CrossRef]
- Fink, J.K.; Leibowitz, L. Thermodynamic and Transport Properties of Sodium Liquid and Vapor; U.S. Department of Energy: Washington, DC, USA, 1995; p. 87. [CrossRef]
- Foust, O.J. Sodium chemistry and physical properties. In Sodium-NaK Engineering Handbook; Gordon and Breach: New York, NY, USA, 1972; Volume I, p. 9. [Google Scholar]
- Din, X.-D.; Michaelides, E.E. Kinetic theory and molecular dynamics simulations of microscopic flows. Phys. Fluids 1997, 9, 3915–3925. [Google Scholar] [CrossRef]
- Wu, X.; Yang, Z.; Duan, Y. Formation and growth of R32/R1234yf nanobubble on smooth surface: Molecular dynamics simulations. J. Mol. Liq. 2022, 348, 118020. [Google Scholar] [CrossRef]
- Alam, M.; Thakur, S.H.; Islam, M.; Hasan, M.N.; Mitsutake, Y.; Monde, M. Atomistic and macroscopic characterization of nanoscale thin film liquid-vapor phase change phenomena. Int. J. Therm. Sci. 2021, 170, 107159. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Wang, S.-Y.; Lu, G.; Wang, X.-D. Explosive boiling of nano-liquid argon films on high temperature platinum walls: Effects of surface wettability and film thickness. Int. J. Therm. Sci. 2018, 132, 610–617. [Google Scholar] [CrossRef]
- Rabbi, K.F.; Tamim, S.I.; Faisal, A.H.M.; Mukut, K.M.; Hasan, M.N. A molecular dynamics study on thin film liquid boiling characteristics under rapid linear boundary heating: Effect of liquid film thickness. In Proceedings of the 7th BSME International Conference on Thermal Engineering, Dhaka, Bangladesh, 22–24 December 2016. [Google Scholar] [CrossRef]
- Yang, K.-S.; Tu, C.-W.; Zhang, W.-H.; Yeh, C.-T.; Wang, C.-C. A novel oxidized composite braided wires wick structure applicable for ultra-thin flattened heat pipes. Int. Commun. Heat Mass Transf. 2017, 88, 84–90. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Wang, S.-Y.; Lu, G.; Wang, X.-D. Effects of wettability on explosive boiling of nanoscale liquid films: Whether the classical nucleation theory fails or not? Int. J. Heat Mass Transf. 2019, 132, 1277–1283. [Google Scholar] [CrossRef]
- Blander, M.; Katz, J.L. Bubble nucleation in liquids. AIChE J. 1975, 21, 833–848. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Cao, Q.; Li, J.; Yu, B.; Tao, W.-Q. Effects of simulation system on the phase transition behavior of liquid film: A molecular dynamics study. J. Mol. Liq. 2020, 311, 113306. [Google Scholar] [CrossRef]
- Hong, F.; Cheng, P.; Wu, H.; Sun, Z. Evaporation/boiling heat transfer on capillary feed copper particle sintered porous wick at reduced pressure. Int. J. Heat Mass Transf. 2013, 63, 389–400. [Google Scholar] [CrossRef]
- Deng, X.; Xu, X.; Song, X.; Li, Q.; Liu, C. Boiling heat transfer of CO2/lubricant on structured surfaces using molecular dynamics simulations. Appl. Therm. Eng. 2023, 219, 119682. [Google Scholar] [CrossRef]
- Ilic, M.; Stevanovic, V.D.; Milivojevic, S.; Petrovic, M.M. Explosive boiling of water films based on molecular dynamics simulations: Effects of film thickness and substrate temperature. Appl. Therm. Eng. 2023, 220, 119749. [Google Scholar] [CrossRef]






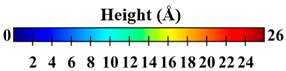
| Surface | Roughness Ratio 1 | Oblique View | Top View | ||
|---|---|---|---|---|---|
| A | 1.00 | 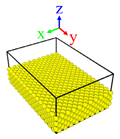 |  | 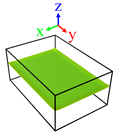 | 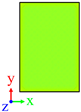 |
 | |||||
| B | 1.03 |  | 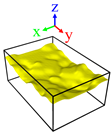 | ||
 |  | ||||
| Simulation Step | Atom Pair | Potential Function | EAM Parameters | 12-6 L-J Parameters | |
|---|---|---|---|---|---|
| (Å) | (eV) | ||||
| First Step | Au-Au | EAM | Ref. [41] | — | — |
| Ag-Ag | EAM | Ref. [41] | — | — | |
| Au-Ag | 12-6 L-J | — | 0.6514 1 | 0.3936 1 | |
| Third Step | Au-Au | 12-6 L-J | — | 2.6370 (Ref. [26]) | 0.441280 (Ref. [26]) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallahzadeh, R.; Bozzoli, F.; Cattani, L.; Pagliarini, L.; Naeimabadi, N.; Azam, M.W. A Molecular Dynamics Perspective on the Impacts of Random Rough Surface, Film Thickness, and Substrate Temperature on the Adsorbed Film’s Liquid–Vapor Phase Transition Regime. Sci 2024, 6, 33. https://doi.org/10.3390/sci6020033
Fallahzadeh R, Bozzoli F, Cattani L, Pagliarini L, Naeimabadi N, Azam MW. A Molecular Dynamics Perspective on the Impacts of Random Rough Surface, Film Thickness, and Substrate Temperature on the Adsorbed Film’s Liquid–Vapor Phase Transition Regime. Sci. 2024; 6(2):33. https://doi.org/10.3390/sci6020033
Chicago/Turabian StyleFallahzadeh, Rasoul, Fabio Bozzoli, Luca Cattani, Luca Pagliarini, Niloofar Naeimabadi, and Muhammad Waheed Azam. 2024. "A Molecular Dynamics Perspective on the Impacts of Random Rough Surface, Film Thickness, and Substrate Temperature on the Adsorbed Film’s Liquid–Vapor Phase Transition Regime" Sci 6, no. 2: 33. https://doi.org/10.3390/sci6020033
APA StyleFallahzadeh, R., Bozzoli, F., Cattani, L., Pagliarini, L., Naeimabadi, N., & Azam, M. W. (2024). A Molecular Dynamics Perspective on the Impacts of Random Rough Surface, Film Thickness, and Substrate Temperature on the Adsorbed Film’s Liquid–Vapor Phase Transition Regime. Sci, 6(2), 33. https://doi.org/10.3390/sci6020033








