Abstract
Energy transformation powers change in the universe. In physical systems, maximal power (rate of energy input or output) may occur only at submaximal efficiency (output/input), or conversely, maximal efficiency may occur only at submaximal power. My review of power and efficiency in living systems at various levels of biological organization reveals that (1) trade-offs (negative correlations) between power and efficiency, as expected in physical systems, chiefly occur for resource-supply systems; (2) synergy (positive correlations) between power and efficiency chiefly occurs for resource use systems, which may result from (a) increasing energy allocation to production versus maintenance as production rate increases and (b) natural selection eliminating organisms that exceed a maximal power limit because of deleterious speed-related effects; (3) productive power indicates species-wide ‘fitness’, whereas efficiency of resource acquisition for production indicates local ‘adaptiveness’, as viewed along a body size spectrum and within clades of related species; (4) covariation of the power and efficiency of living systems occurs across space and time at many scales; (5) the energetic power/efficiency of living systems relates to the rates and efficiencies/effectiveness of nutrient/water uptake/use, the functional performance of various activities, and information acquisition/processing; and (6) a power/efficiency approach has many useful theoretical and practical applications deserving more study.
1. Introduction
Activity of any physical system (i.e., changes in its properties, including its spatial position and that of its parts, its shape or spatial configuration, its physical/energetic composition, and its capture or emittance of energy or materials) involves the uptake and transformation of energy. The fundamental concepts of ‘power’ and ‘efficiency’ describe the rate of energy uptake and transformation driving various kinds of physical activity and the proportional transfer or conversion of energy into work or useful forms of energy, respectively. In short, ‘power’ and ‘efficiency’ refer to the ‘rates’ and ‘ratios’ of energy input and output. Mathematically, physicists describe ‘power’ (P) as being W/t or U/t, where W is work (force x distance), U is the amount of useful energy acquired/produced minus unused heat loss, and t is time [1]. The concept of ‘efficiency’ (E) is described as W/T or U/T, where T is the total energy input. These concepts are based on the first and second laws of thermodynamics (energy cannot be created or destroyed, but only transformed into another form; and no energy transformation is 100% efficient, respectively [2]). Thus, the concepts of power and efficiency are fundamental for understanding the dynamics and energy transformation of all physical systems, both living and non-living (see, e.g., [3,4,5,6,7,8]).
Given the wide-ranging importance of power and efficiency in living systems, I am unable to provide a comprehensive, detailed review of all the diverse theoretical, empirical, and practical applications of these concepts. Instead, I primarily focus on two of the most significant approaches that biologists have used to analyze living systems from a power/efficiency perspective. First, I focus on studies that have examined how power and efficiency covary in various biological and ecological systems. In doing so, I consider the influential view promoted by Odum and Pinkerton over 60 years ago [5] and still advocated today (e.g., [8]) that living systems generally show a trade-off between power and efficiency, like some non-living physical systems under equilibrium conditions (Section 2). According to their “maximum power principle”, maximal power is achieved at submaximal efficiency. Conversely, I also highlight another insufficiently appreciated view that maximal efficiency is achieved at submaximal power, which I call the “maximum efficiency principle”. Both principles, which are derived from observations of non-living physical systems, predict that power and efficiency should covary negatively in living systems (Section 2). As will be seen, however, there are many exceptions to this prediction. In fact, many living systems show a positive correlation between power and efficiency (Section 3). To help explain both negative and positive relationships observed between power and efficiency in living systems, I hypothesize that resource supply systems should usually show negative covariation (trade-offs) between power and efficiency, whereas resource use systems should usually show positive covariation (synergy) between power and efficiency. These predictions are justified mechanistically and supported by abundant empirical evidence in Section 3 and other sections of my review. My discussion of the covariation of power and efficiency in living systems bears on our understanding of many biological patterns and processes, including the thermodynamics of cell metabolism, the energetics and body size scaling of rates of metabolism, growth, reproduction, and locomotion in organisms, of growth and production in populations, and of energy flow in ecosystems (Section 3 and Section 4).
Second, I focus on studies that use the concepts of power and efficiency as measures or indicators of evolutionary fitness or adaptation (Section 5, Section 6 and Section 7). Several biologists have suggested that maximal power (rate of resource use) for production (including specifically reproduction) is a useful energetic index of evolutionary fitness (Section 5 [3,7,9,10,11,12,13]). Furthermore, J. H. Brown and colleagues [14] have argued that the universal action of natural selection favoring maximal power per generation has resulted in species of all sizes having essentially equivalent energetic fitness, a view called the “equal fitness paradigm” (also see [15,16]). By contrast, other scientists have considered energetic or functional efficiency as an appropriate measure, indicator, or result of adaptation (Section 6 [9,17,18,19]). In Section 7, I further discuss how power and efficiency relate to fitness and adaptiveness and how they covary in various organismal and ecological systems over space and time, thereby linking the two major approaches that are emphasized in my review. Specifically, I propose and justify a hypothetical scheme showing how power (fitness) and efficiency (adaptiveness) at the level of species should scale inversely with body size, thus offering a fundamentally different viewpoint than the “equal fitness paradigm” proposed by J. H. Brown and colleagues [14,15,16]. I also show how species-wide power (fitness) and efficiency (adaptiveness) may vary inversely with niche breadth, population stability, and geographical range size within clades of related species. I hypothesize that these patterns are driven, at least in part, by mortality rates that depend on body size and relative habitat stability. In addition, I describe how the power and efficiency of living systems vary in space (geography) and time at various scales (daily, seasonally, ontogenetically, ecologically, and geologically). I thereby provide more evidence of how power and efficiency covary in living systems, as well as new perspectives concerning (1) daily/seasonal variation of the power/efficiency of living systems, (2) ontogenetic shifts in power/efficiency and their possible implications for the evolution of life histories, and (3) macroevolutionary trends in power/efficiency, including the geologically recent origin of high-powered endothermic birds and mammals, all of which deserve further exploration.
In Section 8, I discuss some applications of a power (rate) versus efficiency (effectiveness) perspective to nutrient/water uptake/use, performance of various functional activities, and information acquisition/processing. I hope that this section will stimulate future development of synthetic theory that links rates and efficiencies of the uptake and use of energy, water, nutrients, and information in living systems. In Section 9, I briefly mention some potential practical benefits of a power/efficiency perspective, including maximizing production in fisheries, agriculture, forestry, and human economic systems, as well as improving the effectiveness of microbial bioremediation strategies and bioenergy production. Finally, in Section 10, I summarize the major conclusions of my review. I hope that my analyses and conjectures will stimulate others to further explore the relevance of power and efficiency and their covariation in a variety of living systems at various hierarchical levels of organization, from cells to ecosystems, and over different time scales, from physiological to geological. This subject is of fundamental importance for understanding the dynamics of both living and non-living systems and thus deserves more attention than it has received, including the development of new theory that recognizes the existence of both positive and negative relationships between power and efficiency. I outline some ways that this could be done, including incorporating novel distinctions between negative power/efficiency covariation in resource supply systems versus positive power/efficiency covariation in resource use systems and between power-enhancing fitness versus efficiency-enhancing adaptation. Maximal power theory that has been advocated for decades is insufficient for fully explaining the diverse relationships between power and efficiency that have been observed in living systems.
2. Covariation between Power and Efficiency in Physical Systems
The ecologist Howard T. Odum and physicist Richard Pinkerton [5] described how the maximal power output of Atwood’s machine (a gravity-powered pulley system of opposite falling and rising weights) occurs when the efficiency of energy conversion is less than maximal (apparently not 50% as they say, but 61.8% according to [7]). Thus, maximal power is reached at the expense of submaximal efficiency. They further argued that this trade-off between power and efficiency seen in a simple machine applies to many other kinds of physical energy-transforming systems. They mathematically derived this trade-off for closed thermodynamic systems and claimed that it applies to various kinds of human-made mechanical, electrical, and thermal systems with coupled components. Odum and Pinkerton’s “maximum power principle” (MPP) has been applied to many other kinds of natural physical systems as well [8,20].
However, to be clear, the MPP is a “maximum power at intermediate efficiency principle”. Physical systems may also show a “maximum efficiency at intermediate power principle”, or, for short, a “maximum efficiency principle” (MEP) (Figure 1a). The MEP is exemplified by automobiles and other vehicles of transportation whose fuel use efficiency is maximized at intermediate travel speeds (power) ([4,21], also see Section 3.1). When stopped but engaged, their travel power and efficiency are zero, with all fuel being used for an idling engine (standby costs). As an automobile begins to move and increase its speed, proportionally more fuel is used for movement relative to standby costs, thus increasing both travel power and efficiency. This increase is asymptotic, and eventually, as travel speed increases further, fuel use efficiency declines because of increasing energy-draining, frictional costs (heat loss) apparently associated with the rapid movement of engine parts, air resistance, and resistance of the travel surface to rolling tires.
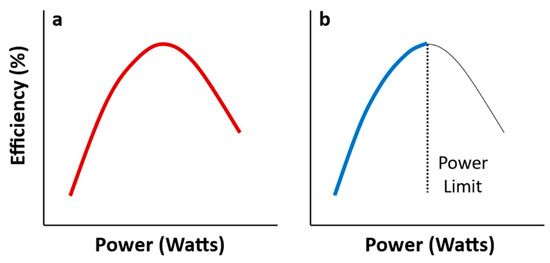
Figure 1.
Covariation between power and efficiency as dictated by a “maximum efficiency principle” (MEP; see text). (a) As power output (Watts = J/s) of a physical system increases, efficiency of conversion of input energy into power output (%) increases and then decreases in a curvilinear (concave downward) way. (b) In biological systems involving growth, reproduction, and locomotion, a limit on maximal power production (dashed vertical line) may cause gross production efficiency (including maintenance costs) to increase positively with increasing production rate in a decelerating (asymptotic) way, as often observed [4]. Compare to Figures 6 and 7.
As noted by Hall and McWhirter [8], the MPP has been inadequately tested (including by Odum himself). Moreover, some reported examples of the MPP are really examples of the MEP, a confusion that should be avoided (see Section 3).
3. Covariation between Power and Efficiency in Living Systems
3.1. Empirical Patterns
Odum and Pinkerton [5] claimed that trade-offs between power and efficiency should apply to living energy-transforming systems, including organismal metabolism, photosynthesis, food capture for maintenance, production in an ecological community, and growth and maintenance of a human civilization. However, only a few unequivocal examples of power–efficiency trade-offs in living systems have been described. For example, Gnaiger [22] claimed that biochemical pathways involved in hypoxic metabolism show an inverse correlation between power and efficiency, but this view has been disputed (see exchange between [19] and [23] and references cited therein). Richman [24] reported an inverse correlation between rates and efficiencies of food assimilation in water fleas (Daphnia), which also occurs in other animals (see Section 3.3). Many vertebrate animals exhibit minimal energy use per minute or distance traveled (and thus maximal efficiency) at intermediate travel speeds [25,26], as do automobiles, airplanes, and helicopters [4,20,26], but these examples follow the “maximum efficiency principle” (MEP), rather than the “maximum power principle” (MPP) of [5,8,20]. Smith [7] suggested that rates and efficiencies of production vary inversely in plants representing different stages of ecological succession, but this hypothesis still requires rigorous testing (also see Section 7.6.4). Harris and colleagues [13] described how the power of net photosynthesis (minus respiratory energy losses) was maximal at intermediate efficiencies ([net primary production]/[gross primary production]) along an elevational gradient in the Luquillo forest of Puerto Rico. Odum [27] also noted that a comparison of experimental phytoplankton communities exposed to different light intensities revealed a humped relationship between the rate and efficiency of primary production, as predicted by the MPP. Lastly, trophic transfer efficiencies (TTEs) from phytoplankton production to zooplankton production tend to be inversely related to the productivity and nutrient loading of freshwater lakes ([28,29]; but see [30]). Similarly, limited data on four freshwater spring ecosystems suggest that TTE from producers to primary consumers (herbivores) tends to decrease, at least approximately, with increasing primary productivity and water temperature (Figure 2). Since increasing temperature increases metabolic rates, this pattern seems to show negative relationships between power (rate of energy use) and efficiency, though temperature effects on TTE may be complicated by different upper temperature tolerances of autotrophs and heterotrophs and increasing dominance of microbial autotrophs that do not provide a sufficient diet for large animals at higher temperatures [31] (also see Section 3.2).
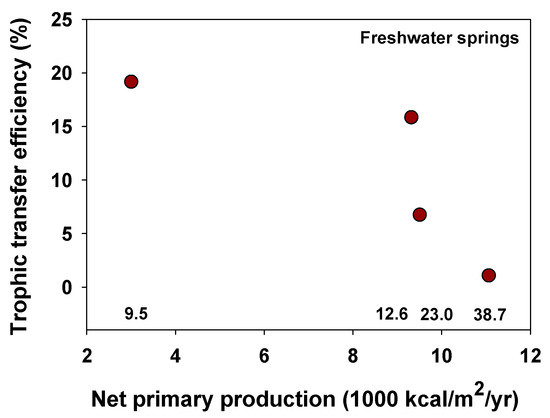
Figure 2.
Trophic transfer efficiencies, defined as (net primary consumer production)/(net producer production), in relation to net primary productivity and water temperature for four freshwater springs (data from [32,33,34,35]). Each red dot represents an individual spring system. Water temperatures (°C) are given above the X-axis line.
By contrast, many energetic studies at the levels of cells, organisms, populations, and communities have reported positive correlations between power and efficiency. At the cellular level, mitochondrial coupling efficiencies (ATP/O) increase with increasing metabolic rates [36,37,38]. In addition, many kinds of microbes, including bacteria, yeasts, and protists, exhibit positive associations between rates and efficiencies of cellular growth [4,39,40,41].
Animal scientists have frequently demonstrated that the rates and efficiencies of production (somatic growth and egg/milk production) and muscular work covary positively in humans and various domestic animals [4,42]. Positive correlations between the speed and efficiency of growth or reproduction have also been described in many other animal species, including hydra [43], nematodes [44], rotifers [45], cladocerans [24], oysters [46], snails [47], echinoderms [48], insects [49,50], fishes [51,52,53,54], birds [55], and laboratory mice [56] (also see Section 7.2). Similar results have been found in a comparison of offspring growth rates and efficiencies during lactation of five species of white-footed mice (Peromyscus and Podomys) and more broadly among 11 rodent species [57]. In addition, increasing light intensity or nutrient levels enhances both the rate and efficiency of tree growth [58] (also see Section 3.3, Section 7.2 and Section 7.6 for other examples of positive covariation of productive power and efficiency in individual organisms).
Additional examples of positive (or non-negative) correlations between power and efficiency occur at the population and community/ecosystem levels. Citing [59], Smith [7] claimed that animals feeding on concentrated food resources both grow faster and have higher production efficiencies relative to species feeding on dispersed food resources. In fact, using log10-transformed data from [59], I calculated a significantly positive relationship between the rate and efficiency of secondary production among 20 animal populations (Figure 3; but see [60]). In aquatic ecosystems, bacterial growth (production) efficiency covaries positively with bacterial growth rate and primary production, increasing from nutrient-poor to nutrient-rich conditions [39]. Photosynthetic efficiency (PE) also correlates positively or non-significantly with the annual net primary production of various terrestrial plant communities, depending on whether PE is based on the total incoming solar radiation striking the landscape or only the solar radiation intercepted by the vegetation, respectively (Figure 4). In either case, no trade-off between power and efficiency is seen. Similarly, net primary production (minus energy costs of respiration) varies in a constant proportion with gross primary production across various forest ecosystems [61,62,63,64], thus revealing no relationship between the rate and efficiency of forest production.
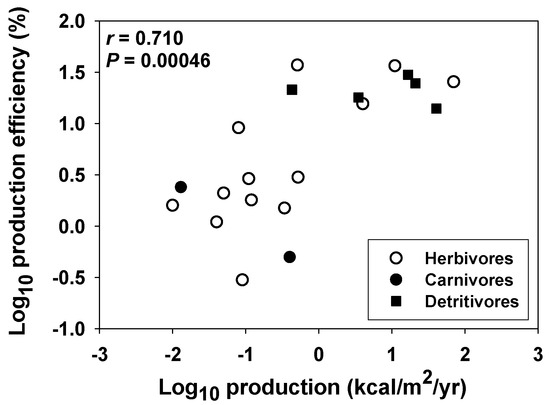
Figure 3.
Positive relationship between the log10-transformed rate and efficiency of secondary production (production/assimilation) among 20 animal populations (data from [59]). Pearson Correlation Coefficient (r) and significance level (p) are shown. The relationship is also significant for the 13 herbivore populations taken alone (r = 0.723; p = 0.0052).
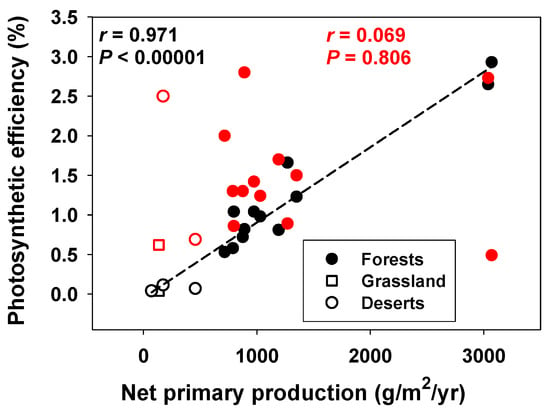
Figure 4.
Positive correlation between photosynthetic efficiency [PE = %NPP/PAR] and net primary production (NPP: g/m2/yr) across 16 terrestrial plant communities (PAR = photosynthetically active solar radiation, which varied over 2-fold among sites from 1.5 to 3.6 × 106 kJ/m2/yr). Pearson Correlation Coefficients (r) and significance levels (p) are shown. The relationship between PE and NPP is also significant for the 12 forest communities taken alone (r = 0.961; p < 0.00001 for dashed line). Also shown is PE/FSC in relation to NPP (red symbols), where FSC = the foliage standing crop (g/m2). Data from [61]. Note that PE represents the photosynthetic efficiency based on the total incoming solar radiation to the landscape, whereas PE/PSC is based approximately (and more realistically) on the solar radiation intercepted by vegetation [61].
Furthermore, a broad comparison of aquatic and terrestrial ecosystems reveals that power and efficiency are positively correlated for energy flow across trophic levels [65]. Ecosystems with rapid mass-specific energy flow from producers to animal consumers (e.g., aquatic plankton communities) exhibit higher trophic transfer efficiencies than do those with low mass-specific energy flow (e.g., terrestrial forest communities). Trophic transfer efficiencies from producers to animal consumers also positively correlate with primary productivity along a latitudinal gradient in the Atlantic Ocean [66] and within each of two groups of terrestrial ecosystems: relatively mesic forest biomes and relatively arid non-forest biomes (Figure 5; note that these positive patterns are obscured when heterogenous aquatic and terrestrial ecosystems having a variety of plant/phytoplankton forms with different levels of palatability are analyzed together; see, e.g., Cebrian [67], who showed a triangular relationship between net primary production (NPP) and the proportion of NPP consumed by herbivores).
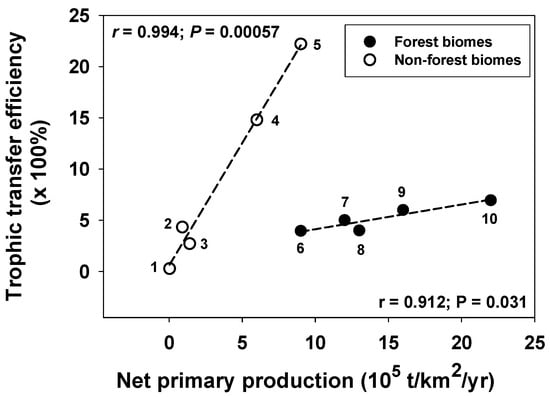
Figure 5.
Positive relationships (shown by dashed lines) between trophic transfer efficiencies from producers to animal consumers (×1000%) and net primary production (metric tons/km2/year) within each of two groups of terrestrial biomes: five relatively mesic forest biomes and five relatively arid non-forest biomes (data from [68]; also see [65]). Pearson Correlation Coefficients (r) and significance levels (p) are shown. 1: Extreme desert, rock, sand, and ice; 2: desert and semi-desert scrub; 3: tundra and alpine; 4: temperate grassland; 5: savanna; 6: boreal forest; 7: temperate deciduous forest; 8: temperate evergreen forest; 9: tropical seasonal forest; 10: tropical rain forest.
3.2. Theoretical Explanations
Clearly, relationships between power and efficiency need not be negative, as predicted by the MPP [5] or MEP (Figure 1a). Why is this so? Watt [19] argued that non-equilibrium living systems cannot be understood simply in terms of equilibrium physical systems (e.g., Atwood’s machine and thermodynamic systems following Carnot’s efficiency theorem). In far-from-equilibrium, open living systems, as the power of an energy transformation process increases, its efficiency may not decrease and may even increase (also see [69,70]). Indeed, natural selection may increase both (see examples in [19]). According to Watt [19], the speed and efficiency of biosynthesis are expected to correlate positively, because they are both promoted by similar changes in biochemical kinetics. In addition, Ho [70] has argued that coherent activities (coupled cyclic flows) in organisms may foster both speed and efficiency of energy mobilization. The same may occur in ecosystems [71].
Also consider that positive associations observed for growth and reproduction in many kinds of animals are often based on whole-body “gross efficiencies” that include costs of maintenance [4]. As production rates increase, proportionately more assimilated food energy is allocated to production versus maintenance, thus increasing production efficiency (also see [24,57]). This pattern resembles the ascending side of the humped relationship of fuel use efficiency versus travel speed observed in automobiles (see Section 2 and Figure 1a). In living systems, somatic maintenance costs are analogous to the standby fuel costs of idling engines. Moreover, when maintenance costs are subtracted, the “net efficiency” of muscular work (minus maintenance costs) shows a humped relationship with climbing speed (data of [72] presented in Figure 24.3 of [4]), bicycling speed [73], and other muscular movements in humans [25,74,75], as predicted by the MEP. Similarly, net growth efficiency shows a humped relationship with rates of growth and food intake in the minnow Phoxinus phoxinus [76]. By contrast, both net and gross efficiencies of offspring growth are positively related to offspring growth rates among rodent species [57]. In this case, the net growth efficiency was calculated by subtracting the maintenance costs of the lactating mother who supplies milk energy to the offspring, but not that of the offspring themselves.
Furthermore, positive correlations between power and efficiency may only be seen in some living systems because the maximization of productive power has been prevented by various intrinsic and extrinsic limiting factors (also see Section 5.2). If so, only the left-hand positive rise of the hump-shaped curve predicted by the MEP may be observed (Figure 1b). Many examples of the efficiency of the conversion of food energy into growth, reproduction, and locomotion showing a positive decelerating relationship with increasing resource input and power output (e.g., [4,39,47,48,50,77,78,79,80]), sometimes with moderate to substantial declines at the highest rations [76,81,82,83,84,85]), support this hypothesis (Figure 6). Therefore, the “principle of diminishing returns” (or “increments”) [4,86] may be consistent with the MEP if it is modified with a maximal power limit. Smith [7] describes further biological and ecological factors that may prevent trade-offs between power and efficiency being observed. In any case, positive or absent correlations between power and efficiency may be as common, or more so, than negative correlations, thus showing that trade-offs between power and efficiency should not be considered a general rule.
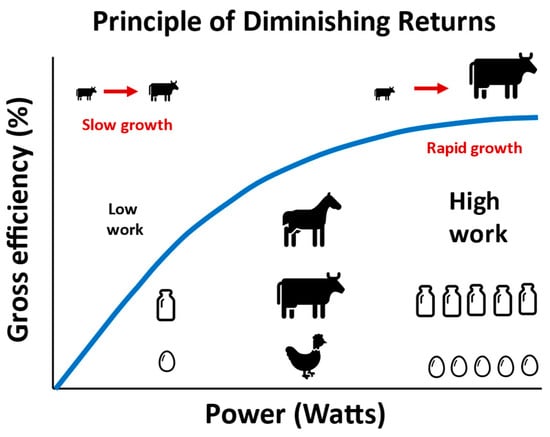
Figure 6.
Schematic representation of positive curvilinear relationships (blue line) between the power (rate) and gross efficiency of somatic growth, muscular work, and production of eggs and milk (includes energy costs of maintenance) in various domestic animals, illustrating the “principle of diminishing returns” (or “increments”) (based on data in [4]). Compare with Figure 1b.
3.3. Covariation of Power and Efficiency in Biological Processes Involving Resource (Energy) Uptake versus Use
To increase an understanding of the diverse patterns of covariation between power and efficiency in living systems, I suggest that biological processes involving resource (energy) uptake should be distinguished from those involving the use of assimilated resources for various biological activities (Figure 7). I contend that biological processes involving resource (energy) uptake should often show negative correlations between power and efficiency for resources of the same type and quality, but positive correlations for resources of different quality. In addition, biological processes involving the use of assimilated resources (energy) should often show positive correlations between power and efficiency. Therefore, covariation between power and efficiency should depend on the resource type and the nature of the biological process being examined.
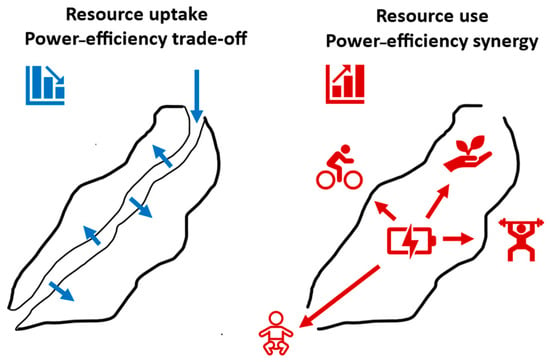
Figure 7.
Schematic representation of organismal resource uptake and use systems that often entail negative versus positive covariation between power and efficiency, respectively. Resource uptake (blue arrows) involves resource acquisition from the external environment and assimilation across gut surfaces into the blood/body. Resource use (red arrows) includes growth, reproduction, and muscular work.
Biological resource uptake across surfaces may become overloaded as resource supply increases. For example, as food intake increases, the assimilation rate (power) across gut surfaces should increase, but assimilation (digestive/absorption) efficiency should decrease, as observed in many kinds of animals (e.g., [4,24,50,82,85,87,88,89,90]). This trade-off between power and efficiency may result from increasing proportions of larger food masses having reduced contact with digestive enzymes and uptake surfaces, thus increasing the relative amount of unassimilated food material passing through the gut [91]. In addition, increases in the rate of movement of food material through the gut decrease the proportional amount that can be absorbed into the body [92,93,94]. The longer food is retained in the gut, the more efficiently it can be digested and absorbed, as observed in avian predators feeding on the same prey [95,96]. However, although rates and efficiency of digestion of the same type of food are usually negatively related, some exceptions exist (e.g., [89,97,98]).
By contrast, when comparing uptake of resources of different quality, positive associations between power and efficiency may be observed. Highly defended or indigestible food sources should entail both lower rates and efficiencies of assimilation of usable energy (nutrients) compared to more digestible food resources, thus yielding a positive correlation between rates and efficiency of energy assimilation across food types, as observed in shrews [99] and crabs [100]. Positive correlations between rates and efficiencies of energy flow from producers to consumers across plankton, grassland, and forest ecosystems [65] may also be explained in this way. Mass-specific rates and efficiencies of energy flow are both lower in forests with large, well-defended, relatively indigestible producers (trees) than in aquatic communities with small, relatively easily consumed, and digested phytoplankton (also see [101,102]).
In addition, the use of assimilated resources (energy) for growth and reproduction should show positive correlations between power and efficiency, as observed in many kinds of animals (see Section 3.1). This is because increases in energy use (power) for growth or reproduction increase the relative allocation of assimilated energy to production versus maintenance (respiration), thus increasing gross production efficiency [4,24,39,57]. Similar increases in gross efficiency occur as the power of muscular work increases [4,25]. The power–efficiency contrast between resource supply and resource use systems is nicely revealed in Daphnia spp. As food ration (and overall rate of energy flow) increases, assimilation efficiency decreases [24], whereas production efficiency (i.e., the proportion of assimilated energy used for growth and reproduction) increases [24,103]. A similar pattern is shown by a rotifer, though at the highest ration levels, production efficiency decreases somewhat [85]. Exceptions may occur when food limitation causes a greater proportional decrease in energy use for maintenance versus production [98]. A complex picture may also emerge if growth efficiency is based on ingested energy, thus preventing the separation of effects of food ration on efficiencies of energy assimilation and conversion to tissue growth [104,105].
However, why do trophic transfer efficiencies (TTEs) vary inversely with production (power) in freshwater ecosystems (Figure 2, and [28,29]) but show positive covariation in marine ecosystems and within each of two groups of comparable terrestrial ecosystems (Figure 4)? Unfortunately, a conclusive answer is not yet available, but I offer three suggestions to stimulate further research. First, consider that these patterns involve both resource uptake and use by animal consumers. Perhaps resource uptake trade-offs between power and efficiency (left image in Figure 7) have predominate effects on animal consumers in aquatic ecosystems, whereas resource use synergy between power and efficiency (right image in Figure 7) has predominate effects on animal consumers in terrestrial ecosystems. This difference may relate in part to the greater ability of herbivores to consume small vulnerable phytoplankton than larger, more protected shrubs and trees (hence the higher TTEs observed in plankton versus shrub/forest ecosystems) [65,101,102]. However, although this hypothesis may help explain the negative relationships between TTE and productivity in the freshwater ecosystems, it cannot explain the positive correlation observed in marine ecosystems. Second, consider that the nearly isothermal freshwater spring ecosystems analyzed in Figure 2 differ greatly in water temperature (range of mean temperatures ≈ 9.0 to 38.7 °C) throughout the year, and thus high maintenance costs related to thermally enhanced metabolic rates may have reduced the proportion of assimilated energy available for animal production, thus decreasing TTE from producers to consumers. This effect may have been less important in the relatively thermally similar subtropical and tropical marine ecosystems compared [67] as well as in the terrestrial ecosystems analyzed, whose often highly fluctuating temperatures were not as distinctly different during the growing season. Therefore, it is possible that the power–efficiency synergy observed in marine plankton ecosystems, forests, and other non-forest terrestrial ecosystems is due to positive correlations between primary production (power) and the proportion of energy assimilated by animal consumers devoted to production versus maintenance, following the effects of higher food energy levels frequently observed in individual animals (Figure 6). Third, the apparent power–efficiency trade-off observed in freshwater springs may be the result of an inverse correlation between temperature and the number of tolerant animal consumers that can survive (see, e.g., [106]). Indeed, a global survey of freshwater springs revealed that over a range of temperatures from 4.5 to 31 °C, macroinvertebrate species richness declines significantly [106]. With fewer consumer species at higher temperatures, the amount of animal production per producer production should decrease. In addition, eutrophic and dystrophic (humic) lakes with low TTEs may experience hypoxia and/or high acidity that reduces zooplankton abundance and productivity [30,107,108]. Thus, stressful abiotic conditions in freshwater lakes may cause low TTEs, rather than being the result of a trade-off with productivity. This hypothesis is supported by a non-negative (positive) correlation between the TTEs and productivity observed in marine plankton ecosystems where stressful hypoxia and acidity were not evident [66].
A distinction between energy-uptake versus energy-use systems may help explain some (but not all) of the variation in relationships between power and efficiency observed in living systems. Further theory, such as that discussed in Section 3.2, is needed to explain fully various patterns of power/efficiency covariation at different levels of biological organization. Although positive covariation between power and efficiency in resource use systems may be explained by the MEP with a maximal power limit (Figure 1b), the contrasting covariation of power and efficiency in resource uptake systems involving the same resource versus resources with different quality is not easily explained by the MEP. For example, negative associations between the rates and efficiency of energy assimilation (digestion) cannot be explained by assuming that they occur only on the right-hand side of the hump-shaped curve predicted by the MEP, because (1) these associations have been observed over a broad range of levels of food (energy) intake and power outputs from near zero to very high [4], and (2) they may be concave upward instead of concave downward (see Figure 5.5 in [4]), contrary to the MEP (Figure 1a).
4. Allometric Scaling of Power and Efficiency in Living Systems
In this section, I draw attention to how the concepts of ‘power’ and ‘efficiency’ have been used in allometric scaling analyses. Although this section represents a sidebar to my discussion so far, it is a useful prelude to Section 7.3.2 and Section 7.7 that consider how the (co)variation of power and efficiency relates to body size. Some investigators have used the term ‘power’ when describing scaling between rates (power) of metabolism, production, or locomotion and body mass (e.g., [21,109,110,111]). Although this use is not problematic, the use of the term ‘efficiency’ in allometric scaling analyses can be. For example, some scientists (especially physicists) describe the hypometric body mass scaling of metabolic rate as showing increased efficiency (economy) of energy use for maintenance in larger animals (e.g., [14,111,112,113,114,115,116]). Moreover, some have proposed that this size-related efficiency or ‘economy of scale’ has been an important factor driving the evolution of larger size (e.g., by allowing larger organisms to survive better through resource-poor periods [112,117,118]). However, this view is misleading (or at least incomplete) in two ways.
First, much theory and evidence indicate that relatively low mass-specific rates of metabolism and other metabolically dependent processes in larger animals relate to various geometric, physical, biological, and ecological constraints, rather than being merely due to natural selection for increased energetic efficiency. For example, to maintain constant body temperatures, endotherms must balance metabolic heat production with heat loss across their body surfaces. Because of their low surface area (SA) to volume (V) ratios, large endotherms have greater problems dissipating heat, thus favoring lower metabolic rates, compared to smaller species [42,119,120]. Indeed, if a steer had the mass-specific metabolic rate of a mouse, its metabolic heat dissipation would cause its surface temperature to exceed the boiling point [42]. In addition, larger organisms may suffer more stringent resource supply limits because of their smaller SA/V ratios (reviewed in [121,122]) and because they must transport resources over greater distances to reach all their metabolizing cells [123], both of which could lower metabolic rate (but see [121,122,124,125]). Ecologically, lower vulnerability to predation, but increased parasitism and intraspecific competition, may also select for slower paces of life (including rates of growth, development, and reproduction) requiring lower rates of metabolism in larger organisms [101,102].
If these and other constraints or selection pressures did not exist, natural selection should cause organisms of all sizes to have similar power outputs (see Section 5) that scale isometrically (loglinear scaling slope = 1). In fact, when constraints related to resource supply or waste removal (including heat dissipation) are temporarily removed during torpor, hibernation, or diapause, or temporarily bypassed during brief episodes of strenuous exercise, metabolic scaling becomes isometric or nearly so [126,127,128,129], i.e., size-related increases in ‘metabolic efficiency’ are reduced or absent.
Second, many kinds of biological efficiencies (e.g., assimilation, growth, and production efficiencies) tend to scale zerometrically or nearly so with animal body mass (loglinear slope ≈ 0) [57,60,130,131], thus showing that in many ways, larger species are not necessarily more efficient than smaller species. In addition, within the unicellular prokaryotes, unicellular eukaryotes, multicellular ectotherms, and multicellular endotherms, production efficiency varies independently of body mass, but it decreases across these evolutionary grades ([132,133]; but see [134]). The principal way in which energetic efficiency may increase with increasing body size is with respect to resource (energy) acquisition from the environment. As will be discussed further in Section 7.3.2, populations of large, protected organisms that experience relatively low mortality rates are more likely to be nearer to the carrying (resource) capacity of their environments (i.e., more regulated by food than predators or other environmental hazards) compared to those of smaller vulnerable organisms that experience high mortality rates. Therefore, the amount of population biomass or energy used relative to environmental resource supply (i.e., the ecological efficiency of converting available environmental resources into productive energy use) may be higher in larger versus smaller organisms.
5. Power and Evolutionary Fitness
This section aims to discuss two major issues: (1) how evolutionary fitness has been equated with energetic power production and (2) how various intrinsic and extrinsic factors may limit and cause variation in (re)productive power among species. In Section 6, I discuss how adaptation has been equated with energetic efficiency or functional effectiveness. In Section 7, I show how both viewpoints can be viewed as correct, if one distinguishes the concepts of fitness and adaptation, often regarded as synonymous, as representing power and efficiency, respectively. Evidence for this dichotomy is presented at the species level, both for a broad body size spectrum and within clades of related species.
5.1. Theory of Universal Evolution of Maximal Power
Since all biological processes depend on metabolic energy, and natural selection favors reproductive success (gene transmission to the next generation), one might argue that natural selection should maximize the acquisition and conversion of resources (energy) into reproduction, i.e., “reproductive power” [3,8,9,10,11,12,13,135,136]. The “struggle for life” described by Darwin [137] can be viewed as a “struggle for acquiring available energy” [138], and those organisms that do this best should outcompete and eventually replace relatively unsuccessful energy gatherers/users [3,9,139,140,141]. Following this viewpoint, some biologists have suggested that the energetic power supporting reproduction (or, more broadly, somatic and reproductive production above maintenance costs) can be considered a useful non-tautological index of evolutionary fitness [10,11,12,13,142]. As such, it is a basic assumption of the “equal fitness paradigm”, which posits that all species, small and large, have evolved to maximize their reproductive power relative to generation time, thus causing them all to have nearly equal energetic fitness, at least in a broad statistical sense [14,15,16] (but see Section 7.3.2).
It is undeniable that an energetic perspective improves our understanding of evolution. Indeed, the field of evolutionary ecology (and specifically life-history evolution) is filled with theories based on the evolutionary ‘optimization’ of resource (energy/nutrient) acquisition and allocation to various vital functions and structures, including reproduction (see, e.g., [89,136,143,144,145,146]). Indeed, nearly a century ago, Fisher ([147], p. 43) famously encouraged the investigation of the evolution of organismal energy budgets by asking what the conditions are that cause organisms to devote more or fewer of their available resources (energy) to reproduction. However, the key word here is ‘optimization’. Natural selection would favor equally high rates of uptake and use of energy for reproduction in all species if there were no constraints on energy acquisition/use or competing demands for energy by other vital organismal activities (e.g., growth and survival) and other species in an ecosystem. However, many kinds of intrinsic and extrinsic constraints and conflicting selection pressures (trade-offs) exist that vary greatly among species, thus preventing an idealistic “Darwinian demon” [148,149] from maximizing reproductive power in all species to the same degree, as evidenced by the great diversity of life histories and associated patterns of energy use (see Section 5.2, Section 5.3, Section 7.3 and Section 7.4). In addition, several studies have shown that within species, various measures of evolutionary fitness may vary negatively as well as positively with rates of energy use (e.g., metabolic rate: [150,151,152,153]). Indeed, some biologists have argued that natural selection should generally favor minimal maintenance costs (basal metabolic rates) whenever possible (e.g., [154]). Moreover, among species, two major indicators of fitness—reproductive rate (intrinsic rate of increase) and survival (longevity)—can vary independently of metabolic rate (e.g., [151,155,156,157]).
In addition, some forms of selection (e.g., sexual selection) do not target increased rates of use of energy resources per se, but rather increased access to other kinds of resources (e.g., mates). Indeed, sexual selection favors the development of exaggerated sexually dimorphic traits that cost relatively little energy to maintain [158,159,160], thus causing a decrease in mass-specific energy use and potentially contributing to hypometric size-scaling of metabolic rate during ontogeny [161]. Thus, selection for sexually dimorphic traits illustrates “cost minimization” [158,160], rather than power maximization.
5.2. Factors Preventing the Attainment of Maximal Power
Lotka [9] himself acknowledged that life maximizes its “energy flux” (power) “as compatible with the constraints to which the system is subject” (p. 148), as also discussed by [8,162]. However, Lotka never fully explained what these constraints are. This section describes some of these intrinsic (biological) and extrinsic (ecological) constraints (Table 1), which are critical not only for understanding the diversity of life histories seen in the natural world (Section 5.3 and Section 7.4), but also for causing physical, functional, or evolutionary limits on power output, thus potentially preventing the manifestation of trade-offs (negative correlations) between power and efficiency predicted to occur by the “maximum efficiency principle” (MEP; see Figure 1b and Section 3). An efficiency–power curve with submaximal power limits may thus be linked to Brody’s “principle of diminishing increments”, as supported by positive decelerating relationships observed between efficiency and power of production and muscular work in many kinds of animals (Figure 6 [4]).

Table 1.
A non-exhaustive list of intrinsic (biological) and extrinsic (ecological) factors that limit power production in living systems. Interactive effects can also occur but are not specified here. Only a sampling of sources is indicated.
5.2.1. Intrinsic Factors
Various intrinsic (biological) factors can limit rates of energy uptake and use for production and muscular work (Table 1; Figure 8). The rate of resource (energy) assimilation is limited by gut capacity (including surface area- and volume-related processes of digestion and absorption); and, in turn, rates of use of assimilated energy for growth, reproduction, and locomotion are limited by (1) finite biosynthetic or biomechanical capacities, biological regulation, and rate-enhanced risks of injury, illness, increased aging, or developmental/functional error; (2) competing demands for energy among growth, reproduction, locomotion, maintenance, repair, and other activities; and (3) loss of energy to pathogens and parasites and defenses induced in response to them. Lynch and colleagues [199] have also suggested that increased frequencies of deleterious mutations in small populations prone to random genetic drift may reduce maximal growth rates, especially in large organisms.
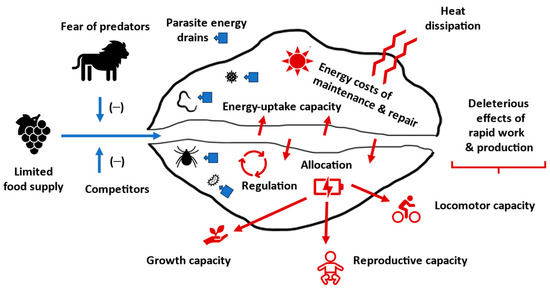
Figure 8.
Schematic representation of various intrinsic (red) and extrinsic (blue) factors that limit rates of production and muscular work (also see Table 1). Arrows refer to flow of energy uptake or use or effects of specific factors on energy flow.
5.2.2. Extrinsic Factors
In natural environments, limited food supply and access to food inhibited by competitors and the fear of predators reduce resource (energy) acquisition, and thus chemical energy ultimately available for power production (Table 1). Parasites and pathogens living in the body also divert resources (energy) away from productive work of the host (Figure 8). All species strive to garner as much energy as they can, which often results in evolutionary “conflicts of self-interest” that inhibit the attainment of maximum power by any individual species. As a result, evolution is a “zero-sum game” [11], causing no species on Earth to usurp all the sun’s energy for itself. As pointed out by Vermeij [139], since most resources are often other species, “acquisition and retention of resources by an individual organism requires that individual to prevent others from obtaining or monopolizing those resources” (p. 221).
The limiting effects of various abiotic and biotic factors in the environment on “reproductive power” has been called the “energy-flow principle” [224,225], which complements the “energy-allocation principle” emphasized in the life history evolution literature [89,182,183,187,190,191,209,226,227]. Both ecological limitations on energy acquisition/uptake and energy allocation to competing demands can whittle down the reproductive power of an organism.
5.3. The Diversification of Reproductive Power: Some Preliminary Thoughts
Lotka [9] himself stated that life can achieve maximal energy flux (power) only if there are abundant resources (also see [228]). However, he failed to articulate the many intrinsic and extrinsic constraints on biological power production, whose variation can help explain the great diversity of reproductive power among species, from tiny bacteria to huge whales (also see Section 7.3). J. H. Brown and colleagues [12] suggested that within a taxonomic group (e.g., Mammalia), specific intermediate body sizes are optimal because they are associated with maximal reproductive power. However, their model used to support this view has been criticized for various logical and empirical reasons [229,230,231,232,233,234], which I will not consider here. Nevertheless, when viewed as total species-wide energy use, energetic fitness or productive power does vary considerably among species, both in relation to body size and independently of it (see Section 7.3 and Section 7.4).
J. H. Brown and colleagues [14] have also claimed that (re)productive power varies interspecifically as a trade-off with generation time. However, I would suggest that this negative covariation arises because both parameters are related to mortality rate, the ultimate driver of life history variation [157,235], but in opposite ways. As body size increases, mortality rate declines (as is well known: see, e.g., [236,237,238,239]; and references cited in [102,235]), because larger organisms are more protected against predators and other environmental hazards than are more vulnerable, small organisms [101,102,157,235]. As a result, smaller organisms have both shorter generation times (they die sooner) and higher reproductive rates to compensate for higher mortality rates than do larger organisms (also see Section 7.7). Species (biotic) interactions may play a fundamental role in causing the opposite allometry of productive power and generation time (also see [101]). Coevolution among species (adaptation and counteradaptation) should be considered when explaining variation in (re)productive power ([240,241,242,243,244], as also discussed in Section 7.3).
6. Efficiency and Evolutionary Adaptation
Evolutionary fitness may be increased by either increasing power (rates of energy intake and use for production) or efficiency (amount of conversion of energy intake into energy use for production) [200,245]. This possibility raises two questions. First, is power or efficiency maximized, or can each be a chief target of natural selection depending on specific environmental conditions? Second, if the latter is true, what are the conditions that favor power versus efficiency? In this section, I discuss how the concept of ‘efficiency’ has been considered a useful quantitative indicator of the level of adaptation (i.e., ‘adaptiveness’) shown by a population or species. In Section 7, I consider how power (fitness) and efficiency (adaptiveness) may be maximized simultaneously or at the expense of the other under specific environmental conditions.
Many biologists have assumed that natural selection maximizes ‘efficiency’ (e.g., [9,120,141,246,247,248]), but this view has been debated. On the one hand, Bock [18] claimed that natural selection favors adaptive features (involving favorable fits with the environment called “synergs”) that cost the least amount of energy to maintain; hence, high adaptiveness involves high efficiency of energy use. He argued that an efficiency measure based on energy required per gram of body mass could be used to estimate the degree of adaptation for a specific biological feature (synerg) among related species, a view considered further in Section 7.3 and Section 7.4. On the other hand, Slobodkin [249] argued that adaptation involves the ‘effectiveness’ of a structure or function, which does not necessarily equate with the ‘efficiency’ of energy use for maintaining/driving a specific structure/function (also see Section 8.2). In short, functional effectiveness may not equate with energetic efficiency (as Bock [18] also acknowledged with respect to specific cases: e.g., the evolution of long tongues may increase the effectiveness of food capture but also increase the energy cost of muscular contraction, thus reducing efficiency).
As Calow [200] noted, ‘efficiency’ is a tricky concept. How it is defined depends on the purpose/objective/needs of the ‘job’ undertaken. It is critical to consider what the input is as well as what the ‘useful’ output is. When doing so, it becomes clear that ‘efficiency’ can be defined in multiple ways. For example, consider growth efficiency, which can be defined as (1) the amount of chemical energy deposited as new tissue mass divided by the amount of food energy ingested, which involves two kinds of efficiency: the efficiency of converting ingested food energy into assimilated energy and the efficiency of converting assimilated energy into new, calorically estimated somatic tissue, (2) the amount of assimilated energy (ingested energy minus that lost in feces) converted into new somatic tissue, (3) the amount of metabolized energy (assimilated energy minus energy lost in urine) converted into new somatic tissue, (4) the amount of metabolized energy converted into new somatic tissue minus that used for maintenance of existing tissues (sometimes called “net growth efficiency”), and (5) the amount of metabolized energy converted into new somatic tissue plus that used to support the cost of biosynthesis [4,57,94,134,224,250,251]. Wieser [134] even wondered whether some efficiency measures are merely “patterns of energy allocation” because evolution does not just optimize production. In any case, how one defines efficiency becomes critical when asking basic questions such as whether endotherms with high energy costs of maintenance have lower production efficiencies than ectotherms (also see Section 7.6.5).
To complicate matters further, increases in one type of efficiency may be associated with decreases in another. For example, Welch [252] reported a negative interspecific correlation between assimilation efficiency (AE) and net growth efficiency (NGE) among various aquatic ectothermic animal species whose energy budgets had been estimated in the laboratory. This trade-off (which is not as apparent when a heterogeneous group of aquatic and terrestrial ectotherms and endotherms are compared [253]) appears to be due to AE and NGE relating oppositely to diet [200,253]. Herbivores/detritivores tend to have low AE but high NGE, whereas faunivores tend to have a high AE but low NGE. Herbivores/detritivores consume relatively indigestible food that causes AE to be low, whereas faunivores consume relatively digestible food that causes AE to be high. By contrast, faunivores must expend more effort searching and capturing their dispersed animal food, thus lowering their NGE because more energy is diverted away from growth to support increased foraging activity, compared to herbivores/detritivores that feed on more accessible, locally concentrated vegetative or detrital food [200,253]. This pattern illustrates the importance of distinguishing resource supply versus use systems (Figure 7). The energetic efficiency of resource supply and use systems may respond very differently to changes in food quantity, quality, and accessibility. Increased food quantity can cause AE to decrease and NGE to increase (also see Section 3.3). Decreased food quality can cause AE to decrease, whereas increased food accessibility can cause NGE to increase. In short, adaptation to various trophic environments does not necessarily involve concordant changes in various kinds of energetic efficiency.
7. Covariation between Power (Fitness) and Efficiency (Adaptation) Revisited
This section has six major goals. First, I recommend that ‘fitness’ and ‘adaptation’ be considered overlapping but distinguishable concepts, which becomes clearer if they are defined in energetic terms, i.e., as representing ‘power’ versus ‘efficiency’ (Section 7.1). Second, I describe examples where natural selection and biochemical/physiological exigencies/constraints have apparently favored positive covariation between fitness-enhancing power and adaptive efficiency in resource use systems (Section 7.2). Third, I describe examples where natural selection and ecophysiological trade-offs have apparently favored negative covariation between fitness-enhancing power and adaptive efficiency in resource supply systems, especially at the whole species level (Section 7.3). Fourth, I further illustrate this third point with a case study of pertinent energetic, ecological, and biogeographic patterns among related species of an exceptionally well-studied genus of mice (Peromyscus) in North America (Section 7.4). Fifth, I describe how energetic power and efficiency vary in space and time for various living systems (Section 7.5 and Section 7.6). Sixth, I attempt a tentative, preliminary synthesis of how and why power and efficiency (co)vary in living systems at various hierarchical levels of biological organization (Section 7.7).
7.1. Fitness as Power and Adaptation as Efficiency
Evolutionary fitness and adaptation are often equated. These terms have been used interchangeably, though there has been much disagreement about their exact meanings, how they should be measured, and even whether they are useful nontautological concepts (see, e.g., [254,255,256,257]). According to Darwin [137], natural selection favors organisms with the highest possible reproductive fitness (i.e., success in producing progeny and thus transmitting genes to the next generation), which is facilitated by adaptations that foster survival, growth, and reproduction in specific environments. Thus, selection favors both increased fitness and adaptation. However, three distinctions between fitness and adaptation can be made, which I believe gives these concepts valuable operational and quantitative value. First, not all fitness-promoting features of an organism enhance adaptive survival, including sexually selected traits that not only do not improve an organism’s adaptive fit to an environment, but also may increase risks of dying from predation or other environmental hazards. Thus, although adaptation can improve fitness, increased fitness need not improve adaptation. Second, selection for increasing fitness is manifested at a regional/global scale that transcends local environments. Any traits that increase the reproductive success, abundance, and geographical spread of a species relative to that of other species enhance ‘fitness’. By contrast, any traits that increase the ability of a species to survive and reproduce in a specific environment enhance ‘adaptation’. Third, at the whole species level, fitness-enhancing traits increase energetic ‘power’ (i.e., the total rate of energy capture and use by a species), whereas adaptive traits increase energetic ‘efficiency’ (i.e., the proportion of available resources in a specific local environment that is captured and converted into production). Thus, asymmetric causation, regional/global versus local scales of application, and power versus efficiency all distinguish fitness from adaptation. These ideas, which focus on applying the concepts of fitness (power) and adaptation (efficiency) to the whole species level, will be further developed in the following sections. How these concepts are used can vary with the level of biological organization (individual, population, and species) and with the time scale [247,254,258]. My approach is not the only one possible (nor should it be), but I believe that it presents some advantages that could facilitate profitable research based on measurable nontautological concepts of fitness and adaptation that can be compared among species.
7.2. Natural Selection May Favor Both Power and Efficiency of Resource Use Systems
Natural selection for increased rates of energy use (power) for production and muscular work should be accompanied by increases in energetic efficiency, as indicated by frequent positive covariations between power and efficiency in resource use systems (see Figure 6; and Section 3). Watt [19] argued that selection favors both power and efficiency in biochemical systems (but see [22,23]). Evolution of faster growth rates in bacteria favors higher energetic efficiency [39,40,80]. Rodent species having higher rates of energetic postnatal growth of their offspring also have higher energetic growth efficiencies [57]. Rates and efficiencies of growth and protein synthesis are positively correlated in fishes [134]. Both production rate and efficiency ([mass-specific biomass production]/[metabolic rate]) covary positively when comparing unicellular prokaryotes, unicellular eukaryotes, and multicellular eukaryotes [132]. In addition, a positive association between power and efficiency may even be seen in corals, where both gross production and (gross production)/(respiration energy expenditure) decrease per polyp with increasing colony size [259]. As suggested in Section 3.2 (Figure 1b), these positive correlations between power and efficiency in resource use systems (Figure 7) may arise because natural selection has eliminated those systems that exceeded a specific power threshold that causes harmful injuries, illness, developmental errors, enhanced aging, and/or functional inefficiency and thus reckless energy wastage (also see Section 3.2 and Section 8.2.1).
7.3. Natural Selection May Favor Power–Efficiency Trade-Offs in Resource Supply Systems
Unlike resource use systems, resource supply systems may often show trade-offs (negative correlations) between power and efficiency (Figure 7). In Section 3.3, I discuss why rates and efficiencies of energy assimilation are often negatively correlated. In the following sections, I review why this may also occur for energy acquisition systems (see Table 2). First, I consider possible factors that may be involved in causing power–efficiency trade-offs in resource acquisition (Section 7.3.1). Second, I consider how power–efficiency trade-offs in resource acquisition may occur along a body size continuum and independently of it (Section 7.3.2).
7.3.1. Possible Factors Causing Power–Efficiency Trade-Offs in Resource Acquisition
Lotka [3,9] claimed that natural selection should favor increased power when resources are abundant and in excess but favor increased efficiency (economy) when resources are scarce and limited (also see [8,22,162,228,260,261]). This view relates to the concept of wasteful versus frugal strategies [262,263]. When resources are abundant, maximization of productive power is a target of natural selection, even if resources are used recklessly and inefficiently, whereas when resources are scarce, maximization of production efficiency is a better strategy because it minimizes the loss of energy that is critically needed to achieve positive energy balance, thus enabling growth and reproduction, albeit at unavoidably low rates. A similar dichotomy of maximizing power versus efficiency of resource use may occur in response to high- versus low-quality resources [264].
In addition, a trade-off between power and efficiency may occur along a continuum from ecological generalists that use a wide variety of resources and habitats to ecological specialists that use a narrow range of resources and habitats. Dietary and habitat generalists have often been considered “jacks of all trades, but masters of none” (e.g., [265,266,267,268,269,270,271]), though exceptions may exist [272,273]. Their ability to acquire numerous kinds of resources may help them to achieve high productive power, but at the cost of not being efficient (well adapted) at using any one resource. By contrast, specialists have evolved to use a specific resource or set of resources with high efficiency, but at the cost of reduced species-level power production. Consistent with this hypothesis, a specialist bee species was found to be a more efficient forager for pollen from its preferred host plant than were four generalist species [274]. Specialized food habits and habitat use are also associated with increased foraging efficiency in other animals, including crabs [275], spiders [276,277,278], insects [279,280,281], and vertebrates [282,283,284] (also see Section 8.3), but exceptions exist, especially when food resources are scarce [285,286]. In addition, herbivorous caterpillars that are trophic generalists exhibit a broad habitat distribution (indicating high species-level productive power and ‘fitness’) but low local population densities (indicating low species-level production efficiency and ‘adaptiveness’), whereas trophic specialists show the opposite pattern [272]. Similar patterns have been reported for aquatic invertebrates [270,287] (however, for further perspective, also see Section 7.3.2 and [288,289,290,291]).


Table 2.
A list of some factors that may cause rates (power) and efficiencies of resource (energy) acquisition to be negatively correlated through the action of natural selection.
Table 2.
A list of some factors that may cause rates (power) and efficiencies of resource (energy) acquisition to be negatively correlated through the action of natural selection.
| Factor | Effect | Sources |
|---|---|---|
| Food quantity | High food: high power; low efficiency Low food: low power; high efficiency | [3,8,9,22,162,228,260,261] |
| Food quality | High quality: high power; low efficiency Low quality: low power; high efficiency | [264] |
| Niche breadth | Generalist: high power; low efficiency Specialist: low power; high efficiency | [265,266,267,268,269,270,271] |
| Population stability | Stable (K-selected): low power; high efficiency Unstable (r-selected): high power; low efficiency | [211,212,213,266] |
Lastly, according to r- and K-selection theory, species living in disturbed or unstable habitats should have highly variable population densities typically below the carrying capacity (K) of their environments that in turn favor high productive power and associated high rates of population increase (r), whereas species living in stable habitats should have relatively stable population densities typically near their environmental carrying capacity (K) that favor high competitive ability and efficient capture and utilization of resources at the expense of low productive power ([211,212,213,266]); but see [292,293,294]. Although r- and K-selection theory has been frequently criticized (see, e.g., [182,183,295]), variation in population dynamics and habitat stability (a core pattern underlying the theory) may help explain not only trade-offs between power and efficiency among related species, but also among species with different body sizes (see Section 7.3.2).
All these factors may have interactive effects that reinforce a dichotomy between high power versus high efficiency. For example, some ecological specialists have become adapted to living on low-quality resources that constrain their productive power (e.g., rodents that specialize in eating low-quality conifer needles at the expense of producing small, slowly developing litters, as compared to related species that eat a wider variety of more nutritious vegetative food [296,297]). In addition, ‘weedy’ species that exploit disturbed and unstable habitats may experience high population fluctuations and thus r-selection that, together with generalized food habits, favor high reproductive outputs. Ecological generalism, high colonization ability, and an ability to live in disturbed habitats are often positively associated (e.g., [243,270,287,298,299,300,301,302,303,304,305,306,307]; but see [308]). By contrast, K-selection in relatively stable habitats may favor ecological specialization [267] and increased efficiency of acquiring resources [212,213,266]. Specialized trophic adaptations in animals tend to be associated with stably abundant, long-lasting, and predictably accessible food resources [309,310,311,312,313].
7.3.2. Possible Trade-Offs between Power and Efficiency along a Body Size Spectrum and within Specific Clades
Predation and other environmental hazards tend to cause greater mortality rates in small versus large organisms [101,102,157,235]. As a result, it can be inferred that the population densities of small organisms should more often be below the resource capacity of their environments (i.e., their carrying capacity K), thus enhancing resource availability per individual, as compared to larger, more protected organisms whose populations should more often be near their K, thus causing intense intraspecific competition for limited resources [101,102,157]. This pattern, which has been canonized as a “Serengeti Rule” [314] because of its clear demonstration in mammals of the Serengeti ecosystem [315,316], is likely common across many kinds of taxa and ecosystems [101], but still needs further testing. Accordingly, one may infer that small organisms with abundant resources should be selected to maximize their power production (energetic fitness), whereas large organisms with limited resources should be selected to maximize their efficiency of resource acquisition (energetic adaptiveness) (Figure 9). This hypothetical size spectrum of power (fitness) to efficiency (adaptation) resembles the proposal that small organisms are r-selected for ‘productivity’, whereas large organisms are K-selected for ‘efficiency’ [212,213], though my scheme does not depend inextricably on the detailed mechanisms of r- and K-selection theory. It also extends the frequent claim that maximization of power versus efficiency depends on resource availability [3,8,9,22,162,228,260,261] by framing it with a body size perspective. In short, a trade-off between power and efficiency of resource acquisition may scale with body size. This view is consistent with the observation that tiny unicellular prokaryotes exhibit the most rapid rates of reproduction and biomolecular turnover in the living world [140].
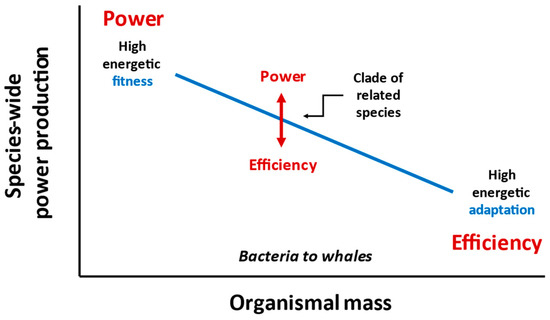
Figure 9.
Hypothetical scheme depicting power (fitness) and efficiency (adaptation) of resource (energy) uptake at the global species level in relation to organismal mass and among related species with similar organismal masses.
Based on the “equal fitness paradigm” (EFP) [14,15,16], one might argue that productive power (energetic fitness) is nearly the same across small and large organisms, thus contradicting the “power/efficiency size spectrum” hypothesized in Figure 9. However, note that the EFP focuses on individual energy use for offspring biomass production (OBP) during a generation of time (G), whereas my scheme focuses on the total productive power (rate of energy uptake/use for growth and reproduction) of whole species (see Section 7.1). I hypothesize that the total mass-specific productive power of a species (i.e., the rate of energy uptake or use for production per individual mass x number of individuals of a species) tends to decrease with increasing body size, whereas the efficiency of acquiring available resource energy (i.e., the proportion of available species or niche specific trophic energy that is captured and assimilated) increases. Two critical departures from the EFP are evident. First, proponents of the EFP define energetic fitness as mass specific OBP × G. Thus, their fitness measure is not a ‘rate’ (power), but the mass-specific amount of energy used during a generation (a variable, relative time measure that scales with body size). My scheme explicitly focuses on the rate (power) of energy uptake for production, which scales negatively with body size (as is consistent with the negative scaling of the rate of population growth [130,133,317,318,319]). Second, my scheme focuses on the species level, rather than the individual organism level, though power production at the two levels may be related (see Section 7.4).
The EFP, as conceived by [14,15,16], and the data upon which it is based, have four other problems. First, its measure of energetic fitness does not explicitly consider variation in the number of breeding events per lifetime. Note that as G (or age at first reproduction as a proxy) increases, the post-maturational lifespan, which may include multiple breeding events, tends to increase disproportionately (log-log slope ≠ 1) in a variety of plant and animal taxa [157,319], a pattern that may cause the EFP to underestimate the energetic fitness of long-lived iteroparous species because it is based on G and not total lifespan. Second, many of the species and major taxa used to calculate the body mass scaling of G were not the same as those used to calculate the body mass scaling of OBP and thus are not strictly comparable. Third, many of the G values that were calculated are not realistic (e.g., values greater than 10 years for many small birds and mammals that do not live nearly that long in nature, on average). Fourth, in the same species of birds and mammals (thus controlling for species composition in two of the major taxa used in the analysis of [14] for which there was sufficient sample size), the mass-specific OBP does not scale inversely with G in a proportionate way (i.e., log-log slope = −1) (Figure 10), as would be expected based on their presumed nearly equal but opposite scaling with body mass [14]. Even though the EFP posits that OBP × G is ‘invariant’ (scaling zerometrically with body mass: log-log slope ≈ 0), it should not be assumed that OBP and G have a proportional 1:1 relationship because both traits vary considerably (by approximately two orders of magnitude), even at the same body size (see Figures 2 and 3 in [14]). Ratios or multiples of other life history traits that appear to be invariants (see, e.g., [319]) may prove not to be so when one trait is related directly to the other (see the many examples described in [157]). As such, the disproportionate relationships between OBP and G observed in birds and mammals indicate that energetic fitness, as defined by [14,15,16], varies with G, and thus is not invariant, as posited by the EFP. In addition, at a given G, OBP may vary by as much as two orders of magnitude (see scatter of points in Figure 10). Furthermore, the body mass scaling of OBP and G do not show quarter-power relationships in birds and mammals, nor are they equally opposite scaling relationships (see Figure 10 legend), as assumed by the EFP [14,15,16].
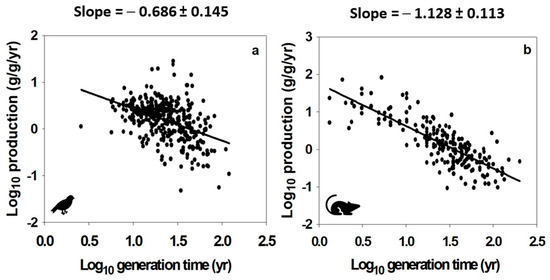
Figure 10.
Mass-specific offspring biomass production (OBE) versus generation time (G) in log-log space for 361 species of birds (a) and 209 species of mammals (b) (data from [14]). The slopes (±95% confidence intervals; p < 0.001) for both relationships are significantly different from −1, assuming that OBE x G is ‘invariant’, as posited by the “equal fitness paradigm” (EFP). In addition, OBE and G do not show quarter-power scaling with dry body mass in log-log space, nor are they equally opposite scaling relationships, further contradicting the EFP (birds: OBE slope = −0.322 ± 0.038; G slope = 0.192 ± 0.026; mammals: OBE slope = −0.320 ± 0.030; G slope = 0.228 ± 0.022; all p < 0.001).
In any case, my measure of energetic fitness (species-wide productive power) is based on the rate of energy uptake for production for all individuals of a species across its entire geographical range. Since microscopic organisms are usually more abundant, and often more widespread [320,321,322,323,324,325,326], than macroscopic organisms (notwithstanding some apparent exceptions [325,327,328], and because of technical difficulties in obtaining reliable data on the abundance and distribution of tiny organisms that are hard to detect and identify [327,328,329,330,331,332]), they should in general also have greater species-level power (fitness), even if individual energetic fitness is similar across body sizes, a plausible hypothesis requiring testing.
In addition, mortality may not only be higher in small, vulnerable versus large, protected organisms, but it may also be proportionately less selective (more random with respect to genotype), thus favoring generalized fitness-/power-enhancing responses of increased rates of growth, development, and reproduction [102,235,254,333,334]. By contrast, although large organisms suffer lower rates of mortality, a larger proportion of their mortality may be selective (nonrandom), thus favoring specific adaptive efficiency-enhancing responses [102,235,333]. The generally greater population stability of large versus small organisms may also promote increased levels of adaptation and efficiency of resource capture [212,213,254] (also see Section 7.7).
In passing, it is worth mentioning that humans are a major exception to the power-versus-efficiency size spectrum depicted in Figure 9. Humans have used special cultural innovations (including the harnessing of fossil fuels) to give them extremely high productive power despite being a relatively large-bodied species [6,261,335,336].
The power–efficiency trade-off may also occur for related species of similar body size in specific clades (Figure 9). Based on their overall greater abundance and total biomass, widespread species have higher species-wide production and thus power (fitness) than geographically restricted related species. In many clades (e.g., white-footed mice in the genus Peromyscus: see Section 7.4), widespread species have achieved their high overall power of energy uptake and use by being generalized ‘opportunistic species’ that exploit new, disturbed, early successional, and seasonally variable environments with abundant resources (at least temporally) and that require relatively little energy-sapping counteradaptation with other relatively few enemy species (e.g., [243,270,298,304,305,307,337]). ‘Hyperabundant’ microbes [305] and animals [307,337] illustrate this pattern well. By contrast, geographically restricted species are often specialized ‘equilibrium species’ that exploit relatively stable habitats and resources in environments requiring considerable counteradaptation against numerous enemy species that reduces their productive power. Many studies have shown positive correlations between niche breadth and geographical range size in various groups of organisms (e.g., [243,270,289,304,338,339,340,341,342,343,344,345,346,347,348]; but see [349,350,351,352]). Both ecological specialization and habitat/population stability should thus favor increased efficiency of resource acquisition in restricted species (also see Section 7.3.1 and Section 7.4). Increased efficiency (adaptiveness) exploiting locally available niche-specific resources for production, in turn, supports greater competitive ability, as experimentally demonstrated in protists (my interpretation of results in [353]) and inferred from natural history observations in white-footed mice (Peromyscus species) (see Section 7.4).
A ‘deep’ (geological) time perspective may also improve an understanding of interspecific trade-offs between power (fitness) and efficiency (adaptation) in four ways. First, widespread ‘powerful’ species tend to have greater geological longevity and lower extinction risk than restricted species (e.g., [354,355,356,357,358,359]), thus further enhancing their species-wide fitness. Second, selective extinction of restricted species that have perilously low population sizes because of inefficient resource acquisition may have been an important higher-order evolutionary process that promoted high trophic efficiency in restricted species. Restricted species may also preferentially occur in stable habitats with stable resources that are conducive to the evolution of adaptive, efficient resource acquisition because they are less likely to go extinct than those found in unstable habitats [360]. Third, isolated populations of generalized widespread species may often evolve into specialized restricted species (e.g., [241,242,243,244,360,361,362,363], because their well-adapted, ‘efficient’ resource acquisition has increased their competitive superiority in stable habitats with predictable resources [364]. Fourth, the evolution of large body size (Cope’s Rule) may be linked to ecological specialization [365], and thereby adaptive efficiency of resource acquisition, as attested by several supporting studies (see Section 7.3.1). If true, this pattern helps to link power–efficiency trade-offs seen among species both in relation to and independently of body size.
7.4. Trade-Offs between Power and Efficiency: A Case Study Based on White-Footed Mice (Peromyscus)
The rodent genus Peromyscus and closely related satellite genera (e.g., Habromys, Isthmomys, Megadontomys, Neotomodon, Osgoodomys, and Podomys, all of which were once considered subgenera of Peromyscus [366,367,368]) constitute an excellent group to test the proposed power versus efficiency scheme described in Section 7.3.2. The geographical range sizes and species-wide power (fitness) of these Peromyscine species vary enormously, from continent-wide (e.g., Peromyscus maniculatus, the most abundant and widespread small mammal in North America [369]; note, however, that this species is regarded as an evolutionarily dynamic species complex, with many recently evolved allopatric subspecies that are approaching species status [370]) to highly localized, some of which are confined to single mountaintops or islands [243,366,371]. Their ecology and biogeography also lend themselves well to testing the niche breadth and habitat stability explanations for power–efficiency trade-offs (Table 2). Widespread Peromyscus species are habitat generalists that occupy broad altitudinal ranges and often new, disturbed, highly seasonal, species-poor habitats, whereas restricted species are usually habitat specialists that occupy relatively narrow altitudinal ranges and usually relatively stable, species-rich habitats [224,243,371]. The widespread species also show r-selected traits such as large litters, small body sizes, rapid development, and short lifespans, whereas restricted species tend to show K-selected traits such as small litters, often larger body sizes, slower development, and longer lifespans [243,372,373,374]. Furthermore, not only do the widespread species exhibit high species-wide productive power just by virtue of their high abundance, but energetic studies also indicate that they tend to have relatively high reproductive power at the individual level as well. Peromyscus maniculatus and P. leucopus, the two most widespread species, not only have relatively high rates of energy expenditure for reproduction [224,375], but their rates of basal and daily (routine) existence metabolism and overall activity levels are also relatively high [224,376,377,378]. By using the strong interspecific relationship between litter size and maternal energy ingested for lactation observed by [224,375], one can show that individual energy uptake for reproduction (reproductive power) correlates positively and highly significantly with geographical range size among Peromyscus species (Figure 11a). The high somatic and reproductive energy fluxes of the widespread species clearly fit the view of their having high energetic fitness (also see Section 7.1).
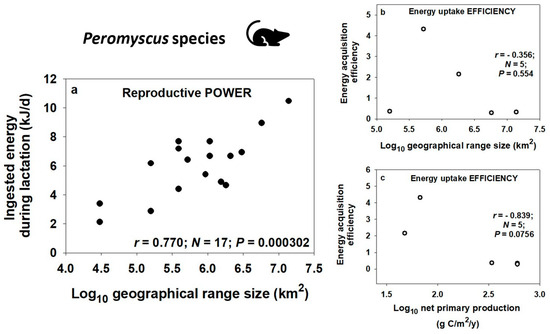
Figure 11.
Reproductive power and energy acquisition efficiency versus geographical range size of Peromyscus (white-footed mice) species (each point represents an individual species). (a) Reproductive power was estimated as mean ingested energy per day by a lactating female (EI), which was calculated from the regression EI = 2.529 (LS) − 1.925 (r = 0.938; N = 5; p = 0.0184) according to the mean litter size (LS) of each species (data from [224,375,376]). (b) Resource acquisition efficiency (RAC) estimated as EI/NPP, where NPP = the net primary productivity of the native habitat of a species given in [378]. (c) RAC versus NPP.
One may question the energetic patterns just described because they are based on laboratory observations. Do the widespread species have higher reproductive power in nature? Although this question requires further research to achieve a definitive answer, three observations support this view. First, litter sizes observed in wild-caught Peromyscus species parallel those observed in the laboratory [224,375]. Second, the annual production of young of three wild species coexisting in the same chaparral habitat in California (thus controlling for environmental differences) was correlated with their geographical range size (from most widespread to least: P. maniculatus—20, P. truei—9, P. californicus—6.2 [379]). Third, wild lactating females of the widespread P. leucopus trapped in a forest near Ithaca, New York state exhibited not only larger mean litter sizes but also higher mean total energy content (kJ) of the ingested food in their stomachs than did those of P. eremicus, a similarly sized, more restricted species trapped in a desert near Portal, Arizona [224].
The hypothetical scheme depicted in Figure 9 predicts that the geographically restricted species of Peromyscus should exhibit a higher degree of adaptation to their local environments, as indexed by a higher efficiency (economy) of resource acquisition for production. Finding evidence for this prediction is more difficult than documenting a correlation between reproductive power and geographical range size, but a comparison of the widespread P. maniculatus and P. leucopus with the relatively restricted P. eremicus is revealing. First, although wild lactating females of P. leucopus and P. eremicus had similar body fat contents (g fat/g lean dry mass) in the field, the fat contents of lactating P. eremicus were significantly higher than those of P. leucopus in the laboratory [224]. This result suggests that when given equal amounts of abundant food, the restricted P. eremicus from a food-poor desert environment had higher efficiency accumulating fat stores than the widespread P. leucopus from a relatively food-rich forest environment. Second, female P. eremicus showed no significant decrease in body fat content during energy-expensive lactation, whereas female P. leucopus did [224], thus suggesting that P. eremicus was more economical with using acquired energy for reproduction. Third, despite living in an environment with scarcer food, wild non-breeding females of P. eremicus were able to ingest slightly more stomach food energy than those of P. leucopus [224], thus suggesting that P. eremicus was more efficient at acquiring limited food resources. Fourth, in the same desert shrub habitat near Portal, Arizona, the restricted desert specialist P. eremicus was more abundant and had higher population production than the coexisting widespread habitat generalist P. maniculatus [380]. Since the two species were living on essentially the same food supply, P. eremicus appeared to show greater efficiency of food acquisition for production than did P. maniculatus. Similar patterns occur for other coexisting widespread and restricted species. For example, the restricted P. keeni (once considered P. oreas and P. sitkensis) is more abundant in its native temperate rainforest habitat in northwestern North America than is the more widespread sympatric P. maniculatus [381]. In addition, the restricted P. gossypinus is more abundant in its specialized habitat (lowland woods and swamps) than the coexisting widespread P. leucopus, which occurs in both lowland and upland forests [382].
Further circumstantial evidence supporting the possibility that restricted species of Peromyscus and other rodents are more efficient resource gatherers than more widespread species is that they tend to have more stable populations often associated with non-seasonal breeding [298,374,383], which should foster K-selection for increased efficiency of resource acquisition ([211,212,213,266]; also see Table 2 and Section 7.3.1). In general, the most restricted species of Peromyscus preferentially occur in relatively stable species-rich tropical and subtropical environments that should favor the evolution of increased competitive ability and associated high efficiency of resource acquisition. As evidence, more restricted specialized species of Peromyscus and other rodents tend to outcompete more widespread generalized (opportunistic) related species [364], often preventing them from invading their native habitat [243,371,381,382].
Another approach is to calculate an index of efficiency of resource acquisition for reproduction by comparing the maternal energy ingested during the lactation (EI) of female mice of widespread and restricted Peromyscus species with the net primary productivity (NPP) of their local environments. I have done this by using data collected from [243,375,376,378]. Data were available for only five species, and they show that two of the three restricted species have higher efficiencies (EI/NPP) than those of the two widespread species (Figure 11b). However, the overall negative correlation between EI/NPP and geographical range size is not significant (r = −0.356; p = 0.554). This efficiency index was also negatively correlated with habitat productivity (Figure 11c), but only with marginal significance (r = −0.839; p = 0.0758). This trend is consistent with the view that limited resource supplies favor the evolution of increased efficiency of resource acquisition (see Section 7.3.1). However, more data are needed that are based on more precise measures of food availability and acquisition, which will be challenging to collect for omnivorous Peromyscus species.
I hope that the above suggestive results will stimulate further research exploring relationships between power/efficiency and the niche breadth, population dynamics, and geographical range size of not only Peromyscus species (a model taxon for such studies), but also related species in other clades. Consistent with the trends observed in Peromyscus, the widespread and versatile racoon Procyon lotor has higher rates of metabolism and reproduction than do other more restricted, specialized Procyonid species [384]. In addition, the most widespread heteromyid rodents have the highest basal metabolic rates in their genera (e.g., Chaetodipus hispidus and Dipodomys ordii [385]), as also occurs in the rodent genus Microtus in North America (M. pennsylvanicus [386]). Furthermore, the widespread M. pennsylvanicus and M. arvalis ingest more food energy for lactation than does the more restricted M. pinetorum (see references cited in [375]). More generally, rates of energy flow (as indicated by basal, daily, and maximal metabolic rates) that can support reproductive power [169,208,243,376,387,388] are positively associated with geographical range size in eutherian mammals [389,390,391]. Reproductive output is also positively correlated with geographical range size in herbaceous plants in France [392] and birds in Britain and New Zealand [393] (other examples are cited in [298]).
7.5. Geography of Power and Efficiency
In general, large/warm/wet geographical areas tend to have higher rates of biological productivity and consumption (power) than smaller/colder/drier areas [68,261], though differences in geographical variation in community energy use among terrestrial vertebrate taxa have been observed [394]. Increases in productivity from polar to tropical regions are well known [68,395,396,397], but geographical patterns of efficiency of resource acquisition and use have been little studied. Forest production efficiency increases with increasing temperature (and decreasing latitude) [398]. Global estimates of efficiency of trophic energy transfer from producers to primary consumers (herbivores) also tend to increase along environmental gradients of increasing temperature and precipitation [65]. Percent consumption or damage of vegetation by herbivores (an indicator of trophic transfer efficiency, TTE) increases with decreasing latitude [399] and toward more productive sites ([400] and references cited therein). The evolution of economical solutions to resource scarcity and/or intense competition for resources is exemplified by the energy conservatism of cave [401,402,403,404] and island animals [101,215,405,406].
Geographical patterns in species diversity may help explain why TTE increases with increasing productivity in terrestrial ecosystems but decreases in freshwater ecosystems. In terrestrial ecosystems, positive covariation of productivity and species diversity [395,407,408] may result in more consumer species being available to eat vegetation at more productive sites. However, in highly productive (eutrophic or thermal) freshwater ecosystems, hypoxia and high temperatures may limit consumer species diversity [31,106], thus lowering TTE from producers to consumers (also see Section 3).
7.6. Temporal Variation in Power and Efficiency
The power production of a living system may vary considerably over time: daily, seasonally, ontogenetically, successionally, and evolutionarily. How this temporal variation is related to energetic efficiency has been little studied empirically. Here, I only touch on this topic to stimulate further research.
7.6.1. Daily Variation in Power Production
In animals, daily variation in power production mainly relates to periods of rest, sleep, torpor, and bouts of activity. Circadian rhythms of activity have been much studied and will not be reviewed here (see, e.g., [409,410]). Notably, animals undergo regular sleep–awake cycles. Sleeping involves minimal activity and power production (though body growth and tissue repair may be hastened somewhat [411]), which may be adaptive at night when diurnal animals cannot effectively find food and avoid predators and other environmental hazards [412,413,414,415]. Although powering down during sleep would seem economical because it reduces energy costs during times of inactivity [413,416,417,418,419], it also reduces time available for acquiring food energy and nutrients for production, and thereby also daily production efficiency, because of a decrease in energy and time spent in engaging in productive work relative to that used for standby (idling) body maintenance, or the “cost of living while doing nothing” [420]. Daily, often lengthy, resting periods clearly show that animals are not geared for continually maximal activity. Indeed, as Elton [421] remarked, many kinds of animals “spend an unexpectedly large proportion of their time doing nothing at all, or at any rate nothing in particular” (pp. 55–56) (also see [422]). And yet, we still understand little why this is so.
Some heterothermic birds and mammals also engage in energy-sparing, daily torpor, involving substantial reductions in body temperature and metabolic rate, when food availability/accessibility is low, predation risk is high, or thermoregulatory costs are exorbitant during cold nights [423,424,425]. This ability to power up and down in relation to the favorableness/harshness of the environment on a moment-by-moment basis nicely illustrates the importance of food availability, predator avoidance, and biological regulation in moderating power production [151,423,424,425,426,427] (also see Table 1 and Section 5.2 and Section 7.6.2).
In addition, the primary production rates and efficiencies of ecosystems may vary during the diel cycle, being maximal during the day (e.g., [32,428,429]). Bacterioplankton growth rates and efficiencies also vary with the daily light cycle [39]. Overall, daily variation in productive activity at both the organismal and ecosystem levels illustrates positive synchronization of power and efficiency, as expected for resource use systems (right-hand side of Figure 7).
7.6.2. Seasonal Variation in Power Production
Seasonal variation in rates and efficiencies of production has been observed at the level of individual organisms, populations, communities, and ecosystems. At the individual level, reproductive activity is highest during relatively warm, resource-rich (spring and summer) months. Since higher rates of offspring production are associated with higher production efficiencies in captive animals (Figure 6 [4,24,25,39,57,103]; also see Section 3.1 and Section 3.3), it is plausible that wild animals should also show synergistic increases in rates and efficiencies of production during favorable growing seasons, as expected for resource use systems (right-hand side of Figure 7). During harsh, food-poor (winter) months, many animals are dormant, thus conserving their limited energy resources until the next growing/breeding season, but at the same time reducing their annual production efficiency (see Section 7.6.1). However, although increased torpor use decreases the rate of energy assimilation, it may increase assimilation (digestive) efficiency, as observed in the Eastern chipmunk (Tamias striatus) [430]. This trade-off between power and efficiency is as expected for resource uptake systems (left-hand side of Figure 7). Thus, many animals annually cycle between periods of high/low rates/efficiencies of assimilation and production that correspond with shifts in energy allocation between growth/reproduction and survival/maintenance. Deciduous trees also power down during the winter months by shedding their production-making solar panel-like leaves. Synergistic seasonal changes in the rate and efficiency of photosynthesis have been observed in various plants (e.g., [431,432]). How seasonality affects annual and seasonal production rates and efficiency should depend on the length of the growing/breeding season. Shorter growing seasons (and thus longer nongrowing seasons, as occur at higher latitudes) should select for trees that have high rates and efficiencies of production during the spring and summer months, as observed [433], while at the same time reducing annual rates and efficiency of production, a plausible hypothesis requiring testing.
At the population level, increased temperature, as occurs during the growing season, increased, or had no effect, on carbon use efficiency in 29 strains of isolated bacteria [434]. Typically, the growth rate of bacterial populations responds more strongly to temperature than does their respiration rate, thus accounting for positive (or non-negative) temperature-related covariation between the rates (power) and efficiency of growth.
At the community/ecosystem levels, cross-season covariation between rates (power) and efficiency of production depends on whether temperature affects rates of production more or less than that of rates of respiration (maintenance metabolism). In several studies, production rates and efficiencies of bacterial communities covaried positively across seasons [39,435,436,437]. However, in one study, during summer when bacterial growth rates were highest, growth efficiency was lowest, because increasing temperature increased respiration rates more than growth rates [438]. Synergistic (and sometimes antagonistic) seasonal changes in rates and efficiencies of primary production (photosynthesis) have also been observed in aquatic and forest ecosystems (e.g., [428,439,440,441]).
In addition, planktonic communities show seasonal changes in trophic transfer efficiencies (TTEs) from phyto- to zooplankton production [442,443]. I further predict that increased seasonality and fluctuations in resource supply (including shorter growing/breeding seasons) should decrease annual TTEs, as supported by an inverse association between annual TTE and seasonality (increased latitude) in forest ecosystems (see Figure 5; and [65]).
7.6.3. Variation in Power Production over a Lifetime
Typically, during early ontogeny (young life stages), animals exhibit faster rates and efficiencies of growth (production) than during later ontogeny (e.g., [4,82,84,444,445,446]; but see [104]), thus showing synergy between power and efficiency, as predicted for resource use systems (right-hand side of Figure 7). Aging trees also show synergistic declines in rates and efficiencies of production [398,447]. Age-related decreases in production efficiency appear to be largely due to increases in maintenance costs of already grown body mass [446].
In ectotherms, according to “developmental cost theory” (DCT: [448]), the relationship between the energy cost of development and temperature depends on the relative thermal sensitivities of developmental time and metabolic rate. This theory predicts that the energy cost of development should be optimally minimal at intermediate temperatures, as has been empirically demonstrated in fishes, crustaceans, and reptiles [448,449]. Since the energy cost of development represents the efficiency of converting food (e.g., yolk) energy into developmental processes, the DCT is consistent with the “maximum efficiency principle” (MEP) where efficiency of fuel use is maximal at intermediate power (speed), which is a function of temperature in ectotherms (see Section 2; Figure 1a).
In mammals, reproductive efficiency (the percent conversion of maternal food into offspring tissue) is usually higher during gestation than lactation, because extrauterine young have greater energy costs of activity and thermoregulation than do intrauterine young, and lactation involves additional energy costs related to the biosynthesis and digestion of milk [450,451]. Therefore, it is not surprising that reproductive efficiency in rodents is positively correlated with the duration of gestation (G) relative to lactation (L) [450]. The marsupial Monodelphis domestica also has a much lower efficiency of litter growth and G/(G + L) than two ecologically comparable eutherian species (Elephantulus rufescens and Echinops telfairi) of similar size (data in [452] analyzed by [450]). These differences in reproductive efficiency may have important ecological and evolutionary implications [450,451,453,454,455]. For example, precocial rodents tend to have higher reproductive efficiencies than altricial rodents [451] that may offset, at least in part, their lower rates and efficiency of offspring production [456]. In addition, reproductive efficiency has been shown to be higher during early versus late lactation of two Peromyscus species in association with the higher relative energetic growth rates of young versus older lactating pups [375].
It would be interesting to examine how and why power and efficiency change during complex life cycles involving metamorphosis of larvae into distinctly different adults. In holometabolous insects with complete metamorphosis, the relatively sedentary larval stages are geared for high productive power (rates of feeding and growth), whereas the highly mobile adult stages are geared for high locomotor power (rates of flying and dispersal) [457,458]. Perhaps this temporal division of labor between growing and moving (flying) has increased the power and efficiency of both by decreasing antagonistic resource allocation, a hypothesis worth testing (also see Section 8.2.2). In support, insect larvae that expend relatively little energy on foraging activity tend to have higher growth efficiencies [50].
A power/efficiency perspective could cast new light on the evolution of complex life cycles, and even life cycles in general. I have already discussed r- and K-selection in terms of a power–efficiency trade-off (see Table 2 and Section 7.3.1, Section 7.3.2 and Section 7.4), but it would also be worthwhile to explore how productive power and efficiency relate to embryonic versus postembryonic development, prenatal versus postnatal development, and lifetime variation in growth (determinate versus indeterminate) and reproduction (semelparous versus iteroparous). It is plausible that protected, sedentary embryonic and fetal life stages should exhibit rapid rates and efficiencies of growth, because they are unimpeded (or relatively little affected) by energy costs of locomotion, homeostasis, and coping with environmental stressors. In support, the energetic conversion efficiencies of embryos and early postnatal or post-hatching developmental stages are among the highest observed in the living world [82,446]. One may also conjecture that semelparous species that expend much energy for a single reproductive event before dying [200,459] should have a higher lifetime reproductive efficiency than iteroparous species that expend smaller amounts of energy per each repeated reproductive event, and thus relatively little compared to lifetime maintenance costs.
7.6.4. Variation in Power Production over Ecological (Successional) Time
In a classic paper, E. P. Odum [460] identified 24 ways that terrestrial plant communities change after disturbance from early to late successional stages, including shifts from small to large plants, r- to K-selection, high colonization ability to high competitive ability, and high mass-specific production (power) to high efficiency of resource (energy/nutrient) use. This scheme dovetails nicely with how power and efficiency appear to trade off along body size gradients and among related widespread generalist and geographically restricted specialist species that occupy habitats of varying stability and successional stage (see Section 7.3 and Section 7.4). However, although successional shifts from power to efficiency have received some theoretical support [7,211,461,462], they have been little studied empirically [463]. Notably, a recent study of phytoplankton communities provides partial empirical support, showing that energy wastage decreases during succession [464], but more research on other communities is clearly needed.
7.6.5. Variation in Power Production over Geological Time
Numerous scientists have claimed that organismal and ecosystem power production (rates of energy use) have increased over geological time. At the organismal level, evolutionary trends toward increased rates of metabolism and activity, culminating in the appearance of high-powered endothermic birds and mammals, have long been the subject of much discussion [261,333,465,466,467,468,469,470,471]. At the ecosystem level, evidence suggesting geological trends toward increased rates of primary production and consumption has also been accumulating [261,467,468,472,473,474,475,476]. Chaisson [477,478] has even claimed that increased mass-specific rates of energy consumption (power) characterize the evolution of complex entities throughout the universe (but see [479]).
To some scientists, the organismal trends support the view that “Evolution is the survival of the powerful” (p. 166 in [462]; also see Section 5.1 and [3,8,9,10,11,12,13,139,140,141,142,480,481]). By contrast, other scientists have argued that evolution has increased the energetic or functional efficiency of organisms (also see Section 6 and [9,141,246,247,248,482]). This would make sense if one assumes that the evolution of increased species diversity (packing) has increased competition for limited resources, thus favoring increased efficiency of resource acquisition/use (see, e.g., [200,266,461]). However, this view assumes that the evolution of increased species richness [474,483] has occurred at a faster rate than the evolution of increased primary productivity, and thus availability of resources, which remains to be determined. J. H. Brown [142] has also argued that the evolution of endothermic animals, which now occur in almost all ecosystems [484], supports the view that evolution has favored increased power over efficiency. As support, many scientists have claimed that energy use for growth/reproduction by high-powered endothermic birds and mammals is relatively inefficient (i.e., energetically wasteful). Although endothermic animals have higher rates of individual growth and population production than ectothermic animals of equivalent size, their production efficiencies are lower [59,60,198,251,261,317,485,486]. Ectotherms with high production efficiencies appear to have an advantage when resources are scarce [485], thus supporting the view that power is favored in resource-rich environments, but efficiency is favored in resource-poor environments (Table 2; Section 7.3.1).
The evolution of endotherms is especially intriguing to consider from a power/efficiency perspective. How this is done depends critically on how one defines efficiency. As noted in Section 6, ‘efficiency’ is a tricky concept [200]. One must clearly specify what the input and the useful output are and provide a justifiable rationale for doing so. An apropos example is the internal combustion engine. Typically, from an anthropocentric viewpoint, one assumes that the useful output is kinetic energy for locomotion, but heat production could also be considered a useful output because it could help one keep warm, especially during winter travel [200]. The same perspective applies to endothermic animals. If biomass production is considered the useful output because it increases reproductive fitness, then populations of endotherms that expend relatively high amounts of energy on maintenance metabolism do have lower production efficiencies than ectotherms of equivalent size. However, if heat production (and its retention) is also considered a useful output because it increases metabolic power and efficiency, then endotherms need not be considered less efficient than ectotherms. A key point is that in endotherms, heat is not merely lost as useless energy; rather, it is essential for maintaining high body temperatures that permit exploitation of cold habitats and nocturnal time periods and that support enhanced rates of muscular activity, food acquisition, digestion, growth, reproduction, and parental care [261,484,487,488,489,490,491,492,493,494,495,496,497]. Heinrich [498] has argued that the maintenance of high, nearly constant body temperatures in many endothermic animals increases the efficiency of their biochemical reactions. In addition, young individual endotherms and ectotherms have comparable efficiencies of converting assimilated energy into growth [82,134,200,499], though during early ontogeny, both endotherms and ectotherms tend to be relatively ectothermic. Moreover, endothermy often permits higher efficiency of resource exploitation, as exemplified by how agile, high-energy goats have outcompeted more sluggish, low-energy tortoises of similar body mass and trophic niche on the Galapagos Islands [500]. The more efficient grazing of goats has reduced the availability of vegetation to tortoises, thus exterminating them in many places [501]. Not surprisingly, endothermic mammals dominate large herbivore and carnivore niches, which are underrepresented by ectothermic reptiles except on oceanic islands [502,503,504,505]. Herbivorous mammals have higher rates of ingestion and assimilation than herbivorous reptiles of equivalent size [506]. Although the Komodo dragon (Varanus komodoensis), the largest carnivorous lizard in the world, has higher population biomass relative to prey population biomass (and thus higher biomass production efficiency) than that of large mammalian carnivores, its resource exploitation efficiency appears to be relatively low because it has no effect on the population dynamics of its prey, unlike that observed for mammalian carnivores that capture more prey per unit time because of their higher activity levels and metabolic needs [505].
Organismal energy budgets are typically viewed in terms of resource acquisition and allocation. According to the “resource allocation principle” [89,182,183,187,226], given finite available resources, more energy that is used for one function is less that is available for another. However, it has not been sufficiently appreciated that different organismal functions may share (recycle) energy, a phenomenon that I have called “resource association” (the third RA: [187]), which is not thermodynamically impossible [6], as one might first think [140,187]. An excellent example of this is when energy used by digestion, locomotion, or production is used again as heat for thermoregulation (i.e., maintenance of a body temperature above the ambient temperature, especially in the cold), sometimes called “compensation” [507,508,509] or thermal “substitution” [510,511,512,513,514,515]. Endotherms are especially adept at thermal substitution, an economical strategy that can save significant amounts of energy [512,513,514,515,516,517]. Indeed, I suggest that resource association played a critical role in the origin of endothermy itself. The earliest ancestral endotherms may have used thermal substitution to maintain elevated body temperatures that enhanced their activity and thermal niche breadth in an economical way with minimal or no increases in metabolic rate, thus constituting an ‘easy’ preadaptation for endothermy. Individual variation in thermal substitution, as observed in mice (Peromyscus leucopus) [516], should have allowed natural selection to readily increase its effectiveness, especially in cold environments. Later in evolution, specific adaptations involving more costly increases in metabolic rate, e.g., thermogenic shivering, as seen in endothermic insects and vertebrates, and various mechanisms of non-shivering thermogenesis, as found in modern birds and mammals, may have furthered the development of endothermy (also see [494,496,497,518,519]).
In short, high-powered endotherms are not necessarily less efficient than ectotherms (also see Section 8.2.3 and [134,245,499,520]). Endothermy has permitted increases in two useful outputs: (1) heat production for thermoregulation enabling increased metabolic power and environmental temperature tolerance [487,492,498] and (2) biomass production for increased rates of growth and reproduction [198,317,486]. Viewed this way, heat production is not just a metabolic waste but a means for increasing energetic power, functional performance, and exploitation of a wide range of resources and habitats. Both heat production and biomass production should be considered important evolutionary and functional assets in a holistic analysis of power and efficiency in endotherms. This viewpoint is not teleological but can be viewed in terms of the action of mindless natural selection (see [496]).
Indeed, based on the power/efficiency spectrum described in Section 7.3.2 (Figure 9), one could argue that evolution over geological time has been largely a story of communities of microscopic organisms with high species-level productive power evolving into communities with additional macroscopic organisms with high species-level efficiencies of resource acquisition for production, thus paralleling trends observed during ecological succession (see Section 7.6.4).
7.7. Synthesis
Here, I attempt to synthesize the major findings discussed in Section 7. I have described how power and efficiency may covary in living systems at various hierarchical levels of organization, but “what is the ultimate driver of these energetic patterns?” Some would say that metabolic rate, as constrained by body size-related resource supply or time limits, drives variation in productive power (e.g., [14,15,16,521,522]), but this leaves open the question of “what ultimately drives metabolic rate?”. I contend that it is mortality rate in conjunction with the availability/accessibility of energy resources (Figure 12; also see Section 7.3.2). Species of small organisms and those living in relatively unstable/ephemeral habitats are subject to high mortality rates that favor (by natural selection) more rapid rates of growth and reproduction (and thus successful transmission of their genes to the next generation) before their imminent death, compared to species of more protected, longer-lived, larger organisms and those living in relatively stable/persistent habitats [101,102,157,235]. This trend is reinforced by intraspecific competition for resources and thus resource availability per individual being positively and negatively correlated with increasing body size and habitat stability, respectively. These ecological trends are inferred from the plausible assumption that the high mortality of species of small organisms or those that live in unstable habitats has caused them to have population densities well below the carrying capacity (K) of their environments, thus decreasing intraspecific competition and increasing resource availability per individual. By contrast, the low mortality of species of large, well-defended organisms or those that live in relatively stable habitats has caused them to have population densities near the carrying capacity (K) of their environments, thus increasing intraspecific competition and decreasing resource availability per individual [101,102,157,212,213,235]. Therefore, it is reasonable to hypothesize that variation in mortality rate has evolutionarily and ecologically caused species of small organisms or those that live in unstable/ephemeral habitats to have relatively high power of resource use for production, in contrast to species of large organisms or those that live in stable/persistent habitats that should have relatively high efficiency of resource uptake for production. In support, power density (W/g) decreases from unicellular eukaryotes to large metazoans [115]. In addition, at the ecosystem level, small heterotrophs consume a greater share of the available energy than do larger heterotrophs in both marine and terrestrial environments [479]. For more details and supporting evidence, see other parts of Section 7. Size-dependent selective mortality may also reinforce the power/efficiency pattern just described. Small organisms are not only subject to greater mortality than larger species, but it has also been suggested that a greater proportion of their mortality is random (non-selective with respect to genotype) [333,334]. Small organisms have responded evolutionarily with generalized increases in reproductive rate [254,333], i.e., power production. By contrast, larger, better defended organisms experience less mortality that is proportionately more selective, thus favoring specific adaptive responses entailing efficient acquisition of environmental resources. I also suggest that species living in relatively unstable, species-poor habitats with fluctuating resources may experience more random mortality than do those in relatively stable, species-rich habitats. Again, the former should evolve generalized increases in productive power, whereas the latter should evolve specific adaptive responses entailing not only efficient resource uptake but also effective counteradaptation against numerous enemy species (also see Section 7.3.2).
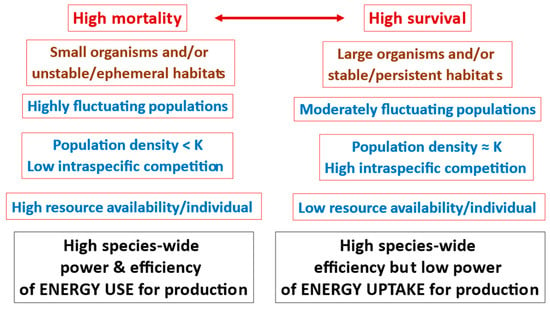
Figure 12.
Hypothetical scheme showing how mortality rate may affect the species-wide, mass-specific power and efficiency of energy use/uptake for production. These effects vary with body size and habitat stability and are mediated by natural selection and secondary ecological effects of mortality rate on intraspecific competition for resources and resource availability per individual. K is the carrying capacity of the environment. See text for more details.
My proposed synthesis has some similarities with other theoretical schemes. For example, Pianka [212] and others [213] have used the theory of r- and K-selection to argue that small species with highly fluctuating populations should be selected for high power, whereas large species with relatively stable populations should be selected for efficiency. However, my hypothetical scheme differs from that of Pianka’s in making a distinction between resource use and resource uptake systems (Figure 7). According to my scheme, species of small organisms or those that live in unstable/ephemeral habitats have evolved both high mass-specific power and efficiency of resource use for production, which follows from the frequent observation that the power and efficiency of resource use systems covary positively in living systems at various levels of biological organization (see Section 3.1, Section 3.3, Section 7.2, Section 7.5 and Section 7.6; and right-hand side of Figure 7). By contrast, I contend that species of large organisms or those that live in stable/persistent habitats have evolved high efficiency, but low species-wide, mass-specific power of resource uptake for production, which follows from the frequent observation that the power and efficiency of resource uptake systems covary negatively in living systems at various levels of biological organization (see Section 3.1, Section 3.3, Section 7.3, Section 7.4 and Section 7.6; and left-hand side of Figure 7).
It is also interesting to compare my scheme with the concepts of general and special adaptation discussed by W. L. Brown [523] and P. J. Darlington [524]. These concepts vaguely resemble my energetic definitions of ‘fitness’ and ‘adaptation’ (see Section 7.1). According to Brown, “general adaptations” are traits that increase the ability of a species to survive and reproduce in multiple environments, whereas “special adaptations” are traits that increase the ability of a species to survive and reproduce in a specific local environment. The global/regional versus local distinction parallels my use of the concepts ‘fitness’ versus ‘adaptation’. Brown [523] also associated general adaptations with good colonization ability, large geographical ranges, and fluctuating populations, whereas special adaptations were associated with ecological specialization and stable populations, thus resembling my contrast between widespread, generalist species with high fitness versus geographically restricted, specialist species with high adaptiveness (see Section 7.1 and Section 7.3). However, Brown did not explicitly state that special adaptations promote efficiency of energy uptake for production. In contrast, he argued that general adaptations include characters that increase system efficiency (not clearly defined) (also see [524]). This notion is the opposite of my distinction between fitness and adaptiveness as representing productive power versus efficiency of resource acquisition for production.
Another way to view my synthetic scheme is to realize that power involves both energy and time. One can increase power by either increasing energy input or output or by decreasing the time involved in obtaining or using a specific amount of energy [462]. Thus, not only can energy availability affect the power and efficiency of a species, but so can a mortality-imposed time limit. Accordingly, vulnerable short-lived species that experience high mortality must engage in rapid growth and reproduction (fast productive speed, even at the expense of reduced efficiency of resource uptake) to ensure their evolutionary success. Protected, longer-lived species can afford more frugal, high-efficiency strategies of resource uptake.
8. Applications of a Power/Efficiency Perspective to Nutrient/Water Uptake/Use, Functional Performance, and Information Processing
So far in my review, I have discussed the power and efficiency of living systems from an energetic perspective, as typically used by physicists for physical energy-transforming systems. However, in complex living systems, analogous perspectives may also be used to understand the dynamics of nutrient/water uptake/use, the strength and effectiveness of performance of various biological functions, and the speed and accuracy of information processing. Since the focus of my review is energetic in nature, I only briefly discuss each of these applications and how they may influence energetic power and efficiency.
8.1. Power (Rate) and Efficiency of Nutrient/Water Uptake and Use
Several studies have examined how the rates and efficiencies of uptake/use of specific elements/nutrients (e.g., carbon, nitrogen, and phosphorus) vary with environmental conditions. For example, the carbon uptake (power) and carbon use efficiency (CUE) of forests increase synergistically with increases in temperature and water availability ([398] but see [397]). By contrast, nitrogen use efficiency (NUE) increases from warm wet terrestrial plant ecosystems with high productivity (forests and grasslands) to cold dry ones with low productivity [525]. NUE is also inversely related to temperature and photon intensity during the growing season [525]. Therefore, covariation between power and efficiency of nutrient use appears to depend on the nutrient considered. Like energy use efficiency, CUE increases with increasing productivity, whereas NUE increases with decreasing productivity. Perhaps this is because nitrogen is essential for the biosynthesis of vital macromolecules (proteins and nucleic acids), and thus its uptake and use must be maintained as high as possible even when resource availability is low. Alternatively, the different responses of CUE and NUE to light and fertilization may reflect different optimization strategies [526].
Nutrient availability can also affect both the power and efficiency of energetic production. For example, bacterial growth rates and efficiency both increase markedly with increasing nutrient availability [39]. In addition, fertilization (increased nitrogen or phosphorus) commonly increases both production and efficiencies of production or radiation conversion in individual plants (e.g., [79,527,528]) and forest ecosystems [58,529], thus paralleling the synergistic effects of food rationing on productive power and efficiency seen in animals (see Section 3 [4,47,48,50,77,78]). The maximization of energy intake in animals, as predicted by optimal foraging models, may also be constrained by nutrient availability [530,531,532,533].
The power/efficiency of uptake/use of energy and water can also interactively affect each other. For example, cactus mice (Peromyscus eremicus) appear to have high efficiencies of both energy acquisition and water use, important indicators of their specialized adaptation to desert habitats (see Section 7.4 and [534]). Furthermore, when dehydrated, these mice conserve water by reducing their energy expenditure and food intake, thus reducing fecal water loss [534]. In general, many desert mammals have low rates and high efficiencies of both water and energy use that are mutually reinforcing (as indicated by efficient water retention and low metabolic rates: see, e.g., [535,536]). In addition, desert scorpions, which are highly effective sit-and-wait, venomous predators, acquire and use energy and water highly economically, thus allowing them to sustain high, stable population densities (and population biomasses that can exceed that of all local vertebrate animals combined) despite the scarcity of food and water [537,538,539,540,541], the epitome of K-selection and high adaptiveness (efficiency of resource acquisition for production), as defined in Section 7.1 and Section 7.3.1.
It is also well known that plant productive power is constrained by a trade-off with water use efficiency. High rates of photosynthesis (carbon uptake and energy production) entail lower water use efficiency because open stomata needed for essential CO2 uptake also increase water loss [542], thus essentially “trading water for carbon” [543].
8.2. Power (Rate) and Effectiveness of Functional Performance
The rates and effectiveness of the performance of specific functional activities may be negatively correlated, which may have important consequences for the covariation of energetic power and efficiency, as discussed in Section 8.2.1. Division of labor in living systems may also affect the power and efficiency of their functional activities, as discussed in Section 8.2.2.
8.2.1. Deleterious Effects of Speed
Increasing the speed of various functional activities (e.g., growth, reproduction, and behavior) may reduce their effectiveness, resulting in injury, enhanced aging, developmental or decision-making mistakes, increased exposure to predators or other environmental hazards, and/or energy wastage. If so, this may help explain why production efficiency often shows a positive asymptotic relationship with productive power (speed) (also see Figure 6 and Section 3.3, Section 7.2, Section 7.5 and Section 7.6), without a decline in efficiency (effectiveness) resulting from a further increase in power, as predicted by the maximum efficiency principle (Figure 1a [5]), because very high-power levels are ‘forbidden’. Natural selection may have eliminated organisms that exceeded a maximal power limit (Figure 1b) because of the deleterious effects produced (also see Table 1 and Section 3.2, Section 5.2 and Section 7.2). Rapid growth may produce developmental errors [89,184,188,201]. Indeed, rapidly growing, small mammals accumulate “epigenetic disorder” more rapidly than do slower growing, large mammals [544]. Rapid growth and reproduction may also hasten aging and mortality, including by increasing tissue/oxidative damage ([94,177,180,184,200,202,203,204,205,545,546,547,548,549] but see [550,551]) and/or exposure to predators or other environmental hazards (Table 1 [136,178,188,217,218]). Animals and humans that run too fast or too long may suffer more physical injuries [4,552,553]. Rapidly performed behaviors may also be associated with decision errors [554,555,556] (also see Section 8.3). Experiments involving hormonal manipulations, genetic engineering, or artificial selection for enhanced rates of growth, reproduction, or locomotion may prove especially useful for testing the hypothetical scheme depicted in Figure 1b (see, e.g., [545,546,557,558]).
8.2.2. Effects of Division of Labor on Power and Efficiency
Division of labor (functional specialization) is commonly believed to enhance performance efficiency in biological and economic systems (e.g., [120,559,560,561,562,563,564]). However, surprisingly, this plausible idea has not been rigorously tested from an energetic point of view in living systems. If this idea, the “division-of-labor efficiency” (DLE) hypothesis, is true, then one may predict that the efficiency of conversion of assimilated energy into a performance activity should be greater when that activity occurs separately (or largely so) from other competing activities. Indirect support for the DLE hypothesis comes from the observation that growth efficiency in immature insects is higher when they engage in relatively little locomotor activity, a competing demand for metabolic energy [50]. Therefore, it follows that a temporal (ontogenetic) division of labor between ‘growing’ during juvenile stages and ‘moving’ during adult stages, as occurs in holometabolous insects, should increase the efficiency of each of these performance activities. As noted in Section 7.6.3, embryonic and prenatal developmental stages may have especially high growth efficiencies because of not having to deal with competing activities, such as locomotion, reproduction, thermoregulation, and other forms of homeostasis. Production efficiency in domestic livestock is also maximized by reducing their activity, as in cages [4].
However, does a spatial division of labor also increase the energetic efficiency of specific performance activities? No one yet knows. Consistent with the DLE hypothesis is the observation that the slime mold (Dictyostelium discoideum) transforms from being unicellular to multicellular when resources become scarce [565], though energetic measurements are still needed to test whether multicellular slime molds are more efficient than unicellular ones. In addition, colonial plants apparently use division of labor to maximize efficient uptake of spatially heterogenous resources [566,567]. If the DLE hypothesis is true, then organisms with more kinds of functionally different cells should be more efficient at using assimilated energy for supporting various life functions than organisms with fewer cell types. Thus, large organisms with many cell types should have lower mass-specific energetic costs for carrying out multiple maintenance functions at rest (i.e., lower resting metabolic rates) than do smaller organisms with fewer cell types. However, this prediction of the DLE hypothesis is contradicted by two observations. First, across all living organisms, from tiny unicellular organisms to huge multicellular organisms, the mean mass-specific metabolic rate of various taxa varies independently of body size ([479,568]; but see [140]) and thus number of cell types [120]. Second, although small and large mammals have the same number of cell types, the mass-specific resting metabolic rate still declines markedly with increasing body mass [120,569], thus showing a dissociation between metabolic efficiency and division of labor. In fact, increased cell-type diversity (division of labor) has been associated with enhanced metabolic intensity (i.e., increased power, rather than efficiency) across all taxonomic groups of life [569], though this view is contradicted by analyses in [479,568]. Nevertheless, “metabolic division of labor” may help to explain why larger colonies of social insects have lower mass-specific energy expenditures, and thus appear to be more efficient energetically, than smaller colonies, thus apparently showing ‘economy of scale’ [570]. We have much to learn about the interrelationships among organismal complexity, body size, and the power and efficiency of various performance activities (for stimulating discussions, see [562,563,565]).
8.2.3. Functional View of Power and Efficiency in Endothermic Animals
In Section 7.6.5, I argued that endothermic animals need not be considered energetically inefficient relative to ectothermic animals. A functional view reinforces this argument. For example, endothermic mammals have evolved multiple structures and functions that are more economical than those of their ectothermic reptilian ancestors, including a more effective masticatory apparatus, external fur (insulation) that conserves energy by reducing heat loss, a more upright gait that improves the efficiency of body support and movement, and a complex kidney that improves the effectiveness of various body functions by controlling body fluid composition [571,572]. In addition, mammals evolved a secondary palate that helped to separate and thus improve the effectiveness of respiration and ingestion, as well as a dental division of labor (heterodonty) that increased the effectiveness of food acquisition and processing compared to the homodonty of reptiles [571,572]. Other avian and mammalian features that improved the effectiveness of various vital functions are discussed in [571,572,573,574]. Birds and mammals are not only relatively powerful, but also efficiently designed for supporting high rates of resource uptake and use.
8.3. Rate and Accuracy of Information Acquisition and Use
To sustain and perpetuate themselves, all living systems require two major commodities: resources (including energy and materials) and information. After countless generations of natural selection, organisms have evolved information-based resource management systems that maximize productive power/efficiency within certain constraints, both intrinsic and extrinsic (see Table 1). Those organisms that most effectively acquire and use information about their external and internal environments to ensure maximally possible resource uptake and use for growth and reproduction will be favored over those that are less informed and thus less effective resource managers. In short, existing organisms have evolved to be “well-informed resource users” [121,187].
However, evolving information-based resource management systems that maximize power/efficiency may be constrained by trade-offs between the speed and accuracy of information acquisition and processing that parallel trade-offs between the power and efficiency of resource (energy) uptake for production. Trade-offs between speed and accuracy occur in many kinds of informational systems at various hierarchical levels of biological organization, including biochemical (e.g., RNA translation and protein synthesis [575,576,577,578] but see [579]), physiological (e.g., neural and sensory processing [580,581,582,583,584]), and behavioral processes (e.g., foraging behavior [279,280,555,584]). Foraging behavior is of special interest here because it involves the integrated acquisition and use of both energy and information. Effective (powerful/efficient) foragers not only obtain the most energy-rich prey with the least amount of cost, but they also manage their ‘optimal foraging’ by obtaining and using relevant information about their prey as quickly/efficiently as they can. Cognitive limitations may cause foraging speed/accuracy trade-offs that can help to explain why trophic specialists are often more efficient at acquiring resources than generalists ([279,280,584]; also see Section 7.3.1).
Based on the above observations, I encourage exploration of how the speed and accuracy of information processing scale with body size. Small organisms with fast paces of life that demand rapid mass-specific rates of resource acquisition should also have faster mass-specific rates of information processing than larger organisms with slower, more energy-conservative lives. Frequently observed hypometric (or zerometric) scaling of genome size and brain mass with body mass (log-log slope < 1 or ≈0) [130,585,586,587,588] is consistent with this view. These patterns suggest that small organisms usually have more information-processing machinery relative to their body size than do larger organisms. In addition, animals with small body size and/or high metabolic rates can detect and react to visual stimuli faster than larger or less energetic animals [589]. Therefore, high informational processing power appears to be linked to high energetic power, but more research is clearly needed.
9. Practical Applications
An understanding of power and efficiency is essential for improving the production of fish [590,591,592], domestic animals [4], agricultural crops [528,593,594,595,596,597], and forests [398,528,529], as well as the effectiveness of microbially powered bioremediation strategies [598,599], bioenergy production [600], and other biotechnology innovations [601,602]. A power/efficiency perspective also provides valuable insight into athletic performance [25,72,73,74,75,603], human economic systems [6,8,21,228,462,480,604,605], and the effects of disturbance, pollution, and climate warming on energy flow through organisms and ecosystems [606,607,608,609]. Thus, studies of power and efficiency have not only great theoretical importance for understanding how living systems work and have evolved but also many practical applications of benefit to human society, a topic that deserves more attention than I can give here.
10. Conclusions
I have attempted to show that a power/efficiency perspective provides useful insight into the tempo, functioning, evolution, and size-scaling of living systems at multiple levels of biological organization, from cells to ecosystems. Positive correlations between energetic power and efficiency are just as common as negative correlations predicted by “maximum power theory” [3,5,8,9,20,462,480,481], thus requiring new theory. Development of new theory should include distinctions between (a) resource supply and resource use systems that often entail negative versus positive correlations between power and efficiency, respectively, and (b) power-enhancing fitness and efficiency-enhancing adaptation and their covariation with body size, habitat stability, and the geographical range size of related species. New synthetic, interdisciplinary theory of power and efficiency in living systems should not only be based on physical, thermodynamic, and/or biochemical constraints as traditionally done, but also incorporate other diverse intrinsic and extrinsic effects, including effects of body size, mortality rates, food quantity/quality, niche breadth, population dynamics, and various evolutionary strategies.
Major observations and conclusions made in my review, all of which require further testing, exploration, and theoretical development, are listed below.
- Although proponents of “maximum power theory” have claimed that the humped relationships of power versus efficiency observed in some physical systems (i.e., maximum power at intermediate efficiency) should also occur in living systems, I argue that the humped relationships of efficiency versus power observed in other physical systems (i.e., maximum efficiency at intermediate power) may also be usefully applied (perhaps more so) to living systems with realistic modifications (e.g., selectively imposed limits on power production; also see conclusion #3 below). Converse relationships between power and efficiency, entailing the “maximum power principle” (MPP) versus the “maximum efficiency principle” (MEP), also deserve attention.
- Negative correlations (trade-offs) between power and efficiency often occur in resource supply systems (e.g., speed versus efficiency of acquisition of environmental resources and their assimilation into the body), whereas positive synergistic correlations between power and efficiency often occur in resource use systems (e.g., speed versus efficiency of growth, reproduction, and muscular work). Positive covariation between the speed and efficiency of productive work can be explained, at least in part, by rate-related increases in the proportion of energy used for productive work versus maintenance (idling costs) of the resource use system.
- Living systems do not universally show maximization of power at the detriment of efficiency. Many intrinsic (physical/biological) and extrinsic (ecological) factors limit power production. As a result, many organisms spend much of their time doing nothing. Positive asymptotic covariation between productive power and efficiency may often occur because natural selection has weeded out living systems that are too speedy, which entails deleterious effects of increased injury, developmental/behavioral mistakes, enhanced aging, increased exposure to predators or other environmental hazards, and/or resource wastage.
- Natural selection may favor either power or efficiency depending on resource quantity/quality, niche breadth, and population stability. Increased productive power is often favored when resources are abundant, organisms are ecological generalists, and populations and habitats are unstable, whereas efficiency of resource acquisition for production is often enhanced when resources are scarce, organisms are ecological specialists, and populations and habitats are relatively stable.
- At the whole species level, ‘fitness’ can be usefully indexed as power production, whereas ‘adaptation’ can be usefully indexed as efficiency of resource acquisition for production. These energetic definitions have the important advantages of being measurable, non-tautological, and comparable among different species. This approach is examined by focusing on variation in power and efficiency along a body size spectrum and among related species in specific clades. I suggest that abundant microscopic organisms subject to high mortality rates have been selected for high productive power (species-level fitness), whereas less abundant macroscopic organisms subject to relatively high resource limitation have been selected for high efficiency of resource acquisition for production (species-level adaptiveness). This power/efficiency size spectrum dovetails nicely with classical r- and K-selection theory. My approach is also supported by a case study of North American white-footed mice (Peromyscus species), where widespread generalist species that often occupy disturbed/unstable habitats promoting r-selection exhibit high productive power (fitness) at both the individual and species (regional/global) levels, whereas geographically restricted specialist species that occupy relatively stable habitats that promote K-selection appear to exhibit high efficiency of resource acquisition for production (adaptiveness at the local population level).
- Productive power and efficiency often increase synergistically with increases in resource abundance both in space and time. Both primary production and the trophic transfer efficiency from primary to secondary production increase along environmental gradients of increasing temperature and water availability. Daily and seasonal changes in resource availability/accessibility are also typically associated with synergistic changes in productive power and efficiency at the individual, population, and ecosystem levels. However, daily/seasonal temperature changes may have varying effects on covariation between productive power and efficiency, depending on the relative thermal sensitivities of production versus maintenance (respiration). Rapid growth during early ontogenetic stages is positively associated with enhanced growth efficiencies. Other features of life cycles (including complex life cycles) may also relate to covariation between productive power and efficiency. However, the ecological succession of terrestrial plant communities appears to involve temporal trade-offs between power and efficiency. Pioneering r-selected species have relatively high mass-specific production rates, whereas climax K-selected species appear to be more efficient at capturing and retaining energy and nutrients. Similar patterns appear to have occurred over geological time, as ecological communities evolved from only having microbes with high species-level productive power to also having macroscopic organisms with relatively high species-level efficiency of resource acquisition for production. By contrast, some scientists have suggested that over geological time, organisms have evolved increased power at the expense of decreased efficiency. Recently evolved endothermic animals are often cited as examples of high-powered, but inefficient, ‘energy-leaking’ living systems. I challenge this view by pointing out that endothermy entails increases in two kinds of useful output, biomass production that enhances reproductive success and heat production (and retention) that amplifies metabolic power and thermal niche breadth. Many biologists have considered heat as merely a metabolic waste that reduces productive efficiency, but endotherms retain much heat for useful purposes. When considering both these useful outputs, endotherms are not necessarily less efficient than ectotherms. Indeed, highly active endotherms may have higher efficiencies of resource exploitation than ectotherms of equivalent size. Furthermore, I argue that the economical ‘recycling’ of heat dissipated from various work processes—including digestion, production, and locomotion—to support regulation of high body temperatures, especially in the cold (called ‘thermal substitution’, a form of ‘resource association’), may have been a preadaptation for the evolution of endothermy itself.
- A power/efficiency perspective may not only be useful from an energetic viewpoint, but also in relation to the nutrient/water uptake/use, functional performance, and information processing of living systems. New general theory of the metabolic, stoichiometric, functional, and informational organization of living systems may benefit from considering power/efficiency covariation of each of these components and their interactions.
- A power/efficiency perspective may also have many practical applications of benefit to human society.
In conclusion, I hope that my review of the (co)variation of power and efficiency in living systems will help to stimulate the development and empirical testing of a general theory of metabolic organization that is applicable to all of life across multiple hierarchical, spatial, and temporal scales (also see [19,115,479,610,611,612]). This theory should focus not just on the maximization of power or efficiency, but rather on the conditions under which each should be maximized within demonstrable functional, ecological, and evolutionary constraints. It should also recognize the rich diversity of relationships between power and efficiency observed in various organismal and ecological systems, as documented throughout my review. A power/efficiency approach promises to provide much insight into the tempo, functioning, and evolution of living systems, small and large.
Funding
This research received no external funding.
Data Availability Statement
All data analyzed in this review can be found in the cited references.
Acknowledgments
I thank two anonymous reviewers for their helpful comments.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics, 10th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Atkins, P. The Laws of Thermodynamics: A Very Short Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Lotka, A.J. Elements of Physical Biology; Williams & Wilkins Company: Baltimore, MD, USA, 1925. [Google Scholar]
- Brody, S. Bioenergetics and Growth with Special Reference to the Efficiency Complex in Domestic Animals; Macmillan: New York, NY, USA, 1945. [Google Scholar]
- Odum, H.T.; Pinkerton, R.C. Time’s speed regulator: The optimum efficiency for maximum power output in physical and biological systems. Am. Sci. 1955, 43, 331–343. [Google Scholar]
- Odum, H.T. Environment, Power, and Society; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- Smith, C.C. When and how much to reproduce: The trade-off between power and efficiency. Am. Zool. 1976, 16, 763–774. [Google Scholar] [CrossRef]
- Hall, C.A.S.; McWhirter, T. Maximum power in evolution, ecology and economics. Philos. Trans. R. Soc. A 2023, 381, 20220290. [Google Scholar] [CrossRef] [PubMed]
- Lotka, A.J. Contribution to the energetics of evolution. Proc. Natl. Acad. Sci. USA 1922, 8, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Van Valen, L. Energy and evolution. Evol. Theory 1976, 1, 179–229. [Google Scholar]
- Van Valen, L. Evolution as a zero-sum game for energy. Evol. Theory 1980, 4, 289–300. [Google Scholar]
- Brown, J.H.; Marquet, P.A.; Taper, M.L. Evolution of body size: Consequences of an energetic definition of fitness. Am. Nat. 1993, 142, 573–584. [Google Scholar] [CrossRef] [PubMed]
- Harris, N.L.; Hall, C.A.S.; Lugo, A.E. A test of the maximum power hypothesis along an elevational gradient in the Luquillo Mountains of Puerto Rico. Ecol. Bull. 2013, 54, 233–243. [Google Scholar]
- Brown, J.H.; Hall, C.A.S.; Sibly, R.M. Equal fitness paradigm explained by a trade-off between generation time and energy production rate. Nat. Ecol. Evol. 2018, 2, 262–268. [Google Scholar] [CrossRef]
- Burger, R.J.; Hou, C.; Hall, C.A.S.; Brown, J.H. Universal rules of life: Metabolic rates, biological times and the equal fitness paradigm. Ecol. Lett. 2021, 24, 1262–1281. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.H.; Burger, J.R.; Hou, C.; Hall, C.A.S. The pace of life: Metabolic energy, biological time, and life history. Integr. Comp. Biol. 2022, 62, 1479–1491. [Google Scholar] [CrossRef] [PubMed]
- Smith, E.A. Human adaptation and energetic efficiency. Hum. Ecol. 1979, 7, 53–74. [Google Scholar] [CrossRef]
- Bock, W.J. The definition and recognition of biological adaptation. Am. Zool. 1980, 20, 217–227. [Google Scholar] [CrossRef]
- Watt, W.B. Power and efficiency as indexes of fitness in metabolic organization. Am. Nat. 1986, 127, 629–653. [Google Scholar] [CrossRef]
- Hall, C.A.S. Energy Return on Investment: A Unifying Principle for Biology, Economics, and Sustainability; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Hooker, J.N. Optimal driving for single-vehicle fuel economy. Transp. Res. A 1988, 22, 183–201. [Google Scholar] [CrossRef]
- Gnaiger, E. Heat dissipation and energetic efficiency in animal anoxibiosis: Economy contra power. J. Exp. Zool. 1983, 228, 471–490. [Google Scholar] [CrossRef]
- Gnaiger, E. Optimum efficiency of energy transformation and the evolution of catabolic pathways. Funct. Ecol. 1992, 6, 234–241. [Google Scholar]
- Richman, S. The transformation of energy by Daphnia pulex. Ecol. Monogr. 1958, 28, 273–291. [Google Scholar] [CrossRef]
- Peyré-Tartaruga, L.A.; Coertjens, M. Locomotion as a powerful model to study integrative physiology: Efficiency, economy, and power relationship. Front. Physiol. 2018, 9, 1789. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lauder, G.V. Energetics of collective movement in vertebrates. J. Exp. Biol. 2023, 226, jeb245617. [Google Scholar] [CrossRef] [PubMed]
- Odum, H.T. Efficiencies, size of organisms, and community structure. Ecology 1956, 37, 592–597. [Google Scholar] [CrossRef]
- Lacroix, G.; Lescher-Moutoué, F.; Bertolo, A. Biomass and production of plankton in shallow and deep lakes: Are there general patterns? Ann. Limnol. 1999, 35, 111–122. [Google Scholar] [CrossRef]
- Gladyshev, M.I.; Sushchik, N.N.; Anishchenko, O.V.; Makhutova, O.N.; Kolmakov, V.I.; Kalachova, G.S.; Kolmakova, A.A.; Dubovskaya, O.P. Efficiency of transfer of essential polyunsaturated fatty acids versus organic carbon from producers to consumers in a eutrophic reservoir. Oecologia 2011, 165, 521–531. [Google Scholar] [CrossRef] [PubMed]
- Karpowicz, M.; Feniova, I.; Gladyshev, M.I.; Ejsmont-Karabin, J.; Górniak, A.; Sushchik, N.N.; Anishchenko, O.V.; Dzialowski, A.R. Transfer efficiency of carbon, nutrients, and polyunsaturated fatty acids in planktonic food webs under different environmental conditions. Ecol. Evol. 2021, 11, 8201–8214. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Springs. In Reference Module in Earth Systems and Environmental Sciences; Elias, S.A., Ed.; Elsevier: Waltham, MA, USA, 2014; pp. 1–78. [Google Scholar]
- Odum, H.T. Trophic structure and productivity of Silver Springs, Florida. Ecol. Monogr. 1957, 27, 55–112. [Google Scholar] [CrossRef]
- Teal, J.M. Community metabolism in a temperate cold spring. Ecol. Monogr. 1957, 27, 283–302. [Google Scholar] [CrossRef]
- Tilly, L.J. The structure and dynamics of Cone Spring. Ecol. Monogr. 1968, 38, 169–197. [Google Scholar] [CrossRef]
- Naiman, R.J. Primary production, standing stock, and export of organic matter in a Mohave Desert thermal stream. Limnol. Oceanogr. 1976, 21, 60–73. [Google Scholar] [CrossRef]
- Boël, M.; Romestaing, C.; Voituron, Y.; Roussel, D. Allometry of mitochondrial efficiency is set by metabolic intensity. Proc. R. Soc. B Biol. Sci. 2019, 286, 20191693. [Google Scholar]
- Boël, M.; Romestaing, C.; Duchamp, C.; Veyrunes, F.; Renaud, S.; Roussel, D.; Voituron, Y. Improved mitochondrial coupling as a response to high mass-specific metabolic rate in extremely small mammals. J. Exp. Biol. 2020, 223, jeb215558. [Google Scholar]
- Barbe, J.; Watson, J.; Roussel, D.; Voituron, Y. The allometry of mitochondrial efficiency is tissue-dependent: A comparison between skeletal and cardiac muscles of birds. J. Exp. Biol. 2023, 226, jeb-246299. [Google Scholar] [CrossRef] [PubMed]
- Del Giorgio, P.A.; Cole, J.J. Bacterial growth efficiency in natural aquatic systems. Annu. Rev. Ecol. Syst. 1998, 29, 503–541. [Google Scholar] [CrossRef]
- Maitra, A.; Dill, K.A. Bacterial growth laws reflect the evolutionary importance of energy efficiency. Proc. Natl. Acad. Sci. USA 2015, 112, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Rogerson, A. The ecological energetics of Amoeba proteus (Protozoa). Hydrobiologia 1981, 85, 117–128. [Google Scholar] [CrossRef]
- Kleiber, M. The Fire of Life: An Introduction to Animal Energetics; John Wiley & Sons: New York, NY, USA, 1961. [Google Scholar]
- Stiven, A.E. The relationship between size, budding rate, and growth efficiency in three species of hydra. Res. Pop. Ecol. 1965, 7, 1–15. [Google Scholar] [CrossRef]
- Schiemer, F. Comparative aspects of food dependence and energetics of freeliving nematodes. Oikos 1983, 41, 32–42. [Google Scholar] [CrossRef]
- Droop, M.R.; Scott, J.M. Steady-state energetics of a planktonic herbivore. J. Mar. Biol. Assoc. UK 1978, 58, 749–772. [Google Scholar] [CrossRef]
- Bayne, B.L.; Svensson, S.; Nell, J.A. The physiological basis for faster growth in the Sydney rock oyster, Saccostrea commercialis. Biol. Bull. 1999, 197, 377–387. [Google Scholar] [CrossRef] [PubMed]
- Ansell, A.D. Experimental studies of a benthic predator-prey relationship. II. Energetics of growth and reproduction, and food-conversion efficiencies, in long-term cultures of the gastropod drill Polinices alderi (Forbes) feeding on the bivalve Tellina tenuis da Costa. J. Exp. Mar. Biol. Ecol. 1982, 61, 1–29. [Google Scholar] [CrossRef]
- Lawrence, J.M. Echinodermata. In Animal Energetics; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; Volume 2, pp. 229–321. [Google Scholar]
- Rollo, C.D. A test of the principle of allocation using two sympatric species of cockroaches. Ecology 1986, 67, 616–628. [Google Scholar] [CrossRef]
- Muthukrishnan, J.; Pandian, T.J. Insecta. In Animal Energetics; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; Volume 1, pp. 373–511. [Google Scholar]
- Biette, R.M.; Geen, G.H. Growth of underyearling sockeye salmon (Oncorhynchus nerka) under constant and cyclic temperatures in relation to live zooplankton ration size. Can. J. Fish. Aquat. Sci. 1980, 37, 203–210. [Google Scholar] [CrossRef]
- Pandian, T.J. Fish. In Animal Energetics; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; Volume 2, pp. 357–465. [Google Scholar]
- Russell, N.R.; Fish, J.D.; Wootton, R.J. Feeding and growth of juvenile sea bass: The effect of ration and temperature on growth rate and efficiency. J. Fish Biol. 1996, 49, 206–220. [Google Scholar] [CrossRef]
- Norin, T.; Clark, T.D. Fish face a trade-off between ‘eating big’ for growth efficiency and ‘eating small’ to retain aerobic capacity. Biol. Lett. 2017, 13, 20170298. [Google Scholar] [CrossRef]
- Brisbin, I.L. Bioenergetics of the breeding cycle of the ring dove. Auk 1969, 86, 54–74. [Google Scholar] [CrossRef]
- Canolty, N.L.; Koong, L.J. Utilization of energy for maintenance and for fat and lean gains by mice selected for rapid postweaning growth rate. J. Nutr. 1976, 106, 1202–1208. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Constraints on the offspring production efficiency of Peromyscus and other rodents. Funct. Ecol. 1990, 4, 223–231. [Google Scholar] [CrossRef]
- Waring, R.H. Estimating forest growth and efficiency in relation to canopy leaf area. Adv. Ecol. Res. 1983, 13, 327–354. [Google Scholar]
- Golley, F.B. Secondary productivity in terrestrial communities. Am. Zool. 1968, 8, 53–59. [Google Scholar] [CrossRef]
- Humphreys, W.F. Production and respiration in animal populations. J. Anim. Ecol. 1979, 48, 427–453. [Google Scholar] [CrossRef]
- Webb, W.L.; Lauenroth, W.K.; Szarek, S.R.; Kinerson, R.S. Primary production and abiotic controls in forests, grasslands, and desert ecosystems in the United States. Ecology 1983, 64, 134–151. [Google Scholar] [CrossRef]
- Waring, R.H.; Landsberg, J.J.; Williams, M. Net primary production of forests: A constant fraction of gross primary production? Tree Physiol. 1998, 18, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Collalti, A.; Prentice, I.C. Is NPP proportional to GPP? Waring’s hypothesis 20 years on. Tree Physiol. 2019, 39, 1473–1483. [Google Scholar] [CrossRef] [PubMed]
- Landsberg, J.J.; Waring, R.H.; Williams, M. The assessment of NPP/GPP ratio. Tree Physiol. 2020, 40, 695–699. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Global patterns of ecological efficiency at the biome-level. Oikos 1991, 61, 439–440. [Google Scholar] [CrossRef]
- Armengol, L.; Calbet, A.; Franchy, G.; Rodríguez-Santos, A.; Hernández-León, S. Planktonic food web structure and trophic transfer efficiency along a productivity gradient in the tropical and subtropical Atlantic Ocean. Sci. Rep. 2019, 9, 2044. [Google Scholar] [CrossRef] [PubMed]
- Cebrian, J. Patterns in the fate of production in plant communities. Am. Nat. 1999, 154, 449–468. [Google Scholar] [CrossRef] [PubMed]
- Whittaker, R.H. Communities and Ecosystems, 2nd ed.; MacMillan: New York, NY, USA, 1975. [Google Scholar]
- McClare, C.W.F. Chemical machines, Maxwell’s demon, and living organisms. J. Theor. Biol. 1971, 30, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Ho, M.W. The Rainbow and the Worm: The Physics of Organisms, 3rd ed.; World Scientific Publishing: Singapore, 2008. [Google Scholar]
- Ho, M.W.; Ulanowicz, R. Sustainable systems as organisms? BioSystems 2005, 82, 39–51. [Google Scholar] [CrossRef]
- Lupton, H.; Hill, A.V. An analysis of the effects of speed on the mechanical efficiency of human muscular movement. J. Physiol. 1923, 57, 337. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, S. The efficiency of bicycle-pedalling, as affected by speed and load. J. Physiol. 1929, 67, 242–255. [Google Scholar] [CrossRef] [PubMed]
- Benedict, F.G.; Cathcart, E.P. Muscular Work: A Metabolic Study with Special Reference to the Efficiency of the Human Body as a Machine; Carnegie Institution of Washington: Washington, DC, USA, 1913. [Google Scholar]
- Hill, A.V. The maximum work and mechanical efficiency of human muscles, and their most economical speed. J. Physiol. 1922, 56, 19–41. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Wootton, R.J. Bioenergetics of growth of a cyprinid, Phoxinus phoxinus (L.): The effect of ration and temperature on growth rate and efficiency. J. Fish Biol. 1988, 33, 763–773. [Google Scholar] [CrossRef]
- Widdows, J. Physiological indices of stress in Mytilus edulis. J. Mar. Biol. Assoc. UK 1978, 58, 125–142. [Google Scholar] [CrossRef]
- Stuart, V. Absorbed ration, respiratory costs and resultant scope for growth in the mussel Aulacomya ater (Molina) fed on a diet of kelp detritus of different ages. Mar. Biol. Lett. 1982, 3, 289–306. [Google Scholar]
- Sinclair, T.R.; Horie, T. Leaf nitrogen, photosynthesis, and crop radiation use efficiency: A review. Crop Sci. 1989, 29, 90–98. [Google Scholar] [CrossRef]
- Eiler, A.; Langenheder, S.; Bertilsson, S.; Tranvik, L.J. Heterotrophic bacterial growth efficiency and community structure at different natural organic carbon concentrations. Appl. Environ. Microbiol. 2003, 69, 3701–3709. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.J.; Bayne, B.L. Some relationships between growth, metabolism and food in the mussel Mytilus edulis. Mar. Biol. 1974, 27, 317–326. [Google Scholar] [CrossRef]
- Calow, P. Conversion efficiencies in heterotrophic organisms. Biol. Rev. 1977, 52, 385–409. [Google Scholar] [CrossRef]
- Allen, J.R.M.; Wootton, R.J. The effect of ration and temperature on the growth of the three-spined stickleback, Gasterosteus aculeatus L. J. Fish Biol. 1982, 20, 409–422. [Google Scholar] [CrossRef]
- Griffiths, C.L.; Griffiths, R.J. Bivalvia. In Animal Energetics; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; Volume 2, pp. 1–88. [Google Scholar]
- Pilarska, J. Eco-physiological studies on Brachionus rubens Ehrb (Rotatoria) III. Energy balances. Pol. Arch. Hydrobiol. 1977, 24, 343–354. [Google Scholar]
- Hodapp, D.; Hillebrand, H.; Striebel, M. “Unifying” the concept of resource use efficiency in ecology. Front. Ecol. Evol. 2019, 6, 233. [Google Scholar] [CrossRef]
- Navarro, J.M.; Winter, J.E. Ingestion rate, assimilation efficiency and energy balance in Mytilus chilensis in relation to body size and different algal concentrations. Mar. Biol. 1982, 67, 255–266. [Google Scholar] [CrossRef]
- Sharma, P.C.; Pant, M.C. An energy budget for Simocephalus vetulus (OF Muller) (Crustacea: Cladocera). Hydrobiologia 1984, 111, 37–42. [Google Scholar] [CrossRef]
- Sibly, R.M.; Calow, P. Physiological Ecology of Animals: An Evolutionary Approach; Blackwell Scientific Publications: London, UK, 1986. [Google Scholar]
- Seale, D.B. Amphibia. In Animal Energetics; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; Volume 2, pp. 467–552. [Google Scholar]
- Afik, D.; Karasov, W.H. The trade-offs between digestion rate and efficiency in warblers and their ecological implications. Ecology 1995, 76, 2247–2257. [Google Scholar] [CrossRef]
- Sibly, R.M. Strategy of digestion and defecation. In Physiological Ecology: An Evolutionary Approach to Resource Use; Townsend, C.R., Calow, P., Eds.; Sinauer Associates: Sunderland, MA, USA, 1981; pp. 109–139. [Google Scholar]
- Raubenheimer, D.; Simpson, S.J. Nutrient transfer functions: The site of integration between feeding behaviour and nutritional physiology. Chemoecology 1998, 8, 61–68. [Google Scholar] [CrossRef]
- Karasov, W.H.; Martínez del Rio, C. Physiological Ecology: How Animals Process Energy, Nutrient, and Toxins; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Hilton, G.M.; Houston, D.C.; Barton, N.W.H.; Furness, R.W.; Ruxton, G.D. Ecological constraints on digestive physiology in carnivorous and piscivorous birds. J. Exp. Zool. A Ecol. Genet. Physiol. 1999, 283, 365–376. [Google Scholar] [CrossRef]
- Hilton, G.M.; Furness, R.W.; Houston, D.C. A comparative study of digestion in North Atlantic seabirds. J. Avian Biol. 2000, 31, 36–46. [Google Scholar] [CrossRef]
- Lawton, J.H. Feeding and food energy assimilation in larvae of the damselfly Pyrrhosoma nymphula (Sulz.) (Odonata: Zygoptera). J. Anim. Ecol. 1970, 39, 669–689. [Google Scholar] [CrossRef]
- Muthukrishnan, J.; Delvi, M.R. Effect of ration levels on food utilisation in the grasshopper Poecilocerus pictus. Oecologia 1974, 16, 227–236. [Google Scholar] [CrossRef] [PubMed]
- Hanski, I. Food consumption, assimilation and metabolic rate in six species of shrew (Sorex and Neomyx). Ann. Zool. Fenn. 1984, 21, 157–165. [Google Scholar]
- Nordhaus, I.; Wolff, M. Feeding ecology of the mangrove crab Ucides cordatus (Ocypodidae): Food choice, food quality and assimilation efficiency. Mar. Biol. 2007, 151, 1665–1681. [Google Scholar] [CrossRef]
- Glazier, D.S. Scaling species interactions: Implications for community ecology and biological scaling theory. Acad. Biol. 2023, 1, 1–20. [Google Scholar] [CrossRef]
- Glazier, D.S. Does death drive the scaling of life? Biol. Rev. 2024. in review. [Google Scholar]
- Glazier, D.S.; Calow, P. Energy allocation rules in Daphnia magna: Clonal and age differences in the effects of food limitation. Oecologia 1992, 90, 540–549. [Google Scholar] [CrossRef] [PubMed]
- Scriber, J.M.; Slansky, F., Jr. The nutritional ecology of immature insects. Annu. Rev. Entomol. 1981, 26, 183–211. [Google Scholar] [CrossRef]
- Straile, D. Gross growth efficiencies of protozoan and metazoan zooplankton and their dependence on food concentration, predator-prey weight ratio, and taxonomic group. Limnol. Oceanogr. 1997, 42, 1375–1385. [Google Scholar] [CrossRef]
- Glazier, D.S. Temperature affects food-chain length and macroinvertebrate species richness in spring ecosystems. Freshw. Sci. 2012, 31, 575–585. [Google Scholar] [CrossRef]
- Karpowicz, M.; Ejsmont-Karabin, J.; Kozłowska, J.; Feniova, I.; Dzialowski, A.R. Zooplankton community responses to oxygen stress. Water 2020, 12, 706. [Google Scholar] [CrossRef]
- Karpowicz, M.; Grabowska, M.; Ejsmont-Karabin, J.; Ochocka, A. Humic lakes with inefficient and efficient transfer of matter in planktonic food webs. Sci. Rep. 2023, 13, 7913. [Google Scholar] [CrossRef]
- Heusner, A.A. Size and power in mammals. J. Exp. Biol. 1991, 160, 25–54. [Google Scholar] [CrossRef]
- Marden, J.H.; Allen, L.R. Molecules, muscles, and machines: Universal performance characteristics of motors. Proc. Natl. Acad. Sci. USA 2002, 99, 4161–4166. [Google Scholar] [CrossRef] [PubMed]
- Alexander, R.M. Models and the scaling of energy costs for locomotion. J. Exp. Biol. 2005, 208, 1645–1652. [Google Scholar] [CrossRef] [PubMed]
- Ahlborn, B.K. Zoological Physics: Quantitative Models of Body Design, Actions, and Physical Limitations of Animals; Springer: Berlin, Germany, 2004. [Google Scholar]
- Bejan, A. The Physics of Life: The Evolution of Everything; St. Martin’s Press: New York, NY, USA, 2016. [Google Scholar]
- Bejan, A.; Almerbati, A.; Lorente, S. Economies of scale: The physics basis. J. Appl. Phys. 2017, 121, 044907. [Google Scholar] [CrossRef]
- Kempes, C.P.; Wolpert, D.; Cohen, Z.; Pérez-Mercader, J. The thermodynamic efficiency of computations made in cells across the range of life. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160343. [Google Scholar] [CrossRef] [PubMed]
- West, G. Scale: The Universal Laws of Life, Growth, and Death in Organisms, Cities, and Companies; Penguin Books: New York, NY, USA, 2017. [Google Scholar]
- Lindstedt, S.L.; Boyce, M.S. Seasonality, fasting endurance, and body size in mammals. Am. Nat. 1985, 125, 873–878. [Google Scholar] [CrossRef]
- Millar, J.S.; Hickling, G.J. Fasting endurance and the evolution of mammalian body size. Funct. Ecol. 1990, 4, 5–12. [Google Scholar] [CrossRef]
- Bartholomew, G.A. Body temperature and energy metabolism. In Animal Physiology: Principles and Adaptations, 4th ed.; Gordon, M.S., Ed.; Macmillan: New York, NY, USA, 1982; pp. 333–406. [Google Scholar]
- Bonner, J.T. Why Size Matters: From Bacteria to Whales; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Glazier, D.S. Metabolic scaling in complex living systems. Systems 2014, 2, 451–540. [Google Scholar] [CrossRef]
- Glazier, D.S. Rediscovering and reviving old observations and explanations of metabolic scaling in living systems. Systems 2018, 6, 4. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Harrison, J.F. Do performance–safety tradeoffs cause hypometric metabolic scaling in animals? Trends Ecol. Evol. 2017, 32, 653–664. [Google Scholar] [CrossRef]
- Glazier, D.S. Variable metabolic scaling breaks the law: From ‘Newtonian’ to ‘Darwinian’ approaches. Proc. R. Soc. B Biol. Sci. 2022, 289, 20221605. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Effects of metabolic level on the body size scaling of metabolic rate in birds and mammals. Proc. R. Soc. B Biol. Sci. 2008, 275, 1405–1410. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Activity affects intraspecific body-size scaling of metabolic rate in ectothermic animals. J. Comp. Physiol. B 2009, 179, 821–828. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. A unifying explanation for diverse metabolic scaling in animals and plants. Biol. Rev. 2010, 85, 111–138. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Scaling of metabolic scaling within physical limits. Systems 2014, 2, 425–450. [Google Scholar] [CrossRef]
- Peters, R.H. The Ecological Implications of Body Size; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Hendriks, A.J. Allometric scaling of rate, age and density parameters in ecological models. Oikos 1999, 86, 293–310. [Google Scholar] [CrossRef]
- DeLong, J.P.; Okie, J.G.; Moses, M.E.; Sibly, R.M.; Brown, J.H. Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. USA 2010, 107, 12941–12945. [Google Scholar] [CrossRef] [PubMed]
- Hatton, I.A.; Dobson, A.P.; Storch, D.; Galbraith, E.D.; Loreau, M. Linking scaling laws across eukaryotes. Proc. Natl. Acad. Sci. USA 2019, 116, 21616–21622. [Google Scholar] [CrossRef] [PubMed]
- Wieser, W. Cost of growth in cells and organisms: General rules and comparative aspects. Biol. Rev. 1994, 69, 1–33. [Google Scholar] [CrossRef]
- Ziółko, M.; Kozłowski, J. Evolution of body size: An optimization model. Math. Biosci. 1983, 64, 127–143. [Google Scholar] [CrossRef]
- Calow, P. Resource utilization and reproduction. In Physiological Ecology; An Evolutionary Approach to Resource Use; Townsend, C.R., Calow, P., Eds.; Sinauer Associates: Sunderland, MA, USA, 1981; pp. 245–270. [Google Scholar]
- Darwin, C. On the Origin of Species; John Murray: London, UK, 1859. [Google Scholar]
- Boltzmann, L. Populare Schriften; Barth: Leipzig, Germany, 1905. [Google Scholar]
- Vermeij, G.J. The evolutionary interaction among species: Selection, escalation, and coevolution. Annu. Rev. Ecol. Syst. 1994, 25, 219–236. [Google Scholar] [CrossRef]
- Milewski, A.V.; Mills, A.J. Does life consistently maximise energy intensity? Biol. Rev. 2010, 85, 859–879. [Google Scholar] [CrossRef] [PubMed]
- Clauss, M.; Müller, D.W.; Codron, D. Within-niche pace of life acceleration as a fundamental evolutionary principle: A mammal pilot test case. Evol. Ecol. Res. 2019, 20, 385–401. [Google Scholar]
- Brown, J.H. Macroecology; University of Chicago Press: Chicago, IL, USA, 1995. [Google Scholar]
- Perrin, N.; Sibly, R.M. Dynamic models of energy allocation and investment. Annu. Rev. Ecol. Syst. 1993, 24, 379–410. [Google Scholar] [CrossRef]
- Pianka, E.R. Evolutionary Ecology, 7th ed.; eBook, 2011. [Google Scholar]
- Humphries, M.M.; McCann, K.S. Metabolic ecology. J. Anim. Ecol. 2014, 83, 7–19. [Google Scholar] [CrossRef]
- Sebens, K.P.; Sarà, G.; Carrington, E. Estimation of fitness from energetics and life-history data: An example using mussels. Ecol. Evol. 2018, 8, 5279–5290. [Google Scholar] [CrossRef]
- Fisher, R.A. The Genetical Theory of Natural Selection; Clarendon Press: Oxford, UK, 1930. [Google Scholar]
- Law, R. Optimal life histories under age-specific predation. Am. Nat. 1979, 114, 339–417. [Google Scholar] [CrossRef]
- Kutschera, U.; Niklas, K.J. Darwin-Wallace Demons: Survival of the fastest in populations of duckweeds and the evolutionary history of an enigmatic group of angiosperms. Plant Biol. 2015, 17, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Burton, T.; Killen, S.S.; Armstrong, J.D.; Metcalfe, N.B. What causes intraspecific variation in resting metabolic rate and what are its ecological consequences? Proc. R. Soc. B Biol. Sci. 2011, 278, 3465–3473. [Google Scholar] [CrossRef]
- Glazier, D.S. Is metabolic rate a universal ‘pacemaker’ for biological processes? Biol. Rev. 2015, 90, 377–407. [Google Scholar] [CrossRef]
- Pettersen, A.K.; Marshall, D.J.; White, C.R. Understanding variation in metabolic rate. J. Exp. Biol. 2018, 221, jeb166876. [Google Scholar] [CrossRef] [PubMed]
- Arnold, P.A.; Delean, S.; Cassey, P.; White, C.R. Meta-analysis reveals that resting metabolic rate is not consistently related to fitness and performance in animals. J. Comp. Physiol. B 2021, 191, 1097–1110. [Google Scholar] [CrossRef] [PubMed]
- Swanson, D.L.; McKechnie, A.E.; Vézina, F. How low can you go? An adaptive energetic framework for interpreting basal metabolic rate variation in endotherms. J. Comp. Physiol. B 2017, 187, 1039–1056. [Google Scholar] [CrossRef] [PubMed]
- De Magalhães, J.P.; Costa, J.; Church, G.M. An analysis of the relationship between metabolism, developmental schedules, and longevity using phylogenetic independent contrasts. J. Gerontol. A Biol. Sci. Med. Sci. 2007, 62, 149–160. [Google Scholar] [CrossRef] [PubMed]
- Stark, G.; Pincheira-Donoso, D.; Meiri, S. No evidence for the ‘rate-of-living’ theory across the tetrapod tree of life. Glob. Ecol. Biogeogr. 2020, 29, 857–884. [Google Scholar] [CrossRef]
- Glazier, D.S. The relevance of time in biological scaling. Biology 2023, 12, 1084. [Google Scholar] [CrossRef]
- Somjee, U. Positive allometry of sexually selected traits: Do metabolic maintenance costs play an important role? BioEssays 2021, 43, 2000183. [Google Scholar] [CrossRef] [PubMed]
- Somjee, U.; Powell, E.C.; Hickey, A.J.; Harrison, J.F.; Painting, C.J. Exaggerated sexually selected weapons maintained with disproportionately low metabolic costs in a single species with extreme size variation. Funct. Ecol. 2021, 35, 2282–2293. [Google Scholar] [CrossRef]
- Dinh, J.P. Large and exaggerated sexually selected weapons comprise high proportions of metabolically inexpensive exoskeleton. Biol. Lett. 2022, 18, 20210550. [Google Scholar] [CrossRef] [PubMed]
- Somjee, U.; Shankar, A.; Falk, J.J. Can sex-specific metabolic rates provide insight into patterns of metabolic scaling? Integr. Comp. Biol. 2022, 62, 1460–1470. [Google Scholar] [CrossRef]
- Sciubba, E. What did Lotka really say? A critical reassessment of the “maximum power principle”. Ecol. Model. 2011, 222, 1347–1353. [Google Scholar] [CrossRef]
- Karasov, W.H. Energetics, physiology and vertebrate ecology. Trends Ecol. Evol. 1986, 1, 101–104. [Google Scholar] [CrossRef] [PubMed]
- Weiner, J. Physiological limits to sustainable energy budgets in birds and mammals: Ecological implications. Trends Ecol. Evol. 1992, 7, 384–388. [Google Scholar] [CrossRef] [PubMed]
- Hammond, K.A.; Diamond, J. Limits to dietary nutrient and intestinal nutrients uptakes in lactating mice. Physiol. Zool. 1994, 67, 282–303. [Google Scholar] [CrossRef]
- Hammond, K.A.; Diamond, J. Maximal sustained energy budgets in humans and animals. Nature 1997, 386, 457–462. [Google Scholar] [CrossRef] [PubMed]
- Bacigalupe, L.D.; Bozinovic, F. Design, limitations and sustained metabolic rate: Lessons from small mammals. J. Exp. Biol. 2002, 205, 2963–2970. [Google Scholar] [CrossRef] [PubMed]
- McNab, B.K. The Physiological Ecology of Vertebrates: A View from Energetics; Cornell University Press: Ithaca, NY, USA, 2002. [Google Scholar]
- Naya, D.E.; Bacigalupe, L.D. Metabolic constraints to resource allocation. In Resource Allocation Theory Applied to Farm Animals; Rauw, W.M., Ed.; CAB International: Wallingford, UK, 2009; pp. 61–71. [Google Scholar]
- Piersma, T.; van Gils, J.A. The Flexible Phenotype: A Body-Centred Integration of Ecology, Physiology, and Behaviour; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Sadowska, J.; Gębczyński, A.K.; Konarzewski, M. Larger guts and faster growth in mice selected for high basal metabolic rate. Biol. Lett. 2021, 17, 20210244. [Google Scholar] [CrossRef] [PubMed]
- Ricklefs, R.E. Adaptation, constraint, and compromise in avian postnatal development. Biol. Rev. 1979, 54, 269–290. [Google Scholar] [CrossRef] [PubMed]
- Hammond, K.A.; Lloyd, K.K.; Diamond, J. Is mammary output capacity limiting to lactational performance in mice? J. Exp. Biol. 1996, 199, 337–349. [Google Scholar] [CrossRef]
- Ricklefs, R.E. Is rate of ontogenetic growth constrained by resource supply or tissue growth potential? A comment on West et al.’s model. Funct. Ecol. 2003, 17, 384–393. [Google Scholar] [CrossRef]
- Speakman, J.R.; Król, E. Limits to sustained energy intake. XIII. Recent progress and future perspectives. J. Exp. Biol. 2011, 214, 230–241. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yang, D.B.; Li, L.; Wang, L.P.; Chi, Q.S.; Hambly, C.; Wang, D.H.; Speakman, J.R. Limits to sustained energy intake. XIX. A test of the heat dissipation limitation hypothesis in Mongolian gerbils (Meriones unguiculatus). J. Exp. Biol. 2013, 216, 3358–3368. [Google Scholar] [CrossRef] [PubMed]
- Eklund, J.; Bradford, G.E. Longevity and lifetime body weight in mice selected for rapid growth. Nature 1977, 265, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Calow, P. The cost of reproduction–a physiological approach. Biol. Rev. 1979, 54, 23–40. [Google Scholar] [CrossRef] [PubMed]
- Calow, P.; Townsend, C.R. Resource utilization in growth. In Physiological Ecology; An Evolutionary Approach to Resource Use; Townsend, C.R., Calow, P., Eds.; Sinauer Associates: Sunderland, MA, USA, 1981; pp. 220–244. [Google Scholar]
- Hirshfield, M.F. An experimental analysis of reproductive effort and cost in the Japanese medaka, Oryzias latipes. Ecology 1980, 61, 282–292. [Google Scholar] [CrossRef]
- Gittleman, J.L.; Thompson, S.D. Energy allocation in mammalian reproduction. Am. Zool. 1988, 28, 863–875. [Google Scholar] [CrossRef]
- Roff, D.A. The Evolution of Life Histories: Theory and Analysis; Chapman and Hall: New York, NY, USA, 1992. [Google Scholar]
- Stearns, S.C. The Evolution of Life Histories; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Arendt, J.D. Adaptive intrinsic growth rates: An integration across taxa. Q. Rev. Biol. 1997, 72, 149–177. [Google Scholar] [CrossRef]
- Zera, A.J.; Harshman, L.G. The physiology of life history trade-offs in animals. Annu. Rev. Ecol. Syst. 2001, 32, 95–126. [Google Scholar] [CrossRef]
- Speakman, J.R. The physiological costs of reproduction in small mammals. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 375–398. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Resource allocation patterns. In Resource Allocation Theory Applied to Farm Animals; Rauw, W.M., Ed.; CAB International: Wallingford, UK, 2009; pp. 22–43. [Google Scholar]
- Dmitriew, C.M. The evolution of growth trajectories: What limits growth rate? Biol. Rev. 2011, 86, 97–116. [Google Scholar] [CrossRef] [PubMed]
- Kooijman, S.A.L.M.; Lika, K. Resource allocation to reproduction in animals. Biol. Rev. 2014, 89, 849–859. [Google Scholar] [CrossRef]
- Ng’oma, E.; Perinchery, A.M.; King, E.G. How to get the most bang for your buck: The evolution and physiology of nutrition-dependent resource allocation strategies. Proc. R. Soc. B Biol. Sci. 2017, 284, 20170445. [Google Scholar] [CrossRef] [PubMed]
- Pontzer, H.; McGrosky, A. Balancing growth, reproduction, maintenance, and activity in evolved energy economies. Curr. Biol. 2022, 32, R709–R719. [Google Scholar] [CrossRef] [PubMed]
- Król, E.; Speakman, J.R. Limits to sustained energy intake VI. Energetics of lactation in laboratory mice at thermoneutrality. J. Exp. Biol. 2003, 206, 4255–4266. [Google Scholar] [CrossRef] [PubMed]
- Król, E.; Murphy, M.; Speakman, J.R. Limits to sustained energy intake. X. Effects of fur removal on reproductive performance in laboratory mice. J. Exp. Biol. 2007, 210, 4233–4243. [Google Scholar] [CrossRef] [PubMed]
- Speakman, J.R.; Król, E. Maximal heat dissipation capacity and hyperthermia risk: Neglected key factors in the ecology of endotherms. J. Anim. Ecol. 2010, 79, 726–746. [Google Scholar] [CrossRef] [PubMed]
- Nord, A.; Nilsson, J.Å. Heat dissipation rate constrains reproductive investment in a wild bird. Funct. Ecol. 2019, 33, 250–259. [Google Scholar] [CrossRef]
- Sadowska, J.; Gȩbczyński, A.K.; Lewoc, M.; Konarzewski, M. Not that hot after all: No limits to heat dissipation in lactating mice selected for high or low BMR. J. Exp. Biol. 2019, 222, jeb204669. [Google Scholar] [CrossRef] [PubMed]
- Ohrnberger, S.A.; Hambly, C.; Speakman, J.R.; Valencak, T.G. Limits to sustained energy intake. XXXII. Hot again: Dorsal shaving increases energy intake and milk output in golden hamsters (Mesocricetus auratus). J. Exp. Biol. 2020, 223, jeb230383. [Google Scholar] [CrossRef] [PubMed]
- Case, T.J. On the evolution and adaptive significance of postnatal growth rates in the terrestrial vertebrates. Q. Rev. Biol. 1978, 53, 243–282. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Trickovic, B.; Kempes, C.P. Evolutionary scaling of maximum growth rate with organism size. Sci. Rep. 2022, 12, 22586. [Google Scholar] [CrossRef] [PubMed]
- Calow, P. Life Cycles: An Evolutionary Approach to the Physiology of Reproduction, Development and Aging; Chapman and Hall: London, UK, 1978. [Google Scholar]
- Leamy, L.; Atchley, W. Directional selection and developmental stability: Evidence from fluctuating asymmetry of morphometric characters in rats. Growth 1985, 49, 8–18. [Google Scholar] [PubMed]
- Speakman, J.R.; Selman, C.; McLaren, J.S.; Harper, E.J. Living fast, dying when? The link between aging and energetics. J. Nutr. 2002, 132, 1583S–1597S. [Google Scholar] [CrossRef] [PubMed]
- Nussey, D.H.; Pemberton, J.M.; Pilkington, J.G.; Blount, J.D. Life history correlates of oxidative damage in a free-living mammal population. Funct. Ecol. 2009, 23, 809–817. [Google Scholar] [CrossRef]
- Ricklefs, R.E. Embryo development and ageing in birds and mammals. Proc. R. Soc. Lond. B Biol. Sci. 2006, 273, 2077–2082. [Google Scholar] [CrossRef] [PubMed]
- Ricklefs, R.E. Life-history connections to rates of aging in terrestrial vertebrates. Proc. Natl. Acad. Sci. USA 2010, 107, 10314–10319. [Google Scholar] [CrossRef] [PubMed]
- Lack, D. The Natural Regulation of Animal Numbers; Oxford University Press: Oxford, UK, 1954. [Google Scholar]
- Glazier, D.S. Effects of food, genotype, and maternal size and age on offspring investment in Daphnia magna. Ecology 1992, 73, 910–926. [Google Scholar] [CrossRef]
- McNab, B.K. Food habits, energetics, and the population biology of mammals. Am. Nat. 1980, 116, 106–124. [Google Scholar] [CrossRef]
- Glazier, D.S. Is fatter fitter? Body storage and reproduction in ten populations of the freshwater amphipod Gammarus minus. Oecologia 2000, 122, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Speakman, J.R. The cost of living: Field metabolic rates of small mammals. Adv. Ecol. Res. 2000, 30, 177–297. [Google Scholar]
- MacArthur, R.H.; Wilson, E.O. The Theory of Island Biogeography; Princeton University Press: Princeton, NJ, USA, 1967. [Google Scholar]
- Pianka, E.R. On r-and K-selection. Am. Nat. 1970, 104, 592–597. [Google Scholar] [CrossRef]
- Southwood, T.R.E. Bionomic strategies and population parameters. In Theoretical Ecology: Principles and Applications, 2nd ed.; May, R.M., Ed.; Sinauer Associates: Sunderland, MA, USA, 1981; pp. 30–52. [Google Scholar]
- Winemiller, K.O.; Rose, K.A. Patterns of life-history diversification in North American fishes: Implications for population regulation. Can. J. Fish. Aquat. Sci. 1992, 49, 2196–2218. [Google Scholar] [CrossRef]
- Adler, G.H.; Levins, R. The island syndrome in rodent populations. Q. Rev. Biol. 1994, 69, 473–490. [Google Scholar] [CrossRef] [PubMed]
- Lima, S.L.; Dill, L.M. Behavioral decisions made under the risk of predation: A review and prospectus. Can. J. Zool. 1990, 68, 619–640. [Google Scholar] [CrossRef]
- Glazier, D.S.; Butler, E.M.; Lombardi, S.A.; Deptola, T.J.; Reese, A.J.; Satterthwaite, E.V. Ecological effects on metabolic scaling: Amphipod responses to fish predators in freshwater springs. Ecol. Monogr. 2011, 81, 599–618. [Google Scholar] [CrossRef]
- Glazier, D.S.; Borrelli, J.J.; Hoffman, C.L. Effects of fish predators on the mass-related energetics of a keystone freshwater crustacean. Biology 2020, 9, 40. [Google Scholar] [CrossRef] [PubMed]
- Forbes, M.R. Parasitism and host reproductive effort. Oikos 1993, 67, 444–450. [Google Scholar] [CrossRef]
- Sheldon, B.C.; Verhulst, S. Ecological immunology: Costly parasite defences and trade-offs in evolutionary ecology. Trends Ecol. Evol. 1996, 11, 317–321. [Google Scholar] [CrossRef] [PubMed]
- Rauw, W.M. Immune response from a resource allocation perspective. Front. Genet. 2012, 3, 267. [Google Scholar] [CrossRef] [PubMed]
- Schmid-Hempel, P. Evolutionary Parasitology: The Integrated Study of Infections, Immunology, Ecology, and Genetics; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- Hvas, M.; Bui, S. Energetic costs of ectoparasite infection in Atlantic salmon. J. Exp. Biol. 2022, 225, jeb243300. [Google Scholar] [CrossRef]
- Glazier, D.S. An Energetic and Ecological Basis for Different Reproductive Rates in Five Species of Peromyscus (mice). Ph.D. Dissertation, Cornell University, Ithaca, NY, USA, 1979. [Google Scholar]
- Glazier, D.S. The Energy Flow Principle and the Evolution of Different Litter Sizes in Five Species of Peromyscus Mice. In Proceedings of the Second International Congress of Systematic and Evolutionary Biology (Abstracts), University of British Columbia, Vancouver, BC, Canada, 17–24 July 1980; p. 212. [Google Scholar]
- Cody, M.L. A general theory of clutch size. Evolution 1966, 20, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Trade-offs between reproductive and somatic (storage) investments in animals: A comparative test of the Van Noordwijk and De Jong model. Evol. Ecol. 1999, 13, 539–555. [Google Scholar] [CrossRef]
- Brown, M.T. The maximum power principle. In Elgar Encyclopedia of Ecological Economics; Rosa, E.P., Ramos-Martín, J., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2023; pp. 363–367. [Google Scholar]
- Kozłowski, J. Energetic definition of fitness? Yes, but not that one. Am. Nat. 1996, 147, 1087–1091. [Google Scholar] [CrossRef]
- Kozłowski, J. Theoretical and empirical status of Brown, Marquet and Taper’s model of species-size distribution. Funct. Ecol. 2002, 16, 540–542. [Google Scholar] [CrossRef]
- Jones, K.E.; Purvis, A. An optimum body size for mammals? Comparative evidence from bats. Funct. Ecol. 1997, 11, 751–756. [Google Scholar] [CrossRef]
- Perrin, N. On body size, and energy and fitness. Funct. Ecol. 1998, 12, 500–502. [Google Scholar] [CrossRef]
- Symonds, M.R.E. Insectivore life histories: Further evidence against an optimum body size for mammals. Funct. Ecol. 1999, 13, 508–513. [Google Scholar] [CrossRef]
- Bokma, F. Evolution of body size: Limitations of an energetic definition of fitness. Funct. Ecol. 2001, 15, 696–699. [Google Scholar] [CrossRef]
- Glazier, D.S. Does death drive the scaling of life? In Scaling in Biology; Enquist, B.J., Kempes, C.P., O’Connor, M.I., Eds.; Santa Fe Institute Press: Santa Fe, NM, USA, 2024; in review. [Google Scholar]
- Peterson, I.; Wroblewski, J.S. Mortality rate of fishes in the pelagic ecosystem. Can. J. Fish. Aquat. Sci. 1984, 41, 1117–1120. [Google Scholar] [CrossRef]
- McGurk, M.D. Natural mortality of marine pelagic fish eggs and larvae: Role of spatial patchiness. Mar. Ecol. Prog. Ser. 1986, 34, 227–242. [Google Scholar] [CrossRef]
- Hirst, A.G.; Kiørboe, T. Mortality of marine planktonic copepods: Global rates and patterns. Mar. Ecol. Progr. Ser. 2002, 230, 195–209. [Google Scholar] [CrossRef]
- McCoy, M.W.; Gillooly, J.F. Predicting natural mortality rates of plants and animals. Ecol Lett. 2008, 11, 710–716. [Google Scholar] [CrossRef]
- Ricklefs, R.E. Clutch size in birds: Outcome of opposing predator and prey adaptations. Science 1970, 168, 599–600. [Google Scholar] [CrossRef] [PubMed]
- Ricklefs, R.E.; Cox, G.W. Taxon cycles in the West Indian avifauna. Am. Nat. 1972, 106, 195–219. [Google Scholar] [CrossRef]
- Ricklefs, R.E.; Cox, G.W. Stage of taxon cycle, habitat distribution, and population density in the avifauna of the West Indies. Am. Nat. 1978, 112, 875–895. [Google Scholar] [CrossRef]
- Glazier, D.S. Ecological shifts and the evolution of geographically restricted species of North American Peromyscus (mice). J. Biogeogr. 1980, 7, 63–83. [Google Scholar] [CrossRef]
- Ricklefs, R.E. A biogeographical perspective on ecological systems: Some personal reflections. J. Biogeogr. 2011, 38, 2045–2056. [Google Scholar] [CrossRef]
- Wieser, W. A new look at energy conversion in ectothermic and endothermic animals. Oecologia 1985, 66, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Pianka, E.R. Natural selection of optimal reproductive tactics. Am. Zool. 1976, 16, 775–784. [Google Scholar] [CrossRef]
- Williams, G.C. Natural Selection: Domains, Levels, and Challenges; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Martin, C. Waste not, want not. Curr. Biol. 2022, 32, R589–R590. [Google Scholar] [CrossRef] [PubMed]
- Slobodkin, L.B. On the inconstancy of ecological efficiency and the form of ecological theories. Trans. Conn. Acad. Sci. 1972, 44, 291–305. [Google Scholar]
- Parry, G.D. The influence of the cost of growth on ectotherm metabolism. J. Theor. Biol. 1983, 101, 453–477. [Google Scholar] [CrossRef] [PubMed]
- Clarke, A. Energy flow in growth and production. Trends Ecol. Evol. 2019, 34, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Welch, H.E. Relationships between assimilation efficiencies and growth efficiencies for aquatic consumers. Ecology 1968, 49, 755–759. [Google Scholar] [CrossRef]
- Ricklefs, R.E.; Miller, G.L. Ecology; Freeman: New York, NY, USA, 2000. [Google Scholar]
- Williams, G.C. Adaptation and Natural Selection: A Critique of Some Current Evolutionary Thought; Princeton University Press: Princeton, NJ, USA, 1966. [Google Scholar]
- Campbell, M. Adaptation and fitness. Stud. Hist. Philos. Sci. A 1983, 14, 59–65. [Google Scholar] [CrossRef]
- Michod, R.E. On fitness and adaptedness and their role in evolutionary explanation. J. Hist. Biol. 1986, 19, 289–302. [Google Scholar] [CrossRef] [PubMed]
- Blanquart, F.; Kaltz, O.; Nuismer, S.L.; Gandon, S. A practical guide to measuring local adaptation. Ecol. Lett. 2013, 16, 1195–1205. [Google Scholar] [CrossRef] [PubMed]
- Thoday, J.M. Components of fitness. Symp. Soc. Exp. Biol. 1953, 7, 95–113. [Google Scholar]
- Kim, K.; Lasker, H.R. Allometry of resource capture in colonial cnidarians and constraints on modular growth. Funct. Ecol. 1998, 12, 646–654. [Google Scholar] [CrossRef]
- Gnaiger, E. Optimum efficiencies of energy transformation in anoxic metabolism. The strategies of power and economy. In Evolutionary Physiological Ecology; Calow, P., Ed.; Cambridge University Press: Cambridge, UK, 1987; pp. 7–36. [Google Scholar]
- Vermeij, G.J. Nature: An Economic History; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Szarski, H. Cell size and the concept of wasteful and frugal evolutionary strategies. J. Theor. Biol. 1983, 105, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Kozłowski, J.; Konarzewski, M.; Czarnoleski, M. Coevolution of body size and metabolic rate in vertebrates: A life-history perspective. Biol. Rev. 2020, 95, 1393–1417. [Google Scholar] [CrossRef]
- Hall, S.R.; Becker, C.R.; Duffy, M.A.; Cáceres, C.E. A power–efficiency trade-off in resource use alters epidemiological relationships. Ecology 2012, 93, 645–656. [Google Scholar] [CrossRef] [PubMed]
- MacArthur, R.H.; Pianka, E.R. On optimal use of patchy environment. Am. Nat. 1966, 100, 603–609. [Google Scholar] [CrossRef]
- MacArthur, R.H. Geographical Ecology: Patterns in the Distribution of Species; Harper & Row: New York, NY, USA, 1972. [Google Scholar]
- Futuyma, D.J.; Moreno, G. The evolution of ecological specialization. Annu. Rev. Ecol. Syst. 1988, 19, 207–233. [Google Scholar] [CrossRef]
- Wilson, D.S.; Yoshimura, J. On the coexistence of specialists and generalists. Am. Nat. 1994, 144, 692–707. [Google Scholar] [CrossRef]
- Caley, M.J.; Munday, P.L. Growth trades off with habitat specialization. Proc. R. Soc. B Biol. Sci. 2003, 270 (Suppl. 2), S175–S177. [Google Scholar] [CrossRef]
- Verberk, W.C.; Van Der Velde, G.; Esselink, H. Explaining abundance–occupancy relationships in specialists and generalists: A case study on aquatic macroinvertebrates in standing waters. J. Anim. Ecol. 2010, 79, 589–601. [Google Scholar] [CrossRef]
- Sudta, C.; Salcido, D.M.; Forister, M.L.; Walla, T.R.; Villamarín-Cortez, S.; Dyer, L.A. Jack-of-all-trades paradigm meets long-term data: Generalist herbivores are more widespread and locally less abundant. Ecol. Lett. 2022, 25, 948–957. [Google Scholar] [CrossRef]
- Remold, S. Understanding specialism when the jack of all trades can be the master of all. Proc. R. Soc. B Biol. Sci. 2012, 279, 4861–4869. [Google Scholar] [CrossRef] [PubMed]
- Sexton, J.P.; Montiel, J.; Shay, J.E.; Stephens, M.R.; Slatyer, R.A. Evolution of ecological niche breadth. Annu. Rev. Ecol. Syst. 2017, 48, 183–206. [Google Scholar] [CrossRef]
- Strickler, K. Specialization and foraging efficiency of solitary bees. Ecology 1979, 60, 998–1009. [Google Scholar] [CrossRef]
- Yamada, S.B.; Boulding, E.G. Claw morphology, prey size selection and foraging efficiency in generalist and specialist shell-breaking crabs. J. Exp. Mar. Biol. Ecol. 1998, 220, 191–211. [Google Scholar] [CrossRef]
- Michálek, O.; Petráková, L.; Pekár, S. Capture efficiency and trophic adaptations of a specialist and generalist predator: A comparison. Ecol. Evol. 2017, 7, 2756–2766. [Google Scholar] [CrossRef] [PubMed]
- García, L.F.; Viera, C.; Pekár, S. Comparison of the capture efficiency, prey processing, and nutrient extraction in a generalist and a specialist spider predator. Sci. Nat. 2018, 105, 30. [Google Scholar] [CrossRef] [PubMed]
- Pompozzi, G.; García, L.F.; Petráková, L.; Pekár, S. Distinct feeding strategies of generalist and specialist spiders. Ecol. Entomol. 2019, 44, 129–139. [Google Scholar] [CrossRef]
- Bernays, E.A.; Funk, D.J. Specialists make faster decisions than generalists: Experiments with aphids. Proc. R. Soc. B Biol. Sci. 1999, 266, 151–156. [Google Scholar] [CrossRef]
- Bernays, E.A.; Singer, M.S.; Rodrigues, D. Foraging in nature: Foraging efficiency and attentiveness in caterpillars with different diet breadths. Ecol. Entomol. 2004, 29, 389–397. [Google Scholar] [CrossRef]
- Egan, S.P.; Funk, D.J. Individual advantages to ecological specialization: Insights on cognitive constraints from three conspecific taxa. Proc. R. Soc. B Biol. Sci. 2006, 273, 843–848. [Google Scholar] [CrossRef] [PubMed]
- Huckins, C.J.F. Functional linkages among morphology, feeding performance, diet and competitive ability in molluscivorous sunfish. Ecology 1997, 78, 2401–2414. [Google Scholar] [CrossRef]
- Jones, M.; Mandelik, Y.; Dayan, T. Coexistence of temporally partitioned spiny mice: Roles of habitat structure and foraging behavior. Ecology 2001, 82, 2164–2176. [Google Scholar] [CrossRef]
- Britt, E.; Bennet, A.F. The energetic advantages of slug specialization in Garter snakes (Genus Thamnophis). Physiol. Biochem. Zool. 2008, 81, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Terraube, J.; Arroyo, B.; Madders, M.; Mougeot, F. Diet specialisation and foraging efficiency under fluctuating vole abundance: A comparison between generalist and specialist avian predators. Oikos 2011, 120, 234–244. [Google Scholar] [CrossRef]
- Korpimäki, E.; Hongisto, K.; Masoero, G.; Laaksonen, T. The difference between generalist and specialist: The effects of wide fluctuations in main food abundance on numbers and reproduction of two co-existing predators. J. Avian Biol. 2020, 51, e02508. [Google Scholar] [CrossRef]
- Mykrä, H.; Heino, J. Decreased habitat specialization in macroinvertebrate assemblages in anthropogenically disturbed streams. Ecol. Complex. 2017, 31, 181–188. [Google Scholar] [CrossRef]
- Brown, J.H. On the relationship between abundance and distribution of species. Am. Nat. 1984, 124, 255–279. [Google Scholar] [CrossRef]
- Novosolov, M.; Rodda, G.H.; North, A.C.; Butchart, S.H.; Tallowin, O.J.; Gainsbury, A.M.; Meiri, S. Population density–range size relationship revisited. Glob. Ecol. Biogeogr. 2017, 26, 1088–1097. [Google Scholar] [CrossRef]
- Sporbert, M.; Keil, P.; Seidler, G.; Bruelheide, H.; Jandt, U.; Aćić, S.; Biurrun, I.; Campos, J.A.; Čarni, A.; Chytrý, M.; et al. Testing macroecological abundance patterns: The relationship between local abundance and range size, range position and climatic suitability among European vascular plants. J. Biogeogr. 2020, 47, 2210–2222. [Google Scholar] [CrossRef]
- Ten Caten, C.; Holian, L.; Dallas, T. Weak but consistent abundance–occupancy relationships across taxa, space and time. Glob. Ecol. Biogeogr. 2022, 31, 968–977. [Google Scholar] [CrossRef]
- Roughgarden, J. Density-dependent natural selection. Ecology 1971, 52, 453–468. [Google Scholar] [CrossRef]
- Mueller, L.D. Density-dependent natural selection does not increase efficiency. Evol. Ecol. 1990, 4, 290–297. [Google Scholar] [CrossRef]
- Joshi, A.; Mueller, L.D. Density-dependent natural selection in Drosophila: Trade-offs between larval food acquisition and utilization. Evol. Ecol. 1996, 10, 463–474. [Google Scholar] [CrossRef]
- Reznick, D.; Bryant, M.J.; Bashey, F. r-and K-selection revisited: The role of population regulation in life-history evolution. Ecology 2002, 83, 1509–1520. [Google Scholar] [CrossRef]
- Hamilton, W.J., III. Reproductive adaptations of the red tree mouse. J. Mamm. 1962, 43, 486–504. [Google Scholar] [CrossRef]
- Vaughan, T.A.; Czaplewski, N.J. Reproduction in Stephens’ woodrat: The wages of folivory. J. Mamm. 1985, 66, 429–443. [Google Scholar] [CrossRef]
- Glazier, D.S. Temporal variability of abundance and the distribution of species. Oikos 1986, 47, 309–314. [Google Scholar] [CrossRef]
- Ebenhard, T. Colonization in metapopulations: A review of theory and observations. Biol. J. Linn. Soc. 1991, 42, 105–121. [Google Scholar] [CrossRef]
- Kitahara, M.; Fujii, K. Biodiversity and community structure of temperate butterfly species within a gradient of human disturbance: An analysis based on the concept of generalist vs. specialist strategies. Popul. Ecol. 1994, 36, 187–199. [Google Scholar] [CrossRef]
- Griffiths, D. Pattern and process in the ecological biogeography of European freshwater fish. J. Anim. Ecol. 2006, 75, 734–751. [Google Scholar] [CrossRef] [PubMed]
- Devictor, V.; Julliard, R.; Jiguet, F. Distribution of specialist and generalist species along spatial gradients of habitat disturbance and fragmentation. Oikos 2008, 117, 507–514. [Google Scholar] [CrossRef]
- Börschig, C.; Klein, A.M.; von Wehrden, H.; Krauss, J. Traits of butterfly communities change from specialist to generalist characteristics with increasing land-use intensity. Basic Appl. Ecol. 2013, 14, 547–554. [Google Scholar] [CrossRef]
- Carscadden, K.A.; Emery, N.C.; Arnillas, C.A.; Cadotte, M.W.; Afkhami, M.E.; Gravel, D.; Livingstone, S.W.; Wiens, J.J. Niche breadth: Causes and consequences for ecology, evolution, and conservation. Q. Rev. Biol. 2020, 95, 179–214. [Google Scholar] [CrossRef]
- Chen, Y.J.; Leung, P.M.; Wood, J.L.; Bay, S.K.; Hugenholtz, P.; Kessler, A.J.; Shelley, G.; Waite, D.W.; Franks, A.E.; Cook, P.L.; et al. Metabolic flexibility allows bacterial habitat generalists to become dominant in a frequently disturbed ecosystem. ISME J. 2021, 15, 2986–3004. [Google Scholar] [CrossRef] [PubMed]
- Stuart-Smith, R.D.; Mellin, C.; Bates, A.E.; Edgar, G.J. Habitat loss and range shifts contribute to ecological generalization among reef fishes. Nat. Ecol. Evol. 2021, 5, 656–662. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.H.; Gibson, L.; Amir, Z.; Chanthorn, W.; Ahmad, A.H.; Jansen, P.A.; Mendes, C.P.; Onuma, M.; Peres, C.A.; Luskin, M.S. The rise of hyperabundant native generalists threatens both humans and nature. Biol. Rev. 2023, 98, 1829–1844. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, D.P.; Simberloff, D. Ecological specialization and susceptibility to disturbance: Conjectures and refutations. Am. Nat. 2002, 159, 606–623. [Google Scholar] [CrossRef] [PubMed]
- Jaenike, J. Resource predictability and niche breadth in the Drosophila quinaria species group. Evolution 1978, 32, 676–678. [Google Scholar] [CrossRef] [PubMed]
- Lacy, R.C. Predictability, toxicity, and trophic niche breadth in fungus-feeding Drosophilidae (Diptera). Ecol. Entomol. 1984, 9, 43–54. [Google Scholar] [CrossRef]
- Jaenike, J. Host specialization in phytophagous insects. Annu. Rev. Ecol. Syst. 1990, 21, 243–273. [Google Scholar] [CrossRef]
- Thompson, J.N. The Coevolutionary Process; University of Chicago Press: Chicago, IL, USA, 1994. [Google Scholar]
- Pekár, S.; Toft, S. Trophic specialisation in a predatory group: The case of prey-specialised spiders (Araneae). Biol. Rev. 2015, 90, 744–761. [Google Scholar] [CrossRef] [PubMed]
- Carroll, S.B. The Serengeti Rules: The Quest to Discover How Life Works and Why It Matters; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Sinclair, A.R.E.; Mduma, S.; Brashares, J.S. Patterns of predation in a diverse predator–prey system. Nature 2003, 425, 288–290. [Google Scholar] [CrossRef]
- Hopcraft, J.G.C.; Olff, H.; Sinclair, A.R.E. Herbivores, resources and risks: Alternating regulation along primary environmental gradients in savannas. Trends Ecol. Evol. 2010, 25, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Fenchel, T. Intrinsic rate of natural increase: The relationship with body size. Oecologia 1974, 14, 317–326. [Google Scholar] [CrossRef] [PubMed]
- Blueweiss, L.; Fox, H.; Kudzma, V.; Nakashima, D.; Peters, R.; Sams, S. Relationships between body size and some life history parameters. Oecologia 1978, 37, 257–272. [Google Scholar] [CrossRef] [PubMed]
- Charnov, E.L. Life History Invariants: Some Explorations of Symmetry in Evolutionary Ecology; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Finlay, B.J.; Esteban, G.F.; Olmo, J.L.; Tyler, P.A. Global distribution of free-living microbial species. Ecography 1999, 22, 138–144. [Google Scholar] [CrossRef]
- Finlay, B.J. Global dispersal of free-living microbial eukaryote species. Science 2002, 296, 1061–1063. [Google Scholar] [CrossRef] [PubMed]
- Finlay, B.J.; Fenchel, T. Cosmopolitan metapopulations of free-living eukaryotes. Protist 2004, 155, 237–244. [Google Scholar] [CrossRef] [PubMed]
- Fenchel, T.; Finlay, B.J. The ubiquity of small species: Patterns of local and global diversity. Bioscience 2004, 54, 777–784. [Google Scholar] [CrossRef]
- Fontaneto, D. Long-distance passive dispersal in microscopic aquatic animals. Mov. Ecol. 2019, 7, 10. [Google Scholar] [CrossRef] [PubMed]
- Azovsky, A.I.; Chertoprud, E.S.; Garlitska, L.A.; Mazei, Y.A.; Tikhonenkov, D.V. Does size really matter in biogeography? Patterns and drivers of global distribution of marine micro-and meiofauna. J. Biogeogr. 2020, 47, 1180–1192. [Google Scholar] [CrossRef]
- Ptatscheck, C.; Traunspurger, W. The ability to get everywhere: Dispersal modes of free-living, aquatic nematodes. Hydrobiologia 2020, 847, 3519–3547. [Google Scholar] [CrossRef]
- Fontaneto, D. (Ed.) Biogeography of Microscopic Organisms: Is Everything Small Everywhere? Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Fontaneto, D.; Hortal, J. At least some protist species are not ubiquitous. Mol. Ecol. 2013, 22, 5053–5055. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fenchel, T. Biogeography for bacteria. Science 2003, 301, 925–926. [Google Scholar] [CrossRef] [PubMed]
- Foissner, W. Biogeography and dispersal of micro-organisms: A review emphasizing protists. Acta Protozool. 2006, 45, 111–136. [Google Scholar]
- Martiny, J.B.H.; Bohannan, B.J.; Brown, J.H.; Colwell, R.K.; Fuhrman, J.A.; Green, J.L.; Horner-Devine, M.C.; Kane, M.; Krumins, J.A.; Kuske, C.R.; et al. Microbial biogeography: Putting microorganisms on the map. Nat. Rev. Microbiol. 2006, 4, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Fenchel, T.; Finlay, B.J.; Esteban, G.F. Cosmopolitan metapopulations? Protist 2019, 170, 314–318. [Google Scholar] [CrossRef] [PubMed]
- Schmalhausen, I.I. Factors of Evolution: The Theory of Stabilizing Selection; Blakiston Company: Philadelphia, PA, USA, 1949. [Google Scholar]
- Bonner, J.T. Randomness in Evolution; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Schramski, J.R.; Gattie, D.K.; Brown, J.H. Human domination of the biosphere: Rapid discharge of the earth-space battery foretells the future of humankind. Proc. Natl. Acad. Sci. USA 2015, 112, 9511–9517. [Google Scholar] [CrossRef] [PubMed]
- Desmond, H.; Ramsey, G. (Eds.) Human Success: Evolutionary Origins and Human Implications; Oxford University Press: Oxford, UK, 2023. [Google Scholar]
- Konno, K. Extremely high relative growth rate makes the cabbage white, Pieris rapae, a global pest with highly abundant and migratory nature. Sci. Rep. 2023, 13, 9697. [Google Scholar] [CrossRef] [PubMed]
- Thompson, K.; Gaston, K.J.; Band, S.R. Range size, dispersal and niche breadth in the herbaceous flora of central England. J. Ecol. 1999, 87, 150–155. [Google Scholar] [CrossRef]
- Morin, X.; Lechowicz, M.J. Niche breadth and range area in North American trees. Ecography 2013, 36, 300–312. [Google Scholar] [CrossRef]
- Slatyer, R.A.; Hirst, M.; Sexton, J.P. Niche breadth predicts geographical range size: A general ecological pattern. Ecol. Lett. 2013, 16, 1104–1114. [Google Scholar] [CrossRef] [PubMed]
- Sheth, S.N.; Angert, A.L. The evolution of environmental tolerance and range size: A comparison of geographically restricted and widespread Mimulus. Evolution 2014, 68, 2917–2931. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Groen, T.A.; Wang, T.; Skidmore, A.K.; Huang, J.; Ma, K. Climatic niche breadth can explain variation in geographical range size of alpine and subalpine plants. Int. J. Geogr. Inf. Sci. 2017, 31, 190–212. [Google Scholar] [CrossRef]
- Kambach, S.; Lenoir, J.; Decocq, G.; Welk, E.; Seidler, G.; Dullinger, S.; Gégout, J.C.; Guisan, A.; Pauli, H.; Svenning, J.C.; et al. Of niches and distributions: Range size increases with niche breadth both globally and regionally but regional estimates poorly relate to global estimates. Ecography 2019, 42, 467–477. [Google Scholar] [CrossRef]
- Sheth, S.N.; Morueta-Holme, N.; Angert, A.L. Determinants of geographic range size in plants. New Phytol. 2020, 226, 650–665. [Google Scholar] [CrossRef] [PubMed]
- Le Feuvre, M.C.; Dempster, T.; Shelley, J.J.; Davis, A.M.; Swearer, S.E. Range restriction leads to narrower ecological niches and greater extinction risk in Australian freshwater fish. Biodivers. Conserv. 2021, 30, 2955–2976. [Google Scholar] [CrossRef]
- Olsen, K.; Svenning, J.C.; Balslev, H. Niche breadth predicts geographical range size and northern range shift in European dragonfly species (Odonata). Diversity 2022, 14, 719. [Google Scholar] [CrossRef]
- Evans, A.; Jacquemyn, H. Range size and niche breadth as predictors of climate-induced habitat change in Epipactis (Orchidaceae). Front. Ecol. Evol. 2022, 10, 894616. [Google Scholar] [CrossRef]
- Jacquemyn, H.; De Coensel, B.; Evans, A.; Wang, D.; Merckx, V.S. The relationship between phylogeny, range size, niche breadth and niche overlap in European orchids (Orchidaceae). J. Biogeogr. 2024, 51, 409–421. [Google Scholar] [CrossRef]
- Gaston, K.J.; Spicer, J.I. The relationship between range size and niche breadth: A test using five species of Gammarus (Amphipoda). Glob. Ecol. Biogeogr. 2001, 10, 179–188. [Google Scholar] [CrossRef]
- Gaston, K.J. The Structure and Dynamics of Geographic Ranges; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Cardillo, M.; Dinnage, R.; McAlister, W. The relationship between environmental niche breadth and geographic range size across plant species. J. Biogeogr. 2019, 46, 97–109. [Google Scholar] [CrossRef]
- Cai, Q.; Welk, E.; Ji, C.; Fang, W.; Sabatini, F.M.; Zhu, J.; Zhu, J.; Tang, Z.; Attorre, F.; Campos, J.A.; et al. The relationship between niche breadth and range size of beech (Fagus) species worldwide. J. Biogeogr. 2021, 48, 1240–1253. [Google Scholar] [CrossRef]
- DeLong, J.P. The maximum power principle predicts the outcomes of two-species competition experiments. Oikos 2008, 117, 1329–1336. [Google Scholar] [CrossRef]
- Liow, L.H. Does versatility as measured by geographic range, bathymetric range and morphological variability contribute to taxon longevity? Glob. Ecol. Biogeogr. 2007, 16, 117–128. [Google Scholar] [CrossRef]
- Payne, J.L.; Finnegan, S. The effect of geographic range on extinction risk during background and mass extinction. Proc. Natl. Acad. Sci. USA 2007, 104, 10506–10511. [Google Scholar] [PubMed]
- Powell, M.G. Geographic range and genus longevity of late Paleozoic brachiopods. Paleobiology 2007, 33, 530–546. [Google Scholar] [CrossRef]
- Heim, N.A.; Peters, S.E. Regional environmental breadth predicts geographic range and longevity in fossil marine genera. PLoS ONE 2011, 6, e18946. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, M.J. How species longevity, intraspecific morphological variation, and geographic range size are related: A comparison using Late Cambrian trilobites. Evolution 2011, 65, 3253–3273. [Google Scholar] [CrossRef]
- Newsome, T.M.; Wolf, C.; Nimmo, D.G.; Kopf, R.K.; Ritchie, E.G.; Smith, F.A.; Ripple, W.J. Constraints on vertebrate range size predict extinction risk. Glob. Ecol. Biogeogr. 2020, 29, 76–86. [Google Scholar] [CrossRef]
- Glazier, D.S. Toward a predictive theory of speciation: The ecology of isolate selection. J. Theor. Biol. 1987, 126, 323–333. [Google Scholar] [CrossRef]
- Wilson, E.O. The nature of the taxon cycle in the Melanesian ant fauna. Am. Nat. 1961, 95, 169–193. [Google Scholar]
- Economo, E.P.; Sarnat, E.M.; Janda, M.; Clouse, R.; Klimov, P.B.; Fischer, G.; Blanchard, B.D.; Ramirez, L.N.; Andersen, A.N.; Berman, M.; et al. Breaking out of biogeographical modules: Range expansion and taxon cycles in the hyperdiverse ant genus Pheidole. J. Biogeogr. 2015, 42, 2289–2301. [Google Scholar] [CrossRef] [PubMed]
- Sriswasdi, S.; Yang, C.C.; Iwasaki, W. Generalist species drive microbial dispersion and evolution. Nat. Commun. 2017, 8, 1162. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S.; Eckert, S.E. Competitive ability, body size and geographical range size in small mammals. J. Biogeogr. 2002, 29, 81–92. [Google Scholar] [CrossRef]
- Raia, P.; Carotenuto, F.; Passaro, F.; Fulgione, D.; Fortelius, M. Ecological specialization in fossil mammals explains Cope’s rule. Am. Nat. 2012, 179, 328–337. [Google Scholar] [CrossRef]
- Carleton, M.D. Systematics and evolution. In Advances in the Study of Peromyscus; Kirkland, G.L., Jr., Layne, J.N., Eds.; Texas Tech University Press: Lubbock, TX, USA, 1989; pp. 7–141. [Google Scholar]
- Miller, J.R.; Engstrom, M.D. The relationships of major lineages within Peromyscine rodents: A molecular phylogenetic hypothesis and systematic reappraisal. J. Mammal. 2008, 89, 1279–1295. [Google Scholar] [CrossRef]
- Platt, R.N.; Amman, B.R.; Keith, M.S.; Thompson, C.W.; Bradley, R.D. What is Peromyscus? Evidence from nuclear and mitochondrial DNA sequences suggests the need for a new classification. J. Mammal. 2015, 96, 708–719. [Google Scholar] [CrossRef] [PubMed]
- McLean, B.S.; Barve, N.; Flenniken, J.; Guralnick, R.P. Evolution of litter size in North America’s most common small mammal: An informatics-based approach. J. Mammal. 2019, 100, 365–381. [Google Scholar] [CrossRef]
- Boria, R.A.; Blois, J.L. Phylogeography within the Peromyscus maniculatus species group: Understanding past distribution of genetic diversity and areas of refugia in western North America. Mol. Phylogenet. Evol. 2023, 180, 107701. [Google Scholar] [CrossRef]
- Baker, R.H. Habitats and distribution. In Biology of Peromyscus (Rodentia); King, J.A., Ed.; Special Publication No. 2; American Society of Mammalogists: Fort Collins, CO, USA, 1968; pp. 98–126. [Google Scholar]
- Modi, W.S. Reproductive tactics among deer mice of the genus Peromyscus. Can. J. Zool. 1984, 62, 2576–2581. [Google Scholar] [CrossRef]
- Martin, L.B.; Weil, Z.M.; Nelson, R.J. Immune defense and reproductive pace of life in Peromyscus mice. Ecology 2007, 88, 2516–2528. [Google Scholar] [CrossRef]
- Wilsterman, K.; Cunningham, K. Evolution in reproductive tempo and investment across the Peromyscus radiation. J. Exp. Zool. A Ecol. Integr. Physiol. 2023, 339, 13–27. [Google Scholar] [CrossRef]
- Glazier, D.S. Energetics of litter size in five species of Peromyscus with generalizations for other mammals. J. Mammal. 1985, 66, 629–642. [Google Scholar] [CrossRef]
- Glazier, D.S. Relationship between metabolic rate and energy expenditure for lactation in Peromyscus. Comp. Biochem. Physiol. A Physiol. 1985, 80, 587–590. [Google Scholar] [CrossRef]
- MacMillen, R.E.; Garland, T., Jr. Adaptive physiology. In Advances in the Study of Peromyscus; Kirkland, G.L., Jr., Layne, J.N., Eds.; Texas Tech University Press: Lubbock, TX, USA, 1989; pp. 143–168. [Google Scholar]
- Mueller, P.; Diamond, J. Metabolic rate and environmental productivity: Well-provisioned animals evolved to run and idle fast. Proc. Natl. Acad. Sci. USA 2001, 98, 12550–12554. [Google Scholar] [CrossRef] [PubMed]
- McCabe, T.T.; Blanchard, B.D. Three Species of Peromyscus; Rood Associates: Santa Barbara, CA, USA, 1950. [Google Scholar]
- Chew, R.M.; Chew, A.E. Energy relationships of the mammals of a desert shrub (Larrea tridentata) community. Ecol. Monogr. 1970, 40, 2–21. [Google Scholar] [CrossRef]
- Sheppe, W. Systematic and ecological relations of Peromyscus oreas and P. maniculatus. Proc. Am. Philos. Soc. 1961, 105, 421–446. [Google Scholar]
- McCarley, H. Distributional relationships of sympatric populations of Peromyscus leucopus and P. gossypinus. Ecology 1963, 44, 784–788. [Google Scholar] [CrossRef]
- Bronson, F.H. Mammalian reproduction: An ecological perspective. Biol. Reprod. 1985, 32, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Mugaas, J.N.; Seidensticker, J.; Mahlke-Johnson, K.P. Metabolic adaptation to climate and distribution of the raccoon Procyon lotor and other Procyonidae. Smithson. Contr. Zool. 1993, 542, 1–34. [Google Scholar] [CrossRef]
- French, A.R. Physiological ecology of the Heteromyidae: Economics of energy and water utilization. In Biology of the Heteromyidae; Genoways, H.H., Brown, J.H., Eds.; American Society of Mammalogists: Fort Collins, CO, USA, 1993; pp. 509–538. [Google Scholar]
- Wunder, B.A. Energetics and thermoregulation. In Biology of New World Microtus; Tamarin, R.H., Ed.; American Society of Mammalogists: Fort Collins, CO, USA, 1985; pp. 812–844. [Google Scholar]
- Sadowska, J.; Gębczyński, A.K.; Konarzewski, M. Basal metabolic rate is positively correlated with parental investment in laboratory mice. Proc. R. Soc. B Biol. Sci. 2013, 280, 20122576. [Google Scholar] [CrossRef] [PubMed]
- Sadowska, J.; Gębczyński, A.K.; Paszko, K.; Konarzewski, M. Milk output and composition in mice divergently selected for basal metabolic rate. J. Exp. Biol. 2015, 218, 249–254. [Google Scholar] [PubMed]
- Agosta, S.J.; Bernardo, J.; Ceballos, G.; Steele, M.A. A macrophysiological analysis of energetic constraints on geographic range size in mammals. PLoS ONE 2013, 8, e72731. [Google Scholar] [CrossRef] [PubMed]
- Hayes, J.P.; Feldman, C.R.; Araújo, M.B. Mass-independent maximal metabolic rate predicts geographic range size of placental mammals. Funct. Ecol. 2018, 32, 1194–1202. [Google Scholar] [CrossRef]
- Boratyński, Z. Energetic constraints on mammalian distribution areas. J. Anim. Ecol. 2021, 90, 1854–1863. [Google Scholar] [CrossRef] [PubMed]
- Van der Veken, S.; Bellemare, J.; Verheyen, K.; Hermy, M. Life-history traits are correlated with geographical distribution patterns of western European forest herb species. J. Biogeogr. 2007, 34, 1723–1735. [Google Scholar] [CrossRef]
- Duncan, R.P.; Blackburn, T.M.; Veltman, C.J. Determinants of geographical range sizes: A test using introduced New Zealand birds. J. Anim. Ecol. 1999, 68, 963–975. [Google Scholar] [CrossRef]
- Carter, B.E.; Alroy, J. The macroecology of community energy use in terrestrial vertebrates. Front. Biogeogr. 2022, 14, e56553. [Google Scholar] [CrossRef]
- Gillman, L.N.; Wright, S.D.; Cusens, J.; McBride, P.D.; Malhi, Y.; Whittaker, R.J. Latitude, productivity and species richness. Glob. Ecol. Biogeogr. 2015, 24, 107–117. [Google Scholar] [CrossRef]
- Chen, M.; Rafique, R.; Asrar, G.R.; Bond-Lamberty, B.; Ciais, P.; Zhao, F.; Reyer, C.P.; Ostberg, S.; Chang, J.; Ito, A.; et al. Regional contribution to variability and trends of global gross primary productivity. Environ. Res. Lett. 2017, 12, 105005. [Google Scholar] [CrossRef]
- Banbury Morgan, R.; Herrmann, V.; Kunert, N.; Bond-Lamberty, B.; Muller-Landau, H.C.; Anderson-Teixeira, K.J. Global patterns of forest autotrophic carbon fluxes. Glob. Change Biol. 2021, 27, 2840–2855. [Google Scholar] [CrossRef]
- Collalti, A.; Ibrom, A.; Stockmarr, A.; Cescatti, A.; Alkama, R.; Fernández-Martínez, M.; Matteucci, G.; Sitch, S.; Friedlingstein, P.; Ciais, P.; et al. Forest production efficiency increases with growth temperature. Nat. Commun. 2020, 11, 5322. [Google Scholar] [CrossRef] [PubMed]
- Coley, P.D.; Barone, J.A. Herbivory and plant defenses in tropical forests. Annu. Rev. Ecol. Syst. 1996, 27, 305–335. [Google Scholar] [CrossRef]
- Wetzel, W.C.; Inouye, B.D.; Hahn, P.G.; Whitehead, S.R.; Underwood, N. Variability in plant–herbivore interactions. Annu. Rev. Ecol. Syst. 2023, 54, 451–474. [Google Scholar] [CrossRef]
- Biswas, J. Metabolic efficiency and regulation of body weight: A comparison between life in hypogean and epigean ecosystems. Int. J. Speleol. 1991, 20, 15–22. [Google Scholar] [CrossRef][Green Version]
- Poulson, T.L. Morphological and physiological correlates of evolutionary reduction of metabolic rate among amblyopsid cave fishes. In The Biology of Hypogean Fishes; Romero, A., Ed.; Springer: Dordrecht, The Netherlands, 2001; pp. 239–249. [Google Scholar]
- Maderspacher, F. White, fat and blind—Economy and evolution in caves. Curr. Biol. 2022, 32, R591–R596. [Google Scholar] [CrossRef]
- Xu, Y.; Jing, Y.; Zhou, J.; Long, R.; Meng, J.; Yang, Y.; Luo, Y. Age, growth, and energy storage of the subterranean fish Triplophysa rosa (Cypriniformes: Nemacheilidae) from Chongqing, China. BMC Ecol. Evol. 2023, 23, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Geiman, C.O.; Long, E.S. Allometric brain reduction in an insular, dwarfed population of black-tailed deer. J. Mamm. Evol. 2023, 30, 673–681. [Google Scholar] [CrossRef]
- Terborgh, J. The ‘island syndrome’ is an alternative state. J. Biogeogr. 2023, 50, 467–475. [Google Scholar] [CrossRef]
- Currie, D.J. Energy and large-scale patterns of animal-and plant-species richness. Am. Nat. 1991, 137, 27–49. [Google Scholar] [CrossRef]
- Bohdalková, E.; Toszogyova, A.; Šímová, I.; Storch, D. Universality in biodiversity patterns: Variation in species–temperature and species–productivity relationships reveals a prominent role of productivity in diversity gradients. Ecography 2021, 44, 1366–1378. [Google Scholar] [CrossRef]
- Palmer, J.D. The Living Clock: The Orchestrator of Biological Rhythms; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Patke, A.; Young, M.W.; Axelrod, S. Molecular mechanisms and physiological importance of circadian rhythms. Nat. Rev. Mol. Cell Biol. 2020, 21, 67–84. [Google Scholar] [CrossRef] [PubMed]
- Oswald, I. Sleep as a restorative process: Human clues. Progr. Brain Res. 1980, 53, 279–288. [Google Scholar]
- Lima, S.L.; Rattenborg, N.C.; Lesku, J.A.; Amlaner, C.J. Sleeping under the risk of predation. Anim. Behav. 2005, 70, 723–736. [Google Scholar] [CrossRef]
- Siegel, J.M. Sleep viewed as a state of adaptive inactivity. Nat. Rev. Neurosci. 2009, 10, 747–753. [Google Scholar] [CrossRef] [PubMed]
- Lesku, J.A.; Aulsebrook, A.E.; Kelly, M.L.; Tisdale, R.K. Evolution of sleep and adaptive sleeplessness. Handb. Behav. Neurosci. 2019, 30, 299–316. [Google Scholar]
- Wichlinski, L.J. Adaptive solutions to the problem of vulnerability during sleep. Evol. Psychol. Sci. 2022, 8, 442–477. [Google Scholar] [CrossRef]
- Berger, R.J.; Phillips, N.H. Energy conservation and sleep. Behav. Brain Res. 1995, 69, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Kelly, M.L.; Collins, S.P.; Lesku, J.A.; Hemmi, J.M.; Collin, S.P.; Radford, C.A. Energy conservation characterizes sleep in sharks. Biol. Lett. 2022, 18, 20210259. [Google Scholar] [CrossRef] [PubMed]
- Lesku, J.A.; Schmidt, M.H. Energetic costs and benefits of sleep. Curr. Biol. 2022, 32, R656–R661. [Google Scholar] [CrossRef] [PubMed]
- Siegel, J.M. Sleep function: An evolutionary perspective. Lancet Neurol. 2022, 21, 937–946. [Google Scholar] [CrossRef] [PubMed]
- Hulbert, A.J.; Else, P.L. Mechanisms underlying the cost of living in animals. Annu. Rev. Physiol. 2000, 62, 207–235. [Google Scholar] [CrossRef] [PubMed]
- Elton, C. Animal Ecology; Macmillan: New York, NY, USA, 1935. [Google Scholar]
- Herbers, J.M. Time resources and laziness in animals. Oecologia 1981, 49, 252–262. [Google Scholar] [CrossRef]
- Turbill, C.; Stojanovski, L. Torpor reduces predation risk by compensating for the energetic cost of antipredator foraging behaviours. Proc. R. Soc. B Biol. Sci. 2018, 285, 20182370. [Google Scholar] [CrossRef] [PubMed]
- Geiser, F. Ecological Physiology of Daily Torpor and Hibernation; Springer: Berlin, Germany, 2021. [Google Scholar]
- Giroud, S.; Habold, C.; Nespolo, R.F.; Mejías, C.; Terrien, J.; Logan, S.M.; Henning, R.H.; Storey, K.B. The torpid state: Recent advances in metabolic adaptations and protective mechanisms. Front. Physiol. 2021, 11, 623665. [Google Scholar] [CrossRef] [PubMed]
- Jastroch, M.; Giroud, S.; Barrett, P.; Geiser, F.; Heldmaier, G.; Herwig, A. Seasonal control of mammalian energy balance: Recent advances in the understanding of daily torpor and hibernation. J. Neuroendocrinol. 2016, 28, jne12437. [Google Scholar] [CrossRef] [PubMed]
- Hrvatin, S.; Sun, S.; Wilcox, O.F.; Yao, H.; Lavin-Peter, A.J.; Cicconet, M.; Assad, E.G.; Palmer, M.E.; Aronson, S.; Banks, A.S.; et al. Neurons that regulate mouse torpor. Nature 2020, 583, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Odum, H.T. Primary production in flowing waters. Limnol. Oceanogr. 1956, 1, 102–117. [Google Scholar] [CrossRef]
- Hoellein, T.J.; Bruesewitz, D.A.; Richardson, D.C. Revisiting Odum (1956): A synthesis of aquatic ecosystem metabolism. Limnol. Oceanogr. 2013, 58, 2089–2100. [Google Scholar] [CrossRef]
- Humphries, M.M.; Thomas, D.W.; Kramer, D.L. Torpor and digestion in food-storing hibernators. Physiol. Biochem. Zool. 2001, 74, 283–292. [Google Scholar] [CrossRef]
- Bourdeau, P.F. Seasonal variations of the photosynthetic efficiency of evergreen conifers. Ecology 1959, 40, 63–67. [Google Scholar] [CrossRef]
- Pollet, B.; Steppe, K.; Dambre, P.; Van Labeke, M.C.; Lemeur, R. Seasonal variation of photosynthesis and photosynthetic efficiency in Phalaenopsis. Photosynthetica 2010, 48, 580–588. [Google Scholar] [CrossRef]
- Jordan, C.F.; Murphy, P.G. A latitudinal gradient of wood and litter production, and its implication regarding competition and species diversity in trees. Am. Midl. Nat. 1978, 99, 415–434. [Google Scholar] [CrossRef]
- Smith, T.P.; Clegg, T.; Bell, T.; Pawar, S. Systematic variation in the temperature dependence of bacterial carbon use efficiency. Ecol. Lett. 2021, 24, 2123–2133. [Google Scholar] [CrossRef] [PubMed]
- Lemée, R.; Rochelle-Newall, E.; Van Wambeke, F.; Pizay, M.D.; Rinaldi, P.; Gattuso, J.P. Seasonal variation of bacterial production, respiration and growth efficiency in the open NW Mediterranean Sea. Aquat. Microb. Ecol. 2002, 29, 227–237. [Google Scholar] [CrossRef]
- Reinthaler, T.; Herndl, G.J. Seasonal dynamics of bacterial growth efficiencies in relation to phytoplankton in the southern North Sea. Aquat. Microb. Ecol. 2005, 39, 7–16. [Google Scholar] [CrossRef]
- Baetge, N.; Behrenfeld, M.J.; Fox, J.; Halsey, K.H.; Mojica, K.D.; Novoa, A.; Stephens, B.M.; Carlson, C.A. The seasonal flux and fate of dissolved organic carbon through bacterioplankton in the Western North Atlantic. Front. Microbiol. 2021, 12, 669883. [Google Scholar] [CrossRef] [PubMed]
- Apple, J.K.; Del Giorgio, P.A.; Kemp, W.M. Temperature regulation of bacterial production, respiration, and growth efficiency in a temperate salt-marsh estuary. Aquat. Microb. Ecol. 2006, 43, 243–254. [Google Scholar] [CrossRef]
- Singh, J.S.; Yadava, P.S. Seasonal variation in composition, plant biomass, and net primary productivity of a tropical grassland at Kurukshetra, India. Ecol. Monogr. 1974, 44, 351–376. [Google Scholar] [CrossRef]
- Turner, D.P.; Urbanski, S.; Bremer, D.; Wofsy, S.C.; Meyers, T.; Gower, S.T.; Gregory, M. A cross-biome comparison of daily light use efficiency for gross primary production. Glob. Change Biol. 2003, 9, 383–395. [Google Scholar] [CrossRef]
- Wehr, R.; Munger, J.W.; McManus, J.B.; Nelson, D.D.; Zahniser, M.S.; Davidson, E.A.; Wofsy, S.C.; Saleska, S.R. Seasonality of temperate forest photosynthesis and daytime respiration. Nature 2016, 534, 680–683. [Google Scholar] [CrossRef] [PubMed]
- Gaedke, U. Ecosystem analysis based on biomass size distributions: A case study of a plankton community in a large lake. Limnol. Oceanogr. 1993, 38, 112–127. [Google Scholar] [CrossRef]
- Gaedke, U.; Straile, D. Seasonal changes of trophic transfer efficiencies in a plankton food web derived from biomass size distributions and network analysis. Ecol. Model. 1994, 75, 435–445. [Google Scholar] [CrossRef]
- Carefoot, T.H. Gastropoda. In Animal Energetics; Pandian, T.J., Vernberg, F.J., Eds.; Academic Press: San Diego, CA, USA, 1987; Volume 2, pp. 89–172. [Google Scholar]
- Almeda, R.; Augustin, C.B.; Alcaraz, M.; Calbet, A.; Saiz, E. Feeding rates and gross growth efficiencies of larval developmental stages of Oithona davisae (Copepoda, Cyclopoida). J. Exp. Mar. Biol. Ecol. 2010, 387, 24–35. [Google Scholar] [CrossRef]
- Rombough, P. The energetics of embryonic growth. Respir. Physiol. Neurobiol. 2011, 178, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Smith, F.W.; Long, J.N. Age-related decline in forest growth: An emergent property. For. Ecol. Manag. 2001, 144, 175–181. [Google Scholar] [CrossRef]
- Marshall, D.J.; Pettersen, A.K.; Bode, M.; White, C.R. Developmental cost theory predicts thermal environment and vulnerability to global warming. Nat. Ecol. Evol. 2020, 4, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Pettersen, A.K.; Nord, A.; While, G.M.; Uller, T. How do fluctuating temperatures alter the cost of development? Funct. Ecol. 2024, 38, 114–125. [Google Scholar] [CrossRef]
- Glazier, D.S. Reproductive efficiency and the timing of gestation and lactation in rodents. Am. Nat. 1990, 135, 269–277. [Google Scholar] [CrossRef]
- Künkele, J. Energetics of gestation relative to lactation in a precocial rodent, the guinea pig (Cavia porcellus). J. Zool. 2000, 250, 533–539. [Google Scholar] [CrossRef]
- Nicoll, M.E.; Thompson, S.D. Basal metabolic rates and energetics of reproduction in therian mammals: Marsupials and placentals compared. Symp. Zool. Soc. Lond. 1987, 57, 7–27. [Google Scholar]
- Low, B.S. Environmental uncertainty and the parental strategies of marsupials and placentals. Am. Nat. 1978, 112, 197–213. [Google Scholar] [CrossRef]
- Emmons, L.H. Observations on litter size and development of some African rainforest squirrels. Biotropica 1979, 11, 207–213. [Google Scholar] [CrossRef]
- Lillegraven, J.A.; Thompson, S.D.; McNab, B.K.; Patton, J.L. The origin of eutherian mammals. Biol. J. Linn. Soc. 1987, 32, 281–336. [Google Scholar] [CrossRef]
- Kam, M.; Khokhlova, I.S.; Degen, A.A. Partitioning of metabolizable energy intake in sucking altricial and precocial rodent pups. J. Zool. 2006, 269, 502–505. [Google Scholar] [CrossRef]
- Wilbur, H.M. Complex life cycles. Annu. Rev. Ecol. Syst. 1980, 11, 67–93. [Google Scholar] [CrossRef]
- Werner, E.E. Size, scaling, and the evolution of complex life cycles. In Size-Structured Populations: Ecology and Evolution; Ebenman, B., Persson, L., Eds.; Springer: Berlin, Germany, 1988; pp. 60–81. [Google Scholar]
- Cole, L.C. The population consequences of life history phenomena. Q. Rev. Biol. 1954, 29, 103–137. [Google Scholar] [CrossRef]
- Odum, E.P. The strategy of ecosystem development: An understanding of ecological succession provides a basis for resolving man’s conflict with nature. Science 1969, 164, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Loreau, M. From Populations to Ecosystems: Theoretical Foundations for a New Ecological Synthesis; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Jordan, C.F. Evolution from a Thermodynamic Perspective: Implications for Species Conservation and Agricultural Sustainability; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Poorter, L.; Amissah, L.; Bongers, F.; Hordijk, I.; Kok, J.; Laurance, S.G.; Lohbeck, M.; Martínez-Ramos, M.; Matsuo, T.; Meave, J.A.; et al. Successional theories. Biol. Rev. 2023, 98, 2049–2077. [Google Scholar] [CrossRef] [PubMed]
- Ghedini, G.; Loreau, M.; Marshall, D.J. Community efficiency during succession. Ecology 2020, 101, 1–11. [Google Scholar] [CrossRef]
- Zotin, A.I.; Konoplev, V.A. Direction of the evolutionary progress of organisms. In Thermodynamic Bases of Biological Processes. Physiological Reactions and Adaptations; Lamprecht, I., Zotin, A.I., Eds.; Walter de Gruyter: Berlin, Germany, 1978; pp. 341–347. [Google Scholar]
- Zotin, A.I.; Lamprecht, I. Aspects of bioenergetics and civilization. J. Theor. Biol. 1996, 180, 207–214. [Google Scholar] [CrossRef] [PubMed]
- Vermeij, G.J. On escalation. Annu. Rev. Earth Planet. Sci. 2013, 41, 1–19. [Google Scholar] [CrossRef]
- Braakman, R.; Follows, M.J.; Chisholm, S.W. Metabolic evolution and the self-organization of ecosystems. Proc. Natl. Acad. Sci. USA 2017, 114, E3091–E3100. [Google Scholar] [CrossRef] [PubMed]
- Zotin, A.A. Energetic macroevolution of vertebrates. Biol. Bull. 2018, 45, 299–309. [Google Scholar] [CrossRef]
- Gavrilov, V.M.; Golubeva, T.B.; Bushuev, A.V. Evolution of metabolic scaling among the tetrapod: Effect of phylogeny, the geologic time of class formation, and uniformity of species within a class. Integr. Zool. 2022, 17, 904–917. [Google Scholar] [CrossRef]
- Gavrilov, V.M.; Golubeva, T.B.; Warrack, G.; Bushuev, A.V. Metabolic scaling in birds and mammals: How taxon divergence time, phylogeny, and metabolic rate affect the relationship between scaling exponents and intercepts. Biology 2022, 11, 1067. [Google Scholar] [CrossRef] [PubMed]
- Bambach, R.K. Seafood through time: Changes in biomass, energetics, and productivity in the marine ecosystem. Paleobiology 1993, 19, 372–397. [Google Scholar] [CrossRef]
- Allmon, W.D.; Martin, R.E. Seafood through time revisited: The Phanerozoic increase in marine trophic resources and its macroevolutionary consequences. Paleobiology 2014, 40, 256–287. [Google Scholar] [CrossRef]
- Antell, G.T.; Saupe, E.E. Bottom-up controls, ecological revolutions and diversification in the oceans through time. Curr. Biol. 2021, 31, R1237–R1251. [Google Scholar] [CrossRef] [PubMed]
- Azevedo-Schmidt, L.; Meineke, E.K.; Currano, E.D. Insect herbivory within modern forests is greater than fossil localities. Proc. Natl. Acad. Sci. USA 2022, 119, e2202852119. [Google Scholar] [CrossRef] [PubMed]
- Crockford, P.W.; On, Y.M.B.; Ward, L.M.; Milo, R.; Halevy, I. The geologic history of primary productivity. Curr. Biol. 2023, 33, 4741–4750. [Google Scholar] [CrossRef] [PubMed]
- Chaisson, E.J. Cosmic Evolution: The Rise of Complexity in Nature; Harvard University Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Chaisson, E.J. Energy rate density as a complexity metric and evolutionary driver. Complexity 2011, 16, 27–40. [Google Scholar] [CrossRef]
- Makarieva, A.M.; Nefiodov, A.V.; Li, B.L. Life’s energy and information: Contrasting evolution of volume-versus surface-specific rates of energy consumption. Entropy 2020, 22, 1025. [Google Scholar] [CrossRef] [PubMed]
- Odum, H.T. Self-organization and maximum empower. In Maximum Power: The Ideas and Applications of H. T. Odum; Hall, C.A.S., Ed.; University Press of Colorado: Denver, CO, USA, 1995; pp. 311–330. [Google Scholar]
- Vermeij, G.J. The Evolution of Power: A New Understanding of the History of Life; Princeton University Press: Princeton, NJ, USA, 2023. [Google Scholar]
- Por, F.D. Animal Achievement. A Unifying Theory of Zoology; Balaban Publishers: Rehovot, Israel, 1994. [Google Scholar]
- Signor, P.W. Biodiversity in geological time. Am. Zool. 1994, 34, 23–32. [Google Scholar] [CrossRef]
- McNab, B.K. Extreme Measures: The Ecological Energetics of Birds and Mammals; University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- Pough, F.H. The advantages of ectothermy for tetrapods. Am. Nat. 1980, 115, 92–112. [Google Scholar] [CrossRef]
- Phillipson, J. Bioenergetic options and phylogeny. In Physiological Ecology; An Evolutionary Approach to Resource Use; Townsend, C.R., Calow, P., Eds.; Sinauer Associates: Sunderland, MA, USA, 1981; pp. 20–45. [Google Scholar]
- Bennett, A.F.; Ruben, J.A. Endothermy and activity in vertebrates. Science 1979, 206, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Farmer, C.G. Parental care: The key to understanding endothermy and other convergent features in birds and mammals. Am. Nat. 2000, 155, 326–334. [Google Scholar] [CrossRef] [PubMed]
- Farmer, C.G. Parental care, destabilizing selection, and the evolution of tetrapod endothermy. Physiology 2020, 35, 160–176. [Google Scholar] [CrossRef] [PubMed]
- Koteja, P. Energy assimilation, parental care and the evolution of endothermy. Proc. R. Society B Biol. Sci. 2000, 267, 479–484. [Google Scholar] [CrossRef] [PubMed]
- Grigg, G.C.; Beard, L.A.; Augee, M.L. The evolution of endothermy and its diversity in mammals and birds. Physiol. Biochem. Zool. 2004, 77, 982–997. [Google Scholar] [CrossRef]
- Clarke, A.; Pörtner, H.O. Temperature, metabolic power and the evolution of endothermy. Biol. Rev. 2010, 85, 703–727. [Google Scholar] [CrossRef] [PubMed]
- Tattersall, G.J. Reptile thermogenesis and the origins of endothermy. Zoology 2016, 119, 403–405. [Google Scholar] [CrossRef] [PubMed]
- Nowack, J.; Giroud, S.; Arnold, W.; Ruf, T. Muscle non-shivering thermogenesis and its role in the evolution of endothermy. Front. Physiol. 2017, 8, 889. [Google Scholar] [CrossRef] [PubMed]
- Lovegrove, B.G. Fires of Life; Yale University Press: New Haven, CT, USA, 2019. [Google Scholar]
- Seebacher, F. Is endothermy an evolutionary by-product? Trends Ecol. Evol. 2020, 35, 503–511. [Google Scholar] [CrossRef] [PubMed]
- Grigg, G.; Nowack, J.; Bicudo, J.E.P.W.; Bal, N.C.; Woodward, H.N.; Seymour, R.S. Whole-body endothermy: Ancient, homologous and widespread among the ancestors of mammals, birds and crocodylians. Biol. Rev. 2022, 97, 766–801. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, B. Why have some animals evolved to regulate a high body temperature? Am. Nat. 1977, 111, 623–640. [Google Scholar] [CrossRef]
- van der Meer, J. Production efficiency differences between poikilotherms and homeotherms have little to do with metabolic rate. Ecol. Lett. 2021, 24, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Hamann, O. On vegetation recovery, goats and giant tortoises on Pinta Island, Galápagos, Ecuador. Biodivers. Conserv. 1993, 2, 138–151. [Google Scholar] [CrossRef]
- Campbell, K.; Donlan, C.J. Feral goat eradications on islands. Conserv. Biol. 2005, 19, 1362–1374. [Google Scholar] [CrossRef]
- Hamilton, J.; Coe, M. Feeding, digestion and assimilation of a population of giant tortoises (Geochelone gigantea (Sehweigger)) on Aldabra atoll. J. Arid Environ. 1982, 5, 127–144. [Google Scholar] [CrossRef]
- Huntly, N. Herbivores and the dynamics of communities and ecosystems. Annu. Rev. Ecol. Syst. 1991, 22, 477–503. [Google Scholar] [CrossRef]
- Van Valkenburgh, B. Major patterns in the history of carnivorous mammals. Annu. Rev. Earth Planet. Sci. 1999, 27, 463–493. [Google Scholar] [CrossRef]
- Jessop, T.S.; Ariefiandy, A.; Forsyth, D.M.; Purwandana, D.; White, C.R.; Benu, Y.J.; Madsen, T.; Harlow, H.J.; Letnic, M. Komodo dragons are not ecological analogs of apex mammalian predators. Ecology 2020, 101, e02970. [Google Scholar] [CrossRef] [PubMed]
- Franz, R.; Hummel, J.; Müller, D.W.; Bauert, M.; Hatt, J.M.; Clauss, M. Herbivorous reptiles and body mass: Effects on food intake, digesta retention, digestibility and gut capacity, and a comparison with mammals. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2011, 158, 94–101. [Google Scholar] [CrossRef] [PubMed]
- Rubner, M. Über Kompensation und Summation von funktionellen Leistungen des Körpers. Sitz. Königl. Preuss. Akad. Wiss. 1910, 16, 316–324. [Google Scholar]
- Wieser, W. Energy allocation by addition and by compensation: An old principle revisited. In Energy Transformations in Cells and Organisms; Wieser, W.l., Gnaiger, E., Eds.; Thieme Verlag Stuttgart: New York, NY, USA, 1989. [Google Scholar]
- Krockenberger, A. Meeting the energy demands of reproduction in female koalas, Phascolarctos cinereus: Evidence for energetic compensation. J. Comp. Physiol. B 2003, 173, 531–540. [Google Scholar] [CrossRef] [PubMed]
- Hart, J.S. Rodents. In Comparative Physiology of Thermoregulation; Whittow, G.C., Ed.; Academic Press: New York: NY, USA, 1971; pp. 1–149. [Google Scholar]
- Chappell, M.A.; Bachman, G.C.; Hammond, K.A. The heat increment of feeding in house wren chicks: Magnitude, duration, and substitution for thermostatic costs. J. Comp. Physiol. B 1997, 167, 313–318. [Google Scholar] [CrossRef]
- Bruinzeel, L.W.; Piersma, T. Cost reduction in the cold: Heat generated by terrestrial locomotion partly substitutes for thermoregulation costs in Knot Calidris canutus. Ibis 1998, 140, 323–328. [Google Scholar] [CrossRef]
- Kaseloo, P.A.; Lovvorn, J.R. Substitution of heat from exercise and digestion by ducks diving for mussels at varying depths and temperatures. J. Comp. Physiol. B 2006, 176, 265–275. [Google Scholar] [CrossRef]
- Humphries, M.M.; Careau, V. Heat for nothing or activity for free? Evidence and implications of activity-thermoregulatory heat substitution. Integr. Comp. Biol. 2011, 51, 419–431. [Google Scholar] [CrossRef]
- González-Medina, E.; Cabello-Vergel, J.; Playà-Montmany, N.; Villegas, A.; Parejo, M.; Abad-Gómez, J.M.; Sánchez-Guzmán, J.M.; Masero, J.A. Going to sleep with a full belly: Thermal substitution by specific dynamic action in shorebirds. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2020, 244, 110689. [Google Scholar] [CrossRef]
- Maloney, C.; Careau, V. Individual variation in heat substitution: Is activity in the cold energetically cheaper for some individuals than others? J. Exp. Biol. 2022, 225, jeb244186. [Google Scholar] [CrossRef] [PubMed]
- McNamara, J.M.; Ekman, J.; Houston, A.I. The effect of thermoregulatory substitution on optimal energy reserves of small birds in winter. Oikos 2004, 105, 192–196. [Google Scholar] [CrossRef]
- Hohtola, E. Shivering thermogenesis in birds and mammals. In Life in the Cold: Evolution, Mechanisms, Adaptation, and Application; Barnes, B.M., Carey, H.V., Eds.; Institute of Arctic Biology, University of Alaska: Fairbanks, AK, USA, 2004; pp. 241–252. [Google Scholar]
- Legendre, L.J.; Davesne, D. The evolution of mechanisms involved in vertebrate endothermy. Philos. Trans. R. Soc. B 2020, 375, 20190136. [Google Scholar] [CrossRef]
- Wieser, W. Low production “efficiency” of homeotherm populations: A misunderstanding. Oecologia 1984, 61, 53–54. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Toward a metabolic theory of ecology. Ecology 2004, 85, 1771–1789. [Google Scholar] [CrossRef]
- Sibly, R.M. Life history. In Metabolic Ecology: A Scaling Approach; Sibly, R.M., Brown, J.H., Kodric-Brown, A., Eds.; Wiley-Blackwell: Chichester, UK, 2012; pp. 57–66. [Google Scholar]
- Brown, W.L., Jr. General adaptation and evolution. Syst. Zool. 1958, 7, 157–168. [Google Scholar] [CrossRef]
- Darlington, P.J., Jr. Area, climate, and evolution. Evolution 1959, 13, 488–510. [Google Scholar] [CrossRef]
- Peng, Y.; Prentice, I.C.; Bloomfield, K.J.; Campioli, M.; Guo, Z.; Sun, Y.; Tian, D.; Wang, X.; Vicca, S.; Stocker, B.D. Global terrestrial nitrogen uptake and nitrogen use efficiency. J. Ecol. 2023, 111, 2676–2693. [Google Scholar] [CrossRef]
- Sterner, R.W.; Elser, J.J. Ecological Stoichiometry: The Biology of Elements from Molecules to the Biosphere; Princeton University Press: Princeton, NY, USA, 2002. [Google Scholar]
- Gimenez, C.; Connor, D.J.; Rueda, F. Canopy development, photosynthesis and radiation-use efficiency in sunflower in response to nitrogen. Field Crops Res. 1994, 38, 15–27. [Google Scholar] [CrossRef]
- Allen, C.B.; Will, R.E.; Jacobson, M.A. Production efficiency and radiation use efficiency of four tree species receiving irrigation and fertilization. For. Sci. 2005, 51, 556–569. [Google Scholar] [CrossRef]
- Harrington, R.A.; Fownes, J.H.; Vitousek, P.M. Production and resource use efficiencies in N-and P-limited tropical forests: A comparison of responses to long-term fertilization. Ecosystems 2001, 4, 646–657. [Google Scholar] [CrossRef]
- Belovsky, G.E. Diet optimization in a generalist herbivore: The moose. Theor. Pop. Biol. 1978, 14, 105–134. [Google Scholar] [CrossRef] [PubMed]
- Owen-Smith, N.; Novellie, P. What should a clever ungulate eat? Am. Nat. 1982, 119, 151–178. [Google Scholar] [CrossRef]
- Van Wieren, S.E. Do large herbivores select a diet that maximizes short-term energy intake rate? For. Ecol. Manag. 1996, 88, 149–156. [Google Scholar] [CrossRef]
- Simpson, S.J.; Sibly, R.M.; Lee, K.P.; Behmer, S.T.; Raubenheimer, D. Optimal foraging when regulating intake of multiple nutrients. Anim. Behav. 2004, 68, 1299–1311. [Google Scholar] [CrossRef]
- Blumstein, D.M.; MacManes, M.D. When the tap runs dry: The physiological effects of acute experimental dehydration in Peromyscus eremicus. J. Exp. Biol. 2023, 226, jeb246386. [Google Scholar] [CrossRef] [PubMed]
- Degen, A.A. Ecophysiology of Small Desert Mammals; Springer: Berlin, Germany, 1997. [Google Scholar]
- Rocha, J.L.; Godinho, R.; Brito, J.C.; Nielsen, R. Life in deserts: The genetic basis of mammalian desert adaptation. Trends Ecol. Evol. 2021, 36, 637–650. [Google Scholar] [CrossRef] [PubMed]
- Polis, G.A.; Farley, R.D. Population biology of a desert scorpion: Survivorship, microhabitat, and the evolution of life history strategy. Ecology 1980, 61, 620–629. [Google Scholar] [CrossRef]
- McCormick, S.J.; Polis, G.A. Prey, predators and parasites. In The Biology of Scorpions; G.A. Polis, Ed.; Stanford University Press: Stanford, CA, USA, 1990; pp. 294–320. [Google Scholar]
- Polis, G.A.; Yamashita, T. The ecology and importance of predaceous arthropods in desert communities. In The Ecology of Desert Communities; Polis, G.A., Ed.; University of Arizona Press: Tucson, AZ, USA, 1991; pp. 180–222. [Google Scholar]
- Lighton, J.R.; Brownell, P.H.; Joos, B.; Turner, R.J. Low metabolic rate in scorpions: Implications for population biomass and cannibalism. J. Exp. Biol. 2001, 204, 607–613. [Google Scholar] [CrossRef] [PubMed]
- Gefen, E. The relative importance of respiratory water loss in scorpions is correlated with species habitat type and activity pattern. Physiol. Biochem. Zool. 2011, 84, 68–76. [Google Scholar] [CrossRef]
- Lawson, T.; Vialet-Chabrand, S. Speedy stomata, photosynthesis and plant water use efficiency. New Phytol. 2019, 221, 93–98. [Google Scholar] [CrossRef] [PubMed]
- Griebel, A.; Bennett, L.T.; Metzen, D.; Pendall, E.; Lane, P.N.; Arndt, S.K. Trading water for carbon: Maintaining photosynthesis at the cost of increased water loss during high temperatures in a temperate forest. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005239. [Google Scholar] [CrossRef]
- Bertucci-Richter, E.M.; Parrott, B.B. The rate of epigenetic drift scales with maximum lifespan across mammals. Nat. Comm. 2023, 14, 7731. [Google Scholar] [CrossRef] [PubMed]
- Wolf, E.; Kahnt, E.; Ehrlein, J.; Hermanns, W.; Brem, G.; Wanke, R. Effects of long-term elevated serum levels of growth hormone on life expectancy of mice: Lessons from transgenic animal models. Mech. Ageing Dev. 1993, 68, 71–87. [Google Scholar] [CrossRef] [PubMed]
- Bartke, A. Can growth hormone (GH) accelerate aging? Evidence from GH-transgenic mice. Neuroendocrinology 2003, 78, 210–216. [Google Scholar] [CrossRef]
- Alonso-Alvarez, C.; Bertrand, S.; Devevey, G.; Prost, J.; Faivre, B.; Sorci, G. Increased susceptibility to oxidative stress as a proximate cost of reproduction. Ecol. Lett. 2004, 7, 363–368. [Google Scholar] [CrossRef]
- Alonso-Alvarez, C.; Bertrand, S.; Faivre, B.; Sorci, G. Increased susceptibility to oxidative damage as a cost of accelerated somatic growth in zebra finches. Funct. Ecol. 2007, 21, 873–879. [Google Scholar] [CrossRef]
- Metcalfe, N.B.; Alonso-Alvarez, C. Oxidative stress as a life-history constraint: The role of reactive oxygen species in shaping phenotypes from conception to death. Funct. Ecol. 2010, 24, 984–996. [Google Scholar] [CrossRef]
- Metcalfe, N.B.; Monaghan, P. Does reproduction cause oxidative stress? An open question. Trends Ecol. Evol. 2013, 28, 347–350. [Google Scholar] [CrossRef]
- Speakman, J.R.; Blount, J.D.; Bronikowski, A.M.; Buffenstein, R.; Isaksson, C.; Kirkwood, T.B.; Monaghan, P.; Ozanne, S.E.; Beaulieu, M.; Briga, M.; et al. Oxidative stress and life histories: Unresolved issues and current needs. Ecol. Evol. 2015, 5, 5745–5757. [Google Scholar] [CrossRef] [PubMed]
- Van Mechelen, W. Running injuries: A review of the epidemiological literature. Sports Med. 1992, 14, 320–335. [Google Scholar] [CrossRef] [PubMed]
- Kessler, D.F. Running FASTER: Changing running technique to reduce stress injuries. Int. J. Athl. Ther. Train. 2020, 25, 49–53. [Google Scholar] [CrossRef]
- MacKay, D.G. The problems of flexibility, fluency, and speed–accuracy trade-off in skilled behavior. Psychol. Rev. 1982, 89, 483–506. [Google Scholar] [CrossRef]
- Chittka, L.; Skorupski, P.; Raine, N.E. Speed–accuracy tradeoffs in animal decision making. Trends Ecol. Evol. 2009, 24, 400–407. [Google Scholar] [CrossRef]
- David, M.; Gillingham, M.A.; Salignon, M.; Laskowski, K.L.; Giraldeau, L.A. Speed–accuracy trade-off and its consequences in a scramble competition context. Anim. Behav. 2014, 90, 255–262. [Google Scholar] [CrossRef]
- Bartke, A. Somatotropic axis, pace of life and aging. Front. Endocrinol. 2022, 13, 916139. [Google Scholar] [CrossRef] [PubMed]
- Kay, J.C.; Colbath, J.; Talmadge, R.J.; Garland, T., Jr. Mice from lines selectively bred for voluntary exercise are not more resistant to muscle injury caused by either contusion or wheel running. PLoS ONE 2022, 17, e0278186. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Clare, A. The division of labor and economic development. J. Dev. Econ. 1996, 49, 3–32. [Google Scholar] [CrossRef]
- Dumville, J.C.; Torano, F.A. Division of labor, efficient? Empirical evidence to support the argument. SAM Adv. Manag. J. 1997, 62, 16–21. [Google Scholar]
- Waibel, M.; Floreano, D.; Magnenat, S.; Keller, L. Division of labour and colony efficiency in social insects: Effects of interactions between genetic architecture, colony kin structure and rate of perturbations. Proc. R. Soc. B Biol. Sci. 2006, 273, 1815–1823. [Google Scholar] [CrossRef]
- Rueffler, C.; Hermisson, J.; Wagner, G.P. Evolution of functional specialization and division of labor. Proc. Natl. Acad. Sci. USA 2012, 109, E326–E335. [Google Scholar] [CrossRef] [PubMed]
- Cooper, G.A.; West, S.A. Division of labour and the evolution of extreme specialization. Nat. Ecol. Evol. 2018, 2, 1161–1167. [Google Scholar] [CrossRef] [PubMed]
- Traxler, M.F.; Rozen, D.E. Ecological drivers of division of labour in Streptomyces. Curr. Opin. Microbiol. 2022, 67, 102148. [Google Scholar] [CrossRef] [PubMed]
- Tannenbaum, E. When does division of labor lead to increased system output? J. Theor. Biol. 2007, 247, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Stueffer, J.F.; De Kroon, H.; During, H.J. Exploitation of environmental hetergeneity by spatial division of labor in a clonal plant. Funct. Ecol. 1996, 10, 328–334. [Google Scholar] [CrossRef]
- Hutchings, M.J.; Wijesinghe, D.K. Patchy habitats, division of labour and growth dividends in clonal plants. Trends Ecol. Evol. 1997, 12, 390–394. [Google Scholar] [CrossRef] [PubMed]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.L.; Chown, S.L.; Reich, P.B.; Gavrilov, V.M. Mean mass-specific metabolic rates are strikingly similar across life’s major domains: Evidence for life’s metabolic optimum. Proc. Natl. Acad. Sci. USA 2008, 105, 16994–16999. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, M.C.; Enquist, B.J. Organismal size, metabolism and the evolution of complexity in metazoans. Evol. Ecol. Res. 2005, 7, 681–696. [Google Scholar]
- Negroni, M.A.; LeBoeuf, A.C. Metabolic division of labor in social insects. Curr. Opin. Insect Sci. 2023, 59, 101085. [Google Scholar] [CrossRef] [PubMed]
- Geist, V. An ecological and behavioural explanation of mammalian characteristics and their implication to therapsid evolution. Z. Säugetierkd. 1972, 37, 1–15. [Google Scholar]
- McFarland, W.N.; Pough, F.H.; Cade, T.J.; Heiser, J.B. Vertebrate Life; Macmillan: New York, NY, USA, 1979. [Google Scholar]
- Kemp, T.S. The origin of mammalian endothermy: A paradigm for the evolution of complex biological structure. Zool. J. Linn. Soc. 2006, 147, 473–488. [Google Scholar] [CrossRef]
- Feldhamer, G.A.; Merritt, J.F.; Krajewski, C.; Rachlow, J.L.; Stewart, K.M. Mammalogy: Adaptation, Diversity, Ecology, 5th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2020. [Google Scholar]
- Lovmar, M.; Ehrenberg, M. Rate, accuracy and cost of ribosomes in bacterial cells. Biochimie 2006, 88, 951–961. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.; Lovmar, M.; Ehrenberg, M. Rate and accuracy of bacterial protein synthesis revisited. Curr. Opin. Microbiol. 2008, 11, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.; Zhang, J.; Ehrenberg, M. Genetic code translation displays a linear trade-off between efficiency and accuracy of tRNA selection. Proc. Natl. Acad. Sci. USA 2012, 109, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Wohlgemuth, I.; Pohl, C.; Mittelstaet, J.; Konevega, A.L.; Rodnina, M.V. Evolutionary optimization of speed and accuracy of decoding on the ribosome. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 2979–2986. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, K.; Kolomeisky, A.B.; Igoshin, O.A. Elucidating interplay of speed and accuracy in biological error correction. Proc. Natl. Acad. Sci. USA 2017, 114, 5183–5188. [Google Scholar] [CrossRef] [PubMed]
- Rinberg, D.; Koulakov, A.; Gelperin, A. Speed-accuracy tradeoff in olfaction. Neuron 2006, 51, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Bogacz, R.; Wagenmakers, E.J.; Forstmann, B.U.; Nieuwenhuis, S. The neural basis of the speed–accuracy tradeoff. Trends Neurosci. 2010, 33, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Heitz, R.P.; Schall, J.D. Neural mechanisms of speed-accuracy tradeoff. Neuron 2012, 76, 616–628. [Google Scholar] [CrossRef] [PubMed]
- Bogacz, R. Speed-accuracy tradeoff. In Encyclopedia of Computational Neuroscience; Jaeger, D., Jung, R., Eds.; Springer: New York, NY, USA, 2022; pp. 3225–3228. [Google Scholar]
- Bernays, E.A. The value of being a resource specialist: Behavioral support for a neural hypothesis. Am. Nat. 1998, 151, 451–464. [Google Scholar] [CrossRef] [PubMed]
- Jerison, H.J. Evolution of the Brain and Intelligence; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Gregory, T.R. Genome size evolution in animals. In The Evolution of the Genome; Gregory, T.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 3–87. [Google Scholar]
- West, G.B.; Brown, J.H. The origin of allometric scaling laws in biology from genomes to ecosystems: Towards a quantitative unifying theory of biological structure and organization. J. Exp. Biol. 2005, 208, 1575–1592. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Genome size covaries more positively with propagule size than adult size: New insights into an old problem. Biology 2021, 10, 270. [Google Scholar] [CrossRef] [PubMed]
- Healy, K.; McNally, L.; Ruxton, G.D.; Cooper, N.; Jackson, A.L. Metabolic rate and body size are linked with perception of temporal information. Anim. Behav. 2013, 86, 685–696. [Google Scholar] [CrossRef] [PubMed]
- Brett, J.R.; Groves, T.D.D. Physiological energetics. In Fish Physiology; Hoar, W.S., Randall, D.J., Brett, J.R., Eds.; Academic Press: New York, NY, USA, 1979; Volume 6, pp. 279–352. [Google Scholar]
- Knights, B. Energetics and fish farming. In Fish Energetics: New Perspectives; Tytler, P., Calow, P., Eds.; Springer: Dordrecht, The Netherlands, 1985; pp. 309–340. [Google Scholar]
- Hancz, C. Feed efficiency, nutrient sensing and feeding stimulation in aquaculture: A review. Acta Agrar. Kaposváriensis 2020, 24, 35–54. [Google Scholar] [CrossRef]
- Loomis, R.S.; Williams, W.A. Maximum crop productivity: An estimate. Crop Sci. 1963, 3, 67–72. [Google Scholar] [CrossRef]
- Penning de Vries, F.W.T.; van Laar, H.H.; Chardon, M.C.M. Bioenergetics of growth of seeds, fruits, and storage organs. In Potential Production of Crops in Different Environments; Smith, W.H., Ed.; International Rice Research Institute: Los Baflos, Philippines, 1983; pp. 37–59. [Google Scholar]
- Ksenzhek, O.S.; Volkov, A.G. Plant Energetics; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Diepenbrock, W. Energy balance in crop production. J. Agric. Sci. Technol. B 2012, 2, 527–533. [Google Scholar]
- Sarkar, D.; Sankar, A.; Devika, O.S.; Singh, S.; Shikha; Parihar, M.; Rakshit, A.; Sayyed, R.Z.; Gafur, A.; Ansari, M.J.; et al. Optimizing nutrient use efficiency, productivity, energetics, and economics of red cabbage following mineral fertilization and biopriming with compatible rhizosphere microbes. Sci. Rep. 2021, 11, 15680. [Google Scholar] [CrossRef] [PubMed]
- Dong, D.; Sun, H.; Qi, Z.; Liu, X. Improving microbial bioremediation efficiency of intensive aquacultural wastewater based on bacterial pollutant metabolism kinetics analysis. Chemosphere 2021, 265, 129151. [Google Scholar] [CrossRef]
- Saeed, M.U.; Hussain, N.; Sumrin, A.; Shahbaz, A.; Noor, S.; Bilal, M.; Aleya, L.; Iqbal, H.M. Microbial bioremediation strategies with wastewater treatment potentialities—A review. Sci. Total Environ. 2022, 818, 151754. [Google Scholar] [CrossRef]
- Ramya, M.; Kumar, P.S. A review on recent advancements in bioenergy production using microbial fuel cells. Chemosphere 2022, 288, 132512. [Google Scholar] [CrossRef] [PubMed]
- Pathak, R.R.; Ahmad, A.; Lochab, S.; Raghuram, N. Molecular physiology of plant nitrogen use efficiency and biotechnological options for its enhancement. Curr. Sci. 2008, 94, 1394–1403. [Google Scholar]
- Steinwand, M.A.; Ronald, P.C. Crop biotechnology and the future of food. Nat. Food 2020, 1, 273–283. [Google Scholar] [CrossRef]
- Cronin, J.; Sleivert, G. Challenges in understanding the influence of maximal power training on improving athletic performance. Sports Med. 2005, 35, 213–234. [Google Scholar] [CrossRef] [PubMed]
- Hall, C.A.; Cleveland, C.J.; Kaufmann, R. Energy and Resource Quality: The Ecology of the Economic Process; Wiley Interscience: New York, NY, USA, 1986. [Google Scholar]
- Costanza, R.; Cumberland, J.H.; Daly, H.; Goodland, R.; Norgaard, R.B. An Introduction to Ecological Economics; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Barneche, D.R.; Hulatt, C.J.; Dossena, M.; Padfield, D.; Woodward, G.; Trimmer, M.; Yvon-Durocher, G. Warming impairs trophic transfer efficiency in a long-term field experiment. Nature 2021, 592, 76–79. [Google Scholar] [CrossRef] [PubMed]
- Eddy, T.D.; Bernhardt, J.R.; Blanchard, J.L.; Cheung, W.W.; Colléter, M.; Du Pontavice, H.; Fulton, E.A.; Gascuel, D.; Kearney, K.A.; Petrik, C.M.; et al. Energy flow through marine ecosystems: Confronting transfer efficiency. Trends Ecol. Evol. 2021, 36, 76–86. [Google Scholar] [CrossRef] [PubMed]
- Baruch, E.M.; Harms, T.K.; Ruhi, A.; Lu, M.; Gaines-Sewell, L.; Sabo, J.L. Food web efficiency in desert streams. Limnol. Oceanogr. 2023, 68, 723–734. [Google Scholar] [CrossRef]
- Seebacher, F.; Bamford, S.M. Warming and pollution interact to alter energy transfer efficiency, performance and fitness across generations in zebrafish (Danio rerio). Sci. Total Environ. 2023, 912, 168942. [Google Scholar] [CrossRef] [PubMed]
- Sousa, T.; Domingos, T.; Kooijman, S.A.L.M. From empirical patterns to theory: A formal metabolic theory of life. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 2453–2464. [Google Scholar] [CrossRef] [PubMed]
- Fridley, J.D. Plant energetics and the synthesis of population and ecosystem ecology. J. Ecol. 2017, 105, 95–110. [Google Scholar] [CrossRef]
- Jusup, M.; Sousa, T.; Domingos, T.; Labinac, V.; Marn, N.; Wang, Z.; Klanjšček, T. Physics of metabolic organization. Phys. Life Rev. 2017, 20, 1–39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).