Development of a Semi-Empirical Model for Estimating the Efficiency of Thermodynamic Power Cycles
Abstract
:1. Introduction
1.1. Power Plants Efficiency
1.2. Brief Literature Review
1.3. The Scope of the Present Work
2. Material and Methods
2.1. Basic Mathematical Background
2.2. Followed Methodology
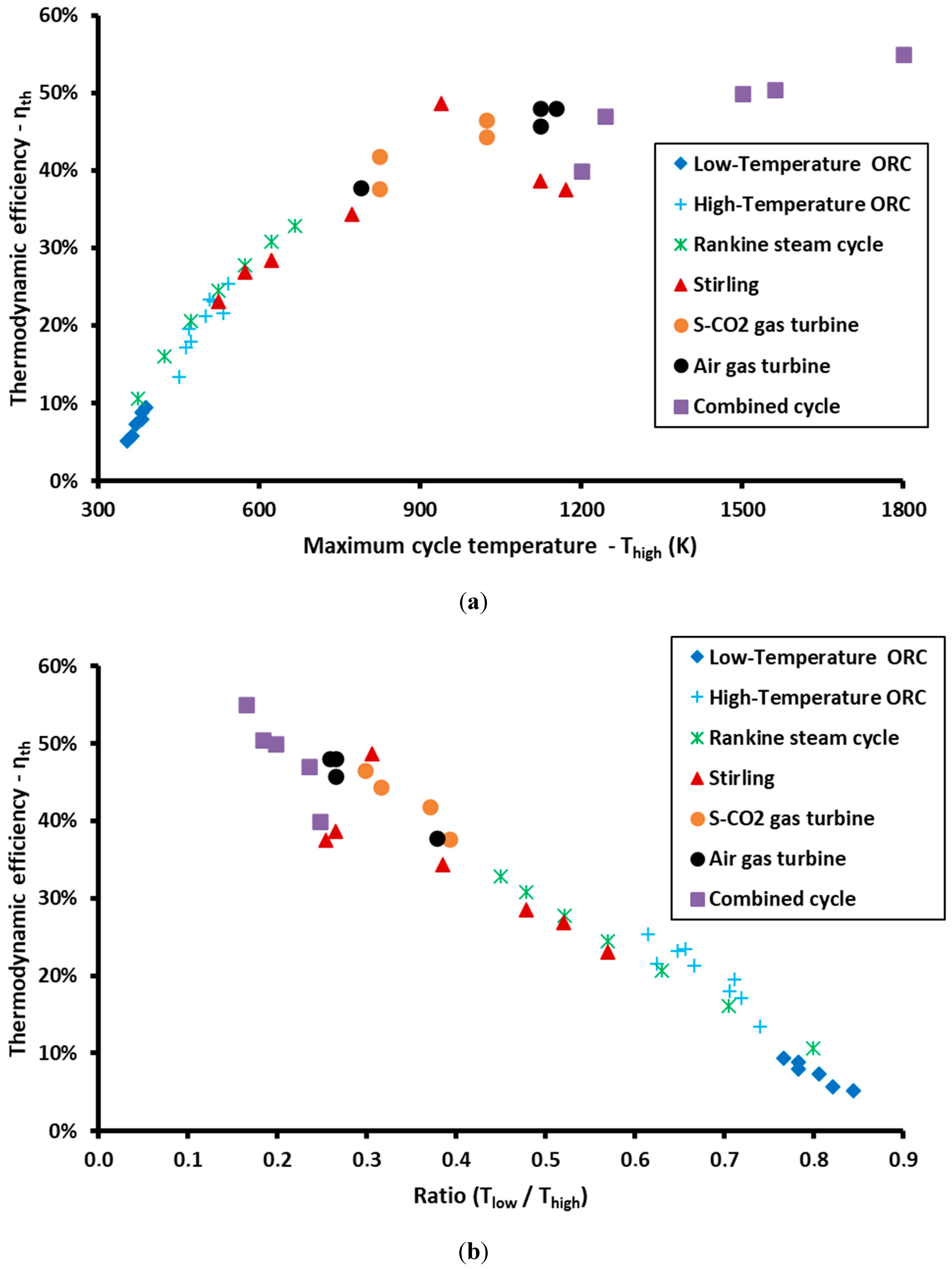
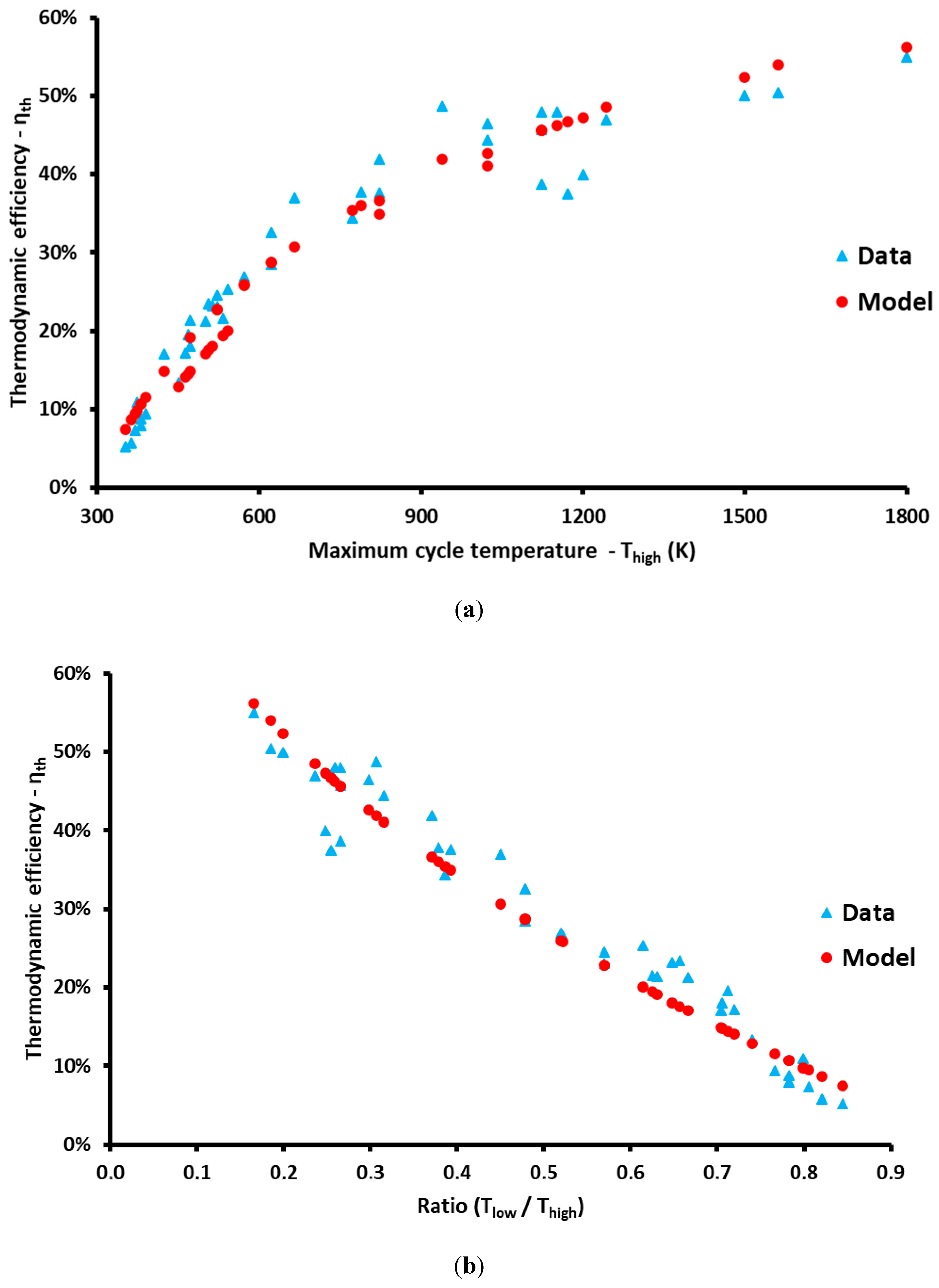
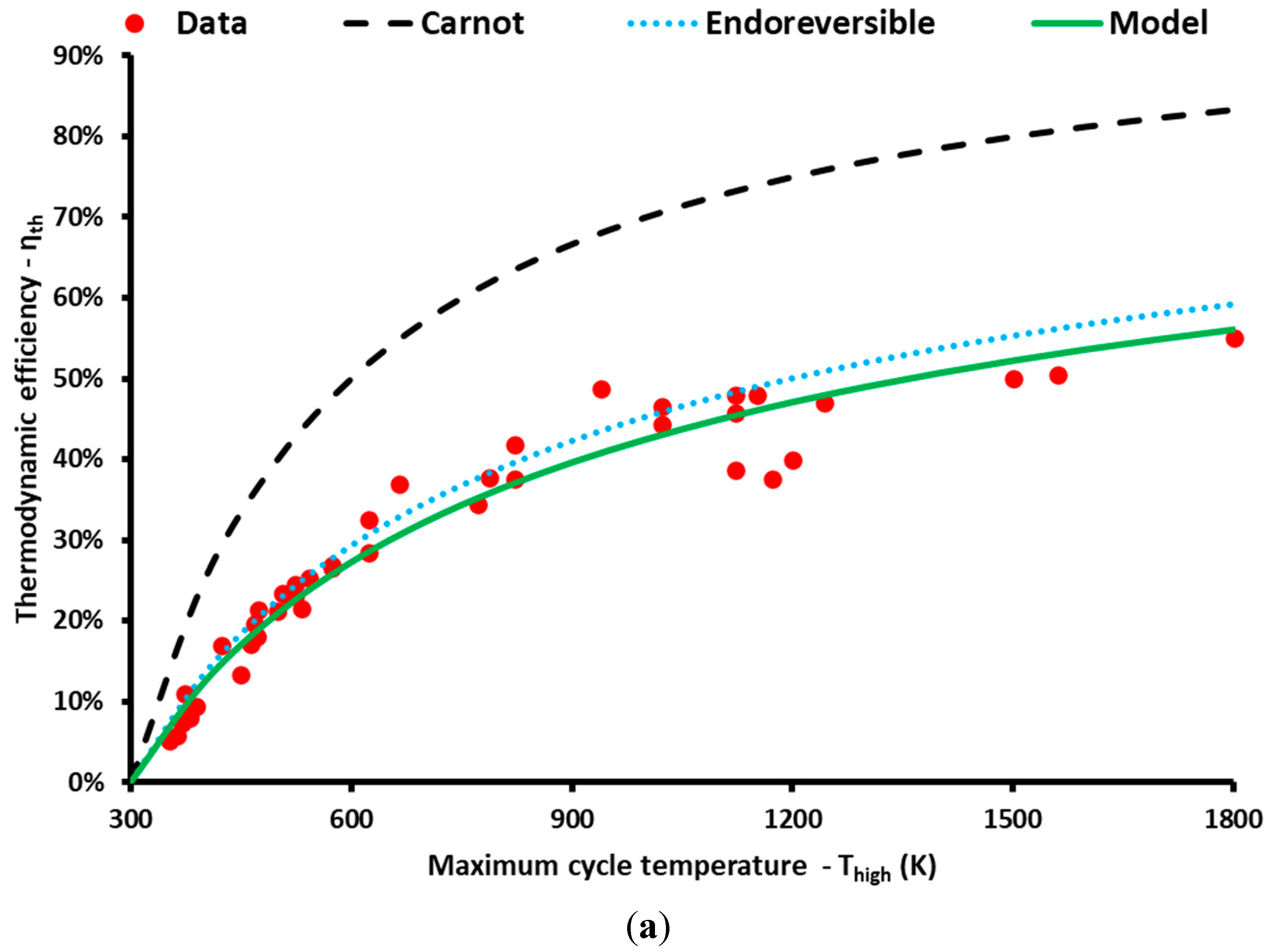
3. Results and Discussion
- ➢
- For the LT-ORC, the total (a) is found at 0.3481 while the reported results indicate a variation from 0.2996 up to 0.3753.
- ➢
- For the HT-ORC, the total (a) is found at 0.5813 while the reported results indicate a variation from 0.4770 up to 0.6399.
- ➢
- For the WS-RC, the total (a) is found at 0.5295 while the reported results indicate a variation from 0.4750 up to 0.5793.
- ➢
- For the Stirling cycle, the total (a) is found at 0.4267 while the reported results indicate a variation from 0.3432 up to 0.5653.
- ➢
- For the SCO2-GT, the total (a) is found at 0.5189 while the reported results indicate a variation from 0.5051 up to 0.5470.
- ➢
- For the Air-GT, the total (a) is found at 0.4808 while the reported results indicate a variation from 0.4617 up to 0.4929.
- ➢
- For the CC, the total (a) is found at 0.4220 while the reported results indicate a variation from 0.3667 up to 0.4440.
4. Conclusions
- ➢
- In the LT-ORC case, the mean (a) is found at 0.3481 while the reported results indicate a variation from 0.2996 up to 0.3753.
- ➢
- In the HT-ORC case, the mean (a) is found at 0.5813 while the reported results indicate a variation from 0.4770 up to 0.6399.
- ➢
- In the WS-RC case, the mean (a) is found at 0.5295 while the reported results indicate a variation from 0.4750 up to 0.5793.
- ➢
- In the Stirling cycle case, the mean (a) is found at 0.4267 while the reported results indicate a variation from 0.3432 up to 0.5653.
- ➢
- In the SCO2-GT case, the mean (a) is found at 0.5189 while the reported results indicate a variation from 0.5051 up to 0.5470.
- ➢
- In the Air-GT case, the mean (a) is found at 0.4808 while the reported results indicate a variation from 0.4617 up to 0.4929.
- ➢
- In the CC case, the mean (a) is found at 0.4220 while the reported results indicate a variation from 0.3667 up to 0.4440.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Superscript of the temperature ratio |
| i | Irreversibility factor |
| R2 | Regression coefficient |
| Thigh | High cycle temperature, K |
| Tlow | Low cycle temperature, K |
| Tm | Medium temperature, K |
| Greek Symbols | |
| ηcarnot | Carnot efficiency |
| ηendor | Endoreversible efficiency |
| ηth | Thermodynamic efficiency |
| ηth,appr | Approximated thermodynamic efficiency |
| Subscripts | |
| max | Maximum reported value for the specific cycle type |
| min | Minimum reported value for the specific cycle type |
| total | Total value for the specific cycle type |
| Abbreviations | |
| Air-GT | Air Gas Turbine |
| CC | Combined Cycle |
| EXPER | Experimental work |
| HT-ORC | High-Temperature Organic Rankine Cycle |
| LT-ORC | Low-Temperature Organic Rankine Cycle |
| ORC | Organic Rankine cycle |
| SCO2-GT | Supercritical Carbon Dioxide Gas Turbine |
| THEOR | Theoretical work |
| WS-RC | Water-Steam Rankine Cycle |
References
- World Energy Outlook—Topics. IEA n.d. Available online: https://www.iea.org/topics/world-energy-outlook (accessed on 26 June 2023).
- Ahmadi, M.H.; Ahmadi, M.A.; Sadatsakkak, S.A. Thermodynamic analysis and performance optimization of irreversible Carnot refrigerator by using multi-objective evolutionary algorithms (MOEAs). Renew. Sustain. Energy Rev. 2015, 51, 1055–1070. [Google Scholar] [CrossRef]
- Topel, M.; Laumert, B. Improving concentrating solar power plant performance by increasing steam turbine flexibility at start-up. Sol. Energy 2018, 165, 10–18. [Google Scholar] [CrossRef]
- Bellos, E. Progress in beam-down solar concentrating systems. Prog. Energy Combust. Sci. 2023, 97, 101085. [Google Scholar] [CrossRef]
- Porto-Hernandez, L.A.; Vargas, J.V.C.; Munoz, M.N.; Galeano-Cabral, J.; Ordonez, J.C.; Balmant, W.; Mariano, A.B. Fundamental optimization of steam Rankine cycle power plants. Energy Convers. Manag. 2023, 289, 117148. [Google Scholar] [CrossRef]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Hernández, A.; Roco, J.M.; Medina, A.; Sánchez-Salas, N. Heat engines and the Curzon-Ahlborn efficiency. Rev. Mex. Fis. 2014, 60, 384. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Yan, Z. Comment on “An ecological optimization criterion for finite-time heat engines” [J. Appl. Phys. 69, 7465 (1991)]. J. Appl. Phys. 1993, 73, 3583. [Google Scholar] [CrossRef]
- Novikov, I.I. The efficiency of atomic power stations (a review). J. Nucl. Energy 1954 1958, 7, 125–128. [Google Scholar] [CrossRef]
- Badescu, V. Simple Upper Bound Efficiencies for Endoreversible Conversion of Thermal Radiation. J. Non-Equilib. Thermodyn. 1999, 24, 196–202. [Google Scholar] [CrossRef]
- Leff, H.S. Thermal Efficiency at Maximum Work Output: New Results for Old Heat Engines. Am. J. Phys. 1987, 55, 602–610. Available online: https://pubs.aip.org/aapt/ajp/article-abstract/55/7/602/1052998/Thermal-efficiency-at-maximum-work-output-New?redirectedFrom=fulltext (accessed on 27 June 2023). [CrossRef]
- Pinho, C. The Curzon-Ahlborn Efficiency of Combined Cycles; Academia: San Francisco, CA, USA, 2003. [Google Scholar]
- Chen, W.Z.; Sun, F.R.; Cheng, S.M.; Chen, L.G. Study on optimal performance and working temperatures of endoreversible forward and reverse carnot cycles. Int. J. Energy Res. 1995, 19, 751–759. [Google Scholar] [CrossRef]
- Iglesias Garcia, S.; Ferreiro Garcia, R.; Carbia Carril, J.; Iglesias Garcia, D. A review of thermodynamic cycles used in low temperature recovery systems over the last two years. Renew. Sustain. Energy Rev. 2018, 81, 760–767. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N.; Mirhadizadeh, S.A. Review of organic Rankine cycle for small-scale applications. Energy Convers. Manag. 2017, 134, 135–155. [Google Scholar] [CrossRef]
- Tzivanidis, C.; Bellos, E.; Antonopoulos, K.A. Energetic and financial investigation of a stand-alone solar-thermal Organic Rankine Cycle power plant. Energy Convers. Manag. 2016, 126, 421–433. [Google Scholar] [CrossRef]
- Karellas, S.; Leontaritis, A.-D.; Panousis, G.; Bellos, E.; Kakaras, E. Energetic and exergetic analysis of waste heat recovery systems in the cement industry. Energy 2013, 58, 147–156. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Pei, G.; Alvi, J.Z.; Ji, J. Analysis of a novel solar electricity generation system using cascade Rankine cycle and steam screw expander. Appl. Energy 2016, 165, 627–638. [Google Scholar] [CrossRef]
- Pramanik, S.; Ravikrishna, R.V. A review of concentrated solar power hybrid technologies. Appl. Therm. Eng. 2017, 127, 602–637. [Google Scholar] [CrossRef]
- Carrillo Caballero, G.E.; Mendoza, L.S.; Martinez, A.M.; Silva, E.E.; Melian, V.R.; Venturini, O.J.; del Olmo, O.A. Optimization of a Dish Stirling system working with DIR-type receiver using multi-objective techniques. Appl. Energy 2017, 204, 271–286. [Google Scholar] [CrossRef]
- Ranieri, S.; Prado, G.A.O.; MacDonald, B.D. Efficiency Reduction in Stirling Engines Resulting from Sinusoidal Motion. Energies 2018, 11, 2887. [Google Scholar] [CrossRef]
- Toghyani, S.; Kasaeian, A.; Ahmadi, M.H. Multi-objective optimization of Stirling engine using non-ideal adiabatic method. Energy Convers. Manag. 2014, 80, 54–62. [Google Scholar] [CrossRef]
- Smith, L.; Nuel, B.; Weaver, S.P.; Berkower, S.; Gross, B. 25 kW Low-Temperature Stirling Engine for Heat Recovery, Solar, and Biomass Applications. In Proceedings of the 17th International Stirling Engine Conference (ISEC), Newcastle upon Tyne, UK, 24–26 August 2016. [Google Scholar]
- Sarkar, J.; Bhattacharyya, S. Optimization of recompression S-CO2 power cycle with reheating. Energy Convers. Manag. 2009, 50, 1939–1945. [Google Scholar] [CrossRef]
- Olumayegun, O.; Wang, M.; Kelsall, G. Closed-cycle gas turbine for power generation: A state-of-the-art review. Fuel 2016, 180, 694–717. [Google Scholar] [CrossRef]
- Ibrahim, T.K.; Mohammed, M.K.; Awad, O.I.; Rahman, M.M.; Najafi, G.; Basrawi, F.; Abd Alla, A.N.; Mamat, R. The optimum performance of the combined cycle power plant: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 459–474. [Google Scholar] [CrossRef]
- Ameri, M.; Ahmadi, P.; Khanmohammadi, S. Exergy analysis of a 420 MW combined cycle power plant. Int. J. Energy Res. 2008, 32, 175–183. [Google Scholar] [CrossRef]
- Polyzakis, A.L.; Koroneos, C.; Xydis, G. Optimum gas turbine cycle for combined cycle power plant. Energy Convers. Manag. 2008, 49, 551–563. [Google Scholar] [CrossRef]

| N/A | Thigh (K) | Tlow (K) | ηth | ηcarnot | ηendor | a | Cycle | Type | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 389 | 298 | 0.0940 | 0.2339 | 0.1247 | 0.3704 | LT-ORC | EXPER | [17] |
| 2 | 381 | 298 | 0.0881 | 0.2178 | 0.1156 | 0.3753 | LT-ORC | EXPER | [17] |
| 3 | 370 | 298 | 0.0737 | 0.1946 | 0.1026 | 0.3538 | LT-ORC | EXPER | [17] |
| 4 | 363 | 298 | 0.0574 | 0.1791 | 0.0939 | 0.2996 | LT-ORC | THEOR | [17] |
| 5 | 353 | 298 | 0.0522 | 0.1558 | 0.0812 | 0.3165 | LT-ORC | EXPER | [18] |
| 6 | 381 | 298 | 0.0794 | 0.2178 | 0.1156 | 0.3367 | LT-ORC | EXPER | [18] |
| 7 | 542 | 333 | 0.2536 | 0.3856 | 0.2162 | 0.6005 | HT-ORC | THEOR | [19] |
| 8 | 507 | 333 | 0.2341 | 0.3432 | 0.1896 | 0.6345 | HT-ORC | THEOR | [19] |
| 9 | 514 | 333 | 0.2316 | 0.3521 | 0.1951 | 0.6069 | HT-ORC | THEOR | [19] |
| 10 | 533 | 333 | 0.2155 | 0.3752 | 0.2096 | 0.5160 | HT-ORC | THEOR | [19] |
| 11 | 500 | 333 | 0.2125 | 0.3340 | 0.1839 | 0.5877 | HT-ORC | THEOR | [19] |
| 12 | 468 | 333 | 0.1957 | 0.2885 | 0.1565 | 0.6399 | HT-ORC | THEOR | [19] |
| 13 | 472 | 333 | 0.1800 | 0.2945 | 0.1601 | 0.5689 | HT-ORC | THEOR | [19] |
| 14 | 463 | 333 | 0.1714 | 0.2808 | 0.1519 | 0.5705 | HT-ORC | THEOR | [19] |
| 15 | 450 | 333 | 0.1338 | 0.2600 | 0.1398 | 0.4770 | HT-ORC | THEOR | [19] |
| 16 | 623 | 298 | 0.3260 | 0.5217 | 0.3084 | 0.5350 | WS-RC | THEOR | [20] |
| 17 | 373 | 298 | 0.1092 | 0.2011 | 0.1062 | 0.5151 | WS-RC | THEOR | [21] |
| 18 | 423 | 298 | 0.1702 | 0.2955 | 0.1607 | 0.5326 | WS-RC | THEOR | [21] |
| 19 | 473 | 298 | 0.2139 | 0.3700 | 0.2063 | 0.5209 | WS-RC | THEOR | [21] |
| 20 | 523 | 298 | 0.2451 | 0.4302 | 0.2452 | 0.4999 | WS-RC | THEOR | [21] |
| 21 | 573 | 299 | 0.2658 | 0.4782 | 0.2776 | 0.4750 | WS-RC | THEOR | [21] |
| 22 | 666 | 300 | 0.3700 | 0.5495 | 0.3288 | 0.5793 | WS-RC | EXPER | [22] |
| 23 | 1123 | 298 | 0.3870 | 0.7346 | 0.4849 | 0.3689 | Stirling cycle | EXPER | [23] |
| 24 | 1172 | 298 | 0.3750 | 0.7457 | 0.4958 | 0.3432 | Stirling cycle | EXPER | [23] |
| 25 | 773 | 298 | 0.3440 | 0.6145 | 0.3791 | 0.4423 | Stirling cycle | THEOR | [24] |
| 26 | 939 | 288 | 0.4873 | 0.6933 | 0.4462 | 0.5653 | Stirling cycle | THEOR | [25] |
| 27 | 623 | 298 | 0.2850 | 0.5217 | 0.3084 | 0.4549 | Stirling cycle | THEOR | [26] |
| 28 | 573 | 298 | 0.2690 | 0.4799 | 0.2788 | 0.4793 | Stirling cycle | THEOR | [26] |
| 29 | 523 | 298 | 0.2310 | 0.4302 | 0.2452 | 0.4670 | Stirling cycle | THEOR | [26] |
| 30 | 823 | 305 | 0.4190 | 0.6294 | 0.3912 | 0.5470 | SCO2-GT | THEOR | [27] |
| 31 | 1023 | 305 | 0.4652 | 0.7019 | 0.4540 | 0.5172 | SCO2-GT | THEOR | [27] |
| 32 | 823 | 323 | 0.3765 | 0.6075 | 0.3735 | 0.5051 | SCO2-GT | THEOR | [27] |
| 33 | 1023 | 323 | 0.4440 | 0.6843 | 0.4381 | 0.5092 | SCO2-GT | THEOR | [27] |
| 34 | 1123 | 298 | 0.4800 | 0.7346 | 0.4849 | 0.4929 | Air-GT | EXPER | [28] |
| 35 | 1123 | 298 | 0.4580 | 0.7346 | 0.4849 | 0.4617 | Air-GT | EXPER | [28] |
| 36 | 1152 | 298 | 0.4800 | 0.7413 | 0.4914 | 0.4836 | Air-GT | EXPER | [28] |
| 37 | 788 | 298 | 0.3780 | 0.6218 | 0.3850 | 0.4883 | Air-GT | EXPER | [28] |
| 38 | 1200 | 298 | 0.4000 | 0.7517 | 0.5017 | 0.3667 | CC | THEOR | [29] |
| 39 | 1500 | 298 | 0.5000 | 0.8013 | 0.5543 | 0.4289 | CC | THEOR | [29] |
| 40 | 1800 | 298 | 0.5500 | 0.8344 | 0.5931 | 0.4440 | CC | THEOR | [29] |
| 41 | 1244 | 293 | 0.4700 | 0.7645 | 0.5147 | 0.4391 | CC | EXPER | [30] |
| 42 | 1561 | 288 | 0.5047 | 0.8155 | 0.5705 | 0.4157 | CC | THEOR | [31] |
| Cycle | atotal | R2 | amin | amax |
|---|---|---|---|---|
| Low-Temperature ORC | 0.3481 | 99.44% | 0.2996 | 0.3753 |
| High-Temperature ORC | 0.5813 | 99.37% | 0.4770 | 0.6399 |
| Water-Steam Rankine cycle | 0.5295 | 99.51% | 0.4750 | 0.5793 |
| Stirling cycle | 0.4267 | 96.47% | 0.3432 | 0.5653 |
| S-CO2 gas turbine | 0.5189 | 99.91% | 0.5051 | 0.5470 |
| Air gas turbine | 0.4808 | 99.93% | 0.4617 | 0.4929 |
| Combined cycle | 0.4220 | 99.63% | 0.3667 | 0.4440 |
| TOTAL | 0.4594 | 98.06% | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellos, E. Development of a Semi-Empirical Model for Estimating the Efficiency of Thermodynamic Power Cycles. Sci 2023, 5, 33. https://doi.org/10.3390/sci5030033
Bellos E. Development of a Semi-Empirical Model for Estimating the Efficiency of Thermodynamic Power Cycles. Sci. 2023; 5(3):33. https://doi.org/10.3390/sci5030033
Chicago/Turabian StyleBellos, Evangelos. 2023. "Development of a Semi-Empirical Model for Estimating the Efficiency of Thermodynamic Power Cycles" Sci 5, no. 3: 33. https://doi.org/10.3390/sci5030033
APA StyleBellos, E. (2023). Development of a Semi-Empirical Model for Estimating the Efficiency of Thermodynamic Power Cycles. Sci, 5(3), 33. https://doi.org/10.3390/sci5030033






