Analysis of Gun Crimes in New York City
Abstract
1. Introduction
- According to a Pew Research Center study, 44% of Americans say they know someone who has been shot, and another 23% say a weapon has been used to threaten or intimidate them or a family member;
- A September 2019 ABC News/Washington Post poll found that six in 10 Americans fear a mass shooting in their community;
- In a March 2018 USA Today/Ipsos poll, 53% of youth aged 13–17 identified gun violence as a “significant concern”, above all other concerns listed in the survey;
- More than 342,439 people were killed by shooting in the United States from 2008 to 2017, which means that one person is killed with a gun in this country every 15 min.
- At the end of 2019, a total of 776 shootings were recorded, both mass and non-mass;
- In August 2020, this number had already been exceeded, with a record of 779 shootings in all the districts of the state of New York, with a total of 942 victims, including injuries and deaths;
- According to the statistics, in the last year, shootings have increased by 38% in New York City, and 77% of shooting victims are people of color;
- Currently, shootings in New York City have been on the rise, with firearm attacks having increased since 2020;
- So far this year, the increase in armed violence in New York has reached 32% compared to the previous year, and a total of 51 deaths have been recorded.
2. State of the Art
3. Materials
- (1)
- The incident_key variable is an identification code of the incident. It was found to be duplicated in some cases, and duplicate codes were removed. Thus, we went from 664 initial observations to 528 observations.
- (2)
- The values of the categorical variables have been recoded with numerical values (see Table A1 of Appendix A).
- (3)
- Treatment of missing data:
- (4)
- Treatment of outliers:
- (5)
- Selection of variables:
4. Methods
- (1)
- Logistic regression [14]: This technique makes it possible to study the association between a categorical or binary dependent variable and a set of categorical or continuous explanatory variables. To achieve this, the probability that the independent variable takes one or the other value is modeled based on the possible combinations of values of the independent variables. The result will be a function that allows us to estimate the parameters by maximum likelihood. This method presents the advantage that allows us to quantify the effects of the predictors on the response through the so-called odds ratio that quantify the change in the probability that the estimated variable belongs to one category or another based on the change of category of each variable included in the model.
- (2)
- Neural networks [15]: This technique makes it possible to obtain underlying relationships in a data set using a model inspired by physical neural networks. The model consists of a set of interrelated nodes of 3 types (input nodes, output nodes, and hidden layers). The input nodes are the independent variables of the model, the output nodes are the dependent variables of the model, and the hidden layers are artificial variables that do not exist in the data. In addition, there is a combination function that allows input nodes to be related to hidden nodes by combining the inputs using weights, and an activation function that defines the output of a node given an input or a set of inputs (for this modifies the result value or imposes a limit that must be exceeded in order to proceed to another neuron).
- (3)
- Decision tree [16]: It is a prediction model similar to a flowchart, where decisions are made based on the discriminant capacity of a variable. Probabilities are assigned to each event and an outcome is determined for each branch. In this way, it is possible to distribute the observations according to their attributes and thus predict the value of the response variable.
- (4)
- Random forest [17]: This technique uses a set of individual decision trees, each trained with a random sample drawn from the original training data using bootstrapping. This implies that each tree is trained with slightly different data. In each individual tree, the observations are distributed by bifurcations (nodes) generating the structure of the tree until reaching a terminal node. The prediction of a new observation is obtained by aggregating the predictions of all the individual trees that make up the model.
- (5)
- Gradient boosting [18]: This technique is based on using a set of individual decision trees, trained sequentially. Each new tree uses information from the previous tree to learn from its mistakes, improving iteration by iteration. To do this, the weights of the observations belonging to the classes of the event of interest are updated through the optimization in the downward direction of a certain loss or error function, managing to give greater relevance in each iteration to the observations misclassified in previous steps. (An attempt is made to minimize the residuals in the decreasing direction by repeating the construction of decision trees, slightly transforming the preliminary predictions.)
5. Results
5.1. Decision Trees
- Data Set A. Target Variable: Staten Island District
- Data Set B. Target Variable: Borough of the Bronx
- Data Set C. Target Variable: Borough of Brooklyn
- Data Set D. Target Variable: Borough of Manhattan
- Data Set E. Target Variable: Borough of Queens
5.2. Logistic Regression
5.3. Neural Networks
5.4. Random Forest
5.5. Gradient Boosting
5.6. Comparation Models
- Set A. Target Variable: Staten Island District
- Set B. Target Variable: District of the Bronx
- Set C. Target Variable: Brooklyn District
- Set D. Target Variable: Manhattan District
- Set E. Target Variable: Queens District
6. Discussion
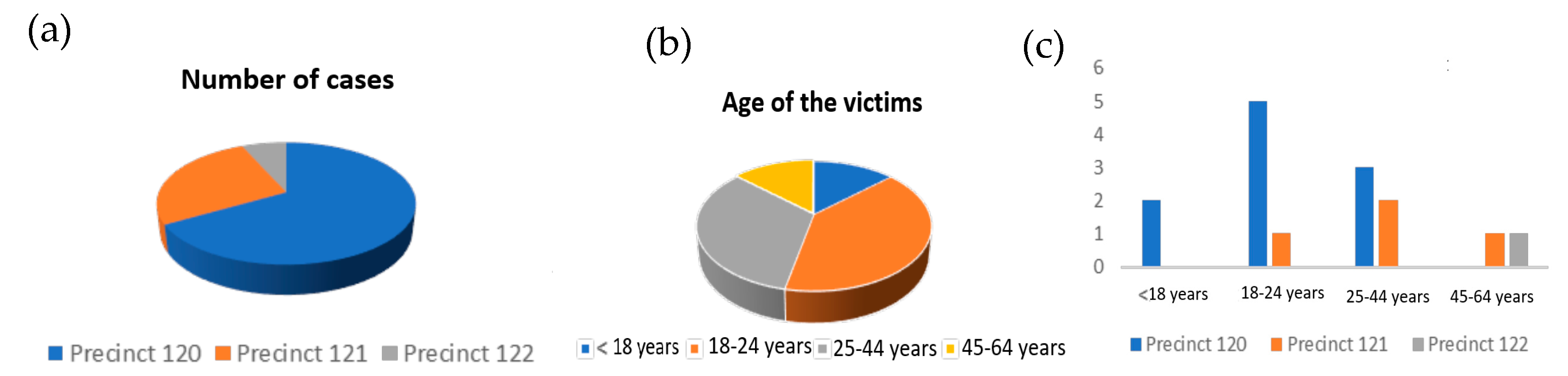
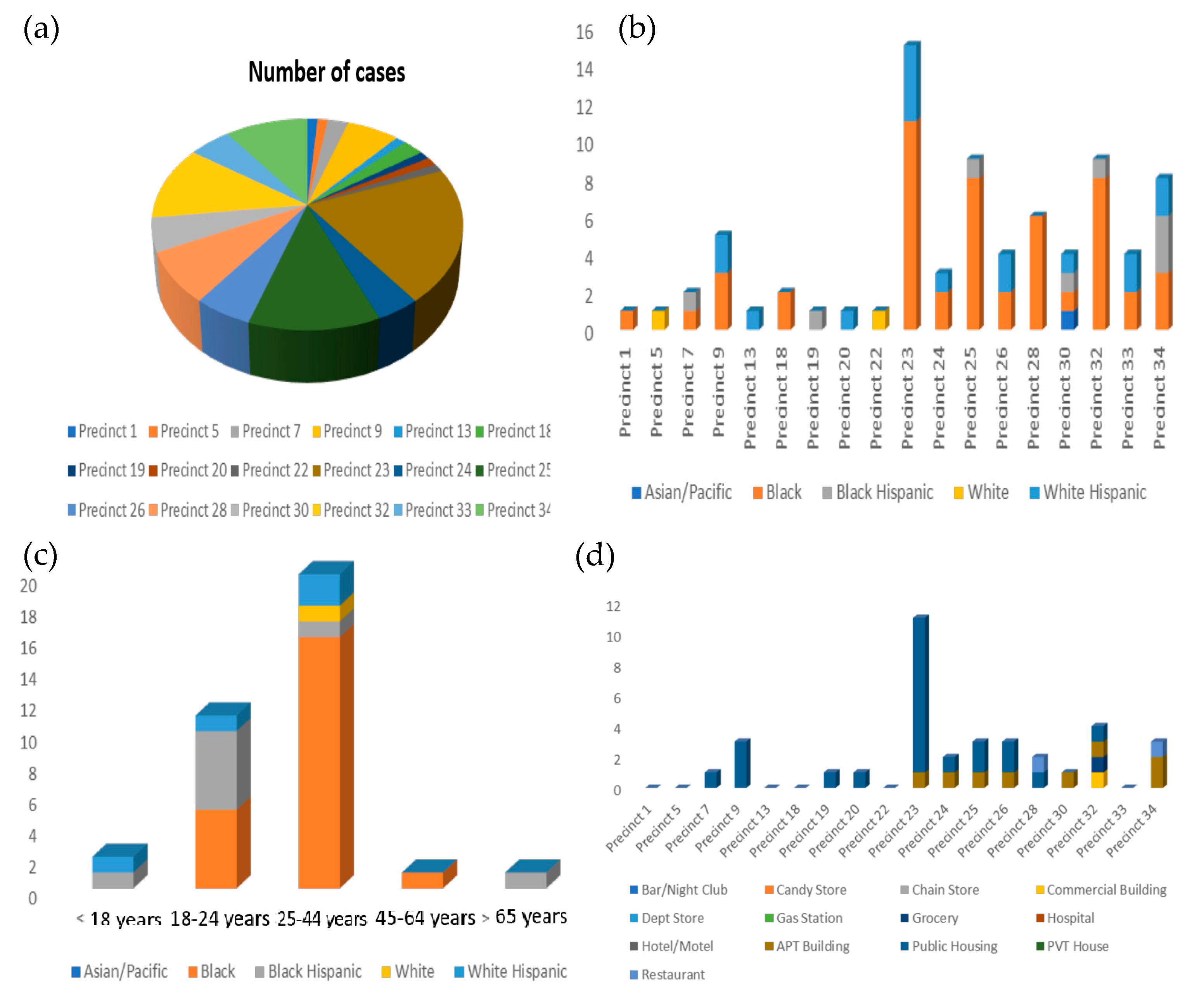
6.1. Staten Island District
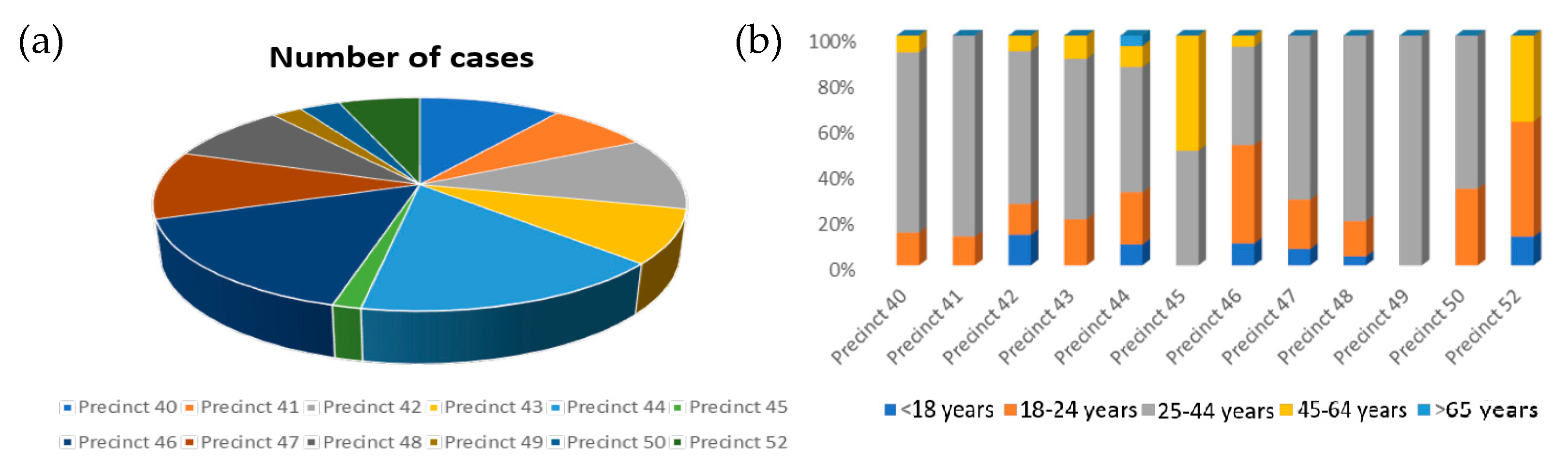
6.2. Bronx District
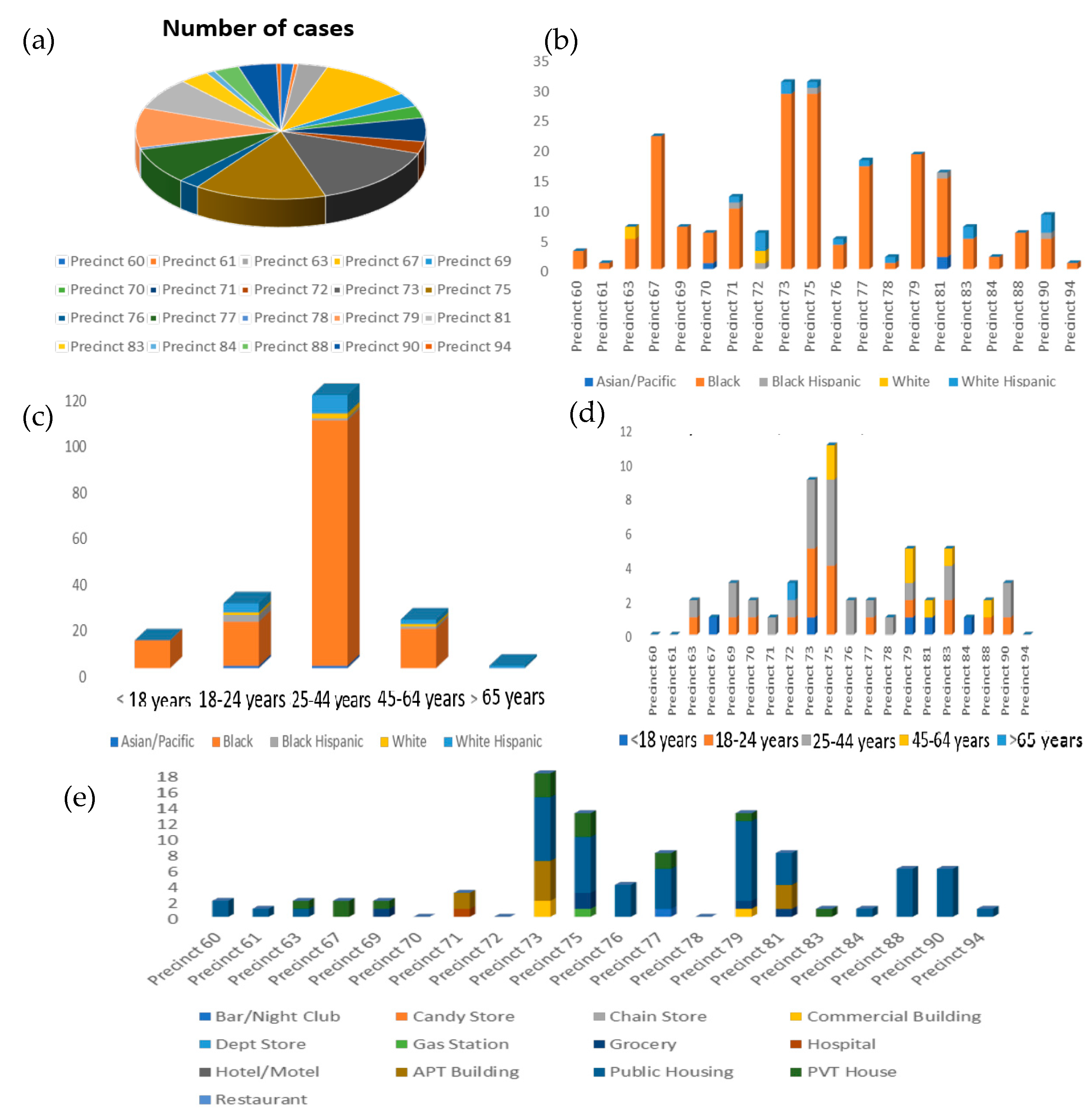
6.3. Brooklyn District
6.4. Manhattan District
6.5. Queens District
7. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Set | Category | Values |
|---|---|---|
| Borough | Staten Island | 1 |
| Bronx | 2 | |
| Brooklyn | 3 | |
| Manhattan | 4 | |
| Queens | 5 | |
| Location-desc | Bar/Night Club | 1 |
| Candy Store | 2 | |
| Chain Store | 3 | |
| Commercial Building | 4 | |
| Dept Store | 5 | |
| Gas Station | 6 | |
| Grocery | 7 | |
| Hospital | 8 | |
| Hotel/Motel | 9 | |
| APT Building | 10 | |
| Public Housing | 11 | |
| PVT House | 12 | |
| Restaurant | 13 | |
| Unclassified | 99 | |
| Statistical_murder_flag | True | 1 |
| False | 2 | |
| Perp_age_group | <18 | 1 |
| 18–24 | 2 | |
| 25–44 | 3 | |
| 45–64 | 4 | |
| 65 | 5 | |
| Unknown | 99 | |
| Perp_race | Asian/Pacific Islander | 1 |
| Black | 2 | |
| Black Hispanic | 3 | |
| White | 4 | |
| White Hispanic | 5 | |
| Unknown | 99 | |
| Perp_sex | M | 1 |
| F | 2 | |
| Vic_age_group | <18 | 1 |
| 18–24 | 2 | |
| 25–44 | 3 | |
| 45–64 | 4 | |
| 65 | 5 | |
| Unknown | 99 | |
| Vic_race | Asian/Pacific Islander | 1 |
| Black | 2 | |
| Black Hispanic | 3 | |
| White | 4 | |
| White Hispanic | 5 | |
| Unknown | 99 | |
| Vic_sex | M | 1 |
| F | 2 |
Appendix B
| Decision Tree | Characteristics | Failure Rate | ROC |
|---|---|---|---|
| Tree 2 | Cut point: ProbChisq p-value: 0.25 Max deep: 22 Sheet size: 17 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.019074 | 0.963 |
| Tree 4 | Cut point: Entropy p-value: 0.25 Max deep: 15 Sheet size: 10 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.019074 | 0.963 |
| Tree 5 | Cut point: ProbChisq p-value: 0.25 Max deep: 12 Sheet size: 8 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.010899 | 0.994 |
| Tree 6 | Cut point: Gini p-value: 0.25 Max deep: 8 Sheet size: 6 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.008174 | 0.989 |
| Tree 12 | Cut point: Gini p-value: 0.25 Max deep: 18 Sheet size: 14 Adjustment p-value: Bonferroni(Before) Deep: Yes | 0.019074 | 0.963 |
| Tree 17 | Cut point: Entropy p-value: 0.25 Max deep: 8 Sheet size: 6 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0 | 1 |
| Decision Tree | Characteristics |
|---|---|
| Tree 20 | Cut point: ProbChisq p-value: 0.20 Max deep: 8 Sheet size: 6 Adjustment p-value: Bonferroni (Before) Deep: Yes |
| Decision Tree | Characteristics | Failure Rate | ROC |
|---|---|---|---|
| Tree 6 | Cut point: ProbChisq p-value: 0.25 Max deep: 20 Sheep size: 16 Adjustment p-value: Bonferroni (After) Deep: Yes | 0.021739 | 0.993 |
| Tree 10 | Cut point: Entropy p-value: 0.25 Max deep: 16 Sheep size: 10 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.005435 | 0.997 |
| Tree 5 | Cut point: Gini p-value: 0.25 Max deep: 12 Sheep size: 8 Adjustment p-value: Bonferroni;no Deep: Yes | 0.013587 | 0.993 |
| Tree 20 | Cut point: ProbChisq p-value: 0.20 Max deep: 8 Sheep size: 6 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.013587 | 0.993 |
| Tree 16 | Cut point: Entropy p-value: 0.25 Max deep: 18 Sheep size: 14 Adjustment p-value: Bonferroni:no Deep: Yes | 0.024457 | 0.998 |
| Tree 8 | Cut point: ProbChisq p-value: 0.25 Max deep: 10 Sheep size: 8 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.013587 | 0.993 |
| Decision Tree | Characteristics | Failure Rate | ROC |
|---|---|---|---|
| Tree 2 | Cut point: ProbChisq p-value: 0.20 Max deep: 22 Sheep size: 17 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.03523 | 0.99 |
| Tree 4 | Cut point: Entropy p-value: 0.25 Max deep: 7 Sheep size: 5 Adjustmen p-value: Bonferroni (Before) Deep: Yes | 0.00271 | 0.999 |
| Tree 12 | Cut point: ProbChisq p-value: 0.25 Max deep: 20 Sheep size: 16 Adjustment p-value: Bonferroni (After) Deep: Yes | 0.03794 | 0.981 |
| Tree 6 | Cut point: Gini p-value: 0.25 Max deep: 8 Sheep size: 6 Adjustment p-value: Bonferroni: No Deep: Yes | 0.00271 | 0.999 |
| Tree 5 | Cut point: Gini p-value: 0.25 Max deep: 12 Sheep size: 8 Adjustment p-value: Bonferroni: No Deep: Yes | 0.00271 | 0.999 |
| Tree 8 | Cut point: ProbChisq p-value: 0.25 Max deep: 10 Sheep size: 8 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.01626 | 0.995 |
| Decision Tree | Characteristics | Failure Rate | ROC |
|---|---|---|---|
| Tree 5 | Cut point: ProbChisq p-value: 0.25 Max deep: 14 Sheet size: 8 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.016304 | 0.954 |
| Tree 6 | Cut point: ProbChisq p-value: 0.25 Max deep: 8 Sheet size: 4 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.002717 | 0.992 |
| Tree 7 | Cut point: Entropy p-value: 0.25 Max deep: 15 Sheet size: 10 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.002717 | 0.992 |
| Tree 9 | Cut point: Gini p-value: 0.15 Max deep: 18 Sheet size: 12 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.013587 | 0.991 |
| Tree 11 | Cut point: Gini p-value: 0.25 Max deep: 23 Sheet size: 15 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.016304 | 0.991 |
| Tree 19 | Cut point: Entropy p-value: 0.25 Max deep: 12 Sheet size: 6 Adjustment p-value: Bonferroni (Before) Deep: Yes | 0.002717 | 0.992 |
References
- Stansfield, R.; Semenza, D.; Steidley, T. Public guns, private violence: The association of city-level firearm availability and intimate partner homicide in the United States. Prev. Med. 2021, 148, 106599. [Google Scholar] [CrossRef] [PubMed]
- Chalfin, A.; LaForest, M.; Kaplan, J. Can precision policing reduce gun violence? evidence from “gang takedowns” in new york city. J. Policy Anal. Manag. 2021, 40, 1047–1082. [Google Scholar] [CrossRef]
- McArdle, A.; Erzen, T. (Eds.) Zero Tolerance: Quality of Life and the New Police Brutality in New York City; NYU Press: New York, NY, USA, 2001. [Google Scholar]
- Sherman, L.W. Reducing gun violence: What works, what doesn’t, what’s promising. Crim. Justice 2001, 1, 11–25. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Kotsiantis, S.B. Decision trees: A recent overview. Artif. Intell. Rev. 2013, 39, 261–283. [Google Scholar] [CrossRef]
- Shaik, A.B.; Srinivasan, S. A brief survey on random forest ensembles in classification model. In International Conference on Innovative Computing and Communications, Proceedings of ICICC 2018, Manila, Philippines, 5-7 January 2018; Springer: Singapore, 2019; Volume 2, pp. 253–260. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2020, 54, 1937–1967. [Google Scholar] [CrossRef]
- Larsen, D.A.; Lane, S.; Jennings-Bey, T.; Haygood-El, A.; Brundage, K.; Rubinstein, R.A. Spatio-temporal patterns of gun violence in Syracuse, New York 2009–2015. PLoS ONE 2017, 12, e0173001. [Google Scholar] [CrossRef] [PubMed]
- James, N.; Menzies, M. Dual-domain analysis of gun violence incidents in the United States. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 111101. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, J.; Mohler, G.; Brantingham, P.J. Association between race, shooting hot spots, and the surge in gun violence during the COVID-19 pandemic in Philadelphia, New York and Los Angeles. Prev. Med. 2022, 165, 107241. [Google Scholar] [CrossRef] [PubMed]
- Kemal, S.; Sheehan, K.; Feinglass, J. Gun carrying among freshmen and sophomores in Chicago, New York City and Los Angeles public schools: The Youth Risk Behavior Survey, 2007–2013. Inj. Epidemiol. 2018, 5, 12–53. [Google Scholar] [CrossRef] [PubMed]
- Messner, S.F.; Galea, S.; Tardiff, K.J.; Tracy, M.; Bucciarelli, A.; Piper, T.M.; Frye, V.; Vlahov, D. Policing, drugs, and the homicide decline in New York City in the 1990s. Criminology 2007, 45, 385–414. [Google Scholar] [CrossRef]
- Sanchez, C.; Jaguan, D.; Shaikh, S.; McKenney, M.; Elkbuli, A. A systematic review of the causes and prevention strategies in reducing gun violence in the United States. Am. J. Emerg. Med. 2020, 38, 2169–2178. [Google Scholar] [CrossRef] [PubMed]
- Goel, S.; Rao, J.M.; Shroff, R. Precinct or prejudice? Understanding racial disparities in New York City’s stop-and-frisk policy. Ann. Appl. Stat. 2016, 10, 365–394. [Google Scholar] [CrossRef]
- Saunders, J.; Hunt, P.; Hollywood, J.S. Predictions put into practice: A quasi-experimental evaluation of Chicago’s predictive policing pilot. J. Exp. Criminol. 2016, 12, 347–371. [Google Scholar] [CrossRef]
- Johnson, B.T.; Sisti, A.; Bernstein, M.; Chen, K.; Hennessy, E.A.; Acabchuk, R.L.; Matos, M. Community-level factors and incidence of gun violence in the United States, 2014–2017. Soc. Sci. Med. 2021, 280, 113969. [Google Scholar] [CrossRef] [PubMed]
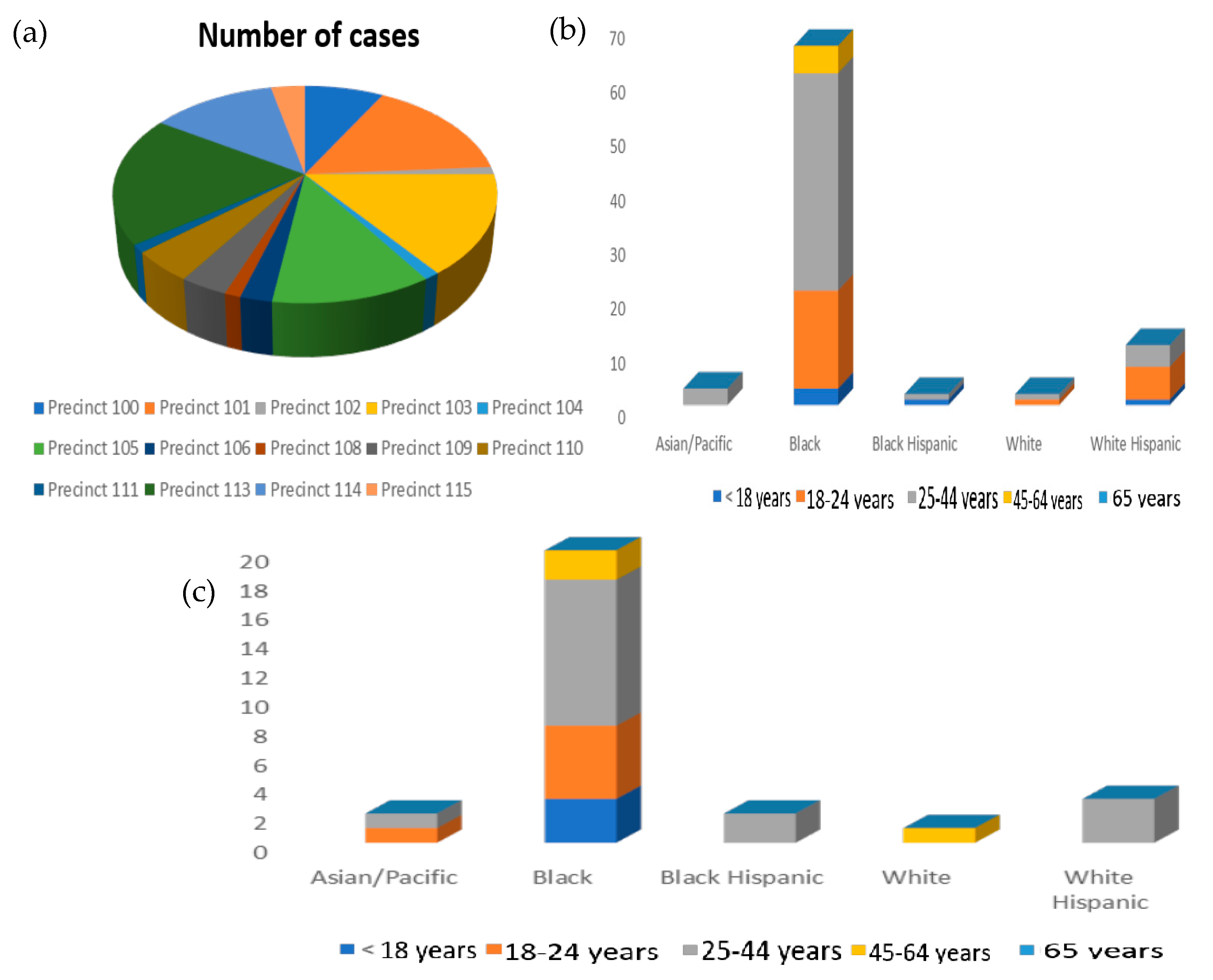
| Variables | Description | Values |
|---|---|---|
| Incident_key | Shooting ID Code | Identifier |
| Borough | District in which the shooting occurred | Staten Island, Queens, Manhattan, Brooklyn, Bronx |
| Precinct | Police area where the shooting occurred | Identifier |
| Jurisdiction | Jurisdiction in which the shooting occurred | Identifier |
| Location Desc | Place/establishment where the shooting took place | Bar/Night Club, Candy Store, Chain Store, Commercial Building, Department Store, Gas Station, Grocery, Hospital, Hotel/Motel, APT Building, PVT House, Restaurant |
| Statistical murder flag | The shooting has caused deaths | yes, no |
| Perp age group | Age group of shooter | <18, 18–24, 25–44, 45–64, 65 and more |
| Perp sex | Sex of the perpetrator of the shooting | male, female |
| Perp race | Race/Ethnicity of shooter | Asian/Pacific Islander, Black, Black Hispanic, White, White Hispanic |
| Vic_age_group | Age group of shooting victims | <18, 18–24, 25–44, 45–64, 65 and more |
| Vic_sex | Victim’s sex | male, female |
| Vic_race | Race/Ethnicity of the victim | Asian/Pacific Islander, Black, Black Hispanic, White, White Hispanic |
| Occur_date | Exact date of the shooting | Date |
| Occur_time | Exact time of the shooting | Time |
| X_coord_cd | X co-ordinate of the center block for the New York State co-ordinate system | Co-ordinate |
| Y_coord_cd | Y co-ordinate of the center block for the New York State co-ordinate system | Co-ordinate |
| Latitude | Latitude co-ordinate for the Global Co-ordinate System | Co-ordinate |
| Longitude | Longitude co-ordinate for the Global Co-ordinate System | Co-ordinate |
| New_georeferenced_column | Georeference | Co-ordinate |
| Model | Characteristics | Failure Rate | AIC | SBC | ROC | AUC |
|---|---|---|---|---|---|---|
| Set A | Logistic regression Selecting variables: No Data partition: 60, 20, 20 Seed: 12,345 | 0.257143 | 630, 2015 | 1812, 262 | 1 | 315 |
| Set B | Logistic regression Selecting variables: No Data partition: 70, 30 Seed: 12,345 | 0 | 734, 2343 | 2167, 502 | 1 | 367 |
| Set C | Logistic regression Selecting variables: No Data partition: 70, 30 Seed: 12,349 | 0 | 7342, 343 | 2162, 643 | 1 | 366 |
| Set D | Logistic regression Selecting variables: No Data partition: 60, 20, 20 Seed: 12,345 | 0.15094 | 632, 169 | 1818, 984 | 1 | 316 |
| Set E | Logistic regression Selecting variables: No Data partition: 70, 30 Seed: 12,345 | 0 | 736, 2025 | 2174, 377 | 1 | 368 |
| Set | Seed | Node Size | Activation Function | Optimization Algorithm | Iterations Early Stopping | Error Objective Variable |
|---|---|---|---|---|---|---|
| B | 12,345 | 4 | Softmax | QUANEW | 10 | 0.14293 |
| B | 43,265 | 7 | Log | LEVMAR | 17 | 0.49966 |
| B | 32,567 | 12 | TanH | LEVMAR | 40 | 0.49433 |
| B | 12,349 | 10 | Softmax | QUANEW | 28 | 0.13941 |
| C | 31,567 | 8 | TanH | LEVMAR | 24 | 0.49999 |
| C | 22,367 | 3 | Log | QUANEW | 44 | 0.49138 |
| C | 67,453 | 7 | Softmax | QUANEW | 12 | 0.17545 |
| C | 11,567 | 10 | Log | LEVMAR | 15 | 0.49998 |
| D | 34,512 | 15 | TanH | QUANEW | 8 | 0.49969 |
| D | 77,156 | 5 | Softmax | LEVMAR | 25 | 0.00294 |
| D | 12,349 | 9 | Log | LEVMAR | 40 | 0.48635 |
| D | 45,447 | 3 | TanH | QUANEW | 28 | 0.49965 |
| E | 21,219 | 2 | Log | LEVMAR | 16 | 0.49678 |
| E | 30,197 | 8 | Softmax | QUANEW | 34 | 0.10472 |
| E | 66,897 | 12 | TanH | QUANEW | 56 | 0.09357 |
| E | 34,565 | 4 | Log | LEVMAR | 22 | 0.44616 |
| Set | Model of Red | Node Size | Activation Function | Optimization Algorithm | Failure Rate | Evaluation ROC |
|---|---|---|---|---|---|---|
| B | NET 1 | 4 | Softmax | QUANEW | 0.24431 | 0.83 |
| B | NET 2 | 7 | Log | LEVMAR | 0.25757 | 0.841 |
| B | NET 3 | 12 | TanH | LEVMAR | 0.74242 | 0.711 |
| B | NET 4 | 4 | TanH | Back Prop (mom = 0.01) | 0.45833 | 0.753 |
| B | NET 5 | 10 | Softmax | QUANEW | 0.22727 | 0.842 |
| C | NET 6 | 8 | TanH | LEVMAR | 0.49242 | 0.705 |
| C | NET 7 | 3 | Log | QUANEW | 0.39962 | 0.882 |
| C | NET 8 | 7 | Softmax | QUANEW | 0.21780 | 0.822 |
| C | NET 9 | 10 | Log | LEVMAR | 0.20833 | 0.714 |
| C | NET 10 | 3 | Tahn | TRUST-REGION | 0.11363 | 0.918 |
| D | NET 11 | 15 | TanH | QUANEW | 0.85227 | 0.58 |
| D | NET 12 | 5 | Softmax | LEVMAR | 1 | |
| D | NET 13 | 9 | Log | LEVMAR | 0.14772 | 0.658 |
| D | NET 14 | 3 | TanH | QUANEW | 0.85227 | 0.407 |
| D | NET 15 | 3 | TanH | Back Prop (mom = 0.01) | 0.85227 | 0.407 |
| E | NET 16 | 2 | Log | LEVMAR | 0.16666 | 0.668 |
| E | NET 17 | 8 | Softmax | QUANEW | 0.16666 | 0.877 |
| E | NET 18 | 12 | TanH | QUANEW | 0.09659 | 0.8 |
| E | NET 19 | 4 | Log | LEVMAR | 0.16666 | 0.767 |
| E | NET 20 | 12 | tanH | TRUST-REGION | 0.10416 | 0.705 |
| Model | Set | Iterations | Node Size | Number of Variables | Average Failure Rate | Average AUC |
|---|---|---|---|---|---|---|
| Bagging1 | A | 100 | 10 | 13 | 0.0136 | 0.99 |
| Bagging2 | B | 100 | 12 | 13 | 0 | 1 |
| Bagging3 | C | 100 | 15 | 13 | 0.0081 | 0.99 |
| Bagging4 | D | 100 | 14 | 13 | 0.0380 | 0.999 |
| Bagging5 | E | 100 | 8 | 13 | 0.0135 | 0.999 |
| RandomForest1 | A | 100 | 12 | 8 | 0.0054 | 1 |
| RandomForest2 | A | 100 | 14 | 11 | 0.0054 | 1 |
| RandomForest3 | A | 100 | 16 | 7 | 0.0163 | 1 |
| RandomForest4 | B | 100 | 10 | 6 | 0 | 1 |
| RandomForest5 | B | 100 | 15 | 9 | 0 | 1 |
| RandomForest6 | B | 100 | 8 | 5 | 0.0272 | 1 |
| RandomForest7 | C | 100 | 12 | 11 | 0 | 0.99 |
| RandomForest8 | C | 100 | 7 | 12 | 0 | 1 |
| RandomForest9 | C | 100 | 15 | 9 | 0.0217 | 0.998 |
| RandomForest10 | D | 100 | 6 | 10 | 0.0163 | 0.999 |
| RandomForest11 | D | 100 | 14 | 6 | 0.0217 | 0.998 |
| RandomForest12 | D | 100 | 9 | 8 | 0.0217 | 0.99 |
| RandomForest13 | E | 100 | 12 | 12 | 0.0054 | 0.998 |
| RandomForest14 | E | 100 | 6 | 5 | 0.0326 | 0.994 |
| RandomForest15 | E | 100 | 9 | 8 | 0.0108 | 1 |
| Model | Set | Iterations | Node Size | Number of Variables | Average Failure Rate | Average AUC |
|---|---|---|---|---|---|---|
| RandomForest1 | A | 100 | 12 | 8 | 0.0054 | 1 |
| RandomForest6 | B | 100 | 8 | 5 | 0.0272 | 1 |
| RandomForest8 | C | 100 | 7 | 12 | 0 | 1 |
| RandomForest10 | D | 100 | 6 | 10 | 0.0163 | 0.999 |
| RandomForest15 | E | 100 | 9 | 8 | 0.0108 | 1 |
| Model | Set | Minimum Number of Observations | Iterations | Shrink | Failure Rate | AUC |
|---|---|---|---|---|---|---|
| GradientBoosting1 | A | 5 | 200 | 0.1 | 0 | 1 |
| GradientBoosting2 | A | 10 | 100 | 0.03 | 0.00545 | 1 |
| GradientBoosting3 | A | 8 | 300 | 0.001 | 0.25613 | 0.986 |
| GradientBoosting4 | A | 4 | 100 | 0.3 | 0 | 1 |
| GradientBoosting5 | B | 5 | 100 | 0.05 | 0 | 1 |
| GradientBoosting6 | B | 13 | 500 | 0.1 | 0 | 1 |
| GradientBoosting7 | B | 5 | 300 | 0.01 | 0.00817 | 1 |
| GradientBoosting8 | B | 7 | 200 | 0.04 | 0 | 1 |
| GradientBoosting9 | C | 8 | 300 | 0.2 | 0 | 1 |
| GradientBoosting10 | C | 5 | 100 | 0.06 | 0.00815 | 0.999 |
| GradientBoosting11 | C | 11 | 400 | 0.003 | 0.0625 | 0.998 |
| GradientBoosting12 | C | 9 | 500 | 0.007 | 0.00815 | 0.999 |
| GradientBoosting13 | D | 13 | 100 | 0.1 | 0 | 1 |
| GradientBoosting14 | D | 6 | 200 | 0.02 | 0.00542 | 1 |
| GradientBoosting15 | D | 4 | 400 | 0.04 | 0 | 1 |
| GradientBoosting16 | E | 8 | 100 | 0.3 | 0 | 1 |
| GradientBoosting17 | E | 10 | 300 | 0.003 | 0.02989 | 0.982 |
| GradientBoosting18 | E | 4 | 200 | 0.07 | 0 | 1 |
| GradientBoosting19 | E | 13 | 500 | 0.03 | 0 | 1 |
| Set | Name Variable | Number of Division Rules | Importance |
|---|---|---|---|
| A | Y_Coord_CD | 8 | 1 |
| Precinct | 10 | 0.9874 | |
| Longitude | 11 | 0.51509 | |
| Latitude | 4 | 0.11659 | |
| Vic_Age_Group | 1 | 0.01146 | |
| B | Y_Coord_CD | 33 | 1 |
| Precinct | 63 | 0.4965 | |
| Longitude | 29 | 0.2609 | |
| Latitude | 9 | 0.0637 | |
| X_Coord_CD | 5 | 0.0214 | |
| Vic_Age_Group | 1 | 0.00727 | |
| C | Precinct | 30 | 1 |
| Y_Coord_CD | 48 | 0.61135 | |
| Longitude | 32 | 0.2736 | |
| X_Coord_CD | 6 | 0.1000 | |
| Incident_key | 13 | 0.06202 | |
| Latitude | 8 | 0.04057 | |
| Location_desc | 6 | 0.03461 | |
| Perp_Age_Group | 3 | 0.02885 | |
| Vic_Age_Group | 1 | 0.02232 | |
| Vic_Race | 1 | 0.00798 | |
| D | Longitude | 60 | 1 |
| Y_Coord_CD | 45 | 0.9158 | |
| Precinct | 59 | 0.90222 | |
| Latitude | 17 | 0.5656 | |
| X_Coord_CD | 8 | 0.4431 | |
| Vic_Race | 13 | 0.1168 | |
| Location_desc | 7 | 0.0788 | |
| Perp_Age_Group | 3 | 0.0709 | |
| Perp_Race | 4 | 0.0636 | |
| Vic_Age_Group | 5 | 0.0473 | |
| E | Longitude | 72 | 1 |
| Precinct | 97 | 0.5829 | |
| Y_Coord_CD | 97 | 0.3996 | |
| Latitude | 22 | 0.1742 | |
| Vic_Race | 5 | 0.0408 | |
| Perp_Race | 3 | 0.0262 | |
| Incident_key | 3 | 0.0249 | |
| X_Coord_CD | 1 | 0.0146 | |
| Perp_Age_Group | 3 | 0.0127 | |
| Vic_Age_Group | 2 | 0.0091 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarasa-Cabezuelo, A. Analysis of Gun Crimes in New York City. Sci 2023, 5, 18. https://doi.org/10.3390/sci5020018
Sarasa-Cabezuelo A. Analysis of Gun Crimes in New York City. Sci. 2023; 5(2):18. https://doi.org/10.3390/sci5020018
Chicago/Turabian StyleSarasa-Cabezuelo, Antonio. 2023. "Analysis of Gun Crimes in New York City" Sci 5, no. 2: 18. https://doi.org/10.3390/sci5020018
APA StyleSarasa-Cabezuelo, A. (2023). Analysis of Gun Crimes in New York City. Sci, 5(2), 18. https://doi.org/10.3390/sci5020018






