Two-Dimensional Model for Consolidation-Induced Solute Transport in an Unsaturated Porous Medium
Abstract
1. Introduction
2. Theoretical Model
2.1. Two-Dimensional Consolidation Model
2.2. Two-Dimensional Solute Transport Model
2.3. Special Case 1: Two-Dimensional Saturated Porous Model
2.4. Special Case 2: One-Dimensional Unsaturated Porous Model
2.5. Special Case 3: One-Dimensional Saturated Model
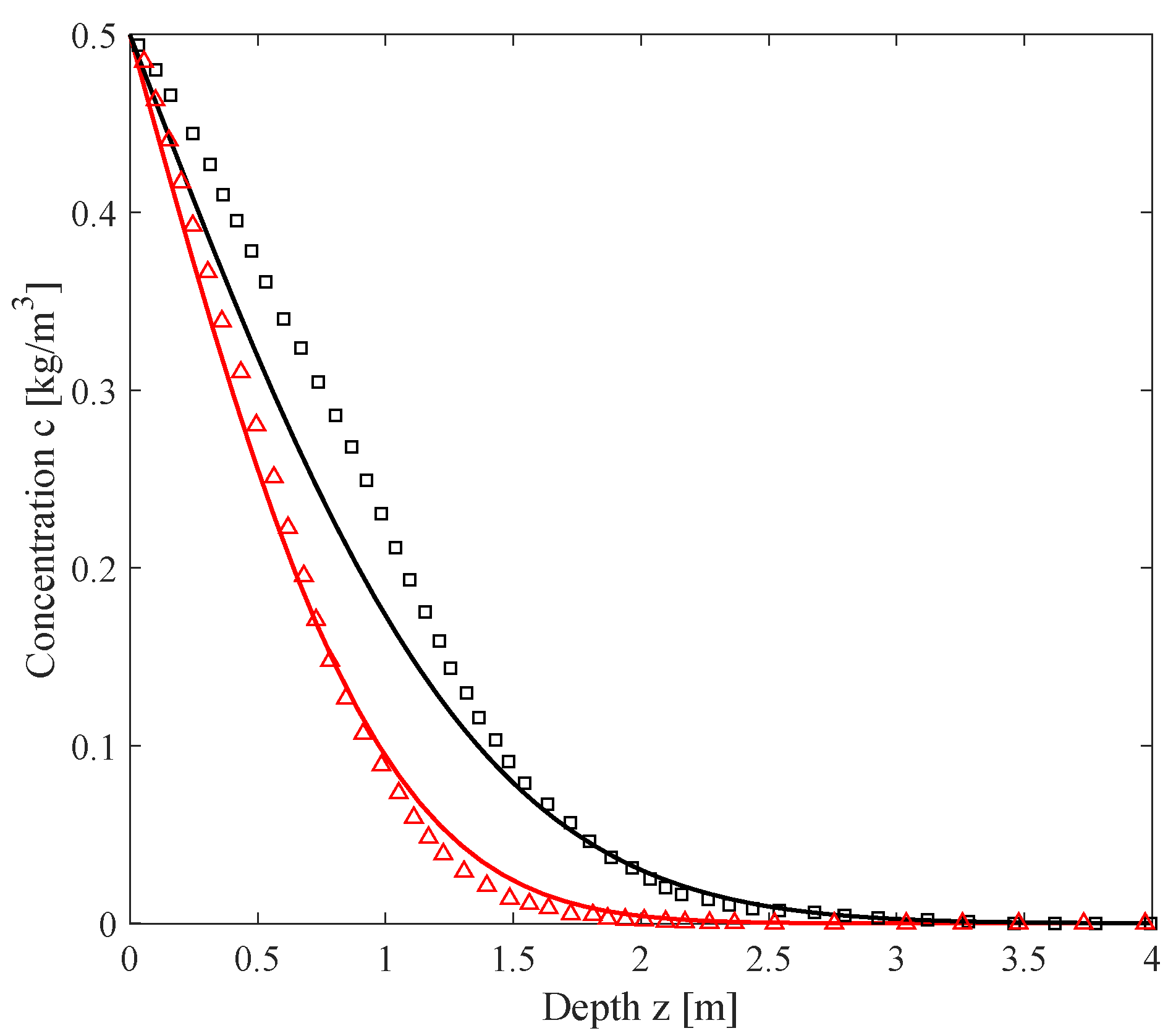
3. Model Validation
4. Results and Discussions
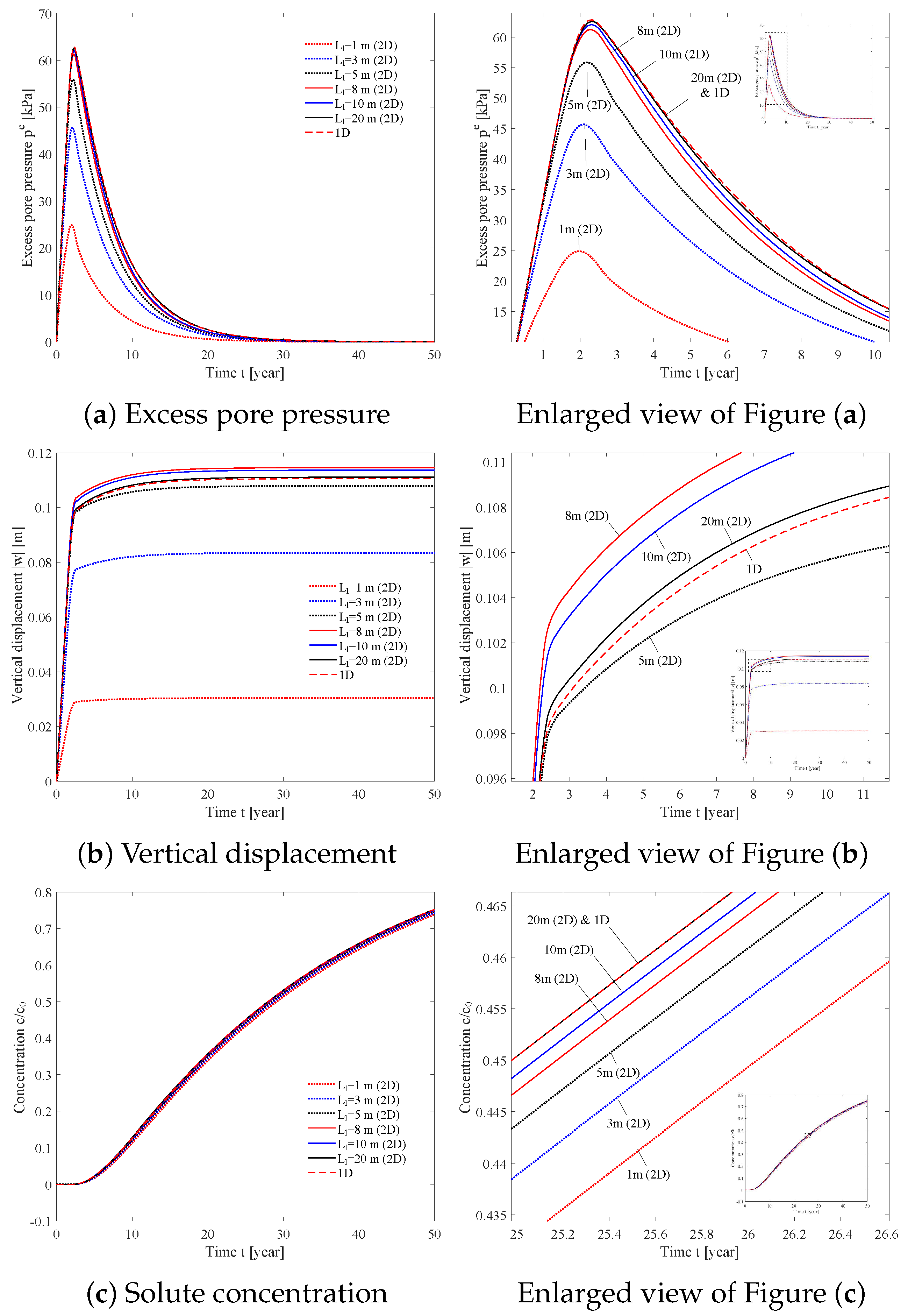
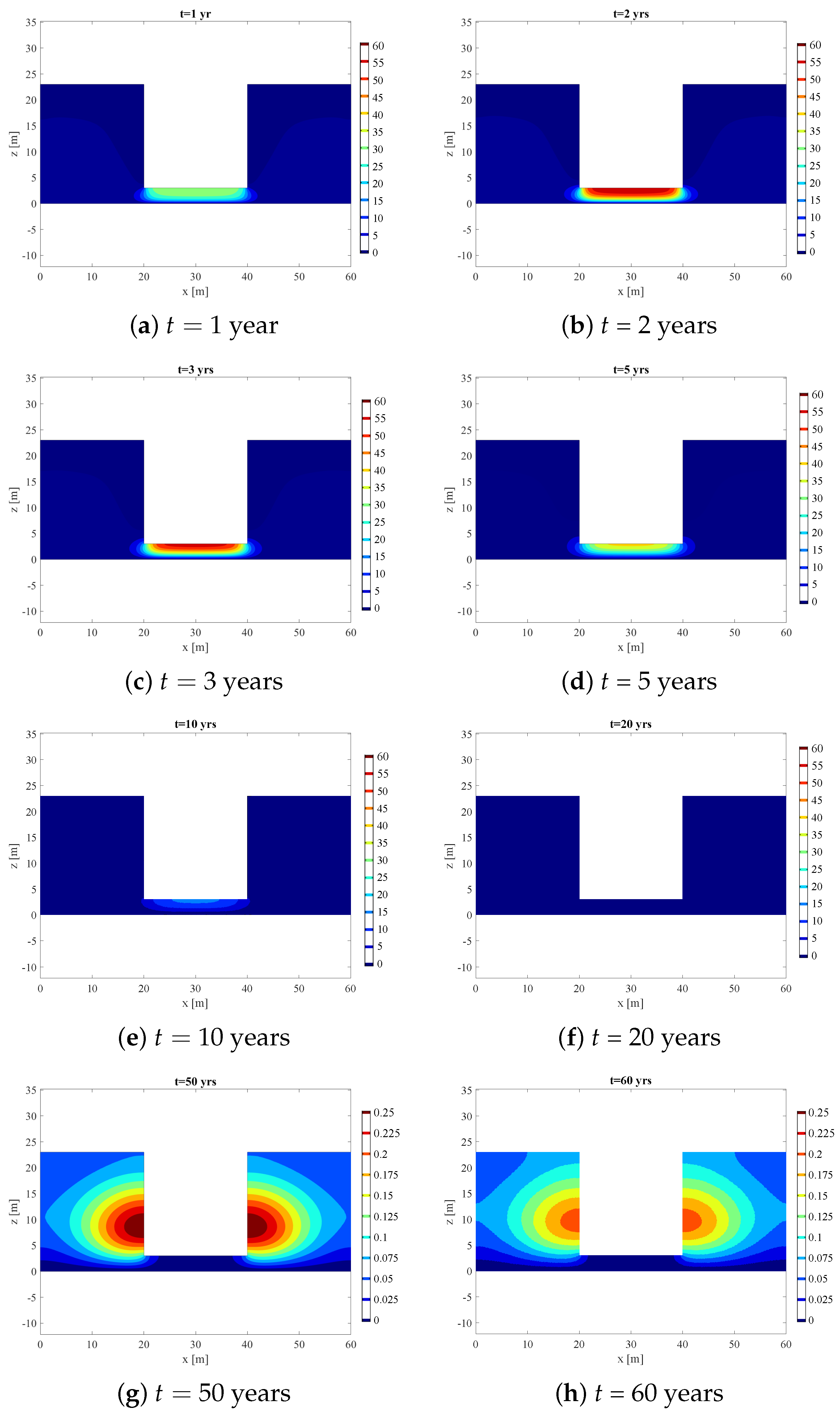
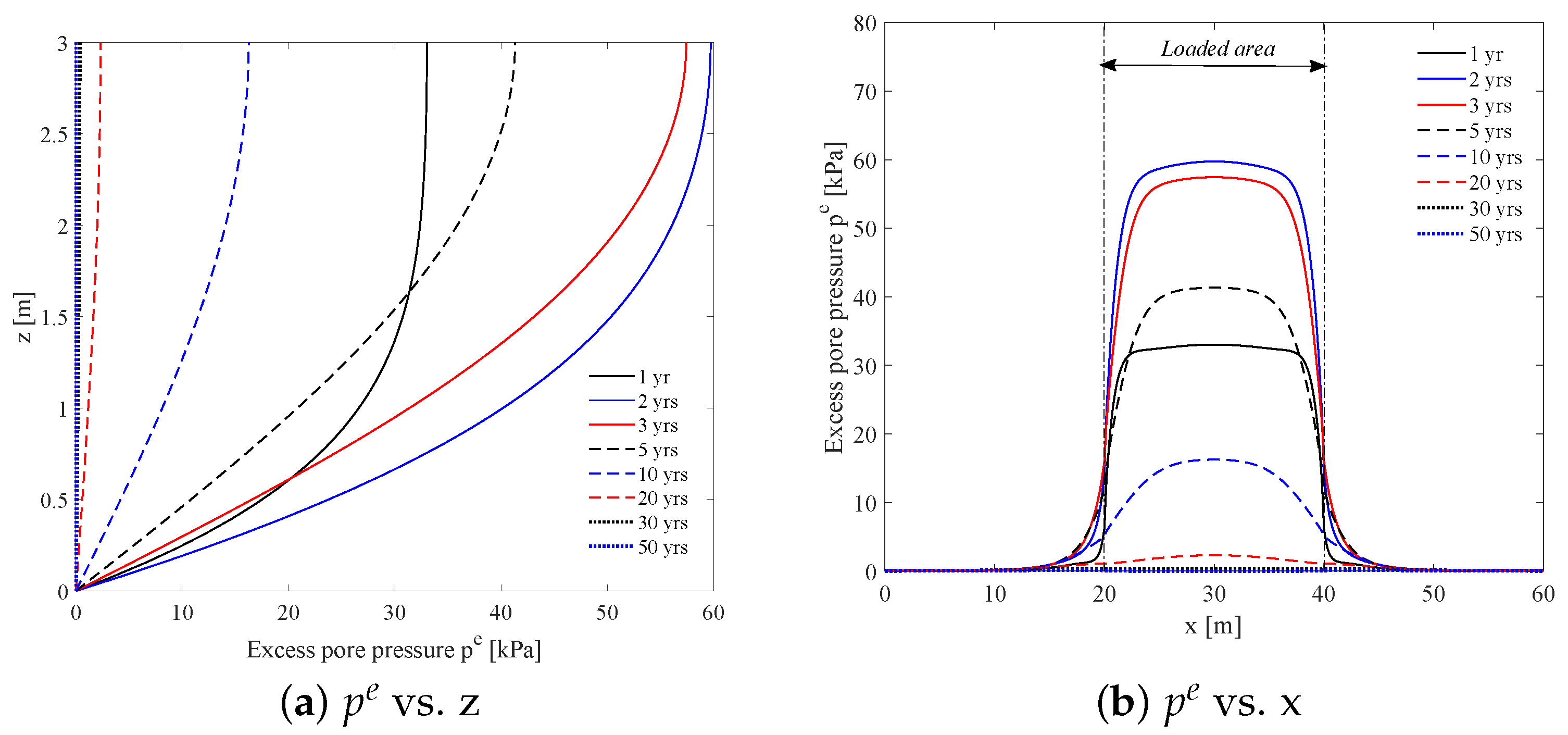
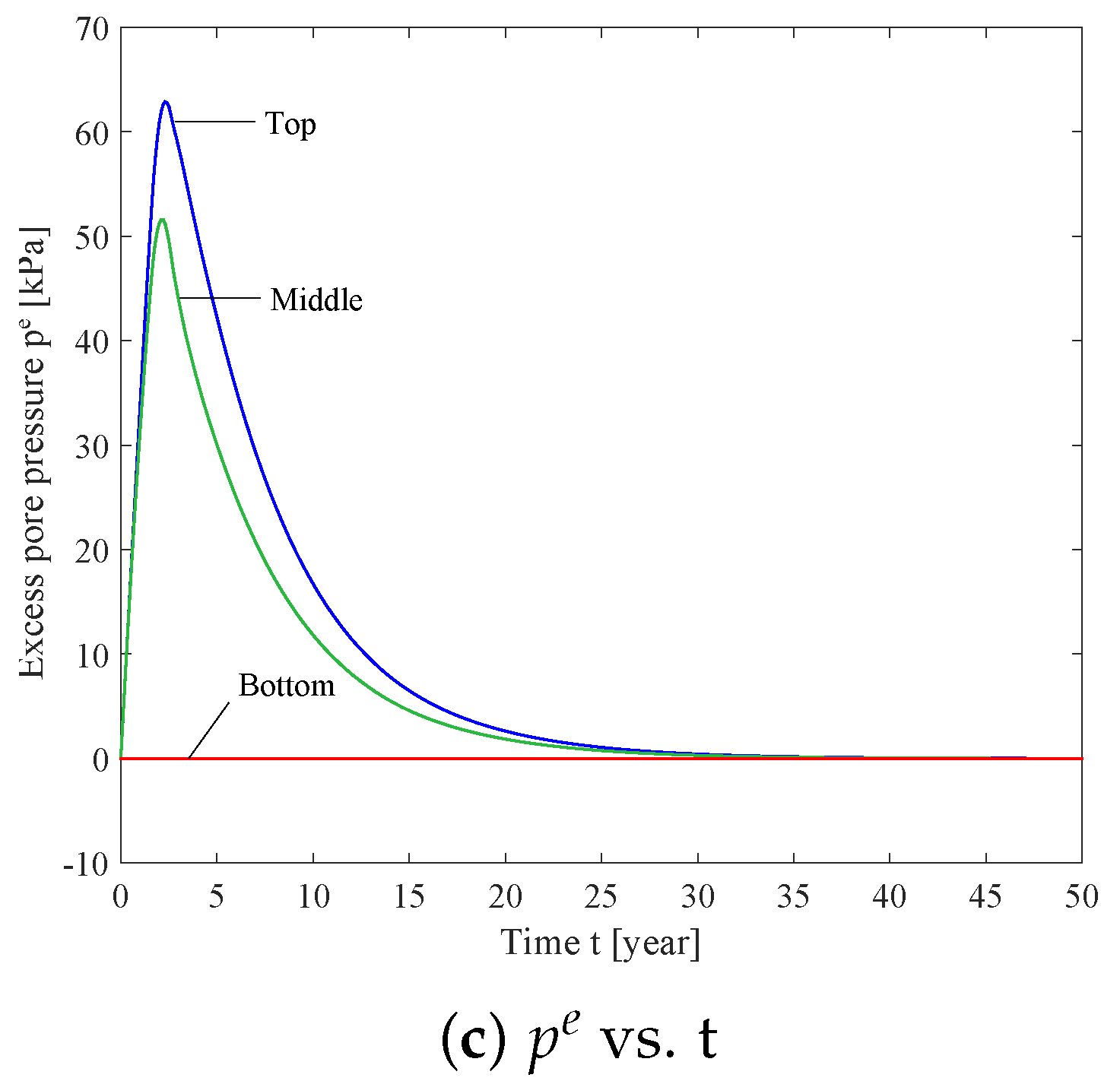
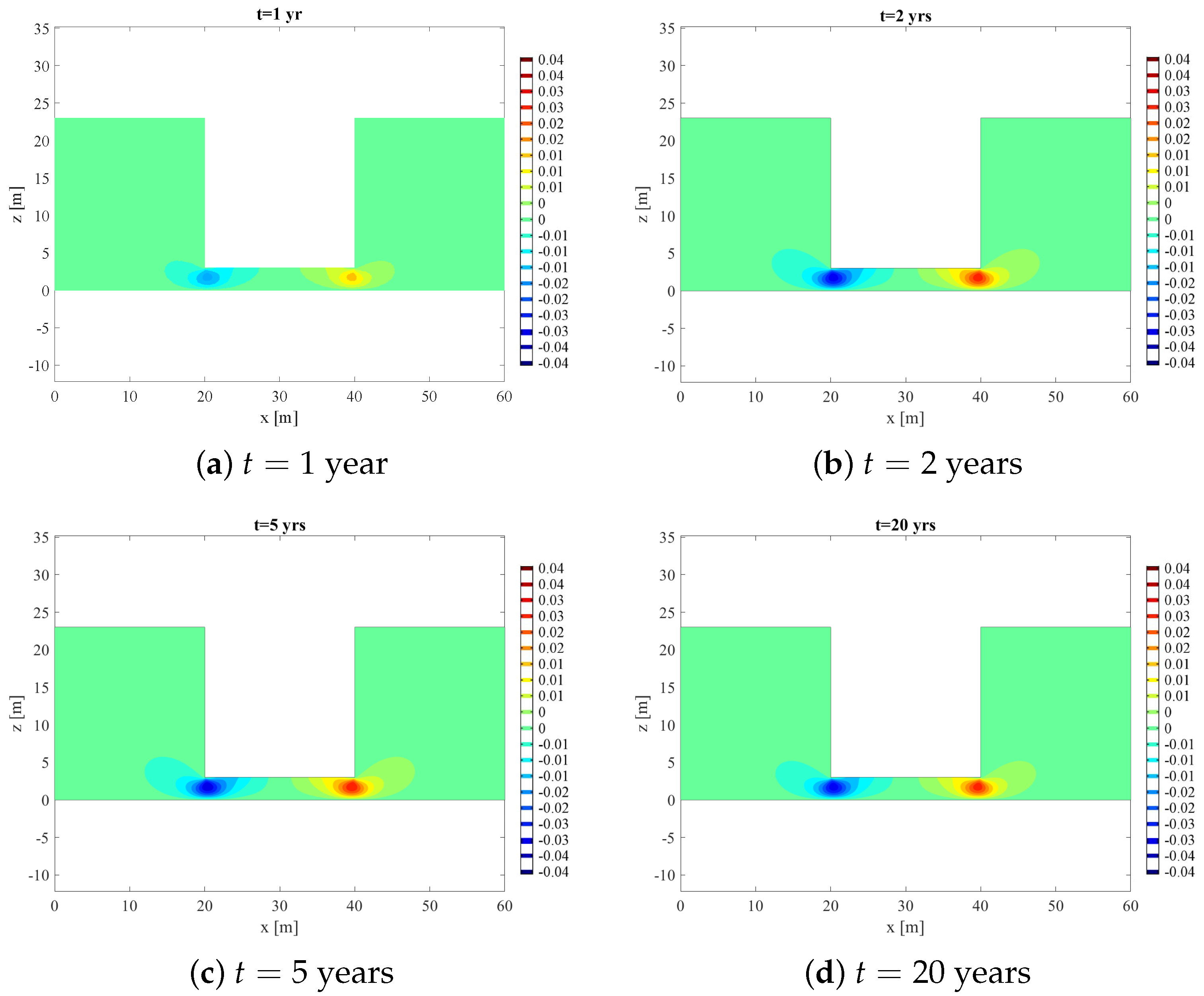
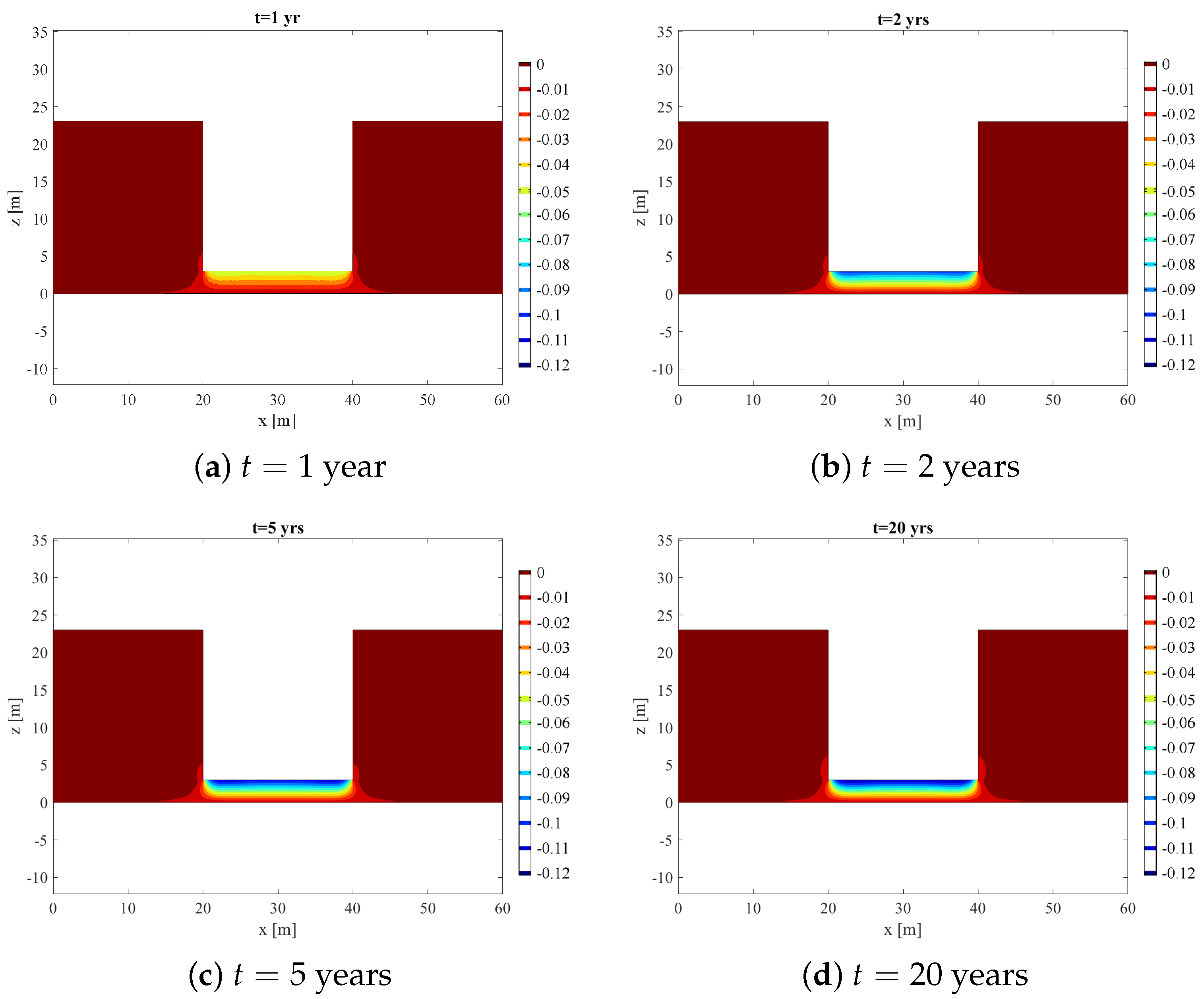
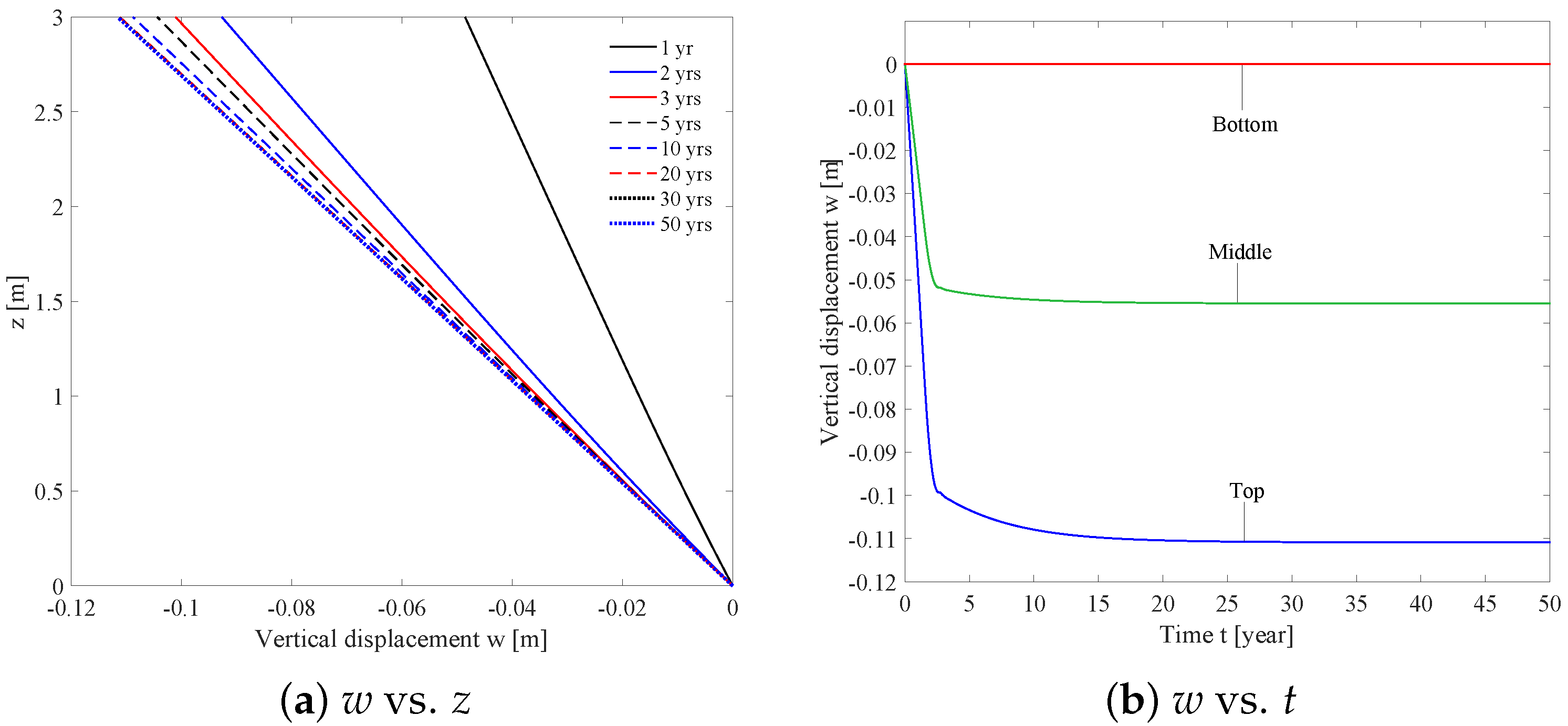
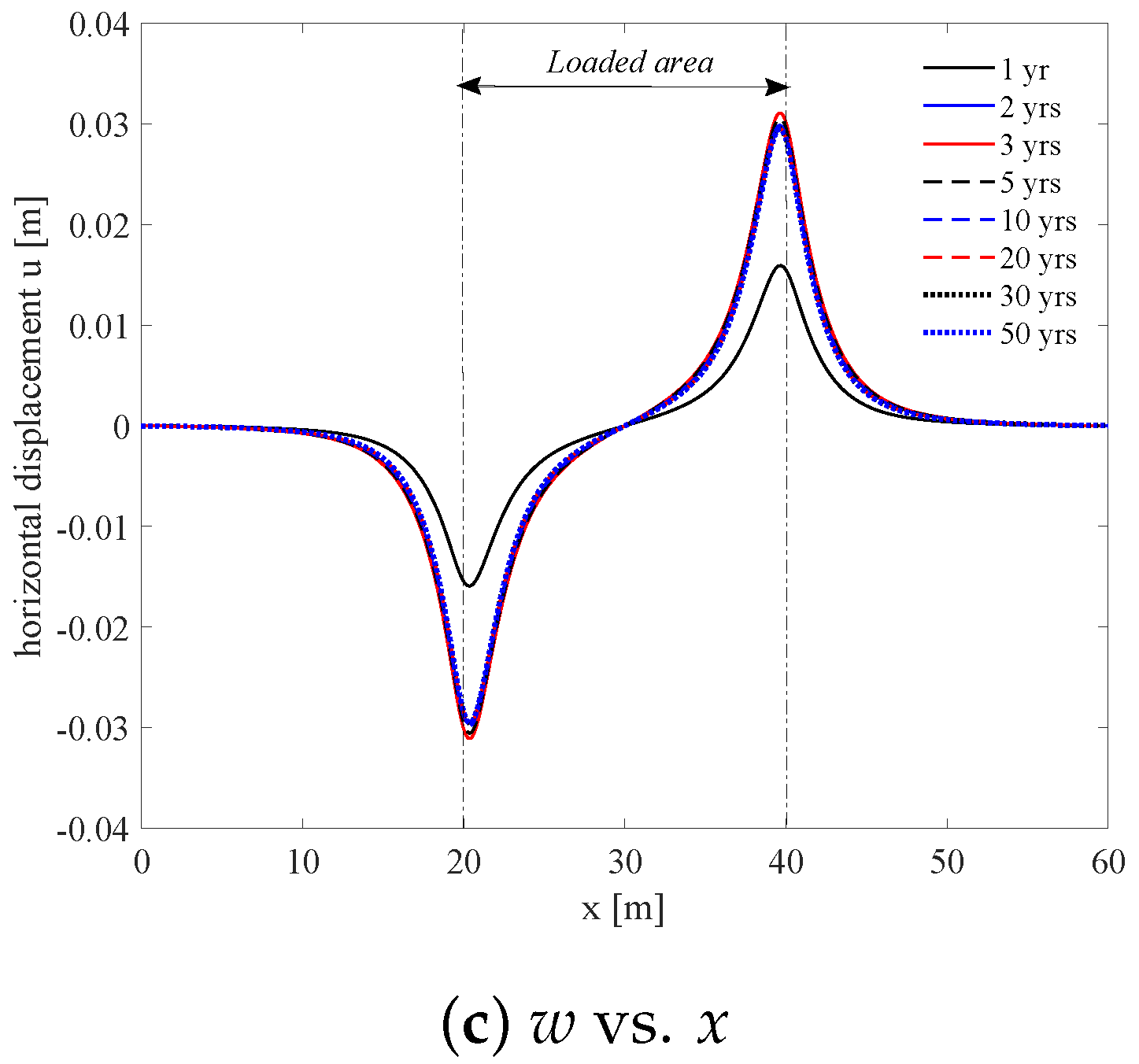
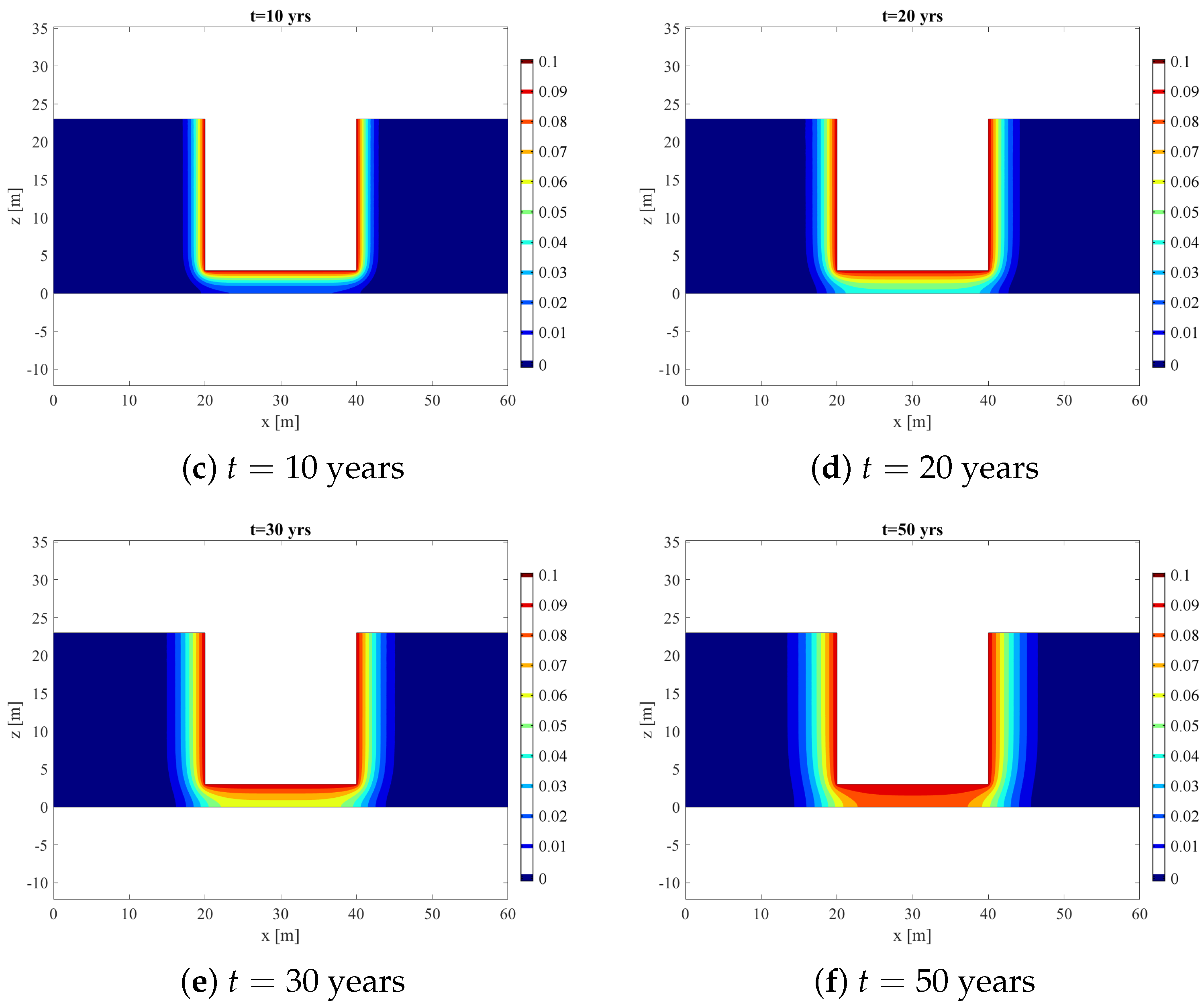
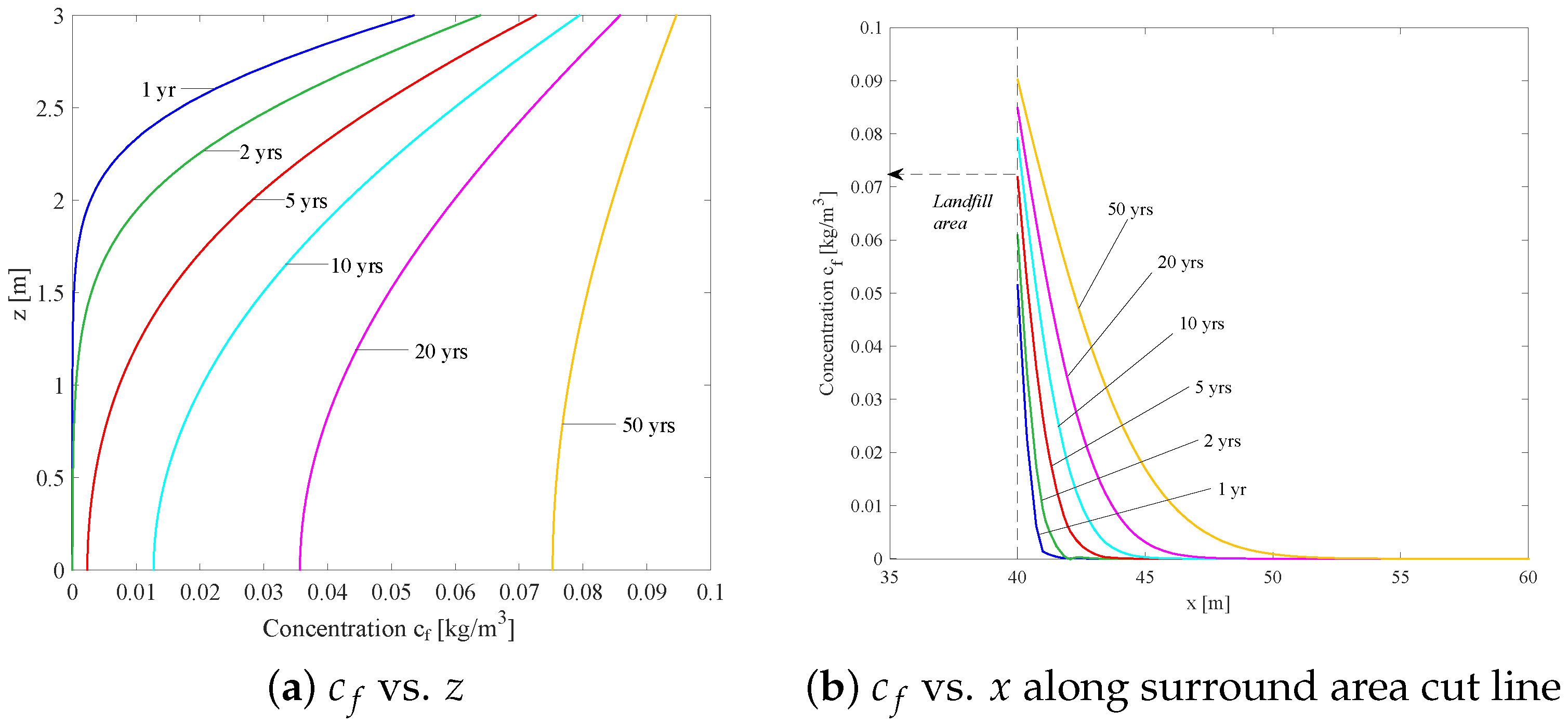
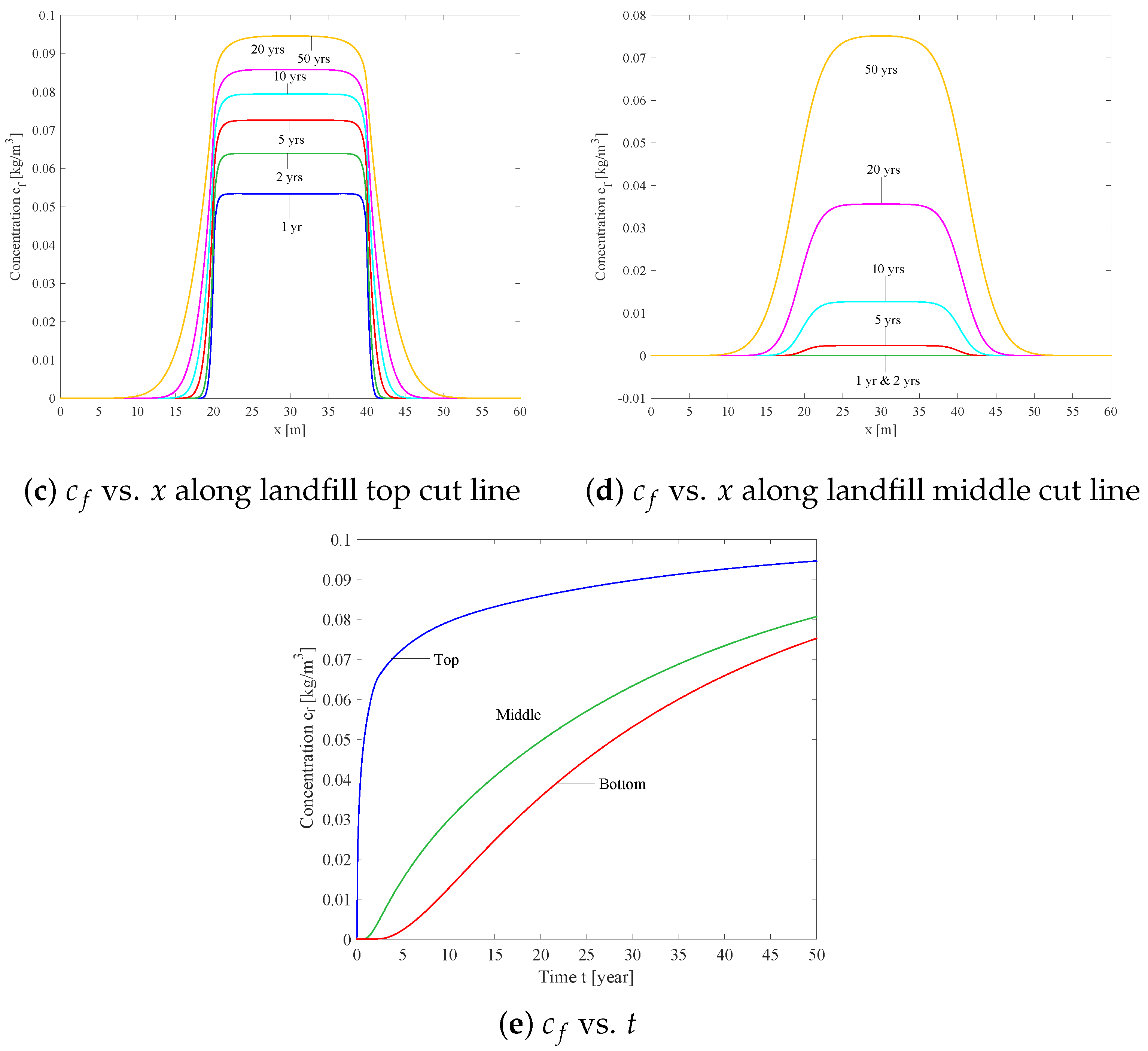
4.1. Homogeneous Soil and Uniform Contaminant Source (2D)
4.2. Point-Source Pollution Study (2D)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier Scientific Publishing Company: New York, NY, USA, 1972. [Google Scholar]
- Barry, D.A. Modelling contaminant transport in the subsurface: Theory and computer programs. In Modelling Chemical Transport in Soil: Natural and Applied Contaminants; Ghadiri, H., Rose, C.W., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1992; pp. 105–144. [Google Scholar]
- Rolle, M.; Hochstetler, D.; Chiogna, G.; Kitanidis, P.K.; Grathwohl, P. Experimental investigation and pore-scale modeling interpretation of compound-specific transverse dispersion in porous media. Transp. Porous Media 2012, 93, 347–362. [Google Scholar] [CrossRef]
- Boso, F.; Bellin, A.; Dumbser, M. Numerical simulations of solute transport in highly heterogeneous formations: A comparison of alternative numerical schemes. Adv. Water Resour. 2013, 52, 178–189. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, H. On different numerical inverse Laplace methods for solute transport problems. Adv. Water Resour. 2015, 75, 80–92. [Google Scholar] [CrossRef]
- Alshawabkeh, A.; Rahbar, N.; Sheahan, T.C.; Tang, G. Volume change effects in solute transport in clay under consolidation. In Proceedings of the Advances in Geotechnical Engineering with Emphasis on Dams, Highway Materials, and Soil Improvement, Ibrid, Jordan, 12–15 July 2004; Volume 1, pp. 105–115. [Google Scholar]
- Potter, L.J.; Savvidou, C.; Gibson, R.E. Consolidation and Pollutant Transport Associated with Slurried Mineral Waste Disposal. In Proceedings of the 1st International Conference on Environmental Geotechnics, Edmonton, AB, Canada, 10–15 July 1994; pp. 525–530. [Google Scholar]
- Smith, D.W. One-dimensional contaminant transport through a deforming porous medium: Theory and a solution for a quasi-steady-state problem. Int. J. Numer. Anal. Methods Geomech. 2000, 24, 693–722. [Google Scholar] [CrossRef]
- Zhang, H.; Jeng, D.S.; Seymour, B.; Barry, D.A.; Li, L. Solute transport in partially-saturated deformable porous media: Application to a landfill clay liner. Adv. Water Resour. 2012, 40, 1–10. [Google Scholar] [CrossRef]
- Terzaghi, K. Erdbaumechanik auf Bodenphysikalischer Grundlage; Deuticke: Vienna, Austria, 1925. [Google Scholar]
- Wu, S.; Jeng, D.S. Numerical modeling of solute transport in deformable unsaturated layered soil. Water Sci. Eng. 2017, 10, 184–196. [Google Scholar] [CrossRef]
- Fox, P.; Berles, J. A piecewise-linear model for large strain consolidation. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 453–475. [Google Scholar] [CrossRef]
- Fox, P. Coupled large strain consolidation and solute transport. I: Model development. J. Geotech. Geoenvironmental Eng. ASCE 2007, 133, 3–15. [Google Scholar] [CrossRef]
- Wu, S.; Jeng, D.S.; Seymour, B. Numerical Modelling of consolidation-induced solute transport in unsaturated soil with dynamic hydraulic conductivity and degree of saturation. Adv. Water Resour. 2020, 135, 103466. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Fang, Y.F. A three-dimensional model coupled mechanical consolidation and contaminant transport. J. Residuals Sci. Technolocy 2016, 13, 121–133. [Google Scholar] [CrossRef] [PubMed]
- Wu, S. Numerical Simulation for Solute Transport in a Deformable Porous Medium. Ph.D. Thesis, Griffith University, Queensland, Australia, 2020. [Google Scholar]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Burnett, R.; Frind, E. An alternating direction Galerkin technique for simulation of groundwater contaminant transport in three dimensions, 2. Dimensionally effects. Water Resour. Res. 1987, 23, 695–705. [Google Scholar] [CrossRef]
- COMSOL. COMSOL Multiphysics, 3rd ed.; COMSOL: Shanghai, China, 2010. [Google Scholar]
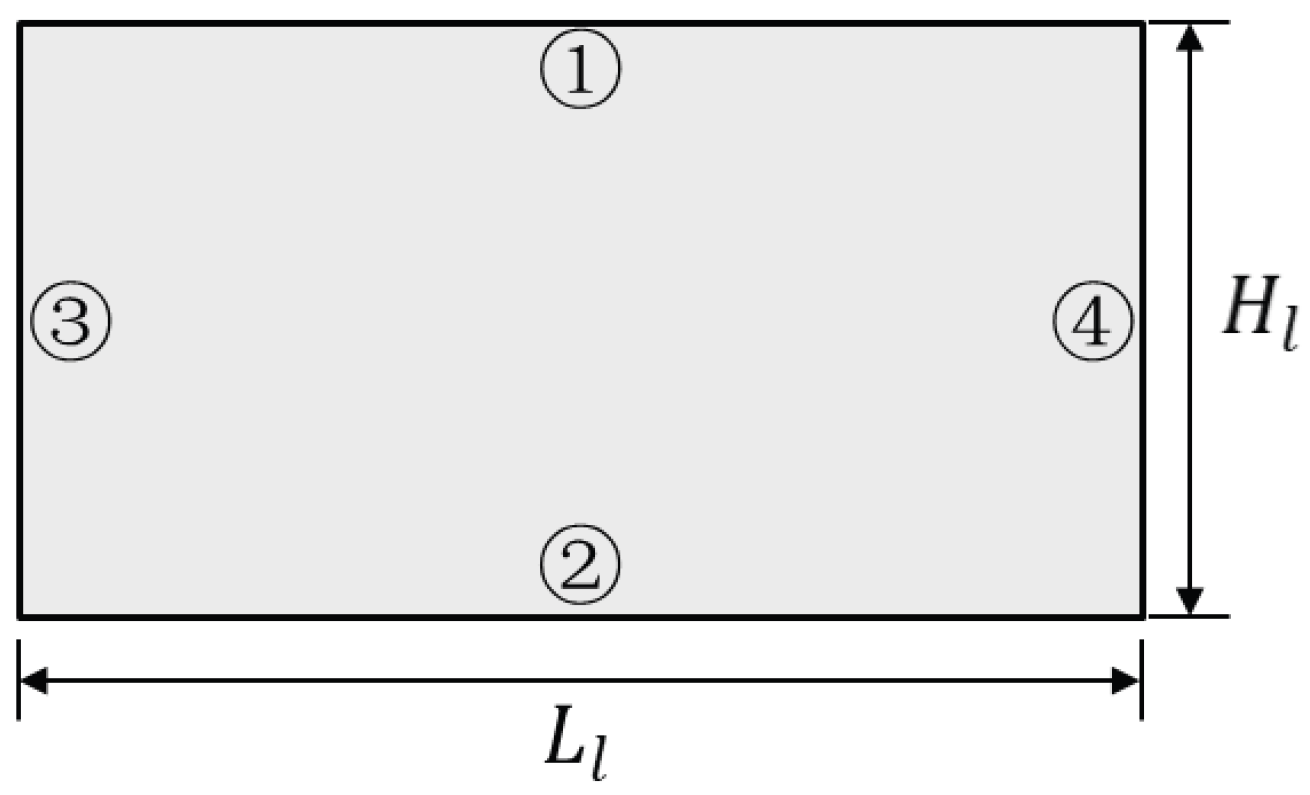
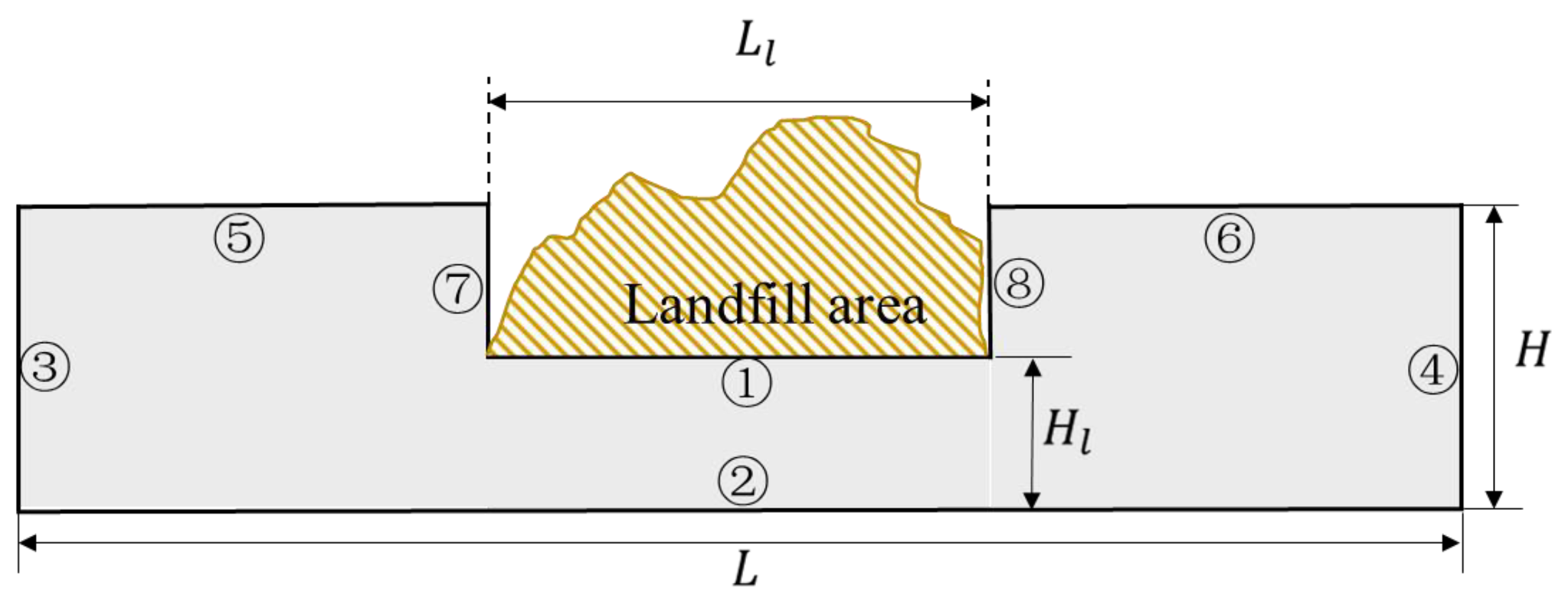



| Boundary Index | BC of | BC of | BC of |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 & 4 | |||
| IC: , and | |||
| Parameter | Value | Description |
|---|---|---|
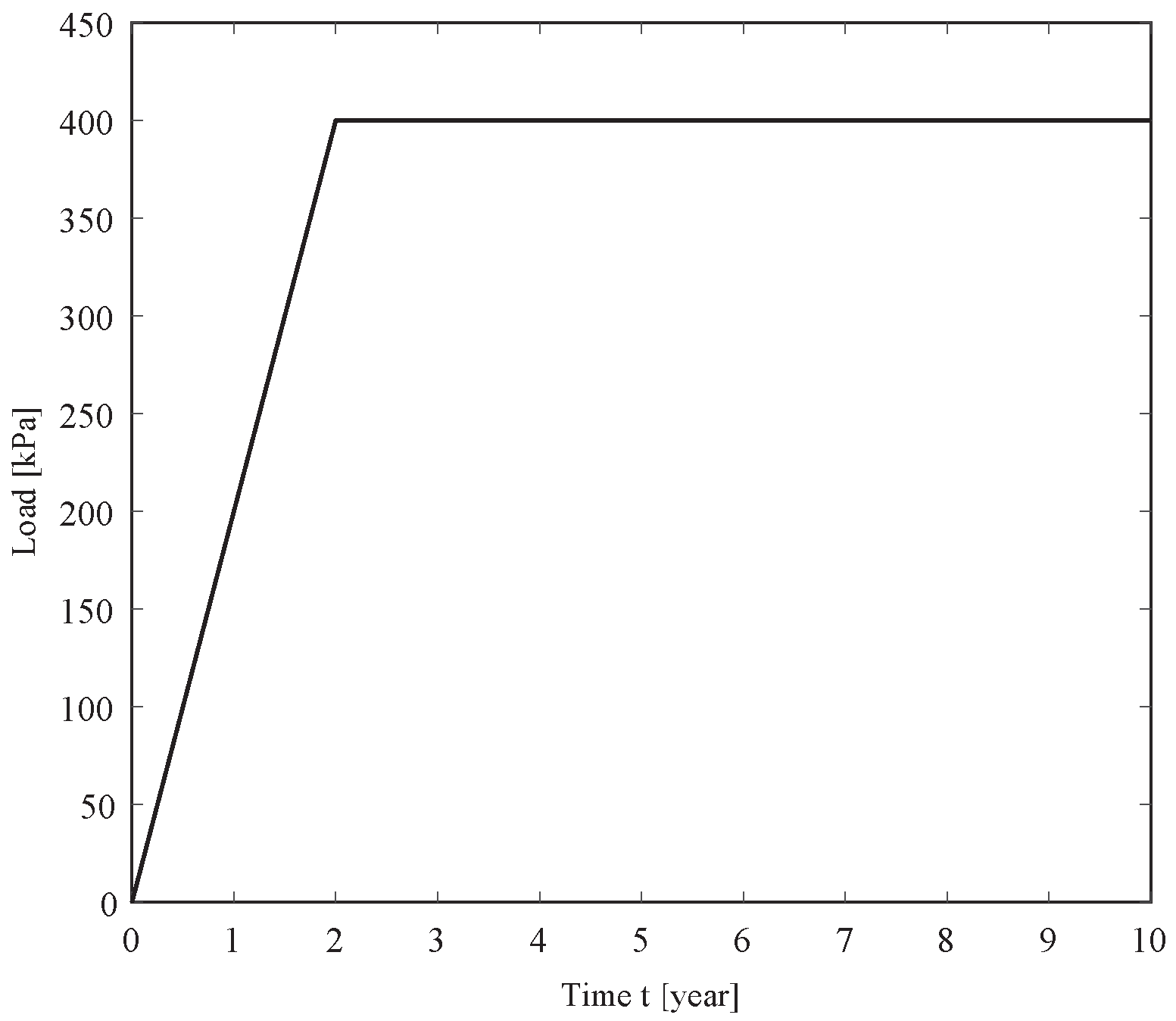
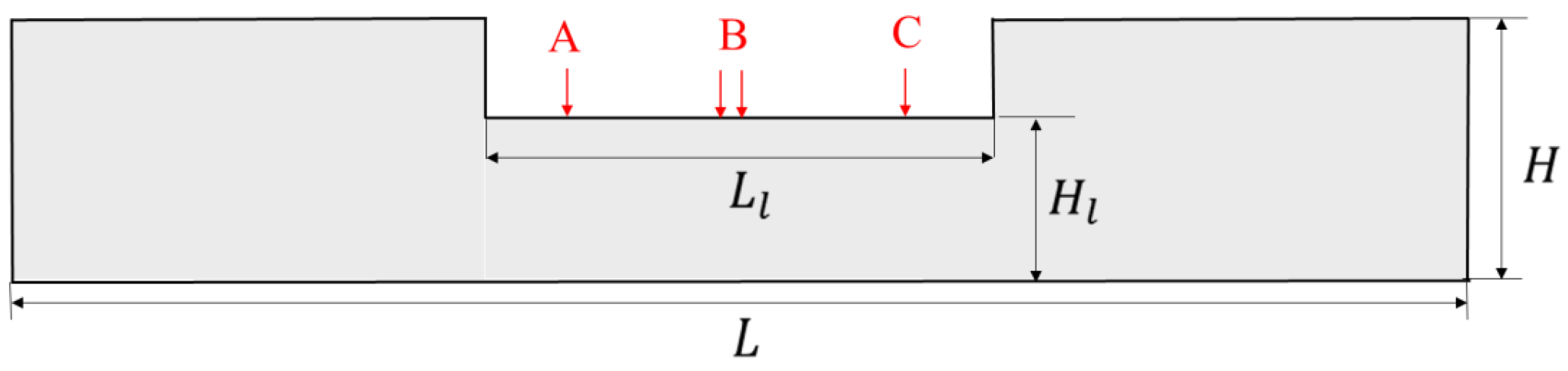
| Referring to Figure 2 | Waste loading | |
| h | 0.0015 m | Thickness of geomembrane |
| 3 m | Depth of soil domain | |
| 1 m, 3 m, 5 m, 8 m, 10 m and 20 m | Width of soil domain | |
| 0.88 | Degree of saturation | |
| 0.33 | Initial porosity | |
| G | Pa | Shear modulus |
| 0.33 | Poisson’s ratio | |
| m/s | Hydraulic conductivity in the x-direction | |
| m/s | Hydraulic conductivity in the z-direction | |
| kg/m | Density of the pore fluid, | |
| varied due to fluid compressibility | ||
| kg/m | Density of the solid phase | |
| 0 | Partitioning coefficient | |
| 0.02 m | Volumetric fraction of dissolved air | |
| within pore water | ||
| m/s | Mass transfer coefficient of geomembrane | |
| m/s | Molecular diffusion coefficient in the clay | |
| 0.1 m | Longitudinal dispersion coefficient | |
| 0.1 m | Transverse dispersion coefficient | |
| 0.1 kg/m | Reference solute concentration |
| Parameter | Value | Description |
|---|---|---|
| 100 kPa | Constant waste loading | |
| 1.0 | Initial degree of saturation | |
| 0.44 | Initial porosity | |
| G | Pa | Shear modulus |
| 0.3 | Poisson’s ratio | |
| m/s | Hydraulic conductivity in x-direction | |
| m/s | Hydraulic conductivity in z-direction | |
| kg/m | Density of the solid phase | |
| kg/m | Partitioning coefficient | |
| m/s | Molecular diffusion coefficient in the clay | |
| 0.5 m | Longitudinal dispersion coefficient | |
| 0.05 m | Transverse dispersion coefficient | |
| 0.5 kg/m | Reference solute concentration |
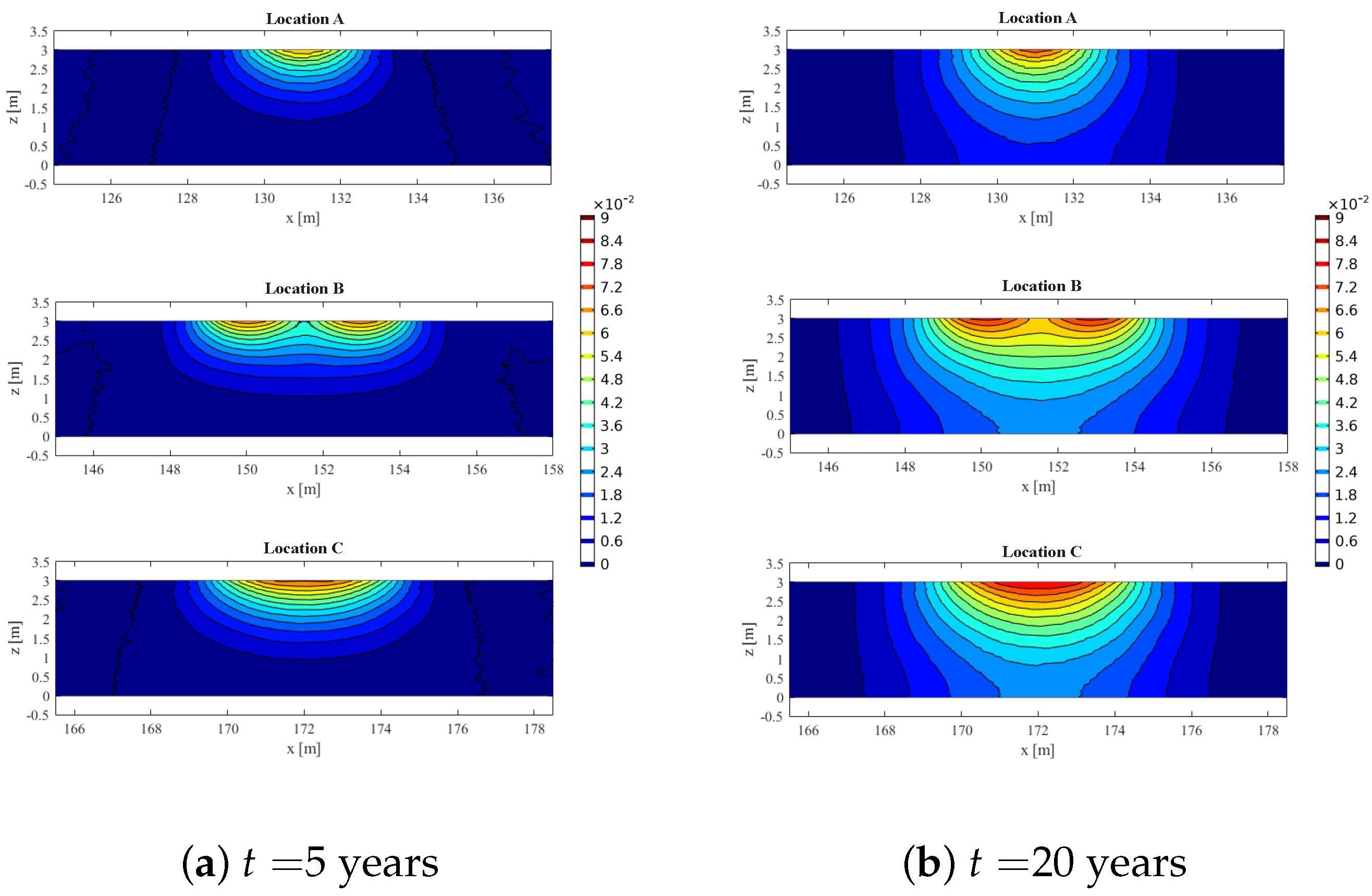
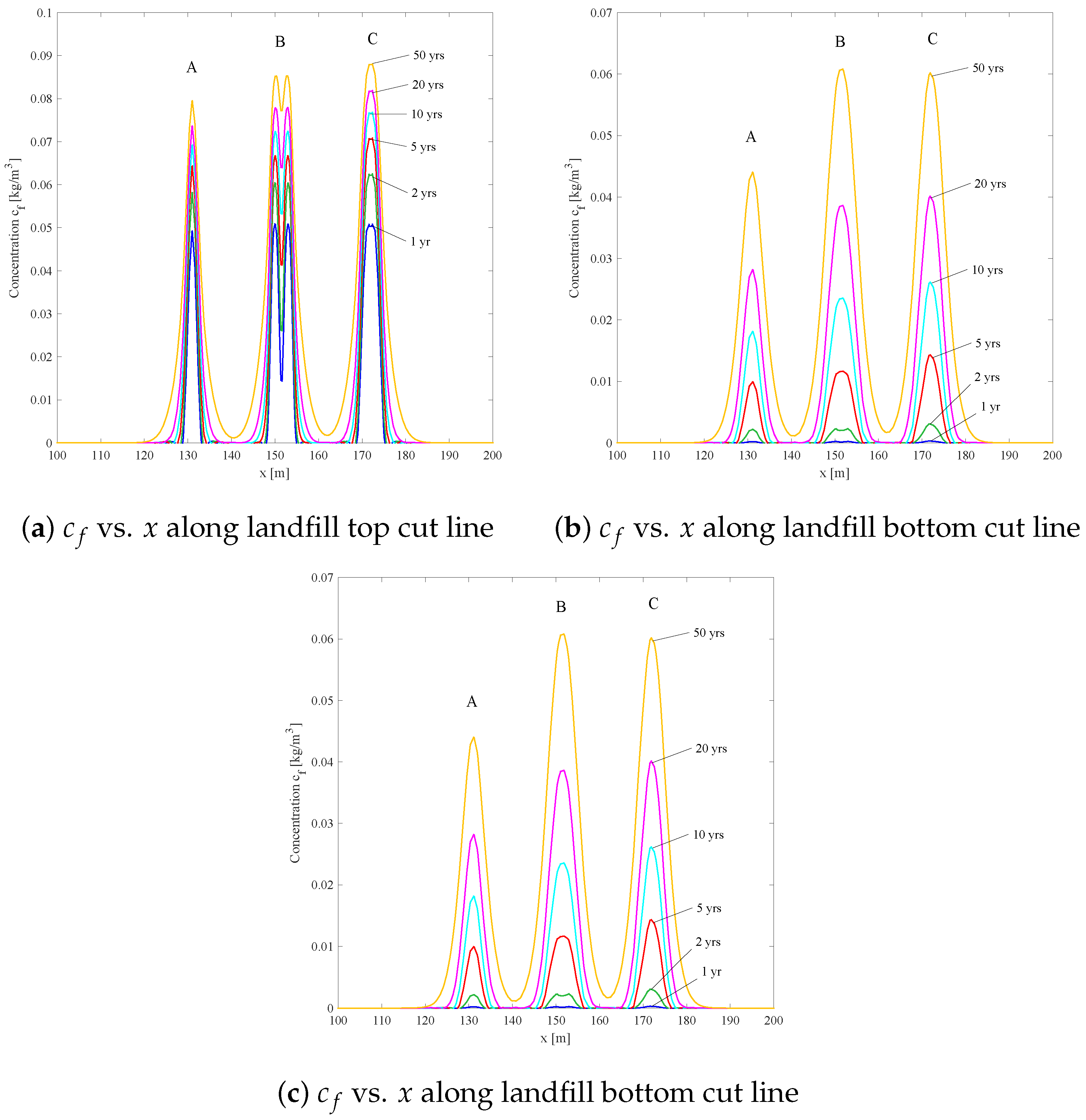
| Location | Pollution Region | Description |
|---|---|---|
| A | 130 m to 132 m | single pollution for 2 m |
| B | 149 m to 151 m | two 2 m pollution points |
| and 152 m to 154 m | that are close to each other | |
| C | 170 m to 174 m | single pollution for 4 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Jeng, D.-S. Two-Dimensional Model for Consolidation-Induced Solute Transport in an Unsaturated Porous Medium. Sci 2023, 5, 16. https://doi.org/10.3390/sci5020016
Wu S, Jeng D-S. Two-Dimensional Model for Consolidation-Induced Solute Transport in an Unsaturated Porous Medium. Sci. 2023; 5(2):16. https://doi.org/10.3390/sci5020016
Chicago/Turabian StyleWu, Sheng, and Dong-Sheng Jeng. 2023. "Two-Dimensional Model for Consolidation-Induced Solute Transport in an Unsaturated Porous Medium" Sci 5, no. 2: 16. https://doi.org/10.3390/sci5020016
APA StyleWu, S., & Jeng, D.-S. (2023). Two-Dimensional Model for Consolidation-Induced Solute Transport in an Unsaturated Porous Medium. Sci, 5(2), 16. https://doi.org/10.3390/sci5020016







