Abstract
A signature of synaptic potentiation conductance has been observed in an α-Fe2O3/p-Si device fabricated using spin coating. The conductance of the device in dark conditions and illumination with a white light source was characterized as a function of the application of a periodic bias (voltage) with a triangular profile. The conductance of the device increases with the number of voltage cycles applied and plateaus to its maximum value of 0.70 μS under dark conditions and 12.00 μS under illumination, and this mimics the analog synaptic weight change with the action potential of a neuron. In the range of applied voltage from 0 V to 0.7 V, the conduction mechanism corresponds to trap-assisted tunneling (TAT) and in the range of 0.7–5 V it corresponds to the Poole–Frenkel emission (PFE). The conductance as a function of electrical pulses was fitted with a Hill function, which is a measure of cooperation in biological systems. In this case, it allows one to determine the turn-on threshold (K) of the device in terms of the number of voltage pulses, which are found to be 3 and 166 under dark and illumination conditions, respectively. The gradual conductance change and activation after a certain number of pulses perfectly mimics the synaptic potentiation of neurons. In addition, the threshold parameter extracted from the Hill equation fit, acting as the number of pulses for synaptic activation, is found to have programmability with the intensity of the light illumination.
1. Introduction
With the proposal of the memristor as the fourth fundamental electrical element [1,2], resistive switching materials—one possible material with which to construct memristors—have been utilized in the construction of artificial electrical synapses that emulate those of the human brain [3,4,5,6]. An adult human brain contains an estimated 1011 neurons and makes nearly 1015 connections through synapses [7,8]; where a synapse connects two neurons, and depending on the characteristics of the electrical stimulus, the weight of the synapse (conductance) either strengthens (potentiation) or weakens (depression) the connectivity between neurons. The conductance of synaptic switches is an analog process that depends on the strength and polarity of the applied stimulus. Generally, repetitive and identical pulses of stimuli (current or voltage) are applied to the synaptic device in order to modulate its weight [9,10]. This is similar to the theoretically predicted behavior of memristors and why they are believed to be a fundamental component of artificial synapses. Ultimately, the suitability of the memristor depends upon the properties of the materials used in their construction.
One of the primary requirements of the material used to construct a memristor for use as an artificial synapse switch is that it exhibits at least two resistance states. The mechanism whereby it changes its resistive state varies from material to material, some examples are valence change [11], electrochemical metallization [12], ferroelectric switching [13], phase change [14], etc. The types of materials used in constructing synaptic devices range from 2D materials [15] to conventional metal/ metal oxide systems such as an Al:HfO2-based memristor that has been shown to have good synaptic potentiation and depression behavior [16] or TiO2-based synaptic devices that have excellent analog memory switching with spike-timing-dependent synaptic plasticity [17]. Other notable material systems are GdOx/Cu:MoOx [18], WOx [19], HfOx/AlOx [20], and AlOx [21]; all of them have been reported to have synaptic potentiation and depression characteristics. The message being that there is almost an infinite combination of materials that can be used in the construction of memristive devices suitable for use as artificial synapses.
Many synaptic devices comprise either low abundance materials or require complex fabrication and post processing methods. As alternative materials, Fe and Fe2O3 are among the most abundant materials on earth and non-toxic [22]. In addition, the band gap of Fe2O3 is centered in the visible range (~2.1 eV) of the light spectrum [23]; therefore, it is suitable for visible light-based applications. Furthermore, it is a low-cost material with fast carrier transport and stability under ambient environment conditions [24]. Consequently, Fe2O3 has been used in various applications including photoelectrochemical water splitting [25], gas sensing [26], lithium-ion batteries [27] (p. 3), etc.
Due to the aforementioned properties of Fe2O3, as well as the fact that oxygen vacancies in metal oxide semiconductors play a vital role in resistive switching behavior [28], we have used it to construct a heterojunction memristor with p-type Si (100). We report on its memristive properties under dark and illuminated conditions and its suitability for use in a synaptic switch. We also examine the oxygen vacancy migration under an applied bias, which is vital to the resistive switching behavior of Fe2O3 [29]. Lastly, we demonstrate that the resistive switching behavior of Fe2O3/Si (100) in the presence of white light widens the switching window, thus producing a unipolar resistive switch that does not require a pulse of opposite polarity to reset.
2. Experimental Details
2.1. Device Fabrication and Characterization
The α-Fe2O3/p-Si samples were prepared using an organic iron solution consisting of 0.5 g of Fe (III) Acetylacetonate (Strem Chemicals, Newburyport, MA, USA, CAS#: 14024-18-1) in 10 mL (50 g/L) of acetone (141 mM). The solution was sonicated for an hour, followed by vortex stirring and filtering. Approximately 10 µL of the solution was spin-coated onto p-Si (100) substrates at 3000 rpm. The solvent was allowed to evaporate, followed by annealing at 500 °C for 1 h in air inside a tube furnace and then allowed to slowly cool to room temperature to avoid cracking of the α-Fe2O3 film. Details and data on the characterization of the α-Fe2O3 film can be found in the Figures S1–S3 from Supplementary Material. Circular gold electrical contacts with an approximate area of 0.071 cm2 were sputtered onto the sample using a shadow mask. The sputter chamber was held at a pressure of 10 mTorr of Ar and deposition was carried out with a plasma power of 25 W. The samples were then annealed at 300 °C in the air for 45 min to form good electrical contact between the Au electrodes and sample.
2.2. Electrical Measurements
Electrical characterization was performed on multiple samples to ensure reproducibility. The electrical measurements were conducted in a dark box equipped with a white light LED for illumination. Current–voltage sweeps (IV curves) were acquired with a triangular voltage waveform and a voltage sweep rate of 0.1 V/s using a Keithley 2425 source meter. A four-wire sense mode was used to acquire pulse–conductance measurements, where the Keithley 2425 source meter was programmed to apply a 5 V pulse with a duration of 10 ms and a period of 100 ms across the outer electrodes, while current was simultaneously measured across the two inner electrodes. A custom Labview program was used to control the source meter and data acquisition.
3. Results and Discussion
Displayed in Figure 1a is a single IV cycle using a triangular waveform of 5 V under dark conditions and illuminated with white light. The IV characteristics of the device are symmetric in forward and reverse bias (only the forward bias region is shown here). The device exhibits a hysteresis loop with unipolar resistive switching, where the area of the loop increases when illuminated with white light with a power density of 268 µW/cm2. The ratio of high resistance state (HRS) to low resistance state (LRS) at 2.5 V bias increased from 1.37 under dark conditions to 1.58 with illumination. Figure 1b,c are the cyclical forward bias voltage and current of the device under dark and illuminated conditions, respectively, where the current progressively increases with each cycle under dark conditions, which is indicative of charge retention [30]. Under illumination, the current initially increases with repeated cycles and then begins to decrease linearly thereafter, which suggests charge trapping that leads to the recombination of electron-hole pairs [31]. Illumination also broadens the current response relative to dark conditions, indicative of greater synaptic habituation [32]. Figure 1d is the conductance as a function of the number of cycles at a bias of 5 V under dark and illuminated conditions. Under dark conditions, the conductance increases linearly until it saturates at 0.11 μS. Under illumination, conductance increases and then decreases nonlinearly for approximately 25 cycles, at which point it decreases linearly. Again, this is an indication of charge trapping leading to electron-hole recombination.
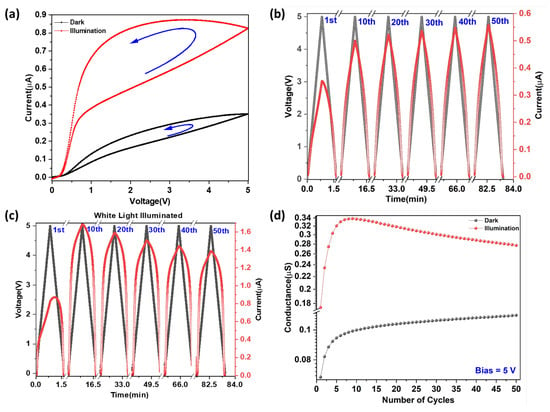
Figure 1.
(a) IV graph in dark and under white light illumination of a single cycle (HRS/LRS = 1.37 for dark and 1.58 for illumination at 2.5 V bias). Selected cycles of 50 applied voltage and measured current cycles as a function of time in (b) dark and (c) with white light illumination. (d) Conductance as a function of number of cycles at 5 V bias in dark and white light illumination.
The switching behavior in Figure 1 can be understood in the context of valence change resistive switching (VCRS) devices [33]. The conduction in a metal–insulator–metal (MIM) VCRS device is a function of the bulk properties of the dielectric (bulk limited) and the electrode–dielectric interfaces (electrode limited). In the dielectric, Poole–Frenkel emission (PFE), hopping conduction, ohmic conduction, space charge limited conduction, ionic conduction and trap-assisted tunneling (TAT) are conduction limiting mechanisms [34], while Schottky emission, direct tunneling (DT), Fowler–Nordheim tunneling, and thermionic-field emission are conduction limiting mechanisms of the electrode-dielectric interfaces. TAT, PFE, and DT conduction mechanisms are schematically represented in Figure 2. We will show that the predominant transport mechanisms in the α-Fe2O3/p-Si device are TAT and PFE.
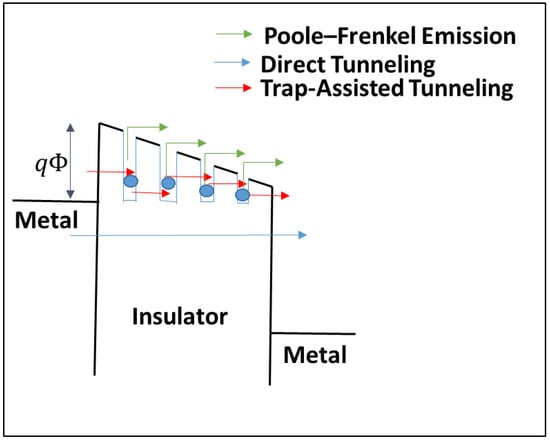
Figure 2.
Schematic diagram showing the mechanisms of charge transport in a metal–insulator–metal structure via Poole–Frenkel emission, trap-assisted tunneling, and direct tunneling.
The trap-assisted tunneling mechanism, unlike DT, is a two-step process in which the carriers are initially trapped by defects or oxygen vacancies and then tunnel through the barrier to another trap and tunnel, etc., where multiple TAT events enable the carrier to cross the insulator, i.e., the carriers tunnel from one trap to another, where each tunneling event is over a fraction of the width of the metal oxide [35]. The generalized equation for TAT current density is a function of the applied electric field and is given by Equation (1),
where is a constant and is the energy of the trap with respect to the conduction band edge of the metal oxide, q is the charge of an electron, m* is the electron effective mass in the oxide, h is Planck’s constant and E is the electric field in the metal [36]. For TAT conduction at a constant temperature, the IV curve can be fit with Equation (2),
a more generalized form of Equation (1), where y and x are current and voltage, respectively.
For conduction by Poole–Frenkel emission, trapped carriers are excited into the conduction band of the metal oxide due to the lowering of the Coulomb barrier by the application of a sufficiently strong electric field. The current density by PFE is given by Equation (3),
where is the density of states in the conduction band, is the applied electric field, is electronic drift mobility, is the depth of the potential of the traps and is the absolute temperature, k is Boltzmann’s constant and q is the charge of an electron [34]. For PFE at a constant temperature, the IV curve can be fit with Equation (4),
a more general form of Equation (3), where once again y and x are current and voltage, respectively.
Figure 3a is the IV curve of the α-Fe2O3/p-Si device for a single cycle with illumination, which can be divided into two regions where either TAT or PFE dominates the conduction. The fit of Equation (2) (TAT) of the IV curve in the voltage range of 0–0.7 V for both ascending and descending bias is displayed in Figure 3b. The fits with Equation (2) up to 0.6 V are excellent for the ascending and descending bias but diverge slightly thereafter, which is attributed to the transition to or from PFE transport, respectively, i.e., 0.6–0.7 V is a region of mixed TAT and PFE carrier conduction. The fit of Equation (4) (PFE) of the IV curve in the voltage range of 0.7–5.0 V for ascending and descending bias is displayed in Figure 3c and is an excellent fit with the experimental data. Based on the qualities of the fits, the conclusion is that trap-assisted tunneling is the primary conduction mechanism below 0.7 V and Poole–Frenkel conduction above 0.7 V, regardless of whether in ascent or descent. The same fits and arguments are true for the IV curve under no illumination, which is not shown here for the sake of brevity.
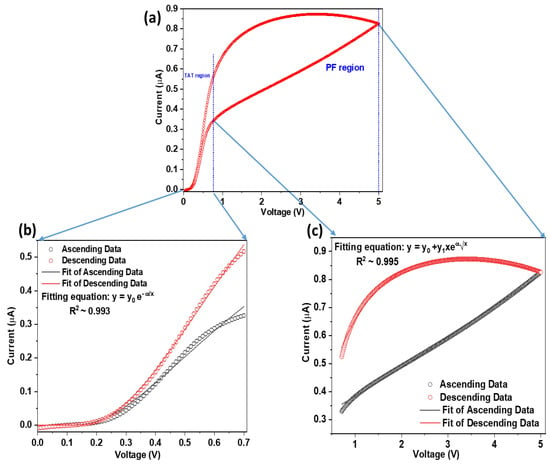
Figure 3.
(a) One IV cycle of the α-Fe2O3/p-Si device with white light illumination. (b) The fitting of the curve in (a) the range of 0–0.7 V with trap-assisted tunneling conduction and (c) in the range of 0.7–5 V with Poole–Frenkel emission conduction. The goodness of the fits (R2) is 99%.
Now that the transport properties of a single cycle of the α-Fe2O3/p-Si device is satisfactorily explained, we turn our attention to the cycle dependence of the device. The hysteresis of the IV curves of the device under dark conditions or illuminated suggests that the device has memristive characteristics [37,38] and, therefore, is useful in the construction of artificial synaptic circuits [39,40,41,42]. As a consequence, we use the Hill equation (Equation 5) [43],
which is a three-parameter nonlinear equation, where indicates the threshold of the independent variable at which the dependent variable reaches half of its maximum and is called the Hill coefficient or cooperativity which indicates the steepness of the curve. This equation is commonly used to describe the drug dose, drug concentration and effect over time in pharmacology [44,45,46]. It is also used in modeling the binding of ligands to a protein molecule, where the Hill coefficient becomes significant. If , the binding of one ligand increases the affinity of binding for further ligands and is called positive cooperation or cooperative binding, and if , the binding of one ligand decreases the affinity of binding for further ligands, which is called negative cooperation or non-cooperative binding [47]. In the present case, we hypothesize that each pulse excites trapped carriers into the conduction band of the Fe2O3, which inhibits further excitation of the carriers due to the fermionic nature of the carriers and provided they are not excitons [48]. The inhibition of further excitation is modeled as a negative cooperative excitation and fitted to the data by fixing the Hill coefficient to n = 0.40 (negative cooperation) for the best fits.
The cooperativity constant was held at 0.40 for the analysis. The fit of the Hill equation of the conductance as a function of the number of pulses for the dark and illuminated conditions is plotted in Figure 4a,b, respectively, with statistics and extracted parameters listed in Table 1. The threshold is found to be ~3 pulses in dark and ~166 pulses when illuminated with white light with an intensity of 1.27 mW/cm2. The threshold can be thought of as the synaptic activation of the device, i.e., the device activates after 3 and 166 pulses of voltage under dark and illuminated conditions, respectively. The maximum conductance, where the conductance begins to plateau, is determined by fitting with the Hill equation. Figure 4c is the maximum of the conductance extracted from the Hill equation fit as a function of incident light intensity, which demonstrates that the maximum conductance increases with increasing intensity of light, reaching a maximum at approximately 1.3 mW/cm2, followed by a decrease to a constant value of approximately 15 μS. Charge trapping and de-trapping are believed to be the mechanisms responsible for conductance switching, where light enhances the phenomena [49]. The presence of different types of trap states (deep and shallow) can have competitive effects on the rate of the number of carries trapping/de-trapping and, hence, conductance saturation, since shallow and deep traps are faster and slower to trap and de-trap the carries, respectively [50,51]. The light intensity not only dictates the number of photo-generated carries but also helps in de-trapping the carries along with phonon and tunneling-assisted de-trapping mechanisms [52]. A 5V pulse, which is in the PFE region, excites the carriers from the trap into the conduction band of the oxide, thereby increasing the conductance with each pulse, but it is limited by the finite density of the trap states and trapped carriers. The hypothesis is that the maximum conductance increases with increasing intensity of light as long as the available and accessible trap states are available to be filled, after that the conductance is no longer intensity dependent and increasing the intensity further only increases the probability of carrier recombination, thereby decreasing the conductance from the maximum and eventually plateauing. The rationale for using the Hill equation to derive the data in Figure 4c is that it better incorporates the competing mechanisms that affect the trapping/de-trapping and excitation/recombination of the carriers. The number of voltage pulses as a function of illumination intensity is plotted in Figure 4d, which shows that the activation of the device is programmable and controlled by the intensity of illumination. As the intensity of light incident on the device increases, the number of pulses of synaptic activation increases, reaches a maximum at 1.3 mW/m2 —the corresponding maximum of the maximum conductance in Figure 4c—and subsequently declines with increasing light intensity. The rise and fall of the number of pulses as a function of light intensity is nonlinear, which is expected because the conductance window is the widest at the maximum of the maximum conductance.
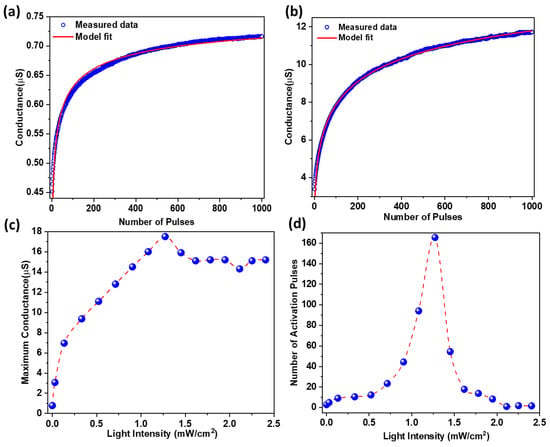
Figure 4.
The conductance as a function of number of pulses for α-Fe2O3/p-Si device when measured (a) under dark conditions, (b) white light illumination with an intensity of 1.27 mW/cm2, (c) maximum conductance based on the fit with the Hill equation as a function of light intensity, and (d) the number of activation pulses for the conductance to plateau as a function of light intensity, also based on the fit with the Hill equation. The Hill coefficient was held at 0.40 for the fits used to obtain the data in (c,d). The triangular electrical pulses with an amplitude of 5 V, a width of 10 ms, and a period of 100 ms were used for all the measurements.

Table 1.
The fitting parameters of the Hill equation used to fit the conductance as a function of the number of pulses under dark conditions and with white light illumination of 1.27 mW/cm2, as well as the corresponding statistics of the fits.
The programmability of the synaptic activation of this device using light intensity, along with the synaptic potentiation with the number of electrical pulses through the device, suggests that this device can be used in artificial synaptic electronics. Although various attributes (pulse period, width, and amplitude dependence) of the synaptic potentiation shown by the device have yet to be investigated, this work serves as a starting point for using the synaptic behavior of an α-Fe2O3/p-Si device in future synaptic electronics.
4. Conclusions
We successfully fabricated a device with promising synaptic electrical character using α-Fe2O3 microcrystalline films on p-type Si (100). Using trap-assisted tunneling and Poole–Frenkel emission models fit to the experimental data, we have demonstrated that the device has two different conduction mechanisms when operated in low (0–0.7 V) and high (0.7–5 V) voltage ranges. Specifically, between the 0–0.7 V range, the dominant conduction mechanism is trap-assisted tunneling and, as the voltage surpasses 0.7 V, carriers trapped in defect sites are excited into the conduction band of α-Fe2O3, at which point the Poole–Frenkel emission conduction mechanism dominates the carrier transport. Based on an analogy of protein-ligand binding, the Hill function has been used to demonstrate that the voltage pulse induced activation of the device under dark conditions is three pulses, while with illumination with a white light of intensity 1.27 mW/cm2 it is 166 pulses. The synaptic potentiation of the device is very interesting and worthy of further investigation. Future studies will examine the temporal variations of the activation with ultra-fast electrical pulses.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sci5010003/s1, Figure S1: SEM micrographs for sample prepared using (a) 28 mM and (b) 141 mM solutions shows variation of the bulk size; Figure S2: (a) EDX mapping of elements and (b) EDX spectra for sample prepared using 28 mM. (c) EDX mapping of elements and (d) EDX spectra for samples prepared using 141 mM solutions. Higher intensity of Fe peak in (d) shows the increased bulk size in the samples; Figure S3: Raman Spectroscopy of the samples prepared using the 28 mM and 141 mM solutions. Peaks that are the signatures of α-Fe2O3 and Si were observed [53,54,55,56,57].
Author Contributions
P.M. contributed to Conceptualization, Data Curation, Formal Analysis, Investigation, Writing–original draft preparation and Visualization. D.N.M. contributed to Writing–review and editing, Supervision and Funding Acquisition. P.W. contributed to data curation, review, and editing. C.M. contributed to sample preparation and data curation. This publication has been read and agreed upon by all contributing authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors would like to acknowledge the U.S. Office of Naval Research for the support of the work (No. N00014-20-1-2433).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jeong, D.S.; Kim, I.; Ziegler, M.; Kohlstedt, H. Towards artificial neurons and synapses: A materials point of view. RSC Adv. 2013, 3, 3169–3183. [Google Scholar] [CrossRef]
- Kuzum, D.; Yu, S.; Wong, H.-S.P. Synaptic electronics: Materials, devices and applications. Nanotechnology 2013, 24, 382001. [Google Scholar] [CrossRef]
- Li, D.; Wu, B.; Zhu, X.; Wang, J.; Ryu, B.; Lu, W.D.; Lu, W.; Liang, X. MoS2 Memristors Exhibiting Variable Switching Characteristics toward Biorealistic Synaptic Emulation. ACS Nano 2018, 12, 9240–9252. [Google Scholar] [CrossRef]
- Yang, X.; Wang, C.; Shang, J.; Zhang, C.; Tan, H.; Yi, X.; Pan, L.; Zhang, W.; Fan, F.; Liu, Y.; et al. An organic terpyridyl-iron polymer based memristor for synaptic plasticity and learning behavior simulation. RSC Adv. 2016, 6, 25179–25184. [Google Scholar] [CrossRef]
- Lee, G.; Baek, J.; Ren, F.; Pearton, S.J.; Lee, G.; Kim, J. Artificial Neuron and Synapse Devices Based on 2D Materials. Small 2021, 17, e2100640. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Chen, Y.; Yi, M.; Zhu, Y.; Li, T.; Liu, L.; Wang, L.; Xie, L.; Huang, W. Recent progress in memristors for stimulating synaptic plasticity. Sci. Sin. Inf. 2018, 48, 115–142. [Google Scholar] [CrossRef]
- Azevedo, F.A.C.; Carvalho, L.R.; Grinberg, L.T.; Farfel, J.M.; Ferretti, R.E.; Leite, R.E.; Filho, W.J.; Lent, R.; Herculano-Houzel, S. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 2009, 513, 532–541. [Google Scholar] [CrossRef]
- Brotherson, S. Understanding Brain Development in Young Children; NDSU Extension Service: Fargo, ND, USA, 2005; Volume 8. [Google Scholar]
- Zhao, L.; Chen, H.-Y.; Wu, S.-C.; Jiang, Z.; Yu, S.; Hou, T.-H.; Wong, H.-S.P.; Nishi, Y. Multi-level control of conductive nano-filament evolution in HfO2 ReRAM by pulse-train operations. Nanoscale 2014, 6, 5698–5702. [Google Scholar] [CrossRef]
- Park, S.; Sheri, A.; Kim, J.; Noh, J.; Jang, J.; Jeon, M.; Lee, B.; Lee, B.R.; Lee, B.H.; Hwang, H. Neuromorphic Speech Systems Using Advanced ReRAM-Based Synapse. In Proceedings of the 2013 IEEE International Electron Devices Meeting, Washington, DC, USA, 9–11 December 2013; pp. 25.6.1–25.6.4. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-Based Resistive Switching Memories—Nanoionic Mechanisms, Prospects, and Challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
- Valov, I.; Kozicki, M.N. Cation-based resistance change memory. J. Phys. Appl. Phys. 2013, 46, 074005. [Google Scholar] [CrossRef]
- Chanthbouala, A.; Garcia, V.; Cherifi, R.O.; Bouzehouane, K.; Fusil, S.; Moya, X.; Xavier, S.; Yamada, H.; Deranlot, C.; Mathur, N.D.; et al. A ferroelectric memristor. Nat. Mater. 2012, 11, 860–864. [Google Scholar] [CrossRef] [PubMed]
- Tuma, T.; Pantazi, A.; Le Gallo, M.; Sebastian, A.; Eleftheriou, E. Stochastic phase-change neurons. Nat. Nanotechnol. 2016, 11, 693–699. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wang, W.; Yang, H. Recent Progress in Synaptic Devices Based on 2D Materials. Adv. Intell. Syst. 2020, 2, 1900167. [Google Scholar] [CrossRef]
- Covi, E.; Brivio, S.; Fanciulli, M.; Spiga, S. Synaptic potentiation and depression in Al:HfO2-based memristor. Microelectron. Eng. 2015, 147, 41–44. [Google Scholar] [CrossRef]
- Seo, K.; Kim, I.; Jung, S.; Jo, M.; Park, S.; Park, J.; Shin, J.; Biju, K.P.; Kong, J.; Lee, K.; et al. Analog memory and spike-timing-dependent plasticity characteristics of a nanoscale titanium oxide bilayer resistive switching device. Nanotechnology 2011, 22, 254023. [Google Scholar] [CrossRef]
- Choi, H.; Jung, H.; Lee, J.; Yoon, J.; Park, J.; Seong, D.J.; Lee, W.; Hasan, M.; Jung, G.Y.; Hwang, H. An electrically modifiable synapse array of resistive switching memory. Nanotechnology 2009, 20, 345201. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.; Jo, S.-H.; Lu, W. Short-Term Memory to Long-Term Memory Transition in a Nanoscale Memristor. ACS Nano 2011, 5, 7669–7676. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Wu, Y.; Jeyasingh, R.; Kuzum, D.; Wong, H.-S.P. An Electronic Synapse Device Based on Metal Oxide Resistive Switching Memory for Neuromorphic Computation. IEEE Trans. Electron Devices 2011, 58, 2729–2737. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, S.; Wong, H.S.P.; Chen, Y.S.; Lee, H.Y.; Wang, S.M.; Gu, P.Y.; Chen, F.; Tsai, M.J. AlOx-Based Resistive Switching Device with Gradual Resistance Modulation for Neuromorphic Device Application. In Proceedings of the 2012 4th IEEE International Memory Workshop, Milan, Italy, 20–23 May 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Smith, K.S.; Huyck, H.L. An Overview of the Abundance, Relative Mobility, Bioavailability, and Human Toxicity of Metals. In The Environmental Geochemistry of Mineral Deposits; Society of Economic Geologists: Littleton, CO, USA, 1997; pp. 29–70. [Google Scholar] [CrossRef]
- Xia, C.; Jia, Y.; Tao, M.; Zhang, Q. Tuning the band gap of hematite α-Fe2O3 by sulfur doping. Phys. Lett. A 2013, 377, 1943–1947. [Google Scholar] [CrossRef]
- Sharma, P.; Jang, J.; Lee, J.S. Key Strategies to Advance the Photoelectrochemical Water Splitting Performance of α-Fe2O3 Photoanode. ChemCatChem 2019, 11, 157–179. [Google Scholar] [CrossRef]
- Sivula, K.; Le, F.; Grätzel, M. Solar Water Splitting: Progress Using Hematite (α-Fe2O3) Photoelectrodes. ChemSusChem 2011, 4, 432–449. [Google Scholar] [CrossRef] [PubMed]
- Mirzaei, A.; Hashemi, B.; Janghorban, K. α-Fe2O3 based nanomaterials as gas sensors. J. Mater. Sci. Mater. Electron. 2016, 27, 3109–3144. [Google Scholar] [CrossRef]
- Chen, J.; Xu, L.; Li, W.; Gou, X. α-Fe2O3 Nanotubes in Gas Sensor and Lithium-Ion Battery Applications. Adv. Mater. 2005, 17, 582–586. [Google Scholar] [CrossRef]
- Sawa, A. Resistive switching in transition metal oxides. Mater. Today 2008, 11, 28–36. [Google Scholar] [CrossRef]
- Zhou, G.; Yang, X.; Xiao, L.; Sun, B.; Zhou, A. Investigation of a submerging redox behavior in Fe2O3 solid electrolyte for resistive switching memory. Appl. Phys. Lett. 2019, 114, 163506. [Google Scholar] [CrossRef]
- Ji, X.; Paulsen, B.D.; Chik, G.K.; Wu, R.; Yin, Y.; Chan, P.K.; Rivnay, J. Mimicking associative learning using an ion-trapping non-volatile synaptic organic electrochemical transistor. Nat. Commun. 2021, 12, 2480. [Google Scholar] [CrossRef] [PubMed]
- Wetzelaer, G.-J.A.H.; Scheepers, M.; Sempere, A.M.; Momblona, C.; Ávila, J.; Bolink, H.J. Trap-Assisted Non-Radiative Recombination in Organic-Inorganic Perovskite Solar Cells. Adv. Mater. 2015, 27, 1837–1841. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, J.; Shi, T.; Zhao, X.; Zhang, X.; Yang, Y.; Wu, F.; Li, Y.; Liu, Q.; Liu, M. A Habituation Sensory Nervous System with Memristors. Adv. Mater. 2020, 32, e2004398. [Google Scholar] [CrossRef]
- Lim, E.; Ismail, R. Conduction Mechanism of Valence Change Resistive Switching Memory: A Survey. Electronics 2015, 4, 586–613. [Google Scholar] [CrossRef]
- Chiu, F.-C. A Review on Conduction Mechanisms in Dielectric Films. Adv. Mater. Sci. Eng. 2014, 2014, 578168. [Google Scholar] [CrossRef]
- Gehring, A. Ausgeführt zum Zwecke der Erlangung des akademischen Grades eines Doktors der technischen Wissenschaften. Ph.D. Thesis, E360—Institut für Mikroelektronik, Stuttgart, Germany, 2003; p. 178. Available online: http://hdl.handle.net/20.500.12708/12170 (accessed on 5 January 2023).
- Houng, M.P.; Wang, Y.H.; Chang, W.J. Current transport mechanism in trapped oxides: A generalized trap-assisted tunneling model. J. Appl. Phys. 1999, 86, 1488–1491. [Google Scholar] [CrossRef]
- Vourkas, I.; Batsos, A.; Sirakoulis, G.C. Spice modeling of nonlinear memristive behavior: Memristor Spice Modeling. Int. J. Circuit Theory Appl. 2015, 43, 553–565. [Google Scholar] [CrossRef]
- Sun, B.; Xiao, M.; Zhou, G.; Ren, Z.; Zhou, Y.N.; Wu, Y.A. Non–zero-crossing current-voltage hysteresis behavior in memristive system. Mater. Today Adv. 2020, 6, 100056. [Google Scholar] [CrossRef]
- Huh, W.; Lee, D.; Lee, C. Memristors Based on 2D Materials as an Artificial Synapse for Neuromorphic Electronics. Adv. Mater. 2020, 32, 2002092. [Google Scholar] [CrossRef]
- Hu, S.G.; Liu, Y.; Chen, T.P.; Liu, Z.; Yu, Q.; Deng, L.J.; Yin, Y.; Hosaka, S. Emulating the paired-pulse facilitation of a biological synapse with a NiOx-based memristor. Appl. Phys. Lett. 2013, 102, 183510. [Google Scholar] [CrossRef]
- Cruz-Albrecht, J.M.; Derosier, T.; Srinivasa, N. A scalable neural chip with synaptic electronics using CMOS integrated memristors. Nanotechnology 2013, 24, 384011. [Google Scholar] [CrossRef]
- Liao, K.; Lei, P.; Tu, M.; Luo, S.; Jiang, T.; Jie, W.; Hao, J. Memristor Based on Inorganic and Organic Two-Dimensional Materials: Mechanisms. Performance, and Synaptic Applications. ACS Appl. Mater. Interfaces 2021, 13, 32606–32623. [Google Scholar] [CrossRef] [PubMed]
- Gesztelyi, R.; Zsuga, J.; Kemeny-Beke, A.; Varga, B.; Juhasz, B.; Tosaki, A. The Hill equation and the origin of quantitative pharmacology. Arch. Hist. Exact Sci. 2012, 66, 427–438. [Google Scholar] [CrossRef]
- Goutelle, S.; Maurin, M.; Rougier, F.; Barbaut, X.; Bourguignon, L.; Ducher, M.; Maire, P. The Hill equation: A review of its capabilities in pharmacological modelling. Fundam. Clin. Pharmacol. 2008, 22, 633–648. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J.G. Kinetics of pharmacologic response I. Proposed relationships between response and drug concentration in the intact animal and man. J. Theor. Biol. 1968, 20, 173–201. [Google Scholar] [CrossRef]
- Mager, D.E.; Wyska, E.; Jusko, W.J. Diversity of Mechanism-Based Pharmacodynamic Models. Drug Metab. Dispos. 2003, 31, 510–518. [Google Scholar] [CrossRef]
- Hunter, C.A.; Anderson, H.L. What is Cooperativity? Angew. Chem. Int. Ed. 2009, 48, 7488–7499. [Google Scholar] [CrossRef] [PubMed]
- Grado-Caffaro, M. Fermionic Behaviour of Excitons in Both Paraboli and Non-Parabolic Semiconductors. Theor. Phys. 2017, 2, 30–33. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, Y.; Chen, Z.; Sun, L.; Wang, J.; Chen, M.; Xu, Z.; Liao, Q.; Zhou, L.; Chen, X.; et al. Phototunable Biomemory Based on Light-Mediated Charge Trap. Adv. Sci. 2018, 5, 1800714. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Z. Charge trapping and detrapping in polymeric materials. J. Appl. Phys. 2009, 106, 123707. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, G.; Liao, R.; Xu, Z. Charge trapping and detrapping in polymeric materials: Trapping parameters. J. Appl. Phys. 2011, 110, 043724. [Google Scholar] [CrossRef]
- Williams, C.K. Kinetics of trapping, detrapping, and trap generation. J. Electron. Mater. 1992, 21, 711–720. [Google Scholar] [CrossRef]
- Chamritski, I.; Burns, G. Infrared- and Raman-Active Phonons of Magnetite, Maghemite, and Hematite: A Computer Simulation and Spectroscopic Study. J. Phys. Chem. B 2005, 109, 4965–4968. [Google Scholar] [CrossRef]
- Das, S.; Hendry, M.J. Application of Raman spectroscopy to identify iron minerals commonly found in mine wastes. Chem. Geol. 2011, 290, 101–108. [Google Scholar] [CrossRef]
- Bersani, D.; Lottici, P.P.; Montenero, A. Micro-Raman investigation of iron oxide films and powders produced by sol-gel syntheses. J. Raman Spectrosc. 1999, 30, 6. [Google Scholar]
- De Faria, D.L.; Venancio Silva, S.; De Oliveira, M.T. Raman microspectroscopy of some iron oxides and oxyhydroxides. J. Raman Spectrosc. 1997, 28, 6. [Google Scholar]
- Li, B.; Yu, D.; Zhang, S.-L. Raman spectral study of silicon nanowires. Phys. Rev. B 1999, 59, 1645–1648. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).