Identification of Long-Term Behavior of Natural Circulation Loops: A Thresholdless Approach from an Initial Response
Abstract
1. Introduction
- Development of a computationally fast algorithm for behavior prediction of NCL systems: The long-term behavior of an NCL system is predicted from the initial transient data.
- Validation of the underlying algorithms on an experimentally validated NCL system simulator: The validation process is based on testing with different sets of system parameters and initial conditions. The test results demonstrate that the performance is independent of the process parameters and that the predictions are consistent with the physics of NCL systems.
2. Description of the Numerical Model
3. Numerical Results
4. Mathematical Theory
4.1. Probabilistic Finite State Automata
- is a (nonempty) finite alphabet, i.e., its cardinality is a positive integer.
- Q is a (nonempty) finite set of states, i.e., its cardinality is a positive integer.
- is a state transition map.
- The set of all words including the empty word ϵ, constructed from symbols in , is denoted as .
- The set of all words, whose suffix (respectively, prefix) is the word w, is denoted as (respectively, ).
- The set of all words of (finite) length ℓ is denoted as , where ℓ is a positive integer.
- The deterministic FSA G is called the underlying FSA of the PFSA K.
- The probability map is called the morph function (also known as symbol generation probability function) that satisfies the condition: for all which can be converted to a morph matrix Π
- The state transition probability mass function is constructed by combining δ and π, which can be structured as a state transition probability matrix . In that case, the PFSA can also be described as the triple .
4.2. D-Markov Machines
- Alphabet size (): To separate out the regimes in the feature space, a larger alphabet size is preferred but more data is required for training the model. For the purpose of this paper, an alphabet size was sufficient.
- Depth (D) in the D-Markov machine: Sometimes, a higher value of the Markov depth D may lead to better results. However, this comes at the expense of increased computational time, due to larger dimension of the space and the need for more training. In this work, has been chosen to keep lower word lengths and smaller PFSAs which leads to faster training and testing.
- Choice of Feature: The feature needs to be one that best captures the nature (e.g., texture) of the signal. The morph matrix (which for is identical to the state transition matrix ) has been chosen as the feature, because it is easily computed and captures the pertinent dynamics embedded in the signal.
4.3. Hidden Markov Modeling for Classification
- (1)
- is the state-transition probability matrix, where is the finite number of hidden states belonging to the set N of hidden states:where and .
- (2)
- is the probability density of the observation given the state:
- (3)
- is the probability distribution of the initial state : , where is a vector with and .
5. Problem Formulation and Algorithm Development
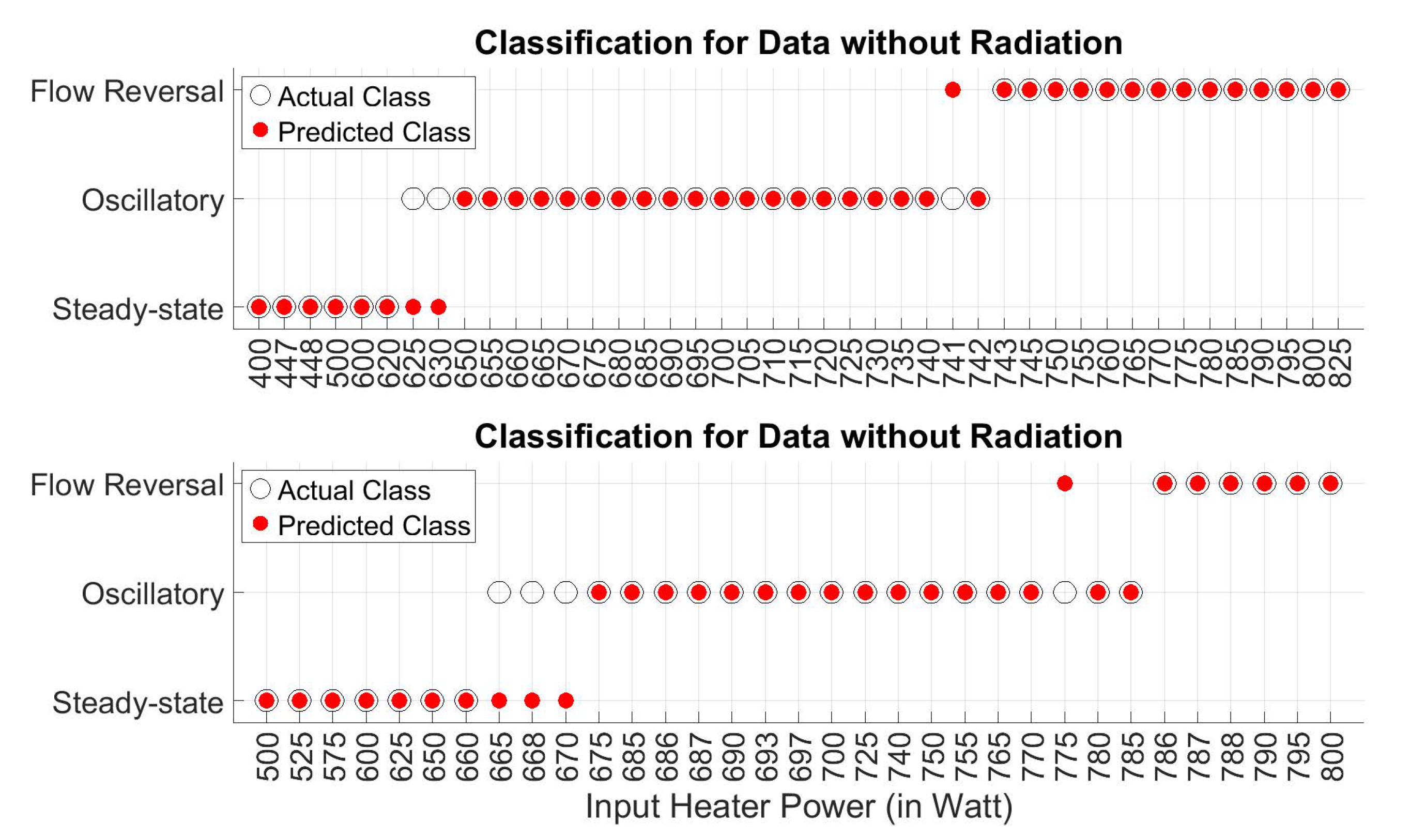
5.1. Regime Classification
5.2. Identification of System Nature
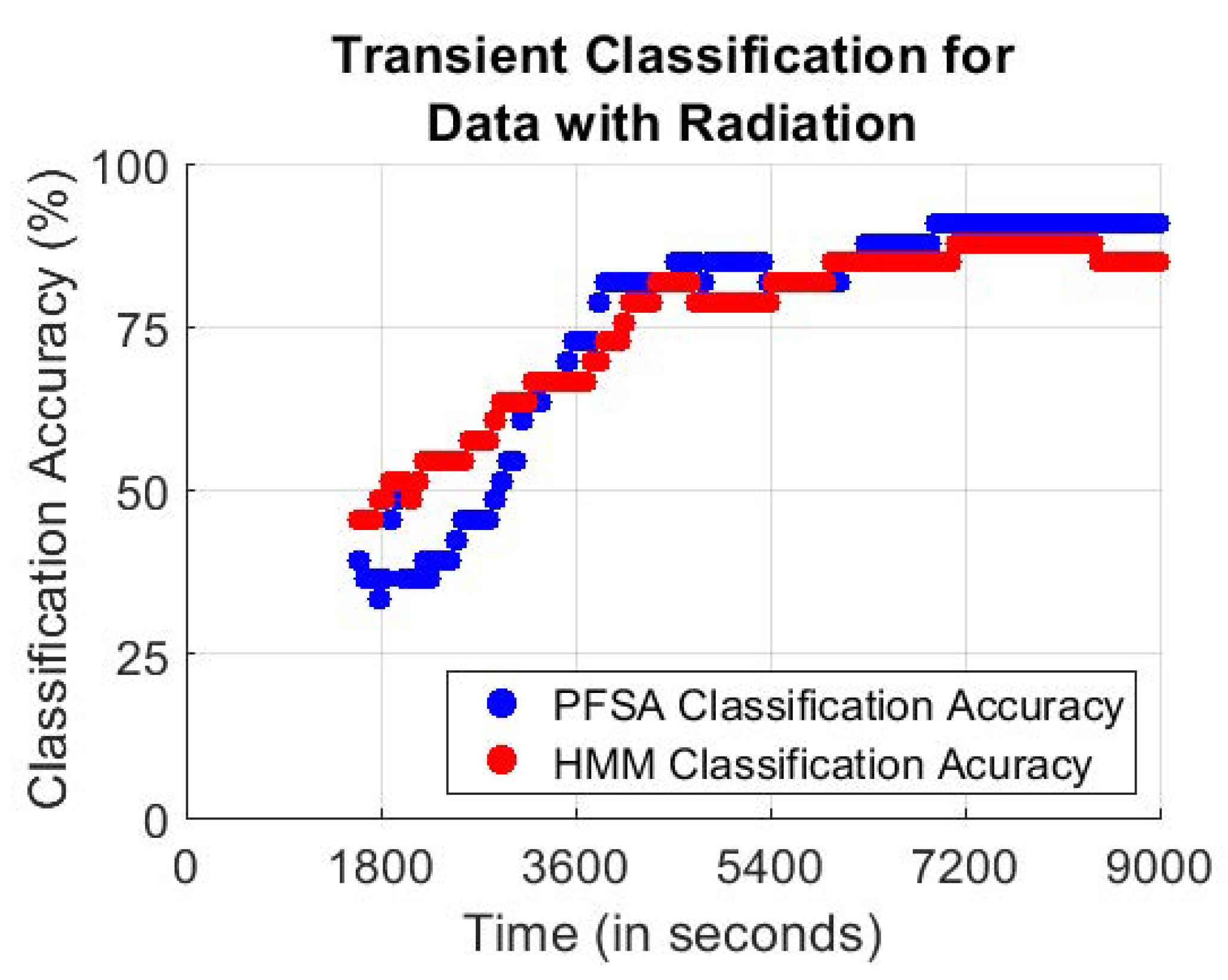
6. Results and Discussions
6.1. Classification Accuracy
6.2. Computation Overhead
6.3. Efficacy of Identification/Classification
7. Summary, Conclusions, and Future Work
- (1)
- Investigation of the efficacy of the PFSA algorithms using data from other experimental and industrial NCL systems and more simulations with varying geometry parameters.
- (2)
- Enhancement of the PFSA algorithms to accommodate smaller data window lengths (i.e., faster detection and identification of regimes).
- (3)
- Investigation of other regime identification/classification methods, such as different configurations of neural networks.
- (4)
- Quantitative analysis of the effects of radiative and convective heat transfer on operational characteristics of NCL systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Internal surface area of the loop through which heat transfer takes place area (m2) | |
| Surface area through which heat transfer takes place in the cooler (m2) | |
| Surface area through which heat loss takes place to the ambient (m2) | |
| Specific heat of fluid at constant pressure (J/kg· K) | |
| Specific heat of wall at constant pressure (J/kg· K) | |
| Specific heat of coolant at constant pressure (J/kg· K) | |
| Internal loop diameter (m) | |
| Outer loop diameter (m) | |
| Change in length (m) | |
| f | Friction factor |
| g | Gravitational acceleration (m/s2) |
| Loop fluid mass-flux (kg/m· s) | |
| Coolant mass-flux (kg/m· s) | |
| Grashof number | |
| Graetz number | |
| Heat transfer coefficient between the fluid and wall (W/m· K) | |
| Heat transfer coefficient between wall and ambient (W/m· K) | |
| Radiation heat transfer coefficient (W/m· K) | |
| Heat transfer coefficient between wall and coolant (W/m· K) | |
| Thermal conductivity of the fluid (W/m· K) | |
| Thermal conductivity of the wall (W/m· K) | |
| Thermal conductivity of heat exchanger (W/m· K) | |
| Total loop length (m) | |
| Loop height (m) | |
| Nusselt number | |
| Prandtl number | |
| Q | Heat input (W) |
| Rayleigh number | |
| Reynolds number | |
| t | Time (s) |
| Temperature of fluid (°C) | |
| Loop wall temperature (°C) | |
| Coolant temperature (°C) | |
| Reference temperature (°C) | |
| Ambient temperature (°C) | |
| The component of the fluid velocity in the z–direction (m/s) | |
| Volume of the wall except heater and cooler section (m3) | |
| Volume of the wall in the heater section (m3) | |
| Volume of the heat exchanger (m3) | |
| Thermal volumetric expansion coefficient (K) | |
| Dynamic viscosity of the fluid (kg/m· s) | |
| Dynamic viscosity of the fluid at the surface (kg/m· s) | |
| Kinematic viscosity of the fluid (m/s) | |
| Fluid density (kg/m) | |
| Wall density (kg/m) | |
| Coolant density (kg/m) |
References
- Vijayan, P.; Austregesilo, H.; Teschendorff, V. Simulation of the unstable oscillatory behavior of single-phase natural circulation with repetitive flow reversals in a rectangular loop using the computer code ATHLET. Nucl. Eng. Des. 1995, 155, 623–641. [Google Scholar] [CrossRef]
- Vijayan, P. Experimental observations on the general trends of the steady state and stability behaviour of single-phase natural circulation loops. Nucl. Eng. Des. 2002, 215, 139–152. [Google Scholar] [CrossRef]
- Vijayan, P.; Sharma, M.; Saha, D. Steady state and stability characteristics of single-phase natural circulation in a rectangular loop with different heater and cooler orientations. Exp. Therm. Fluid Sci. 2007, 31, 925–945. [Google Scholar] [CrossRef]
- Misale, M.; Tagliafico, L. The transient and stability behaviour of single-phase natural circulation loops. Heat Technol. 1987, 5, 101–116. [Google Scholar]
- Misale, M.; Garibaldi, P.; Tarozzi, L.; Barozzi, G.S. Influence of thermal boundary conditions on the dynamic behaviour of a rectangular single-phase natural circulation loop. Int. J. Heat Fluid Flow 2011, 32, 413–423. [Google Scholar] [CrossRef]
- Misale, M. Experimental study on the influence of power steps on the thermohydraulic behavior of a natural circulation loop. Int. J. Heat Mass Transf. 2016, 99, 782–791. [Google Scholar] [CrossRef]
- Cammi, A.; Luzzi, L.; Pini, A. The influence of the wall thermal inertia over a single-phase natural convection loop with internally heated fluids. Chem. Eng. Sci. 2016, 153, 411–433. [Google Scholar] [CrossRef]
- Goudarzi, N.; Talebi, S. Heat removal ability for different orientations of single-phase natural circulation loops using the entransy method. Ann. Nucl. Energy 2018, 111, 509–522. [Google Scholar] [CrossRef]
- Desrayaud, G.; Fichera, A.; Lauriat, G. Two-dimensional numerical analysis of a rectangular closed-loop thermosiphon. Appl. Therm. Eng. 2013, 50, 187–196. [Google Scholar] [CrossRef]
- Krishnani, M.; Basu, D.N. Computational stability appraisal of rectangular natural circulation loop: Effect of loop inclination. Ann. Nucl. Energy 2017, 107, 17–30. [Google Scholar]
- Nayak, A.; Vijayan, P.; Saha, D.; Raj, V.V. Mathematical modelling of the stability characteristics of a natural circulation loop. Math. Comput. Model. 1995, 22, 77–87. [Google Scholar] [CrossRef]
- Der Lee, J.; Pan, C.; Chen, S.W. Nonlinear dynamic analysis of a two-phase natural circulation loop with multiple nuclear-coupled boiling channels. Ann. Nucl. Energy 2015, 80, 77–94. [Google Scholar]
- Luzzi, L.; Misale, M.; Devia, F.; Pini, A.; Cauzzi, M.T.; Fanale, F.; Cammi, A. Assessment of analytical and numerical models on experimental data for the study of single-phase natural circulation dynamics in a vertical loop. Chem. Eng. Sci. 2017, 162, 262–283. [Google Scholar] [CrossRef]
- Goyal, V.; Hassija, V.; Pandey, V.; Singh, S. Non-linear dynamics of single phase rectangular natural circulation loop. Prog. Nucl. Energy 2020, 130, 103530. [Google Scholar] [CrossRef]
- Elton, D.; Arunachala, U.; Vijayan, P. Investigations on the dependence of the stability threshold on different operating procedures in a single-phase rectangular natural circulation loop. Int. J. Heat Mass Transf. 2020, 161, 120264. [Google Scholar]
- du Toit, C.G. Fundamental evaluation of the effect of pipe diameter, loop length and local losses on steady-state single-phase natural circulation in square loops using the 1D network code Flownex. Therm. Sci. Eng. Prog. 2021, 22, 100840. [Google Scholar] [CrossRef]
- Dass, A.; Gedupudi, S. Numerical investigation on the heat transfer coefficient jump in tilted single-phase natural circulation loop and coupled natural circulation loop. Int. Commun. Heat Mass Transf. 2021, 120, 104920. [Google Scholar] [CrossRef]
- Saha, R.; Sen, S.; Mookherjee, S.; Ghosh, K.; Mukhopadhyay, A.; Sanyal, D. Experimental and numerical investigation of a single-phase square natural circulation loop. J. Heat Transf. 2015, 137, 121010. [Google Scholar] [CrossRef]
- Saha, R.; Ghosh, K.; Mukhopadhyay, A.; Sen, S. Dynamic characterization of a single phase square natural circulation loop. Appl. Therm. Eng. 2018, 128, 1126–1138. [Google Scholar] [CrossRef]
- Saha, R.; Ghosh, K.; Mukhopadhyay, A.; Sen, S. Flow reversal prediction of a single-phase square natural circulation loop using symbolic time series analysis. Sādhanā 2020, 45, 1–11. [Google Scholar]
- Daw, C.; Fenney, C.; Tracy, E. A review of symbolic analysis of experimental data. Rev. Sci. Instrum. 2003, 74, 915–930. [Google Scholar] [CrossRef]
- Dupont, P.; Denis, F.; Esposito, Y. Links between probabilistic automata and hidden Markov models: Probability distributions, learning models and induction algorithms. Pattern Recognit. 2005, 38, 1349–1371. [Google Scholar] [CrossRef]
- Ray, A. Symbolic dynamic analysis of complex systems for anomaly detection. Signal Process. 2004, 84, 1115–1130. [Google Scholar] [CrossRef]
- Mukherjee, K.; Ray, A. State splitting and merging in probabilistic finite state automata for signal representation and analysis. Signal Process. 2014, 104, 105–119. [Google Scholar] [CrossRef]
- Sarkar, S.; Chakravarthy, S.; Ramanan, V.; Ray, A. Dynamic data-driven prediction of instability in a swirl-stabilized combustor. Int. J. Spray Combust. Dyn. 2016, 8, 235–253. [Google Scholar] [CrossRef]
- Bhattacharya, C.; O’Connor, J.; Ray, A. Data-driven Early Detection of Thermoacoustic Instability in a Multi-nozzle Combustor. Combust. Sci. Technol. 2020, 1–32. [Google Scholar] [CrossRef]
- Ghalyan, N.F.; Ray, A. Symbolic Time Series Analysis for Anomaly Detection in Measure-invariant Ergodic Systems. J. Dyn. Syst. Meas. Control 2020, 142, 061003. [Google Scholar] [CrossRef]
- Jha, D.; Virani, N.; Reimann, J.; Srivastav, A.; Ray, A. Symbolic analysis-based reduced order Markov modeling of time series data. Signal Process. 2018, 149, 68–81. [Google Scholar] [CrossRef]
- Li, Y.; Jha, D.K.; Ray, A.; Wettergren, T.A. Information-Theoretic Performance Analysis of Sensor Networks via Markov Modeling of Time Series Data. IEEE Trans. Cybern. 2018, 48, 1898–1909. [Google Scholar] [CrossRef]
- Najkar, N.; Razzazi, F.; Sameti, H. A novel approach to HMM-based speech recognition systems using particle swarm optimization. Math. Comput. Model. 2010, 52, 1910–1920. [Google Scholar] [CrossRef]
- Oates, T.; Firoiu, L.; Cohen, P. Using dynamic time warping to bootstrap HMM-based clustering of time series. In Sequence Learning; Springer: New York, NY, USA, 2000; pp. 35–52. [Google Scholar]
- Ali, S.S.; Ghani, M.U. Handwritten Digit Recognition Using DCT and HMMs. In Proceedings of the 2014 12th International Conference on Frontiers of Information Technology, Islamabad, Pakistan, 17–19 December 2014; pp. 303–306. [Google Scholar]
- Bhattacharya, C.; Ray, A. Data-driven Detection and Classification of Regimes in Chaotic Systems via Hidden Markov Modeling. ASME Lett. Dyn. Syst. Control 2021, 1, 021009. [Google Scholar] [CrossRef]
- Mondal, S.; Bhattacharya, C.; Ghalyan, N.F.; Ray, A. Real-Time Monitoring and Diagnostics of Anomalous Behavior in Dynamical Systems. In Dynamics and Control of Energy Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 301–327. [Google Scholar]
- Basu, D.N.; Bhattacharyya, S.; Das, P. Effect of heat loss to ambient on steady-state behaviour of a single-phase natural circulation loop. Appl. Therm. Eng. 2007, 27, 1432–1444. [Google Scholar] [CrossRef]
- Basu, D.N.; Bhattacharyya, S.; Das, P. Effect of geometric parameters on steady-state performance of single-phase NCL with heat loss to ambient. Int. J. Therm. Sci. 2008, 47, 1359–1373. [Google Scholar] [CrossRef]
- Rajagopalan, V.; Ray, A. Symbolic time series analysis via wavelet-based partitioning. Signal Process. 2006, 86, 3309–3320. [Google Scholar] [CrossRef]
- Subbu, A.; Ray, A. Space Partitioning via Hilbert Transform for Symbolic Time Series Analysis. Appl. Phys. Lett. 2008, 92, 084107. [Google Scholar] [CrossRef]
- Mor, B.; Garhwal, S.; Kumar, A. A Systematic Review of Hidden Markov Models and Their Applications. Arch. Comput. Methods Eng. 2020. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Murphy, K. Machine Learning: A Probabilistic Perspective, 1st ed.; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2007. [Google Scholar]
- Bhattacharya, C.; Ray, A. Online Discovery and Classification of Operational Regimes from an Ensemble of Time Series Data. J. Dyn. Syst. Meas. Control 2020, 142, 114501. [Google Scholar] [CrossRef]

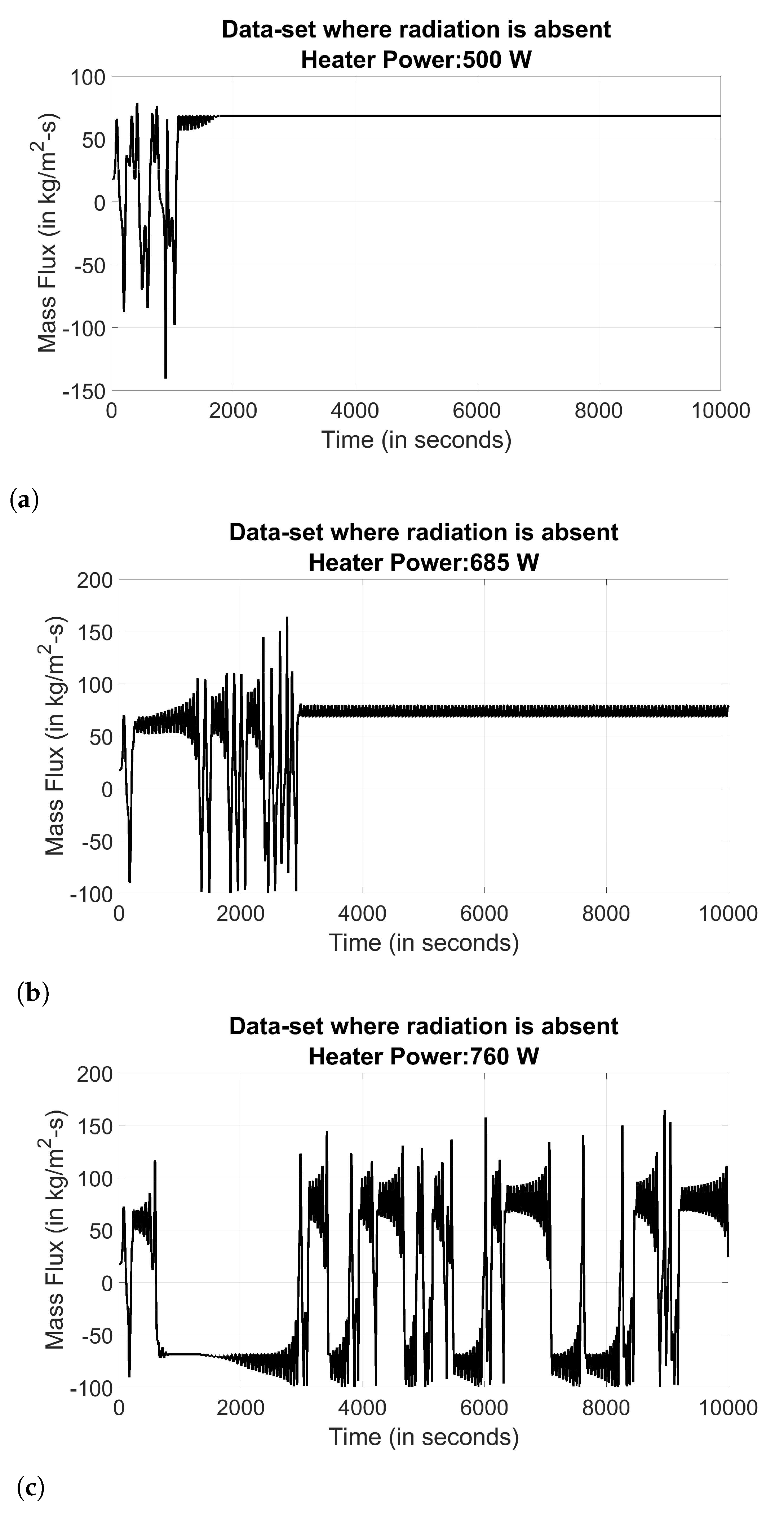
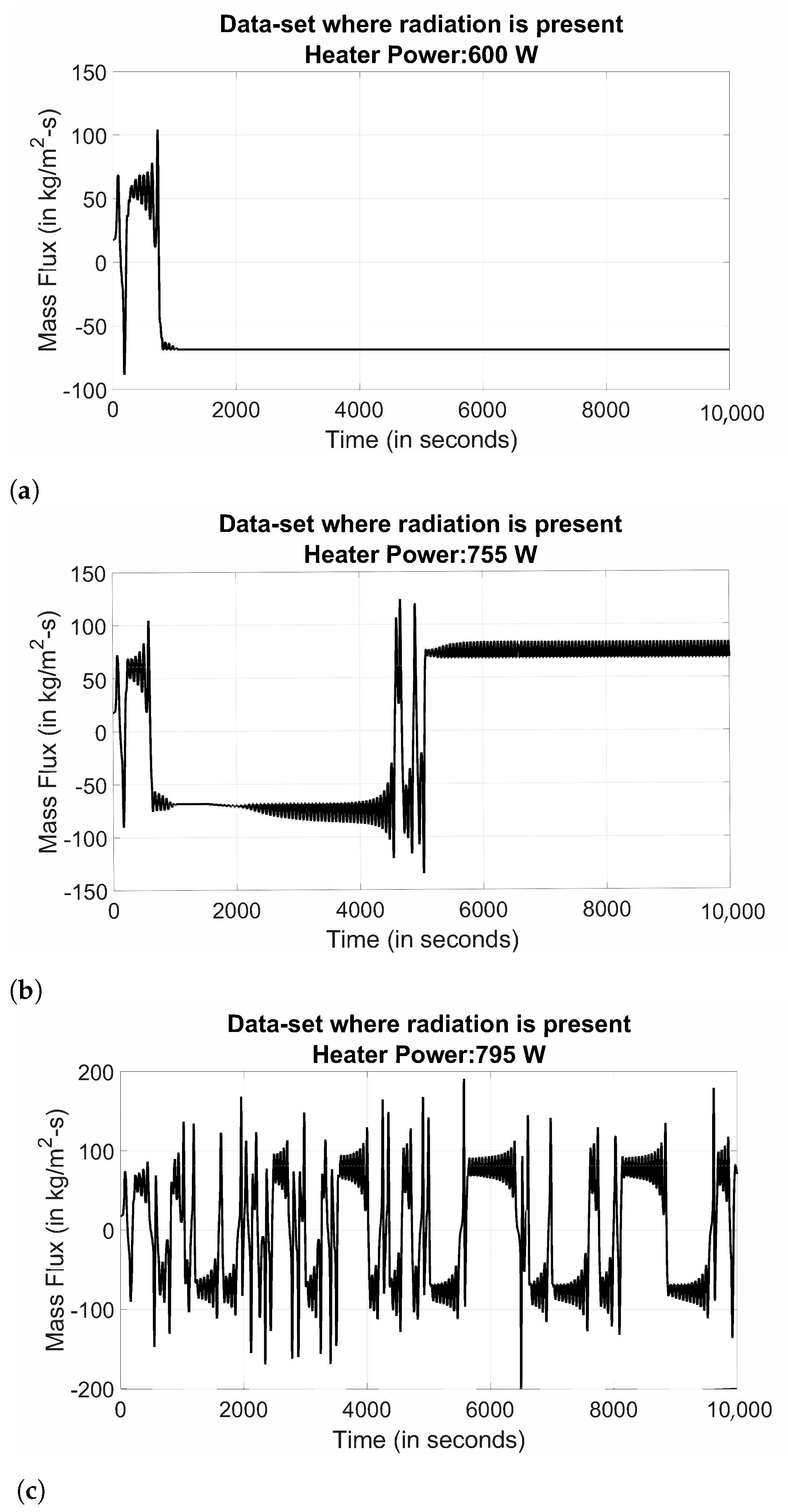


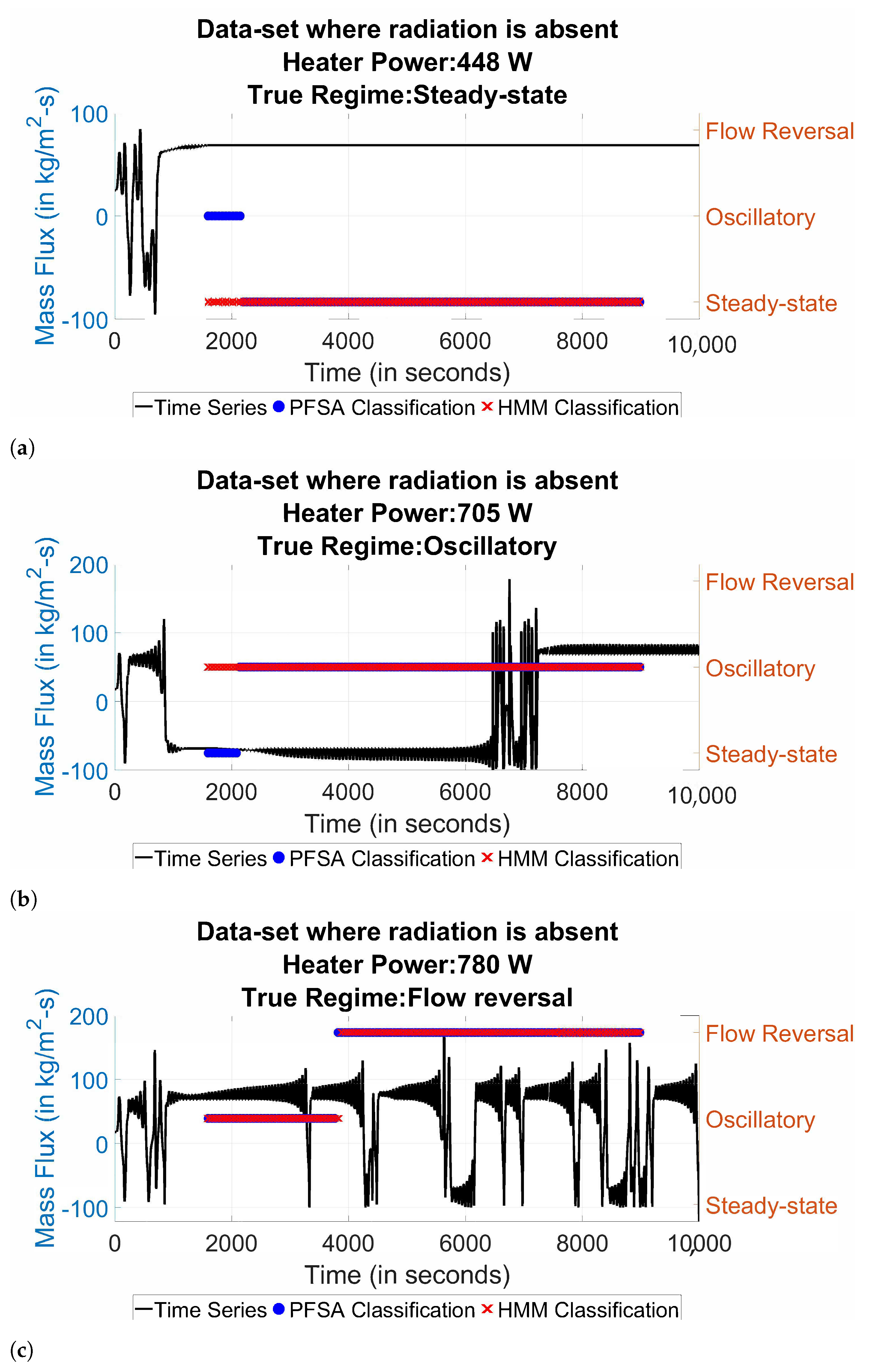
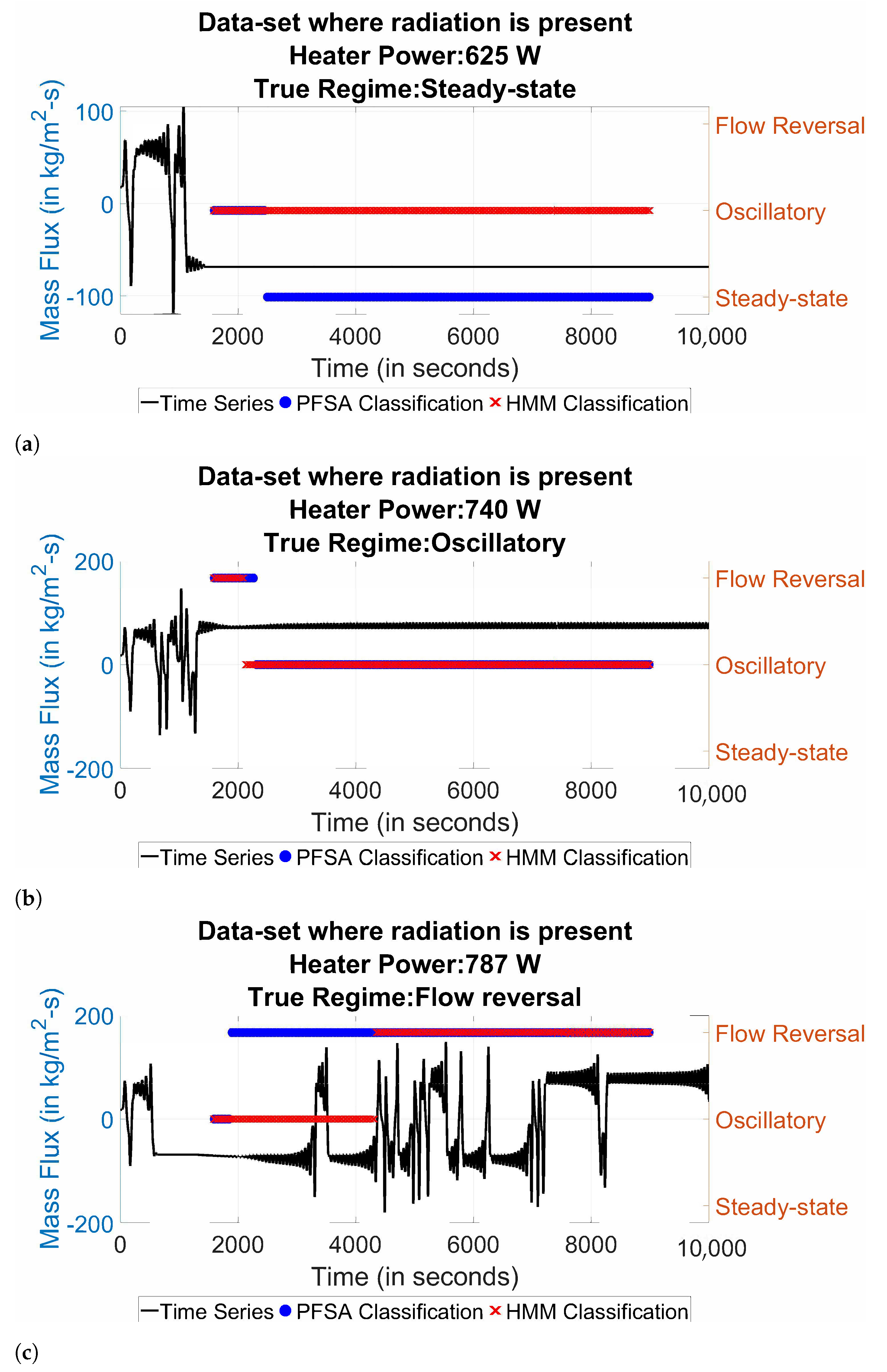
| Change-Point for Steady-State to Oscillatory | Change-Point for Oscillatory to Flow-Reversal | |
|---|---|---|
| Without radiation heat loss | 625 W | 743 W |
| With radiation heat loss | 665 W | 786 W |
| PFSA Method: Classified as | HMM Method: Classified as | |||||
|---|---|---|---|---|---|---|
| SS | OL | FR | SS | OL | FR | |
| Truly SS | 100% | 0 | 0 | 73.33% | 16.67% | 10.00% |
| Truly OL | 0 | 79.55% | 20.45% | 1.82% | 76.82% | 21.36% |
| Truly FR | 0 | 0 | 100% | 0 | 7.86% | 92.14% |
| PFSA Method: Classified as | HMM Method: Classified as | |||||
|---|---|---|---|---|---|---|
| SS | OL | FR | SS | OL | FR | |
| Truly SS | 100% | 0 | 0 | 83.33% | 16.67% | 0 |
| Truly OL | 0 | 79.55% | 20.45% | 0 | 95.65% | 4.35% |
| Truly FR | 0 | 0 | 100% | 0 | 7.14% | 92.86% |
| PFSA Method: Classified as | HMM Method: Classified as | |||||
|---|---|---|---|---|---|---|
| SS | OL | FR | SS | OL | FR | |
| Truly SS | 100% | 0 | 0 | 71.43% | 28.57% | 0 |
| Truly OL | 5% | 90% | 5% | 5% | 85% | 10% |
| Truly FR | 0 | 0 | 100% | 0 | 0 | 100% |
| PFSA | HMM | |
|---|---|---|
| Training Time per Time Series (in ms) | 18.7 | 5252.89 |
| Testing Time per Time Series (in ms) | 22.8 | 67.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharya, C.; Saha, R.; Mukhopadhyay, A.; Ray, A. Identification of Long-Term Behavior of Natural Circulation Loops: A Thresholdless Approach from an Initial Response. Sci 2021, 3, 14. https://doi.org/10.3390/sci3010014
Bhattacharya C, Saha R, Mukhopadhyay A, Ray A. Identification of Long-Term Behavior of Natural Circulation Loops: A Thresholdless Approach from an Initial Response. Sci. 2021; 3(1):14. https://doi.org/10.3390/sci3010014
Chicago/Turabian StyleBhattacharya, Chandrachur, Ritabrata Saha, Achintya Mukhopadhyay, and Asok Ray. 2021. "Identification of Long-Term Behavior of Natural Circulation Loops: A Thresholdless Approach from an Initial Response" Sci 3, no. 1: 14. https://doi.org/10.3390/sci3010014
APA StyleBhattacharya, C., Saha, R., Mukhopadhyay, A., & Ray, A. (2021). Identification of Long-Term Behavior of Natural Circulation Loops: A Thresholdless Approach from an Initial Response. Sci, 3(1), 14. https://doi.org/10.3390/sci3010014








