Analysis of Avoided Level Crossing Muon Spin Resonance Spectra of Muoniated Radicals in Anisotropic Environments: Estimation of Muon Dipolar Hyperfine Parameters for Lorentzian-like Δ₁ Resonances

Abstract

Avoided level crossing muon spin resonance (ALC-$\mu$SR) is used to characterize muoniated free radicals. These radicals are used as probes of the local environment and reorientational motion of specific components in complex systems. The parameter that provides information about the anisotropic motion is the motionally-averaged muon dipolar-hyperfine coupling constant ($⟨D_{\mu }^{\Vert }⟩$). The ALC-$\mu$SR spectra of muoniated radicals in anisotropic environments frequently have Lorentzian-like ${\mathsf{\Delta }}_1$ resonances, which makes it challenging to extract $⟨D_{\mu }^{\Vert }⟩$. In this paper, we derive a means to estimate $|⟨D_{\mu }^{\Vert }⟩|$ from ALC-$\mu$SR spectra with Lorentzian-like resonances by measuring the amplitude, width, and position of the ${\mathsf{\Delta }}_1$ resonance and the amplitude, width, and position of a ${\mathsf{\Delta }}_0$ resonance. Numerical simulations were used to test this relationship for radicals with a wide range of muon and proton hyperfine parameters. We use this methodology to determine $|⟨D_{\mu }^{\Vert }⟩|$ for the Mu adducts of the cosurfactant 2-phenylethanol in ${\mathrm{C}}_{12}$E₄ bilayers. From this we determined the amplitude of the anisotropic reorientational motion of the cosurfactant.

1. Introduction

Muoniated radicals can be formed by the addition of muonium (Mu), a one-electron atom that behaves chemically like a light isotope of hydrogen, to unsaturated bonds [1]. Muoniated radicals can be used as highly polarized spin labels in complex systems where they can provide information about the dynamics and local environment of specific components. Muoniated radicals can be characterized using a magnetic resonance technique called avoided level crossing muon spin resonance (ALC-$\mu$SR). There are several advantages of muon spin labeling compared with traditional labeling using nitroxides or other persistent radicals and characterization using EPR spectroscopy:

• The muoniated radicals are produced in situ.
• The production of the muoniated radicals does not require a complicated mixture of harsh chemicals like Fenton’s reagent or by radiolysis with electrons or $\gamma$-rays, where multiple reactive species are produced and scavengers must be added.
• There are only a few muoniated radicals in the sample at any given instant. This means that bimolecular termination reactions can be ignored, so kinetics are always of first or pseudo-first order, and radicals can be studied under conditions where they are highly mobile.
• Muoniated radicals that can be observed are generally the primary radical products of the Mu addition reaction.
• The 100% spin polarization of an ensemble of muons is preserved during the formation of the muoniated radicals, which makes the muon a polarized spin label in the radical.
• Muoniated radicals are less perturbing probes than stable nitroxide spin labels. This is because the structure of the muoniated radical is generally much closer to that of the parent compound than the nitroxide radical is.

The ALC-$\mu$SR technique has been extensively reviewed [1], so only a brief summary is given here. The technique involves measuring the time-integrated asymmetry (A) of the positrons emitted by the decay of the muons as a function of the applied magnetic field. A is proportional to the time-integrated muon polarization, ${\overline{P}}_z$. Resonances occur when spin states are mixed through the isotropic or anisotropic components of the hyperfine coupling constant (hfcc). We typically observe two types of resonances, which are characterized by the selection rule $\mathsf{\Delta }M$ = 0 and $\pm 1$, where M is the sum of the $m_z$ quantum numbers of the muon, electron, and nuclear spins. The resonances are referred to as ${\mathsf{\Delta }}_0$ and ${\mathsf{\Delta }}_1$ resonances, respectively. The ${\mathsf{\Delta }}_1$ resonance field is given by:

$$B_{\mathrm{res}}^{{\mathsf{\Delta }}_1}=\frac{1}{2}\left[\frac{A_{\mu }}{{\gamma }_{\mu }}-\frac{A_{\mu }}{{\gamma }_{\mathrm{e}}}\right],$$

(1)

where $A_{\mu }$ is the muon hfcc and ${\gamma }_{\mu }$ and ${\gamma }_{\mathrm{e}}$ are the muon and electron gyromagnetic ratios, respectively [2]. The ${\mathsf{\Delta }}_0$ resonance field depends on both the muon hfcc and the proton hfcc, $A_{\mathrm{p}}$, and is given by:

$$B_{\mathrm{res}}^{{\mathsf{\Delta }}_0}=\frac{1}{2}\left[\frac{A_{\mu }-A_{\mathrm{p}}}{{\gamma }_{\mu }-{\gamma }_{\mathrm{p}}}-\frac{A_{\mu }+A_{\mathrm{p}}}{{\gamma }_{\mathrm{e}}}\right],$$

(2)

where ${\gamma }_{\mathrm{p}}$ is the nuclear gyromagnetic ratio [2]. The second term is small in comparison with the first term, so the ${\mathsf{\Delta }}_0$ resonance field is approximately

$$B_{\mathrm{res}}^{{\mathsf{\Delta }}_0}\approx \frac{1}{2}\left[\frac{A_{\mu }-A_{\mathrm{p}}}{{\gamma }_{\mu }-{\gamma }_{\mathrm{p}}}\right],$$

(3)

${\mathsf{\Delta }}_1$ resonances can provide information about the anisotropic motion of muoniated radicals. There have been very detailed studies of motion, chemical reactions, and electron spin flips on ALC-$\mu$SR spectra [3]. We will consider a muoniated radical where the muon has an axially symmetric hyperfine tensor, i.e., it can be described in terms of the parallel muon dipolar hfcc ($D_{\mu }^{\Vert }$) and the perpendicular muon dipolar hfcc ($D_{\mu }^{\perp }$).

$$D_{\mu }^{\Vert }=-2D_{\mu }^{\perp }$$

(4)

because the dipolar tensor is traceless. An axially symmetric hyperfine tensor can arise from rapid rotation of the radical around a single axis. Additional motion of the radical will further average the dipolar coupling. We denote this by the use of angled brackets and refer to this as the motionally-averaged muon dipolar hfcc ($〈D_{\mu }^{\Vert }〉$). If one can determine the value of $〈D_{\mu }^{\Vert }〉$ from ALC-$\mu$SR spectra, it provides important information about the restricted reorientational motion of muoniated spin probes, and hence, of the closely related parent compound.

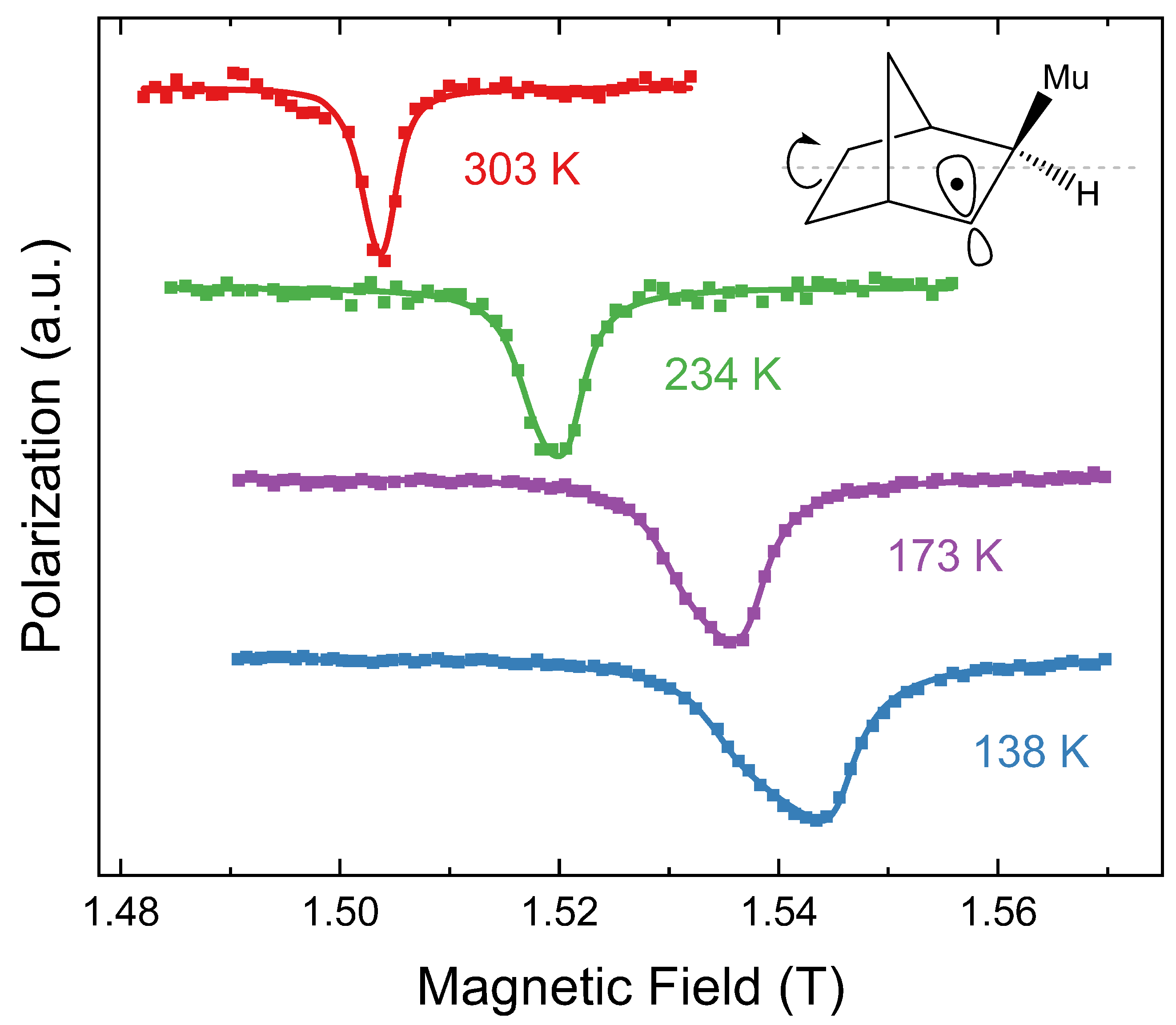
When the ${\mathsf{\Delta }}_1$ resonance has an anisotropic shape, it is possible to determine $〈D_{\mu }^{\Vert }〉$ by fitting this resonance using expressions derived by Roduner and coworkers. A classic example of asymmetric ${\mathsf{\Delta }}_1$ resonances is in the ALC-$\mu$SR spectra of norbornene (Figure 1) [4]. The ${\mathsf{\Delta }}_1$ resonance is anisotropic at low temperatures and becomes roughly Lorentzian at high temperatures due to the decreasing magnitude of $〈D_{\mu }^{\Vert }〉$ that arises from more isotropic reorientational motion of the radical.

Asymmetric resonances like those shown in Figure 1 are rare. We more frequently obtain spectra where the ${\mathsf{\Delta }}_1$ resonances are roughly Lorentzian. In this situation, it is not possible to determine $〈D_{\mu }^{\Vert }〉$ as it is a strongly correlated fit parameter with the damping rate. There have been claims to determine $〈D_{\mu }^{\Vert }〉$ by fitting Lorentzian-like resonances with powder patterns, but this often results in overparamaterized fits and the obtained values not being physically realistic [5]. This is especially true when dealing with the non-linear background in ALC-$\mu$SR spectra that arises from positron spiraling in the applied magnetic field. The issue is that these studies looked at the ${\mathsf{\Delta }}_1$ and ${\mathsf{\Delta }}_0$ resonances independently. To properly fit the resonances, it is necessary to examine the ${\mathsf{\Delta }}_1$ and ${\mathsf{\Delta }}_0$ resonances simultaneously. This is because the parameters of the ${\mathsf{\Delta }}_0$ resonance constrain the values for fitting the ${\mathsf{\Delta }}_1$ resonance. This approach was used to determine $〈D_{\mu }^{\Vert }〉$ by numerically simulating ALC-$\mu$SR spectra and finding the best match with the experimental spectra [6], but this approach is very difficult if there are multiple resonances due to several muoniated radicals and is computationally expensive, especially when there is hyperfine coupling to multiple nuclei. We are seeking a simplified model where one can obtain an approximate value of $|〈D_{\mu }^{\Vert }〉|$ when Lorentzian-like resonances are observed. In this paper, we use the analytical expressions for radicals undergoing a chemical reaction to a state-off resonance to show that one can use the position, amplitude, and width of the ${\mathsf{\Delta }}_1$ resonance and the position, amplitude, and width of a ${\mathsf{\Delta }}_0$ resonance to estimate $|〈D_{\mu }^{\Vert }〉|$. We then use numerical simulations to verify the relationship for chemical reactions to a state-off resonance and find it is also valid for radicals undergoing electron spin flips. We use the results of the simulations to derive an empirical relationship that can be used to extract $|〈D_{\mu }^{\Vert }〉|$ from spectra with Lorentzian-like resonances regardless of the relaxation mechanism. We show that this can be applied to determine the $|〈D_{\mu }^{\Vert }〉|$ values of the three Mu adducts of 2-phenylethanol interacting with the L_α phase of C₁₂E₄ bilayers [7]. We use these values along with DFT calculations to determine the amplitude of the anisotropic reorientational motion of the cosurfactant 2-phenylethanol. This method can be used to study the reorientational motion of specific components in complex systems such as soft matter [6,7] and radicals in zeolites [8].

2. ${\mathsf{\Delta }}_{\mathbf{0}}$ Resonances

We will first begin by considering the ${\mathsf{\Delta }}_0$ resonances. We are interested in the change of the time-integrated muon polarization ($\mathsf{\Delta }{\overline{P}}_z^{{\mathsf{\Delta }}_0}$) as a function of the applied magnetic field [2]. There is an analytical expression for radicals undergoing chemical reaction. It does not account for electron spin flips [9] and neglects the usually small effect of $〈D_{\mu }^{\Vert }〉$ on the resonance field.

$$\mathsf{\Delta }{\overline{P}}_z^{{\mathsf{\Delta }}_0}\left(B\right)=\frac{(2h_{\mathrm{R}}/N){\left({\nu }_r^{{\mathsf{\Delta }}_0}\right)}^2}{{(\lambda /2\pi )}^2+{\left({\nu }_r^{{\mathsf{\Delta }}_0}\right)}^2+{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2{(B-B_{\mathrm{res}}^{{\mathsf{\Delta }}_0})}^2}$$

(5)

$h_{\mathrm{R}}$ is the fraction of muons forming the muoniated radical (i.e., $0\le h_{\mathrm{R}}\le 1$), and N is the dimension of the Pauli spin operator matrix, which depends on the number of spins with $I>0$ in the radical. $h_{\mathrm{R}}/N$ cannot be measured independently but is a common factor in the ${\mathsf{\Delta }}_1$ resonance. In this paper, we will only consider radicals where the ${\mathsf{\Delta }}_0$ resonances are due to protons, i.e., $I_{\mathrm{p}}$ = 1/2. There is an oscillating signal in the time domain. $\lambda$ is the relaxation rate of the oscillating signal, and the frequency on resonance (${\nu }_r^{{\mathsf{\Delta }}_0}$) is

$${\nu }_r^{{\mathsf{\Delta }}_0}=\frac{c{A}_{\mu }{A}_{\mathrm{p}}}{2{\gamma }_{\mathrm{e}}{B}_{\mathrm{res}}^{{\mathsf{\Delta }}_0}}$$

(6)

where $c=\sqrt{I_{\mathrm{p}}(I_{\mathrm{p}}+1)-M(M-1)}$ and $I_{\mathrm{p}}\ge M\ge (-I_{\mathrm{p}}+1)$ [2]. When dealing with a single proton, c = 1. When dealing with two equivalent protons, $c=\sqrt{2}$.

The relaxation of the oscillating signal can have multiple sources. A ubiquitous contribution is the radioactive decay of the muon, which has a lifetime of 2.2 $\mathsf{\mu }$s. There is also a contribution from inhomogeneity in the magnetic field. It can also be due to the chemical reaction of the radical, which takes the muoniated radical out of the resonance condition. In this case, the relaxation is given by:

$${\lambda }^{\prime }=k\left[\mathrm{X}\right]$$

(7)

where k is the second-order rate constant and [X] is the concentration of the molecule “X” that the muoniated radical is reacting with [1]. Relaxation can also be caused by electron spin flips. The unpaired electron is coupled to the muon via the hyperfine interaction, so electron spin relaxation will also lead to relaxation of the muon spin via the indirect interaction. One can refer to studies of the spin relaxation of the muoniated ethyl radical in the gas phase [10]. In high magnetic fields and in the fast fluctuation limit, the muon spin relaxation rate is proportional to the inverse electron correlation time and will depend on $D_{\mu }^{\Vert }$.

Resonances in ALC-$\mu$SR spectra are often fit with Lorentzian functions, which have the form:

$$L\left(x\right)=\frac{1}{\pi }\frac{(\mathsf{\Gamma }/2)}{{(\mathsf{\Gamma }/2)}^2+{(x-x_0)}^2}$$

(8)

where $x_0$ is the center of the resonance and $\mathsf{\Gamma }$ is a parameter specifying the full width at half maximum (FWHM). This function has an area of 1. Equation (5) can be rewritten in the form of a Lorentzian:

$$\mathsf{\Delta }{\overline{P}}_z^{{\mathsf{\Delta }}_0}\left(B\right)=\left[\frac{2\pi h_{\mathrm{R}}{({\nu }_r^{{\mathsf{\Delta }}_0})}^2}{N{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2\sqrt{\frac{{(\lambda /2\pi )}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}+\frac{{({\nu }_r^{{\mathsf{\Delta }}_0})}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}}}\right]\times \left[\frac{(1/\pi )\sqrt{\frac{{(\lambda /2\pi )}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}+\frac{{({\nu }_r^{{\mathsf{\Delta }}_0})}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}}}{\left[\frac{{(\lambda /2\pi )}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}+\frac{{({\nu }_r^{{\mathsf{\Delta }}_0})}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}\right]+{(B-B_{\mathrm{res}}^{{\mathsf{\Delta }}_0})}^2}\right]$$

(9)

The term in the first square brackets corresponds to the area, $A_0$. The term in the second square brackets is a Lorentzian with an area of one and a full width half maximum (${\mathsf{\Gamma }}_0$) given by:

$${\mathsf{\Gamma }}_0=2\sqrt{\frac{{(\lambda /2\pi )}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}+\frac{{({\nu }_r^{{\mathsf{\Delta }}_0})}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2}}$$

(10)

Combining the expressions for $A_0$ and ${\mathsf{\Gamma }}_0$ gives:

$$A_0=\left[\left(\frac{h_{\mathrm{R}}}{N}\right)\frac{4\pi {({\nu }_r^{{\mathsf{\Delta }}_0})}^2}{{({\gamma }_{\mu }-{\gamma }_{\mathrm{p}})}^2{\mathsf{\Gamma }}_0}\right]$$

(11)

We substitute in the expression for ${\nu }_r^{{\mathsf{\Delta }}_0}$ (Equation (6)) and then solve for $h_{\mathrm{R}}/N$. This will be the same for the ${\mathsf{\Delta }}_1$ resonance and all ${\mathsf{\Delta }}_0$ resonances.

$$\frac{h_{\mathrm{R}}}{N}=\frac{{\gamma }_{\mathrm{e}}^2}{4\pi c^2}\frac{{(A_{\mu }-A_{\mathrm{p}})}^2}{A_{\mu }^2{A}_{\mathrm{p}}^2}{A}_0{\mathsf{\Gamma }}_0$$

(12)

3. ${\mathsf{\Delta }}_{\mathbf{1}}$ Resonances

The total change of the time-integrated muon polarization as a function of applied magnetic field due to a ${\mathsf{\Delta }}_1$ resonance in a radical undergoing chemical reaction (including a factor two for the two muon spin flips between energy level pairs in the same electron spin subsystem) is given by [2]:

$$\mathsf{\Delta }{\overline{P}}_z^{{\mathsf{\Delta }}_1}(B,\theta )=\frac{2·(2h_{\mathrm{R}}/N){\left({\nu }_r^{{\mathsf{\Delta }}_1}\right)}^2}{{(\lambda /2\pi )}^2+{\left({\nu }_r^{{\mathsf{\Delta }}_1}\right)}^2+{\gamma }_{\mu }^2{(B-B_{\mathrm{res}}^{{\mathsf{\Delta }}_1})}^2}$$

(13)

where the frequency on resonance (${\nu }_r^{{\mathsf{\Delta }}_1}$) is

$${\nu }_r^{{\mathsf{\Delta }}_1}=\frac{3}{4}〈D_{\mu }^{\Vert }〉sin\theta cos\theta$$

(14)

We combine the two preceding equations and integrate over $\theta$ from 0 to $\pi$. This gives:

$$\mathsf{\Delta }{\overline{P}}_z^{{\mathsf{\Delta }}_1}\left(B\right)=4\left(\frac{h_{\mathrm{R}}}{N}\right){\left(\frac{3〈D_{\mu }^{\Vert }〉}{4}\right)}^2{\int }_0^{\pi /2}\frac{{sin}^3\theta {cos}^2\theta \mathrm{d}\theta }{\left[{\left(\frac{\lambda }{2\pi }\right)}^2+{\left(\frac{3〈D_{\mu }^{\Vert }〉}{4}\right)}^2{sin}^2\theta {cos}^2\theta \right]+{\gamma }_{\mu }^2{(B-B_{\mathrm{res}}^{{\mathsf{\Delta }}_1})}^2}$$

(15)

$$=4\left(\frac{h_{\mathrm{R}}}{N}\right){\int }_0^{{\displaystyle \frac{\pi }{2}}}{\displaystyle \frac{{sin}^3\theta {cos}^2\theta }{\kappa +{sin}^2\theta {cos}^2\theta }}\mathrm{d}\theta$$

(16)

$$=4\left(\frac{h_{\mathrm{R}}}{N}\right){\int }_0^1\frac{(x^2-x^4)}{\kappa +(x^2-x^4)}\mathrm{d}x$$

(17)

$$=4\left({\displaystyle \frac{h_R}{N}}\right)\left(1-{\displaystyle \frac{(d^2-1)}{2\sqrt{2}d}}·\left({\displaystyle \frac{arctan\left(\sqrt{{\displaystyle \frac{2}{d-1}}}\right)}{\sqrt{d-1}}}+{\displaystyle \frac{artanh\left(\sqrt{{\displaystyle \frac{2}{d+1}}}\right)}{\sqrt{d+1}}}\right)\right)$$

(18)

with

$$d=\sqrt{1+4\kappa }$$

$$\kappa =\frac{{\left(\frac{\lambda }{2\pi }\right)}^2+{\gamma }_{\mu }^2{(B-B_{\mathrm{res}}^{{\mathsf{\Delta }}_1})}^2}{{\left(\frac{3〈D_{\mu }^{\Vert }〉}{4}\right)}^2}$$

(19)

The exact solution (Equation (18)) is defined for $〈D_{\mu }^{\Vert }〉\ne 0$ and has a Lorentzian-like form for $\lambda >|〈D_{\mu }^{\Vert }〉|$. This form is inconvenient for fitting, especially in the case of overlapping resonances from different radical types. A ’clean’ Lorentzian (Equation (8)) would have the advantage of having a mathematically tractable expression and providing uncorrelated fit parameters A and $\mathsf{\Gamma }$ over a wide range of parameters $\lambda$ and $〈D_{\mu }^{\Vert }〉$. We have chosen to approximate the integral in Equation (18) by applying Simpson’s rule for two integration intervals. This, of course, is a very rough approximation but sufficient to obtain a first estimate for $〈D_{\mu }^{\Vert }〉$ during an experiment, which can then be used in the off-line refinement of the analysis or molecular modeling. In this approximation, we ignore the generally small angular dependence of $B_{\mathrm{res}}^{{\mathsf{\Delta }}_1}$ and restrict the analysis to sufficiently symmetric lineshapes only.

$${\int }_0^1\frac{(x^2-x^4)}{\kappa +(x^2-x^4)}\mathrm{d}x\approx \frac{2}{3}{\left[\frac{(x^2-x^4)}{\kappa +(x^2-x^4)}\right]}_{x=\frac{1}{2}}={\displaystyle \frac{2}{16\kappa +3}}$$

(20)

Hence

$$\mathsf{\Delta }{\overline{P}}_z^{{\mathsf{\Delta }}_1}\left(B\right)\approx 4\left(\frac{h_{\mathrm{R}}}{N}\right){\displaystyle \frac{2}{16\kappa +3}}$$

(21)

In this approximation, the ${\mathsf{\Delta }}_1$ resonance is a Lorentzian with a full width at half maximum (${\mathsf{\Gamma }}_1$) of

$${\mathsf{\Gamma }}_1=\frac{1}{{\gamma }_{\mu }}\sqrt{{\left(\frac{\lambda }{\pi }\right)}^2+\frac{27}{64}{〈D_{\mu }^{\Vert }〉}^2}$$

(22)

and an area ($A_1$) given by:

$$A_1={\displaystyle \frac{9\pi }{16}}\left(\frac{h_{\mathrm{R}}}{N}\right){\displaystyle \frac{{〈D_{\mu }^{\Vert }〉}^2}{{\gamma }_{\mu }^2}}{\displaystyle \frac{1}{{\mathsf{\Gamma }}_1}}$$

(23)

We then substitute the expression for $h_{\mathrm{R}}/N$ derived from the ${\mathsf{\Delta }}_0$ resonance (Equation (12)) into the preceding equation and rearrange to give:

$$|〈D_{\mu }^{\Vert }〉|=\left[\sqrt{\frac{64}{9}}\frac{{\gamma }_{\mu }}{{\gamma }_{\mathrm{e}}}\right]x\approx 0.0129x$$

(24)

where

$$x=\frac{A_{\mu }{A}_{\mathrm{p}}}{(A_{\mu }-A_{\mathrm{p}})}\sqrt{\frac{A_1{\mathsf{\Gamma }}_1}{\left[A_0/c^2\right]{\mathsf{\Gamma }}_0}}$$

(25)

This allows us to estimate $|〈D_{\mu }^{\Vert }〉|$ from the resonance field, width, and area of the ${\mathsf{\Delta }}_1$ and ${\mathsf{\Delta }}_0$ resonances.

4. Simulations

ALC-$\mu$SR spectra were simulated using the program Quantum [11] to test Equation (24). This was done for chemical reactions and electron spin flips at a rate of ${\lambda }_{\mathrm{e}}$. Although there is no analytical expression for the ${\mathsf{\Delta }}_1$ resonance for a radical undergoing electron spin flips, we are assuming that this process will have a similar form to chemical reactions. 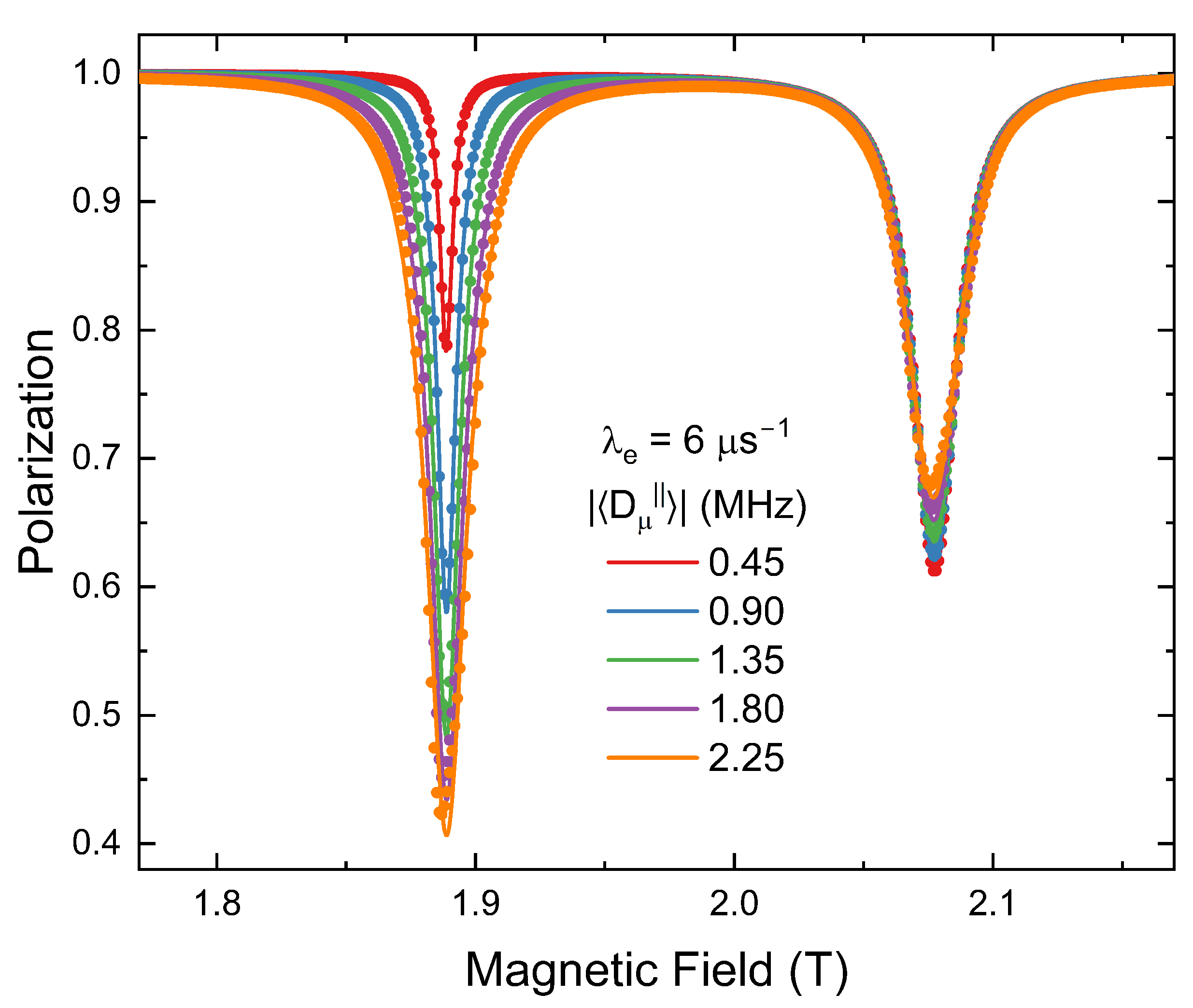Examples of simulated spectra are shown in Figure 2. Electron spin relaxation results in larger amplitude resonances than a chemical reaction to a diamagnetic state. This is due to additional polarization loss to the other electron manifold.

Several hundred ALC-$\mu$SR spectra were simulated with a range of values for $|〈D_{\mu }^{\Vert }〉|$, $\lambda$, and ${\lambda }_{\mathrm{e}}$. Examples are shown in Figure 3. We simulated spectra for a muoniated radical with one proton and used a range of muon and proton hfccs typical of muoniated cyclohexadienyl radicals. The values we used are listed in

Table 1. Hyperfine parameters used for simulation of ALC-$\mu$SR spectra using Quantum [11].

Radical	${\mathit{A}}_{\mathsf{\mu }}$ (MHz)	${\mathit{A}}_{\mathbf{p}}$ (MHz)
R1	514.4	126.0
R2	475.0	116.4
R3	435.0	106.6
R4	395.0	96.8
R5	355.0	87.0

. The largest values are for C₆H₆Mu in liquid benzene at 298 K [12]. We have also simulated spectra for a muoniated radical with two equivalent protons undergoing electron spin flips. We used hyperfine parameters for the pseudo-methyl group of the muoniated $tert$-butyl radical at 297.1 K [13]. These simulations take substantially longer than those with one proton, so there are only a few examples. Simulating chemical reactions for a muoniated radical with two protons was prohibitively time-consuming and is not included. The simulated ALC-$\mu$SR spectra were fit with two Lorentzian functions: one to determine $A_1$, ${\mathsf{\Gamma }}_1$, and $B_{\mathrm{res}}^{{\mathsf{\Delta }}_1}$, and the second to determine $A_0$, ${\mathsf{\Gamma }}_0$, and $B_{\mathrm{res}}^{{\mathsf{\Delta }}_0}$. We used these values to calculate x using Equation (25). 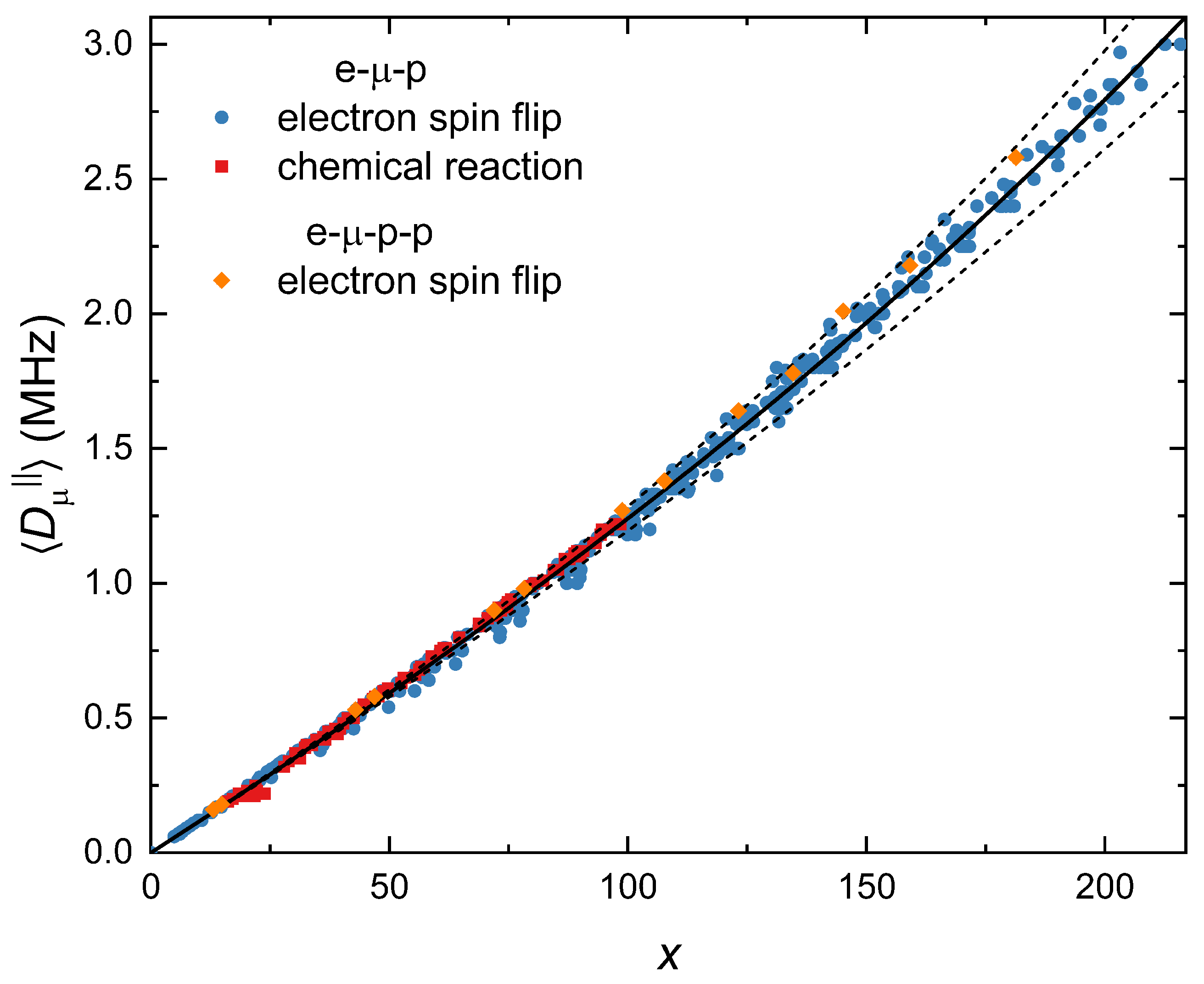We then plotted $|〈D_{\mu }^{\Vert }〉|$ versus x (Figure 4). Lorentzian resonances are obtained when $|〈D_{\mu }^{\Vert }〉|$ is small compared with $\lambda$ or ${\lambda }_{\mathrm{e}}$. We have only included spectra where the resonances are not noticeably asymmetric.

The simulations show that for small values of $|〈D_{\mu }^{\Vert }〉|$, it is proportional to x. The slope is ≈0.0125, which is incredibly close to the predicted slope of 0.0129 (Equation (24)), given the rough approximation of the integral. This is true for both chemical reactions and electron spin relaxation. It also holds for a range of isotropic muon and proton hyperfine coupling constants and the number of equivalent protons. The relationship deviates from linearity at larger $|〈D_{\mu }^{\Vert }〉|$ values. Nevertheless, we can use this to estimate $|〈D_{\mu }^{\Vert }〉|$ for particular values of $A_1$, ${\mathsf{\Gamma }}_1$, $B_{\mathrm{res}}^{{\mathsf{\Delta }}_1}$, $A_0$, ${\mathsf{\Gamma }}_0$, and $B_{\mathrm{res}}^{{\mathsf{\Delta }}_0}$. The best fit line is $|〈D_{\mu }^{\Vert }〉|\approx$$c_1·x+c_2·x^2+c_3·x^3$, where $c_1$ = $1.114\left(1\right)\times {10}^{-2}$ MHz⁻¹, $c_2$ = $6.5\left(22\right)\times {10}^{-6}$ MHz⁻², and $c_3$ = $3.1\left(8\right)\times {10}^{-8}$ MHz⁻³. This empirical relationship is independent of the relaxation mechanism as long as the resonances are not noticeably asymmetric and do not depend on the isotropic hyperfine parameters. The dotted lines in Figure 4 correspond to one standard deviation error in the fit. The error in the estimation increases with x, going from ≈1% for small $〈D_{\mu }^{\Vert }〉$ to ≈7% when $〈D_{\mu }^{\Vert }〉$ is 3 MHz. The uncertainty in $〈D_{\mu }^{\Vert }〉$ will be larger than this due to the errors associated with the measured parameters used to calculate x.

5. Anisotropic Motion of 2-Phenylethanol in the ${\mathrm{L}}_{\mathsf{\alpha }}$ Phase of ${\mathrm{C}}_{\mathbf{12}}$${\mathrm{E}}_{\mathbf{4}}$ Bilayers

We have previously used ALC-$\mu$SR to study the interaction of 2-phenylethanol cosurfactant with C₁₂E₄ bilayers (Figure 5). The experimental methodology is described in ref. [7]. We have used the model derived in this paper to estimate the dipolar muon hfccs of the three Mu adducts of 2-phenylethanol (ortho, meta, and para) and then use these parameters to estimate the extent of anisotropic reorientational motion of the cosurfactant. The values of $|〈D_{\mu }^{\Vert }〉|$ estimated using Equation (24) are listed in

Table 2. Fitted parameters for the Mu adducts of 2-phenylethanol in C₁₂E₄ bilayers at 308 K and the corresponding dipolar muon hyperfine coupling constants.

Parameter	Ortho	Meta	Para
$A_1$	$2.19\left(7\right)\times {10}^{-5}$	$0.77\left(7\right)\times {10}^{-5}$	$2.29\left(9\right)\times {10}^{-5}$
${\mathsf{\Gamma }}_1$ (T)	$3.08\left(12\right)\times {10}^{-3}$	$3.06\left(38\right)\times {10}^{-3}$	$5.02\left(22\right)\times {10}^{-3}$
$B_{\mathrm{res}}^{{\mathsf{\Delta }}_1}$ (T)	1.82182(4)	1.87932(11)	1.83632(8)
$A_0$	$1.59\left(3\right)\times {10}^{-4}$	$1.08\left(2\right)\times {10}^{-4}$	$0.58\left(3\right)\times {10}^{-4}$
${\mathsf{\Gamma }}_0$ (T)	$1.39\left(2\right)\times {10}^{-2}$	$1.33\left(3\right)\times {10}^{-2}$	$1.32\left(6\right)\times {10}^{-2}$
$B_{\mathrm{res}}^{{\mathsf{\Delta }}_0}$ (T)	2.00334(7)	2.06485(7)	2.01943(17)
$|〈D_{\mu }^{\Vert }〉|$ (MHz)	0.33	0.25	0.75

.

We have assumed that the muoniated radicals are rotating rapidly around a preferred axis, which generates an axially symmetric hyperfine tensor, and that wobbling of the rotation axis further averages the dipolar hyperfine coupling constants. We assume that the rotation axis wobbles randomly within a cone of half-angle ${\theta }_{\mathrm{C}}$ (restricted random walk model [14]). The vibrationally-averaged muon dipolar coupling constant becomes [15]:

$$〈D_{\mu }^{\Vert }〉=D_{\mu }^{\Vert }\left(\frac{cos{\theta }_{\mathrm{C}}+{cos}^2{\theta }_{\mathrm{C}}}{2}\right)$$

(26)

Since we know $|〈D_{\mu }^{\Vert }〉|$, we can determine ${\theta }_{\mathrm{C}}$ if $D_{\mu }^{\Vert }$, the value for pure uniaxial rotation, is known. We cannot measure $D_{\mu }^{\Vert }$, so we estimate it using DFT calculations.

We performed DFT calculations on the ortho, meta, and para isomers of the muoniated methylcyclohexadienyl radical, which are formed by Mu addition to toluene. These are simplified models for the Mu adducts of 2-phenylethanol. The static muon dipolar hyperfine coupling constants were obtained from DFT calculations performed with the Gaussian 09 package of programs [16]. The structures were optimized using the unrestricted B3LYP functional and the 6-311+G(d,p) basis set. Muonium was treated as an isotope of hydrogen with a magnetic moment of 8.890597 ${\mu }_N$. The light mass of the muon was treated in a manner suggested by Roduner [17]. The structure was first optimized with no constraints. The structure was then reoptimized with the bond corresponding to the C-Mu bond constrained at a length 4.9% longer than the optimized value. This method has been benchmarked for several muoniated cyclohexadienyl-type radicals [18]. It produces isotropic muon and methylene proton hfccs within a few percent of the experimental values.

The components of the theoretical dipolar muon-hyperfine coupling constants ($B_{\mu }^{aa}$, $B_{\mu }^{bb}$, and $B_{\mu }^{cc}$) of the Mu adducts of toluene are listed in

Table 3. Calculated dipolar hfccs (UB3LYP/6-311+G(d,p) with 4.9% isotope effect) for the Mu adducts of toluene. Reported values are the static hyperfine components, the averaged values for rapid uniaxial rotation about a rotation axis that is in the plane of the six-membered ring and at an angle of 8.3^° to the long axis of the molecule (the C_methyl-C_para vector), and the averaged values for wobbling of the rotation axis.

Radical	${\mathit{B}}_{\mathsf{\mu }}^{\mathit{aa}}$, ${\mathit{B}}_{\mathsf{\mu }}^{\mathit{bb}}$, ${\mathit{B}}_{\mathsf{\mu }}^{\mathit{cc}}$ (MHz)	${\mathit{D}}_{\mathsf{\mu }}^{\Vert }$ (MHz)	$〈{\mathit{D}}_{\mathsf{\mu }}^{\Vert }〉$ (MHz)${ }^{\mathit{a}}$
Ortho	−10.65, 0.85, 9.80	1.73	0.25
Meta	−11.17, −0.89, 12.06	1.51	0.22
Para	−10.69, −0.62, 11.31	5.44	0.78

^a ${\theta }_{\mathrm{C}}$ = 76.5^°.

. Each atom has its own coordinate system where the hyperfine tensor is diagonal. The value of $D_{\mu }^{\Vert }$ for fast uniaxial rotation was calculated using the method reported by Weil and Bolton [19].

$$D_{\mu }^{\Vert }={\left[{\mathbf{n}}^{\mathrm{T}}·\mathbf{A}·{\mathbf{A}}^{\mathrm{T}}·\mathbf{n}\right]}^{1/2}-A_{\mu }$$

(27)

where $\mathbf{n}$ is the rotation axis, ${\mathbf{n}}^{\mathrm{T}}$ is its transpose, $\mathbf{A}$ is the hyperfine tensor, and ${\mathbf{A}}^{\mathrm{T}}$ is its transpose. The rotation axis is transformed from the molecular coordinate system to the coordinate system of the muon-hyperfine tensor. These values are listed in Table 3.

We have assumed that the rotation axis is the same for all radicals. The best agreement between experiment and theory is when the rotation axis is in the plane of the six-membered ring and at an angle of 8.3^° to the long axis of the molecule (the C_methyl-C_para vector), and ${\theta }_{\mathrm{C}}$ has a value of 76.5^° (Table 3). This results in the $〈D_{\mu }^{\Vert }〉$ values for the ortho and meta isomers being smaller than the para isomer, which agrees with the experiment. The results show that 2-phenylethanol is undergoing large-amplitude reorientational motion even while incorporated in C₁₂E₄ bilayers. This suggests that 2-phenylethanol is not located deep within the bilayer but is instead near the oil-water interface.

6. Conclusions

We have developed an empirical expression that can be used to estimate the motionally-averaged muon dipolar hyperfine coupling constant in the case where one observes ${\mathsf{\Delta }}_1$ and ${\mathsf{\Delta }}_0$ resonances that are approximately Lorentzian. This is a frequently encountered situation using ALC-$\mu$SR spectroscopy. $|〈D_{\mu }^{\Vert }〉|$ was predicted to be proportional to x, which depends on the amplitude, width, and position of the ${\mathsf{\Delta }}_1$ resonance and the amplitude, width, and position of the ${\mathsf{\Delta }}_0$ resonance. Numerical simulations with a wide range of hyperfine parameters were used to test the relationship between $|〈D_{\mu }^{\Vert }〉|$ and x. It is linear for small values of $|〈D_{\mu }^{\Vert }〉|$ and can be described by a cubic equation over the entire range: $|〈D_{\mu }^{\Vert }〉|\approx$$c_1·x+c_2·x^2+c_3·x^3$, where $c_1$ = $1.114\left(1\right)\times {10}^{-2}$ MHz⁻¹, $c_2$ = $6.5\left(22\right)\times {10}^{-6}$ MHz⁻², and $c_3$ = $3.1\left(8\right)\times {10}^{-8}$ MHz⁻³. This expression was then used to estimate $|〈D_{\mu }^{\Vert }〉|$ for the Mu adducts of 2-phenylethanol in the L_α phase of C₁₂E₄ bilayers at 308 K. The $|〈D_{\mu }^{\Vert }〉|$ values indicate 2-phenylethanol is undergoing large amplitude reorientational motion when incorporated in C₁₂E₄ bilayers.