Abstract
In this review work, the passage of charged and neutral beams through dielectric capillary guides is described from a uniform point of view of beams channeling in capillaries. The motion of beams into the hollow channels formed by the inner walls of capillaries is mainly determined by multiple small-angle scattering (reflection) and can be described in the approximation of surface channeling. It is shown that the surface interaction potential in the case of micro- and nano-capillaries is actually conditioned by the curvature of the reflecting surface. After presenting the analysis of previously performed studies on X-rays propagation into capillaries, which is valid for thermal neutrons, too, the surface channeling formalism is also developed for charged particle beams, in particular, moving in curved cylindrical capillaries. Alternative theories explaining experimental results on the beams passage through capillaries are based on simple thermodynamic estimates, on various diffusion models, and on the results of direct numerical simulations as well. Our work is the first attempt to explain the effective guiding of a charged beam by a capillary from the general standpoint of quantum mechanics, which made it possible to analytically explore the interaction potential for surface channeling. It is established that, depending on the characteristics of a projectile and a dielectric forming the channel, the interaction potential can be either repulsive or attractive; the limiting values of the potential function for the corresponding cases are determined. It has been demonstrated that the surface channeling behaviour can help in explaining the efficient capillary guiding for radiations and beams.
1. Introduction
Channeling is usually associated with the passage of beams of charged particles in crystals oriented along the direction of particle motion (see in [1,2,3,4,5,6,7,8]), when the angle between the particle momentum and selected axis (or plane) of the crystal does not exceed a certain fixed value determined by the critical angle [9,10] (also known as Lindhard angle). (To describe a deep penetration of charged particles into the crystals [11,12,13,14], J. Lindhard first introduced and developed a continuous potential formalism based on multiple small-angle scattering of charged particles by the axis (or plane) atoms of aligned crystals, defining in such a way the phenomenology for crystal channeling [15]). This condition is necessarily to fulfil in order to establish a special kind of the particle motion, typically an undulating one, associated with the crystal lattice. In other words, under these conditions, the motion of a particle in an aligned crystal can be described within the quantum-mechanical principles in the form of a bound motion defined by a potential well [16,17]. The potential well, in both shape and depth, is determined by the averaged potential of the crystal lattice in its dependence on the crystal orientation, planar or axial. Historically, channeling is most often associated with the passage of charged particles in crystals, where the ordered arrangement of atoms in planes or axes forms dedicated channels for the associated movement of particles. In reality, the channels to trap charged and neutral particles can be of various origins characterised by strong electromagnetic fields with a distinguished spatial structure that determines the long narrow potential channel. Thus, the channeling formalism can be applied to describe the motion of particles in various media, for instance, in laser and plasma channels (see [18,19,20,21,22] and Refs. in the review paper [23]), as well as the propagation of radiations in self-organised subsystems [24,25,26,27].
From a simple consideration, it becomes obvious that the possibility of manX-ray radiationipulating particle beams in a wide spectrum of energies and impulses by means of channeling gives rise to a whole class of applied problems exploiting the effect of particle channeling in the external electromagnetic field. The first in this series that should be mentioned is the possibility of effective deflection of a beam of charged particles in bent crystals [28,29]. A beam of particles bound in the channeling mode moves along curved channels, which makes it possible to deflect beams of high-energy particles at large angles, which serves as the basis for creating crystal collimators and beam focusing systems, as well as for extracting particles from storage rings [30,31]. Speaking about channeling of charged particles in strong external electromagnetic fields, one cannot fail to also mention the possibility of using this phenomenon to create a powerful source of electromagnetic radiation in a wide frequency range, from soft X-ray to -gamma radiation, channeling radiation [32,33]. The trajectory of a channeled particle represents a rapidly oscillating flight pass with a small amplitude that induces the projectile to emit the photons of a certain energy range [5,8,34,35,36].
Until now, controlling the beams of charged and neutral particles, which in fact determines the development of technologies for accelerators, storage rings, and colliders, as well as for novel powerful beam and radiation sources, remains relevant, directing us to fundamental research on the interaction of beams and radiations in external electromagnetic fields of various origins (for details see in the recent comprehensive review [37] and Refs. therein). Usually, electromagnetic fields for beam optics are generated by special devices known as dipoles, quadrupoles, solenoids, etc., including various types of magnets and laser-plasma sources, which are characterised by a rather complex design [38,39]. Most often, solids are used as simple collimators, scatterers, mirrors, and absorbers. However, solids, or any dense media, are characterised by strong electromagnetic fields in the bulk volume as well as in the immediate vicinity of their surfaces. The natural field gradients in solids can be very high, going beyond the technical capabilities implemented in common specialised scientific instruments. Strong fields generated by solid specimens of a certain geometry can provide an additional tool to manipulate the beams and radiations, giving them the required characteristics to be utilised in many types of fundamental and applied research [40].
Recently, capillaries or capillary structures of various configurations have come to be seen as one of the most promising techniques for the formation of particle or radiation beams. Despite the difference in the physics of propagation processes of particles and radiations in capillaries, a clear example is capillary X-ray optics (for the physics of X-ray radiation propagation in capillaries, see [41]), which has grown from a beautiful idea into a widely used tool to handle X-ray radiation [42,43,44,45,46]. In fact, even before the development of capillary/polycapillary X-ray optics, the possibility for using curved reflecting surfaces as an alternative practice to shape ion beams was proposed [47] and successfully discussed [48,49] (see [50]). Based on the physics of charged particle channeling in crystals, the interaction of an incident ion with a reflecting surface was described in the approximation of a continuous atomic potential of the surface. (We have to note that the term a surface channeling was introduced in the research on theoretical treatments of ion scattering by solid crystalline surfaces in [51], and successfully on an experimental proof of the phenomenon existence in [52]. However, these studies have examined the projectile motion into the bulk surface region of the crystal as channeling along length paths through the solid). Having confirmed very small angles of efficient ion reflection from a smooth, flat surface, in order to increase the angles of beam deflection, the use of curved surfaces, in particular, dielectric capillaries, was proposed regardless of the change in the beam charge characteristics (see [53] and Refs. therein). However, these studies were not properly continued, while the further exploitation of capillaries (or capillary bundles) is presently known in relation to the beams of X-rays and thermal neutrons [54,55,56,57].
On the contrary, since the first observations of propagation of atoms and ions into dielectric capillaries [58,59], this topic has increasingly attracted the attention of physicists. Analysing the ion motion in a hollow core of micro-capillary that involves various scattering processes by the capillary inner-wall surface, it is shown that the main contribution to the fraction of reflected particles is made by projectiles impinging on the surface at glancing angles of incidence. Successfully, the effective transmission of the beams by the capillary is explained by the fact that when the ion beam passes through the capillary, some fraction of the beam first settles on the inner surface of the capillary and, accumulating there, creates a repulsive potential, which becomes a channel-guiding potential for a charged particle [59,60]. Apart from general mechanisms for electromagnetic interaction of charged projectiles with the reflecting surface, as shown, guiding efficiency is strongly related to the surface curvature (capillary diameter) [61]. A decrease in the guiding channel diameter from micrometer sizes to nanometer ones makes the transport mechanism a bit different, requesting strong non-linear features of scattering to be involved into consideration for correct interpretation of the results of capillary guiding [62,63,64,65]. However, independently of the surface curvature, the drift mechanism of ions-guiding has been recognised to be supreme on the charge diffusion mechanism. Additionally, it has been demonstrated that dielectric capillaries can transmit ion beams without any change in both the ion kinetic energy and the ion charge [66]. Capillary guiding peculiarities have been also studied for electron beams, revealing similar elastic and inelastic features of scattering by the inner capillary surface, while a time evolution of transmitted intensity for electrons remains essentially different from that of ions [67,68,69,70,71,72,73,74,75,76,77].
The undoubted interest in the development of new methods for shaping particle beams based on capillary systems [78,79,80,81,82,83] has resulted in a wide spectrum of experimental activities dedicated to this phenomenon, while theoretical works counts disproportionally much less published articles ([84,85] and Refs. therein). Known theoretical studies mainly aim at simulating the motion of charged particle beams inside capillary insulators using either the Monte Carlo method or direct numerical calculations [60,64,65,86,87,88,89,90]. Alternative theories on the motion of charged beams in both macro- and micro-capillaries are based on simple thermodynamic estimates within common diffusion models.
Below, we present a brief introduction to the phenomenon of channeling, i.e., crystal channeling, and to the concept of continuous potential, starting from which the mirror grazing reflection mechanism is described within the theory of beams and radiations channeling along a smooth amorphous surface, so-called surface channeling. Applied to the dielectric capillary guides, the surface channeling phenomenon explains efficient grazing-incident transmission as well as deflection or shaping of charged and neutral beams. In this work, based on the physics of surface channeling along a curved surface, we, for the first time, analytically describe the process of interaction of a charged particle with the inner wall of a dielectric capillary on the basis of quantum mechanics. In combination with the existing theories and models of transmission of particle beams by dielectric capillaries, the developed theory of surface channeling of particles along strongly curved reflective surfaces will serve as an additional factor for a more complete and complex description of the capillary guiding phenomenon.
2. Surface Channeling: Basic Principles
2.1. Basics of Channeling
Channeling is generally known as a special type of charged particle motion in crystals, when the particle momentum and one of the main crystallographic directions (defined by unique Miller index) coincide within a very small angular deviation close to some critical angle [10]. To describe this phenomenon, let us consider the interaction of a charged particle in a medium composed of the constituent atoms. The interaction of a charged particle with a crystal atom is defined by the potential
with the charges of the particle and the medium atom (e is the electron charge), and the Thomas–Fermi screening function with the screening parameter, for instance, defined as (≃ Å is the Bohr radius). The screening function has been determined by many authors in various approchimations, while one of the most applied is known as Moliere’s screening function [91,92]
where , , which have been below used for simple analytical estimations.
Under the channeling conditions, a charged particle (the projectile) moves at very small angle to one crystallographic axis (row), formed by many atoms in a chain, simultaneously undergoing a small-angle multiple scattering by a huge number of the chain atoms (Figure 1, left). In other words, the projectile interacts with a whole atomic chain that mathematically can be expressed as “smearing out” the potential of one atom along the chain z
from which it is seen that the potential depends only on the distance of the projectile from the axis . At the Moliere’s approximation for the screening function, this expression determines the continuous axial potential (the atomic potential averaged along the axis)
where d is the interatomic distance for the crystal axis and is the modified Bessel function of the 2nd kind.
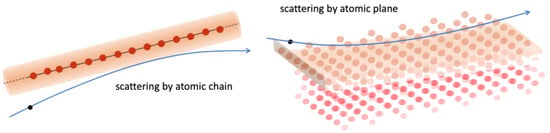
Figure 1.
Scattering of a charged particle by a chain or a plane of crystal atoms. At grazing incidence, the interaction can be described by the averaged over the chain or plane atomic potential, i.e., the continuous axial or planar potential.
Obviously, similar considerations are valid when the crystal is oriented along one of the crystallographic planes, which is also composed of the crystal atoms (Figure 1, right). Averaging the atomic potential over the plane atoms determines the corresponding continuous planar potential
Here, is the bulk atomic density of the crystal, and is the interplanar distance (the distance between the adjacent planes) for selected crystal orientation (∼ Å). Simple analysis shows essential difference in the potential extreme values for the axial and planar cases, slowly growing with the crystal nuclear charge .
To perform correct calculations, for both cases of charged particles channeling in crystals, the approximated expressions of the continuous potential should be modified, taking into account the thermal vibrations of crystal atoms. Thus, the updated Formulas (4) and (5), i.e., thermally averaged continuous potentials, depend on the amplitude of thermal vibrations of atoms, which is, in turn, a function of Debay temperature (see in [93,94]). Moreover, precise expressions for the continuous potentials of a crystal count the contribution of a sufficient number of neighbour atomic planes or axes characterised by equivalent Miller index (Figure 2) [95]. A set of continuous potentials for selected crystal orientation forms a well emphasised periodic potential, which consists of successfully repeated potential wells, the minima of which are situated either at the axis (plane) positions or between the neighbour axes (planes). The positions of the potential well extremes are determined by the channeled particle charge. Due to this feature, the opposite charged particles become differently redistributed in the transverse plane. This is why negatively charged particles, moving in the vicinity of atomic axes or planes, suffer much stronger scattering by crystal atoms in comparison with positively charged particles, which are mostly distant from the axes or planes. Obviously, the potential wells for a selected particle charge become the potential barriers for the particles of an opposite charge.
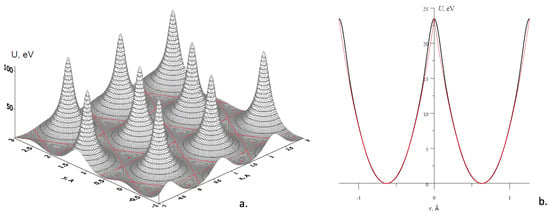
Figure 2.
Continuous potentials at axial and planar channeling of relativistic positrons in crystals. (a) Axial channeling in diamond C<111> at a room temperature; (b) Planar channeling in diamond C(110) at a room temperature. The parabolic approximation for a planar potential shown in red reveals good enough fitting that may simplify the analytical analysis for rapid estimations. For both cases the minima of the potential wells are formed in a less-atomic-dense space in the transverse cross-section to the direction of channeling. Reproduced from [95].
As aforementioned, at channeling, the projectile will be trapped in a channeling regime when the angle between its momentum and selected crystallographic direction is smaller than the critical angle of channeling, Lindhard angle, . This angle is defined by the equality of the transverse energy of a channeled particle and the depth of potential well, ≃ (≲1 mrad for relativistic light particles). Various regimes of a channeling motion in a monocrystal are shown in Figure 3, from which we can see that each channeling regime is characterised by well defined beam-to-crystal mutual orientation. The requirements for crystal channeling are very strict according to the beam characteristics, too; the beam divergence should preferably less than the critical angle (or comparable), ≲.
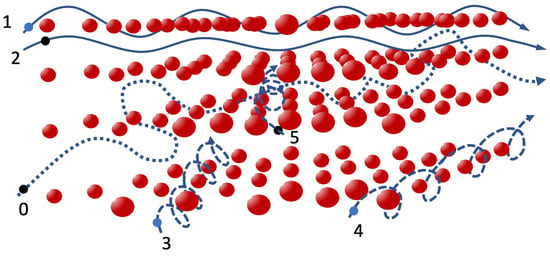
Figure 3.
Various channeling regimes for positively and negatively charged particles in crystals. 0—amorphous orientation; 1—planar orientation for a negative charge; 2—planar orientation for a positive charge; 3 and 4—axial orientation for a negative charge; and 5—axial orientation for a positive charge.
2.2. Small-Angle Multiple Scattering by Smooth Flat or Curved Surface
At the particle channeling in crystals, we deal with the conform interaction of a charged particle with crystals atoms of either axis or plane, i.e., axial or planar channeling. In first approximation, the interaction potential is formed by the atoms within one channel, while remained atoms of the crystal bulk weakly contribute, mostly defining the periodicity of continuous potential. On the contrary, when the particle is reflected by the crystal surface (or amorphous smooth surface), in order to determine the interaction potential with an amorphous medium, even at the small-angle scattering with respect to the medium surface (grazing incidence), one should count the contribution by all medium atoms. In other words, the scattering potential of a surface, i.e., the surface potential, can be defined in the following form [96]
where the variables x and define the distances perpendicular to the surface plane, the first from the surface in the vacuum and the second into the medium. The volume integration in the medium can be simplified by integrating many-sliced planar potentials of Equation (5) over , where each plane is parallel to the reflecting surface. The obtained interaction potential of the particle with the amorphous surface
is similar to the continuous planar potential in the crystal but lower by the barrier height.
Reflection from a smooth surface can be used to deflect a beam at large angles through multiple low-angle reflections. Since each reflection is specular at a small angle , the beam intensity remains practically unchanged. For effective deflection of a beam with the transverse dimension d, the surface must be curved with the radius of curvature that satisfies the condition . This condition also determines the required surface length for deflection at a certain angle.
Beam deflection can also be done using a channel formed by two curved surfaces. However, in order to deflect a beam of the same transverse size over equal angle, we need the length of the surfaces forming a channel-guide, which is comparable with the length of a single surface reflector. However, the channel-guide, if the surface-formed samples are thick enough, provides an advantage only in a beam collimation at the exit end of the channel.
The situation may change significantly if capillary is used as a guide [50]. In this case, the beam can be deflected through a fixed angle at a much shorter channel length, although the condition for efficient transport remains unchanged, ( and are the capillary bending radius and the capillary channel diameter, respectively). This is due to the possibility of surface channeling of particles along various spiral-like trajectories (valid for some approximations); the radii of curvature are less than the bending radius of the capillary, (for extremely low limit we have ).
3. X-ray Surface Channeling in Capillaries
Transmission of X-rays by capillaries of various diameters has been intensively studied in the last 35 years (see in the review paper [57]). These studies confirmed the predicted high efficiency of the radiation transmission by the capillaries, which thus became very promising new optics capable to deflect or bend intense X-ray beams. (As known, X-ray reflection at grazing incidence permits efficient radiation deflection by a small angle, which has been utilised in multiple X-ray reflection optical instruments for X-ray beam bending over large angles (Figure 4). Applied to capillaries, it becomes decisive in designing novel X-ray capillary optical elements). However, additionally to the development of capillary/polycapillary optics, a single capillary of desired geometry exhibits a unique tool for investigating the dispersion features of X-ray radiation by a surface [41,97,98,99].

Figure 4.
Grazing small-angle reflection (a) applied for curved surfaces (b) permits radiation bending over large angles via multiple small-angle reflections. This principle is even more efficient for bent capillaries (c).
To describe the radiation propagation into capillaries, it must be noted that in widely used capillary systems, the sizes of channels (micrometer-sizes) essentially exceeds the effective wavelength of the radiation that is transmitted. It allows the radiation dispersion at multiple-reflection propagation of the radiation down the capillary channel to be analysed within the ray optics approximation, which, in turn, for very small grazing angles, exposes the picture of whispering gallery modes (surface channeling modes) [100,101,102,103,104,105]. The modern technology for manufacturing capillary optical systems enables extremely small channel diameters (nanometer-sizes) to be reached at the drawing process [56,106]. Propagation of radiation in such small guides is expressed in bulk channeling modes instead of surface ones [107].
Generally, to explain all peculiarities recorded experimentally, we have to apply the wave optics methods in description of the processes of radiation spreading down the capillaries [108,109,110,111]. The characteristics of radiation scattering inside capillaries can be evaluated from the solution of a wave propagation equation. Neglecting the roughness correction at the radiation reflection from the capillary inner surface, the wave equation in the transverse plane to the propagation direction is written as follows
in which the transverse part of the radiation field is defined from the equation , . Here, E is the electromagnetic field amplitude, which describes the radiation; is the radiation wave vector; and , is the dielectric permittivity (—no absorption). At grazing incidence , we get for the transverse wave vector. Hence, the effective interaction potential is defined by the channel geometry
We can see that at , which defines the critical angle for total external reflection, so-called Fresnel’s angle. Moreover, we can generalise the wave Equation (8), extending its application to a massive particle motion, the Schrödinger equation, in a specified potential well . Obviously, if the effective potential of radiation interaction in a guide is determined by the guiding channel, the description of radiation propagation down the channel is similar to the particle channeling phenomenon [10]. Hence, applying the channeling theory to describe the radiation propagation in a media with the potential (9), the wave Equation (8) can be solved for the case of -channels as well as for n-guides. The only difference in description of radiation channeling in - and n-capillaries is due to the origin of the interaction potential. The bound radiation propagation in a -channel is related to the surface potential, which in the case of a curved surface reveals a potential well. For n-channels, on the contrary, we deal with the so-called bulk channeling, which is very similar to the crystal channeling of charged particles.
At a curved reflecting surface, the effective potential reveals an additional contribution strongly related to the surface curvature. To describe new expected features due to the surface profile, we have to consider the fact that the reflection of an electromagnetic wave occurs on an extended area defined by both the longitudinal part ∼ (c is the light velocity), which is much greater than the atomic distances, and the transverse part, which is a layer of the electric field penetration ∼. Hence, we can evaluate the radiation reflection by splitting the radiation scattering in the reflecting surface area into coherent and incoherent parts. The first one describes a well known mirror reflection, while the second is responsible for the radiation absorption in the reflecting layer. However, if the reflecting surface is curved, a simple algebra in curved coordinates brings us to the modified interaction potential [97,112]
in which we have an additional term absent in the effective potential expression for a plane surface, . This term can be considered as a centrifugal potential energy of the photon, i.e., as if the photon receives a certain angular momentum when reflected from a curved surface. The presence of an additional term in the expression for the effective potential replaces the step potential with a known barrier by an attractive potential with a known potential well that is schematically represented in Figure 5.

Figure 5.
The profiles of the effective potentials at the reflection of X-rays by plane and curved surfaces (the scheme is reproduced from [41]). (A) The potential barrier for a plane surface; (B) Once the reflecting surface is curved, the reflection potential reveals an additional potential energy; (C) The potential barrier for a curved surface.
Further, we can estimate the limits when the wave peculiarities become important in description of the radiation propagation in capillaries [97]. If we imagine the motion of a photon inside a capillary through multiple grazing reflections from the inner wall of the capillary, then the imaginary trajectory of a photon is a kind of spiral with two limiting curvature values, from the inner radius of the capillary to the curvature radius of entire capillary (defined by the capillary bending angle). Generally, for a photon with the wave vector propagating along a curved surface with the curvature radius (), we can define a longitudinal wave vector, , as well as a transverse wave vector , (Figure 6). Hence, the wave approximation can be applied to the description of the radiation reflection for the part of radiation propagating at very sliding angles within the above-surface layer ∼, i.e.,
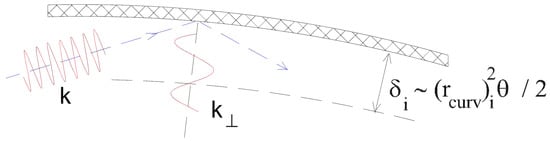
Figure 6.
Illustration of the relativity for the case of grazing reflection from the curved surface. It explains the surface channeling phenomenon as a modal regime of propagation along curved surface (reproduced from [41]).
The relation (11) defines the condition for surface-bound propagation of X-rays—surface channeling— along the curved surface of the inner capillary wall. This phenomenon is known as whispering gallery one [41,113,114,115].
Since in the case of capillary systems the principal waveguide is a hollow cylindrical tube (a circular guide), the interaction potential is determined by Equation (10) with the radiation polarisability parameter (for simplicity, the absorption is considered to be negligible ). The solution of the wave equation
demonstrates the wave-guiding character of radiation propagation in the channel () [99,116]. Here, is the Airy function, and is the arbitrary unit characterising the capillary substance. Expression (12) describes the radiation modes in a capillary, i.e., the surface channeling states, that propagate close to the waveguide wall. Figure 7 shows an example of the spatial radiation distribution for two different capillary radii. This solution reveals that the wave functions are damped both inside the channel wall and moving from the wall towards the center.
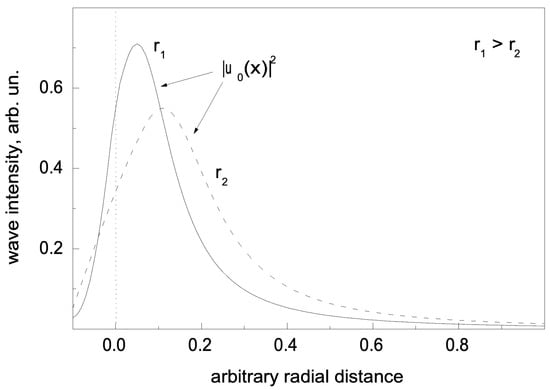
Figure 7.
The radial distributions of main radiation mode for capillaries of various radii. The radius decrease results in a shift of the maximum towards the capillary center. The wall surface position is shown by the dotted line (reproduced from [99]).
The characteristic radial size of the main grazing mode () results in , and we can conclude that the typical radial size may overcome the wavelength , whereas the curvature radius in the trajectory plane exceeds the inner channel radius, : (for example, for a capillary channel with the radius ).
We have to underline here that, as seen from the spatial distributions of surface modes, the decrease in the capillary channel diameter, i.e., the increase in the reflecting surface curvature, results in the “extrusion” of the surface bound modes to the center of the waveguide. Hence, almost all radiation power is concentrated in a hollow channel region, providing a small radiation power attenuation along the capillary waveguide wall. However, being negligible for -guides, in case of n-guides, the tunneling phenomenon, i.e., the radiation penetration deep into the cladding responsible for the radiation cross of the guide wall, should be taken into account.
4. Charged Beam Surface Channeling
4.1. Charged Beam Guiding in Dielectric Capillary
Describing the interaction of a charged particle with the surface of a reflecting dielectric is undoubtedly a complex task. The main reason for this is the necessity of taking into account the contribution to the total scattering process by different components of dielectric determined by both atomic and electronic subsystems [40,117].
Let us consider the electromagnetic field in a nonmagnetic substance of the permittivity that occupies the infinite space with a cylindrical cavity of radius inside (Figure 8). Then, in absence of free currents and charges, based on Maxwell’s equations, the Fourier components of the field scalar and vector potentials are defined by the following equation
where is the part of the Laplace operator of the coordinates transverse to the axis, which coincides with the cavity longitudinal axis, and the field potentials satisfy the following gauge relation
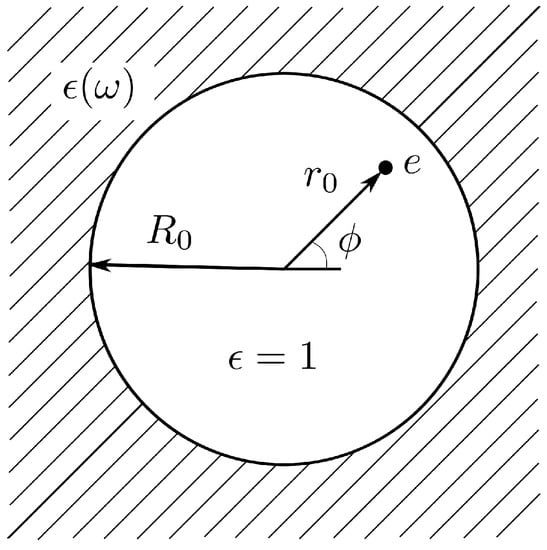
Figure 8.
Scheme of a cylindric cavity of radius in the infinite dielectric, characterised by the permittivity , with a particle of the charge e moving inside the cavity. For the cavity, we choose .
To characterise the damping surface waves excited at the boundary cavity interface, the condition of continuity of the electric and magnetic fields components tangential to the interface has to be used, from which one can derive the complex dispersion law
written in the notations and , where and are the modified Bessel functions and n is the integer.
To solve Equation (15) analytically is a rather routine procedure; therefore, let us examine two physically significant limiting cases determined by the parameter , the ratio of the capillary radius to the wavelength of surface excitations . For , Equation (15) can be solved only at , while at the solution can be presented in the form of a series expansion in powers of a small parameter . For large , i.e., for the wavelengths , the dispersion relation slightly differs from the case of a flat reflecting plane [117]. Thus, if we neglect the wavelengths , the frequency of surface excitations is assumed to be constant, while the wave vector varies within the range with the cut-off frequency .
At these assumptions, the charged particle interaction with the cavity surface is described by the scalar potential operator of surface excitations
where the excitation amplitudes and are defined by the modified Bessel functions in the hollow and the cladding parts of the capillary guide ( is the boson-operator), respectively. To get the amplitudes, we solve the electrostatic problem for a scalar potential of a charge e inside an infinite cylindrical cavity
which is valid at the following interface matching conditions:
where is the static dielectric constant, and the potential is presented as a sum .
4.2. Interaction Potential at Surface Channeling of Charged Beams
Since we deal with a charge moving in a cylindrical cavity, the potential energy of interaction with the atomic system of a dielectric can be calculated as the sum of Coulomb potentials presented in a Fourier series split at the cut-off frequency [94]
where are, respectively, the charges and radius-vectors of the particle p and the surface nuclei and electrons j, and is the normalization volume. The 1st term describes the interaction at small distances that does not allow the averaging at calculations (for instance, for metals, is of the order of the atom size [118]), while the 2nd—at , i.e., the interaction with collective surface excitations, can be evaluated by averaging single interaction features over all the system. As aforementioned, the latter is described by the potential operator (16). The 1st term of Equation (18), in turn, is described as a sum of potential energies for the particle interaction with the screened surface atoms [119], that, in view of the equation of motion for a particle, transforms into the averaged atomic potential of the surface.
Generally, for a particle of charge e and mass m moving inside a cylindrical hollow cavity formed by an infinite insulator, we can write the Hamiltonian in the form
where is the radius-vector in the transverse plane , while the -axis coincides with the cavity longitudinal axis. Here, is the particle field operator (fermion-operator) and is the operator describing the particle interaction with the surface excitations (boson-operator). The potential energy of the atom-particle interaction corresponds to the 1st term of Equation (18), while the operator corresponds to the energy of non-interacting surface excitations. The particle field operator is defined by the sum over the quantum states of motion
where is the annihilation operator; k is the z-projection of the charged particle wave vector; and are the radial and azimuthal quantum numbers (). Successfully, the wave function can be divided into longitudinal and transverse components
with the cavity longitudinal size L.
In our case, the particle longitudinal energy is much greater than the transverse one . Hence, following the calculation procedure presented in the paper [120] but simplified for one-dimensional freedom, the effective Hamiltonian is defined by the matrix element
where
The real part of Equation (22) is responsible for elastic processes in a complex potential energy, while its imaginary part is responsible for inelastic ones. The latter calculates the energy loss of a particle, normalised by traveled distance, as a function of distance to the cavity axis. The energy loss of a particle due to the interaction with surface plasmons can be calculated in the form of asymptotic expansion of the Bessel functions [121,122] ()
where is the particle-to-plane distance.
Using Equation (22), the equation of transverse motion inside a cavity can be written in the following way
which actually describes the channeled motion. Indeed, neglecting the change in the particle longitudinal momentum results in averaging the atomic potential over the surface plane. The surface potential is calculated by summing the potentials of individual atoms, where the number of atoms per unit length along the cavity axis is much greater than unity ( is the dielectric atomic density). After integration over the surface, the 2nd term in Equation (25) becomes dependent only on the distance from the cavity axis .
When the equation for elastic processes is solved, we consider only the real part of induced potential, while the potential imaginary part leads to a finite lifetime for each quantum state. Thus, the induced potential with the amplitude of surface excitations is defined by
where means the principal value of the integral and v is the charge velocity.
Hence, the effective potential for a channeled particle inside a cylindrical cavity is determined by the averaged and induced potentials, . The 1st term is evaluated as a continuous potential via known technique in channeling physics [10,93] and does not result in any unexpected behaviours, while the 2nd one brings us to new features.
Analysis of general induced potential for two extreme cases, and , has shown new, but expected, peculiarities in the interaction potential of a charged projectile with a curved capillary surface [123]. At , the induced potential is defined as follows
the graph dependence of which is shown in Figure 9. On the contrary, at the induced potential is evaluated by the expression at
where the function is characterised by some local maximum. It permits the potential minimum position to be revealed at with the minimum value of the induced potential (Figure 10). If we define formally that the ratio is a certain “cyclotron frequency” for a particle flying in a capillary, then we can conclude that at the plasmon frequencies much lower than the cyclotron one , the interaction potential of the particle with the surface is a reflective barrier. On the contrary, when the plasmon frequencies of the dielectric surface exceed the cyclotron frequency of the moving particle , the interaction potential becomes attractive.
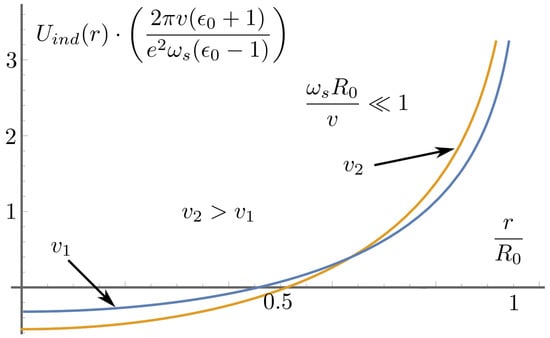
Figure 9.
Dimensionless induced potential versus the distance from the cavity axis at the condition , while a concrete plotting is for and , with the characteristic value ∼ corresponding the cavity radius ∼ cm.
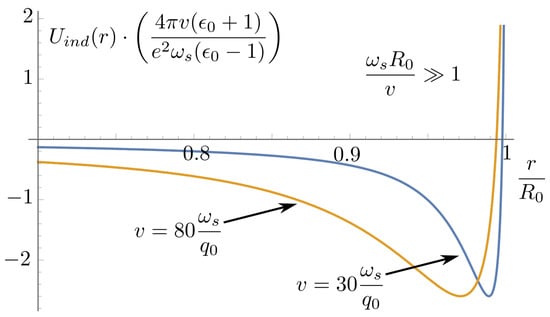
Figure 10.
Dimensionless induced potential versus the distance from the cavity axis at the condition . Two curves correspond different values of longitudinal velocity. As can be seen, at the particle velocity increase the potential shape does not change, and the curve minimum tends to the cavity center.
Moreover, it is notable that if the particle velocity increases, the potential minimum position very slowly shifts closer to the cavity center, keeping the potential shape itself practically unchanged. At the cavity surface, the induced potential logarithmically diverges , while at the cavity center it is equal to
In both cases considered, approaching the cavity surface, the induced potential increases. However, the induced potential must be cut off for the distances ∼; therefore, assuming ∼1, the maximum value of the induced potential in both limits can be estimated as
in which the logarithms do not essentially contribute to the value of induced potential. That allows us in further estimates to omit the logarithmic factors, i.e., ∼.
Equation (26) is obtained in view of smallness of the transverse energy in comparison with the longitudinal one, , which also imposes definite restrictions on the particle longitudinal velocity v. Supposing the maximum of transverse energy to be equal to the maximum of induced potential, we can write the limitation for longitudinal energy as well as for normalised longitudinal speed of a particle . For example, for a channeled electron moving inside a cavity characterised by surface oscillations of a plasma frequency ∼ , the reduced potential is valid under the condition eV. In turn, it corresponds to the velocity constraint , where the upper limit should be correlated with the applicability of nonrelativistic description.
As follows from Equation (30), the maximum value of induced potential depends mainly on the particle charge and its longitudinal velocity, resulting in the estimate ∼ meV for electron. Hence, the magnitude of the induced potential for one particle is not large in comparison with the averaged atomic potential ∼10 eV. However, it might be essentially different for a beam (multi-particle) passing through the cavity.
The presented analysis leads to the important conclusion that surface channeling of charged beams in capillaries demonstrates the same features as those at channeling of radiation in capillaries. Namely, in addition to very similar definition of the interaction potentials, a decrease in the capillary diameter at fixed beam parameters leads to the ejection (expulsion) of particles towards the center of the guiding channel. This property manifests itself in the case of a repulsive potential (Figure 9) as well as an attractive one (Figure 10). The latter can have a very important application since it will significantly increase the efficiency of beam passage through capillaries.
5. Conclusions
Nowadays, the radiation waveguides are in a wide use to shape the electromagnetic beams of a wide frequency range. This makes the radio and optical waveguides extremely attractive for various applications. On the contrary, X-ray waveguides are still mainly in the research stage of development.
As is known, generally, the solution of Maxwell equations describing propagation of electromagnetic waves in media with a step-function index of refraction and results in forming a discrete set of the modes [124]. Applied to capillary guides, our analysis of X-ray radiation propagation into the guides of various shapes shows that all the observed features can be described within the unified theory of X-ray channeling: surface channeling in -size guides and bulk channeling inn-size guides [105]. The ratio between the transverse wavelength of radiation and the effective size of a guide, i.e., , in other words, the ratio between the diffraction and Fresnel angles, herein determines the main criterion defining character of radiation propagation. If this ratio is small, the ray optics approximation is valid, and we deal with the large number of bound states. In turn, at , a few modes will be formed in a quantum well of the interaction potential, along with just a single mode, for . Solution of the wave equation of the radiation propagation in such guides, moreover, demonstrates that at the center of a guide the flux peaking of x radiation, i.e., the increase of the channeling state intensity in the center of a guide, should take place [125]. This feature is a proper channeling phenomenon [33] and can be explained only by the modal regime of radiation propagation. The latter is of particular interest to researchers.
Obviously, all the considerations taken for X-rays should be valid for thermal neutrons. Some of them have been already proved [41,126,127].
A similar problem of interaction of a charged particle with the inner surface of a cylindrical cavity in an infinite insulator has been also analysed based on the Hamiltonian formalism. We have succeeded in reducing the interaction potential for a charged particle in the field of surface excitations. Neglecting excitations of the wavelengths comparable to the cavity radius, the interaction potential has been explicitly written revealing its complex nature. An imaginary part of the potential leads to a finite width of the energy levels and is not examined in a general form. However, as an example, the energy losses of a particle per unit of traveled distance are obtained at its interaction with surface plasmons. The analysis of a real part of the potential, instead, has been carried out for two limiting cases.
We have shown for the first time that at the limit , the induced potential of interaction of a charged particle with the cavity surface acts as a scattering potential (forming a reflecting barrier), while at , it reveals a potential well near the surface. The width of the potential well depends on the speed of the particle, i.e., the higher the speed of the particle, the wider the well. In both cases considered, the real potential logarithmically tends to plus infinity. The maximum value of the induced potential mainly depends on the particle charge and its longitudinal velocity. The estimates performed show that the averaged atomic potential is much higher than that induced for one particle, while for a beam of many particles channeled in a capillary, the maximum value of the induced potential is expected to be essentially different.
The theoretical results obtained for charged particles allow us to explain within unique approach (model) different features of charged particles transmission by capillaries of various diameters. These characteristics might be absolutely opposite to the results obtained if described within simple thermodynamic principles for particle diffusion models. The latter makes it necessary to use different models to describe the results of the same experiment. The proposed theory, in our opinion, will help to circumvent these difficulties.
We hope that this work, in addition to known theories and models, will lead to a better understanding of the physics of surface channeling of charged particles along curved surfaces, will allow a better understanding of the process of effective transmission of particle beams by capillaries, and will contribute to the continuation of active research on the formation of charged particle beams by capillary structures.
Author Contributions
Conceptualization, S.D. and A.D.; methodology, S.D. and A.D.; software, S.D. and A.D.; validation, S.D. and A.D.; formal analysis, S.D. and A.D.; investigation, S.D. and A.D.; data curation, S.D. and A.D.; writing—original draft preparation, S.D. and A.D.; writing—review and editing, S.D.; visualisation, A.D.; supervision, S.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
One of the authors (SD) would like to acknowledge the support of the Competitiveness Program of the National Research Nuclear University MEPhI (Moscow).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dearnaley, G. The Channeling of Ions through Detectors (Preprint Oct. 1963). IEEE Trans. Nucl. Sci. 1964, 11, 249–253. [Google Scholar] [CrossRef]
- Davies, J. Lectures on Channelling Ion Implantation and Atomic Collisions; Lectures on Mathematics and Physics: Physics; Tata Institute of Fundamental Research: Mumbai, India, 1974. [Google Scholar]
- Kumakhov, M.A.; Shirmer, G. Atomic Collisions in Crystals; G. & B. Sci. Pub. Ltd.: London, UK, 1979. [Google Scholar]
- Feldman, L.; Mayerand, J.; Picraux, S. Materials Analysis by Ion Channeling; Academic Press: London, UK, 1982. [Google Scholar]
- Baryshevsky, V.G. Channeling, Radiation and Reactions in Crystals at High Energies; BSU: Minsk, Belarus, 1982. (In Russian) [Google Scholar]
- Davies, J.A. The Channeling Phenomenon and Some of Its Applications. Phys. Scr. 1983, 28, 294–302. [Google Scholar] [CrossRef]
- Ohtsuki, Y.H. Charged Beam Interaction with Solids; Taylor & Francis Ltd.: London, UK; New York, NY, USA, 1983. [Google Scholar]
- Kalashnikov, N.P. Coherent Interactions of Charged Particles in Single Crystals. Scattering and Radiative Processes in Single Crystals; Harwood Acad. Pub.: London, UK; New York, NY, USA, 1988. [Google Scholar]
- Lindhard, J. Motion of swift charged particles, as influenced by strings of atoms in crystals. Phys. Lett. 1964, 12, 126–128. [Google Scholar] [CrossRef]
- Lindhard, J. Influence of Crystal Lattice on Motion of Energetic Charged Particles. Kongel. Dan. Vidensk. Selsk. Mat.-Fys. Medd. 1965, 34, 1. [Google Scholar]
- Piercy, G.R.; Brown, F.; Davies, J.A.; McCorgo, M. Experimental Evidence for the Increase of Heavy Ions Ranges by Channeling in Crystalline Structure. Phys. Rev. Lett. 1963, 10, 399–400. [Google Scholar] [CrossRef]
- Lutz, H.; Sizmann, R. Super Ranges of Fast Ions in Copper Single Crystals. Phys. Lett. 1963, 5, 113–114. [Google Scholar] [CrossRef]
- Robinson, M.; Oen, O. Computer Studies of the Slowing Down of Energetic Atoms in Crystals. Phys. Rev. 1963, 132, 2385–2398. [Google Scholar] [CrossRef]
- Beeler, J.R., Jr.; Besco, D.G. Range and Damage Effects of Tunnel Tragectories in a Wurtzite Structure. J. Appl. Phys. 1963, 34, 2873–2878. [Google Scholar] [CrossRef]
- Brandt, W. Channeling in Crystals. Sci. Am. 1968, 218, 91. [Google Scholar] [CrossRef]
- Lervig, P.; Lindhard, J.; Nielsen, V. Quantal Treatment of Directional Effects for Energetic Charged Partciles in Crystal Lattices. Nucl. Phys. 1967, A96, 481–504. [Google Scholar] [CrossRef]
- Andersen, J.U.; Andersen, S.K.; Augustyniak, W.M. Channeling of electrons and positrons. Kongel. Dan. Vidensk. Selsk. Mat.-Fys. Medd. 1977, 39, 1–58. [Google Scholar]
- Borisov, A.B.; Borovskiy, A.V.; Korobkin, V.V.; Prokhorov, A.M.; Shiryaev, O.B.; Shi, X.M.; Luk, T.S.; McPherson, A.; Solem, J.C.; Boyer, K.; et al. Observation of relativistic and charge-displacement self-channeling of intense subpicosecond ultraviolet (248 nm) radiation in plasmas. Phys. Rev. Lett. 1992, 68, 2309–2312. [Google Scholar] [CrossRef] [PubMed]
- Frolov, E.; Dik, A.; Dabagov, S. Dynamics of electrons acceleration in presence of crossed laser field. Nucl. Instrum. Meth. B 2013, 309, 157–161. [Google Scholar] [CrossRef]
- Dabagov, S.B.; Dik, A.V.; Frolov, E.N. Channeling of electrons in a crossed laser field. Phys. Rev. ST Accel. Beams 2015, 18, 064002. [Google Scholar] [CrossRef]
- Frolov, E.; Dik, A.; Dabagov, S. Space charge effect simulation at electrons channeling in laser fields. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 402, 220–222. [Google Scholar] [CrossRef]
- Dabagov, S.; Frolov, E.; Dik, A. Space charge influence on particles channeling in optical lattice. Phys. Lett. B 2019, 790, 77–80. [Google Scholar] [CrossRef]
- Dabagov, S.B. Advanced Channeling Technologies in Plasma and Laser Fields. EPJ Web Conf. 2018, 167, 01002. [Google Scholar] [CrossRef]
- Esarey, E.; Sprangle, P.; Krall, J.; Ting, A. Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE J. Quantum Electron. 1997, 33, 1879–1914. [Google Scholar] [CrossRef]
- Davis, J.; Borisov, A.B.; Boyer, K.; Rhodes, C.K. Multikilovolt channelled X-ray propagation in water. J. Phys. B At. Mol. Opt. Phys. 2005, 38, L309–L313. [Google Scholar] [CrossRef]
- Bezryadina, A.; Hansson, T.; Gautam, R.; Wetzel, B.; Siggins, G.; Kalmbach, A.; Lamstein, J.; Gallardo, D.; Carpenter, E.J.; Ichimura, A.; et al. Nonlinear Self-Action of Light through Biological Suspensions. Phys. Rev. Lett. 2017, 119, 058101. [Google Scholar] [CrossRef]
- Schirber, M. Bacteria form waveguides. Physics 2017, 10, 90. [Google Scholar] [CrossRef]
- Carrigan, R.A. Single Crystals and Short-Lived Particles. Phys. Rev. Lett. 1975, 35, 206–209. [Google Scholar] [CrossRef]
- Tsyganov, E. Some Aspects of the Mechanism of a Charged Particle Penetration through a Monocrystal; Fermilab preprint TM-682; Fermilab: Batavia, IL, USA, 1976. [Google Scholar]
- Biryukov, V.M.; Chesnokov, Y.A.; Kotov, V.I. Crystal Channeling and Its Application at High-Energy Accelerators; Springer: Berlin, Germany, 1997. [Google Scholar]
- Scandale, W.; Taratin, A. Channeling and volume reflection of high-energy charged particles in short bent crystals. Crystal assisted collimation of the accelerator beam halo. Phys. Rep. 2019, 815, 1–107. [Google Scholar] [CrossRef]
- Kumakhov, M. On the theory of electromagnetic radiation of charged particles in a crystal. Phys. Lett. A 1976, 57, 17–18. [Google Scholar] [CrossRef]
- Beloshitsky, V.V.; Komarov, F.F. Electromagnetic Radiation of Relativistic Channeling Particles (The Kumakhov Effect). Phys. Rep. 1982, 93, 117–197. [Google Scholar] [CrossRef]
- Saenz, A.; Uberall, H. (Eds.) Coherent Radiation Sources; Springer: Berlin, Germany, 1985. [Google Scholar]
- Baier, V.N.; Katkov, V.M.; Strakhovenko, V.M. High Energy Electromagnetic Processes in Oriented Single Crystals; World Scientific: Singapore, 1998. [Google Scholar]
- Rullhusen, P.; Artru, X.; Dhez, P. Novel Radiation Sources Using Relativistic Electrons: From Infrared to X-rays (Series in Mathematical Biology and Medicine); World Scientific: Singapore, 1998. [Google Scholar]
- Shiltsev, V.; Zimmermann, F. Modern and future colliders. Rev. Mod. Phys. 2021, 93, 015006. [Google Scholar] [CrossRef]
- Minty, M.G.; Zimmermann, F. Measurement and Control of Charged Particle Beams; Particle Acceleration and Detection; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Zimmermann, R.; Seidling, M.; Hommelhoff, P. Charged particle guiding and beam splitting with auto-ponderomotive potentials on a chip. Nat. Commun. 2021, 12, 390. [Google Scholar] [CrossRef]
- Gras-Marti, A.; Urbassek, H.M.; Arista, N.R.; Flores, F. (Eds.) Interaction of Charged Particles with Solids and Surfaces; Nato ASI Series; Springer: Boston, MA, USA, 1991; Volume 271. [Google Scholar] [CrossRef]
- Dabagov, S.B. Channeling of neutral particles in micro- and nanocapillaries. Phys.-Uspekhi 2003, 46, 1053–1075. [Google Scholar] [CrossRef]
- Thiel, D.; Stern, E.; Bilderback, D.; Lewis, A. Focusing of synchrotron radiation using tapered glass capillaries. Phys. B Condens. Matter 1989, 158, 314–316. [Google Scholar] [CrossRef]
- Kumakhov, M. Channeling of photons and new X-ray optics. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 1990, 48, 283–286. [Google Scholar] [CrossRef]
- Engström, P.; Larsson, S.; Rindby, A.; Buttkewitz, A.; Garbe, S.; Gaul, G.; Knöchel, A.; Lechtenberg, F. A submicron synchrotron X-ray beam generated by capillary optics. Nucl. Instrum. Meth. A 1991, 302, 547–552. [Google Scholar] [CrossRef]
- Thiel, D.J.; Bilderback, D.H.; Lewis, A.; Stern, E.A. Submicron concentration and confinement of hard X-rays. Nucl. Instrum. Meth. A 1992, 317, 597–600. [Google Scholar] [CrossRef]
- Bilderback, D.H.; Thiel, D.J.; Pahl, R.; Brister, K.E. X-ray Applications with Glass-Capillary Optics. J. Synchrotron Radiat. 1994, 1, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Kumakhov, M.A. Deflection of charged beams by surface channeling. Tech. Phys. Lett. 1979, 5, 689–692. (In Russian) [Google Scholar]
- Akkerman, A.F.; Chubisov, M. Simulation of particles deflection by surface channeling. Tech. Phys. Lett. 1981, 51, 2152–2155. (In Russian) [Google Scholar]
- Kumakhov, M.A.; Sabirov, A.S. Theory of ion reflection from amorphous surface at low glancing angles. Radiat. Eff. 1989, 107, 197–225. [Google Scholar] [CrossRef]
- Kumakhov, M.A. Radiation of Channeled Particles in Crystals; Energoatomizdat: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Mashkova, E.S.; Molchanov, V.A. Medium-energy ion scattering by solid surfaces part II. Radiat. Eff. 1974, 23, 215–270. [Google Scholar] [CrossRef]
- Sizmann, R.; Varelas, C. Surface Channeling. Nucl. Instrum. Methods 1976, 132, 633–638. [Google Scholar] [CrossRef]
- Kumakhov, M.; Komarov, F. Multiple reflection from surface X-ray optics. Phys. Rep. 1990, 191, 289–350. [Google Scholar] [CrossRef]
- Bilderback, D.H. Review of capillary X-ray optics from the 2nd International Capillary Optics Meeting. X-ray Spectrom. 2003, 32, 195–207. [Google Scholar] [CrossRef]
- Kumakhov, M. (Ed.) Kumakhov Optics and Applications; SPIE Selected Papers; Proc. SPIE: Washington, WA, USA, 2000; Volume 4155. [Google Scholar]
- Khounsary, A.; MacDonald, C.A. Focusing Polycapillary Optics and Their Applications. X-ray Opt. Instrum. 2010, 2010, 867049. [Google Scholar] [CrossRef]
- Dabagov, S.B.; Gladkikh, Y.P. Advanced channeling technologies for X-ray applications. Radiat. Phys. Chem. 2019, 154, 3–16. [Google Scholar] [CrossRef]
- Winter, H. Scattering of atoms and ions from insulator surfaces. Prog. Surf. Sci. 2000, 63, 177–247. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Bremer, J.H.; Hoffmann, V.; Hellhammer, R.; Fink, D.; Petrov, A.; Sulik, B. Transmission of 3 keV Ne7+ Ions through Nanocapillaries Etched in Polymer Foils: Evidence for Capillary Guiding. Phys. Rev. Lett. 2002, 88, 133201. [Google Scholar] [CrossRef]
- Schiessl, K.; Palfinger, W.; Tőkési, K.; Nowotny, H.; Lemell, C.; Burgdörfer, J. Simulation of guiding of multiply charged projectiles through insulating capillaries. Phys. Rev. A 2005, 72, 062902. [Google Scholar] [CrossRef]
- Stolterfoht, N. Comparison of ion guiding through nanocapillaries and macrocapillaries in insulating materials. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2015, 354, 51–55. [Google Scholar] [CrossRef]
- Hellhammer, R.; Sobocinski, P.; Pešić, Z.; Bundesmann, J.; Fink, D.; Stolterfoht, N. Interaction of slow highly charged ions with the inner surface of nanocapillaries. Nucl. Instrum. Meth. B 2005, 232, 235–243. [Google Scholar] [CrossRef]
- Pokhil, G.; Vokhmyanina, K. Drift model of ion beam guiding using capillaries. J. Surf. Investig. 2008, 2, 237–240. [Google Scholar] [CrossRef]
- Stolterfoht, N. Simulation and analysis of ion guiding through a nanocapillary in insulating polymers. Phys. Rev. A 2013, 87, 012902. [Google Scholar] [CrossRef]
- Stolterfoht, N. Simulations of ion-guiding through insulating nanocapillaries of varying diameter: Interpretation of experimental results. Atoms 2020, 8, 48. [Google Scholar] [CrossRef]
- Giglio, E.; Guillous, S.; Cassimi, A.; Zhang, H.; Nagy, G.; Tokési, K. Evolution of the electric potential of an insulator under charged particle impact. Phys. Rev. A 2017, 95, 030702. [Google Scholar] [CrossRef]
- Schiessl, K.; Tőkési, K.; Solleder, B.; Lemell, C.; Burgdörfer, J. Electron Guiding through Insulating Nanocapillaries. Phys. Rev. Lett. 2009, 102, 163201. [Google Scholar] [CrossRef] [PubMed]
- Dassanayake, B.S.; Das, S.; Ayyad, A.; Tanis, J.A. Electron transmission through a single glass macrocapillary: Dependence on energy and time. Phys. Scr. 2011, T144, 014041. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J.; Yu, D.Y.; Yang, B.; Wu, Y.H.; Zhang, M.W.; Ruan, F.F.; Cai, X.H. Transmission of electrons through a tapered glass capillary. Phys. Scr. 2011, T144, 014023. [Google Scholar] [CrossRef]
- Wickramarachchi, S.; Dassanayake, B.; Keerthisinghe, D.; Ayyad, A.; Tanis, J. Electron transmission through a microsize tapered glass capillary. Nucl. Instrum. Meth. B 2011, 269, 1248–1252. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Tanis, J. Significant differences in ion and electron guiding through highly insulating capillaries. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2018, 421, 32–37. [Google Scholar] [CrossRef]
- Das, S.; Dassanayake, B.; Winkworth, M.; Baran, J.; Stolterfoht, N.; Tanis, J. Inelastic guiding of electrons in polymer nanocapillaries. Phys. Rev. A—At. Mol. Opt. Phys. 2007, 76, 042716. [Google Scholar] [CrossRef]
- Dassanayake, B.; Das, S.; Bereczky, R.; Tokési, K.; Tanis, J. Energy dependence of electron transmission through a single glass macrocapillary. Phys. Rev. A—At. Mol. Opt. Phys. 2010, 81, 020701. [Google Scholar] [CrossRef]
- Wickramarachchi, S.; Ikeda, T.; Dassanayake, B.; Keerthisinghe, D.; Tanis, J. Electron-beam transmission through a micrometer-sized tapered-glass capillary: Dependence on incident energy and angular tilt angle. Phys. Rev. A 2016, 94, 022701. [Google Scholar] [CrossRef]
- Vokhmyanina, K.; Kubankin, A.; Myshelovka, L.; Zhang, H.; Kaplii, A.; Sotnikova, V.; Zhukova, M. Transport of accelerated electrons through dielectric nanochannels in PET films. J. Instrum. 2020, 15, C04003. [Google Scholar] [CrossRef]
- Vokhmyanina, K.; Myshelovka, L.; Sotnikova, V.; Kubankina, A.; Pyatigor, A.; Kubankin, A.; Grigoriev, Y. A Study of the Transmission of 10-keV Electrons through a Ceramic Macrochannel. Tech. Phys. Lett. 2021, 47, 51. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Wulfkühler, J.P.; Heisig, J.; Tajmar, M. Electron guiding in macroscopic borosilicate capillaries with large bending angles. Sci. Rep. 2021, 11, 8345. [Google Scholar] [CrossRef] [PubMed]
- Nebiki, T.; Yamamoto, T.; Narusawa, T.; Breese, M.; Teo, E.; Watt, F. Focusing of MeV ion beams by means of tapered glass capillary optics. J. Vac. Sci. Technol. Vac. Surf. Film. 2003, 21, 1671–1674. [Google Scholar] [CrossRef]
- Ikeda, T.; Kanai, Y.; Kojima, T.M.; Iwai, Y.; Kambara, T.; Yamazaki, Y.; Hoshino, M.; Nebiki, T.; Narusawa, T. Production of a microbeam of slow highly charged ions with a tapered glass capillary. Appl. Phys. Lett. 2006, 89, 163502. [Google Scholar] [CrossRef]
- Ikeda, T.; Kojima, T.; Iwai, Y.; Kanai, Y.; Kambara, T.; Nebiki, T.; Narusawa, T.; Yamazaki, Y. Production of a nm sized slow HCI beam with a guiding effect. J. Phys. Conf. Ser. 2007, 58, 68–73. [Google Scholar] [CrossRef]
- Zhou, C.; Simon, M.; Ikeda, T.; Guillous, S.; Iskandar, W.; Méry, A.; Rangama, J.; Lebius, H.; Benyagoub, A.; Grygiel, C.; et al. Transmission of slow highly charged ions through glass capillaries: Role of the capillary shape. Phys. Rev. A—At. Mol. Opt. Phys. 2013, 88, 050901. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, Y. Beam diameter effects on the transmission of 1-MeV protons through an insulating macrocapillary. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2020, 482, 1–5. [Google Scholar] [CrossRef]
- Ikeda, T. Applications of microbeams produced by tapered glass capillary optics. Quantum Beam Sci. 2020, 4, 22. [Google Scholar] [CrossRef]
- Lemell, C.; Burgdörfer, J.; Aumayr, F. Interaction of charged particles with insulating capillary targets—The guiding effect. Prog. Surf. Sci. 2013, 88, 237–278. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Yamazaki, Y. Guiding of charged particles through capillaries in insulating materials. Phys. Rep. 2016, 629, 1–107. [Google Scholar] [CrossRef]
- Schiessl, K.; Lemell, C.; Tökési, K.; Burgdörfer, J. Simulation of charged particle guiding through insulating nanocapillaries. J. Phys. Conf. Ser. 2009, 194, 012069. [Google Scholar] [CrossRef]
- Schiessl, K.; Palfinger, W.; Lemell, C.; Burgdörfer, J. Simulation of guiding of highly charged projectiles through insulating nanocapillaries. Nucl. Instrum. Meth. B 2005, 232, 228–234. [Google Scholar] [CrossRef]
- Liu, S.; Stolterfoht, N.; Zhao, Y. Simulated transmission of a 1-MeV proton microbeam through an insulating macrocapillary. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2019, 458, 28–32. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, Y. Simulations of transmission of 1 MeV protons through an insulating macrocapillary. J. Phys. Appl. Phys. 2020, 53. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, Y. Simulations of 1-MeV proton transmission through an insulating conical macrocapillary: Further insight into transmission mechanisms. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2021, 491, 1–6. [Google Scholar] [CrossRef]
- Moliere, G. Theorie der Streuung schneller geladener Teilchen I Einzelstreuung am abgeschirmten Coulomb-Feld. Z. Naturforschung A 1947, A2, 133–145. [Google Scholar] [CrossRef]
- Bethe, H.A. Molière’s Theory of Multiple Scattering. Phys. Rev. 1953, 89, 1256–1266. [Google Scholar] [CrossRef]
- Gemmell, D.S. Channeling and Related Effects in the Motion of Charged Particles Through Crystals. Rev. Mod. Phys. 1974, 46, 129–227. [Google Scholar] [CrossRef]
- Madelung, O. Solid State Theory, Russian ed.; Translated from O. Madelung, Festköpertheorie I, II, Spriger-Verlag 1972; Nauka: Moscow, Russia, 1980. [Google Scholar]
- Dabagov, S.B.; Zhevago, N.K. On radiation by relativistic electrons and positrons channeled in crystals. Riv. Nuovo C. 2008, 31, 491–529. [Google Scholar] [CrossRef]
- Kumakhov, M.A. Interaction potential of a particle with amorphous surface. Tech. Phys. Lett. 1983, 9, 1314–1316. (In Russian) [Google Scholar]
- Dabagov, S.B. Redistribution of X-rays Trapped in Bound States by Capillary Systems; Preprint IROS-1/1992; IROS: Moscow, Russia, 1992. [Google Scholar]
- Cappuccio, G.; Dabagov, S.; Pifferi, A.; Gramaccioni, C. Divergence Behaviour Due to Surface Channeling in Capillary Optics. Appl. Phys. Lett. 2001, 78, 2822–2824. [Google Scholar] [CrossRef]
- Dabagov, S.B. Wave theory of X-ray scattering in capillary structures. X-ray Spectrom. 2003, 32, 179–185. [Google Scholar] [CrossRef]
- Dabagov, S.B.; Kumakhov, M.A. X-ray channeling in capillary systems. Proc. SPIE 1995, 2515, 124–133. [Google Scholar] [CrossRef]
- Dabagov, S.; Kumakhov, M.; Nikitina, S. On the Interference of X-rays in Multiple Reflection Optics. Phys. Lett. A 1995, 203, 279–282. [Google Scholar] [CrossRef]
- Burattini, E.; Dabagov, S.B. Channeling of X-rays in capillary systems: I. General principles. Nuovo C. B 2001, 116, 361–370. [Google Scholar]
- Burattini, E.; Dabagov, S.B.; Monti, F. Channeling of X-rays in capillary systems. II. Quantum-wave approach. Nuovo C. B 2002, 117, 769–779. [Google Scholar]
- Bukreeva, I.; Popov, A.; Pelliccia, D.; Cedola, A.; Dabagov, S.B.; Lagomarsino, S. Wave-Field Formation in a Hollow X-ray Waveguide. Phys. Rev. Lett. 2006, 97, 184801. [Google Scholar] [CrossRef]
- Dabagov, S.; Uberall, H. On X-ray waveguiding in nanochannels: Channeling formalism. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 580, 756–763. [Google Scholar] [CrossRef]
- Kumakhov, M.A. (Ed.) X-ray and Neutron Capillary Optics II; Proc. SPIE: Washington, WA, USA, 2004; Volume 5943. [Google Scholar]
- Dabagov, S.B. From surface down to bulk X-ray channeling. AIP Conf. Proc. 2003, 652, 89–98. [Google Scholar] [CrossRef]
- Dabagov, S.B.; Kumakhov, M.A.; Nikitina, S.V.; Murashova, V.A.; Fedorchuk, R.V.; Yakimenko, M.N. Observation of Interference Effects at the Focus of an X-ray Lens. J. Synch. Irradiat. 1995, 2, 132–135. [Google Scholar] [CrossRef]
- Artemiev, N.; Artemiev, A.; Kohn, V.; Smolyakov, N. Coherent Phenomenon in Reflection of Radiation by an Uneven Mirror. Phys. Scr. 1998, 57, 228. [Google Scholar] [CrossRef][Green Version]
- Dabagov, S.B.; Marcelli, A. Single-reflection regime of X-rays that travel into a monocapillary. Appl. Opt. 1999, 38, 7494–7497. [Google Scholar] [CrossRef]
- Kukhlevsky, S.V.; Flora, F.; Marinai, A.; Nyitray, G.; Ritucci, A.; Palladino, L.; Reale, A.; Tomassetti, G. Diffraction of X-ray beams in capillary waveguides. Nucl. Instrum. Meth. B 2000, 168, 276–282. [Google Scholar] [CrossRef]
- Liu, C.; Golovchenko, J.A. Surface Trapped X-rays: Whispering-Gallery Modes at λ = 0.7 Å. Phys. Rev. Lett. 1997, 79, 788–791. [Google Scholar] [CrossRef]
- Vinogradov, A.V.; Kovalev, V.F.; Kozhevnikov, I.V.; Pustovalov, V.V. Diffraction theory for grazing modes in concave mirrors and resonators at X-ray wavelengths. Sov. Phys. Tech. Phys. 1985, 30, 335–339. [Google Scholar]
- Dabagov, S.B.; Marcelli, A.; Murashova, V.A.; Svyatoslavsky, N.L.; Fedorchuk, R.V.; Yakimenko, M.N. Coherent and incoherent components of a synchrotron radiation spot produced by separate capillaries. Appl. Opt. 2000, 39, 3338–3343. [Google Scholar] [CrossRef] [PubMed]
- Bongaerts, J.; David, C.; Drakopoulos, M.; Zwanenburg, M.; Wegdam, G.; Lackner, T.; Keymeulen, H.; Van der Veen, J. Propagation of a partially coherent focused X-ray beam within a planar X-ray waveguide. J. Synchrotron Radiat. 2002, 9, 383–393. [Google Scholar] [CrossRef]
- Alexandrov, Y.; Dabagov, S.; Kumakhov, M.; Murashova, V.; Fedin, D.; Fedorchuk, R.; Yakimenko, M. Peculiarities of photon transmission through capillary systems. Nucl. Instrum. Meth. B 1998, 134, 174–180. [Google Scholar] [CrossRef]
- Devreese, J.T.; Kunz, A.B.; Collins, T.C. (Eds.) Elementary Excitations in Solids, Molecules and Atoms. Part B, Chapter—Electron Interaction with Surface Modes by G. D. Mahan; Nato ASI Subseries B; Springer: New York, NY, USA, 1974; Volume 2. [Google Scholar] [CrossRef]
- Ashkroft, N.; Mermin, N. Solid State Physics, Russian ed.; Translated from N.W. Ashkroft, N.D. Mermin, Solid State Physics, Saunders College Publ. 1976; Nauka: Moscow, Russia, 1980. [Google Scholar]
- Dedkov, G.V. Interatomic potentials of interactions in radiation physics. Phys.-Uspekhi 1995, 38, 877–910. [Google Scholar] [CrossRef]
- Kawai, R.; Itoh, N.; Ohtsuki, Y. Inelastic Scattering of Ions at the Surface. Surf. Sci. 1982, 114, 137–146. [Google Scholar] [CrossRef]
- Nunez, R.; Echenique, P.; Ritchie, R. The energy loss of energetic ions moving near a solid surface. J. Phys. C Solid State Phys. 1980, 13, 4229–4246. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972; Nauka: Moscow, Russia, 1979. (In Russian) [Google Scholar]
- Dabagov, S.B.; Dik, A.V. On channeling of charged particles in a single dielectric capillary. arXiv 2021, arXiv:2109.03524. [Google Scholar]
- Metzger, T.H. Squeezing X-ray Photons. Science 2002, 297, 205–206. [Google Scholar] [CrossRef] [PubMed]
- Dabagov, S.B.; Uberall, H. On X-ray channeling in narrow guides. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2008, 266, 3881–3887. [Google Scholar] [CrossRef]
- Ioffe, A.; Dabagov, S.; Kumakhov, M. Effective neutron bending at large angles. Neutron News 1995, 6, 20–21. [Google Scholar] [CrossRef]
- Pogossian, S.P.; Gall, H.L. Neutron and X-ray propagation laws in thin film waveguides. Opt. Commun. 1995, 114, 235–241. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).