Laser Peening Analysis of Aluminum 5083: A Finite Element Study
Abstract
:1. Introduction
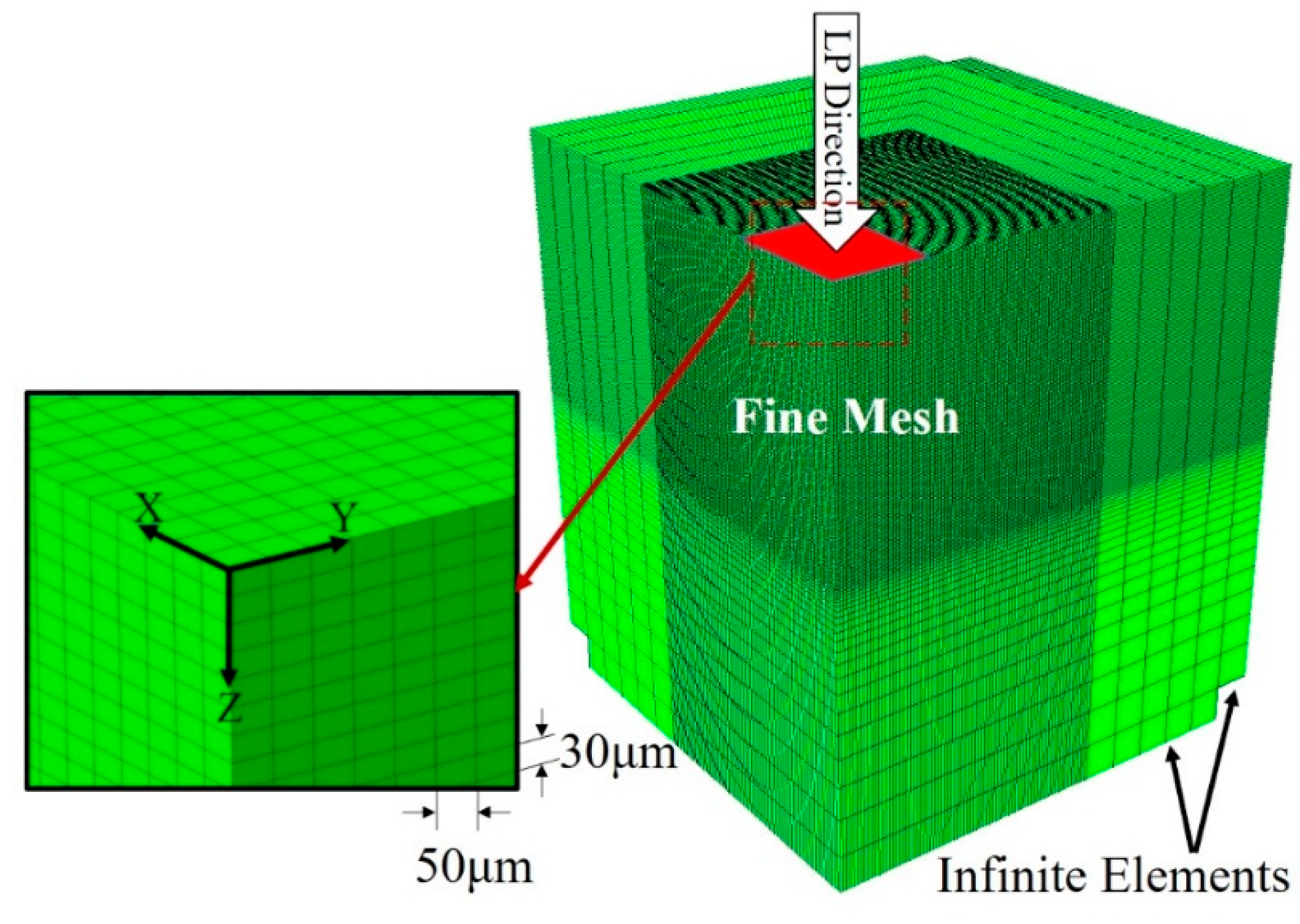
2. 3D Simulation of the Laser Peening Process
3. Experiments
3.1. LP Process
3.2. Residual Stress Measurement
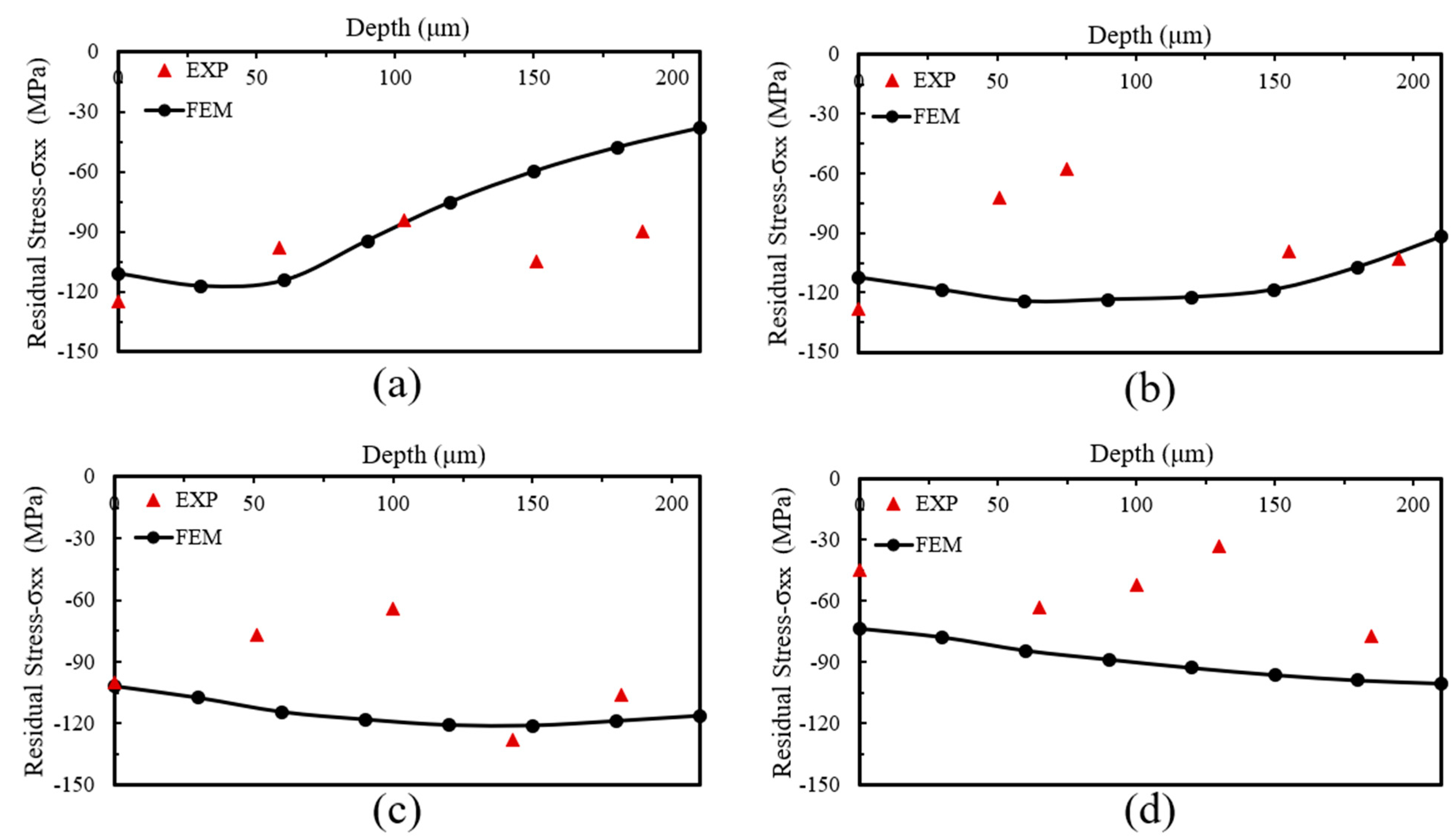
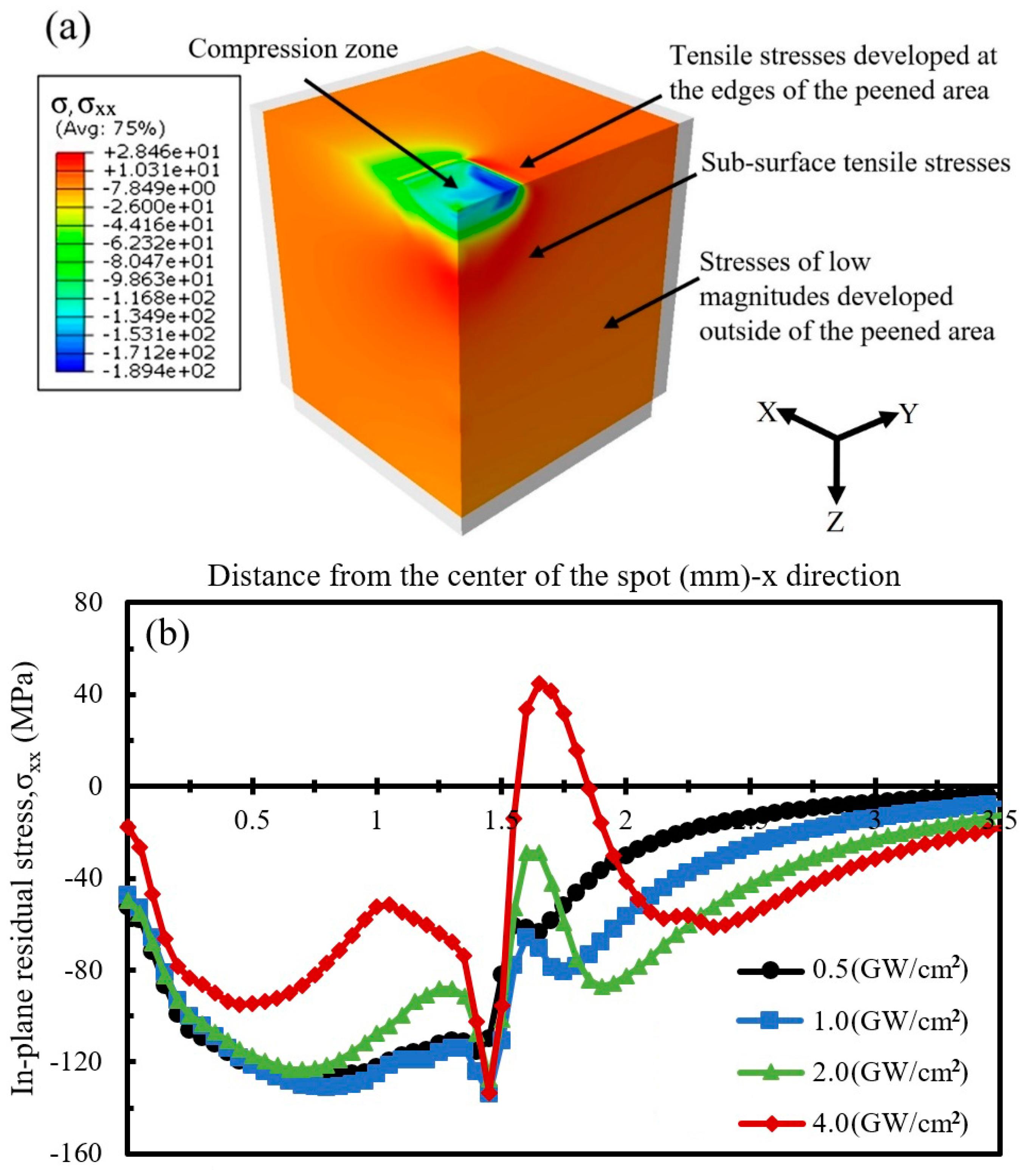
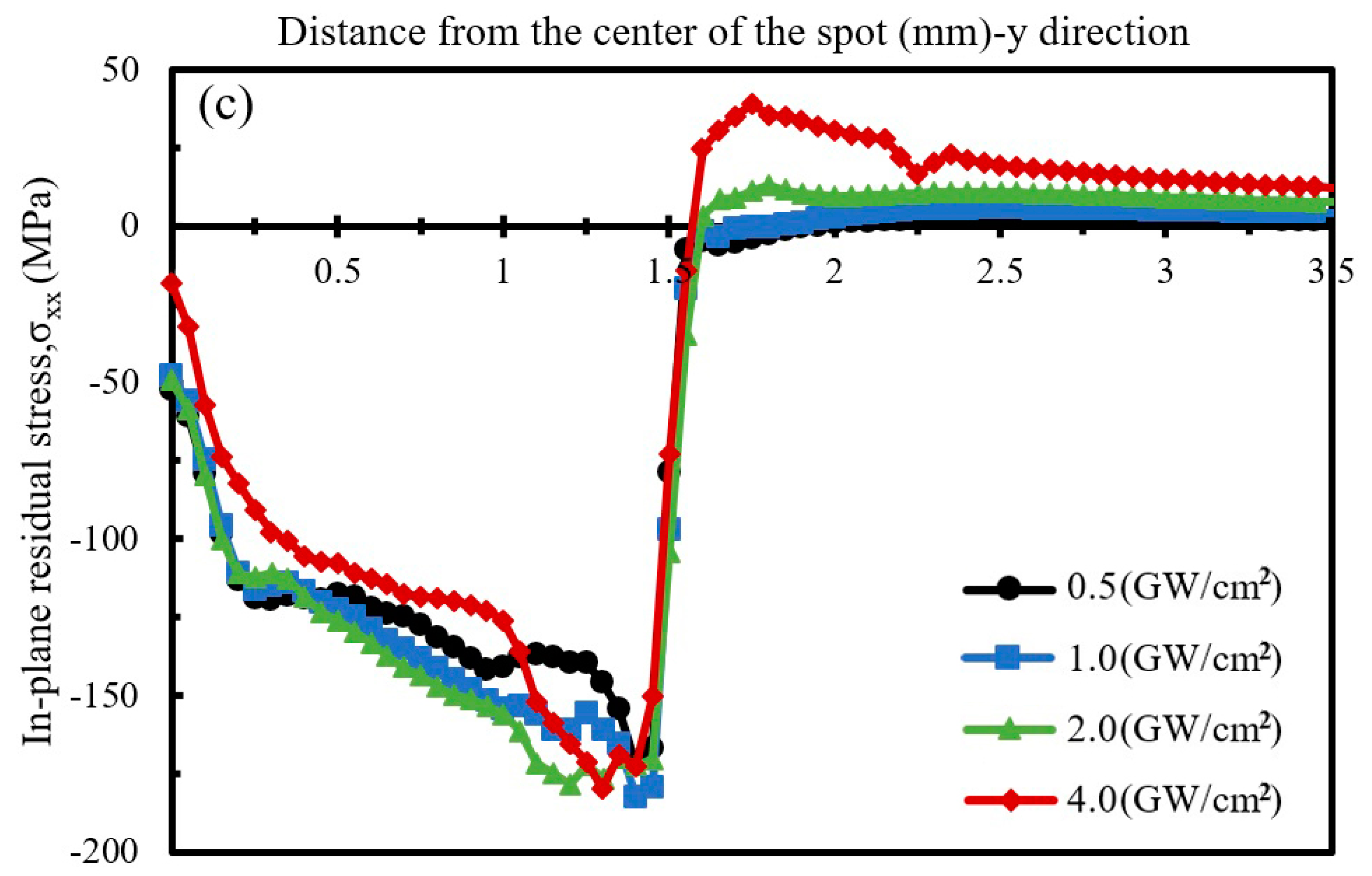
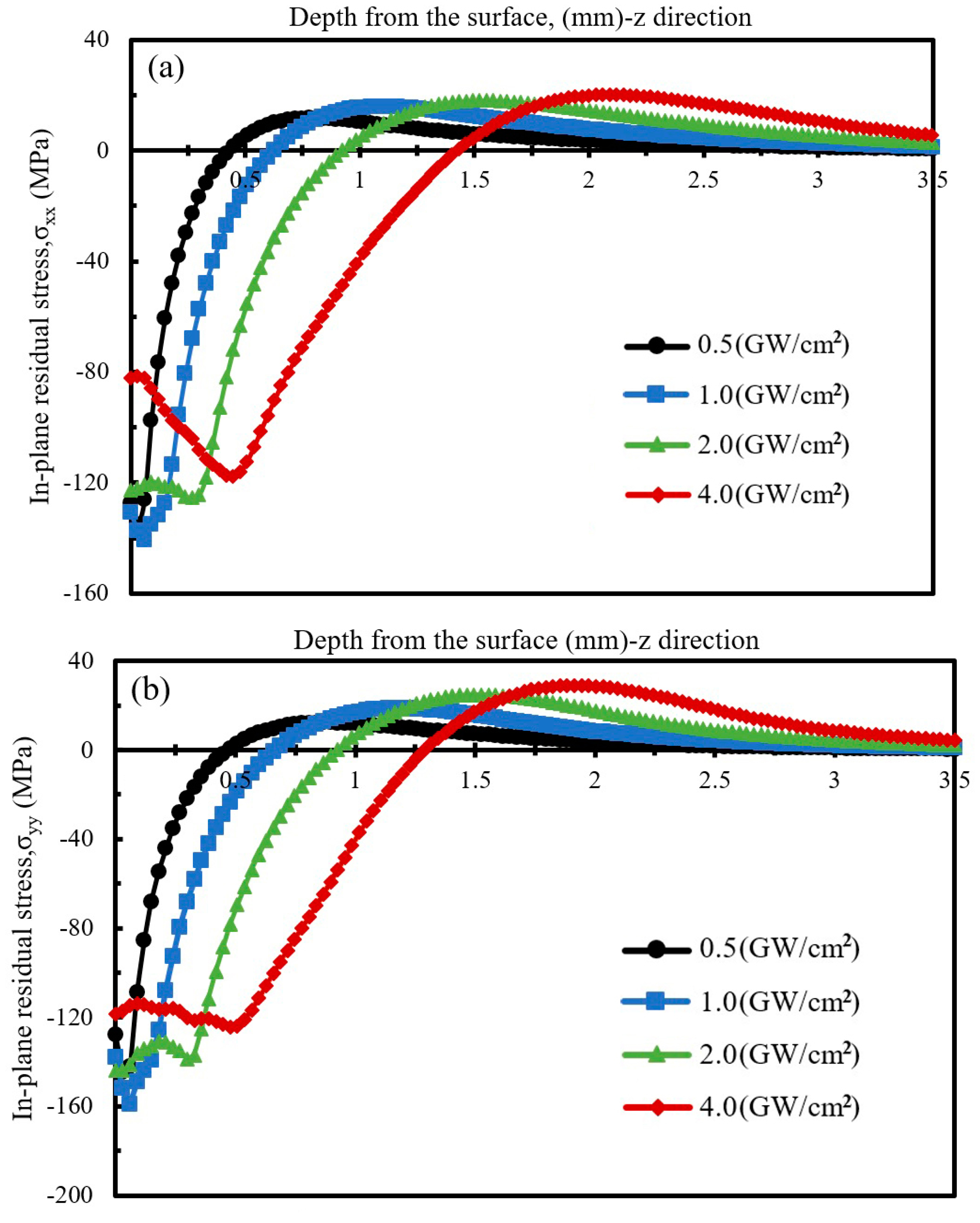
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bachmann, A.L.; Dickey, M.D.; Lazarus, N. Making Light Work of Metal Bending: Laser Forming in Rapid Prototyping. Quantum Beam Sci. 2020, 4, 44. [Google Scholar] [CrossRef]
- Gujba, A.K.; Medraj, M. Laser Peening Process and Its Impact on Materials Properties in Comparison with Shot Peening and Ultrasonic Impact Peening. Materials 2014, 7, 7925–7974. [Google Scholar] [CrossRef] [Green Version]
- Thiede, T.; Mishurova, T.; Evsevleev, S.; Serrano-Munoz, I.; Gollwitzer, C.; Bruno, G. 3D Shape Analysis of Powder for Laser Beam Melting by Synchrotron X-ray CT. Quantum Beam Sci. 2019, 3, 3. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Xue, P.; Lan, Q.; Meng, G.; Ren, Y.; Yang, Z.; Xu, P.; Liu, Z. Recent research and development status of laser cladding: A review. Opt. Laser Technol. 2021, 138, 106915. [Google Scholar] [CrossRef]
- Shobu, T.; Shiro, A.; Kono, F.; Muramatsu, T.; Yamada, T.; Naganuma, M.; Ozawa, T. Internal Strain Distribution of Laser Lap Joints in Steel under Loading Studied by High-Energy Synchrotron Radiation X-rays. Quantum Beam Sci. 2021, 5, 17. [Google Scholar] [CrossRef]
- Munther, M.; Martin, T.; Tajyar, A.; Hackel, L.; Beheshti, A.; Davami, K. Laser shock peening and its effects on microstructure and properties of additively manufactured metal alloys: A review. Eng. Res. Express 2020, 2, 022001. [Google Scholar] [CrossRef]
- Bagheri, S.; Guagliano, M. Review of shot peening processes to obtain nanocrystalline surfaces in metal alloys. Surf. Eng. 2009, 25, 3–14. [Google Scholar] [CrossRef]
- Hayashi, M.; Okido, S.; Suzuki, H. Residual Stress Distribution in Water Jet Peened Type 304 Stainless Steel. Quantum Beam Sci. 2020, 4, 18. [Google Scholar] [CrossRef] [Green Version]
- Malaki, M.; Ding, H. A review of ultrasonic peening treatment. Mater. Des. 2015, 87, 1072–1086. [Google Scholar] [CrossRef]
- Peyre, P.; Chaieb, I.; Braham, C. FEM calculation of residual stresses induced by laser shock processing in stainless steels. Model. Simul. Mater. Sci. Eng. 2007, 15, 205–221. [Google Scholar] [CrossRef]
- Yang, C.; Hodgson, P.D.; Liu, Q.; Ye, L. Geometrical effects on residual stresses in 7050-T7451 aluminum alloy rods subject to laser shock peening. J. Mater. Process. Technol. 2008, 201, 303–309. [Google Scholar] [CrossRef]
- Chupakhin, S.; Klusemann, B.; Huber, N.; Kashaev, N. Application of design of experiments for laser shock peening process optimization. Int. J. Adv. Manuf. Technol. 2019, 102, 1567–1581. [Google Scholar] [CrossRef]
- Palma, T.; Munther, M.; Sharma, M.; Hackel, L.; Beheshti, A.; Davami, K. Nanomechanical Characterization of Laser Peened Additively Manufactured Inconel 718 Superalloy. Adv. Eng. Mater. 2019, 21, 1900499. [Google Scholar] [CrossRef]
- Ren, X.; Chen, B.; Jiao, J.; Yang, Y.; Zhou, W.; Tong, Z. Fatigue behavior of double-sided laser shock peened Ti-6Al-4V thin blade subjected to foreign object damage. Opt. Laser Technol. 2020, 121, 105784. [Google Scholar] [CrossRef]
- Kalainathan, S.; Prabhakaran, S. Recent development and future perspectives of low energy laser shock peening. Opt. Laser Technol. 2016, 81, 137–144. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, Z.; Hu, J. 3-D FEM simulation of laser shock processing. Surf. Coat. Technol. 2006, 201, 1426–1435. [Google Scholar] [CrossRef]
- Braisted, W.; Brockman, R. Finite element simulation of laser shock peening. Int. J. Fatigue 1999, 21, 719–724. [Google Scholar] [CrossRef]
- Ding, K.; Ye, L. FEM simulation of two sided laser shock peening of thin sections of Ti-6Al-4V alloy. Surf. Eng. 2003, 19, 127–133. [Google Scholar] [CrossRef]
- Peyre, P.; Sollier, A.; Chaieb, I.; Berthe, L.; Bartnicki, E.; Braham, C.; Fabbro, R. FEM simulation of residual stresses induced by laser Peening. Eur. Phys. J. Appl. Phys. 2003, 23, 83–88. [Google Scholar] [CrossRef]
- Xiao, Y. Effect of laser shock peening on bending fatigue performance of AISI 9310 steel spur gear. Opt. Laser Technol. 2017, 94, 15–24. [Google Scholar] [CrossRef]
- Hfaiedh, N.; Peyre, P.; Song, H.; Popa, I.; Ji, V.; Vignal, V. Finite element analysis of laser shock peening of 2050-T8 aluminum alloy. Int. J. Fatigue 2015, 70, 480–489. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Ren, X.; Yang, Y.; Tong, Z.; Asuako Larson, E. Finite element analysis of laser shock peening induced near-surface deformation in engineering metals. Opt. Laser Technol. 2019, 119, 105608. [Google Scholar] [CrossRef]
- Cao, Y.; Shin, Y.C.; Wu, B. Parametric study on single shot and overlapping laser shock peening on various metals via modeling and experiments. J. Manuf. Sci. Eng. Trans. ASME 2010, 132, 0610101–06101010. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, W.; Tong, Z.; Chen, L.; Yang, X.; Larson, E.A.; Ren, X. Electrochemical Corrosion Behavior of 5083 Aluminum Alloy Subjected to Laser Shock Peening. J. Mater. Eng. Perform. 2019, 28, 6081–6091. [Google Scholar] [CrossRef]
- Sun, S. Laser Shock Peening Process to Prevent Stress Corrosion Cracking of 5xxx Aluminum Alloys. Embargoed Master’s Thesis, University of Nebraska-Lincoln, Lincoln, NE, USA, April 2018. [Google Scholar]
- Ballard, P.; Fournier, J.; Fabbro, R.; Frelat, J. Residual Stresses Induced By Laser-Shocks. J. Phys. IV 1991, 1, C3-487–C3-494. [Google Scholar] [CrossRef]
- Fabbro, R.; Fournier, J.; Ballard, P.; Devaux, D.; Virmont, J. Physical study of laser-produced plasma in confined geometry. J. Appl. Phys. 1990, 68, 775–784. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R. Laser shock processing: A review of the physics and applications. Opt. Quantum Electron. 1995, 27, 1213–1229. [Google Scholar] [CrossRef]
- Elwasli, F.; Zemzemi, F.; Mkaddem, A.; Mzali, S.; Mezlini, S. A 3D multi-scratch test model for characterizing material removal regimes in 5083-Al alloy. Mater. Des. 2015, 87, 352–362. [Google Scholar] [CrossRef]
- Boteler, J.M.; Dandekar, D.P. Dynamic response of two strain-hardened aluminum alloys. J. Appl. Phys. 2006, 100, 054902. [Google Scholar] [CrossRef]
- Wei, X.L.; Ling, X. Numerical modeling of residual stress induced by laser shock processing. Appl. Surf. Sci. 2014, 301, 557–563. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, Y.J.; Lee, J.W.; Yoo, S.H. Study on effect of time parameters of laser shock peening on residual stresses using FE simulation. J. Mech. Sci. Technol. 2014, 28, 1803–1810. [Google Scholar] [CrossRef]
- Ding, K. Three-dimensional dynamic finite element analysis of multiple laser shock peening processes. Surf. Eng. 2003, 19, 351–358. [Google Scholar] [CrossRef]
- Bikdeloo, R.; Farrahi, G.H.; Mehmanparast, A.; Mahdavi, S.M. Multiple laser shock peening effects on residual stress distribution and fatigue crack growth behaviour of 316 L stainless steel. Theor. Appl. Fract. Mech. 2020, 105, 102429. [Google Scholar] [CrossRef]
- Sealy, M.P.; Guo, Y.B. Surface integrity and process mechanics of laser shock peening of novel biodegradable magnesium-calcium (Mg-Ca) alloy. J. Mech. Behav. Biomed. Mater. 2010, 3, 488–496. [Google Scholar] [CrossRef]
- Sun, R.; Li, L.; Zhu, Y.; Zhang, L.; Guo, W.; Peng, P.; Li, B.; Guo, C.; Liu, L.; Che, Z.; et al. Dynamic response and residual stress fields of Ti6Al4V alloy under shock wave induced by laser shock peening. Model. Simul. Mater. Sci. Eng. 2017, 25, 065016. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, Y.J.; Kim, J.S. Effects of simulation parameters on residual stresses for laser shock peening finite element analysis. J. Mech. Sci. Technol. 2013, 27, 2025–2034. [Google Scholar] [CrossRef]
- Hu, Y.; Gong, C.; Yao, Z.; Hu, J. Investigation on the non-homogeneity of residual stress field induced by laser shock peening. Surf. Coat. Technol. 2009, 203, 3503–3508. [Google Scholar] [CrossRef]
- Li, P.; Huang, S.; Xu, H.; Li, Y.; Hou, X.; Wang, Q.; Fu, W.; Fang, Y. Numerical simulation and experiments of titanium alloy engine blades based on laser shock processing. Aerosp. Sci. Technol. 2015, 40, 164–170. [Google Scholar] [CrossRef]
- Achintha, M.; Nowell, D. Eigenstrain modelling of residual stresses generated by laser shock peening. J. Mater. Process. Technol. 2011, 211, 1091–1101. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R.; Merrien, P.; Lieurade, H.P. Laser shock processing of aluminium alloys. Application to high cycle fatigue behaviour. Mater. Sci. Eng. A 1996, 210, 102–113. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tajyar, A.; Holtham, N.; Brooks, N.; Hackel, L.; Sherman, V.; Beheshti, A.; Davami, K. Laser Peening Analysis of Aluminum 5083: A Finite Element Study. Quantum Beam Sci. 2021, 5, 34. https://doi.org/10.3390/qubs5040034
Tajyar A, Holtham N, Brooks N, Hackel L, Sherman V, Beheshti A, Davami K. Laser Peening Analysis of Aluminum 5083: A Finite Element Study. Quantum Beam Science. 2021; 5(4):34. https://doi.org/10.3390/qubs5040034
Chicago/Turabian StyleTajyar, Ali, Noah Holtham, Nicholas Brooks, Lloyd Hackel, Vincent Sherman, Ali Beheshti, and Keivan Davami. 2021. "Laser Peening Analysis of Aluminum 5083: A Finite Element Study" Quantum Beam Science 5, no. 4: 34. https://doi.org/10.3390/qubs5040034
APA StyleTajyar, A., Holtham, N., Brooks, N., Hackel, L., Sherman, V., Beheshti, A., & Davami, K. (2021). Laser Peening Analysis of Aluminum 5083: A Finite Element Study. Quantum Beam Science, 5(4), 34. https://doi.org/10.3390/qubs5040034






