Nanopore Formation in CeO2 Single Crystal by Ion Irradiation: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Simulation Method
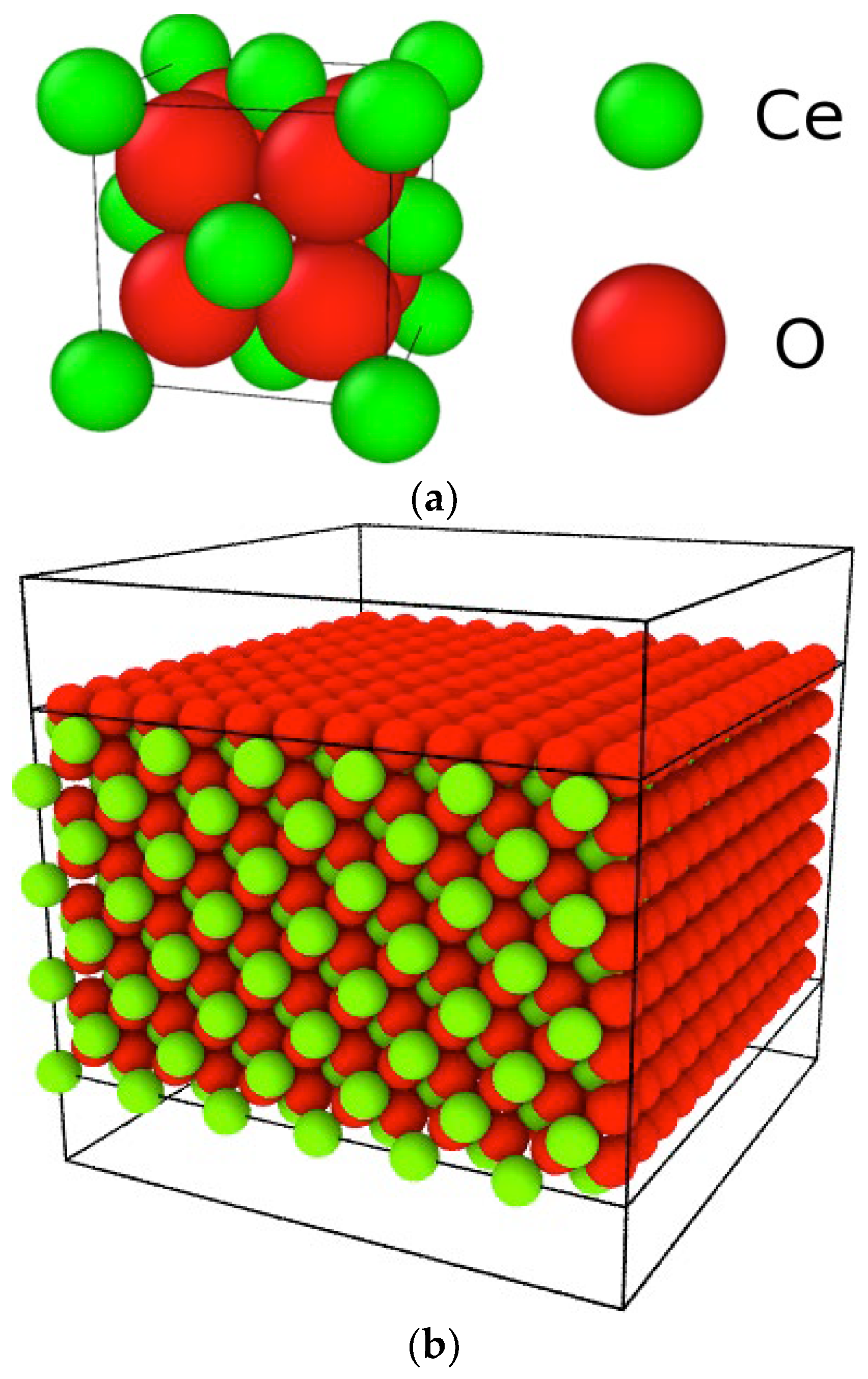
2.1. Molecular Dynamics
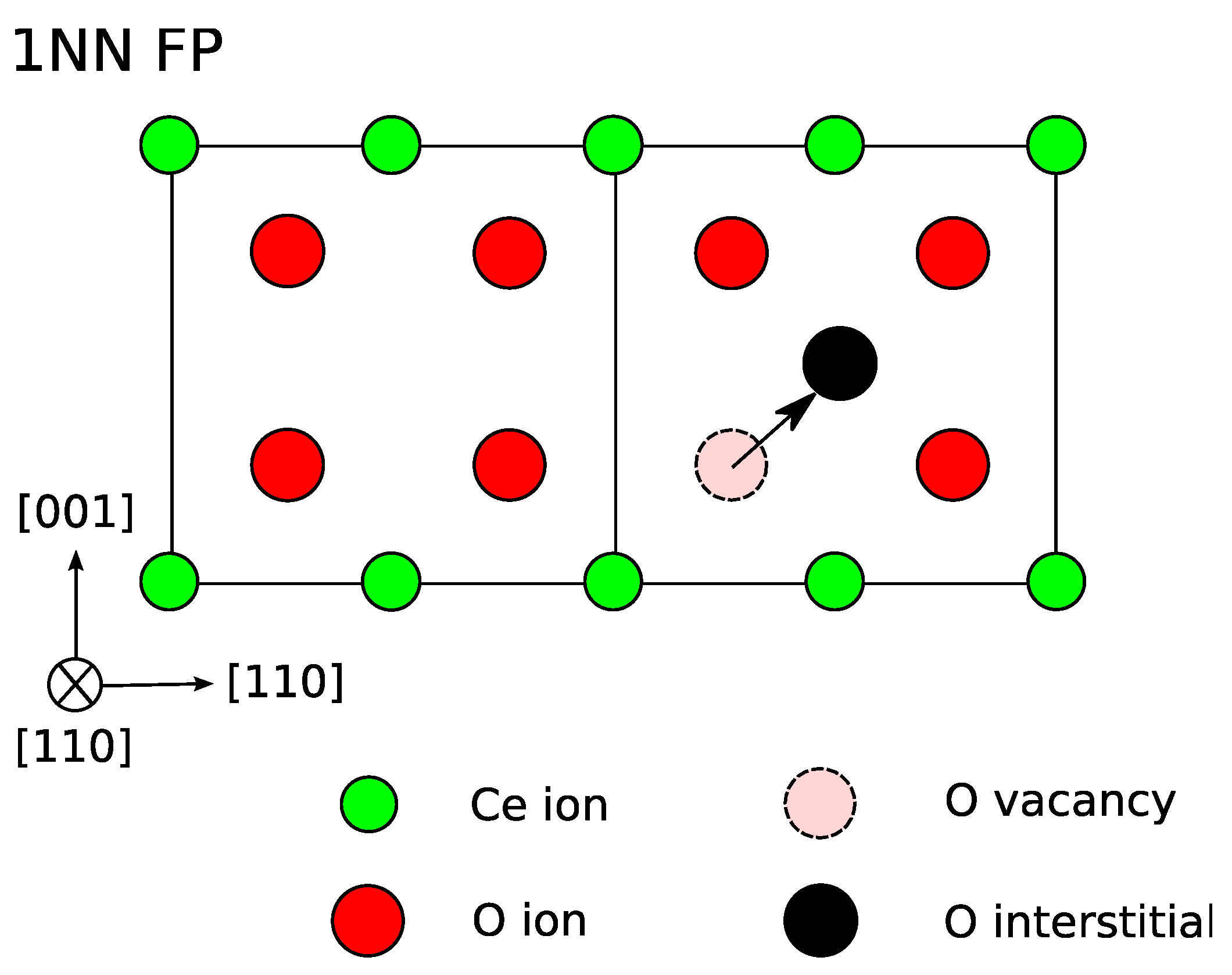
2.2. Structure Analysis
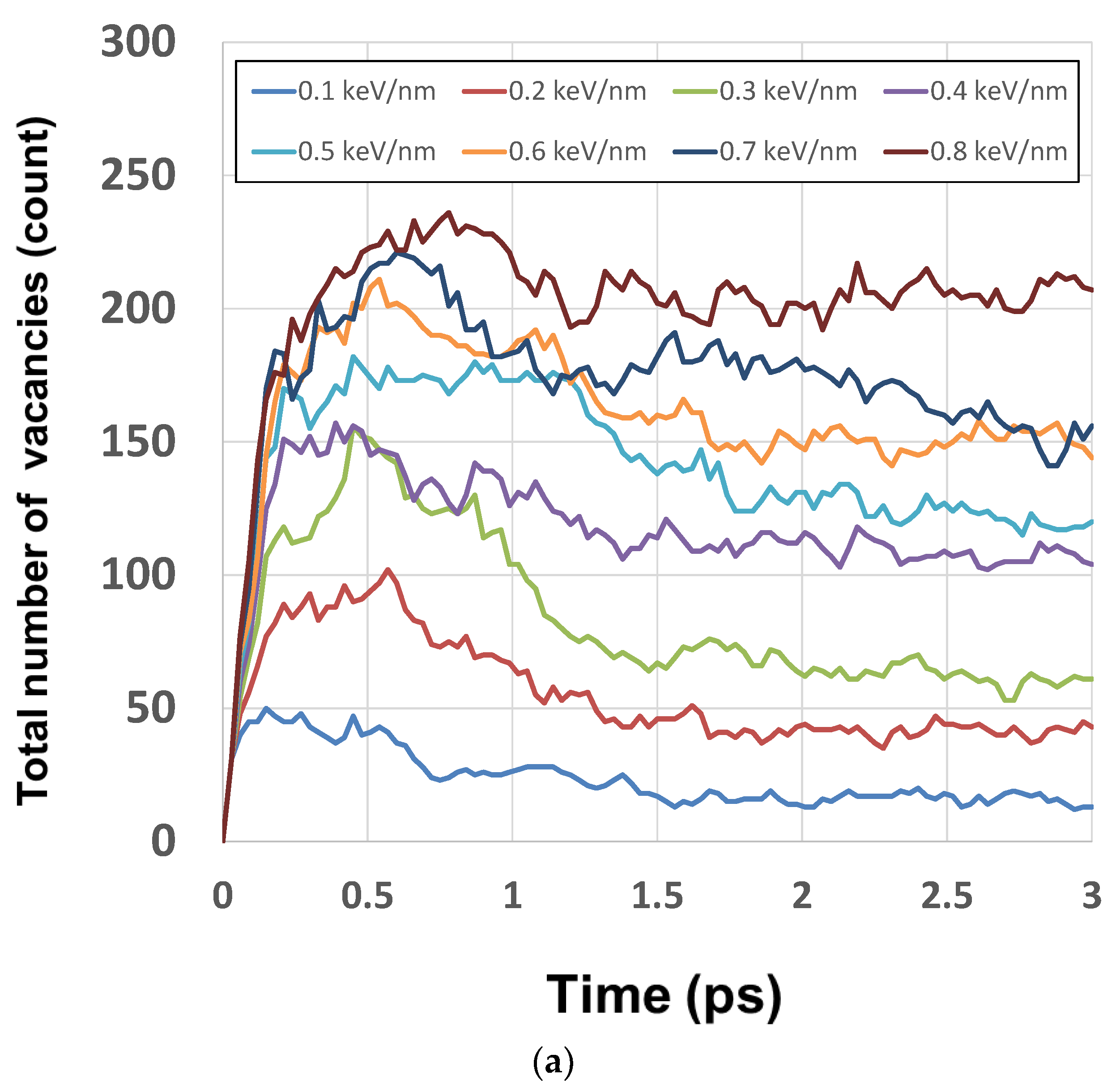
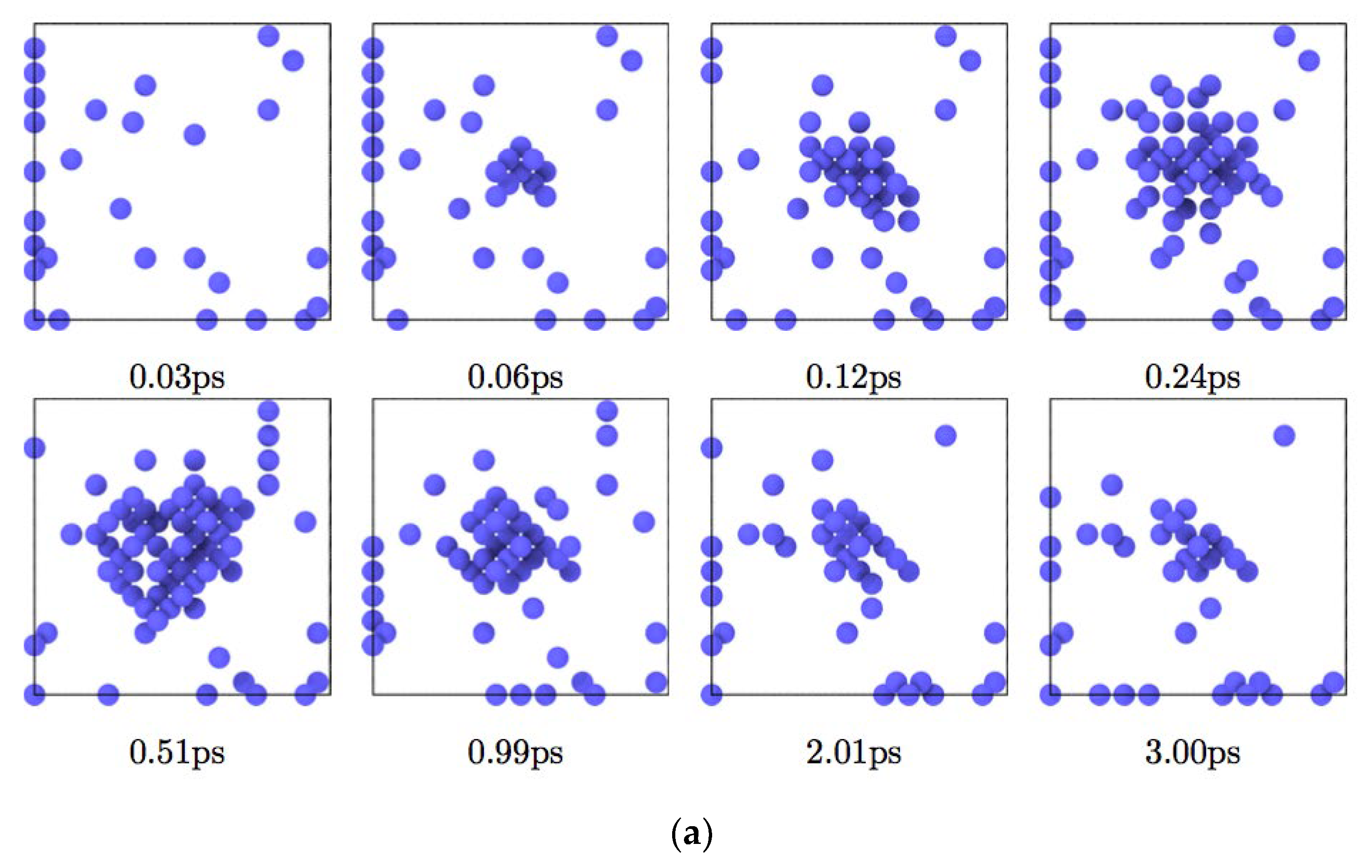
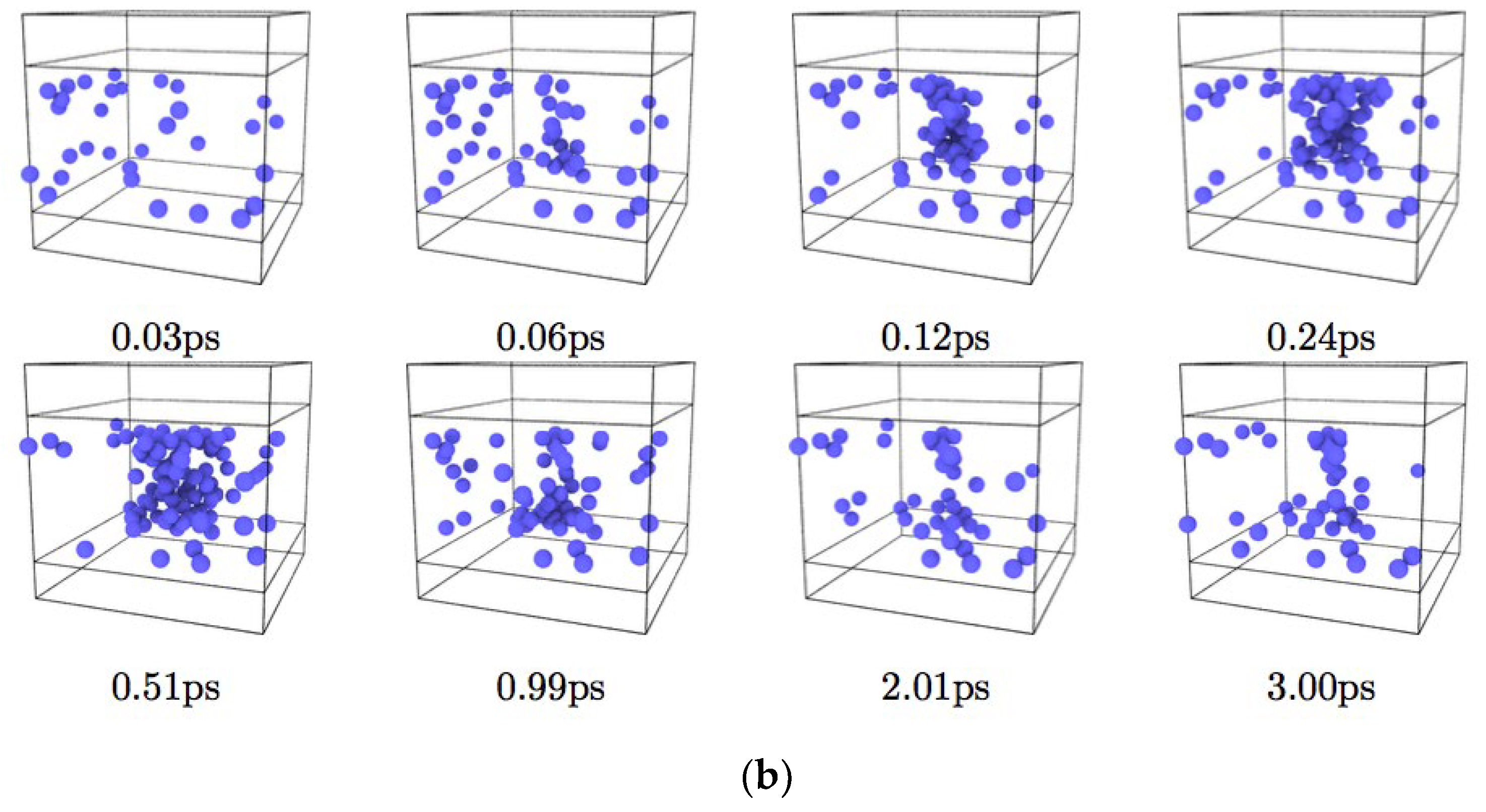
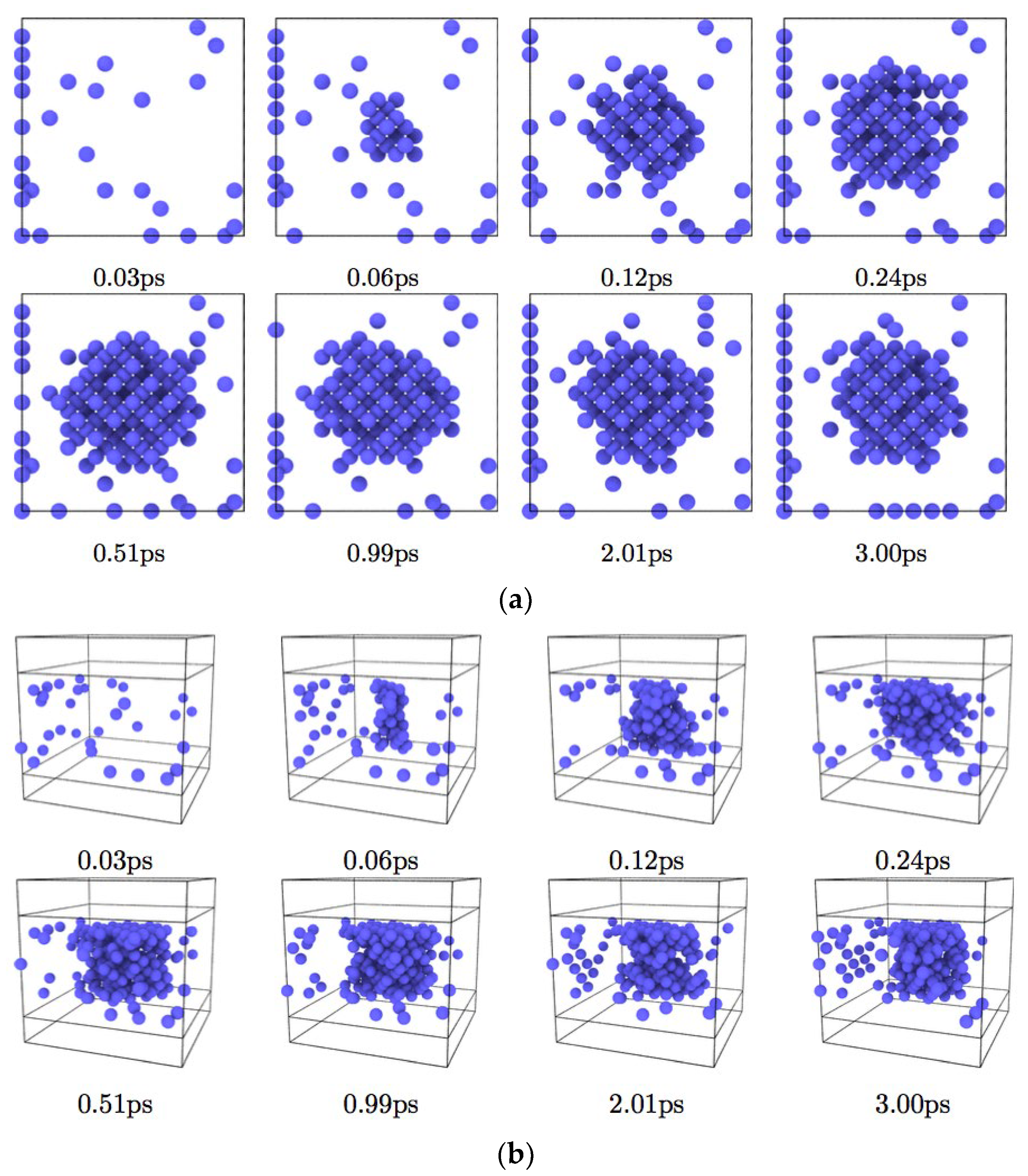
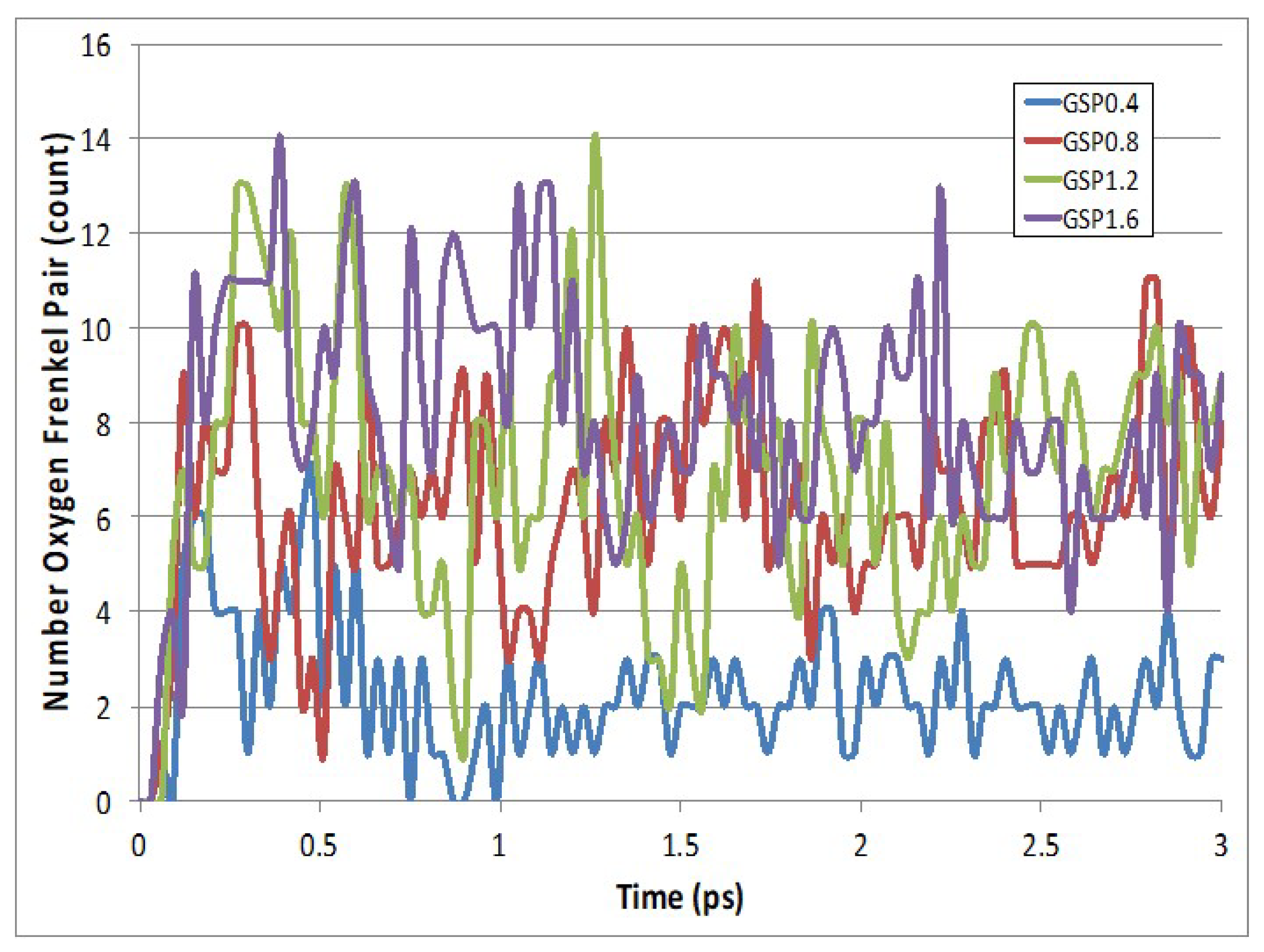
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Schattat, B.; Bolse, W.; Klaumuenzer, S.; Zizak, I.; Scholz, R. Cylindrical nanopores in NiO induced by swift heavy ions. Appl. Phys. Lett. 2005, 87, 173110. [Google Scholar] [CrossRef]
- Jensen, J.; Dunlop, A.; Della-Negra, S.; Pascard, H. Tracks in YIG induced by MeV C 60 ions. Nucl. Instrum. Methods B 1998, 135, 295–301. [Google Scholar] [CrossRef]
- Ishikawa, N.; Okubo, N.; Taguchi, T. Experimental evidence of crystalline hillocks created by irradiation of CeO2 with swift heavy ions: TEM study. Nanotechnology 2015, 26, 355701. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Taguchi, T.; Kitamura, A.; Szenes, G.; Toimil-Molares, M.E.; Trautmann, C. TEM analysis of ion tracks and hillocks produced by swift heavy ions of different velocities in Y3Fe5O12. J. Appl. Phys. 2020, 127, 055902. [Google Scholar] [CrossRef]
- Costantini, J.-M.; Lelong, G.; Guillaumet, M.; Gourier, D.; Takaki, S.; Ishikawa, N.; Watanabe, H.; Yasuda, K. Optical reflectivity of ion-irradiated cerium dioxide sinters. J. Appl. Phys. 2019, 126, 175902. [Google Scholar] [CrossRef]
- Costantini, J.-M.; Gutierrez, G.; Watanabe, H.; Yasuda, K.; Takaki, S.; Lelong, G.; Guillaumet, M.; Weber, W.J. Optical spectroscopy study of modifications induced in cerium dioxide by electron and ion irradiations. Philos. Mag. 2019, 99, 1695–1714. [Google Scholar] [CrossRef] [Green Version]
- Palomares, R.I.; Shamblin, J.; Tracy, C.L.; Neuefeind, J.; Ewing, R.C.; Trautmann, C.; Lang, M. Defect accumulation in swift heavy ion-irradiated CeO2 and ThO2. J. Mater. Chem. A 2017, 5, 12193. [Google Scholar] [CrossRef]
- Graham, J.T.; Zhang, Y.; Weber, W.J. Irradiation-induced defect formation and damage accumulation in single crystal CeO2. J. Nucl. Mater. 2018, 498, 400–408. [Google Scholar] [CrossRef]
- Shelyug, A.; Palomares, R.I.; Lang, M.; Navrotsky, A. Energetics of defect production in fluorite-structured CeO2 induced by highly ionizing radiation. Phys. Rev. Mater. 2018, 2, 093607. [Google Scholar] [CrossRef]
- Costantini, J.-M.; Miro, S.; Touati, N.; Binet, L.; Wallez, G.; Lelong, G.; Guillaumet, M.; Weber, W.J. Defects induced in cerium dioxide single crystals by electron irradiation. J. Appl. Phys. 2018, 123, 025901. [Google Scholar] [CrossRef]
- Cureton, W.F.; Palomares, R.I.; Walters, J.; Tracy, C.L.; Chen, C.-H.; Ewing, R.C.; Baldinozzi, G.; Lian, J.; Trautmann, C.; Lang, M. Grain size effects on irradiated CeO2, ThO2, and UO2. Acta Mater. 2018, 160, 47–56. [Google Scholar] [CrossRef]
- Maslakov, K.I.; Teterin, Y.A.; Popel, A.J.; Teterin, A.Y.; Ivanov, K.E.; Kalmykov, S.N.; Petrov, V.G.; Petrov, P.K.; Farnan, I. XPS study of ion irradiated and unirradiated CeO2 bulk and thin film samples. Appl. Surf. Sci. 2018, 448, 154–162. [Google Scholar] [CrossRef]
- Cureton, W.F.; Palomares, R.I.; Tracy, C.L.; O’Quinn, E.C.; Walters, J.; Zdorovets, M.; Ewing, R.C.; Toulemonde, M.; Lang, M. Effects of irradiation temperature on the response of CeO2, ThO2, and UO2 to highly ionizing radiation. J. Nucl. Mater. 2019, 525, 83–91. [Google Scholar] [CrossRef]
- Abanades, S.; Flamant, G. Thermochemical hydrogen production from a two-step solar driven water-splitting cycle based on cerium oxides. Sol. Energy 2006, 80, 1611–1623. [Google Scholar] [CrossRef]
- Sasajima, Y.; Onuki, H.; Ishikawa, N.; Iwase, A. Computer simulation of high-energy-ion irradiation of SiO2. Trans. MRS-J. 2013, 38, 497–502. [Google Scholar]
- Sasajima, Y.; Ajima, N.; Osada, T.; Ishikawa, N.; Iwase, A. Molecular dynamics simulation of fast particle irradiation to the Gd2O3-doped CeO2. Nucl. Instrum. Methods B 2013, 316, 176–182. [Google Scholar] [CrossRef]
- Sasajima, Y.; Osada, T.; Ishikawa, N.; Iwase, A. Computer simulation of high-energy-ion irradiation of uranium dioxide. Nucl. Instrum. Methods B 2013, 314, 195–201. [Google Scholar] [CrossRef]
- Sasajima, Y.; Ajima, N.; Osada, T.; Ishikawa, N.; Iwase, A. Molecular dynamics simulation of fast particle irradiation to the single crystal CeO2. Nucl. Instrum. Methods B 2013, 314, 202–207. [Google Scholar] [CrossRef]
- Sasajima, Y.; Ajima, N.; Kaminaga, R.; Ishikawa, N.; Iwase, A. Structure analysis of the defects generated by a thermal spike in single crystal CeO2: A molecular dynamics study. Nucl. Instrum. Methods B 2019, 440, 118–125. [Google Scholar] [CrossRef]
- Yablinsky, C.A.; Devanathan, R.; Pakarinen, J.; Gan, J.; Severin, D.; Trautmann, C.; Allen, T. Characterization of swift heavy ion irradiation damage in ceria. J. Mater. Res. 2015, 30, 1473–1484. [Google Scholar] [CrossRef]
- Medvedev, N.A.; Rymzhanov, R.A.; Volkov, A.E. Time-resolved electron kinetics in swift heavy ion irradiated solids. J. Phys. D 2015, 48, 355303. [Google Scholar] [CrossRef]
- Rymzhanov, R.A.; Medvedev, N.; Volkov, A.E. Damage threshold and structure of swift heavy ion tracks in Al2O3. J. Phys. D Appl. Phys. 2017, 50, 475301. [Google Scholar] [CrossRef]
- Rymzhanova, R.A.; Medvedev, N.; Volkova, A.E.; O’Connell, J.H.; Skuratova, V.A. Overlap of swift heavy ion tracks in Al2O3. Nucl. Instrum. Methods B 2018, 435, 121–125. [Google Scholar] [CrossRef]
- Rymzhanova, R.A.; Gorbunovd, S.A.; Medvedeve, N.; Volkova, A.E. Damage along swift heavy ion trajectory. Nucl. Instrum. Methods B 2019, 440, 25–35. [Google Scholar] [CrossRef]
- Rymzhanov, R.A.; Medvedev, N.; O’Connell, J.H.; Janse van Vuuren, A.; Skuratov, V.A.; Volkov, A.E. Recrystallization as the governing mechanism of ion track formation. Sci. Rep. 2019, 9, 3837. [Google Scholar] [CrossRef] [PubMed]
- Rymzhanov, R.A.; O’Connell, J.H.; Janse van Vuuren, A.; Skuatov, V.A.; Medvedev, N.; Volkov, A.E. Insight into picosecond kinetics of insulator surface under ionizing radiation. J. Appl. Phys. 2020, 127, 015901. [Google Scholar] [CrossRef]
- Karlušić, M.; Rymzhanov, R.A.; O’Connell, J.H.; Bröckers, L.; Tomić, L.K.; Siketić, Z.; Fazinić, S.; Dubček, P.; Jakšić, M.; Provatas, G.; et al. Mechanisms of surface nanostructuring of Al2O3 and MgO by grazing incidence irradiation with swift heavy ions. Surf. Interfaces 2021, 27, 101508. [Google Scholar] [CrossRef]
- Inaba, H.; Sagawa, R.; Hayashi, H.; Kawamura, K. Molecular dynamics simulation of gadolinia-doped ceria. Solid State Ion. 1999, 122, 95–103. [Google Scholar] [CrossRef]
- Sadus, R.J. Molecular Simulation of Fuids–Theory, Algorithms and Object-Orientation; Elsevier: Amsterdam, The Netherlands, 2002; p. 305. [Google Scholar]
- Shiiyama, K.; Yamamoto, T.; Takahashi, T.; Guglielmetti, A.; Chartier, A.; Yasuda, K.; Matsumura, S.; Yasunaga, K.; Meis, C. Molecular dynamics simulations of oxygen Frenkel pairs in cerium dioxide. Nucl. Instrum. Methods B 2010, 268, 2980–2983. [Google Scholar] [CrossRef]
- Yasunaga, K.; Yasuda, K.; Matsumura, S.; Sonoda, T. Electron energy-dependent formation of dislocation loops in CeO2. Nucl. Instrum. Methods B 2008, 266, 2877–2881. [Google Scholar] [CrossRef]
- Takaoka, H. Ionized Cluster Beam Technique for Deposition and Epitaxy. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 23 July 1981; pp. 45–50. [Google Scholar] [CrossRef]
- Yamada, I.; Takaoka, H. Ionized Cluster Beams: Physics and Technology. Jpn. J. Appl. Phys. 1993, 32, 2121. [Google Scholar] [CrossRef]



| Parameters | Ce 4+ | O 2− |
|---|---|---|
| z | 2.700 | −1.350 |
| a (nm) | 0.1330 | 0.1847 |
| b (nm) | 0.00454 | 0.0166 |
| c (J0.5(nm)3mol−0.5) | 0.00 | 1.294 |
| f0 | 4.07196 | 4.07196 |
| Type (NN: Nearest Neighbor) | Distance (nm) |
|---|---|
| 1NN | 0.234 |
| 2NN | 0.449 |
| 3NN | 0.590 |
| 4NN | 0.703 |
| 5NN | 0.800 |
| 6NN | 0.887 |
| 7NN | 0.966 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sasajima, Y.; Kaminaga, R.; Ishikawa, N.; Iwase, A. Nanopore Formation in CeO2 Single Crystal by Ion Irradiation: A Molecular Dynamics Study. Quantum Beam Sci. 2021, 5, 32. https://doi.org/10.3390/qubs5040032
Sasajima Y, Kaminaga R, Ishikawa N, Iwase A. Nanopore Formation in CeO2 Single Crystal by Ion Irradiation: A Molecular Dynamics Study. Quantum Beam Science. 2021; 5(4):32. https://doi.org/10.3390/qubs5040032
Chicago/Turabian StyleSasajima, Yasushi, Ryuichi Kaminaga, Norito Ishikawa, and Akihiro Iwase. 2021. "Nanopore Formation in CeO2 Single Crystal by Ion Irradiation: A Molecular Dynamics Study" Quantum Beam Science 5, no. 4: 32. https://doi.org/10.3390/qubs5040032
APA StyleSasajima, Y., Kaminaga, R., Ishikawa, N., & Iwase, A. (2021). Nanopore Formation in CeO2 Single Crystal by Ion Irradiation: A Molecular Dynamics Study. Quantum Beam Science, 5(4), 32. https://doi.org/10.3390/qubs5040032







