Coherent, Short-Pulse X-ray Generation via Relativistic Flying Mirrors

Abstract

Coherent, Short X-ray pulses are demanded in material science and biology for the study of micro-structures. Currently, large-sized free-electron lasers are used; however, the available beam lines are limited because of the large construction cost. Here we review a novel method to downsize the system as well as providing fully (spatially and temporally) coherent pulses. The method is based on the reflection of coherent laser light by a relativistically moving mirror (flying mirror). Due to the double Doppler effect, the reflected pulses are upshifted in frequency and compressed in time. Such mirrors are formed when an intense short laser pulse excites a strongly nonlinear plasma wave in tenuous plasma. Theory, proof-of-principle, experiments, and possible applications are addressed.

1. Introduction

A mirror moving at very high speed and the reflection from such a mirror were discussed by Einstein in this historical paper in 1905 [1], as a thought experiment at that time. Within the framework of special relativity the mechanism of relativistic flying mirrors (RFMs) was investigated and explained clearly. Although researchers did not know how to realize fast moving mirrors experimentally, the problem of relativistic reflection attracted many researchers for a long time. The reasons are that the problem raises several interesting discussions on conditions e.g., frequency upshifts, energy conservation, superluminal cases, etc. Einstein’s mirror was an ideal object, which reflected 100% of the incident radiation. Afterwards, researchers thus considered more realistic cases and parameters including the reflectivity and transmissivity. Later there was active work on how to realize such mirrors and applications of the RFMs for obtaining higher frequency radiation and even coherent, short pulse radiation.

Recently, the realization of such relativistically fast moving mirrors has become feasible thanks to the progress of knowledge and technology. The implementation of such moving mirrors can be performed by employing an ionization front, an oscillating mirror solid density plasma, double-sided mirrors, relativistic electron spikes formed in underdense plasma, etc. In this paper, we review the RFMs and the experimental implementation of such mirrors including the possible applications of mirrors [2]. Detailed theory and literature can be found in [3]. The organization of the paper is as follows. In Section 2 a brief theoretical description on the reflection of an incident electromagnetic wave from a moving mirror is given. In Section 3, we review several ideas and experiments to realize relativistically moving mirrors. Section 4 discusses the possible applications of relativistic mirrors, especially for generating coherent X-rays and the problems to be solved in the future. A conclusion is presented in Section 5.

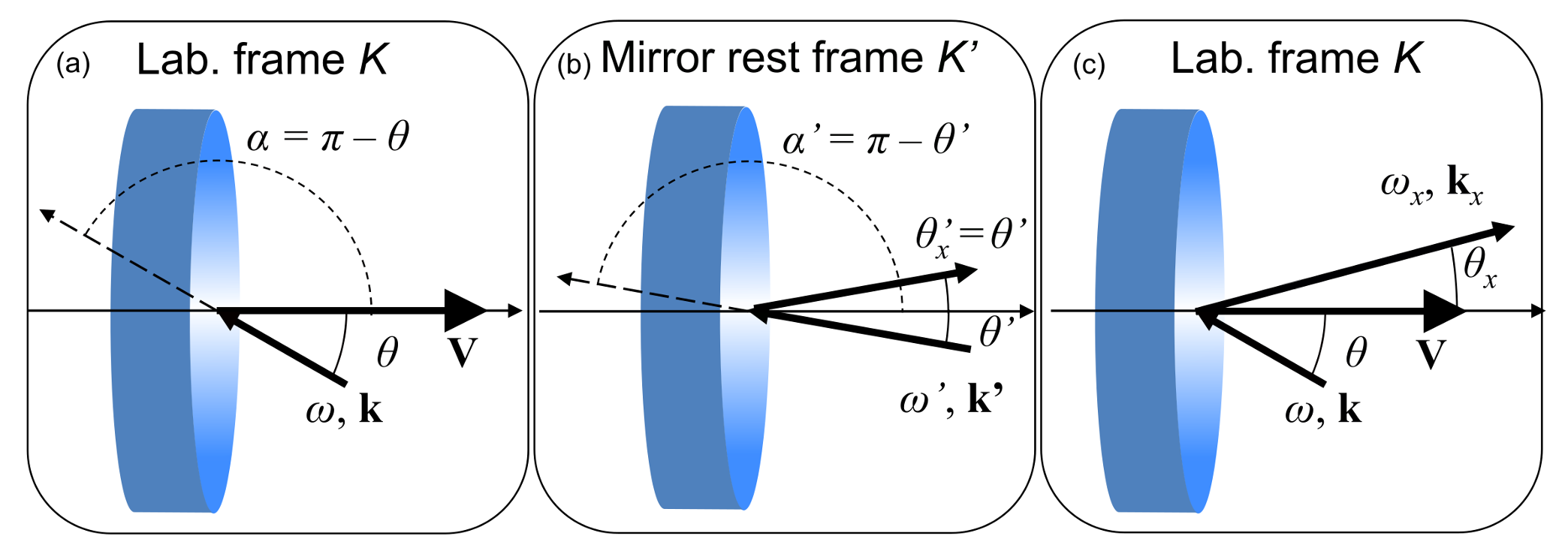
2. Theory of Relativistic Mirrors

Relativistic mirrors interact with electromagnetic waves. Let us derive the relationship between the reflection angle and frequency of the reflected light. The mirror is propagating along the positive direction with the velocity of $\mathbf{V}=\beta c$, where c is the speed of light in vacuum. Light with the frequency $\omega$ is incident on the mirror at an angle $\alpha$ as seen in Figure 1. We then consider this situation in the mirror rest frame by performing a Lorentz transformation $x^{\prime }=\gamma (x-\beta ct),y^{\prime }=y,z^{\prime }=z,t^{\prime }=\gamma (t-\beta x/c)$, where prime (^′) denotes the variables in the rest frame K and $\gamma ={(1-{\beta }^2)}^{-1/2}$ is the relativistic factor of the mirror. The light phase $\varphi =\omega t-\mathbf{k}·\mathbf{r}$ is Lorentz invariant, where $\mathbf{k}$ is the wave vector of the light and $\mathbf{r}$ is the position vector. We obtain

$$\omega t-\frac{\omega }{c}(x\cos \alpha +y\sin \alpha )={\omega }^{\prime }{t}^{\prime }-\frac{{\omega }^{\prime }}{c}(x^{\prime }\cos {\alpha }^{\prime }+y^{\prime }\sin {\alpha }^{\prime }),$$

(1)

and

$${\omega }^{\prime }=\omega \gamma (1-\beta \cos \alpha ),$$

(2)

$$\cos {\alpha }^{\prime }=\frac{\cos \alpha -\beta }{1-\beta \cos \alpha }.$$

(3)

In the mirror rest frame K z^′, the angle of reflection is same as that of incidence and the frequency does not change; thus we obtain ${\alpha }^{\prime }=\pi -{\theta }^{\prime }$, ${\omega }_r^{\prime }={\omega }^{\prime }$. Finally, we return to the laboratory frame by the inverse Lorentz transformation and obtain

$$\cos {\theta }_x=\frac{2\beta +(1+{\beta }^2)\cos \theta }{1+{\beta }^2+2\beta \cos \theta },$$

(4)

and

$${\omega }_x=\omega \frac{1+\beta \cos \theta }{1-\beta \cos {\theta }_x}\approx \left(4{\gamma }^2{\cos }^2\frac{\theta }{2}\right)\omega .$$

(5)

The approximation at the end of Equation (5) applies when the velocity of the mirror is ultra-relativistic ($\gamma \gg 1$). The pulse duration of the reflected pulse is shortened by the same factor $\approx 4{\gamma }^2{\cos }^2(\theta /2)$ as the frequency upshift, because the number of light cycles is Lorentz invariant.

3. Several Implementations of Relativistic Flying Mirrors

3.1. Relativistic Charged Beam

Motz considered radiation from electron beams interacting with an undulator, i.e., alternating sinusoidal static magnetic field [4]. Later a proof-of-concept experiment was demonstrated by Granatstein et al. [5]. In this paper, the term relativistic mirror was coined. They used a pulsed electron gun with the voltage of 1 MV and the duration of 60 ns. A radio frequency (RF) pulse was incident on the incoming electron beam to generate Doppler shifted radiation. The reflection of the radiation in coherent manner was not clearly mentioned as such short electron pulses were not available at that time.

The latest accelerator advances allow generating electron beams having durations of tens of femtoseconds so that the coherent reflection from them will be expected to be in the terahertz-frequency range. For higher frequency radiation, the self-amplified spontaneous emission (SASE) regime of free-electron laser is now used at X-ray free-electron laser facilities [6]. In this regime, a tens of femtosecond electron bunch develops into many micro bunches with lengths of the order of the emitting radiation wavelength; thus this process can be considered to be equivalent to multiple moving electron mirrors.

Recently, Sasao proposed to use relativistic ion beams in storage rings as very bright gamma beam sources by the double Doppler effect [7]. The difference to electron beams is the larger cross section (∼${10}^9$ times compared to Thomson cross section) thanks to the internal structure of partially ionized ions.

3.2. Propagating Ionization Front

Another method was proposed by Semenova in 1967 [8], where an intense laser pulse can generate a propagating ionization front in gas media. Similarly a recombination front can be used. In these cases each electron does not have relativistic velocity but the front speed can be relativistic, such as the group velocity of the drive laser in media. The refractive index difference between the plasma and unionized media causes reflection. However, the scale length of the ionization front should be smaller than the incoming wavelength; otherwise the reflection coefficient decreases. This requires relatively high intensity and high contrast ratio for the pump laser.

The experiment of the transmission through the front was conducted by Kuo using two microwaves crossing in a gas filled chamber [9]. The frequency of 3.27 GHz was transmitted through plasma and the frequency upshift of 1.5 GHz was observed.

Savage et al. used an ultraviolet laser to produce an ionization front in a gas filled microwave cavity. The incoming radio frequency of the 34.8 GHz pulse was reflected and a large upshift of 116 GHz was detected [10].

This concept is further developed using a static electric or magnetic field as an input because the static field looks like a traveling wave in the rest frame of a moving mirror [11,12,13,14]. This concept is called the DC to AC converter (DARC) and has been demonstrated. This can be a tunable electromagnetic radiation source in the THz regime.

Note that the transmitted light also undergoes the frequency upshift as ${\omega }_t=\omega [1+{\omega }_p^2/(4{\omega }^2)]$, where ${\omega }_t$ is the transmitted frequency and ${\omega }_p$ is the plasma frequency.

3.3. Moving Boundary of Impedance in Nonlinear Transform Line

Itoh and Soda showed another implementation of a moving boundary in a simple setup in 1979 [15]. They used a nonlinear transmission line loaded with variable capacitance diodes. The speed of the boundary was estimated and was ∼20% of the speed of light. In the experiment a transmitted microwave was detected instead of the reflected one because the parameters used in the experiment did not allow the reflection. A microwave of 200 MHz was transmitted to upshifted radiation of ∼230 MHz and downshifted to 180 MHz in good agreement with the theory. Note that there exists a transmitted wave in this case and it can be upshifted in a similar way as described in the previous section.

3.4. Moving Boundary of Electron-Hole Plasma in Semiconductors

In semiconductors electron-hole pairs are created by irradiating light whose photon energy is higher than the band gap of the semiconductor. The electron-hole plasma front serves as a moving boundary and thus can reflect incoming long-wavelength radiation [16]. This scheme was later well demonstrated by Bae et al. in 2009 [17]. They used a 532-nm Nd:YAG laser pulses to excite moving mirrors on silicon-on-insultator substrate. The incident mirowaves ranging from 9 GHz to 18 GHz were successfully upshifted to 40–68 GHz showing the upshifting factor of 3.82.

Recently, a Ti:sapphire (centered at 0.8 μm) was used as a pump and THz radiation was reflected by the moving carrier in silicon [18]. Kohno et al. used a Ti:sapphire laser (1.5 mJ, 800 nm, 55 fs) to generate carriers in a silicon target and counter-propagating THz waves (centered at 0.52 THz). They detected the reflected pulse by using the electro-optical sampling (EOS) method. The EOS provided the reflected waveform. The upshift factor in the experiment was 1.18 ± 0.02, which is smaller than the theoretical estimate (1.8 ± 0.6). They suggested the reduction of the upshift factor was due to the prepulse that preceded the main (highest peak) pulse in time.

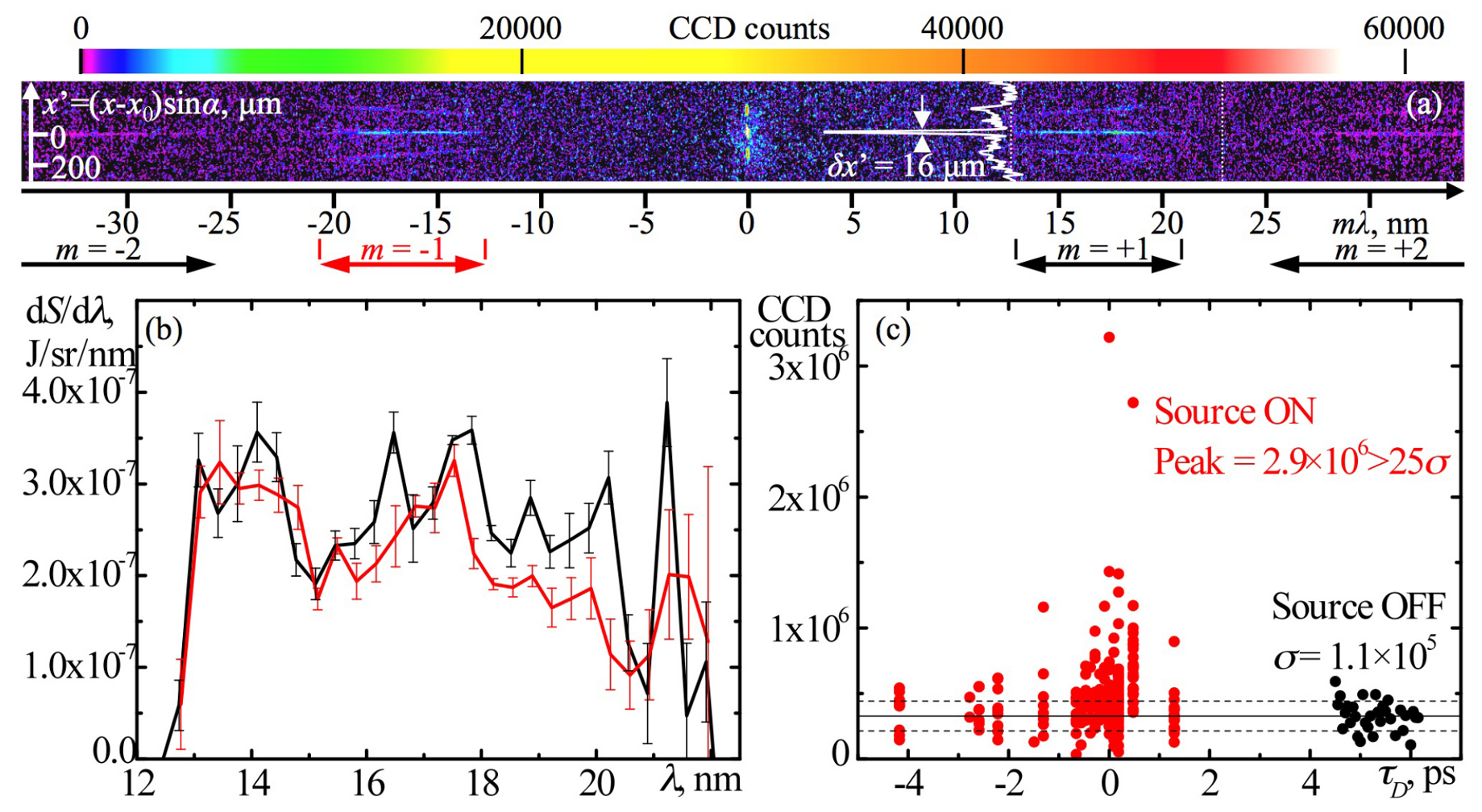
3.5. Oscillating Mirror/Sliding Mirror

When an intense laser is irradiated onto a solid, an electron sheet coherently moves perpendicular to the surface of the target. This electron sheet can serve as an oscillating mirror. The oscillation leads to the Doppler up- and down-shift of the frequency [19]. The model also predicts harmonics generation from such mirrors. In addition, attosecond pulse trains are expected to be generated during the interaction using particle-in-cell (PIC) simulations [20,21].

The sliding mirror model is similar to the oscillating mirror however, the plasma density is higher so that the electron sheet moves not along the target normal, but along the target surface (sliding). Within the model Pirozhkov et al. analyzed and found the optimum condition for generating attosecond pulses [22,23].

The reflection from oscillating mirrors was demonstrated by Dromey et al. in 2006 using a high-contrast 10²⁰ W/cm² intensity laser pulse with a double plasma mirror [24]. They observed up to 238th harmonic of the initial laser frequency where the spectrum decays with a power law as expected by the theory. Later Dromey et al. observed nearly diffraction limited harmonics radiation in the wavelength of 20–40 nm [25].

Simulations and experiments [26] suggest that reflected pulses exhibit attosecond pulse trains and thus such radiation can be used for ultrafast dynamics of matter. Isolated attosecond pulses can also be generated [23] or selected from the attosecond pulse trains [27].

3.6. A Thin Foil Mirror Driven by an Intense Laser Light Pressure

Esirkepov et al. proposed that a thin solid-density foil serves as double-sided accelerating mirror [28]. Double-sided means that the front surface, where an intense drive pulse shines, reflects the drive pulse and the frequency is downshifted while the rear surface works as an upshifting mirror for the incoming laser. This effect will be dominant when the drive pulse is intense enough to trigger a radiation pressure acceleration of the foil. Kulagin et al. [29] proposed using a thin electron layer pushed out of the thin foil target by the laser pulse as a relativistic mirror for frequency up-shifting of the counter-propagating electromagnetic wave. The stability of such mirrors was analyzed by Bulanovit et al. [30].

A part of the principle of the method was demonstrated by Kiefer et al. in 2013 using 10- and 50-nm-thick foils as targets [31]. An intense driving pulse (∼5 J, 55 fs) was focused onto the target at the peak intensity of $6\times {10}^{20}$ W/cm² and another weak laser pulse (∼2 mJ, 55 fs) was focused onto the opposite side of the target at the intensity of $1\times {10}^{15}$ W/cm². Frequencies of 8th to 15th harmonics of the fundamental laser frequency were observed as shown in Figure 2. The wavelengths of the reflected signal ranged from 50 nm to 100 nm. The upshift factor was ∼10 and the reflectivity of the mirror was estimated to be 5 × ${10}^{-5}$ in terms of photon number.

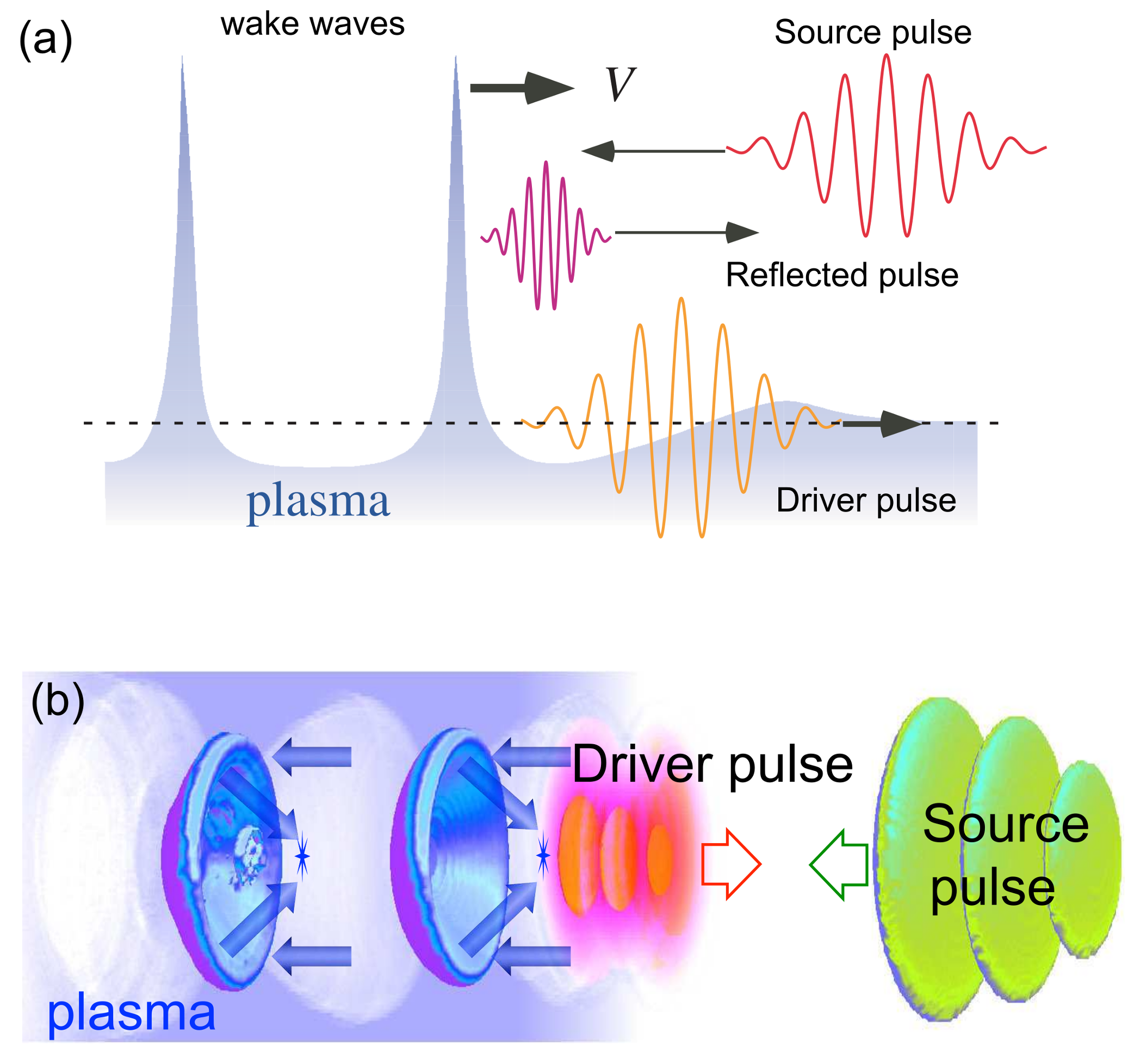
3.7. Breaking Wake Waves

Bulanov et al. proposed to use a breaking wake wave driven by an intense, short laser pulse as a relativistic mirror in 2003 [32]. The electron density driven by the laser pulse becomes spiky as seen in Figure 3 and even has a bent (focusing parabolic) structure due to the nonlinear response of the plasma electron oscillation caused by the Gaussian intensity profile of the drive laser as seen in Figure 3b. Thus, the reflected pulse is not only upshifted but focused by this moving parabolic mirror.

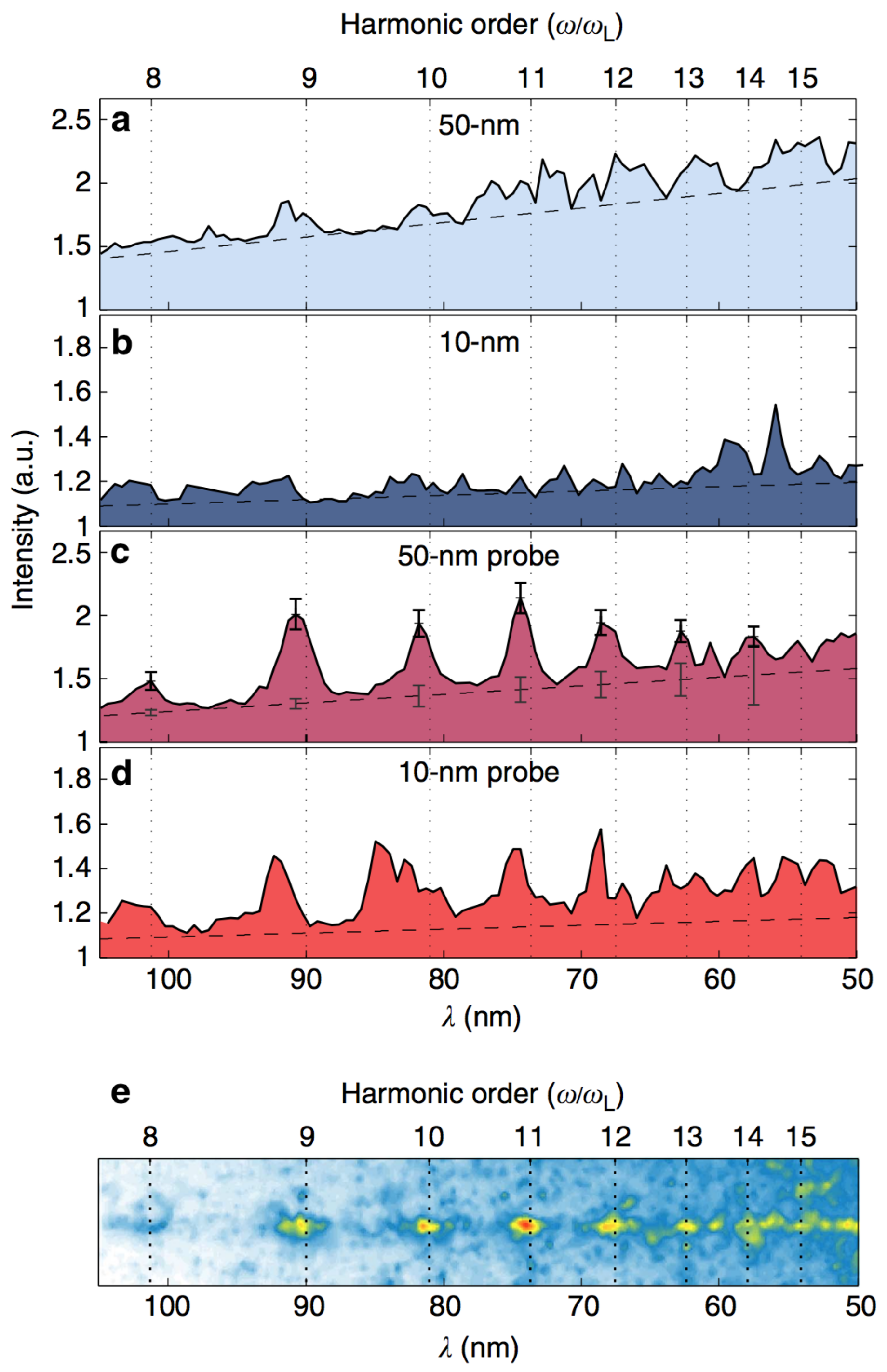
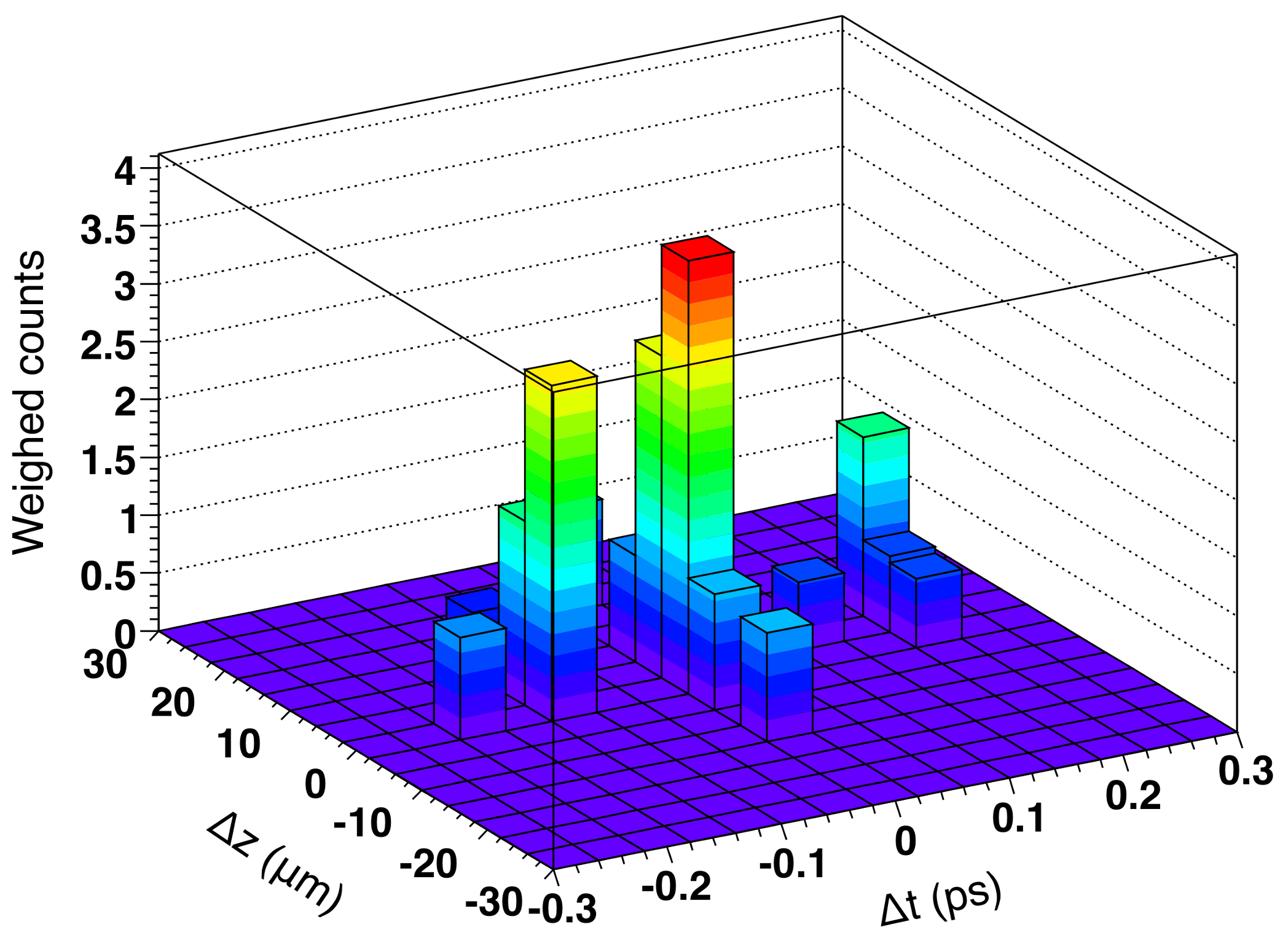
A proof-of-principle experiment was performed using a Ti:sapphire laser by Kando et al. and Pirozhkov et al. in 2007 [33,34]. A 210 mJ, 76 fs driver pulse produced wake waves in helium plasma and the source pulse was incident to the wake or relativistic flying mirrors at the angle of 45°. The reflected signals were observed when the two pulses collided in time and space properly as shown in Figure 4. The upshift factors were 50–110.

The reflectivity of the mirror is theoretically given in [32,35,36]. For a delta-function and cusp density profiles, the reflectivities in terms of photon number are scaled as ${\gamma }^{-3}$ and ${\gamma }^{-4}$, respectively. This theoretical estimate of the reflectivity for the cusp case was confirmed in 2009 [37,38]. In the experiment the obtained spectra are shown in Figure 5 and the estimated reflectivity was $R_{cusp}=2.3\times {10}^{-5}$, which is nearly half of the theoretical calculation.

3.8. Superluminal Mirrors

One may consider what happens if the velocity of the mirror is greater than the speed of light. Since the moving front is faster than the propagating wave there is no reflected pulse. There exist two propagating waves with the frequency shifted. This is not a fantasy, but such superluminal mirrors can actually be realized in ionizing plasma, with wake waves propagating in plasma having a density up-ramp, etc. Lampe et al. discussed this problem [39]. Later, the superluminal mirror theory was developed by Bu et al. [40].

Hashimshony et al. demonstrated the reflection by superluminous ionization fronts in 2001 [41] using semiconductor plasma, because the refractive index is larger than unity; thus it is easy to fullfil superluminous conditions. The ionization front was created by irradiating a Ti:sapphire laser (0.8 μm, 100 fs) onto the target with the angle of incidence of 20 degrees. In the experiment, an electrostatic field was applied in the semiconductor and was converted into an electromagnetic wave (0.3–10 THz).

4. Applications of Relativistic Flying Mirrors

RFMs have attracted many researchers for a century mainly because of the interest in the mechanism of how to realize them. Later researchers conceived that this scheme is favorable to obtain higher frequency radiation and short pulse duration. As the technology progresses the frequency range shifts from microwave to soft X-rays increasing the importance of the applications. Recent demonstration tends to obtain attosecond, coherent X-ray pulses using short infrared laser pulses as source beams.

In order to reflect incoming electromagnetic radiation completely, the mirror should be dense enough, or overdense. The plasma density should be higher than the critical density $n_e=\pi /(r_e{\lambda }^2)$, where $r_e$ is the classical electron radius and $\lambda$ is the wavelength of the radiation in the mirror rest frame. For a thin foil, the total reflectivity condition is derived by Vshivkov et al. [42]. As we have seen in the previous section, many RFMs are created by irradiating intense infrared laser pulses, thus creating high reflectivity is difficult for high frequency radiation since the frequency is upshifted. Thus the ionization front method works in the longer wavelength region of THz. In contrast, the oscillating mirror or wake waves use a highly nonlinear shape of the density profile. Even though the density is lower than the critical density, the nonlinear shape (singularities) can reflect the electromagnetic waves. This effect can be considered a manifestation of burst intensification by singularity emitting radiation (BISER) [43], where the singularity created by the driver pulse is driven by the source pulse.

Although the demonstrated photon numbers in the experiments are still low for practical applications the scaling law can suggest that more photons are expected. Increasing the photon number is left for future development. Note that there exists an application for improving temporal coherence of X-ray free-electron lasers (XFEL) by seeding into the XFEL amplifier. So far the seeding from high order harmonics using near infrared laser pulses is limited to around the tens of nanometer range. The required seed power $P_{seed}$ for the XFEL must be much larger than its shot noise power $P_n$. In [44] $P_{seed}\approx$ 1.5 MW and $P_n\approx$ 5 kW is shown for a seeded XFEL at ∼10 keV. A relativistic flying mirror operated at $\gamma$ = 50 with a source pulse of ${\lambda }_s$ = 800 nm, 100 mJ, 100 fs with a driver pulse of 800 nm, $a_0$ = 10 (6 J, 20fs) can produce a reflected pulse of approximately 10 GW. Therefore, the RFM can offer shorter wavelength, fully coherent X-ray pulses for seeded XFELs.

The second application is using these mirrors for intensifying the radiation as it was proposed by Bulanov et al. [32]. As we see the RFMs offer shortening the pulse duration by the $4{\gamma }^2$ factor. The reflection coefficient in terms of photon number is $\sim {\gamma }^{-3}-{\gamma }^{-4}$, which means the energy reflection coefficient is $\sim {\gamma }^{-1}-{\gamma }^{-2}$. Taking advantage of the focusing property of the RFMs we will obtain an additional intensification factor of ${\gamma }^2$, because we can assume that the reflected pulse can be focused down to the diffraction limited size in the rest frame of the mirror, i.e., $r=\lambda /(2\gamma )$. Including all the above effects, we can still expect the intensification of the reflected pulse to be ${\gamma }^2-{\gamma }^3$. Before reaching a high intensity, like the Schwinger limit, Koga et al. discussed the potential usage of RFM for measuring photon-photon scattering [45], which is a long-standing problem in physics. In this view, spherical relativistic mirrors [46] have certain advantages. Although the high upshifted photon energy of 19.6 keV, alignment, and spherical focusing present challenges, spherical relativistic mirrors colliding three photon beams for stimulated scattering at driver pulse powers of 655 TW for each beam and a total source pulse energy of 3 mJ (1 mJ per pulse) could achieve 2.96 scattered photons per shot [45].

Using the RFM concept to test the black hole information paradox has been recently proposed by Chen and Mourou [47]. The fundamental idea is that accelerating mirrors can mimic black holes using the equivalence principle. Once such a situation can be obtained in a terrestrial environment, controlled experiments will provide much more knowledge about black hole physics.

5. Conclusions

We have reviewed the topics on the reflection from mirrors moving nearly at the speed of light. Such relativistic flying mirrors have been analyzed theoretically, numerically, and experimentally during the century after the discovery of special relativity.

Recently, several schemes to realize such relativistic flying mirrors have been proposed and fundamental features of the RFMs have been demonstrated. The upshifting factors demonstrated in the experiments range from 1 to 100 and even 1000 when an oscillating mirror was used. The reflectivities are measured to be on the order of 10⁻⁵ in terms of photon number but more systematic measurement is demanded. In addition, an increase of the reflected photon number is critical for practical applications for ultrafast imaging, etc.