Numerical Investigation of the Axial Load Capacity of Cold-Formed Steel Channel Sections: Effects of Eccentricity, Section Thickness, and Column Length
Abstract
1. Introduction
2. The Design Criteria Are Based on the Direct Strength Method (DSM)
2.1. Global Buckling
2.2. Local Buckling
2.3. Distortional Buckling
3. Finite Element Modelling (FEM)
3.1. General
3.2. Mesh Size and Element Type
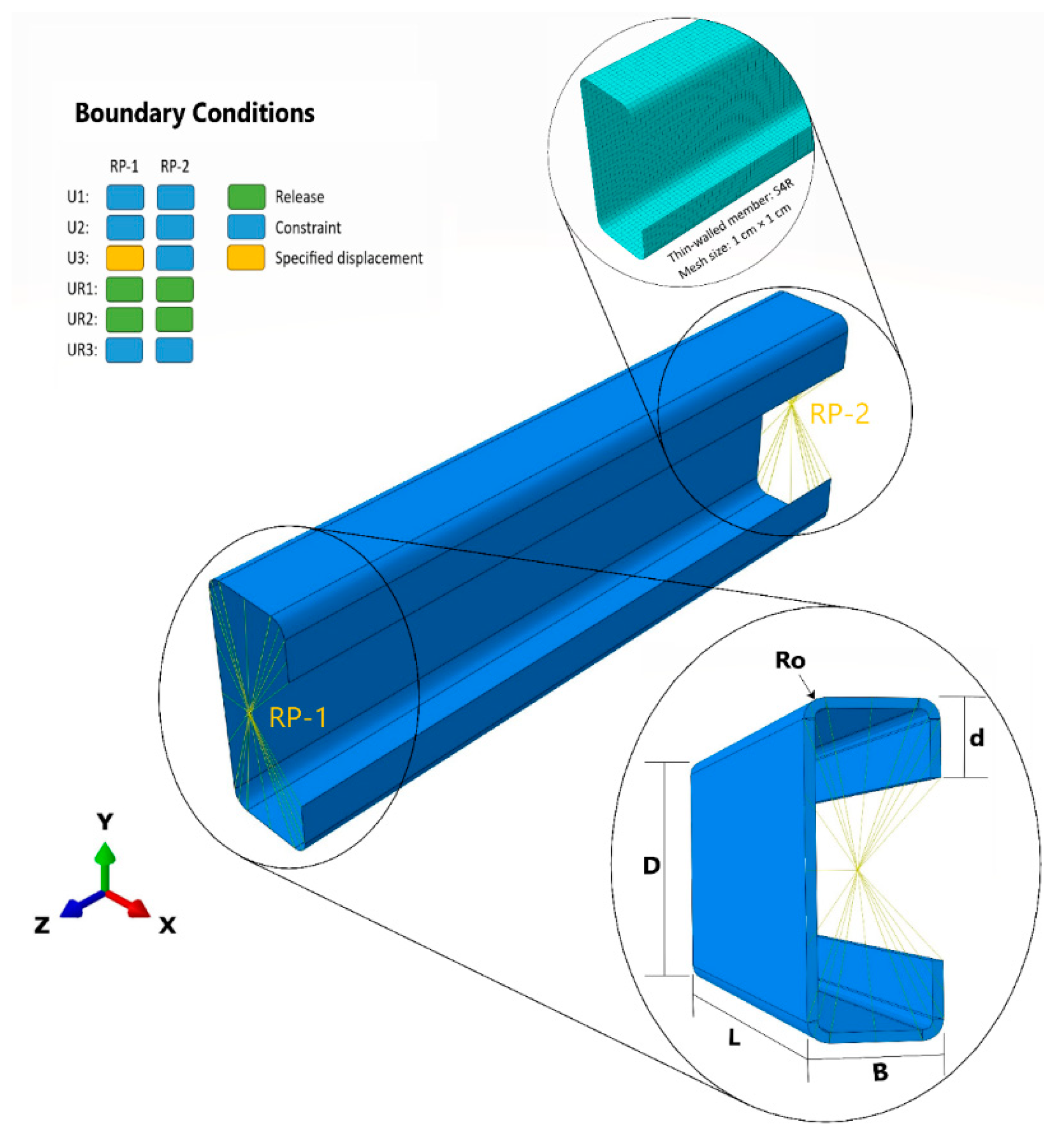
3.3. Loading Method and Boundary Conditions
4. Validation of the Developed Finite Element Models
4.1. Specimen Design
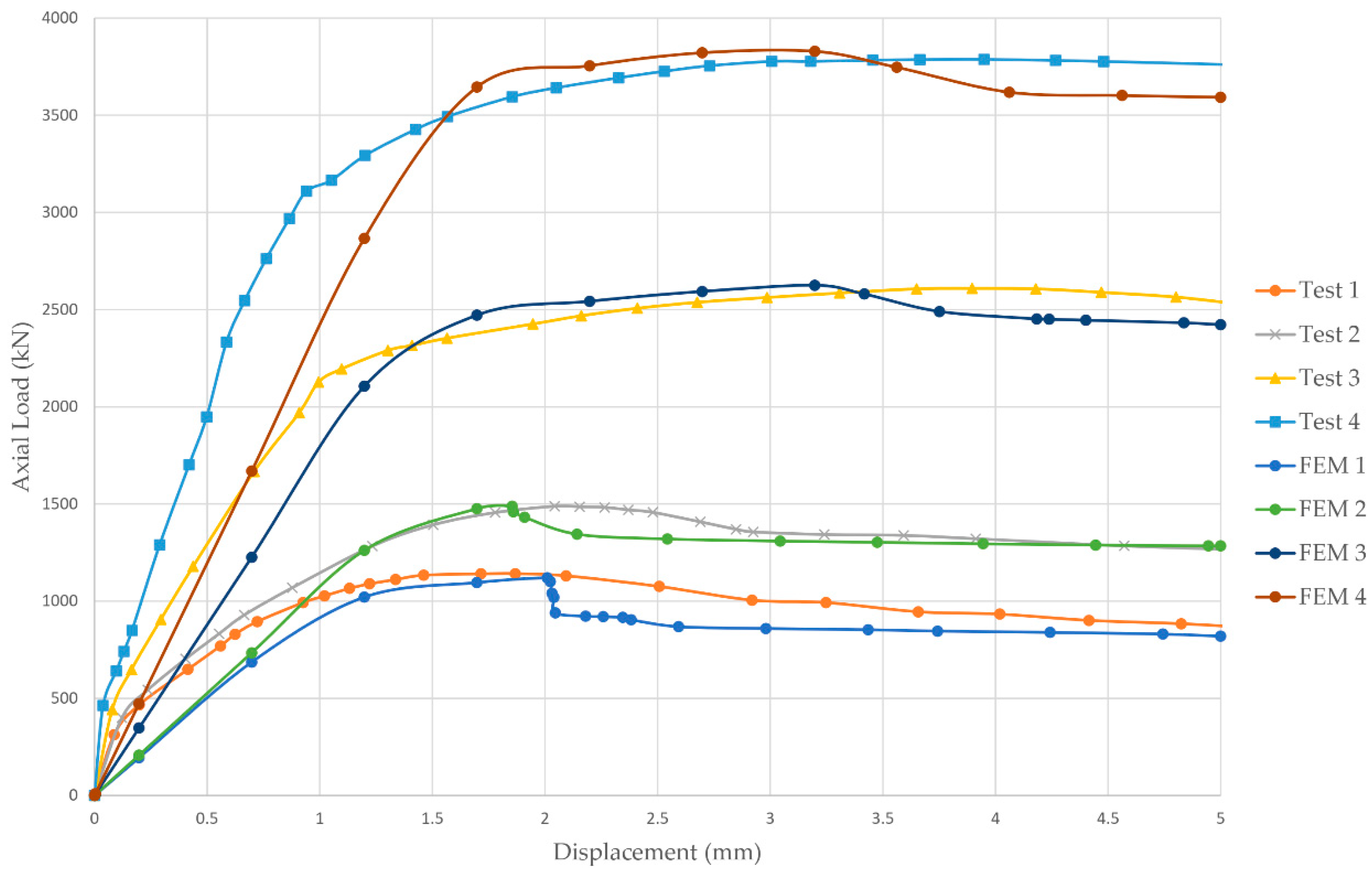
4.2. Test Results Analysis
4.3. Material Properties and Geometry
4.4. Comparison of Various Findings
4.5. Verification of Finite Element Model
5. Parametric Study and Result
5.1. General
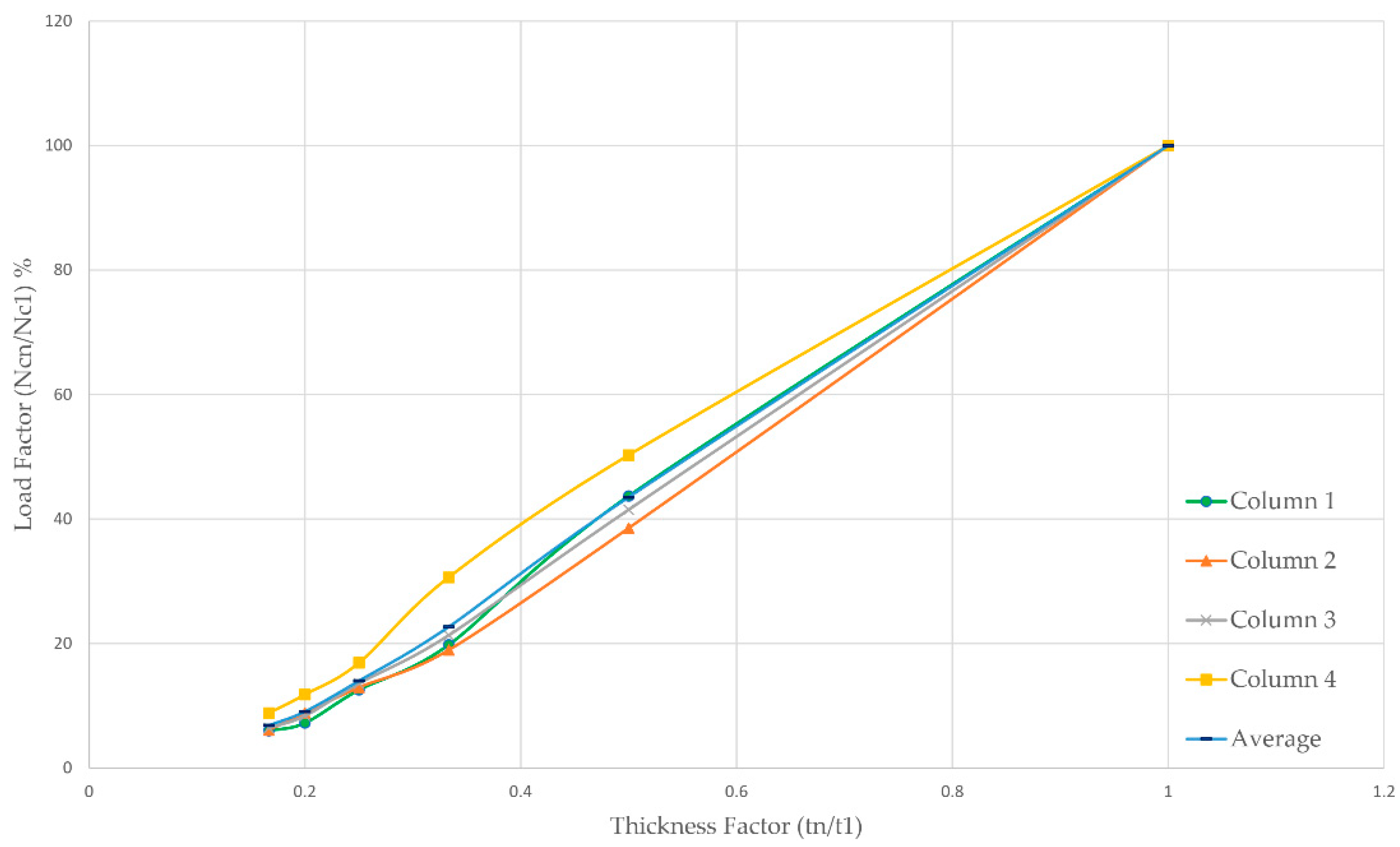
5.2. The Effect of Member Thickness
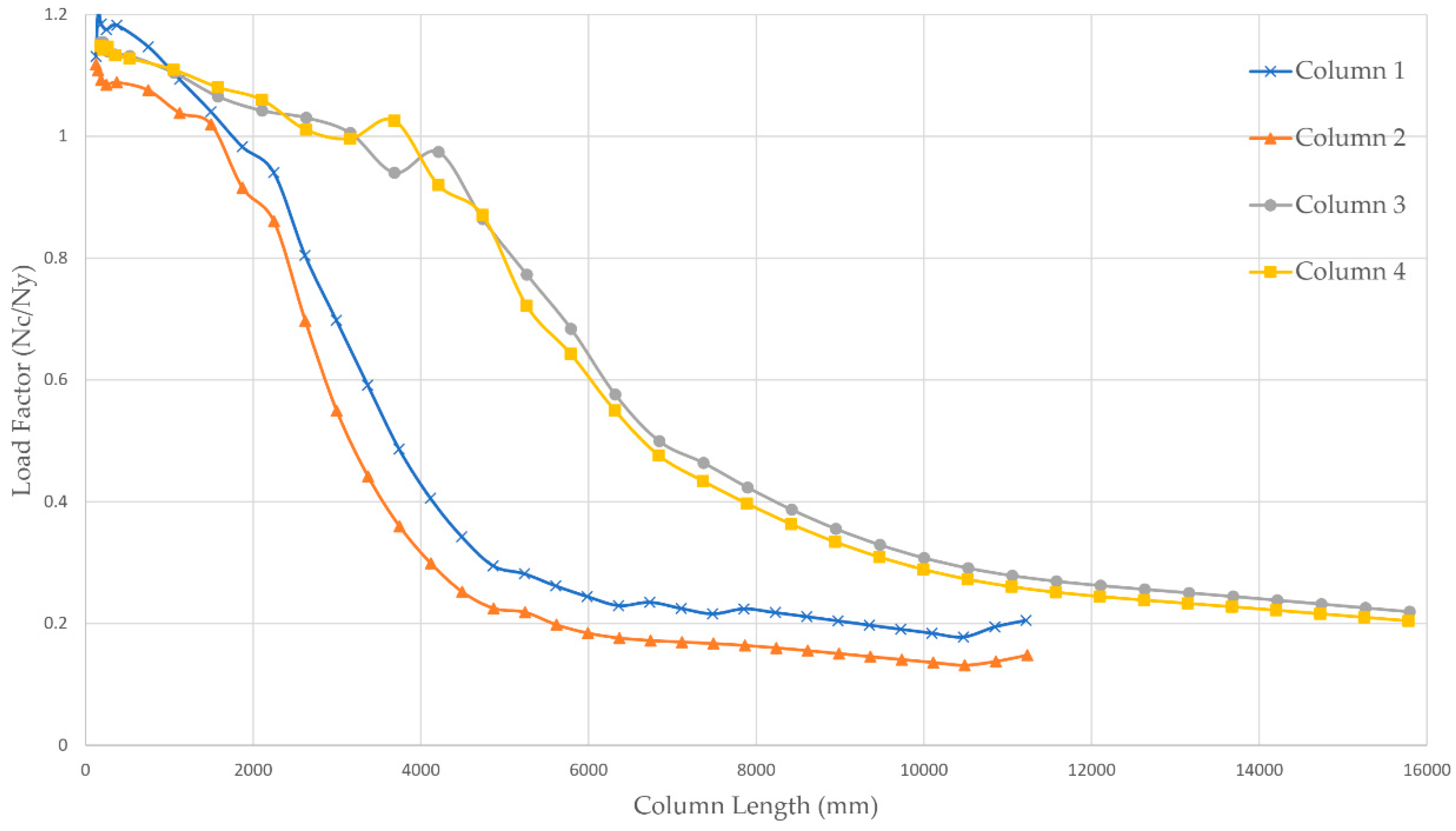
5.3. The Effect of Member Length
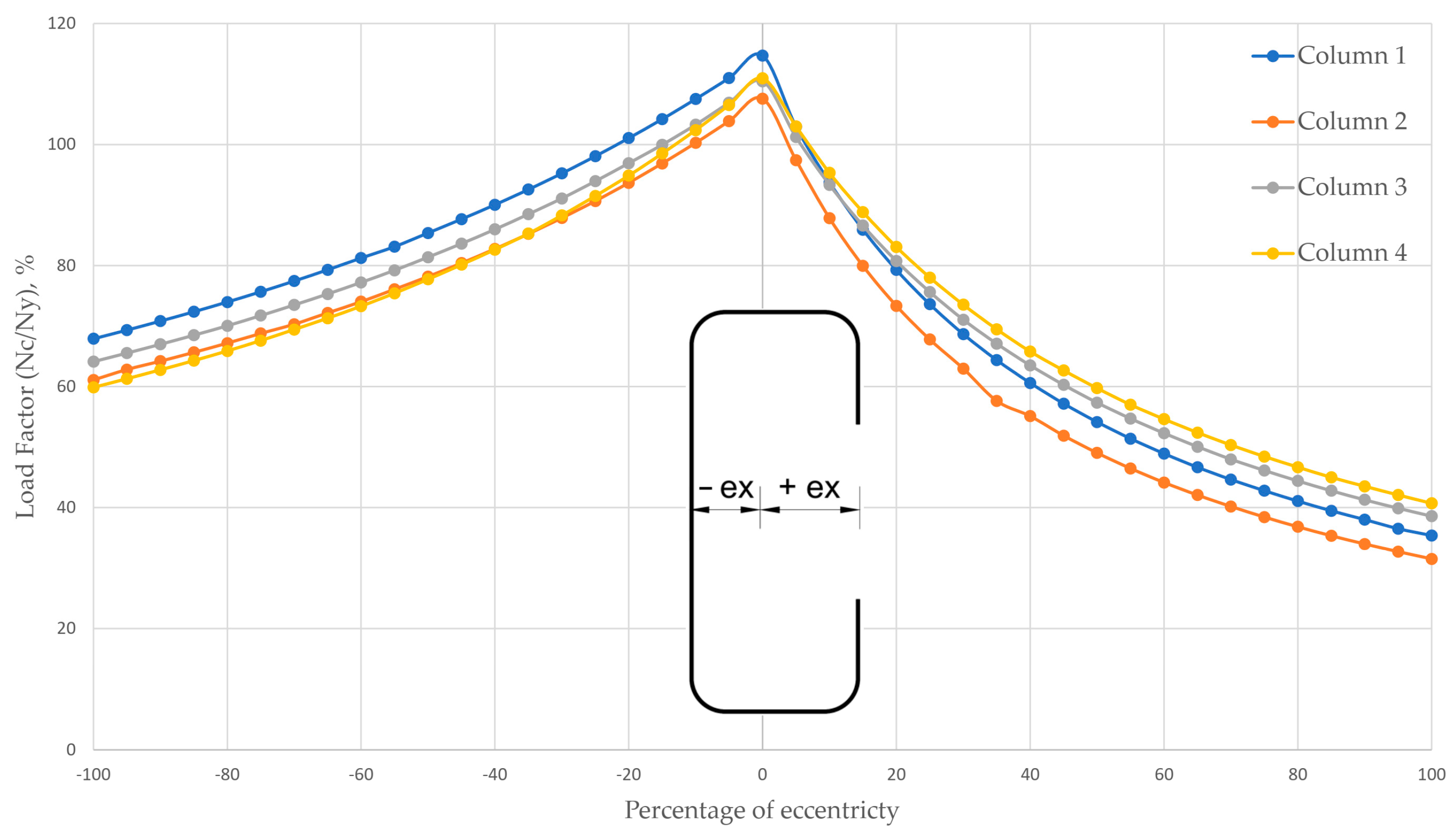
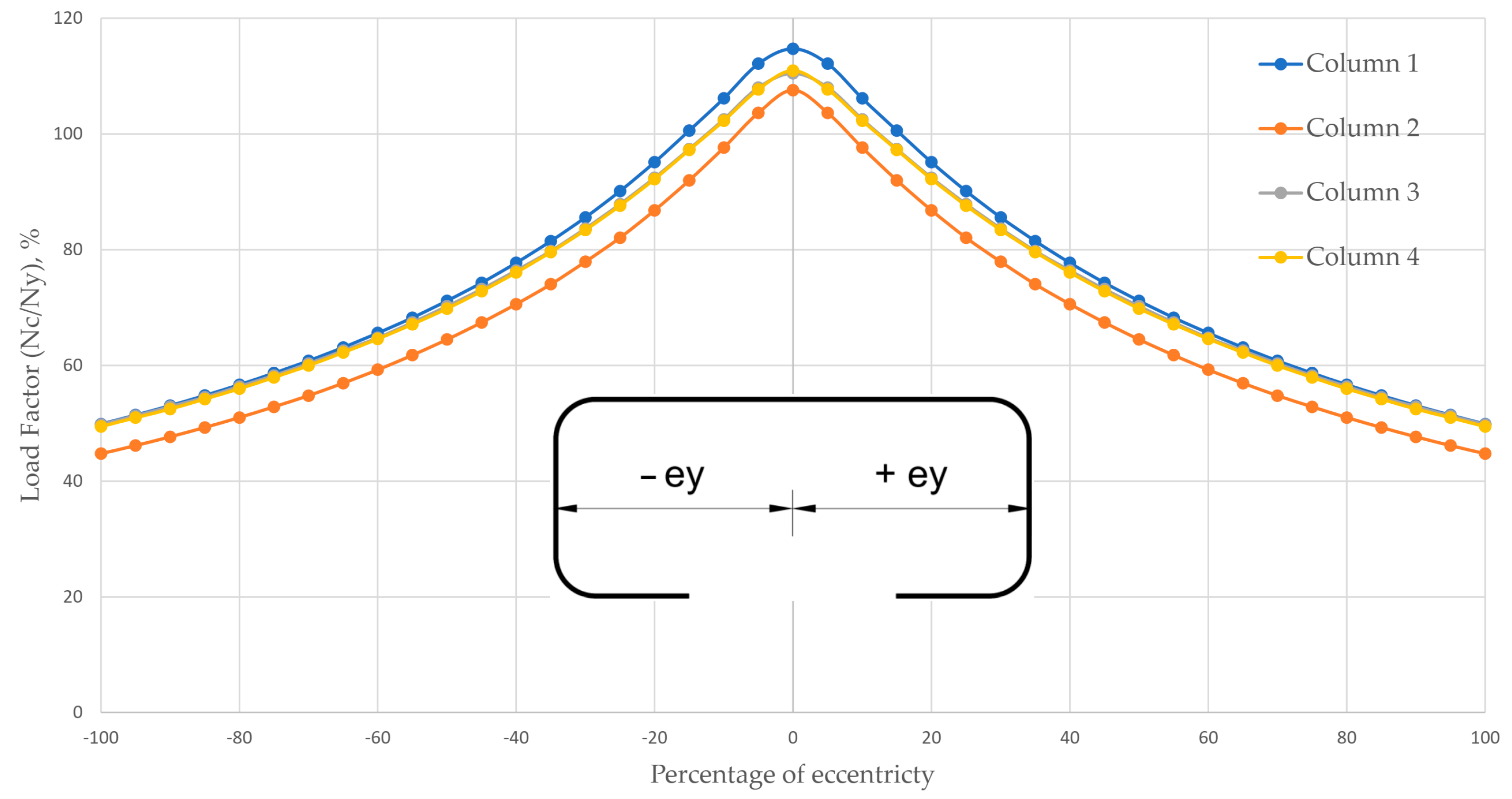
5.4. The Effect of Eccentricity from the Centroid
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Meaning |
| AS/NZS | Australian/New Zealand Standard |
| AISI | American Iron and Steel Institute |
| DSM | Direct Strength Method |
| EWM | Effective Width Method |
| FEM | Finite Element Model |
| CFS | Cold-Formed Steel |
| CFSC | Cold-Formed Steel Channel |
| GMNIA | Geometric and Material Nonlinear (Second-order) Inelastic Analysis with Imperfections |
| RP | Reference Point |
| S | Sample standard deviation |
| LB | Local Buckling |
| DB | Distortional Buckling |
| GB | Global Buckling |
| F | Flexural |
| T | Tortional |
| FT | Flexural-Tortional |
| LD | Local-Distortional |
| λc; λl; λd | non-dimensional slenderness |
| Nce | The nominal member capacity of a member in compression for flexural, torsional or flexural-torsional buckling |
| Noc | Least of the elastic compression member buckling load in flexural, torsional and flexural-torsional buckling |
| Ny | Nominal yield capacity of the member in compression |
| Ncl | The nominal member capacity of a member in compression for local buckling |
| Nol | Elastic local buckling load |
| Ncd | The nominal member capacity of a member in compression for distortional buckling |
| Nod | Elastic distortional compression member buckling load |
| fy | Compressive yield stress |
| Ag | Gross area of the cross-section |
References
- Sang, L.; Zhou, T.; Zhang, L.; Zhang, T.; Wang, S. Local buckling in cold-formed steel built-up I-section columns: Experiments, numerical validations and design considerations. Structures 2023, 47, 134–152. [Google Scholar] [CrossRef]
- Zhao, J.; Lai, B.L.; Fan, S.; Liu, M.; Li, C. Numerical simulation of local-distortional buckling behavior of lipped C-section stainless steel columns. J. Constr. Steel Res. 2023, 211, 108148. [Google Scholar] [CrossRef]
- Rasmussen, K.J.R. Bifurcation of locally buckled members. Thin-Walled Struct. 1997, 28, 117–154. [Google Scholar] [CrossRef]
- Dai, Y.; Roy, K.; Fang, Z.; Raftery, G.M.; Ghosh, K.; Lim, J.B.P. A critical review of cold-formed built-up members: Developments, challenges, future directions. J. Build. Eng. 2023, 76, 107255. [Google Scholar] [CrossRef]
- Khezri, M.; Rasmussen, K.J.R. Buckling Mode Decomposition of Built-up Members by the Modal Finite Strip Method (mFSM). In Proceedings of the Annual Stability Conference Structural Stability Research Council, Charlotte, NC, USA, 11–14 April 2023; Available online: https://cloud.aisc.org/SSRC/2023/Khezri_et_al_SSRC_2023.pdf (accessed on 18 August 2024).
- Qadir, S.J.; Nguyen, V.B.; Hajirasouliha, I. Design optimisation for cold rolled steel beam sections with web and flange stiffeners. J. Constr. Steel Res. 2024, 213, 108375. [Google Scholar] [CrossRef]
- Selvam, J.; Vajravelu, A.; Nagapan, S.; Arumugham, B.K. Analyzing the Flexural Performance of Cold-Formed Steel Sigma Section Using ABAQUS Software. Sustainability 2023, 15, 4085. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, S.; Li, C.; Peng, J.; Li, J. Research on the local-distortional interaction buckling capacity of stainless steel lipped C-section columns. Structures 2023, 48, 2003–2023. [Google Scholar] [CrossRef]
- Martins, A.D.; Peres, N.; Jacinto, P. Gonçalves An Assessment of the Eurocode 3 Simplified Formulas for Distortional Buckling of Cold-Formed Steel Lipped Channels. Appl. Sci. 2024, 14, 4924. [Google Scholar] [CrossRef]
- Li, S.; Liang, Y.; Zhao, O. Cross-section behaviour and design of press-braked ferritic stainless steel channel sections under combined compression and major-axis bending moment. Thin-Walled Struct. 2023, 188, 110775. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Y.; Zhao, O. Cross-sectional behaviour of press-braked S690 high strength steel slender channel section stub columns under minor-axis combined loading. J. Constr. Steel Res. 2023, 210, 108050. [Google Scholar] [CrossRef]
- Ma, J.L.; Pandey, M.; Chan, T.M.; Young, B. Design of cold-formed high strength steel square and rectangular hollow section beam–columns. Thin-Walled Struct. 2023, 185, 110483. [Google Scholar] [CrossRef]
- Li, Q.Y.; Young, B. Design of cold-formed steel built-up open section members under combined compression and bending. Thin-Walled Struct. 2022, 172, 108890. [Google Scholar] [CrossRef]
- He, Z.; Peng, S.; Zhou, X.; Li, Z.; Yang, G. Zhang Design recommendation of cold-formed steel built-up sections under concentric and eccentric compression. J. Constr. Steel Res. 2024, 212, 108255. [Google Scholar] [CrossRef]
- He, Z.; Peng, S.; Zhou, X.; Yang, G.; Schafer, B.W. Failure characteristics of cold-formed steel built-up sections with web stiffeners under axial and eccentric compression. Thin-Walled Struct. 2023, 182, 110269. [Google Scholar] [CrossRef]
- Zhao, J.; He, J.; Chen, B.; Zhang, W.; Yu, S. Test and direct strength method on slotted perforated cold-formed steel channels subjected to eccentric compression. Eng. Struct. 2023, 285, 116082. [Google Scholar] [CrossRef]
- AISI S100-16 (R2020) w/S3-22; North American Specification for the Design of Cold-Formed Steel Structural Members 2016 Edition (Reaffirmed 2020) with Supplement 3, 2020 Edition. AISI: Washington, DC, USA, 2016. Available online: https://www.buildusingsteel.org/wp-content/uploads/2023/06/AISI-S100-16-2020-wS3-22.pdf (accessed on 22 August 2024).
- AISI S100-16 (2020) w/S2-20; North American Specification for the Design of Cold-Formed Steel Structural Members 2016 Edition (Reaffirmed 2020) with Supplement 2, 2020 Edition. AISI: Washington, DC, USA, 2016. Available online: https://www.buildusingsteel.org/wp-content/uploads/2023/06/AISI-S100-16-2020-wS2-20.pdf (accessed on 22 August 2024).
- AS/NZS 4600: 2018; Cold-Formed Steel Structures. AS: Sydney, Australia; NZS: Wellington, New Zealand, 2018. Available online: https://www.standards.govt.nz/shop/asnzs-46002018 (accessed on 22 August 2024).
- Bilheiro, E.; Filho, F.; Landesmann, A.; Camotim, D. DSM design of CFS lipped channel columns undergoing distortional-global interaction at elevated temperatures. In Proceedings of the Annual Stability Conference Structural Stability Research Council, Charlotte, NC, USA, 11–14 April 2023; Available online: https://www.researchgate.net/publication/370400597_DSM_Design_of_CFS_Lipped_Channel_Columns_undergoing_Distortional-Global_Interaction_at_Elevated_Temperatures (accessed on 22 August 2024).
- He, Z.; Jian, Y.; Zhou, X.; Jin, S. Local-distortional interactive behavior and design of cold-formed steel C-sections with & without slotted holes. J. Build. Eng. 2023, 79, 107812. [Google Scholar] [CrossRef]
- AISI D100-08; Cold-Formed Steel Design. American Iron and Steel Institute: Washington, DC, USA, 2008. Available online: https://scholarsmine.mst.edu/ccfss-aisi-spec/159/ (accessed on 22 August 2024).
- Yu, W.-W.; LaBoube, R.A.; Chen, H. Cold-Formed Steel Design, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020; Available online: https://www.wiley.com/en-us/Cold-Formed+Steel+Design%2C+5th+Edition-p-9781119487395 (accessed on 22 August 2024).
- Dubina, D.; Ungureanu, V.; Landolfo, R. Eurocode 3: Part 1–3, 1st ed.; ECCS—European Convention for Constructional Steelwork: Brussels, Belgium, 2012. [Google Scholar]
- Georgantzia, E.; Gkantou, M.; Kamaris, G.S. Aluminium alloy channel columns: Testing, numerical modelling and design. Thin-Walled Struct. 2023, 182, 110242. [Google Scholar] [CrossRef]
- Ananthi, G.B.G.; Roy, K.; Ghosh, K.; Poologanathan, K.; Lim, J.B.P. An investigation on stiffened cold-formed steel unequal angle box section columns. J. Build. Eng. 2023, 76, 106989. [Google Scholar] [CrossRef]
- Mei, Y.; Cui, Y.; Ma, C.; Sun, Y.; Su, A. Tests, numerical simulations and design of G550 high strength cold-formed steel lipped channel section columns failing by interactive buckling. Thin-Walled Struct. 2023, 192, 111172. [Google Scholar] [CrossRef]
- Zhang, P.; Alam, M.S. Assessment of buckling strength curves in Direct Strength Method for estimating axial strengths of Cold-formed Steel members considering average yield stresses of cross-sections Thin-Walled Struct. 2023, 188, 110823. Thin-Walled Struct. 2023, 188, 110823. [Google Scholar] [CrossRef]
- Chen, B.; Wang, Y.; Lim, J.B.P. Behaviour And Design of Cold-Formed Steel Channel Sections with Strengthened Web Holes Under Different Loadings: A Review. In Proceedings of the Ninth International Conference on Thin-Walled Structures—ICTWS2023, Sydney, Australia, 29 November–1 December 2023; Available online: https://www.ictws2023.org.au/wp-content/uploads/2023/11/48308-Chen.pdf (accessed on 18 August 2024).
- Dassault Systèmes. ABAQUS. 2024. Available online: https://www.3ds.com/products/simulia/abaqus (accessed on 18 August 2024).
- Kechidi, S.; Fratamico, D.C.; Schafer, B.W.; Castro, J.M.; Bourahla, N. Simulation of screw connected built-up cold-formed steel back-to-back lipped channels under axial compression. Eng. Struct. 2020, 206, 110109. [Google Scholar] [CrossRef]
- Li, Q.Y.; Young, B. Numerical investigation and design of cold-formed steel built-up section beam-column members under moment gradients. Eng. Struct. 2023, 283, 115746. [Google Scholar] [CrossRef]
- Vy, S.T.; Mahendran, M.; Sivaprakasam, T. Built-up back-to-back cold-formed steel compression members failing by local and distortional buckling. Thin-Walled Struct. 2021, 159, 107224. [Google Scholar] [CrossRef]
- Fu, X.; Xu, W.; Yu, S.; Mei, X. Experimental Research on the Cold-Forming Effect of Cold-Formed Thick-Walled Steel. Buildings 2023, 13, 1201. [Google Scholar] [CrossRef]
- Hasanali, M.; Mojtabaei, S.M.; Hajirasouliha, I.; Clifton, G.C.; Lim, J.B.P. More accurate design equations for cold-formed steel members subjected to combined axial compressive load and bending. Thin-Walled Struct. 2023, 185, 110588. [Google Scholar] [CrossRef]
- He, Y.; Dai, L.; Ren, C. Buckling analyses of cold-formed steel lipped channel members under minor-axis eccentric load. J. Constr. Steel Res. 2023, 211, 108181. [Google Scholar] [CrossRef]
- Yılmaz, Y.; Öztürk, F.; Demir, S. Buckling behavior of cold-formed steel sigma and lipped channel section beam-columns: Experimental and numerical investigation. J. Constr. Steel Res. 2024, 214, 108456. [Google Scholar] [CrossRef]
- Miller, B.H.T.; Member, A.; Pekoz, T. Load-Eccentricity Effects on Cold-Formed Steel Lipped-Channel Columns. J. Struct. Eng. 1994, 120, 805–823. [Google Scholar] [CrossRef]
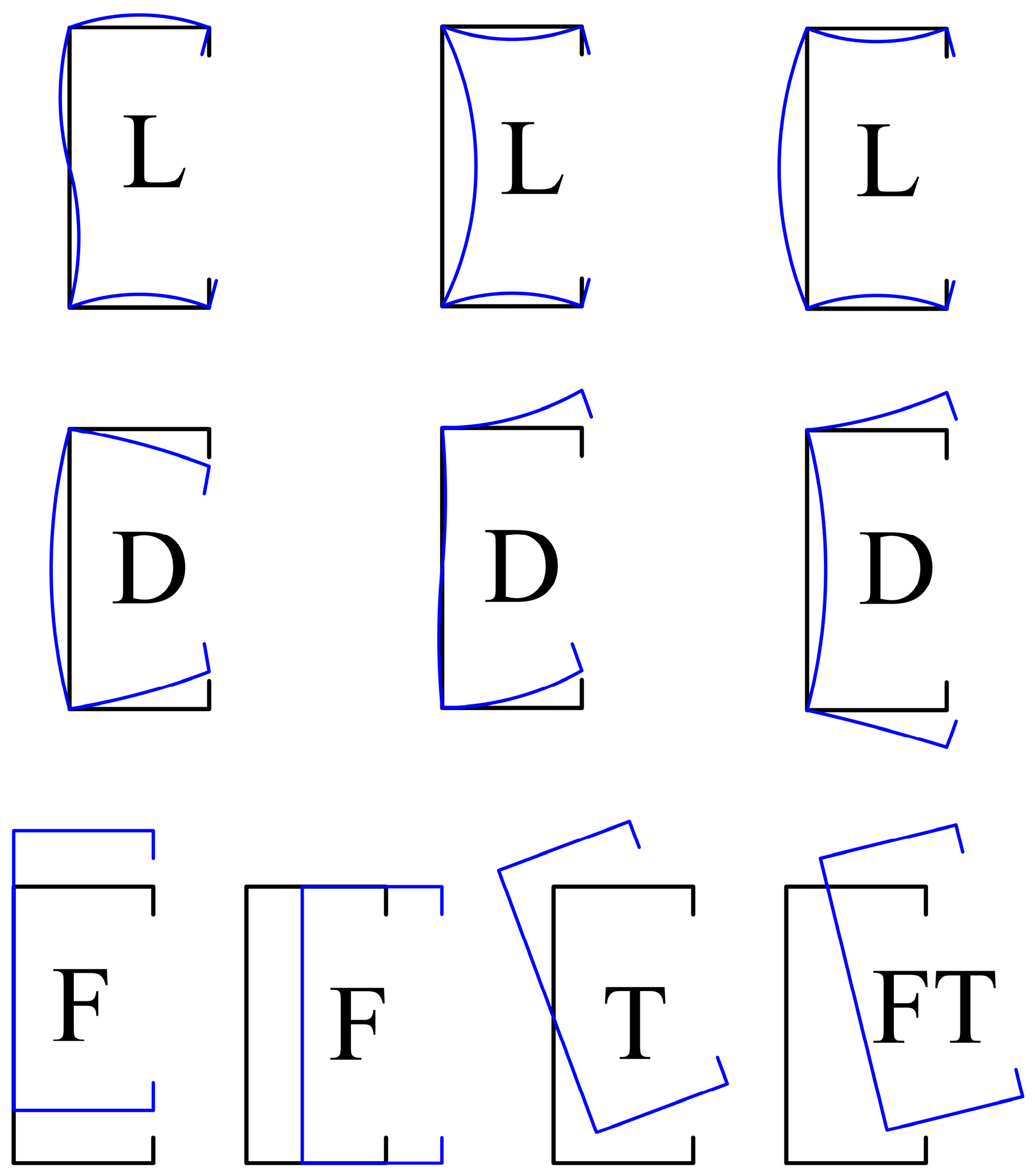


| Columns | D | B | d | t | Ro | L | X | Y | A | Fy | E | Ny |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mm | mm2 | MPa | GPa | kN | ||||||||
| Column 1 | 253.5 | 80.5 | 50.1 | 7.43 | 14.9 | 748 | 28.2 | 126.8 | 3461 | 297.9 | 202 | 1031 |
| Column 2 | 255.2 | 80.7 | 50.3 | 7.81 | 15.1 | 749 | 28.3 | 127.6 | 3645 | 381.6 | 205 | 1391 |
| Column 3 | 361.1 | 141.5 | 83.9 | 11.33 | 22.4 | 1053 | 53.7 | 180.6 | 8360 | 295.7 | 210 | 2472 |
| Column 4 | 343.5 | 144.8 | 97.1 | 15.51 | 30.1 | 1052 | 59.1 | 171.8 | 11274 | 316.3 | 208 | 3566 |
| Columns | Nc[AISI & AS/NZS] | Nc[TEST] | Nc[FEM] | Nc[FEM]/Nc[TEST] | Nc[AISI & AS/NZS]/Nc[TEST] |
|---|---|---|---|---|---|
| kN | kN | kN | % | % | |
| Column 1 | 944 | 1142 | 1073 | 94 | 83 |
| Column 2 | 1252 | 1488 | 1455 | 98 | 92 |
| Column 3 | 2338 | 2609 | 2536 | 97 | 90 |
| Column 4 | 3394 | 3787 | 3713 | 98 | 90 |
| Average | 96.8 | 88.5 | |||
| S | 0.0187 | 0.0401 |
| Columns | n = 1:6 | tn = t1/n | X | Ncn | Ncn/Nc1 |
|---|---|---|---|---|---|
| mm | mm | kN | % | ||
| Column 1 | 1 | 7.43 | 28.23 | 1073 | 100 |
| 2 | 3.72 | 27.92 | 469 | 44 | |
| 3 | 2.48 | 27.83 | 212 | 20 | |
| 4 | 1.86 | 27.78 | 135 | 13 | |
| 5 | 1.49 | 27.75 | 77 | 7 | |
| 6 | 1.24 | 27.73 | 64 | 6 | |
| Column 2 | 1 | 7.81 | 28.28 | 1455 | 100 |
| 2 | 3.91 | 27.96 | 561 | 39 | |
| 3 | 2.60 | 27.85 | 276 | 19 | |
| 4 | 1.95 | 27.80 | 188 | 13 | |
| 5 | 1.56 | 27.77 | 129 | 9 | |
| 6 | 1.30 | 27.75 | 89 | 6 | |
| Column 3 | 1 | 11.33 | 53.70 | 2536 | 100 |
| 2 | 5.67 | 53.38 | 1052 | 41 | |
| 3 | 3.78 | 53.27 | 541 | 21 | |
| 4 | 2.83 | 53.22 | 344 | 14 | |
| 5 | 2.27 | 53.19 | 212 | 8 | |
| 6 | 1.89 | 53.17 | 163 | 6 | |
| Column 4 | 1 | 15.51 | 59.12 | 3713 | 100 |
| 2 | 7.76 | 58.78 | 1867 | 50 | |
| 3 | 5.17 | 58.67 | 1138 | 31 | |
| 4 | 3.88 | 58.62 | 627 | 17 | |
| 5 | 3.10 | 58.59 | 438 | 12 | |
| 6 | 2.59 | 58.57 | 328 | 9 | |
| Average | 1 | 100% | |||
| 2 | 44% | ||||
| 3 | 23% | ||||
| 4 | 14% | ||||
| 5 | 9% | ||||
| 6 | 7% | ||||
| Short Columns | Long Columns | ||||||
|---|---|---|---|---|---|---|---|
| Columns | n = 1:6 | Ln = L1/n | Ncn | Ncn/Nc1 | Ln = L1 × n | Ncn | Ncn/Nc1 |
| mm | N | % | mm | N | % | ||
| Column 1 | 1 | 748 | 1073 | 100 | 748 | 1073 | 100 |
| 2 | 374 | 1106 | 103 | 1496 | 973 | 91 | |
| 3 | 249 | 1100 | 102 | 2244 | 880 | 82 | |
| 4 | 187 | 1108 | 103 | 2992 | 653 | 61 | |
| 5 | 150 | 1125 | 105 | 3740 | 455 | 42 | |
| 6 | 125 | 1058 | 99 | 4488 | 320 | 30 | |
| Column 2 | 1 | 749 | 1455 | 100 | 749 | 1455 | 100 |
| 2 | 375 | 1473 | 101 | 1498 | 1380 | 95 | |
| 3 | 250 | 1467 | 101 | 2247 | 1164 | 80 | |
| 4 | 187 | 1478 | 102 | 2996 | 744 | 51 | |
| 5 | 150 | 1500 | 103 | 3745 | 487 | 33 | |
| 6 | 125 | 1513 | 104 | 4494 | 341 | 23 | |
| Column 3 | 1 | 1053 | 2536 | 100 | 1053 | 2536 | 100 |
| 2 | 527 | 2599 | 102 | 2106 | 2392 | 94 | |
| 3 | 351 | 2604 | 103 | 3159 | 2308 | 91 | |
| 4 | 263 | 2616 | 103 | 4212 | 2262 | 89 | |
| 5 | 211 | 2650 | 104 | 5265 | 1774 | 70 | |
| 6 | 176 | 2650 | 104 | 6318 | 1322 | 52 | |
| Column 4 | 1 | 1052 | 3713 | 100 | 1052 | 3713 | 100 |
| 2 | 526 | 3775 | 102 | 2104 | 3548 | 96 | |
| 3 | 351 | 3793 | 102 | 3156 | 3335 | 90 | |
| 4 | 263 | 3840 | 103 | 4208 | 3080 | 83 | |
| 5 | 210 | 3823 | 103 | 5260 | 2417 | 65 | |
| 6 | 175 | 3844 | 104 | 6312 | 1841 | 50 | |
| Average | 1 | 100% | 100% | ||||
| 2 | 102% | 94% | |||||
| 3 | 102% | 86% | |||||
| 4 | 103% | 71% | |||||
| 5 | 104% | 53% | |||||
| 6 | 103% | 39% | |||||
| Direction from Centroid to Web | Direction from Centroid to Lip | Direction from Centroid to Top Flange | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Columns | N = 0:100% | X | Ncn | Ncn/Nc0 | X | Ncn | Ncn/Nc0 | Y | Ncn | Ncn/Nc0 |
| mm | kN | % | mm | kN | % | mm | kN | % | ||
| Column 1 | 0 | 28 | 1073 | 100 | 28 | 1073 | 100 | 0 | 1073 | 100 |
| 10 | 25 | 1006 | 94 | 33 | 877 | 82 | 13 | 993 | 93 | |
| 20 | 23 | 945 | 88 | 39 | 742 | 69 | 25 | 890 | 83 | |
| 30 | 20 | 891 | 83 | 44 | 642 | 60 | 38 | 801 | 75 | |
| 40 | 17 | 842 | 79 | 49 | 567 | 53 | 51 | 727 | 68 | |
| 50 | 14 | 799 | 74 | 54 | 507 | 47 | 63 | 666 | 62 | |
| 60 | 11 | 760 | 71 | 60 | 458 | 43 | 76 | 614 | 57 | |
| 70 | 8 | 724 | 68 | 65 | 418 | 39 | 89 | 569 | 53 | |
| 80 | 6 | 692 | 64 | 70 | 384 | 36 | 101 | 530 | 49 | |
| 90 | 3 | 662 | 62 | 75 | 356 | 33 | 114 | 496 | 46 | |
| 100 | 0 | 635 | 59 | 81 | 331 | 31 | 127 | 466 | 43 | |
| Column 2 | 0 | 28 | 1455 | 100 | 28 | 1455 | 100 | 0 | 1455 | 100 |
| 10 | 25 | 1357 | 93 | 34 | 1189 | 82 | 13 | 1321 | 91 | |
| 20 | 23 | 1268 | 87 | 39 | 992 | 68 | 26 | 1175 | 81 | |
| 30 | 20 | 1189 | 82 | 44 | 852 | 59 | 38 | 1054 | 72 | |
| 40 | 17 | 1120 | 77 | 49 | 746 | 51 | 51 | 955 | 66 | |
| 50 | 14 | 1058 | 73 | 54 | 664 | 46 | 64 | 872 | 60 | |
| 60 | 11 | 1002 | 69 | 60 | 597 | 41 | 77 | 802 | 55 | |
| 70 | 8 | 951 | 65 | 65 | 544 | 37 | 89 | 741 | 51 | |
| 80 | 6 | 909 | 62 | 70 | 498 | 34 | 102 | 690 | 47 | |
| 90 | 3 | 869 | 60 | 75 | 460 | 32 | 115 | 645 | 44 | |
| 100 | 0 | 827 | 57 | 81 | 427 | 29 | 128 | 606 | 42 | |
| Column 3 | 0 | 54 | 2536 | 100 | 54 | 2536 | 100 | 0 | 2536 | 100 |
| 10 | 48 | 2371 | 93 | 62 | 2143 | 85 | 18 | 2354 | 93 | |
| 20 | 43 | 2225 | 88 | 71 | 1854 | 73 | 36 | 2122 | 84 | |
| 30 | 38 | 2091 | 82 | 80 | 1631 | 64 | 54 | 1920 | 76 | |
| 40 | 32 | 1974 | 78 | 89 | 1458 | 57 | 72 | 1754 | 69 | |
| 50 | 27 | 1868 | 74 | 98 | 1316 | 52 | 90 | 1612 | 64 | |
| 60 | 21 | 1772 | 70 | 106 | 1201 | 47 | 108 | 1487 | 59 | |
| 70 | 16 | 1687 | 67 | 115 | 1102 | 43 | 126 | 1385 | 55 | |
| 80 | 11 | 1608 | 63 | 124 | 1019 | 40 | 144 | 1294 | 51 | |
| 90 | 5 | 1538 | 61 | 133 | 948 | 37 | 162 | 1214 | 48 | |
| 100 | 0 | 1472 | 58 | 142 | 886 | 35 | 181 | 1143 | 45 | |
| Column 4 | 0 | 59 | 3713 | 100 | 59 | 3713 | 100 | 0 | 3713 | 100 |
| 10 | 53 | 3427 | 92 | 68 | 3190 | 86 | 17 | 3424 | 92 | |
| 20 | 47 | 3176 | 86 | 76 | 2781 | 75 | 34 | 3087 | 83 | |
| 30 | 41 | 2956 | 80 | 85 | 2461 | 66 | 52 | 2792 | 75 | |
| 40 | 35 | 2766 | 74 | 93 | 2202 | 59 | 69 | 2546 | 69 | |
| 50 | 30 | 2602 | 70 | 102 | 2000 | 54 | 86 | 2337 | 63 | |
| 60 | 24 | 2453 | 66 | 111 | 1829 | 49 | 103 | 2162 | 58 | |
| 70 | 18 | 2324 | 63 | 119 | 1685 | 45 | 120 | 2007 | 54 | |
| 80 | 12 | 2206 | 59 | 128 | 1563 | 42 | 137 | 1874 | 50 | |
| 90 | 6 | 2101 | 57 | 136 | 1457 | 39 | 155 | 1756 | 47 | |
| 100 | 0 | 2004 | 54 | 145 | 1363 | 37 | 172 | 1655 | 45 | |
| Average | 0% | 100% | 100% | 100% | ||||||
| 10% | 93% | 83% | 92% | |||||||
| 20% | 87% | 71% | 83% | |||||||
| 30% | 82% | 62% | 74% | |||||||
| 40% | 77% | 55% | 68% | |||||||
| 50% | 73% | 50% | 62% | |||||||
| 60% | 69% | 45% | 57% | |||||||
| 70% | 65% | 41% | 53% | |||||||
| 80% | 62% | 38% | 50% | |||||||
| 90% | 60% | 35% | 46% | |||||||
| 100% | 57% | 33% | 44% | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussein, D.B.; Hussein, A.B. Numerical Investigation of the Axial Load Capacity of Cold-Formed Steel Channel Sections: Effects of Eccentricity, Section Thickness, and Column Length. Infrastructures 2024, 9, 142. https://doi.org/10.3390/infrastructures9090142
Hussein DB, Hussein AB. Numerical Investigation of the Axial Load Capacity of Cold-Formed Steel Channel Sections: Effects of Eccentricity, Section Thickness, and Column Length. Infrastructures. 2024; 9(9):142. https://doi.org/10.3390/infrastructures9090142
Chicago/Turabian StyleHussein, Diyari B., and Ardalan B. Hussein. 2024. "Numerical Investigation of the Axial Load Capacity of Cold-Formed Steel Channel Sections: Effects of Eccentricity, Section Thickness, and Column Length" Infrastructures 9, no. 9: 142. https://doi.org/10.3390/infrastructures9090142
APA StyleHussein, D. B., & Hussein, A. B. (2024). Numerical Investigation of the Axial Load Capacity of Cold-Formed Steel Channel Sections: Effects of Eccentricity, Section Thickness, and Column Length. Infrastructures, 9(9), 142. https://doi.org/10.3390/infrastructures9090142






