The Influence of Open-Ground Floors on the Impact of RC Columns Due to Seismic Pounding from Adjacent Lower-Height Structures

Abstract

The substantial influences of masonry infills used as partition walls on the seismic behavior of multistory reinforced concrete (RC) structures have long been recognized. Thereupon, in this study, considering open-ground floors due to a lack of infills (pilotis configuration), the structural pounding phenomenon between adjoining RC buildings with unequal story levels and unequal total heights is investigated. Emphasis is placed on the impact of the external columns of the higher structure, which suffer from the slabs of adjoining shorter buildings. The developing maximum shear forces of the columns due to the impact are discussed and compared with the available shear strength. Furthermore, it is stressed that the structures are partially in contact, as is the case in most real adjacent structures; therefore, the torsional vibrations brought about due to the pounding phenomenon are examined by performing 3D nonlinear dynamic analyses (asymmetric pounding). In this study, an eight-story RC frame structure that is considered to be fully infilled or has an open-ground floor interacts with shorter buildings with n_s stories, where n_s = 6, 3, and 1. Two natural seismic excitations are used, with each one applied twice—once in the positive direction and once in the negative direction—to investigate the influence of seismic directionality on the asymmetric pounding effect. Finally, from the results of this study, it is concluded that the open-ground story significantly increases the shear capacity demands of the columns that suffer the impact and the inelastic rotation demands of the structure, whereas these demands further increase as the stories of the adjoining shorter building increase.

1. Introduction

It is widely accepted that the distributions of the masonry infills along the height of reinforced concrete (RC) buildings strongly influence the seismic behavior and overall seismic capacity of these structures. In recent decades, the effect of structural irregularities on the seismic response of these structures has been the object of many research studies. A distinction between irregularity in plan and irregularity in elevation characterizes the literature [1], although a combination of both types often exists. Nevertheless, recent reviews of the research progress on the seismic behavior of RC buildings with plan or vertical irregularities imply that research activities in vertically asymmetric structures are limited in comparison to corresponding plan irregularity activities [2].

In particular, through many field observations conducted after severe earthquakes, it has become a common conception that the lack of infills on the ground floor has a crucial role in the seismic response of RC buildings. Focusing on vertical irregularities or irregularities in elevation, different distributions of mass, stiffness, and strength with respect to the height of the RC structures have been investigated to gain insight and clarify critical issues for the seismic behavior, analysis, and design of these structures [3,4].

In this respect, the morphology of the first floor has a crucial role in the seismic response of RC structures. Thereon, it is noted that an open-ground story may cause the following [5]: (a) a soft story effect, which means increased deformation in the frame members of the open-ground story because it may have lower stiffness, or (b) a weak story effect, which means lower lateral strength and discontinuities in the flow of lateral seismic shear in the open-ground story.

This irregular structural morphology with respect to elevation is referred to as open first story or pilotis, and it has been the object of several research studies. In general, thorough examination studies of the results of past earthquakes concluded that such irregularities on the first floor of such structures are the main cause of severe damage or even collapse. Kirac et al. [6] reported that the main cause of 59.67% of the damaged buildings from the Kocaeli–Izmit earthquake (1999 Turkey) is attributed to soft first-story configurations.

The seismic inelastic response of RC structures with an open-ground story has been the subject of many analytical studies [7,8]. Furthermore, it has been indicated [9] that in multistory RC buildings, the damage distribution is not only significantly changed by the presence of the infills but also depends on the performance level at which the seismic assessment is performed. Furthermore, the results of nonlinear analyses have indicated that at different limit states, different concluding remarks regarding the sensitivity of the response parameters to the modeling variables of infilled RC frames are obtained [9,10]. In 2006, Repapis et al. [11] presented a new methodology for the evaluation of structural overstrength, global ductility, and the available behavioral factors of existing RC buildings.

On the other hand, another common cause of damage, repeatedly observed during earthquakes, is the interaction of adjacent structures. Many field surveys conducted after severe seismic events in global areas have confirmed that pounding between structures built in contact or those in close proximity to each other frequently results in severe damage or even collapse initiation [1]. The first cases of damage or even failure due to pounding were reported after earthquakes in Alaska, 1964; Managua, 1972; and Mexico City, 1985 [12,13]; and thence in Loma Prieta, 1989; Alkyonides, Greece, 1981; and Kalamata, Greece 1986.

Densely populated city centers usually consist of large blocks that include multistorey RC buildings that are built in contact with one another, although seismic codes recommend seismic gaps between structures [14,15]. Therefore, it has to be further stressed that within a block, land ownerships are not equal and are varied with respect to plans. Therefore, it is most probable that adjacent buildings within a block are in contact with one another in an asymmetrical manner or even only partly in contact. Thus, as Mazza and Labernarda [16], Karayannis and Naoum [17], and Manoukas and Karayannis [18] analytically investigated, during earthquake excitations, a building laterally restrained in an asymmetrical manner due to a stiff adjacent structure usually experiences vibrations that include torsional oscillations. This phenomenon has been pointed out in the recent literature [17,18], and it is referred to as asymmetric pounding.

Moreover, buildings that often exhibit undesired and, in some cases, disastrous behavior during earthquakes are those with L-shaped floor plans, which are frequently built on city block corners and elsewhere. The two structural parts of this type of building, due to its highly uneven lateral stiffness in each of the two directions, tend to laterally vibrate in an entirely different manner. Consequently, severe seismic events result in structural damage or even complete failure in the structural section where the building’s common corner is located [1,19]. In order to mitigate the consequences of this problematic configuration, these buildings are constructed as two separate structures that are in contact with one another. Nevertheless, this settlement has resulted in asymmetric seismic pounding phenomena occurring between two parts of the structural complex. Structural subsystems of a building may also frequently induce torsional oscillations from one to another due to asymmetrical pounding. Jankowski and Mahmood—in their analytical investigation of Olive View Hospital—have pointed out this problem [20,21].

In light of these observations, the seismic behavior and interactions between adjacent structures were studied first between single-degree-of-freedom systems [22], and soon after, the phenomenon between multistory buildings was also studied [23,24,25]. In the latter case, the floor slabs of the first structure come into contact with the floor slabs of the other structure because the story levels of the two structures are the same. Following this, a significant step forward in the investigation of the phenomenon was the study of the interaction between adjoining multistory structures with different story heights [25,26]. In the case of interaction between buildings with different story heights, the slabs of one structure collide with the external columns of the other. It is apparent that this type of interaction is the most dangerous one because the impact on the external columns within their deformable height can cause severe damage or even failure under certain conditions. Recently, the seismic pounding of isolated structures has also been studied. Rayegani and Nouri [27,28] proposed the application of innovative magnetorheological dampers and demonstrated their efficiency in considerably mitigating the damage due to pounding.

The consequences of the phenomenon of the interaction between adjacent structures become even more severe for multistory buildings with irregular open-ground-story morphology (pilotis configuration). Furthermore, it is stressed that the interaction between multistory RC buildings with pilotis configurations and adjoining shorter multistory structures with different story levels and total heights is a common case that has not yet been thoroughly investigated.

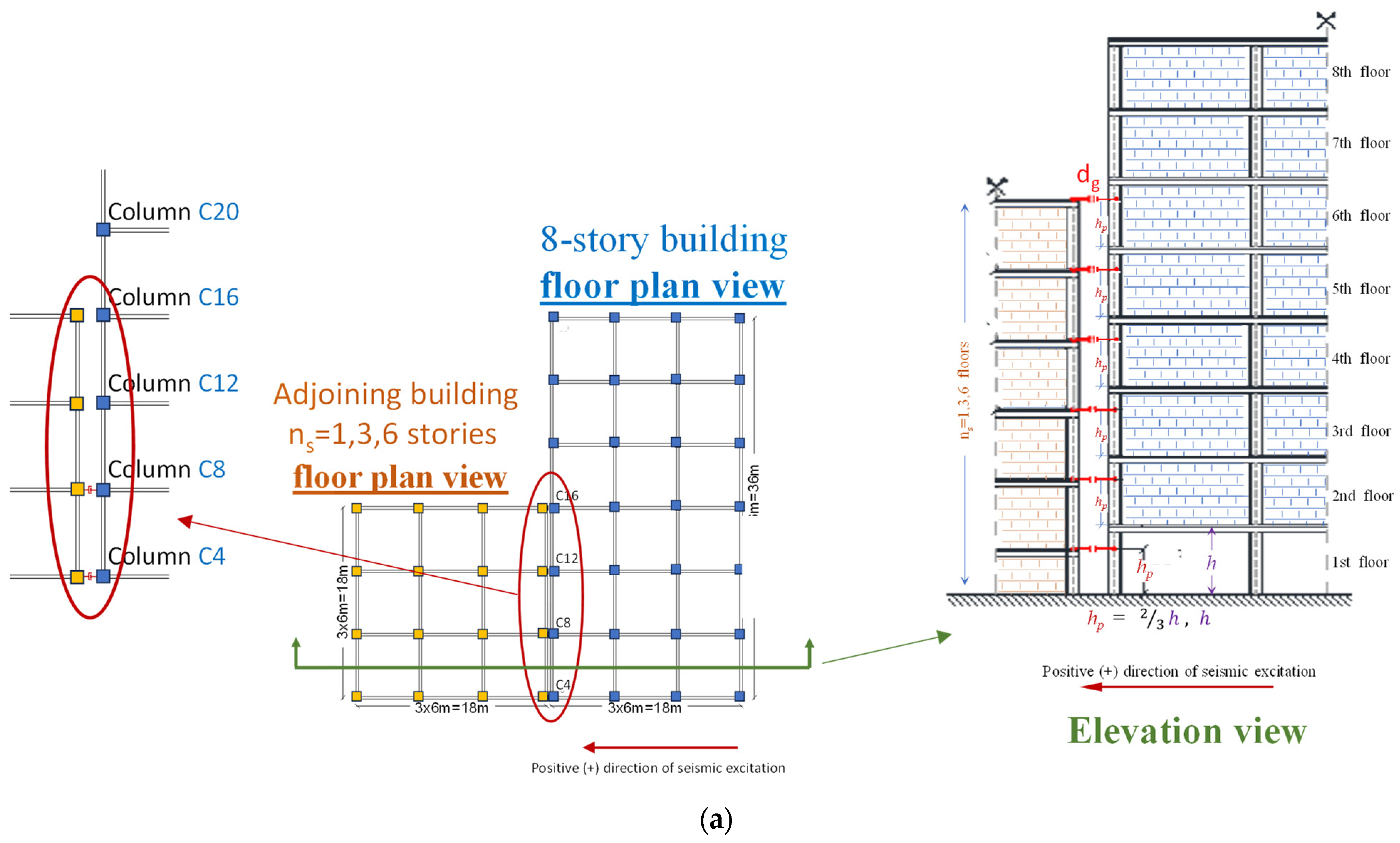
Herein, an eight-story RC building considered (a) fully infilled and (b) with an open-ground floor is studied. The building interacts with shorter buildings with different story levels; these have n_s stories, where n_s = 1, 3, 6 (Figure 1a). Based on the obtained results, it is concluded that the open-ground floor configuration significantly increases the capacity demands of the columns that suffer impacts in terms of shear strength and the inelastic rotation demands of the structure as a whole, whereas the total height of the shorter building strongly influences these results.

Thereupon, for the adequate study of this problem, more than 400 pounding pairs with structures that have equal story levels (type A or slab-to-slab pounding) and 400 pounding pairs with structures that have unequal story levels (type B or slab-to-column pounding) were thoroughly investigated. Furthermore, all pounding cases were examined for two natural seismic excitations, and each excitation was considered with respect to two directions (plus and minus direction). Moreover, the existence of various gap distances between the interacting eight-story building and the other structure, as well as the influence of several other parameters, is also studied in some cases.

2. Structural Modeling and Analysis

The presented study mainly highlights the influence of the open-ground floor configuration on the consequences and the severity of the impact of the RC columns due to the interaction phenomenon. Pounding occurs between two structures that are partly in contact, as shown in Figure 1a. Due to the non-symmetric restraints of lateral oscillations between the structures, it is apparent that pounding induces torsional oscillations in the structures; therefore, 3D analyses are adopted for the attempted investigation.

The eight-story RC building is designed with the following parameters, in compliance with medium ductility levels according to EC8: seismic acceleration at 0.3 g and an overall behavior factor of 3.9. The dimensions and the longitudinal reinforcements of the columns are presented in

Table 1. Characteristics and longitudinal reinforcements of the columns of the 8-story building.

Floors	External Column Cross-Section * (Reinforcements)	Internal Column Cross-Section * (Reinforcements)
1st and 2nd	50/50 (12∅20)	50/50 (12∅20)
3rd	45/45 (12∅20)	45/45 (12∅20)
4th	35/35 (12∅20)	45/45 (12∅20)
5th	30/30 (12∅20)	40/40 (12∅20)
6th	30/30 (8∅20)	40/40 (8∅20)
6th	30/30 (8∅20)	35/35 (8∅20)
7th	30/30 (8∅16)	35/35 (8∅16)

* Cross-sections in cm/cm.

.

A special focus was given to the idealization of the real behavior of the impact area between the structures. A spring-type element with zero length was employed for the numerical simulation of the impact. The spring element remained idle until special conditions induced its activation. Hereupon, in the event that a node of the first structure coincides with the corresponding node of the other structure at a time step of the performed analysis, the conditions are fulfilled, and the activation of the spring element is induced; it is considered that the impact takes place within this time step.

The mechanical characteristics of the spring element adopted herein include three distinct response parts: (a) the negative direction of the x-axis, which represents the case that the two structures sway away from the other. (b) The positive direction of the x-axis includes two parts, and it represents the case in which structures move closer to one another. The first part of the positive direction exists when there is a predefined gap between the interacting structures, and it is equal to this gap. In the case where the two structures approach one another if the sum of the absolute values of their displacements is less than the predefined gap, the spring element still remains inactive. (c) On the contrary, if structures move closer to one another and the sum of the absolute values of their displacements is equal to the gap, then the impact takes place within this time step.

A quantitative approach to the stiffness of the spring cannot be objectively obtained because the geometrical characteristics of the surfaces that suffer the hit are more or less unknown, and the materials under impact are also undefined. Nevertheless, from the literature, it is observed that the response of the interacting buildings is not noticeably sensitive, even with respect to major changes in the adopted spring stiffness and damping values [17,31,32,33]. Thus, in Reference [17], the time history of the torsional moment at the base floor of an eight-story building was studied with respect to pounding phenomena with a two-story building in relation to different stiffness values (k) of the spring elements. It was concluded that significantly different stiffness values (0.5k, k, 2k) did not really influence the results in the examined cases. After some tests that confirmed the aforementioned conclusion, k = 10⁹ kN/m and c = 0 kNsec/m values were selected for the element stiffness and damping values, respectively. Furthermore, it was stressed that in slab-to-column impacts, major damage can be introduced to columns that suffer the hit. On the contrary, the local damage inflicted on the crushed building material of the slab of the adjoining structure is not considered noteworthy.

The computer software SAP2000v.23, which is widely accepted, is employed for nonlinear earthquake analyses; these are performed for the requirements of this investigation. The slabs of the buildings are not directly modeled. Their diaphragmatic behavior is taken into account via the appropriate constraints available in the software. Each beam and column is modeled via a single linear finite element, with the exception of the columns suffering the hit, which are divided into two elements connected at the impact points. Elements with lumped plasticity with respect to the plastic hinges at their ends have been adopted for the simulation of nonlinear column and beam behavior, whereas 3D interaction surfaces are utilized for obtaining RC cross-sections. Moment–rotation relations are represented via simplified bilinear curves after yielding stiffness values equal to a small percentage of the initial stiffness values without pinching.

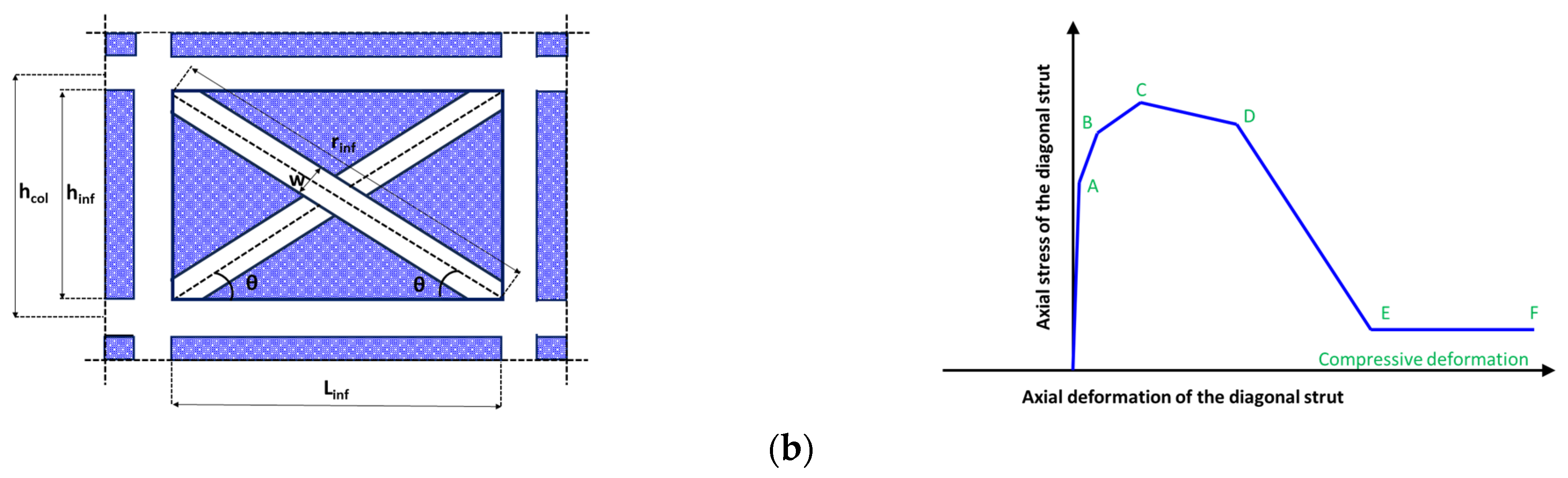
For the simulation of the infills, an equivalent strut model is employed (Figure 1b). This takes into account the response of the infill masonry to a certain degree of accuracy. It includes a degrading branch and residual strength (Figure 1b). It is important that these elements only exhibit axial response and not flexural properties. The proper evaluation of the diagonal struts’ characteristics is a significant issue. Experimental results from Karayannis et al. [29,30] are utilized for the evaluation of the stress–strain behavior curve of the struts, whereas the recommendations provided in FEMA356 are adopted for their effective width [26,34].

The total number of finite elements used differs relative to the pounding case. The total number ranges from 1408 to 2080 finite elements, including the spring elements that simulate the impact areas. Given the properties of the structural members and the modeling assumptions adopted, a finer discretization would not modify the results.

Finally, it is worth noting that the buildings are designed to fulfill the criterion of Eurocode 8, Part 1, Section 4.4.2.2(2), in all stories; thus, second-order (P-Δ) effects are neglected.

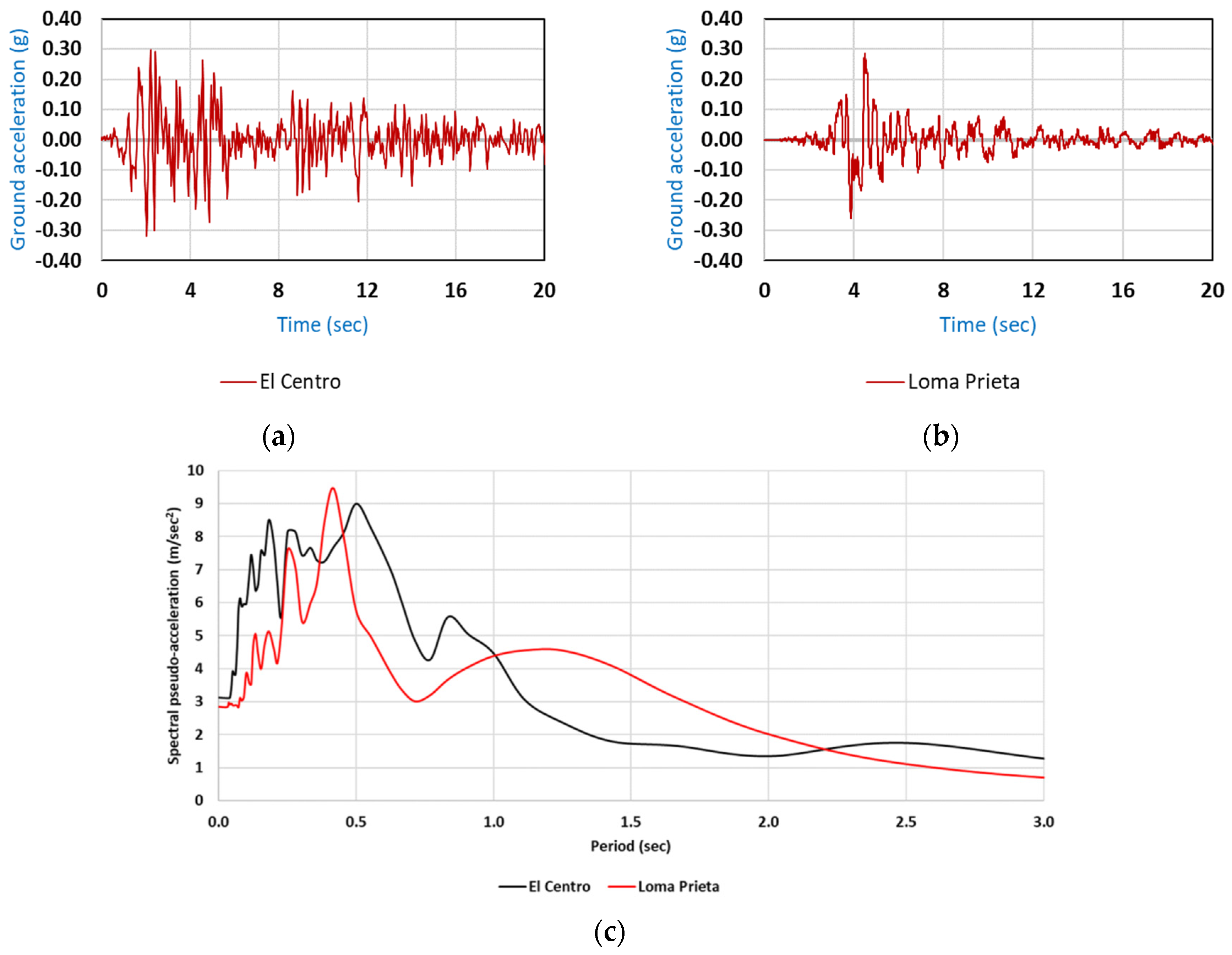
All interaction cases are examined for two recorded acceleration seismic excitations that are presented in Figure 2, and each analysis has been performed twice, first considering the seismic excitation in the positive and then in the negative direction. This arrangement is necessary because the results proved that before the analysis, it was not clear which direction of the earthquake was critical for each examined interaction case.

The excitations of El Centro 1940 and Loma Prieta 1989 were used in the performed analyses. These excitations are selected because their Peak Ground Acceleration is almost equal to the design ground acceleration of the buildings. Furthermore, the response spectra of both excitations (Figure 2c) experience the maximum spectral values around the period range, delimiting the constant branch of the Eurocode 8 design spectrum. Thus, these excitations can be considered representative of the seismic hazard of the buildings.

As mentioned, the computer software SAP2000v.23 is employed for the nonlinear step-by-step earthquake analyses performed for the needs of this investigation. Furthermore, it is also noted that the incremental dynamic analysis procedure is a very useful and powerful computational tool that is widely used in earthquake engineering [35]. However, in this study, because the main objective of the authors is to evaluate the structural response and the pounding phenomenon under seismic excitations corresponding to the design earthquake load of the buildings, step-by-step analyses have been performed.

3. Results and Discussion

3.1. Influence of Open-Ground Story on the Deformations Induced by the Pounding Effect

The influence of the open-ground story (pilotis configuration) on the developing story rotations and story displacements induced by the pounding effect is examined herein. The time history results of the interaction between the eight-story RC structure and a single-story RC infilled frame structure are presented in Figure 3. The two adjoining structures are partially in contact in an asymmetric manner, as shown in Figure 1. The contact points are located at a height h_p equal to two-thirds of the total height of the eight-story structure’s ground story columns, which is within the deformable length of external columns C4 and C8 (Figure 1a).

The choice of the impact point location is based on field observations, which indicated that the impact very often takes place at about two-thirds of the column’s height. In particular, in city centers, it is very common that the ground floor of many multistory reinforced concrete buildings is used as a store. Usually, these stores include a mezzanine floor (a low-height floor between the ground level and the first floor); because of this, the total height of the ground floor is almost 5 m. Nevertheless, the height of the ground floor of the adjacent structure is usually 3 to 3.5 m. Thus, in the case of seismic pounding between the two structures, the impact point is within the deformable length of the columns of the first building and is situated at a height close to two-thirds of their total height (since 3–3.5/5 is 0.6–0.7). It is expected that modifying the impact point’s location would considerably affect the results. The quantification of this influence is an issue of considerable interest, which is beyond the scope of the present paper.

The seismic excitation El Centro 1940 applied in the negative direction was used for the presented analyses. In the first analysis, the eight-story structure is considered to be fully filled, and the results are represented in Figure 3 via the black lines. In the second analysis, this structure is considered with the open-ground story (pilotis configuration), and the results are represented via the red lines of the figure. In particular, Figure 3a presents the time histories of the first-story rotations of the eight-story structure that is considered to be fully infilled and had an open-ground story during the El Centro seismic event. It can be observed that the structure with an open-ground story (pilotis) exhibits over 10 times higher maximum rotations compared to the rotation of the same structure with fully infilled configurations. Furthermore, Figure 3b shows the time histories of the first-story displacements during the same excitation. It can be observed that the maximum displacement of the first story of the pilotis structure is more than 3 times higher compared to the displacement of the same structure that is considered fully infilled.

The influence of the open-ground story on the rotation of the first story induced by the pounding effect between the eight-story RC structure and a shorter structure with six, three, or a single story are presented in Figure 4, Figure 5, and Figure 6, respectively, for the El Centro excitation with respect to the negative direction. In all examined cases, the two 3D structures are in contact in an asymmetric manner, as shown in Figure 1a.

In particular, as shown in Figure 4, the time histories of the first-story rotations of the eight-story structure due to pounding with a six-story RC structure are presented for two ground-story configurations of the tall structure: (1) The fully infilled structure is represented by black dashed lines, and (2) the open-ground-story structure (pilotis configuration) is represented by red solid lines. Furthermore, it is stressed that the influence of the open-ground story on the developing rotation of the first story of the eight-story structure is examined for two types of pounding: (a) slab-to-column pounding (Figure 4a) and (b) slab-to-slab pounding (Figure 4b). Based on the results shown in Figure 4, it is emphasized that in both types of pounding—slab-to-column (Figure 4a) and slab-to-slab (Figure 4b)—the maximum rotations developed in the open-ground-story case (red lines) are at least 10 times higher than the maximum rotations developed in the corresponding fully infilled eight-story structure cases.

Furthermore, in Figure 5, the time histories of the first-story rotations of the eight-story structure due to pounding with a three-story RC structure are presented for two configurations of a tall structure’s ground story: (1) The fully infilled structure is represented by black dashed lines, and (2) the open-ground-story structure (pilotis configuration) is represented by red solid lines. Moreover, the influence of the open-ground story on the developing rotation of the first story of the eight-story structure is examined for two types of pounding: (a) slab-to-column pounding (Figure 5a) and (b) slab-to-slab pounding (Figure 5b). Based on the results shown in Figure 5, it is emphasized that in both types of pounding—slab-to-column (Figure 5a) and slab-to-slab (Figure 5b)—the maximum rotations developed in the open-ground-story cases (red lines) are at least 12 times higher than the maximum rotations developed in the corresponding fully infilled eight-story structure cases.

Finally, in Figure 6, the time histories of the first-story rotations of the eight-story structure due to pounding with a stiff single-story structure are presented for two ground-story tall structure configurations: (1) The fully infilled structure is represented by black lines, and (2) the open-ground-story structure (pilotis configuration) is represented by red lines. Here, the influence of the open-ground story on the developing rotation of the first story of the eight-story structure is examined for two types of pounding: (a) slab-to-column pounding (Figure 6a) and (b) slab-to-slab pounding (Figure 6b). Based on the results shown in Figure 6, it is emphasized that in both types of pounding—slab-to-column (Figure 6a) and slab-to-slab (Figure 6b)—the maximum rotations developed in the open-ground-story cases (red lines) are at least 10 times higher than the maximum rotations developed in the corresponding fully infilled eight-story structure cases.

The pounding phenomena between the eight-story building and shorter structures are studied in Figure 7 in terms of story drifts along the height of the eight-story building. The El Centro excitation in the negative direction is used. The influence of the open-ground story on the observed drift is apparent. On the other hand, it seems that the number of stories of the shorter structure does not significantly influence the developing drift.

3.2. Influence of Open-Ground Story on the Observed Shears of the External Columns Due to Pounding Effects

In Figure 8, the influence of the open-ground story (pilotis) on the pounding effect between the eight-story structure and a six-story building is examined. In particular, in Figure 8a, the maximum shear forces of external column C4 of all stories of the fully infilled eight-story structure—including the ones that suffer pounding impacts—are presented relative to the response without pounding effects (free vibration—blue dashed line) and for the case with the pounding effect (solid red line). Similarly, in Figure 8b, the maximum shear forces of all stories of the eight-story structure with open-ground-story configuration are presented for the response without pounding effects (free vibration—blue dashed line) and with pounding effects (solid red line). In both cases, the pounding effect increases the influence of the developing shear force.

Nevertheless, from the comparison of Figure 8a and Figure 8b, it is concluded that in the case of open-ground-floor configuration (Figure 8b), the pounding effect dramatically increases the maximum shear forces developing in the floors of the eight-story structure, whereas, in the case of the fully infilled structure (Figure 8a), the corresponding increase due to the pounding effect is substantially lower.

In Figure 9, the influence of the open-ground story (pilotis) on the pounding effect between the eight-story structure and a three-story building is examined. Similarly, in Figure 10, the influence of the open-ground story (pilotis) on the pounding effect between the eight-story structure and a single-story building is examined. In particular, in Figure 9a and Figure 10a, the maximum shear forces of all stories of the fully infilled eight-story structure are presented with respect to the response without pounding effects (free vibration—blue dashed line) and with pounding effects (solid red line).

Similarly, in Figure 9b and Figure 10b, the maximum shear forces of all stories of the eight-story structure with open-ground-story configuration are presented with respect to the response without pounding effects (free vibration—blue dashed line) and with pounding effects (solid red line). From a comparison between the pounding case between the eight-story structure and the three-story structure (Figure 9a,b) and the pounding case between the eight-story structure and a single-story building (Figure 10a,b), it is easily concluded that in the case of open-ground-floor configuration (Figure 9b and Figure 10b), the pounding effect dramatically increases the maximum shear forces developing in the floors of the eight-story structure, whereas in the case of the fully infilled structure (Figure 9a and Figure 10a), the corresponding increase is lower due to the pounding effect.

4. Influence of the Total Height of the Shorter Structure

It has been repeatedly reported that the consequences of the pounding effect between two adjoining structures with different total heights are significantly affected by the total height of the shorter structure [18,26]. In Figure 11, the influence of the total height of the adjacent shorter structure on the developing maximum shear forces of column C4—which suffers the impact—is presented for the eight-story pilotis building with respect to the El Centro excitation’s positive direction. From Figure 11, it is deduced that in the examined cases, the developing maximum story forces of the column that suffers the impact from the slabs of the shorter structure are increased as the total height of the shorter structure increases.

Thus, in the pounding case of the eight-story structure with respect to a six-story structure, the maximum shear force of column C4 in the second story is almost 25% higher than the maximum shear of the same column in the case of pounding relative to a three-story structure. Nevertheless, no safe conclusions can be obtained regarding the influence of small changes in the number of stories on the demands for shear strength.

5. Influence of the Direction of Seismic Excitation on the Pounding Effect

The study of pounding effects is mainly based on inelastic seismic analyses, and other studies have always carried out analyses by considering either the positive or negative direction of the seismic excitation. Apparently, this consideration is quite reasonable in the symmetric configuration case of interacting structures. Nevertheless, in common cases in which the structural system of the interacting structures as a whole is not a symmetric configuration, this simplification is not justified. Consequently, reversing the direction (negative direction) of the seismic excitation and performing a new inelastic analysis leads to different results compared to the first analysis with a positive seismic excitation direction.

The entire issue is essential or even critical in the case of 3D pounding between adjacent multistory structures that are asymmetrically in contact with one another (Figure 1). This subject was studied by Manoukas and Karayannis for the first time [18,26], and it has been reported as the directionality of seismic excitations. In these studies, it is suggested that for interactions between multistory RC structures, inelastic analyses must be performed twice, and the examined pounding case has to be examined with respect to both directions (positive and negative) of each seismic excitation.

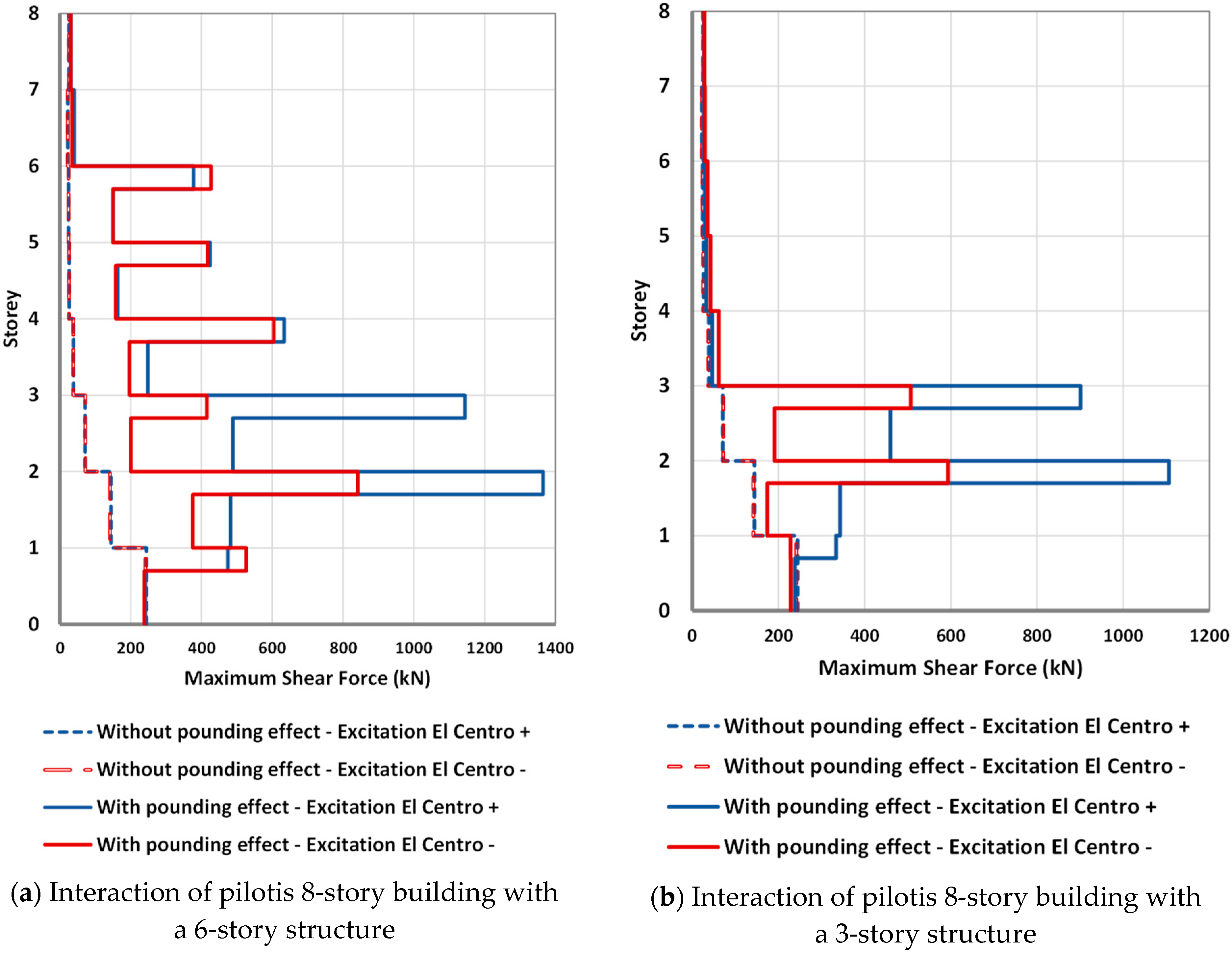
This recommendation is once again justified in the present paper, where the two accelerograms used are applied along both x-axis directions. In Figure 12, the developing maximum shear forces of external column C4 of the eight-story structure, including the ones that suffer the pounding hit, are presented with respect to the following: (a) interaction of the eight-story structure with a six-story structure (Figure 12a) and (b) interaction of the eight-story structure with a three-story structure (Figure 12b). In each interaction, the shear forces for the El Centro seismic excitation in the positive (blue lines) and negative directions (red lines) are presented with respect to the response of the eight-story structure without the pounding effect (dashed lines) and with the pounding effect (solid lines). From the presented results, it is apparent that the direction of the seismic excitation significantly influences the developing shear forces without being known before the analysis which direction, positive or negative, is the critical one for each examined pounding case. Consequently, both directions of each ground motion must be taken into account.

Thereupon, in the case of pounding between the eight-story structure and a six-story structure (Figure 12a), it is observed that the third-story column exhibits due to the positive direction of the excitation almost 2.5 times higher shear force compared to the shear force developed in the same column due to the negative seismic excitation direction. Similarly, in the case of pounding between the eight-story and three-story structure (Figure 12b), it is observed that the second-story column exhibits due to the positive direction of the excitation almost 2 times higher shear force compared to the shear force developed in the same column due to the negative seismic excitation direction.

6. Shear Capacity Demands of the Columns That Suffer the Pounding Impact

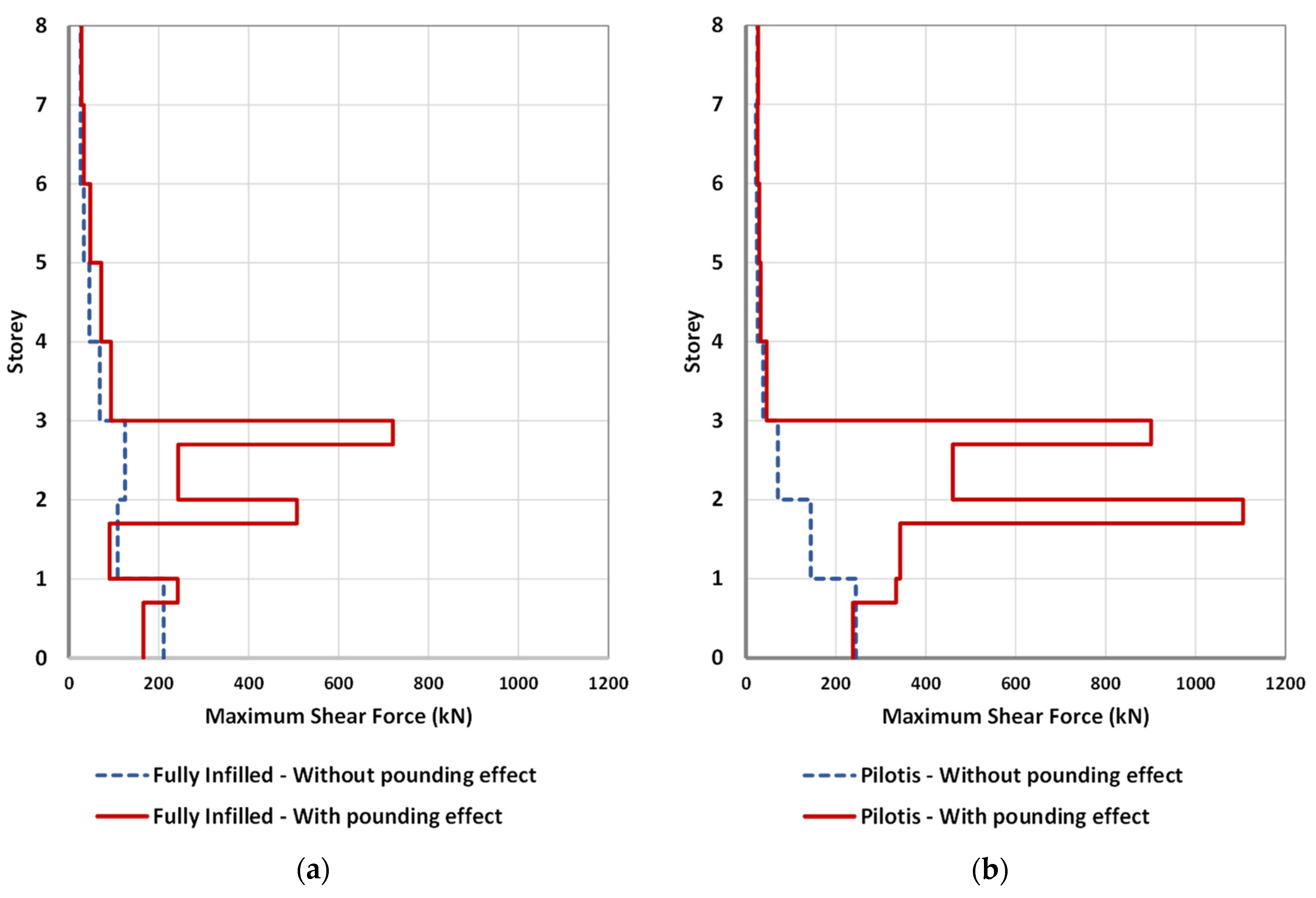
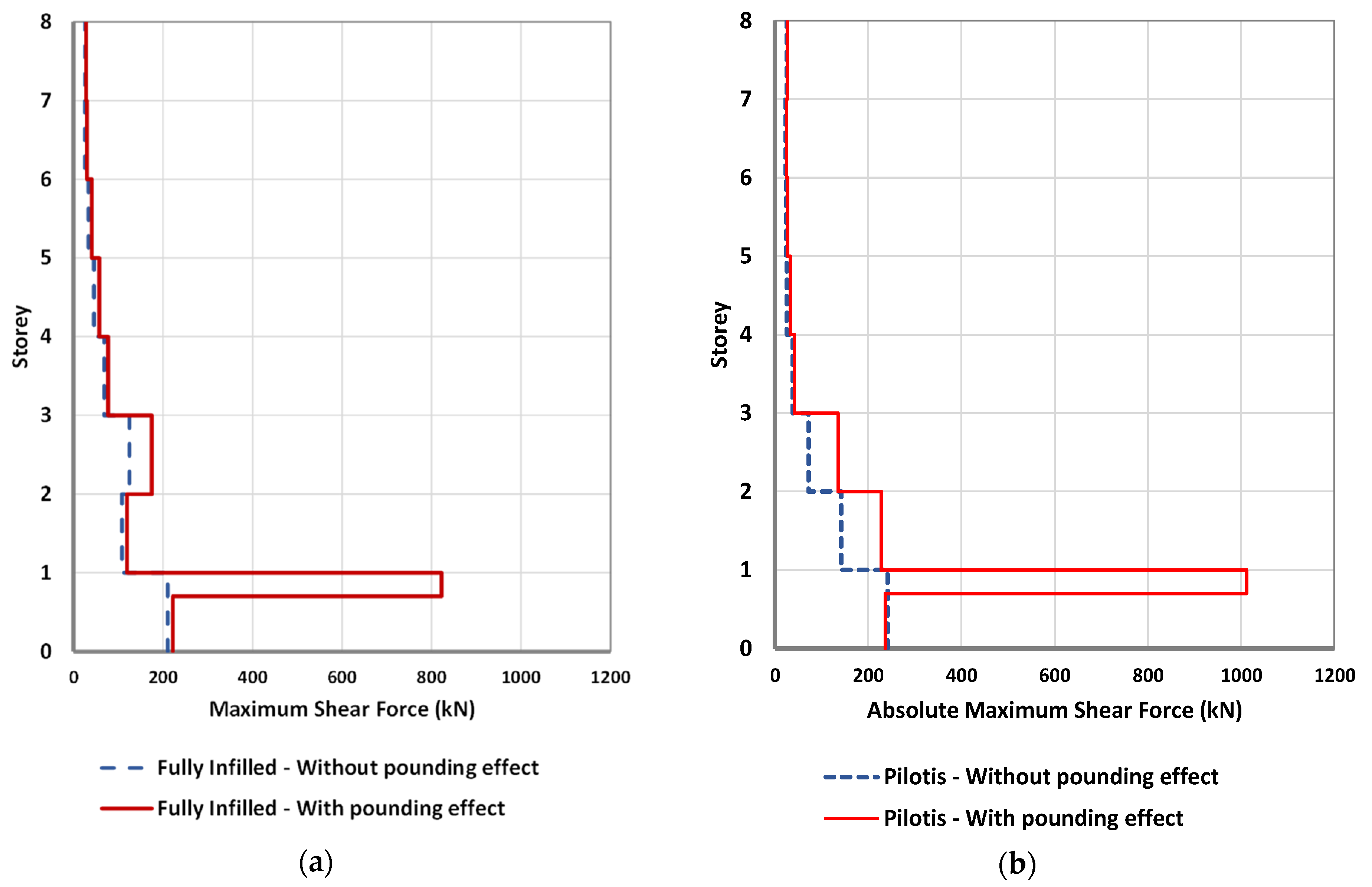
The most important issue with respect to the safety of interacting structures is to compare developing demands in the shear forces of columns that suffer impacts from the slabs of adjoining structures with the available shear strength. The interaction results of the slab-to-column cases between the eight-story reinforced concrete frame building and a stiff adjacent single-story building and between the eight-story building and a stiff three-story structure are presented in Figure 13 and Figure 14, respectively. In these interaction cases, the structures are partly in contact, as shown in Figure 1a. The eight-story structure is considered to be (a) fully infilled and (b) with open first story (pilotis configuration).

The critical point in these cases is that the element that suffers impacts in multiple time steps during seismic excitations develops a critical shear situation. In contrast, it is observed that flexural inelastic deformation demands are easily satisfied. Based on these observations and the dangerous brittle character of the shear failure, this study conducted a thorough examination of the developing shear forces of the columns that suffer the impact, and a comparison with the considered available shear strength was carried out.

Herein, the shear strength of the columns is estimated according to Eurocode 2 provisions [36], and it is based on the following considerations: stirrups according to Eurocode 2 [36] for non-critical regions, calculations of the shear strength due to stirrups, and estimations of shear strength relative to concrete (Eurocode 2 [36]) without stirrups. Here, it is noted that the shear strength of the reinforced concrete elements, according to Eurocode 2, depends on the angle θ of the developing cracks with respect to the axis of the element (low limit—crack angle of θ = 45°; upper limit—crack angle of θ = 22°). Thereupon, the uncertain character of the assumed strength is stressed, especially in the case where angle θ is equal to 22°; considering that θ is equal to 22°, the highest shear strength is obtained.

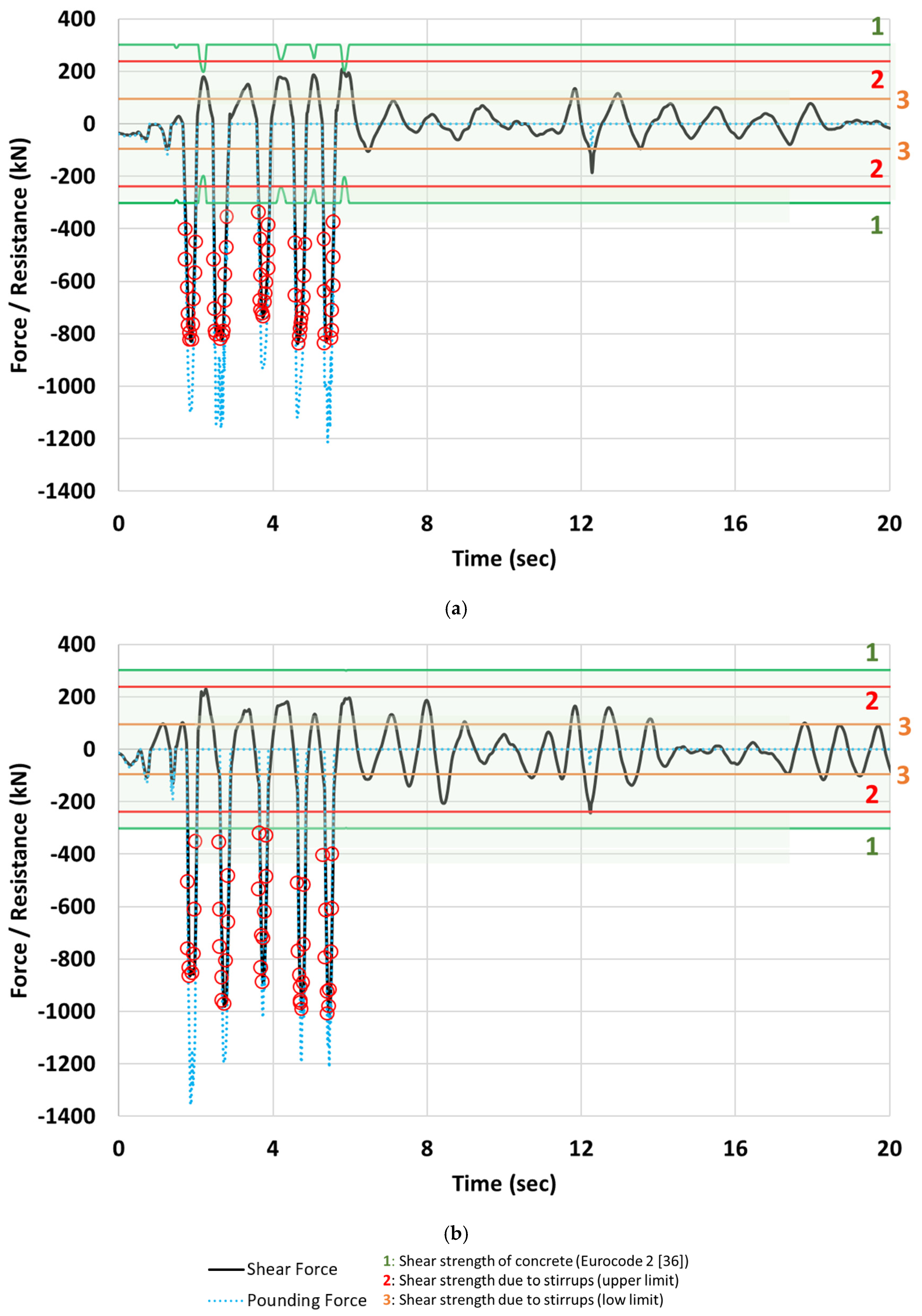
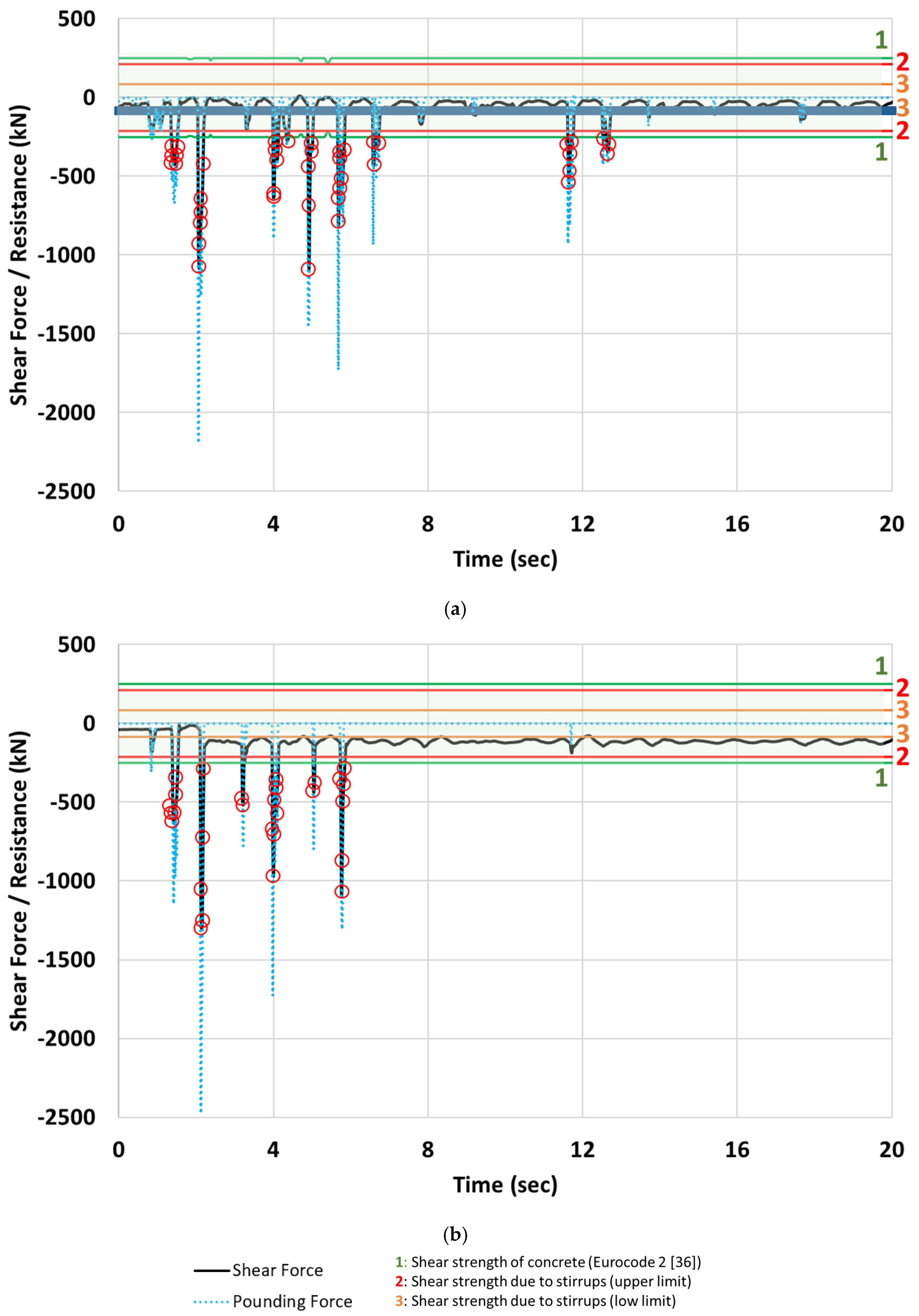
Interaction between the eight-story reinforced concrete structure and a stiff single-story building is examined in Figure 13 in terms of the developing shear forces at the impact point of external column C4 located at the ground floor of the eight-story structure (Figure 1a). The time histories of the developing shear forces during the El Centro 1940 excitation considered in the negative direction are presented for the case of the fully infilled eight-story structure (Figure 13a) and for the case where the ground floor of the eight-story structure is an open story (Figure 13b) whereas masonry infills are considered in the other stories (pilotis configuration). In these figures, the developing shear demand is presented at each time step of the analysis, and it is compared to the available shear capacity as it is estimated based on the provisions of Eurocodes 2 [36] and 8 [14]. As observed, there are five short time periods comprising 10 to 20-time steps, within which the developing shear demands due to the pounding impact exceed 2 or even 3 times the estimated shear capacity of the column. It is emphasized that in the case of the interaction between the eight-story pilotis structure and the single-story building (Figure 13b), the demands are even higher than those of the fully infilled eight-story structure, underlying this way the fact that pilotis configuration excessively increases the shear demands, frequently resulting in brittle local failure and the collapse initiation of the entire structure.

Interaction between the eight-story reinforced concrete structure and a stiff three-story building is examined in Figure 14 in terms of the developing shear forces at the impact point of external column C4, which is located on the ground floor of the eight-story structure (Figure 1a). The time histories of the developing shear forces during the El Centro 1940 excitation considered in the positive direction are presented for the case of the fully infilled eight-story structure (Figure 14a) and for the case where the ground floor of the eight-story structure is an open story (Figure 14b) whereas masonry infills are considered in the other stories (pilotis configuration). In these figures, the developing shear demand is presented at each time step of the analysis, and it is compared to the available shear capacity [14,36]. As observed, there are many time periods—comprising 3- to 10-time steps—within which the developing shear demands due to the pounding impact exceed 2 or even 4 times the estimated shear capacity of the column. Furthermore, it is emphasized that in the interaction case between the eight-story pilotis structure (Figure 14b) and a three-story building, the demands are even higher than the ones of the fully infilled eight-story structure, underlying this way, the fact that pilotis configuration excessively increases the shear demands, frequently resulting in brittle local failure and the collapse initiation of the entire structure.

In order to highlight the correlation between developing shear and pounding forces—namely, the forces transferred from one interacting structure to another via contact elements—the latter are also plotted in Figure 13 and Figure 14. Obviously, pounding forces are directly correlated with other critical response quantities as well.

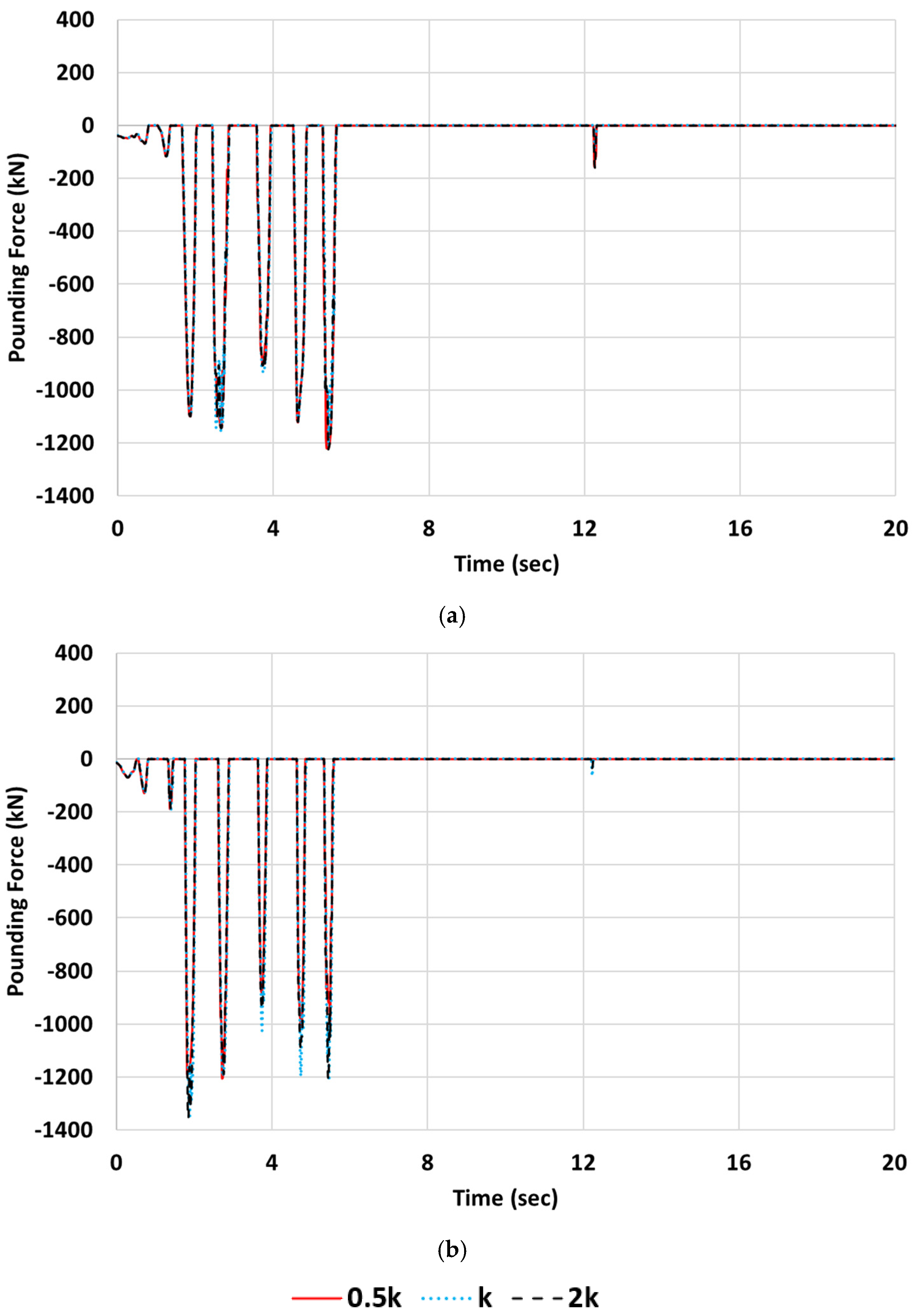
As discussed in Section 2, the response of the interacting buildings is not noticeably sensitive, even relative to major changes in the adopted values of the contact element’s stiffness [17,31,32,33]. In the framework of the present study, some confirmation tests were carried out. Indicatively, the pounding forces acting on the ground story column of the eight-story buildings interacting with a stiff single-story structure due to El Centro negative excitation are illustrated in Figure 15. The dashed cyan line—also plotted in Figure 13—represents the developing pounding forces with respect to a contact element stiffness value that is equal to k, while the solid red and dashed black lines represent the developing forces for stiffness values equal to 0.5k and 2k, respectively (k = 10⁹ kN/m). It is apparent that the pounding forces are not considerably affected by the stiffness value.

7. Concluding Remarks

An extensive study was conducted with respect to pounding phenomena between adjoining multistory structures that are in contact in an asymmetric manner, and a step-by-step nonlinear 3D analysis was carried out.

Herein, eight-story RC buildings considered (a) with an open-ground story and (b) fully infilled are interacting with shorter buildings with different story levels having n_s = 1, 3, 6 stories. Both slab-to-slab and slab-to-column pounding types are examined. Considering the common but most damaging case of slab-to-column pounding, it is concluded that the total height of the shorter building highly influences the shear capacity demands of the upper column, which suffers impacts.

Therefore, in all slab-to-column cases, it has to be stressed that the shear forces that develop in the column that suffers the impact in the open-ground-story structure are substantially higher compared to the corresponding ones developed in fully infilled structures.

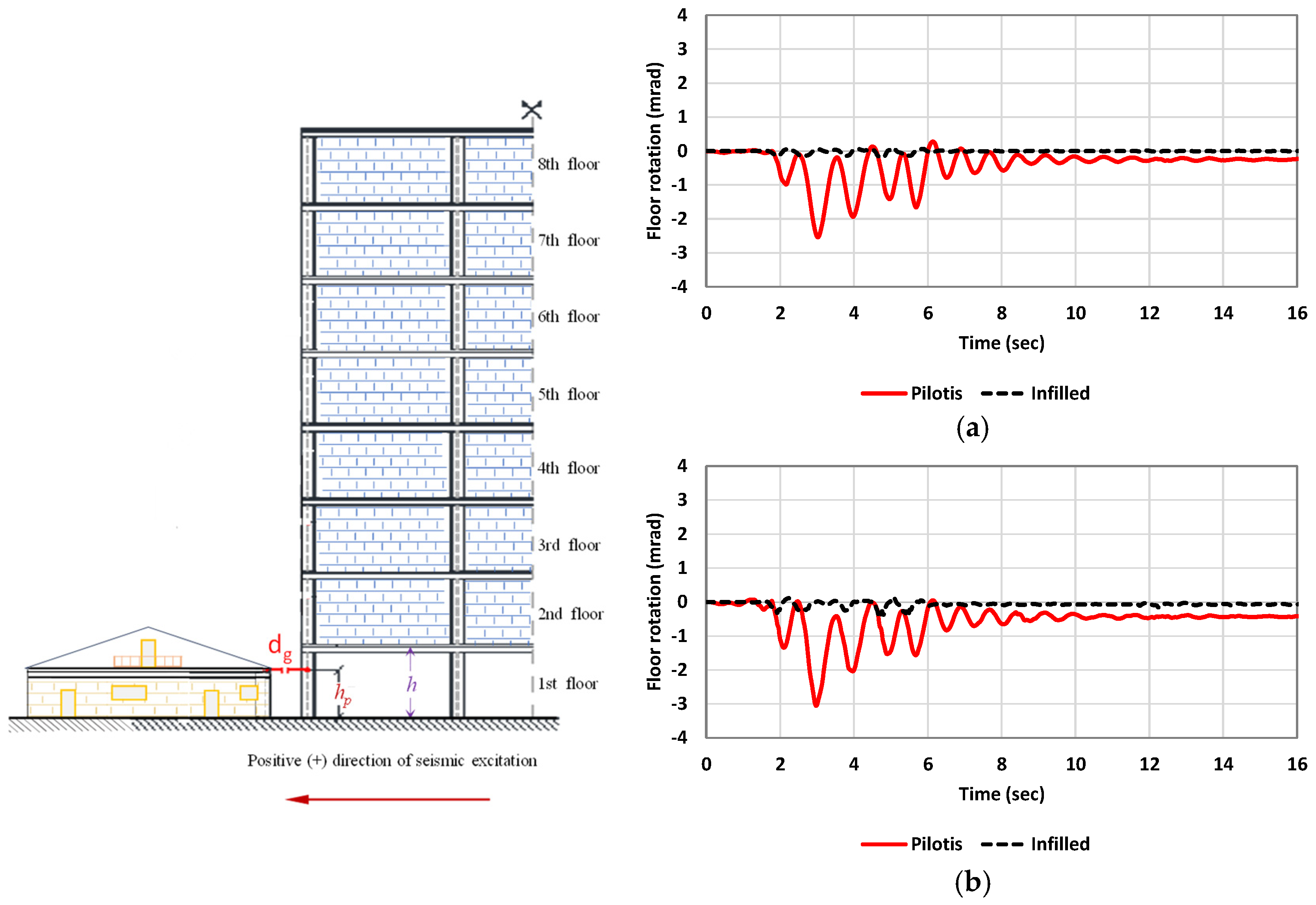
The asymmetric pounding phenomenon of adjoining buildings due to the asymmetric and partial contact between them results in rotational vibrations. The observed rotations of the first story increased substantially in the examined interaction cases of the eight-story building with an open-ground story (pilotis).

Furthermore, considering the developing story drifts, it is deduced that they are mainly influenced by the ground story configuration (infilled or open-ground story), whereas the height (number of stories) of the second shorter structure in the examined cases exhibits a less important influence.

As a final conclusion, it is emphasized that the open-ground-story configuration significantly increases the shear capacity demands of the columns that suffer impacts and the inelastic deformation demands of the structure as a whole.

The aforementioned derivations could result in specific design recommendations, which might be useful for engineering practitioners. For example, when ensuring a sufficient separation gap between the adjacent structures is not possible, the adequate and proper placement of shear walls relative to the floor plan may limit displacements, including the rotation of diaphragms. This measure is also efficient for mitigating the unfavorable effects of the pilotis configuration. Furthermore, the utilization of dampers is a promising alternative solution.