Using Multiple Machine Learning Models to Predict the Strength of UHPC Mixes with Various FA Percentages
Abstract
1. Introduction
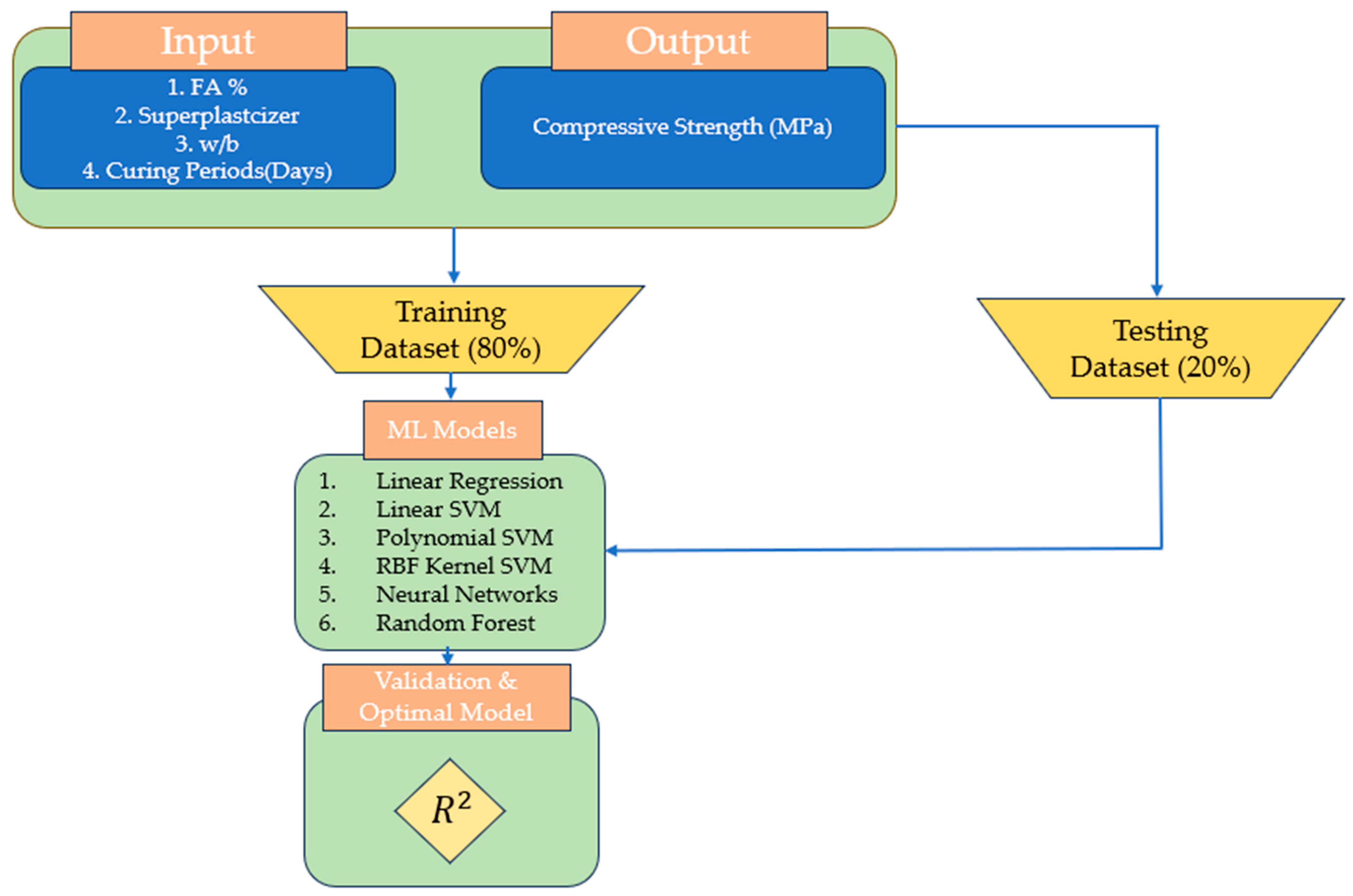
2. Methodology
2.1. Data Collection
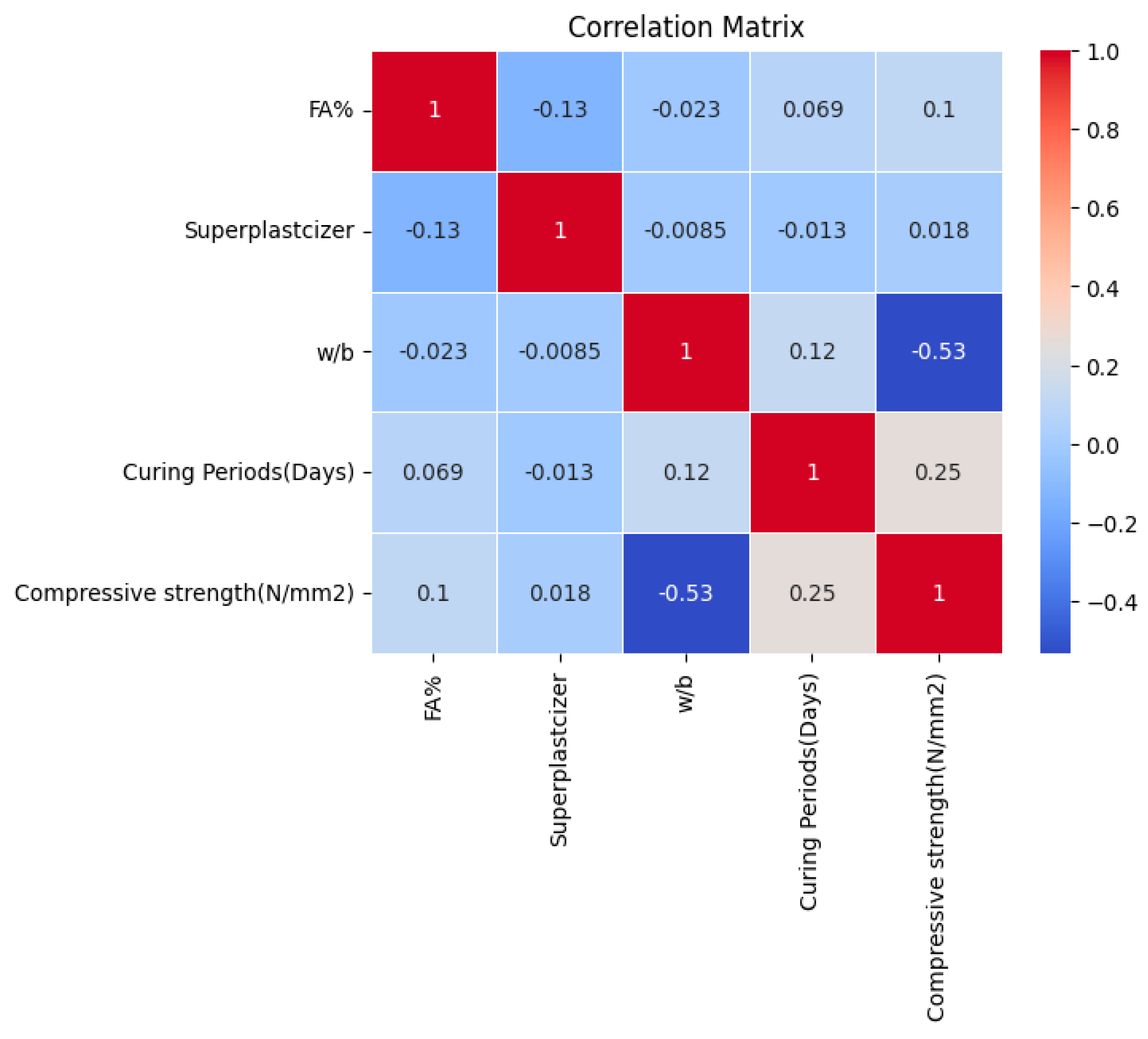
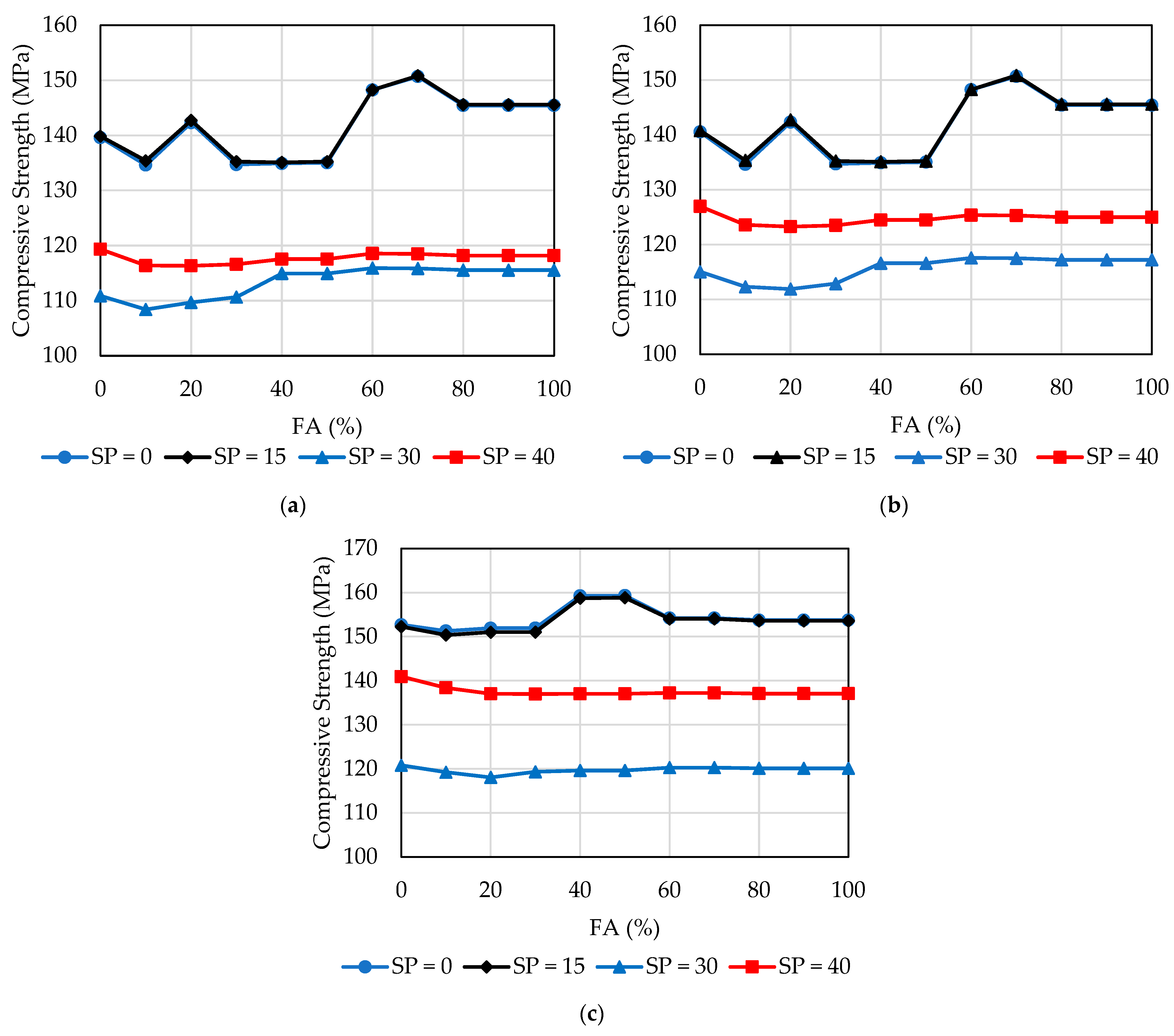
2.2. Data Visualization
2.3. Data Normalization
2.3.1. Unnormalized Techniques
2.3.2. Min-Max Normalization
2.3.3. Z-Score Normalization
2.4. Machine Learning Techniques
2.4.1. Linear Regression
2.4.2. Support Vector Machine (SVM)
2.4.3. Random Forest
2.4.4. Artificial Neural Networks (ANN)
2.5. Model Performance Evaluation
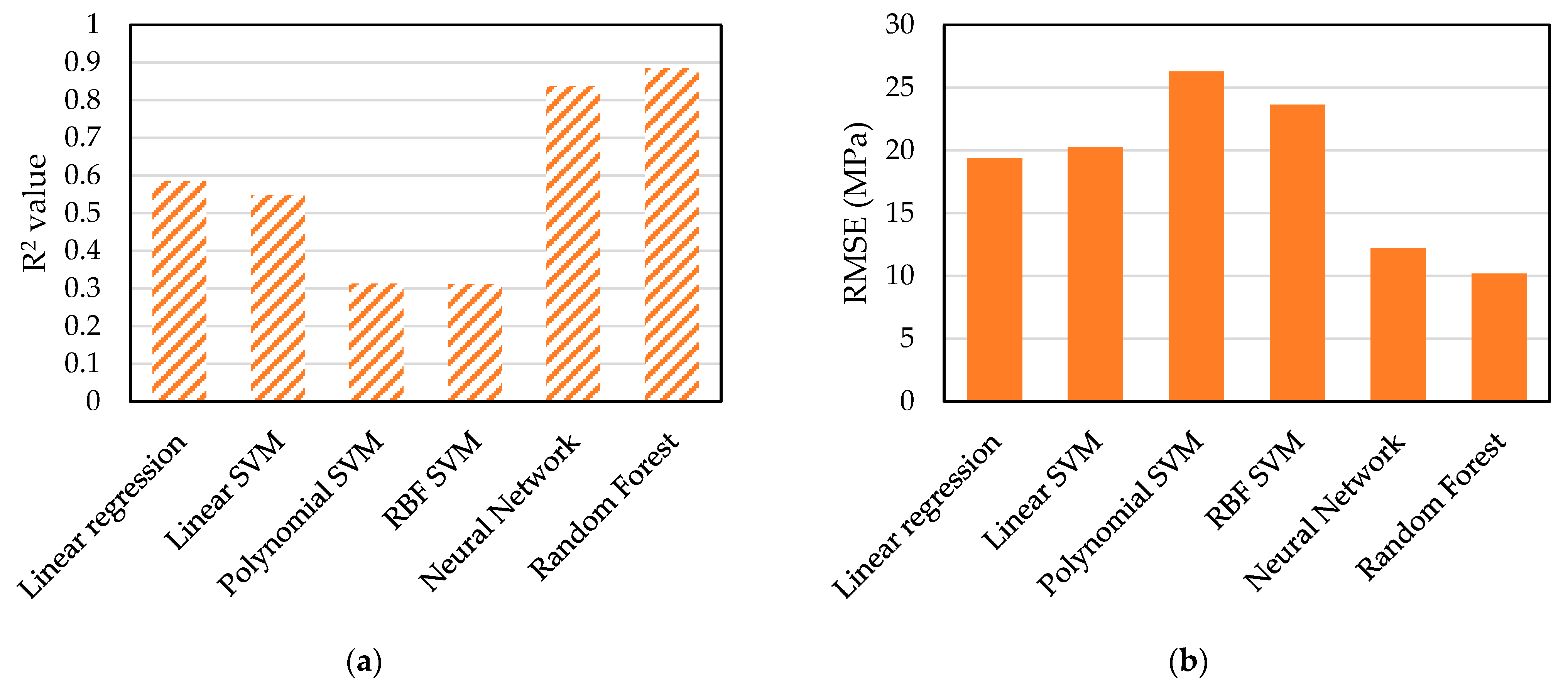
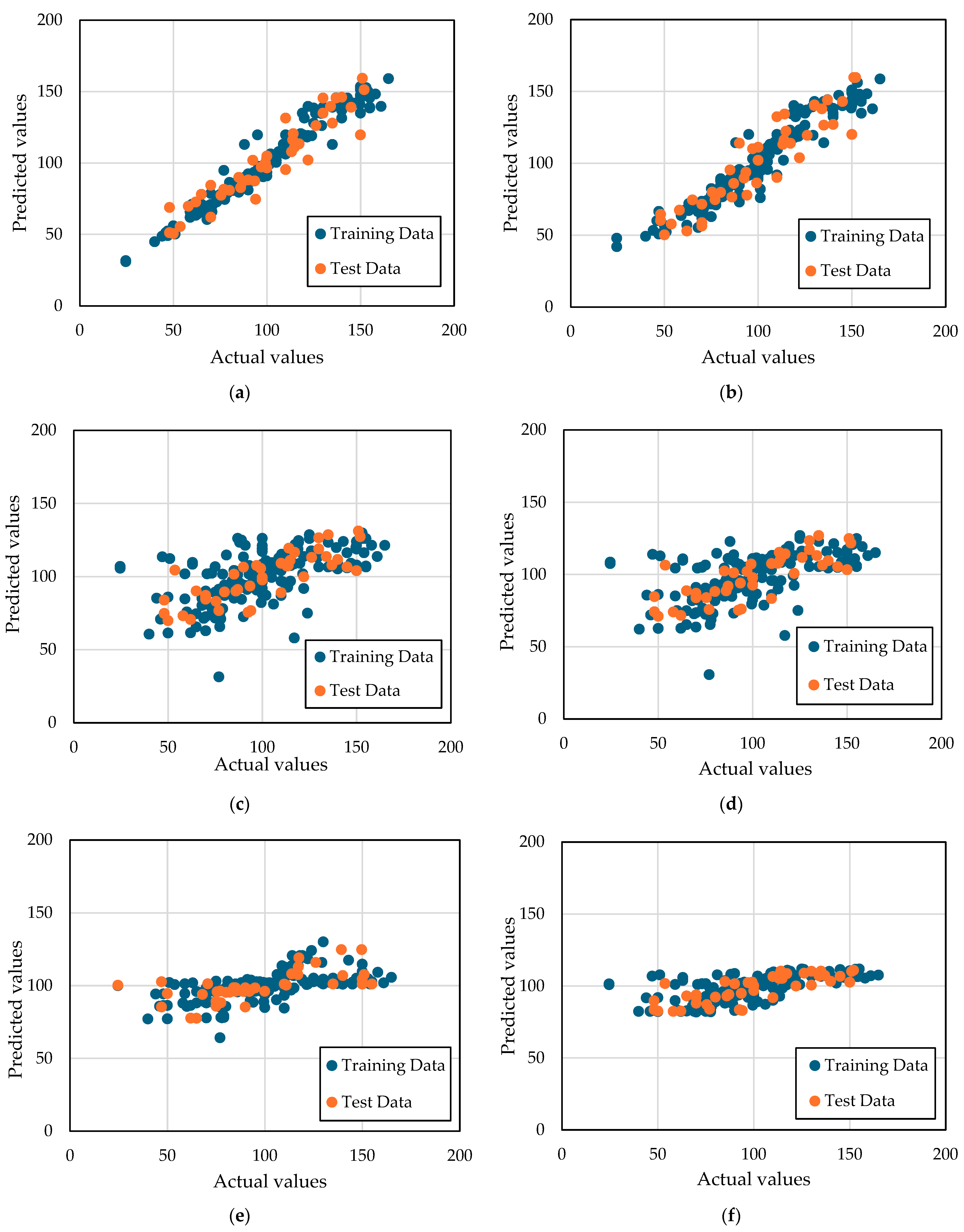
3. Results and Discussion
4. Parametric Study
5. Conclusions
- The Random Forest ML model emerged as the top performer in predicting UHPC’s strength with an R2 value of 0.8857. This was achieved due to the Random Forest model being able to capture complex nonlinear relationships inherent in the dataset. The results achieved with the model emphasize the value of leveraging advanced algorithms that can handle multidimensional data and interaction effects more effectively than simple traditional models.
- Traditional modelling techniques such as Linear Regression and SVMs showed limited capability in accurately predicting UHPC strength where the best model out of them had an accuracy of 0.5844. This limitation points to the difficulties of applying linear or margin-based models to phenomena characterized by complex interactions and nonlinear dependencies. This highlights the importance of considering the relationship between the different variables before applying the models. Variables like w/b ratio and superplasticizer have a complex relationship with UHPC’s strength that cannot be captured with a simple traditional model like linear regression.
- The research emphasizes the necessity of broadening the scope of data collection to include a wider array of conditions, processing parameters, and material compositions. The parametric study was performed but limited by the variety of data in the dataset. After 120 days the predictive model was not able to predict the increase in strength of the concrete.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Reference | FA (%) | Superplasticizer (kg/m3) | w/b | Curing Period (Days) | Compressive Strength (MPa) |
|---|---|---|---|---|---|
| Ferdosian et al. [19] | 0 | 0 | 0.2 | 28 | 150 |
| 10 | 0 | 0.2 | 28 | 140 | |
| 15 | 0 | 0.2 | 28 | 145 | |
| 20 | 0 | 0.2 | 28 | 155 | |
| 25 | 0 | 0.2 | 28 | 137 | |
| 30 | 0 | 0.2 | 28 | 137 | |
| 35 | 0 | 0.2 | 28 | 140 | |
| 20 | 0 | 0.2 | 28 | 145 | |
| 20 | 0 | 0.2 | 28 | 145 | |
| 25 | 0 | 0.2 | 28 | 155 | |
| 30 | 0 | 0.2 | 28 | 150 | |
| Chen et al. [20] | 0 | 30.2 | 0.2 | 1 | 59 |
| 0 | 30.2 | 0.2 | 7 | 95.7 | |
| 0 | 30.2 | 0.2 | 28 | 106.3 | |
| 0 | 30.2 | 0.2 | 56 | 108.8 | |
| 0 | 30.2 | 0.2 | 90 | 114.1 | |
| 0 | 30.2 | 0.2 | 1 | 70.7 | |
| 0 | 30.2 | 0.2 | 7 | 97.4 | |
| 0 | 30.2 | 0.2 | 28 | 113.2 | |
| 0 | 30.2 | 0.2 | 56 | 113.8 | |
| 0 | 30.2 | 0.2 | 90 | 118.1 | |
| 20 | 30.2 | 0.2 | 1 | 53.7 | |
| 20 | 30.2 | 0.2 | 7 | 99.2 | |
| 20 | 30.2 | 0.2 | 28 | 109.9 | |
| 20 | 30.2 | 0.2 | 56 | 110.3 | |
| 20 | 30.2 | 0.2 | 90 | 117.5 | |
| 30 | 30.2 | 0.2 | 1 | 24.6 | |
| 30 | 30.2 | 0.2 | 7 | 101.2 | |
| 30 | 30.2 | 0.2 | 28 | 114.8 | |
| 30 | 30.2 | 0.2 | 56 | 117.2 | |
| 30 | 30.2 | 0.2 | 90 | 119.3 | |
| 40 | 30.2 | 0.2 | 1 | 24.6 | |
| 40 | 30.2 | 0.2 | 7 | 101.2 | |
| 40 | 30.2 | 0.2 | 28 | 114.8 | |
| 40 | 30.2 | 0.2 | 56 | 117.2 | |
| 40 | 30.2 | 0.2 | 90 | 119.3 | |
| 0 | 34.2 | 0.2 | 1 | 72.8 | |
| 0 | 34.2 | 0.2 | 7 | 102.8 | |
| 0 | 34.2 | 0.2 | 28 | 113.8 | |
| 0 | 34.2 | 0.2 | 56 | 126.2 | |
| 0 | 34.2 | 0.2 | 90 | 139.3 | |
| 0 | 34.2 | 0.2 | 1 | 72.8 | |
| 0 | 34.2 | 0.2 | 7 | 102.8 | |
| 0 | 34.2 | 0.2 | 28 | 113.8 | |
| 0 | 34.2 | 0.2 | 56 | 126.2 | |
| 0 | 34.2 | 0.2 | 90 | 139.3 | |
| 0 | 34.2 | 0.2 | 1 | 73.2 | |
| 0 | 34.2 | 0.2 | 7 | 102.3 | |
| 0 | 34.2 | 0.2 | 28 | 115.2 | |
| 0 | 34.2 | 0.2 | 56 | 129.3 | |
| 0 | 34.2 | 0.2 | 90 | 149.7 | |
| Alsalman et al. [22] | 0 | 5.11 | 0.4 | 3 | 40 |
| 0 | 5.11 | 0.4 | 7 | 50 | |
| 0 | 5.11 | 0.4 | 28 | 65 | |
| 0 | 5.11 | 0.4 | 56 | 78 | |
| 0 | 5.11 | 0.4 | 91 | 79 | |
| 0 | 5.11 | 0.4 | 210 | 79 | |
| 30 | 4.77 | 0.3 | 3 | 48 | |
| 30 | 4.77 | 0.3 | 7 | 59 | |
| 30 | 4.77 | 0.3 | 28 | 75 | |
| 30 | 4.77 | 0.3 | 56 | 85 | |
| 30 | 4.77 | 0.3 | 91 | 87 | |
| 30 | 4.77 | 0.3 | 210 | 89 | |
| 40 | 4.75 | 0.3 | 3 | 44 | |
| 40 | 4.75 | 0.3 | 7 | 50 | |
| 40 | 4.75 | 0.3 | 28 | 65 | |
| 40 | 4.75 | 0.3 | 56 | 88 | |
| 40 | 4.75 | 0.3 | 91 | 86 | |
| 40 | 4.75 | 0.3 | 210 | 87 | |
| 0 | 6.77 | 0.3 | 3 | 68 | |
| 0 | 6.77 | 0.3 | 7 | 71 | |
| 0 | 6.77 | 0.3 | 28 | 85 | |
| 0 | 6.77 | 0.3 | 56 | 97 | |
| 0 | 6.77 | 0.3 | 91 | 100 | |
| 0 | 6.77 | 0.3 | 210 | 100 | |
| 40 | 4.24 | 0.3 | 3 | 68 | |
| 40 | 4.24 | 0.3 | 7 | 70 | |
| 40 | 4.24 | 0.3 | 28 | 86 | |
| 40 | 4.24 | 0.3 | 56 | 97 | |
| 40 | 4.24 | 0.3 | 91 | 100 | |
| 40 | 4.24 | 0.3 | 210 | 100 | |
| Hakeem et al. [37] | 0 | 0 | 0.15 | 28 | 161 |
| 40 | 0 | 0.15 | 28 | 150 | |
| 60 | 0 | 0.15 | 28 | 158 | |
| 80 | 0 | 0.15 | 28 | 143 | |
| 100 | 0 | 0.15 | 28 | 130 | |
| Haque & Kayali [43] | 0 | 6 | 0.4 | 7 | 62 |
| 0 | 6 | 0.4 | 14 | 70 | |
| 0 | 6 | 0.4 | 28 | 77.5 | |
| 10 | 6 | 0.35 | 7 | 70 | |
| 10 | 6 | 0.35 | 14 | 77.5 | |
| 10 | 6 | 0.35 | 28 | 94 | |
| 10 | 6 | 0.35 | 56 | 99.5 | |
| 15 | 6 | 0.35 | 7 | 58 | |
| 15 | 6 | 0.35 | 14 | 65 | |
| 15 | 6 | 0.35 | 28 | 73.5 | |
| 0 | 7.5 | 0.35 | 7 | 69 | |
| 0 | 7.5 | 0.35 | 14 | 75 | |
| 0 | 7.5 | 0.35 | 28 | 92.5 | |
| 0 | 7.5 | 0.35 | 56 | 106 | |
| 10 | 7.5 | 0.25 | 7 | 84 | |
| 10 | 7.5 | 0.25 | 14 | 93.5 | |
| 10 | 7.5 | 0.25 | 28 | 111 | |
| 10 | 7.5 | 0.25 | 56 | 121.5 | |
| 15 | 7.5 | 0.3 | 7 | 75.5 | |
| 15 | 7.5 | 0.3 | 14 | 89 | |
| 15 | 7.5 | 0.3 | 28 | 102 | |
| 15 | 7.5 | 0.3 | 56 | 113.5 | |
| Hasnat & Ghafoori [38] | 0 | 0 | 0.15 | 1 | 63 |
| 0 | 0 | 0.15 | 7 | 105 | |
| 0 | 0 | 0.15 | 28 | 134 | |
| 0 | 0 | 0.15 | 90 | 153 | |
| 10 | 0 | 0.15 | 1 | 63 | |
| 10 | 0 | 0.15 | 7 | 102 | |
| 10 | 0 | 0.15 | 28 | 129 | |
| 10 | 0 | 0.15 | 90 | 152 | |
| 30 | 0 | 0.15 | 1 | 51 | |
| 30 | 0 | 0.15 | 7 | 90 | |
| 30 | 0 | 0.15 | 28 | 126 | |
| 30 | 0 | 0.15 | 90 | 153 | |
| 40 | 0 | 0.15 | 1 | 47 | |
| 40 | 0 | 0.15 | 7 | 81 | |
| 40 | 0 | 0.15 | 28 | 119 | |
| 40 | 0 | 0.15 | 90 | 151 | |
| Wang et al. [39] | 0 | 0 | 0.1 | 28 | 88 |
| 0 | 0 | 0.12 | 28 | 135 | |
| 0 | 0 | 0.15 | 28 | 122 | |
| 0 | 0 | 0.18 | 28 | 110 | |
| 0 | 0 | 0.2 | 28 | 95 | |
| 0 | 0 | 0.23 | 28 | 88 | |
| 0 | 0 | 0.25 | 28 | 80 | |
| 0 | 0 | 0.3 | 28 | 70 | |
| 20 | 0 | 0.1 | 28 | 125 | |
| 20 | 0 | 0.12 | 28 | 155 | |
| 20 | 0 | 0.15 | 28 | 145 | |
| 20 | 0 | 0.18 | 28 | 135 | |
| 20 | 0 | 0.2 | 28 | 130 | |
| 20 | 0 | 0.23 | 28 | 115 | |
| 20 | 0 | 0.25 | 28 | 110 | |
| 20 | 0 | 0.3 | 28 | 110 | |
| 40 | 0 | 0.1 | 28 | 125 | |
| 40 | 0 | 0.12 | 28 | 135 | |
| 40 | 0 | 0.15 | 28 | 130 | |
| 40 | 0 | 0.18 | 28 | 120 | |
| 40 | 0 | 0.2 | 28 | 110 | |
| 40 | 0 | 0.23 | 28 | 105 | |
| 40 | 0 | 0.25 | 28 | 100 | |
| 40 | 0 | 0.3 | 28 | 100 | |
| 0 | 0 | 0.35 | 3 | 50 | |
| 0 | 0 | 0.35 | 7 | 62 | |
| 0 | 0 | 0.35 | 28 | 48 | |
| 0 | 0 | 0.35 | 90 | 80 | |
| 8 | 0 | 0.35 | 3 | 46 | |
| 8 | 0 | 0.35 | 7 | 75 | |
| 8 | 0 | 0.35 | 28 | 60 | |
| 8 | 0 | 0.35 | 90 | 100 | |
| 15 | 0 | 0.35 | 3 | 47 | |
| 15 | 0 | 0.35 | 7 | 90 | |
| 15 | 0 | 0.35 | 28 | 77 | |
| 15 | 0 | 0.35 | 90 | 110 | |
| 0 | 0 | 0.25 | 3 | 75 | |
| 0 | 0 | 0.25 | 7 | 70 | |
| 0 | 0 | 0.25 | 28 | 90 | |
| 0 | 0 | 0.25 | 90 | 90 | |
| 8 | 0 | 0.25 | 3 | 85 | |
| 8 | 0 | 0.25 | 7 | 87 | |
| 8 | 0 | 0.25 | 28 | 95 | |
| 8 | 0 | 0.25 | 90 | 97 | |
| 15 | 0 | 0.25 | 3 | 92 | |
| 15 | 0 | 0.25 | 7 | 100 | |
| 15 | 0 | 0.25 | 28 | 100 | |
| 15 | 0 | 0.25 | 90 | 100 | |
| Wu et al. [40] | 0 | 0 | 0.2 | 3 | 98 |
| 0 | 0 | 0.2 | 7 | 122 | |
| 0 | 0 | 0.2 | 28 | 150 | |
| 0 | 0 | 0.2 | 90 | 154 | |
| 20 | 0 | 0.2 | 3 | 85 | |
| 20 | 0 | 0.2 | 7 | 105 | |
| 20 | 0 | 0.2 | 28 | 135 | |
| 20 | 0 | 0.2 | 90 | 150 | |
| 40 | 0 | 0.2 | 3 | 85 | |
| 40 | 0 | 0.2 | 7 | 105 | |
| 40 | 0 | 0.2 | 28 | 140 | |
| 40 | 0 | 0.2 | 90 | 165 | |
| 60 | 0 | 0.2 | 3 | 75 | |
| 60 | 0 | 0.2 | 7 | 93 | |
| 60 | 0 | 0.2 | 28 | 140 | |
| 60 | 0 | 0.2 | 90 | 150 | |
| Yazici [41] | 0 | 45 | 0.2 | 28 | 117 |
| 20 | 45 | 0.3 | 28 | 122 | |
| 40 | 45 | 0.4 | 28 | 124 | |
| 60 | 45 | 0.5 | 28 | 117 | |
| 80 | 45 | 0.65 | 28 | 77 | |
| Jaturapitakkul et al. [42] | 15 | 6 | 0.3 | 7 | 70 |
| 15 | 6 | 0.3 | 28 | 80 | |
| 15 | 6 | 0.3 | 56 | 90 | |
| 15 | 6 | 0.3 | 90 | 95 | |
| 15 | 6 | 0.3 | 180 | 100 | |
| 25 | 5.3 | 0.3 | 7 | 70 | |
| 25 | 5.3 | 0.3 | 28 | 82 | |
| 25 | 5.3 | 0.3 | 56 | 92 | |
| 25 | 5.3 | 0.3 | 90 | 95 | |
| 25 | 5.3 | 0.3 | 180 | 100 | |
| 35 | 4.3 | 0.3 | 7 | 70 | |
| 35 | 4.3 | 0.3 | 28 | 80 | |
| 35 | 4.3 | 0.3 | 56 | 88 | |
| 35 | 4.3 | 0.3 | 90 | 93 | |
| 35 | 4.3 | 0.3 | 180 | 100 | |
| 50 | 3.2 | 0.3 | 7 | 70 | |
| 50 | 3.2 | 0.3 | 28 | 77 | |
| 50 | 3.2 | 0.3 | 56 | 84 | |
| 50 | 3.2 | 0.3 | 90 | 87 | |
| 50 | 3.2 | 0.3 | 180 | 91 |
References
- Wu, Z.; Shi, C.; He, W.; Wang, D. Uniaxial Compression Behavior of Ultra-High Performance Concrete with Hybrid Steel Fiber. J. Mater. Civ. Eng. 2016, 28, 06016017. [Google Scholar] [CrossRef]
- Habel, K.; Viviani, M.; Denarié, E.; Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cem. Concr. Res. 2006, 36, 1362–1370. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, D.J.; Ryu, G.S.; Koh, K.T. Tensile behavior of Ultra High Performance Hybrid Fiber Reinforced Concrete. Cem. Concr. Compos. 2012, 34, 172–184. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Z.; Xiao, J.; Wang, D.; Huang, Z.; Fang, Z. A review on ultra high performance concrete: Part I. Raw materials and mixture design. Constr. Build. Mater. 2015, 101, 741–751. [Google Scholar] [CrossRef]
- Kim, H.; Moon, B.; Hu, X.; Lee, H.; Ryu, G.S.; Koh, K.T.; Joh, C.; Kim, B.S.; Keierleber, B. Construction and performance monitoring of innovative ultra-high-performance concrete bridge. Infrastructures 2021, 6, 121. [Google Scholar] [CrossRef]
- Ali, B.; Farooq, M.A.; El Ouni, M.H.; Azab, M.; Elhag, A.B. The combined effect of coir and superplasticizer on the fresh, mechanical, and long-term durability properties of recycled aggregate concrete. J. Build. Eng. 2022, 59, 105009. [Google Scholar] [CrossRef]
- Arshad, S.; Sharif, M.B.; Irfan-Ul-Hassan, M.; Khan, M.; Zhang, J.-L. Efficiency of Supplementary Cementitious Materials and Natural Fiber on Mechanical Performance of Concrete. Arab. J. Sci. Eng. 2020, 45, 8577–8589. [Google Scholar] [CrossRef]
- Abdalla, J.A.; Hawileh, R.A.; Bahurudeen, A.; Jyothsna, G.; Sofi, A.; Shanmugam, V.; Thomas, B. A comprehensive review on the use of natural fibers in cement/geopolymer concrete: A step towards sustainability. Case Stud. Constr. Mater. 2023, 19, e02244. [Google Scholar] [CrossRef]
- RHawileh, R.A.; Mhanna, H.H.; Abdalla, J.A.; AlMomani, D.; Esrep, D.; Obeidat, O.; Ozturk, M. Properties of concrete replaced with different percentages of recycled aggregates. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Mantawy, I.; Chennareddy, R.; Genedy, M.; Taha, M.R. Polymer Concrete for Bridge Deck Closure Joints in Accelerated Bridge Construction. Infrastructures 2019, 4, 31. [Google Scholar] [CrossRef]
- Kurniati, E.O.; Kim, H.-J. Utilizing Industrial By-Products for Sustainable Three-Dimensional-Printed Infrastructure Applications: A Comprehensive Review. Infrastructures 2023, 8, 140. [Google Scholar] [CrossRef]
- Eisa, A.S.; Sabol, P.; Khamis, K.M.; Attia, A.A. Experimental Study on the Structural Response of Reinforced Fly Ash-Based Geopolymer Concrete Members. Infrastructures 2022, 7, 170. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Quadri, S.S.; Abdalla, J.A.; Assad, M.; Thomas, B.S.; Craig, D.; Naser, M.Z. Residual mechanical properties of recycled aggregate concrete at elevated temperatures. Fire Mater. 2023, 48, 138–151. [Google Scholar] [CrossRef]
- Abdalla, J.A.; Hawileh, R.A.; Tariq, R.; Abdelkhalek, M.; Abbas, S.; Khartabil, A.; Khalil, H.T.; Thomas, B.S. Achieving concrete sustainability using crumb rubber and GGBS. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Abdalla, J.A.; Nawaz, W.; Zadeh, A.S.; Mirghani, A.; Al Nassara, A.; Khartabil, A.; Shantia, M. Effects of Replacing Cement with GGBS and Fly Ash on the Flexural and Shear Performance of Reinforced Concrete Beams. Pr. Period. Struct. Des. Constr. 2024, 29, 04024011. [Google Scholar] [CrossRef]
- Tariq, H.; Siddique, R.M.A.; Shah, S.A.R.; Azab, M.; Rehman, A.U.; Qadeer, R.; Ullah, M.K.; Iqbal, F. Mechanical Performance of Polymeric ARGF-Based Fly Ash-Concrete Composites: A Study for Eco-Friendly Circular Economy Application. Polymers 2022, 14, 1774. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Xiao, R.; Zhang, M.; Hu, W.; Bai, Y.; Huang, B. A laboratory investigation of steel to fly ash-based geopolymer paste bonding behavior after exposure to elevated temperatures. Constr. Build. Mater. 2020, 254, 119267. [Google Scholar] [CrossRef]
- Khan, M.; Ali, M. Improvement in concrete behavior with fly ash, silica-fume and coconut fibres. Constr. Build. Mater. 2019, 203, 174–187. [Google Scholar] [CrossRef]
- Ferdosian, I.; Camões, A.; Ribeiro, M. High-volume fly ash paste for developing ultra-high performance concrete (UHPC). Cienc. Tecnol. Dos Mater. 2017, 29, e157–e161. [Google Scholar] [CrossRef]
- JChen, J.; Ng, P.; Li, L.; Kwan, A. Production of High-performance Concrete by Addition of Fly Ash Microsphere and Condensed Silica Fume. Procedia Eng. 2017, 172, 165–171. [Google Scholar] [CrossRef]
- Nath, P.; Sarker, P. Effect of Fly Ash on the Durability Properties of High Strength Concrete. Procedia Eng. 2011, 14, 1149–1156. [Google Scholar] [CrossRef]
- Alsalman, A.; Dang, C.N.; Hale, W.M. Development of ultra-high performance concrete with locally available materials. Constr. Build. Mater. 2017, 133, 135–145. [Google Scholar] [CrossRef]
- Gong, N.; Zhang, N. Predict the compressive strength of ultra high-performance concrete by a hybrid method of machine learning. J. Eng. Appl. Sci. 2023, 70, 107. [Google Scholar] [CrossRef]
- Hu, X.; Shentu, J.; Xie, N.; Huang, Y.; Lei, G.; Hu, H.; Guo, P.; Gong, X. Predicting triaxial compressive strength of high-temperature treated rock using machine learning techniques. J. Rock Mech. Geotech. Eng. 2023, 15, 2072–2082. [Google Scholar] [CrossRef]
- Zhang, Y.; An, S.; Liu, H. Employing the optimization algorithms with machine learning framework to estimate the compressive strength of ultra-high-performance concrete (UHPC). Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 97–108. [Google Scholar] [CrossRef]
- Qian, Y.; Sufian, M.; Accouche, O.; Azab, M. Advanced machine learning algorithms to evaluate the effects of the raw ingredients on flowability and compressive strength of ultra-high-performance concrete. PLoS ONE 2022, 17, e0278161. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Deifalla, A.F.; Kamiński, P.; Dyczko, A. Compressive Strength Evaluation of Ultra-High-Strength Concrete by Machine Learning. Materials 2022, 15, 3523. [Google Scholar] [CrossRef] [PubMed]
- Abuodeh, O.R.; Abdalla, J.A.; Hawileh, R.A. Assessment of compressive strength of Ultra-high Performance Concrete using deep machine learning techniques. Appl. Soft Comput. 2020, 95, 106552. [Google Scholar] [CrossRef]
- Khan, M.; Lao, J.; Dai, J.-G. Comparative study of advanced computational techniques for estimating the compressive strength of UHPC. J. Asian Concr. Fed. 2022, 8, 51–68. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, M.; Shang, X.; Xiong, Y.; Zhang, Y. Predicting the Compressive Strength of UHPC with Coarse Aggregates in the Context of Machine Learning. Case Stud. Constr. Mater. 2023, 19, e02627. [Google Scholar] [CrossRef]
- Marani, A.; Jamali, A.; Nehdi, M.L. Predicting Ultra-High-Performance Concrete Compressive Strength Using Tabular Generative Adversarial Networks. Materials 2020, 13, 4757. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Yu, Z.; Zhu, Y.; Huang, S.; Luo, Q.; Zhang, S. Effect of Lithium-Slag in the Performance of Slag Cement Mortar Based on Least-Squares Support Vector Machine Prediction. Materials 2019, 12, 1652. [Google Scholar] [CrossRef] [PubMed]
- Solhmirzaei, R.; Salehi, H.; Kodur, V.; Naser, M.Z. Machine learning framework for predicting failure mode and shear capacity of ultra high performance concrete beams. Eng. Struct. 2020, 224, 111221. [Google Scholar] [CrossRef]
- Abellan-Garcia, J. Four-layer perceptron approach for strength prediction of UHPC. Constr. Build. Mater. 2020, 256, 119465. [Google Scholar] [CrossRef]
- Fan, D.; Yu, R.; Fu, S.; Yue, L.; Wu, C.; Shui, Z.; Liu, K.; Song, Q.; Sun, M.; Jiang, C. Precise design and characteristics prediction of Ultra-High Performance Concrete (UHPC) based on artificial intelligence techniques. Cem. Concr. Compos. 2021, 122, 104171. [Google Scholar] [CrossRef]
- Serna, P.; Llano-Torre, A.; Martí-Vargas, J.R.; Navarro-Gregori, J. (Eds.) Fibre Reinforced Concrete: Improvements and Innovations RILEM-fib International Symposium on FRC (BEFIB) in 2020; RILEM Bookseries; Springer: Berlin/Heidelberg, Germany, 2021; Available online: http://www.springer.com/series/8781 (accessed on 5 January 2024).
- Hakeem, I.Y.; Althoey, F.; Hosen, A. Mechanical and durability performance of ultra-high-performance concrete incorporating SCMs. Constr. Build. Mater. 2022, 359, 129430. [Google Scholar] [CrossRef]
- Hasnat, A.; Ghafoori, N. Properties of ultra-high performance concrete using optimization of traditional aggregates and pozzolans. Constr. Build. Mater. 2021, 299, 123907. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, D.; Chen, H. The role of fly ash microsphere in the microstructure and macroscopic properties of high-strength concrete. Cem. Concr. Compos. 2017, 83, 125–137. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W. Comparative study on flexural properties of ultra-high performance concrete with supplementary cementitious materials under different curing regimes. Constr. Build. Mater. 2017, 136, 307–313. [Google Scholar] [CrossRef]
- Yazici, H. The effect of curing conditions on compressive strength of ultra high strength concrete with high volume mineral admixtures. Build. Environ. 2007, 42, 2083–2089. [Google Scholar] [CrossRef]
- Jaturapitakkul, C.; Kiattikomol, K.; Sata, V.; Leekeeratikul, T. Use of ground coarse fly ash as a replacement of condensed silica fume in producing high-strength concrete. Cem. Concr. Res 2004, 34, 549–555. [Google Scholar] [CrossRef]
- Haque, M.; Kayali, O. Properties of high-strength concrete using a fine fly ash. Cem. Concr. Res. 1998, 28, 1445–1452. [Google Scholar] [CrossRef]
- Christopher, M. Bishop, Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Schölkopf, B.; Burges, C.J.; Smola, A.J. Advances in Kernel Methods: Support Vector Learning; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Chin-Chung, C. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar]
- Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel Methods in Machine Learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Burges, C.J.C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Schölkopf, B. Kernel Principal Component Analysis. In Proceedings of the Artificial Neural Networks—ICANN’97, Lausanne, Switzerland, 8–10 October 1997; pp. 583–588. [Google Scholar]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification. 2016. Available online: https://www.csie.ntu.edu.tw/~cjlin/ (accessed on 10 January 2024).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safieh, H.; Hawileh, R.A.; Assad, M.; Hajjar, R.; Shaw, S.K.; Abdalla, J. Using Multiple Machine Learning Models to Predict the Strength of UHPC Mixes with Various FA Percentages. Infrastructures 2024, 9, 92. https://doi.org/10.3390/infrastructures9060092
Safieh H, Hawileh RA, Assad M, Hajjar R, Shaw SK, Abdalla J. Using Multiple Machine Learning Models to Predict the Strength of UHPC Mixes with Various FA Percentages. Infrastructures. 2024; 9(6):92. https://doi.org/10.3390/infrastructures9060092
Chicago/Turabian StyleSafieh, Hussam, Rami A. Hawileh, Maha Assad, Rawan Hajjar, Sayan Kumar Shaw, and Jamal Abdalla. 2024. "Using Multiple Machine Learning Models to Predict the Strength of UHPC Mixes with Various FA Percentages" Infrastructures 9, no. 6: 92. https://doi.org/10.3390/infrastructures9060092
APA StyleSafieh, H., Hawileh, R. A., Assad, M., Hajjar, R., Shaw, S. K., & Abdalla, J. (2024). Using Multiple Machine Learning Models to Predict the Strength of UHPC Mixes with Various FA Percentages. Infrastructures, 9(6), 92. https://doi.org/10.3390/infrastructures9060092








