Abstract
This study determines the equivalent stress intensity factor (SIF) model that best fits the experimental behavior of low-carbon steel under mixed modes ( and ). The study assessed Tanaka, Richard, and Pook’s equivalent SIF models. The theoretical values used for comparison correspond to the experimental results in a modified C(T) geometry by machining a hole ahead of the crack tip subjected to fatigue loads with a load ratio of R = 0.1. The comparison involved the SIF for six experimental points and the values computed through the numerical simulation. The Paris, Klesnil, and Modified Forman–Newman crack growth models were used with each equivalent SIF to analyze the prediction in the estimated number of cycles. The Klesnil model showed the closest prediction since the error between the calculated and experimentally recorded number of cycles is the lowest. However, the material behavior reflects a reduced crack propagation rate attributed to plasticity in the crack tip. The results suggest that Asaro equivalent SIF conservatively estimates the element lifespan with increasing errors from 2.3% at the start of growth to 27% at the end of the calculation. This study sheds light on the accuracy and limitations of different equivalent SIF models, providing valuable insights for structural integrity assessments in engineering applications.
1. Introduction
The widely accepted Paris rule correlates the stress intensity factor (SIF) with crack length advance per cycle. However, the Paris rule is commonly established under mode loading. Therefore, when more than one loading mode is present, a crack increment rule under mixed modes and an angle prediction criterion is needed [1,2]. This is one rule to quantify crack length increment and another to quantify crack direction [3]. In the case of mixed-mode fracture, SIFs appear in orthogonal directions, each contributing to crack growth and crack kinking. Several equivalent SIF (Keq) models are based on different principles [4]. Consequently, it is necessary to identify the Keq models that best account for the combination loading modes [5]. Therefore, when more than one loading is present, the choice of Keq impacts the crack growth rate [6]. Previous studies [7,8] suggest a significant decrease in the toughness of metals when mixed-mode failures occur.
Recently, the importance of Keq in fatigue crack growth has been acknowledged in aluminum samples [9,10] and both aluminum and steel specimens [11]. Additionally, numerical studies [12] investigated the effects of mode-mixity in surface cracks, observing a difference in crack growth rate under mixed modes in steel. Moreover, Berrios-Barcena et al. [13] reproduced FCG in a double cantilever sample of low-carbon steel. Further research by Dirik and T. Yalçinkaya [14] tested the Tanaka model against numerical simulations. Compact tension (CT) samples were subjected to mode , , and loading where Pook’s and Richard’s Keq models were calculated [15]. On the other hand, Sajith et al. [16] compared various Keq models using the Paris rule and found an acceptable agreement for the Tanaka and Irwin models. Furthermore, Zhan and Zhang [17] explored various crack growth models considering load amplitude. Additionally, Silva et al. [18] focused on the Tanaka Keq model combined with the Paris rule, finding a good correlation but lacking comparison to other models. Finally, Tavares and Castro [10] compared several Keq models in an Al sample but only in combination with the Paris rule; hence, load inversion ratio, fatigue threshold, and fracture toughness were left out of the analysis. Consequently, the literature review revealed no consensus on the Keq model that best describes fatigue crack growth (FCG).
The structural integrity of an element is characterized by how it experiences failure, which is categorized into three fracture modes: mode , where the stresses act perpendicular to the crack, generating the separation of the opposing faces; mode , characterized by shear stresses causing in-plane crack edge displacement; and mode , involving out-of-plane stress, usually associated with elements subjected to torsion [4]. Figure 1 shows an example of the three opening modes occurring simultaneously. In linear elastic fracture mechanics (LEFM), the stress field ahead of the crack tip is described by the SIF in each direction. Additionally, LEFM provides tools to assess the lifespan of mechanical elements with flaws [14]. Moreover, a crack is a flaw in a solid, which can be produced by a stress gradient, corrosion, plastic deformation, fatigue [4], or thickness reduction [19], which requires adequate stress and time [14]. A body subjected to alternating loads, below its elastic limit, presents a localized plastic phenomenon known as fatigue, which causes the crack to grow in length and change its direction if more than one stress direction is involved [1,2]. Mixed-mode loading may also occur due to multiaxial loads, a stress concentrator, or a crack. Furthermore, the fracture toughness (Kc) measures the material’s resistance to crack propagation [20] as a parameter for assessing failure in cracked bodies. However, in practical case scenarios, a body is subjected to multiaxial loads, and therefore it is necessary to consider a mixed-mode fracture [21]. Here is where the models to quantify the combination of SIF under mixed modes come into play [5].
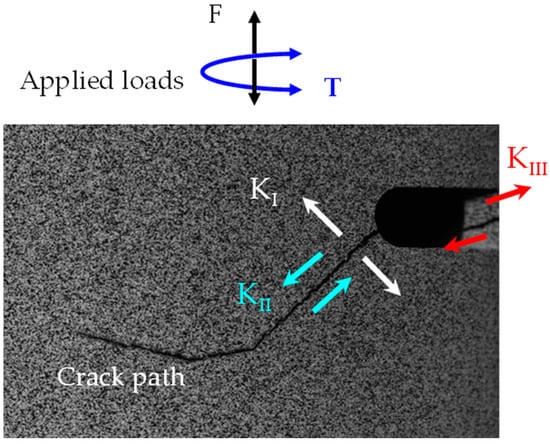
Figure 1.
Example of tubular specimen subjected to fully inversed axial (F) and torque (T) loads showing three opening modes. Adapted from [3].
Moreover, FCG is usually conducted using analytical methods for simple loading cases, numerical methods [12,13,14], a combination of both, or even with non-parametric models [22]. A review of some of them can be found in [23]. The choice of the Keq may impact crack growth prediction. In this study, we compare the finite element method implemented in ANSYS’s (Separating Morphing and Adaptive Remeshing Technology (SMART)) with the dual boundary element method (BEM), which is implemented and described elsewhere [24] for FCG under mixed modes ( and ).
In this paper, a comparison is made between three Keq models combined with three FCG models, each covering different zones of the Paris plot. There has been a lack of studies concurrently exploring multiple Keq models with different crack growth models to assess the combination that best matches experimental results. This study seeks to fill this void by providing a comprehensive analysis that evaluates the performance of different Keq and crack growth model combinations under varying experimental conditions. Additionally, numerical results are validated with experimental data from the literature at ambient temperature.
2. Background
This section provides the formulations used on the paper.
2.1. Equivalent SIF Models
Despite the wide variety of models available, this paper evaluates three, each with a distinct formulation. Some models are experiment-based, while others are based on numerical data fitting.
The Tanaka criterion [25,26] is derived from the Weertman dislocation model [27], which determines that crack propagation occurs when strains in the plastic zone reach the critical value. Equation (1) represents the formula for the Tanaka model, which has demonstrated a close correlation between experimental and numerical results, particularly for steel specimens [28].
where Ki is the SIF and is the Poisson ratio. Moreover, Asaro’s analysis of stresses at the crack tip derived from the consideration of the release of potential energy [29] is represented by Equation (2). Furthermore, due to the influence of the Poisson ratio, this model depends on either plane stress or plain conditions if mode is present.
Pook [30] proposed the value of Keq for the formula shown in Equation (3) for a beam subjected to three-point bending. Although the tests on the specimen initially anticipated a dominant mode , the crack tip rotation occurred until it was eventually aligned with the specimen’s side.
Accordingly, one can see that an appropriate equivalent SIF model defines the accuracy of the lifespan estimation [31].
2.2. Crack Growth Models
Understanding crack growth is essential for assessing the lifespan of structural components. This section examines three models.
The Paris rule, shown in Equation (4), establishes a relationship between the crack growth rate and the equivalent SIF [32], where a corresponds to the crack size and N to the number of cycles and the constants C and m depend on the material, geometry, and test conditions. However, this model is only valid for stable crack growth and does not account for the load inversion rate [33].
The Klesnil–Lukas model, represented by Equation (5), introduces the concept of the fracture threshold, Kth, which is particularly useful in cases where the applied load either does not cause crack growth or barely exceeds the threshold value. The constants C and m remain consistent with those in the Paris rule [34].
A more detailed model, the Modified Forman–Newman, can describe the three regions of crack growth by incorporating the threshold and fracture toughness, , as depicted in Equation (6).
where the additional constants , , and are adjusted to experimental results and R represents the load reversal ratio.
Figure 2 illustrates the comparison between the Paris, Klesnil, and Modified Forman–Newman models for R = 0.1. The Klesnil model exhibits conservative behavior in Region . As it enters Region II, its trend converges with the Paris rule. Finally, the modified Forman–Newman model predicts less conservatively, with higher growth rates, and can predict unstable growth in Region . In all models, the lifespan of each crack increment Δa or increment in cycles ΔN can be estimated by separating variables in Equation (4). In the case scenario of mixed-mode loading, the crack increment is a function of Keq or ΔKeq for alternating loads [2]. Integrating the Paris rule yields Equation (7), incorporating established parameters and introducing the variable T to accommodate additional terms alongside the constants C and m as described in the Klesnil–Lukas and Forman–Newman models.
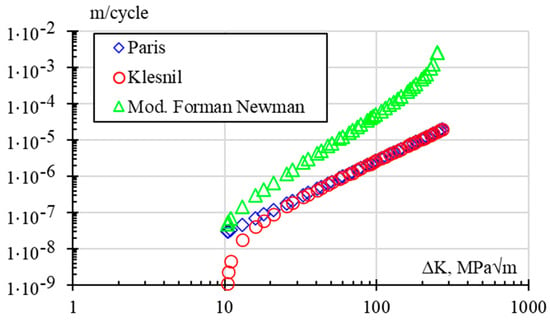
Figure 2.
Comparison of crack propagation models: Paris, Klesnil, and Modified Forman–Newman.
Moreover, fully defining the crack path under mixed modes requires establishing the crack kinking angle , as shown in Equation (8). The model is derived from the maximum tangential stress (MTS) criterion [14]. Recent evaluations of several models based on experimental data concluded that, in some cases, the computational cost could be high despite reducing the error in prediction [2].
3. Materials and Methods
A modified C(T) specimen data, as shown in Figure 3, was retrieved from the literature [35], where SIFs were experimentally estimated for different crack lengths. The sample was made of low-carbon steel and had a material composition detailed in Table 1. The specimen was drilled to modify the stress fields ahead of the crack tip, inducing mixed modes and . Sample dimensions are shown in Figure 3a.
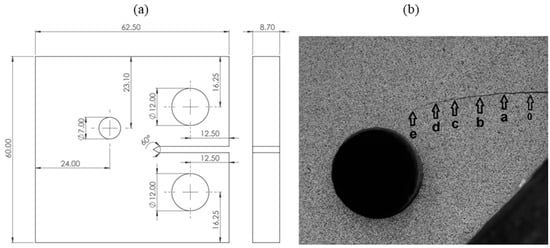
Figure 3.
Modified C(T) specimen; (a) dimensions in [mm] accordance with ASTM E647, (b) location of six reported intervals named 0 to e [30].

Table 1.
Material composition for modified C(T) sample.
The modified C(T) specimen initially developed a horizontal crack, which later curved due to the influence of the drilled hole. The SIF ranges in modes and were found by fitting displacement fields to Williams’ displacement model in an infinite plate using the digital image correlation (DIC) technique, as extensively detailed in [35]. Thus, calculations were conducted for six crack lengths, designated as 0, a, b, c, d, and e, respectively, as illustrated in Figure 3b, with numerical values in Table 2. Extensive details about SIF calculations are available in [35].

Table 2.
Experimental parameters C(T) sample [35].
Once the experimental results were available for evaluating the numerical models, obtaining the crack growth constants was necessary, as depicted in Table 3. For the Paris rule, tests with R = 0.1 are required. As for the Forman and Modified Forman–Newman models, data for low-carbon plain steels can be found in the literature [36].

Table 3.
Crack growth models parameters [22].
Therefore, to assess the equivalent SIF models, both the Finite Element Method (FEM) and the Dual Boundary Element Method (DBEM) [37] were employed. ANSYS introduced the SMART methodology, which allows for dynamic mesh adjustments during the simulation progression [9]. This technology has been recently assessed and successfully compared to experimental results [38]. The geometry, as illustrated in Figure 3a, was modeled in ANSYS, using quadratic tetrahedral meshing, with an influence sphere of 20 mm around the crack tip and element size of 0.5 mm, this resulted in a mesh comprising 127,305 nodes and 91,640 elements shown in Figure 4a. Boundary conditions consisted of free cylindrical support in the radial direction and an average bearing load of 5420 N. The analysis configuration involved 15 steps, aligning with the experimental crack length.
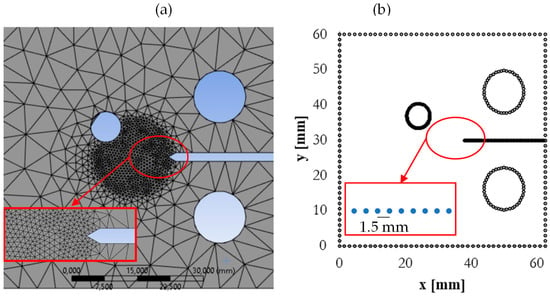
Figure 4.
Mesh details for the modified C(T) sample achieved by; (a) FEM; (b) BEM.
On the other hand, the DBEM simplifies 2D problems to one dimension, facilitating meshing and reducing computational costs [37]. The GID 16.0.7 software was used for the geometric modeling, as shown in Figure 4b, which displays the mesh nodes. Boundary conditions were set for a plane stress problem, resulting in 458 nodes and 229 elements. The lower left corner was fixed in both directions, and the upper left corner was constrained in the x-direction. Elements of 0.5 mm in length were used at the crack tip, and the mesh was refined by implementing 30 elements around the drilled hole, which the crack tip approached as it grew. The implementation of the DBEM method was carried out using an in-house code described somewhere else [24]. It was noted that the computation time was shorter than with FEM. Each simulation lasted approximately 18 s, unlike FEM simulations, which took about 15.37 min using the same computer.
4. Results
4.1. Parametric Models
Table 4 displays the SIF values obtained using the equivalent SIF models previously described. Employing the presented crack growth models is feasible based on the results obtained. Since the crack increment Δa is known, Equation (7) can be applied to determine the estimated number of cycles N. This procedure was executed for each growth model. As a result, graphs illustrate the calculated number of cycles for each interval about the experimentally recorded cycles and the percentage error.

Table 4.
Equivalent SIF (MPa√m) models results from experimental values.
4.2. Paris Rule
In this case, a conservative prediction is obtained (Figure 5). The error decreases after the third interval once the curvature of the crack becomes noticeable. The SIF model with the lowest mean percentage error, 40.9, corresponds to the one presented by Tanaka.
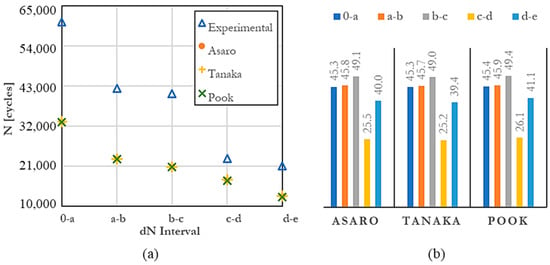
Figure 5.
Estimated cycles with the Paris rule; (a) Numerical vs. dN interval; (b) Mean percentage error concerning each interval of dN.
4.3. Modified Forman Newman
When evaluating the Forman–Newman model (Figure 6), the prediction for the first interval diverges from the conservative trend. However, subsequent intervals exhibit a deviation from the experimental results. At the point of the highest growth rate, the prediction tends to be conservative. Notably, both projections are significantly close in the fourth interval. Beyond this point, as the crack curve assumes higher values, indicating the onset of unstable crack growth. However, the number of experimental cycles remains higher. This phenomenon could be attributed to the yielding at the crack tip due to the material’s ductility.
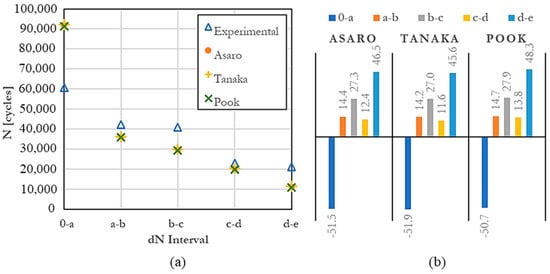
Figure 6.
Estimated cycles with the Modified Forman–Newman model; (a) Numerical vs. dN interval; (b) Mean percentage error with respect to each interval of dN.
4.4. Klesnil
Finally, the growth model that presented the lowest average error percentage was Klesnil. This behavior can be attributed to the influence of the fatigue threshold, , indicating that its predictions are more accurate for cracks propagating in Regions and . When comparing the material’s toughness with the recorded values, it becomes evident that the material is in the transition zone towards Region , where the growth rate tends to stabilize. Moreover, by using Paris’s constants, Klesnil incorporates a specific R. In Figure 7, a conservative trend in cycle predictions is observable, consistent with the previous models, and it satisfactorily aligns with the recorded experimental value in the fourth interval.
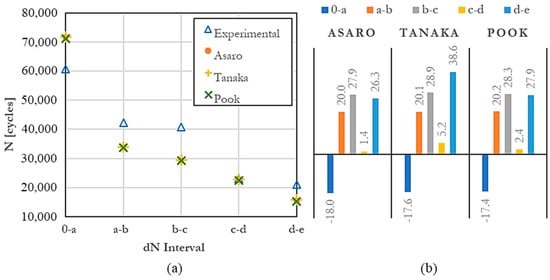
Figure 7.
Estimated cycles with the Klesnil model; (a) Numerical vs. dN interval; (b) Mean percentage error concerning each interval of dN.
The results obtained from the growth models reveal that Asaro’s SIF model demonstrated the lowest average percentage error for each of the proposed crack growth models, as shown in Figure 8.
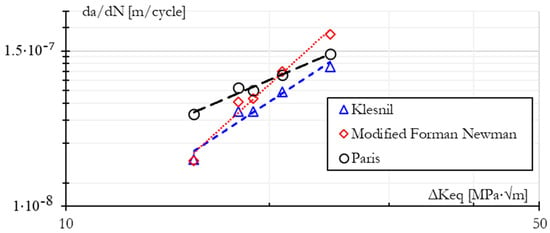
Figure 8.
Fatigue crack growth using Keq Asaro.
The Klesnil model yields intermediate results compared to the other models during the initial intervals. As the growth rate increases, all three models tend to linearize. Upon closer examination of the Klesnil model, its proximity to Kth might be the cause. It is noteworthy that both this model and the Modified Forman–Newman model only consider mode in their adjustment parameters, as there is no specific methodology to calculate them in mixed modes. However, studies suggest that the initial crack propagation energy is higher when the mixed mode is present, especially when the presence of KII is noticeable and KI decreases [39].
Figure 9 compares the most suitable combination of the crack growth model and equivalent SIF (Asaro–Klesnil) with the experimentally obtained data. The results tend to be slightly conservative, with a difference of 10% in the total number of cycles. This trend can be attributed to various phenomena that smooth the crack tip, due to either the material’s chemical or morphological composition or additional overload conditions [40].
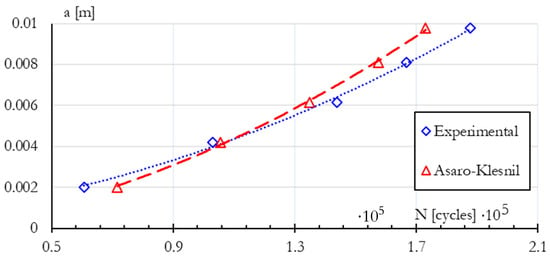
Figure 9.
Crack growth models using Asaro–Klesnil.
4.5. Numerical FEM
Following the acquisition of the results from the two numerical methods, the comparison is depicted in Figure 10 alongside the experimental results. Figure 10a shows a similarity in the increase in the SIF concerning the crack size between the FEM simulation and the experimental results. This factor is related to the ratio between the crack size and the specimen width. However, In Figure 10b, this trend does not persist, possibly due to the relatively low values attained by . In FEM, results are computed concerning the immediately preceding interval, requiring the establishment of a new coordinate system at each evaluated point. During the final measured intervals, the crack exhibits its highest curvature about the initial measurement point. However, when measured from the immediately preceding point, the curvature is minimal. These results are reflected in the values recorded by FEM, although the simulation shows a trajectory similar to experiments [2].
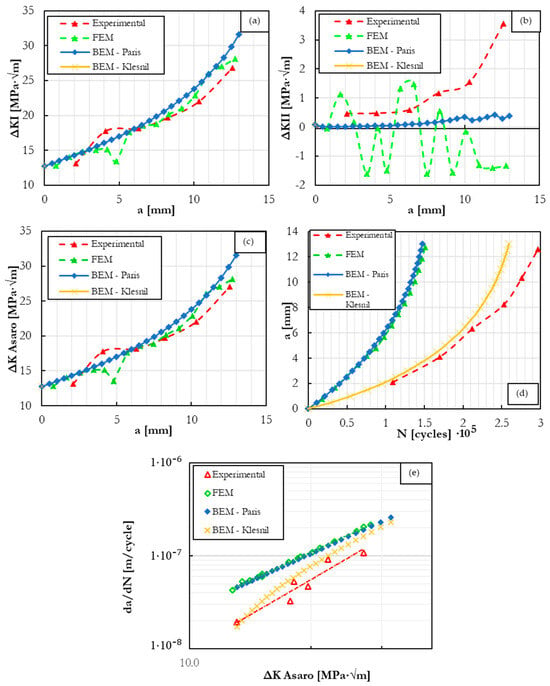
Figure 10.
(a) a [mm]; (b) a [mm]; (c) a [mm]; (d) e) .
Figure 10c displays the results of the equivalent SIF concerning the crack size. FEM results are higher compared to the experimental ones, as the values of were also high. However, accelerated growth is observed after reaching 35% of the total crack size. The results associated with the SIF and crack size are similar in the numerical methods and experimental results. Figure 10d illustrates that the simulations yield a conservative result regarding the relationship between the crack size and the number of cycles. This is because the SIF values are close, and this difference is reflected in the growth rate, especially in the growth constants, as shown in Figure 10e. The experimental growth rate was slower; this is evident in the first reported value for the equivalent SIF, which is practically equal but experimentally corresponded to 109,000 cycles, while in the FEM simulation, it was reached at 18,100 cycles.
4.6. Numerical BEM
The results of the BEM numerical method are split into two groups: the results with the Paris rule (BEM–Paris) and Klesnil (BEM–Klesnil). In Figure 10a, the reported values of ΔKI are higher than the experimentally reported ones; however, they exhibit a similar trend to the FEM values. Figure 10a shows that the reported values for ΔKII are near zero. However, the experimental values measured the horizontal deformation of the specimen, while neither of the two numerical methods accurately estimated this value; in the case of the programs, none calculates it this way. Additionally, the values of ΔKI and ΔKII are equal in the case of BEM–Paris and BEM–Klesnil. In Figure 10c, the trend exhibits a behavior similar to Figure 10a because ΔK Asaro predominates over the influence of ΔKI. In Figure 10d, in the case of BEM–Paris, the results are equal to those reported by FEM, which also employs the same growth model, and when determining the crack propagation, the Keq is the same.
In contrast, in the BEM–Klesnil combination, the crack propagation rate is slower at the beginning; this may reflect some plasticity ahead of the crack tip [41]. In this case, the reported values are close to the experimental ones. It is important to emphasize that for this figure, the implemented growth constants were those of mode reported in Table 3. Finally, in Figure 10e, where the growth rate is presented concerning the equivalent SIF, the results of BEM–Paris are the same as those of FEM for the reasons discussed earlier. A slow initial growth in BEM–Klesnil can be observed.
Additionally, some of the points overlap with the experimental ones. However, the general experimental growth continues to present a lower rate. In this case, new constants are proposed for mode /, for which a potential adjustment was made, obtaining the constants C and m reported in Table 5.

Table 5.
Mixed-mode Paris constants for experimental data.
Simulations were rerun but implementing the constants reported in Table 5. In this case, the values of ΔKI and ΔKII are minimal; thus, we omitted these graphs for practicality. Figure 11a illustrates that all the results, except BEM–Klesnil, overlap. However, as the propagation progresses, the results converge as Region II develops. Figure 11b demonstrates that both numerical methods present acceptable predictions, even slightly conservative compared to the experimental results. If specific constants are known for mixed modes, it is possible to use the Paris rule. In this case, the Klesnil model predicts a conservative number of almost double cycles. This is because, in this case, the constants already consider slow growth. This model is appropriate if the specimen presents slow propagation and only the Paris constants are known for mode .
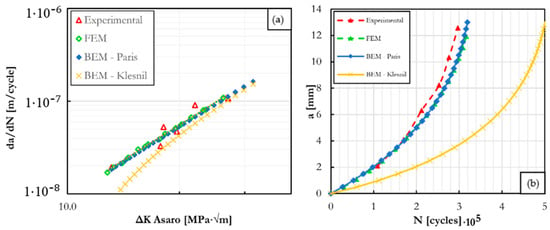
Figure 11.
Crack growth implementing mixed mode constants; (a) ; (b) .
5. Discussion
Tavares and Castro [10] recently argued that although different SIF may yield the same, different KI/KII ratios may produce different FCG rates. In Table 3, we showed a decrease in growth constants for . This implies a potential reduction in mixed-mode Paris constants. Such a trend is consistent with the findings of Heirani and Farhangdoost [42], where changes in constants were noted based on the severity of the applied mixed mode. However, a definitive trend was not identified, attributing the variation to shifts in force distribution throughout the body as the mixed modes become more pronounced. Nevertheless, it is evident that alterations in loading conditions, such as changes in mode mixity, can lead to corresponding adjustments in growth constants, as highlighted before [43].
The experimental data acquired through DIC were processed and compared with numerical methods FEM and BEM (see Figure 10a,b). The results unveiled a consistent trend of higher values in FEM, aligning with other studies [44]. However, it has been shown that FEM cannot reproduce conditions such as fatigue-induced plasticity, crack roughness, debris, friction, crack flank interlocking, and the microstructural effect on the crack path [45]. Their impact on LEFM parameters can be seen when selecting the experimental data to work with. For example, choosing the full field displacement may capture the plasticity in the very near region potentially leading to higher KI, or it may yield negative KI values if the fields are in compression. Alternatively, choosing points behind the crack tip may pick the effect of crack roughness and crack flank interlocking [46,47], which may shadow KII. Additionally, the CP was satisfactorily studied somewhere else [47]. Of course, these scenarios are out of scope, but they are worth mentioning.
Other researchers [48] have encountered similar results, addressing them by implementing a theta-method in FEM simulations to calculate values and computing the crack opening displacement factor (COD) using DIC data or the J integral to avoid the plasticity fields around the crack tip [46]. However, in our experience, the J integral implementation for mixed-mode fields has been a challenge. Similarly, in the study by [49], it was resolved through a hybrid experimental–computational approach. The FEM robustness and RPIM (Reduced-Order Proper Orthogonal Decomposition Integration Method) computations were experimentally validated, through Thermal Stress Analysis (TSA), with the achieved SIF solution. Such an approach appears suitable for cases of mixed-mode loading and could serve as a potential solution for this issue.
Regarding , the simulations did not show a specific trend, potentially due to their low magnitudes. However, a consistent pattern emerged, showing higher values for both and in FEM [50], as reported in Figure 10d. For future studies, it is essential to recognize that achieving convergence between experimental and computational results may require the implementation of alternative algorithms.
The sample’s thickness and the assumption of plain strain conditions influence the accuracy of computational predictions. Despite the sample’s relatively small thickness (only 8.7 mm), the assumptions regarding plain strain conditions influenced the computational results. In the BEM simulations, the superficial calculation led to lower values than experimental findings [51], see Figure 10c. This discrepancy suggests that the idealized conditions assumed in the computational model may not fully represent the real-world behavior of the material.
Examining the relationship between crack size and the number of cycles, the discrepancy reaches 100% at its peak. This can be attributed to crack tip-induced plasticity, as the material is a low-carbon steel. According to the COD formulation, the plasticity mechanisms governing crack closure [52] are proportional to the SIF but inversely proportional to r0.5, significantly influencing the experimental growth slope [53] as shown in Figure 10e.
6. Conclusions
Three fatigue crack growth rules (Paris, Klesnil–Lukas, and Modified Forman–Newman) were tested with experimental data from the literature combined with three equivalent SIF models (Asaro, Pook, and Tanaka). It was found that the equivalent Stress Intensity Factor (SIF) model proposed by Asaro exhibits the lowest percentage error in predicting cycle differentials among the evaluated growth models, with a mean error within the range of 18.4–41.2%. Asaro, Tanaka, and Pook’s models exhibit close results, originating from maximum stress theoretical principles, resulting in conservative predictions for Experimental and values compared to ASTM E647-23, which are notably lower in the initial three intervals (where mostly mode is present), leading to slower crack propagation. This phenomenon may be attributed to localized plasticity.
If specific constants are known for mixed modes, it is possible to use the Paris rule. When not available, the Klesnil fatigue crack growth model showed the smallest range of error in predicting cycle differentials, ranging from 18.4% to 22.1%. The total cycle count calculation using the Asaro equivalent SIF model showed slightly conservative behavior, with a satisfactory adjustment of 10%. The Klesnil growth model offered closer predictions due to its ability to model regions and of crack propagation. Observing the material’s propagation threshold, SIF values indicated that the data reside at the entry limit of Region .
DIC-acquired and processed experimental data were compared against commercial FEM and BEM numerical methods using SIF as a benchmark. The comparison revealed a higher value in FEM, agreeing with other studies [39]. Differences were attributed to idealized conditions in the simulations, notably impacting values without a specific trend. Notably, BEM’s over-the-surface calculations led to lower values, as shown in Figure 10c.
Author Contributions
Conceptualization J.G.D.-R. and M.d.J.M., Software E.G.-G. and J.A.M.-V., Writing—original draft E.G.-G., J.A.M.-V. and O.R.B.-B., Writing—review & editing J.G.D.-R. and M.d.J.M., Formal analysis J.G.D.-R., E.G.-G., J.A.M.-V., O.R.B.-B. and M.d.J.M., Investigation J.G.D.-R., E.G.-G. and J.A.M.-V., Methodology J.G.D.-R., E.G.-G. and J.A.M.-V., Supervision M.d.J.M. and O.R.B.-B., Visualization E.G.-G. and J.A.M.-V., Validation E.G.-G. and J.A.M.-V., Resources J.G.D.-R., E.G.-G., J.A.M.-V., O.R.B.-B. and M.d.J.M., Funding acquisition J.G.D.-R., E.G.-G., J.A.M.-V., O.R.B.-B. and M.d.J.M., Data curation J.G.D.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is available upon reasonable request.
Acknowledgments
The authors acknowledge the editors and reviewers’ effort revising the manuscript. The help of C. A. Hernández solving some simulation issues is greatly appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mróz, K.P.; Mróz, Z. On crack path evolution rules. Eng. Fract. Mech. 2010, 77, 1781–1807. [Google Scholar] [CrossRef]
- Díaz, J.G.; Freire, J.L.d.F. LEFM crack path models evaluation under proportional and non-proportional load in low carbon steels using digital image correlation data. Int. J. Fatigue 2022, 156, 106687. [Google Scholar] [CrossRef]
- Bouchard, P.O.; Bay, F.; Chastel, Y. Numerical modelling of crack propagation: Automatic remeshing and comparison of different criteria. Comput. Methods Appl. Mech. Eng. 2003, 192, 3887–3908. [Google Scholar] [CrossRef]
- Richard, H.A.; Sander, M. Fatigue Crack Growth: Detect—Assess—Avoid; Springer: Berlin/Heidelberg, Germany, 2016; Volume 227. [Google Scholar]
- Radaj, D.; Vormwald, M. Advanced Methods of Fatigue Assessment, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Sajith, S.; Murthy, K.S.R.K.; Robi, P.S. Fatigue crack growth and life prediction under mixed-mode loading. AIP Conf. Proc. 2018, 1943, 020068. [Google Scholar] [CrossRef]
- Floros, I.S.; Tserpes, K.I.; Löbel, T. Mode-I, mode-II and mixed-mode I + II fracture behavior of composite bonded joints: Experimental characterization and numerical simulation. Compos. B Eng. 2015, 78, 459–468. [Google Scholar] [CrossRef]
- Srinivas, M.; Kamat, S.V. Effect of strain rate on fracture toughness of mild steel. Mater. Sci. Technol. 2001, 17, 529–535. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory. Materials 2022, 15, 363. [Google Scholar] [CrossRef]
- Tavares, S.M.O.; de Castro, P.M.S.T. Equivalent Stress Intensity Factor: The Consequences of the Lack of a Unique Definition. Appl. Sci. 2023, 13, 4820. [Google Scholar] [CrossRef]
- Kanth, S.A.; Harmain, G.A.; Jameel, A. Modeling of Nonlinear Crack Growth in Steel and Aluminum Alloys by the Element Free Galerkin Method. Mater. Today Proc. 2018, 5, 18805–18814. [Google Scholar] [CrossRef]
- Yarullin, R.R.; Yakovlev, M.M.; Boychenko, N.V.; Lyadov, N.M. Effect of mixed-mode loading on surface crack propagation in steels. Eng. Fract. Mech. 2024, 295, 109717. [Google Scholar] [CrossRef]
- Berrios-Barcena, D.R.; Franco-Rodríguez, R.; Rumiche-Zapata, F.A. Calibration of nasgro equation for mixed-mode loading using experimental and numerical data. Rev. Fac. Ing. Univ. Antioq. 2019, 97, 65–77. [Google Scholar] [CrossRef]
- Dirik, H.; Yalçinkaya, T. Crack path and life prediction under mixed mode cyclic variable amplitude loading through XFEM. Int. J. Fatigue 2018, 114, 34–50. [Google Scholar] [CrossRef]
- Martins, R.F.; Ferreira, L. Stress intensity factors KI, KII, KIII, Keq, induced at the crack tip of CT specimens subjected to torsional loading. Procedia Struct. Integr. 2020, 28, 74–83. [Google Scholar] [CrossRef]
- Sajith, S.; Krishna Murthy, K.S.R.; Robi, P.S. Prediction of Accurate Mixed Mode Fatigue Crack Growth Curves using the Paris’ Law. J. Inst. Eng. India Ser. C 2019, 100, 165–174. [Google Scholar] [CrossRef]
- Zhan, W.; Lu, N.; Zhang, C. A new approximate model for the R-ratio effect on fatigue crack growth rate. Eng. Fract. Mech. 2014, 119, 85–96. [Google Scholar] [CrossRef]
- Silva, A.L.L.; de Jesus, A.M.P.; Xavier, J.; Correia, J.A.F.O.; Fernandes, A.A. Combined analytical-numerical methodologies for the evaluation of mixed-mode (I + II) fatigue crack growth rates in structural steels. Eng. Fract. Mech. 2017, 185, 124–138. [Google Scholar] [CrossRef]
- Abduljabbar, A.; Khazal, H.; Hassan, A.K.F. Experimental study on repair of cracked pipe under internal pressure. Period. Eng. Nat. Sci. PEN 2022, 10, 67. [Google Scholar] [CrossRef]
- Zhu, X.-K.; Joyce, J.A. Review of fracture toughness (G, K, J, CTOD, CTOA) testing and standardization. Eng. Fract. Mech. 2012, 85, 1–46. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhang, B.C.; Li, Q. A review on mixed mode fracture of metals. Eng. Fract. Mech. 2020, 235, 107126. [Google Scholar] [CrossRef]
- Wang, B.; Xie, L.; Song, J.; Zhao, B.; Li, C.; Zhao, Z. Curved fatigue crack growth prediction under variable amplitude loading by artificial neural network. Int. J. Fatigue 2021, 142, 105886. [Google Scholar] [CrossRef]
- Surendran, M.; Natarajan, S.; Palani, G.S.; Bordas, S.P.A. Linear smoothed extended finite element method for fatigue crack growth simulations. Eng. Fract. Mech. 2019, 206, 551–564. [Google Scholar] [CrossRef]
- Mantilla Villalobos, J.A.; Poveda Díaz, D.E.; del Jesús Martínez, M. Estimación del factor de intensidad de esfuerzo en una probeta wedge splitting bajo carga estática mediante el método de elementos finitos. Respuestas 2021, 26, 53–61. [Google Scholar] [CrossRef]
- Tanaka, K. Fatigue crack propagation from a crack inclined to the cyclic tensile axis. Eng. Fract. Mech. 1974, 6, 493–507. [Google Scholar] [CrossRef]
- Wang, H.; Tanaka, S.; Oterkus, S.; Oterkus, E. Study on two-dimensional mixed-mode fatigue crack growth employing ordinary state-based peridynamics. Theor. Appl. Fract. Mech. 2023, 124, 103761. [Google Scholar] [CrossRef]
- Weertman, J. Rate of growth of fatigue cracks calculated from the theory of infinitesimal dislocations distributed on a plane. Int. J. Fract. 1984, 26, 308–315. [Google Scholar] [CrossRef]
- Sajith, S.; Shukla, S.S.; Murthy, K.S.R.K.; Robi, P.S. Mixed mode fatigue crack growth studies in AISI 316 stainless steel. Eur. J. Mech. A/Solids 2020, 80, 103898. [Google Scholar] [CrossRef]
- Newman, C.J.; Raju, I.S. Stress intensity factor equations for cracks in three-Dimensional finite bodies. ASTM Spec. Tech. Publ. 1983, 791, 238–265. [Google Scholar]
- Pook, L.P. The Significance of Mode I Branch Cracks for Combined Mode Failure. In Fracture and Fatigue; Elsevier: Amsterdam, The Netherlands, 1980; pp. 143–153. [Google Scholar] [CrossRef]
- Kim, J.-H.; Paulino, G.H. T-stress, mixed-mode stress intensity factors, and crack initiation angles in functionally graded materials: A unified approach using the interaction integral method. Comput. Methods Appl. Mech. Eng. 2003, 192, 1463–1494. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Fluids Eng. Trans. ASME 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Branco, R.; Antunes, F.V.; Martins Ferreira, J.A.; Silva, J.M. Determination of Paris law constants with a reverse engineering technique. Eng. Fail. Anal. 2009, 16, 631–638. [Google Scholar] [CrossRef]
- Klesnil, M.; Lukáš, P. Influence of strength and stress history on growth and stabilisation of fatigue cracks. Eng. Fract. Mech. 1972, 4, 77–92. [Google Scholar] [CrossRef]
- Díaz Rodríguez, J.G.; Gonzales, G.; Ortiz Gonzalez, J.A.; Freire, J. Analysis of Mixed-mode Stress Intensity Factors using Digital Image Correlation Displacement Fields. In Proceedings of the 24th ABCM International Congress of Mechanicl Engineering, ABCM, Curitiba, Brazil, 3–8 December 2017. [Google Scholar] [CrossRef]
- Ferreira, S.E.; Castro, J.T.P.; Meggiolaro, M.A. Fatigue crack growth predictions based on damage accumulation ahead of the crack tip calculated by strip-yield procedures. Int. J. Fatigue 2018, 115, 89–106. [Google Scholar] [CrossRef]
- Portela, A.; Aliabadi, M.H.; Rooke, D.P. The dual boundary element method: Effective implementation for crack problems. Int. J. Numer. Methods Eng. 1992, 33, 1269–1287. [Google Scholar] [CrossRef]
- Fageehi, Y.A.; Alshoaibi, A.M. Investigating the Influence of Holes as Crack Arrestors in Simulating Crack Growth Behavior Using Finite Element Method. Appl. Sci. 2024, 14, 897. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhang, B.; Bian, Y.; Li, C.Q. Fracture resistance characteristics of mild steel under mixed mode I-II loading. Eng. Fract. Mech. 2021, 258, 108044. [Google Scholar] [CrossRef]
- Cruces, A.S.; Mokhtarishirazabad, M.; Moreno, B.; Zanganeh, M.; Lopez-Crespo, P. Study of the biaxial fatigue behaviour and overloads on S355 low carbon steel. Int. J. Fatigue 2020, 134, 105466. [Google Scholar] [CrossRef]
- Palacios-Pineda, L.M.; Hernandez-Reséndiz, J.E.; Martínez-Romero, O.; Hernandez Donado, R.J.; Tenorio-Quevedo, J.; Jiménez-Cedeño, I.H.; López-Vega, C.; Olvera-Trejo, D.; Elías-Zúñiga, A. Study of the Evolution of the Plastic Zone and Residual Stress in a Notched T-6061 Aluminum Sample. Materials 2022, 15, 1546. [Google Scholar] [CrossRef] [PubMed]
- Heirani, H.; Farhangdoost, K. Mixed mode I/II fatigue crack growth under tensile or compressive far-field loading. Mater. Res. Express 2017, 4, 116505. [Google Scholar] [CrossRef]
- Shukla, S.S.; Murthy, K.S.R.K. A study on the effect of different Paris constants in mixed mode (I/II) fatigue life prediction in Al 7075-T6 alloy. Int. J. Fatigue 2023, 176, 107895. [Google Scholar] [CrossRef]
- Sabsabi, M.; Giner, E.; Fuenmayor, F.J. Experimental fatigue testing of a fretting complete contact and numerical life correlation using X-FEM. Int. J. Fatigue 2011, 33, 811–822. [Google Scholar] [CrossRef]
- Proudhon, H.; Basseville, S. Finite element analysis of fretting crack propagation. Eng. Fract. Mech. 2011, 78, 685–694. [Google Scholar] [CrossRef][Green Version]
- Gonzáles, G.L.G.; Diaz, J.G.; González, J.A.O.; Castro, J.T.P.; Freire, J.L.F. Determining SIFs Using DIC Considering Crack Closure and Blunting. In Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2017; Volume 4, pp. 25–36. [Google Scholar] [CrossRef]
- Díaz-Rodríguez, J.G.; Pertúz-Comas, A.D.; Bohórquez-Becerra, O.R.; Braga, A.M.B.; Prada-Parra, D. Plastic Zone Radius Criteria for Crack Propagation Angle Evaluated with Experimentally Obtained Displacement Fields. Buildings 2024, 14, 495. [Google Scholar] [CrossRef]
- Pop, O.; Meite, M.; Dubois, F.; Absi, J. Identification algorithm for fracture parameters by combining DIC and FEM approaches. Int. J. Fract. 2011, 170, 101–114. [Google Scholar] [CrossRef]
- Farahani, B.V.; Tavares, P.J.; Moreira, P.M.G.P.; Belinha, J. Stress intensity factor calculation through thermoelastic stress analysis, finite element and RPIM meshless method. Eng. Fract. Mech. 2017, 183, 66–78. [Google Scholar] [CrossRef]
- Vázquez, J.; Navarro, C.; Domínguez, J. Two dimensional versus three dimensional modelling in fretting fatigue life prediction. J. Strain Anal. Eng. Des. 2016, 51, 109–117. [Google Scholar] [CrossRef]
- Blanco, E.; Martínez, M.; González, J.; González, M. Análisis numérico del crecimiento de grieta por fatiga del CPVC: Efecto de la temperatura y frecuencia de carga. Rev. UIS Ing. 2019, 18, 177–186. [Google Scholar] [CrossRef]
- Kibey, S.; Sehitoglu, H.; Pecknold, D.A. Modeling of fatigue crack closure in inclined and deflected cracks. Int. J. Fract. 2004, 129, 279–308. [Google Scholar] [CrossRef]
- Nicholls, D.J. the Relation Between Crack Blunting and Fatigue Crack Growth Rates. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 459–467. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).