A Method for Measuring the Mass of a Railroad Car Using an Artificial Neural Network

Abstract

The fast, convenient, and accurate determination of railroad cars’ load mass is critical to ensure safety and allow asset counting in railway infrastructure. In this paper, we propose a method for modeling the mechanical deformations that occur in the rail web under the influence of a static load transmitted through a railway wheel. According to the proposed method, a railroad car’s weight can be determined from the rail deformation values. A solid model of a track section, including a railroad tie, rail, and wheel, is developed, and a multi-physics simulation technique that allows for the determination of the values of deformations and mechanical stresses in the strain gauge installation areas is presented. The influence of the loaded mass, the temperature of the rail, and the wheel position relative to the strain gauge location is considered. We also consider the possibility of using artificial neural networks to determine railroad cars’ weight without specifying the coordinates of the wheel position. The effect of noise in the data on the accuracy of determining the railroad car weight is considered.

1. Introduction

Monitoring the mass of railway cars is an important component of ensuring the control and safety of railway transportation and ease of asset counting [1,2]. The use of railroad cars with masses exceeding the allowable limit reduces the expected life of the track without repairs [3,4], and asymmetric loading (greater loading of the wheel on one side of the axle) can lead to the derailment of trains [5,6].

A railway-weighing system that does not require embedment in the railway track structure during installation and that is capable of performing dynamic weighing (so-called WIM—weigh in motion) is a promising object for development and study [7,8]. An analysis of current scientific publications on this topic allows us to conclude that researchers most commonly suggest using strain gauges [9,10,11,12,13], piezoelectric sensors [14], or fiber-optic sensors based on Bragg gratings [15,16]. One study [17] provided a general literature review on the application of optical-fiber-based structural-health-monitoring systems in railway infrastructure and its possible integration with an AI technique. Due to their fragility, fiber sensors are never used without packaging, which decreases their measurement accuracy. To correct the error and improve the measurement accuracy, a strain transfer theory was developed to establish the quantitative strain relationship between the sensing fiber and the monitoring material. In [18], a state-of-the-art review on the strain transfer theory, considering optical-fiber-based sensors developed for civil structures, is provided. In [19], an optimization design method based on the strain transfer theory, considering industrialized optical-fiber-based sensors, was investigated, and a case analysis of employing the developed sensors to monitor the complex deformation of asphalt pavement was conducted.

Sensors are commonly installed on the rail web (the side of the rail), but other positions may also be chosen, e.g., the rail pads or rail ties [20]. Strain, i.e., the mechanical deformation relative to a reference condition, is one of the most accepted measured quantities within the structural monitoring and assessment field [21,22]. Strain gauges show less sensitivity to train speed variations than other sensors [13]. In addition, they are used to evaluate various values of bending and shear deformation [12]. For example, ref. [23] was devoted to the development of a method which allows for accurate and reliable railroad measurements of wheel–rail contact vertical forces and shear strains in rails by using a combination of four strain gauges. The method proposed in [24] allows for the identification of the axle weight and axle spacing in regard to the train speed, as well as gross train weight using strain sensors embedded in the bridge structure (bridge weigh-in-motion (BWIM)). The bridge strain values at the points of sensor installment, the integral area of the strain data, and the second derivatives of the strains were used to calculate moving train load characteristics analytically through the influence line technique, while numerical simulation and case study measurements proved the method’s feasibility. However, the axle weight determination that was performed exhibited errors, and the presented method was required as a preprocessing step for operation. In [12], a deep learning-based axle weight measurement system was developed for bridges using strain gauge data as an alternative approach to weigh-in-motion. The authors emphasized that essential information from strain gauges can be evaluated for maintenance and further research.

The computational complexity of the model directly depends on the type of problem being solved: static or dynamic. Reducing the problem to static load calculation makes it possible to reduce the computing resource requirements and is quite common among other authors [9,16]. As was shown in [9], with a decrease in the railroad car speed and an increase in the quality of the railway track, the contribution of the dynamic component tends toward zero and can be neglected. In addition, static weighing is characterized by a higher accuracy compared with dynamic weighing [25], and it has significantly less sensitivity to the influence of external factors (train acceleration, redistribution of loads, and ground subsidence). In turn, the method of axial weighing is versatile, since the result does not depend on the size of the cars and the number of their bogies or wheelsets (axles). In addition, it is efficient since it involves simple installation using standard sensors. The deformation of a rail during the passage of a rail car on it is also affected by the properties of the ballast on which the rails and railroad ties are located. In [11], special attention was paid to the mechanical properties of railway tracks. The track model consisted of three layers of materials with different mechanical properties: rail, ties, and ballast. Geometrical dimensions, the material density, Young’s modulus, and Poisson’s ratio were considered, while the rail and the railroad tie were connected through elastic elements (springs) with particular stiffness and damping coefficients, and the ballast was connected to a fixed base (the Earth) through elastic elements with a particular stiffness coefficient. After analyzing the simulation results for various combinations of stiffness and damping coefficients, the authors concluded that the contribution of these track parameters to the obtained values of the dynamic loads on the track is insignificant. In the proposed work, the contribution of the track understructure to the static loads experienced by the rail was not considered.

The consideration of the temperature component of mechanical deformations seems to be justified, since the rail tracks in the Russian Federation, in particular, are operated in a wide temperature range. It is well known that considering and controlling the thermal expansion of rails is an important issue in track installation; an error could lead to the track buckling, which is dangerous and requires immediate repair. Reference [26] found that, in the cold season, the rail temperature is approximately equal to the ambient air temperature, and in the warm season, it exceeds the ambient air temperature by 20 °C. In [10], the authors used both data from strain gauge sensors mounted on a rail and data from a temperature sensor; however, the results presented for the correlation of the temperature and mechanical deformations seem to be ambiguous. In [27], the influence of the bitumic road pavement temperature on the error in determining the weight of a vehicle using a WIM system embedded into the road pavement was examined. Based on an analysis of experimental data collected from three types of sensors for six months, the authors concluded that the influence of the sensor’s intrinsic error ranged from −12% to +2% and the influence of the change in the pavement parameter (sensor external error) ranged from −30% to +20% over a temperature change range from −20 °C to +30 °C. The authors proposed using a nonlinear model that uses the stiffness coefficient for the road surface and the speed of the vehicle and its weight as the main parameters. In the authors’ opinion, such WIM systems need two temperature sensors: one at the beginning and one at the end of the road surface section under consideration.

The data obtained in real conditions during the axial static weighing of a railroad car with a system based on strain gauges inevitably contain noise. Errors in measuring the signals from strain gauges are included in the data [13]. In addition, static weighing in its pure form is rarely used due to its economic inexpediency, and weighing often occurs in motion, at a low train speed. In this case, the contribution of the dynamic component becomes difficult to predict. It seems impractical to account for such parameters as the quality of the track, properties of the wheels of the train, and variations in speed during the weighing process. The use of neural networks in railroad car scales and WIM systems, if they work successfully with data containing noise, is a promising area of research [28].

A large number of scientific studies are devoted to attempts to use neural networks to determine the weight of railroad vehicles, their number of axles, and their speed and movement type. In most of these studies, vibrations when vehicles drive over a bridge were investigated and simulated. For example, in [29], the problem of training deep convolutional networks on data from accelerometers installed on the road surface of an automobile bridge was considered in detail. The data were transformed into spectral images obtained using the short-time Fourier transform (STFT), Wigner–Ville transform (WVT), and continuous wavelet transform (CWT) methods. The authors managed to achieve accuracies for determining the mass (three classes), speed (three classes), and vehicle type (two classes) of 98.2%, 98.8%, and 99.5%, respectively, for data obtained from a scaled model of the bridge and vehicle. Note that, with an increase in the measured values of the mass and speed, it will be necessary to increase either the number of classes or the step according to these values. Maintaining high accuracy is possible only if a significant increase in the training set is achieved.

Reference [30] was also devoted to determining the mass of a vehicle passing over a bridge. The authors trained an LSTM neural network on deformation data at six points in the bridge structure, obtained via modeling three scenarios of the passage of vehicles on the bridge with LS-DYNA^®. In total, the authors received 45,000 frames for three scenarios. After training on data containing 0.1–2.0% noise, the neural network determined the mass of the vehicle with an accuracy of 61.3–81.3%, depending on the scenario. In [31], artificial neural networks (ANN) were applied to forecast the weights of cargo trains a year in advance based on known cargo weights for the three preceding years. For training the network, error measures such as the root mean square error and mean absolute percentage error were used, which were obtained from predictive modeled values and the actual values of cargo weights. Three training algorithms were considered, and the best in terms of relative, absolute, and network errors proved to be the Levenberg–Marquardt algorithm. Moreover, no sensor data were used for the network training, and there was no information on how correct the forecasted trend turned out to be.

In [32], a system for determining wheel load using two pairs of sensors—a shaft pin sensor and strain gauge sensor—was proposed. The authors combined data from both types of sensors on one graph. During the experiments, the load mass did not change, and the speed varied within small limits. Thus, the graph represents the reaction of the sensors to the passage of the wheel along the studied section of the track. The article proposed a method for refining the mass of a loaded wheel, determined by the sensors, using correction factors fitted by a neural network. The hybrid methodology proposed in [33] includes several approaches at once: custom loss functions of neural networks combined with residuals derived after the application of the finite element method for solving direct and inverse problems. Despite the versatility and relative simplicity of the methodology, it cannot be used for nonlinear cases, and its usage for solving complex problems is time-consuming due to the empirical nature of the search and the necessity of choosing a neural network architecture. In [34], back propagation neural networks were trained on real data collected from a weighing platform and two types of bridges. It was proven that the usage of artificial neural networks allows for an increased effectiveness in vehicle weight identification.

Our aim in this study was to determine the masses of loaded railroad cars accurately and automatically. The rest of this article is presented as follows. In Section 2, the designed finite element model of the wheel–rail–tie system, the proposed simulation technique, and an explanation of how neural networks can be used to determine railcar weight are described. Section 3 is devoted to the Static Structural and Steady-State Thermal mode simulation results and their analysis as well as confirmation of the application feasibility of the ANN. Finally, key conclusions are summarized in Section 4.

2. Proposed Methodology

According to the proposed method, firstly, a finite element model of the track structure fragment was designed, including a rail fragment, two rail ties, and a rail wheel corresponding to actual existing infrastructure objects. Then, the simulation was carried out in the Static Structural and Steady-State Thermal modes of ANSYS^® CAD. Finally, the comprehensive array of the obtained simulation results containing data about strains, temperatures, coordinates, and load masses was used to train the neural network. Eventually, the properly trained ANN was capable of determining the value of a load based on strain data with sufficiently high accuracy, taking into account possible noise and operating independently of the wheel coordinates relative to the strain gauge positions.

2.1. Finite Element Model

To simulate static loads that occur on a rail under the influence of car weight, a solid model was developed, as shown in Figure 1a. The rail fragment corresponding to the section of the railway track on which the static weight sensors were mounted was rigidly connected to two railroad ties that were fixed from below. The solid-state model was geometrically similar to real structures—an R50-type rail [35] and a solid-rolled railway wheel for freight cars with a tread diameter of 920 mm [36], which are used in the Russian Federation. Thus, the correct shape of the contact patch was preserved in the model (Figure 1b). The railroad tie spacing was 510 mm.

A sketch of the proposed model is shown in Figure 2. On the rail web, symmetrically to the center of the studied rail fragment at the points where strain gauges are usually attached, there are two pairs of strain measurement points: points 1 and 2 on the outside of the rail web and points 3 and 4 on the inside. Points 1 and 3 are located at a distance of 100 mm from the symmetry line, closer to the left tie, while points 2 and 4 are located at a distance of 100 mm from the symmetry line, closer to the right tie. Since the problem is symmetrical with respect to the strain measurement points, simulation of the wheel moving towards the center of the rail (line of symmetry, see Figure 2) was carried out. While various types of rail deformations can be measured in wheel–rail contact studies, like bends or shears [12,23], this requires relatively complex algorithms for post-processing, and only vertical strains need to be measured for wheel load identification. This is why this study only took into account the values of the vertical deformations, although during the simulation, three axes’ deformation values as well as mechanical stress values were obtained.

2.2. Simulation Technique

To collect the rail deformation data, the simulation was conducted under the following conditions: the wheel moved along the rail sequentially and discretely at 11 different points from the origin coordinates (the left edge of the rail) to the line of symmetry; the step between the points was 50 mm; at each point, the load on the wheel varied discretely from 2500 kg to 12,500 kg in increments of 500 kg. This mass range approximately corresponds to the load on a single wheel in different scenarios, from an empty car to the most loaded standard four-axle railroad car. Since the deformation of the wheel was not considered in this work, the load mass was specified by defining a point mass or correspondingly changing the density of the wheel material. For each of the mass and coordinate combinations, a static analysis was carried out, and the vertical deformation of the rail at four points was calculated as a result.

Simulation results were obtained with ANSYS^® CAD for five rail temperature values: 22 °C, 40 °C, 50 °C, −10 °C, and −20 °C. It was assumed that 22 °C is a standard temperature; 40 °C and 50 °C are the temperatures of a heated rail in the summer season when the air temperature is 20 °C and 30 °C, respectively; and −10 °C and −20 °C are the temperatures of a rail in the winter season, which are equal to the air temperature [26]. In the case of the standard temperature, the rail was only loaded with the mass of the car, which was transmitted through the wheel. In other cases, coupled Steady-State Thermal–Static Structural problems were solved, in which mechanical stresses and deformations caused by temperature were used as initial loads in solving the static problem of calculating the rail deformations induced by the loaded wheel. Thus, in contrast to conventional models, this model takes into account the temperature deformations of the rail and also uses accurate three-dimensional models of the railway wheel and rail without simplifying the geometry, which results in an accurate contact patch between the wheel and the rail and allows for stress distributions and strain values of the rail material that are close to the actual values to be obtained.

For each combination of loaded wheel mass, temperature, and wheel position on the rail, strain values were obtained along the y-axis, coinciding with the direction of gravitational acceleration (which was taken into account during the simulation) at four strain measurement points. We proceeded with the assumption that the strain values at these points were uniquely correlated with the electrical voltage values obtained from the strain gauges.

2.3. Using a Neural Network to Determine Load Mass

In this part of the study, we considered the potential of using neural networks in WIM systems and the importance of the temperature of the rail and coordinates when training a neural network.

To determine the importance of coordinates in the measurement of deformations, the following model experiment was carried out. From the complete simulation dataset containing 1155 unique combinations of values for four strain measurement points, only the values corresponding to the standard temperature of the rail (T = 22 °C) were selected. Random white Gaussian noise was added to the remaining 231 combinations of values for the four strain measurement points.

The magnitude of the noise was estimated as follows. It is known that in real-life railway-weighing systems or railroad car scales, for example, those used in Russia, the RTV-D, VTV, or M8300, the readout discreteness or the division value, which determines the weighing accuracy, depend on factors such as the maximum permissible speed of the train during weighing and the maximum load (the upper limit of the mass determined during weighing). The value of one division could be 200 kg with a maximum load of 100,000 kg. The value of 100,000 kg corresponds to the upper limit of the range of loaded masses studied in this work for four-axle railroad cars. In terms of a single wheel, the division value used was 25 kg (200/8). Based on the differences in deformations that occurred at the measurement points, with and without taking into account the influence of this additional mass, the relative strain measurement error corresponding to such a division value (200 kg) was determined, which ranged from 0.2% (for the largest loaded mass within the range under study) to 1% (for the smallest mass) of the simulation results for the strain values, and which determines the amount of added noise. Thus, for this study, it was assumed that the data obtained from strain gauges in railroad scales were noisy, with an average noise value of 1%. Other noise values were taken for research purposes.

An array of data containing noise were obtained from the original data in accordance with the formula:

$$d_{noise}=d\pm d·\epsilon$$

(1)

where d is the original data, ɛ is the standard deviation with the mathematical expectation being equal to zero, and d_noise is the noised data.

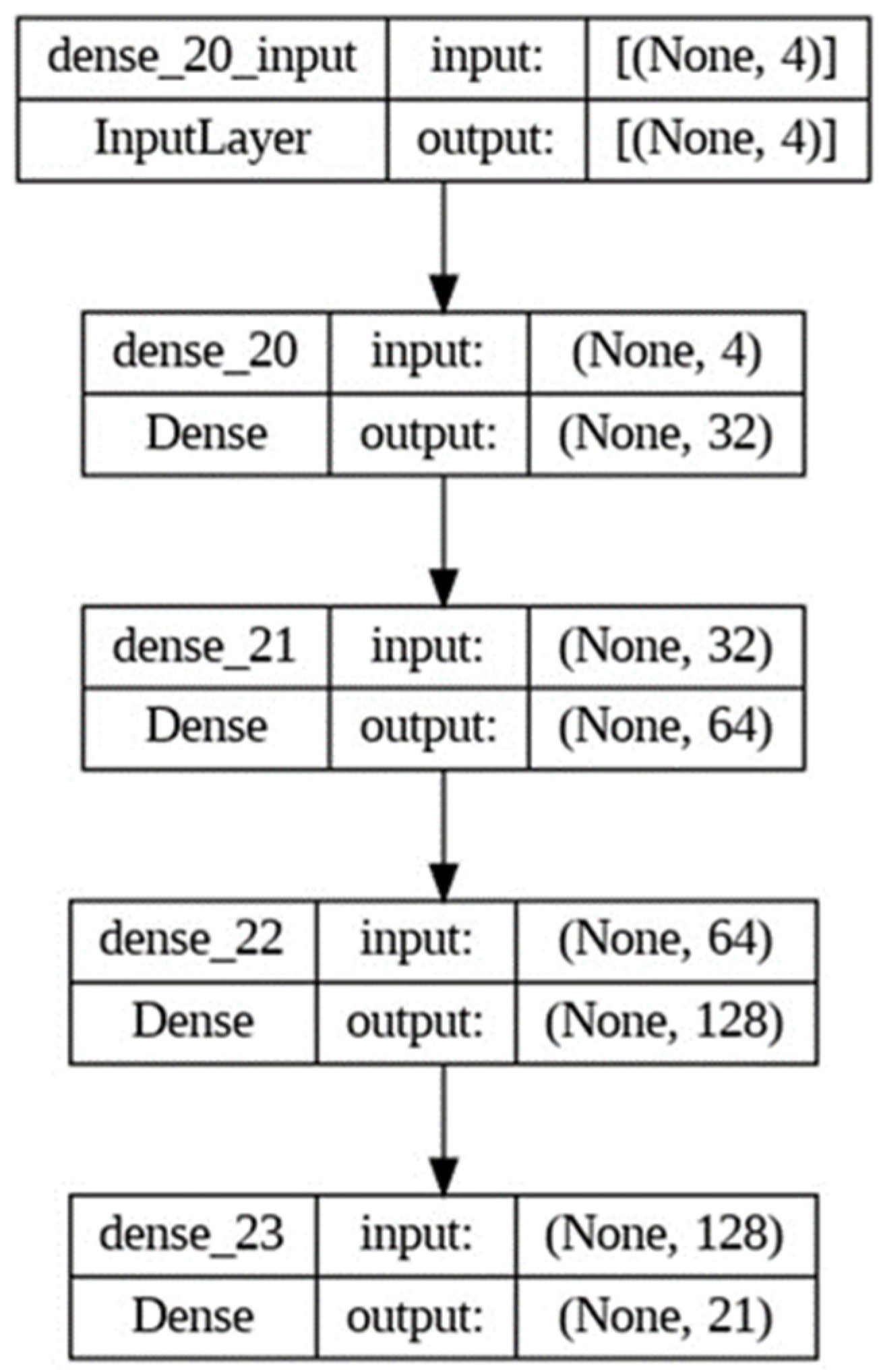
Using 1000 randomly generated noise arrays, 23,100 combinations of strain values for four measurement points containing noise were obtained and used to train the neural network. The network was trained only on the strain values observed at four strain measurement points and the load mass values, which were categorized into 21 categories: category 0 corresponds to a mass of 2500 kg and category 20 to a mass of 12,500 kg. Thus, the input data of the neural network were vertical strains (obtained from simulation or the sensors in the case of real operation) and the output data were specified load masses. There were no coordinate values in the training data. The temperature of the rail was taken into account indirectly, since the data were initially filtered by the value of 22 °C. The described data were divided into training and test samples at a standard 80/20 ratio. The scheme of the used neural network is shown in Figure 3.

This neural network is a simple multilayer perceptron model consisting of four layers. The first fully connected input layer consists of neurons with the ReLU activation function and receives the strain value at four strain measurement points. The next three layers are also fully connected with the ReLU activation function, while the number of neurons gradually increases from 32 to 128. The last fully connected layer is the output layer and consists of 21 neurons with the softmax activation function, according to the number of classes. The neural network was trained for 40 epochs.

3. Results and Discussion

The mechanical deformation values, corresponding to four locations where strain gauges would be expected to be installed on the rail web, were obtained during simulation. The data array comprises strain values for all combinations of the load masses, temperatures, and wheel coordinates. Based on these data, the characteristics of the deformations were plotted and analyzed. The accuracy of the neural network in terms of the simulation results was checked for different noise levels, and corresponding confusion matrices were visualized.

3.1. Results of Finite Element Model Simulation

Figure 4a shows the dependences of the vertical deformations of the rail at strain measurement points 1 and 4 on the coordinates for various values of the mass loaded on the wheel at a standard rail temperature (22 °C). Figure 4b,c shows similar dependences obtained for when the rail temperature was 50 °C and −20 °C.

The symmetry of the simulated system with respect to the sensor pairs (Figure 2) made it possible to use the values of deformation at strain measurement point 2 to plot a deformation versus coordinate graph at strain measurement point 1 for coordinate values located to the right of the symmetry line. The values of deformation at strain measurement point 3 were used to plot a deformation versus coordinate graph at strain measurement point 4 for the same reasons. The graphs for strain measurement points 2 and 3 are mirror images of the graphs for strain measurement points 1 and 4 and, therefore, are not shown here.

As can be seen from Figure 4a, the influence of the loaded mass on the deformation value depends on the location of the wheel on the rail. When the wheel was above the middle of the railroad tie, the effect of the mass on the deformation was almost zero, and an intersection of characteristics could be seen in this area. As the center of the wheel approached the locations of the strain gauges, the effect of the mass on the deformations became increasingly significant, and the steepest sections of the characteristics for strain measurement point 1 were observed in an area approximately corresponding to coordinates ranging from 250 mm (when the wheel moved off the railroad tie) to 350 mm (i.e., not reaching 50 mm up to strain measurement point 1) and from 550 mm to 750 mm, while the curves’ peaks were at approximately 450 mm. The steepest sections of the characteristics for strain measurement point 4 corresponded to coordinates ranging from 250 mm to 450 mm and from 650 mm to 750 mm, while the largest absolute strain values corresponded approximately to the point with a coordinate of 550 mm. Thus, in measurement by strain gauges when the wheel moves along the rail, the areas between the ties and sensors can be considered as the most suitable areas in terms of the degree of influence of the mass on the resulting deformations.

However, the exact placement of railroad cars and their wheelsets relative to the sensors and ties during static weighing, or determining the required time to perform measurements during dynamic weighing, is a non-trivial task. In this study, we investigated the possibility of developing a wheel-load determination system that takes into account the influence of external factors (in this case, the rail temperature) and does not require exact positioning. Whether the rail temperature measurement is direct (when a temperature sensor is installed together with strain gauges [10,27]) or indirect, for example, by using different coefficients at different times of the year, these values could be used when analyzing the output electrical voltage values of strain gauges.

Figure 4b,c shows that the shapes of the coordinate–deformation curves are approximately the same for different temperatures; however, a change in the ranges of the measured deformations is noticeable. In the case of standard conditions (T = 22 °C), rail deformations could exceed 100 µm, and their direction coincided with the direction of gravity, while in the areas where rails cross railroad ties, the deformation values tended toward zero. As the temperature rose, the rail slightly bent upwards; therefore, in the measured range of the loaded masses, the degree of influence of the mass on the deformation was weaker than the degree of influence of the temperature, and the rail was deformed, but in the direction opposite to that of gravity. In the region of the ties, the value of the deformation of the rail was 120 μm as a result, while in the middle of the rail section between two ties, due to mutual compensation, the strain was, on the contrary, the smallest (approximately 25 μm). In the case of negative temperatures (T = −20 °C, winter period, when the rail temperature is approximately equal to the ambient temperature [26]), the rail slightly bent downward, and this deformation was added to the deformation exerted by the loaded wheel, so the entire range of deformations was located in the negative value region, and the greatest absolute value of deformation exceeded 240 µm.

The dependences of the deformations at deformation measurement point 4 on the coordinate and loaded mass for different temperatures of the rail are shown in Figure 4d. As can be seen, there were no intersections between the three-dimensional surfaces formed by the sets of deformations for various combinations of loaded masses and coordinates corresponding to different temperatures of the rail (the graphs have no common points), so it could be concluded that temperature makes the combination of parameters unique and is needed to indirectly determine the loaded mass. The use of temperature as a parameter is also justified because it has a significant effect on the amount of strain recorded by strain gauges, which is noticeable in Figure 4a–d.

3.2. Results of the Artificial Neural Network Application

The results of training the neural network show that, with a noise level not exceeding 1% (which corresponds to a relative error in measuring the deformations at the lowest value of the loaded mass of 2500 kg and taking into account the value of the division value in the railway scales used in practice), it is possible to determine the category of the load mass with an accuracy of 78% or greater. With a noise level within 0.1%, the neural network correctly determined the category of the load mass in 100% of cases.

A graph of the dependence of the accuracy of test data classification by a neural network on the noise level with and without taking into account the temperature of the rail is shown in Figure 5. Figure 6, Figure 7 and Figure 8 show the confusion matrices of the networks trained on test data for noise values of 0.1%, 1%, and 10%, respectively.

To determine the importance of taking into account the temperature of the rail, the neural network was trained on the entire data array at temperatures of 22 °C, 40 °C, 50 °C, −10 °C, and −20 °C, while leaving the remaining parameters of the neural network unchanged. At a noise level of 1%, the accuracy of determining the category of load mass was 27%, and at a noise level of 0.1%, the accuracy of determining the category of load mass was 54%. The analysis of these results allows us to conclude that considering the temperature of a rail when measuring deformation in order to determine the load mass can significantly affect the accuracy of the scales, especially in cases where full automation of such system is assumed or a neural network is used.

4. Conclusions

In this paper, a method for determining the masses of railroad loads based on combinations of mass categories and corresponding strain values obtained from simulation results for four strain measurement points was proposed. The influence of the rail temperature on the deformations that occur under the influence of a loaded wheel was studied. A technique for using an artificial neural network to analyze the load on a railway wheel by combining four values of mechanical deformation of the rail web material with the addition of random noise to these values was presented. It was suggested that the use of a trained artificial neural network can reduce the requirements for the quality of sensors and signal processing systems. The following conclusions can be drawn:

• Thermal loads affect the mechanical stress and the deformation values obtained when the considered static problem of the load transmitted through the railroad wheel to the rail has been solved;
• The surfaces plotted as a function of deformations versus the coordinates, corresponding to the position of the wheel geometric center, and the mass of the loaded wheel for different temperatures, do not intersect; that is, the deformation values for this combination are unique. Therefore, the combination of the four strain values will also be unique, which will allow the mass of the loaded wheel to be determined from these values;
• Determining the mass of a loaded wheel using the proposed method based on neural networks does not require specifying the exact value of the coordinates. The accuracy of determining the mass without using coordinate data is high enough at 78% with a noise level as high as 1% of the measured deformation values and a relatively large number of categories;
• Despite the declared applicability of the proposed method, it has some limitations: while there is no need to know the exact location of the wheel to determine the mass, the railroad car should still be positioned so that the wheel is placed between two ties; the usage of a neural network implies a probabilistic choice of preliminary specified categories corresponding to loaded mass rather than a true measurement; and finally, additional factors like temperature should be taken into account when determining mass as, otherwise, the accuracy could be too low.

The proposed approach could be useful for automated mass determination in railway infrastructure based on the simple installment of a set of typical sensors using machine learning, as it does not require precise rail car positioning. Further development of this research area could consider the improvement of the designed models and refinement of the boundary conditions. So far, only simulation data have been used for neural network training, but field tests on the track are planned in the future to check the feasibility and accuracy of the proposed model.