Abstract
Roller-compacted concrete (RCC) pavements have been the subject of studies focused on their increasing deterioration over time due to the influence of vehicular loading and ambient factors in humidity and temperature conditions ranging from medium to low (40% relative humidity and 25 °C temperature). Therefore, it is necessary to understand how they behave under various relative humidity and temperature conditions since these parameters vary in each geographic region. In this context, this research focused on analyzing the effect of drying shrinkage on RCC pavements under the influence of vehicular loading using a computational model calibrated with data obtained under typical ambient conditions. For this purpose, laboratory experiments were performed, numerical modeling was used, and the results for RCC pavements were validated using statistical analysis. The results revealed validated models providing moisture content and drying shrinkage curves. These results also underline the importance of considering ambient effects when calculating pavement stresses as a response variable in structural designs. In particular, these effects are highlighted as they can generate changes in pavement stresses of up to 10%, emphasizing the relevance of the models proposed in this study as they consider this phenomenon when predicting the performance and durability of RCC pavements.
1. Introduction
Pavements are fundamental structures that have significantly contributed to improving the quality of life in society, facilitating connections between communities with reasonable travel times, especially compared with unpaved roads. Research in this field has been crucial, leading to notable developments, such as using sustainable and environmentally friendly materials with self-repairing capabilities, de-icing during winter properties [1], and the ability to receive signals that identify vehicle speeds and loads [2]. In addition, progress has been made in the in situ evaluation of the mechanical properties of pavements using non-destructive techniques, allowing the determination of their remaining service life and the appropriate methods for their rehabilitation [3,4].
Research has also focused on improving surface characteristics to ensure user comfort and safety and exploring construction alternatives to reduce the carbon footprint [5]. A wide variety of pavements exist, each with its advantages and limitations depending on its application. For example, flexible pavements are the most widely used worldwide on high-speed roads but have slow or static load limitations [6]. Slab, continuous, and roller-compacted concrete (RCC) pavements are often more effective [7,8].
The latter has obtained a noticeable trend worldwide because many countries are inclined to implement RCC for pavements, adopting this modality in different categories. Precisely, areas such as ports, intermodal facilities [9,10], heavy industrial areas, light industrial areas, airport service areas, arterial streets, and local streets have positioned themselves as favorites for such incorporation. This preference suggests that these areas are considered vital or conducive for RCC. In contrast, the categories of widening (over-widening) and shoulders [11] and timber facilities, composting areas, and storage yards have been noticeably less popular, which could be linked to technological and infrastructural particularities, or individual countries’ priorities.
The study of RCC for pavements has gained relevance in the last decades, specifically in its shrinkage behavior, exploring the analysis of RCC with blast furnace slag additions as a partial replacement for cement and its repercussions on shrinkage with different aggregate origins, finding better behavior in limestones [12]. In addition, the long-term shrinkage of RCC with granulated blast furnace slag (GGBFS) addition under various temperature exposures has been found [13] to significantly affect the strength development of concrete. At 14 days, concrete cured at 50 °C and 70 °C showed higher strength than that cured at 25 °C due to the acceleration in the kinetics of strength development at higher temperatures. Moreover, adding GGBFS showed a more significant variation in early-age strength, especially at higher temperatures. At low temperatures, the mix with GGBFS gained strength more slowly than the ordinary Portland cement mix. However, at higher temperatures, early-age strength development was rapid, particularly with higher levels of GGBFS. In addition, the results showed that temperature considerably impacted the development of shrinkage strain during early exposure to drying. Finally, there is a multivariate model for predicting the shrinkage strain of concrete based on temperature, time, and the percentage of GGBFS. This model can estimate the shrinkage strain within the 95% prediction range.
On the other hand, not all possible solutions to shrinkage are promising, as in the case of adding tire rubber, which did not help but increased drying shrinkage slightly more compared with the control RCC without tire rubber [14]. However, adding modified rubber particles to RCC improved its plasticity, mechanical properties, and freezing resistance and reduced the pore volume. The authors established that the optimum volume of modified rubber particles to add to the RCC mix was 5%, and they analyzed the working performance, mechanical properties, and durability of rubber RCC, compressive strength, flexural strength, drying shrinkage, and freezing resistance [15].
When analyzing the mechanical and permeability properties of RCC pavements reinforced with different types of synthetic fibers and crimped steel fiber, the authors found that increasing the fiber volume from 0.5 to 1% can reduce the drying shrinkage rate and improve the flexural strength of fiber-reinforced RCC. However, water sorptivity and porosity increased with the substitution of fibers in RCC blends. The water sorptivity of the samples was highly dependent on the type and surface geometry of the fibers. In addition, the porosity increased when fibers with a high aspect ratio were used [16].
Conversely, in situ thermal properties and early-stage RCC pavement performance have been studied in Louisiana, USA, aiming to develop a mechanistic–empirical-based RCC thickness design procedure to quantify the combined effect of traffic and ambient loading on RCC. The key findings include the following: (i) RCC is less susceptible to early-stage cracking due to a lower water–cement ratio, reduced shrinkage, and early strength gain from roller compaction, and (ii) optimal shear joint spacing to prevent shrinkage cracking and become cost-effective is required [17].
The background on the subject presents some significant incidences in the performance of RCC for pavements in the short [18] and long terms [19]. Also, climate actions and traffic loading influence the RCC shrinkage phenomenon, causing curling that results in slab elevation and loss of contact with the ground. Likewise, studies have demonstrated that the stress increases to up to 500% for a crack width of 0.5 mm under 40% relative humidity and a 25 °C temperature [20,21]. Nonetheless, this stress depends on the climate conditions, i.e., the relative humidity and temperature variations, which are particular to each zone, and the medium–low values (40% relative humidity and 25 °C temperature) or the fact that the conditions most studies focus on are not always present. Therefore, there is a need to know the behavior of RCC for pavement at a range of relative humidity values since the variation in this parameter is particular to each zone, and the medium–low relative humidity and temperature conditions are not always present.
Currently, the design of concrete pavements, specifically RCC for pavements, does not consider in its sizing criteria the decrease in performance due to concrete drying shrinkage [8], leading to a lack of knowledge of its impact on the pavements [22]. This is counterproductive for an RCC pavement [23], since its reparation is usually greater than that of conventional concrete pavements [24], i.e., the North American standard for jointed plain concrete pavement (JPCP) [24,25] or the French standard, including BC (Chaussées á delles non armées et non goujonnées (unreinforced and ungrooved slab pavements)) and BCg (Chaussées á delles non armées et goujonnées (unreinforced and doweled slab pavements)) [26]. It must be noted that joints usually used to anticipate shrinkage cracks in JPCP pavements (BC or BCg) are infrequent in RCC for pavements [8,27].
Hence, the alternative approach that is able to represent reality is using physical models at a 1:1 scale or computational modeling. The latter has historically achieved reliable results in highway engineering, such as bridges, tunnels, and pavements [28,29,30]. Furthermore, when the correct method was chosen, it was applied successfully to find the calibration constants necessary to study a real structure.
Finally, the study of drying shrinkage in RCC has been an area of interest for a long time. However, until now, no notable response has been identified at different times, such as at advanced stages of material maturity, especially under relative humidity and temperature variations. Accordingly, this study aims to address this gap, focusing on how these ambient conditions specifically influence the drying shrinkage of RCCs for pavements. Furthermore, it also aims to contribute to the knowledge of the structural design of RCC pavements, as there are uncertainties regarding their behavior under conditions different from the typical ones, i.e., in situations where the relative humidity differs from 40% and the temperature varies from 25 °C [20,21].
2. Methodology
The methodology is divided into three main steps:
- Materials and laboratory tests: This step describes the materials used and the laboratory test procedures in detail. These tests are essential to calibrate the results obtained under controlled conditions.
- Computational modeling of laboratory tests: In this phase, computational modeling replicates and analyzes the laboratory test results. It allows for a deeper understanding of the data obtained.
- Computational modeling and validation of RCC pavement results: In this last step, computational modeling is used to evaluate the performance of an RCC pavement [31] under different conditions, including corner loading and various ambient conditions, such as (i) 85% relative humidity at 25 °C, (ii) 10% relative humidity at 40 °C, and (iii) 20% relative humidity at 25 °C. These conditions reflect specific water vapor levels in the air (17, 5, and 4 g of water vapor per kilogram of air, respectively) (Figure 1). This step aims to determine the maximum stresses experienced by the pavement under corner loading.
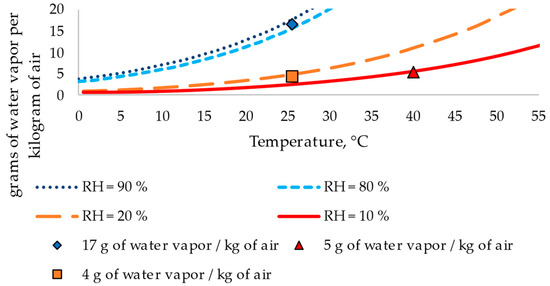 Figure 1. Relative humidity (RH), temperature (T), and g of water vapor/kg of air behavior. Source: [32].
Figure 1. Relative humidity (RH), temperature (T), and g of water vapor/kg of air behavior. Source: [32].
Finally, the RCC pavement results are validated using inferential statistical methods. This validation allows the establishment of the effect of the ambient setting on the structural design of the RCC pavement.
2.1. Materials and Laboratory Tests
The investigation was carried out using a standard RCC pavement mix. This mix had an optimum moisture content (OMC) of 5.65% [33] and a maximum dry density (Mdd) of 2.583 g/cm3, determined with a Proctor compaction test (ASTM D1557-12) [34]. The aggregates used were of the limestone type, with a specific gravity of 2.775 (ASTM C128-15) (ASTM. ASTM C127-15) [35,36] and an absorption of 0.472%, and complied with the particle size distribution specified in the PCA construction standards [37,38,39] (Figure 2).

Figure 2.
Gradation for roller-compacted concrete (RCC) pavement.
The cement was a Portland composite (CEM II/A-M (L-V 42.5 R)) [40,41], constituted of >80% clinker, <13% fly ash, >6% limestone, and between 0 and 1% minor components.
The laboratory tests were carried out (as shown in Figure 3), complying with the subsequent computational modeling requirements. Modeling was performed using the ABAQUS software focused on analyzing RCC shrinkage in pavements under various climatic conditions and vehicular loads at corners. The following tests were performed:

Figure 3.
Laboratory procedures.
- A moisture content test;
- A free shrinkage strain test;
- A compressive strength test;
- A flexural strength test;
- An elastic modulus test.
These tests were carried out after curing the RCC mix submerged in water for 90 days and then subjecting it to various climatic conditions for different periods of exposure with intervals of 0, 1, 4, 7, 14, 28, 42, 56, 70, 84, and 90 days. Three specimen replicates were employed per ambient condition.
Following the laboratory procedures, specimens with dimensions of 100 mm × 300 mm × 300 mm were fabricated following a series of well-defined steps:
- The preparation of the molds;
- The preparation of the RCC mix;
- Compaction in two equal phases, with 1 min consolidation per layer, totaling at 4 min with the maneuvers. The compaction was performed using a plate compactor (Universidad de Granada, Spain) with a contact surface equal to the mold [42,43].
Once the RCC mixture reached the desired consistency, the specimens were subjected to a curing period underwater at a temperature of 23 ± 2 °C for 90 days [20,21,44]. Subsequently, they were placed in various controlled ambient conditions that maintained specific relative humidity and temperature levels according to the required time intervals.
The moisture content [44,45] (Figure 4) of each specimen was determined with a gravimetric test at intervals of 0, 1, 4, 7, 14, 28, 42, 56, 70, 84, and 90 days in replicates of three samples for each ambient condition. This measurement was performed on 10 mm thick pieces (now categorized as thin sections) cut from cubes (100 mm × 100 mm × 100 mm) obtained from specimens of 100 mm × 300 mm × 300 mm. Therefore, the procedure continued with the following steps: (1) The thin section was weighed. (2) The thin section was sealed with gray American adhesive tape on the four sides, the top and bottom faces remaining free. (3) The thin section was weighed with gray American adhesive tape. (4) The remaining 10 mm high section was sealed with gray American adhesive tape on five sides, except the top surface, as it has to be in contact with the bottom side of the thin section. (5) The two parts of the cube were joined together with yellow polyvinyl tape to keep it as a complete cube and to allow regular moisture content transit. Ayano et al. [46] conducted a study on the impact of voids on moisture transfer in sliced specimens. They compared the moisture diffusion coefficient between a stack of these sliced specimens and a solid sample, concluding that the effect of the gap between the slices is minimal. (6) The cubes were placed in climatic chambers (Universidad de Granada, Spain). (7) The cubes were removed from the climatic chambers to measure the weight of the thin sections. For this purpose, the yellow polyvinyl tape was removed, and the weights of the thin sections were registered. (8) The pieces were then retaped with new tape and placed in the chambers again. (9) The steps from point 7 were repeated until the measurement on day 90 was completed. (10) Then, after point 9, the weights of the thin sections were measured without American gray adhesive tape. (11) The thin sections were dried in an oven at 110 °C (INDELAB, Spain) until they reached a constant weight. (12) Finally, the daily moisture content () in the thin sections was calculated according to Equation (1), as follows:

Figure 4.
Moisture content test.
The difference between the initial weight () (corresponding to day zero) and the weight measured on a specific day was calculated (). Subsequently, this difference was divided by the product of three factors:
- (i)
- The density of the thin section (p);
- (ii)
- The difference between the weight of the untaped thin section at day zero () and day 90 (), divided by the multiplication of the density (p) and thickness () of the thin section;
- (iii)
- The thickness of the thin section ().
The result of this division was subtracted from a value of 1 (1 represents 100% saturation) (Equation (1)).
Shrinkage beams (Figure 5) (ELE International, Milton Keynes, UK) (ASTM C157/C157M-17) [47] were obtained by cutting specimens with dimensions of 100 mm × 100 mm × 285 mm from specimens of 100 mm × 300 mm × 300 mm. As in the case of the cubes, they were subjected to controlled relative humidity and temperature conditions, as illustrated in Figure 5. However, in this case, the beams were only sealed on the sides to allow their computational modeling without being affected by surface stresses and internal compressions, as described in the drying process [20,21,44]. This methodology proved crucial to accurately measuring the strain due to shrinkage.

Figure 5.
Free shrinkage strain test.
The measurement time intervals were consistent with those applied to the cubes concerning their moisture content. The test procedure comprised the following steps:
- Measure the displacement of the beams with the frame fixed;
- Place the beams in the climatic chambers;
- Remove the beams from the climatic chambers to measure their displacement;
- Reposition the beams in the climatic chambers.
These steps were repeated at intervals of 0, 1, 4, 7, 14, 28, 42, 56, 70, 84, and 90 days. Once these measurements were completed, the daily strain due to shrinkage was calculated by taking the difference between the height of the beam in the wet state and also in the dry state and dividing this value by the original dimensions of the beam in the wet state.
Compression tests (Ibertest, Madrid, Spain), as shown in Figure 6, were carried out using cubes (100 mm × 100 mm × 100 mm) that were obtained from cutting slabs (100 mm × 300 mm × 300 mm) (ASTM C39/C39M-21) (BS EN 12390-3:2019-TC) [48,49]. The test procedure was developed as follows:

Figure 6.
Compressive strength test.
- The cubes were placed in climatic chambers for 90 days;
- They were subjected to a compression test in a universal machine (Universidad de Granada, Spain) with a loading rate of 0.25 MPa/s;
- The compressive strength was determined using the maximum load in the contact zone.
As depicted in Figure 7 (ASTM C78/C78M-21) [50], the modulus of rupture and flexural elasticity were evaluated in specimens subjected to shrinkage tests. A universal machine (Universidad de Granada, Spain) with a center point loading device and a fixed support and roller system was used. The beams were tested at a loading rate of 0.02 MPa/s. Calculations for these parameters were based on:

Figure 7.
Flexural strength test.
- The modulus of rupture for the maximum load, considering the distance from the support to the plane of break and the transverse dimensions of the beams;
- The elastic modulus for the load, considering the span, the transverse dimensions, and the strain in the lower fibers of the beams.
2.2. Computational Modeling of Laboratory Tests
The moisture content test results were analyzed using back-calculation solid finite element computational models (Figure 8). The finite element used in the research was a finite brick element (DC3D8) with three degrees of freedom per node (UX, UY, and UZ) and an eight-node linear heat transfer brick. Furthermore, the material was represented with the constitutive thermal modeling. The modeling consisted (Figure 9) of the following: (1) A cube (100 mm × 100 mm × 100 mm) with a 3D modeling space of a deformable type and with a solid shape was created; (2) the material behaviors were selected; (3) in the steps manager section, the initial, as well as the heat transfer (transient), procedures were selected; (4) in the step editing section, a 90-day interval and size increase were defined; (5) the configuration of the output field request manager was performed; (6) the sink temperature interaction and film coefficient on the surface accessible to the cube ambient was applied; (7) the loading was set to represent an initial saturation of 100%; (8) the mesh was established to define the element type, shape, and technique; (9) the job was set for data checking and submission; and (10) finally, the results were established to determine the temperature (equivalent to the moisture content) in relation to time. The procedure was repeated until results similar to those registered in the laboratory were obtained. Therefore, the calibration was developed by changing the material properties, specifically the temperature and conductivity. These variables represented the moisture content and moisture diffusivity [51], respectively.

Figure 8.
Cube sample for moisture content test for the finite element method (FEM).
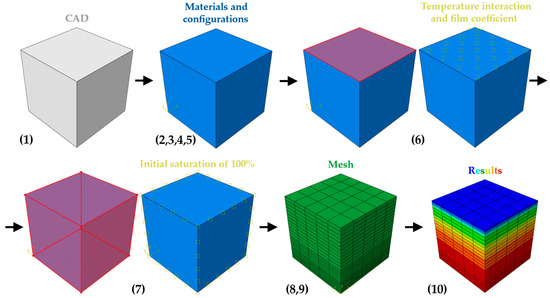
Figure 9.
Computational modeling of the moisture content test.
Based on the laboratory results of the drying shrinkage test beams, back-calculation models were performed to calculate the hygral contraction coefficients [21]. The finite elements used in the research were (i) a finite brick element (DC3D8) [52] with three degrees of freedom per node (UX, UY, and UZ) and an eight-node linear heat transfer brick and thermal constitutive modeling, and (ii) a finite brick (C3D8) with three degrees of freedom per node (UX, UY, and UZ), an eight-node linear brick, and constitutive modeling of concrete damaged plasticity (CDP) [53]. The modeling consisted (Figure 10) of the following: (1) The beam model with the properties of moisture diffusivity and moisture content, calculated in the computational model of the moisture content test, was initially created; (2) for the mechanical modeling, the beam with a 3D modeling space, deformable type, and solid shape was chosen; (3) the material behaviors were selected; (4) in the steps manager section, the initial as well as the static and general procedures were included; (5) in the step editing section, an interval of 90 days and the size increase were defined; (6) the configuration of the output field request manager was carried out; (7) the loading was set to represent an initial saturation of 100%, the boundary conditions (Figure 11), the support system adjusted to how the beam shrinkage measurement framework test works, and the moisture content development over 90 days; (8) the mesh was established to define the element type, shape, and technique; (9) the job was set for data checking and submission; and (10) the results were set to establish the strain (equivalent to the shrinkage strain) concerning time.

Figure 10.
Computational modeling of the free shrinkage strain test.
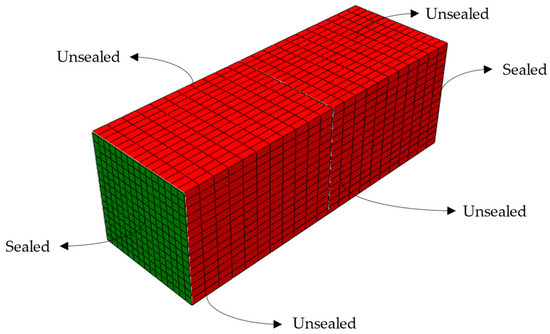
Figure 11.
Beam sample used for the free shrinkage strain test employing the finite element method (FEM).
The procedure was repeated as many times as necessary until results similar to those recorded in the laboratory were obtained. Therefore, the calibration was developed by changing the material properties, specifically the expansion coefficient and temperature. These variables represented the hygral contraction coefficients and moisture content.
2.3. Computational Modeling and Validation of RCC Pavement Results
An investigation was carried out in the field of RCC pavements, involving a structure composed of a subgrade, base, and RCC layer, with the specific thicknesses detailed in Table 1. It is essential to mention that the boundary condition for the subgrade was considered semi-infinite. In Table 1, information about the elastic modulus of the base, the foundation stiffness per subgrade area [54], Poisson’s ratio (which has no significant impact on the pavement behavior) [55], and the thicknesses of the structure are provided.
Also, the RCC layer was designed with a rectangular shape based on previous research [21], with planar dimensions of 3.4 m × 20 m, a width that is common in both the United States [56] and Europe [57] and a length that was selected to consider the continuous behavior of the RCC pavement, as illustrated in Figure 12.

Figure 12.
Roller-compacted concrete (dark grey), base (yellow), and subgrade.

Table 1.
Thicknesses, foundation stiffness per area, elastic modulus, and Poisson’s ratio of the roller-compacted concrete (RCC) pavement.
Table 1.
Thicknesses, foundation stiffness per area, elastic modulus, and Poisson’s ratio of the roller-compacted concrete (RCC) pavement.
| Layer | Thickness, m | Foundation Stiffness per Area, MPa/m | Elastic Modulus, MPa | Poisson’s Ratio |
|---|---|---|---|---|
| RCC | 0.20 | - | 49,779 to 52,526 * | 0.18 |
| Base | 0.15 | - | 8000 | 0.30 |
| Subgrade | Semi-infinite | 60 | - | - |
* The specific value for each mixture is shown in Figure 13.

Figure 13.
Displacement–load curves and elastic moduli of the roller-compacted concrete material subjected to various ambient conditions.
Laboratory tests obtained the displacement–load curves and the elastic modulus and represented the mechanical behavior of the RCC mixture. The conclusions derived from these results are presented in the results section.
In a further approach, the RCC pavement behavior was modeled considering both conditions, i.e., with and without the influence of the ambient conditions. Corner loading was applied, as this is one of the most critical design conditions for RCC pavements. Based on pavement history and development, this study implemented the following vehicle loading configuration: a design axle of 80 KN US (using half of the axle at the pavement corner), a uniformly distributed contact pressure of 0.700 MPa, a rectangular contact area of 0.120 m × 0.240 m, and a tire spacing of 0.240 m.
A computational model of the RCC pavement was proposed to address this research, considering the drying moisture content and the free shrinkage strain calculated in back calculations. A constitutive model incorporating heat transfer (HT) and concrete-damaged plasticity (CDP) was applied to develop the moisture content and vehicular loading [53].
Once the models were completed, statistical methods were applied as an alternative to verify the results obtained, seeking to determine if there were significant differences in the maximum principal stress of the pavement as a function of different relative humidity and temperature values. As a starting point, an exploration was carried out to determine if the data complied with the assumptions of normality and the homogeneity of variances. This was performed using the Kolmogorov–Smirnov test [58], which especially applied to samples comprising more than 50 data per group.
The test for normality and the homogeneity of variances was based on the null hypothesis, which states that the values follow a normal distribution, implying that the population means are equal. Otherwise, the alternative hypothesis was considered.
When the data met the assumptions of a normal distribution and homogeneous variance, a two-factor ANOVA test [59] was used as the definitive method to determine if there were significant differences between groups. If not, the Kruskal–Wallis rank-sum test [60,61] was used, complemented with the Mann–Whitney post hoc test [62] as a subsequent analysis. The latter was used when there were more than two independent samples, non-homogeneous variances, and a non-normally distributed population.
The Mann–Whitney post hoc test was used to compare pairs of ambient conditions, and its null hypothesis stated that there were no significant differences between the two ambient conditions. This hypothesis was rejected if the significance value exceeded the 0.05 threshold.
3. Results and Discussion
3.1. Laboratory Results
Figure 13 shows the displacement–load curves and elastic moduli of the flexural strength test for each ambient condition of the RCC material. The results obtained were similar in behavior for each ambient condition since the graphs presented a constant behavior from the beginning until the end of the failure. Furthermore, the elastic moduli, i.e., the slopes, showed slight differences, marginally lower in samples subjected to dry curing than those cured in wet conditions, exhibiting variations of approximately 5% under different ambient conditions. These results suggest that a reduction in relative humidity and temperature moderately affects the properties of RCC. Finally, the results pertain to mixes with compressive strengths of 80.94, 77.23, and 80.22 MPa. These strengths were determined using compression tests conducted in ambient conditions of 85% relative humidity at 25 °C, 10% relative humidity at 40 °C, and 20% relative humidity at 25 °C, respectively.
Figure 14 shows the results of the evolution of moisture content versus days of curing for the wet and dry ambient cases (i.e., at different temperatures and relative humidities). Specifically, differences of up to 80% were observed between wet and dry ambient conditions. Additionally, compared with the intermediate condition (reference or typical values), the percentage of variation was 26% for wet conditions and 50% for dry. Also, the influence of any ambient condition was accentuated in the first days, but after 50 days, stable behavior was registered. The results show an essential effect on the material because the study found three moisture content behaviors over 90 days. Accordingly, the influence of the stresses of the material on the RCC pavement was established and is presented and discussed in the following sections. Finally, essential consonances were obtained with previous studies [20,44], as was the case for the intermediate condition, since they maintained similar behaviors for each situation studied and demonstrated the adequacy and similarity of the results measured in this research and the effect in each ambient condition.
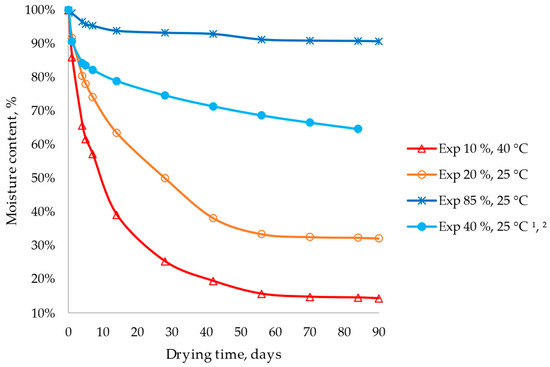
Figure 14.
Experimental (Exp) moisture profiles with different relative humidity and temperature values for wet and dry ambient conditions. 1 [20]; 2 [21].
Figure 15 shows the results of the evolution of free shrinkage strain versus days of curing for the wet and dry ambient conditions (at different temperatures and relative humidities). The shrinkage due to drying was identical at the beginning for each ambient condition up to day 7. Then, the dry conditions separated from the wet ones by approximately 52%. Subsequently, the dry condition with 10% RH at 40 °C stabilized and separated from the 20% RH at 25 °C on day 42, establishing a variation of up to 30%. This last finding determined that the temperature over 90 days was the variable with the most significant influence on drying shrinkage because the water content per kilogram of air was similar in all the dry conditions in this study. This phenomenon is attributed to a more pronounced development of shrinkage at the onset, as evidenced in Figure 15, consistent with previous findings by Gholami et al. [19] and Saluja et al. [13]. These studies indicate that early drying exposure significantly impacts shrinkage strain development. However, it must be noted that mixes of RCC for pavements, following a 90-day curing period submerged underwater and exposure to the environment for another 90 days, tend to stabilize in a shorter period at higher temperatures. This behavior suggests a potential for expansion, a topic that warrants further study.
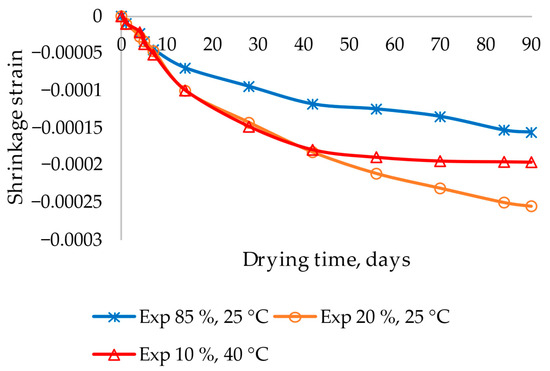
Figure 15.
Evolution of the experimental (Exp) free shrinkage strain of the roller-compacted concrete material under different wet and dry ambient conditions.
After 90 days, the wet conditions of 85% RH at 25 °C and dry conditions of 20% RH at 25 °C began to stabilize, showing a variation of 64%. This allowed recording that all the ambient conditions studied varied between 25 and 30%. Therefore, this study determined that the moisture content and drying shrinkage acting on the material according to the climatic record changed after seven days and reached stability from 42 to 90 days.
3.2. Validation of the Laboratory Computational Models
According to the laboratory results and the finite element computational modeling, Figure 16 presents the evolution of the moisture content versus days of curing for wet and dry ambient conditions. The graphs show an essential similarity as the numerical curves attempt to fit over the experimental ones, determining that the validation was successful. Therefore, the 85% RH at 25 °C condition was the best for the computational model calibrated in the investigation because it was equal to the experimental one. The curves of 20% RH at 25 °C and 10% RH at 40 °C were comparable in the first days. However, they separated slightly until they became stable after 90 days, determining a variation of 2 to 3%, respectively. These results agree with those found in state-of-the-art studies [44] because the reference measurement (40% RH at 25 °C) obtained up to 9% variation in the first days. Then, after 42 days, the numerical and experimental results were equal.

Figure 16.
Evolution of the numerical (employing the finite element method (FEM)) and experimental (Exp) moisture profiles under different relative humidity and temperature conditions. Results according to the ABAQUS modeling. 1 [20]; 2 [21].
These results allowed the analysis of how ambient conditions affect moisture content and its interaction with drying shrinkage, which, in turn, contributes to understanding pavement stresses and their impact when subjected to vehicle loading.
Figure 17a–c illustrates the moisture content distribution at 90 days in two different ambient conditions: wet (85% RH at 25 °C) and dry (20% RH at 25 °C and 10% RH at 40 °C). In Figure 17a, the surface moisture content in the wet ambient condition coincides with the experimental conditions, registering at 86%. In contrast, in Figure 17b,c, the moisture content ranges between 16 and 25% under dry conditions. These data reveal a significant change in the moisture distribution at depths of 10 to 15 mm in dry ambient conditions, where values range between 10 and 15%. In addition, when varying the moisture content of the curing ambient condition, the change was 5%. Consequently, it is concluded that the relationship between relative humidity and temperature in wet conditions had a lower impact compared with a dry ambient condition.

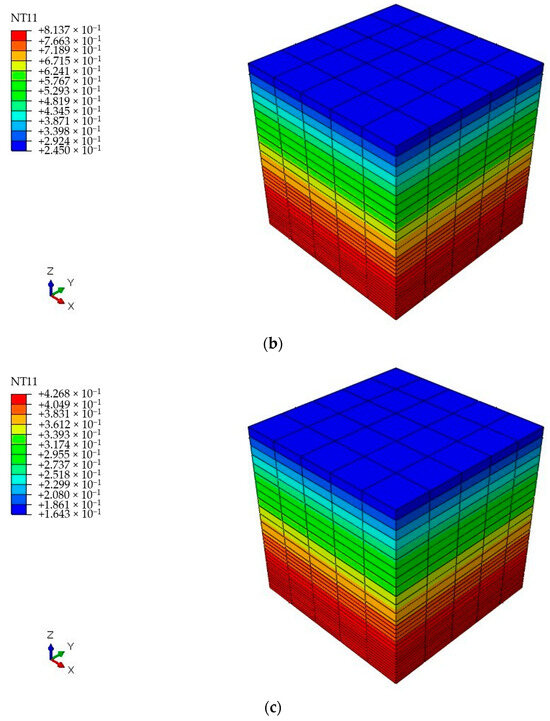
Figure 17.
Moisture content after 90 days for cubes of 100 mm × 100 mm × 100 mm: (a) ambient condition of 85% RH and 25 °C; (b) ambient condition of 20% RH and 25 °C; and (c) ambient condition of 10% RH and 40 °C.
Figure 18 exhibits the evolution of the free shrinkage strain over the days of curing from an experimental and numerical perspective for wet and dry ambient conditions. The finite-element-based computational modeling curves resemble those obtained experimentally, concluding that the models were validated satisfactorily. In particular, the ambient conditions with 85% RH and 25 °C showed an optimal calibration curve, practically coinciding with the experimental data. Moreover, the curves corresponding to 20% RH and 25 °C were almost identical during the first days, with an overall variation of 4%. On the other hand, the curves corresponding to 10% RH and 40 °C presented a slight variation of up to 7% from the beginning until day 56. Then, they maintained constant stability until the last measurement day, showing consistent behavior.

Figure 18.
Evolution of the numerical (employing the finite element method (FEM)) and experimental free shrinkage strain under different relative humidity and temperature conditions.
Overall, the results of the shrinkage strain due to drying indicate that the material responds significantly to ambient conditions. Furthermore, its interaction with the moisture content is evident since the models agree remarkably well with the experimental data.
Figure 19a–c represents the strain distribution due to free shrinkage over a 90-day period along axis 3 of the beam center, which coincides with the z-direction of the model for three different ambient conditions: wet (85% RH and 25 °C) and dry (20% RH and 25 °C, and 10% RH and 40 °C). In the wet ambient conditions (Figure 19a), the strain due to free shrinkage was more significant in the center of the section, extending along the beam until day 90. In contrast, when cured in dry conditions (Figure 19b,c), a uniform behavior was detected throughout the specimen after 90 days of exposure under this ambient condition. This result coincides with the ones expressed in Figure 16 and Figure 18, where the moisture content and shrinkage strain stabilize after 90 days. Between the 20% RH and 25 °C and 10% RH and 40 °C conditions, there was no significant change in the strain distribution due to shrinkage along the beam. However, a considerable change was observed in the shrinkage log, reaching a variation of 30%. On the other hand, in the curing ambient conditions with 85% RH and 25 °C, the difference was manifested at the end of the beam, registering a change of up to 64% compared with dry conditions. Consequently, the relationship between relative humidity and temperature in dry conditions exerts a more significant effect than in wet ambient conditions.

Figure 19.
Shrinkage strain after 90 days for beams of 100 mm × 100 mm × 285 mm: (a) ambient condition of 85% RH and 25 °C; (b) ambient condition of 20% RH and 25 °C; and (c) ambient condition of 10% RH and 40 °C.
3.3. Computational Modeling and Results Validation Using Inferential Statistics
3.3.1. Model of Behavior under Corner Loading
Figure 20, Figure 21 and Figure 22 illustrate the behavior of RCC pavements subjected to corner loading over a one-year analysis, both with and without considering the effect of the ambient conditions. In each figure, the maximum principal stresses are presented. These are related to the maximum inelastic principal strain of the pavement, i.e., cracking.

Figure 20.
Maximum principal stress (MPa) of the pavement under corner loading (a) without being subjected to ambient conditions of 85% RH and 25 °C and (b) being subjected to ambient conditions of 85% RH and 25 °C.

Figure 21.
Maximum principal stress (MPa) of the pavement under corner loading (a) without being subjected to ambient conditions of 20% RH and 25 °C and (b) being subjected to ambient conditions of 20% RH and 25 °C.


Figure 22.
Maximum principal stress (MPa) of the pavement under corner loading (a) without being subjected to an ambient condition of 10% RH and 40 °C and (b) being subjected to an ambient condition of 10% RH and 40 °C.
Figure 20a, Figure 21a and Figure 22a show that the stress distribution was uniform throughout the pavement, except for the areas around the corner loads when the ambient impact was not considered. However, the stress distribution varied along the pavement surface when considering climatic conditions (Figure 20b, Figure 21b and Figure 22b). The stresses at the corners of the pavement were found to experience variations of 8.452% at 85% RH and 25 °C, 9.550% at 10% RH and 40 °C, and 9.577% at 20% RH and 25 °C.
Therefore, it is evident that by not considering the influence of the ambient surroundings, there was an annual increase in the maximum principal stresses, agreeing with the analyses and reflections of various authors [63], especially in working situations under conditions of 40% RH and 25 °C [20].
3.3.2. Influence of the Curing Time
Figure 23 presents the evolution of the maximum principal stress in the pavement after applying a corner load throughout the curing period, considering ambient and no ambient conditions. The results show remarkable differences in the pavement stresses when no vehicle load was used, with increases of up to 158 times in the 85% RH and 25 °C conditions, 220 times in the 20% RH and 25 °C conditions, and an increase of up to 209 times in the 10% RH and 40 °C conditions.
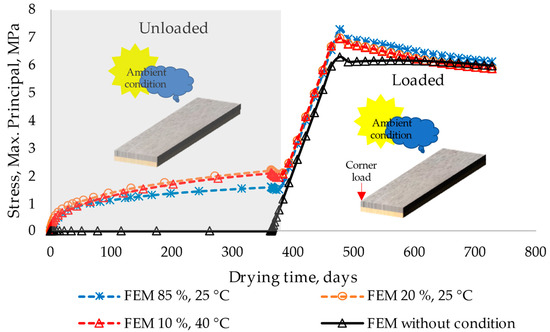
Figure 23.
Numerical maximum principal stress of the pavement under corner loading subjected to different relative humidity and temperature conditions employing the finite element method (FEM).
However, it is relevant to note that these stress increases were reduced when the vehicle load was applied at the corner of the pavement, registering an increase factor of 1.10 under the influence of the ambient conditions. This is because the loading at the corner acts in the opposite direction to the shrinkage caused by the drying of the material. Therefore, this study reveals that the pavement is impacted before a vehicular load is applied on the corner. Furthermore, simultaneous loading in this area significantly decreased the stresses that could lead to pavement failure.
Figure 20, Figure 21 and Figure 22 illustrate the behavior of RCC pavements subjected to corner loading over a one-year analysis, with and without considering the effect of the ambient conditions. In each figure, the maximum principal stresses are presented and are related to the maximum inelastic principal strain of the pavement, i.e., cracking.
Additionally, Figure 23 highlights that when subjected to ambient loads, pavement stresses experience a significant effect as the curves depart from non-ambient conditions. This observation was supported by the Kruskal–Wallis analysis, which showed that the p-values were less than 0.05, as detailed in Table 2 and Table 3. However, the results differed when comparing the curves under ambient conditions, as they showed similarities. This finding was confirmed by the Kruskal–Wallis and Mann–Whitney post hoc tests, where the p-values were found to be more significant than 0.05, as detailed in Table 4 and Table 5, indicating that no appreciable effect was observed between the different ambient conditions.

Table 2.
Kolmogorov–Smirnov normality test for maximum principal stress in a pavement under corner loading with or without relative humidity and temperature conditions.

Table 3.
Kruskal–Wallis rank-sum test of maximum principal stress results in pavement.

Table 4.
Kruskal–Wallis rank-sum test of maximum principal stress results in pavement under corner loading.

Table 5.
Post hoc Mann–Whitney test of maximum principal stress results in pavement under corner loading.
Therefore, the results suggest that analyzing and designing an RCC pavement with an intermediate condition is possible, implying a 200-fold increase in stresses due to shrinkage and a 1.10-fold increase under vehicular loads at the corner, with findings that agree with previous research [21].
4. Conclusions
The current investigation evaluated the effects of relative humidity and temperature on the drying shrinkage of roller-compacted concrete (RCC) pavements subjected to vehicular loading. For this purpose, moisture content and drying shrinkage tests were performed for 90 days. In addition, from the experimental results, calibrated models were developed using the finite element method. Also, a pavement stress analysis was carried out using inferential statistics. From the results obtained, the following conclusions are drawn:
- This study validates the effectiveness of finite element method models in accurately replicating moisture content and drying shrinkage curves, staying within standard limits (10% for moisture content and 7% for drying shrinkage). This outcome is crucial for understanding how relative humidity and temperature impact roller-compacted concrete used in pavements under typical ambient conditions.
- This study revealed that in dry conditions, temperature has a more significant influence than in wet conditions. This is due to the stabilization of the shrinkage curve after 56 days of curing in an ambient condition with 10% relative humidity and 40 °C, in contrast with an ambient condition with 20% relative humidity and 25 °C. Thus, this coincides with the moisture stabilization time, which is also 56 days.
- Ambient effects are crucial in analyzing maximum stresses in pavements: stress increases by a factor of 1.10 with vehicular load and ambient conditions but escalates to 158 times in wet conditions and 220 times in dry conditions with ambient factors alone. Therefore, vehicular load mitigates the impacts of shrinkage and moisture.
- In practice, it is feasible to design roller-compacted concrete pavements for intermediate ambient conditions, as no significant differences were found between wet and dry ambient conditions. The designs should consider a 1.10 increase in stress due to vehicular loading at the corners of the pavement.
Author Contributions
Conceptualization, J.P.-D. and M.S.-S.; methodology, J.P.-D. and M.S.-S.; software, J.P.-D.; validation, F.M.-N.; formal analysis, J.P.-D.; investigation, J.P.-D.; resources, M.S.-S.; data curation, F.M.-N.; writing—original draft preparation, J.P.-D. and M.S.-S.; writing—review and editing, M.S.-S.; visualization, F.M.-N.; supervision, M.S.-S.; project administration, F.M.-N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CEM II/A-M | Portland composite cement |
| E | Flexural elasticity |
| f’c | Compressive strength |
| FEM | Finite element method |
| GGBF | Ground granulated blast furnace |
| Mdd | Maximum dry density |
| Mr | Modulus of rupture |
| OMC | Optimum moisture content |
| RCC | Roller-compacted concrete |
| RH | Relative humidity |
| T | Temperature |
References
- Leiva-Padilla, P.; Moreno-Navarro, F.; Iglesias, G.; Rubio-Gamez, M.C. A Review of the contribution of mechanomutable asphalt materials towards addressing the upcoming challenges of asphalt pavements. Infrastructures 2020, 5, 23. [Google Scholar] [CrossRef]
- Moreno-Navarro, F.; Sierra-Carrillo de Albornoz, F.J.; Sol-Sánchez, M.; Rubio-Gámez, M.C. MASAI: Sustainable, automated and intelligent asphalt materials. The way to the next generation of asphalt pavements. Road Mater. Pavement Des. 2023, 24 (Suppl. S1), 486–505. [Google Scholar] [CrossRef]
- Garbowski, T.; Pożarycki, A. Multi-level backcalculation algorithm for robust determination of pavement layers parameters. Inverse Probl. Sci. Eng. 2017, 25, 674–693. [Google Scholar] [CrossRef]
- Karlaftis, A.G.; Badr, A. Predicting asphalt pavement crack initiation following rehabilitation treatments. Transp. Res. Part C Emerg. Technol. 2015, 55, 510–517. [Google Scholar] [CrossRef]
- Mattinzioli, T.; Sol-Sanchez, M.; Moreno-Navarro, F.; Rubio-Gamez, M.C.; Martinez, G. Benchmarking the embodied environmental impacts of the design parameters for asphalt mixtures. Sustain. Mater. Technol. 2022, 32, e00395. [Google Scholar] [CrossRef]
- Moreno, F.; Sol, M.; Martín, J.; Pérez, M.; Rubio, M.C. The effect of crumb rubber modifier on the resistance of asphalt mixes to plastic deformation. Mater. Des. 2013, 47, 274–280. [Google Scholar] [CrossRef]
- Aghaeipour, A.; Madhkhan, M. Mechanical properties and durability of roller compacted concrete pavement (RCCP)—A review. Road Mater. Pavement Des. 2020, 21, 1775–1798. [Google Scholar] [CrossRef]
- Harrington, D.; Abdo, F.; Adaska, W.; Hazaree, C.V.; Ceylan, H. Guide for Roller-Compacted Concrete Pavements. Available online: http://lib.dr.iastate.edu/intrans_reports (accessed on 2 April 2021).
- Mickevič, R.; Vaitkus, A. Application of roller-compacted concrete in freight terminals. Moksl. Liet. Ateitis 2020, 12, 1–5. [Google Scholar] [CrossRef]
- Smallridge, M.; Elbaz, M. RCC pavement success at mobile container terminal. Ports 2010: Building on the Past, Respecting the Future. In Proceedings of the 12th Triannual International Conference 2010, Jacksonville, FL, USA, 25–28 April 2010; pp. 901–911. [Google Scholar]
- Kim, Y.S. Roller-compacted concrete shoulder construction on interstate highway in Georgia. Transp. Res. Rec. 2007, 2040, 71–79. [Google Scholar] [CrossRef]
- Saluja, S.; Kaur, K.; Goyal, S.; Bhattacharjee, B. Assessing the effect of GGBS content and aggregate characteristics on drying shrinkage of roller compacted concrete. Constr. Build. Mater. 2019, 201, 72–80. [Google Scholar] [CrossRef]
- Saluja, S.; Kaur, K.; Goyal, S.; Bhattacharjee, B. Long-term drying shrinkage of GGBFS-incorporated RCC under various temperature exposures. J. Mater. Civ. Eng. 2021, 33, 04021122. [Google Scholar] [CrossRef]
- Jingfu, K.; Chuncui, H.; Zhenli, Z. Strength and shrinkage behaviors of roller-compacted concrete with rubber additives. Mater. Struct./Mater. Constr. 2009, 42, 1117–1124. [Google Scholar] [CrossRef]
- Li, Z.-X.; Chen, Y.-Z.; Guo, T.-T.; Huang, F.-H.; Chang, Y.-M.; Niu, X.-J. Pavement Performance and Mechanism of Action for Modified Rubber Roller Compacted Concrete. Zhongguo Gonglu Xuebao/China J. Highw. Transp. 2023, 36, 39–48. [Google Scholar] [CrossRef]
- Pourjahanshahi, A.; Madani, H.; Emadi, M. Assessing flexural and permeability performance of roller-compacted concrete pavement (RCCP) reinforcing with different types of synthetic fibres and crimped steel fibre. Aust. J. Civ. Eng. 2023, 21, 167–181. [Google Scholar] [CrossRef]
- Mahdi, M.; Wu, Z.; Liu, Y.L.; Sobhani, M.G. Investigation of in situ thermal properties and early-age pavement behavior in the design and performance evaluation of roller compacted concrete pavement in Louisiana, U.S. Transp. Res. Rec. 2023, 2677, 10. [Google Scholar] [CrossRef]
- Sok, T.; Kim, Y.K.; Park, J.Y.; Lee, S.W. Evaluation of early-age strains and stresses in roller-compacted concrete pavement. J. Traffic. Transp. Eng. Engl. Ed. 2021, 9, 93–105. [Google Scholar] [CrossRef]
- Gholami, N.; Modarres, A. Shrinkage behaviour of superplasticised RCCP and its relationship with internal temperature. Int. J. Pavement Eng. 2019, 20, 12–23. [Google Scholar] [CrossRef]
- Jafarifar, N.; Pilakoutas, K.; Bennett, T. The effect of shrinkage cracks on the load bearing capacity of steel-fibre-reinforced roller-compacted-concrete pavements. Mater. Struct./Mater. Constr. 2016, 49, 2329–2347. [Google Scholar] [CrossRef]
- Jafarifar, N. Shrinkage Behaviour of Steel-Fibre-Reinforced-Concrete Pavements. Available online: https://etheses.whiterose.ac.uk/7475/1/PhD%20Thesis-%20Naeimeh%20Jafarifar-%20Corrected%20Version.pdf (accessed on 26 January 2021).
- Pittman, D.W.; Ragan, S.A. Drying shrinkage of roller-compacted concrete for pavement applications. ACI Mater. J. 1998, 95, 19–26. [Google Scholar]
- Hejazi, S.M.; Abtahi, S.M.; Safaie, F. Investigation of thermal stress distribution in fiber-reinforced roller compacted concrete pavements. J. Ind. Text. 2016, 45, 896–914. [Google Scholar] [CrossRef]
- AASHTO. Mechanistic-Empirical Pavement Design Guide. A Manual of Practice; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2015. [Google Scholar]
- AASHTO. AASHTO (2008) Pavement Design Guide A Manual of Practice; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2008. [Google Scholar]
- LCPC-SETRA. Chaussée en Béton, Guide Technique. Paris: LCPC-SETRA. 2000. Available online: https://en.calameo.com/read/001587962fa82bd755fe6 (accessed on 8 April 2021).
- Pittman, D.W.; Mccullough, B.F. Development of a roller-compacted concrete pavement crack and joint spacing model. Transp. Res. Rec. 1997, 1568, 52–64. [Google Scholar] [CrossRef]
- Adwan, I.; Milad, A.; Memon, Z.A.; Widyatmoko, I.; Zanuri, N.A.; Memon, N.A.; Yusoff, N.I.M. Asphalt pavement temperature prediction models: A review. Appl. Sci. 2021, 11, 3794. [Google Scholar] [CrossRef]
- An, H.; Liu, H.; Han, H. Hybrid Finite-Discrete Element Modelling of Excavation Damaged Zone Formation Process Induced by Blasts in a Deep Tunnel. Adv. Civ. Eng. 2020, 2020, 7153958. [Google Scholar] [CrossRef]
- Pizarro, A.; Manfreda, S.; Tubaldi, E. The science behind scour at bridge foundations: A review. Water 2020, 12, 374. [Google Scholar] [CrossRef]
- Zdiri, M.; Abriak, N.-E.; Ouezdou, M.B.; Loulizi, A.; Neji, J. Numerical modeling of a roller compacted concrete pavement under vehicular loading. Int. J. Pavement Res. Technol. 2009, 2, 188–195. [Google Scholar]
- Tartarini, F.; Schiavon, S.; Cheung, T.; Hoyt, T. CBE Thermal Comfort Tool: Online tool for thermal comfort calculations and visualizations. SoftwareX 2020, 12, 100563. [Google Scholar] [CrossRef]
- Shafigh, P.; Hashemi, M.; Nam, B.H.; Koting, S. Optimum moisture content in roller-compacted concrete pavement. Int. J. Pavement Eng. 2020, 21, 1769–1779. [Google Scholar] [CrossRef]
- ASTM. ASTM D1557-12; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Modified Effort (56,000 ft-lbf/ft 3 (2700 kN-m/m3). ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar] [CrossRef]
- ASTM. ASTM C128-15; Standard Test Method for Relative Density (Specific Gravity) and Absorption of Fine Aggregate. ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- ASTM. ASTM C127-15; Standard Test Method for Relative Density (Specific Gravity) and Absorption of Coarse Aggregate. ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- Portland Cement Association. Guide Specification for Construction of Roller-Compacted Concrete Pavements, Illinois. June 2004. Available online: https://www.chaneyenterprises.com/files/productdocs/Guidetorcc.PDF (accessed on 10 September 2021).
- Chhorn, C.; Lee, S.W. Influencing compressive strength of roller-compacted concrete. Proc. Inst. Civ. Eng.-Constr. Mater. 2018, 171, 3–10. [Google Scholar] [CrossRef]
- ASTM. ASTM C33/C33M-18; Standard Specification for Concrete Aggregates. ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar] [CrossRef]
- Hashemi, M.; Shafigh, P.; Bin Karim, M.R.; Atis, C.D. The effect of coarse to fine aggregate ratio on the fresh and hardened properties of roller-compacted concrete pavement. Constr. Build. Mater. 2018, 169, 553–566. [Google Scholar] [CrossRef]
- Ministerio de Fomento. RC-16 Instrucción Para la Recepción de Cementos. Ministerio de la Presidencia. 2016. Available online: https://www.mitma.gob.es/recursos_mfom/boea20166167.pdf (accessed on 1 September 2021).
- García-Travé, G.; Martinez-Echevarria, M.J.; Gámez, M.C.R.; Navarro, F.M. Bituminous mix response to plastic deformations: Comparison of the Spanish NLT-173 and UNE-EN 12697-22 wheel-tracking tests|Análisis comparativo del comportamiento de una mezcla bituminosa frente a deformaciones plásticas, atendiendo a los ensayos NLT. Dyna 2012, 79, 51–57. [Google Scholar]
- García Travé, G.M. Análisis Comparativo del Comportamiento Mecánico de Mezclas Bituminosas: Normativa NLT-Normativa UNE-EN: Para la Obtención del Título de Doctor por la Universidad de Granada; Editorial Universidad de Granada: Granada, Spain, 2013. [Google Scholar]
- Jafarifar, N.; Pilakoutas, K.; Bennett, T. Moisture transport and drying shrinkage properties of steel-fibre-reinforced-concrete. Constr. Build. Mater. 2014, 73, 41–50. [Google Scholar] [CrossRef]
- Asad, M.; Baluch, M.H.; Al-Gadhib, A.H. Drying shrinkage stresses in concrete patch repair systems. Mag. Concr. Res. 1997, 49, 283–293. [Google Scholar] [CrossRef]
- Ayano, T.; Wittmann, F.H. Drying, moisture distribution, and shrinkage of cement-based materials. Mater. Struct. 2002, 35, 134–140. [Google Scholar] [CrossRef]
- ASTM. ASTM C157/C157M-17; Standard Test Method for Length Change of Hardened Hydraulic-Cement Mortar and Concrete. ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar] [CrossRef]
- ASTM. ASTM C39/C39M-21; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2021. [Google Scholar] [CrossRef]
- British Standards Institution. BS EN 12390-3:2019; TC: Tracked Changes. Testing Hardened Concrete. Compressive Strength of Test Specimens. British Standards Institution: London, UK, 2019. Available online: https://shop.bsigroup.com/ProductDetail/?pid=000000000030407444 (accessed on 10 January 2021).
- ASTM. ASTM C78/C78M-21; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2021. [Google Scholar] [CrossRef]
- Asad, M. Computational Modelling of Shrinkage in Repaired Concrete. King Fahd University of Petroleum and Minerals. 1995. Available online: https://eprints.kfupm.edu.sa/id/eprint/2591/1/S_M_F_14.pdf (accessed on 7 April 2021).
- Pegg, E.C.; Gill, H.S. An open source software tool to assign the material properties of bone for ABAQUS finite element simulations. J. Biomech. 2016, 49, 3116–3121. [Google Scholar] [CrossRef] [PubMed]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Liao, S.S.C. Estimating the coefficient of subgrade reaction for plane strain conditions. Proc. Inst. Civ. Eng. Geotech. Eng. 1995, 113, 166–181. [Google Scholar] [CrossRef]
- Hou, X.; Silberschmidt, V.V. Metamaterials with Negative Poisson’s Ratio: A Review of Mechanical Properties and Deformation Mechanisms. In Mechanics of Advanced Materials: Analysis of Properties and Performance; Springer: Switzerland, 2015; pp. 155–179. [Google Scholar] [CrossRef]
- AASHTO. A Policy on Geometric Design of Highways and Streets, 7th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2018; Available online: https://aashtojournal.org/2018/09/28/aashto-releases-7th-edition-of-its-highway-street-design-green-book/ (accessed on 11 November 2022).
- Brewer, J.; German, J.; Krammes, R.; Movassaghi, K.; Okamoto, J.; Otto, S.; Ruff, W.; Sillan, S.; Stamatiadis, N.; Walters, R. Geometric Design Practices for European Roads, Washington, DC, USA. 2001. Available online: https://international.fhwa.dot.gov/Pdfs/Geometric_Design.pdf (accessed on 4 November 2023).
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures; Chapman and Hall/CRC: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Spangl, B.; Kaiblinger, N.; Ruckdeschel, P.; Rasch, D. Minimal sample size in balanced ANOVA models of crossed, nested, and mixed classifications. Commun. Stat. Theory Methods 2021, 52, 1728–1743. [Google Scholar] [CrossRef]
- Sahu, P.K.; Pal, S.R.; Das, A.K. Estimation and Inferential Statistics; Springer: New Delhi, India, 2015; pp. 1–317. [Google Scholar] [CrossRef]
- Korosteleva, O. Nonparametric Methods in Statistics with SAS Applications; Taylor & Francis Ltd.: London, UK, 2013. [Google Scholar] [CrossRef]
- Ho, R. Handbook of Univariate and Multivariate Data Analysis and Interpretation with SPSS; Chapman and Hall/CRC: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Sok, T.; Hong, S.J.; Kim, Y.K.; Lee, S.W. Evaluation of load transfer characteristics in roller-compacted concrete pavement. Int. J. Pavement Eng. 2020, 21, 796–804. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).